JoSDW: Combating Noisy Labels by Dynamic Weight
Abstract
:1. Introduction
- This article selects reliable samples through a small loss sample strategy by using relative loss and multi-class loss, subdivides it, and proposes a distinction between pure samples and complex samples based on the prediction consistency in the multi-view of the sample.
- In this paper, a dynamic weight is set between the pure sample and the complex sample to reduce the weight of the noise sample. While deepening the neural network, the complex sample weight is gradually reduced. The dynamic weight is determined based on the results of the previous round of iterative training.
- By providing comprehensive experimental results, we show that our method outperforms the most advanced methods on noisy datasets. In addition, extensive ablation studies are conducted to verify the effectiveness of our method.
2. Related Work
2.1. Co-Teaching
2.2. Disagreement and Agreement
2.3. Contrastive Learning
3. The Proposed Method
3.1. Network
3.2. Loss Function
- Classification loss
- Contrastive loss
3.3. Sample Selection
- Small loss sample selection
- Pure sample
- Complex sample
3.4. Dynamic Weight
4. Experiments
4.1. Results on MNIST
4.2. Results on CIFAR-10
4.3. Results on CIFAR-100
4.4. Ablation Study
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Wang, L.; Li, W.; Agustsson, E.; Van Gool, L. Webvision database: Visual learning and understanding from web data. arXiv 2017, arXiv:1708.02862. [Google Scholar]
- Mahajan, D.; Girshick, R.; Ramanathan, V.; He, K.; Paluri, M.; Li, Y.; Bharambe, A.; Van Der Maaten, L. Exploring the limits of weakly supervised pretraining. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 181–196. [Google Scholar]
- Kuznetsova, A.; Rom, H.; Alldrin, N.; Uijlings, J.; Krasin, I.; Pont-Tuset, J.; Kamali, S.; Popov, S.; Malloci, M.; Kolesnikov, A. The open images dataset v4. Int. J. Comput. Vis. 2020, 128, 1956–1981. [Google Scholar] [CrossRef] [Green Version]
- Tanno, R.; Saeedi, A.; Sankaranarayanan, S.; Alexander, D.C.; Silberman, N. Learning from noisy labels by regularized estimation of annotator confusion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11244–11253. [Google Scholar]
- Arnaiz-González, Á.; Fernández-Valdivielso, A.; Bustillo, A.; de Lacalle, L.N.L. Using artificial neural networks for the prediction of dimensional error on inclined surfaces manufactured by ball-end milling. Int. J. Adv. Manuf. Technol. 2016, 83, 847–859. [Google Scholar] [CrossRef]
- Jacob, E.; Astorga, J.; Jose Unzilla, J.; Huarte, M.; Garcia, D.; Lopez de Lacalle, L.N. Towards a 5G compliant and flexible connected manufacturing facility. Dyna 2018, 93, 656–662. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Niles-Weed, J.; Razavian, N.; Fernandez-Granda, C. Early-learning regularization prevents memorization of noisy labels. arXiv 2020, arXiv:2007.00151. [Google Scholar]
- Andres, B.; Gorka, U.; Perez, J. Smart optimization of a friction-drilling process based on boosting ensembles. J. Manuf. Syst. 2018, 48, 108–121. [Google Scholar]
- Reed, S.; Lee, H.; Anguelov, D.; Szegedy, C.; Erhan, D.; Rabinovich, A. Training deep neural networks on noisy labels with bootstrapping. arXiv 2014, arXiv:1412.6596. [Google Scholar]
- Tanaka, D.; Ikami, D.; Yamasaki, T.; Aizawa, K. Joint optimization framework for learning with noisy labels. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5552–5560. [Google Scholar]
- Arpit, D.; Jastrzębski, S.; Ballas, N.; Krueger, D.; Bengio, E.; Kanwal, M.S.; Maharaj, T.; Fischer, A.; Courville, A.; Bengio, Y. A closer look at memorization in deep networks. In Proceedings of the International Conference on Machine Learning, Singapore, 24–26 February 2017; pp. 233–242. [Google Scholar]
- Jiang, L.; Zhou, Z.; Leung, T.; Li, L.-J.; Fei-Fei, L. Mentornet: Learning data-driven curriculum for very deep neural networks on corrupted labels. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 2304–2313. [Google Scholar]
- Shen, Y.; Sanghavi, S. Learning with bad training data via iterative trimmed loss minimization. In Proceedings of the International Conference on Machine Learning, Zhuhai, China, 22–24 February 2019; pp. 5739–5748. [Google Scholar]
- Han, B.; Yao, Q.; Yu, X.; Niu, G.; Xu, M.; Hu, W.; Tsang, I.; Sugiyama, M. Co-teaching: Robust training of deep neural networks with extremely noisy labels. arXiv 2018, arXiv:1804.06872. [Google Scholar]
- Yu, X.; Han, B.; Yao, J.; Niu, G.; Tsang, I.; Sugiyama, M. How does disagreement help generalization against label corruption? In Proceedings of the International Conference on Machine Learning, Zhuhai, China, 22–24 February 2019; pp. 7164–7173. [Google Scholar]
- Malach, E.; Shalev-Shwartz, S. Decoupling “when to update” from “how to update”. arXiv 2017, arXiv:1706.02613. [Google Scholar]
- Wei, H.; Feng, L.; Chen, X.; An, B. Combating noisy labels by agreement: A joint training method with co-regularization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 13726–13735. [Google Scholar]
- Chen, Y.; Shen, X.; Hu, S.X.; Suykens, J.A.K. Boosting Co-teaching with Compression Regularization for Label Noise. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Nashville, TN, USA, 19–25 June 2021; pp. 2688–2692. [Google Scholar]
- Kumar, M.P.; Packer, B.; Koller, D. Self-Paced Learning for Latent Variable Models. In Proceedings of the NIPS, Vancouver, BC, Canada, 6–11 December 2010; p. 2. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. arXiv 2020, arXiv:2002.05709. [Google Scholar]
- Grill, J.-B.; Strub, F.; Altché, F.; Tallec, C.; Richemond, P.H.; Buchatskaya, E.; Doersch, C.; Pires, B.A.; Guo, Z.D.; Azar, M.G. Bootstrap your own latent: A new approach to self-supervised learning. arXiv 2020, arXiv:2006.07733. [Google Scholar]
- Hadsell, R.; Chopra, S.; LeCun, Y. Dimensionality reduction by learning an invariant mapping. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; pp. 1735–1742. [Google Scholar]
- Li, Y.; Hu, P.; Liu, Z.; Peng, D.; Zhou, J.T.; Peng, X. Contrastive clustering. In Proceedings of the 2021 AAAI Conference on Artificial Intelligence (AAAI), Virtual, 2–9 February 2021. [Google Scholar]
- Oord, A.v.d.; Li, Y.; Vinyals, O. Representation learning with contrastive predictive coding. arXiv 2018, arXiv:1807.03748. [Google Scholar]
- Schroff, F.; Kalenichenko, D.; Philbin, J. Facenet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 815–823. [Google Scholar]
- Gutmann, M.; Hyvärinen, A. Noise-contrastive estimation: A new estimation principle for unnormalized statistical models. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Setti Ballas, Italy, 13–15 May 2010; pp. 297–304. [Google Scholar]
- Blum, A.; Mitchell, T.M. Combining Labeled and Unlabeled Sata with Co-Training. In Proceedings of the Eleventh Annual Conference on Computational Learning Theory, COLT 1998, Madison, WI, USA, 24–26 July 1998. [Google Scholar]
- Sindhwani, V.; Niyogi, P.; Belkin, M. A co-regularization approach to semi-supervised learning with multiple views. In Proceedings of the ICML Workshop on Learning with Multiple Views, Bonn, Germany, 11 August 2005; pp. 74–79. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 30 December 2021).
- Goldberger, J.; Ben-Reuven, E. Training deep neural-networks using a noise adaptation layer. In Proceedings of the ICLR 2017 Conference, Toulon, France, 24–26 April 2017. [Google Scholar]
- Kiryo, R.; Niu, G.; du Plessis, M.C.; Sugiyama, M. Positive-unlabeled learning with non-negative risk estimator. arXiv 2017, arXiv:1703.00593. [Google Scholar]





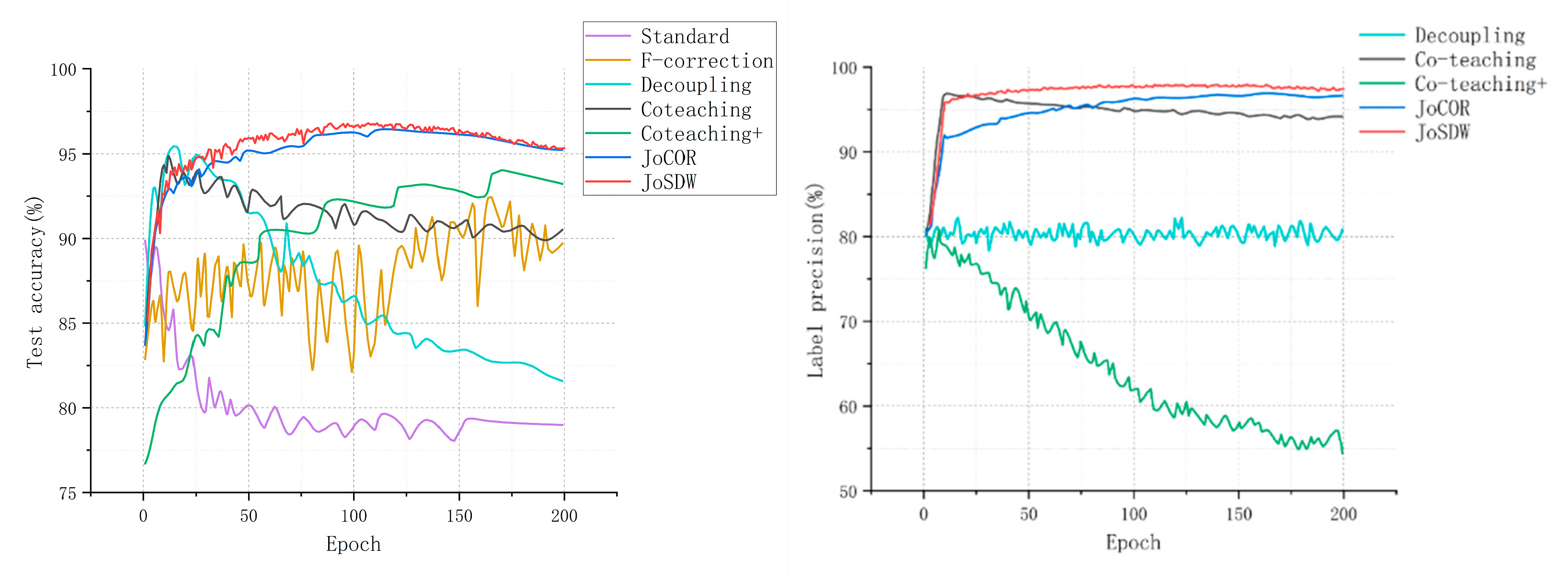










| Baselines | Description |
|---|---|
| F-correction | F-correction corrects the label predictions by the label transition matrix. |
| Decoupling | Decoupling only uses instances with different predictions from the two classifiers to update the parameters. |
| Co-teaching | Co-teaching trains two networks simultaneously and let them cross-update. |
| Co-teaching+ | Co-teaching+ trains two networks simultaneously and lets them cross-update when the two networks predict disagreement. |
| JoCOR | JoCOR trains two networks at the same time and sets a contrast loss between the two networks to facilitate the two grids to reach an “Agreement”. |
| Decoupling | Co-Teaching | Co-Teaching+ | JoCOR | JoSDW | |
|---|---|---|---|---|---|
| Small loss | X | √ | √ | √ | √ |
| Cross update | X | √ | √ | X | X |
| Disagreement | √ | X | √ | X | √ |
| Agreement | X | X | X | √ | √ |
| Dynamic weight | X | X | X | X | √ |
| Datasets | # of Class | # of Train | # of Test | Size |
|---|---|---|---|---|
| Mnist | 10 | 60,000 | 10,000 | 28 × 28 |
| CIFAR-10 | 10 | 50,000 | 10,000 | 32 × 32 |
| CIFAR-100 | 100 | 50,000 | 10,000 | 32 × 32 |
| MLP | CNN |
|---|---|
| Gray Image 28 × 28 | RGB Image 32 × 32 |
| 28 × 28→256, ReLU | 3 × 3, 64 BN, ReLU 3 × 3, 64 BN, ReLU 2 × 2 Max-pool |
| 3 × 3, 128 BN, ReLU 3 × 3, 128 BN, ReLU 2 × 2 Max-pool | |
| 3 × 3, 196 BN, ReLU 3 × 3, 196 BN, ReLU 2 × 2 Max-pool | |
| 256→10 | 256→100 |
| Noise Settings | Standard | F-Correction | Decoupling | Co-Teaching | Co-Teaching+ | JoCOR | JoSDW |
|---|---|---|---|---|---|---|---|
| Symmetry-20% | 79.56 | 95.38 | 93.16 | 95.1 | 97.81 | 98.06 | 98.24 |
| Symmetry-50% | 52.66 | 92.74 | 69.79 | 89.82 | 95.8 | 96.64 | 97.23 |
| Symmetry-80% | 23.43 | 72.96 | 28.51 | 79.73 | 58.92 | 84.89 | 90.31 |
| Asymmetry-40% | 79 | 89.77 | 81.84 | 90.28 | 93.28 | 95.24 | 95.38 |
| Noise Settings | Standard | F-Correction | Decoupling | Co-Teaching | Co-Teaching+ | JoCOR | JoSDW |
|---|---|---|---|---|---|---|---|
| Symmetry-20% | 69.18 | 68.74 | 69.32 | 78.23 | 78.71 | 85.73 | 86.28 |
| Symmetry-50% | 42.71 | 42.19 | 40.22 | 71.3 | 57.05 | 79.41 | 79.75 |
| Symmetry-80% | 16.24 | 15.88 | 15.31 | 25.58 | 24.19 | 27.78 | 32.31 |
| Asymmetry-40% | 69.43 | 70.6 | 68.72 | 73.78 | 68.84 | 76.36 | 77.04 |
| Noise Settings | Standard | F-Correction | Decoupling | Co-Teaching | Co-Teaching+ | JoCOR | JoSDW |
|---|---|---|---|---|---|---|---|
| Symmetry-20% | 35.14 | 37.95 | 33.1 | 43.73 | 49.27 | 53.01 | 53.28 |
| Symmetry-50% | 16.97 | 24.98 | 15.25 | 34.96 | 40.04 | 43.49 | 45.25 |
| Symmetry-80% | 4.41 | 2.1 | 3.89 | 15.15 | 13.44 | 15.49 | 14.01 |
| Asymmetry-40% | 27.29 | 25.94 | 26.11 | 28.35 | 33.62 | 32.7 | 34.63 |
| Index | Methods | Label Precision |
|---|---|---|
| 1 | JoSDW-S | 81.12 |
| 2 | JoSDW-SD | 84.96 |
| 3 | JoSDW | 86.28 |
| Index | Methods | Label Precision |
|---|---|---|
| 1 | JoSDW-S | 95.03 |
| 2 | JoSDW-SD | 96.66 |
| 3 | JoSDW | 97.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xu, H.; Xiao, J.; Bian, M. JoSDW: Combating Noisy Labels by Dynamic Weight. Future Internet 2022, 14, 50. https://doi.org/10.3390/fi14020050
Zhang Y, Xu H, Xiao J, Bian M. JoSDW: Combating Noisy Labels by Dynamic Weight. Future Internet. 2022; 14(2):50. https://doi.org/10.3390/fi14020050
Chicago/Turabian StyleZhang, Yaojie, Huahu Xu, Junsheng Xiao, and Minjie Bian. 2022. "JoSDW: Combating Noisy Labels by Dynamic Weight" Future Internet 14, no. 2: 50. https://doi.org/10.3390/fi14020050
APA StyleZhang, Y., Xu, H., Xiao, J., & Bian, M. (2022). JoSDW: Combating Noisy Labels by Dynamic Weight. Future Internet, 14(2), 50. https://doi.org/10.3390/fi14020050





