A Fairness Index Based on Rate Variance for Downlink Non-Orthogonal Multiple Access System

Abstract

Aiming at the resource allocation problem of a non-orthogonal multiple access (NOMA) system, a fairness index based on sample variance of users’ transmission rates is proposed, which has a fixed range and high sensitivity. Based on the proposed fairness index, the fairness-constrained power allocation problem in NOMA system is studied; the problem is decoupled into the intra cluster power allocation problem and the inter cluster power allocation problem. The nonconvex optimization problem is solved by the continuous convex approximation (SCA) method, and an intra and inter cluster power iterative allocation algorithm with fairness constrained is proposed to maximize the total throughput. Simulation results show that the proposed algorithm can take into account intra cluster, inter cluster, and system fairness, and maximize the system throughput on the premise of fairness.

1. Introduction

Non-orthogonal multiple access (NOMA) has the advantages of high spectral efficiency, low delay, large connection volume, and good compatibility. It has been proposed and become a trending research topic in the context of 5G, and it is also an alternative technology for 6G [1]. Power domain non-orthogonal multiple access (PD-NOMA) distributes different levels of power to different users, so that each user can transmit data in the same frequency band and use resources at the same time [2,3,4], so as to improve the spectral efficiency, energy efficiency, and other performance of the system. References [5,6,7] introduce cooperative communication technology to NOMA and carried out relevant research on energy efficiency, power allocation, and multi-user symbol detection.

In recent years, scholars have studied power allocation and user clustering in NOMA systems. References [8,9,10,11,12,13,14] study the power allocation problem in the downlink NOMA system with the goal of maximizing energy efficiency. References [15,16,17,18,19,20,21] study the power allocation problem in NOMA system with the goal of maximizing throughput. References [22,23] apply intelligent optimization algorithms to NOMA user clustering, which can achieve greater throughput and energy efficiency. Since the resource allocation problem in NOMA system is a mixed integer programming problem, references [24,25,26] decouple the resource allocation problem into two sub problems: user clustering and power allocation. The above literature only researches the system throughput and energy efficiency, ignoring the fairness between users in the system.

Fairness is a key issue in the resource allocation process of a communication system. The fairness of a wireless communication system is defined as how to allocate radio resources fairly among users. In a NOMA system, allocating more resources to users with better channel conditions can obtain greater system throughput. However, it is unfair for users with weak channel conditions. Jain et al. proposed a quantitative measure of fairness index (Jain index) in the network [27]. In the Jain index, fairness value is a number belonging to the range of [$\frac{1}{K}$, 1], where K is the number of users in the typical system. As can be seen, the lower bound of Jain index is affected by the number of users in the system. Reference [28] proposed a fairness index (GUI index) based on the difference between user rate and fair rate. In the GUI index, the fair rate is related to the power allocation in the system, and the fair value can reach the maximum only when all users obtain the fair rate. Although the GUI fairness index can reflect the user power distribution well, its lower bound is affected by the number of users and user channel conditions in the system. Based on the Jain index, references [29,30] proposed power allocation schemes with the weighted sum of throughput and fairness as the optimization objective and power allocation schemes based on the channel gain ratio of paired users, respectively. Based on the proportional fairness constraint, an iterative algorithm for joint subcarrier and user power allocation with the goal of maximizing throughput is proposed in [31]. A price-based power allocation algorithm using game theory is proposed in [32]. A power allocation scheme constrained by the minimum fairness of edge users is proposed in [33]. A power allocation scheme aiming at maximizing the minimum fairness to achieve a compromise between complexity and throughput is proposed in [34]. References [29,30,31,32,33,34] focus on improving the overall fairness of the system but cannot reflect the fairness requirements of individual user cluster. Since the lower bound of the Jain fairness index is affected by the number of users in the system, and the GUI fairness index is affected by the power allocation and channel conditions, the Jain index and GUI index are not suitable for systems with changing number of users and channel conditions. In view of the above, this paper studies the fairness index of a NOMA system and proposes a new fairness index based on sample variance of users’ transmission rates of a downlink NOMA system. The proposed index and Jain index are based on the rate, that is, the closer the user rate in the system, the greater the fairness, while the GUI index is related to the user power allocation in the system, that is, the greater the user rate with more power allocation, the greater the fairness. The other difference between the proposed index and the other two indexes is that, when the rate of one user in the system is equal to the transmission rate of the system and the rate of other users is 0, the proposed fairness index is 0, and the Jain fairness index is 1/K, while the GUI fairness index needs to meet the equal power allocation and the same channel conditions of all users before it can be taken as 0. In general, the fairness index based on rate variance can evaluate the fairness of systems with different user numbers and has better sensitivity. The comparison of our proposed fairness index with Jain index and GUI index is given in

Table 1. Comparison of our proposed fairness index with other indexes.

Fairness Index	Value Range	Fairness Criteria
proposed fairness index	[0, 1]	rate
Jain index	$[\frac{1}{K}$, 1]	rate
GUI index	[0, 1]	channel state and power allocation

.

Based on the proposed fairness index, this paper studies the power allocation problem of a downlink NOMA system and proposes a joint power allocation algorithm intra and inter clusters to maximize throughput based on fairness constraints.

The paper is organized as follows. First, the system model is discussed. Second, the new fairness index based on sample variance of users’ transmission rates is introduced. Third, the power allocation problem of maximizing system throughput is studied under the constraints of minimum intra and inter cluster fairness. Finally, simulation results followed by the conclusion are provided.

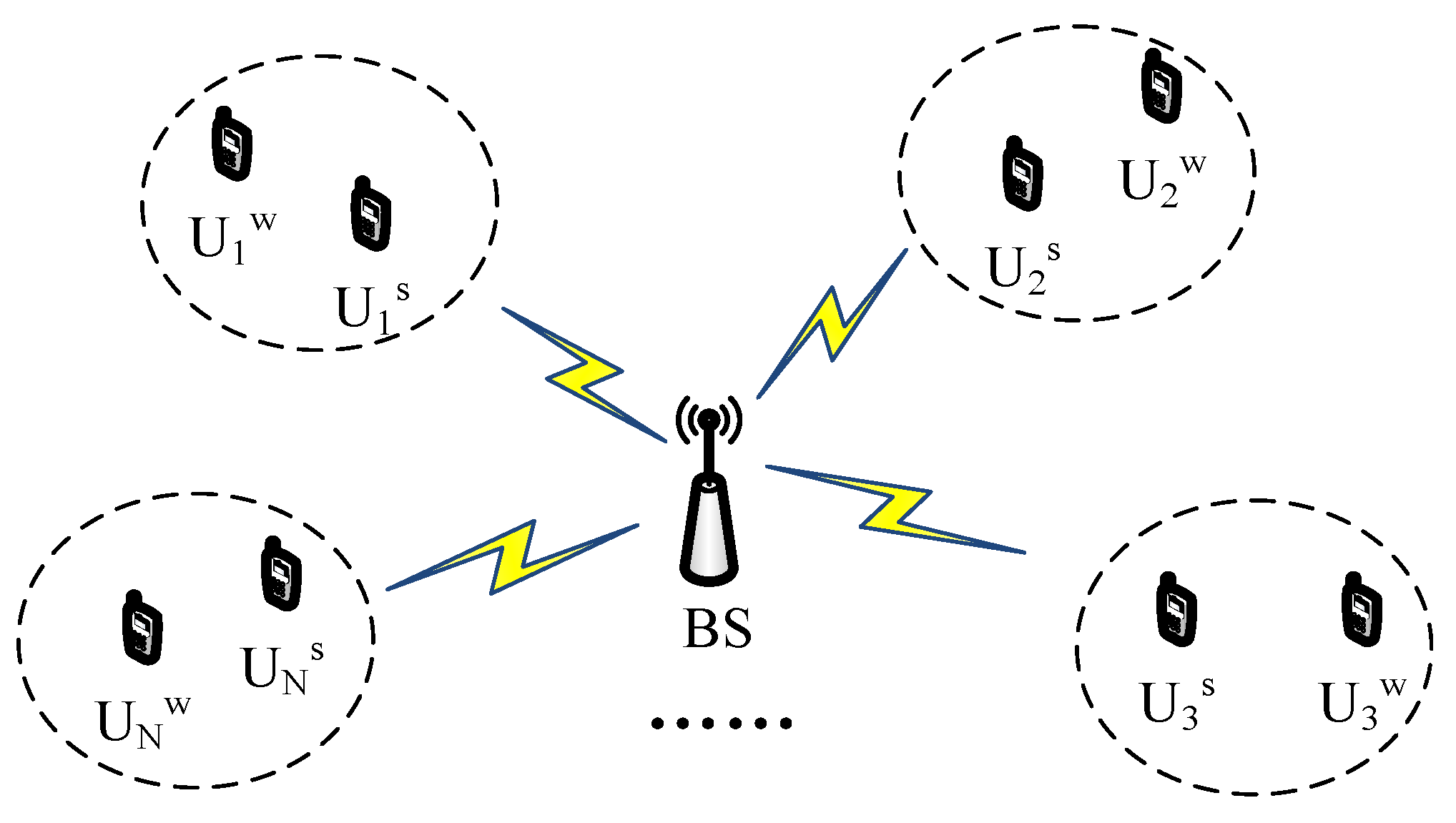
2. System Model

Consider a downlink NOMA system, a single antenna base station (BS) is deployed in the regional center with a radius of R. BS provides services for $M\left(M=2\times N,N\in {\mathrm{N}}^{+}\right)$ active users in the area, where N represents the number of user clusters, and the set of active users is represented as $\mathit{U}=\left\{U_1,U_2,\dots ,U_M\right\}$. Assuming that the BS completely knows the channel state information (CSI), $h_m$ represents the channel gain between the BS and the user $m$, and the set of user channel gains is expressed as $\mathit{H}=\{h_1,h_2,\dots ,h_M\}$. A distributed user clustering algorithm is adopted among users [35]. First, the users are sorted according to the channel gain from large to small, $\mathit{Us}=\left\{U_1^s,U_2^s,\dots ,U_N^s\right\}$ represents the strong channel gain user set, and $\mathit{Uw}=\left\{U_1^w,U_2^w,\dots ,U_N^w\right\}$ represents the weak channel gain user set, $U_n^s$ and $U_n^w$ will be paired into a cluster, where $n\in [1,N]$. The clustered downlink NOMA system is shown in Figure 1.

Assuming that the transmit power of the BS is P_t, the bandwidth is W, and the channel bandwidth of the nth cluster is W_n, BS transmits superimposed coded signals to the n-th cluster, then the signals received by strong channel gain user $U_n^s$ and weak channel gain user $U_n^w$ are, respectively:

$$y_n^s=h_n^s\sqrt{p_n^s}{x}_n^s+h_n^s\sqrt{p_n^w}{x}_n^w+{\eta }_n^s$$

(1)

$$y_n^w=h_n^w\sqrt{p_n^s}{x}_n^s+h_n^w\sqrt{p_n^w}{x}_n^w+{\eta }_n^w$$

(2)

where, $h_n^s$ represents the channel gain between BS and $U_n^s$ in the n-th cluster, $h_n^w$ represents the channel gain between BS and $U_n^w$ in the n-th cluster. $p_n^s$ and $p_n^w$ represent the transmit power of $U_n^s$ and $U_n^w$ allocated by BS, respectively. $x_n^s$ and $x_n^w$ represent the received signal of $U_n^s$ and $U_n^w$ transmitted by BS, respectively. ${\eta }_n^s$ and ${\eta }_n^w$ are Gaussian white noise with unilateral power spectral density n₀. Using the successful interference cancellation (SIC) technology to decode the received signal, $U_n^w$ can obtain a transmission rate as:

$$R_{c-n}^w=W_n{\log }_2\left(1+\frac{|h_n^w{|}^2{p}_n^w}{|h_n^w{|}^2{p}_n^s+W_n{n}_0}\right)$$

(3)

$U_n^s$ can obtain a transmission rate as:

$$R_{c-n}^s=W_n{\log }_2(1+\frac{|h_n^s{|}^2{p}_n^s}{W_n{n}_0})$$

(4)

The throughput of the n-th cluster is:

$$R_{c-n}=R_{c-n}^s+R_{c-n}^w$$

(5)

3. Fairness Index Based on Rate

For the above system, the rate set of M users is defined as R = {R₁, …R_m, …, R_M}, and the total throughput of the system can be defined as:

$$R_{sum}={\displaystyle \sum _{m=1}^M{R}_m}$$

(6)

The average transmission rate of all users is:

$$\overline{R}=\raisebox{1ex}{$R_{sum}$}\!\left/ \!\raisebox{-1ex}{$M$}\right.$$

(7)

The mean square value of users’ transmission rates is:

$$\overline{R^2}=\frac{1}{M}{\displaystyle \sum _{m=1}^M{R}_m{}^2}$$

(8)

The sample variance of users’ transmission rates T can be expressed as:

$$S^2=\frac{1}{M-1}{\displaystyle \sum _{m=1}^M{(R_m-\overline{R})}^2}$$

(9)

The fairness index related to sample variance of users’ transmission rate is designed as:

$$F=1-\frac{S^2}{\overline{R^2}}$$

(10)

Index F has the following properties:

(1)

When the transmission rates of all users in the system are equal, the maximum value of F can be obtained (F_max = 1).

(2)

The minimum value of F can be obtained (F_min = 0) when only one user’s transmission rate is not 0 and all the other users’ rates are 0.

(3)

The value range of F has nothing to do with the number of users, channel conditions, or transmission power, but only with the distribution of users’ transmission rates.

For the system shown in Figure 1, the average throughput of the n-th cluster is:

$$\overline{R_c}=\frac{{\displaystyle \sum _{n=1}^N{R}_{c-n}}}{N}$$

(11)

The mean square value of transmission rate of N clusters is:

$$\overline{R_c^2}=\frac{{\displaystyle \sum _{n=1}^N{R}_{c-n}{}^2}}{N}$$

(12)

Referring to the sample variance of transmission rates given in (10), intra cluster fairness F_c−n and inter cluster fairness F_c are respectively defined as follows:

$$\begin{array}{cc}{F}_{c-n}& =1-\frac{{\left[R_{c-n}^{\mathrm{s}}-\frac{1}{2}(R_{c-n}^{\mathrm{s}}+R_{c-n}^w)\right]}^2+{\left[R_{c-n}^w-\frac{1}{2}(R_{c-n}^{\mathrm{s}}+R_{c-n}^w)\right]}^2}{\frac{1}{2}\left[{\left(R_{c-n}^{\mathrm{s}}\right)}^2+{\left(R_{c-n}^w\right)}^2\right]}\hfill \\ & =1-\frac{{\left(R_{c-n}^{\mathrm{s}}-R_{c-n}^w\right)}^2}{{\left(R_{c-n}^{\mathrm{s}}\right)}^2+{\left(R_{c-n}^w\right)}^2}=\frac{2}{\frac{R_{c-n}^{\mathrm{s}}}{R_{c-n}^w}+\frac{R_{c-n}^w}{R_{c-n}^s}}\hfill \end{array}$$

(13)

$$F_c=1-\frac{{{\displaystyle {\sum }_{n=1}^N(R_{c-n}-\overline{R_c})}}^2}{(N-1)\overline{R_c^2}}$$

(14)

4. Power Allocation under Fairness Constraints

In this section, the power allocation problem of maximizing system throughput is studied under the constraints of minimum intra and inter cluster fairness. Power allocation includes inter cluster power allocation and intra cluster user power allocation. The problem can be described as:

$$\begin{array}{l}\begin{array}{ccc}& P0& \end{array}\underset{p_n^s,p_n^w}{\max }{R}_{sum}={\displaystyle \sum _{n=1}^N(R_{c-n}^{\mathrm{s}}+R_{c-n}^w)}\\ s.t.\begin{array}{cc}& \end{array}C1:{\displaystyle \sum _{n=1}^N(p_n^s+p_n^w)}=P_t\\ \begin{array}{ccc}& & \end{array}C2:0<p_n^s<p_n^w<P_t,n\in [1,N]\\ \begin{array}{ccc}& & \end{array}C3:F_{\mathrm{c}-n}\ge {\phi }_{c-n},n\in [1,N]\\ \begin{array}{ccc}& & \end{array}C4:F_c\ge {\phi }_c\end{array}$$

(15)

where ${\phi }_{c-n}$ represents the lower bound of fairness among users in the n-th cluster, ${\phi }_c$ represents the lower bound of fairness between clusters. C1 ensures that the power allocated to all user clusters is equal to the total transmit power of the BS; C2 represents the power magnitude relationship between strong and weak users; C3 gives the lower bound of fairness among users in the n-th cluster, ${\phi }_{c-n}\in [0,1]$; C4 gives the lower bound of fairness between clusters, ${\phi }_c\in [0,1]$.

If the power allocated to the n-th cluster by the BS is p_n, then the power allocated to strong channel gain user is $p_n^s={\alpha }_n^s{p}_n$, and the power allocated to weak channel gain user is $p_n^w={\alpha }_n^w{p}_n$, where ${\alpha }_n^s$ and ${\alpha }_n^w$ represent the power allocation factor for the strong channel gain user and the weak channel gain, respectively. For convenience, the problem P0 is decoupled into two sub problems: power allocation intra cluster and power allocation inter clusters.

4.1. Power Allocation Intra Cluster

The power allocation intra cluster can be expressed as:

$$\begin{array}{l}\begin{array}{ccc}& P1& \end{array}\underset{{\alpha }_n^s,{\alpha }_n^w}{\max }{R}_{c-n}=R_{c-n}^s+R_{c-n}^w\\ s.t.\begin{array}{cc}& \end{array}C1:{\alpha }_n^s+{\alpha }_n^w=1\\ C2:0<{\alpha }_n^s\le 0.5\\ C3:0.5\le {\alpha }_n^w<1\\ C4:F_{c-n}\ge {\phi }_{c-n},n\in [1,N]\end{array}$$

(16)

According to Equation (13), F_c−n can be expressed as:

$$F_{c-n}=2/\left(x+\frac{1}{x}\right)$$

(17)

where $x=R_{c-n}^s/R_{c-n}^w$, $x\in \left(0,+\infty \right)$. When $x=1$, $F_{c-n}=1$, set ${\alpha }_n^s={\alpha }_{equal}$ at this time. Let ${\alpha }_n^s=0.5$, then set $F_{c-n}={\phi }_{mid}$. If ${\alpha }_n^s\in (0,{\alpha }_{equal})$, F_n monotonically increases, and $F_n\in [0,1]$. If ${\alpha }_n^s\in \left[{\alpha }_{equal},0.5\right)$, F_n monotonically decreasing, and $F_n\in \left({\phi }_{mid},1\right]$. According to the principle of PD-NOMA, the greater the power allocated to strong channel gain user, the smaller the fairness and the greater the throughput in the cluster. Combined with the above analysis, if ${\phi }_{c-n}\in \left[0,{\phi }_{mid}\right]$, the throughput in the cluster is the largest when ${\alpha }_n^s=0.5$; if ${\phi }_{c-n}\in \left({\phi }_{mid},1\right]$, then the throughput in the cluster is the largest when $F_{c-n}={\phi }_{c-n}$. According to Equation (16), we can get:

$$x=\frac{1}{{\phi }_{c-n}}\times \left[{\left(1-{\phi }_{c-n}{}^2\right)}^{\frac{1}{2}}+1\right]$$

(18)

According to $R_{c-n}^s/R_{c-n}^w=x$, ${\alpha }_n^s$ can be obtained.

Based on the above analysis, the intra cluster power allocation algorithm is as follows.

Algorithm 1: Intra cluster power allocation algorithm under fairness constraint

Input: ${\phi }_{c-n}$, $p_n$, $h_n^s$, $h_n^w$, $n_0$ and $W_n$. Output: ${\alpha }_n^s$ and ${\alpha }_n^w$

1: if ${\phi }_{c-n}\in [0,{\phi }_{mid}]$,${\alpha }_n^s=0.5$, turn to step 3; 2: if ${\phi }_{c-n}\in ({\phi }_{mid},1]$, $x_0=\frac{1}{{\phi }_{c-n}}\times \left[{\left(1-{\phi }_{c-n}{}^2\right)}^{\frac{1}{2}}+1\right]$, according to $R_{c-n}^s/R_{c-n}^w=x_0$, get ${\alpha }_n^s$; 3: ${\alpha }_n^w=1-{\alpha }_n^s$;

4: end.

4.2. Power Allocation Inter Cluster

The power allocation intra cluster can be expressed as:

$$\begin{array}{l}\begin{array}{c}\end{array}P2\begin{array}{c}\end{array}\underset{{\left\{p_n\right\}}_{n=1}^N}{\max }{R}_{sum}={\displaystyle \sum _{n=1}^N{R}_{c-n}}\\ s.t.\begin{array}{cc}& \end{array}C1:{\displaystyle \sum _{n=1}^N{p}_n}=P_t\\ C2:p_n\in (0,P_t)\\ C3:F_c\ge {\phi }_c\end{array}$$

(19)

In this paper, continuous convex approximation (SCA) [29] is used to deal with the non-convex problem in P2. According to Equations (11), (12), and (14), the constraint of C3 can be written as the following equivalent inequality:

$${({\displaystyle \sum _{n=1}^N{R}_{c-n}})}^2/{\displaystyle \sum _{n=1}^N{R}_{c-n}{}^2}\ge ({\phi }_c+\frac{1}{N-1})(N-1)$$

(20)

Introducing a set of relaxation variables r₁, r₂, …, r_n, we can get the optimization problem P3 equivalent to P2:

$$\begin{array}{l}\begin{array}{c}\end{array}P3\begin{array}{c}\end{array}\underset{{\{p_n,r_n\}}_{n=1}^N}{\max }{\displaystyle \sum _{n=1}^N{r}_n}\\ s.t.\begin{array}{cc}& \end{array}C1:{\displaystyle \sum _{n=1}^N{p}_n}=P_t\\ C2:p_n\in (0,P_t)\\ C3:R_{c-n}\ge r_n,n\in [1,N]\\ C4:{({\displaystyle \sum _{n=1}^N{r}_n})}^2/{\displaystyle \sum _{n=1}^N{r}_n{}^2}\ge ({\phi }_c+\frac{1}{N-1})(N-1)\end{array}$$

(21)

Relaxation variables γ and θ are introduced to make ${\left(\sum r_n\right)}^2\ge \gamma {\theta }^2$ and $\sum r_n{}^2\le {\theta }^2$. The equivalent inequality of C4 can be obtained:

$$\gamma \ge \left({\phi }_c+\frac{1}{N-1}\right)\left(N-1\right)$$

(22)

Using the first-order approximate Taylor series, the approximate equivalent inequality of ${\left(\sum r_n\right)}^2\ge \gamma {\theta }^2$ is:

$$\sum r_n\ge \sqrt{{\gamma }^{\left(i-1\right)}}{\theta }^{\left(i-1\right)}+0.5\frac{1}{\sqrt{{\gamma }^{\left(i-1\right)}}}{\theta }^{\left(i-1\right)}\left(\gamma -{\gamma }^{\left(i-1\right)}\right)+\sqrt{{\gamma }^{\left(i-1\right)}}\left(\theta -{\theta }^{\left(i-1\right)}\right)$$

(23)

where ${\gamma }^{\left(i-1\right)}$ and ${\theta }^{\left(i-1\right)}$ represent the approximate value of γ and θ at iteration i, respectively. $\sum r_n{}^2\le {\theta }^2$ can be approximately expressed as:

$$\theta \ge {\Vert {\left[\begin{array}{cc}{r}_1& r_2\end{array}\cdots \begin{array}{cc}{r}_{N-1}& r_N\end{array}\right]}^T\Vert }_2$$

(24)

P3 can be further equivalent to:

$$\begin{array}{l}\begin{array}{c}\end{array}P4\begin{array}{c}\end{array}\underset{\gamma ,\theta ,{\{p_n,r_n\}}_{n=1}^N}{\max }{\displaystyle \sum _{n=1}^N{r}_n}\\ s.t.C1:{\displaystyle \sum _{n=1}^N{p}_n}=P_t\\ \begin{array}{ccc}& & \end{array}C2:p_n\in \left(0,P_t\right)\\ \begin{array}{ccc}& & \end{array}C3:R_{c-n}\ge r_n,n\in [1,N]\\ \begin{array}{ccc}& & \end{array}C4:{\left({\displaystyle \sum _{n=1}^N{r}_n}\right)}^2/{\displaystyle \sum _{n=1}^N{r}_n{}^2}\ge \left({\phi }_c+\frac{1}{N-1}\right)\left(N-1\right)\\ \begin{array}{ccc}& & \end{array}C5:\gamma \ge \left({\phi }_c+\frac{1}{N-1}\right)\left(N-1\right)\\ \begin{array}{ccc}& & \end{array}C6:\sum r_n\ge \sqrt{{\gamma }^{\left(i-1\right)}}{\theta }^{\left(i-1\right)}+0.5\frac{1}{\sqrt{{\gamma }^{\left(i-1\right)}}}{\theta }^{\left(i-1\right)}\left(\gamma -{\gamma }^{\left(i-1\right)}\right)+\sqrt{{\gamma }^{\left(i-1\right)}}\left(\theta -{\theta }^{\left(i-1\right)}\right)\\ \begin{array}{ccc}& & \end{array}C7:\theta \ge {\Vert {\left[\begin{array}{cc}{r}_1& r_2\end{array}\cdots \begin{array}{cc}{r}_{N-1}& r_N\end{array}\right]}^T\Vert }_2\end{array}$$

(25)

Based on the above analysis, the inter cluster power allocation algorithm is as follows.

Algorithm 2: Inter cluster power allocation algorithm under fairness constraint

Input: $P_t$, ${\phi }_c$, ${\left\{{\alpha }_n^s,{\alpha }_n^w\right\}}_{n=1}^N$, H, W, n0, i

Output: $\gamma ,\theta ,{\left\{p_n,r_n\right\}}_{n=1}^N$

1: if i = 1, initialize ${\left\{p_n\right\}}_n^N$$,p_n^{i-1}=P_t/N$; else, turn to step 5;

2: according to $r_n^{i-1}=R_{c-n}$, n ∊ [1, N], calculate ${\left\{r_n\right\}}_{n=1}^N$;

3: initialize θ, ${\theta }^{i-1}={\Vert {\left[\begin{array}{cc}{r}_1^{i-1}& r_2^{i-1}\end{array}\cdots \begin{array}{cc}{r}_{N-1}^{i-1}& r_N^{i-1}\end{array}\right]}^T\Vert }_2$;

4: initialize γ, ${\gamma }^{i-1}=\left({\phi }_c+\frac{1}{N-1}\right)\left(N-1\right)$;

5: using sequential quadratic programming method to solve problems P4 with nonlinear constraints, get $\gamma ,\theta ,{\left\{p_n,r_n\right\}}_{n=1}^N$;

6: end.

4.3. Joint Power Allocation Intra and Inter Cluster

The intra and inter cluster power allocation algorithms are optimization algorithms under the given inter cluster and intra cluster power allocation coefficient, respectively. The intra and inter cluster power allocation can be iteratively carried out alternately, so that the system can obtain the maximum throughput that meets the minimum fairness condition. Based on the above ideas, this paper proposes a joint intra and inter cluster power allocation algorithm, where ε represents the iterative error tolerance.

Algorithm 3: Joint power allocation inter and intra cluster under fairness constraints

Input: $P_t$, ${\phi }_c$, ${\left\{{\phi }_{c-n}\right\}}_{n=1}^N$, $H$, $W$, $n_0,\epsilon$, $i=0$ Output: ${\left\{p_n,{\alpha }_n^s,{\alpha }_n^w\right\}}_{n=1}^N$ 1: initialize ${\left\{p_n^0=P_t/N\right\}}_{n=1}^N$, execute Algorithm 1 and get ${\left\{{\left({\alpha }_n^s\right)}^0,{\left({\alpha }_n^w\right)}^0\right\}}_{n=1}^N$, calculate $R_{sum}^0$; 2: i = i + 1; 3: bring ${\left\{{\left({\alpha }_n^s\right)}^{i-1},{\left({\alpha }_n^w\right)}^{i-1}\right\}}_{n=1}^N$$\mathrm{into}\mathrm{Algorithm}2\mathrm{and}\mathrm{get}{\left\{p_n^i\right\}}_{n=1}^N$; 4: for n = 1: N; 5: substitute ${\left\{p_n^i\right\}}_{n=1}^N$$\mathrm{into}\mathrm{Algorithm}1\mathrm{and}\mathrm{get}{\left({\alpha }_n^s\right)}^i,{\left({\alpha }_n^w\right)}^i$; 6: end; 7: calculate $R_{sum}^i$; 8: if $\left|R_{sum}^i-R_{sum}^{i-1}\right|>\epsilon$, turn to step 2; 9: output ${\left\{p_n^i,{\left({\alpha }_n^s\right)}^i,{\left({\alpha }_n^w\right)}^i\right\}}_{n=1}^N$;

10: end.

5. Simulation and Analysis

In this section, simulations based on MATLAB are used to verify the effectiveness of the proposed fairness index and joint power allocation algorithm. We suppose that BS is located in the center of the cellular area, and users are randomly distributed around BS. The channels between users and BS are Rayleigh channels [22], the mean value of channel coefficients being 0 and the variance being 1. Simulation parameters are shown in

Table 2. Simulation parameters.

Parameter	Value
BS transmit power Pt	40 dBm
total bandwidth W	1 MHz
cell radius D	500 m
path loss exponent λ	5
noise unilateral power spectral density	−174 dBm/Hz
error tolerance ε	0.001
lower bound of intra cluster fairness	0.7
lower bound of inter cluster fairness	0.7

.

Figure 2 shows the curves of the proposed fairness index, Jain index, and GUI index with the power allocation factor for strong channel gain user (α_s). For convenience, it is assumed that the number of users is 2, in which the strong channel gain users are 250 m away from the BS and the weak channel gain users are 350 m away from the BS.

As can be seen from Figure 2, the proposed fairness index and Jain index [24] are convex curves, while GUI index is a concave curve. This is because the proposed fairness index and Jain index are based on the rate, that is, the closer the user rate in the system, the greater the fairness. The GUI fairness index is related to user power allocation in the system, that is, the greater the rate of users with more power allocation, the greater the fairness. From the perspective of fairness value range, the lower bound of Jain index is affected by the number of users, which is suitable for analyzing systems with a fixed number of users. The lower bound of GUI fairness index is affected by the number of users and channel conditions, which is suitable for analyzing systems with fixed number of users and channel conditions. The range of the proposed fairness index is not affected by the number of users and channel conditions. Thus, it is more sensitive to the changes of resource allocation in the system and suitable for analyzing systems with changing number of users and channel conditions.

Figure 3 compares the throughput of the proposed algorithm, the algorithm in reference [30] (the algorithm of Abd-Elnaby 2021), and the fractional transmit power allocation (FTPA) algorithm under different user numbers. The algorithm in reference [30] is a power allocation algorithm based on channel gain of paired users, the power allocation factor of strong channel gain users in the n-th cluster is ${\alpha }_n^s=0.5e^{-3\mu }$, where $\mu =\left|h_n^w\right|/\left|h_n^s\right|$. As can be seen from Figure 3, with the increase of the number of users, the throughput advantage of the proposed algorithm becomes more and more obvious. When the number of users M = 60, the throughput of the proposed algorithm is 1.9135 × 10⁴ bps, the throughput of the algorithm in reference [30] is 1.5044 × 10⁴ bps, and the throughput of FTPA algorithm is 1.7512 × 10⁴ bps. The throughput of the proposed algorithm increased by about 24% compared with reference [30]. The reason is that the intra cluster user power allocation factor in the algorithm of reference [30] is a fixed coefficient based on the channel coefficient, which limits the range of throughput optimization.

Figure 4 compares the system fairness of the proposed algorithm, the algorithm in reference [30], and the FTPA algorithm under different user numbers. It can be seen that with the increase of the number of users, the fairness of the system gradually tends to be stable. The reason is that as the number of users in the system gradually increases, the channel gain difference between users gradually decreases. It can be seen from the figure that the proposed algorithm in this paper has significantly higher system fairness.

Figure 5 shows the change trend of system throughput with φ_c−n and φ_c. The value range of φ_c−n and φ_c is [0.05, 0.9]. As can be seen from Figure 5, the throughput decreases with the increase of the minimum fairness intra and inter clusters, and the downward trend gradually slows down. When φ_c is small, the throughput can be increased by reducing φ_c−n. When φ_c is large, the reduction of φ_c−n cannot obtain significant throughput gain. In practical applications, the system throughput can be improved by reasonably adjusting the minimum fairness constraints of one aspect according to the different needs of inter and intra cluster user fairness in different scenarios.

6. Conclusions

Aiming at the resource allocation problem of a downlink NOMA system, this paper proposes a fairness index based on the sample variance of users’ transmission rates, and designs a fairness constrained intra and inter cluster joint power allocation algorithm based on the proposed fairness index, which can maximize the system throughput under the minimum fairness constraint. The simulation results show that the proposed fairness index has a fixed value range and good sensitivity, which is suitable for comparing the fairness between systems with different user numbers. Different from the traditional power allocation scheme, this algorithm can take into account intra cluster fairness, inter cluster fairness, and system fairness, and has greater flexibility.