1. Introduction
A plethora of data-driven business processes, governmental and educational systems, and the rapid adoption of Industry 4.0 digital technologies [
1], such as cloud platforms, the Internet of Things (IoT), computationally extensive AI and ML techniques, augmented reality (AR), big data streaming services, blockchain, robotics, and 3D technologies [
2], are accelerating the demand for and complexity of data center (DC) industries. This trend has recently been bolstered by the emergence of COVID-19, which has increased the global demand for social networking, online education, and video conferencing, a trend that appears to be continuing [
3]. As data center demand and complexity increase, so do operational management challenges, making it more difficult for operators to maintain service reliability and availability. Energy management is one of the most common and complex challenges. According to A. S. Andrae and T. Edler [
4], if appropriate measurements are not taken, data centers are expected to consume up to 21% of the global demand; however, if necessary, measurements are taken, this figure could be reduced to 8% by 2030. Hence, a new solution is required to optimize DC operations and energy efficiency.
The emergence of IoT and intelligent technologies have recently enabled the automation of DC operations management by tracking operations parameters and generating massive amounts of streaming data over time, allowing DC operators to make data-driven decisions. However, the massive amount of streaming data must be transformed into actionable information to optimize DC operations. Thus far, commonly used methods for modeling DC operations and analyzing data streams are based on heuristic, statistical, and mathematical models. These models are reactive and incapable of processing massive amounts of data streams with complex and non-linear interactions [
5] in such a complex data center environment. Recently, artificial intelligence and machine learning technologies being increasingly leveraged in the data center industries to model and process massive amounts of streaming data into actionable information. Google implemented a simple neural network, ML approach for predicting power usage effectiveness (PUE), which assisted in configuring controllable parameters and resulted in a 40% cooling efficiency enhancement [
6]. Research by A. Grishina et al. [
7] was also conducted on thermal characterization and analysis using ML to enhance DC energy efficiency. Although many more AI and ML-based research studies have been conducted to optimize DC energy efficiency and operations at different layers, relevant feature selection has rarely been discussed. However, relevant feature selection is the backbone for effectively modeling DC operations with the objectives of improving model performance, reducing computational expense, and providing insight into the underlying patterns. To the best of our knowledge, although several feature selection methods have been discussed in various domains, they have rarely been discussed in the context of the DC industries. Therefore, identifying relevant features in the context of DCs is essential for mining the underlying patterns and effectively modeling DC operations. Hence, this paper establishes Shapley Additive exPlanation (SHAP) value-assisted Feature Selection (FS) method, which is rarely discussed in the literature. SHAP was initially proposed by Lundberg and Lee [
8] for explainable AI (XAI) in the field of AI and machine learning techniques. Recently, SHAP showed promising results in FSS methods for identifying relevant features by explaining the contributions of each feature toward developing an accurate model. Why SHAP? SHAP is a unique class of additive feature attribution values with consistent, missingness, and accuracy properties that computes feature importance based on the game theory concept. It is a model-agnostic method that can be applied to any machine learning or deep learning model. Hence, the ultimate goal of this paper is to identify relevant features based on their importance, which is computed using SHAP in relation to the specified target variables. We compared SHAP’s effectiveness with several widely used feature selection methods. To demonstrate the feature selection analysis, we conducted experiments using operational management data streams obtained from an HPC DC: the ENEA-CRESCO6 cluster with 20,832 cores from Italy. The data streams consist of energy consumption, cooling system, and environment-related operational features. In this paper, we use data center energy demand and ambient temperature target variables to demonstrate the FS process in the context of data center industries, allowing for the effective modeling and optimization of DC operations.
The contributions of this paper are: (i) Establishing SHAP-values-assisted feature automation method in the context of a data center with non-linear and complex system interactions and configurations to identify relevant features for effectively modeling and optimizing DC operations. This enables DC operators to better understand their DC operational patterns, allowing them to accurately characterize and optimize their DC operations in a cost-effective way. (ii) Enables accurately characterize and identify the underlying patterns and relationships of features in relation to the target variables, allowing operators to make informed decisions. (iii) Analyzing the effectiveness of various importance-based feature selection methods and selecting the best one that allows for the identification of relevant features in relation to the target variables. (iv) Finally, we identify the best feature selection technique for DC characterizations and operational optimizations that attempts to capture significant features, improve model performance, and reduce computational expense. We also analyze and characterize feature dependency and interactions to better understand how a particular feature affects the modeling of the target variable and DC operations.
We compared the proposed method to other commonly used feature selection methods. The top ten features of each feature selection method were then chosen, and the predictive models were retrained to identify the best feature selection method in the context of the data center industries. Hence, the best feature selection method is the one which results in better model performance and reduced computational expenses. The main contribution of this paper is therefore to identify and establish essential feature selection methods in the context of data centers to effectively model and reduce the computational expenses of machine learning models for the optimization and characterization of DC operations.
The remaining sections of this paper are structured as follows:
Section 2 provides a literature review in relation to feature selection techniques, focusing on the techniques used in the FSS space.
Section 3 describes the methodology used in this paper.
Section 4 presents the experimental results and discussion, and
Section 5 provides conclusions and describes future works of the author.
2. A Theoretical Review of Feature Selection Methods
In a given data stream,
D, with
n features, 2
npossible feature subsets can be generated. However, all these subsets may not be relevant for modeling and mining important patterns. Some features may appear to be equidistant, redundant, irrelevant, or noisy. To overcome these challenges, there are two special methods used to identify relevant features [
9]. The first method is feature extraction/dimensional reduction, which transforms the original input feature into a reduced representation set. The second method is feature selection, which identifies relevant subsets while preserving the original information [
10,
11]. Hence, in this paper, we focus on feature selection methods for identifying relevant features in the context of a data center. The main classes of feature selection (FS) methods are wrapper methods, embedded methods, and filter methods [
12]. Wrapper methods use the model’s performance as a score to select relevant feature subsets [
13]. Although wrappers are effective methods, they are computationally expensive and in some case pros to overfilting [
14]. On the other hand, embedded feature selection methods are applied during the model training process and are associated with a specific learning algorithm [
11,
12]. Filter methods are another model-independent feature selection method that are typically applied in the preprocessing steps [
15].
The best method, however, is usually determined depending on the problem identified. Data center operational management data streams are multivariate time series problems. The data streams are sequences of observations, denoted as
xi (
t); [
i = 1,
n;
t = 1,
…,
T] [
16], in which
x represents observations,
i represents measurements taken at each time point,
t,
n is the maximum index, and the maximum time length is
T. The time series can be a univariate time series (UTS) problem or a multivariate time series (MTS) problem. It may be an MTS if the number of features,
n, is greater than or equal to 2, and it may be a UTS if n=1. This paper focuses on an MTS because the data center operations management data streams at hand are stored in a multi-dimensional matrix represented as
m ∗
n, where
n represents features in the data streams and
m represents rows in the data streams. The target variables for the data center ambient temperature and data center energy demand are determined not only by their previous history but also by several other operational factors. The interaction between streams over time is the key to the complexity of the MTS problem. Thus, feature subset selection (FSS) entails identifying relevant features from given data streams with three main objectives. The objectives are: To provide insights into the data, reduce computational expense, and improve model performance [
12]. To achieve these objectives, many studies have been conducted to identify relevant features in regression problems. For example, wrapper methods such as recursive feature elimination (RFE) and backward feature elimination (BFE) take input in the form of a single-column vector of the matrix. However, MTS data streams are stored in the form of a multidimensional matrix, which may lose important information during vectorization.
Additionally, MTS data streams typically contain complex correlations between features over time that make it difficult to apply wrapper and embedded feature selection methods to MTS problems.
Filter methods are correlation-based feature selection techniques that are effective on time series or continuous variables that compute correlations among different features and the target variable. Using correlation-based methods such as Pearson, Spearman, and Kendall, filter methods identify relevant features that have high correlations to the target variable. Filter methods identify relevant FSSs related to the target variable based on distance, dependency, and consistency [
17]. Commonly used correlation-based methods are the Pearson, Spearman, and Kendall methods, as well as the mutual information (MI) method. The Pearson correlation is the most widely used filter method for measuring the linear relationship between two variables. The Spearman and Kendall correlation methods, which employ non-parametric tests, are better suited for non-normally distributed data [
18]. The degree of correlation between two variables is measured by the Spearman correlation, whereas the Kendall method measures and computes the interdependency between features [
19]. Hence, the Kendall method is more accurate feature at identifying dependencies and correlations in relation to the target variable than Spearman method. [
19]. Spearman correlation can be effective for non-linear and non-time series data but shows poor results in the domain of MTS problems. Another study used a feature selection method based on Pearson correlation and symmetrical uncertainty scores to compute non-linear and linear interactions between features and the target variable [
20]. In this context, a correlated but important feature may be overthrown, leading to the wrong conclusion. Another well-known feature selection method is the mutual information (MI)-based method, which measures the uncertainty of random variables, termed Shannon’s entropy [
21]. A recent feature subset selection method based on merit score, also implemented by Kathirgamanathan and P. Cunningham [
22], was used to identify relevant features in the MTS domain. In general, correlation-based feature selection (CFS) techniques are not effective in MTS problems [
23]. As a CFS technique requires input streams in the form of vector representations, it may result in the loss of important information during vectorization. Recently, importance-based feature selection methods have been used in different domains, including the MTS domain. Commonly used methods are random forest (RF)- and extreme gradient boosting (XGB)-based feature importance ranking methods. For example, Zhen Yang et al. [
24] used the random forest method with Gini feature importance ranking to identify relevant features related to PUE prediction. However, these methods suffer from a high frequency and cardinality of features. This paper establishes SHAP value-assisted relevant feature selection for effectively modeling and characterizing DC operations.
3. Methodology
This paper focuses only on supervised learning methods because modeling DC energy demand and ambient temperature predictions are treated as time series regression problems. To effectively model the problems, we applied Shapley Additive exPlanation (SHAP) additive feature attribution value-assisted feature selection method to identify relevant features based on various feature importance rankings.
Section 3.2 presents the description and implementation procedures of the SHAP-assisted feature selection. In the feature-importance-based approach, input features are assigned a score based on how useful they are at predicting the target variables. The top-ranked features are the most significant features for modeling the specified target problem. We compared the effectiveness of the SHAP value-assisted feature selection method introduced in this paper with the following several commonly used importance-based feature selection methods: (i) Random Forest with Gini Feature Importance Ranking (RFGFIR) (mean decrease impurity), (ii) Random Forest permutation-based Feature Importance Ranking (RFPFIR), (iii) Random Forest with SHAP-values-based Feature Importance Ranking (RFSVFIR), (iv) XGB with Gain-based Feature Importance Ranking (XGBGFIR), (v) XGB with Permutation-based Feature Importance Ranking (XGBPFIR), and (vi) XGB with SHAP-values-based Feature Importance Ranking (XGBSVFIR). The methods were tested and validated using a real dataset from an HPC data center, a CRESCO6 cluster consisting of 20,832 cores. The dataset was divided into a 7:3 ratio for training and testing while preserving the time order.
Table 1 illustrates the dataset’s features and descriptions. Then we trained the models using the first 70% of the dataset, applied the feature selection methods, and ranked the important features in prior orders. The models were retrained, being with the highest-ranked features from each feature selection method, and their performance and learning rate of the feature selection were compared. This was performed
n − 1 times. Finally, the topmost important features with good model performance and fair computational expenses were kept. The experimental procedures are detailed in
Section 3.2 in
Figure 1. To validate the feature selection methods, we applied the 30% testing set of the dataset. We then retrained and compared the methods’ performance and learning rate using the top 10 most important features of each feature selection method. To evaluate and compared the feature selection methods, we applied to mean absolute average error (MAPE), mean absolute error (MAE), and root mean squared error (RMSE) evaluation criteria. The method with the lowest error and computational expenses was selected as the best method for the identification of relevant features to effectively model DC operations. In this paper, we generally adhered to the conceptual framework illustrated in
Figure 1. The following three steps were systematically applied: (i) Dataset and preprocessing as described in
Section 3.1, (ii) Introduction to SHAP feature attribution value-assisted relevant feature selection procedures as described in
Section 3.2, and (iii) the machine learning models used to evaluate the feature selection methods presented in
Section 3.3.
3.1. Datasets and Descriptions
The dataset used in this paper was obtained from the ENEA CRESCO6 cluster, a data center consisting of 434 computing nodes with 20,832 cores. Each node consists of two Intel Xeon Platinum 8160 CPUs (represented as CPU1 and CPU2), each with 24 cores and a total of 192 GB of RAM, corresponding to 4 GB/core and operating at a clock frequency of 2.1 GHz. The ENEA CRESCO6 cluster has been operating since 2018. The cluster has a nominal computing power of 1.4 PFLOPS and is based on the Lenovo Think System SD530 platform. The nodes are linked with an Intel Omni-Path network and have 15 switches of 48 ports each at 100 Gb/s with a latency equal to 1 µs of bandwidth. For monitoring and management purposes, each computing server/node of CRESCO6 is instrumented with onboard sensors. These sensors read the values of the operational parameters of the equipment for the entire calculation server/node. These sensors monitor temperatures at different sections of the nodes (e.g., CPU, RAM, fans, rotation speeds, and the volume of air passing through the nodes) and the energy demand.
The data are read via an intelligent platform management interface (IPMI), which is a CONFLUENT software package directly installed on the cluster computing nodes and stores the acquired values in a MySQL database. Cooling system parameters such as inlet temperature, outlet temperature, relative humidity, airflow, and fan speed are also monitored using the onboard sensors of the refrigerating machine. There are also several sensors installed around the cluster to monitor the environmental conditions around the data center. These sensors measure temperature- and humidity-related parameters. The data streams related to computing nodes, cooling, and environmental parameters are stored in a MySQL database with separate tables. In this experiment, we used annual data streams from 2020. These data streams were collected in a matter of seconds or minutes. The datasets were then organized, standardized, and sensitized, and missing values were interpolated. Next, the datasets were resampled into 15 min intervals equal in length, and the available tables of data composing the datasets were aligned. Finally, the datasets were aggregated into one table and shaped as (35,136, 50): that is, 35,136 rows and 50 features/columns.
Table 1 provides the features and descriptions of the dataset.
The above-mentioned features represented the totals and averages of the values of the data points, which were derived from each sensor’s data stream. In addition to the features listed in
Table 1, we included time covariate features in the time series, which have a significant impact on model performance. The included covariates are hours, weekdays, weekends, months, and quarters, which could have a greater impact and improve the modeling performance of the target variables. Hence, the final data streams used in the application of the feature selection methods were shaped (35,136, 55). Note that the time stamp measure was an index, and the actual features were 54 columns, shaped as (35,136, 54).
3.2. Shapley Additive exPlanation (SHAP)-Based FSS Method
Shapley Additive exPlanation (SHAP) is one of the additive feature attribution values methods initially proposed by Lundberg and Lee (2017) and was designed for explainable AI (XAI) [
8]. The explanation level is focused on comprehending how a model makes decisions based on its features and from each learned component. SHAP is a class of additive feature attribution methods that are model-agnostic and can be applied to any machine learning and deep learning model by attributing the importance of each input feature. In comparison to other additive feature attribution methods, such as LIM [
25] and DeepLIFT [
26], SHAP has a unique approach that satisfies the accuracy, missingness, and consistency properties of feature attribution. In SHAP, feature importance can be computed using ideas from game theory concepts. The model explanation can be computed at global and local levels. The model’s global explanation assists in better understanding which features are important, as well as the interactions between different features. It is also more aligned with human intuition and is more effective at mining influential features. Hence, this paper introduces SHAP-values-assisted feature selection to identify relevant features with respect to the specified target variables in the context of a data center.
The SHAP-assisted feature selection procedures used in this paper are depicted in
Figure 1. The procedures were: (i) data collection and preprocessing; (ii) training the models using all features in the initial interaction; (iii) applying SHAP, computing the Shapley values of each feature, and ranking them in ascending priority order; (iv) training the models
n times, beginning with the topmost features and continuing until the optimal subset is found with respect to each of the aforementioned methods; and (v) selecting the optimal feature subset to effectively model the target problem with the most predictable feature subset to optimize DC operations. In general, Shapley values can be computed as a unified measure of feature importance, which is the average of the marginal contributions of features from all conceivable coalitions. For example, we can compute the Shapley value of a given feature,
n, in each dataset, D. The value of the feature is replaced by a value from another instance of the model, and all possible outcomes are considered to compare the original prediction with the new prediction. Hence, the average between the new value and the original value represents the importance of feature
n to the final prediction. For example, the Shapley value estimation of the
jth feature with
i combinations of features, target feature
x,
j index, data streams
D with matrix
X, and predictive model
f, Shapley value for
x is computed as follows:
where
ϕij is the average Shapley value of the
jth feature with the
ith feature,
fˆ(
x+j) is the prediction for target x with a random number of feature values, including
jth feature, and
fˆ(
x−j) is the coalition without the
jth feature. In general, to compute the Shapley value of the
jth feature that is target
x, the equation is given as follows:
The importance of all features is computed in the same way and is ranked based on their Shapley value in a prior order. As shown in the following iterations, the model is then trained using the most important features, beginning from the top and continuing until the optimal feature subset is found.
1st interaction: i1 = f1
2nd interaction: i2 = f1, f2
nth interaction: in = f1, f2, f3,…,fn
Finally, the optimal feature subset can be found and used to effectively model the target problem. The following
Figure 1 shows the overall conceptual framework of the process.
Figure 1.
The flow of SHAP assisted FSS method. Relevant feature selection and analysis processes in the context of the DC operations. The colors represent different tasks.
Figure 1.
The flow of SHAP assisted FSS method. Relevant feature selection and analysis processes in the context of the DC operations. The colors represent different tasks.
Depending on the machine learning model architecture, various SHAP approximation methods are available. These are the kernelSHAP, Gradient SHAP, and TreeSHAP approximations for decision-tree-based machine learning models, and the DeepSHAP approximation for deep learning approaches. In this paper, we used RF- and XGB-tree-based prediction models with TreeSHAP to identify and validate feature selection methods in the context of a data center. TreeSHAP is the fastest method when compared to others because it has optimized hy-perparameters with RF and XGB decision tree models.
3.3. Machine Learning Models
The use of machine learning (ML) and deep learning (DL) technologies to optimize data center operations has increased. Identifying relevant features in relation to a specific problem is critical for effectively modeling and optimizing DC operations using these technologies. Hence, this paper demonstrates an importance-based, relevant FSS with RF and XGB predictive models. The models’ implementations are described in the following
Section 3.3.1 and
Section 3.3.2.
3.3.1. Random Forest (RF)
Random Forest (RF) is an ensemble machine learning algorithm that is commonly used in regression problems. It was initially proposed by Ho (1995) [
27] and was further extended by L. Breiman (2001) [
28]. Bootstrap aggregation is used to train the algorithm. Each tree is trained on a random subset of the examples with replacement. In this case, each tree learner is shown a different subset of the training data, and the same observation can be chosen multiple times in a sample [
29]. In general, the algorithm follows these steps: (i) in RF,
n number of random samples are generated from the given data set and have
k records; (ii) individual decision trees are constructed for each sample; (iii) each decision tree generates sequential output; and (iv) the final output is then considered as an average for classification and regression, respectively. As our study concerns a multivariate time series (MTS) regression problem, we fitted several decision tree classifiers to different sub-samples of the data set and then averaged the predictions. This could improve the predictive accuracy and avoid the overfitting of the RF regression model. During model implementation, the values of the hyperparameters typically have a significant impact on the performance and behavior of the model. Hence, the hyperparameters for the RF algorithm were explored and tuned as follows: the maximum depth of trees was 5, and the estimator, or forest, in the trees was 200, with the rest remaining as defaults.
3.3.2. Extreme Gradient Boosting (XGB)
Extreme gradient boosting (XGB) is an ensemble ML model that provides efficient and effective implementation of gradient boosting, which is widely used ML algorithms in both classification and regression problems [
30], with regularization to objectively reduce variance and bias. Due to its ability to perform parallel computation on a single machine, XGBoost is at least ten times faster than existing gradient boosting implementations [
9]. It can perform a variety of objective functions, such as regression, classification, and ranking. It also has features for performing cross-validation and identifying important variables [
30]. The hyperparameters for XGB ere explored and tuned as follows: the maximum depth was 5, the estimator was 200, and the learning rate was 0.01.
3.4. Model Performance Evaluation Criteria
In regression, the model error is the difference between the actual sample and the predicted values. The following evaluation criteria were used to determine the model’s performance:
- (i)
Mean absolute error (MAE): this is the arithmetic mean of the absolute values of the errors, representing the deviation from actual values. The computational equation is given as follows:
- (ii)
Root mean squared error (RMSE): a popular performance evaluation metric for models. It can be interpreted as the standard deviation of the forecast errors.
- (iii)
Mean absolute percentage error (MAPE): the total of each period’s individual absolute prediction error divided by the actual values. The RMSE and MAPE are computed as follows, respectively:
Execution time: the time it takes for the model to learn and predict based on the given input variables, where is the predictive value at time point i and yi is the actual value. The execution time in this paper is the computational time when SHAP is applied to the trained models. Lower MAE, RMSE, and MAPE values indicate better performance of the model in predicting energy demand and ambient temperature.
4. Results and Discussion
The SHAP-assisted feature selection method established in this paper has been discussed and compared to several importance-based feature selection methods. Feature importance is computed and scored for all input features with a given machine learning model. A higher score indicates that the specific feature contributes more to the problem’s modeling effectiveness and efficiency. We compared the SHAP-values-assisted feature selection method with other commonly used methods to determine its suitability and effectiveness for identifying relevant features to effectively mine and optimize data center operations, allowing data center operators to perform data-driven service reliability and availability improvements. To demonstrate the feature selection process in the context of data center industry, we used two widely used machine learning regression models: the RF and XGB prediction models. We decided to use these methods to identify relevant features in the context of data centers because they are widely used for feature selection processes, they are faster, and, when compared to others, the TreeSHAP approximation method has optimized hyperparameters with RF and XGB. The hyperparameter values of the models and the FSS have a significant impact on the models’ behavior and performance. Hence, the hyperparameters for each method were tuned as follows: for the RF-based feature selection methods, the maximum depth of the trees was 5 and the estimator, or forest, in the trees was 200; the rest were left as defaults. For the XGB feature selection methods, the maximum depth was 5, the estimator was 200, and the learning rate was 0.01; the rest was left as defaults. All the feature selection methods were fitted and computed in Python. Initially, the models were trained using 70% of the total data streams, considering all input features. Following that, we applied feature selection methods to the trained model to compute the importance of each feature and rank them in priority order. The most important feature received the highest score and was ranked first. We trained the models after computing and ranking features based on their importance for each feature selection method, starting with the topmost-ranked feature and continuing n times to find the optimal feature subset from each feature selection method. The order of ranked features and the combination of optimal subsets for each feature selection method may differ due to the nature of the machine learning models. To evaluate the feature selection methods, we created a testing set comprising 30% of the total data streams with all input features. We then selected the top ten most important features from each feature selection method and retrained the ML model’s performance and learning rate to demonstrate the suitability of the FSS methods. We used three evaluation criteria to determine and compare the suitability of each feature selection method. These were the MAE, RMSE, and MAPE evaluation metrics.
Hence, the suitable feature selection method is then the method which will produce the most predictable feature subset with the best model performance and computational expense in the context of a data center industry. The results in
Table 2 and
Table 3 are based on the top ten most important features chosen from each feature selection method. The results demonstrate how to determine which feature selection method is best suited to identifying relevant features with respect to the specified target variables in the context of a data center. Note that we selected the ambient temperature and energy demand of the data center as target variables to explore the feature selection process, allowing us to extract the underlying patterns that enable the maintenance of data center operations. Hence, the results in
Table 2 and
Table 3 pertain to the ambient temperature and energy demand target variables, respectively.
Table 2 and
Table 3 demonstrate the performance and computational expenses of the models implemented for predicting the data center ambient temperature and energy demand, respectively, that were retrained with the top ten most important features obtained from each feature selection method. The feature selection methods presented in this paper are RFGFIR, RFPFIR, RFSVFIR, XGBGFIR, XGBPFIR, and XGBSVFIR, as shown above in
Table 2 and
Table 3. RFGFIR is a method that computes feature importance during the model training process, making it computationally fast but error prone.
Table 2 and
Table 3 demonstrate that RFGFIR had a fair speed but lower performance than others. On the other hand, RFPFIR can be used to identify relevant features by using permuted samples out-of-bag to compute feature importance (OOB). To compute feature importance, this method requires a trained model and test samples. It shuffles each feature by chance and quantifies the changes in the model’s effectiveness. The feature that has a significant impact on model performance is the most important feature for effectively modeling the target problem. As is shown in
Table 2 and
Table 3, RFPFIR outperformed RFGFIR but had a high computational cost. XGBGFIR and XGBPFIR are two others commonly used, importance-based feature selection methods. Like RFGFIR, XGBGFIR can be computed during the model training process using an importance attribute technique. Its value is computed as the average gain across all tree splits. XGBPFIR, on the other hand, requires a trained model and test data to compute the feature importance by permuting samples. XGBGFIR randomly shuffles each feature and calculates the changes in model performance. In this case, the most important feature is the one with significant impact on model performance. As demonstrated in
Table 2 and
Table 3, XGBPFIR outperformed XGBGFIR, RFGFIR, and RFPFIR in terms of performance at a reasonable speed. However, these methods suffer from a high frequency and cardinality of features in the relevant feature selection process, which may result in wrong conclusions.
The SHAP-values-assisted FSS method introduced in this paper, on the other hand, outperformed the other methods for identifying relevant features in the context of a data center. According to the conceptual framework of the SHAP-assisted feature selection process presented in
Section 3.3, it is model-agnostic and can be used with any machine learning model. In this paper, we used TreeSHAP with RF and XGB models to demonstrate FSS methods.
Hence,
Table 2 and
Table 3 demonstrate that the RFSVFIR and XGBSVFIR which are SHAP-values-assisted FSS methods outperformed other methods, demonstrating lower errors and fair speed. RFSVFIR performed with an MAE of 0.42, RMSE of 0.237, MAPE of 0.018, and an MAE of 1.368, RSME of 6.657, and MAPE of 0.005 at predicting the DC ambient temperature and DC energy demand target variables, respectively, with a fair computational speed. XGBSVFIR, on the other hand, predicted the DC ambient temperature and DC energy demand target variables with lower errors of a MAE of 0.401, RMSE of 0.245, MAPE of 0.0035, and a MAE of 0.451, RSME of 0.235, and MAPE of 0.004, respectively, with fair computational speed. When we compared XGBSVFIR with RFSVFIR, XGBSVFIR outperformed RFSVFIR, demonstrating a better performance and fair computational expenses. Hence, SHAP with XGB feature selection was faster when compared with SHAP with RF due to the capacity for parallel computation in XGB. Furthermore, due to its optimized hyperparameter with TreeSHAP [
31]. Hence, as demonstrated by the experimental results in
Table 2 and
Table 3, XGBSVFIR is the best-suited FSS method in the context of a data center for identifying the relevant operational features and underlying patterns to effectively model and optimize DC operations.
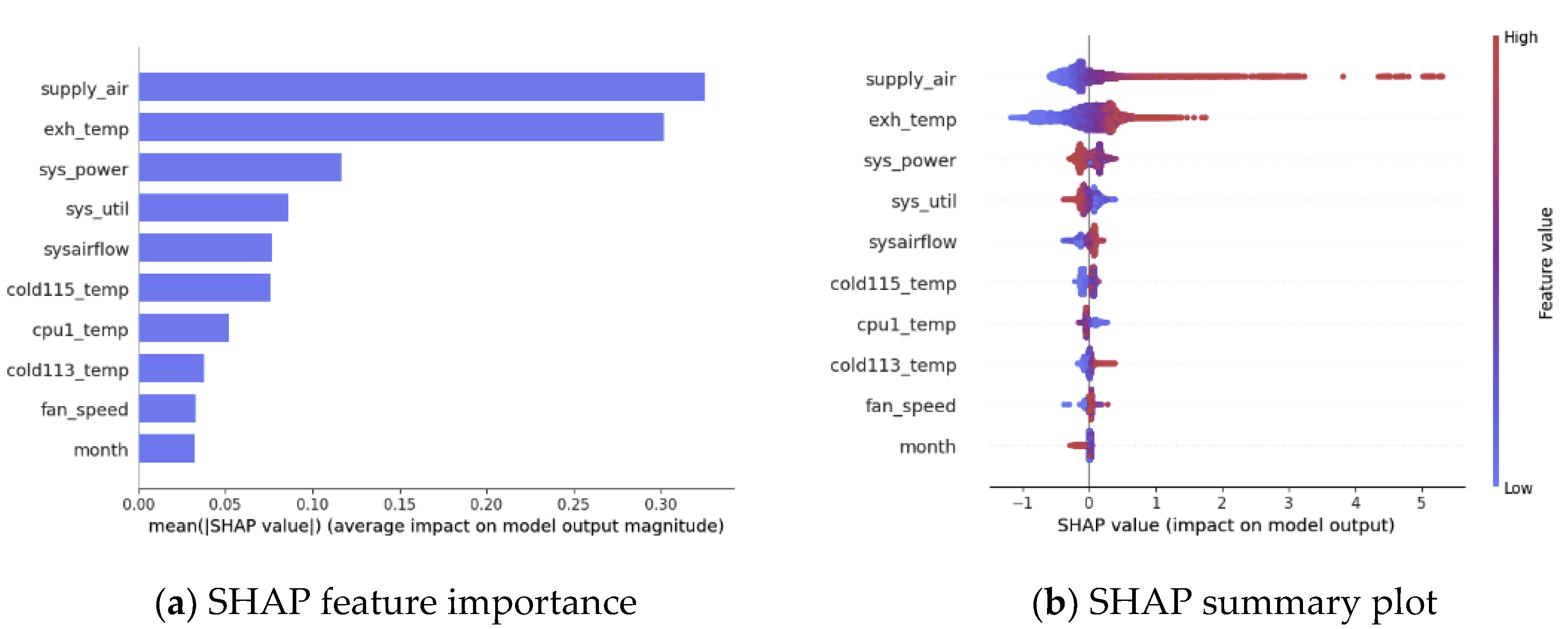
To visualize the experimental results of the most suitable FSS method, we relied on three plots: SHAP feature importance, SHAP summary, and partial dependency plots. Hence, the graphs are based on the XGBSVFIR feature selection method. SHAP feature importance plots visualize features based on their feature importance, which is prioritized with high, absolute Shapley values. The feature importance of each feature is computed as the average absolute Shapley value of each feature across the data streams, as below:
Following the Shapley value results, we sorted the feature importance from highest to lowest and plotted the graph.
Figure 2a and
Figure 3a illustrate the SHAP feature importance plots based on the XGBSVFIR method at predicting the data center ambient temperature (amb_temp) and energy demand (dcenergy) target variables, respectively. The y-axes represent the names of the features and x-axis represents the Shapley values. The Shapley values indicate how much each feature influences the prediction of the target variable. Although SHAP feature importance is useful for visualizing the importance of features, it does not provide further information, aside from the importance. SHAP summary plots can provide additional information about the effects of each feature on the target variable. The SHAP summary plot provides the dispersion information of Shapley per each feature.
Figure 2b and
Figure 3b display SHAP summary plots of the features used to predict data center ambient temperature and energy demand, respectively. The y-axis displays feature names and Shapley values, while the vertical line represents the accumulated density. The feature effect is represented by two colors: red for the greatest influence and blue for the least influence. In general, the topmost features are the most predictable.
For example, the supply air is an inlet temperature supplied by the cooling system. It allows the data center to maintain an ambient temperature. Exhaust temperature is dissipated temperature from the computing nodes that should be effectively returned to the computer room air conditioning (CRAC) unit while maintaining the data center’s ambient temperature and improving equipment efficiencies. Hence, supply_air and exh_temp are the topmost important features at predicting amb_temp while optimizing DC operations.
Figure 2a,b below are plots of the top ten most important features for predicting amb_temp over 2000 data samples.
Figure 3a,b below show the importance of SHAP features and SHAP summary plots of features in relation to the data center energy demand target variables. Note that these figures are based on 2000 samples taken from the testing sets. The result shows that the main energy consumers in the data center are the computing nodes, which are represented by sys_power, the total power consumption of the calculation nodes in the center. Hence, sys_power is the topmost influential feature at predicting the data center energy demand. Time-based covariates such as quarter, months, and days have a greater impact on data center energy consumption.
Furthermore, we present SHAP dependency plots that can provide the necessary information to understand the feature interactions and underlying patterns. The Shapley interaction of features can be computed as below:
The Shapley interaction of a single feature can be computed by subtracting from the model’s main feature impact:
where
s denotes the average value of all coalitions and
X denotes the feature matrix.
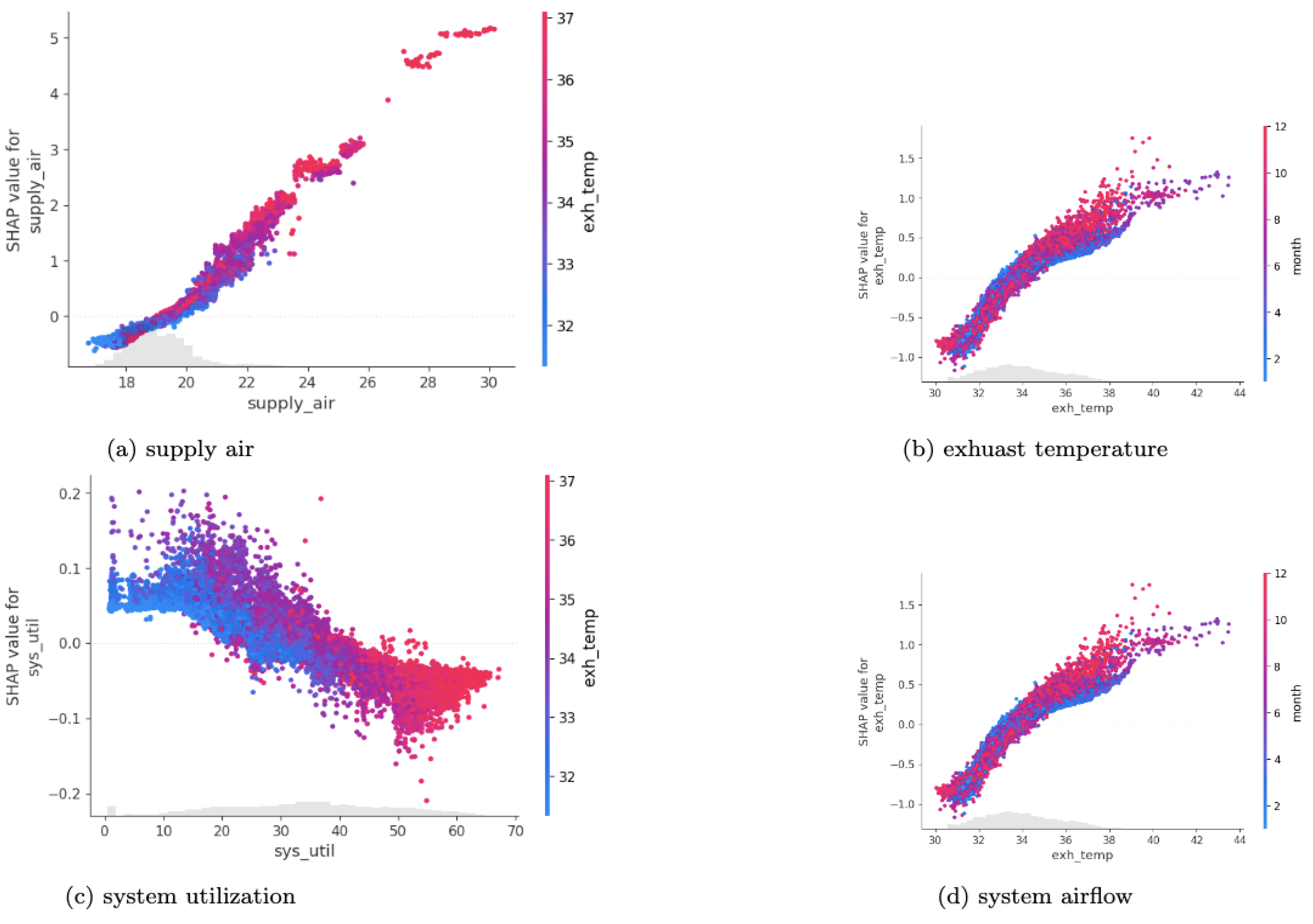
Figure 4 and
Figure 5 depict SHAP feature dependency plots, which show the interactions of features and their impact on predicting the target variable. For example,
Figure 4a–d illustrates the interaction between supply_air and exh_temp, exh_temp with covariate month, syst_util with exh_temp, and sysairflow with cpu2_temp. The indexed feature name is positioned on the x-axis, and the Shapley values are positioned on the y-axis. The vertical lines represent the accumulated information density. The colors represent the interaction of the features and their impact on predicting the target variable. The red color represents the feature’s higher effect, while the blue color represents the feature’s lower effect. For example, as the supply air temperature rises, the exhaust temperature in the data center rises as well, which has a greater impact on predicting the ambient temperature.
Similarly,
Figure 5 illustrates the SHAP feature dependency plots to demonstrate feature interaction and the underlying pattern analysis with respect to the data center energy demand target variables. The following subfigures, a–d, illustrate the SHAP feature interactions and pattern analysis. In addition to sys power, the time covariate features of quarter, months, and days, as well as the data center cooling system fan speed to supply inlet temperature, have a greater impact on the data center’s energy consumption. As a result, the following subfigures are based on these important features and their interactions with other dependent patterns. The Shapley values of the feature are positioned on the y-axis and the feature is positioned on the x-axis, while the interaction feature information is accumulated on the vertical line. The red color represents the highest feature effect, while the blue color represents the lowest effect in predicting the target variable. For example,
Figure 5a demonstrates how the covariate quarter feature interacts with the data center’s return air or outlet temperature in the first quarter, indicating that the outlet temperature is good at predicting energy demand.