Streaming and Elastic Traffic Service in 5G-Sliced Wireless Networks and Mutual Utilization of Guaranteed Resource Units

Abstract

Researchers of 5G-sliced Wireless Networks are faced with the task of achieving, at the same time, (i) mandatory isolation among network slices and (ii) the effective utilization of resource at Fifth Generation Base Station (gNB). This article proposes the second version of the Preemption-based service Prioritization (PP2) scheme that merges the capabilities of the classical Resource Reservation (RR) and Service Prioritization (SP) schemes and realizes the coexistence of non-TCP streaming and TCP elastic traffic at gNB. Analytical methods are given for Dynamic Resource Sharing (DRS) and Dynamic Resource Reallocation (DRR) with data rate reduction and service preemption. As main results, under some baseline scenario, the PP2 scheme, in comparison with RR, does increase the admission probability up to 99.999% at the system while ensuring 100% in system capacity utilization.

1. Introduction

Four years after the Network Slicing (NS) official launch alongside other technologies (by far not the least important creations for Fifth Generation Base Stations (gNBs) [1,2,3,4,5,6,7,8]), major advances in the wireless telecommunication industry have been achieved with NS at the core, harboring features such as the inherently flexible Resource Reservation (RR) and/or Service Prioritization (SP) access scheme [1,2,4,6,8,9,10,11,12,13,14]. Unfortunately, these schemes do not completely enable NS’s capabilities at the gNB: the RR proves especially inefficient during network outages, and the SP does not ensure NS’s utmost important property—the slices’ effective isolation. For the review, we refer the reader to [10].

The NS concept, standardized by Third Generation Partnership Project (3GPP) and implemented by Docomo and Ericsson, aims at efficient resource utilization while meeting the slices’ aggregated Quality of Service (QoS) requirements [1,3,4,5,6,7]. To achieve its goal, NS first needs to overcome the above-mentioned RR and SP inefficiencies. An obvious solution, and by far the simplest, seems to be to just interconnect the RR isolation capability and SP efficient resource utilization in a Preemption-based service Prioritization (PP) scheme, so-called by research [10]. The setback at this point is that the PP scheme performs the expected job exclusively among slices, with each slice providing customers with non-TCP streaming service at a gNB.

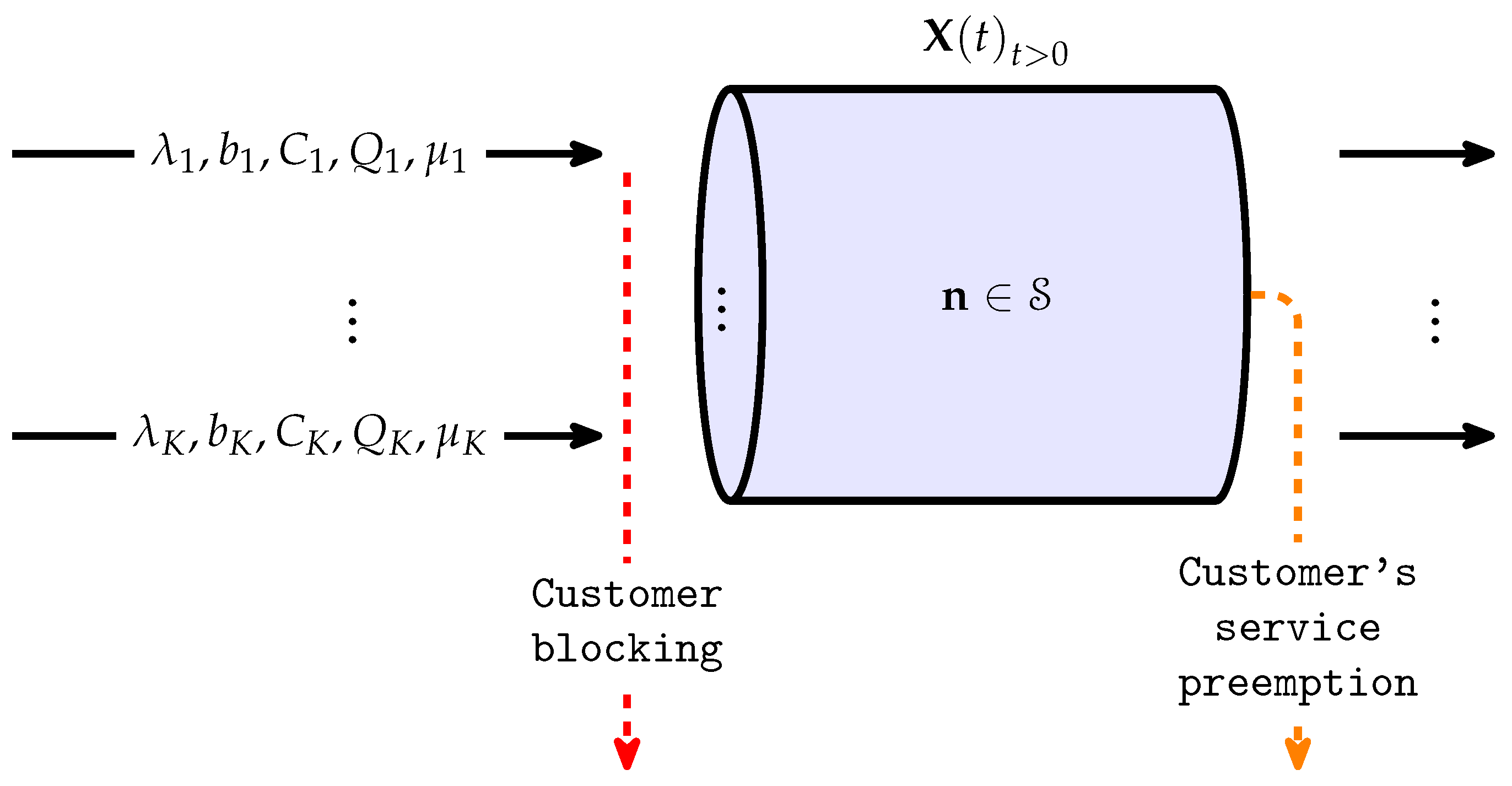
The current research aimed to develop the second version of the PP (PP2) scheme—an improvement or adaptation of the PP scheme in order to allow the simultaneous provision of non-TCP streaming and TCP elastic services at a gNB. Thus, the remainder of this paper is outlined as follows. First, the system model, together with the optimization problem and solution, is presented in Section 2. Next, the mathematical model is constructed, and the relevant system Key Performance Indicators (KPIs) are described in Section 3. Then, an accurate comparison of the PP2 scheme with the widely utilized RR is conducted in Section 4. Finally, this paper is concluded in Section 5.

2. System Model

Let us consider the coexistence of multiple slices at one Fifth Generation Base Station (gNB), each providing either non-TCP streaming or TCP elastic service (non-TCP streaming or TCP elastic slice) to customers (Figure 1). Thus, we consider a system model with a <<service-type-based slice>> [3,4,9]. We denote the following notation:

• $C,0<C<\infty$—the total system capacity;
• $\mathcal{K}=\left\{\begin{array}{c}1,\dots ,K\end{array}\right\}$—the finite set of slices in the system;
• ${\mathcal{K}}_{\mathrm{s}}\subseteq \mathcal{K},\left|{\mathcal{K}}_{\mathrm{s}}\right|=K_{\mathrm{s}}$—the subset of non-TCP streaming slices;
• ${\mathcal{K}}_{\mathrm{e}}\subseteq \mathcal{K},{\mathcal{K}}_{\mathrm{s}}\cap {\mathcal{K}}_{\mathrm{e}}=\varnothing ,{\mathcal{K}}_{\mathrm{s}}\cup {\mathcal{K}}_{\mathrm{e}}=\mathcal{K},\left|{\mathcal{K}}_{\mathrm{e}}\right|=K_{\mathrm{e}}$—the subset of TCP elastic slices;
• $C_k,0<C_k\le C,{\sum }_{i=1}^K{C}_i\ge C,k\in \mathcal{K}$—the overall capacity of slice k;
• $Q_k,0\le Q_k\le C_k,{\sum }_{i=1}^K{Q}_i\le C$—the guaranteed capacity of slice k.

We note that the model is built at the top level of abstraction, without particular attention paid to the configuration details at the lower layers of the OSI/ISO model. Thus, we consider the bitrate (one bit per second) as the resource unit (r.u.) since the Quality of Service (QoS) requirements for services are primarily specified in terms of bitrate. From this point of view, the slice capacity is measured in r.u.

Let the customer flow at a slice $k\in \mathcal{K}$ be a Poisson flow with intensity ${\lambda }_k\left[{\displaystyle \frac{\mathrm{customers}}{\mathrm{time}\mathrm{units}(\mathrm{t}.\mathrm{u}.)}}\right]$. We assume that a customer flow $k_{\mathrm{s}}\in {\mathcal{K}}_{\mathrm{s}}$ is characterized by the service time with intensity ${\mu }_{k_{\mathrm{s}}}\left[{\displaystyle \frac{\mathrm{customers}}{\mathrm{t}.\mathrm{u}.}}\right]$ and constant data rate $b_{k_{\mathrm{s}}}\left[{\displaystyle \frac{\mathrm{r}.\mathrm{u}.}{\mathrm{customer}}}\right]$, while a customer flow $k_{\mathrm{e}}\in {\mathcal{K}}_{\mathrm{e}}$ denotes an exponentially distributed random size of the transmitted data block with parameter ${\mu }_{k_{\mathrm{e}}}^{-1}\left[\mathrm{size}\mathrm{units}(\mathrm{s}.\mathrm{u}.)\right]$ and minimum data rate $b_{k_{\mathrm{e}}}\left[{\displaystyle \frac{\mathrm{r}.\mathrm{u}.}{\mathrm{customer}}}\right]$. Let us note that r.u. are expressed in s.u. per t.u. $\left({\displaystyle \frac{\mathrm{s}.\mathrm{u}.}{\mathrm{t}.\mathrm{u}.}}\right)$.

Table 1. The characteristics of a customer flow $k\in \mathcal{K}$.

Flow k	${\mathit{\lambda }}_{\mathit{k}},0<{\mathit{\lambda }}_{\mathit{k}}<\mathit{\infty }$	${\mathit{\mu }}_{\mathit{k}}^{-1},0<{\mathit{\mu }}_{\mathit{k}}^{-1}<\mathit{\infty }$	${\mathit{b}}_{\mathit{k}},0<{\mathit{b}}_{\mathit{k}}\le {\mathit{C}}_{\mathit{k}}$	${\mathit{\rho }}_{\mathit{k}},0<{\mathit{\rho }}_{\mathit{k}}<\mathit{\infty }$
$k\in {\mathcal{K}}_{\mathrm{s}}$ (Streaming service)	Intensity of the customers’ arrival	Mean service time of one customer	Constant data rate of one customer	Offered load ${\lambda }_k{\mu }_k^{-1}$
$k\in {\mathcal{K}}_{\mathrm{e}}$ (Elastic service)	Intensity of the data blocks’ arrival	Mean size of one data block	Minimum data rate of one customer	Offered load ${\lambda }_k{\mu }_k^{-1}$

groups the characteristics of the flows in the system.

Let us denote the following:

• $D_k=⌊C{b}_k^{-1}⌋,0<D_k<\infty ,k\in \mathcal{K}$—the maximum number of customers in slice k, given that equality $C_k=C$ holds;
• $M_k=⌊C_k{b}_k^{-1}⌋,0<M_k\le D_k$—the maximum number of customers in slice k;
• $N_k=⌊Q_k{b}_k^{-1}⌋,0<N_k\le M_k$—the guaranteed number of customers in slice k;
• $n_k,0\le n_k\le M_k$—the number of customers in slice k;
• $\mathbf{n}:={\left(n_1,\dots ,n_K\right)}^T,\mathbf{n}\in \mathsf{\Omega }$—the gNB state, with the state space

  $$\begin{array}{c}\mathsf{\Omega }=\left\{\mathbf{n}\in {\left(\mathbb{N}\cup \left\{0\right\}\right)}^K:\sum _{k=1}^K{n}_k{b}_k\le C\right\},{\left(z\right)}^{+}=\left\{\begin{array}{cc}\hfill z,& z>0;\hfill \\ \hfill 0,& z\le 0;\hfill \end{array}\right.\end{array}$$

  (1)
• $c_k\left(\mathbf{n}\right),0\le c_k\left(\mathbf{n}\right)\le C_k$—the capacity share of slice k;
• $x_k\left(\mathbf{n}\right)=n_k^{-1}{c}_k\left(\mathbf{n}\right),n_k>0$—the data rate allocated to each customer in slice k (with this, we assume the uniform allocation of the capacity share of slice k).

According to [15], the state space $\mathsf{\Omega }={\mathsf{\Omega }}^{\max }\cup {\mathsf{\Omega }}^{\mathrm{opt}}$, where ${\mathsf{\Omega }}^{\max }$ denotes the feasible states that all customers can be allocated the maximum data rates:

$$\begin{array}{c}{\mathsf{\Omega }}^{\max }=\left\{\mathbf{n}\in \mathsf{\Omega }:\sum _{k_{\mathrm{s}}\in {\mathcal{K}}_{\mathrm{s}}}{n}_{k_{\mathrm{s}}}{b}_{k_{\mathrm{s}}}+\sum _{k_{\mathrm{e}}\in {\mathcal{K}}_{\mathrm{e}}}{n}_{k_{\mathrm{e}}}{C}_{k_{\mathrm{e}}}\le C\right\};\end{array}$$

(2)

and ${\mathsf{\Omega }}^{\mathrm{opt}}=\mathsf{\Omega }\setminus {\mathsf{\Omega }}^{\max }$ denotes all other feasible states.

We note that two essential slicing features are illustrated in the states of ${\mathsf{\Omega }}^{\mathrm{opt}}$:

• The total system capacity is occupied, which ensures that an r.u. is not idle if it can be used to provide services with the highest quality;
• The optimization of r.u. utilization can be performed while ensuring slice isolation for guaranteed QoS.

We denote ${\mathcal{K}}_{\mathrm{v}}\left(\mathbf{n}\right)\subseteq \mathcal{K},\mathbf{n}\in \mathsf{\Omega }$ as the subset of slices violating the mandatory isolation among the slices (slice violators) in an arbitrary system state $\mathbf{n}$. Thus, a slice violator is a slice (non-TCP streaming or TCP elastic slice) that uses r.u. guaranteed to another slice (slice owner—also non-TCP streaming or TCP elastic slice) during time intervals when those r.u. are not required/claimed by the other slice due to a lack of customers.

We assume that the guaranteed capacity of a slice $k_{\mathrm{o}}\in \mathcal{K}$ (slice owner) could be utilized by slices violators $k_{\mathrm{v}}\in {\mathcal{K}}_{\mathrm{v}}\left(\mathbf{n}\right)$ in arbitrary system state $\mathbf{n}$. With this feature, QoS management and isolation among slices can be a problem in the system. Therefore, we propose an analytical solution method—the Dynamic Resource Reallocation (DRR). Through capacity share reduction, DRR can preempt customers’ service in slices violators $k_{\mathrm{v}}$, whenever required for a customer admission to slice owner $k_{\mathrm{o}}$. We assume that DRR starts its job from slice violator $k_{\mathrm{v}}$ with the lowest Priority Level (PL) and keeps up until the required capacity is gathered [10,11]. To gather capacity shares of non-TCP streaming slices violators ($k_{\mathrm{v}}\in {\mathcal{K}}_{\mathrm{s}}$), DRR utilizes service preemption [10], while for TCP elastic slices violators ($k_{\mathrm{v}}\in {\mathcal{K}}_{\mathrm{e}}$), it does so after reducing the data rate allocated to each customer in TCP elastic slices violators $k_{\mathrm{v}}$ down to the minimum [11,15]. The DRR method is analytically described in Definition 2.

A depiction of the considered K-dimensional Queueing System (QS) is given by the scheme model in Figure 1.

Let us assume that in arbitrary system state $\mathbf{n}\in \mathsf{\Omega }$, ${\mathcal{K}}^{+}\left(\mathbf{n}\right)=\left\{k\in \mathcal{K}:n_k>0\right\}$ and ${\mathcal{K}}_{\mathrm{e}}^{+}\left(\mathbf{n}\right)=\left\{k_{\mathrm{e}}\in {\mathcal{K}}_{\mathrm{e}}:n_{k_{\mathrm{e}}}>0\right\}$.

Note that each non-TCP streaming slice can be seen as ‘TCP elastic-friendly’ [16], meaning that the minimum data rate allocated to one customer equals the maximum, which makes it constant. Thus, following [11], we consider the next optimization problem with a utility function of the log type that was proposed by Kelly [17] for proportionally fair Dynamic Resource Sharing (DRS), which, in our case, coincides with max–min fairness ([18], pp. 111–204):

$$\begin{array}{c}\sum _{k\in {\mathcal{K}}^{+}\left(\mathbf{n}\right)}{W}_k\left(n_k\right)n_{k}ln\left(x_k\right)⟶\max ,\end{array}$$

(3)

$$\begin{array}{c}\mathrm{subject}\mathrm{to}\sum _{k\in {\mathcal{K}}^{+}\left(\mathbf{n}\right)}{x}_k{n}_k=C,\hfill \end{array}$$

(4)

$$\begin{array}{c}\mathrm{over}\mathbf{x}\in \mathcal{P}=\left\{\mathbf{x}={\left(x_1,\dots ,x_K\right)}^T:\underset{k\in {\mathcal{K}}^{+}\left(\mathbf{n}\right)}{\bigwedge }\left(b_k\le x_k\le C_k\right)\right\},\end{array}$$

(5)

where $W_k\left(n_k\right)=\left\{\begin{array}{cc}\hfill 1,& n_k\le N_k;\hfill \\ \hfill n_k^{-1}{N}_k,& n_k>N_k.\hfill \end{array}\right.,k\in \mathcal{K}$, denotes the weight functions [15].

We propose an analytical DRS solution method, allocating a data rate to each customer in the considered system.

Definition 1.

The DRS method is described by the following recursive sequence of numbers:

$$\begin{array}{c}{w}_k^{\left(0\right)}\left(\mathbf{n}\right)=\left\{\begin{array}{c}{n}_k{b}_k,k\in {\mathcal{K}}_{\mathrm{s}},\hfill \\ \min \left(n_k{b}_k,Q_k\right),k\in {\mathcal{K}}_{\mathrm{e}},\hfill \end{array}\right.k=\overline{1,K},\end{array}$$

(6)

$$\begin{array}{c}{w}_k^{\left(l\right)}\left(\mathbf{n}\right)=\left\{\begin{array}{c}{w}_k^{(l-1)}\left(\mathbf{n}\right)r_k^{(l-1)}\left(\mathbf{n}\right),k\in {\mathcal{K}}_{\mathrm{s}},\hfill \\ \min \left(C_k,w_k^{(l-1)}\left(\mathbf{n}\right)+{\left(C-\sum _{i=1}^K{w}_i^{(l-1)}\left(\mathbf{n}\right)\right)}^{+}{r}_k^{(l-1)}\left(\mathbf{n}\right)\right),k\in {\mathcal{K}}_{\mathrm{e}},\hfill \end{array}\right.l=\overline{1,K_{\mathrm{e}}+1},\end{array}$$

(7)

where

$$\begin{array}{c}{r}_k^{\left(0\right)}\left(\mathbf{n}\right)=\left\{\begin{array}{c}1,k\in {\mathcal{K}}_{\mathrm{s}},\hfill \\ {\left({\displaystyle \frac{n_k\mathrm{I}\left({\sum }_{i=1}^K{\left(n_i-N_i\right)}^{+}=0\right)}{{\sum }_{j\in {\mathcal{K}}_{\mathrm{e}}}{n}_j}}+{\displaystyle \frac{{\left(n_k-N_k\right)}^{+}\mathrm{I}\left({\sum }_{i=1}^K{\left(n_i-N_i\right)}^{+}>0\right)}{{\sum }_{j\in {\mathcal{K}}_{\mathrm{e}}}{\left(n_j-N_j\right)}^{+}}}\right)}^{+},k\in {\mathcal{K}}_{\mathrm{e}},\hfill \end{array}\right.\end{array}$$

(8)

$$\begin{array}{c}{r}_k^{\left(l\right)}\left(\mathbf{n}\right)=\left\{\begin{array}{c}1,k\in {\mathcal{K}}_{\mathrm{s}},\hfill \\ {\left({\displaystyle \frac{n_k}{{\sum }_{j\in {\mathcal{K}}_{\mathrm{e}}}{n}_j\mathrm{I}\left(C_j-w_j^{\left(l\right)}\left(\mathbf{n}\right)>0\right)}}\right)}^{+},k\in {\mathcal{K}}_{\mathrm{e}},\hfill \end{array}\right.\end{array}$$

(9)

given $\mathrm{I}\left(\mathit{event}A\right)=\left\{\begin{array}{cc}\hfill 1,& \mathit{if}A\mathit{occurs},\hfill \\ \hfill 0,& \mathit{otherwise},\hfill \end{array}\right.$, which is the indicator function. Let us denote the following:

• $c_k\left(\mathbf{n}\right):=w_k^{(K_{\mathrm{e}}+1)}\left(\mathbf{n}\right)$—the capacity share of slice k in arbitrary system state $\mathbf{n}\in \mathsf{\Omega }$;
• ${\sum }_{k=1}^K{c}_k\left(\mathbf{n}\right)=c_1\left(\mathbf{n}\right)+\dots +c_K\left(\mathbf{n}\right)$—the allocated capacity of the system;
• $C-{\sum }_{k=1}^K{c}_k\left(\mathbf{n}\right)$—the unallocated capacity of the system.

Explanations for Definition 1 are given by the illustrations in Figure 2.

Let us denote ${\mathbf{e}}_k,k\in \mathcal{K}$ as the k-th row of a $K\times K$ identity matrix.

Given the above DRS method, we organize the Radio Admission Control (RAC) scheme in such a way that, upon a customer’s arrival at a slice $k\in \mathcal{K}$ in arbitrary system state $\mathbf{n}\in \mathsf{\Omega }$, three paths are available:

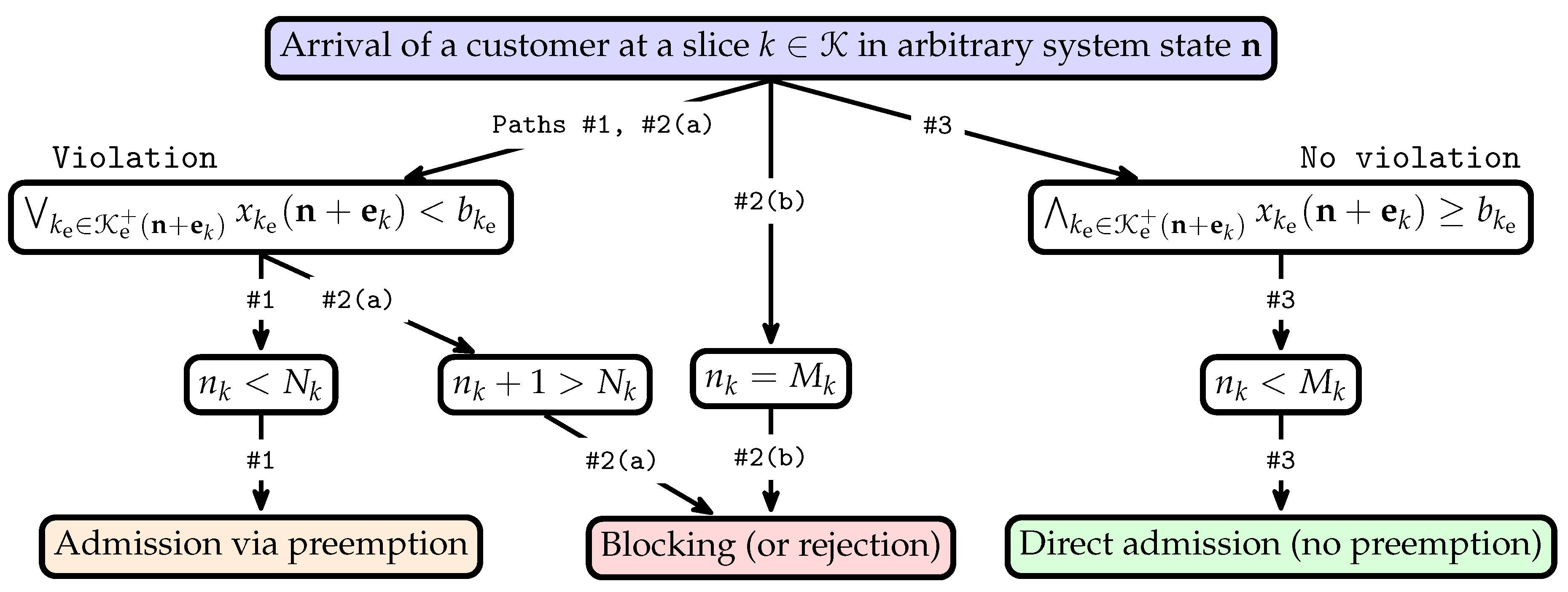
• Admission via preemption—when the data rate allocated to each customer in any of the TCP elastic slices will be less than the minimum, and the number of customers in the slice k is less than guaranteed.
• Blocking (or rejection) in two cases:

  (a)

  When the data rate allocated to each customer in any of the TCP elastic slices will be less than the minimum, and the number of customers in the slice k will be more than that guaranteed.

  (b)

  When the number of customers in the slice k is equal to the maximum.

• Direct admission (no preemption)—when the data rate allocated to each customer in each TCP elastic slice will be equal or more than the minimum, and the number of customers in the slice k is less than the maximum.

A depiction of the RAC scheme for accessing a slice $k\in \mathcal{K}$ is given in Figure 3.

Let us assume that in arbitrary system state $\mathbf{n}$, ${\mathcal{K}}_{\mathrm{v}}\left(\mathbf{n}\right)=\left\{k_{\mathrm{v}}\in \mathcal{K}:n_{k_{\mathrm{v}}}>N_{k_{\mathrm{v}}}\right\}$.

We analytically describe the DRR method governing the preemption for a customer admission to a slice owner $k_{\mathrm{o}}\in \mathcal{K}$ in arbitrary system state $\mathbf{n}\in \mathsf{\Omega }$. We denote the following:

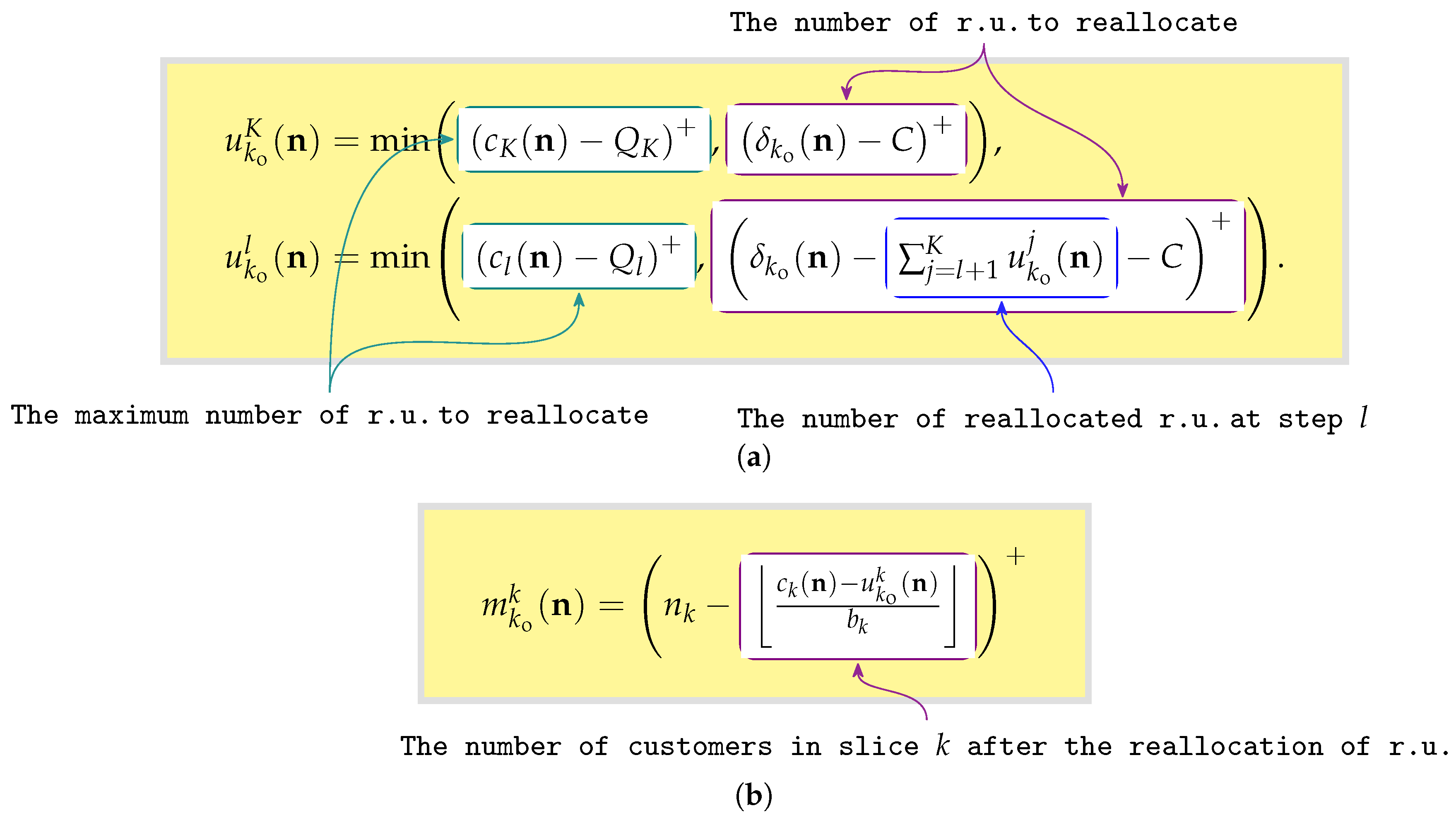
• $u_{k_{\mathrm{o}}}^{k_{\mathrm{v}}}\left(\mathbf{n}\right),k_{\mathrm{v}}\in {\mathcal{K}}_{\mathrm{v}}\left(\mathbf{n}\right)$—the capacity share of slice violator $k_{\mathrm{v}}$ to reallocate for a customer admission to slice owner $k_{\mathrm{o}}$;
• $m_{k_{\mathrm{o}}}^{k_{\mathrm{v}}}\left(\mathbf{n}\right)$—the corresponding number of customers to preempt.

Definition 2.

The DRR method is based on the following sequence of numbers in arbitrary system state $\mathbf{n}\in \mathsf{\Omega }$:

$$\begin{array}{c}{u}_{k_{\mathrm{o}}}^K\left(\mathbf{n}\right)=\min \left({\left(c_K\left(\mathbf{n}\right)-Q_K\right)}^{+},{\left({\delta }_{k_{\mathrm{o}}}\left(\mathbf{n}\right)-C\right)}^{+}\right),k_{\mathrm{o}}\in \mathcal{K},\end{array}$$

(10)

$$\begin{array}{c}{u}_{k_{\mathrm{o}}}^l\left(\mathbf{n}\right)=\min \left({\left(c_l\left(\mathbf{n}\right)-Q_l\right)}^{+},{\left({\delta }_{k_{\mathrm{o}}}\left(\mathbf{n}\right)-\sum _{j=l+1}^K{u}_{k_{\mathrm{o}}}^j\left(\mathbf{n}\right)-C\right)}^{+}\right),l=\overline{K-1,1},\end{array}$$

(11)

with ${\delta }_{k_{\mathrm{o}}}\left(\mathbf{n}\right)={\sum }_{j=1}^K{c}_j\left(\mathbf{n}\right)+b_{k_{\mathrm{o}}}$ means that we require capacity $b_{k_{\mathrm{o}}}$. Therefore, we obtain

$$m_{k_{\mathrm{o}}}^k\left(\mathbf{n}\right)={\left(n_k-⌊{\displaystyle \frac{c_k\left(\mathbf{n}\right)-u_{k_{\mathrm{o}}}^k\left(\mathbf{n}\right)}{b_k}}⌋\right)}^{+},k\in \mathcal{K}.$$

(12)

Using the DRR method for a customer admission to a slice owner $k_{\mathrm{o}}\in \mathcal{K}$ in an arbitrary system state $\mathbf{n}\in \mathsf{\Omega }$, one may note the following:

• $0\le u_{k_{\mathrm{o}}}^{k_{\mathrm{v}}}\left(\mathbf{n}\right)\le C_{k_{\mathrm{v}}}-Q_{k_{\mathrm{v}}},0\le m_{k_{\mathrm{o}}}^{k_{\mathrm{v}}}\left(\mathbf{n}\right)\le M_{k_{\mathrm{v}}}-N_{k_{\mathrm{v}}},k_{\mathrm{v}}\in {\mathcal{K}}_{\mathrm{v}}\left(\mathbf{n}\right)$—the capacity share of slice violator $k_{\mathrm{v}}$ to reallocate cannot exceed $C_{k_{\mathrm{v}}}-Q_{k_{\mathrm{v}}}$, which means that the corresponding number of customers to preempt cannot exceed $M_{k_{\mathrm{v}}}-N_{k_{\mathrm{v}}}$;
• $0\le {\sum }_{j=1}^K{u}_{k_{\mathrm{o}}}^j\left(\mathbf{n}\right)\le b_{k_{\mathrm{o}}}$—the total capacity to reallocate cannot exceed the data rate $b_{k_{\mathrm{o}}}$.

Explanations for Definition 2 are given by the illustrations in Figure 4.

Given the above-described RAC scheme and the analytical DRS and DRR methods as fundaments of the second version of the Preemption-based service Prioritization (PP2), we can move to the mathematical model construction in the next section.

3. Mathematical Model

According to the Radio Admission Control (RAC) scheme given in Section 2 and considering the Poisson flows of customers, the system behavior can be described by the K-dimensional Markov process $\mathbf{X}\left(t\right)={\left(\begin{array}{c}{X}_1\left(t\right),\dots ,X_K\left(t\right),t>0\end{array}\right)}^T$, where $X_k\left(t\right),k\in \mathcal{K}$, is the number of customers in slice k at time t over the system state space

$$\begin{array}{c}\mathcal{S}=\left\{\mathbf{n}\in \mathsf{\Omega }:\underset{k_{\mathrm{e}}\in {\mathcal{K}}_{\mathrm{e}}^{+}\left(\mathbf{n}\right)}{\bigwedge }\left(x_{k_{\mathrm{e}}}\left(\mathbf{n}\right)\ge b_{k_{\mathrm{e}}}\right),\sum _{k=1}^K{\left(n_k-M_k\right)}^{+}=0,\sum _{k=1}^K{c}_k\left(\mathbf{n}\right)\le C\right\}.\end{array}$$

(13)

We note that system state space $\mathcal{S}$ contains several subspaces ([19], pp. 66–100), ([20], pp. 2–14). For a slice $k\in \mathcal{K}$, we denote the following:

• ${\mathcal{S}}_k^{\left(1\right)}$—the state subspace for a direct admission (no preemption) of a customer;
• ${\mathcal{S}}_k^{\left(2\right)}$—the state subspace for an admission via preemption;
• ${\overline{\mathcal{S}}}_k$—the state subspace for blocking (or rejection):

  $$\begin{array}{c}{\mathcal{S}}_k^{\left(1\right)}=\left\{\mathbf{n}\in \mathcal{S}:\underset{k_{\mathrm{e}}\in {\mathcal{K}}_{\mathrm{e}}^{+}\left(\mathbf{n}+{\mathbf{e}}_k\right)}{\bigwedge }\left(x_{k_{\mathrm{e}}}\left(\mathbf{n}+{\mathbf{e}}_k\right)\ge b_{k_{\mathrm{e}}}\right),n_k<M_k\right\},\end{array}$$

  (14)

  $$\begin{array}{c}{\mathcal{S}}_k^{\left(2\right)}=\left\{\mathbf{n}\in \mathcal{S}:\underset{k_{\mathrm{e}}\in {\mathcal{K}}_{\mathrm{e}}^{+}\left(\mathbf{n}+{\mathbf{e}}_k\right)}{\bigvee }\left(x_{k_{\mathrm{e}}}\left(\mathbf{n}+{\mathbf{e}}_k\right)<b_{k_{\mathrm{e}}}\right),n_k<N_k\right\},\end{array}$$

  (15)

  $$\begin{array}{c}{\overline{\mathcal{S}}}_k=\left\{\mathbf{n}\in \mathcal{S}:\underset{k_{\mathrm{e}}\in {\mathcal{K}}_{\mathrm{e}}^{+}\left(\mathbf{n}+{\mathbf{e}}_k\right)}{\bigvee }\left(x_{k_{\mathrm{e}}}\left(\mathbf{n}+{\mathbf{e}}_k\right)<b_{k_{\mathrm{e}}}\right),n_k+1>N_k\vee n_k=M_k\right\},\end{array}$$

  (16)

  $$\begin{array}{c}\mathcal{S}={\mathcal{S}}_k^{\left(1\right)}\cup {\mathcal{S}}_k^{\left(2\right)}\cup {\overline{\mathcal{S}}}_k.\end{array}$$

  (17)

Given the above-defined state space $\mathcal{S}$ and its subspaces, the RAC function for the customers flow $k\in \mathcal{K}$ can be described as $f_k\left(\mathbf{n}\right)=\left\{\begin{array}{cc}\hfill 1,& \mathbf{n}\in {\mathcal{S}}_k^{\left(1\right)}\cup {\mathcal{S}}_k^{\left(2\right)},\hfill \\ \hfill 0,& \mathrm{otherwise}\left(\mathbf{n}\in {\overline{\mathcal{S}}}_k\right),\hfill \end{array}\right.,\mathbf{n}\in \mathcal{S}$.

Let ${\mathbf{m}}_k\left(\mathbf{n}\right):={\left(\begin{array}{c}{m}_k^1\left(\mathbf{n}\right),\dots ,m_k^K\left(\mathbf{n}\right)\end{array}\right)}^T,k\in \mathcal{K},\mathbf{n}\in \mathcal{S}$.

A depiction of the system state transition diagram between $\mathbf{n}\in \mathcal{S}$ and all its neighbors $\mathbf{n}+{\mathbf{e}}_k,\mathbf{n}-{\mathbf{e}}_k,\mathbf{n}+{\mathbf{e}}_k-{\mathbf{m}}_k\left(\mathbf{n}\right),\mathbf{n}-{\mathbf{e}}_k+{\mathbf{m}}_k\left(\mathbf{n}\right)$ is provided in Figure 5.

Let ${\mathbf{p}}^T:={\left(\begin{array}{c}p\left(\mathbf{n}\right)\end{array}\right)}_{\mathbf{n}\in \mathcal{S}}$ denote the stationary probability distribution of the Markov process $\mathbf{X}\left(t\right)$, with $p\left(\mathbf{n}\right),\mathbf{n}\in \mathcal{S}$, denoting the stationary probability that the system is in state $\mathbf{n}$. We can describe ${\mathbf{p}}^T$ using a system of equilibrium equations:

$$\begin{array}{c}p\left(\mathbf{n}\right)\left(\sum _{k=1}^K{n}_k{\mu }_k\left(\mathrm{I}\left(k\in {\mathcal{K}}_{\mathrm{s}}\right)+x_k\left(\mathbf{n}\right)\mathrm{I}\left(k\in {\mathcal{K}}_{\mathrm{e}}\right)\right)+\sum _{k=1}^K{\lambda }_k\mathrm{I}\left(\mathbf{n}\in {\mathcal{S}}_k^{\left(1\right)}\right)+\sum _{k=1}^K{\lambda }_k\mathrm{I}\left(\mathbf{n}\in {\mathcal{S}}_k^{\left(2\right)}\right)\right)=\hfill \\ =\sum _{k=1}^{K}p\left(\mathbf{n}-{\mathbf{e}}_k\right){\lambda }_k\mathrm{I}\left(\mathbf{n}-{\mathbf{e}}_k\in {\mathcal{S}}_k^{\left(1\right)}\right)+\sum _{k=1}^{K}p\left(\mathbf{n}-{\mathbf{e}}_k+{\mathbf{m}}_k\left(\mathbf{n}\right)\right){\lambda }_k\mathrm{I}\left(\mathbf{n}-{\mathbf{e}}_k+{\mathbf{m}}_k\left(\mathbf{n}\right)\in {\mathcal{S}}_k^{\left(2\right)}\right)+\\ \hfill +\sum _{k=1}^{K}p\left(\mathbf{n}+{\mathbf{e}}_k\right)\left(n_k+1\right){\mu }_k\left(\mathrm{I}\left(k\in {\mathcal{K}}_{\mathrm{s}}\right)+x_k\left(\mathbf{n}+{\mathbf{e}}_k\right)\mathrm{I}\left(k\in {\mathcal{K}}_{\mathrm{e}}\right)\right)\mathrm{I}\left(\mathbf{n}\in {\mathcal{S}}_k^{\left(1\right)}\right),\end{array}$$

(18)

with the intrinsic normalization condition ${\sum }_{\mathbf{n}\in \mathcal{S}}p\left(\mathbf{n}\right)=1$.

Due to the implementation of the Dynamic Resource Reallocation (DRR) method with service preemption, the Markov process $\mathbf{X}\left(t\right)$ is not reversible. Therefore, we can numerically compute the stationary probability distribution ${\mathbf{p}}^T$ using an iterative method ([21], pp. 103–204) ([22], pp. 106–179) [23,24,25] to solve Equation (18) rewritten as ${\mathbf{p}}^T\mathbf{A}={\mathbf{0}}^T,{\mathbf{p}}^T\mathbf{1}=1$, where $\mathbf{A}={\left(\begin{array}{c}a\left(\mathbf{n},\mathbf{s}\right)\end{array}\right)}_{\mathbf{n},\mathbf{s}\in \mathcal{S}}$ is the infinitesimal matrix (the matrix of transition intensities):

$$\begin{array}{c}a\left(\mathbf{n},\mathbf{s}\right)=\left\{\begin{array}{c}{\lambda }_k,\mathbf{s}=\mathbf{n}+{\mathbf{e}}_k,\mathbf{n}\in {\mathcal{S}}_k^{\left(1\right)},k=\overline{1,K},\hfill \\ {\lambda }_k,\mathbf{s}=\mathbf{n}+{\mathbf{e}}_k-{\mathbf{m}}_k\left(\mathbf{n}\right),\mathbf{n}\in {\mathcal{S}}_k^{\left(2\right)},k=\overline{1,K},\hfill \\ n_k{\mu }_k\left(\mathrm{I}\left(k\in {\mathcal{K}}_{\mathrm{s}}\right)+x_k\left(\mathbf{n}\right)\mathrm{I}\left(k\in {\mathcal{K}}_{\mathrm{e}}\right)\right),\mathbf{s}=\mathbf{n}-{\mathbf{e}}_k,k=\overline{1,K},\hfill \\ -\sum _{k=1}^K{\lambda }_k\mathrm{I}\left(\mathbf{n}\in {\mathcal{S}}_k^{\left(1\right)}\right)-\sum _{k=1}^K{\lambda }_k\mathrm{I}\left(\mathbf{n}\in {\mathcal{S}}_k^{\left(2\right)}\right)-\sum _{k=1}^K{n}_k{\mu }_k\left(\mathrm{I}\left(k\in {\mathcal{K}}_{\mathrm{s}}\right)+x_k\left(\mathbf{n}\right)\mathrm{I}\left(k\in {\mathcal{K}}_{\mathrm{e}}\right)\right),\mathbf{s}=\mathbf{n},\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(19)

Once the stationary probability distribution ${\mathbf{p}}^T$ is obtained, one can compute the system Key Performance Indicators (KPIs) using expressions in analytic form. We analyze the system functioning in terms of the utilization and accessibility KPIs [3]. Let us denote the following:

• $N_k,k\in \mathcal{K}$—the mean number of customers in slice k;
• $N$—the mean number of customers in the system;
• ${\mathrm{P}}_k$—the admission probability at slice k (the probability of an event ${\mathcal{S}}_k^{\left(1\right)}\cup {\mathcal{S}}_k^{\left(2\right)}$);
• $\mathrm{P}$—the admission probability at the system;
• ${\varphi }_{Q_k}$—the guaranteed capacity utilization in slice k;
• ${\varphi }_{b_{k_{\mathrm{e}}}},k_{\mathrm{e}}\in {\mathcal{K}}_{\mathrm{e}}$—the minimum data rate utilization in TCP elastic slice $k_{\mathrm{e}}$;
• ${\varphi }_C$—the total system capacity utilization:

  $$\begin{array}{c}{N}_k=\sum _{\mathbf{n}\in \mathcal{S}}p\left(\mathbf{n}\right)n_k,k\in \mathcal{K},\end{array}$$

  (20)

  $$\begin{array}{c}N=\sum _{\mathbf{n}\in \mathcal{S}}p\left(\mathbf{n}\right)\sum _{k=1}^K{n}_k=\sum _{k=1}^K{N}_k,\end{array}$$

  (21)

  $$\begin{array}{c}{\mathrm{P}}_k=\sum _{\mathbf{n}\in {\mathcal{S}}_k^{\left(1\right)}\cup {\mathcal{S}}_k^{\left(2\right)}}p\left(\mathbf{n}\right)=\sum _{\mathbf{n}\in \mathcal{S}\setminus {\overline{\mathcal{S}}}_k}p\left(\mathbf{n}\right),\end{array}$$

  (22)

  $$\begin{array}{c}\mathrm{P}=\sum _{\mathbf{n}\in \mathcal{S}\setminus {\bigcap }_{k=1}^K{\overline{\mathcal{S}}}_k}p\left(\mathbf{n}\right),\end{array}$$

  (23)

  $$\begin{array}{c}{\varphi }_{Q_k}={\displaystyle \frac{1}{Q_k}}\sum _{\mathbf{n}\in \mathcal{S}}p\left(\mathbf{n}\right)c_k\left(\mathbf{n}\right),\end{array}$$

  (24)

  $$\begin{array}{c}{\varphi }_{b_{k_{\mathrm{e}}}}={\displaystyle \frac{1}{b_{k_{\mathrm{e}}}}}\sum _{\mathbf{n}\in \mathcal{S}}p\left(\mathbf{n}\right)x_{k_{\mathrm{e}}}\left(\mathbf{n}\right),k_{\mathrm{e}}\in {\mathcal{K}}_{\mathrm{e}},\end{array}$$

  (25)

  $$\begin{array}{c}{\varphi }_C={\displaystyle \frac{1}{C}}\sum _{\mathbf{n}\in \mathcal{S}}p\left(\mathbf{n}\right)\sum _{k=1}^K{c}_k\left(\mathbf{n}\right).\end{array}$$

  (26)

Once the KPI are computed, one can move to their analysis in the next section.

4. Numerical Analysis

In this section, we provide a comparative analysis of the model developed in Section 2 and Section 3, which is the second version of the Preemption-based service Prioritization (PP2) scheme, versus the Resource Reservation (RR) [10]. We use the expression $\Delta :=\left|{\displaystyle \frac{{\mathrm{KPI}}_{\mathrm{PP}2}-{\mathrm{KPI}}_{\mathrm{RR}}}{{\mathrm{KPI}}_{\mathrm{RR}}}}\right|\times 100\%$ to denote the relative gain or loss in terms of a given KPI.

Let us consider a case example of three slices coexisting in a system ($K=3$). Let $C=100$ resource units (r.u.). For simplicity, we assume $C_k,Q_k,b_k,k=1,2,3$, are expressed in percentages of number C [26,27]. Let us regroup the input parameters in

Table 2. Input data for KPI analysis, given the uniform offered loads ${\rho }_k=\rho =\overline{1,300},k=1,2,3$.

Slice (Traffic)	Parameter	Value RR Scheme	Value PP2 Scheme	Unit
1, 2 (Streaming)	$C_1,Q_1,b_1,C_2,Q_2,b_2$	$35,35,4,35,35,3$	$40,35,4,40,35,3$	% of C
	${\mu }_1,{\mu }_2,{\lambda }_1,{\lambda }_2$	$60,30,\rho {\mu }_1,\rho {\mu }_2$		customers/time units (t.u.)
3 (Elastic)	$C_3,Q_3,b_3$	$30,30,5$	$75,30,5$	% of C
	${\mu }_3^{-1}$	10		size units (s.u.)
	${\lambda }_3$	$\rho {\mu }_1$		customers/t.u.

.

As one can guess from Table 2, we compared the classical RR scheme (Complete Partitioning, where $C_k=Q_k,k=1,2,3$, with $C_1+C_2+C_3=100\%\mathrm{of}C$) [5,6,8] and the PP2 scheme with an overlap of 5% of C for each non-TCP streaming slice $1,2$ and 45% of C for TCP elastic slice 3. The Priority Levels (PLs) were set as shown in the first column of Table 1 to make non-TCP streaming slices $1,2$ gain the most from the Dynamic Resource Reallocation (DRR) method with data rate reduction (Definition 2). Note that the PLs are used only under PP2. The comparison results for the utilization and accessibility KPIs described in Equations (20)–(26) are depicted in Figure 6, Figure 7 and Figure 8.

The main results of the comparative analysis are summarized as follows. The PP2 scheme application under the baseline parameters in Table 2 shows several gains (✓) and one loss (✗) in terms of utilization and accessibility KPI:

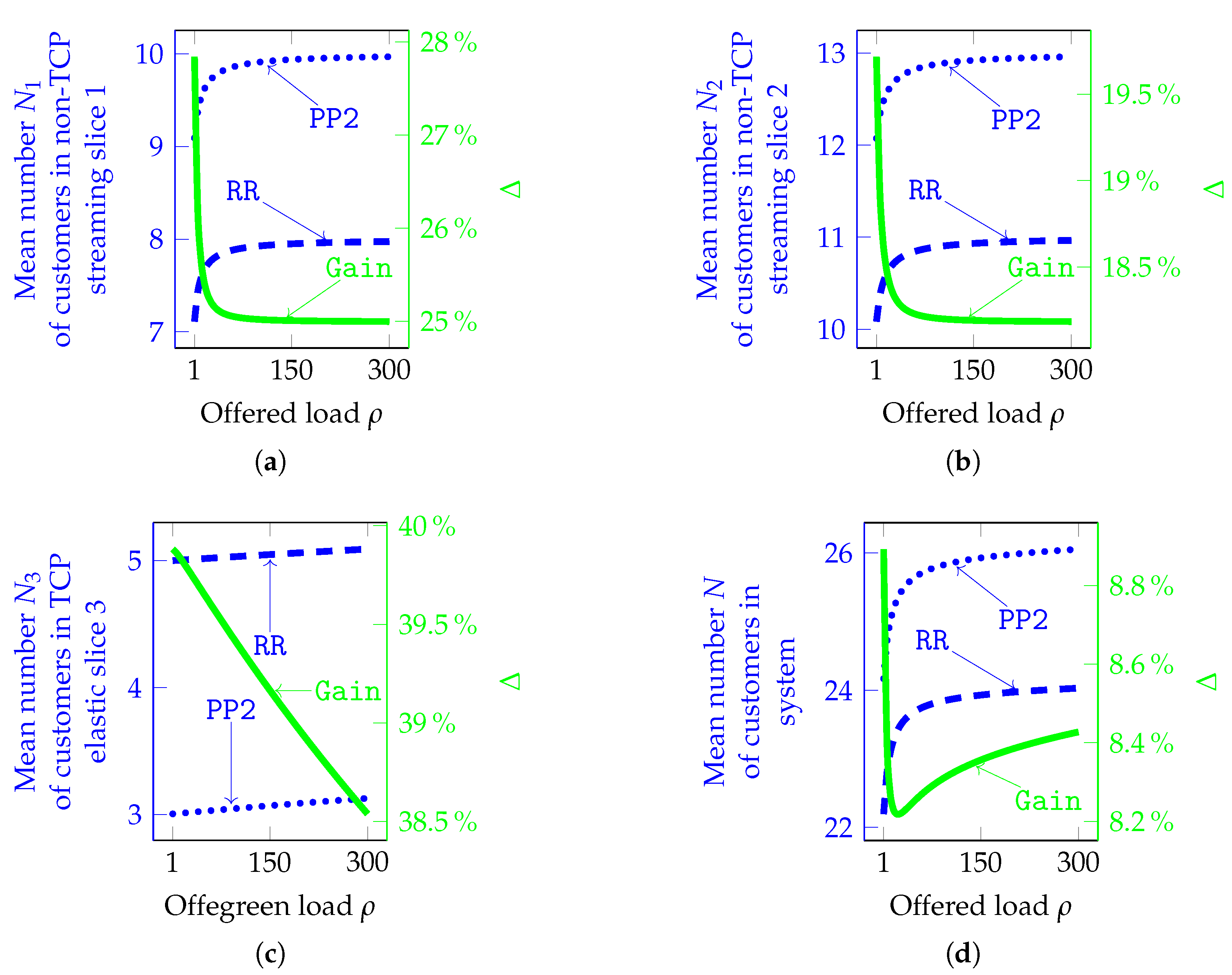
• ✓ The mean number of customers in non-TCP streaming slice 1 can increase up to 28% (Figure 6a);
• ✓ The mean number of customers in non-TCP streaming slice 2 can increase up to 19.75% (Figure 6b);
• ✓ The mean number of customers in TCP elastic slice 3 can decrease down to 40% (Figure 6c);
• ✓ The mean number of customers in system can increase up to 9% (Figure 6d);
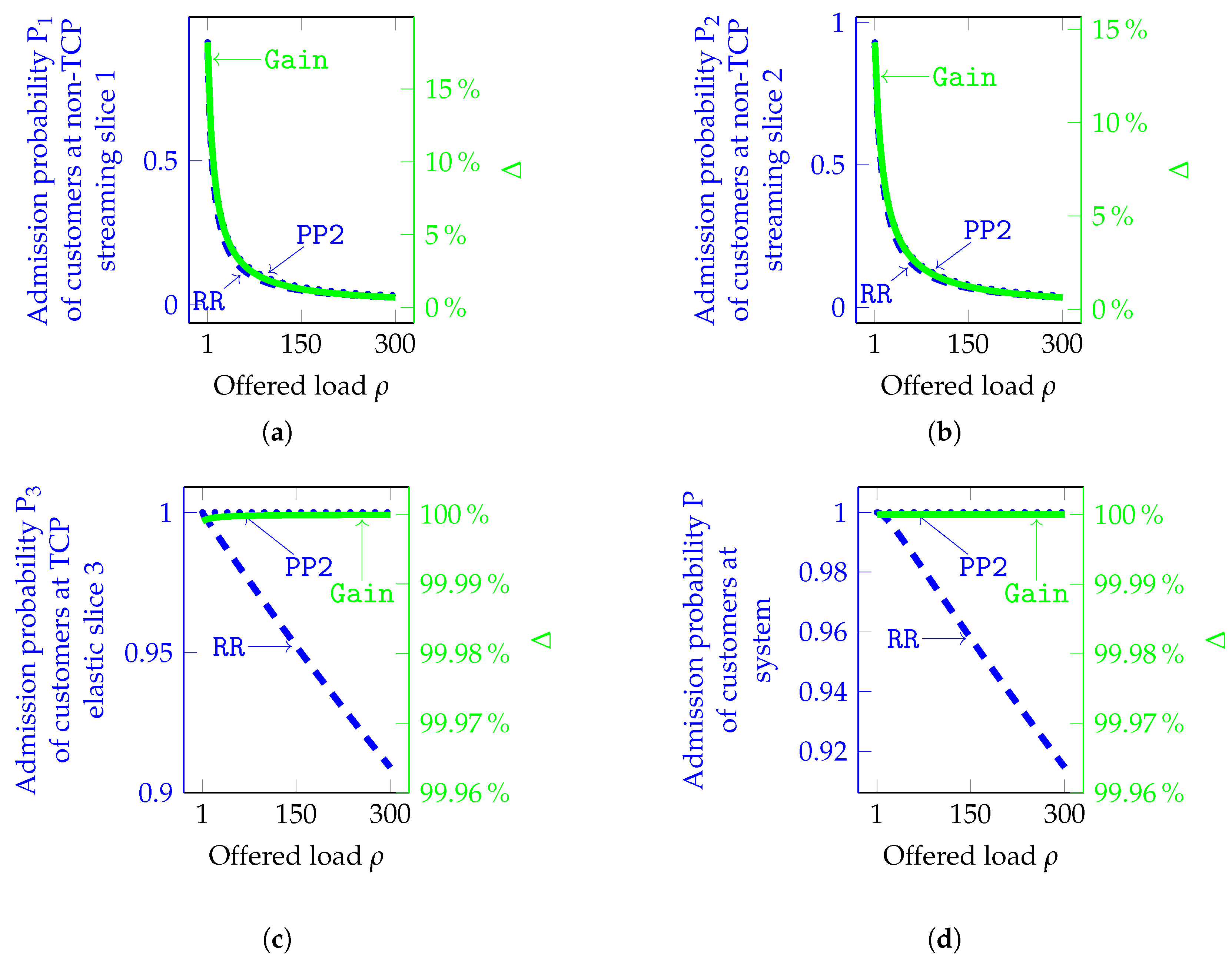
• ✓ The admission probability of customers at non-TCP streaming slice 1 can increase up to 17.5% (Figure 7a);
• ✓ The admission probability of customers at non-TCP streaming slice 2 can increase up to 15% (Figure 7b);
• ✓ The admission probability of customers at TCP elastic slice 3 can increase up to 99.999% (Figure 7c);
• ✓ The admission probability of customers at the system can increase up to 99.999% (Figure 7d);
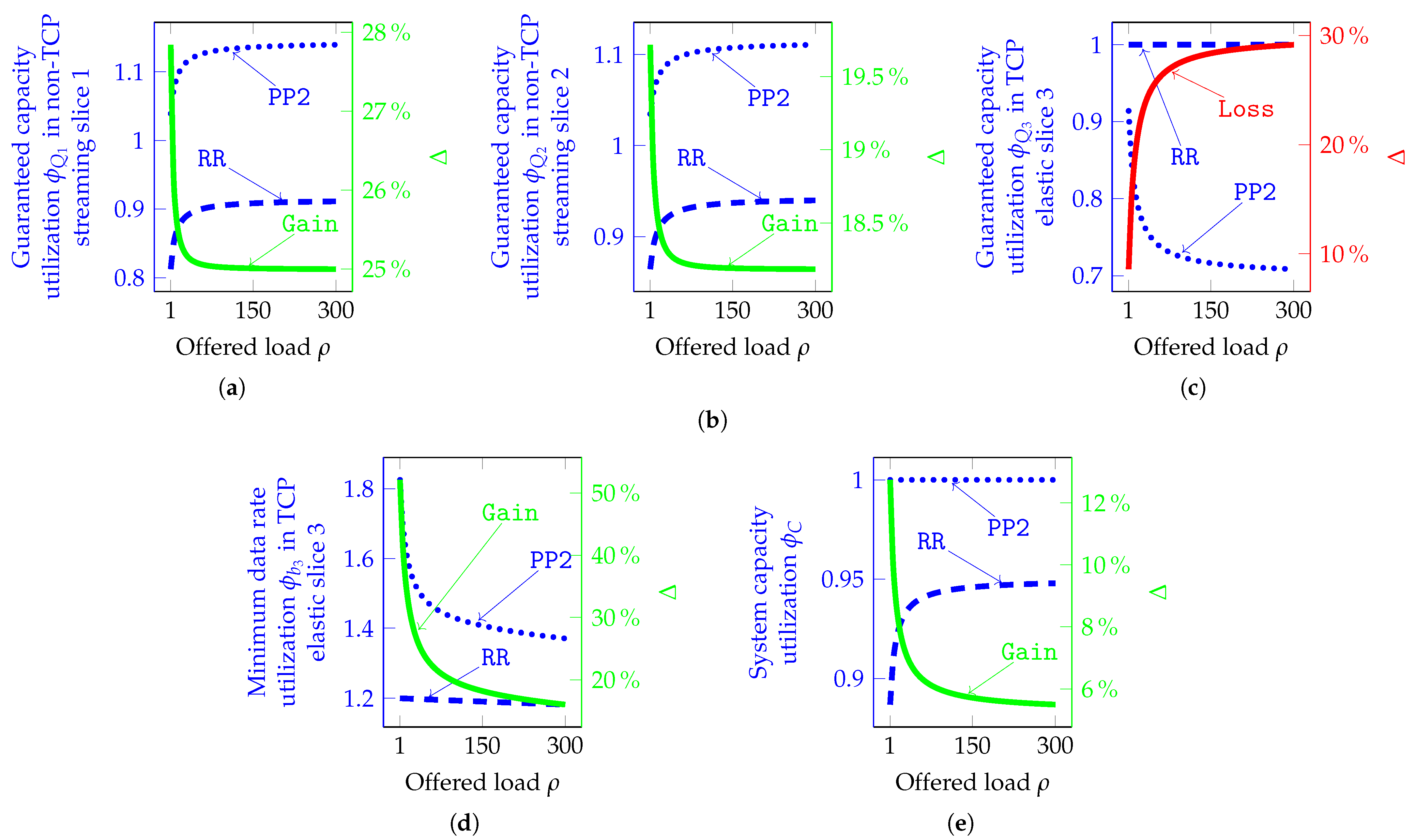
• ✓ The guaranteed capacity utilization in non-TCP streaming slice 1 can increase up to 28% (Figure 8a);
• ✓ The guaranteed capacity utilization in non-TCP streaming slice 2 can increase up to 19.75% (Figure 8b);
• ✗ The guaranteed capacity utilization in TCP elastic slice 3 can decrease down to 30% (Figure 8c);
• ✓ The minimum data rate utilization in TCP elastic slice 3 can increase up to 52% (Figure 8d);
• ✓ The total system capacity utilization can increase up to 13% (Figure 8e).

The obtained results are analyzed as follows. Under the PP2 scheme, non-TCP streaming slices $1,2$ can service more customers than guaranteed—shown by the PP2 utilization curve above the horizontal unit in Figure 8a,b, which is corroborated by the PP2 curve above the RR curve in Figure 6a,b. This is due to the DRR method reducing (down toward the minimum data rate) the data rate of each customer in TCP elastic slice 3—shown by the PP2 utilization curve below the horizontal unit in Figure 8c. Even with this, as expected by allowing an overlap of 45% of C for TCP elastic slice 3 (Table 2), each of its customers can be allocated almost the double of the minimum data rate—shown by the PP2 utilization curve above the horizontal unit and above the RR utilization curve in Figure 8d, which leads to fast service—shown by the PP2 curve below the RR curve in Figure 6c. At last, the system capacity is constantly 100% utilized—shown by the PP2 utilization curve remaining at the horizontal unit in Figure 8e.

5. Conclusions

The current research developed the second version of the Preemption-based service Prioritization (PP2) scheme—an improvement of the previous PP [10]. Unlike PP, which optimizes resource utilization among slices, with each providing non-TCP streaming service (non-TCP streaming slice), PP2 realizes the same among slices, each providing either non-TCP streaming or TCP elastic service (TCP elastic slice). PP2 is based on analytically described Dynamic Resource Sharing (DRS) and Dynamic Resource Reallocation (DRR) methods—DRS ensures fair resource allocation, while DRR reduces the capacity share of the slices violating the mandatory isolation among the slices (slice violators). The main feature of PP2 is the mutual utilization of the guaranteed capacity of all slices. Given some baseline scenario, the comparison of PP2 versus the classical Resource Reservation (RR) shows (i) an increase up to 99.999% in the admission probability at the system and (ii) a constant system capacity utilization at 100%.

As a next research topic, one can consider the application of Service Prioritization (SP) schemes and Priority Levels (PLs) on all TCP elastic slices in system capacity utilization. As another interesting subject, one can research the benefits of introducing the maximum data rate of customers with less than the overall capacity into all TCP elastic slices.

In general, unlike the previous PP scheme, PP2 can be used at various levels in smart cities, farms, and buildings to efficiently manage or supply available water, energy, etc.