Abstract
With the innovation of wireless communication technology and the surge of data in mobile networks, traditional routing strategies need to be improved. Given the shortcomings of existing opportunistic routing strategies in transmission performance and security, this paper proposes a community opportunistic routing decision-making method based on the trust model. This algorithm calculates the node’s trust value through the node’s historical forwarding behavior and then calculates the node’s trust value based on the trust model. Thresholds and trust attenuation divide dynamic security communities. For message forwarding, nodes in the security community are prioritized as next-hop relay nodes, thus ensuring that message delivery is always in a safe and reliable environment. On this basis, better relay nodes are further selected for message forwarding based on the node centrality, remaining cache space, and remaining energy, effectively improving the message forwarding efficiency. Through node trust value and community cooperation, safe and efficient data transmission is achieved, thereby improving the transmission performance and security of the network. Through comparison of simulation and opportunistic network routing algorithms, compared with traditional methods, this strategy has the highest transmission success rate of 81% with slightly increased routing overhead, and this algorithm has the lowest average transmission delay.
1. Introduction
With the advancement of 5G network communication technology, the widespread adoption of mobile devices such as smartphones and tablets has become ubiquitous in daily life [1]. Consequently, there has been a substantial surge in data generation. The escalating volume of data coupled with the progressively intricate network landscape has imposed heightened demands on both data transmission efficiency and security [2]. Traditional mobile self-organizing networks typically necessitate the pre-confirmation of a complete transmission link prior to communication. However, real-world scenarios often entail frequent mobility and uneven distribution of mobile devices, leading to challenges such as network communication disruptions [3]. Given the complexity of traditional mobile self-organizing networks in adapting to the dynamic shifts in wireless networks, researchers both domestically and internationally have shifted their focus towards the exploration of opportunistic networks [4].
As a delay-tolerant network, opportunistic networks lack fixed communication lines between nodes. Nodes within opportunistic networks employ a store-carry-forward mechanism for data forwarding, rendering the network mobile, open, and sparse [5]. Presently, opportunistic networks find application in various domains such as wildlife research [6], vehicle networking [7], and post-disaster communications [8]. Concurrently, within human society, individuals utilizing mobile devices imbue these networks with social attributes, thus forming social opportunistic networks [9].
Contemporary studies on opportunistic networks predominantly harness node contextual data, including geographical locations [10] and social networks [11], to earmark efficient next-hop relay nodes, thereby enhancing the network’s transmission capabilities. However, these investigations tend to overlook the perilous influence of malicious and selfish nodes on the network’s integrity [12,13]. Given the reliance of opportunistic networks on the proactive engagement of all nodes for data transmission [14], they are particularly prone to security breaches. This underscores the necessity of not only choosing nodes based on their transmission efficacy but also ensuring the security credentials of these next-hop relay nodes.
Moreover, the prevailing approach within opportunistic network research is to prioritize nodes with the highest transmission efficiency for relay purposes to achieve optimal local transmission outcomes [15]. This strategy neglects the potential strain on central nodes, which, when overly relied upon for data forwarding, face considerable storage pressure [16]. This, in turn, can lead to data congestion and the rapid depletion of node energy, necessitating further exploration into opportunistic network data transmission strategies. Opportunistic network forwarding requires nodes to cache data until an encounter with the destination node occurs [17]. Nonetheless, the mobile devices comprising these networks are typically constrained by limited computational power, storage capacity, and energy, frequently resulting in buffer overflows and data loss [18]. Particularly, flooding-based routing algorithms are prone to causing network congestion, node depletion, and delays in data transmission [19]. Thus, identifying strategies to alleviate backbone network transmission pressures and prolong network longevity, while ensuring the selection of efficient and secure relay nodes, presents a novel challenge in the realm of opportunistic networks.
In response to the aforementioned challenges, this paper proposes a secure community algorithm based on the trust model. The algorithm computes node trust values based on historical interaction records, reflecting node performance within the opportunistic network. These records facilitate the prediction of subsequent node forwarding behavior. Subsequently, dynamic security communities are delineated using trust thresholds and decay. During message forwarding, nodes prioritize relay nodes within security communities, considering node centrality, remaining cache space, and energy levels. This selection of secure and efficient relay nodes alleviates network congestion, prolongs node lifespan, and enhances data transmission efficiency within the opportunistic network, thereby improving network service quality and user experience.
This study contributes as follows:
- (1)
- This study introduces the notion of delineating secure communities grounded in node trust, coupled with a delineated methodology for computing node trust derived from historical interactions. It further advances the segmentation of dynamic secure communities predicated on trust thresholds and trust decay, aiming to fortify the efficacy of community segmentation and facilitate secure data transmissions.
- (2)
- We propose a novel routing algorithm that determines next-hop relay nodes by leveraging secure community divisions, node centrality, residual cache capacity, and remaining energy levels. This algorithm enhances data transmission success rates, alleviates network congestion, and prolongs network longevity.
- (3)
- Simulation experiments substantiate that the secure community opportunistic routing algorithm, underpinned by the trust model, surpasses conventional algorithms in network data transmission, showcasing a superior transmission success rate and diminished transmission delays.
2. Related Works
The inception of opportunistic networks can be traced back to early delay-tolerant networks [20], first conceptualized at EXOR in 2005 [21]. Presently, both domestic and international academic research endeavors pertaining to opportunistic networks primarily delve into their social characteristics [22]. The proposed algorithm significantly enhances the data transmission performance within opportunistic networks. Subsequently, the following section will delve into various existing opportunistic routing algorithms.
In opportunistic networks, routing algorithms are commonly categorized into non-context-aware and context-aware routing algorithms [23]. Non-context-aware routing algorithms often resort to flooding for data transmission, resulting in the proliferation of redundant message copies within the network, consequently leading to elevated message forwarding delays and increased energy consumption [24]. The Epidemic [25] algorithm stands as a classic non-context-aware routing algorithm, modeled after the spread of infectious diseases. Although effective in reducing network transmission delay under optimal resource conditions, the Epidemic algorithm struggles to deliver favorable outcomes in natural environments due to network congestion with increasing node density.
To address the limitations of the Epidemic algorithm, the Spray and Wait algorithm was introduced, fixing the number of message copies N at the outset [26]. This algorithm comprises two stages: the spray stage, where the source node broadcasts N copies of the message, and the wait stage, where nodes carrying message copies wait in the network. However, the challenge lies in setting the optimal number of message copies, as too few copies may hinder message delivery, while an excessive number may exacerbate forwarding delays and energy consumption.
Context-aware routing algorithms select the next-hop relay node based on user contextual information, such as geographical location, historical data, and social relationships [27]. Nonetheless, these algorithms often necessitate extensive information and intricate computations, contributing to additional transmission delays and energy consumption. In BubbleRap [28], nodes are segregated into different communities, with preference given to nodes within the same community as the destination node when selecting the next-hop relay node. However, over time, this algorithm may witness the formation of large, encompassing communities, diminishing the significance of community division. Furthermore, prioritizing nodes with high centrality for data forwarding may lead to node congestion and rapid energy depletion.
Wu et al. [29] proposed the Edge Collaborative Cache Trust Community (ECTC) routing algorithm, which employs comprehensive trust indicators to partition trust communities. This algorithm utilizes explicit labels for direct trust and calculates node similarities through inter-node paths for indirect trust. Trusted relay nodes assist in cache cooperative transmission by trusting neighbor nodes (edge nodes) with surplus cache space within the community. Simulation experiments validate the efficacy of the Edge Collaborative Cache Trust Community (ECTC) routing algorithm in improving message transmission success rates and reducing network overhead.
Table 1 provides a comprehensive analysis of existing relevant research. Building upon the exploration of the aforementioned methodologies, this paper introduces a more effective approach to achieve secure and efficient data transmission within opportunistic networks.

Table 1.
Summary of related work.
3. Trust Community Routing Algorithm
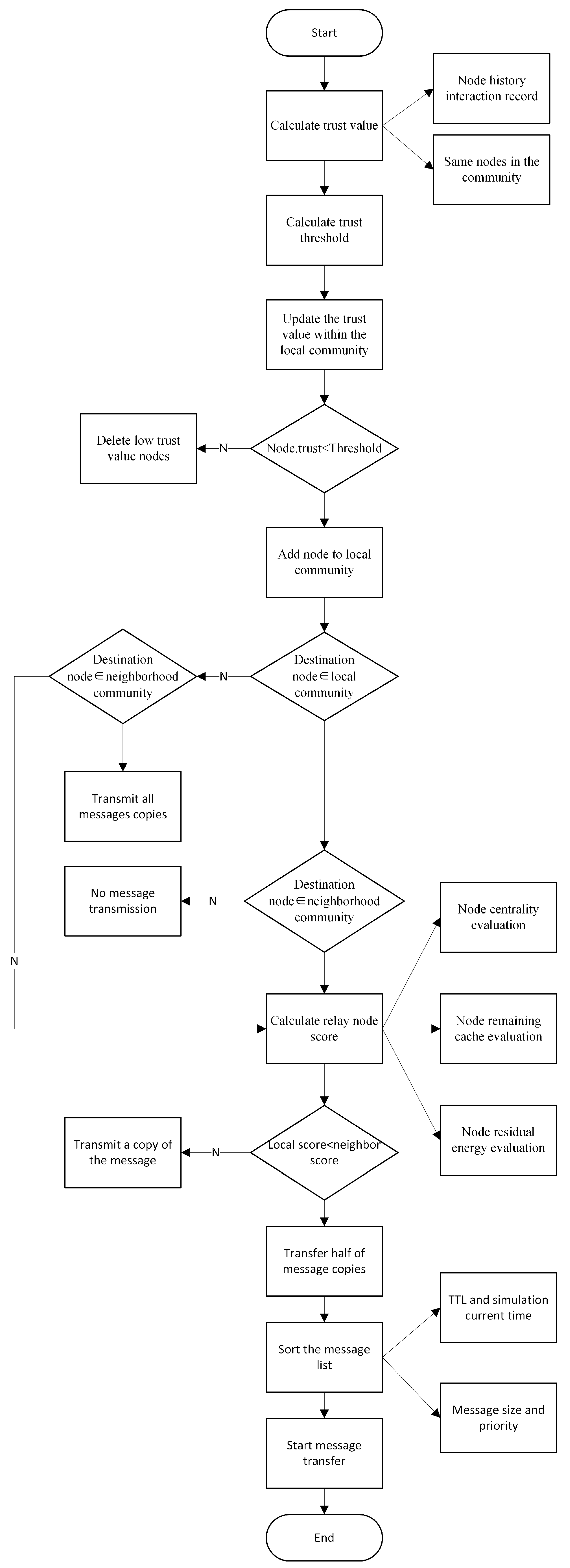
In this section, we present a detailed exposition of the Secure Community Opportunistic Network algorithm based on the trust model. This algorithm primarily encompasses three pivotal steps: (1) calculation of node trust degree; (2) construction of the security community; (3) selection of forwarding nodes. Initially, nodes involved in this study locally store historical interaction records, enabling prediction of subsequent node forwarding behavior and computation of the node’s direct trust value. The node’s indirect trust value is then determined by assessing the identical nodes within the node community, culminating in the derivation of the node’s comprehensive trust value. Subsequently, a trusted community is established based on the cumulative trust value, with the maintenance of trust communities facilitated through periodic updates employing trust value decay. Finally, leveraging the concepts of local and global centrality in conjunction with the node’s residual energy and cache space, relay nodes are meticulously selected from neighboring nodes, facilitating sequential data transmission in accordance with message priority.
The calculation of node trust value forms the foundational underpinning for constructing a secure community, ensuring message transmission predominantly occurs within safe communities. Moreover, the selection of relay nodes within the security community based on high centrality, residual energy, and cache space expedites data transmission while mitigating network congestion. The iterative coordination of the three algorithms encompassing node trust value calculation, trust community division, and relay node selection collectively contribute to achieving efficient data transmission.
3.1. Node Trust Degree Measurement
In an opportunistic network, message transmission relies on the store-carry-forward mechanism, necessitating active participation and collaboration among network nodes. However, ensuring the absence of malicious nodes among these entities is imperative to avert the risks of network attacks. Thus, the assessment of node trustworthiness and the selection of trusted nodes form the cornerstone of secure message transmission. To this end, this paper advocates leveraging the historical forwarding behavior of nodes to quantify node trust, thereby identifying reliable relay nodes conducive to safe transmission. The calculation of node trust entails a comprehensive consideration of both direct and indirect trust. Direct trust is evaluated based on the node’s historical interaction records, while indirect trust pertains to those of other nodes within the local community.
Definition 1.
Node trust.
This parameter indicates the potential for neighboring nodes to assist in the successful forwarding of messages by the focal node. For any pair of nodes, A and B, within the opportunistic network, the trust value between nodes is computed as depicted in Formula (1):
among them, represents the comprehensive trust degree of node A towards node B, denotes the direct trust, signifies the indirect trust, and serves as the weight factor.
Definition 2.
Direct Trust.
This paper employs the Bayesian trust model to forecast the subsequent forwarding behavior of nodes. The Bayesian trust model conceptualizes trust as a random variable following the distribution, leveraging the node’s historical interaction records as the prior distribution, and computing the posterior distribution to predict the node’s future forwarding behavior. The parameter in the distribution is determined by the number of successful historical node interactions, while the parameter is influenced by the number of failed interactions. The expectation of this distribution is then utilized to depict the Bayesian trust of the node. Bayesian trust offers an intuitive representation of a node’s message forwarding success rate and future forwarding tendencies. A higher value indicates a node’s greater capability in forwarding messages. The calculation formula is articulated as follows:
where represents the number of successful node interactions, and represents the number of failed node interactions. By utilizing Formula (2), this study thoroughly examines the node’s three historical interaction records to compute the node’s direct trust degree. The calculation formula for direct trust is expressed as follows:
where is calculated by incorporating the historical interaction records between node B and all other nodes in the network into Formula (2). This value can effectively depict the overall forwarding behavior of node B within the social opportunistic network. is computed by integrating the historical interaction record of node B receiving messages sent by node A into Formula (2), thus reflecting node B’s proficiency in receiving messages from node A. Similarly, is derived from the historical interaction records of node B forwarding messages received from node A, illustrating node B’s capability in successfully forwarding messages from node A. The coefficients , , and represent different weight coefficients, whose values can be adjusted according to various network environments. For instance, in a network that prioritizes the overall behavior of nodes, the value of can be elevated. The direct trust degree comprehensively evaluates the historical forwarding behavior of the relay node towards other nodes in the network, its reception behavior of messages from the designated node, and its transmission behavior of messages provided by the designated node. Such a comprehensive evaluation enables a more accurate prediction of subsequent forwarding behavior within social opportunistic networks.
Definition 3.
Indirect trust.
In social opportunistic networks, aside from evaluating the node’s own trustworthiness towards neighboring nodes, it is imperative to also account for the trustworthiness of nodes within the node’s local community towards neighboring nodes. This study proposes utilizing the average trust value of the same node within the node’s local community as the node’s indirect trust value. The calculation formula is delineated as follows:
where n represents the count of identical nodes in the local community of both node A and node B, while signifies the comprehensive trust value of node A towards the identical node j within the local community.
3.2. Node Community Division
Partitioning security communities according to node trust values enables nodes to prioritize selecting trusted nodes within these communities as next-hop relay nodes during information transmission, thereby enhancing the security of message delivery. Given the inability of nodes within opportunistic networks to ascertain the global network status and to mitigate the storage burden arising from excessive community information retention, this study advocates for nodes to solely maintain a local community table locally. Furthermore, dynamic trust thresholds are employed for community organization, calculated by averaging the trust values of all neighboring nodes. The calculation formula is articulated as follows:
where m represents the number of links established by node A, and denotes the comprehensive trust value of node A towards the neighbor node i at the opposite end of the link.
Additionally, as time progresses, nodes persist in adding other network nodes to their local communities. With the expansion of a node’s local community table, the significance of community division decreases. When a node’s local community encompasses most of the network nodes, community division becomes irrelevant. To tackle this issue, this paper adopts a decay function to update the trust values of nodes in the local table and eliminates nodes below the trust threshold to mitigate community redundancy. The decay function for node trust value is detailed as follows:
where denotes the most recent comprehensive trust value of node A concerning node B, signifies the current system time, and denotes the time of the last trust value update. denotes the decay function.
By employing dynamic trust thresholds and trust value attenuation, we can establish robust security communities, mitigating the formation of overly expansive communities within social opportunistic networks and guaranteeing the efficacy of community segmentation. The steps for dividing the security community are outlined as follows:
- Step 1:
- The node maintains two sets locally: the acquaintance set and the local community. Upon encountering other nodes in the network, it initiates the calculation of the node’s trust value and determines the corresponding trust threshold.
- Step 2:
- Nodes exceeding the trust threshold are incorporated into the node’s acquaintance set and local community.
- Step 3:
- The node traverses its acquaintance set, computes the trust value for each neighboring node within this set using the transitive trust formula, and includes nodes surpassing the trust threshold into its local community.
- Step 4:
- The trust value gradually diminishes over time. Prior to data transmission, the node updates the trust value of nodes within both the acquaintance set and the local community. Nodes falling below the threshold are subsequently removed from both sets.
3.3. Routing and forwarding Strategy
Nodes within the security community exhibit a high level of trust. To enhance the efficiency of message transmission while ensuring the security of node communication, it becomes imperative to designate nodes with stronger forwarding capabilities from the security community as the subsequent relay nodes. This study opts for nodes with elevated centrality, determined through both global and local centrality concepts, as the subsequent relay nodes.
Definition 4.
Node centrality.
This paper utilizes the node’s neighbor count to compute its global centrality (Algorithm 1). A higher global centrality implies increased likelihood of interaction with other nodes, thereby providing more opportunities for message forwarding. Local centrality, on the other hand, is determined by the number of neighbor nodes belonging to the local community. Greater local centrality indicates a heightened chance of encountering nodes within the local community, facilitating easier message forwarding to the destination node within that community. The calculation formula for node centrality is articulated as follows:
where represents the global centrality of node A, denotes the local centrality of node A, signifies the neighboring node of node A, encompasses all nodes in the social opportunistic network, and denotes the neighboring nodes belonging to the local community of node A.
| Algorithm 1: Community division |
 |
However, over-reliance on high-centrality nodes for message transmission may lead to node buffer overflow and message transmission failure. Simultaneously, due to the small size and low-energy characteristics of wireless devices, depending excessively on high-centrality nodes for message transmission may rapidly deplete node energy, eventually resulting in node failure and network collapse. Therefore, in addition to considering node centrality, this paper comprehensively incorporates node residual energy and node residual cache to select the next hop relay node. The selection formula for the next hop relay node is as follows:
where represents the score of the relay node. A higher score indicates a greater likelihood for the node to be selected as the next-hop relay node. denotes the global centrality, while signifies the local centrality of node A. denotes the remaining cache of the node, whereas represents the maximum cache capacity of the node. represents the remaining energy of the node, and indicates the maximum energy of the node. designates the message’s destination node, and characterizes the local community of the relay node. The coefficients , , and are weight factors adjustable to meet the requirements of the network environment.
To further mitigate the risk of buffer overflow and potential message loss during message forwarding, this paper introduces additional adjustments to the message queue order based on priority. Messages are then forwarded according to their assigned priority levels. The calculation formula for determining message priority is provided below:
where represents the priority of message forwarding, denotes the current simulation time, indicates the message creation time, and represents the message’s life cycle. A larger value of indicates a longer forwarding time in the network, approaching the message’s expiration time, thereby necessitating prioritized delivery. denotes the priority label of the message itself, while indicates the message size. A higher value of corresponds to a higher priority for messages with a unit size. The weight coefficients and are utilized in the algorithm.
The message-forwarding process of the routing algorithm proceeds as follows:
- Step 1:
- If the neighbor node’s local community does not include the message’s destination node, and this node’s local community contains the message’s destination node, the message will not be forwarded.
- Step 2:
- If the neighbor node’s local community contains the message’s destination node, while this node’s local community does not, all messages will be transmitted to the neighbor node.
- Step 3:
- If neither the neighbor node’s local community nor this node’s local community includes the message’s destination node, compare the Scorerel of the neighbor node and this node using Formula (9). If the neighbor node’s Scorerel is higher, half of the messages will be transmitted; otherwise, one will be subtracted.
- Step 4:
- If both the neighbor node’s local community and this node’s local community contain the message’s destination node, compare the Scorerel of the neighbor node and this node using Formula (10). If the neighbor node’s Scorerel is higher, half of the messages will be transmitted; otherwise, one will be subtracted.
- Step 5:
- During message transmission, prioritize messages in the message queue based on their , with higher priority messages being forwarded first.
Figure 1 delineates the operational workflow of the Secure Community Trust Model (SCTM) routing algorithm. Initially, the algorithm deduces the trust values of neighboring nodes by examining historical interaction records and interactions with identical nodes within the local community. Subsequently, it computes the trust threshold for the security community and purges nodes from the local community that fall below this trust threshold following an update of the community nodes’ trust values. After the inclusion of nodes surpassing the trust threshold into the local community, the Algorithm 2 proceeds to select relay nodes and allocate message copies, taking into consideration the node’s community affiliation, centrality, remaining cache, and residual energy. The process culminates with the initiation of message transmission, preceded by the organization of the message queue.
| Algorithm 2: Forwarding strategy |
 |
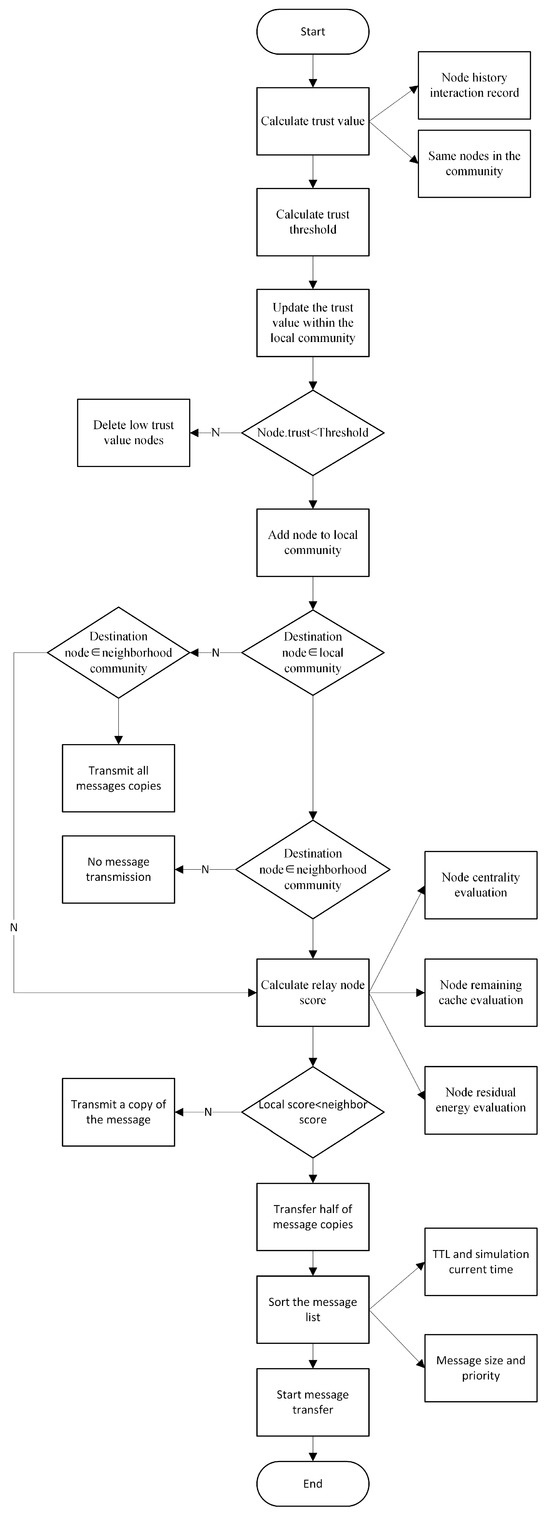
Figure 1.
Algorithm flowchart.
During the preparation of this work the author used GPT−4 in order to polish the language of the paper. After using this tool/service, the author reviewed and edited the content as needed and takes full responsibility for the content of the publication.
4. Performance Evaluation
This study employs THE ONE simulator to conduct experiments on the Secure Community Opportunistic Network (SCTM) routing algorithm based on the trust model. THE ONE simulator, written in Java, is specifically designed for simulating opportunistic networks. The TCR algorithm is evaluated based on three key indicators: network transmission success rate, average transmission delay, and routing overhead. Additionally, traditional routing algorithms, including Direct (direct transmission algorithm), Epdic (Epidemic algorithm), Spray (Spray and Wait algorithm), and the community routing algorithm BubbleRap, were selected for comparative analysis.
The experimental setup includes an AMD Ryzen 7 5800H CPU, NVIDIA GeForce RTX 3060 GPU, 16 GB × 4 DDR4 memory, and Windows 10 Home Basic 64 bit operating system. Table 2 illustrates the simulation parameters configured by THE ONE simulator for the experiment. The simulated map used in this study is derived from the actual map of Helsinki within THE ONE simulator. The simulation duration is set to 6 h, covering an area of 4500 m × 3400 m. A total of 1000 nodes are involved in the simulation, utilizing the SHORTESTPATHMAPBASEDMOVEMENT node motion model with movement speeds ranging from 0.8 m/s to 1.8 m/s, and a maximum transmission range of 10 m for each node. The message size varies from 500 Kb to 1 Mb, with a data packet sending interval of 25S to 35S. The Time To Live is set to 300 M, and each message is replicated 10 times.

Table 2.
Simulation parameters.
To compare and analyze the performance of five routing algorithms—SCTM, Direct, Epdic, Spray, and BubbleRap—in opportunistic networks, this study will evaluate them based on three key indicators: transmission success rate, average transmission delay, and routing overhead.
Transmission success rate (deliveryratio): This parameter denotes the ratio of successfully delivered messages during transmission to the total number of messages generated by the source node within the network.
Transmission delay (latency_avg): This parameter represents the average transmission time needed for messages to traverse from the source node to the destination node within the network. A smaller value indicates a more robust transmission capability of the routing algorithm.
Routing overhead (overhead): This parameter denotes the ratio of messages forwarded by nodes in the network to the total number of successfully transmitted messages. A higher routing overhead implies increased costs for nodes in accomplishing message forwarding and greater resource utilization.
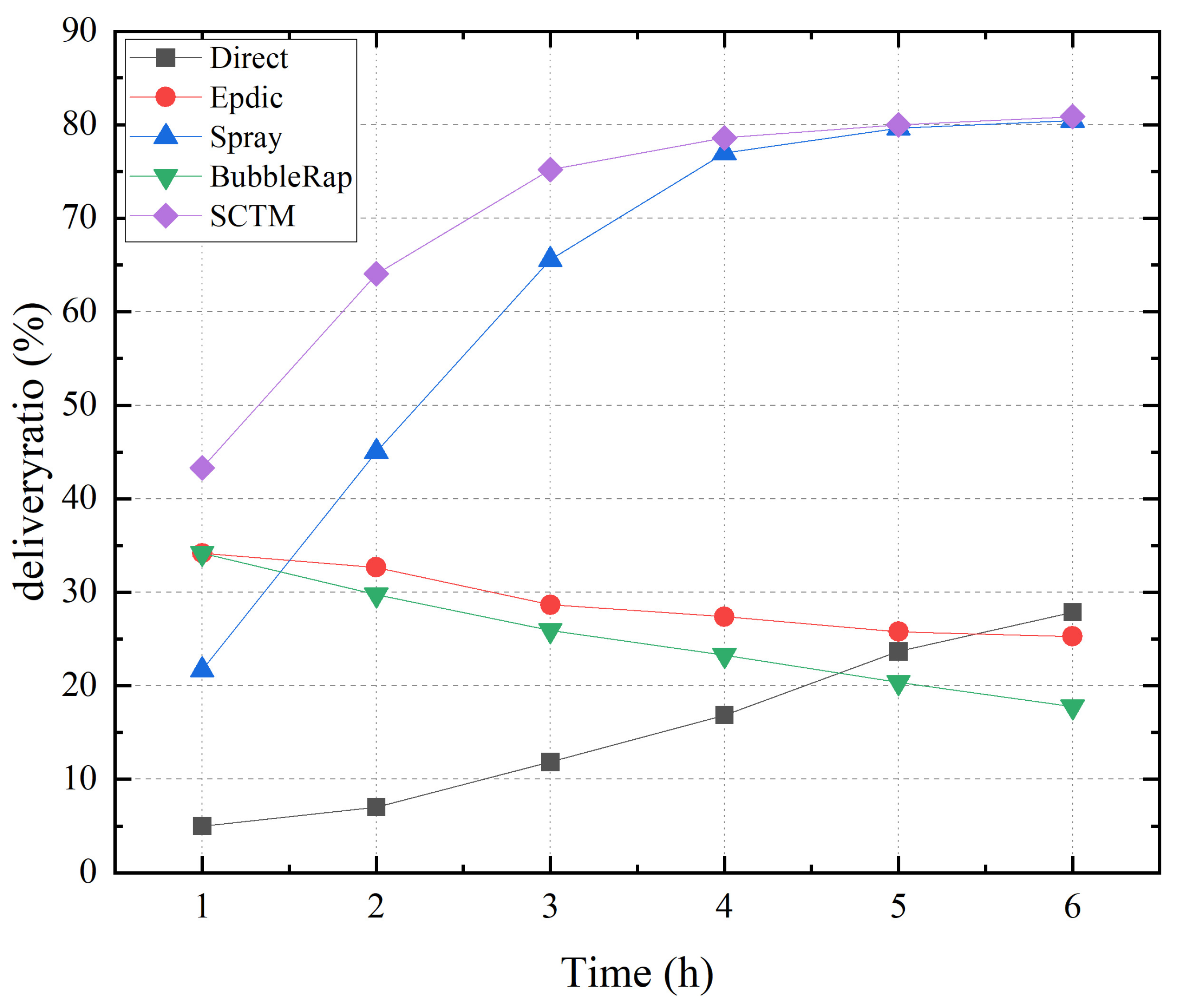
Figure 2 illustrates the correlation between transmission success rate and simulation time for the Direct, Epdic, Spray, BubbleRap, and SCTM routing algorithms. The SCTM algorithm, employing community division and selection of nodes with superior forwarding behavior and higher centrality as next-hop relay nodes, achieves the highest transmission success rate, peaking at approximately 81%. Conversely, the Epdic and BubbleRap algorithms, employing flooding forwarding strategies, experience a decline in transmission success rate over time due to the accumulation of redundant messages in the network, resulting in increased message losses. The Spray algorithm, employing a limited copy forwarding strategy, outperforms the Epdic and BubbleRap algorithms in transmission success rate. Meanwhile, the Direct algorithm, solely delivering messages to the destination node, exhibits a low and gradually increasing forwarding success rate over time.
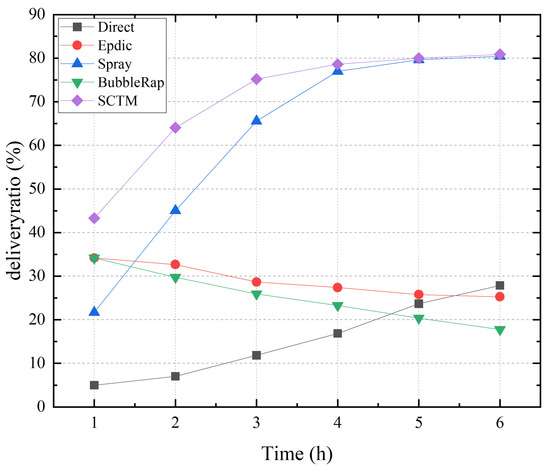
Figure 2.
Deliveryratio and simulation time.
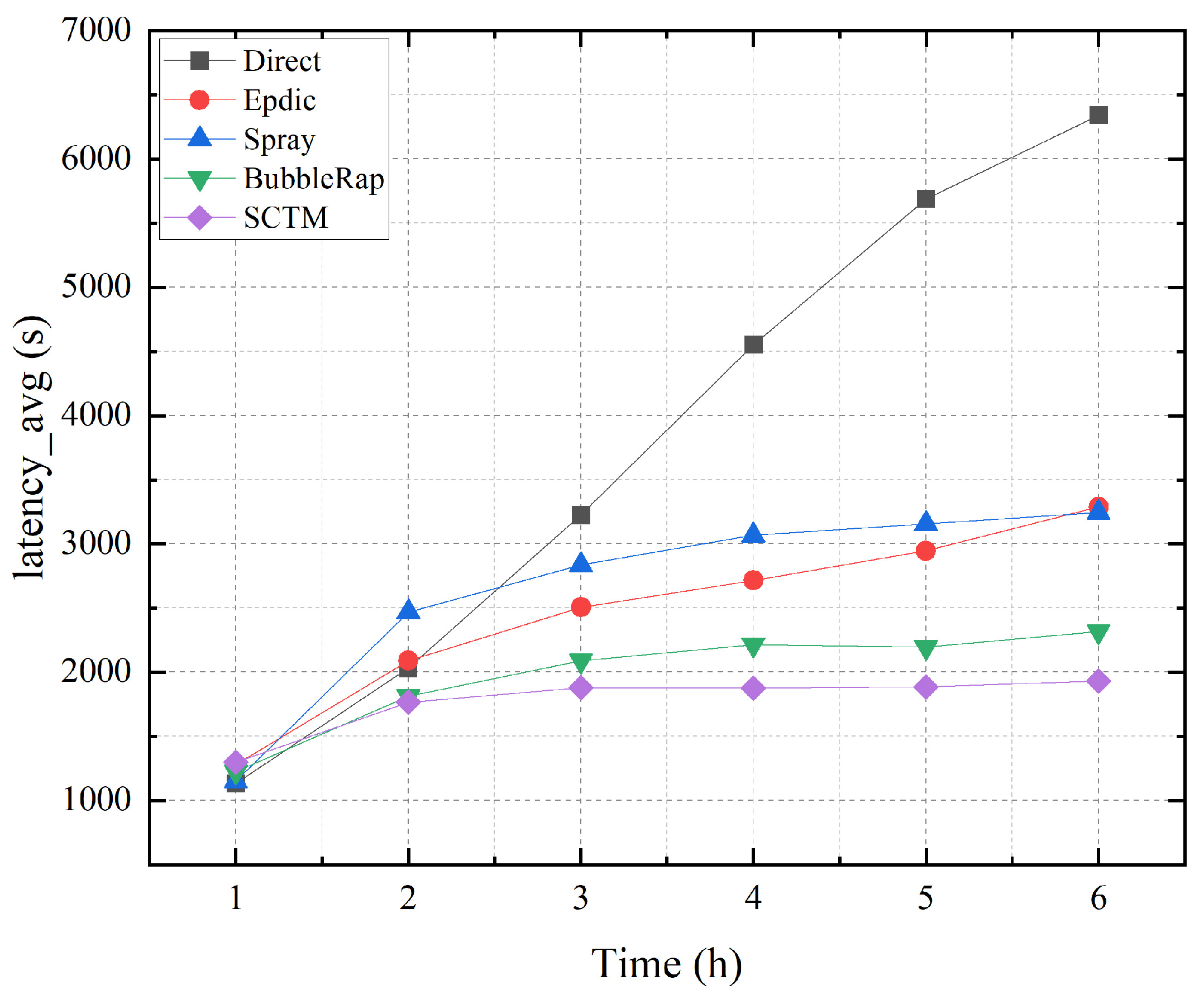
Figure 3 illustrates the average transmission delay observed with the Direct, Epdic, Spray, BubbleRap, and SCTM routing algorithms. Initially, the forwarding of data packets in the network is random, leading to varied delays. However, as time progresses, the average transmission delay gradually stabilizes. Notably, the Direct algorithm exhibits the highest transmission delay due to its inherent characteristic of exclusively routing data to the destination node. In contrast, algorithms such as Epdic and BubbleRap, characterized by flooding forwarding strategies, demonstrate relatively lower average delays in successfully transmitted data packets. Moreover, owing to community division, the BubbleRap algorithm outperforms the Epdic algorithm in terms of transmission delay. Nonetheless, with the increasing number of data packets circulating in the network, the forwarding delay of these algorithms gradually escalates. On the other hand, the Spray and SCTM algorithms employ copy forwarding limitations, resulting in consistently stable average transmission delays. Particularly, the SCTM algorithm leverages historical interaction records to establish trust-based communities, ensuring efficient selection of next-hop relay nodes while considering node centrality. Consequently, the SCTM algorithm achieves the lowest average transmission delay, affirming the efficacy of community division in optimizing network performance.
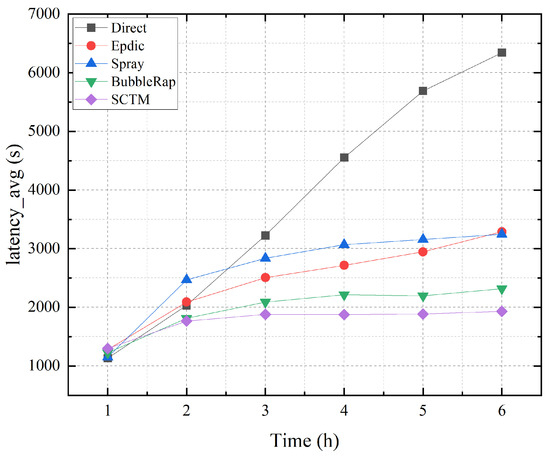
Figure 3.
Latency_avg and simulation time.
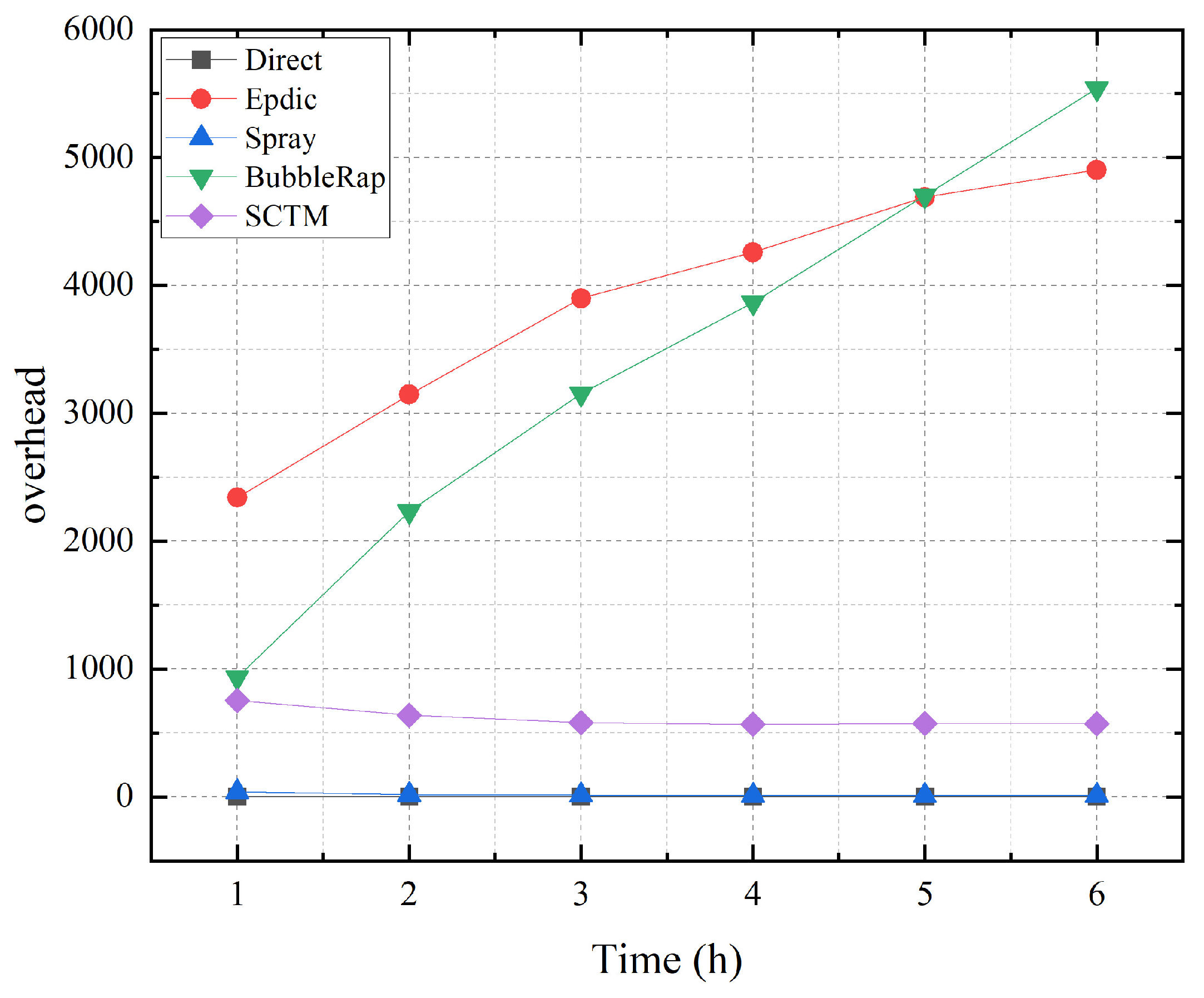
As depicted in Figure 4, the Direct algorithm exclusively routes data directly to the destination node, resulting in a routing overhead of 0. Conversely, the Spray algorithm’s forwarding behavior is determined by the number of message copies held by each node. When a node holds only one message copy, it ceases forwarding before reaching the destination node. Meanwhile, the Epdic and BubbleRap algorithms consistently exhibit high routing overheads owing to their flooding forwarding strategies. In contrast, the SCTM algorithm employs a community-based approach to limit copy forwarding. Despite also restricting the number of message copies, the SCTM algorithm stands apart from the Spray algorithm by considering additional factors such as node community, centrality, remaining cache, and energy levels. Consequently, the SCTM algorithm selects more optimal relay nodes for message forwarding.
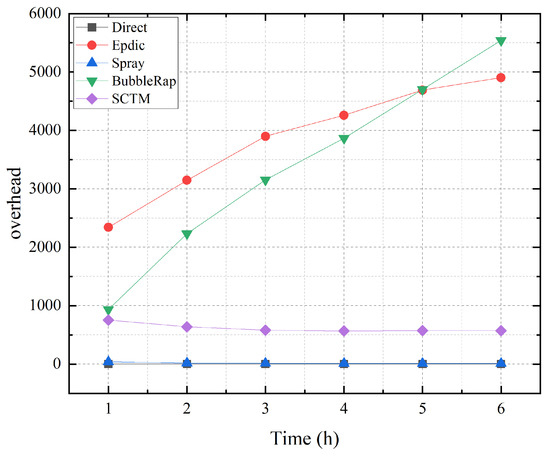
Figure 4.
Overhead and simulation time.
In social opportunistic networks, the cache size of nodes significantly influences routing algorithm performance. Hence, this study conducts a comparative experimental analysis by adjusting node cache sizes to explore their impact.
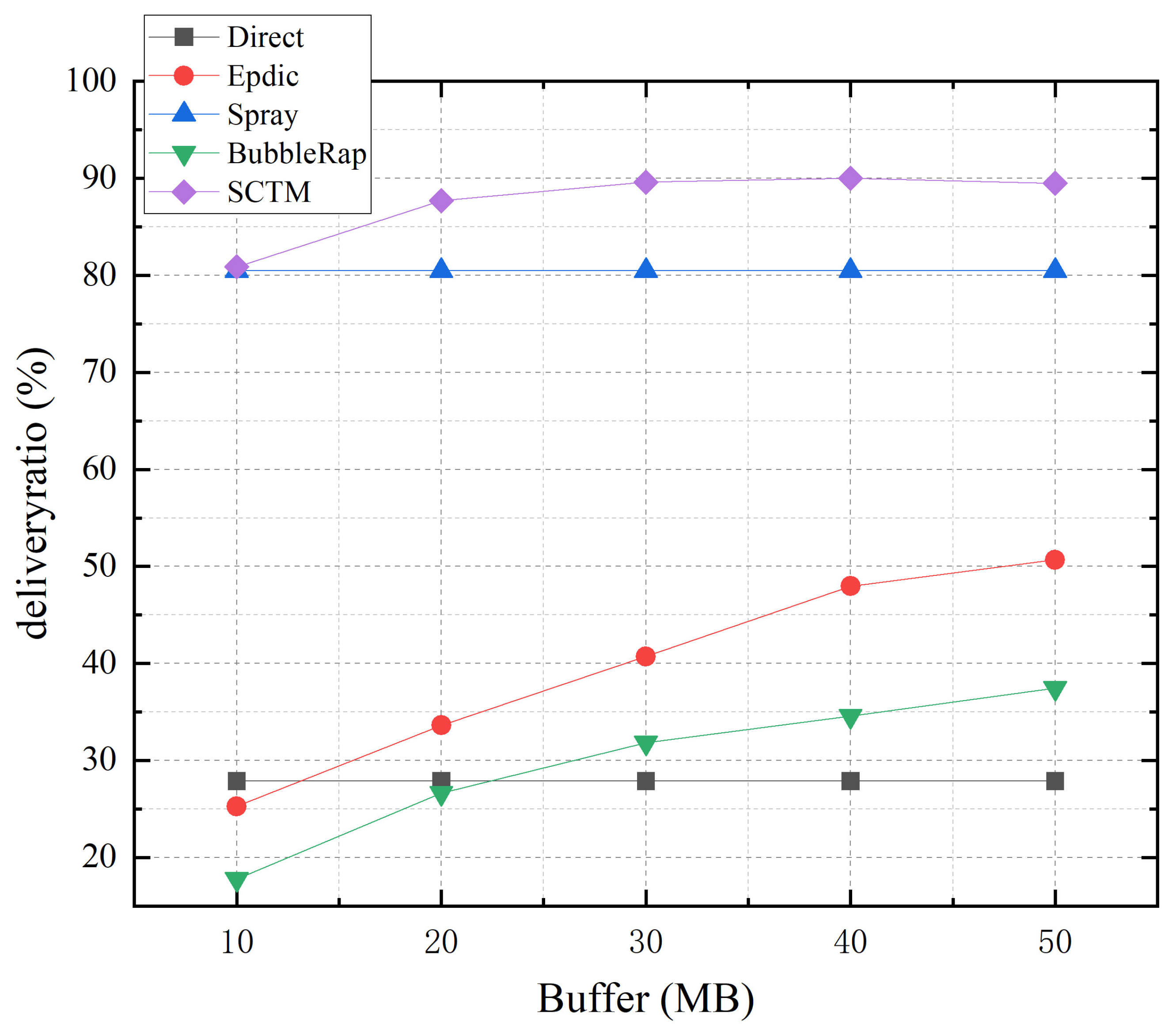
Figure 5 illustrates the relationship between transmission success rate and node cache for the Direct, Epdic, Spray, BubbleRap, and SCTM routing algorithms. As depicted, with an increase in node cache size, the forwarding success rate of SCTM, Epdic, and BubbleRap algorithms experiences a significant rise, while that of the Direct and Spray algorithms remains relatively unchanged. This divergence arises because the Direct and Spray algorithms do not generate redundant message copies during message forwarding. Instead, the Spray algorithm implements limited copy forwarding by attributing messages with representations, thereby minimizing the number of message copies transmitted across the network and alleviating caching pressure on nodes. Conversely, the Epdic and BubbleRap algorithms produce numerous message copies during transmission, leading to cache pressure and subsequent message loss, thus reducing transmission success rates. Increasing node cache size effectively mitigates this issue, improving the forwarding success rate of these algorithms. Although the SCTM algorithm employs restricted copy forwarding, it selects relay nodes with higher centrality, thus enhancing forwarding efficiency. Augmenting node cache size alleviates caching pressure on the backbone network and further improves forwarding success rates. Notably, when node cache size reaches 30MB, the SCTM algorithm achieves a transmission success rate of approximately 90%, demonstrating its lower dependency on node cache size.
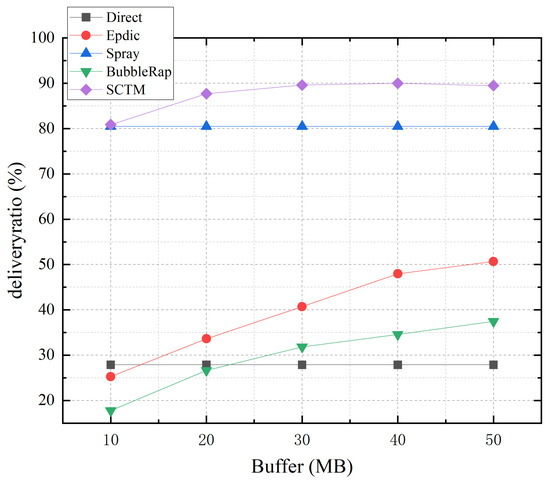
Figure 5.
Deliveryratio and node buffer.
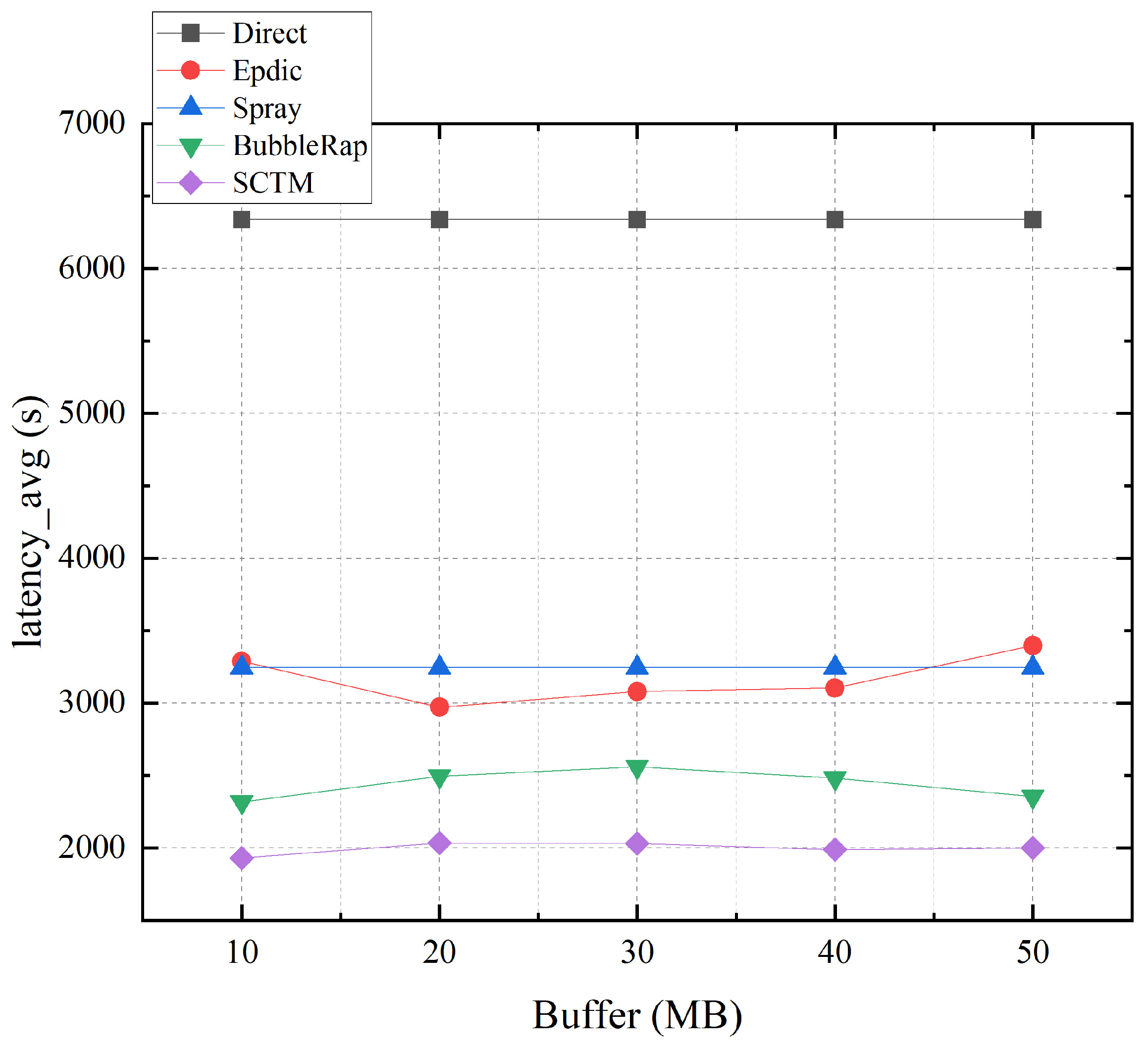
Figure 6 depicts the relationship between average transmission delay and node cache. Notably, the Direct and Spray algorithms exhibit minimal dependency on node cache, with average transmission delay maintaining stability. Contrarily, while the Epdic and BubbleRap algorithms alleviate network congestion with increasing node cache, nodes storing more messages prolong the survival time of messages that should otherwise be discarded due to tardiness, resulting in a slight reduction in algorithmic average delay. The SCTM algorithm selects next-hop relay nodes based on considerations of node centrality and remaining cache. Although increasing node cache mitigates cache pressure on highly central nodes, these nodes typically maintain low residual cache levels after receiving numerous messages. Consequently, the SCTM algorithm may opt for nodes with lower centrality but higher residual cache when selecting next-hop relay nodes, leading to a modest increase in average forwarding delay, albeit remaining at a low level.
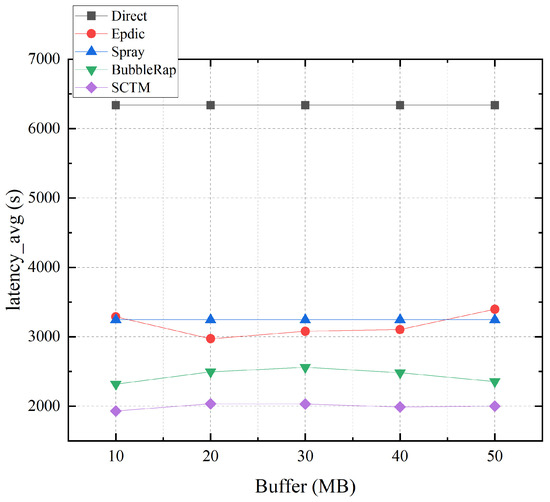
Figure 6.
Latency_avg and node buffer.
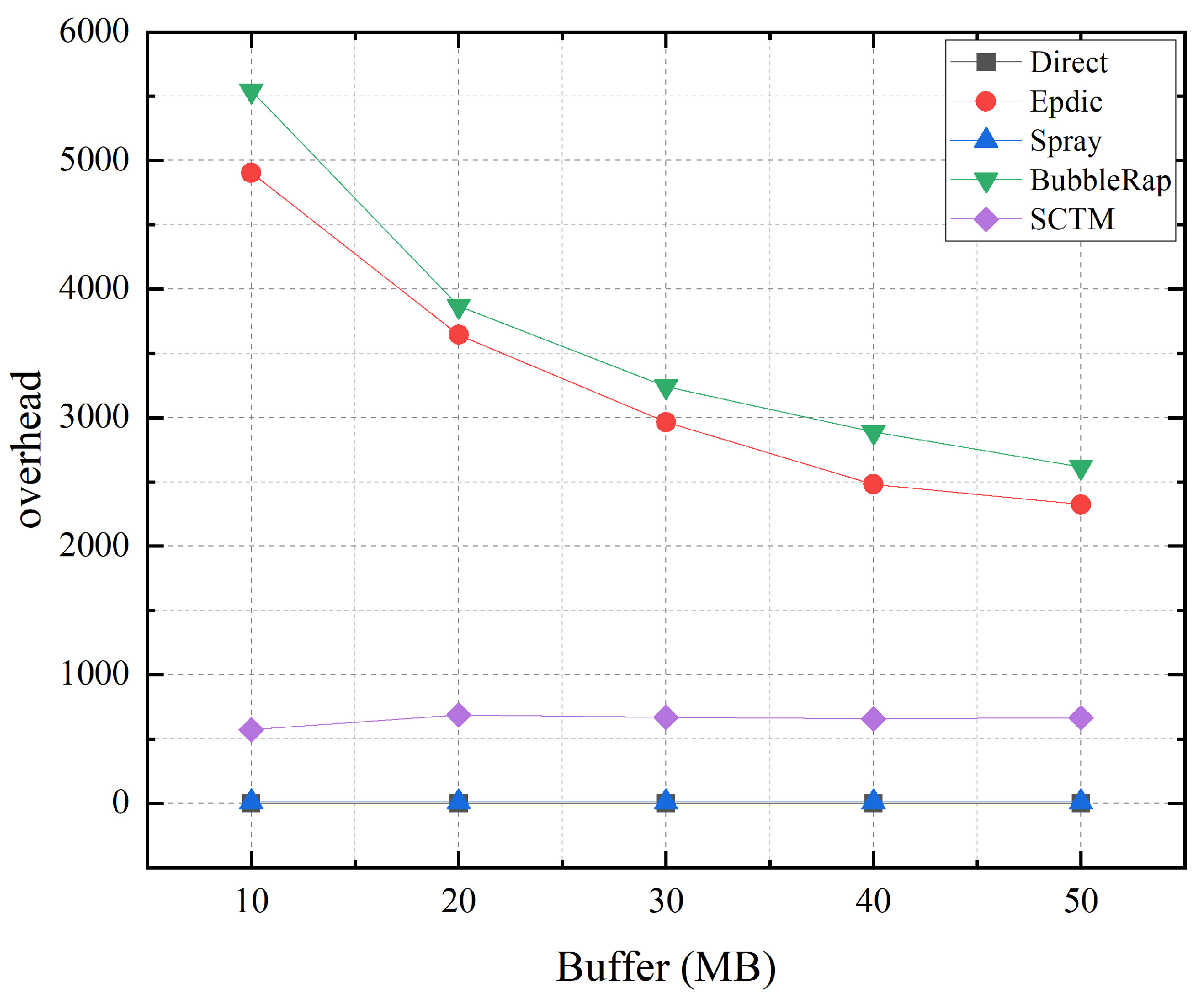
As illustrated in Figure 7, the increased node cache of the Epdic and BubbleRap algorithms results in fewer messages being discarded due to buffer overflow, leading to a reduction in the number of forwarding instances required for successful message transmission and a significant decrease in routing overhead. Conversely, the SCTM algorithm’s strategy of selecting nodes with low centrality but ample remaining cache space as next-hop relay nodes leads to messages traversing more nodes and being forwarded more frequently, resulting in a slight increase in routing overhead. Meanwhile, the Direct and Spray algorithms exhibit minimal changes.
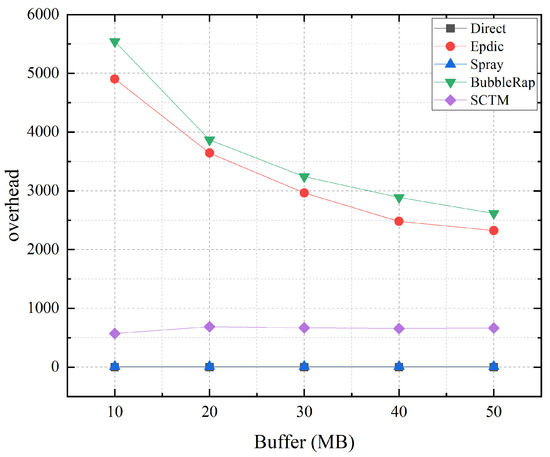
Figure 7.
Overhead and node buffer.
Furthermore, this study investigates both node-sparse and node-dense networks in real-world scenarios. Comparative experiments were conducted by adjusting the number of nodes in the network during simulation.
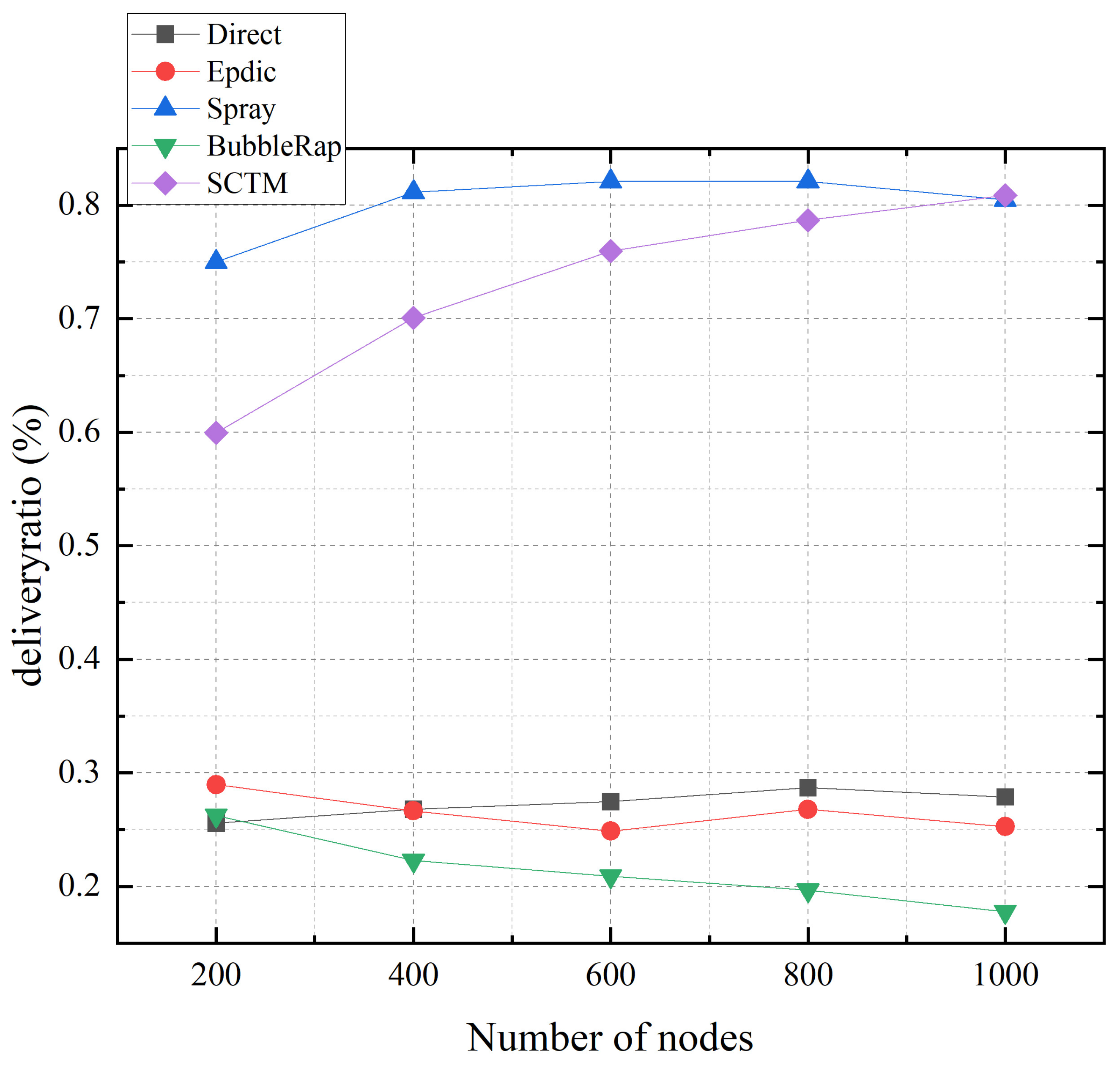
Figure 8 illustrates the relationship between the transmission success rate and the number of nodes for the Direct, Epdic, Spray, BubbleRap, and SCTM routing algorithms. With an increase in the number of nodes, the transmission success rate of the SCTM algorithm exhibits a gradual rise. This phenomenon arises from the heightened frequency of node interactions as the network expands. Consequently, the SCTM algorithm adeptly identifies superior forwarding nodes, leading to a sustained enhancement in transmission success rate throughout the network. Notably, when the network comprises 1000 nodes, the transmission success rate surpasses that of the Spray algorithm. Conversely, the Epdic and BubbleRap algorithms, utilizing flooding forwarding strategies, witness an escalation in redundant message copies within the network due to increased message forwarding, thereby diminishing the transmission success rate. As for the Direct and Spray algorithms, their average transmission delay hinges on the encounter probability between the message-carrying node and the destination node, with minimal influence from the network size. Moreover, the transmission success rate of these algorithms stabilizes over time, largely dictated by the encounter probability between the message-carrying node and the destination node.
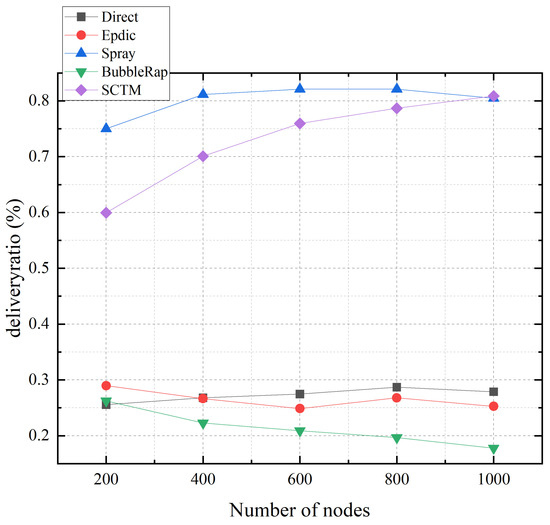
Figure 8.
Deliveryratio and node numbers.
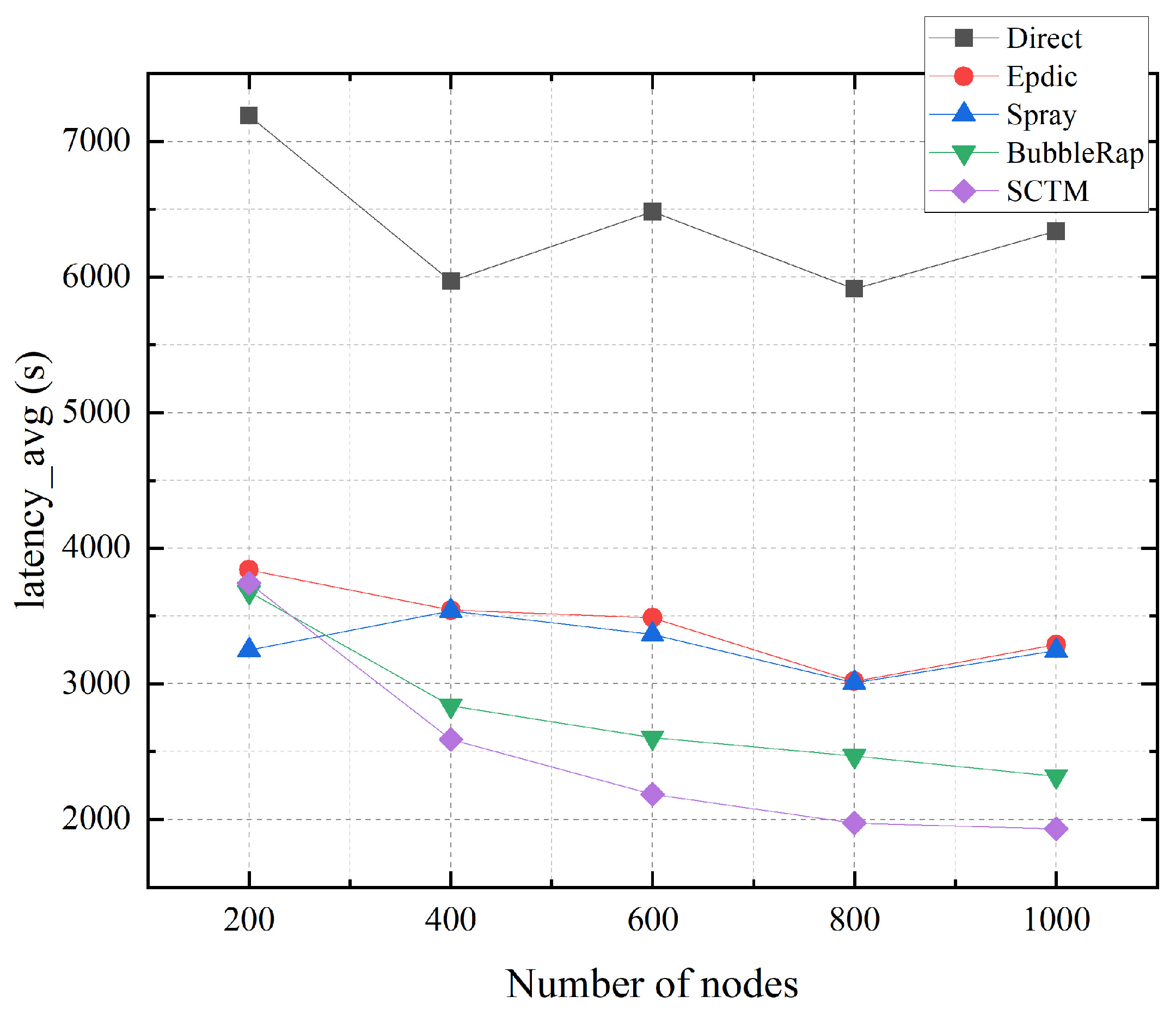
Figure 9 depicts the relationship between the average transmission delay and the number of nodes. As the network expands, node interactions become more frequent, thereby increasing opportunities for message forwarding. Consequently, the average transmission delays witnessed substantial reductions in the Epdic, BubbleRap, and SCTM algorithms. Notably, owing to community division, the average transmission delays in the BubbleRap and SCTM algorithms exhibit further decline, showcasing a clear and continuous descent. Conversely, in the Epdic algorithm, the surge in network message forwarding leads to a proliferation of message copies, consequently resulting in an initial decline followed by an eventual increase in transmission delay. Meanwhile, the average transmission delay observed in the Direct and Spray algorithms is contingent upon the encounter probability between the message-carrying node and the destination node, with minimal impact from the network size.
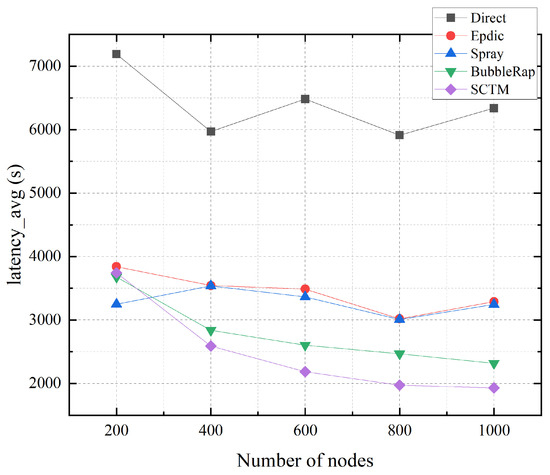
Figure 9.
Latency_avg and node numbers.
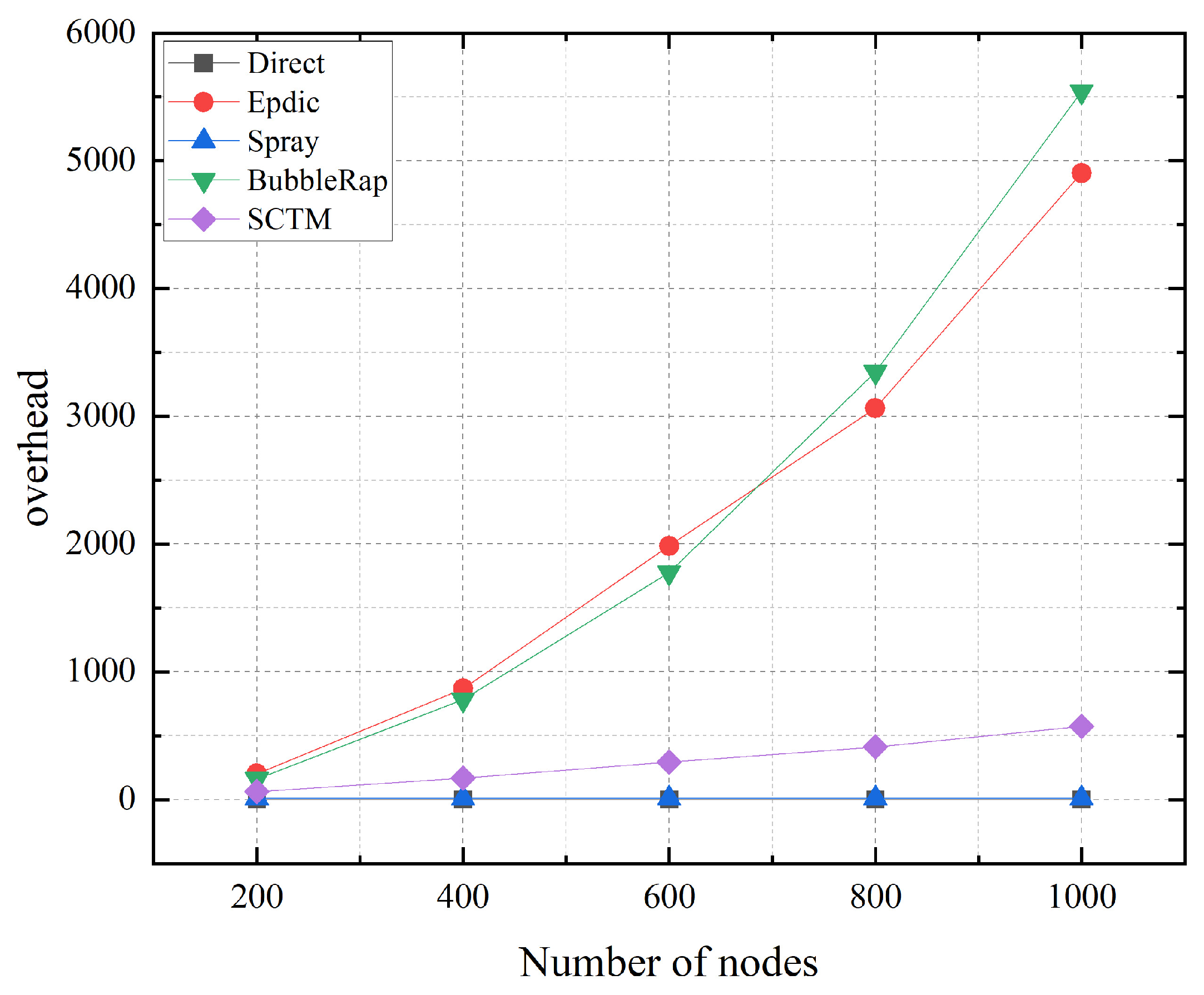
As depicted in Figure 10, the Direct and Spray algorithms maintain a fixed number of message copies, with the Spray algorithm halting message forwarding upon generating a single copy. Consequently, the number of nodes in the network profoundly impacts these algorithms, albeit with minimal effect. In contrast, the flooding forwarding approach adopted by the Epdic and BubbleRap algorithms leads to an upsurge in message forwarding with increasing node count, resulting in network congestion and elevated routing overhead. Conversely, the SCTM algorithm demonstrates a proportional increase in message forwarding as the number of nodes rises. However, owing to community division and meticulous selection of next-hop relay nodes, the SCTM algorithm experiences only marginal increments in routing overhead.
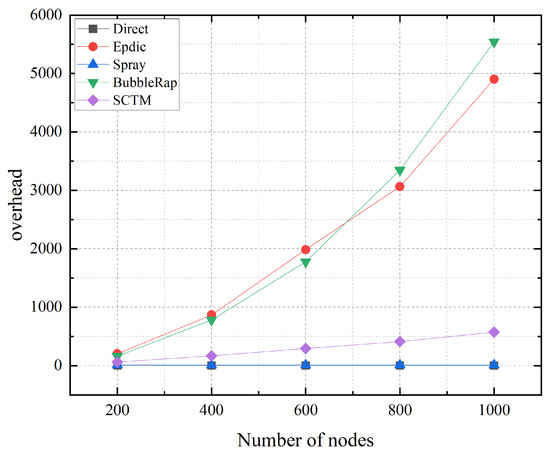
Figure 10.
Overhead and node numbers.
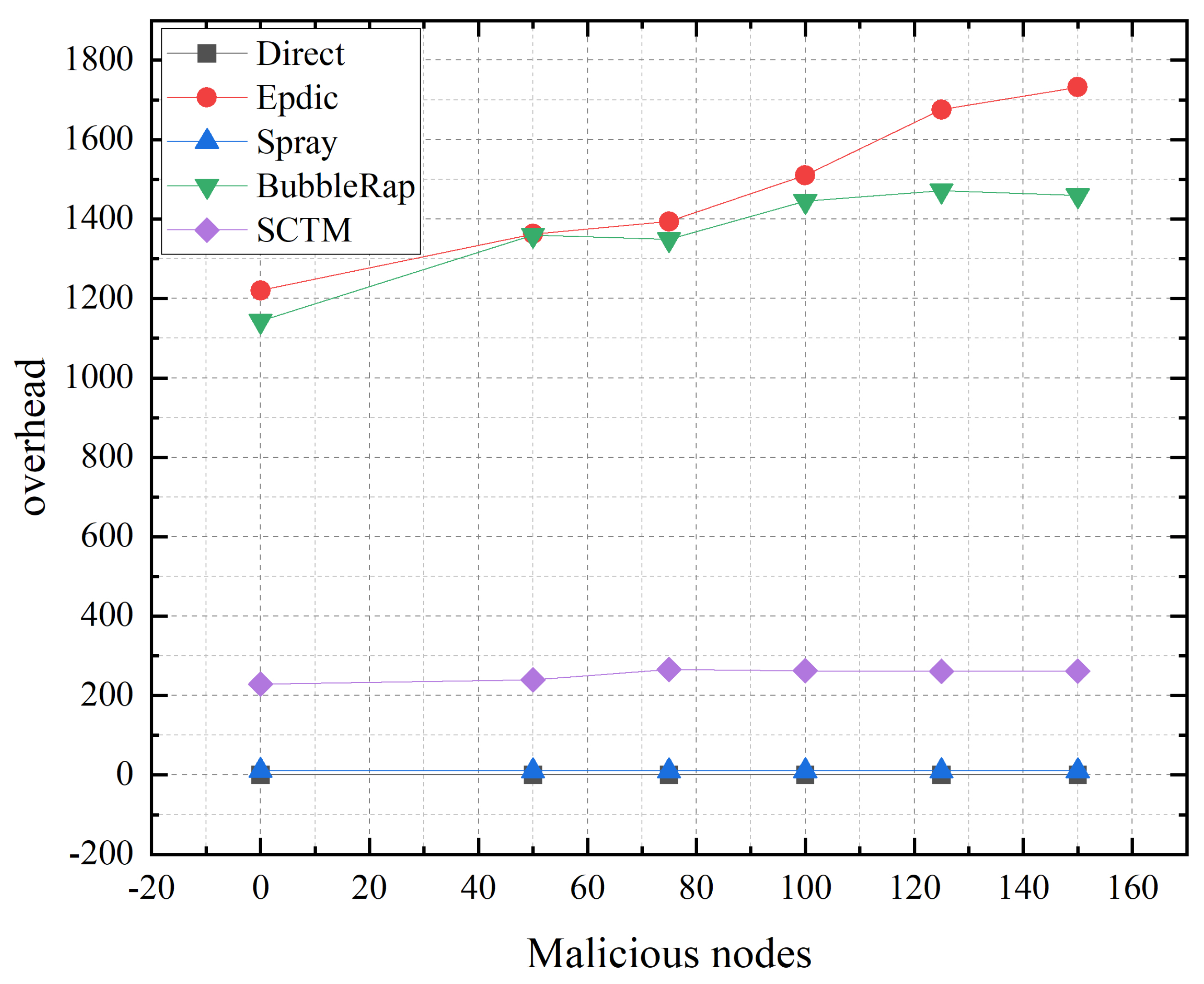
To evaluate the resilience of opportunistic routing algorithms against malicious node attacks, this study introduces a subset of specialized nodes within the simulation framework, designed to mimic a black hole attack by solely accepting messages without further dissemination. A comparative analysis was undertaken by establishing a baseline of 500 operational nodes within the opportunistic network, followed by a systematic variation in the quantity of malicious nodes introduced. This approach facilitates a comprehensive understanding of the algorithm’s performance under the duress of adversarial conditions.
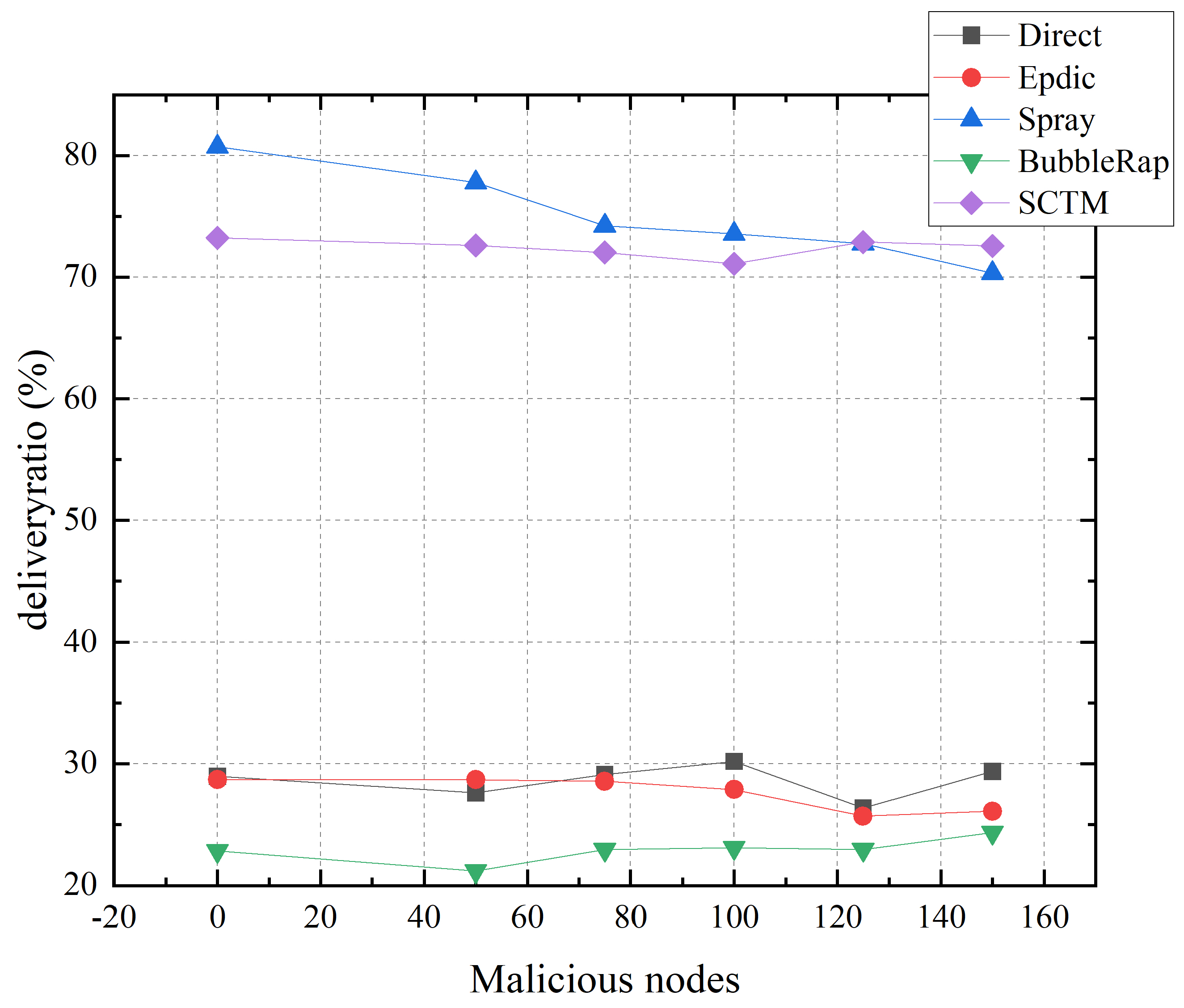
As can be seen from Figure 11, the Direct algorithm, which exclusively delivers messages to the intended destination node, exhibits minimal susceptibility to the influence of malicious nodes. In contrast, the Epdic and BubbleRap algorithms, employing a flooding forwarding strategy, experience a nuanced impact from malicious activities. While the deliberate loss of packets by malicious nodes can inadvertently reduce network congestion by diminishing the volume of redundant messages, it concurrently risks the malicious discarding of messages destined for successful delivery, resulting in negligible fluctuations in the transmission success rate. The Spray algorithm, predicated on the random selection of next-hop relay nodes, encounters a marked decrease in the transmission success rate when malicious nodes intercept and halt the propagation of message copies within the opportunistic network. Conversely, the SCTM algorithm, by prioritizing nodes within a secure community for next-hop selection, effectively insulates against malicious nodes, which are precluded from the secure community due to their detrimental behaviors, thereby maintaining a stable transmission success rate. Simulation outcomes reveal that the SCTM algorithm possesses the capability to detect and exclude malicious nodes from the opportunistic network, offering robust defense against malevolent attacks. Notably, even with the presence of 150 malicious nodes, the SCTM algorithm achieves the highest transmission success rate of 73%, underscoring its effectiveness in safeguarding communication integrity within opportunistic networks.
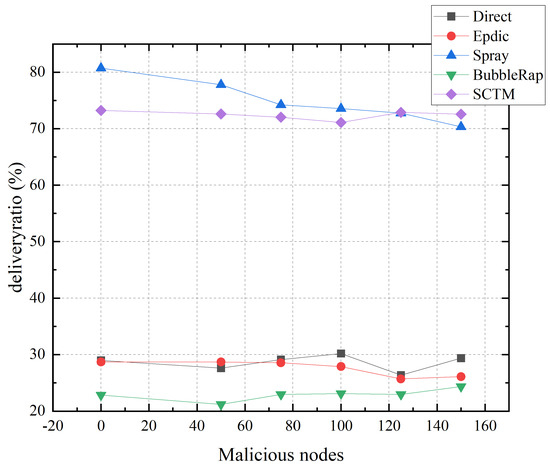
Figure 11.
Deliveryratio and malicious nodes.
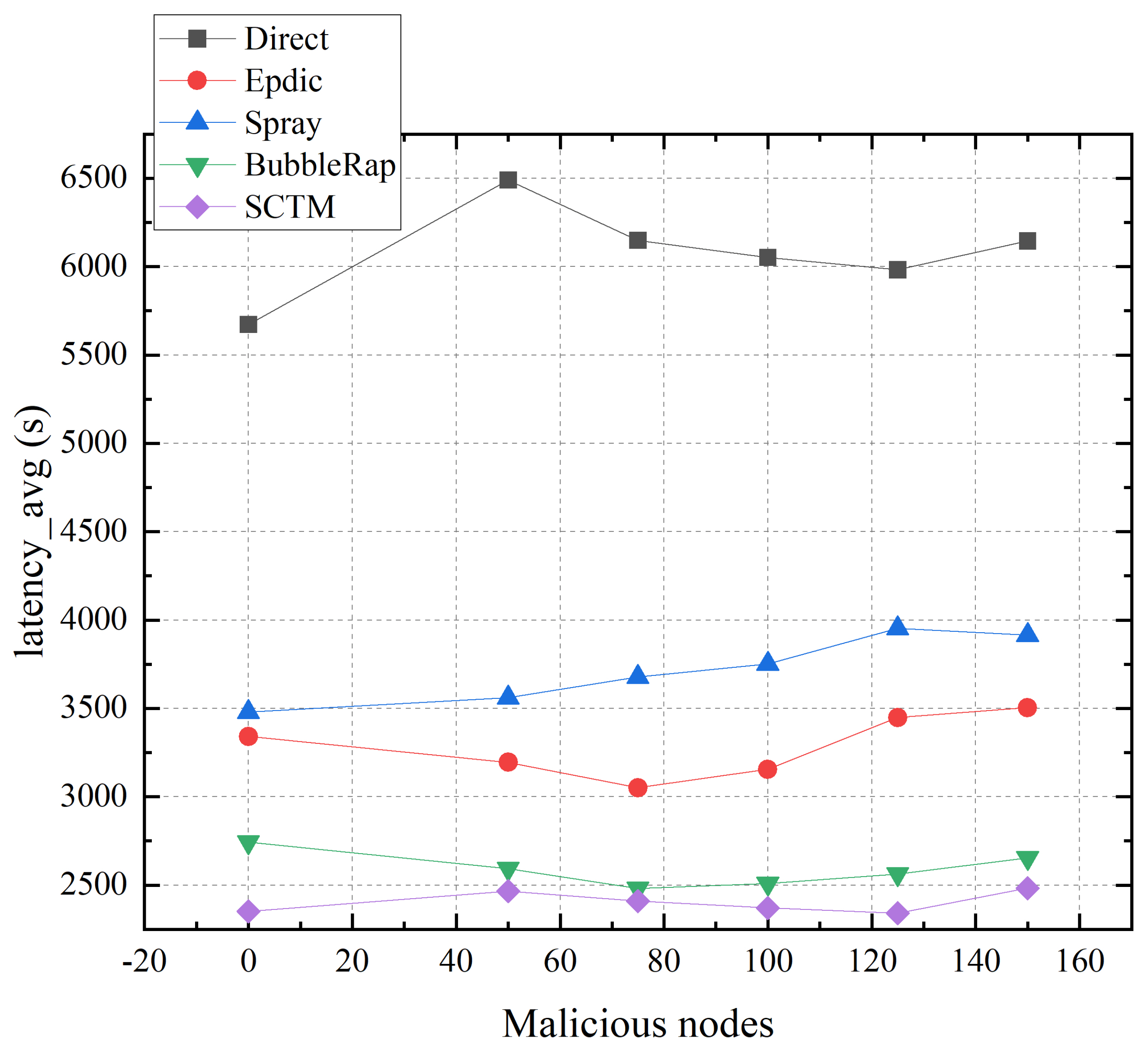
As illustrated in Figure 12, the average transmission delay for the Epdic and BubbleRap algorithms initially decreases and subsequently increases with the rising number of malicious nodes. This trend is attributable to the flooding forwarding strategy employed by both algorithms, which engenders significant network redundancy. Such redundancy congests the network, whereas a judicious amount of malicious packet loss can alleviate transmission pressure, thus reducing the average transmission delay. However, an excessive presence of malicious nodes leads to the potential discard of messages en route to the destination node, resulting in an augmented average transmission delay. Conversely, as the prevalence of malicious nodes escalates, the Spray algorithm experiences a notable increase in delay due to malicious message dropping. Meanwhile, the SCTM algorithm maintains the lowest average transmission delay, benefitting from the division of secure communities. The transmission efficiency of the Direct algorithm, predicated on the probabilistic encounters of nodes, exhibits minimal susceptibility to malicious nodes.
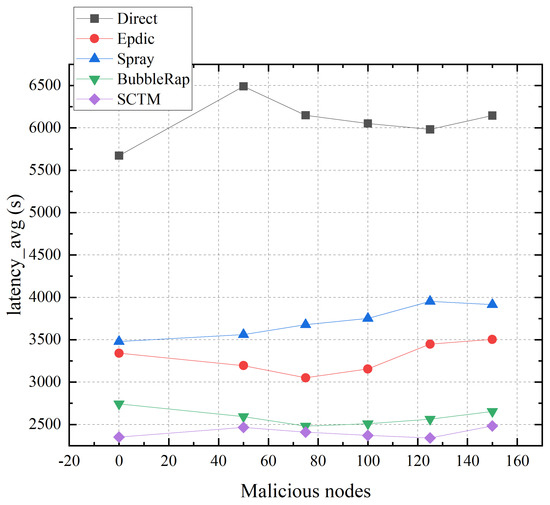
Figure 12.
Latency_avg and malicious nodes.
Figure 13 delineates that the Direct and Spray algorithms, which adopt a restricted copy forwarding strategy, show negligible impact on routing overhead from the presence of malicious nodes. In contrast, due to malicious packet loss, the Epdic and BubbleRap algorithms necessitate the successful transmission of over 100 messages to the destination node, causing routing overhead to escalate with an increase in malicious nodes. The SCTM algorithm, which segments communities based on dynamic security thresholds, experiences a lowering of trust thresholds and an expansion of the node’s local community in the presence of malicious nodes. Nonetheless, by considering node centrality in the selection of the next hop relay node, the SCTM algorithm manages to ensure message delivery to the destination with fewer transmissions, thereby maintaining low routing overhead despite the challenges posed by malicious nodes.
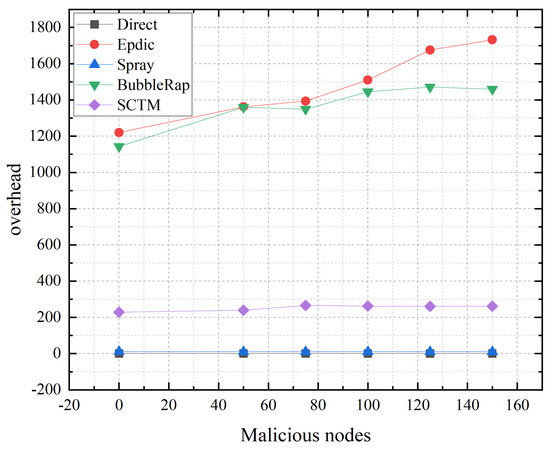
Figure 13.
Overhead and malicious nodes.
Discussion: Table 3 presents a performance evaluation of various algorithms following a six-hour simulation in a scenario with 1000 nodes within the opportunistic network and a node cache size of 30 MB. The Secure Community Trust Model (SCTM) algorithm outperforms others in terms of both transmission success rate and average transmission delay. This superiority is attributed to its strategy of limiting message copies and its preference for selecting nodes with closer connections to the destination node for message forwarding, which leads to a marginally higher routing overhead compared to the Direct and Spray algorithms. Notably, the SCTM algorithm enhances the transmission success rate by 125% over the Epdic algorithm, while cutting routing overhead by 77%. In comparison with the Spray algorithm, it also reduces the average transmission delay by 37%, marking a substantial improvement over its counterparts. Moreover, the SCTM algorithm orchestrates secure community divisions, prioritizing nodes within the security community for relay node selection and taking into account factors such as node centrality, remaining cache, and energy levels. This approach ensures the selection of safer and more efficient nodes for relay purposes. Simulation findings corroborate the SCTM algorithm’s capability to adeptly identify and exclude malicious nodes from the network, effectively counteracting malicious threats and sustaining algorithmic stability.

Table 3.
Comparison table between SCTM algorithm and existing algorithms.
5. Conclusions
This study introduces a robust Secure Community Trust Model (SCTM) algorithm for opportunistic network routing, premised on a trust-based framework. The foundation of this model lies in the premise that nodes exhibiting commendable forwarding behavior in historical interactions are likely to maintain similar efficacy in future communications. To counteract malicious activities within opportunistic networks, the SCTM algorithm leverages the historical interaction records between nodes and their counterparts within the same local community to compute a trust score. This score facilitates the dynamic segmentation of secure communities via adaptable trust thresholds and decay functions, ensuring message propagation remains within a safeguarded network milieu. To augment message forwarding efficiency, mitigate the transmission load on the network backbone, and prevent network congestion and node failure, the SCTM algorithm employs a constrained replica forwarding tactic. This approach strategically segments message replicas by evaluating node centrality, residual cache capacity, and remaining energy levels, thus optimizing the routing and forwarding process. Simulation outcomes underscore the SCTM algorithm’s superiority over comparative algorithms, demonstrating an unmatched transmission success rate of 81% and minimal transmission delays, all while maintaining low network overhead. Notably, the SCTM algorithm exhibits proficiency in detecting and isolating malicious nodes, thereby safeguarding against hostile intrusions and preserving algorithmic stability. Future investigations will delve into more sophisticated trust models to bolster data transmission security, scrutinize social affiliations among nodes, and develop routing strategies that are simultaneously low latency, energy-efficient, and highly effective.
Author Contributions
Conceptualization, J.L. and B.S.; Methodology, J.L.; Software, B.S.; Validation, J.L. and B.S.; Formal Analysis, J.L.; Investigation, B.S.; Resources, B.S.; Data Curation, B.S.; Writing—Original Draft Preparation, J.L.; Writing—Review and Editing, B.S.; Visualization, J.L.; Supervision, B.S.; Project Administration, B.S.; Funding Acquisition, B.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author, J.L., upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Khalil, A.; Zeddini, B. A Secure Opportunistic Network with Efficient Routing for Enhanced Efficiency and Sustainability. Future Internet 2024, 16, 56. [Google Scholar] [CrossRef]
- Khan, N.A.; Brohi, S.N.; Zaman, N. Ten deadly cyber security threats amid COVID-19 pandemic. Authorea Prepr. 2023. [Google Scholar] [CrossRef]
- Su, B.; Zhu, B. TBMOR: A lightweight trust-based model for secure routing of opportunistic networks. Egypt. Inform. J. 2023, 24, 205–214. [Google Scholar] [CrossRef]
- Yu, L.; Xu, G.; Zhang, N.; Wei, F. Opportunistic Network Routing Strategy Based on Node Individual Community. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Chen, W.; Letaief, K.B.; Cao, Z. Opportunistic network coding for wireless networks. In Proceedings of the 2007 IEEE International Conference on Communications; IEEE: Piscataway, NJ, USA, 2007; pp. 4634–4639. [Google Scholar]
- Ayele, E.D.; Meratnia, N.; Havinga, P.J. An asynchronous dual radio opportunistic beacon network protocol for wildlife monitoring system. In Proceedings of the 2019 10th IFIP International Conference on New Technologies, Mobility and Security (NTMS), Canary Islands, Spain, 24–26 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–7. [Google Scholar]
- Teranishi, Y.; Kimata, T.; Kawai, E.; Harai, H. Hybrid cellular-DTN for vehicle volume data collection in rural areas. In Proceedings of the 2019 IEEE 43rd Annual Computer Software and Applications Conference (COMPSAC), Milwaukee, WI, USA, 15–19 July 2019; IEEE: Piscataway, NJ, USA, 2019; Volume 1, pp. 276–284. [Google Scholar]
- Fu, X.; Yao, H.; Postolache, O.; Yang, Y. Message forwarding for WSN-assisted opportunistic network in disaster scenarios. J. Netw. Comput. Appl. 2019, 137, 11–24. [Google Scholar] [CrossRef]
- Guan, P.; Wu, J. Effective data communication based on social community in social opportunistic networks. IEEE Access 2019, 7, 12405–12414. [Google Scholar] [CrossRef]
- Wang, T.; Cui, J.; Chang, Y.; Huang, F.; Yang, Y. Dynamic Co-Operative Energy-Efficient Routing Algorithm Based on Geographic Information Perception in Opportunistic Mobile Networks. Electronics 2024, 13, 868. [Google Scholar] [CrossRef]
- Yuwei, Z.; Satoshi, F. Acceleration of Sociality-Aware Message Routing in Opportunistic Networks. In Proceedings of the 2023 Eleventh International Symposium on Computing and Networking Workshops (CANDARW), Matsue, Japan, 27–30 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 45–51. [Google Scholar]
- Wang, X.; Wang, X.; Hao, F.; Min, G.; Wang, L. Efficient coupling diffusion of positive and negative information in online social networks. IEEE Trans. Netw. Serv. Manag. 2019, 16, 1226–1239. [Google Scholar] [CrossRef]
- Yao, L.; Man, Y.; Huang, Z.; Deng, J.; Wang, X. Secure routing based on social similarity in opportunistic networks. IEEE Trans. Wirel. Commun. 2015, 15, 594–605. [Google Scholar] [CrossRef]
- Rashidibajgan, S.; Hupperich, T.; Doss, R.; Förster, A. Secure and privacy-preserving structure in opportunistic networks. Comput. Secur. 2021, 104, 102208. [Google Scholar] [CrossRef]
- Liu, D.; Tan, X. A novel routing algorithm based on probability prediction for mobile opportunistic networks. In Proceedings of the Fourth International Conference on Signal Processing and Computer Science (SPCS 2023), Guilin, China, 25–27 August 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12970, pp. 840–845. [Google Scholar]
- Singh, M.; Verma, A.; Verma, P. Encounter Count and Interaction Time-Based Routing Protocol for Opportunistic Networks. SN Comput. Sci. 2023, 5, 43. [Google Scholar] [CrossRef]
- Zhang, Z.; Krishnan, R. An overview of opportunistic routing in mobile ad hoc networks. In Proceedings of the MILCOM 2013—2013 IEEE Military Communications Conference, San Diego, CA, USA, 18–20 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 119–124. [Google Scholar]
- Liao, Z.; Hu, W.; Huang, J.; Wang, J. Joint multi-user DNN partitioning and task offloading in mobile edge computing. Ad. Hoc. Netw. 2023, 144, 103156. [Google Scholar] [CrossRef]
- Xu, Q.; Su, Z.; Zhang, K.; Ren, P.; Shen, X.S. Epidemic information dissemination in mobile social networks with opportunistic links. IEEE Trans. Emerg. Top. Comput. 2015, 3, 399–409. [Google Scholar] [CrossRef]
- Trifunovic, S.; Kouyoumdjieva, S.T.; Distl, B.; Pajevic, L.; Karlsson, G.; Plattner, B. A decade of research in opportunistic networks: Challenges, relevance, and future directions. IEEE Commun. Mag. 2017, 55, 168–173. [Google Scholar] [CrossRef]
- Biswas, S.; Morris, R. ExOR: Opportunistic multi-hop routing for wireless networks. In Proceedings of the 2005 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, Philadelphia, PA, USA, 22–26 August 2005; pp. 133–144. [Google Scholar]
- Wu, J.; Yu, G.; Guan, P. Interest characteristic probability predicted method in social opportunistic networks. IEEE Access 2019, 7, 59002–59012. [Google Scholar] [CrossRef]
- Chakchouk, N. A survey on opportunistic routing in wireless communication networks. IEEE Commun. Surv. Tutor. 2015, 17, 2214–2241. [Google Scholar] [CrossRef]
- Kuppusamy, V. Performance analysis of epidemic routing in destination-less oppnets. In Proceedings of the 2018 IEEE 19th International Symposium on “A World of Wireless, Mobile and Multimedia Networks” (WoWMoM), Chania, Greece, 12–15 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–3. [Google Scholar]
- Yahaya, B.; Momoh, M.O.; Ibrahim, Y.; Shobowale, K.O.; Abubakar, Z.M. Congestion Control on the Epidemic Routing Protocol for Opportunistic Networks. Niger. J. Eng. 2023, 30, 87. [Google Scholar]
- Garg, P.; Dixit, A.; Sethi, P. Performance comparison of fresh and spray & wait protocol through one simulator. IT Ind. 2021, 9, 1–6. [Google Scholar]
- Bhajantri, L.B. Context Aware Data Aggregation in Distributed Sensor Networks. Context 2016, 6, 46–51. [Google Scholar]
- Jain, S.; Yadav, P. Controlled replication based bubble rap routing algorithm in delay tolerant network. In Proceedings of the Smart and Innovative Trends in Next Generation Computing Technologies: Third International Conference, NGCT 2017, Dehradun, India, 30–31 October 2017; Revised Selected Papers, Part II 3. Springer: Berlin/Heidelberg, Germany, 2018; pp. 70–87. [Google Scholar]
- Wu, X.; Chang, L.; Luo, J.; Wu, J. Efficient edge cache collaboration transmission strategy of opportunistic social network in trusted community. IEEE Access 2021, 9, 51772–51783. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).