Abstract
In this work, we present a new protocol that accomplishes multiparty quantum private comparison leveraging maximally entangled triplets. Our intention was to develop a protocol that can be readily executed by contemporary quantum computers. This is possible because the protocol uses only triplets, irrespective of the number n of millionaires. Although it is feasible to prepare multiparticle entangled states of high complexity, this is overly demanding on a contemporary quantum apparatus, especially in situations involving multiple entities. By relying exclusively on states, we avoid these drawbacks and take a decisive step toward the practical implementation of the protocol. An important quantitative characteristic of the protocol is that the required quantum resources are linear both in the number of millionaires and the amount of information to be compared. Additionally, our protocol is suitable for both parallel and sequential execution. Ideally, its execution is envisioned to take place in parallel. Nonetheless, it is also possible to be implemented sequentially if the quantum resources are insufficient. Notably, our protocol involves two third parties, as opposed to a single third party in the majority of similar protocols. Trent, commonly featured in previous multiparty protocols, is now accompanied by Sophia. This dual setup allows for the simultaneous processing of all n millionaires’ fortunes. The new protocol does not rely on a quantum signature scheme or pre-shared keys, reducing complexity and cost. Implementation wise, uniformity is ensured as all millionaires use similar private circuits composed of Hadamard and CNOT gates. Lastly, the protocol is information-theoretically secure, preventing outside parties from learning about fortunes or inside players from knowing each other’s secret numbers.
1. Introduction
The pursuit of quantum computers with quantitative characteristics that surpass classical computers remains ongoing. Although this aspiration has not yet been achieved, there are certain important facts, such as IBM’s 127-qubit Eagle [1], 433-qubit Osprey [2], and the more recent 1121-qubit Condor [3], which indicate remarkable progress. Hopefully, the pace toward the quantum world has accelerated. Clearly, the present level of our quantum technology has matured significantly to warrant serious consideration for the design and implementation of cryptographic protocols. In this perspective, it is not surprising that quantum cryptographic methods have gained immense popularity since the landmark work by Bennett and Brassard [4], where the quantum key distribution was introduced for the first time. Furthermore, Shor [5] and Grover’s [6] famous quantum algorithms have demonstrated the potential vulnerability of many widely used security algorithms against quantum computers. In developing cryptographic systems that are secure against both quantum and classical computers, two fundamental approaches can be identified. One approach, often referred to as post-quantum or quantum-resistant cryptography, advocates for reliance on problems that are believed to be, but not yet formally proven to be, computationally hard. The other approach, commonly called quantum cryptography, advocates for reliance on the properties of quantum mechanics and thus takes advantage of nature’s own fundamental laws in order to achieve security. Today one can easily identify many active areas of research, such as quantum key distribution (see [4,7,8,9] and the more recent [10]), quantum secret sharing [11,12,13,14], quantum teleportation [15,16], and quantum-secure direction communication [17,18,19], to name just a few.
Another notable direction that aims to achieve the tenets of privacy and security through quantum mechanics is quantum private comparison (QPC from now on), initiated by Yang and Wen in their pioneering work [20]. Yang and Wen were the first to present a quantum protocol that enables Alice and Bob to find out if their private numbers are equal, without any party gaining additional information in case the numbers are different. This problem can be traced back to the fundamental works [21,22] by Yao, wherein the millionaires’ problem was introduced: two millionaires wish to know who is richer, but without divulging any information about the precise amount of their fortune to the other one. Following this line of thought, Boudot [23] proposed a classical protocol for the socialist millionaires’ problem, where two millionaires desire to find out if they are equally rich. Yang and Wen’s protocol is based on EPR pairs for comparing information with respect to equality and employs the help of a third party (TP). Almost simultaneously, the authors in [24] proposed an alternative QPC protocol utilizing triplets. In [25], a QPC protocol that relies on W triplets, and also uses a third party, was presented. Later, another QPC protocol using Bell states and a third party appeared in [26].
In [27,28,29,30,31], the authors proposed different QPC protocols, having as a common characteristic the fact that they utilize entangled states, such as , GHZ states, or highly entangled six-qubit states. The authors in [32] presented the first semi-quantum private comparison protocol for participants who compare their secrets without any quantum capability, and under an almost dishonest third-party. Similarly, in [33], an improved semi-quantum private comparison protocol was introduced, achieving a higher security level. There have also been different approaches, e.g., the authors in [34] do not use entanglement but still require a semi-honest third party as the QPC protocol proposed in [35] makes use of random rotation angles. Recently, a practical quantum-secure protocol for the socialist millionaires’ problem based on single photons was introduced, with emphasis on the ease of implementation with current technology [36]. For more pointers on the subject, the interested reader may consult the comprehensive survey [37]. Sophisticated quantum protocols for magnitude comparison have also been proposed in [38,39,40,41,42,43]; all these protocols envision d-level quantum systems and also require a third party. Typically, d is assumed to be greater than a certain threshold, which, in practice, considerably complicates their implementation on contemporary quantum computers based on qubits.
Chang et al. in [44] were the first to devise a clever generalization to n parties that requires -class states and the prior distribution of a secret key to each of the n parties. This inspired researchers to design more multiparty quantum private comparison (MQPC for short) protocols. Along this direction, the authors in [45] proposed a different MQPC protocol based on a d-level quantum system. Similarly, the researchers in [46] introduced an MPQC protocol with an almost dishonest third party that requires a d-level quantum system, where also d is assumed greater than the largest number slated for comparison. Subsequently, in [47], an enhanced MQPC protocol was introduced that uses -type states for n participants. Ye and Ye in [41] came up with a sophisticated MQPC protocol also based on a d-level quantum system. One of the novelties of their protocol was the creative utilization of two semi-honest third parties that eliminate the need for pre-shared keys between each pair. Other notable MQPC protocols were proposed in [42], relying on d-level states; in [48], exploiting properties of quantum homomorphic encryption; and in [49,50]. In constructing secure QPC protocols, there are certain obstacles. It has been shown in [51] that unconditionally secure classical computation involving two parties is not possible for certain categories of functions. Despite the fact that things are different in the quantum setting [52], Lo has demonstrated that it is impossible to securely evaluate the equality function in a two-party scenario [53]. This has necessitated the introduction of further assumptions, typically in the form of a semi-honest third party.
Given the current level of technology and the challenging issues that must still be overcome, today a hybrid approach, combining classical and quantum techniques to leverage the strengths of both paradigms, may be a fruitful solution. Toward this end, the sophisticated classical algebraic scheme introduced in [54] can offer many practical advantages. The new protocol we propose was designed from a computer scientist perspective that now or in the near future will be endowed with a quantum computer powerful enough to run a QMEP for a modest number of participants. The technological challenges and intricate implementation issues, such as the complexity of operations and the ability to control and measure the entangled states accurately, are not in the least underestimated, but from the point of view of an active quantum practitioner that is given a working apparatus, they may be assumed solved at least to a certain satisfactory degree. To make its presentation more easygoing for the reader, we describe it as a quantum game, something quite usual in the literature. The role of the millionaires is assumed by the famous Alice and her clones, which star alongside Sophia and Trent, who play the two third parties that are required for the secure implementation of the protocol. Quantum games were introduced in the two pioneering works [55,56] that go back to 1999. Since then, they have gained remarkable acceptance, mainly due to the fact that quantum strategies are often superior to classical ones [57,58,59,60]. The famous Prisoner’s Dilemma game provides a convincing example in this regard [56].
This article introduces a novel protocol, aptly named GHZ3MQPEC, that accomplishes a multiparty quantum private comparison relying exclusively on triplets. In designing this protocol, our fundamental concern has been to come up with an algorithm that can be easily run on today’s quantum computers. We achieved this aim by utilizing only triplets for any number n of millionaires. While more complex multiparticle entangled states, not to mention high-dimensional quantum states, are possible, they are difficult to generate with existing quantum technology, leading to an extended preparation time and complexity, especially in cases where the number of players becomes arbitrarily large. Of course, there is a plethora of classes of entangled states, such as W states, cluster states, and graph states, to name just a few. Within the circuit model paradigm, GHZ states can be easily produced, given a powerful enough quantum computer, like the 1121-qubit Condor [3]. Technically, this is accomplished by employing efficient circuits that require only steps to prepare the state (see [61]). This is particularly true for states, being the simplest in their class.
The GHZ3QPEC protocol makes quite modest demands on the quantity of quantum resources needed. As shown in Section 6.1, the number of qubits grows linearly both in the number of millionaires n and in the number m of qubits within each quantum register, reflecting the magnitude of the numbers to be compared. This allows the protocol to seamlessly scale with respect to both the number of players and the volume of information processed. This further attests to the potential of the GHZ3MQPEC protocol for practical implementation. Another advantage of the protocol concerns its suitability for parallel as well as sequential execution. Although the execution of the quantum part of the protocol is envisioned to take place completely in parallel, it is also possible to be implemented sequentially. So, if the quantum resources are insufficient for the implementation of the protocol in one go, it is possible to partition the n of millionaires into smaller groups and process these groups sequentially, even to the point of executing the protocol serially for one millionaire at a time. Another distinguishing feature of our protocol is the existence of two third parties. Trent, featured in many previous multiparty protocols, is now accompanied by Sophia. The existence of two parties enables the simultaneous processing of all n millionaires’ fortunes in one go. In addition to the possibility of either parallel or sequential execution, this protocol is flexible enough to accommodate both localized and distributed settings, a capability that stems from its inherent use of entanglement. In the first case, all players physically are assumed to be at the same geographical location, whereas, in the second case, the players are in different spatial locations.
It is worth mentioning that the GHZ3MQPEC protocol does not rely on a quantum signature scheme, or pre-shared keys, which reduces its complexity and cost. Moreover, the protocol guarantees consistency in its implementation because every millionaire uses pretty much the same private quantum circuit. With this architecture, a fully modular quantum system with identical modules is established. All private quantum circuits use only the ubiquitous CNOT and Hadamard quantum gates, which make them easy to build on modern quantum computers. Finally, it goes without saying that outside parties cannot learn any information about the millionaires’ fortunes, inside players cannot know the secret numbers of other players, and the GHZ3MQPEC protocol is shown to be information-theoretically secure.
Organization
This document is structured as follows: Section 2 offers a brief summary of the key concepts, setting the stage for grasping our protocol. A thorough explanation of the hypotheses that support the GHZ3MQPEC protocol is provided in Section 3. The GHZ3MQPEC protocol is formally outlined in Section 4. An illustrative example that demonstrates how the protocol functions is presented in Section 5, while the issues of efficiency and security are examined in Section 6. The document wraps up with a recap and a discussion on the more intricate aspects of the protocol in Section 7.
2. Preliminary Concepts
2.1. States
Numerous quantum protocols can be characterized as interactions among familiar fictional characters, typically identified as Alice, Bob, Charlie, etc., and in this particular case, Sophia and Trent besides Alice. The players are engaged in efforts to exchange information in a manner that is both private and secure. Generally, secure communication is achieved through a combination of classical authenticated channels and quantum channels. The transmission of confidential information typically occurs via the quantum channel, employing a variety of techniques, followed by the exchange of messages through a classical public channel to complete the protocol. During this process, an adversary, commonly called Eve, may attempt to intercept this communication and extract any available information. In such scenarios, the primary advantage of quantum cryptography over classical methods lies in the protection afforded to the communicating parties during the information transmission through the quantum channel, which is grounded in fundamental principles of quantum mechanics, including the no-cloning theorem [62] and the concept of entanglement monogamy, among others.
Entanglement is the cornerstone of numerous quantum protocols, including the one discussed in this paper, and could potentially become the standard approach to quantum cryptography in the future thanks to its wide range of uses across the entire domain. It is a key concept in quantum mechanics and can be represented mathematically as the sum of two or more product states. GHZ states are a prominent class of maximally entangled states, involving three or more qubits. At its core, quantum entanglement suggests that quantum particles can become linked together, and the state of one particle can instantly affect the state of another, regardless of the distance between them. For those interested in exploring this topic further, standard textbooks like [63,64,65] are a great resource for a more in-depth explanation.
The Hadamard and CNOT gates, two common quantum gates, can be used to create states on modern quantum computers, as demonstrated by the power of the most recent IBM quantum computers [2,3]. n qubits, CNOT gates, and one Hadamard gate applied to the first qubit are needed to implement such a circuit. To build effective GHZ circuits, we follow [61], which provides a workable approach that requires only steps to prepare the state. Our new protocol employs triplets. A state is formally expressed by the following formula. To make clear that entanglement requires three separate entities, we use the subscripts A, S, and T to indicate which qubit belongs to Alice, Sophie, and Trent. Following this convention, qubits denoted by belong to Alice, those denoted by belong to Sophie, and those denoted by belong to Trent:
In view of the scope of the proposed protocol, it is necessary to use m triplets because a single triplet will not suffice. The mathematical description of the state of a composite system containing m triplets is shown below (see also [14,66]):
In writing Formula (2), the following notation is used:
- is the binary set .
- To differentiate syntactically the bit vector from the bit , the bit vector is written in boldface. A bit vector of length m is a sequence of n bits: . There is also the special zero bit vector , in which all the bits are zero; that is, .
- Each bit vector serves as the binary form of one of the basis kets that constitute the computational basis of the underlying -dimensional Hilbert space.
- As we have previously explained, to avoid ambiguity, we rely on the subscripts A, S, and T to indicate which qubits belong to Alice, Sophie, and Trent’s quantum registers, respectively.
2.2. Inner Product Modulo 2 Operation
Inner product modulo 2 is a binary operation defined on bit vectors of equal length. This operation requires two bit vectors as inputs and returns their inner product, denoted by . Assuming that and , then is given by
where the symbol := stands for “is defined as”, and ⊕ is addition modulo 2. This operation is employed in many important formulae of quantum computation and information. One such fundamental formula is given below; it concerns the application of the m-fold Hadamard on an arbitrary ket , and we shall use it during the detailed analysis of our quantum protocol. This formula is proved in many textbooks, such as [63,67]:
An important property of the inner product modulo 2 operation is a special type of symmetry that can be used to partition the set of bit vectors into two subsets of equal cardinality. Specifically, any constant bit vector of , other than , exhibits the following property: for exactly half of the bit vectors , , and for the remaining half, . Clearly, is an exception to the above rule because if , then for all , . In accordance with [68], this fact is henceforth referred to as the Characteristic Inner Product (CIP) property:
For our protocol, and also the purpose of creating decoys, we utilize two other signature states, namely and , defined as
During the execution of the protocol itself, all measurements are carried out in relation to the computational basis . However, during the test for eavesdropping detection, decoys are also measured with respect to the Hadamard basis.
3. The Setup
This paper introduces a novel protocol designed to practically and efficiently accomplish a multiparty quantum private equality comparison using only states. Henceforth, for succinctness, we shall refer to this protocol with the acronym GHZ3MQPEC. In this section, we give an in-depth explanation of the whole setup and the hypotheses that guarantee the correct implementation of GHZ3MQPEC.
3.1. The Actors
Before we formally introduce the players involved in the GHZ3MQPEC, we clarify one important notion, that of the semi-honest player. After it was established that it is impossible to compute the equality function securely in situations involving two parties [53], it became clear that to achieve a secure private comparison, additional assumptions must be put forth. In the literature, the most well-known such assumption is that of a semi-honest third party. Definition 1 clarifies what this entails.
Definition 1
(Semi-honest player). A semi-honest player exhibits the following traits:
- Always executes the protocol faithfully.
- Cannot conspire with any other player.
- Cannot be corrupted by an outside entity.
- Keeps track of all intermediate calculations and may attempt to steal information from the records.
To put it another way, a semi-honest player sticks to the rules of the protocol so as to assist the interested parties in doing the equality comparison but is also interested in learning their personal information.
The GHZ3MQPEC protocol evolves as a game played by players, where n is an arbitrarily large positive integer. So, without further ado, we list the actors and the rules governing their behavior below:
- (A1)
- There are n players, the millionaires, who are designated by Alice0, …, Alicen−1. Each Alicei, , desires to find out whether her fortune is equal or not to the fortune of every other Alicej, , but without ever divulging her actual fortune to any other in-game player or outside eavesdropper. For the needs of the protocol, the millionaires’ fortunes are represented in binary and not in decimal. In particular, Alicei’s fortune is designated by the bit vector , . There is a catch, however, in the whole setup. The millionaires, in case their fortunes turn out to be different, must not be able to infer any additional information besides the fact that they are different, not even a single bit of the other player’s fortune.To allow for more generality, the millionaires are assumed to be in different locations.
- (A2)
- Additionally, there are two semi-honest third parties, Sophia and Trent, whose participation is essential for the correct implementation of the protocol. So, in total, this game involves players, all in different regions of space.
- (A3)
- Sophia’s role is critical as we explain now. The rationale behind the GHZ3MQPEC protocol is the following: instead of Alicei and Alicej directly comparing their fortunes and , , they both compare their fortune with a fixed but secret number . If , then , whereas if , then . Sophia is responsible for randomly choosing a secret number and embedding it into the global entanglement. It goes without saying that Sophia must never reveal her secret number to any other in-game player or outside eavesdropper.
- (A4)
- Trent’s role is also essential. First of all, he is responsible for the generation of the triplets and their distribution to the players according to the entanglement distribution scheme explained in Definition 2. Moreover, at the end of the protocol, he determines for each Alicei, , whether her fortune is equal or not to that of every other Alicej, . Trent must only announce the corresponding decision in the form of a single bit, e.g., YESi,j or NOi,j. Trent must never reveal the private measurements and records he used to arrive at his decisions to any other in-game player or outside eavesdropper.
- (A5)
- All players agree beforehand on the number m of qubits sufficient to store their fortunes , , and Sophia’s secret number .
We clarify that the millionaires do not wish to compare their fortunes in terms of relative size, i.e., to establish which one is greater than the other; just to know if they are equal or not.
Furthermore, as is the norm in the literature, it is presumed that the quantum channel operates as an ideal channel, characterized by the absence of noise and the retention of the particle. This simplifying assumption overlooks critical practical challenges such as losses, decoherence, specific ambient conditions in free-space channels, and the optical fibers. We fully understand the utmost importance of such issues related to noise, channel loss, control of entanglement, and scalability, which affect the practical implementation of any entanglement-based quantum protocol. Nonetheless, we believe that such issues are outside the modest scope of this article, which is focused on establishing the theoretical merits of the new protocol. Additionally, the classical channels are regarded as authenticated channels, wherein the transmitted message remains public but is impervious to alteration by any adversary.
3.2. The Entanglement Distribution Scheme
The implementation of the GHZ3MQPEC protocol requires a versatile composite system consisting of smaller subsystems. The unique feature of this configuration is the entanglement of the corresponding qubits in the state across all triplets of associated quantum registers. This is an immediate consequence of the employed Uniform Distribution Scheme, as explained in the next Definition 2.
Definition 2
(Uniform Distribution Scheme). The Uniform Distribution Scheme stipulates the following:
- Alicei, , is endowed with an m-qubit input register .
- For every Alicei, Sophia, and Trent, each utilize an m-qubit input register corresponding to Alicei, denoted by and , , respectively.
- For every Alicei, , Trent generates triplets entangled in the state. Trent keeps the first qubit p and transmits the second and third qubits q and r to Sophia and Alicei, respectively.
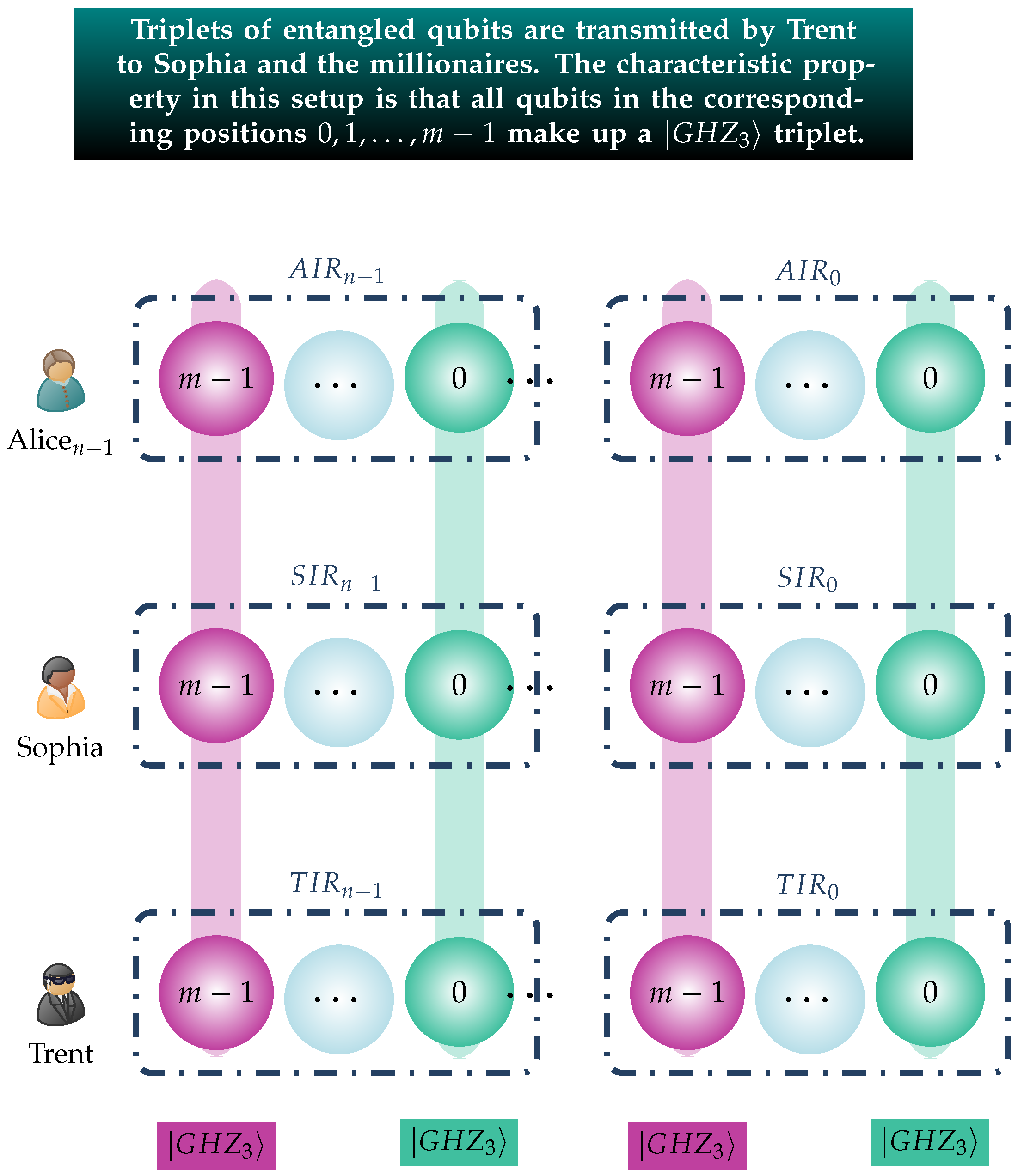
This scheme effectively creates for every Alicei, , a triplet of quantum registers, namely . These associated registers are strongly linked because their corresponding qubits are maximally entangled in the state. This is visualized in Figure 1, which conveys this setup, whereby the qubits that belong to the same triplet are painted in the same color.
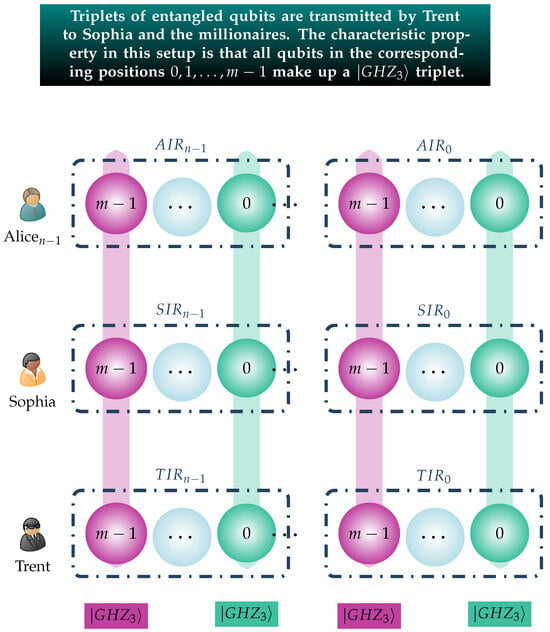
Figure 1.
This figure visualizes the fact that in every triplet of quantum registers , the m qubits in the corresponding positions belong to the same triplet. To make this point clear, they are drawn with the same color.
In this composite system, each register holds m qubits. It is important to emphasize that the spatial arrangement of the registers, whether they are co-located or dispersed across various locations, is of no consequence. The entanglement effect derived from the m triplets will produce the required correlations, regardless of whether the composite system is confined to a single area or is fully distributed. This distinctive characteristic of entanglement enables us to conceptualize the entire setup as a cohesive system. Any practical implementation of the GHZ3MQPEC protocol will require Trent to also prepare decoys. This technique is ubiquitous in the literature and is, typically, referred to as the decoy technique. There are many well-written expositions that thoroughly explain the specifics; we refer to [20,26,36,41,43,44,47,69], to cite just a few. The idea is that if the party responsible for the generation of the entangled triplets also produces decoys randomly chosen from one of the states, it is possible to discover the presence of an eavesdropper. These decoys are randomly inserted into the transmitted sequence(s). We have not mentioned the decoys in Definition 2 to avoid clutter and make the main idea of the protocol easier to grasp.
4. The GHZ3MQPEC Protocol
Our aim in the current section is to provide a thorough presentation of the new protocol. The protocol is designed to accomplish a quantum private equality comparison among an arbitrarily large number n of millionaires using only states. From now on, we shall refer to it simply by its acronym GHZ3MQPEC. Its most important characteristic traits are outlined below:
- Ease of implementation. Besides EPR pairs, triplets are arguably the easiest maximally entangled states that can be produced by a modern quantum apparatus. The fact that, irrespective of the number n of millionaires, the GHZ3MQPEC protocol can be executed with triplets exclusively guarantees the feasibility of its implementation.
- Efficiency and scalability. The forthcoming mathematical analysis in Section 6 corroborates the efficiency of the GHZ3MQPEC protocol. Moreover, one of its most important qualitative features is that the required quantum resources scale linearly both in the number n of millionaires and the number m of qubits necessary to store their fortunes, which further enhances its potential applicability.
- Parallel or sequential execution. Although the execution of the quantum part of the GHZ3MQPEC protocol is envisioned to take place completely in parallel, it is also possible to be implemented sequentially. So, if the quantum resources do not suffice for the execution of the protocol in one go, it is possible to partition the n of millionaires into smaller groups and process these groups sequentially, even to the point of executing the protocol serially for one millionaire at a time.
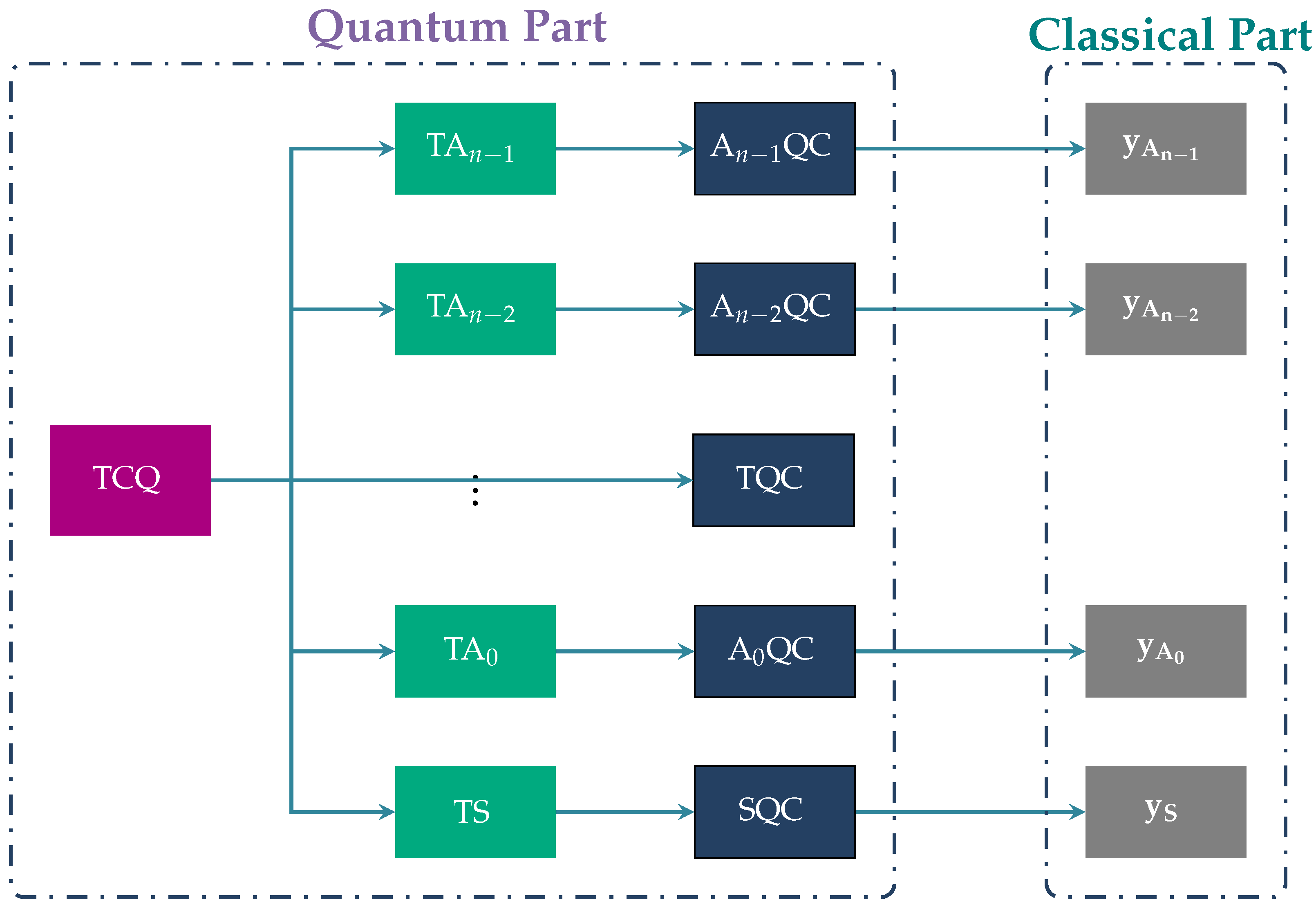
Box 1 gives a succinct outline of the intuition behind the GHZ3MQPEC protocol, and Box 2 explains how GHZ3MQPEC can be simplified in the special case of 2 millionaires. A useful overview of the GHZ3MQPEC protocol is also given by the block diagram of Figure 2, containing the actions taking place during the execution of the protocol. Our protocol consists of an initial quantum part followed by a classical part. The former takes place through quantum channels and the latter through public classical channels. Table 1 below contains the acronyms that appear in Figure 2.
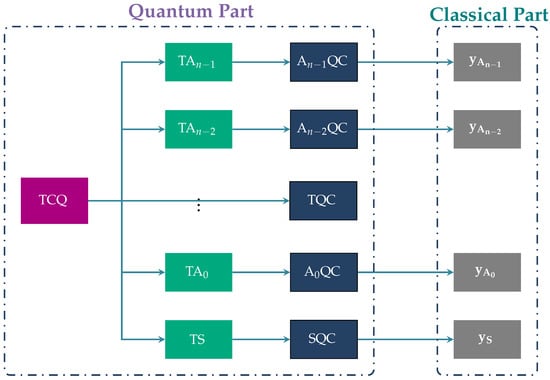
Figure 2.
The above figure presents the block diagram of the GHZ3MQPEC protocol. For the acronyms appearing in the figure, we refer to Table 1.

Table 1.
This table contains the acronyms appearing in the block diagram of Figure 2.
Box 1. The intuition behind the GHZ3MQPEC protocol
The GHZ3MQPEC protocol uses entanglement. It is the phenomenon of entanglement that allows for the secret and untraceable encoding of information in the global state of the composite quantum system. The precise mathematical formulation of the correlations among the individual subsystem as encoded into the global state takes the form given by Equation (17), which we call the Hadamard Entanglement Property.
The other prevalent idea is that instead of having Alicei and Alicej directly comparing their fortunes and , , they can both compare their fortune with a fixed but secret number . If , then , whereas if , then . Sophia is responsible for randomly choosing a secret number and embedding it into the global entanglement. It goes without saying that Sophia must never reveal her secret number .
Box 2. The special case of 2 millionaires
>To compare the fortunes of millionaires, Sophia serves as a secret, albeit fixed, point of reference. To give a geometric analogy, one could say that Sophia is the center of a collection of virtual concentric circles and those millionaires that possess the same fortune are points of the same circle. Thus, for , Sophia is indispensable.
Nonetheless, in the very special case where , which is when there are only 2 millionaires, Sophia becomes unnecessary. In this case, Trent alone suffices. We explain how the protocol and the corresponding quantum setup become simpler in such a special case in Section 7.
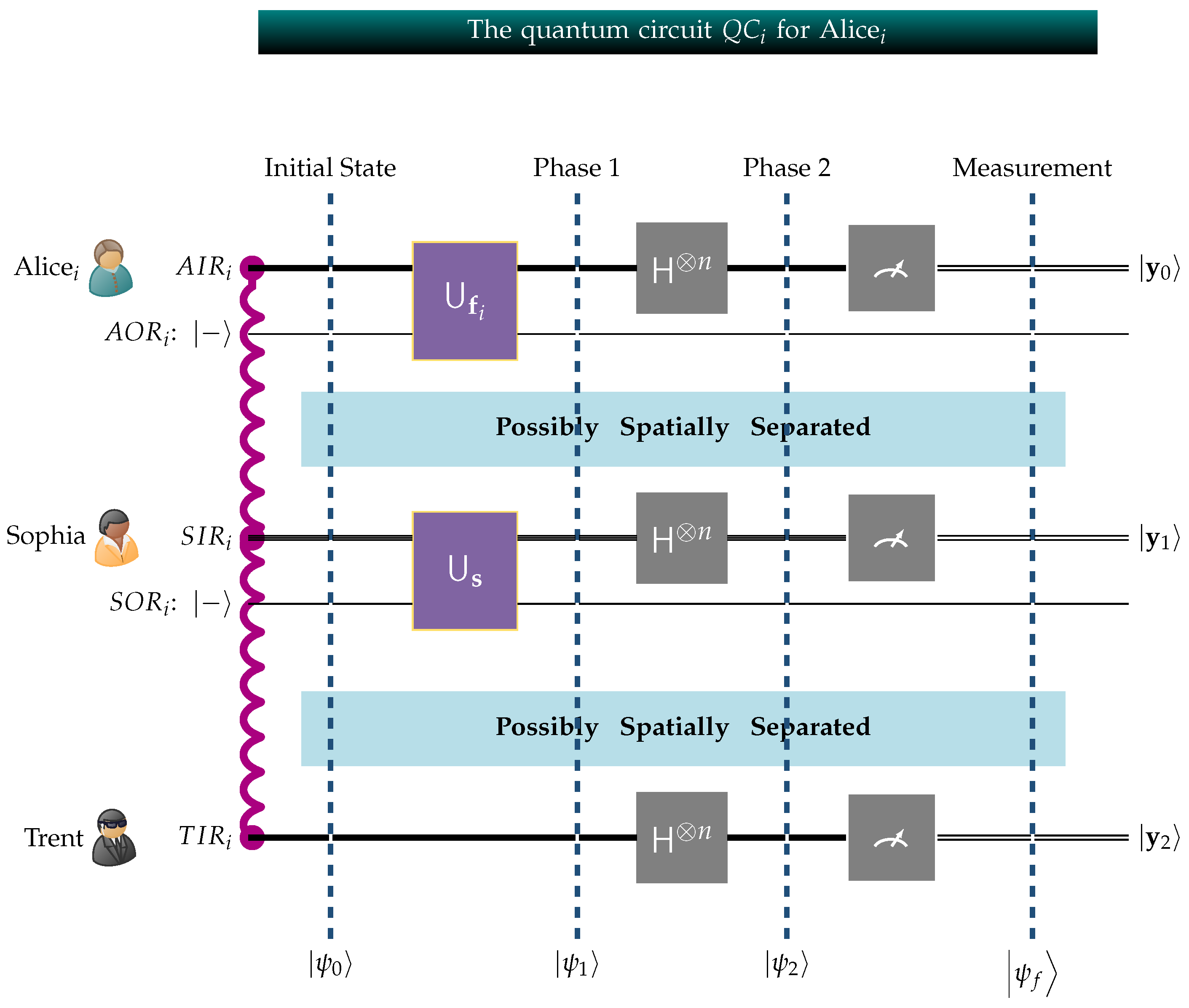
The quantum circuit that implements the GHZ3MQPEC protocol for Alicei is designated by , and is visualized in Figure 3. Considering the depiction of the quantum circuit , , in Figure 3, we note the following conventions:
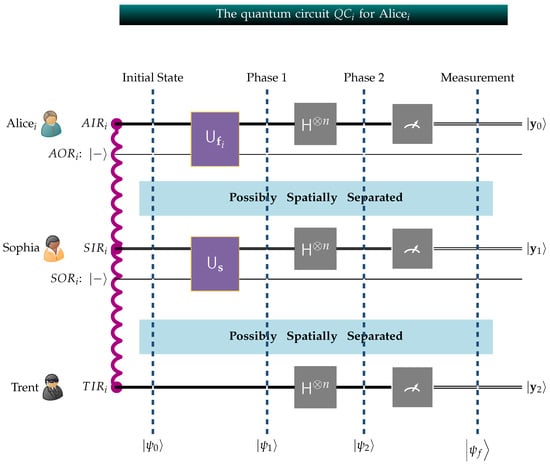
Figure 3.
The above circuit , , embeds Alicei’s fortune and Sophia’s secret number into the global state of the system. The potentially spatially separated private circuits operated by Alicei, Sophia, and Trent are linked due to entanglement, indicated by the wavy red line connecting , and , and form one composite system.
- For consistency, all quantum circuits follow the Qiskit [70] convention with respect to the order of qubits. Qiskit adheres to the little-endian qubit-indexing scheme, positioning the least significant qubit on the right side. Consequently, in the figure, the least significant qubit is placed at the top, while the most significant qubit is located at the bottom.
- is the quantum circuit corresponding to Alicei.
- , and are the input registers, each containing m qubits, in the local private circuits of Trent, Sophia, and Alicei, respectively. Their corresponding qubits are entangled, a fact that is visually indicated by the wavy red line connecting them.
- is Sophia’s single-qubit output register that is initialized to . Analogously, is Alicei’s single-qubit output register also initialized to .
- is the m-fold Hadamard transform.
- Alicei, , Sophia, and Trent act on their local circuits in a private and secret manner. Alicei’s private circuit is structurally similar to Sophia’s, but there is a critical difference. Alicei encodes her fortune into the global state of the system using an appropriate unitary transform . Similarly, Sophia embeds her secret number into the global system through her unitary transform . Since, in general, , the unitary transforms and are different.
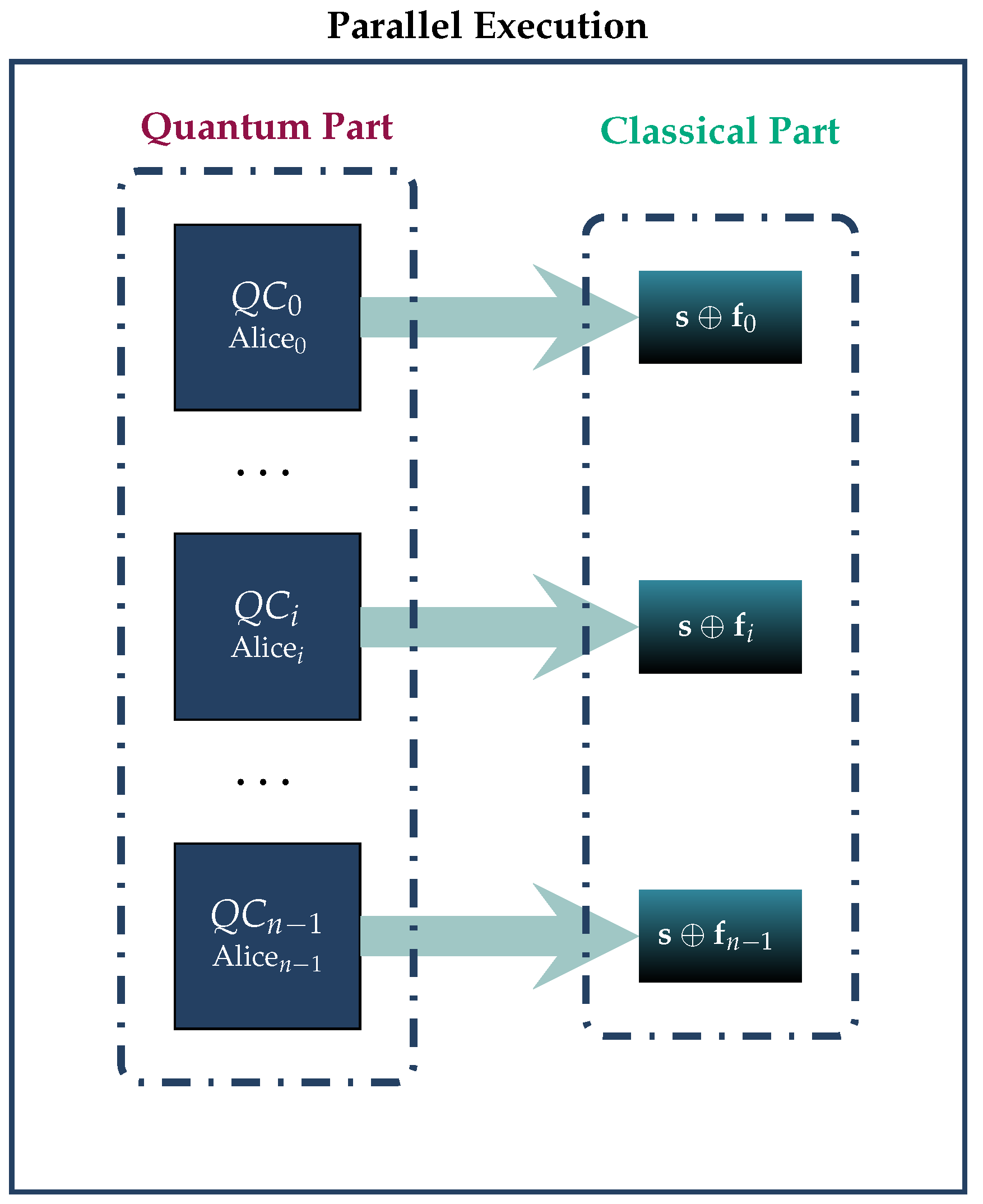
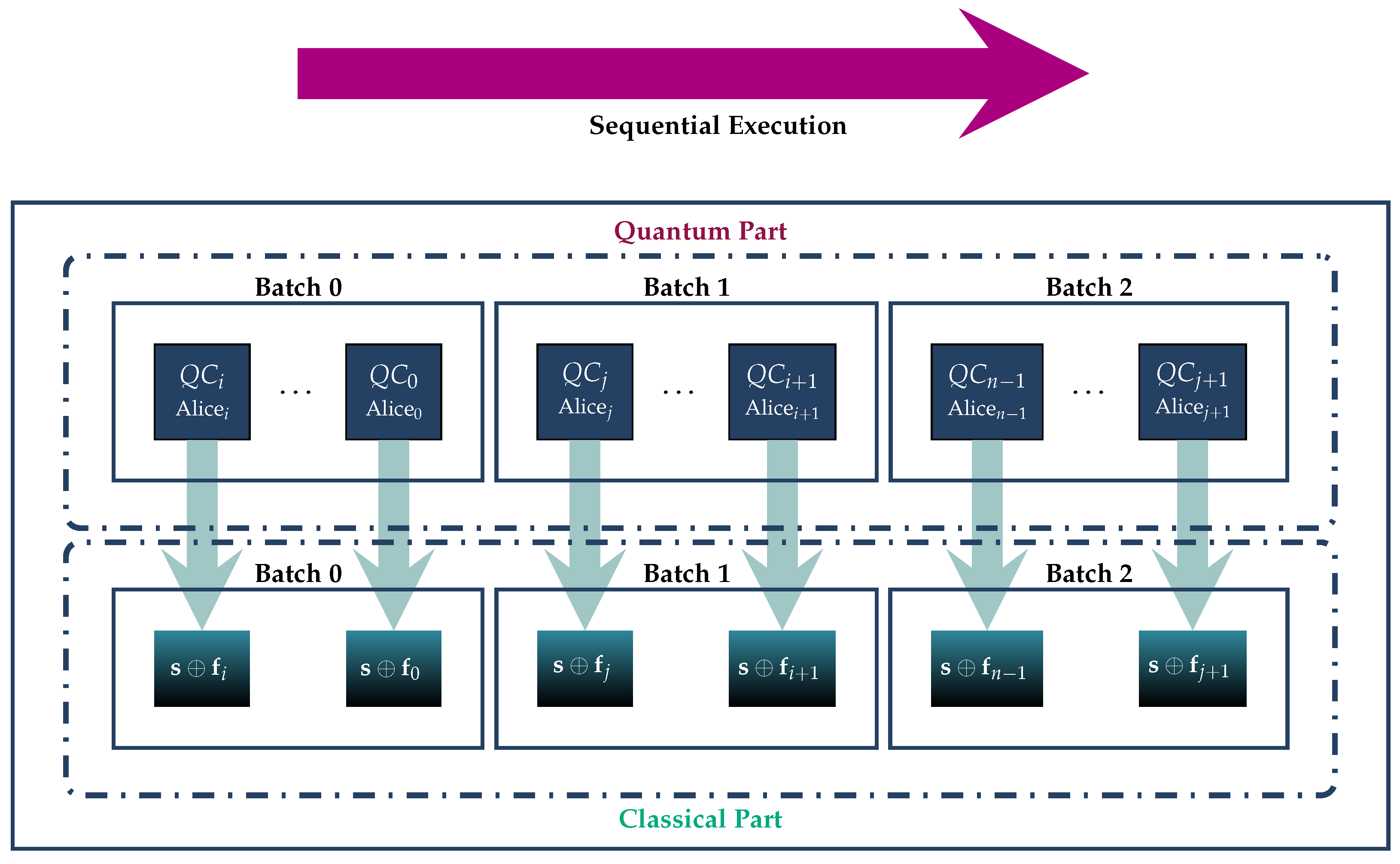
Ideally, assuming sufficient quantum resources, we shall employ a parallel array of n such circuits , as visualized in Figure 4. In case this is not feasible, due to a lack of adequate resources, it is possible to employ these circuits in sequential batches, as we show in Figure 5. All quantum circuits , , are structurally identical, their only possible difference being in unitary transform that embeds Alicei’s fortune into the system. Obviously, if Alicei and Alicej’s fortunes and , , are equal, the corresponding unitary transforms and are the same; otherwise, they are different.
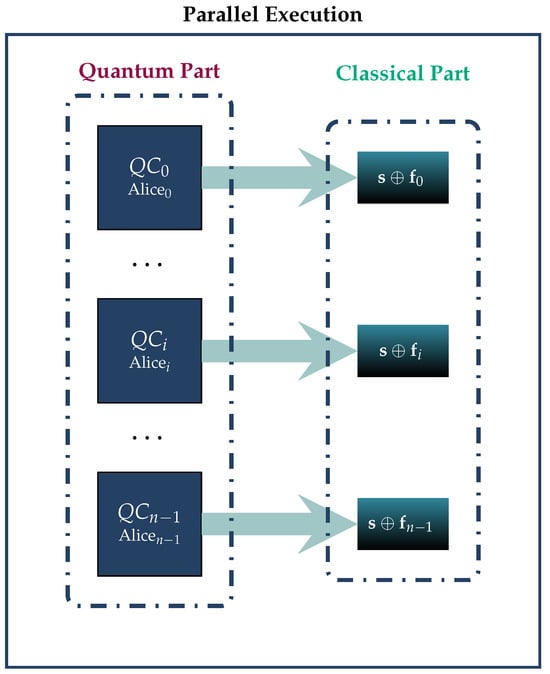
Figure 4.
In the ideal scenario, the GHZ3MQPEC protocol can be executed entirely in parallel by employing a parallel array of n circuits .
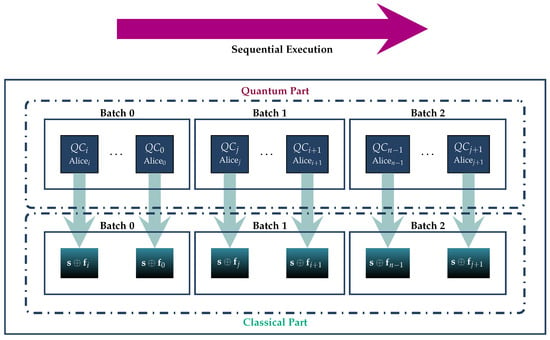
Figure 5.
If the lack of resources precludes the parallel implementation of the protocol, the n circuits can be partitioned in sequential batches. In this example, are partitioned into 3 batches. The circuits within each batch are employed simultaneously, but the 3 batches are executed sequentially.
Utilizing (2), the start state of the quantum circuit depicted in Figure 3 can be expressed as
As mentioned previously, throughout our analysis, we shall use the subscripts T, S, and i to clarify that we refer to the kets in the private circuits of Trent, Sophia, and Alicei, respectively. Hopefully, this practice will enhance readability and avoid any ambiguity.
The execution of the protocol commences in earnest by having Sophia and Alicei act on their private circuits via their secret unitary transforms and . By doing so, both of them encode their secret numbers into the entangled state of the global circuit. Let us emphasize that Sophia and Alicei’s actions result in the embedding of their private numbers into the entanglement of the three input registers of the distributed circuit.
Sophia’s transform is based on the scheme →, which, for the particular circuit , becomes
The intuition behind Alicei’s unitary transform is quite similar since it implements the scheme →, which, for our circuit , assumes the following explicit form:
The cumulative effect of both unitary transforms sends the quantum circuit into the next state :
At the conclusion of Phase 1, Sophia and Alicei have untraceably integrated their confidential numbers and , which are known solely to them, into the state of the entangled quantum system. The next step is to extract this information, enabling Trent to compare the wealth of the millionaires. To retrieve the embedded private data, Trent, Sophia, and Alicei perform the m-fold Hadamard transform on their input registers, as illustrated in Figure 3. As a result, by the end of Phase 2, the system’s state has transitioned to :
At this point, the use of Equation (4) allows us to expand , , and , as shown below:
By substituting the previous relations, we may rewrite as
This last formula can be written in a more readable form in view of the CIP property for bit vectors (recall Formulae (5) and (6)). In this specific setting, the application of these properties leads to the following reasoning:
- If , or, equivalently, ≠, the sumappearing in (14) becomes just 0.
- If , or, equivalently, =, the sumbecomes
Thus, can be written in the simpler form given below:
where
The relationship expressed by (17) is identified as the Hadamard Entanglement Property, which connects the input registers of Trent, Sophia, and Alicei. This relationship emerges as a consequence of the initial entanglement present among these input registers. By the time Phase 2 is concluded, Sophia and Alicei have encoded their private values, and , as the modulo 2 sum within the state of the system, thereby imposing this correlation on the contents of the input registers.
The GHZ3MQPEC protocol’s quantum portion is completed when Trent, Sophia, and Alicei perform measurements on their input registers with respect to the computational basis. Through this process, the composite system’s state collapses to :
We note that both output registers and remain in their initial state throughout the execution of the protocol. In that sense, they could be ignored and removed from (18). It is expedient to point out that our reasoning is valid no matter whether the private circuits of the players are in the same locality or are spatially distributed. This is because the previous equations derive their validity from the fact that the input registers are entangled in the first place. In the presence of entanglement, the distance among the players is irrelevant.
From now on, the GHZ3MQPEC protocol uses only classical authenticated communication channels. The following actions allow Trent to complete the multiparty equality comparison among the n millionaires and announce his decision in the form of a single bit for every pair of Alicei and Alicej, ; namely, YESi,j if or NOi,j if .
- (D1)
- Sophia and Alicei send to Trent the measured contents of their input registers and , respectively. The communication takes place via authenticated classical channels, which means that the transmitted messages become public knowledge but cannot be modified by an adversary.
- (D2)
- Trent, as was stipulated in (A4) of Section 3.1, never divulges the measured contents of his input register to any other in-game player or outside eavesdropper. This implies that only Trent has the complete information to compute the modulo 2 sum according to (19).
- (D3)
- The same procedure is repeated for every millionaire Alice0, …, Alicen−1. This enables Trent to calculate the sequence of n modulo 2 sums , …, . We note that Trent, as was ordained in (A4), never reveals the aforementioned sequence to any other in-game player or outside eavesdropper. The following obvious identityis the key to determine whether two fortunes and , , are equal or not. Finally, Trent broadcasts through classical channels a sequence of of bits that carry the information YESi,j or NOi,j, , depending on whether or .
To obtain a better feeling for the inner workings of the GHZ3MQPEC protocol, we present an illustrative example in the next section.
5. The GHZ3MQPEC Protocol in Action
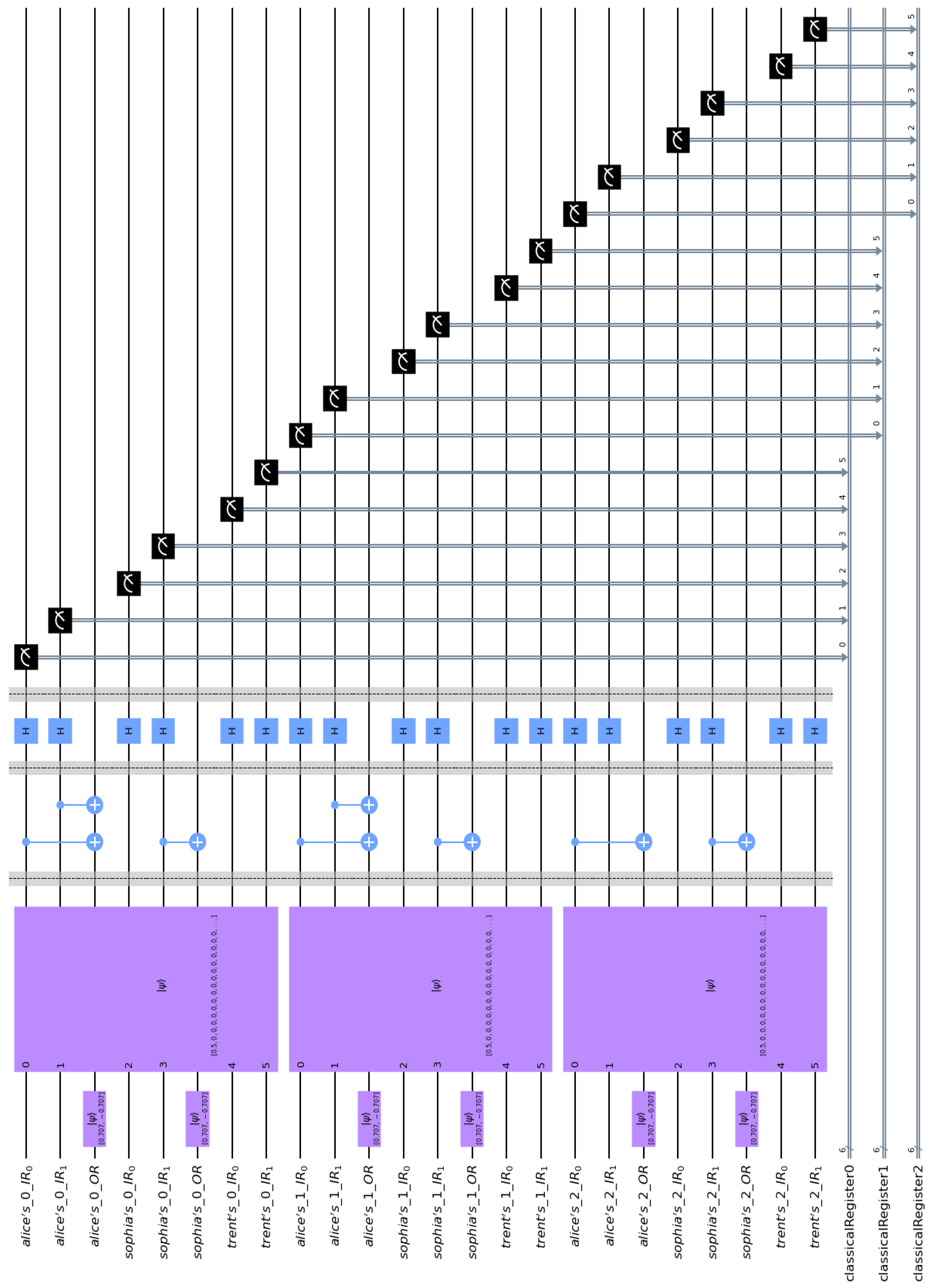
This section contains an example that demonstrates and explains the operation of the GHZ3MQPEC protocol. For practical reasons, this is a small-scale example utilizing 24 qubits. A bigger example, involving more qubits, would result in unintelligible figures that would obstruct the readability and understanding of the quantum circuit. This example, which faithfully follows the abstract quantum circuit of Figure 3, was implemented in Qiskit [70], and the resulting quantum circuit is shown in Figure 6.
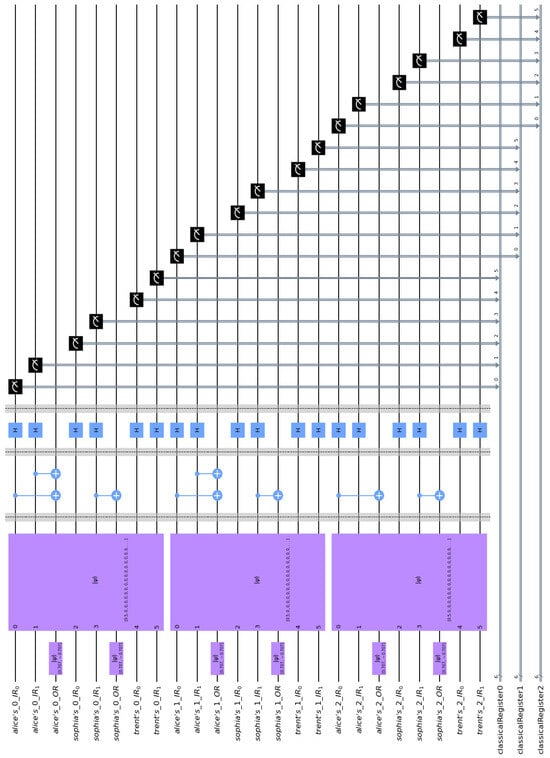
Figure 6.
This circuit, created with Qiskit, implements the GHZ3MQPEC protocol for 3 millionaires, Alice0, Alice1, and Alice2. Their fortunes were chosen so that they can be represented with qubits.
We assume that millionaires Alice0, Alice1, and Alice2 with private fortunes , , and want to compare their fortunes in one go with the mediation of Sophia, whose secret number is , and Trent. To keep the qubit count low, we opted for input registers that have two qubits, i.e., . So, we employ a parallel array of three circuits , , and , corresponding to Alice0, Alice1, and Alice2, respectively. Below we explain the acronyms used in Figure 6.
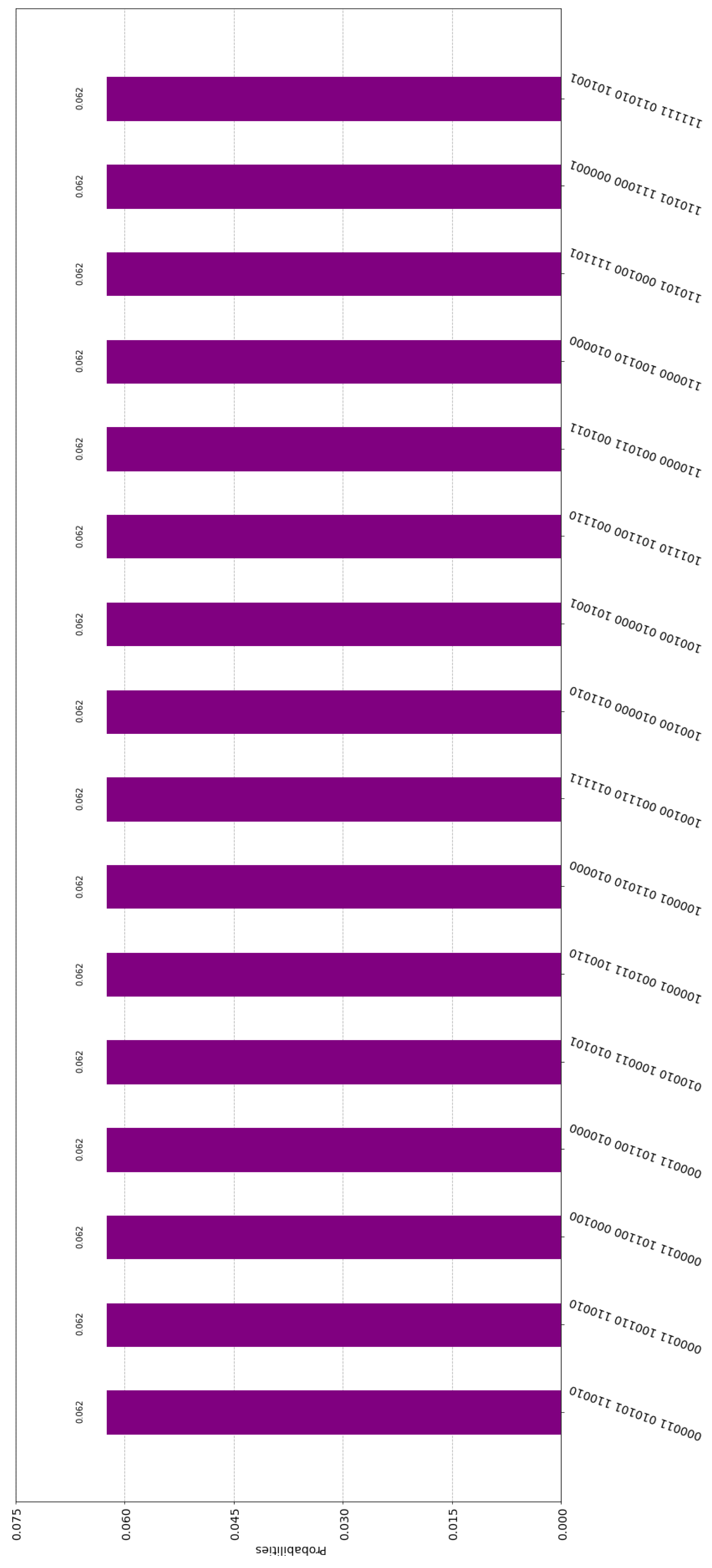
Alice0, Alice1, Alice2, and Sophia embed their private numbers in the global state of the entangled system. The embedding is trivially implemented using exclusively CNOT gates. When they measure their input registers, Alice0, Alice1, Alice2, Sophia, and Trent obtain one of the = 16,777,216 outcomes, all with equal probability. Due to evident technical constraints, it is not feasible to present all these outcomes, as doing so would lead to a figure that is difficult to interpret. Therefore, we illustrate only 16 of them in Figure 7.
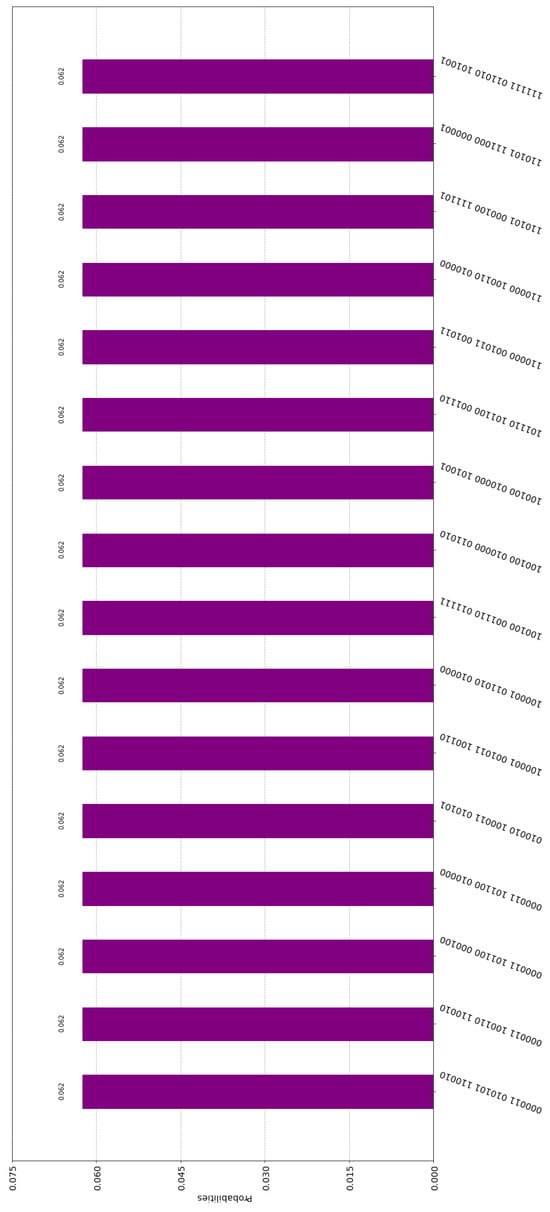
Figure 7.
This figure contains a few potential measurements and their associated probabilities for the circuit shown in Figure 6.
consists of the following components:
- Alice0’s input register alice’s_0_IR containing two qubits.
- Alice0’s single-qubit output register alice’s_0_OR initialized at .
- Sophia’s input register sophia’s_0_IR containing two qubits.
- Sophia’s single-qubit output register sophia’s_0_OR initialized at .
- Trent’s input register trent’s_0_IR containing two qubits.
- trent’s_0_IR, sophia’s_0_IR, and alice’s_0_IR are initialized in the entangled state .
- The three classical registers (each containing two bits) used by Alice0, Sophia, and Trent to store their measurements, are collectively referred to as the classicalRegister0 with a total capacity of six bits.
consists of the following components:
- Alice1’s input register alice’s_1_IR containing two qubits.
- Alice1’s single-qubit output register alice’s_1_OR initialized at .
- Sophia’s input register sophia’s_1_IR containing two qubits.
- Sophia’s single-qubit output register sophia’s_1_OR initialized at .
- Trent’s input register trent’s_1_IR containing two qubits.
- trent’s_1_IR, sophia’s_1_IR, and alice’s_1_IR are initialized in the entangled state .
- The three classical registers (each containing two bits) used by Alice1, Sophia, and Trent to store their measurements, are collectively referred to as the classicalRegister1 with a total capacity of six bits.
consists of the following components:
- Alice2’s input register alice’s_2_IR containing two qubits.
- Alice2’s single-qubit output register alice’s_2_OR initialized at .
- Sophia’s input register sophia’s_2_IR containing two qubits.
- Sophia’s single-qubit output register sophia’s_2_OR initialized at .
- Trent’s input register trent’s_2_IR containing two qubits.
- trent’s_0_IR, sophia’s_2_IR, and alice’s_2_IR are initialized in the entangled state .
- The three classical registers (each containing two bits) used by Alice2, Sophia, and Trent to store their measurements are collectively referred to as the classicalRegister2 with a total capacity of six bits.
It is straightforward to verify that all outcomes satisfy the Hadamard Entanglement Property, as quantified by (19). To explain this point beyond any doubt, let us focus on the histogram of Figure 7 and, specifically, on the value of the label of the first bar, which is 

 . The label consists of three parts:
. The label consists of three parts:  , corresponding to the contents of classicalRegister2;
, corresponding to the contents of classicalRegister2;  , corresponding to the contents of the classicalRegister1; and
, corresponding to the contents of the classicalRegister1; and  , corresponding to the contents of the classicalRegister0. This ordering is a direct consequence of the way the quantum circuit in Figure 6 was constructed, i.e., the bits of classicalRegister2 are more significant than those of classicalRegister1, which in turn are more significant than those of classicalRegister0.
, corresponding to the contents of the classicalRegister0. This ordering is a direct consequence of the way the quantum circuit in Figure 6 was constructed, i.e., the bits of classicalRegister2 are more significant than those of classicalRegister1, which in turn are more significant than those of classicalRegister0.


 . The label consists of three parts:
. The label consists of three parts:  , corresponding to the contents of classicalRegister2;
, corresponding to the contents of classicalRegister2;  , corresponding to the contents of the classicalRegister1; and
, corresponding to the contents of the classicalRegister1; and  , corresponding to the contents of the classicalRegister0. This ordering is a direct consequence of the way the quantum circuit in Figure 6 was constructed, i.e., the bits of classicalRegister2 are more significant than those of classicalRegister1, which in turn are more significant than those of classicalRegister0.
, corresponding to the contents of the classicalRegister0. This ordering is a direct consequence of the way the quantum circuit in Figure 6 was constructed, i.e., the bits of classicalRegister2 are more significant than those of classicalRegister1, which in turn are more significant than those of classicalRegister0.- classicalRegister0 is the collective name for the three classical registers (each containing two bits) used by Trent, Sophia, and Alice0 to store their measurements. Therefore, the contents of
 are analyzed as shown below:
This means that , , and . Sophia and Alice0 send to Trent and via authenticated classical channels. So, Trent has the complete information to compute the modulo 2 sum of , , and and conclude that
are analyzed as shown below:
This means that , , and . Sophia and Alice0 send to Trent and via authenticated classical channels. So, Trent has the complete information to compute the modulo 2 sum of , , and and conclude that according to (19).
according to (19). - Reasoning in exactly the same way for classicalRegister1 and classicalRegister2, it is straightforward to see that Trent arrives at the additional conclusions
Ergo, Trent ascertains that Alice0 and Alice1’s fortunes are equal but different from Alice2’s fortune. We emphasize that Sophia, as stipulated in (A3), never reveals her secret number , so Trent cannot infer from . Likewise, Trent never divulges or the modulo 2 sum to any other in-game player or outside eavesdropper, as ordained by (A4) and (D3). Thus, no entity can gain any information about the millionaires’ fortunes. Hopefully, our in-depth analysis demonstrates that it is very easy to extend the present example either by increasing the capacity m of the registers or by increasing the number of millionaires n.
6. Efficiency and Security Analysis
We proceed now to examine the efficiency and security aspects of the GHZ3MQPEC protocol. Its efficiency is, we believe, one of the strong points, as we demonstrate in the next Section 6.1.
6.1. Efficiency
A common metric for quantifying the qubit efficiency of quantum protocols is the ratio , which compares the total number of transmitted “useful” classical bits to the total number of qubits employed [71,72]. For multiparty quantum private comparison protocols, this measure must be suitably adjusted and defined as follows (see, for instance, [36,73]):
where stands for the number of classical bits required to represent the fortunes of the millionaires, and is the number of qubits the protocol uses. At this point, we must clarify that the measure does not include the decoys, as is the norm in the literature.
In the case of the GHZ3MQPEC protocol, we assumed that each millionaire requires m bits to store her fortune. Taking into account the fact that there are n millionaires, we see that
To accomplish this task, our protocol requires qubits for each millionaire, which means that for n millionaires, it requires
qubits in total. Therefore, the efficiency of the GHZ3MQPEC protocol is
In the derivation of the above result, we used the fact that for large values of m, a realistic assumption in a real-life scenario, it holds that . These efficiency results are what is to be expected in multiparty quantum private comparison protocols based on GHZ entanglement. This fact can be verified by consulting the relevant literature [36,73,74,75,76].
Let us emphasize that the quantum resources required by our GHZ3MQPEC protocol, as given by Formula (27), grow linearly in both parameters n, expressing the number of millionaires, and m, quantifying the number of qubits that suffice to represent in binary any of the millionaires’ fortunes. This can be more formally stated as follows:
This proves the ability of the GHZ3MQPEC protocol to scale in the most efficient way possible with both parameters n and m and thus be amenable to practical implementation.
It should be noted though that, given the modest number of qubits in modern quantum computers, there are practical limitations to scaling. For instance, higher m values may prove challenging. We should point out that as m increases, it becomes increasingly difficult to ensure the desired entanglement states and to maintain control over the entire composite system. This could potentially restrict the practical application of our protocol on today’s quantum computers.
6.2. Security
This subsection analyzes the security aspects of the GHZ3MQPEC protocol and proves that it is information-theoretically secure. Our proof is given in a format that is pretty much the norm in the relevant literature. It is expedient to distinguish between external and participants’ attacks. By external attack, we refer to an attack by an outside eavesdropper, namely Eve, whereas by participants’ attack, we mean an attack by any of the players that participate in the protocol.
6.2.1. External Attack
Before we lay out the formal analysis regarding the possible actions undertaken by Eve in her effort to breach the security of the GHZ3MQPEC protocol and obtain some useful information, it is essential to recall two standard detection techniques that are among the first line of defense against malicious adversaries.
- (DT1)
- Eavesdropping detection. A typical scheme for the detection of a possible eavesdropper is to have the source responsible for the generation and distribution of the entangled particles, the triplets in our case, also produce decoy photons randomly chosen from one of the states, which are randomly embedded into the transmission sequences. Eve, by meddling with the transmission sequences, and unaware of the positions of the decoys, will invariably cause errors that are easily detectable by the legitimate players upon a typical verification check. This technique, which is referred to as the decoy technique, has been extensively studied in the literature [20,26,36,41,43,44,47,69].
- (DT2)
- Entanglement validation. The effective execution of any protocol based on entanglement relies fundamentally on the presence of entanglement itself. In the absence of assured entanglement, the operational integrity of the protocol is jeopardized. The process of validating entanglement may yield two possible results. Should entanglement be confirmed, the protocol is then able to advance and successfully fulfill its designated purpose. The inability to confirm entanglement suggests a lack of the essential entanglement itself. This situation may arise due to either the presence of noisy quantum channels or intentional disruption by an adversary. No matter what the underlying reason might be, the only appropriate course of action is to cease the current execution and restart the entire process, ensuring that corrective measures are put in place. Given its importance, the validation of entanglement has been extensively examined by numerous researchers. The GHZ3MQPEC protocol follows the advanced techniques described in previous studies, and in particular [77,78,79,80,81,82].
We shall now examine the most prominent tactics that the external eavesdropper Eve might utilize.
- (Attack1)
- Measure and Resend. Eve intercepts the qubits as they are being transmitted from Trent to Sophia, and Alicei, , measures them and then returns them to the intended recipients in this kind of attack. However, there is no information encoded in the triplets. Therefore, Eve will be unable to find any information by doing this. Additionally, the legitimate players will be able to identify a malicious presence with ease if they use the decoy technique. As a result, the protocol is immune to attacks of this kind.
- (Attack2)
- Intercept and Resend. Eve’s approach in this scenario involves intercepting the particles while they are being transmitted from Trent to Sophia and Alicei, where . Due to the no-cloning theorem, she is unable to create copies of these particles. Consequently, she opts to prepare and send new qubits to the designated recipients. Eve does not learn anything by measuring the triplets because, as we have already mentioned, they carry no information at all during the protocol’s transmission phase. Additionally, the legitimate players can deduce the existence of an eavesdropper thanks to the decoy technique. So, the GHZ3MQPEC protocol is also safe from such an attack.
- (Attack3)
- Entangle and Measure. Eve starts this kind of attack by intercepting the qubits of the triplets during their transmission. In contrast to the previous types of attack, in this case, Eve refrains from measuring these qubits; instead, she entangles them with her ancilla state before forwarding the relevant qubits to Sophia and Alicei. Following this, Eve remains inactive until the protocol concludes, at which point she measures her qubits, aiming to extract valuable information. However, the result of her efforts leads to a situation where, rather than achieving an even distribution of triplets among Trent, Sophia, and Alicei, she ends up with m quadruples distributed evenly among Trent, Sophia, Alicei, and herself. Consequently, during the classical portion of the protocol, when Sophia and Alicei relay their measurements to Trent via the public channel, Eve will be unable to compute the correct modulo 2 sum. This is due to her lack of access to Trent’s private bit vector , which Trent does not transmit through the public channel. As a result, Eve will again be unsuccessful in acquiring any information.
- (Attack4)
- PNS. One of the most potent attack methods that Eve can use against any quantum protocol at the moment is the photon number splitting attack (PNS), which was first described in [83] and subsequently examined in [84,85]. Contemporary photon sources exhibit a known flaw: at times, they might generate several identical photons rather than a single one. Consequently, Eve could intercept the pulses originating from Trent during the distribution of the triplets, retain one photon from the multiphoton pulse for her own use, and transmit the remaining photons to Sophia and Alicei without being noticed during the transmission phase. Nonetheless, this situation resembles the Entangle and Measure attack analyzed above. Again, instead of triplets evenly distributed among the three legitimate actors, there are quadruples evenly distributed among Trent, Sophia, Alicei, and Eve. Eve becomes an active fourth player in the game but fails to uncover any useful information for the reason explained above.
6.2.2. Participants’ Attack
In this subsection, we examine the scenario in which one of the players in this game seeks to acquire information regarding the wealth of one of the millionaires. It is useful to categorize the following situations based on the dishonest participant attempting to obtain unauthorized information:
- Alicei
- Let us assume that Alicei, , intercepts the qubits during their transmission from Trent to Sophia and another Alicej, . Alicei has the option to measure them and send them back to their intended recipients or transmit new, previously prepared qubits to their intended recipients. Taking into consideration the fact that the triplets contain no information at all, we see that, in both cases, Alicei will fail to gain any information. Moreover, the decoy technique will allow the legitimate players to infer that someone has tampered with the transmitted sequences.Another scenario for Alicei is to intercept the qubits from the triplets during their transmission from Trent to Sophia and Alicej, , and, without measuring them, entangle them with her ancilla state. Then, Alicei forwards the relevant qubits to Sophia and Alicej and waits for the quantum part of the protocol to finish. At this point, she measures her qubits in the hope of gaining useful information. The critical flaw in Alicei’s strategy is that her actions result in having quadruples evenly distributed among Trent, Sophia, Alicej, and Alicei instead of having triplets evenly distributed among Trent, Sophia, and Alicej. Ultimately, Alicei will fail to compute the correct modulo 2 sum as the classical portion of the protocol unfolds, the reason being that Alicei will not know Trent’s private bit vector . Recall that Trent never divulges or the modulo 2 sum to any other in-game player or outside eavesdropper, as ordained by (A4) and (D3). Once again, Alicei fails to gain any information. Therefore, the GHZ3MQPEC protocol is immune to attacks by Alicei, .
- Sophia
- Let us assume that Sophia intercepts the particles en route from Trent to Alicei. Sophia has the option to measure these particles and subsequently return them to Alicei, or alternatively, she may send new qubits that she has prepared in advance to Alicei. Since the triplets carry no information, Sophia will not gain any information in any of the earlier cases. Additionally, the other legitimate players will be able to identify the tampering thanks to the use of the decoy technique.Another possibility for Sophia is to intercept the qubits from the triplets during their transmission from Trent to Alicei and entangle them with her ancilla state, without measuring them. Sophia sends corresponding qubits to Alicei and waits for the protocol to finish. Then, she measures her qubits, expecting to uncover some information. The problem with this strategy is that Sophia’s tampering has resulted in having quadruples evenly distributed among Trent, Sophia, and Alicei, instead of having triplets. Ultimately, Sophia will fail to compute the correct modulo 2 sum as the classical portion of the protocol unfolds because she will not know Trent’s private bit vector . We recall that Trent never divulges or the modulo 2 sum to any other in-game player or outside eavesdropper, as dictated by (A4) and (D3). Consequently, the GHZ3MQPEC protocol is impervious to attacks by Sophia.
- Trent
- Trent cannot surmise Sophia’s secret number because Sophia, as stipulated in (A3), never reveals her secret number . Moreover, the fundamental premise of the protocol is that Alicei, , never divulges her private fortune . Hence, although Trent knows the modulo 2 sum , he can infer neither nor . Thus, the GHZ3MQPEC protocol cannot be compromised by Trent.
Information theoretically, the GHZ3MQPEC protocol is secure, as proved by the above concise security analysis.
6.3. Comparative Assessment
In this section, we present an informative comparative assessment of the GHZ3MQPEC protocol with respect to some notable previous protocols designed to address the private equality comparison problem for an arbitrary number n of millionaires, and also for the special case of two millionaires. We gathered in Table 2 the most important design choices for multiparty quantum private comparison protocols, such as the choice of entanglement, the use or not of unitary operations, and the reliance on QKD schemes, the latter adding extra complexity and overhead to the protocol itself. Last, but not least, we included the important efficiency metric. The results contained in Table 2 highlight the novelties incorporated in the GHZ3MQPEC protocol and corroborate its most important qualitative and quantitative traits.

Table 2.
Comparison among GHZ3MQPEC and previous multiparty quantum private comparison protocols.
7. Discussion and Conclusions
This paper presents the innovative GHZ3MQPEC protocol that accomplishes a multiparty quantum private comparison leveraging maximally entangled triplets. We list below some of the most important advantages of the protocol.
- The primary aim of this protocol is to be easily executable by modern quantum computers. This is achieved by employing only triplets, regardless of the number of participants. Though high-dimensional quantum states and more intricate multiparticle entangled states are feasible, their creation is challenging given the current state of quantum technology, leading to longer preparation times, particularly in situations involving many players. By exclusively using states, which are simpler to produce than Bell states, these issues are mitigated, advancing the practical implementation of the protocol.
- A key quantitative feature of this protocol is that the number of players and the volume of data being compared determine the required quantum resources, which scale linearly, further demonstrating its practicality. Notably, the GHZ3MQPEC protocol can be executed in both parallel and sequential modes. While the quantum operations are intended to run in parallel, sequential execution is also possible if quantum resources are insufficient, allowing the participants to be divided into smaller groups for sequential processing.
- Additionally, the protocol does not depend on a quantum signature scheme or pre-shared keys, which simplify and reduce its cost. Implementation is further streamlined as all participants use identical private quantum circuits consisting of Hadamard and CNOT gates, making it straightforward to implement on contemporary quantum computers.
- Crucially, the protocol ensures that external parties cannot access any information about the participants’ values, and participants themselves cannot learn each other’s secret numbers. The protocol is demonstrated to be information-theoretically secure.
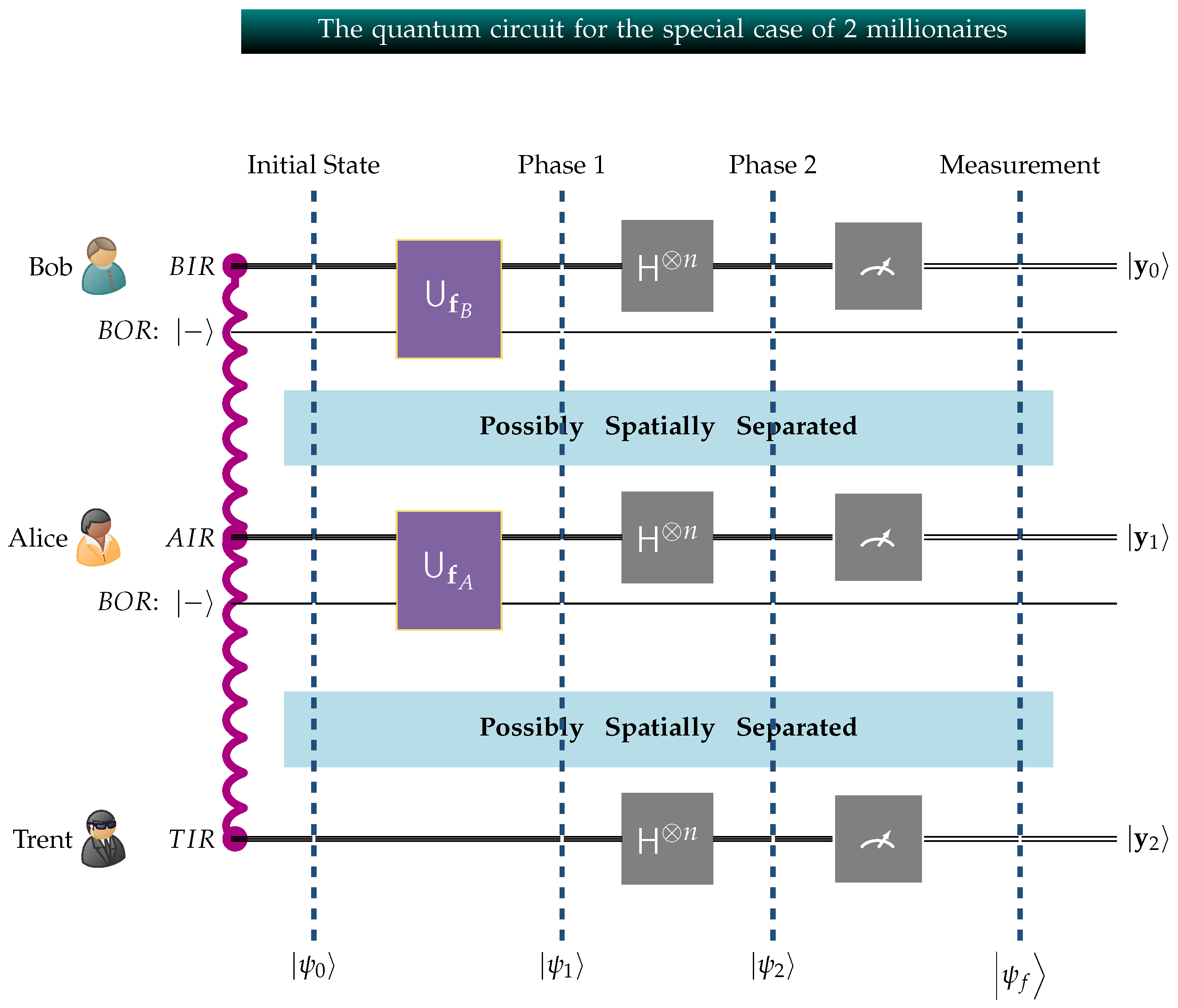
In closing, we briefly mention the special case , which is when there are only two millionaires, say Alice and Bob. As we mentioned in Section 3, in such a case Sophia becomes unnecessary and Trent alone suffices. The GHZ3MQPEC protocol can be easily simplified to function without the presence of Sophia, using the quantum circuit shown in Figure 8. Obviously, the whole mathematical description of the protocol, its quantitative characteristics, and its security remain unaffected.
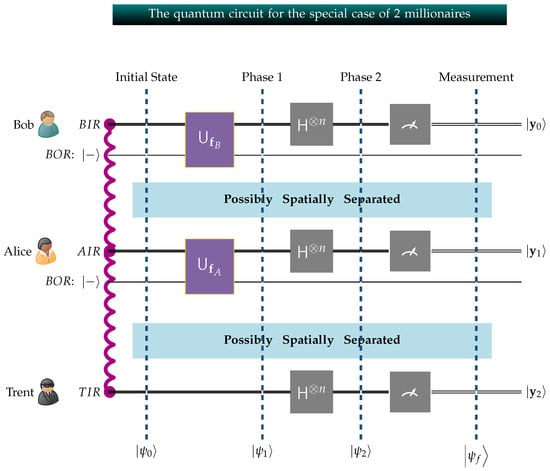
Figure 8.
The above circuit embeds Alice and Bob’s fortunes and into the entangled system. The private circuits operated by Alice, Bob, and Trent are linked due to entanglement, indicated by the wavy red line connecting , and , and form one composite system.
The current state of affairs, regarding the availability of quantum computers with a sufficient number of qubits, undoubtedly imposes certain limitations on the practical execution of any quantum protocol, including, of course, GHZ3MQPEC. Moreover, it should be noted that measuring m triplets simultaneously can be challenging and may call for sophisticated multichannel detection systems, which raises the complexity of the implementation. Hopefully, the upcoming generation of quantum computers will address many of these practical issues and allow for increased scalability.
Author Contributions
Conceptualization, T.A. and A.S.; methodology, T.A.; validation, A.S.; formal analysis, A.S.; investigation, T.A.; writing—original draft preparation, T.A. and A.S.; writing—review and editing, T.A. and A.S.; visualization, A.S.; supervision, T.A.; project administration, T.A. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chow, J.; Dial, O.; Gambetta, J. IBM Quantum Breaks the 100-Qubit Processor Barrier. 2021. Available online: https://www.ibm.com/quantum/blog/127-qubit-quantum-processor-eagle (accessed on 2 March 2024).
- Newsroom, I. IBM Unveils 400 Qubit-Plus Quantum Processor. 2022. Available online: https://newsroom.ibm.com/2022-11-09-IBM-Unveils-400-Qubit-Plus-Quantum-Processor-and-Next-Generation-IBM-Quantum-System-Two (accessed on 2 March 2024).
- Gambetta, J. The Hardware and Software for the Era of Quantum Utility Is Here. 2023. Available online: https://www.ibm.com/quantum/blog/quantum-roadmap-2033 (accessed on 2 March 2024).
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 9–12 December 1984; pp. 175–179. [Google Scholar]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Grover, L. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on the Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Mermin, N.D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 1992, 68, 557–559. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Ampatzis, M.; Andronikos, T. QKD Based on Symmetric Entangled Bernstein-Vazirani. Entropy 2021, 23, 870. [Google Scholar] [CrossRef] [PubMed]
- Hillery, M.; Bužek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829. [Google Scholar] [CrossRef]
- Cleve, R.; Gottesman, D.; Lo, H.K. How to share a quantum secret. Phys. Rev. Lett. 1999, 83, 648. [Google Scholar] [CrossRef]
- Karlsson, A.; Koashi, M.; Imoto, N. Quantum entanglement for secret sharing and secret splitting. Phys. Rev. A 1999, 59, 162. [Google Scholar] [CrossRef]
- Ampatzis, M.; Andronikos, T. A Symmetric Extensible Protocol for Quantum Secret Sharing. Symmetry 2022, 14, 1692. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Deng, F.G.; Long, G.L.; Liu, X.S. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 2003, 68, 042317. [Google Scholar] [CrossRef]
- Deng, F.G.; Long, G.L. Secure direct communication with a quantum one-time pad. Phys. Rev. A 2004, 69, 052319. [Google Scholar] [CrossRef]
- Wang, C.; Deng, F.G.; Li, Y.S.; Liu, X.S.; Long, G.L. Quantum secure direct communication with high-dimension quantum superdense coding. Phys. Rev. A 2005, 71, 044305. [Google Scholar] [CrossRef]
- Yang, Y.G.; Wen, Q.Y. An efficient two-party quantum private comparison protocol with decoy photons and two-photon entanglement. J. Phys. A Math. Theor. 2009, 42, 055305. [Google Scholar] [CrossRef]
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science (sfcs 1982), Washington, DC, USA, 3–5 November 1982. [Google Scholar] [CrossRef]
- Yao, A.C.C. How to generate and exchange secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science (sfcs 1986), Toronto, ON, Canada, 27–29 October 1986. [Google Scholar] [CrossRef]
- Boudot, F.; Schoenmakers, B.; Traoré, J. A fair and efficient solution to the socialist millionaires’ problem. Discret. Appl. Math. 2001, 111, 23–36. [Google Scholar] [CrossRef]
- Chen, X.B.; Xu, G.; Niu, X.X.; Wen, Q.Y.; Yang, Y.X. An efficient protocol for the private comparison of equal information based on the triplet entangled state and single-particle measurement. Opt. Commun. 2010, 283, 1561–1565. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.B.; Jiang, Z.T. An efficient protocol for the quantum private comparison of equality with W state. Opt. Commun. 2011, 284, 3160–3163. [Google Scholar] [CrossRef]
- Tseng, H.Y.; Lin, J.; Hwang, T. New quantum private comparison protocol using EPR pairs. Quantum Inf. Process. 2011, 11, 373–384. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.B.; Jiang, Z.T.; Cao, Y.Z. A Protocol for the Quantum Private Comparison of Equality with χ-Type State. Int. J. Theor. Phys. 2011, 51, 69–77. [Google Scholar] [CrossRef]
- Jia, H.Y.; Wen, Q.Y.; Li, Y.B.; Gao, F. Quantum Private Comparison Using Genuine Four-Particle Entangled States. Int. J. Theor. Phys. 2011, 51, 1187–1194. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.B.; Jiang, Z.T.; Cao, Y.Z.; Cui, W. New Quantum Private Comparison Protocol Using χ-Type State. Int. J. Theor. Phys. 2012, 51, 1953–1960. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.B. Quantum Private Comparison Based on GHZ Entangled States. Int. J. Theor. Phys. 2012, 51, 3596–3604. [Google Scholar] [CrossRef]
- Ji, Z.X.; Ye, T.Y. Quantum Private Comparison of Equal Information Based on Highly Entangled Six-Qubit Genuine State. Commun. Theor. Phys. 2016, 65, 711–715. [Google Scholar] [CrossRef]
- Chou, W.H.; Hwang, T.; Gu, J. Semi-quantum private comparison protocol under an almost-dishonest third party. arXiv 2016, arXiv:1607.07961. [Google Scholar] [CrossRef]
- He, Z.; Lou, X. Security analysis and improvement in a semi-quantum private comparison without pre-shared key. Quantum Inf. Process. 2023, 22, 150. [Google Scholar] [CrossRef]
- Chen, X.B.; Su, Y.; Niu, X.X.; Yang, Y.X. Efficient and feasible quantum private comparison of equality against the collective amplitude damping noise. Quantum Inf. Process. 2012, 13, 101–112. [Google Scholar] [CrossRef]
- Zi, W.; Guo, F.; Luo, Y.; Cao, S.; Wen, Q. Quantum Private Comparison Protocol with the Random Rotation. Int. J. Theor. Phys. 2013, 52, 3212–3219. [Google Scholar] [CrossRef]
- Hou, M.; Wu, Y. Single-photon-based quantum secure protocol for the socialist millionaires’ problem. Front. Phys. 2024, 12, 1364140. [Google Scholar] [CrossRef]
- Liu, W.; Liu, C.; Wang, H.; Jia, T. Quantum Private Comparison: A Review. IETE Tech. Rev. 2013, 30, 439. [Google Scholar] [CrossRef]
- Jia, H.Y.; Wen, Q.Y.; Song, T.T.; Gao, F. Quantum protocol for millionaire problem. Opt. Commun. 2011, 284, 545–549. [Google Scholar] [CrossRef]
- Lin, S.; Sun, Y.; Liu, X.F.; Yao, Z.Q. Quantum private comparison protocol with d-dimensional Bell states. Quantum Inf. Process. 2012, 12, 559–568. [Google Scholar] [CrossRef]
- Zhang, W.W.; Li, D.; Zhang, K.J.; Zuo, H.J. A quantum protocol for millionaire problem with Bell states. Quantum Inf. Process. 2013, 12, 2241–2249. [Google Scholar] [CrossRef]
- Ye, C.Q.; Ye, T.Y. Multi-party quantum private comparison of size relation with d-level single-particle states. Quantum Inf. Process. 2018, 17, 252. [Google Scholar] [CrossRef]
- Cao, H.; Ma, W.; Lü, L.; He, Y.; Liu, G. Multi-party quantum privacy comparison of size based on d-level GHZ states. Quantum Inf. Process. 2019, 18, 287. [Google Scholar] [CrossRef]
- Wu, W.; Zhao, Y. Quantum private comparison of size using d-level Bell states with a semi-honest third party. Quantum Inf. Process. 2021, 20, 155. [Google Scholar] [CrossRef]
- Chang, Y.J.; Tsai, C.W.; Hwang, T. Multi-user private comparison protocol using GHZ class states. Quantum Inf. Process. 2013, 12, 1077–1088. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.B.; Wang, X.M. Multi-party Quantum Private Comparison Protocol Using d-Dimensional Basis States Without Entanglement Swapping. Int. J. Theor. Phys. 2013, 53, 1085–1091. [Google Scholar] [CrossRef]
- Huang, S.L.; Hwang, T.; Gope, P. Multi-party quantum private comparison with an almost-dishonest third party. Quantum Inf. Process. 2015, 14, 4225–4235. [Google Scholar] [CrossRef]
- Hung, S.M.; Hwang, S.L.; Hwang, T.; Kao, S.H. Multiparty quantum private comparison with almost dishonest third parties for strangers. Quantum Inf. Process. 2016, 16, 36. [Google Scholar] [CrossRef]
- Zhang, J.W.; Xu, G.; Chen, X.B.; Chang, Y.; Dong, Z.C. Improved multiparty quantum private comparison based on quantum homomorphic encryption. Phys. A Stat. Mech. Its Appl. 2023, 610, 128397. [Google Scholar] [CrossRef]
- Zhao-Xu, J.; Tian-Yu, Y. Multi-party quantum private comparison based on the entanglement swapping of d-level cat states and d-level Bell states. Quantum Inf. Process. 2017, 16, 177. [Google Scholar] [CrossRef]
- Ye, T.Y.; Hu, J.L. Multi-Party Quantum Private Comparison Based on Entanglement Swapping of Bell Entangled States within d-Level Quantum System. Int. J. Theor. Phys. 2021, 60, 1471–1480. [Google Scholar] [CrossRef]
- Colbeck, R. Impossibility of secure two-party classical computation. Phys. Rev. A 2007, 76, 062308. [Google Scholar] [CrossRef]
- Crépeau, C.; Gottesman, D.; Smith, A. Secure multi-party quantum computation. In Proceedings of the Thiry-Fourth Annual ACM Symposium on Theory of Computing, STOC02, Montreal, QC Canada, 19–21 May 2002., STOC02. [CrossRef]
- Lo, H.K. Insecurity of quantum secure computations. Phys. Rev. A 1997, 56, 1154–1162. [Google Scholar] [CrossRef]
- Sonnino, G.; Sonnino, A. Efficient Multiparty Protocols Using Generalized Parseval’s Identity and the Theta Algebra. In Proceedings of the 2022 7th International Conference on Mathematics and Computers in Sciences and Industry (MCSI), Athens, Greece, 22–24 August 2022. [Google Scholar] [CrossRef]
- Meyer, D.A. Quantum strategies. Phys. Rev. Lett. 1999, 82, 1052. [Google Scholar] [CrossRef]
- Eisert, J.; Wilkens, M.; Lewenstein, M. Quantum games and quantum strategies. Phys. Rev. Lett. 1999, 83, 3077. [Google Scholar] [CrossRef]
- Andronikos, T.; Sirokofskich, A.; Kastampolidou, K.; Varvouzou, M.; Giannakis, K.; Singh, A. Finite Automata Capturing Winning Sequences for All Possible Variants of the PQ Penny Flip Game. Mathematics 2018, 6, 20. [Google Scholar] [CrossRef]
- Andronikos, T.; Sirokofskich, A. The Connection between the PQ Penny Flip Game and the Dihedral Groups. Mathematics 2021, 9, 1115. [Google Scholar] [CrossRef]
- Andronikos, T. Conditions that enable a player to surely win in sequential quantum games. Quantum Inf. Process. 2022, 21, 268. [Google Scholar] [CrossRef]
- Kastampolidou, K.; Andronikos, T. Quantum Tapsilou—A Quantum Game Inspired by the Traditional Greek Coin Tossing Game Tapsilou. Games 2023, 14, 72. [Google Scholar] [CrossRef]
- Cruz, D.; Fournier, R.; Gremion, F.; Jeannerot, A.; Komagata, K.; Tosic, T.; Thiesbrummel, J.; Chan, C.L.; Macris, N.; Dupertuis, M.A.; et al. Efficient Quantum Algorithms for GHZ and W States, and Implementation on the IBM Quantum Computer. Adv. Quantum Technol. 2019, 2, 1900015. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Yanofsky, N.S.; Mannucci, M.A. Quantum Computing for Computer Scientists; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Wong, T.G. Introduction to Classical and Quantum Computing; Rooted Grove: Omaha, USA, 2022. [Google Scholar]
- Ampatzis, M.; Andronikos, T. Quantum Secret Aggregation Utilizing a Network of Agents. Cryptography 2023, 7, 5. [Google Scholar] [CrossRef]
- Mermin, N. Quantum Computer Science: An Introduction; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Andronikos, T.; Sirokofskich, A. One-to-Many Simultaneous Secure Quantum Information Transmission. Cryptography 2023, 7, 64. [Google Scholar] [CrossRef]
- Deng, F.G.; Li, X.H.; Zhou, H.Y. Efficient high-capacity quantum secret sharing with two-photon entanglement. Phys. Lett. A 2008, 372, 1957–1962. [Google Scholar] [CrossRef]
- Qiskit. Qiskit Open-Source Toolkit for Useful Quantum. Available online: https://www.ibm.com/quantum/qiskit (accessed on 2 March 2024).
- Tsai, C.W.; Hsieh, C.R.; Hwang, T. Dense coding using cluster states and its application on deterministic secure quantum communication. Eur. Phys. J. D 2011, 61, 779–783. [Google Scholar] [CrossRef]
- Hwang, T.; Hwang, C.C.; Tsai, C.W. Quantum key distribution protocol using dense coding of three-qubit W state. Eur. Phys. J. D 2011, 61, 785–790. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, W.F.; Zhang, S.B. Efficient multiparty quantum private comparison protocol based on single photons and rotation encryption. Quantum Inf. Process. 2023, 22, 272. [Google Scholar] [CrossRef]
- Banerjee, A.; Pathak, A. Maximally efficient protocols for direct secure quantum communication. Phys. Lett. A 2012, 376, 2944–2950. [Google Scholar] [CrossRef]
- Joy, D.; Surendran, S.P.; Sabir, M. Efficient deterministic secure quantum communication protocols using multipartite entangled states. Quantum Inf. Process. 2017, 16, 157. [Google Scholar] [CrossRef]
- Song, X.; Wen, A.; Gou, R. Multiparty Quantum Private Comparison of Size Relation Based on Single-Particle States. IEEE Access 2019, 7, 142507–142514. [Google Scholar] [CrossRef]
- Neigovzen, R.; Rodó, C.; Adesso, G.; Sanpera, A. Multipartite continuous-variable solution for the Byzantine agreement problem. Phys. Rev. A 2008, 77, 062307. [Google Scholar] [CrossRef]
- Feng, Y.; Shi, R.; Zhou, J.; Liao, Q.; Guo, Y. Quantum Byzantine Agreement with Tripartite Entangled States. Int. J. Theor. Phys. 2019, 58, 1482–1498. [Google Scholar] [CrossRef]
- Wang, W.; Yu, Y.; Du, L. Quantum blockchain based on asymmetric quantum encryption and a stake vote consensus algorithm. Sci. Rep. 2022, 12, 8606. [Google Scholar] [CrossRef]
- Yang, Z.; Salman, T.; Jain, R.; Pietro, R.D. Decentralization Using Quantum Blockchain: A Theoretical Analysis. IEEE Trans. Quantum Eng. 2022, 3, 4100716. [Google Scholar] [CrossRef]
- Qu, Z.; Zhang, Z.; Liu, B.; Tiwari, P.; Ning, X.; Muhammad, K. Quantum detectable Byzantine agreement for distributed data trust management in blockchain. Inf. Sci. 2023, 637, 118909. [Google Scholar] [CrossRef]
- Ikeda, K.; Lowe, A. Quantum protocol for decision making and verifying truthfulness among N-quantum parties: Solution and extension of the quantum coin flipping game. IET Quantum Commun. 2023, 4, 218–227. [Google Scholar] [CrossRef]
- Huttner, B.; Imoto, N.; Gisin, N.; Mor, T. Quantum cryptography with coherent states. Phys. Rev. A 1995, 51, 1863. [Google Scholar] [CrossRef]
- Lütkenhaus, N. Security against individual attacks for realistic quantum key distribution. Phys. Rev. A 2000, 61, 052304. [Google Scholar] [CrossRef]
- Brassard, G.; Lütkenhaus, N.; Mor, T.; Sanders, B.C. Limitations on practical quantum cryptography. Phys. Rev. Lett. 2000, 85, 1330. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).