Advanced Trajectory Analysis of NASA’s Juno Mission Using Unsupervised Machine Learning: Insights into Jupiter’s Orbital Dynamics
Abstract
1. Introduction
2. Related Work
3. Problem Statement
4. Data Source and Pre-Processing
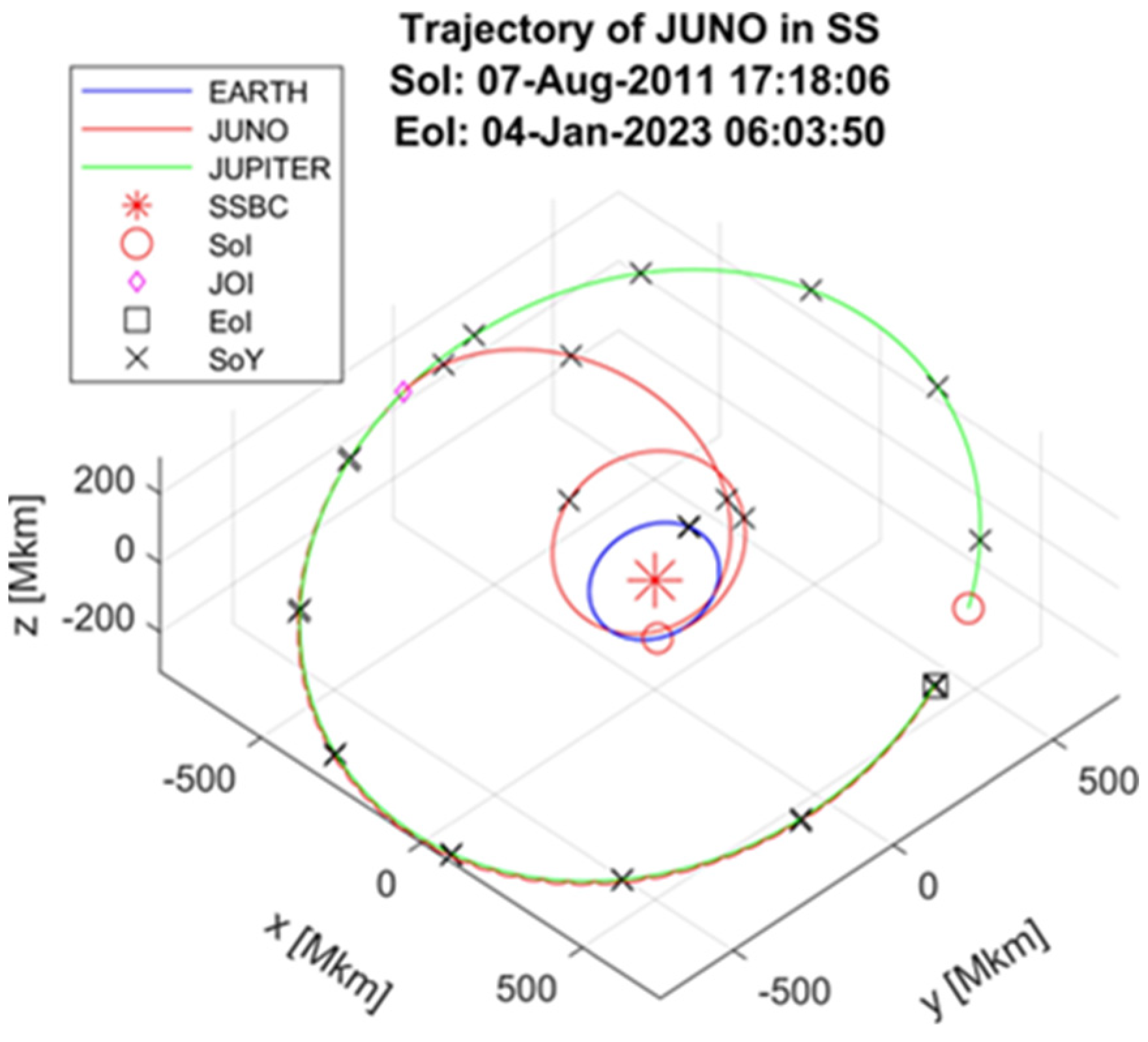
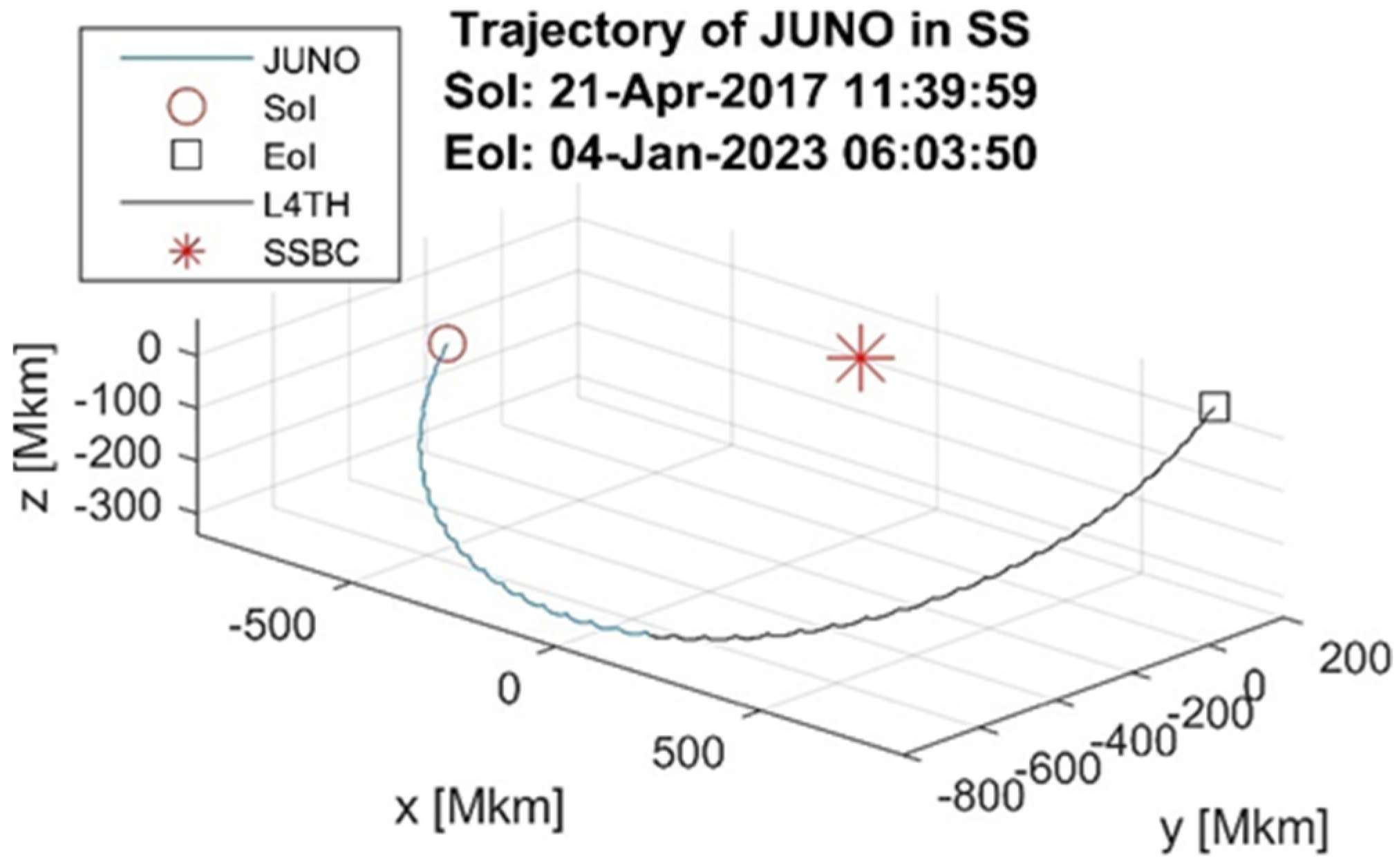
5. Juno Trajectory Geometry
5.1. Trajectory Components
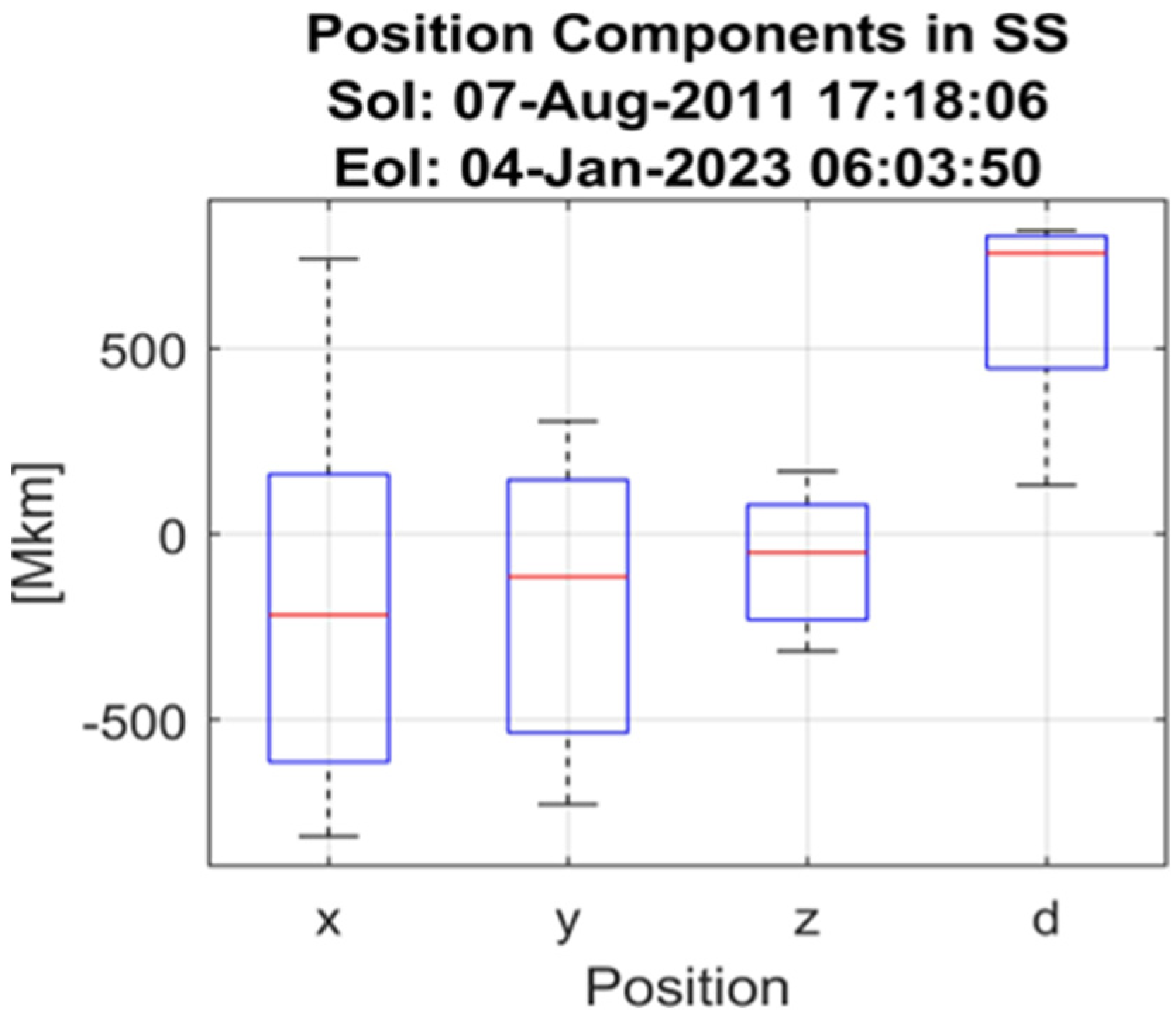
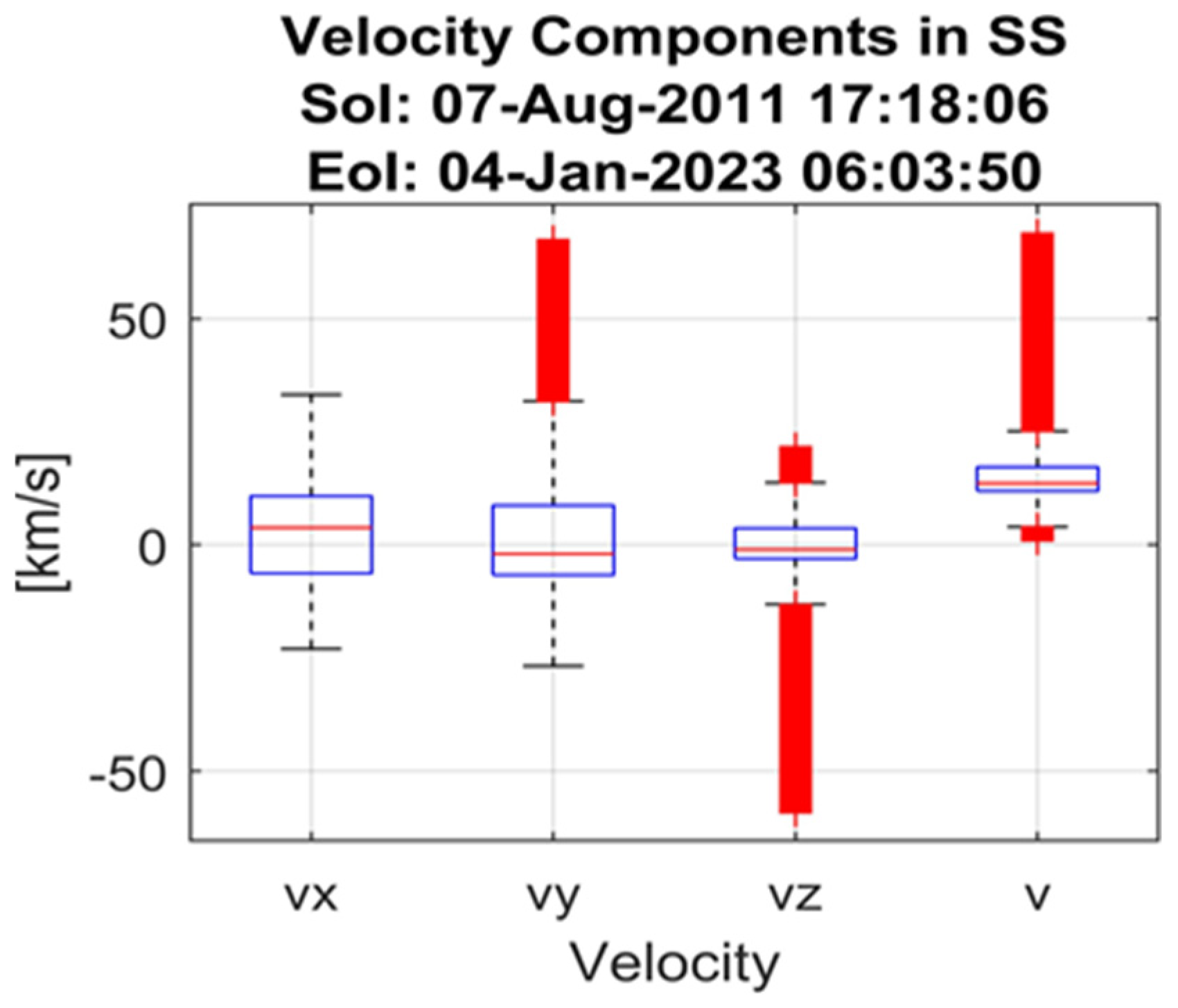
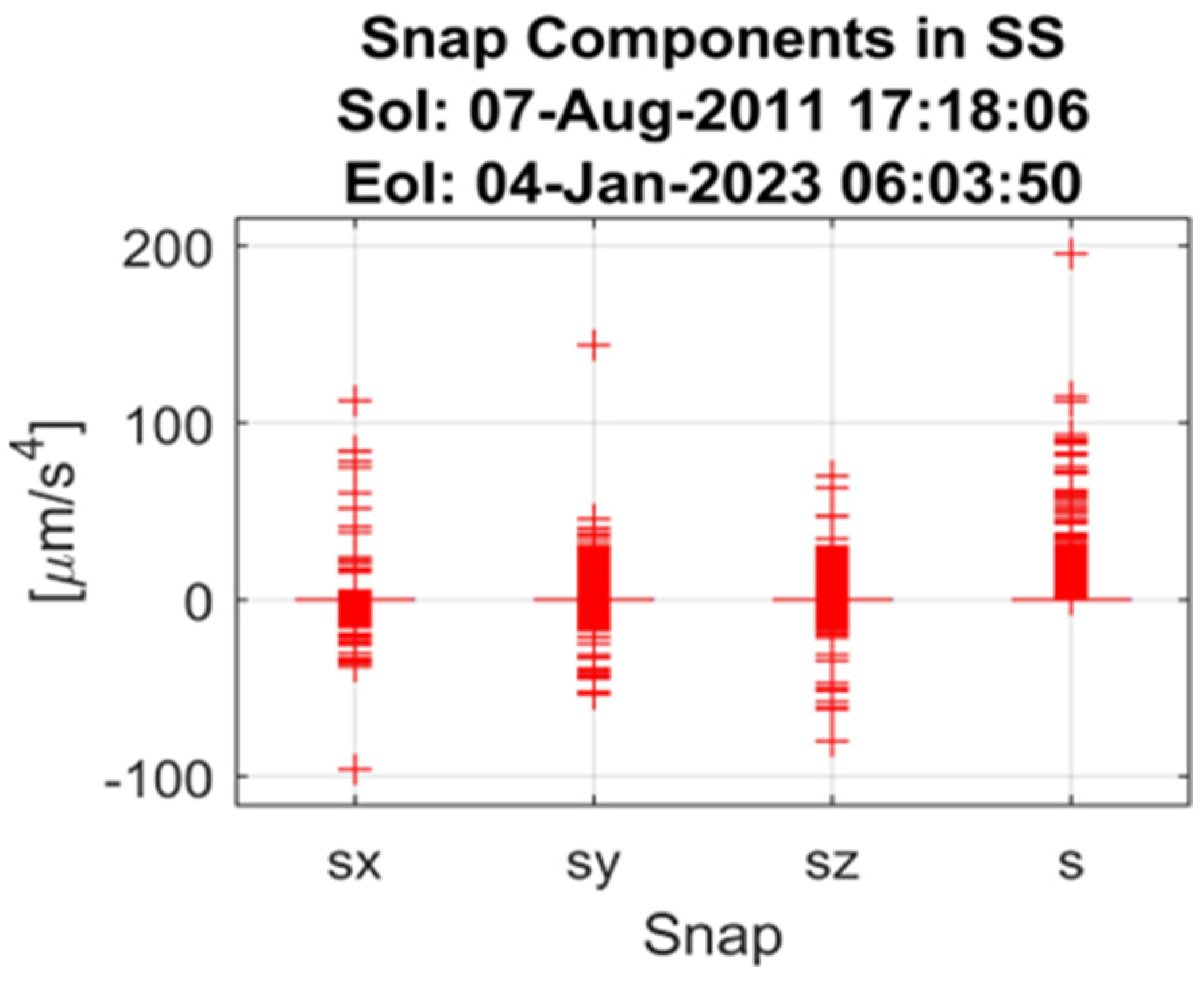
5.2. Statistical Properties of Position, Velocity and Acceleration Components
- The center line of the box represents the median, which is the middle value when the data are ordered from least to greatest.
- The box itself encompasses the middle 50% of the data, also known as the interquartile range (IQR). The lower boundary of the box corresponds to the first quartile (Q1), while the upper boundary indicates the third quartile (Q3).
- Lines extending from the box, called whiskers, typically reach up to 1.5 times the IQR from the quartiles. These whiskers capture most of the remaining data points.
- Any data points falling outside the whiskers are considered outliers and are plotted individually as circles or asterisks.
- Center: The typical value of the acceleration derivative.
- Spread: How much the data vary around the center.
- Skewness: If the distribution leans toward positive or negative values.
- Outliers: Any extreme values in the dataset.
6. Methodology
- (i)
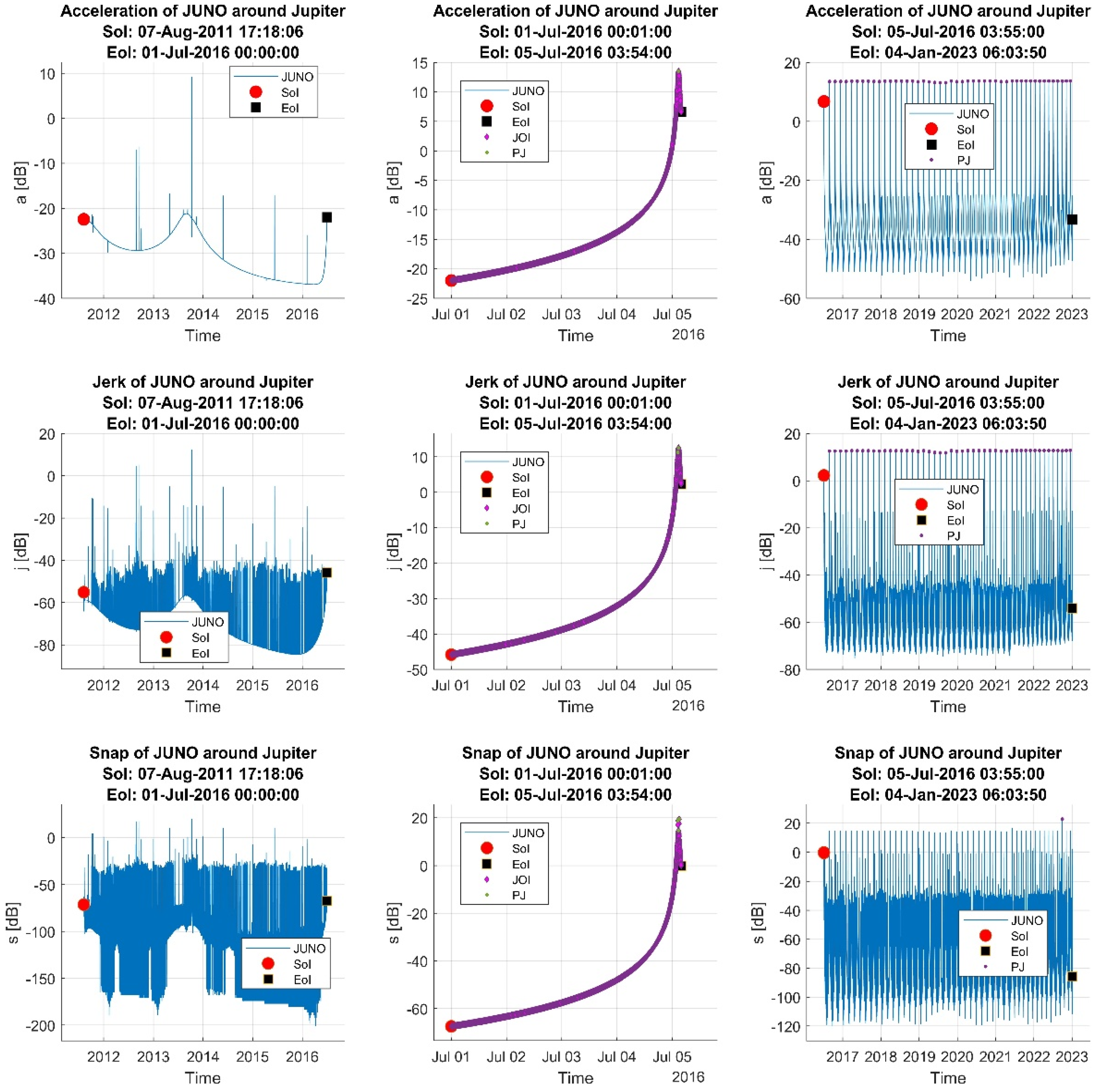
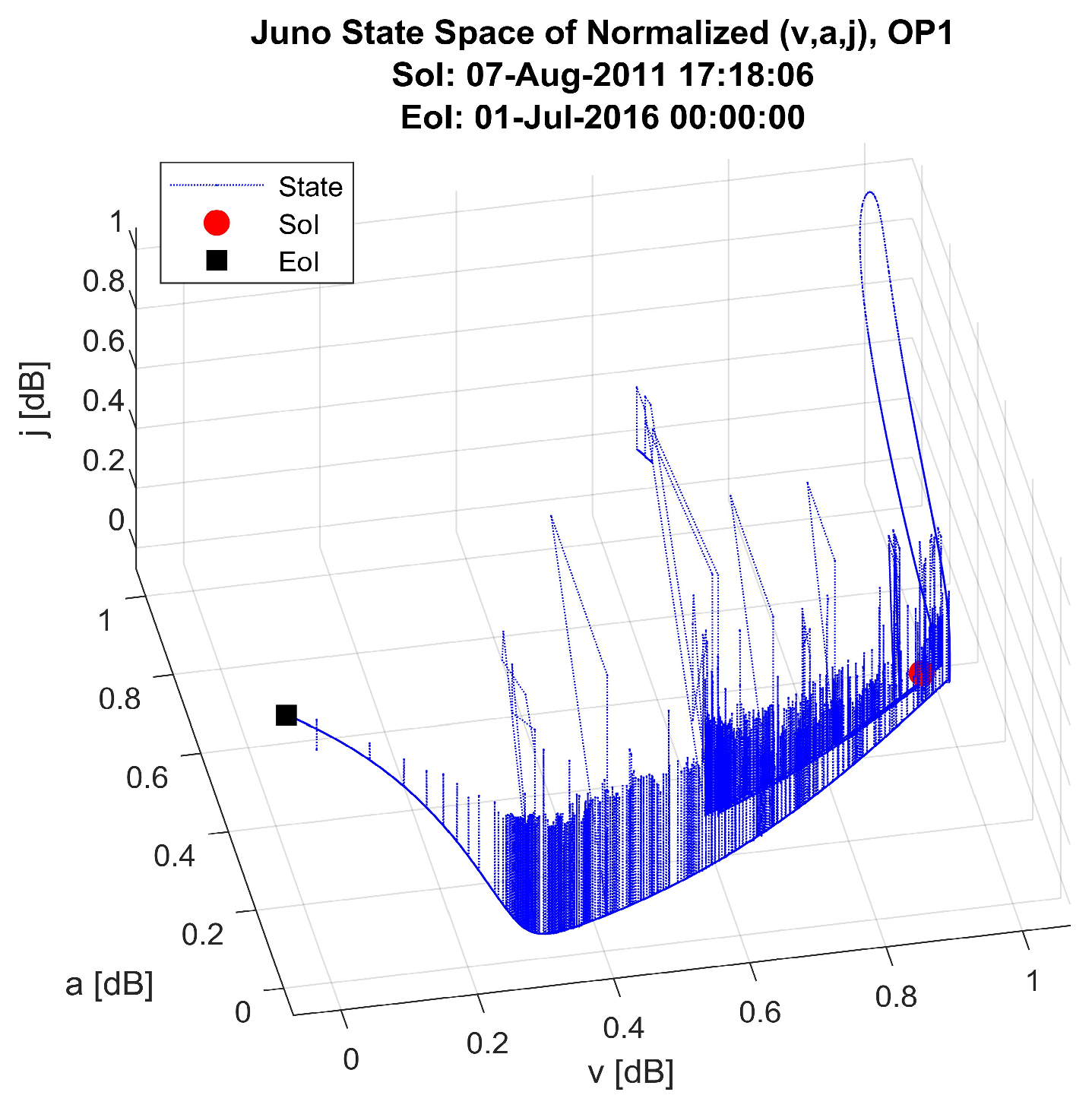
- OP1: Before the JOI phase, Juno’s trajectory is a smoothed 3D curve in the solar system. This phase lasts approximately five years after the launch from the Earth. The reference system is the solar system.
- (ii)
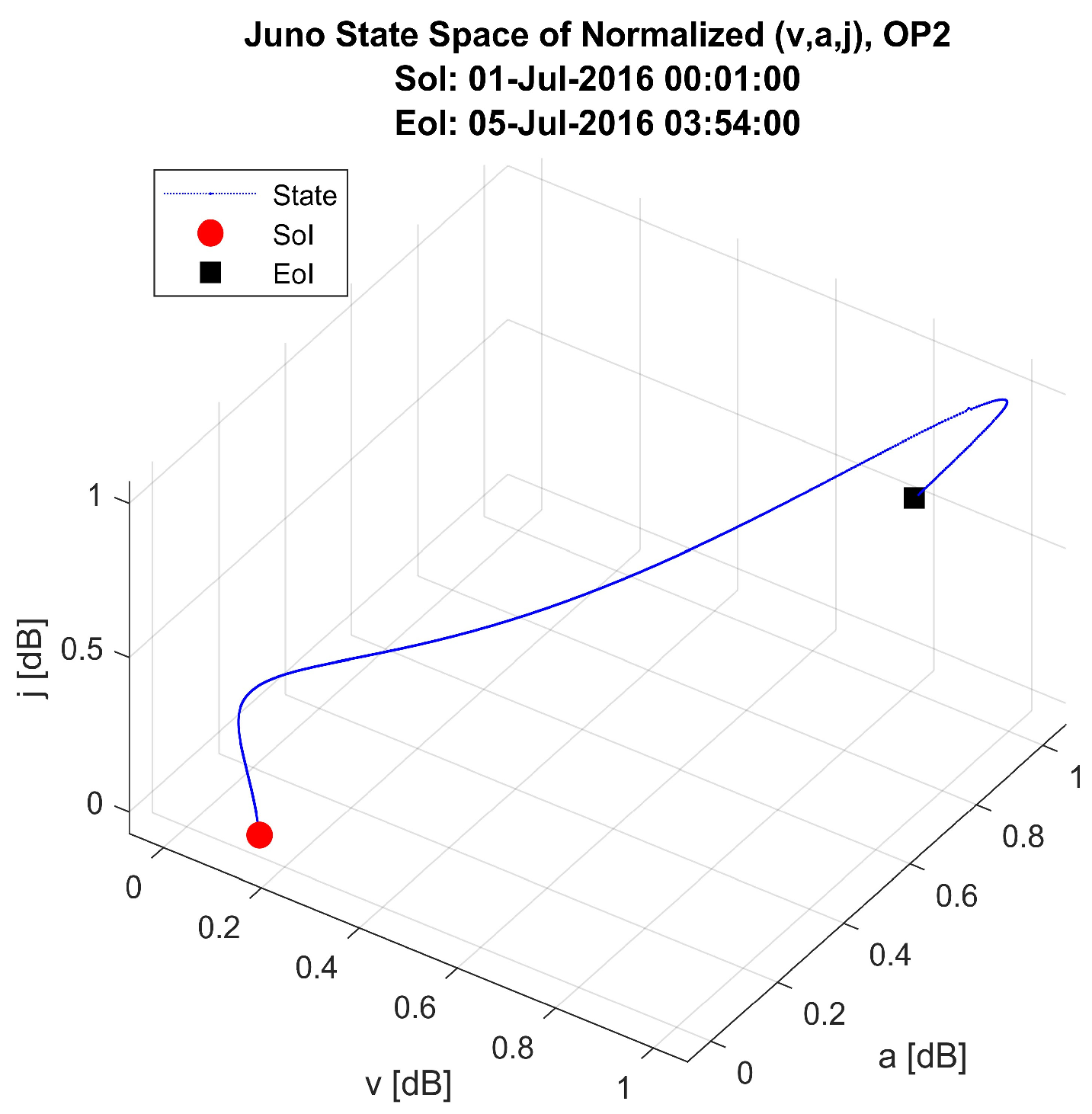
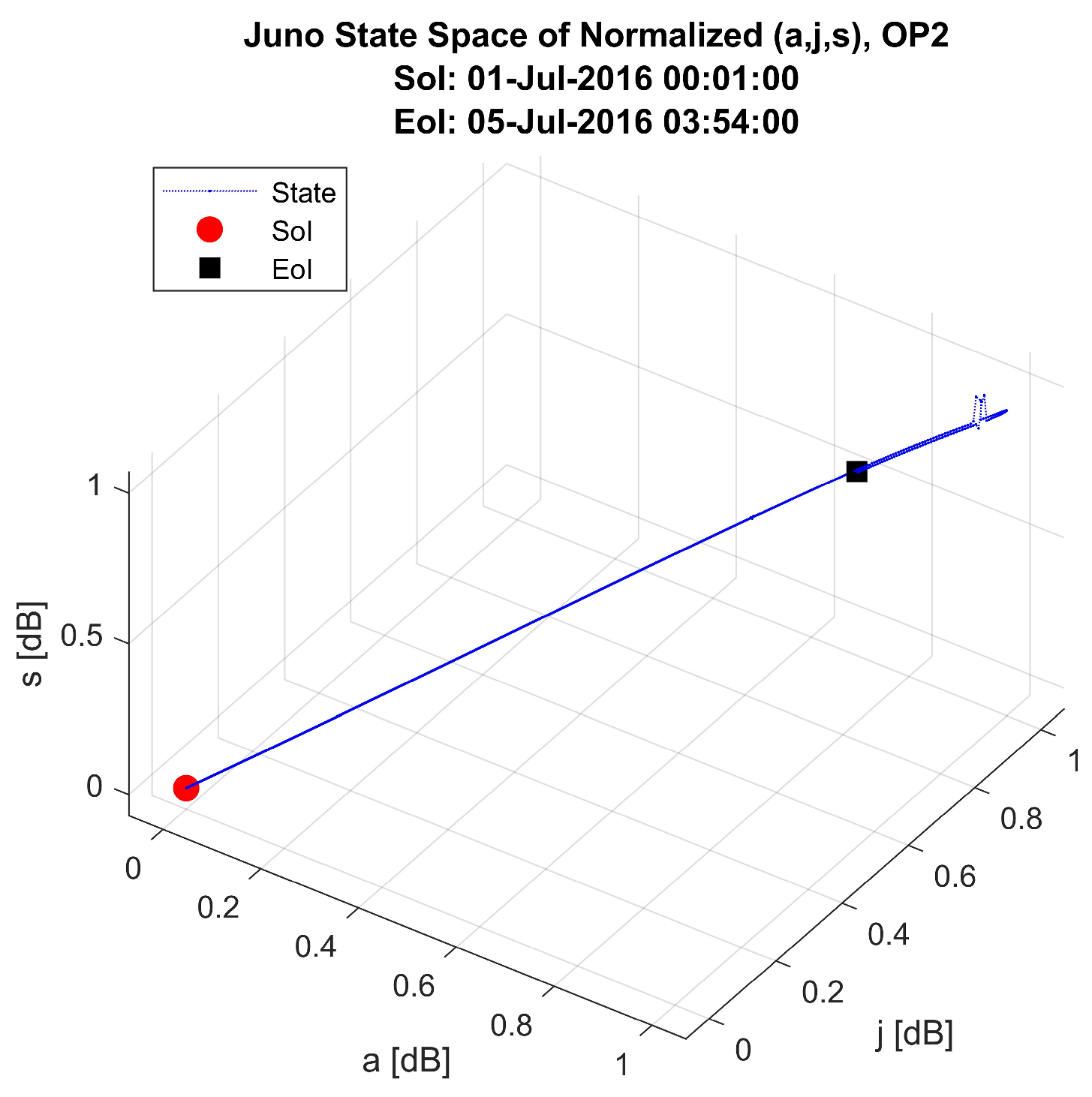
- OP2: In the JOI phase, Juno approaches Jupiter and, based on the gravity effects, starts, step-by-step, to move around it. The reference system remains the solar system.
- (iii)
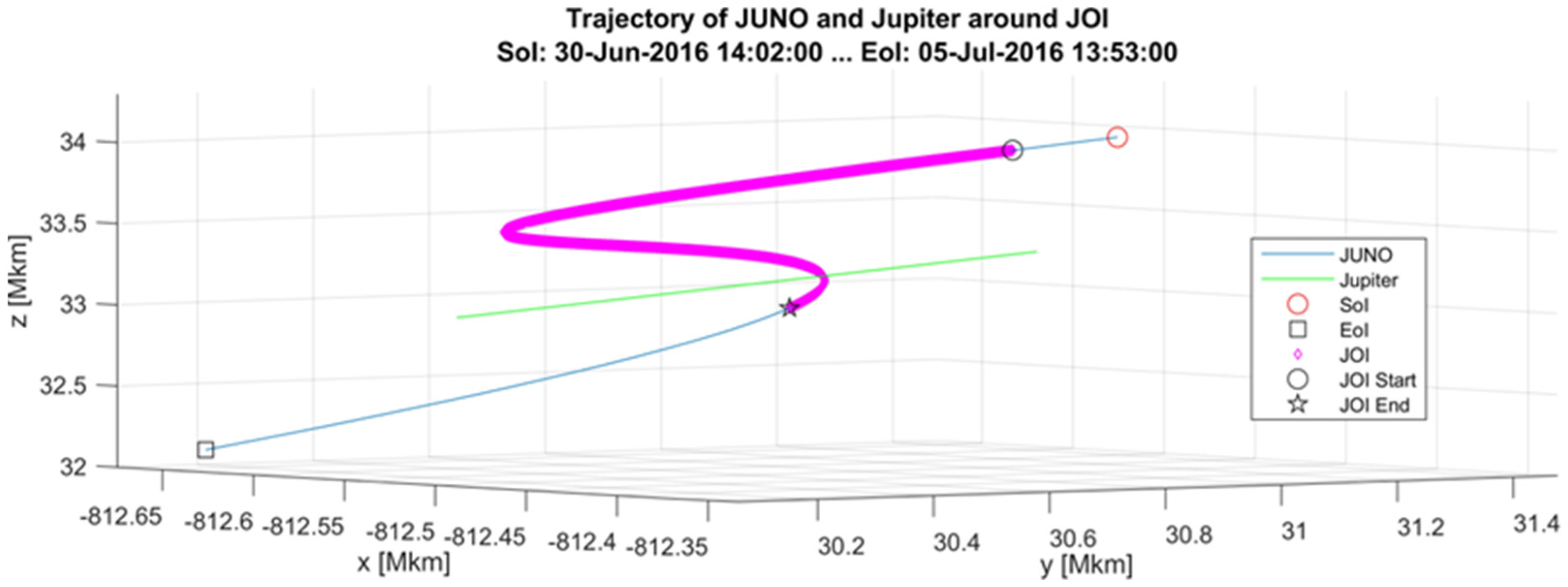
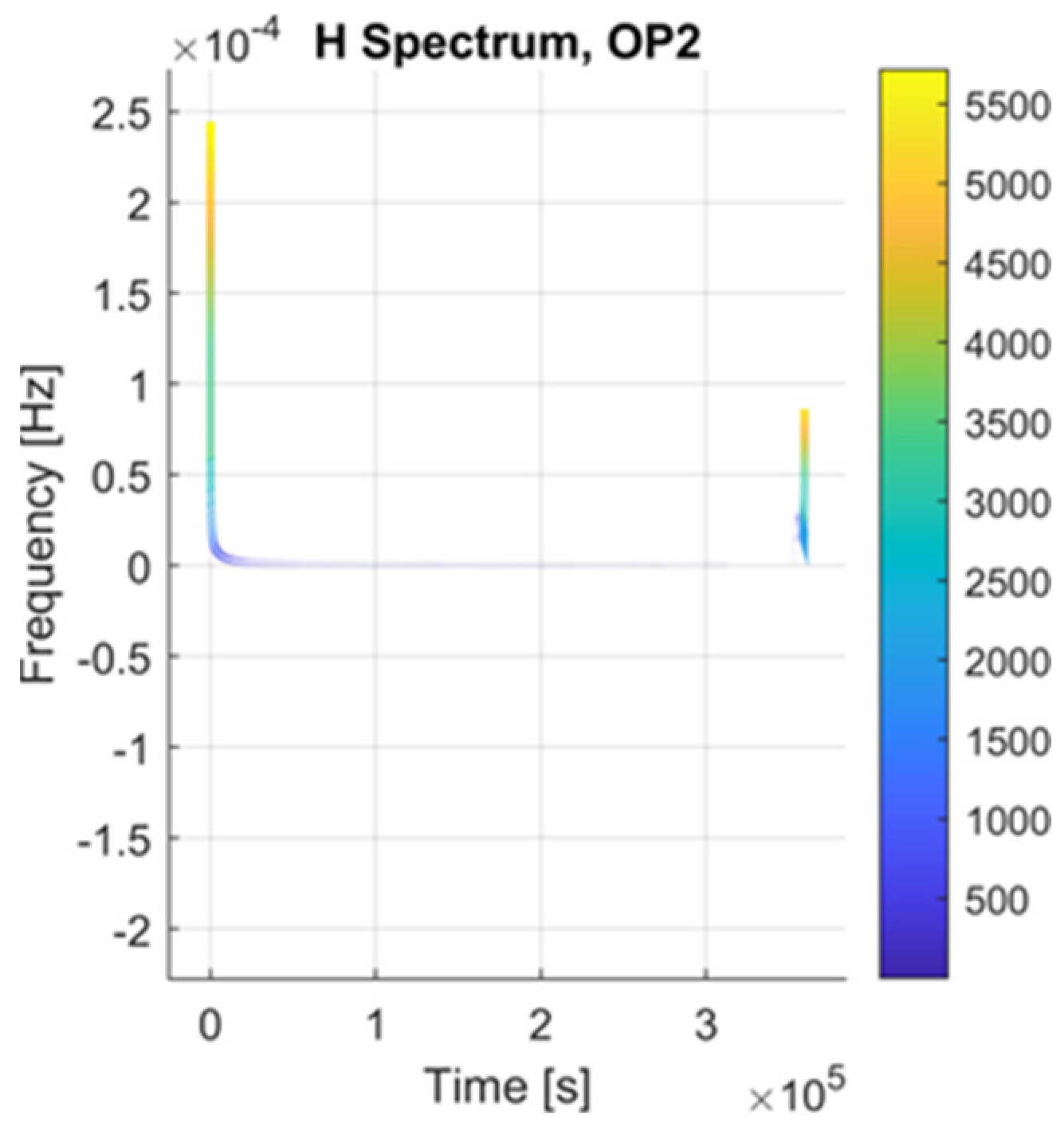
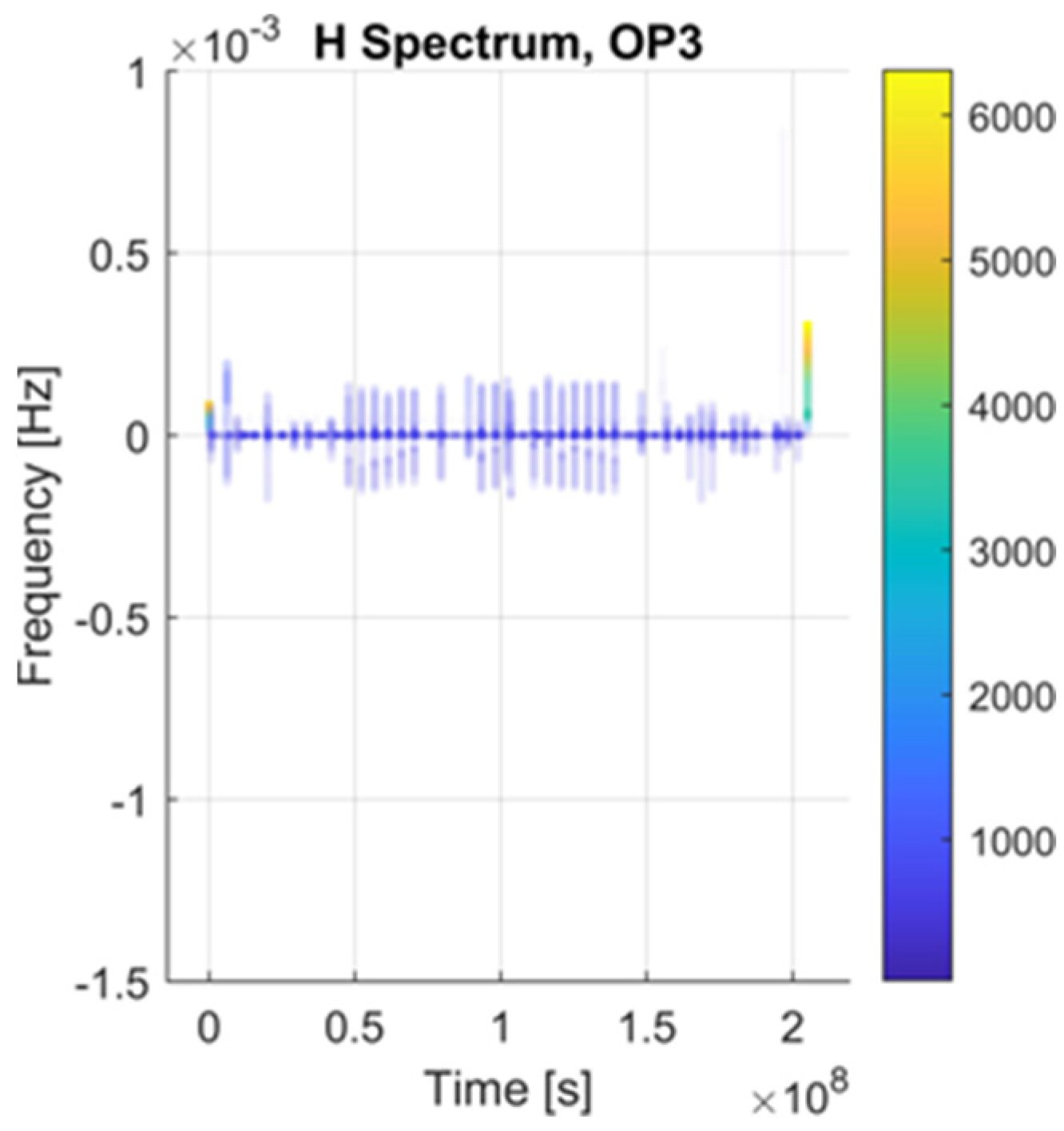
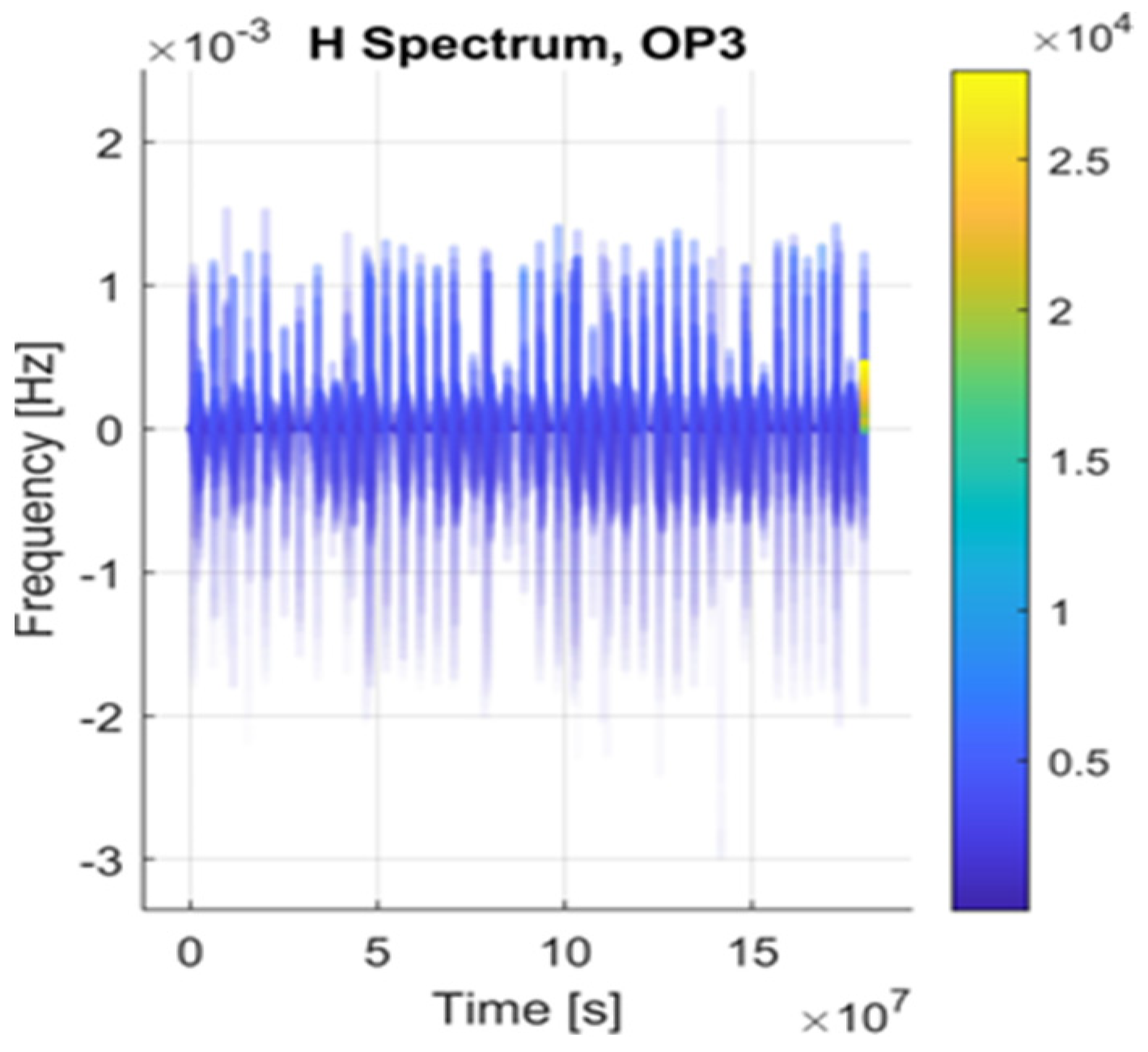
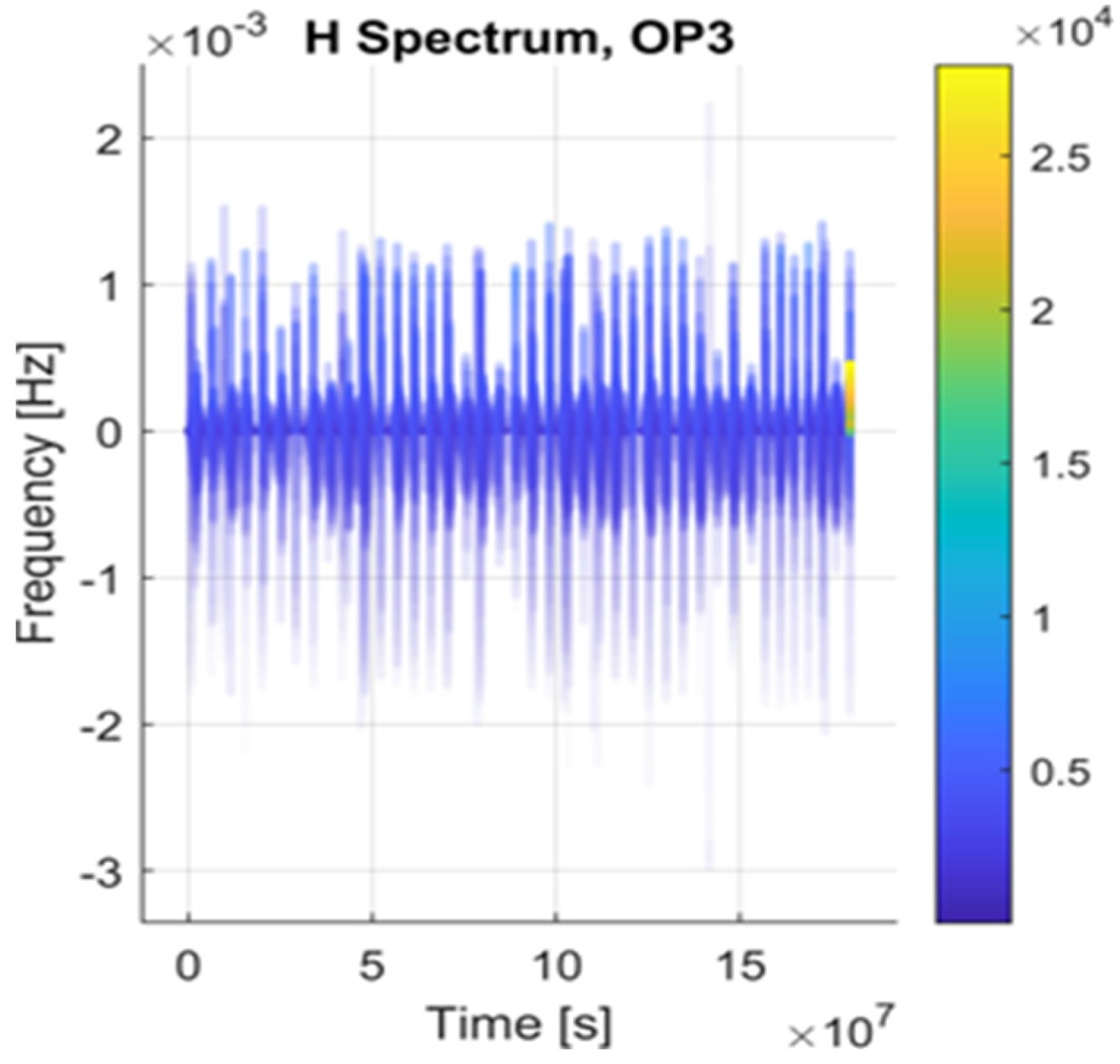
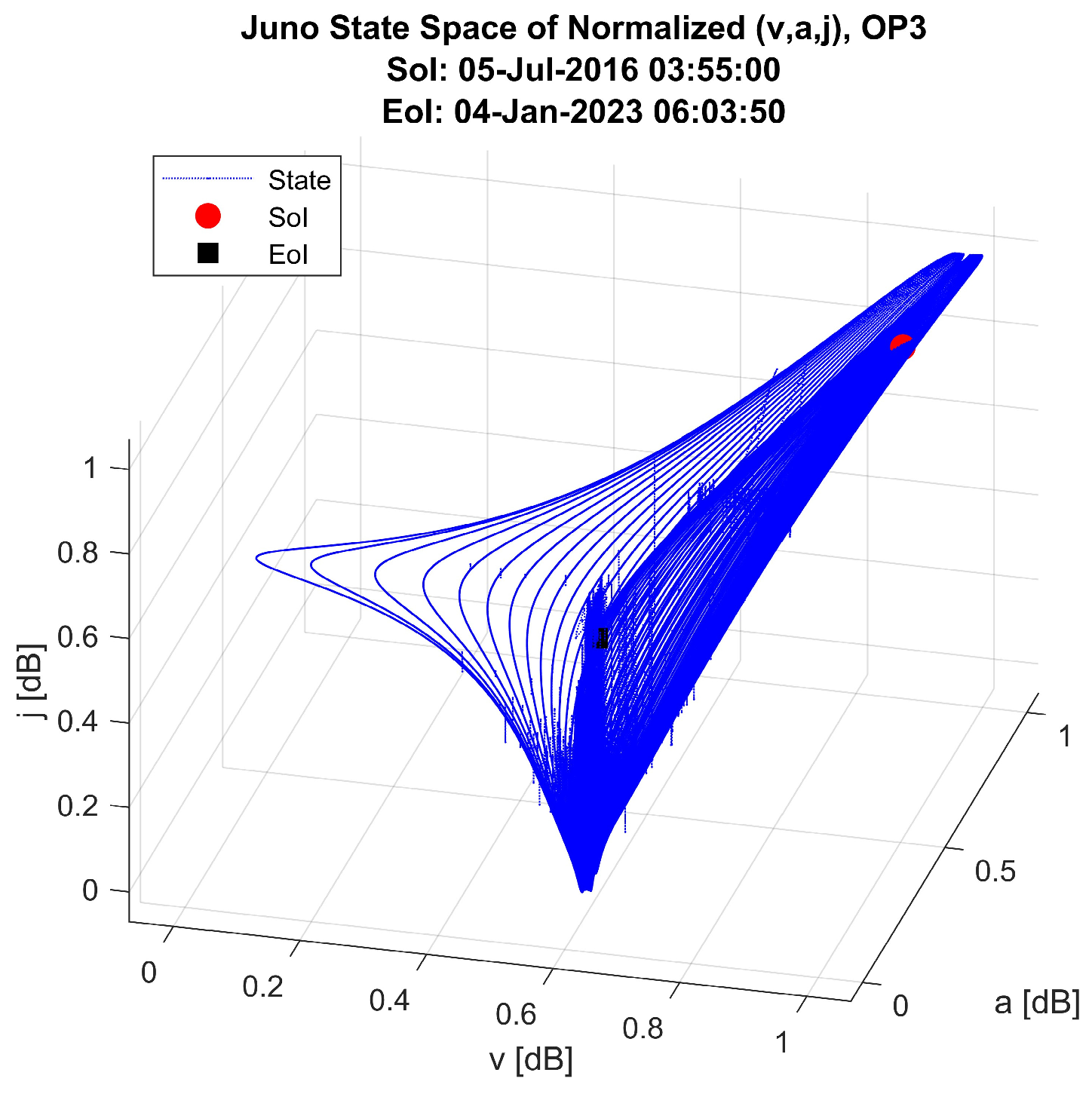
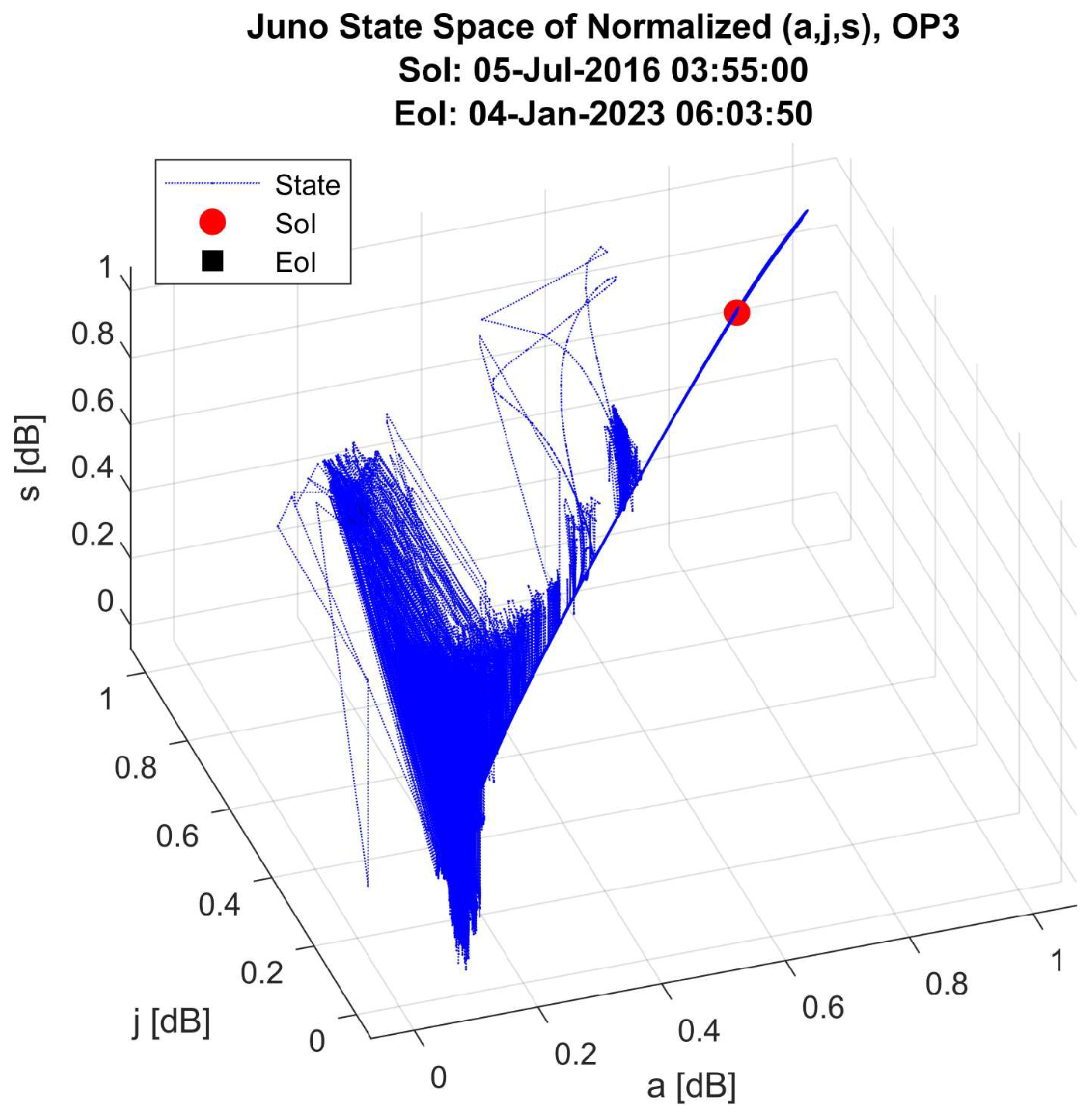
- OP3: After the JOI phase in the solar reference system, Juno has a helicoid orbit in 3D with Jupiter in the gravity center (see Figure 3). In a time of weeks, the trajectory of Juno around Jupiter is an ellipse, with one of the focal points being Jupiter. It should be mentioned that this trajectory modifies slowly on the scale of several months or years, and this relative trajectory is slowly modifying over time, too. An overview of the applied methods is given in Table 2. Evaluation of the acceleration, jerk, and snap is considered in each operation phase to be relative to the barycenter of the solar system. Trajectory modification is considered an extreme event (EE).
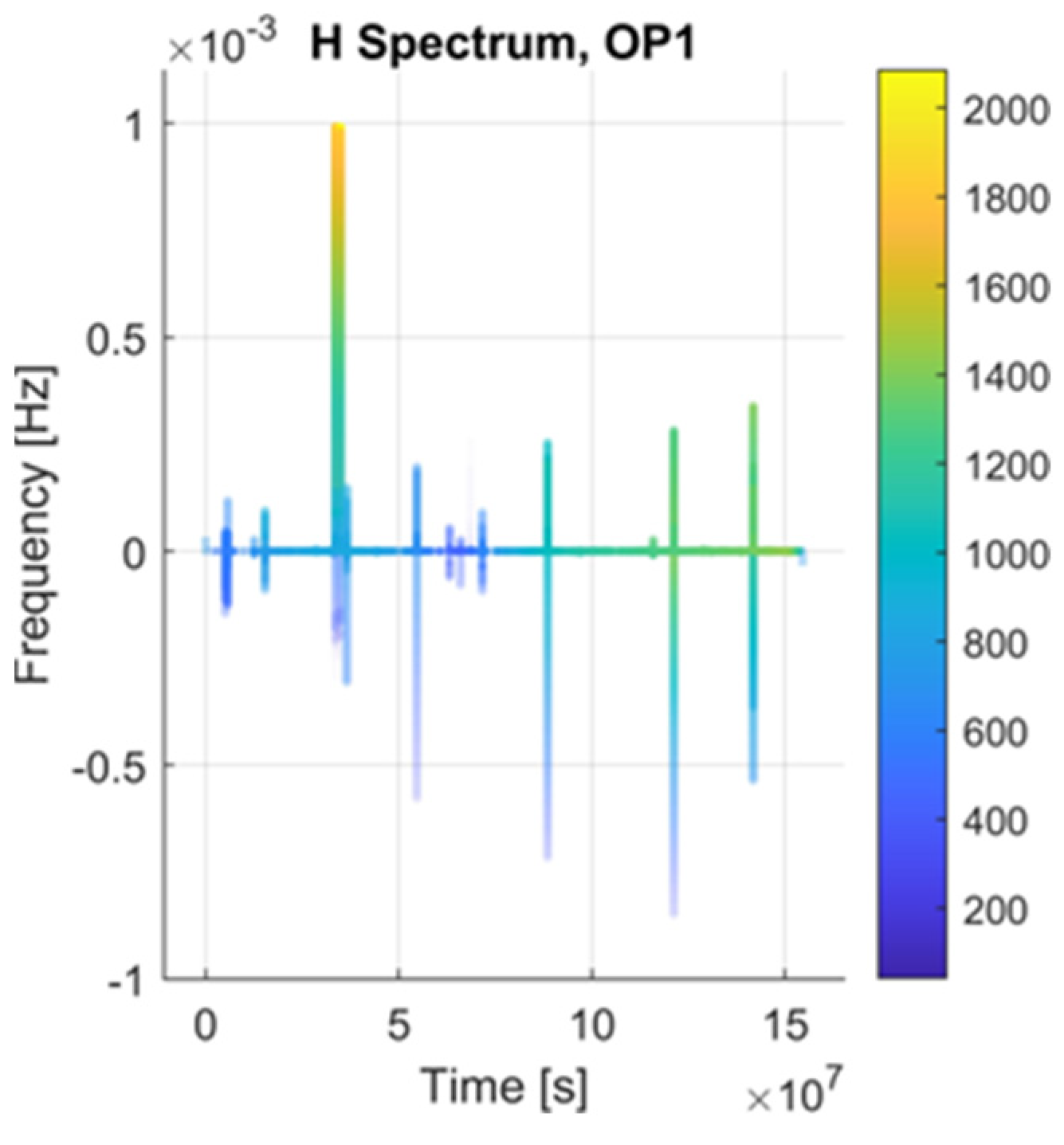
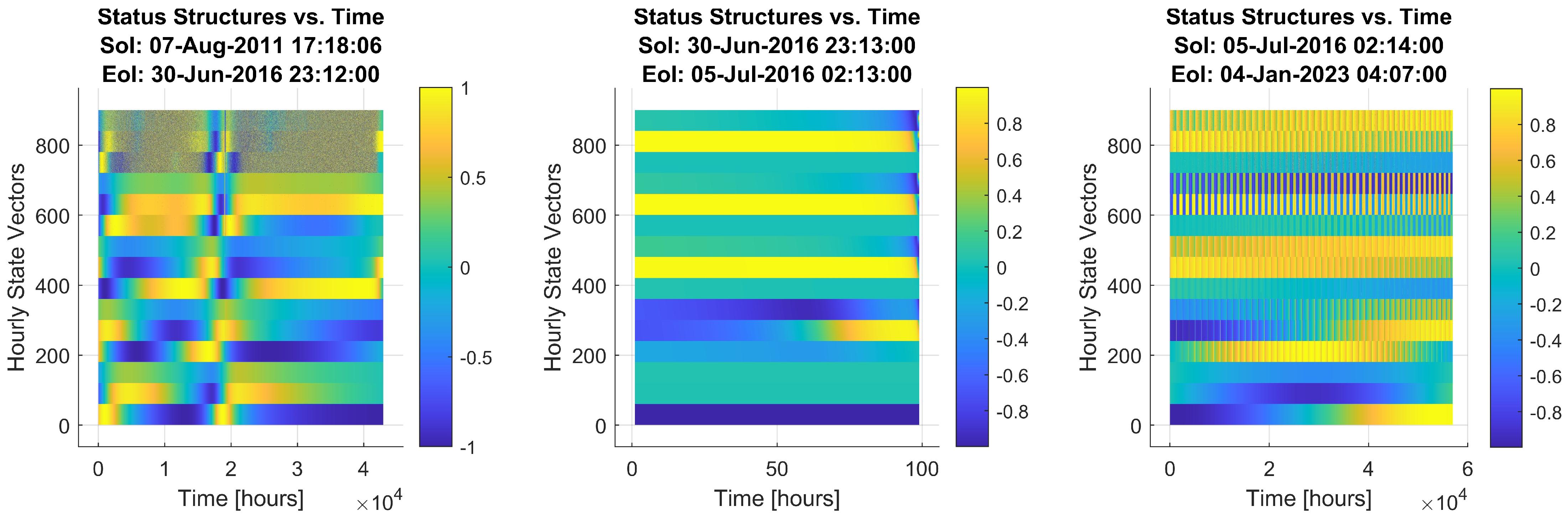
6.1. Detection of Trajectory Modification
6.2. State Space Analysis and Discussion
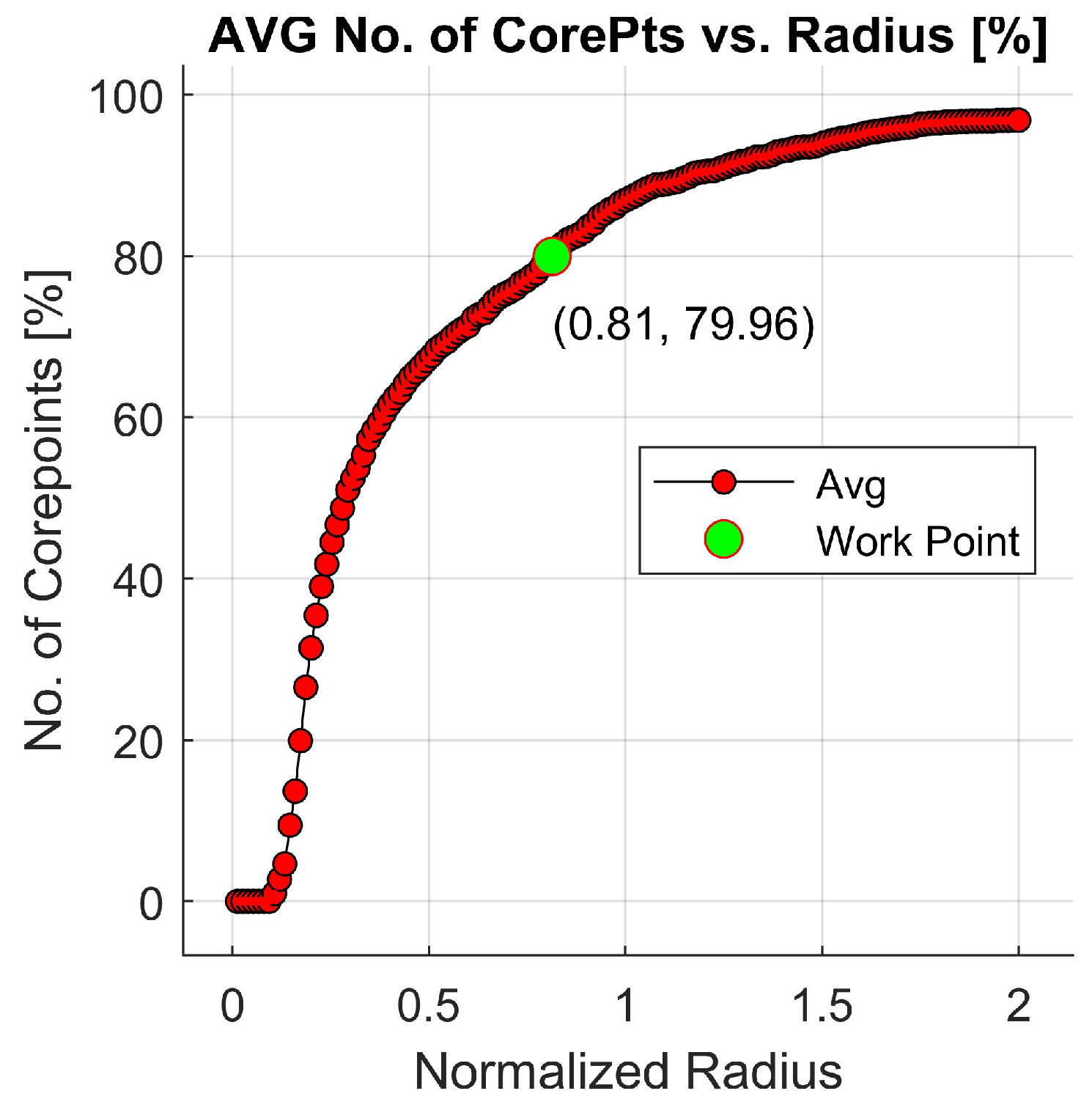
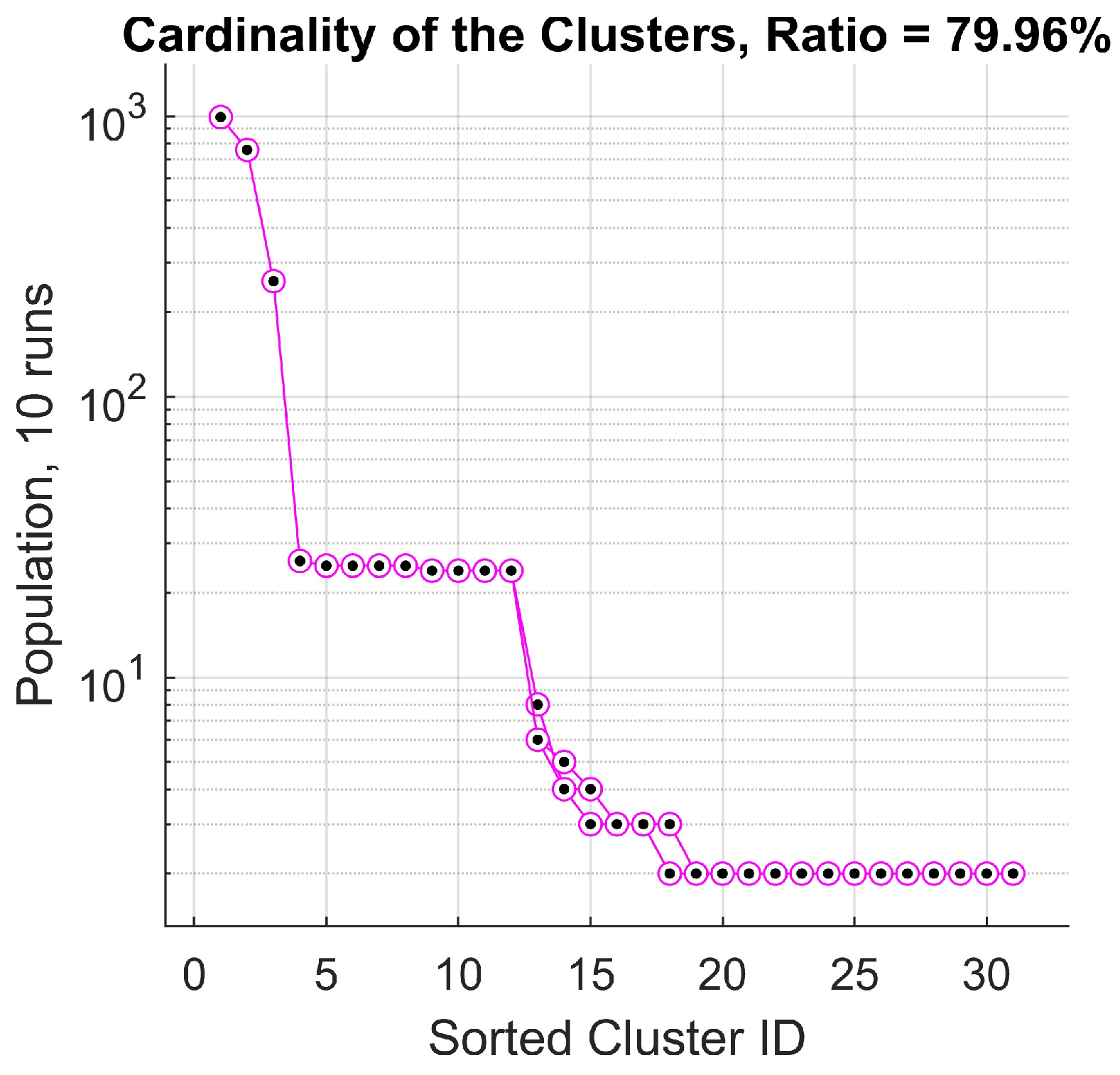
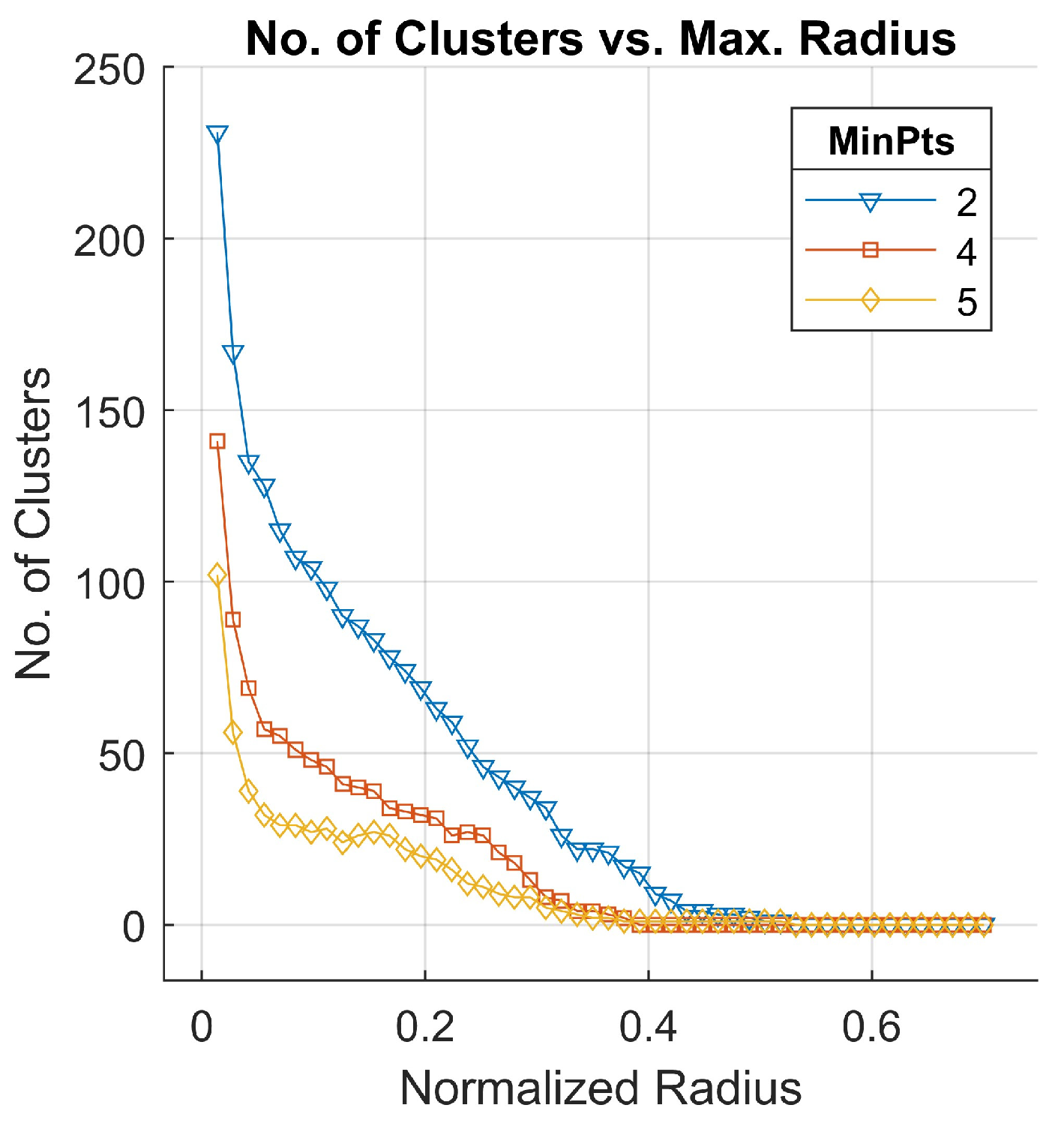
6.3. Cauterization Analysis and Discussion
7. Conclusions
8. Limitations and Future Work
- Adapting our methods for real-time trajectory analysis and anomaly detection during ongoing missions.
- Integrating machine learning techniques to further enhance the prediction accuracy and pattern recognition in trajectory data.
- Extending our approach to analyze and optimize multi-body trajectories for future complex mission designs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yamaguchi, T.; Mimasu, Y.; Tsuda, Y.; Funase, R.; Sawada, H.; Mori, O.; Morimoto, M.Y.; Takeuchi, H.; Yoshikawa, M. Trajectory analysis of solar sail spacecraft considering the large uncertainty of solar radiation pressure. In Proceedings of the ISSFD21, Advances in the Astronautical Sciences, Toulouse, France, 28 September–2 October 2009; Volume 134, pp. 123–142. [Google Scholar]
- Elmer, J.; Jones, B.L.; Nagin, D.S. Using the Beta distribution in group-based trajectory models. BMC Med. Res. Methodol. 2018, 18, 152. [Google Scholar] [CrossRef] [PubMed]
- Föhn, M.; Galli, A.; Vorburger, A.; Tulej, M.; Lasi, D.; Riedo, A.; Fausch, R.; Althaus, M.; Brungger, S.; Fahrer, P.; et al. Description of the Mass Spectrometer for the Jupiter Icy Moons Explorer Mission. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 6–13 March 2021. [Google Scholar] [CrossRef]
- Matousek, S. The Juno new frontiers mission. Acta Astronaut. 2007, 61, 932–939. [Google Scholar] [CrossRef]
- Grammier, R.S. A look inside the Juno Mission to Jupiter. In Proceedings of the 2009 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2009; pp. 1–10. [Google Scholar]
- Nybakken, R. The Juno mission to Jupiter—A pre-launch update. In Proceedings of the 2011 Aerospace Conference, Big Sky, MT, USA, 5–12 March 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–8. [Google Scholar]
- Nybakken, R. The Juno mission to Jupiter launch campaign and early cruise report. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012; pp. 1–14. [Google Scholar]
- Lewis, J. Juno spacecraft operations lessons learned for early cruise mission phases. In Proceedings of the 2014 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2014; pp. 1–20. [Google Scholar]
- Stephens, S.K. The Juno mission to Jupiter: Lessons from cruise and plans for orbital operations and science return. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–20. [Google Scholar]
- Demyanov, V.V.; Yasyukevich, Y.V.; Klimenko, M.V.; Klimenko, V.V.; Sergeeva, M.A. The second-order derivative of GPS carrier phase as a promising means for ionospheric scintillation research. Pure Appl. Geophys. 2019, 176, 4555–4573. [Google Scholar] [CrossRef]
- Juuso, E.; Karioja, K.; Nissilä, J. Real order derivatives and spectral norms in fault detection. In Proceedings of the 5th International Conference on Maintenance, Condition Monitoring and Diagnostics, Oulu, Finland, 16–17 February 2021; Juuso, E., Galar, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2023. MCMD 2021. pp. 105–116. [Google Scholar] [CrossRef]
- Presser, T.; Dasgupta, A.; Erwin, D.; Oberai, A. Diffusion models for generating ballistic spacecraft trajectories. arXiv 2024, arXiv:2405.11738. [Google Scholar]
- Yu, Z.; Chen, W.; Yu, W. Analytical trajectory prediction of high-eccentricity spacecraft transfer orbits considering J2 perturbation. Aerosp. Sci. Technol. 2024, 153, 109462. [Google Scholar] [CrossRef]
- Briden, J.; Johnson, B.; Linares, R.; Cauligi, A. Diffusion policies for generative modeling of spacecraft trajectories. arXiv 2025, arXiv:2501.00915. [Google Scholar]
- Acton, C.H.; Bachman, N.; Elson, L.S.; Semenov, B.; Wright, E.L. SPICE: A real example of data system reuse to reduce the costs of ground data systems development and mission operations. In Proceedings of the 2003 IEEE Aerospace Conference, Big Sky, MT, USA, 8–15 March 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 1–9. [Google Scholar]
- Space Studies Board. Data Management and Computation—Volume I: Issues and Recommendations; National Academies Press: Washington, DC, USA, 1982. [Google Scholar] [CrossRef]
- Panuju, D.R.; Paull, D.J.; Griffin, A.L. Change detection techniques based on multispectral images for investigating land cover dynamics. Remote Sens. 2020, 12, 1781. [Google Scholar] [CrossRef]
- García, S.; Luengo, J.; Herrera, F. Data preparation basic models. In Data Preprocessing in Data Mining; Springer: Cham, Switzerland, 2015; pp. 39–57. [Google Scholar] [CrossRef]
- Thompson, P.F.; Abrahamson, M.; Ardalan, S.; Bordi, J.J. Reconstruction of Earth flyby by the Juno spacecraft. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Santa Fe, NM, USA, 26–30 January 2014; No. AAS 14-435. American Astronautical Society: Springfield, VA, USA, 2014. [Google Scholar]
- Kowalkowski, T.; Johannesen, J.; Lam, T. Launch period development for the Juno mission to Jupiter. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2008; p. 7369. [Google Scholar]
- Stephens, S.K. Juno at Jupiter: The mission and its path to unveiling secrets of the history of the solar system. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; pp. 1–19. [Google Scholar] [CrossRef]
- Pavlak, T.A.; Frauenholz, R.B.; Helfrich, C.E.; Kangas, J.A.; Bordi, J.J. Maneuver design for the Juno mission: Inner cruise. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, San Diego, CA, USA, 4–7 August 2014; p. 4149. [Google Scholar]
- Chang, X.H.; Cui, P.Y.; Cui, H.T. Research on autonomous navigation method of deep space cruise phase based on the Sun observation. Yuhang Xuebao/J. Astronaut. 2010, 31, 1017–1023. [Google Scholar]
- Pavlak, T.A.; Bhat, R.S.; Stumpf, P.W. Maneuver Operations During Juno’s Approach, Orbit Insertion, and Early Orbit Phase. In Proceedings of the 27th AAS/AIAA Space Flight Mechanics Meeting, AAS 17-422, San Antonio, TX, USA, 5–9 February 2017; Advances in the Astronautical Sciences (AAS) series. American Astronautical Society (AAS): Springfield, VA, USA, 2017; Volume 161. [Google Scholar]
- Janssen, M.A.; Oswald, J.E.; Brown, S.T.; Gulkis, S.; Levin, S.M.; Bolton, S.J.; Wang, C.C. MWR: Microwave radiometer for the Juno mission to Jupiter. Space Sci. Rev. 2017, 213, 139–185. [Google Scholar] [CrossRef]
- Lee, M.; Weidner, R.J. Juno mission simulation. In Proceedings of the 2008 IEEE Aerospace Conference 2008, Big Sky, MT, USA, 1–8 March 2008; pp. 1–9. [Google Scholar]
- Bordi, J.; Bryant, L. Conjunction Assessment Plans for the Juno Earth Flyby. NASA Technical Reports Server; 2013. Available online: https://ntrs.nasa.gov/citations/20150007245 (accessed on 22 January 2025).
- Dawson, S.; Stella, P.; McAlpine, W.; Smith, B. JUNO photovoltaic power at Jupiter. In Proceedings of the 10th International Energy Conversion Engineering Conference, Atlanta, GA, USA, 30 July–1 August 2012; p. 3833. [Google Scholar] [CrossRef][Green Version]
- Bolton, S.J.; Lunine, J.; Stevenson, D.; Connerney, J.E.P.; Levin, S.; Owen, T.C.; Bagenal, F.; Gautier, D.; Ingersoll, A.P.; Orton, G.S.; et al. The Juno mission. Space Sci. Rev. 2017, 213, 5–37. [Google Scholar] [CrossRef]
- Soriano, M.; Finley, S.; Jongeling, A.; Fort, D.; Goodhart, C.; Rogstad, D.; Navarro, R. Spacecraft-to-Earth communications for Juno and Mars Science Laboratory critical events. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012; pp. 1–11. [Google Scholar] [CrossRef]
- Ardalan, S.; Bordi, J.; Bradley, N.; Farnocchia, D.; Takahashi, Y.; Thompson, P. Juno Orbit Determination Experience During First Year at Jupiter. NASA Technical Reports Server; 2017. Available online: https://ntrs.nasa.gov/citations/20210007704 (accessed on 22 January 2025).
- Pavlak, T.A.; Johannesen, J.R.; Bordi, J.J. Juno Trajectory Redesign Following PRM Cancellation. NASA Technical Reports Server; 2017. Available online: https://ntrs.nasa.gov/citations/20210007701 (accessed on 22 January 2025).
- Helled, R.; Stevenson, D.J.; Lunine, J.I.; Bolton, S.J.; Nettelmann, N.; Atreya, S.; Guillot, T.; Militzer, B.; Miguel, Y.; Hubbard, W.B. Revelations on Jupiter’s formation, evolution and interior: Challenges from Juno results. Icarus 2022, 378, 114937. [Google Scholar] [CrossRef]
- Jorgensen, J.L.; Benn, M.; Connerney, J.E.P.; Denver, T.; Jorgensen, P.S.; Andersen, A.C.; Bolton, S.J. Distribution of interplanetary dust detected by the Juno spacecraft and its contribution to the zodiacal light. J. Geophys. Res. Planets 2021, 126, e2020JE006509. [Google Scholar] [CrossRef]
- Feng, H.; Liu, Y. Trajectory based detection of forest-change impacts on surface soil moisture at a basin scale [Poyang Lake Basin, China]. J. Hydrol. 2014, 514, 337–346. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Zeileis, A.; Culvenor, D. Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef]
- Wilde, M.; Kwok Choon, S.; Grompone, A.; Romano, M. Equations of motion of free-floating spacecraft-manipulator systems: An engineer’s tutorial. Front. Robot. AI 2018, 5, 41. [Google Scholar] [CrossRef] [PubMed]
- Kirk, D.E. Optimal Control Theory: An Introduction; Courier Corporation: North Chelmsford, MA, USA, 2012; pp. 3–17. [Google Scholar]
- Liu, B. A fast density based clustering algorithm for large databases. In Proceedings of the IEEE Fifth International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006; pp. 226–231. [Google Scholar]
- Ping, Y.; Tian, Y.-J.; Zhou, Y.-J.; Yang, Y.-X. Convex decomposition-based cluster labeling method for support vector clustering. J. Comput. Sci. Technol. 2012, 27, 428–442. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; AAAI Press: Washington, DC, USA, 1996; pp. 226–231. [Google Scholar]
- Iorio, L. A possible new test of general relativity with Juno. Class. Quantum Gravity 2013, 30, 195011. [Google Scholar] [CrossRef]





| Activity Name | Start Date | End Date |
|---|---|---|
| Pre-Launch | 2 August 2011 | 5 August 2011 |
| Launch | 5 August 2011 | 8 August 2011 |
| Inner Cruise 1 | 8 August 2011 | 10 October 2011 |
| Inner Cruise 2 | 10 October 2011 | 28 May 2013 |
| Inner Cruise 3 | 28 May 2013 | 5 November 2013 |
| Earth Flyby (short event) | 9 October 2013 | 9 October 2013 |
| Quiet Cruise | 5 November 2013 | 5 January 2016 |
| Jupiter Approach | 5 January 2016 | 30 June 2016 |
| Jupiter Orbit Insertion (JOI) | 1 July 2016 | 5 July 2016 |
| Capture Orbits | 5 July 2016 | 19 October 2016 |
| Period Reduction Maneuver | 19 October 2016 | 20 October 2016 |
| Orbits 1–2 | 20 October 2016 | 9 November 2016 |
| Science Orbits | 9 November 2016 | 11 October 2017 |
| Deorbit | 11 October 2016 | 16 October 2017 |
| Extended Mission | 1 August 2021 | 30 September 2025 |
| Operation Phase | OP1 | OP2 | OP3 |
|---|---|---|---|
| Acceleration (a) | Relative to SSBC for a, j and s in every operation phase (OP1:3) | ||
| Jerk (j) | |||
| Snap (s) | |||
| Event | |||
| EE condition | |||
| Reference system | Solar system | ||
| Operation Phase | OP1 | OP2 | OP3 |
|---|---|---|---|
| Start of OP | 7 August 2021 17:18:06 | 1 July 2016 00:00:01 | 5 July 2016 03:55:00 |
| End of OP | 1 July 2016 00:00:00 | 5 July 2016 03:54:00 | 4 January 2023 06:03:51 |
| Event condition | Hz | ||
| EE condition |
| Operation Phase | Extreme Event Dates |
|---|---|
| OP1 (No. of EE = 9) | 2012 01 21T02:19:59; 2012 02 05T01:24:59; 2012 09 19T23:18:59 2012 09 19T23:20:59; 2013 03 11T14:19:59; 2014 03 23T10:23:59 2014 03 23T10:25:59; 2014 11 15T12:06:00; 2014 11 15T12:08:00 |
| OP2 (No. of EE = 2) | 2016 07 01T00:00:59 (JOI Start); 2016 07 05T03:53:59 (JOI End) |
| OP3 (No. of EE = 12) | 2016 07 13T18:02:00; 2016 10 25T17:59:00; 2017 02 22T16:59:59 2017 02 22T17:43:59; 2018 01 09T15:59:59; 2018 03 01T17:01:59 2019 08 16T03:26:00; 2019 10 14T21:46:00; 2019 10 14T21:51:00 2019 10 14T21:52:00; 2019 12 31T23:57:00; 2020 05 04T11:59:59 |
| Accuracy of EE Detection/Operation Phase | OP1 | OP2 | OP3 |
|---|---|---|---|
| DBSCAN | 98.8% | 98.2% | 97.4% |
| OPTICS | 99.3% | 99.1% | 98.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
ALDabbas, A.; Mustafa, Z.; Gal, Z. Advanced Trajectory Analysis of NASA’s Juno Mission Using Unsupervised Machine Learning: Insights into Jupiter’s Orbital Dynamics. Future Internet 2025, 17, 125. https://doi.org/10.3390/fi17030125
ALDabbas A, Mustafa Z, Gal Z. Advanced Trajectory Analysis of NASA’s Juno Mission Using Unsupervised Machine Learning: Insights into Jupiter’s Orbital Dynamics. Future Internet. 2025; 17(3):125. https://doi.org/10.3390/fi17030125
Chicago/Turabian StyleALDabbas, Ashraf, Zaid Mustafa, and Zoltan Gal. 2025. "Advanced Trajectory Analysis of NASA’s Juno Mission Using Unsupervised Machine Learning: Insights into Jupiter’s Orbital Dynamics" Future Internet 17, no. 3: 125. https://doi.org/10.3390/fi17030125
APA StyleALDabbas, A., Mustafa, Z., & Gal, Z. (2025). Advanced Trajectory Analysis of NASA’s Juno Mission Using Unsupervised Machine Learning: Insights into Jupiter’s Orbital Dynamics. Future Internet, 17(3), 125. https://doi.org/10.3390/fi17030125







