Online Parameters Identification and State of Charge Estimation for Lithium-Ion Battery Using Adaptive Cubature Kalman Filter
Abstract
:1. Introduction
2. Battery Model and Parameter Identification
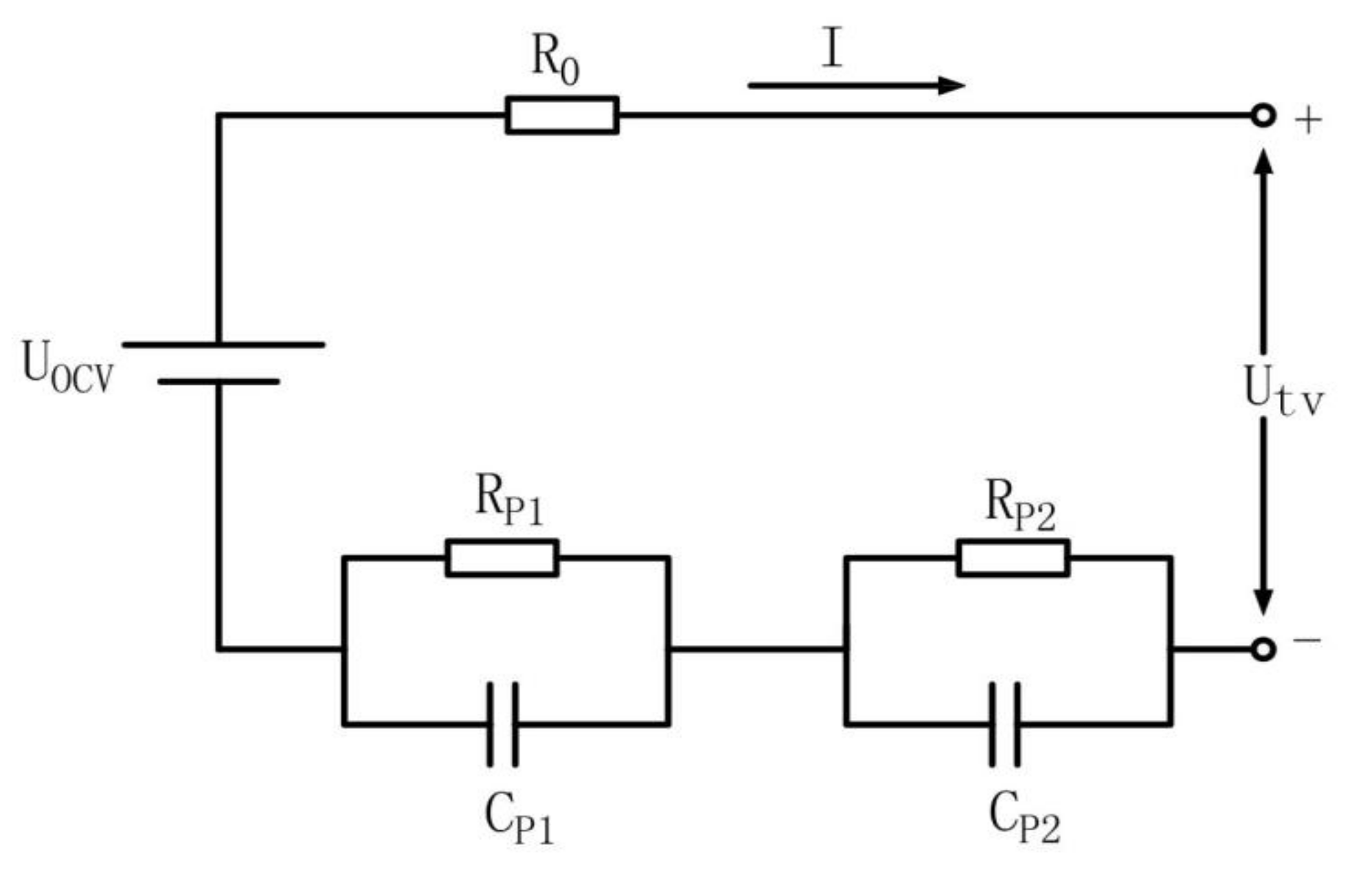
2.1. Battery Model
2.2. Model Parameter Identification
2.2.1. Identification of Open Circuit Voltage
- Charge the battery fully. At this time SOC = 1 and the measured battery voltage is recorded as OCV.
- Discharge at 1 C until SOC = 0.95 and rest for 30 min. Measure the battery voltage and record it as the open circuit voltage of SOC = 0.95.
- Step (2) is repeated until SOC = 0.05 and the battery voltage corresponding to each SOC is recorded.
2.2.2. Parameter Identification with Vector Forgetting Factor Recursive Least Squares Algorithm
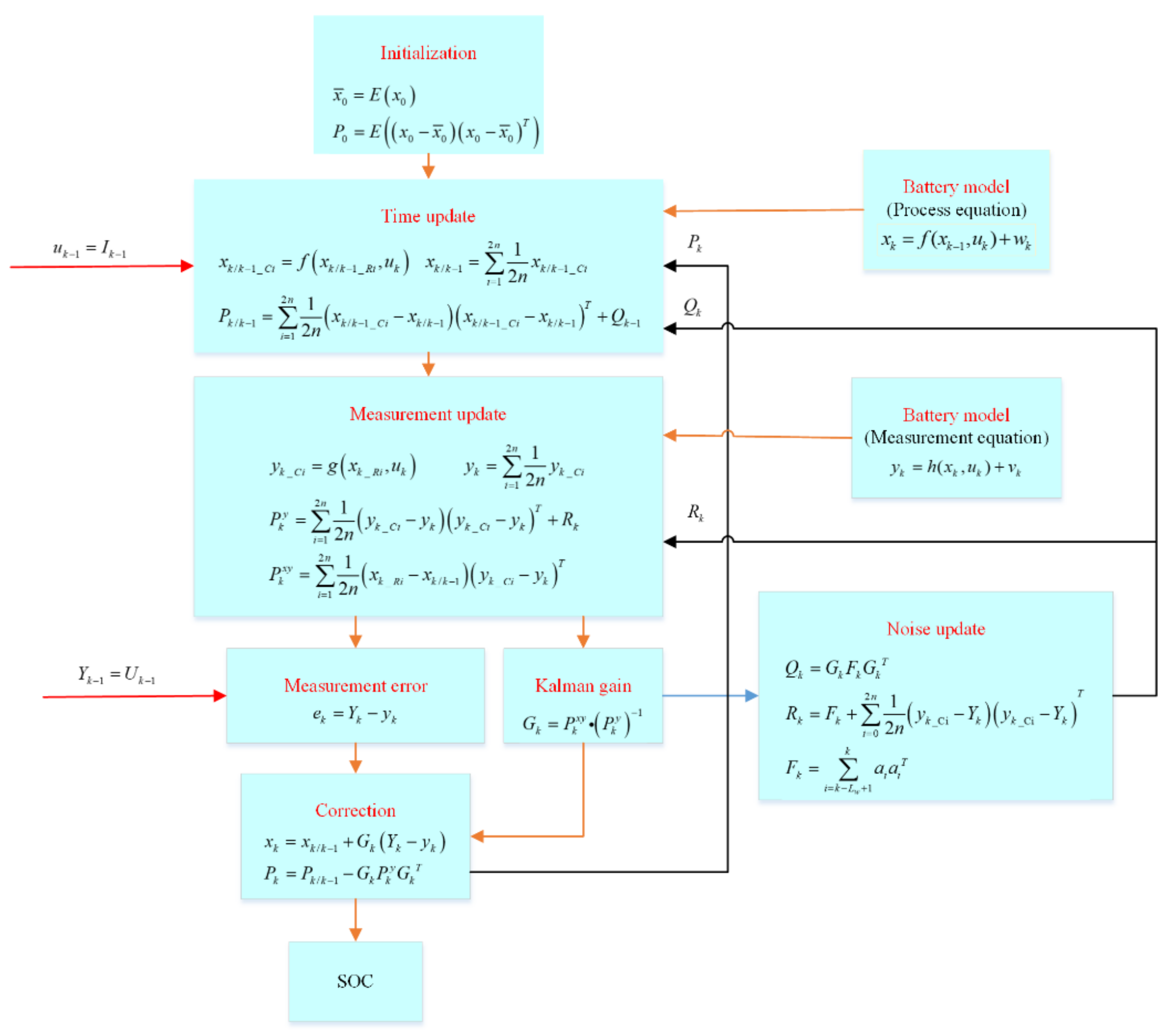
3. Adaptive Cubature Kalman Filter Algorithm
4. Results and Discussion
4.1. Experimental Setup
4.2. Comparison of Two Battery Models
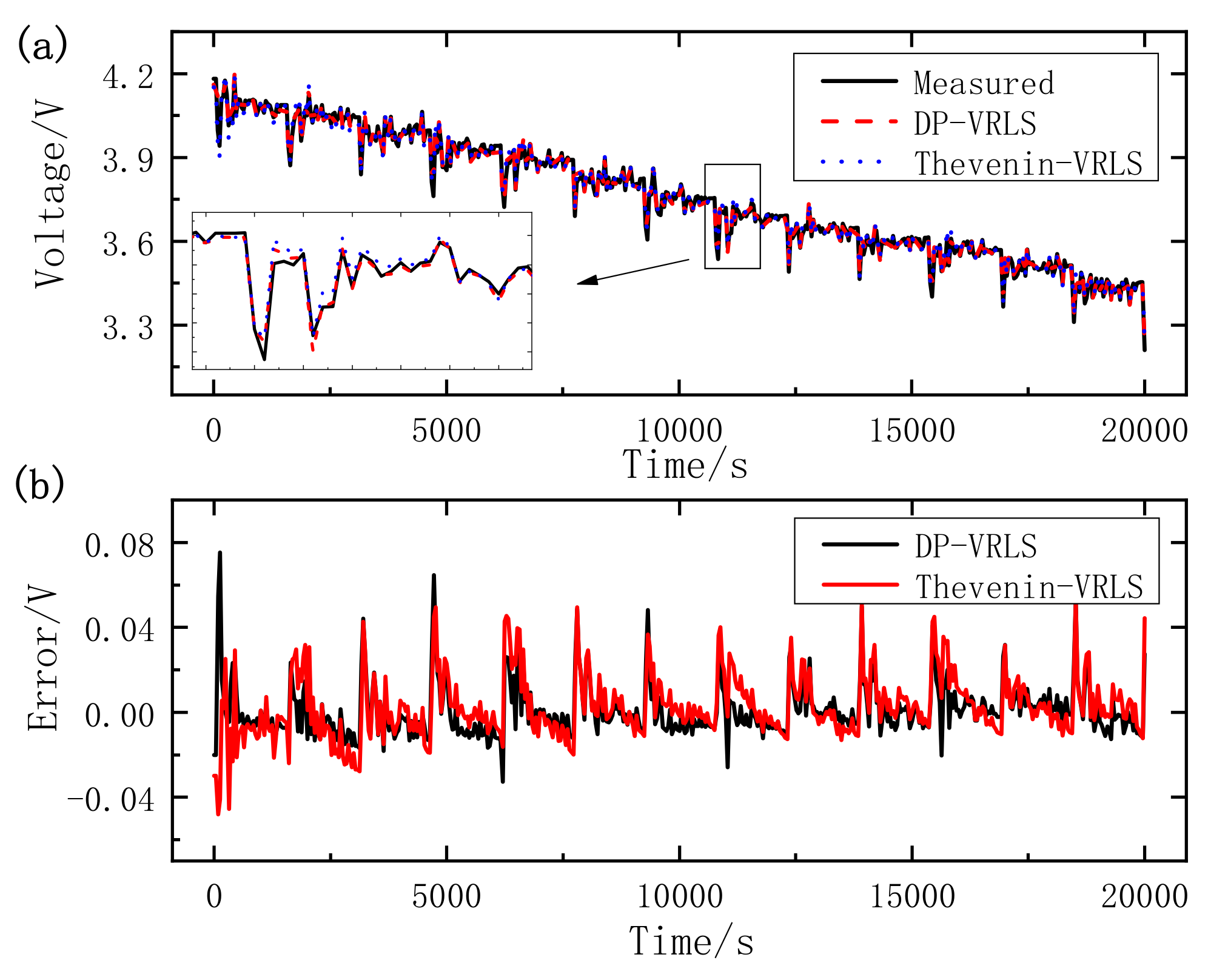
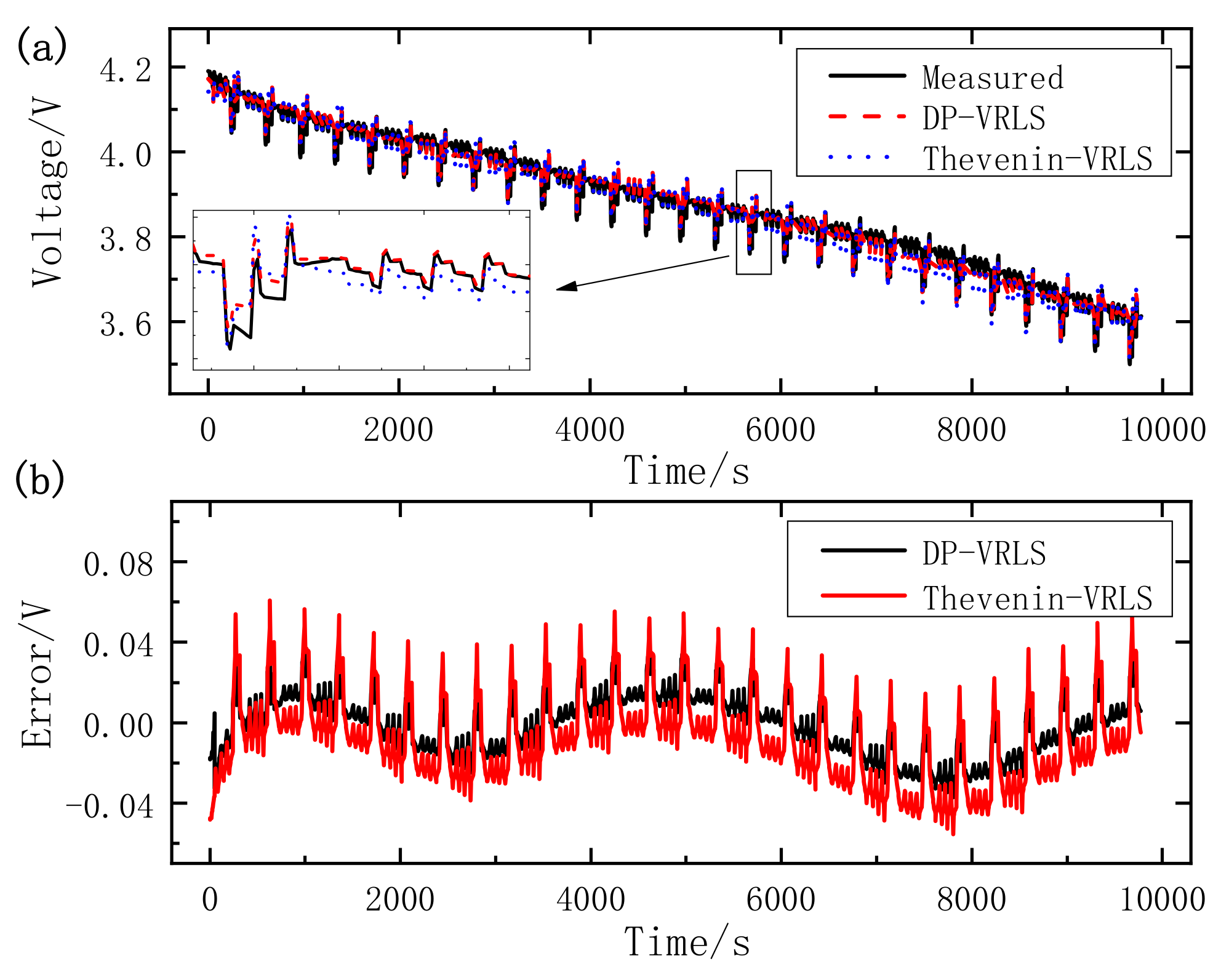
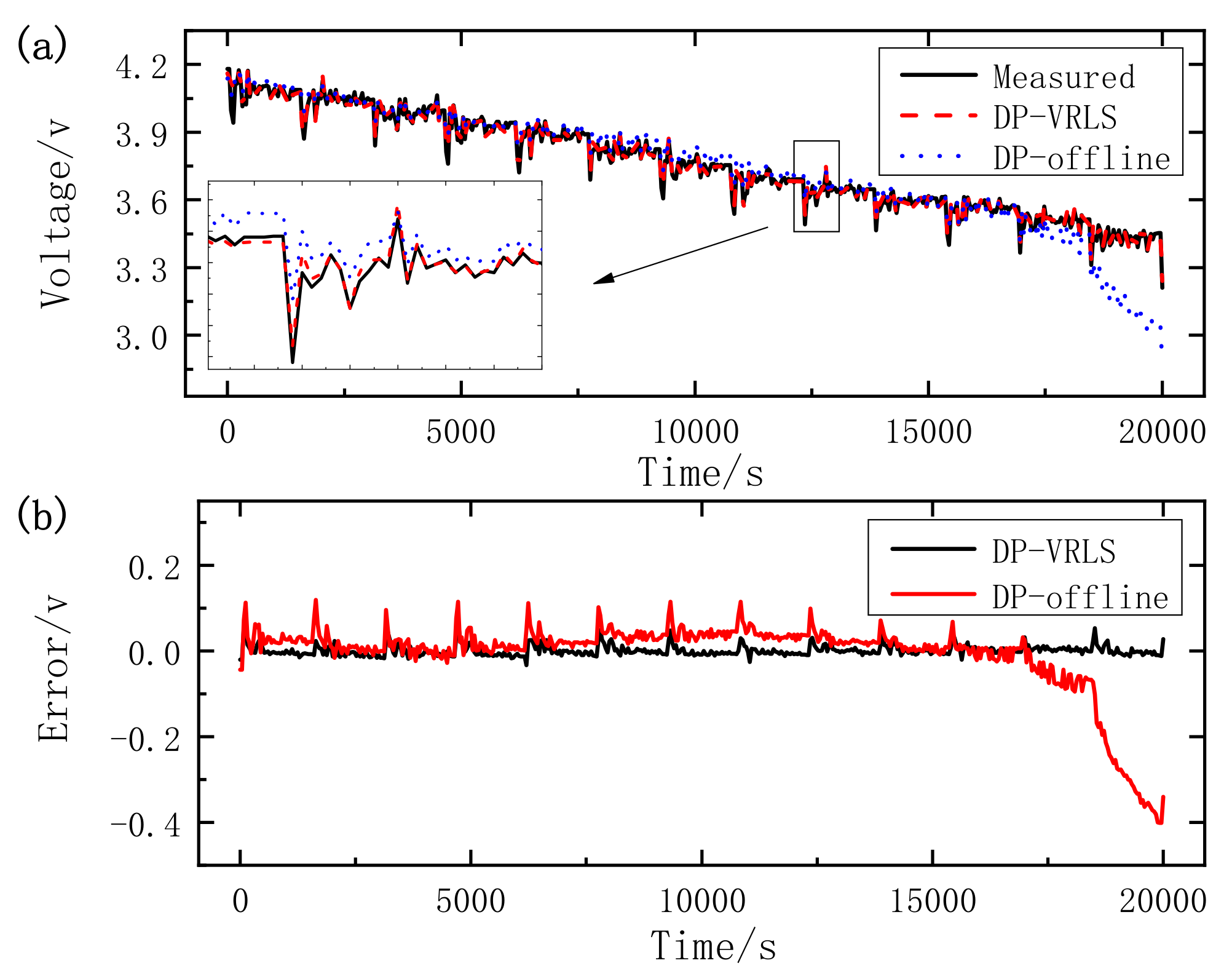
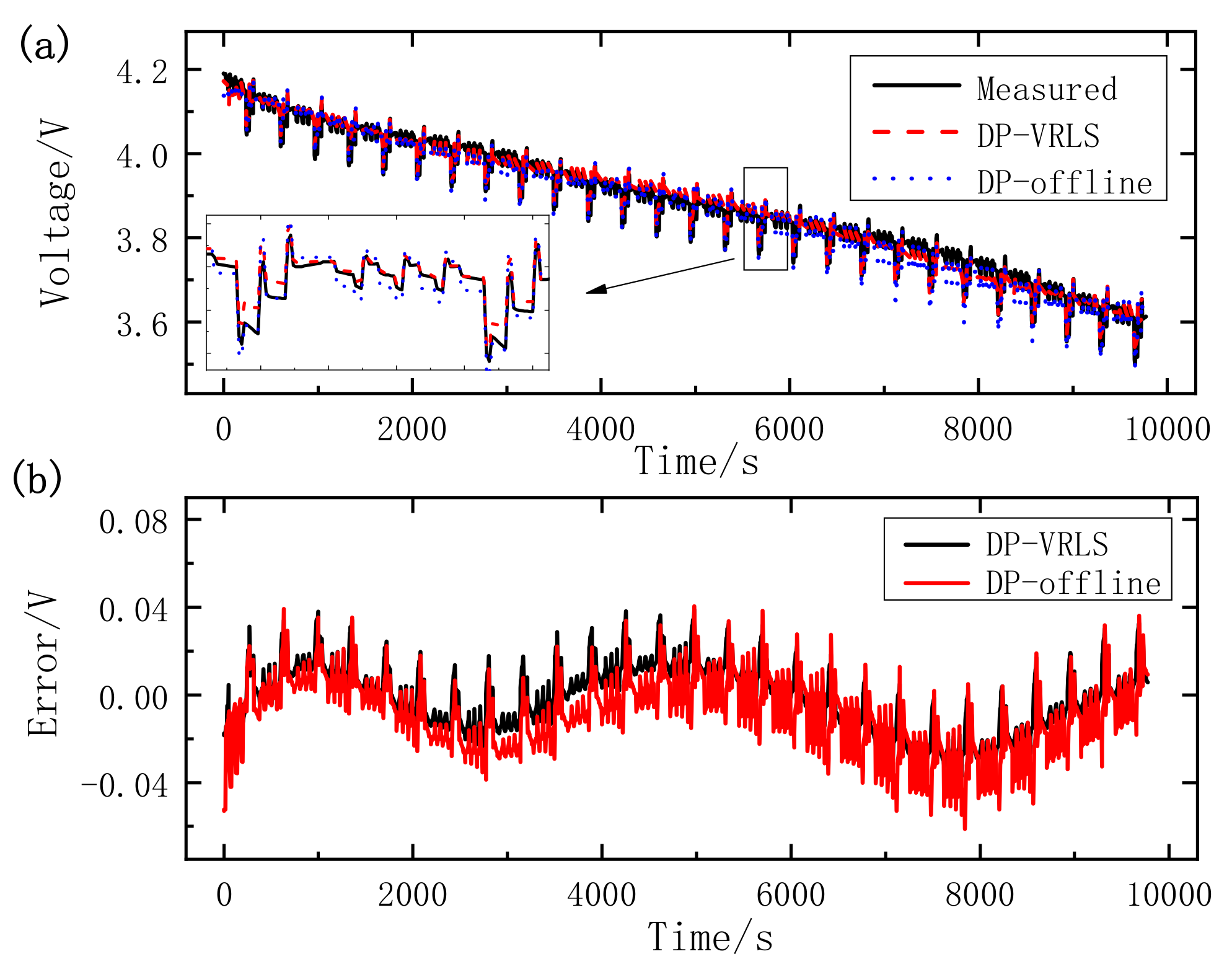
4.3. Comparison of Two Parameter Identification Methods
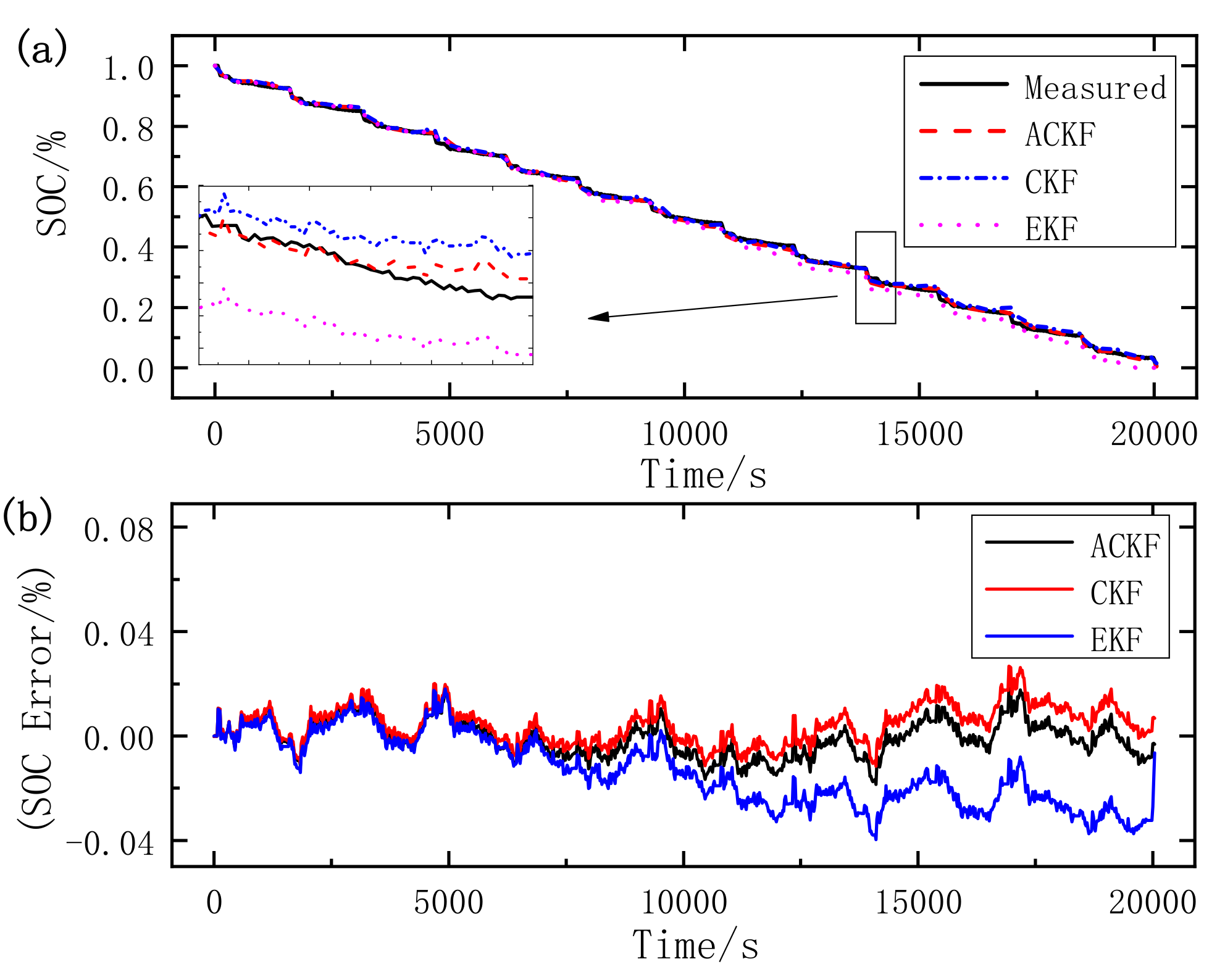
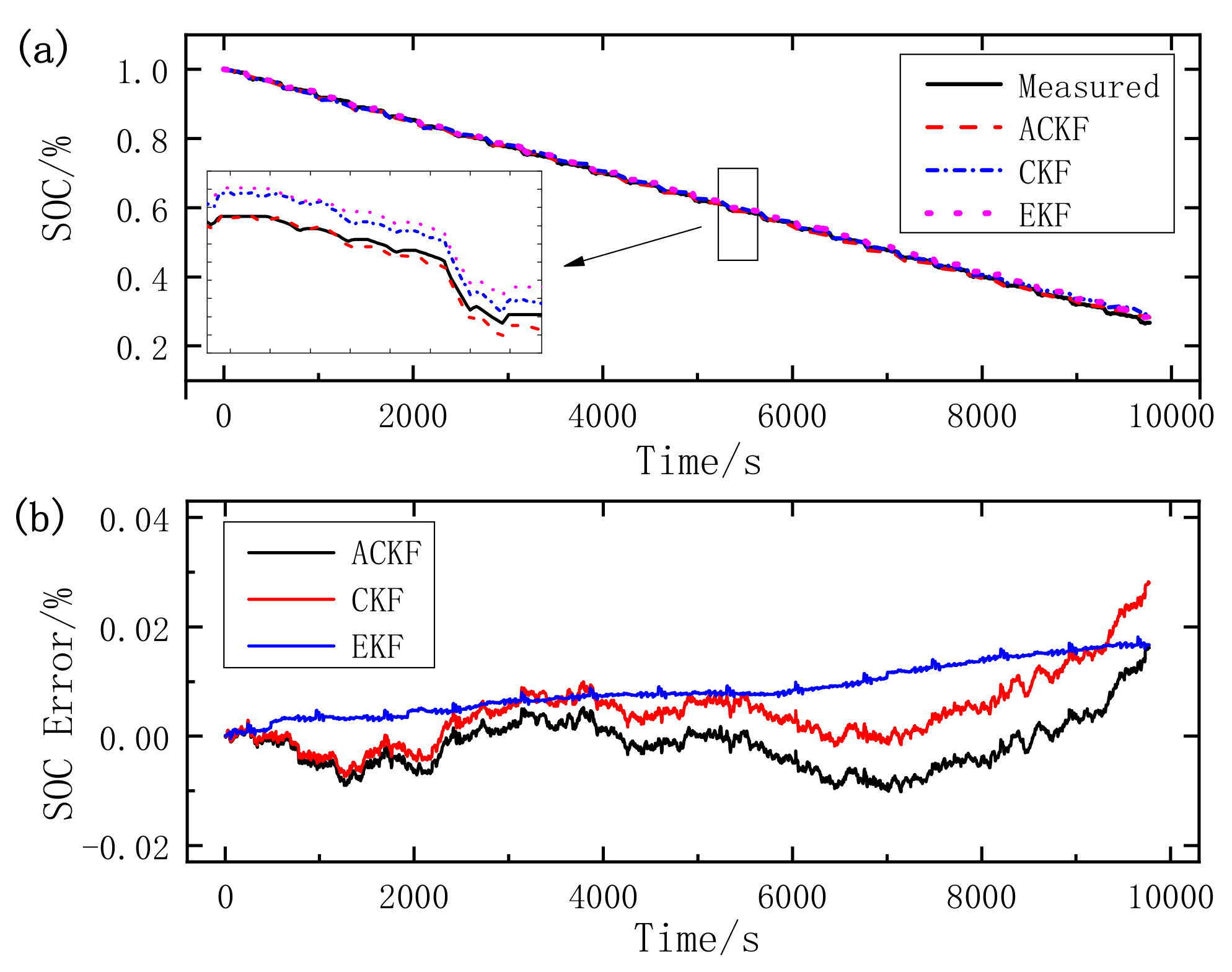
4.4. Comparison of SOC Estimation with Different Algorithms
5. Conclusions
- (1)
- By comparing the estimated terminal voltage of the Thevenin model and DP model, we can conclude that on the one hand, the Thevenin model and DP model can be adopted to the dynamic and complex condition. On the other hand, the DP model has higher accuracy and better dynamic performance compared with the Thevenin model.
- (2)
- Online parameter identification based on VRLS has an improvement for voltage estimation over the offline parameter identification of the HPPC test, and it is shown that the proposed VRLS has a more accurate parameter identification ability.
- (3)
- Experiments based on the two typical dynamic operating cycles are used to evaluate the superiority of the proposed algorithm compared with EKF and CKF in terms of accuracy and stability. The maximum errors of ACKF are 1.85% in UDDS and 1.64% in DST, the MAEs are 0.59% in UDDS and 0.39% in DST, and the RMSEs are 0.72% in UDDS and 0.49% in DST. The estimation accuracy is relatively high and the maximum error, MAE, RMSE of ACKF are all smaller than those of EKF and CKF. The results show that the ACKF has a satisfactory performance in SOC estimation, and has better accuracy and stability than EKF and CKF. To conclude, the VRLS-ACKF is capable of obtaining accurate SOC estimation and terminal voltage prediction with satisfying stability, which is suitable to implement in the real application. For future work, the proposed algorithm will be applied in BMS to verify its practicality.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACKF | Adaptive cubature Kalman filter |
| AUKF | Adaptive unscented Kalman filter |
| BMS | Battery Management System |
| CKF | Cubature Kalman filter |
| DP | Dual polarization |
| DST | Dynamic Stress Test |
| ECMs | Equivalent circuit models |
| EKF | Extended Kalman filter |
| EVS | Electric vehicles |
| HPPC | Hybrid pulse power characterization |
| KF | Kalman filter |
| MAE | Mean Absolute Error |
| OCV | Open Circuit Voltage |
| PNGV | Partnership for a New Generation of Vehicle |
| RLS | Recursive least square |
| RMSE | Root Mean Square Error |
| SOC | State of charge |
| UKF | Unscented Kalman filter |
| VRLS | Vector forgetting factor recursive least squares |
References
- Cuma, M.U.; Koroglu, T. A comprehensive review on estimation strategies used in hybrid and battery electric vehicles. Renew. Sustain. Energy Rev. 2015, 42, 517–531. [Google Scholar] [CrossRef]
- Guo, X.; Xu, X.; Geng, J.; Hua, X.; Gao, Y.; Liu, Z. SOC Estimation with an Adaptive Unscented Kalman Filter Based on Model Parameter Optimization. Appl. Sci. 2019, 9, 4177. [Google Scholar] [CrossRef] [Green Version]
- Saw, L.H.; Ye, Y.; Tay, A.A.O. Integration issues of lithium-ion battery into electric vehicles battery pack. J. Clean. Prod. 2016, 113, 1032–1045. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, G.; Xie, Z.; He, Y.; Lu, X. Lithium battery SOC estimation based on whale optimization algorithm and unscented Kalman filter. J. Renew. Sustain. Energy 2020, 12, 065501. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W. State of the Art of Lithium-Ion Battery SOC Estimation for Electrical Vehicles. Energies 2018, 11, 1820. [Google Scholar] [CrossRef] [Green Version]
- Peng, N.; Zhang, S.; Guo, X.; Zhang, X. Online parameters identification and state of charge estimation for lithium-ion batteries using improved adaptive dual unscented Kalman filter. Int. J. Energy Res. 2021, 45, 975–990. [Google Scholar] [CrossRef]
- Hu, X.; Zou, C.; Zhang, C.; Li, Y. Technological Developments in Batteries: A Survey of Principal Roles, Types, and Management Needs. IEEE Power Energy Mag. 2017, 15, 20–31. [Google Scholar] [CrossRef]
- Farmann, A.; Waag, W.; Marongiu, A.; Sauer, D.U. Critical review of on-board capacity estimation techniques for lithium-ion batteries in electric and hybrid electric vehicles. J. Power Sources 2015, 281, 114–130. [Google Scholar] [CrossRef]
- Guo, X.; Kang, L.; Yao, Y.; Huang, Z.; Li, W. Joint Estimation of the Electric Vehicle Power Battery State of Charge Based on the Least Squares Method and the Kalman Filter Algorithm. Energies 2016, 9, 100. [Google Scholar] [CrossRef]
- She, C.; Wang, Z.; Sun, F.; Liu, P.; Zhang, L. Battery Aging Assessment for Real-World Electric Buses Based on Incremental Capacity Analysis and Radial Basis Function Neural Network. IEEE Trans. Ind. Inform. 2020, 16, 3345–3354. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Xu, L.; Ouyang, M.; Han, X.; Lu, L.; Lin, C. Online management of lithium-ion battery based on time-triggered controller area network for fuel-cell hybrid vehicle applications. J. Power Sources 2010, 195, 3338–3343. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, X.; Li, G. State of charge estimation for pulse discharge of a LiFePO4 battery by a revised Ah counting. Electrochim. Acta 2015, 151, 63–71. [Google Scholar] [CrossRef]
- Huang, S.-J.; Huang, B.-G.; Pai, F.-S. An approach to measurements of electrical characteristics of lithium-ion battery with open-circuit voltage function. IET Power Electron. 2012, 5, 1968–1975. [Google Scholar] [CrossRef]
- Luzi, M.; Frattale Mascioli, F.M.; Paschero, M.; Rizzi, A. A White-Box Equivalent Neural Network Circuit Model for SoC Es-timation of Electrochemical Cells. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 371–382. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, Y.; Qi, H. State of charge estimation of LiFePO4 batteries based on online parameter identification. Appl. Math. Model. 2016, 40, 6040–6050. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Peng, H.; Ning, Z.; Mu, Z.; Sun, C. Comparative Research on RC Equivalent Circuit Models for Lithium-Ion Batteries of Electric Vehicles. Appl. Sci. 2017, 7, 1002. [Google Scholar] [CrossRef] [Green Version]
- Nejad, S.; Gladwin, D.T.; Stone, D.A. A systematic review of lumped-parameter equivalent circuit models for real-time esti-mation of lithium-ion battery states. J. Power Sources 2016, 316, 183–196. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network. Energy 2019, 175, 66–75. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Z.; Lu, Z.; Li, J.; Ji, B.; Wei, H.; Pan, H. A Novel State-of-Charge Estimation Method of Lithium-Ion Batteries Combining the Grey Model and Genetic Algorithms. IEEE Trans. Power Electron. 2018, 33, 8797–8807. [Google Scholar] [CrossRef] [Green Version]
- Luzi, M.; Paschero, M.; Rizzi, A.; Maiorino, E.; Frattale Mascioli, F.M. A Novel Neural Networks Ensemble Approach for Modeling Electrochemical Cells. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 343–354. [Google Scholar] [CrossRef]
- Wang, K.; Feng, X.; Pang, J.; Ren, J.; Duan, C.; Li, L. State of Charge (SOC) Estimation of Lithium-ion Battery Based on Adaptive Square Root Unscented Kalman Filter. Int. J. Electrochem. Sci. 2020, 15, 9499–9516. [Google Scholar]
- Shuai, W.; Li, E.; Wang, H. An equivalent circuit model of a deformed Li-ion battery with parameter identification. Int. J. Energy Res. 2020, 44, 8372–8387. [Google Scholar] [CrossRef]
- Xia, B.; Chen, G.; Zhou, J.; Yang, Y.; Huang, R.; Wang, W.; Lai, Y.; Wang, M.; Wang, H. Online Parameter Identification and Joint Estimation of the State of Charge and the State of Health of Lithium-Ion Batteries Considering the Degree of Polarization. Energies 2019, 12, 2939. [Google Scholar] [CrossRef] [Green Version]
- Long, H.; Zhu, C.; Huang, B.; Piao, C.; Sun, Y. Model Parameters Online Identification and SOC Joint Estimation for Lithium-Ion Battery Based on a Composite Algorithm. J. Electr. Eng. Technol. 2019, 14, 1485–1493. [Google Scholar] [CrossRef]
- Xia, B.; Zheng, W.; Zhang, R.; Lao, Z.; Sun, Z. A Novel Observer for Lithium-Ion Battery State of Charge Estimation in Electric Vehicles Based on a Second-Order Equivalent Circuit Model. Energies 2017, 10, 1150. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, J.; Zhao, P.; Kang, J.; Yan, F.; Du, C. Correlation between the model accuracy and model-based SOC estimation. Electrochim. Acta 2017, 228, 146–159. [Google Scholar] [CrossRef]
- Groot, J.; Swierczynski, M.; Stan, A.I.; Kær, S.K. On the complex ageing characteristics of high-power LiFePO4/graphite battery cells cycled with high charge and discharge currents. J. Power Sources 2015, 286, 475–487. [Google Scholar] [CrossRef]
- Tan, Y.; Luo, M.; She, L.; Cui, X. Joint Estimation of Ternary Lithium-ion Battery State of Charge and State of Power Based on Dual Polarization Model. Int. J. Electrochem. Sci. 2020, 15, 1128–1147. [Google Scholar] [CrossRef]
- Sun, X.; Ji, J.; Ren, B.; Xie, C.; Yan, D. Adaptive Forgetting Factor Recursive Least Square Algorithm for Online Identification of Equivalent Circuit Model Parameters of a Lithium-Ion Battery. Energies 2019, 12, 2242. [Google Scholar] [CrossRef] [Green Version]
- Ren, B.; Xie, C.; Sun, X.; Zhang, Q.; Yan, D. Parameter identification of a lithium-ion battery based on the improved recursive least square algorithm. IET Power Electron. 2020, 13, 2531–2537. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Chen, Z.; He, H. A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion polymer battery in electric vehicles. Appl. Energy 2014, 113, 463–476. [Google Scholar] [CrossRef]
- Partovibakhsh, M.; Liu, G. An Adaptive Unscented Kalman Filtering Approach for Online Estimation of Model Parameters and State-of-Charge of Lithium-Ion Batteries for Autonomous Mobile Robots. IEEE Trans. Control Syst. Technol. 2015, 23, 357–363. [Google Scholar] [CrossRef]
- Yu, Q.; Xiong, R.; Lin, C.; Shen, W.; Deng, J. Lithium-Ion Battery Parameters and State-of-Charge Joint Estimation Based on H-Infinity and Unscented Kalman Filters. IEEE Trans. Veh. Technol. 2017, 66, 8693–8701. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Guo, H.; Ding, Y. Modeling for Lithium-Ion Battery used in Electric Vehicles. Proc. Eng. 2011, 15, 2869–2874. [Google Scholar] [CrossRef] [Green Version]
- Lao, Z.; Xia, B.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. A Novel Method for Lithium-Ion Battery Online Parameter Identification Based on Variable Forgetting Factor Recursive Least Squares. Energies 2018, 11, 1358. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Z.; Tian, J.; Li, D.; Tian, Y. An Online State of Charge Estimation Algorithm for Lithium-Ion Batteries Using an Improved Adaptive Cubature Kalman Filter. Energies 2018, 11, 59. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, Q.; Chen, J.; Zheng, J. State-of-Charge Observer Design for Batteries With Online Model Parameter Identification: A Robust Approach. IEEE Trans. Power Electron. 2020, 35, 5820–5831. [Google Scholar] [CrossRef]
- He, Z.; Yang, Z.; Cui, X.; Li, E. A Method of State-of-Charge Estimation for EV Power Lithium-Ion Battery Using a Novel Adaptive Extended Kalman Filter. IEEE Trans. Veh. Technol. 2020, 69, 14618–14630. [Google Scholar] [CrossRef]
- Xia, B.; Lao, Z.; Zhang, R.; Tian, Y.; Chen, G.; Sun, Z.; Wang, W.; Sun, W.; Lai, Y.; Wang, M.; et al. Online Parameter Identification and State of Charge Estimation of Lithium-Ion Batteries Based on Forgetting Factor Recursive Least Squares and Nonlinear Kalman Filter. Energies 2018, 11, 3. [Google Scholar] [CrossRef] [Green Version]
- Yu, Q.; Xiong, R.; Lin, C. Online Estimation of State-of-charge Based on the H infinity and Unscented Kalman Filters for Lithium Ion Batteries. Energy Proc. 2017, 105, 2791–2796. [Google Scholar] [CrossRef]
- Wang, T.; Chen, S.; Ren, H.; Zhao, Y. Model-based unscented Kalman filter observer design for lithium-ion battery state of charge estimation. Int. J. Energy Res. 2018, 42, 1603–1614. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S.; Hurd, T.R. Cubature Kalman Filtering for Continuous-Discrete Systems: Theory and Simulations. IEEE Trans. Signal Process 2010, 58, 4977–4993. [Google Scholar] [CrossRef]
- Peng, J.; Luo, J.; He, H.; Lu, B. An improved state of charge estimation method based on cubature Kalman filter for lithium-ion batteries. Appl. Energy 2019, 253, 113520. [Google Scholar] [CrossRef]
- Xu, W.; Xu, J.; Yan, X. Lithium-ion battery state of charge and parameters joint estimation using cubature Kalman filter and particle filter. J. Power Electron. 2020, 20, 292–307. [Google Scholar] [CrossRef]
- Xiong, R.; Zhang, Y.; He, H.; Zhou, X.; Pecht, M.G. A Double-Scale, Particle-Filtering, Energy State Prediction Algorithm for Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2017, 65, 1526–1538. [Google Scholar] [CrossRef]
- Pei, Y.; Biswas, S.; Fussell, D.S.; Pingali, K. An elementary introduction to Kalman filtering. Commun. ACM 2019, 62, 122–133. [Google Scholar] [CrossRef] [Green Version]
- Claude, F.; Becherif, M.; Ramadan, H.S. Experimental validation for Li-ion battery modeling using Extended Kalman Filters. Int. J. Hydrogen Energy 2017, 42, 25509–25517. [Google Scholar] [CrossRef]
- Ouyang, Q.; Ma, R.; Wu, Z.; Xu, G.; Wang, Z. Adaptive Square-Root Unscented Kalman Filter-Based State-of-Charge Estimation for Lithium-Ion Batteries with Model Parameter Online Identification. Energies 2020, 13, 4968. [Google Scholar] [CrossRef]
- He, H.; Qin, H.; Sun, X.; Shui, Y. Comparison Study on the Battery SoC Estimation with EKF and UKF Algorithms. Energies 2013, 6, 5088–5100. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman Filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Sun, X.; An, Y.; Zhang, X.; Wei, T.; Ma, Y. Online parameters identification and state of charge estimation for lithium-ion capacitor based on improved Cubature Kalman filter. J. Energy Storage 2019, 24, 100810. [Google Scholar] [CrossRef]

| i | λ0i | λ1i | τi |
|---|---|---|---|
| 1 | 0.998 | 0.98 | 500 |
| 2 | 0.995 | 0.99 | 500 |
| 3 | 0.99 | 0.97 | 500 |
| 4 | 0.998 | 0.98 | 500 |
| 5 | 0.995 | 0.99 | 500 |
| Step 1. Initialize the parameters: |
| Step 2. Calculate the state variables and the predicted value of covariance matrix: |
| Step 3. Update the gain: |
| Step 4. Update the state variables and covariance matrix: where , and E is a unit vector of the fifth order. |
| Items | Parameters |
|---|---|
| Cathode materials | LiNi1-x-yCoxMnyO2 |
| Nominal capacity (Ah) | 35 |
| Rated voltage (V) | 3.7 |
| Maximal continuous discharge current (C) | 3 |
| Maximal pulse discharge current (C) | 5 (30 s) |
| Upper/lower cut-off voltage (V) | 4.2/2.5 |
| Condition | Algorithm | Maximum Error/V | MAE/V | RMSE/V |
|---|---|---|---|---|
| UDDS | DP-VRLS | 0.0754 | 0.0087 | 0.0126 |
| Thevenin-VRLS | 0.0525 | 0.0106 | 0.0149 | |
| DP-offline | 0.4014 | 0.0486 | 0.0907 | |
| DST | DP-VRLS | 0.0389 | 0.0123 | 0.0147 |
| Thevenin-VRLS | 0.0606 | 0.0185 | 0.0227 | |
| DP-offline | 0.0612 | 0.0152 | 0.0192 |
| Condition | Algorithm | Maximum Error | MAE | RMSE |
|---|---|---|---|---|
| UDDS | ACKF | 0.0185 | 0.0059 | 0.0072 |
| CKF | 0.0268 | 0.0067 | 0.0084 | |
| EKF | 0.0399 | 0.0156 | 0.0188 | |
| DST | ACKF | 0.0164 | 0.0039 | 0.0049 |
| CKF | 0.0283 | 0.0056 | 0.0077 | |
| EKF | 0.0181 | 0.0085 | 0.0096 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Luo, M.; Tan, Y.; Cui, X. Online Parameters Identification and State of Charge Estimation for Lithium-Ion Battery Using Adaptive Cubature Kalman Filter. World Electr. Veh. J. 2021, 12, 123. https://doi.org/10.3390/wevj12030123
Li W, Luo M, Tan Y, Cui X. Online Parameters Identification and State of Charge Estimation for Lithium-Ion Battery Using Adaptive Cubature Kalman Filter. World Electric Vehicle Journal. 2021; 12(3):123. https://doi.org/10.3390/wevj12030123
Chicago/Turabian StyleLi, Wei, Maji Luo, Yaqian Tan, and Xiangyu Cui. 2021. "Online Parameters Identification and State of Charge Estimation for Lithium-Ion Battery Using Adaptive Cubature Kalman Filter" World Electric Vehicle Journal 12, no. 3: 123. https://doi.org/10.3390/wevj12030123
APA StyleLi, W., Luo, M., Tan, Y., & Cui, X. (2021). Online Parameters Identification and State of Charge Estimation for Lithium-Ion Battery Using Adaptive Cubature Kalman Filter. World Electric Vehicle Journal, 12(3), 123. https://doi.org/10.3390/wevj12030123







