Recent Advances in Multi-Phase Electric Drives Model Predictive Control in Renewable Energy Application: A State-of-the-Art Review
Abstract
:1. Introduction
2. Multi-Phase Machine Model
3. Classical MPC Schemes in a Multi-Phase Machine
3.1. Model Predictive Current Control
3.2. Model Predictive Torque Control
3.3. Model Predictive Speed Control
4. Advanced Control Schemes of MPC in the Multi-Phase Machine
4.1. MPC of the Multi-Phase Machine with Simplified Cost Function
4.2. MPC of the Multi-Phase Machine with Harmonic Current Suppression
4.3. MPC of the Multi-Phase Machine with Computational Complexity Reduction
4.4. MPC of the Multi-Phase Machine with Robustness Improvement
4.5. MPC of Multi-Phase Machines with Fault-Tolerant Operation
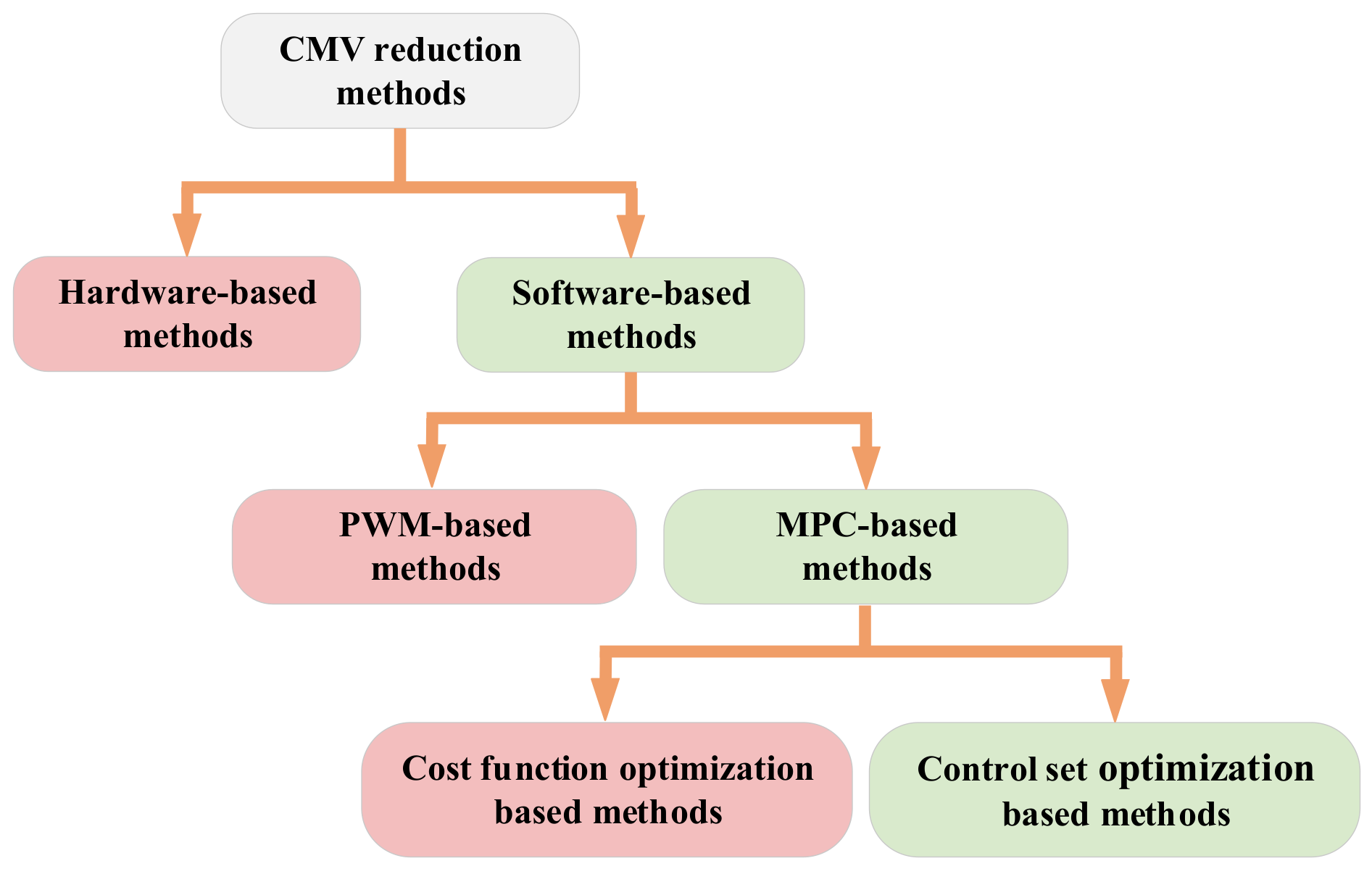
4.6. MPC of Multi-Phase Machines with CMV Reduction
4.7. MPC of Multi-Phase Machines with ZSC Reduction
5. Future Trends of MPC for Multi-Phase Machines
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shao, L.; Hua, W.; Dai, N.; Tong, M.; Cheng, M. Mathematical modeling of a 12-phase flux-switching permanent-magnet machine for wind power generation. IEEE Trans. Ind. Electron. 2016, 63, 504–516. [Google Scholar] [CrossRef]
- Rodas, J. A brief survey of model predictive current control techniques for six-phase induction machines. In Proceedings of the 2021 IEEE CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Valparaíso, Chile, 6–9 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, C.; Tao, W.; Wang, J.; Liu, G. Virtual-stator-flux-based direct torque control of five-phase fault-tolerant permanent-magnet motor with open-circuit fault. IEEE Trans. Power Electron. 2020, 35, 5007–5017. [Google Scholar] [CrossRef]
- Barrero, F.; Duran, M.J. Recent advances in the design, modeling, and control of multiphase machines—Part I. IEEE Trans. Ind. Electron. 2016, 63, 449–458. [Google Scholar] [CrossRef]
- Duran, M.J.; Barrero, F. Recent advances in the design, modeling, and control of multiphase machines—Part II. IEEE Trans. Ind. Electron. 2016, 63, 459–468. [Google Scholar] [CrossRef]
- Berm, M.; Mart, C.; Gonz, I.; Dur, M.J.; Barrero, F. Predictive current control in electrical drives: An illustrated review with case examples using a five-phase induction motor drive with distributed windings. IET Electr. Power Appl. 2020, 14, 1291–1310. [Google Scholar]
- Cao, B.; Grainger, B.M.; Wang, X.; Zou, Y.; Reed, G.F.; Mao, Z.-H. Direct torque model predictive control of a five-phase permanent magnet synchronous motor. IEEE Trans. Power Electron. 2021, 36, 2346–2360. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model predictive control for power converters and drives: Advances and trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Flores-Bahamonde, F.; Acuna, P.; Novak, M.; Zhang, Y.; Tarisciotti, L.; Davari, S.A.; Zhang, Z.; et al. Latest advances of model predictive control in electrical drives—Part I: Basic concepts and advanced strategies. IEEE Trans. Power Electron. 2022, 37, 3927–3942. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Davari, S.A.; Rodas, J.; Valencia, D.F.; Elmorshedy, M.; Wang, F.; Zuo, K.; Tarisciotti, L.; et al. Latest advances of model predictive control in electrical drives—Part II: Applications and benchmarking with classical control 4methods. IEEE Trans. Power Electron. 2022, 37, 5047–5061. [Google Scholar] [CrossRef]
- Li, X.; Xue, Z.; Zhang, L.; Hua, W. A low-complexity three-vectorbased model predictive torque control for spmsm. IEEE Trans. Power Electron. 2021, 36, 13002–13012. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Xie, W.; Wang, F.; Dou, M.; Kennel, R.M.; Lorenz, R.D.; Gerling, D. Deadbeat model-predictive torque control with discrete space-vector modulation for pmsm drives. IEEE Trans. Ind. Electron. 2017, 64, 3537–3547. [Google Scholar] [CrossRef]
- Li, X.; Xue, Z.; Yan, X.; Zhang, L.; Ma, W.; Hua, W. Low-complexity multivector-based model predictive torque control for pmsm with voltage preselection. IEEE Trans. Power Electron. 2021, 36, 11726–11738. [Google Scholar] [CrossRef]
- Fretes, H.; Rodas, J.; Doval-Gandoy, J.; Gomez, V.; Gomez, N.; Novak, M.; Rodriguez, J.; Dragicevic, T. Pareto optimal weighting factor design of predictive current controller of a six-phase induction machine based on particle swarm optimization algorithm. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 207–219. [Google Scholar] [CrossRef]
- Levi, E. Multiphase electric machines for variable-speed applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Cervone, A.; Dordevic, O.; Brando, G. General approach for modeling and control of multiphase pmsm drives. IEEE Trans. Power Electron. 2021, 36, 10490–10503. [Google Scholar] [CrossRef]
- Zhao, Y.; Lipo, T. Space vector pwm control of dual three-phase induction machine using vector space decomposition. IEEE Trans. Ind. Appl. 1995, 31, 1100–1109. [Google Scholar] [CrossRef]
- Muduli, U.R.; Chikondra, B.; Behera, R.K. Space vector pwm based dtc scheme with reduced common mode voltage for five-phase induction motor drive. IEEE Trans. Power Electron. 2022, 37, 114–124. [Google Scholar] [CrossRef]
- Bhowate, A.; Aware, M.V.; Sharma, S. Speed sensor-less predictive torque control for five-phase induction motor drive using synthetic voltage vectors. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2698–2709. [Google Scholar] [CrossRef]
- Tomlinson, M.; Mouton, H.T.; Kennel, R.; Stolze, P. A fixed switching frequency scheme for finite-control-set model predictive control—Concept and algorithm. IEEE Trans. Ind. Electron. 2016, 63, 7662–7670. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J.; Gao, X.; Tian, W.; Zhou, L.; Rodriguez, J.; Kennel, R. Continuous control set predictive speed control of spmsm drives with short prediction horizon. IEEE Trans. Power Electron. 2022, 37, 10166–10177. [Google Scholar] [CrossRef]
- Norambuena, M.; Rodriguez, J.; Zhang, Z.; Wang, F.; Garcia, C.; Kennel, R. A very simple strategy for high-quality performance of ac machines using model predictive control. IEEE Trans. Power Electron. 2019, 34, 794–800. [Google Scholar] [CrossRef]
- Mart, C.; Arahal, M.R.; Barrero, F.; Duran, M.J. Five-phase induction motor rotor current observer for finite control set model predictive control of stator current. IEEE Trans. Ind. Electron. 2016, 63, 4527–4538. [Google Scholar] [CrossRef]
- Lim, C.S.; Levi, E.; Jones, M.; Rahim, N.A.; Hew, W.P. Fcs-mpc-based current control of a five-phase induction motor and its comparison with 6pi-pwm control. IEEE Trans. Ind. Electron. 2014, 61, 149–163. [Google Scholar] [CrossRef]
- Riveros, J.A.; Barrero, F.; Levi, E.; Duran, M.J.; Toral, S.; Jones, M. Variable-speed five-phase induction motor drive based on predictive torque control. IEEE Trans. Ind. Electron. 2013, 60, 2957–2968. [Google Scholar] [CrossRef]
- Mousa, H.H.H.; Youssef, A.-R.; Mohamed, E.E.M. Model predictive speed control of five-phase pmsg based variable speed wind generation system. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 304–309. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, C. A simplified model predictive control for a dual three-phase pmsm with reduced harmonic currents. IEEE Trans. Ind. Electron. 2018, 65, 9079–9089. [Google Scholar] [CrossRef]
- Yu, F.; Liu, X.; Zhu, Z.; Mao, J. An improved finite-control-set model predictive flux control for asymmetrical six-phase pmsms with a novel duty-cycle regulation strategy. IEEE Trans. Energy Convers. 2021, 36, 1289–1299. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, H.; Fan, M.; He, L.; Xie, M.; Chen, R.; Norambuena, M.; Rodríguez, J. Multiple-voltage-vector model predictive control with reduced complexity for multilevel inverters. IEEE Trans. Transp. Electrif. 2020, 6, 105–117. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, B. Double vectors model predictive torque control without weighting factor based on voltage tracking error. IEEE Trans. Power Electron. 2018, 33, 2368–2380. [Google Scholar] [CrossRef]
- Xue, C.; Song, W.; Feng, X. Finite control-set model predictive current control of five-phase permanent-magnet synchronous machine based on virtual voltage vectors. IET Electr. Power Appl. 2017, 11, 836–846. [Google Scholar] [CrossRef]
- Liu, S.; Liu, C. Virtual-vector-based robust predictive current control for dual three-phase pmsm. IEEE Trans. Ind. Electron. 2021, 68, 2048–2058. [Google Scholar] [CrossRef]
- Liu, X.; Jin, W.; Li, Z.; Hao, Z.; Kennel, R. Simplified predictive torque control of five phase permanent magnet motor with non-sinusoidal back-emf. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018. [Google Scholar]
- Luo, Y.; Liu, C. Model predictive control for a six-phase pmsm motor with a reduced-dimension cost function. IEEE Trans. Ind. Electron. 2019, 67, 969–979. [Google Scholar] [CrossRef]
- Wang, W.; Song, Z.; Liu, Y.; Liu, C. Decoupled modulation scheme for harmonic current suppression in five-phase pmsm. IEEE Trans. Power Electron. 2022, 37, 8795–8799. [Google Scholar] [CrossRef]
- Wang, F.; Xie, H.; Chen, Q.; Davari, S.A.; Rodr, J.; Kennel, R. Parallel predictive torque control for induction machines without weighting factors. IEEE Trans. Power Electron. 2020, 35, 1779–1788. [Google Scholar] [CrossRef]
- Davari, S.A.; Norambuena, M.; Nekoukar, V.; Garcia, C.; Rodriguez, J. Even-handed sequential predictive torque and flux control. IEEE Trans. Ind. Electron. 2020, 67, 7334–7342. [Google Scholar] [CrossRef]
- Xiong, S.; Li, J. Cascade Model Predictive Current Control for Five-Phase Permanent Magnet Synchronous Motor. IEEE Access 2022, 10, 88812–88820. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, S.; Ren, G.; Yao, C.; Ma, G. A cascaded band based model predictive current control for pmsm drives. IEEE Trans. Ind. Electron. 2022, 70, 3503–3514. [Google Scholar] [CrossRef]
- Musunuru, N.S.P.; Srirama, S. Cascaded predictive control of a single power supply-driven four-level open-end winding induction motor drive without weighting factors. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2858–2867. [Google Scholar] [CrossRef]
- Dragičević, T.; Novak, M. Weighting factor design in model predictive control of power electronic converters: An artificial neural network approach. IEEE Trans. Ind. Electron. 2018, 66, 8870–8880. [Google Scholar] [CrossRef]
- Yao, C.; Sun, Z.; Xu, S.; Zhang, H.; Ren, G.; Ma, G. Optimal parameters design for model predictive control using an artificial neural network optimized by genetic algorithm. In Proceedings of the 2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1–3 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Wan, Y.; Dragicevic, T.; Mijatovic, N.; Li, C.; Rodriguez, J. Reinforcement learning based weighting factor design of model predictive control for power electronic converters. In Proceedings of the 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 20–22 November 2021; pp. 738–743. [Google Scholar] [CrossRef]
- Yao, C.; Sun, Z.; Xu, S.; Zhang, H.; Ren, G.; Ma, G. ANN optimization of weighting factors using genetic algorithm for model predictive control of PMSM drives. IEEE Trans. Ind. Appl. 2022, 58, 7346–7362. [Google Scholar] [CrossRef]
- Bhowate, A.; Aware, M.V.; Sharma, S. Predictive torque control algorithm for a five-phase induction motor drive for reduced torque ripple with switching frequency control. IEEE Trans. Power Electron. 2020, 35, 7282–7294. [Google Scholar] [CrossRef]
- Xu, Y.; Zheng, B.; Wang, G.; Yan, H.; Zou, J. Current harmonic suppression in dual three-phase permanent magnet synchronous machine with extended state observer. IEEE Trans. Power Electron. 2020, 35, 12166–12180. [Google Scholar] [CrossRef]
- Gon, P.F.C.; Cruz, S.M.A.; Mendes, A.M.S. Fixed and variable amplitude virtual vectors for model predictive control of six-phase pmsms with single neutral configuration. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, VIC, Australia, 13–15 February 2019; pp. 267–273. [Google Scholar] [CrossRef]
- Du, Y.; Ji, J.; Zhao, W.; Tao, T.; Xu, D. Self-adapted model predictive current control for five-phase open-end winding pmsm with reduced switching loss. IEEE Trans. Power Electron. 2022, 37, 11007–11018. [Google Scholar] [CrossRef]
- Ren, Y.; Zhu, Z.Q. Enhancement of steady-state performance in directtorque-controlled dual three-phase permanent-magnet synchronous machine drives with modified switching table. IEEE Trans. Ind. Electron. 2015, 62, 3338–3350. [Google Scholar] [CrossRef]
- Yang, G.; Yang, J.; Li, S.; Wang, Y.; Hussain, H.; Deng, R.; Yan, L. A sequential direct torque control scheme for seven-phase induction machines based on virtual voltage vectors. IEEE Trans. Ind. Appl. 2021, 57, 3722–3734. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, C. A flux constrained predictive control for a six-phase pmsm motor with lower complexity. IEEE Trans. Ind. Electron. 2019, 66, 5081–5093. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, C. Multi-vector-based model predictive torque control for a six-phase pmsm motor with fixed switching frequency. IEEE Trans. Energy Convers. 2019, 34, 1369–1379. [Google Scholar] [CrossRef]
- Aciego, J.J.; Gonz, I.; Duran, M.J. Model predictive control of six-phase induction motor drives using two virtual voltage vectors. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 321–330. [Google Scholar] [CrossRef]
- Goncalves, P.; Cruz, S.; Mendes, A. Bi-subspace predictive current control of six-phase pmsm drives based on virtual vectors with optimal amplitude. Electr. Power Appl. IET 2019, 13, 1672–1683. [Google Scholar] [CrossRef]
- Aciego, J.J.; Prieto, I.G.; Duran, M.J.; Bermudez, M.; SalasBiedma, P. Model predictive control based on dynamic voltage vectors for six-phase induction machines. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2710–2722. [Google Scholar] [CrossRef]
- González-Prieto, A.; González-Prieto, I.; Duran, M.J. Smart voltage vectors for model predictive control of six-phase electric drives. IEEE Trans. Ind. Electron. 2021, 68, 9024–9035. [Google Scholar] [CrossRef]
- Gonzalez, O.; Ayala, M.; Romero, C.; Delorme, L.; Rodas, J.; Gregor, R.; Gonzalez-Prieto, I.; Durán, M.J. Model predictive current control of sixphase induction motor drives using virtual vectors and space vector modulation. IEEE Trans. Power Electron. 2022, 37, 7617–7628. [Google Scholar] [CrossRef]
- Saeed, M.S.R.; Song, W.; Huang, L.; Yu, B. Double-vector-based finite control set model predictive control for five-phase pmsms with high tracking accuracy and dc-link voltage utilization. IEEE Trans. Power Electron. 2022, 37, 15234–15244. [Google Scholar] [CrossRef]
- González-Prieto, A.; González-Prieto, I.; Duran, M.J.; Aciego, J.J.; SalasBiedma, P. Current harmonic mitigation using a multi-vector solution for mpc in six-phase electric drives. IEEE Access 2021, 9, 117761–117771. [Google Scholar] [CrossRef]
- Wang, W.; Liu, C.; Liu, S.; Zhao, H. Model predictive torque control for dual three-phase pmsms with simplified deadbeat solution and discrete space-vector modulation. IEEE Trans. Energy Convers. 2021, 36, 1491–1499. [Google Scholar] [CrossRef]
- Gonzalez, O.; Ayala, M.; Doval-Gandoy, J.; Rodas, J.; Rivera, M. Predictivefixed switching current control strategy applied to six-phase induction machine. Energies 2019, 12, 2294. [Google Scholar] [CrossRef]
- Ayala, M.; Doval-Gandoy, J.; Gonzalez, O.; Rodas, J.; Gregor, R.; Rivera, M. Experimental stability study of modulated model predictive current controllers applied to six-phase induction motor drives. IEEE Trans. Power Electron. 2021, 36, 13275–13284. [Google Scholar] [CrossRef]
- Ayala, M.; Doval-Gandoy, J.; Rodas, J.; Gonzalez, O.; Gregor, R.; Rivera, M. A novel modulated model predictive control applied to six-phase induction motor drives. IEEE Trans. Ind. Electron. 2021, 68, 3672–3682. [Google Scholar] [CrossRef]
- Gonzalez-Prieto, A.; Martin, C.; Gonzalez-Prieto, I.; Duran, M.J.; Carrillo-Ríos, J.; Aciego, J.J. Hybrid multivector fcs–mpc for six-phase electric drives. IEEE Trans. Power Electron. 2022, 37, 8988–8999. [Google Scholar] [CrossRef]
- Liu, S.; Liu, C. Direct harmonic current control scheme for dual three-phase pmsm drive system. IEEE Trans. Power Electron. 2021, 36, 11647–11657. [Google Scholar] [CrossRef]
- Ye, D.; Li, J.; Qu, R.; Lu, H.; Lu, Y. Finite set model predictive mtpa control with vsd method for asymmetric six-phase pmsm. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Wang, W.; Fan, Y.; Chen, S.; Zhang, Q. Finite control set model predictive current control of a five-phase PMSM with virtual voltage vectors and adaptive control set. CES Trans. Electr. Mach. Syst. 2018, 2, 136–141. [Google Scholar] [CrossRef]
- Yu, B.; Song, W.; Yang, K.; Guo, Y.; Saeed, M.S.R. A computationally efficient finite control set model predictive control for multiphase pmsm drives. IEEE Trans. Ind. Electron. 2022, 69, 12066–12076. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, C. Elimination of harmonic currents using a reference voltage vector based-model predictive control for a six-phase pmsm motor. IEEE Trans. Power Electron. 2019, 34, 6960–6972. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Xu, Z.; Wang, W.; Wang, B.; Zou, Z. Deadbeat predictive current control-based fault-tolerant scheme for dual three-phase pmsm drives. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1591–1604. [Google Scholar] [CrossRef]
- Huang, W.; Hua, W.; Yin, F.; Yu, F.; Qi, J. Model predictive thrust force control of a linear flux-switching permanent magnet machine with voltage vectors selection and synthesis. IEEE Trans. Ind. Electron. 2019, 66, 4956–4967. [Google Scholar] [CrossRef]
- Hua, W.; Chen, F.; Huang, W.; Zhang, G.; Wang, W.; Xia, W. Multivectorbased model predictive control with geometric solution of a five-phase flux-switching permanent magnet motor. IEEE Trans. Ind. Trial Electron. 2020, 67, 10035–10045. [Google Scholar] [CrossRef]
- Tao, T.; Zhao, W.; He, Y.; Zhu, J.; Tan, H.; Xue, R. Multivector predictive current control for five-phase pm motor by using hybrid duty modulation technology. IEEE Trans. Transp. Electrif. 2020, 6, 1603–1612. [Google Scholar] [CrossRef]
- Lin, X.; Huang, W.; Jiang, W.; Zhao, Y.; Zhu, S. Deadbeat direct torque and flux control for permanent magnet synchronous motor based on stator flux oriented. IEEE Trans. Power Electron. 2020, 35, 5078–5092. [Google Scholar] [CrossRef]
- Wang, W.; Liu, C.; Zhao, H.; Song, Z. Improved deadbeat-direct torque and flux control for pmsm with less computation and enhanced robustness. IEEE Trans. Ind. Electron. 2022, 70, 2254–2263. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, C. Model predictive torque control of an open-end winding pmsm with reduced computation time. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Wei, X.; Liang, Z.; Kennel, R.; Rodriguez, J. Spacevector-optimized predictive control for dual three-phase pmsm with quick current response. IEEE Trans. Power Electron. 2022, 37, 4453–4462. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, C. Model predictive control for a six-phase pmsm with high robustness against weighting factor variation. IEEE Trans. Ind. Appl. 2019, 55, 2781–2791. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, G. Predictive dtc strategy with fault-tolerant function for six-phase and three-phase pmsm series-connected drive system. IEEE Trans. Ind. Electron. 2018, 65, 9101–9112. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, X.; Niu, S. A hybrid two-stage control solution for sixphase pmsm motor with improved performance. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 5435–5445. [Google Scholar] [CrossRef]
- Li, T.; Ma, R. An improved deadbeat predictive current control for five phase pmsm. In Proceedings of the 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 20–22 November 2021; pp. 562–569. [Google Scholar] [CrossRef]
- Yan, L.; Wang, F.; Tao, P.; Zuo, K. Robust predictive torque control of permanent magnet synchronous machine using discrete hybrid prediction model. IEEE Trans. Energy Convers. 2020, 35, 2240–2248. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z. Simple robust model predictive current control for pmsm drives without flux linkage parameter. IEEE Trans. Ind. Electron. 2022, 70, 3515–3524. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, S.; Zhang, C. Improved model predictive current control for spmsm drives with parameter mismatch. IEEE Trans. Ind. Electron. 2020, 67, 852–862. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Hackl, C.M.; Kennel, R.; Rodriguez, J. Efficient directmodel predictive control with discrete-time integral action for pmsgs. IEEE Trans. Energy Convers. 2019, 34, 1063–1072. [Google Scholar] [CrossRef]
- Fu, R. Robust predictive current control of dual three-phase pmsm using prediction error correction. In Proceedings of the 2021 IEEE International Conference 14on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 20–22 November 2021; pp. 576–581. [Google Scholar] [CrossRef]
- Yao, X.; Zhang, F.; Wang, J.; Huang, S.; Wang, Y.; Ma, H. Improved predictive torque control of pmsm considering inductance parameter mismatch. In Proceedings of the 2021 IEEE International Electric Machines Drives Conference (IEMDC), Hartford, CT, USA, 17–20 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Mohamed, Y.A.-R.I.; El-Saadany, E.F. An improved deadbeat current control scheme with a novel adaptive self-tuning load model for a three-phase pwm voltage-source inverter. IEEE Trans. Ind. Electron. 2007, 54, 747–759. [Google Scholar] [CrossRef]
- Mwasilu, F.; Jung, J.-W. Enhanced fault-tolerant control of interior pmsms based on an adaptive ekf for ev traction applications. IEEE Trans. Power Electron. 2016, 31, 5746–5758. [Google Scholar] [CrossRef]
- Gao, S.; Dong, H.; Ning, B.; Tang, T.; Li, Y. Nonlinear mapping-based feedback technique of dynamic surface control for the chaotic pmsm using neural approximation and parameter identification. IET Control. Theory Appl. 2018, 12, 819–827. [Google Scholar] [CrossRef]
- Jabbour, N.; Mademlis, C. Online parameters estimation and autotuning of a discrete-time model predictive speed controller for induction motor drives. IEEE Trans. Power Electron. 2019, 34, 1548–1559. [Google Scholar] [CrossRef]
- Liu, Z.-H.; Jing, L.; Li, X.-H.; Zhang, Y.-J. Cooperative particle swarm optimization with ics and its application to parameter identification of pmsm. In Proceedings of the 2012 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012; pp. 1303–1308. [Google Scholar] [CrossRef]
- Sun, X.; Cao, J.; Lei, G.; Guo, Y.; Zhu, J. A robust deadbeat predictive controller with delay compensation based on composite sliding-mode observer for pmsms. IEEE Trans. Power Electron. 2021, 36, 10742–10752. [Google Scholar] [CrossRef]
- Perera, A.; Nilsen, R. A.; Nilsen, R. A method based on prediction-error-gradients to estimate pmsm parameters online. In IEEE IAS Annual Meeting 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Mehreganfar, M.; Saeedinia, M.H.; Davari, S.A.; Garcia, C.; Rodriguez, J. Sensorless predictive control of afe rectifier with robust adaptive inductance estimation. IEEE Trans. Ind. Inform. 2019, 15, 3420–3431. [Google Scholar] [CrossRef]
- Saeed, M.S.R.; Song, W.; Yu, B. Robustness improvement of deadbeat model predictive control for five-phase pmsm drives. In Proceedings of the 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020; pp. 1336–1341. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, C.; Liu, S.; Song, Z. A new cascaded adaptive deadbeat control method for pmsm drive. IEEE Trans. Ind. Electron. 2022, 70, 3384–3393. [Google Scholar] [CrossRef]
- Perera, A.; Nilsen, R. Gauss-newton: A prediction-error-gradient based algorithm to track PMSM parameters online. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Brosch, A.; Hanke, S.; Wallscheid, O.; Bocker, J. Data-driven recursive least squares estimation for model predictive current control of permanent magnet synchronous motors. IEEE Trans. Power Electron. 2021, 36, 2179–2190. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Z.; Cheng, Y.; Wang, Y. Robust model predictive current control based on inductance and flux linkage extraction algorithm. IEEE Trans. Veh. Technol. 2020, 69, 14893–14902. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, S.; Zhang, C.; Galassini, A.; Degano, M. Improved model predictive current control for spmsm drives using current update mechanism. IEEE Trans. Ind. Electron. 2020, 68, 1938–1948. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Cui, X.; Wang, Y.; Zhang, C.; Li, Z.; Zhou, Y. Novel deadbeat predictive current control for pmsm with parameter updating scheme. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2065–2074. [Google Scholar] [CrossRef]
- Yan, L.; Wang, F.; Dou, M.; Zhang, Z.; Kennel, R.; Rodríguez, J. Active disturbance-rejection-based speed control in model predictive control for induction machines. IEEE Trans. Ind. Electron. 2020, 67, 2574–2584. [Google Scholar] [CrossRef]
- Wang, F.; Wang, J.; Kennel, R.M.; Rodríguez, J. Fast speed control of ac machines without the proportional-integral controller: Using an extended high-gain state observer. IEEE Trans. Power Electron. 2019, 34, 9006–9015. [Google Scholar] [CrossRef]
- Yan, L.; Dou, M.; Hua, Z.; Zhang, H.; Yang, J. Robustness improvement of fcs-mptc for induction machine drives using disturbance feedforward technique. IEEE Trans. Power Electron. 2019, 34, 2874–2886. [Google Scholar] [CrossRef]
- Wang, J.; Wang, F.; Wang, G.; Li, S.; Yu, L. Generalized proportional integral observer based robust finite control set predictive current control for induction motor systems with time-varying disturbances. IEEE Trans. Ind. Inform. 2018, 14, 4159–4168. [Google Scholar] [CrossRef]
- Xiong, C.; Xu, H.; Guan, T.; Zhou, P. A constant switching frequency multiple-vector-based model predictive current control of five-phase pmsm with nonsinusoidal back emf. IEEE Trans. Ind. Electron. 2020, 67, 1695–1707. [Google Scholar] [CrossRef]
- Gon, P.F.C.; Cruz, S.M.A.; Mendes, A.M.S. Suppression of steadystate errors in predictive current control of six-phase pmsm drives. In Proceedings of the 2020 International Conference on Smart Energy Systems and Technologies (SEST), Istanbul, Turkey, 7–9 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Bermudez, M.; Arahal, M.R.; Duran, M.J.; Gonzalez-Prieto, I. Model predictive control of six-phase electric drives including arx disturbance estimator. IEEE Trans. Ind. Electron. 2021, 68, 81–91. [Google Scholar] [CrossRef]
- An, X.; Liu, G.; Chen, Q.; Zhao, W.; Song, X. Robust predictive current control for fault-tolerant operation of five-phase pm motors based on online stator inductance identification. IEEE Trans. Power Electron. 2021, 36, 13162–13175. [Google Scholar] [CrossRef]
- Yu, K.; Wang, Z.; Hua, W.; Cheng, M. Robust cascaded deadbeat predictive control for dual three-phase variable-flux pmsm considering intrinsic delay in speed loop. IEEE Trans. Ind. Electron. 2022, 69, 12107–12118. [Google Scholar] [CrossRef]
- Gon, P.F.; Cruz, S.M.; Mendes, A.M.S. Disturbance observer based predictive current control of six-phase permanent magnet synchronous machines for the mitigation of steady-state errors and current harmonics. IEEE Trans. Ind. Electron. 2022, 69, 130–140. [Google Scholar] [CrossRef]
- Lin, C.-K.; Liu, T.-H.; Yu, J.-t.; Fu, L.-C.; Hsiao, C.-F. Model-free predictive current control for interior permanent-magnet synchronous motor drives based on current difference detection technique. IEEE Trans. Ind. Electron. 2014, 61, 667–681. [Google Scholar] [CrossRef]
- Lin, C.-K.; Yu, J.-T.; Lai, Y.-S.; Yu, H.-C. Improved model-free predictive current control for synchronous reluctance motor drives. IEEE Trans. Ind. Electron. 2016, 63, 3942–3953. [Google Scholar] [CrossRef]
- Wang, P.; Yuan, X.; Zhang, C. An improved model free predictive current control for pmsm with current prediction error variations. IEEE Access 2022, 10, 54537–54548. [Google Scholar] [CrossRef]
- Carlet, P.G.; Tinazzi, F.; Bolognani, S.; Zigliotto, M. An effective modelfree predictive current control for synchronous reluctance motor drives. IEEE Trans. Ind. Appl. 2019, 55, 3781–3790. [Google Scholar] [CrossRef]
- Yu, F.; Zhou, C.; Liu, X.; Zhu, C. Model-free predictive current control for three-level inverter-fed ipmsm with an improved current difference updating technique. IEEE Trans. Energy Convers. 2021, 36, 3334–3343. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, J.; Huang, L. Model-free predictive current control of pmsm drives based on extended state observer using ultralocal model. IEEE Trans. Ind. Electron. 2021, 68, 993–1003. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, H.; Yao, H. Model-free control of surface mounted pmsm drive system. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 175–180. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, H.; Zhang, H. Model-free deadbeat predictive current control of a surface-mounted permanent magnet synchronous motor drive system. J. Power Electron. 2018, 18, 103–115. [Google Scholar]
- Agoro, S.; Husain, I. Model-free predictive current and disturbance rejection control of dual three-phase pmsm drives using optimal virtual vector modulation. IEEE J. Emerg. Sel. Top. Power Electron. 2022. [Google Scholar] [CrossRef]
- Jin, N.; Chen, M.; Guo, L.; Li, Y.; Chen, Y. Double-vector model-free predictive control method for voltage source inverter with visualization analysis. IEEE Trans. Ind. Electron. 2022, 69, 10066–10078. [Google Scholar] [CrossRef]
- Norambuena, M.; Lezana, P.; Rodriguez, J. A method to eliminate steadystate error of model predictive control in power electronics. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2525–2530. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, L.; Wang, J.; Gao, X.; Li, Z.; Zhang, Z. Robust predictive current control of permanent-magnet synchronous motors with newly designed cost function. IEEE Trans. Power Electron. 2020, 35, 10778–10788. [Google Scholar] [CrossRef]
- Siami, M.; Khaburi, D.A.; Abbaszadeh, A.; Rodríguez, J. Robustness improvement of predictive current control using prediction error correction for permanent-magnet synchronous machines. IEEE Trans. Ind. Electron. 2016, 63, 3458–3466. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Wang, Q. Robust predictive current control with parallel compensation terms against multi-parameter mismatches for pmsms. IEEE Trans. Energy Convers. 2020, 35, 2222–2230. [Google Scholar] [CrossRef]
- Fu, R. Robust model predictive flux control of pmsm drive using a compensated stator flux predictor. IEEE Access 2021, 9, 136736–136743. [Google Scholar] [CrossRef]
- Wang, F.; Zuo, K.; Tao, P.; Rodríguez, J. High performance model predictive control for pmsm by using stator current mathematical model self regulation technique. IEEE Trans. Power Electron. 2020, 35, 13652–13662. [Google Scholar] [CrossRef]
- He, C.; Hu, J.; Li, Y. Robust predictive current control for pmsm drives with parameter mismatch. In Proceedings of the 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 20–22 November 2021; pp. 542–546. [Google Scholar] [CrossRef]
- Xu, C.; Han, Z.; Lu, S. Deadbeat predictive current control for permanent magnet synchronous machines with closed-form error compensation. IEEE Trans. Power Electron. 2020, 35, 5018–5030. [Google Scholar] [CrossRef]
- Dai, S.; Wang, J.; Sun, Z.; Chong, E. Model inaccuracy analysis and compensation of stationary frame-based deadbeat predictive current control for high-speed pmsm drives. IEEE Trans. Transp. Electrif. 2022, 8, 2654–2666. [Google Scholar] [CrossRef]
- Lu, H.; Li, J.; Qu, R.; Ye, D.; Lu, Y. Fault-tolerant predictive control of six-phase PMSM drives based on pulse-width modulation. IEEE Trans. Ind. Electron. 2019, 66, 4992–5003. [Google Scholar] [CrossRef]
- Liu, G.; Song, C.; Chen, Q. Fcs-mpc-based fault-tolerant control of fivephase ipmsm for mtpa operation. IEEE Trans. Power Electron. 2020, 35, 2882–2894. [Google Scholar] [CrossRef]
- Wang, X.; Liu, G.; Chen, Q.; Farahat, A.; Song, X. Multivectors model predictive control with voltage error tracking for five-phase PMSM short-circuit fault-tolerant operation. IEEE Trans. Transp. Electrif. 2022, 8, 675–687. [Google Scholar] [CrossRef]
- Lu, H.; Li, J.; Qu, R.; Ye, D.; Xiao, L. Reduction of unbalanced axial magnetic force in postfault operation of a novel six-phase double-stator axialflux pm machine using model predictive control. IEEE Trans. Ind. Appl. 2017, 53, 5461–5469. [Google Scholar] [CrossRef]
- Huang, W.; Hua, W.; Fan, Q. Performance analysis and comparison of two fault-tolerant model predictive control methods for five-phase pmsm drives. CES Trans. Electr. Mach. Syst. 2021, 5, 311–320. [Google Scholar] [CrossRef]
- Guzman, H.; Duran, M.J.; Barrero, F.; Bogado, B.; Toral, S. Speed control of five-phase induction motors with integrated open-phase fault operation using model-based predictive current control techniques. IEEE Trans. Ind. Electron. 2014, 61, 4474–4484. [Google Scholar] [CrossRef]
- Guzman, H.; Duran, M.J.; Barrero, F.; Zarri, L.; Bogado, B.; Prieto, I.G.; Arahal, M.R. Comparative study of predictive and resonant controllers in fault-tolerant five-phase induction motor drives. IEEE Trans. Ind. Electron. 2016, 63, 606–617. [Google Scholar] [CrossRef]
- Huang, W.; Hua, W.; Chen, F.; Yin, F.; Qi, J. Model predictive current control of open-circuit fault-tolerant five-phase flux-switching permanent magnet motor drives. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1840–1849. [Google Scholar] [CrossRef]
- Huang, W.; Hua, W.; Chen, F.; Hu, M.; Zhu, J. Model predictive torque control with svm for five-phase pmsm under open-circuit fault condition. IEEE Trans. Power Electron. 2020, 35, 5531–5540. [Google Scholar] [CrossRef]
- Huang, W.; Hua, W.; Chen, F.; Qi, J.; Zhu, J. Performance improvement of model predictive current control of fault-tolerant five-phase flux-switching permanent magnet motor drive. IEEE Trans. Ind. Appl. 2019, 55, 6001–6010. [Google Scholar] [CrossRef]
- Huang, W.; Hua, W.; Chen, F.; Zhu, J. Enhanced model predictive torque control of fault-tolerant five-phase permanent magnet synchronous motor with harmonic restraint and voltage preselection. IEEE Trans. Ind. Electron. 2020, 67, 6259–6269. [Google Scholar] [CrossRef]
- Tao, T.; Zhao, W.; Du, Y.; Cheng, Y.; Zhu, J. Simplified fault-tolerant model predictive control for a five-phase permanent-magnet motor with reduced computation burden. IEEE Trans. Power Electron. 2020, 35, 3850–3858. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, W.; Tang, H.; Tao, T.; Saeed, S. Improved fault-tolerant model predictive torque control of five-phase pmsm by using deadbeat solution. IEEE Trans. Energy Convers. 2022, 37, 210–219. [Google Scholar] [CrossRef]
- Tao, T.; Zhao, W.; He, Y.; Cheng, Y.; Saeed, S.; Zhu, J. Enhanced faulttolerant model predictive current control for a five-phase pm motor with continued modulation. IEEE Trans. Power Electron. 2021, 36, 3236–3246. [Google Scholar] [CrossRef]
- Saeed, S.; Zhao, W.; Wang, H.; Tao, T.; Khan, F. Fault-tolerant deadbeat model predictive current control for a five-phase pmsm with improved svpwm. Chin. J. Electr. Eng. 2021, 7, 111–123. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, C. Pre- and post-fault tolerant operation of a six-phase pmsm motor using fcs-mpc without controller reconfiguration. IEEE Trans. Veh. Technol. 2019, 68, 254–263. [Google Scholar] [CrossRef]
- González-Prieto, I.; Durán, M.J.; Bermúdez, M.; Barrero, F.; Martín, C. Assessment of virtual-voltage-based model predictive controllers in sixphase drives under open-phase faults. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2634–2644. [Google Scholar] [CrossRef]
- Sun, X.; Li, T.; Tian, X.; Zhu, J. Fault-tolerant operation of a six-phase permanent magnet synchronous hub motor based on model predictive current control with virtual voltage vectors. IEEE Trans. Energy Convers. 2022, 37, 337–346. [Google Scholar] [CrossRef]
- Bhowate, A.; Aware, M.; Sharma, S.; Tatte, Y. Predictive torque control for five phase induction motor drive with common mode voltage reduction. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 1730–1735. [Google Scholar] [CrossRef]
- Duran, M.J.; Riveros, J.A.; Barrero, F.; Guzman, H.; Prieto, J. Reduction of common-mode voltage in five-phase induction motor drives using predictive control techniques. IEEE Trans. Ind. Appl. 2012, 48, 2059–2067. [Google Scholar] [CrossRef]
- Dabour, S.M.; Abdel-Khalik, A.S.; Ahmed, S.; Massoud, A. Model predictive control for common-mode voltage reduction and third-harmonic current injection techniques with five-phase inverters. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 1310–1315. [Google Scholar] [CrossRef]
- Iqbal, A.; Alammari, R.; Mosa, M.; Abu-Rub, H. Finite set model predictive current control with reduced and constant common mode voltage for a five-phase voltage source inverter. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 479–484. [Google Scholar] [CrossRef]
- Bhowate, A.; Aware, M.V.; Sharma, S. Predictive torque control of five-phase induction motor drive using successive cost functions for cmv elimination. IEEE Trans. Power Electron. 2021, 36, 14133–14141. [Google Scholar] [CrossRef]
- Yu, B.; Song, W.; Guo, Y.; Li, J.; Saeed, M.S.R. Virtual voltage vector-based model predictive current control for five-phase VSIs with common-mode voltage reduction. IEEE Trans. Transp. Electrif. 2021, 7, 706–717. [Google Scholar] [CrossRef]
- Vu, H.-C.; Lee, H.-H. Model-predictive current control scheme for sevenphase voltage-source inverter with reduced common-mode voltage and current harmonics. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3610–3621. [Google Scholar] [CrossRef]
- Yu, B.; Song, W.; Li, J.; Li, B.; Saeed, M.S.R. Improved finite control set model predictive current control for five-phase vsis. IEEE Trans. Power Electron. 2021, 36, 7038–7048. [Google Scholar] [CrossRef]
- Yu, B.; Song, W.; Guo, Y.; Saeed, M.S.R. A finite control set model predictive control for five-phase pmsms with improved dc-link utilization. IEEE Trans. Power Electron. 2022, 37, 3297–3307. [Google Scholar] [CrossRef]
- Lai, Y.-S.; Shyu, F.-S. Optimal common-mode voltage reduction pwm technique for inverter control with consideration of the dead-time effects-part i: Basic development. IEEE Trans. Ind. Appl. 2004, 40, 1605–1612. [Google Scholar] [CrossRef]
- Kwak, S.; Mun, S.-K. Model predictive control methods to reduce common- mode voltage for three-phase voltage source inverters. IEEE Trans. Power Electron. 2015, 30, 5019–5035. [Google Scholar] [CrossRef]
- Kwak, S.; Mun, S. Common-mode voltage mitigation with a predictive control method considering dead time effects of three-phase voltage source inverters. Power Electron. IET 2014, 8, 1690–1700. [Google Scholar] [CrossRef]
- Guo, L.; Jin, N.; Gan, C.; Xu, L.; Wang, Q. An improved model predictive control strategy to reduce common-mode voltage for two-level voltage source inverters considering dead-time effects. IEEE Trans. Ind. Electron. 2019, 66, 3561–3572. [Google Scholar] [CrossRef]
- Guo, L.; Jin, N.; Gan, C.; Luo, K. Hybrid voltage vector preselection-based model predictive control for two-level voltage source inverters to reduce the common-mode voltage. IEEE Trans. Ind. Electron. 2020, 67, 4680–4691. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, X.; Yuan, X.; Wu, X. Low-complexity model-predictive control for a nine-phase open-end winding pmsm with dead-time compensation. IEEE Trans. Power Electron. 2022, 37, 8895–8908. [Google Scholar] [CrossRef]
- Zhu, B.; Rajashekara, K.; Kubo, H. Predictive torque control with zero-sequence current suppression for open-end winding induction machine. In Proceedings of the 2015 IEEE Industry Applications Society Annual Meeting, Addison, TX, USA, 18–22 October 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Eshwar, K.; Thippiripati, V.K. Weighting-factorless predictive torque control scheme for dual inverter fed open-end-winding pmsm with single dc source. IEEE Trans. Power Electron. 2021, 36, 12968–12978. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, W. Model predictive full-torque control for the openwinding pmsm system driven by dual inverter with a common dc bus. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1541–1554. [Google Scholar] [CrossRef]
- Lin, X.; Huang, W.; Jiang, W.; Zhao, Y.; Wu, X.; Zhu, S. Predictive torque control for open-end winding pmsm with common dc bus based on weighting factorless and finite control set optimization. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1479–1493. [Google Scholar] [CrossRef]
- Xu, D.; Zhao, W.; Tang, H.; Song, X.; Xue, R. Three-vector-based model predictive current control with zero-sequence current suppression for openwinding lpmvm drives. IEEE Trans. Veh. Technol. 2021, 70, 225–236. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; He, Y. A novel model predictive current control method for open-winding pmsg fed by dual inverter. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 7–10 October 2018; pp. 1450–1454. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, W.; Xu, C.; Li, Y.; Wang, Y.; Gao, D. 3-d vector-based model predictive current control for open-end winding pmsg system with zero-sequence current suppression. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 242–258. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Wang, K.; Zhang, W.; Gao, D. Model predictive control of the open-winding pmsg system based on three-dimensional reference voltage-vector. IEEE Trans. Ind. Electron. 2020, 67, 6312–6322. [Google Scholar] [CrossRef]
- Cheng, Y.; Sun, D.; Chen, W.; Nian, H. Model predictive current control for an open-winding pmsm system with a common dc bus in 3-d space. IEEE Trans. Power Electron. 2020, 35, 9597–9607. [Google Scholar] [CrossRef]
- Saeed, M.S.R.; Song, W.; Yu, B.; Xie, Z.; Feng, X. Low-complexity deadbeat model predictive current control for open-winding pmsm drive with zero-sequence current suppression. IEEE Trans. Transp. Electrif. 2021, 7, 2671–2682. [Google Scholar] [CrossRef]
- Musunuru, N.S.P.; Srinivas, S. Elimination of dead time effects on common mode voltage in an open-end winding induction motor drive under low speed operation using a simplified model predictive control. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 1195–1204. [Google Scholar] [CrossRef]
- Cheng, L.; Hu, J.; Jing, S. Dual-vector predictive current control of open-end winding pmsm with zero-sequence current hysteresis control. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 184–195. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Zhang, C.; Zhou, Y.; Zhang, C. An improved deadbeat predictive current control scheme for open-winding permanent magnet 27synchronous motors drives with disturbance observer. IEEE Trans. Power Electron. 2021, 36, 4622–4632. [Google Scholar] [CrossRef]
- Mousavi, M.S.; Davari, S.A.; Nekoukar, V.; Garcia, C.; Rodriguez, J. Computationally efficient model-free predictive control of zero-sequence current in dual inverter fed induction motor. IEEE J. Emerg. Sel. Top. Power Electron. 2022. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, S.; Zhang, C.; Degano, M.; Buticchi, G.; Galassini, A. Improved finite-state model predictive current control with zero-sequence current suppression for oew-spmsm drives. IEEE Trans. Power Electron. 2020, 35, 4996–5006. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, C.; Zhang, S. Torque ripple suppression for open-end winding permanent-magnet synchronous machine drives with predictive current control. IEEE Trans. Ind. Electron. 2020, 67, 1771–1781. [Google Scholar] [CrossRef]
- Saeed, M.S.R.; Song, W.; Yu, B. Reduced complexity model predictive control for five-phase open winding pmsm drive. In Proceedings of the 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 20–22 November 2021; pp. 353–358. [Google Scholar] [CrossRef]
- Wang, H.; Wu, X.; Zheng, X.; Yuan, X. Virtual voltage vector based model predictive control for a nine-phase open-end winding pmsm with a common dc bus. IEEE Trans. Ind. Electron. 2022, 69, 5386–5397. [Google Scholar] [CrossRef]
- Immovilli, F.; Bianchini, C.; Lorenzani, E.; Bellini, A.; Fornasiero, E. Evaluation of combined reference frame transformation for interturn fault detection in permanent-magnet multiphase machines. IEEE Trans. Ind. Electron. 2015, 62, 1912–1920. [Google Scholar] [CrossRef]
- Gon, P.F.C.; Cruz, S.M.A.; Mendes, A.M.S. Online diagnostic method for the detection of high-resistance connections and open-phase faults in six-phase pmsm drives. IEEE Trans. Ind. Appl. 2022, 58, 345–355. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Xu, Z.; Cheng, M.; Wang, W.; Hu, Y. Comprehensive diagnosis and tolerance strategies for electrical faults and sensor faults in dual three-phase pmsm drives. IEEE Trans. Power Electron. 2019, 34, 6669–6684. [Google Scholar] [CrossRef]
- Huang, W.; Du, J.; Hua, W.; Bi, K.; Fan, Q. A hybrid model-based diagnosis approach for open-switch faults in pmsm drives. IEEE Trans. Power Electron. 2022, 37, 3728–3732. [Google Scholar] [CrossRef]
- Huang, W.; Du, J.; Hua, W.; Lu, W.; Bi, K.; Zhu, Y.; Fan, Q. Current-based open-circuit fault diagnosis for pmsm drives with model predictive control. IEEE Trans. Power Electron. 2021, 36, 10695–10704. [Google Scholar] [CrossRef]
- Huang, W.; Luo, L.; Du, J.; Xiang, B.; Mei, S.; Zhou, L.; Fan, Q. Opencircuit fault detection in pmsm drives using model predictive control and cost function error. IEEE Trans. Transp. Electrif. 2022, 8, 2667–2675. [Google Scholar] [CrossRef]
- Hu, K.; Meng, X.; Liu, Z.; Xu, J.; Lin, G.; Tong, L. Flux-based open-switch fault diagnosis and fault tolerance for im drives with predictive torque/flux control. IEEE Trans. Transp. Electrif. 2022, 8, 4595–4606. [Google Scholar] [CrossRef]
- González-Prieto, I.; Duran, M.J.; Rios-Garcia, N.; Barrero, F.; Martin, C. Open-switch fault detection in five-phase induction motor drives using model predictive control. IEEE Trans. Ind. Electron. 2018, 65, 3045–3055. [Google Scholar] [CrossRef]
- Zhao, S.; Blaabjerg, F.; Wang, H. An overview of artificial intelligence applications for power electronics. IEEE Trans. Power Electron. 2021, 36, 4633–4658. [Google Scholar] [CrossRef]
- Akpolat, A.N.; Habibi, M.R.; Dursun, E.; Kuzucuoğlu, A.E.; Yang, Y.; Dragičević, T.; Blaabjerg, F. Sensorless control of dc microgrid based on artificial intelligence. IEEE Trans. Energy Convers. 2021, 36, 2319–2329. [Google Scholar] [CrossRef]

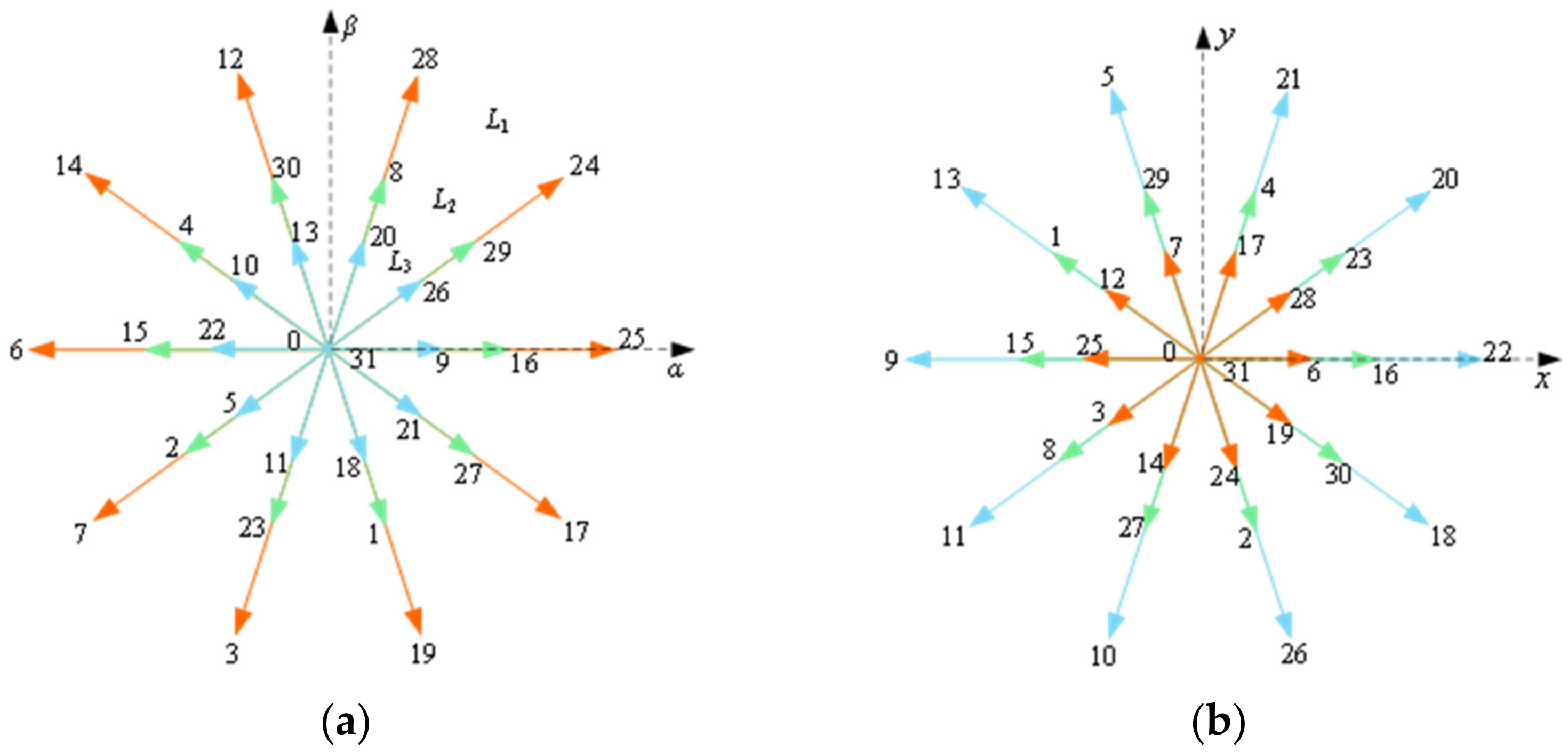
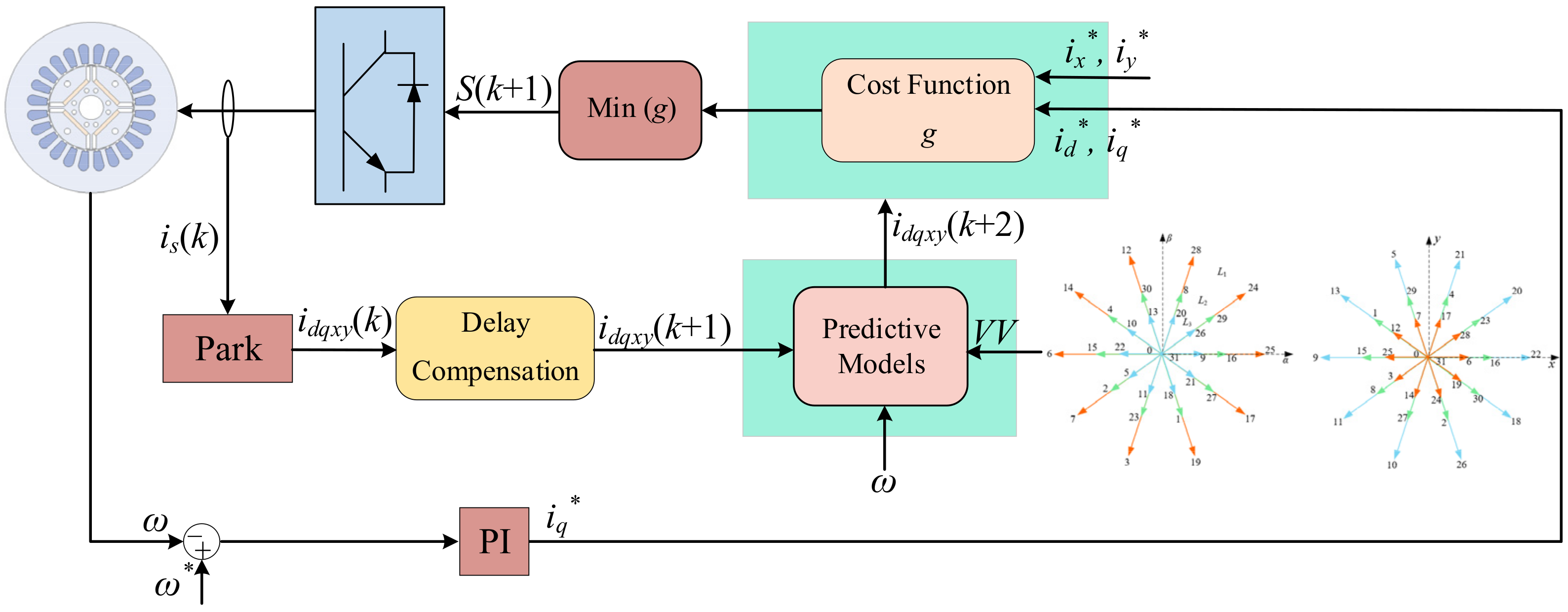
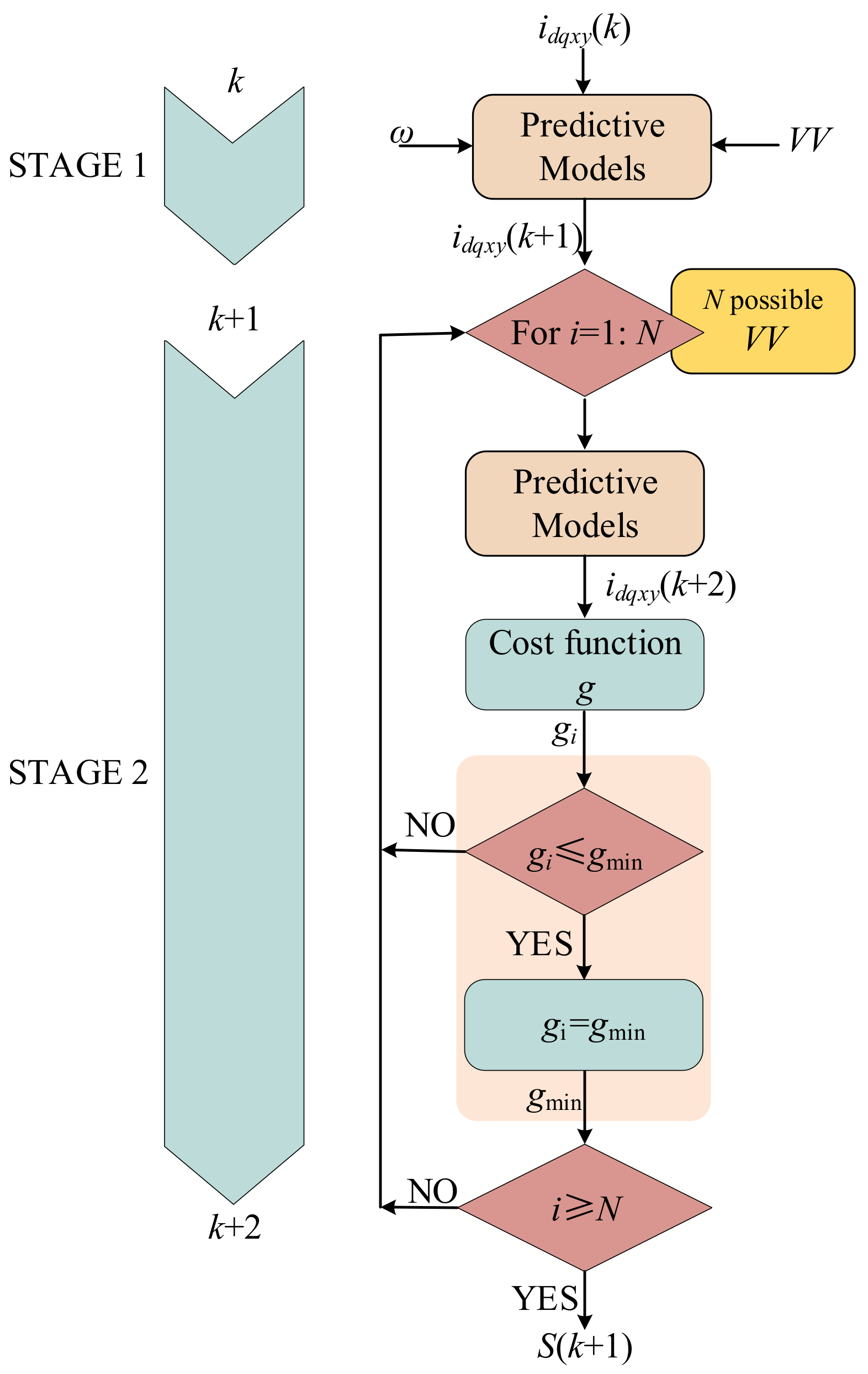


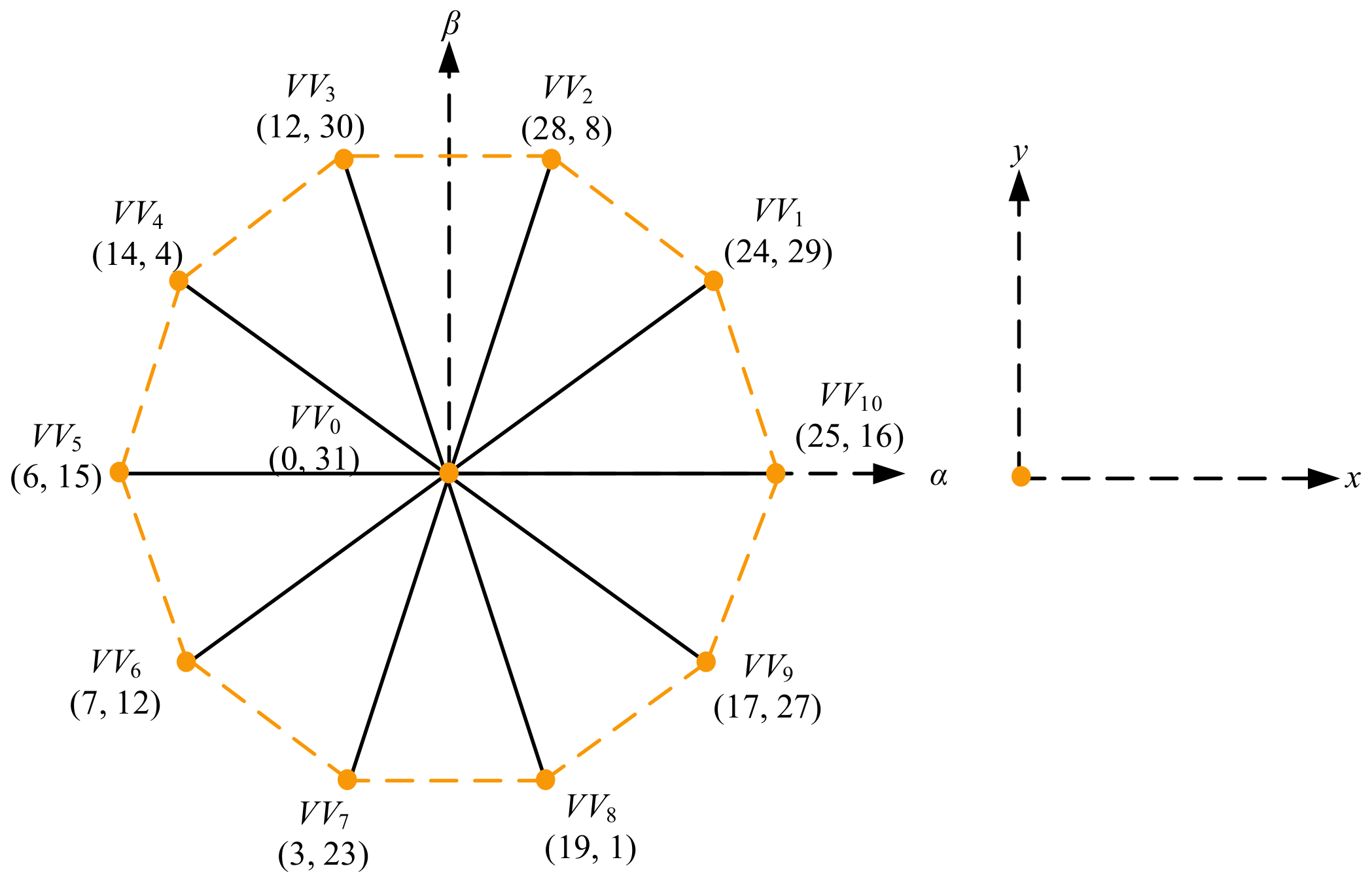
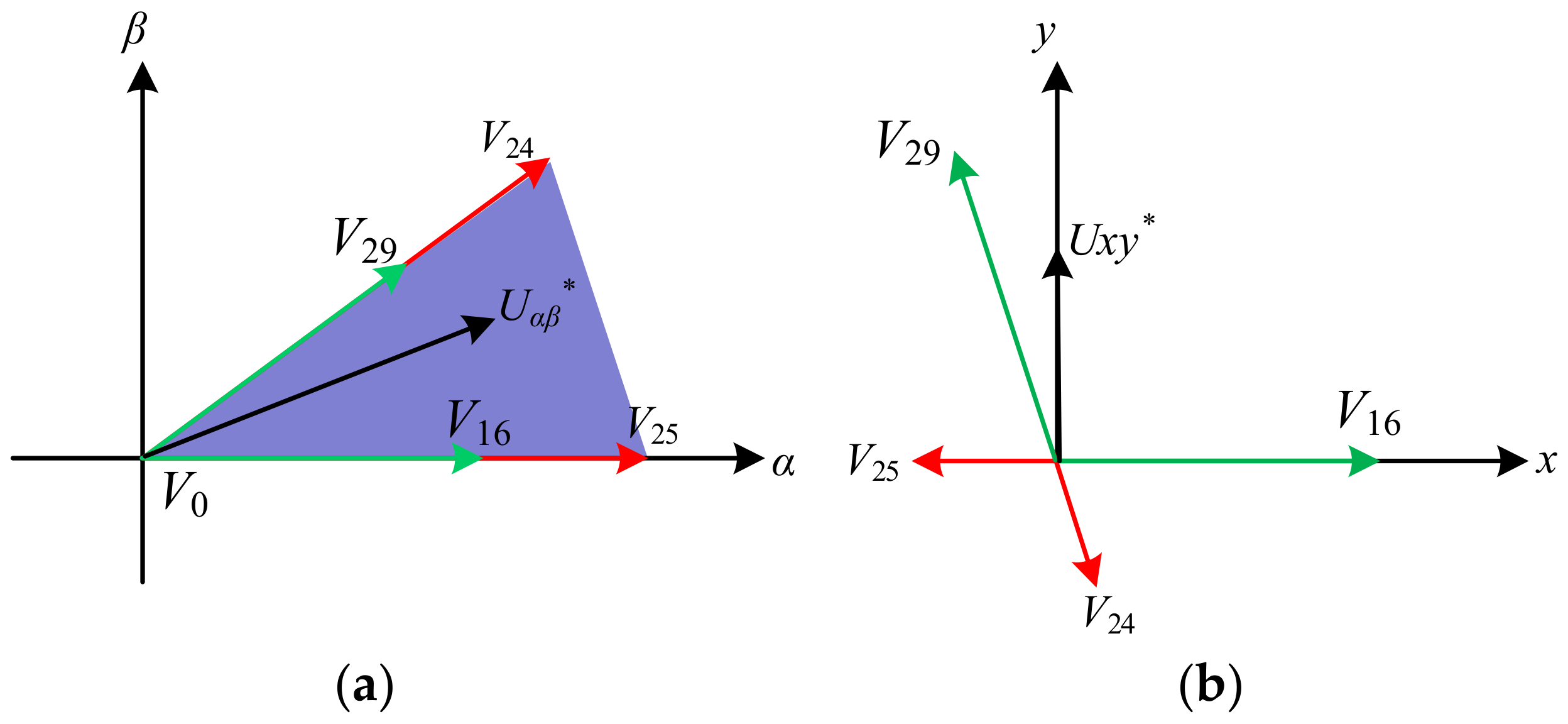
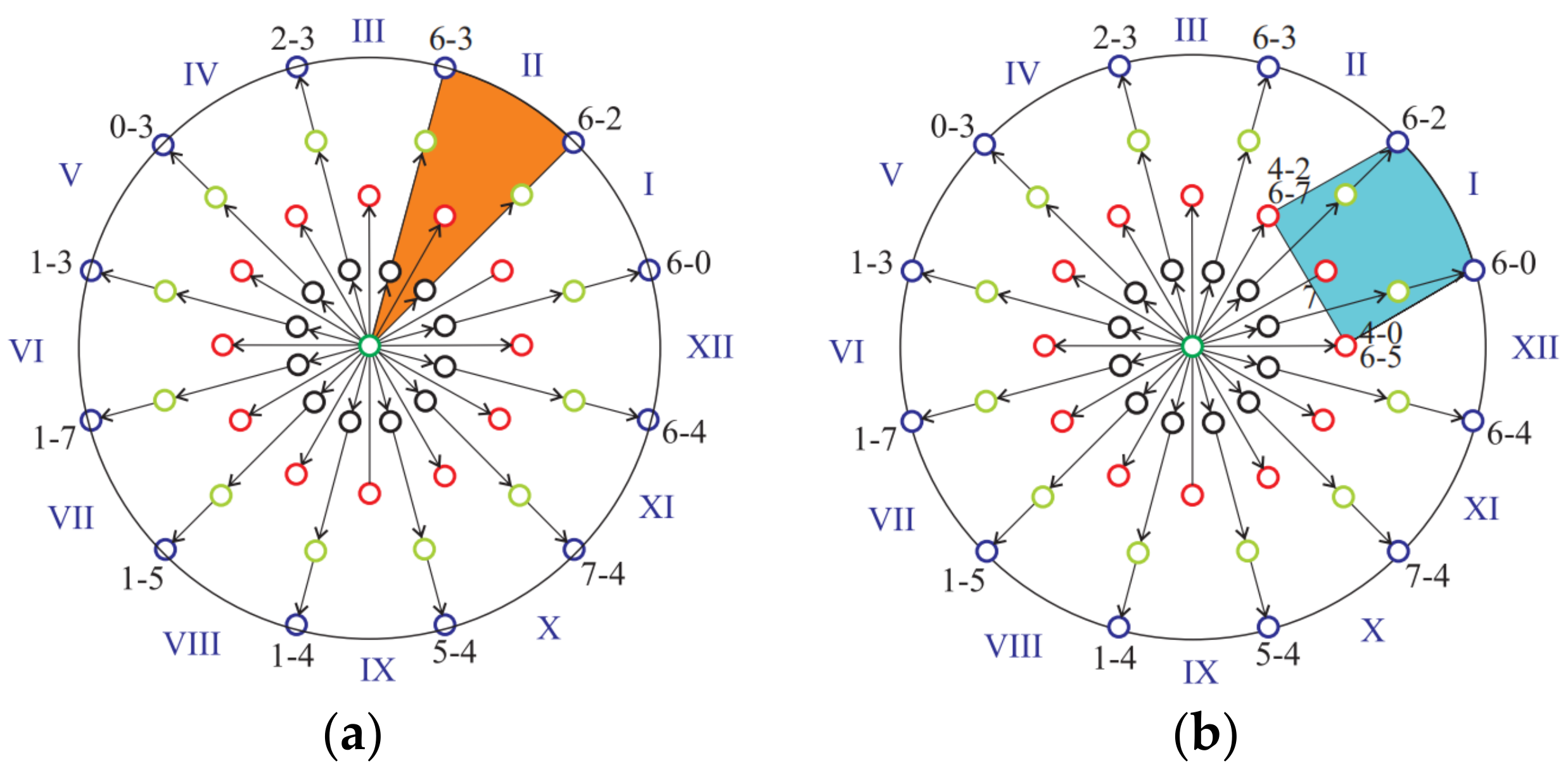

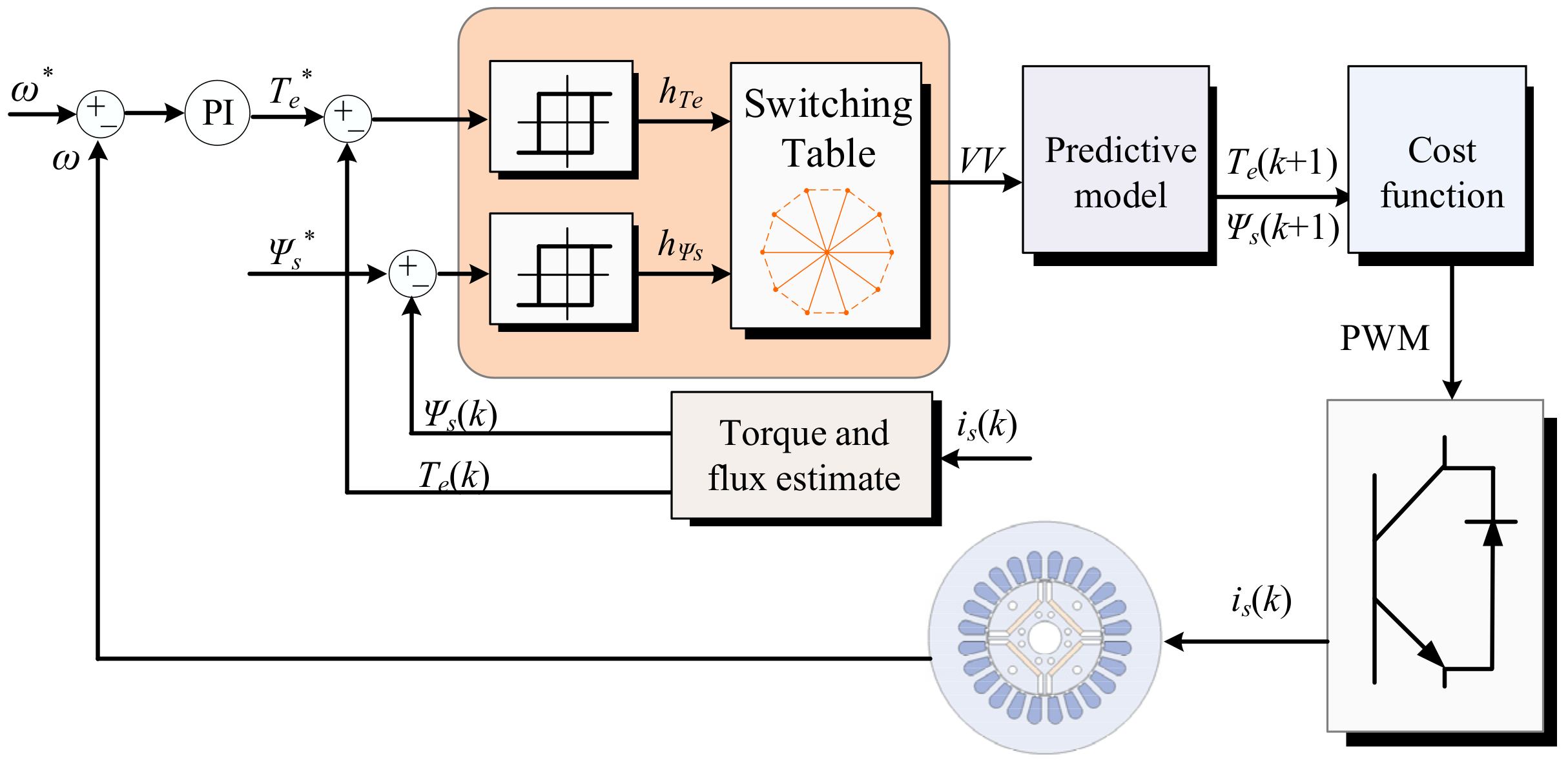
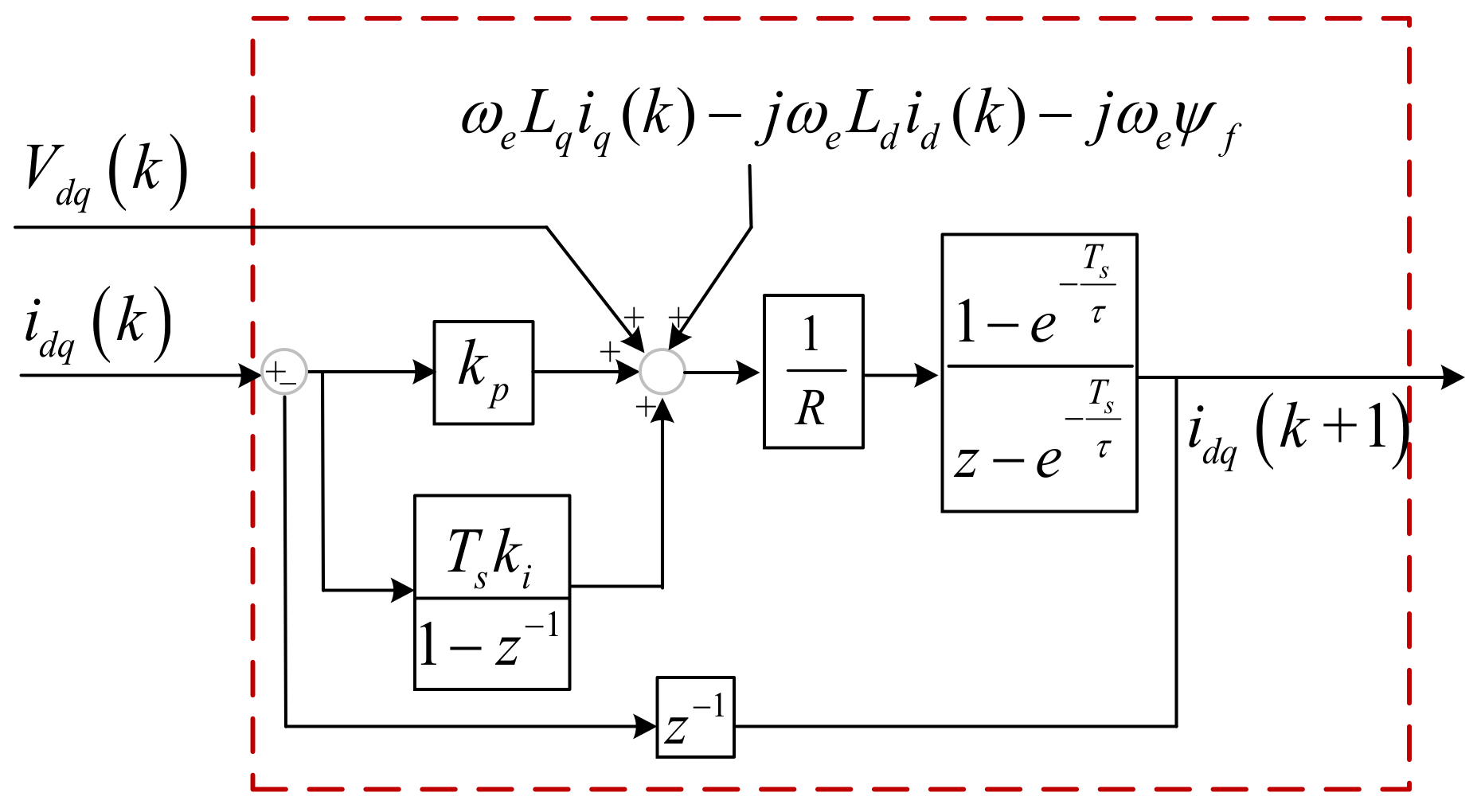
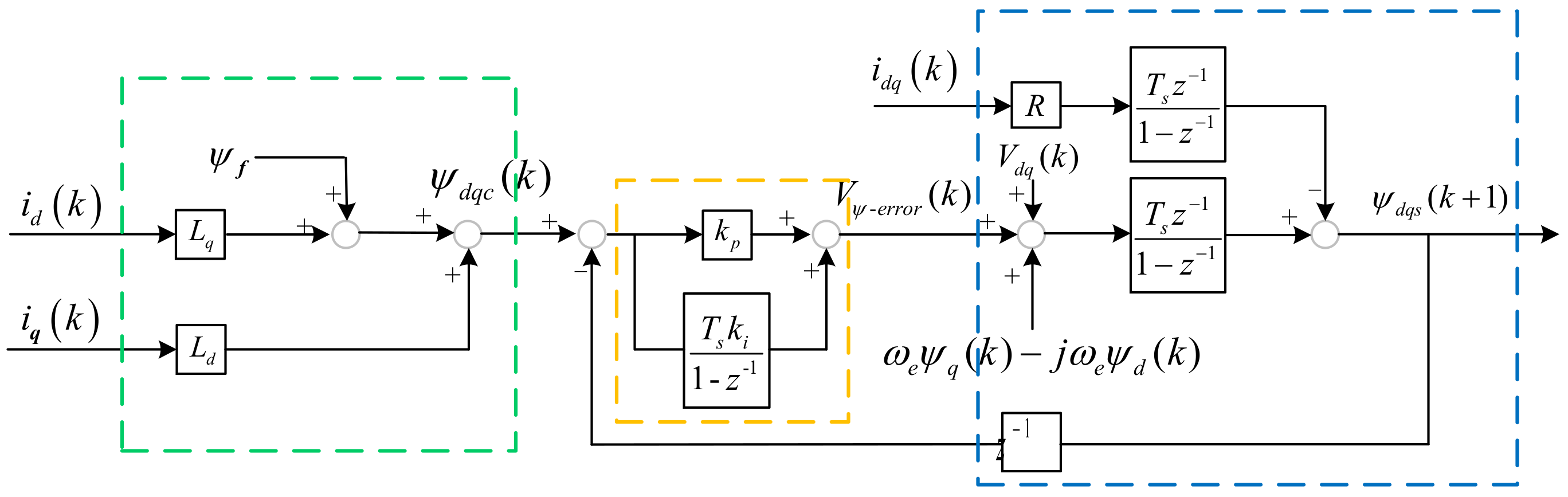
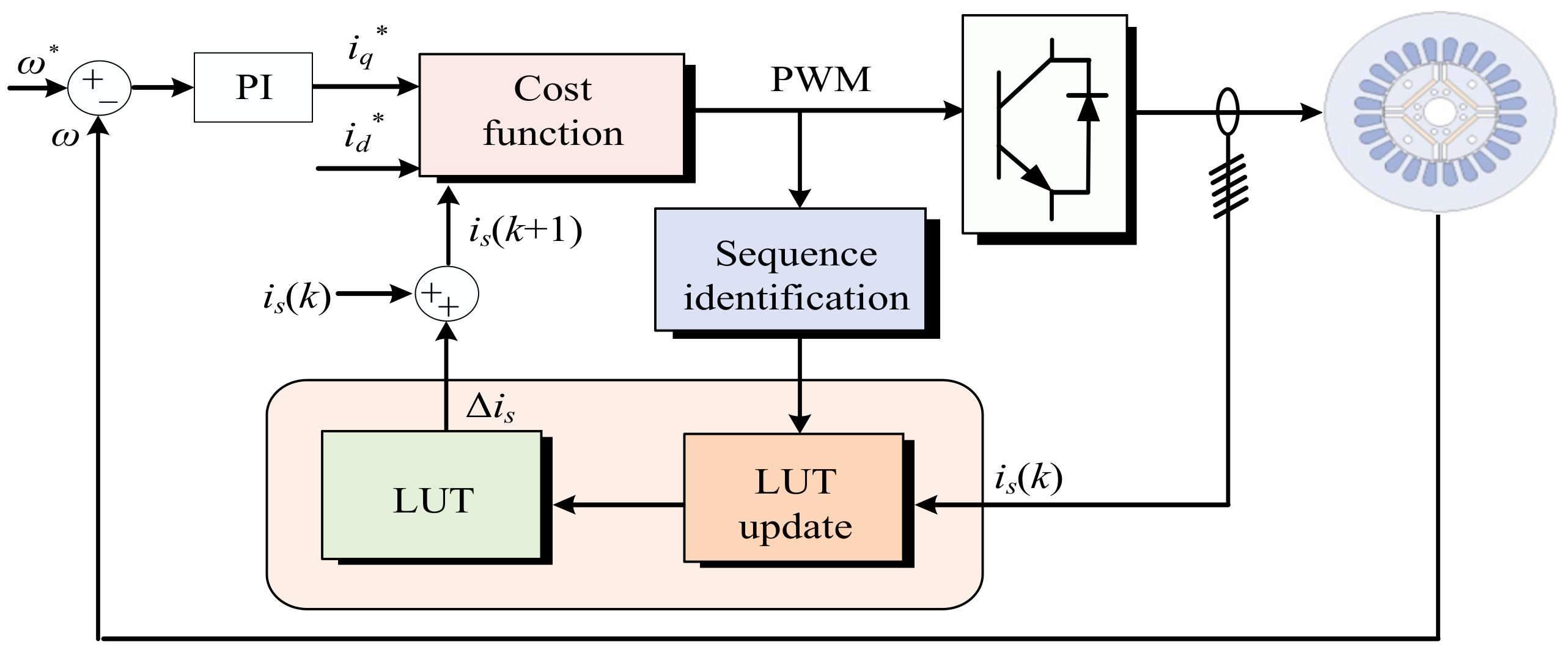
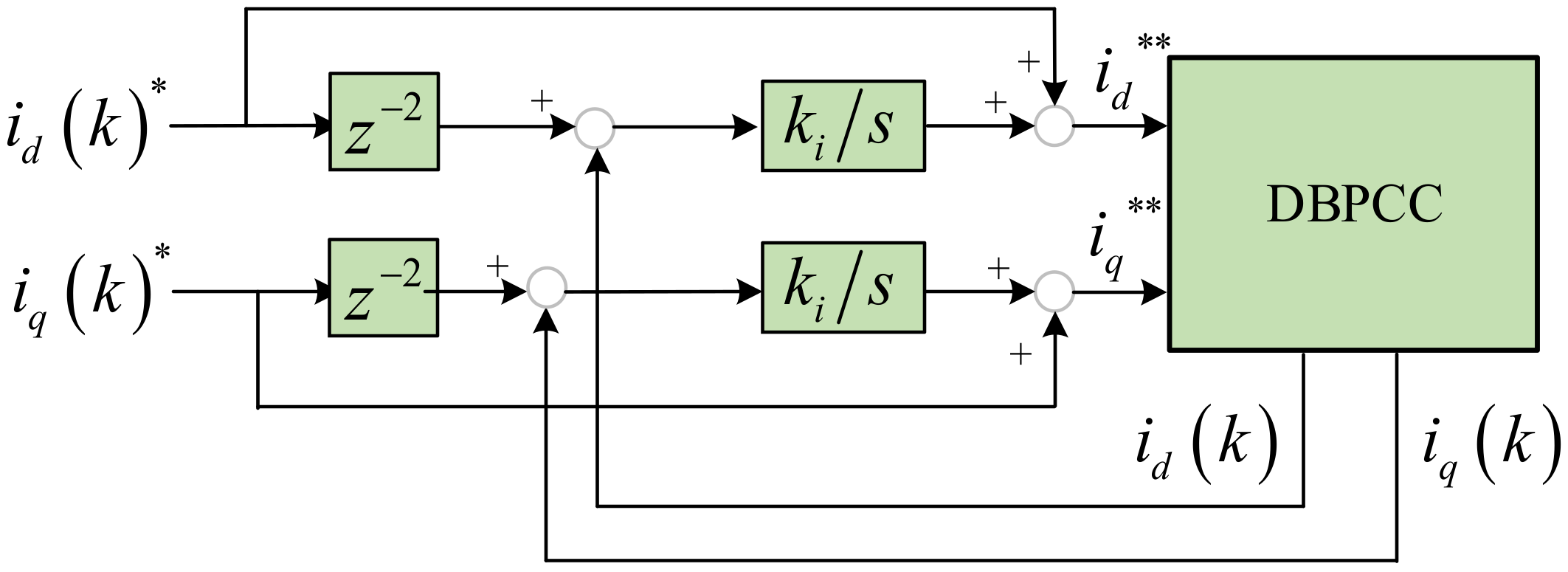
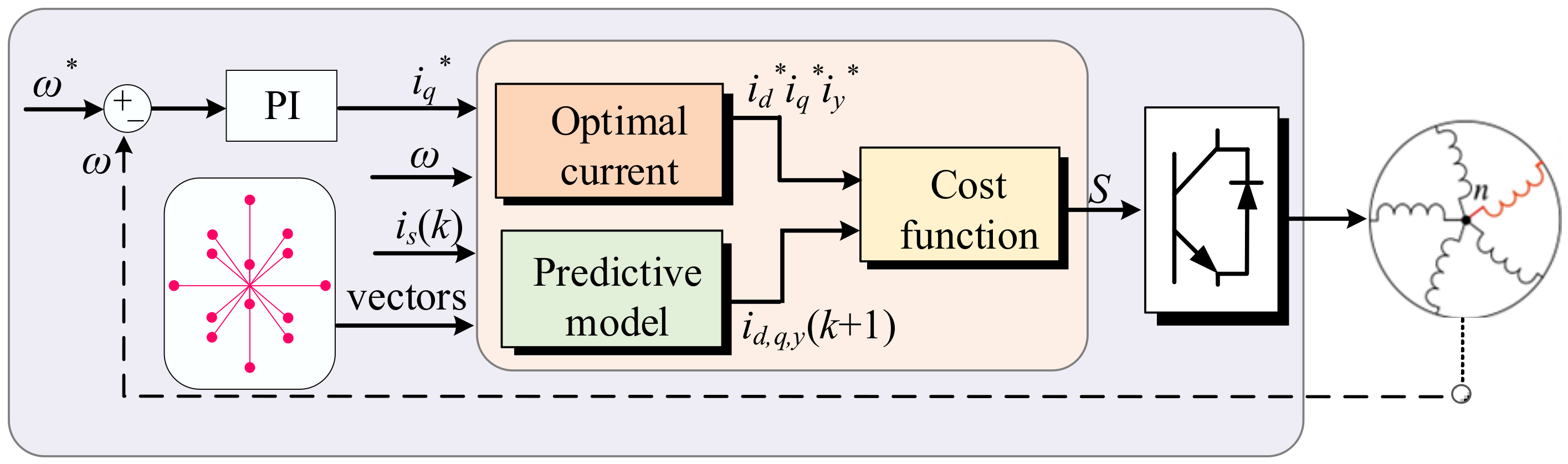
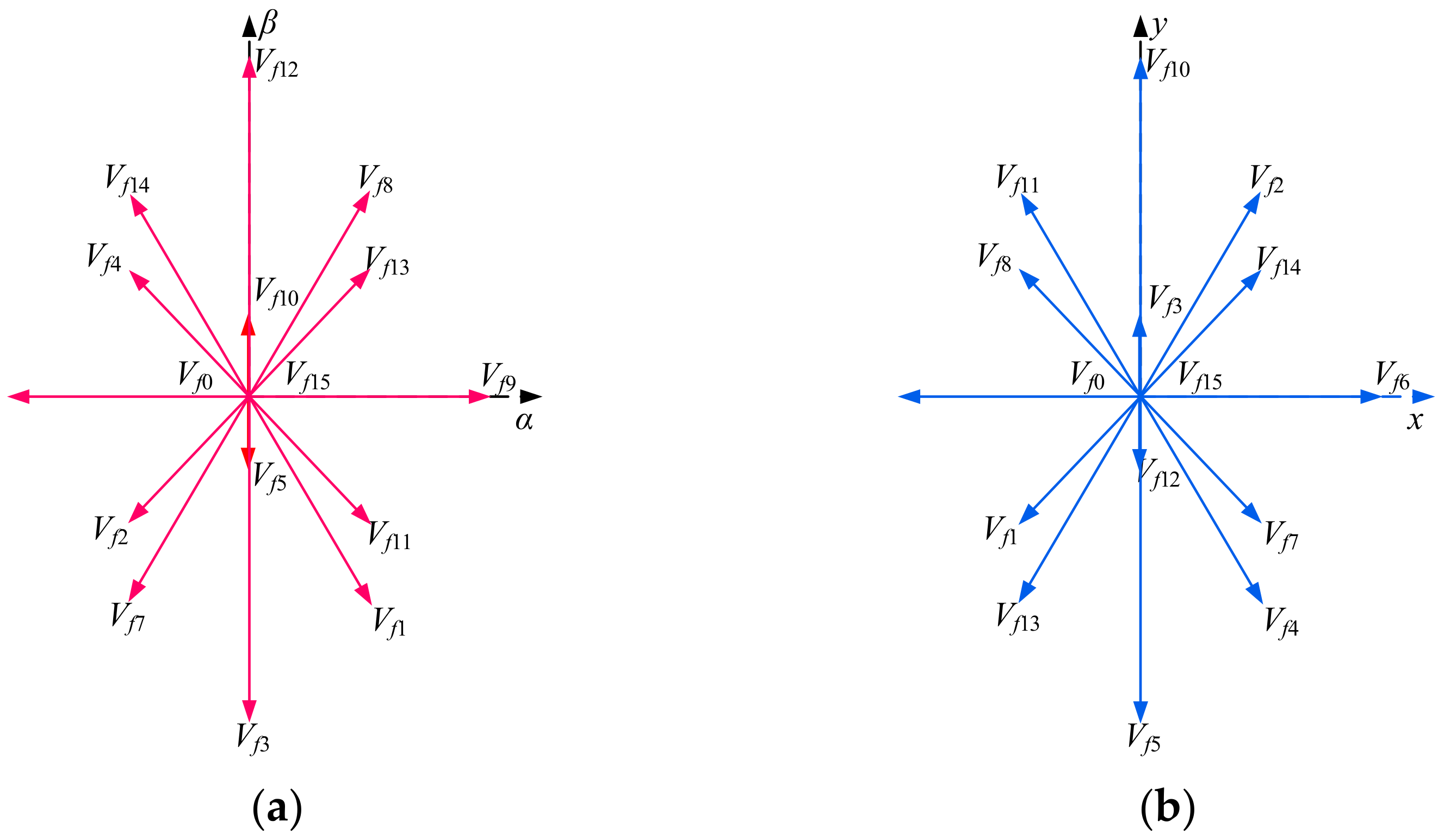
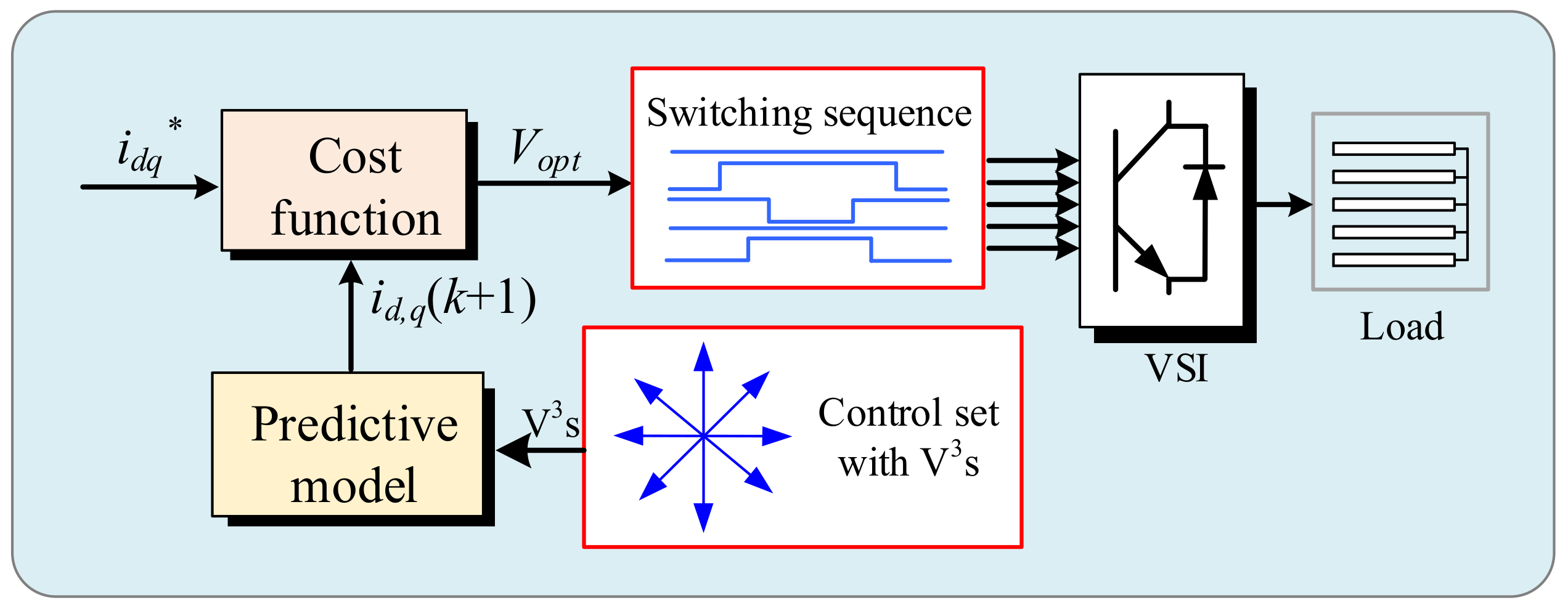
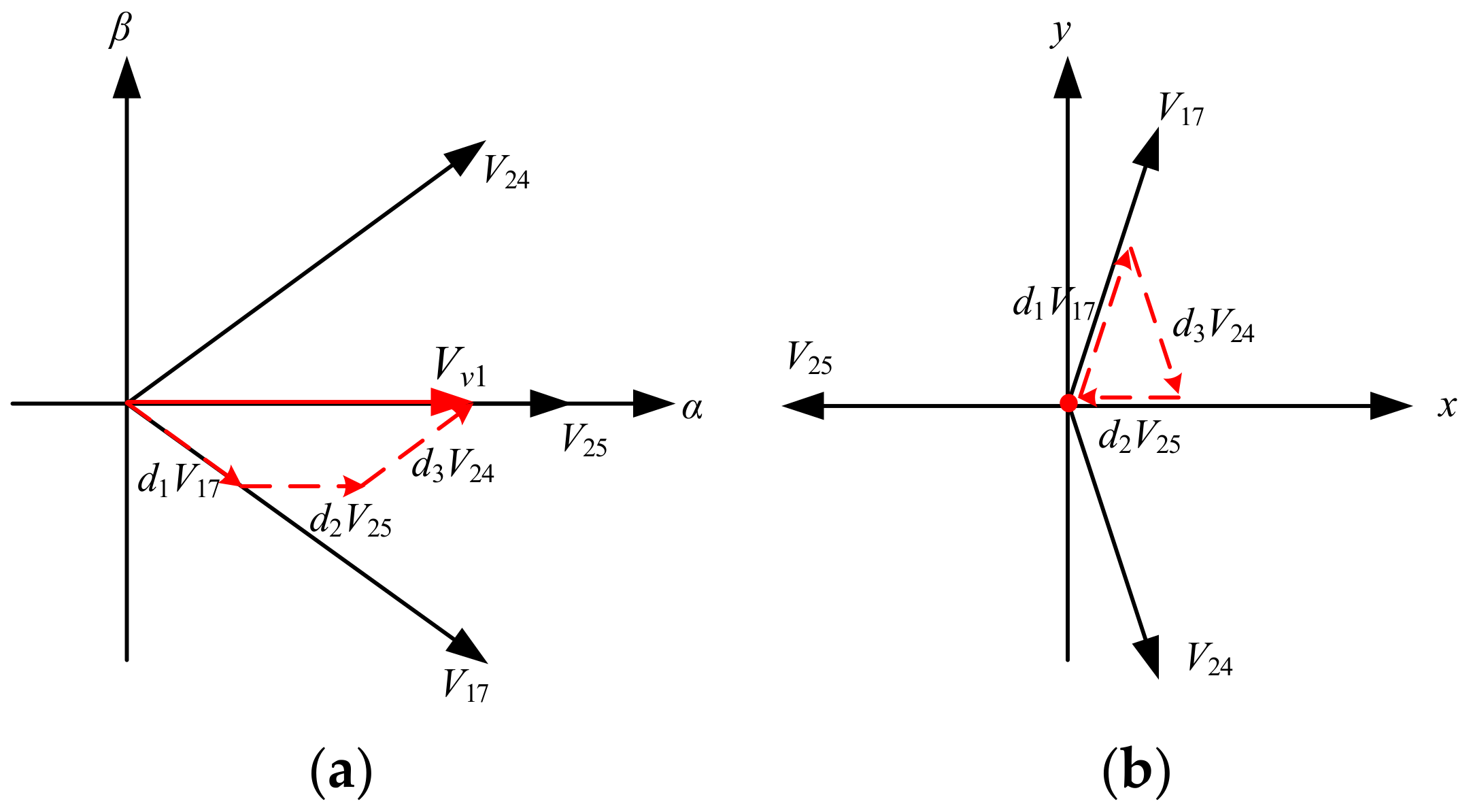
| Control Methods | Advantages | Disadvantages |
|---|---|---|
| V3s-based method [67,68,69] | Simplified CF and prediction model | Non-standard switching sequence |
| Deadbeat solution [70,71,72,73,74,75] | Good performance and accurate vector selection | Poor robustness |
| Torque and flux error-based methods [76,77,78,79,80] | Simple structure and good robustness | Rough vector selection |
| Control Methods | Complexity | Disadvantages |
|---|---|---|
| Improved prediction model [81,82,83,84,85,86,87] | Low | Model dependency |
| Parameter identification [88,89,90,91,92,93,94,95,96,97,98,99,100,101,102] | Medium | Complex tuning work |
| Disturbance observer [103,104,105,106,107,108,109,110,111,112] | High | Model dependency Complex tuning work |
| Model-free predictive control [113,114,115,116,117,118,119,120,121,122] | Slight high | Sensor accuracy dependency Sampling frequency dependency |
| Change the structure of the controller [123,124,125,126,127,128,129,130,131] | Low | Model dependency |
| Control Methods | Advantages | Disadvantages |
|---|---|---|
| Reduced-order transformation-based methods [137,138,139,140,141,142,143,144,145,146] | Accurate modeling and good performance | Complex structure |
| Without changing structure-based methods [147,148,149] | Easy to implement and natural transition before and after the fault | Poor performance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, Z.; Niu, S.; Chau, A.M.H.; Luo, Y.; Lin, H.; Li, X. Recent Advances in Multi-Phase Electric Drives Model Predictive Control in Renewable Energy Application: A State-of-the-Art Review. World Electr. Veh. J. 2023, 14, 44. https://doi.org/10.3390/wevj14020044
Xue Z, Niu S, Chau AMH, Luo Y, Lin H, Li X. Recent Advances in Multi-Phase Electric Drives Model Predictive Control in Renewable Energy Application: A State-of-the-Art Review. World Electric Vehicle Journal. 2023; 14(2):44. https://doi.org/10.3390/wevj14020044
Chicago/Turabian StyleXue, Zhiwei, Shuangxia Niu, Aten Man Ho Chau, Yixiao Luo, Hongjian Lin, and Xianglin Li. 2023. "Recent Advances in Multi-Phase Electric Drives Model Predictive Control in Renewable Energy Application: A State-of-the-Art Review" World Electric Vehicle Journal 14, no. 2: 44. https://doi.org/10.3390/wevj14020044
APA StyleXue, Z., Niu, S., Chau, A. M. H., Luo, Y., Lin, H., & Li, X. (2023). Recent Advances in Multi-Phase Electric Drives Model Predictive Control in Renewable Energy Application: A State-of-the-Art Review. World Electric Vehicle Journal, 14(2), 44. https://doi.org/10.3390/wevj14020044






