Instrumentation of an Electronic–Mechanical Differential for Electric Vehicles with Hub Motors
Abstract
:1. Introduction
2. Background
3. Materials and Methods
3.1. Hub Motors
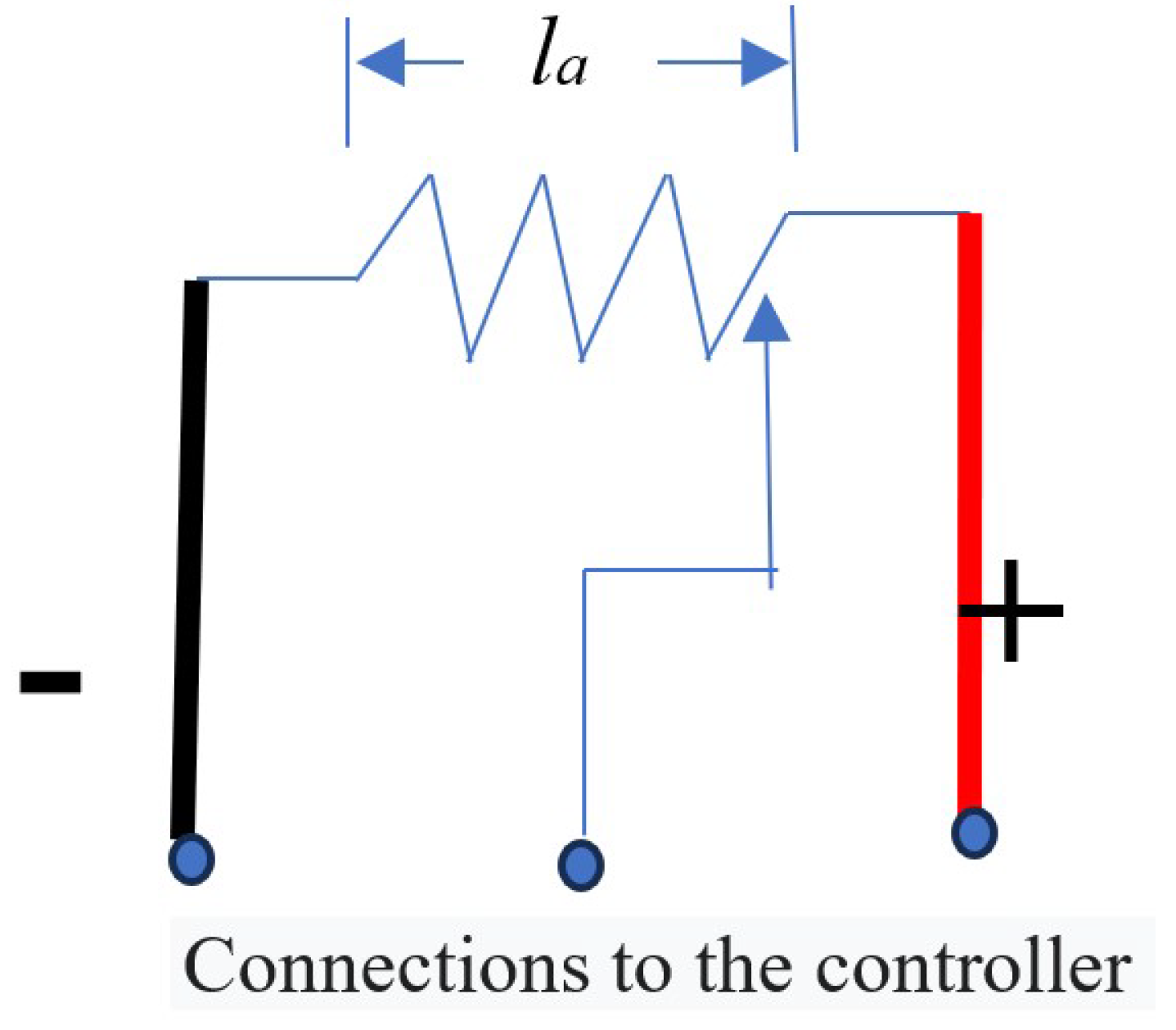
3.2. Controllers
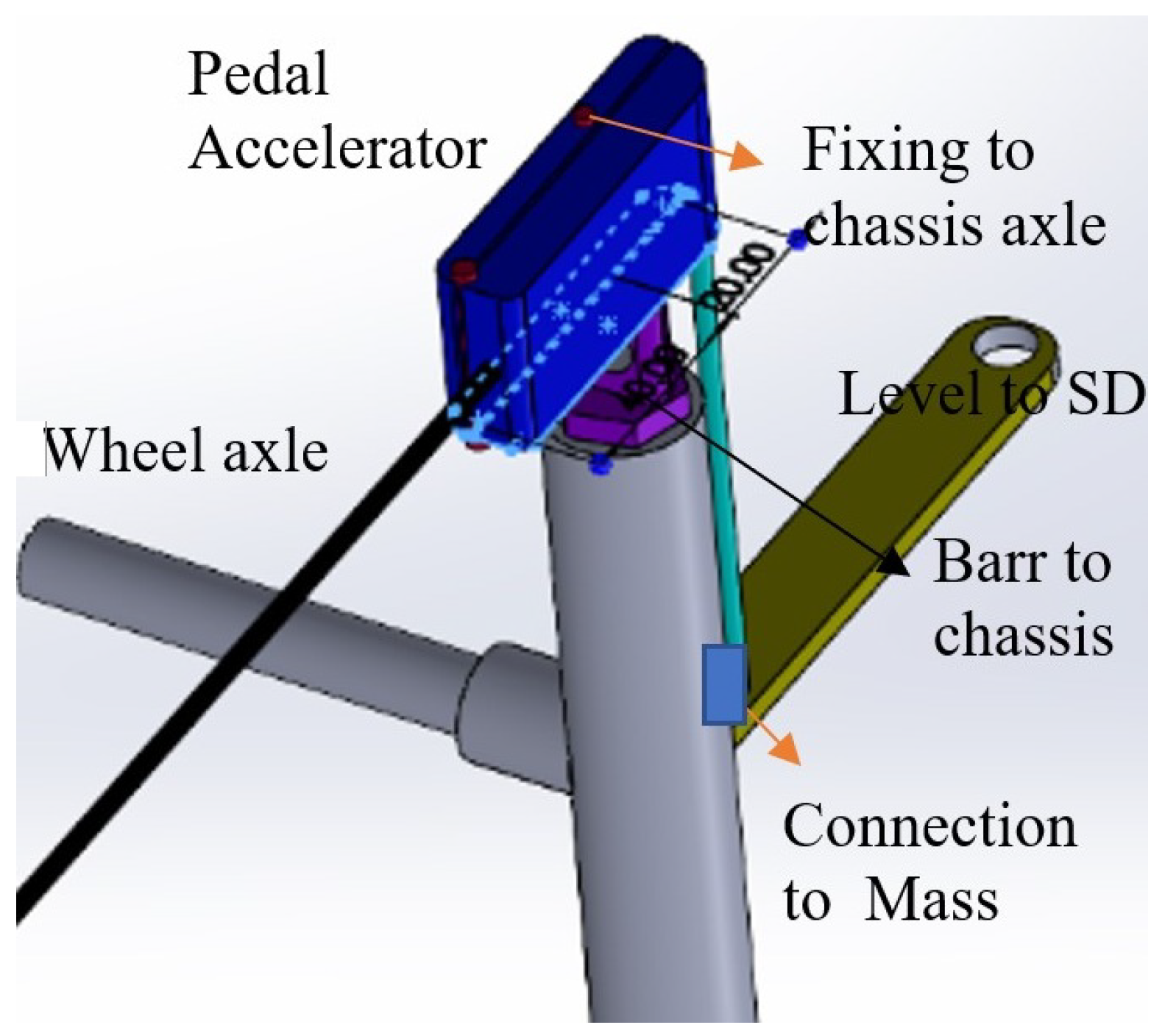
3.3. Accelerators
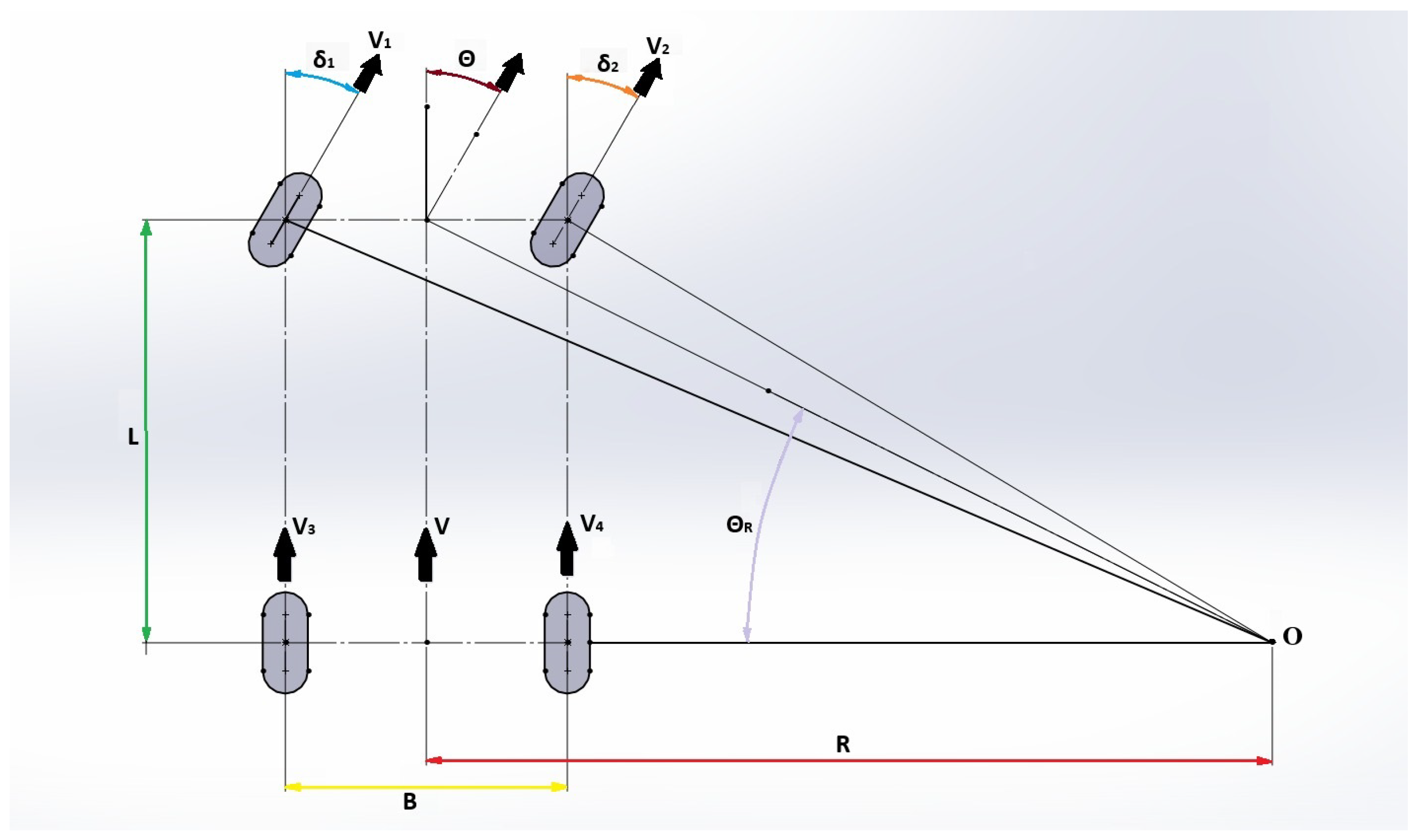
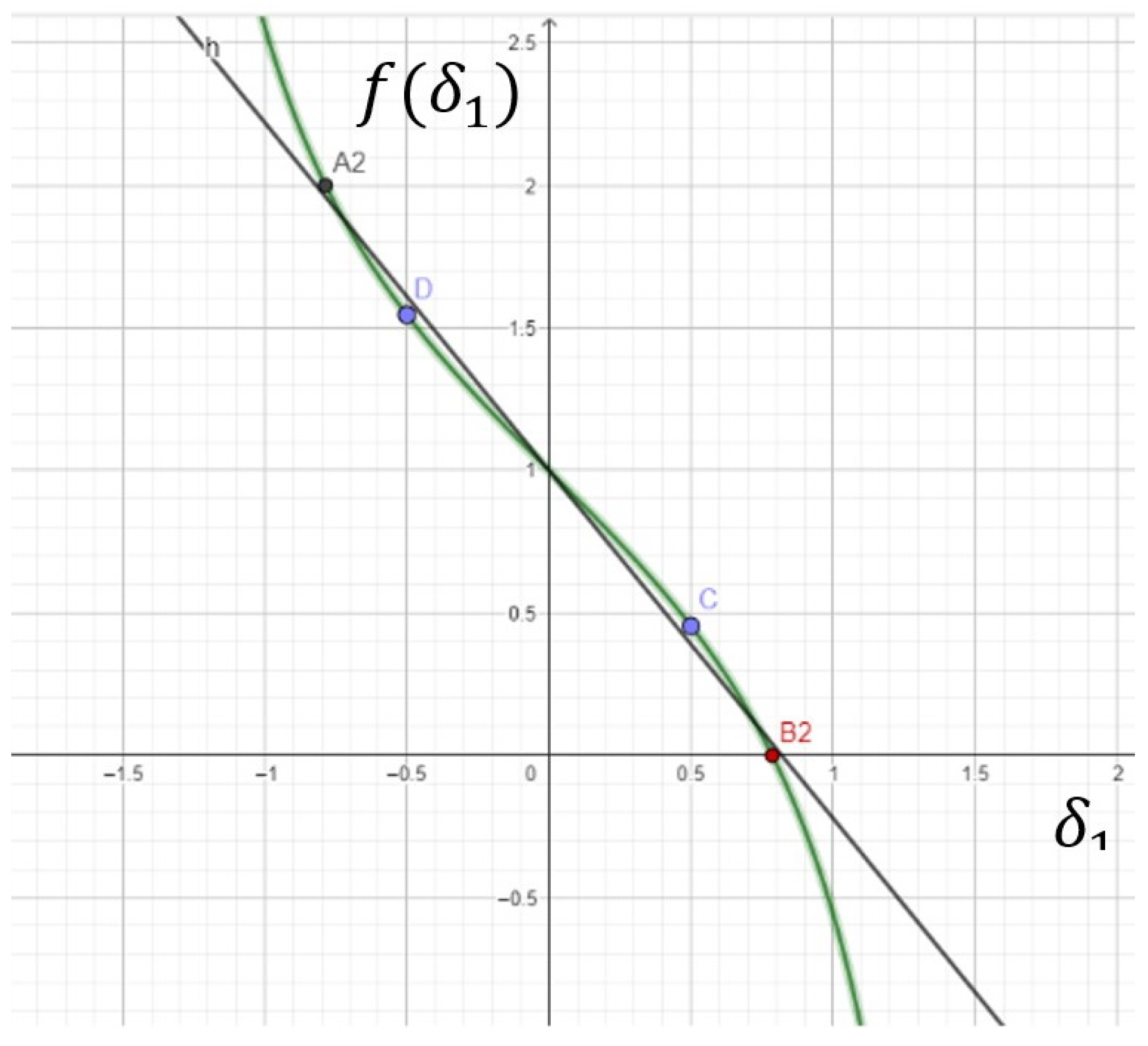
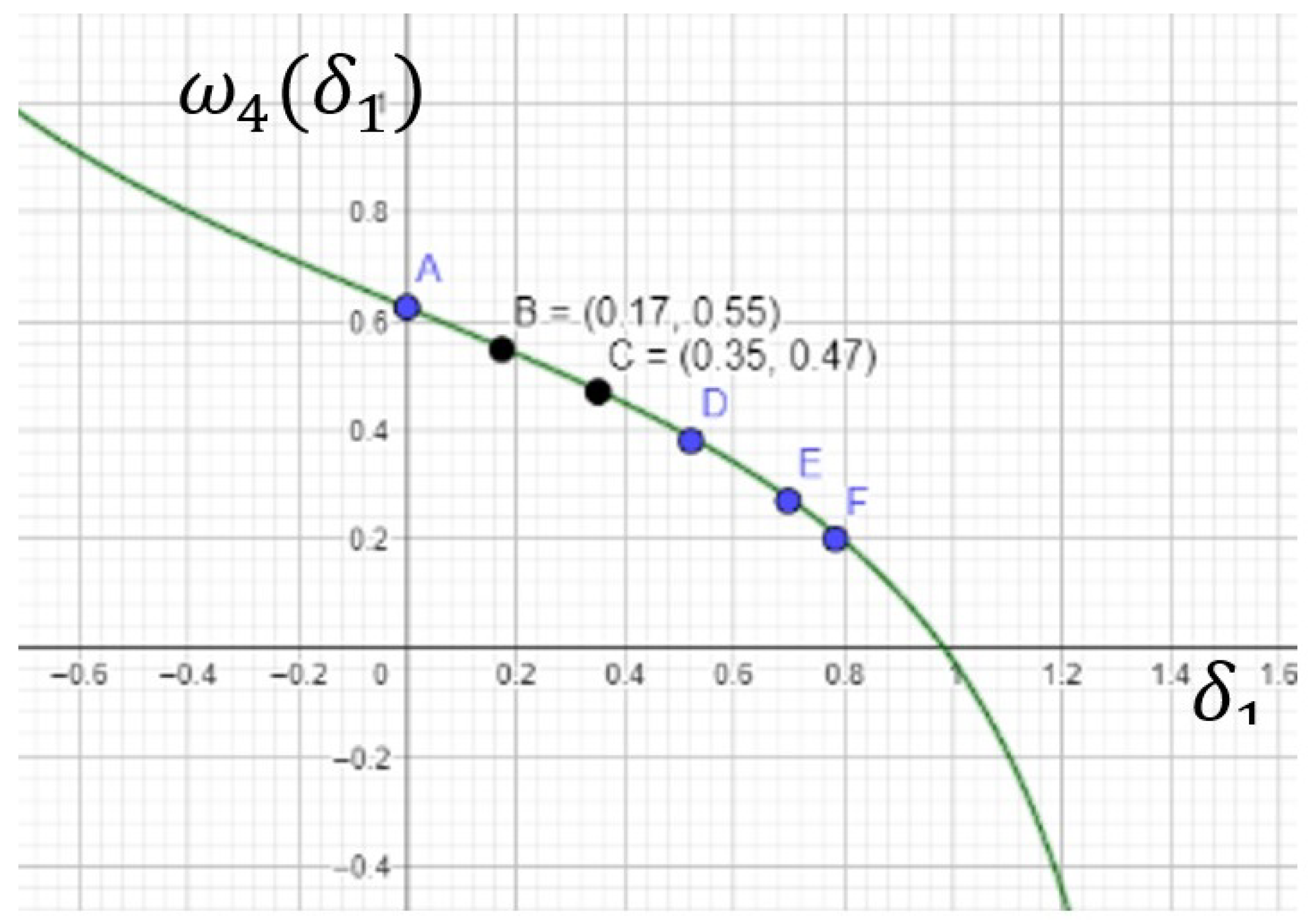
3.4. Calculations of Speed Ratios
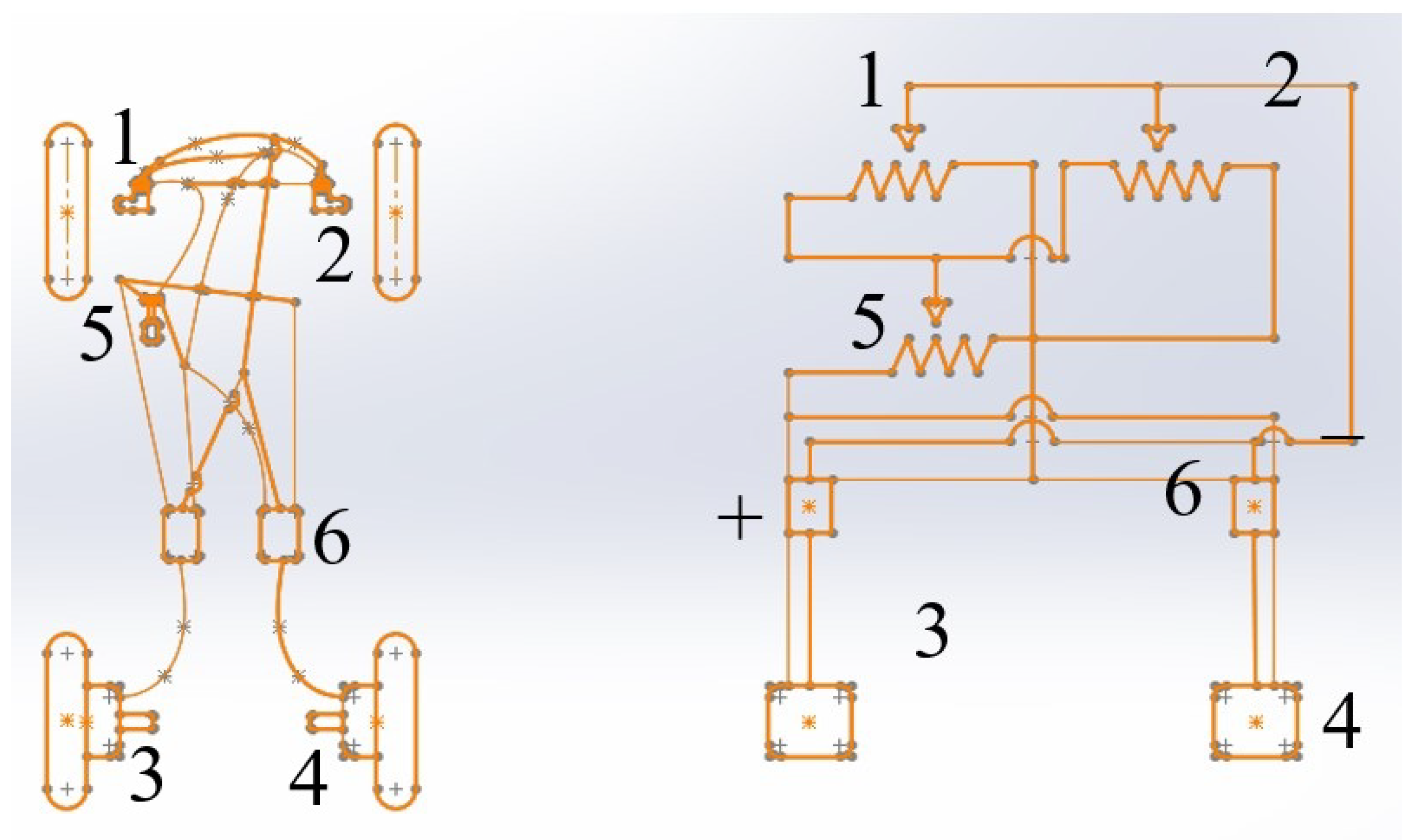
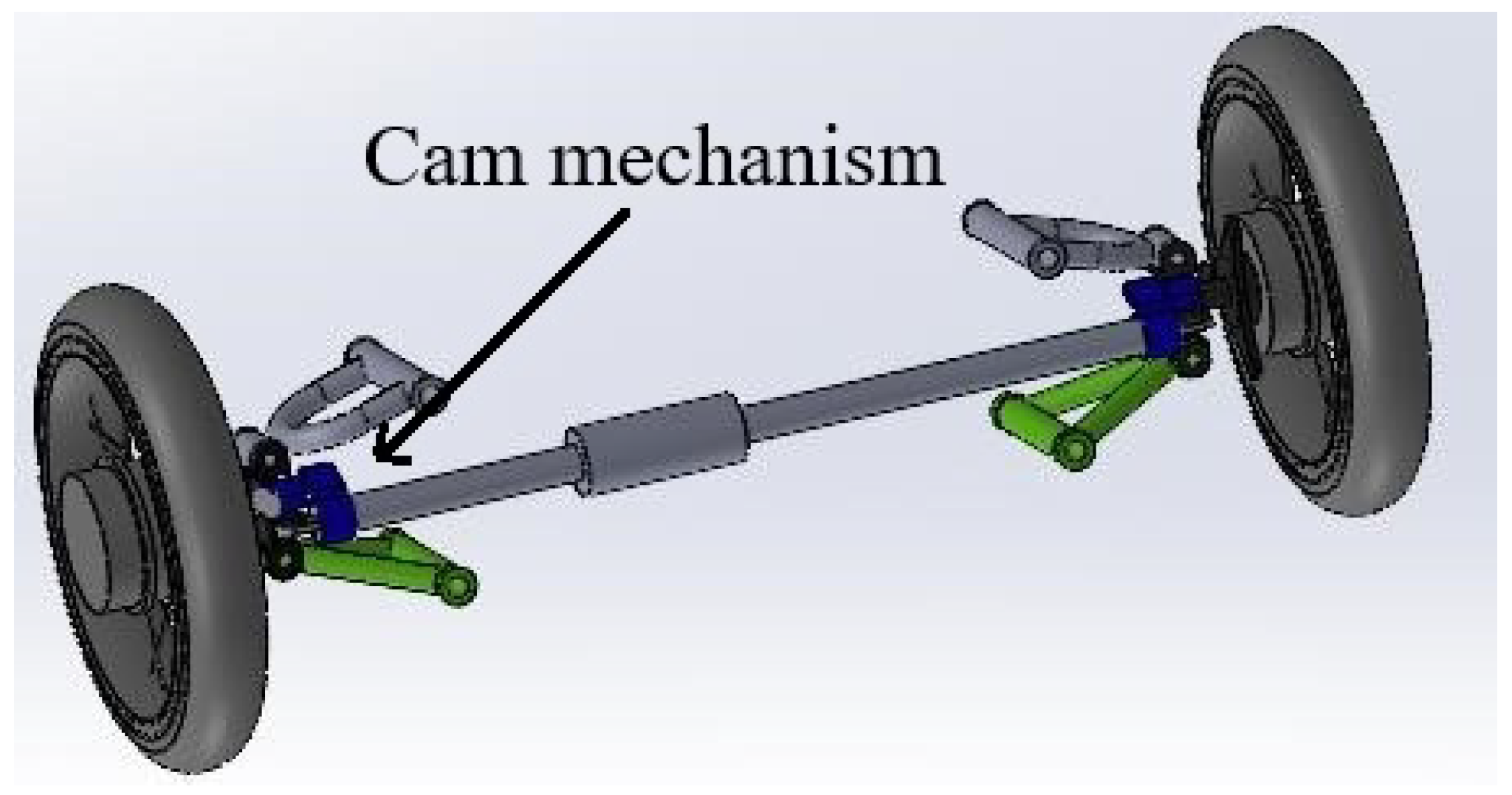
3.5. Electronic–Mechanical Differential
4. Results
Mechanism Design
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A Critical Review of Thermal Issues in Lithium-Ion Batteries. J. Electrochem. Soc. 2011, 158, R1. [Google Scholar] [CrossRef]
- Crouse, W.H. Transmisión y Caja de Cambios del Automóvil; McGraw-Hill: Barcelona, Spain, 1984; ISBN 9788426702289. [Google Scholar]
- Sharma, S.; Pegu, R.; Barman, P. Electronic Differential for Electric Vehicle with Single Wheel Reference. In Proceedings of the 2015 1st Conference on Power, Dielectric and Energy Management at NERIST (ICPDEN), Itanagar, India, 10–11 January 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Hashemnia, N.; Asaei, B. Comparative Study of Using Different Electric Motors in the Electric Vehicles. In Proceedings of the 18th International Conference on Electrical Machines, Vilamoura, Portugal, 6–9 September 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Deepak, K.; Frikha, M.A.; Benômar, Y.; Baghdadi, M.E.; Hegazy, O. In-Wheel Motor Drive Systems for Electric Vehicles: State of the Art, Challenges, and Future Trends. Energies 2023, 16, 3121. [Google Scholar] [CrossRef]
- Linares-Flores, J.; Castro-Heredia, O.; Garcia-Rodriguez, C. Diseño e Implementación de un Diferencial Electrónico para un Vehículo Eléctrico de Tracción de Cuatro Ruedas. 2022. Available online: http://repositorio.utm.mx:8080/jspui/handle/123456789/406 (accessed on 1 January 2022).
- Moazen, M.; Sharifian, M.B.B.; Sabahi, M. Electric Differential for an Electric Vehicle with 4WD/2WS Ability. In Proceedings of the 2016 24th Iranian Conference on Electrical Engineering (ICEE), Shiraz, Iran, 10–12 May 2016; pp. 751–756. [Google Scholar]
- Reséndiz Barrón, A.J.; Ramos Pérez, M.A.; Salas Flores, A.; García Rodriguez, F.J. Design and manufacture of electric vehicle body with solar panels for urban use. Rev. Cienc. Tecnol. 2025, 8, 1–14. [Google Scholar] [CrossRef]
- Contò, C.; Bianchi, N. E-Bike Motor Drive: A Review of Configurations and Capabilities. Energies 2013, 16, 160. [Google Scholar] [CrossRef]
- Kahveci, H.; Okumus, H.; Ekici, H. An Electronic Differential System Using Fuzzy Logic Speed Controlled In-Wheel Brushless DC Motors. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013; pp. 881–885. [Google Scholar] [CrossRef]
- Haddoun, A.; Benbouzid, M.; Diallo, D.; Jamel, R.A.J.; Srairi, K. Design and Implementation of an Electric Differential for Traction Application. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010. [Google Scholar] [CrossRef]
- Tabbache, B.; Kheloui, A.; Benbouzid, M. An Adaptive Electric Differential for Electric Vehicles Motion Stabilization. IEEE Trans. Veh. Technol. 2022, 60, 104–110. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J. Design and Evaluation on Electric Differentials for Overactuated Electric Ground Vehicles with Four Independent In-Wheel Motors. IEEE Trans. Veh. Technol. 2012, 60, 1534–1542. [Google Scholar] [CrossRef]
- Tuncay, R.N.; Ustun, O.; Yilmaz, M.; Gokce, C.; Karakaya, U. Design and Implementation of an Electric Drive System for In-Wheel Motor Electric Vehicle Applications. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011. [Google Scholar] [CrossRef]
- Magallán, G.A.; Bisheimer, D.A.H.G.; García, G.O. Implementación de un Diferencial Electrónico para Vehículos Eléctricos con un Único Controlador DSP. In Proceedings of the En las actas del Congreso [In XII Reunión de Trabajo en Procesamiento de la Información y Control], Córdoba, Spain, 16–18 October 2007; ISBN 9789871242238. [Google Scholar]
- Clavero-Ordóñez, L.; Fernández-Ramos, J.; Gago-Calderón, A. Electronic Differential System for Light Electric Vehicles with Two Inwheel Motors. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’18), Salamanca, Spain, 21–23 March 2018; pp. 326–329. [Google Scholar] [CrossRef]
- Aghili, F. Fault-Tolerant Torque Control of BLDC Motors. IEEE Trans. Power Electron. 2011, 26, 355–363. [Google Scholar] [CrossRef]
- Yıldırım, M.; Kurum, H. Electronic Differential System for an Electric Vehicle with Four In-Wheel PMSM. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020. [Google Scholar] [CrossRef]
- Draou, A. Electronic Differential Speed Control for Two In-Wheels Motors Drive Vehicle. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013; pp. 764–769. [Google Scholar]
- Perez-Pinal, F.J.; Cervantes, I.; Emadi, A. Stability of Electric Differential for Traction Applications. IEEE Trans. Veh. Technol. 2009, 58, 3224–3233. [Google Scholar] [CrossRef]
- Moazen, M.; Sabahi, M. Electric Differential for an Electric Vehicle with Four Independent Driven Motors and Four Wheels Steering Ability Using Improved Fictitious Master Synchronization Strategy. J. Oper. Autom. Power Eng. 2014, 2, 141–150. [Google Scholar]
- Yang, Y.P.; Xing, X.Y. Design of Electric Differential System for an Electric Vehicle with Dual Wheel Motors. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 4414–4419. [Google Scholar] [CrossRef]
- Aggarwal, A. Electronic Differential in Electric Vehicle. Int. J. Sci. Eng. Res. 2013, 4, 1322–1330. [Google Scholar]
- Koladia, D. Mathematical Model to Design Rack and Pinion Ackerman Steering Geometry. Int. J. Sci. Eng. Res. 2014, 5, 716–720. [Google Scholar]






| f | ||||
|---|---|---|---|---|
| 1 | 0 | 625 | ||
| 0.882 | 0.354 | 551.25 | ||
| 0.7575 | 0.7275 | 473.43 | ||
| 0.6151 | 1.1547 | 384.46 | ||
| 0.4411 | 1.6767 | 275.72 | ||
| 0.3334 | 1.999 | 208.75 |
| 0 | 625 | ||
| 0.31 | 548 | ||
| 0.733 | 470 | ||
| 1.15 | 390 | ||
| 1.675 | 280 | ||
| 2.09 | 210 |
| 0 | 0 | 0 | |
| 12.4 | 0.589 | 11.24 | |
| 0.75 | 0.724 | 0.86 | |
| 0.4 | 1.44 | 0.18 | |
| 0.1 | 1.55 | 0.062 | |
| 4.55 | 0.598 | 4.82 | |
| 0.41 | 0.98 | 0.336 |
| f | |||||
|---|---|---|---|---|---|
| 1 | 0 | 215 | 450 | ||
| 0.93 | 0.2 | 200.78 | 420.25 | ||
| 0.889 | 0.333 | 191.13 | 400.05 | ||
| 0.771 | 0.687 | 165.76 | 346.95 | ||
| 0.636 | 1.092 | 136.74 | 287.55 | ||
| 0.472 | 1.584 | 101.52 | 212.4 | ||
| 0.371 | 1.887 | 79.76 | 166.95 |
| 215 | 450 | ||
| 200 | 420 | ||
| 190 | 400 | ||
| 166 | 345 | ||
| 135 | 287 | ||
| 101 | 210 | ||
| 79 | 167 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reséndiz Barrón, A.J.; Flores, Y.J.; García-Rodríguez, F.J.; Medina, A.; Serrano Huerta, D.A. Instrumentation of an Electronic–Mechanical Differential for Electric Vehicles with Hub Motors. World Electr. Veh. J. 2025, 16, 179. https://doi.org/10.3390/wevj16030179
Reséndiz Barrón AJ, Flores YJ, García-Rodríguez FJ, Medina A, Serrano Huerta DA. Instrumentation of an Electronic–Mechanical Differential for Electric Vehicles with Hub Motors. World Electric Vehicle Journal. 2025; 16(3):179. https://doi.org/10.3390/wevj16030179
Chicago/Turabian StyleReséndiz Barrón, Abisai Jaime, Yolanda Jiménez Flores, Francisco Javier García-Rodríguez, Abraham Medina, and Daniel Armando Serrano Huerta. 2025. "Instrumentation of an Electronic–Mechanical Differential for Electric Vehicles with Hub Motors" World Electric Vehicle Journal 16, no. 3: 179. https://doi.org/10.3390/wevj16030179
APA StyleReséndiz Barrón, A. J., Flores, Y. J., García-Rodríguez, F. J., Medina, A., & Serrano Huerta, D. A. (2025). Instrumentation of an Electronic–Mechanical Differential for Electric Vehicles with Hub Motors. World Electric Vehicle Journal, 16(3), 179. https://doi.org/10.3390/wevj16030179







