Developing a Unified Framework for PMSM Speed Regulation: Active Disturbance Rejection Control via Generalized PI Control
Abstract
1. Introduction
- This paper refines the equivalent transformation of ADRC to ensure that each component in the equivalent model retains a clear physical interpretation, thereby enhancing the intuitive understanding of ADRC.
- This paper systematically examines and establishes the equivalence relationships between the HESO and CESO. By providing a clear correspondence between these observer structures, the findings offer deeper insights into the role of observers within ADRC.
2. System Modeling
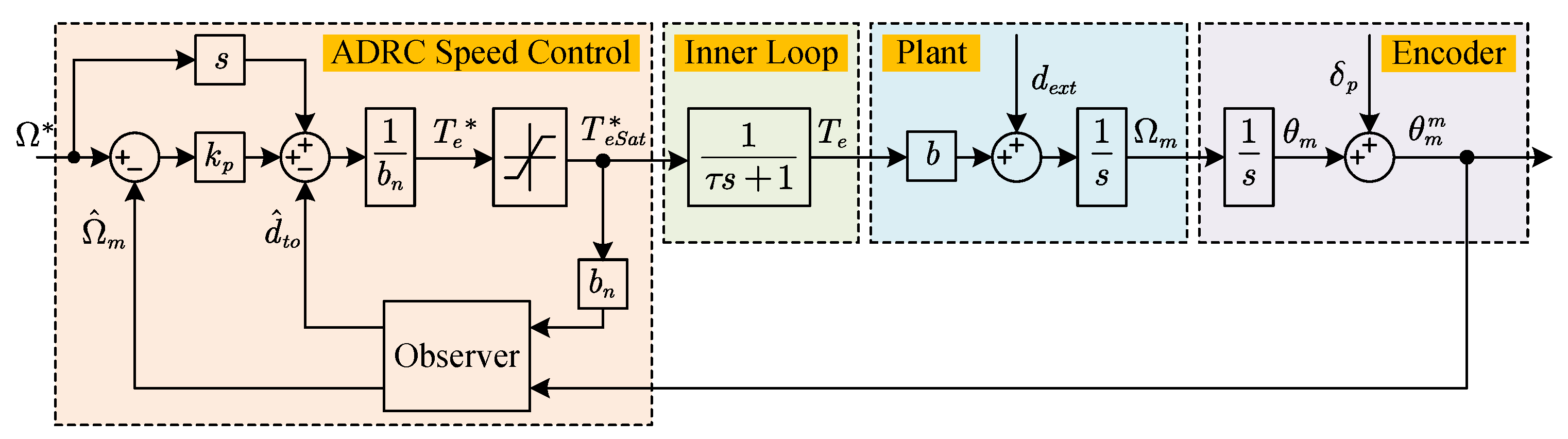
2.1. ADRC Speed Regulation System Construction
2.1.1. Physical System Modeling
2.1.2. ADRC Control Strategy
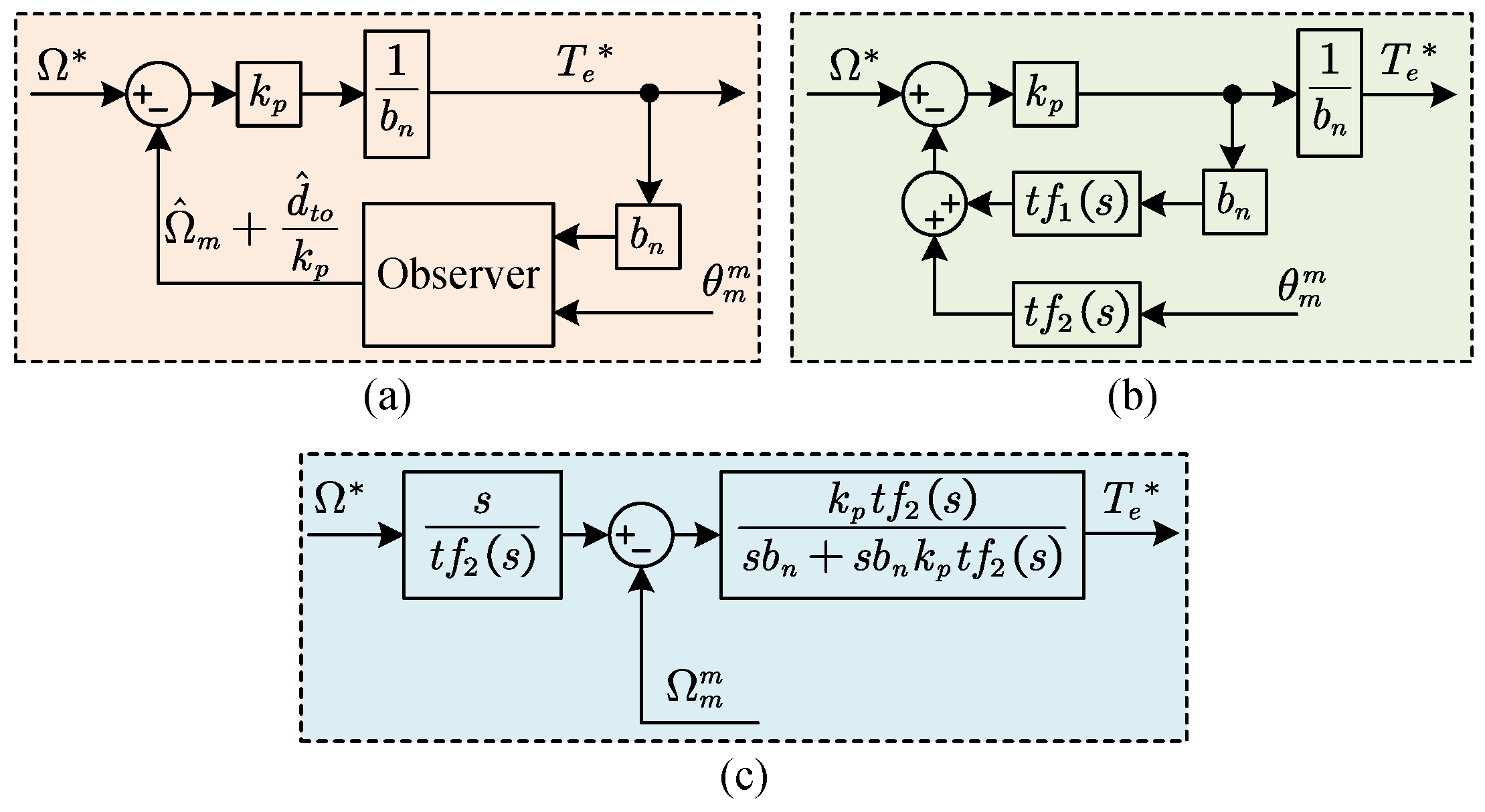
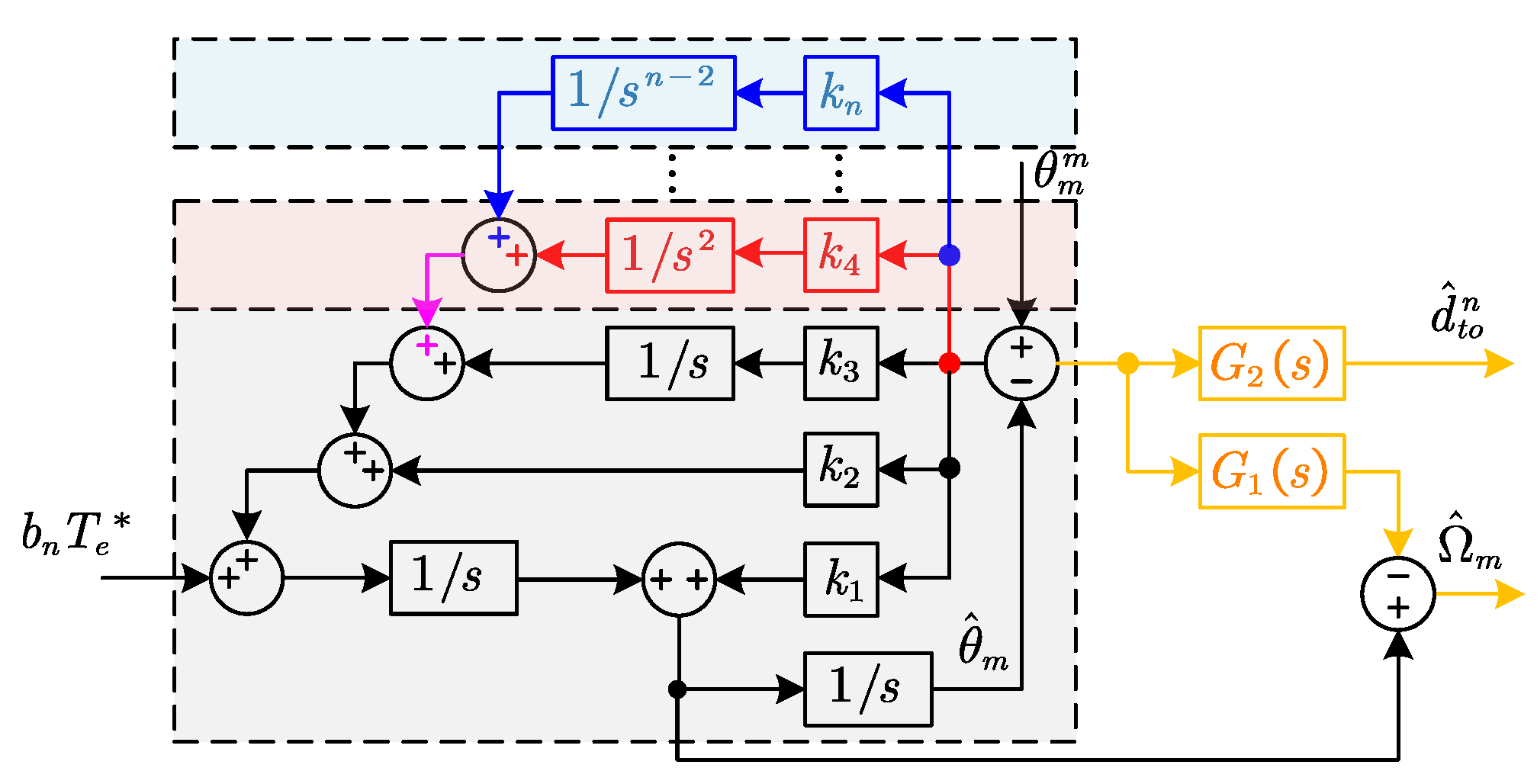
2.2. Equivalent Model Construction
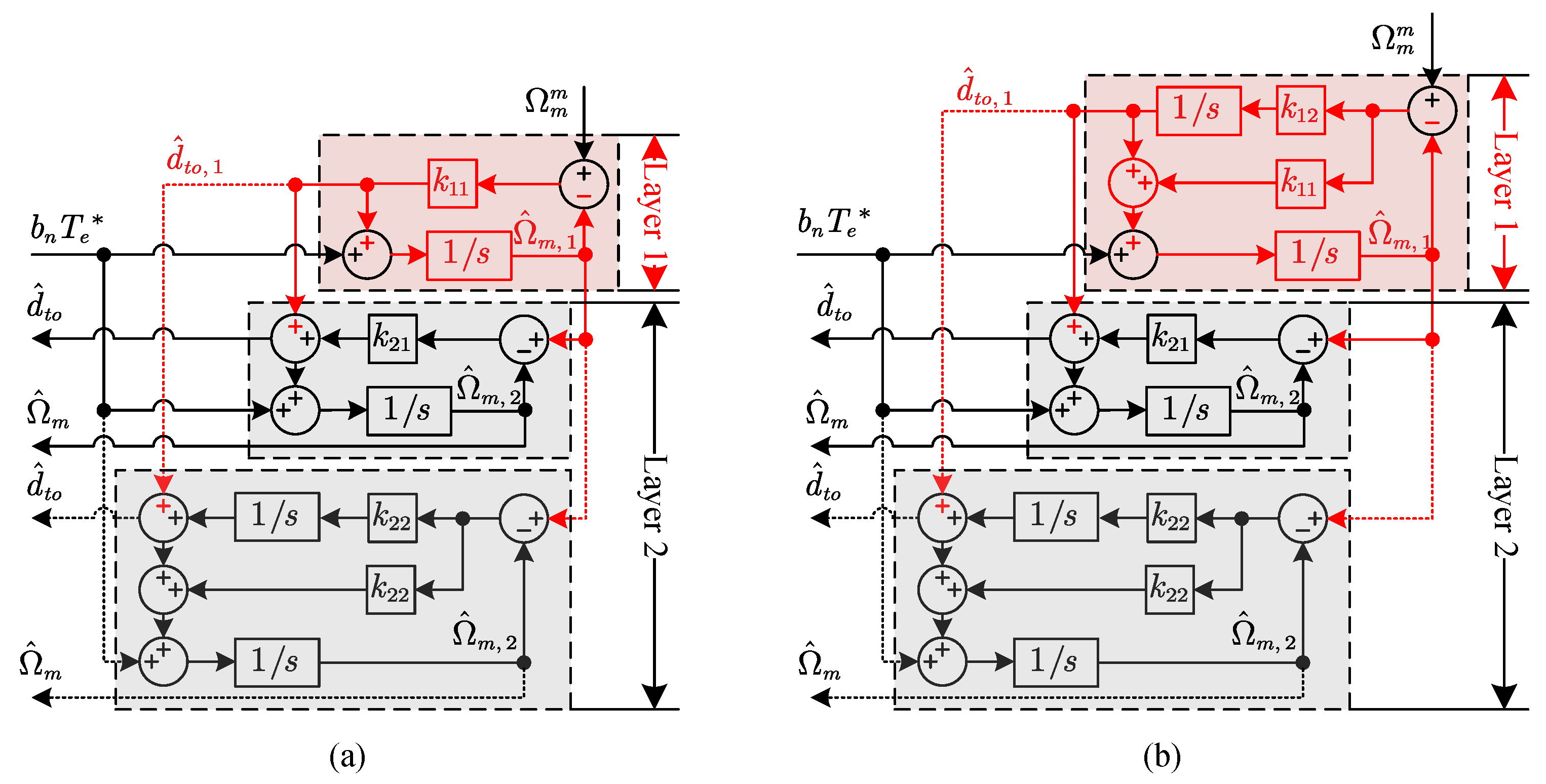
2.3. Observer Construction
3. Frequency-Domain Analysis
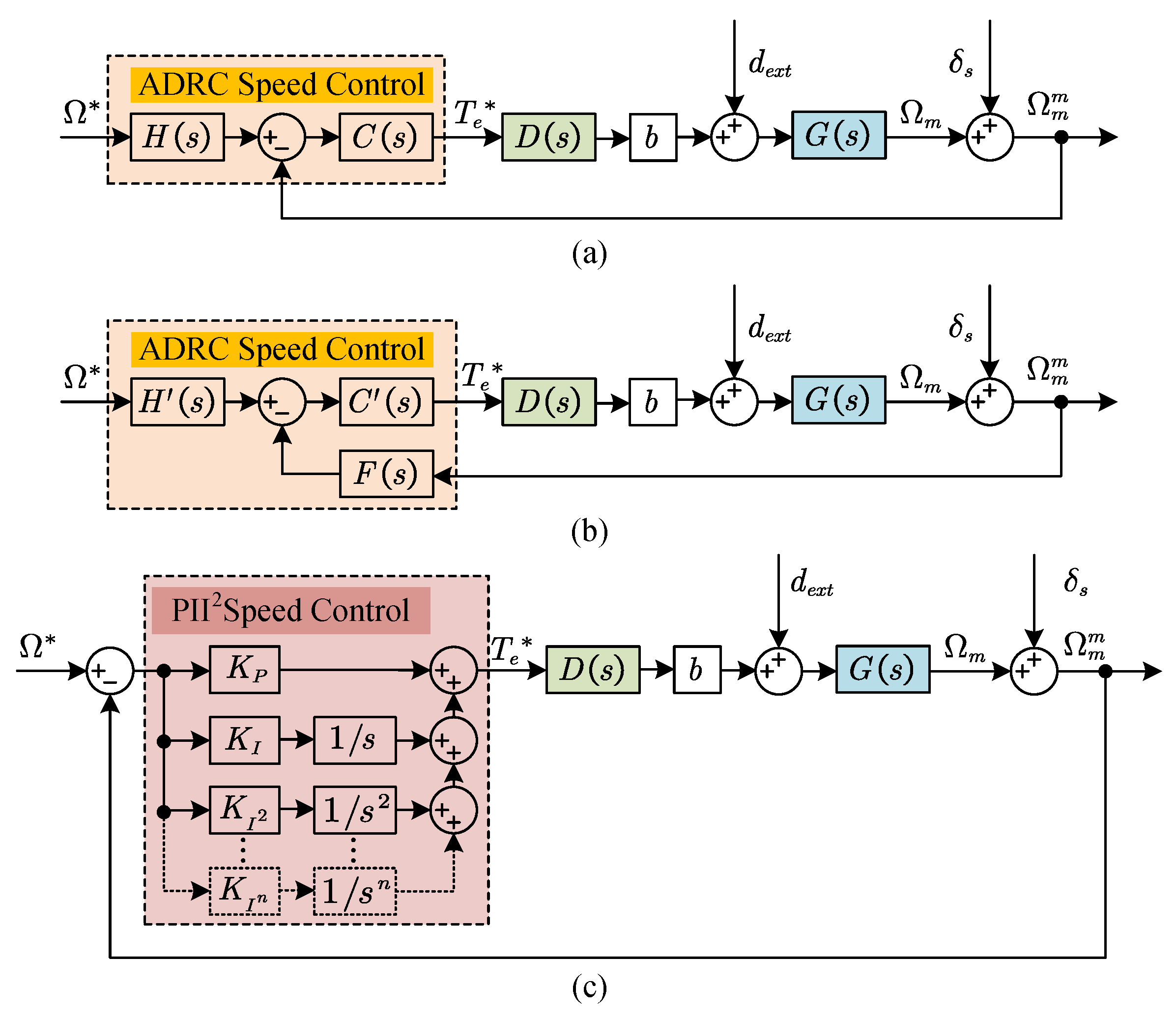
3.1. Analysis of the Equivalence of ADRC and Generalized PI Control
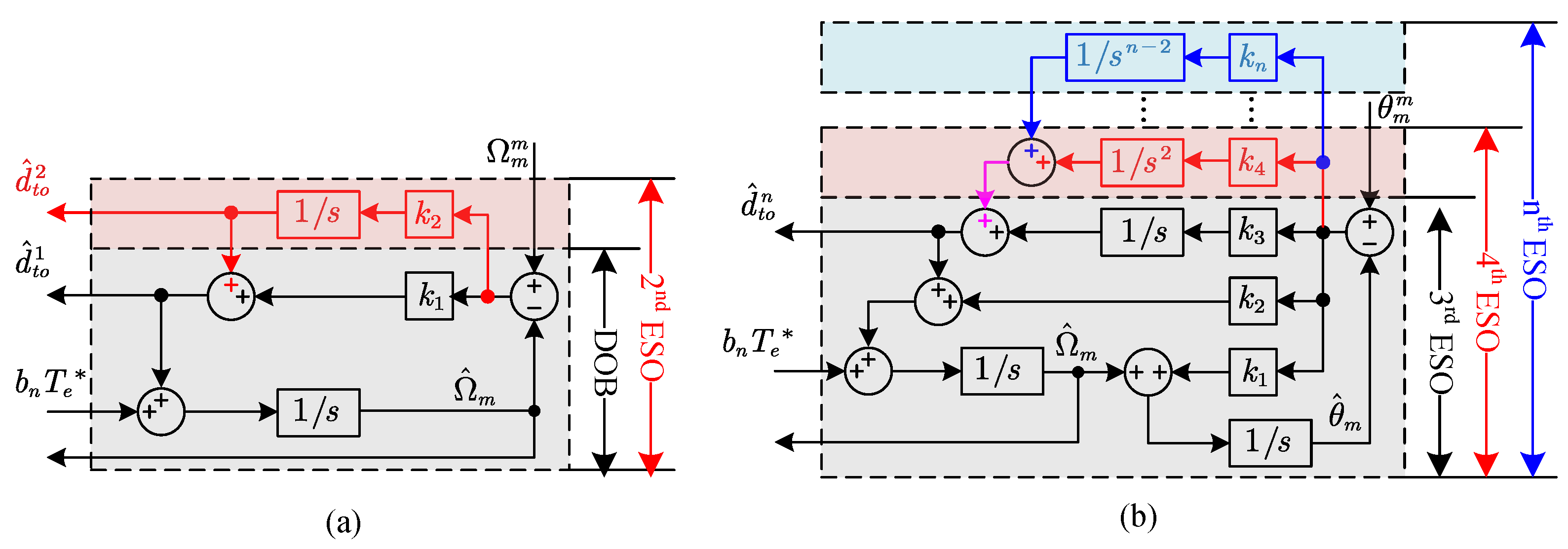
3.2. Analysis of ADRC with HESO and CESO
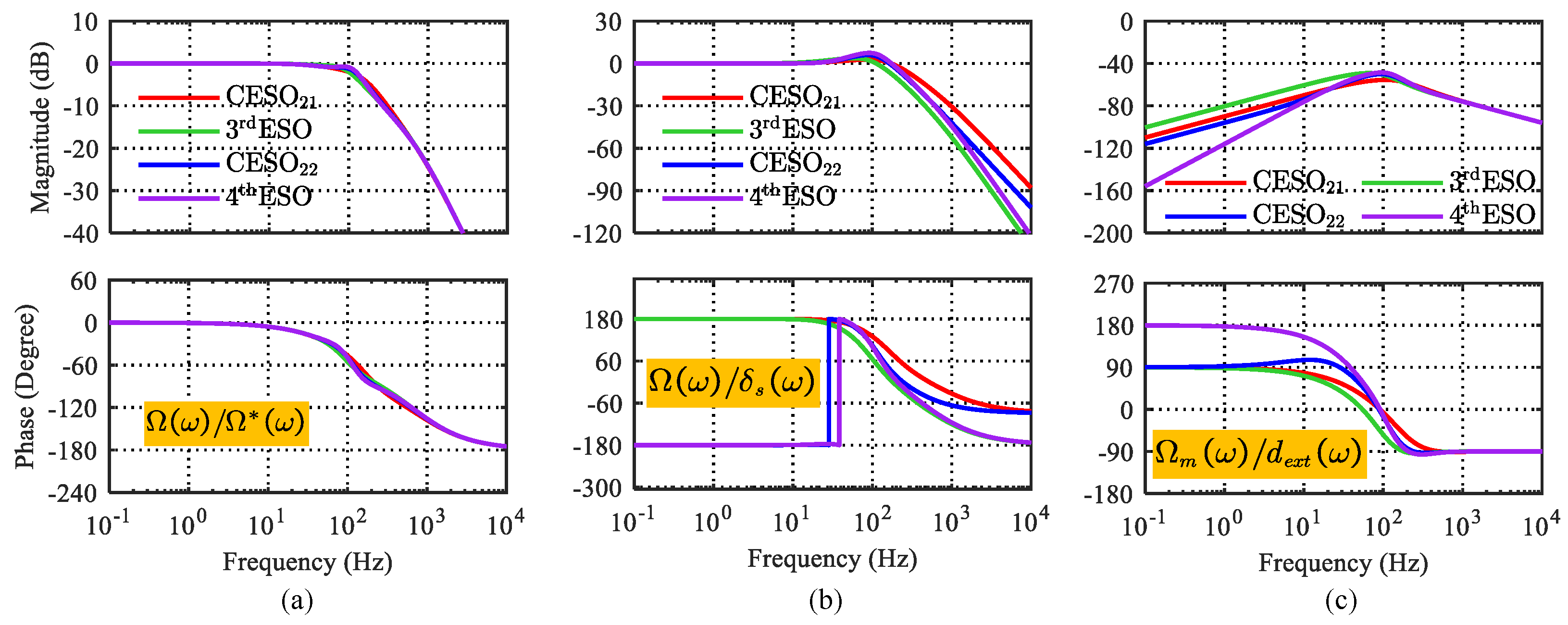
3.3. System Performance Analysis
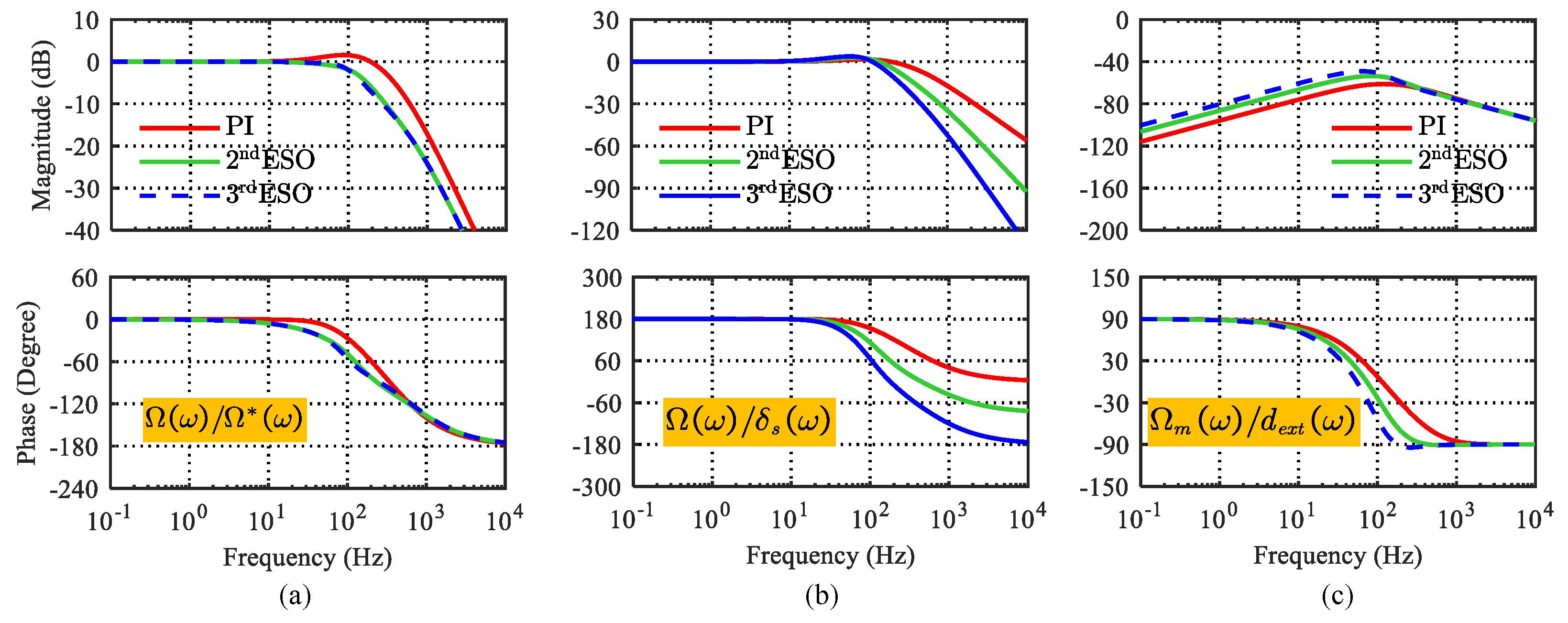
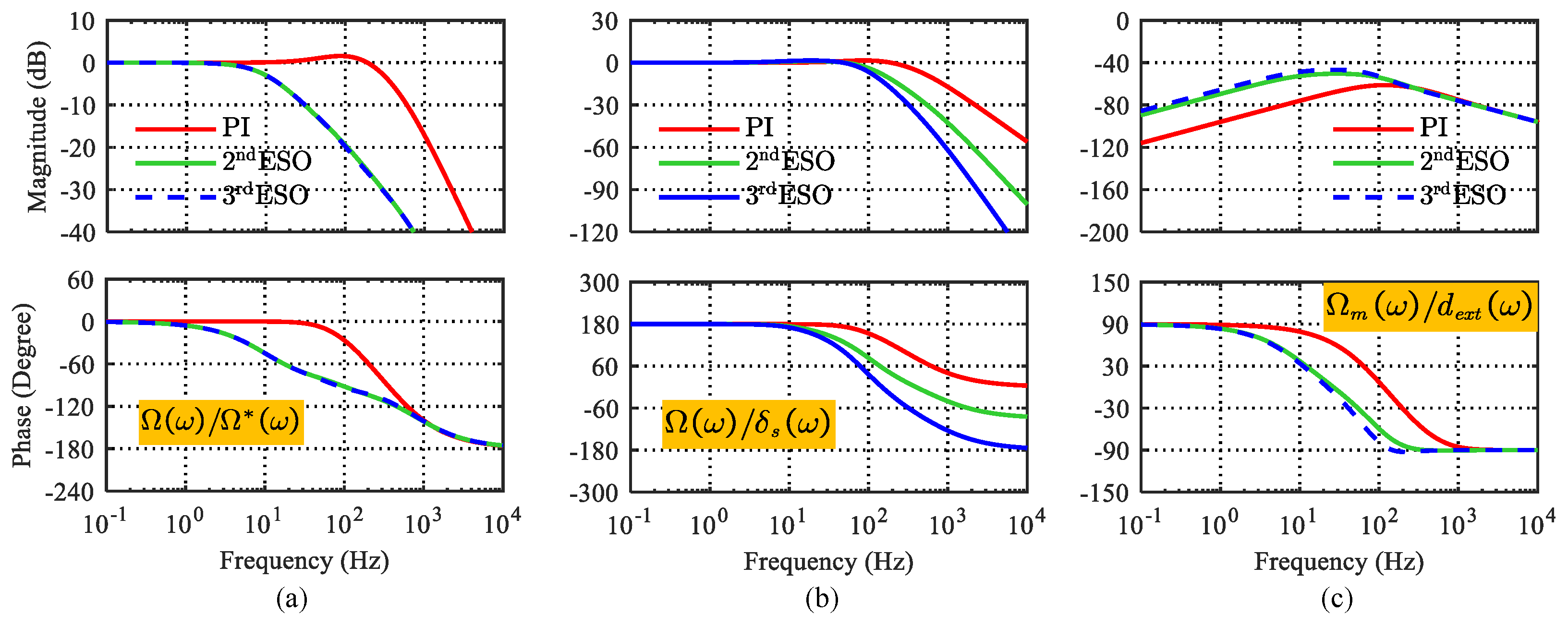
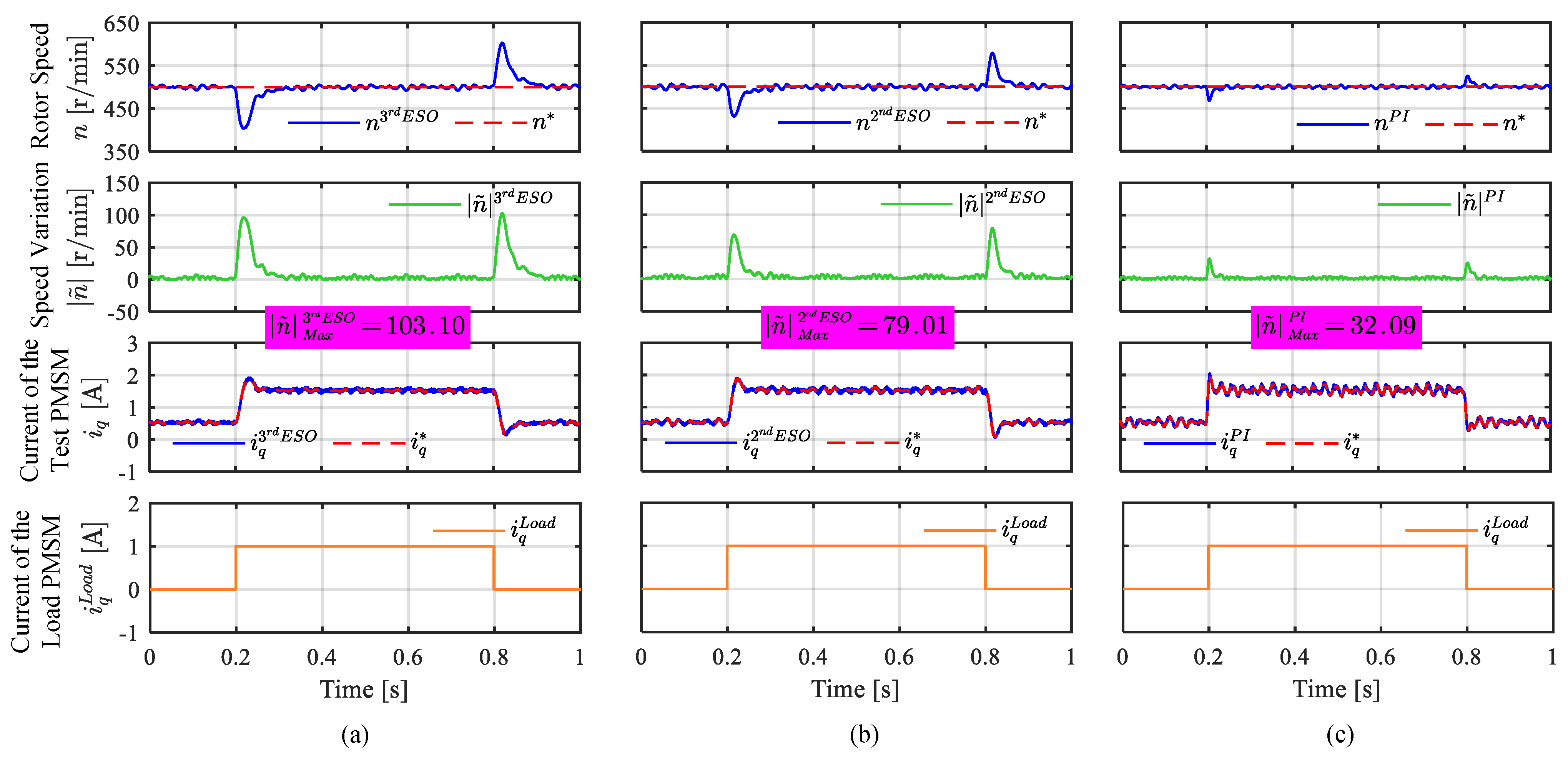
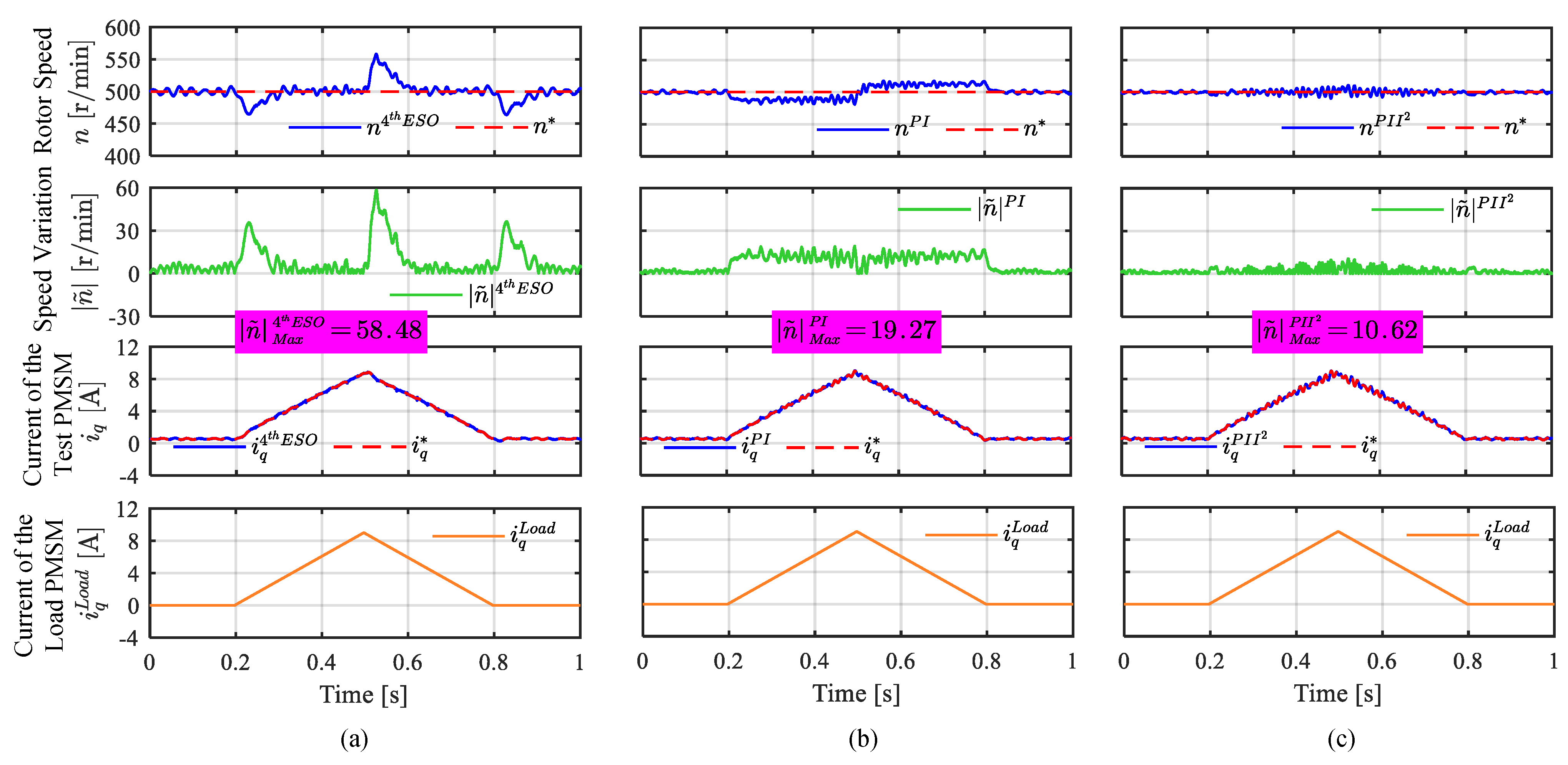
3.3.1. Comparative Analysis of ADRC and Generalized PI Control
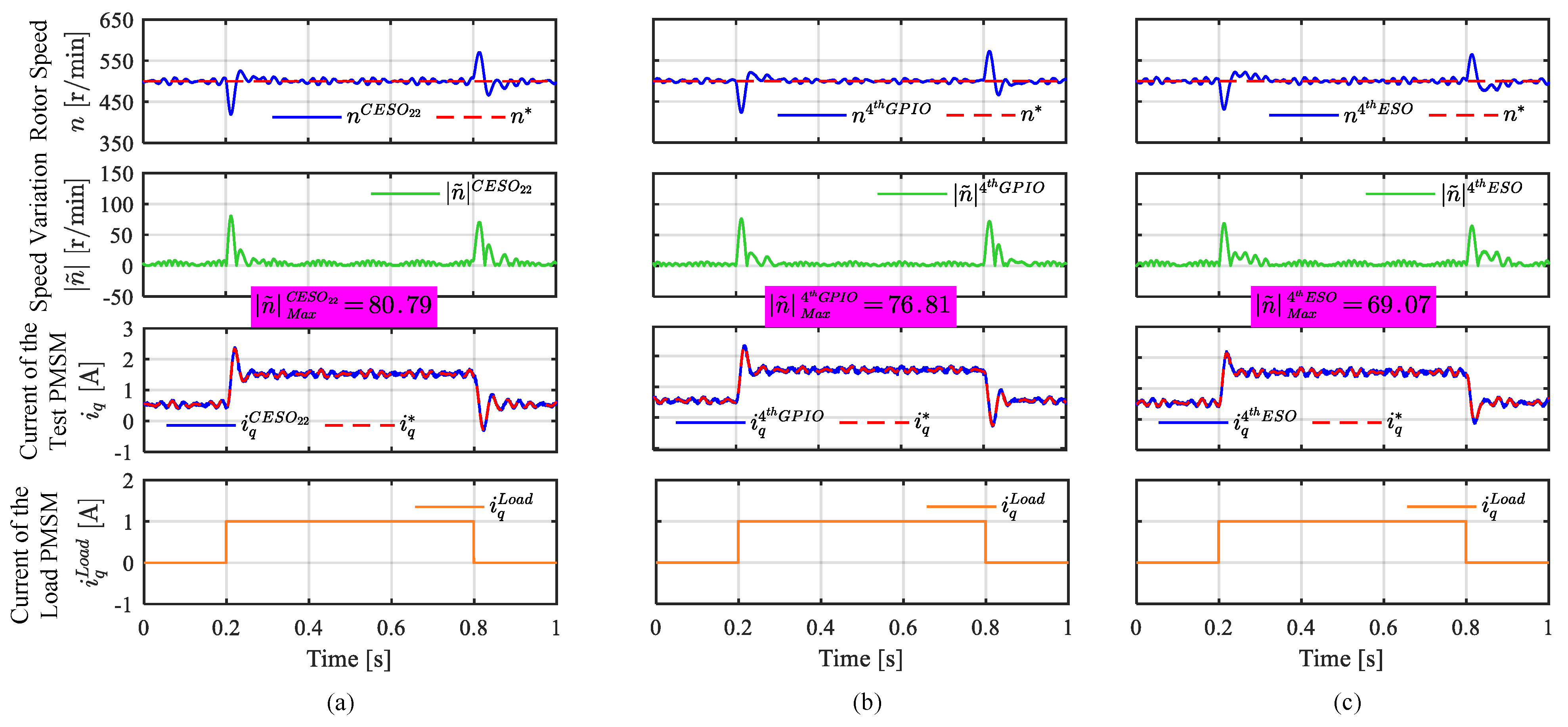
3.3.2. Comparative Analysis of CESO and HESO
4. Experimental Results
4.1. Test Bench Setup
4.2. Comparative Experiments on ADRC and Generalized PI Controller
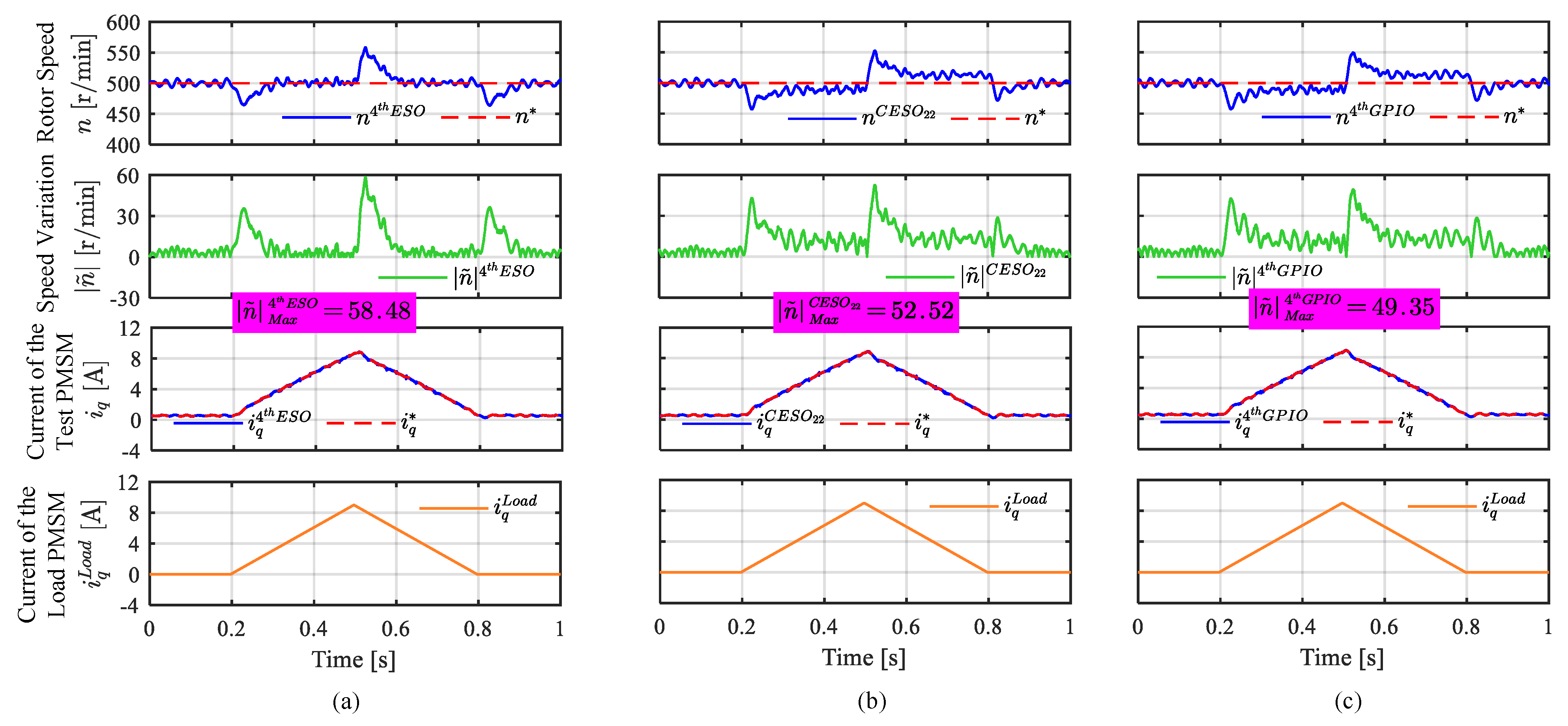
4.3. Comparative Experiments on ADRC with Different Observer Structures
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| b | Reciprocal of the actual rotor inertia | Reciprocal of the nominal rotor inertia | |
| B | Viscous damping | External disturbance | |
| Total disturbance | Estimated total disturbance | ||
| Estimated total disturbance of the ith ESO | Speed tracking error | ||
| J | Actual rotor inertia | Nominal rotor inertia | |
| Integral control gain of the generalized PI controller | Double integral control gain of the generalized PI controller | ||
| Proportional control gain of ADRC | Proportional control gain of the generalized PI controller | ||
| d-axis inductance | q-axis inductance | ||
| Rated speed | Pole pair number | ||
| Rated power | Stator resistance | ||
| Electric torque | Torque reference | ||
| Load torque | Rated torque | ||
| Rated voltage | Position measurement noise | ||
| Speed measurement noise | Rotor flux | ||
| Time constant of the inner loop | Measured position from the encoder | ||
| Estimated position | Position estimation error | ||
| Cut-off frequency of the LPF | Bandwidth of the generalized PI controller | ||
| Rotor angular speed | Rotor angular speed reference | ||
| Bandwidth of the observer | Rotor angular speed in the frequency domain | ||
| Measured rotor angular speed | Estimated rotor angular speed | ||
| Rotor angular speed reference in the frequency domain | Speed estimation error | ||
| Input speed error of the ith ESO | Estimated speed of the ith ESO | ||
| Damping ratio of the LPF |
References
- Fang, S.; Wang, Y.; Wang, W.; Chen, Y.; Chen, Y. Design of permanent magnet synchronous motor servo system based on improved particle swarm optimization. IEEE Trans. Power Electron. 2021, 37, 5833–5846. [Google Scholar] [CrossRef]
- Cao, D.; Zhao, W.; Ji, J.; Wang, Y. Parametric equivalent magnetic network modeling approach for multiobjective optimization of PM machine. IEEE Trans. Ind. Electron. 2020, 68, 6619–6629. [Google Scholar] [CrossRef]
- Song, W.; Li, J.; Ma, C.; Xia, Y.; Yu, B. A simple tuning method of PI regulators in FOC for PMSM drives based on deadbeat predictive conception. IEEE Transp. Electrif. 2024, 10, 9852–9863. [Google Scholar]
- Hori, Y. Disturbance suppression on an acceleration control type DC servo system. In Proceedings of the PESC ’88 Record, 19th Annual IEEE Power Electronics Specialists Conference, Kyoto, Japan, 11–14 April 1988; pp. 222–229. [Google Scholar]
- Huba, M.; Vrancic, D.; Bistak, P. PID control with higher order derivative degrees for IPDT plant models. IEEE Access 2020, 9, 2478–2495. [Google Scholar] [CrossRef]
- Espina, J.; Arias, A.; Balcells, J.; Ortega, C. Speed anti-windup PI strategies review for field oriented control of permanent magnet synchronous machines. In Proceedings of the 2009 Compatibility and Power Electronics, Badajoz, Spain, 20–22 May 2009; pp. 279–285. [Google Scholar]
- Chen, W.-H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2015, 63, 1083–1095. [Google Scholar]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 989–994. [Google Scholar]
- Xiong, J.; Fu, X. Extended Two-State Observer-Based Speed Control for PMSM With Uncertainties of Control Input Gain and Lumped Disturbance. IEEE Trans. Ind. Electron. 2023, 71, 6172–6182. [Google Scholar]
- Wu, Z.; Li, D.; Liu, Y.; Chen, Y. Performance analysis of improved ADRCs for a class of high-order processes with verification on main steam pressure control. IEEE Trans. Ind. Electron. 2022, 70, 6180–6190. [Google Scholar]
- Lin, G.; Wang, F.; He, Y.; Rodríguez, J. A Cascaded Extended State Observer for Three-level Back-to-back Converter with Surface Mounted Permanent Magnet Synchronous Motor. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–6. [Google Scholar]
- Niu, Z.; Zuo, Y.; Wang, H.; Zhang, L.; Zhu, X.; Lee, C.H.T. Improved Low-frequency Disturbance Rejection Property for Position Control of PMSM Using Generalized Extended State Observer. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 4739–4748. [Google Scholar] [CrossRef]
- Babayomi, O.; Zhang, Z. Model-free predictive control of power converters with cascade-parallel extended state observers. IEEE Trans. Ind. Electron. 2022, 70, 10215–10226. [Google Scholar] [CrossRef]
- Babayomi, O.; Zhang, Z.; Li, Z. Model-Free Predictive Control of DC-DC Boost Converters: Sensor Noise Suppression with Hybrid Extended State Observers. IEEE Trans. Power Electron. 2023, 39, 245–259. [Google Scholar]
- Ahmad, S.; Ali, A. On active disturbance rejection control in presence of measurement noise. IEEE Trans. Ind. Electron. 2021, 69, 11600–11610. [Google Scholar]
- Li, H.; Yu, J. Anti-disturbance control based on cascade ESO and sliding mode control for gimbal system of double gimbal CMG. IEEE Access 2019, 8, 5644–5654. [Google Scholar]
- Li, H.; Zheng, S.; Ning, X. Precise control for gimbal system of double gimbal control moment gyro based on cascade extended state observer. IEEE Trans. Ind. Electron. 2017, 64, 4653–4661. [Google Scholar] [CrossRef]
- Wang, H.; Zuo, Y.; Zhao, C.; Cao, H.; Lee, C.H.T. Improved Disturbance Rejection Ability for Speed Control of PMSM Drives Using a Modified Cascaded Extended State Observer. IEEE J. Emerg. Sel. Top. Power Electron. 2024; early access. [Google Scholar] [CrossRef]
- Samad, T. A survey on industry impact and challenges thereof [technical activities]. IEEE Control Syst. Mag. 2017, 37, 17–18. [Google Scholar]
- Jin, H.; Song, J.; Lan, W.; Gao, Z. On the characteristics of ADRC: A PID interpretation. Sci. China Inf. Sci. 2020, 63, 2029201. [Google Scholar]
- Lin, P.; Wu, Z.; Liu, K.-Z.; Sun, X.-M. A class of linear–nonlinear switching active disturbance rejection speed and current controllers for PMSM. IEEE Trans. Power Electron. 2021, 36, 14366–14382. [Google Scholar]
- Lin, P.; Wu, Z.; Fei, Z.; Sun, X.-M. A generalized PID interpretation for high-order LADRC and cascade LADRC for servo systems. IEEE Trans. Ind. Electron. 2021, 69, 5207–5214. [Google Scholar]
- Cao, H.; Deng, Y.; Zuo, Y.; Li, H.; Wang, J.; Liu, X.; Lee, C.H.T. Unified Interpretation of Active Disturbance Rejection Control for Electrical Drives. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 3433–3437. [Google Scholar] [CrossRef]


| ESO Order | In Time Domain | In Frequency Domain | Gains |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 to n |
| ESO Order | Transit Process | Controller |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
| ESO Order | Low-Pass Filter with Its Setting | ||
|---|---|---|---|
| 1 | 1 | ||
| 2 | |||
| 3 | |||
| 4 | |||
| ESO Order | Controller with Its Gain Setting | |||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| Symbol | Value | Symbol | Value |
|---|---|---|---|
| Rated power | 1 (kW) | Rated speed | 3000 (r/min) |
| Rated voltage | 220 (V) | Rated torque | 1 (Nm) |
| Pole pair number | 5 | Stator resistance | 1 () |
| d-axis inductance | 2.7 (mH) | q-axis inductance | 5.7 (mH) |
| Rotor flux | 0.55 (Wb) | Motor inertia J | 5.58 × () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zuo, Y.; Zhao, C.; Lee, C.H.T. Developing a Unified Framework for PMSM Speed Regulation: Active Disturbance Rejection Control via Generalized PI Control. World Electr. Veh. J. 2025, 16, 193. https://doi.org/10.3390/wevj16040193
Wang H, Zuo Y, Zhao C, Lee CHT. Developing a Unified Framework for PMSM Speed Regulation: Active Disturbance Rejection Control via Generalized PI Control. World Electric Vehicle Journal. 2025; 16(4):193. https://doi.org/10.3390/wevj16040193
Chicago/Turabian StyleWang, Huanzhi, Yuefei Zuo, Chenhao Zhao, and Christopher H. T. Lee. 2025. "Developing a Unified Framework for PMSM Speed Regulation: Active Disturbance Rejection Control via Generalized PI Control" World Electric Vehicle Journal 16, no. 4: 193. https://doi.org/10.3390/wevj16040193
APA StyleWang, H., Zuo, Y., Zhao, C., & Lee, C. H. T. (2025). Developing a Unified Framework for PMSM Speed Regulation: Active Disturbance Rejection Control via Generalized PI Control. World Electric Vehicle Journal, 16(4), 193. https://doi.org/10.3390/wevj16040193









