Research on Energy-Saving Control Strategy of Nonlinear Thermal Management System for Electric Tractor Power Battery Under Plowing Conditions
Abstract
1. Introduction
2. Materials and Methods
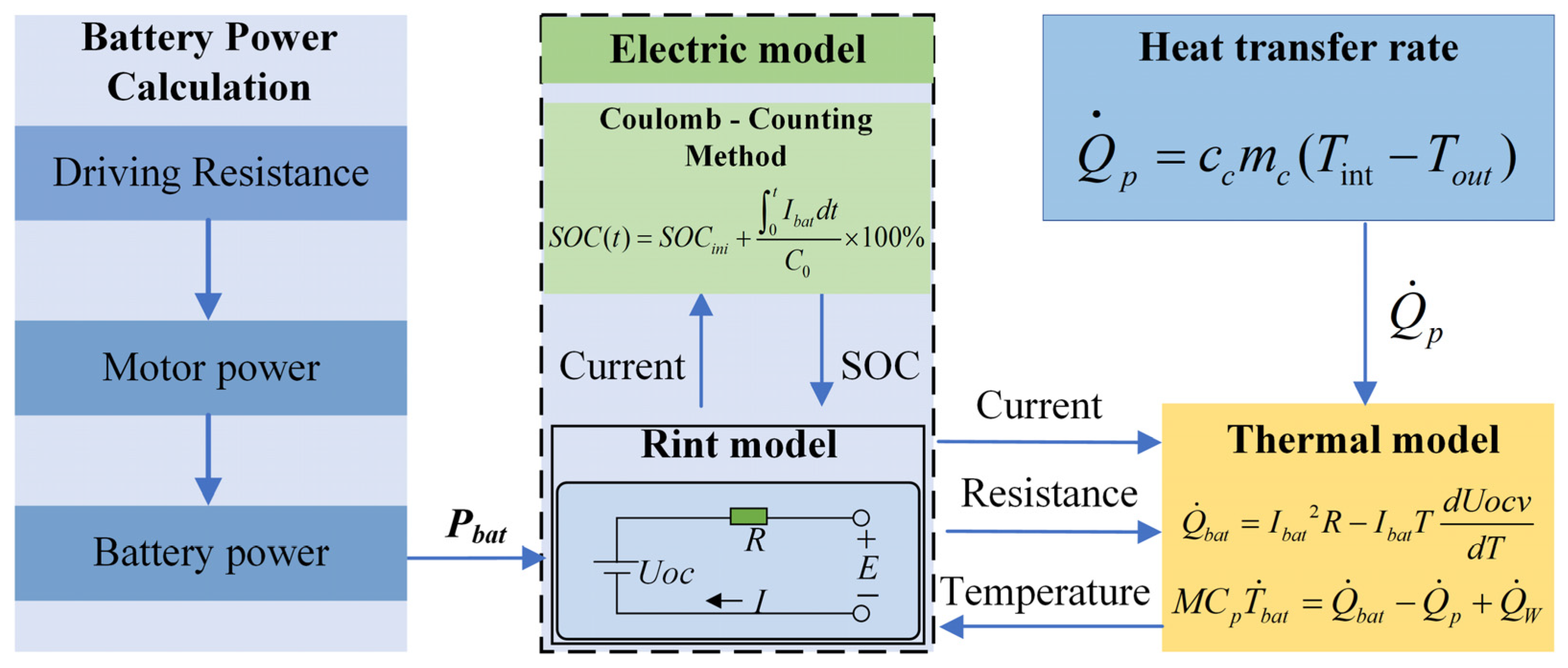
2.1. Battery Electro–Thermal Coupling Model
2.1.1. Battery Power Calculation Model
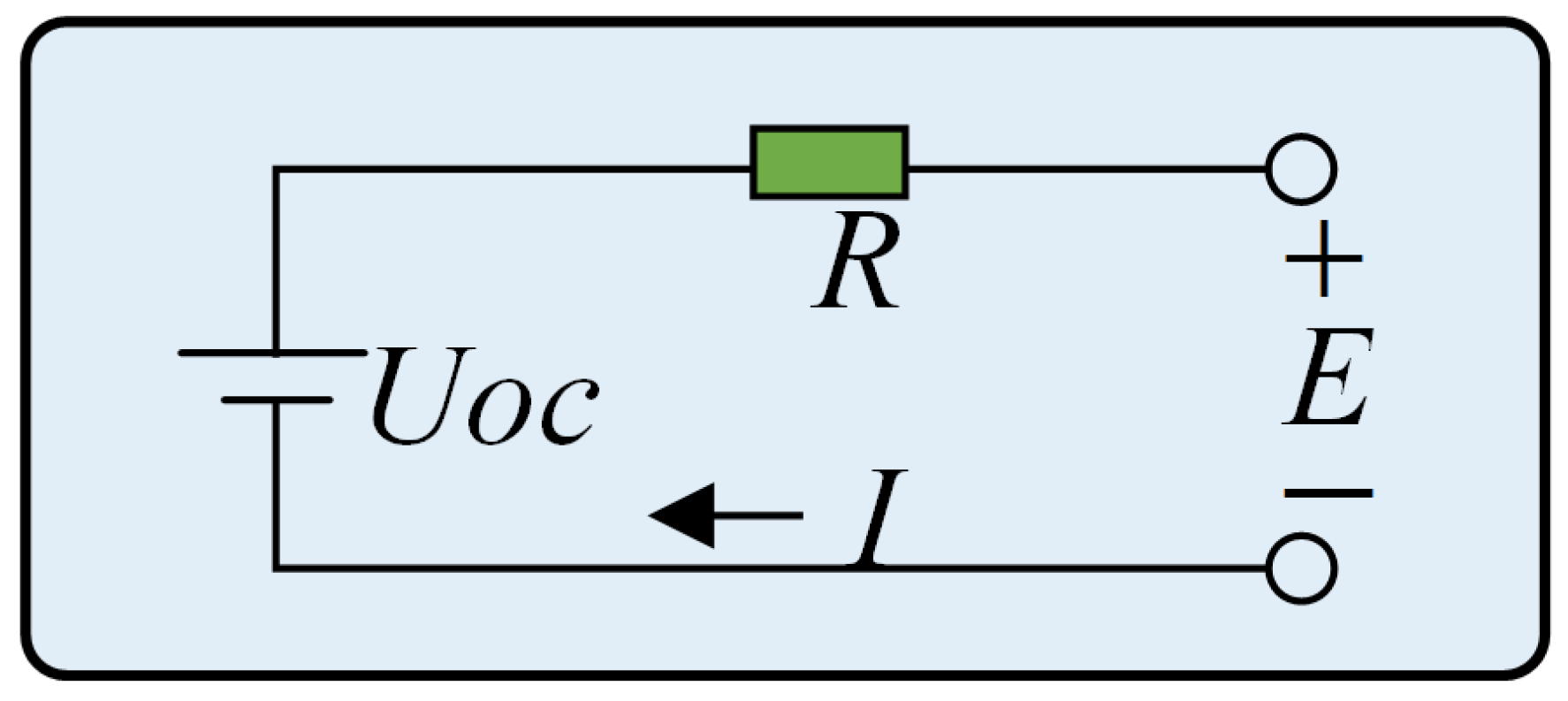
2.1.2. Electrical Model
2.1.3. Battery Heat Production Rate Modeling
2.2. Battery Thermal Management System Modeling
2.2.1. The Coolant Circuit Model
2.2.2. Heat Exchanger Model
2.2.3. Refrigerant Circuit Model
2.3. Battery Thermal Management System Model
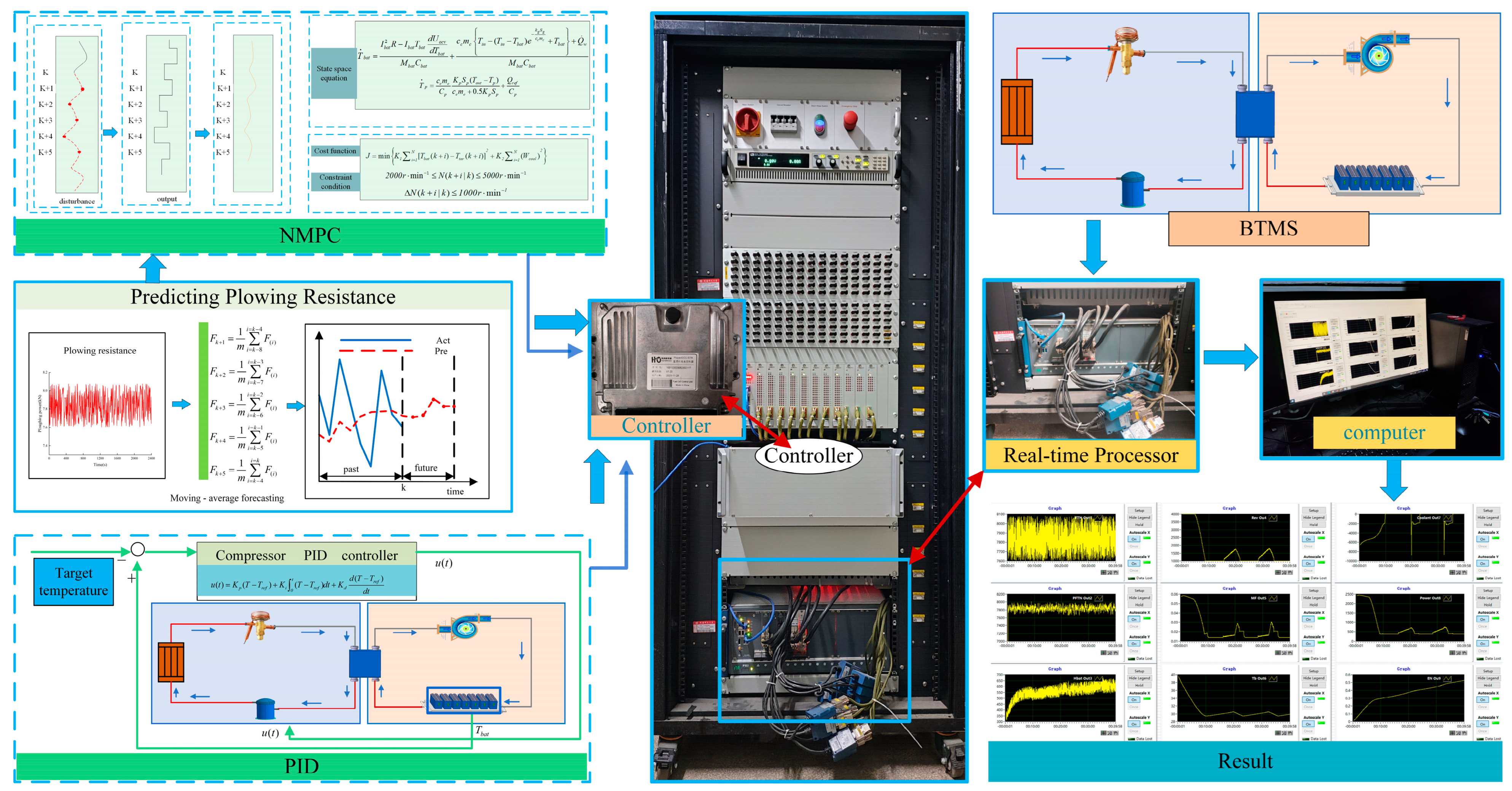
2.3.1. Temperature Control Strategy of Battery Thermal Management System Based on NMPC
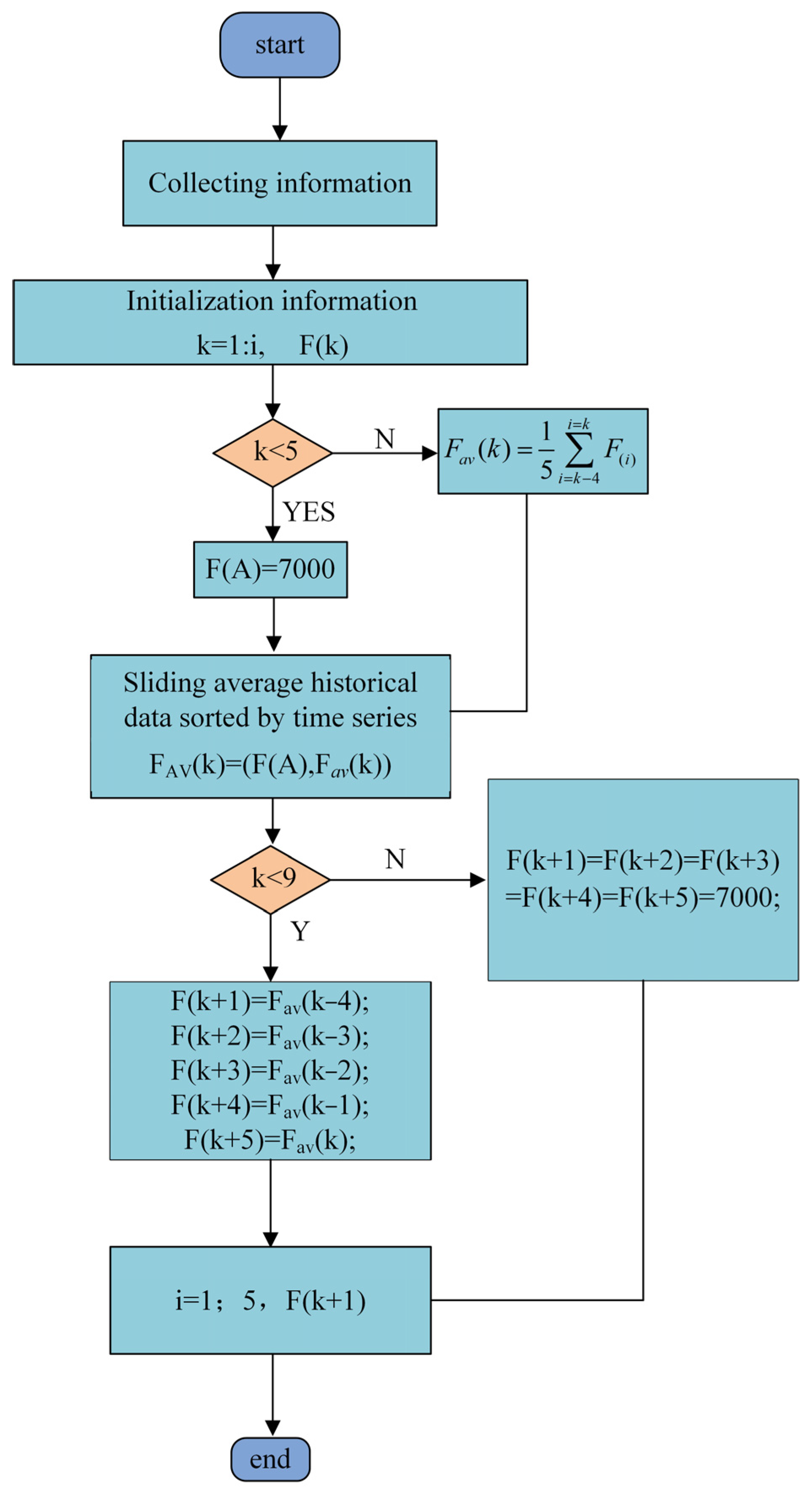
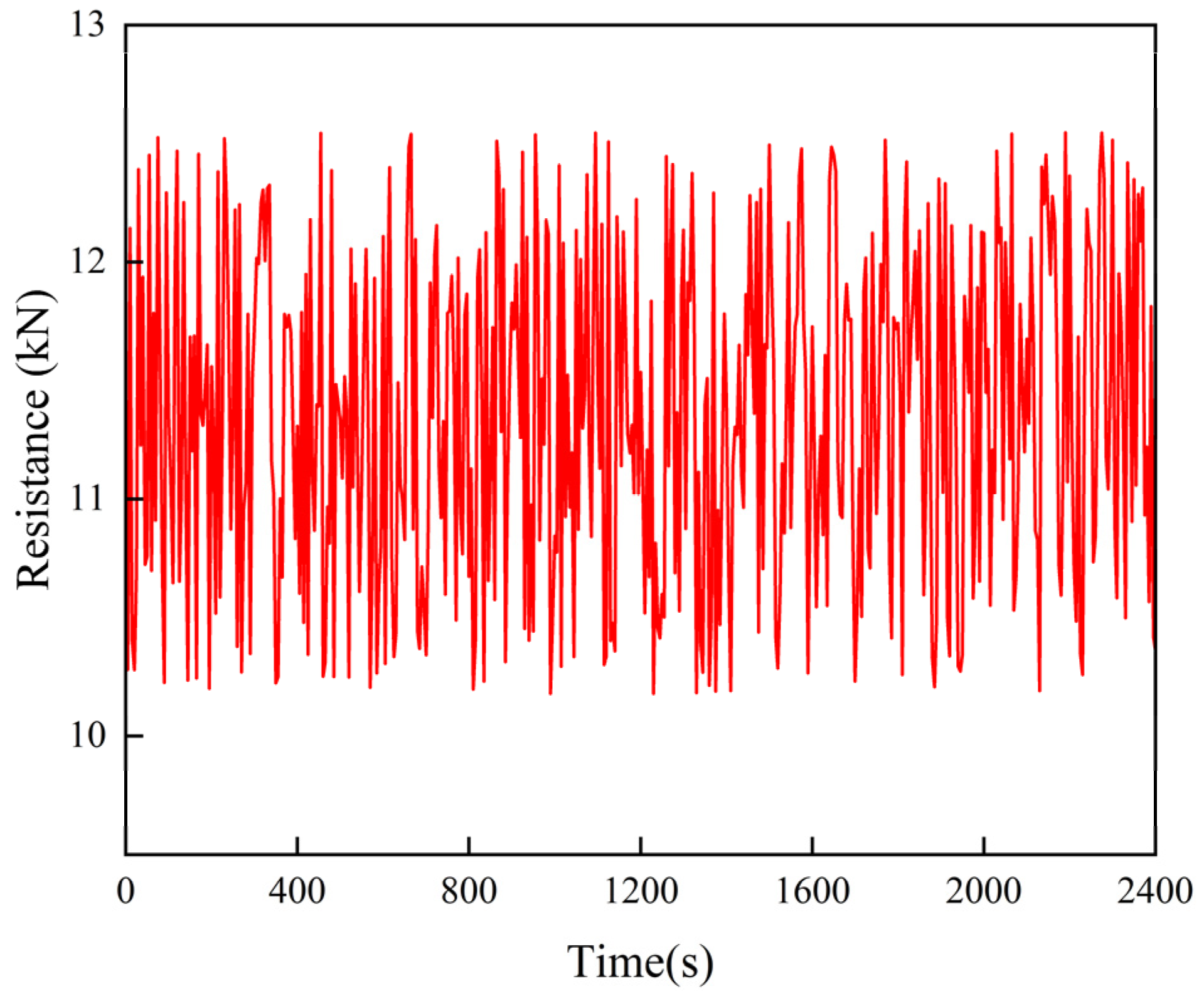
2.3.2. Prediction of Plow Resistance Based on Moving Average Window Theory
2.3.3. PID-Based Temperature Control Strategy for Battery Thermal Management System
3. Results and Discussion
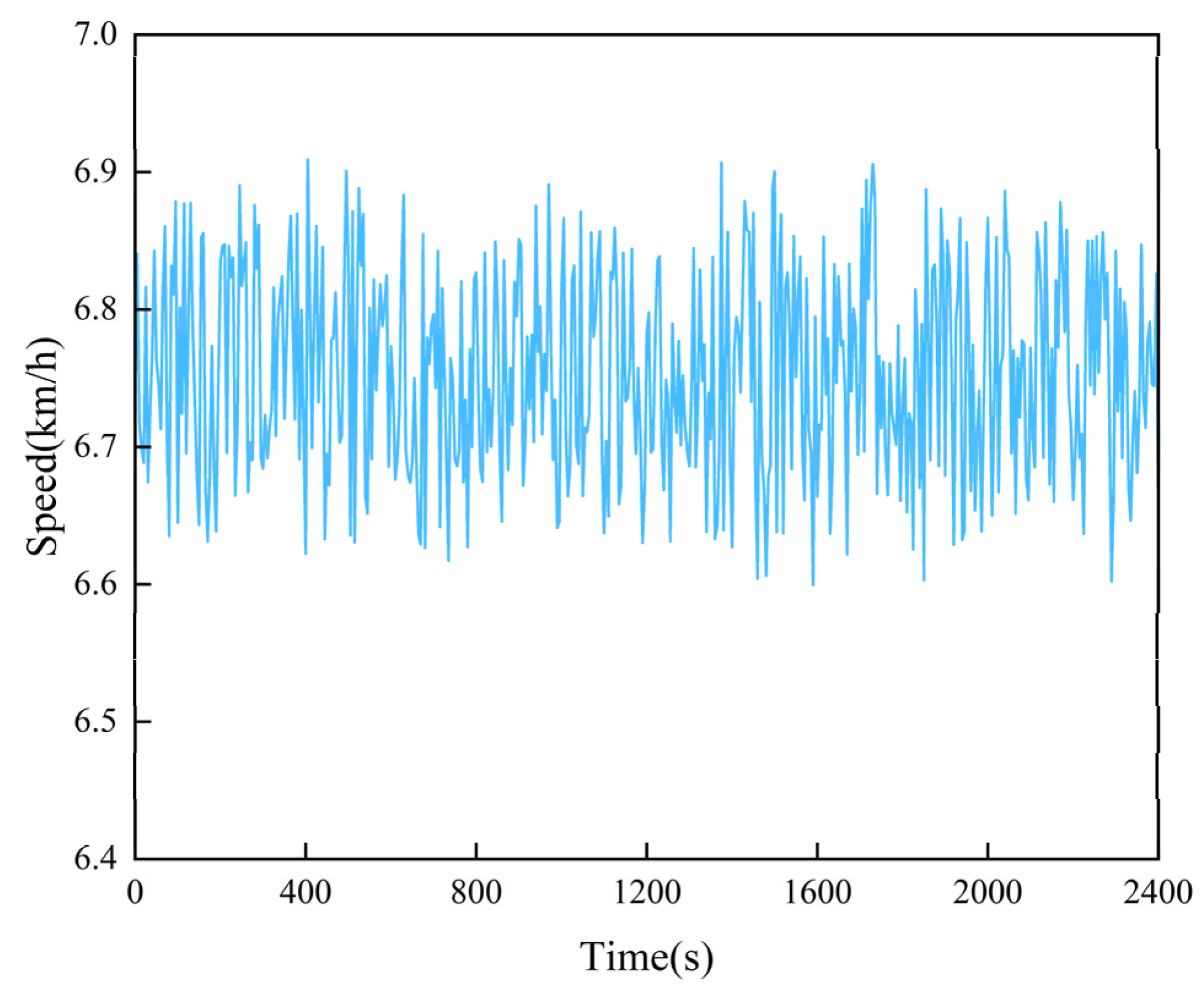
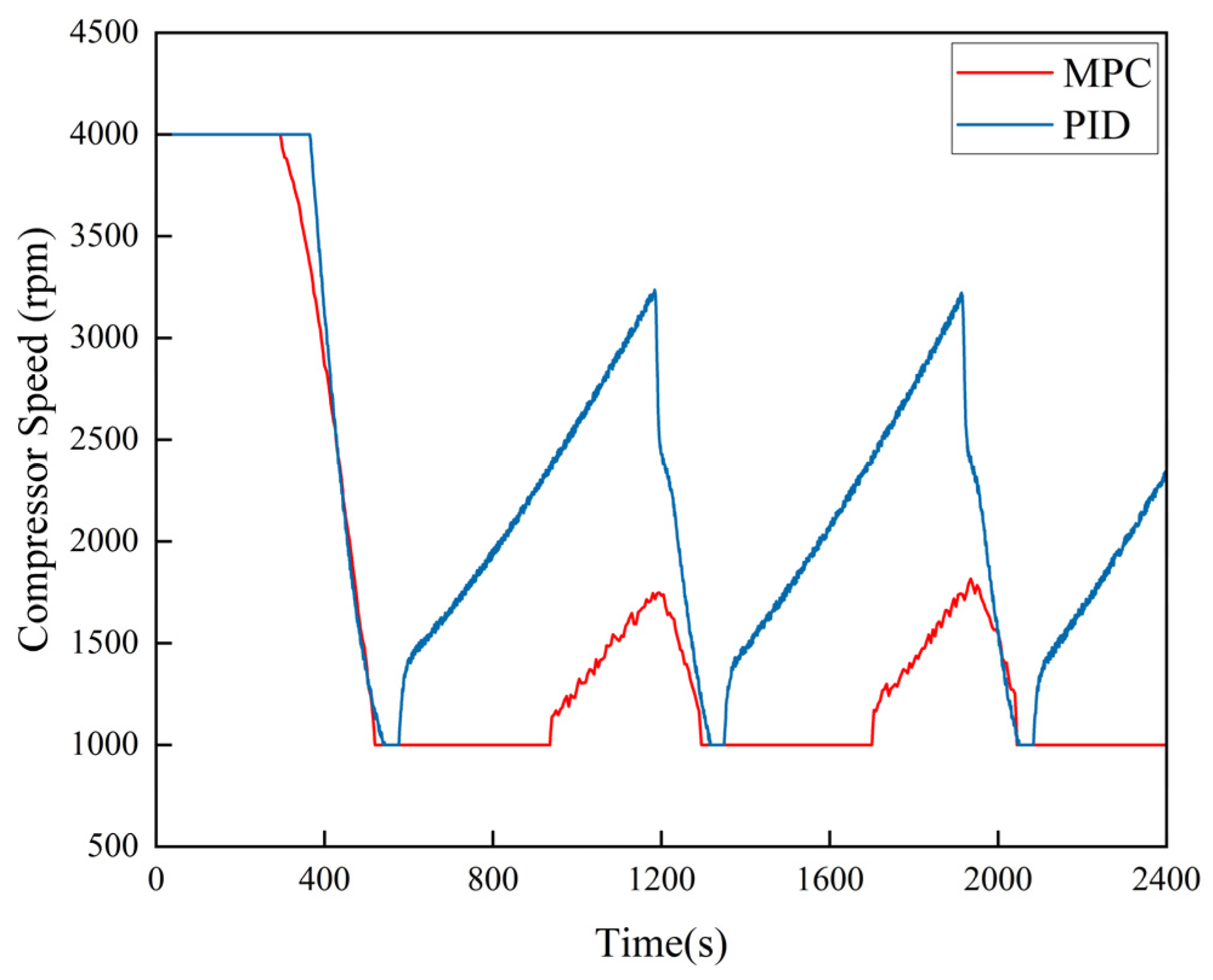
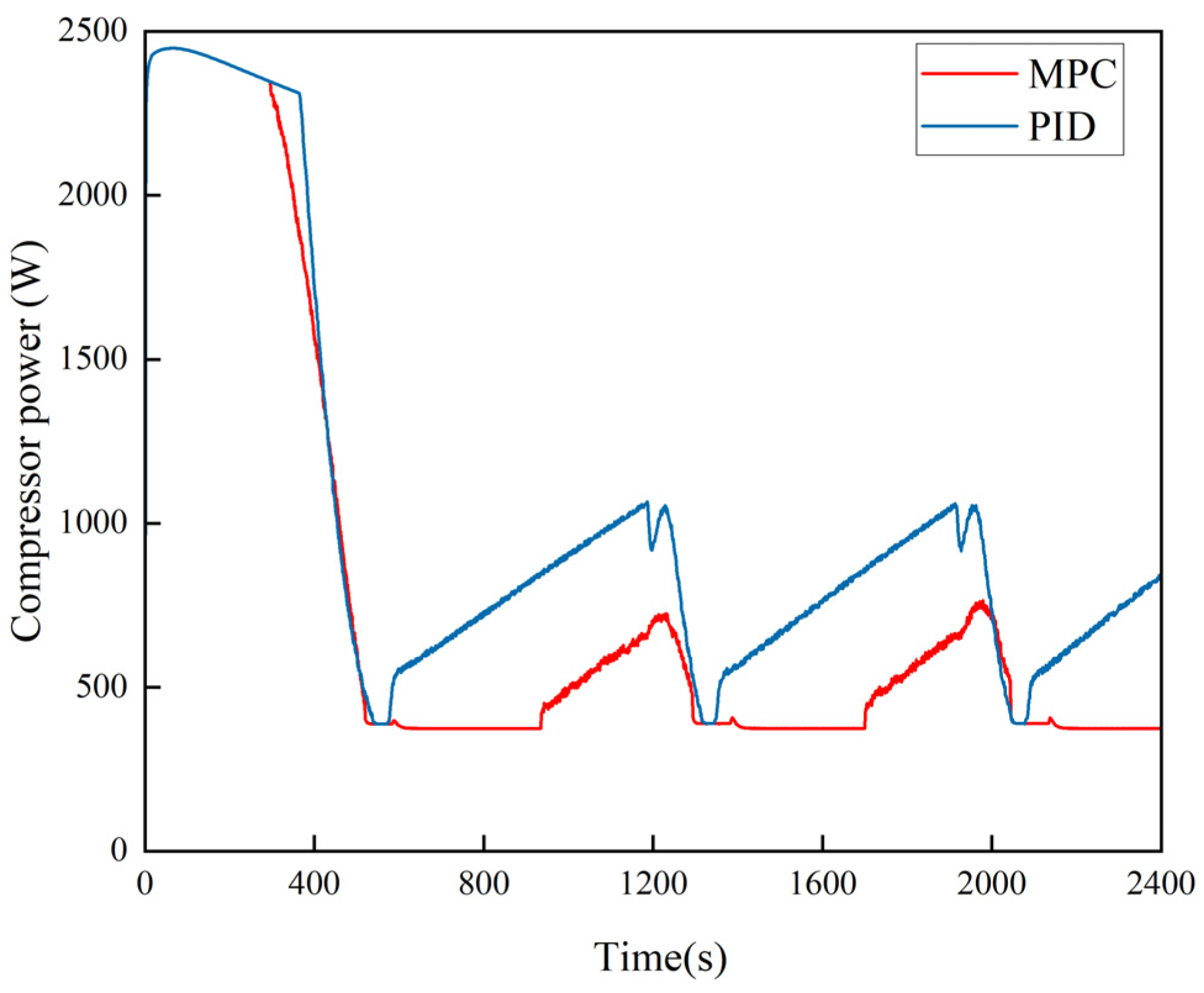
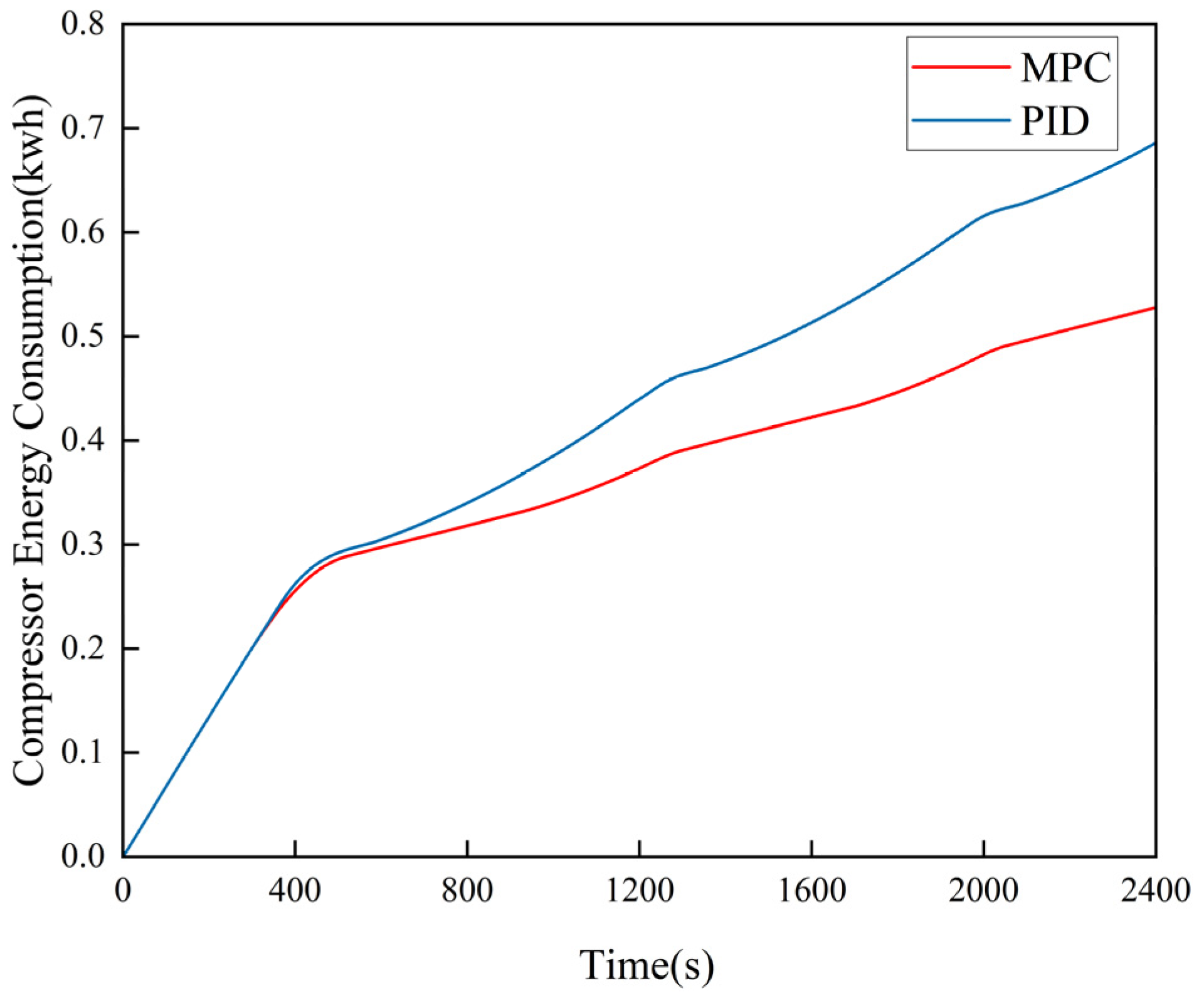
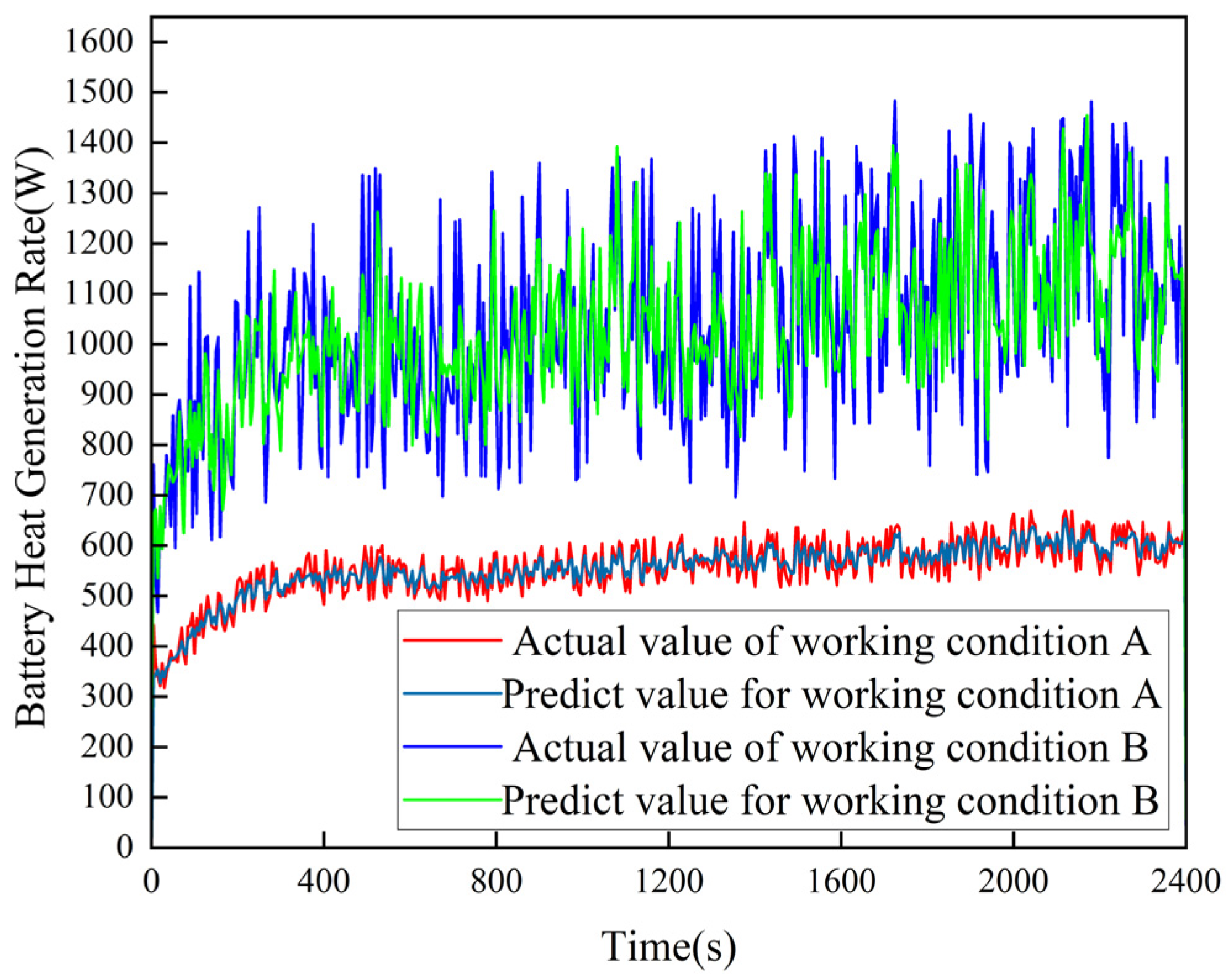
3.1. Simulation Verification
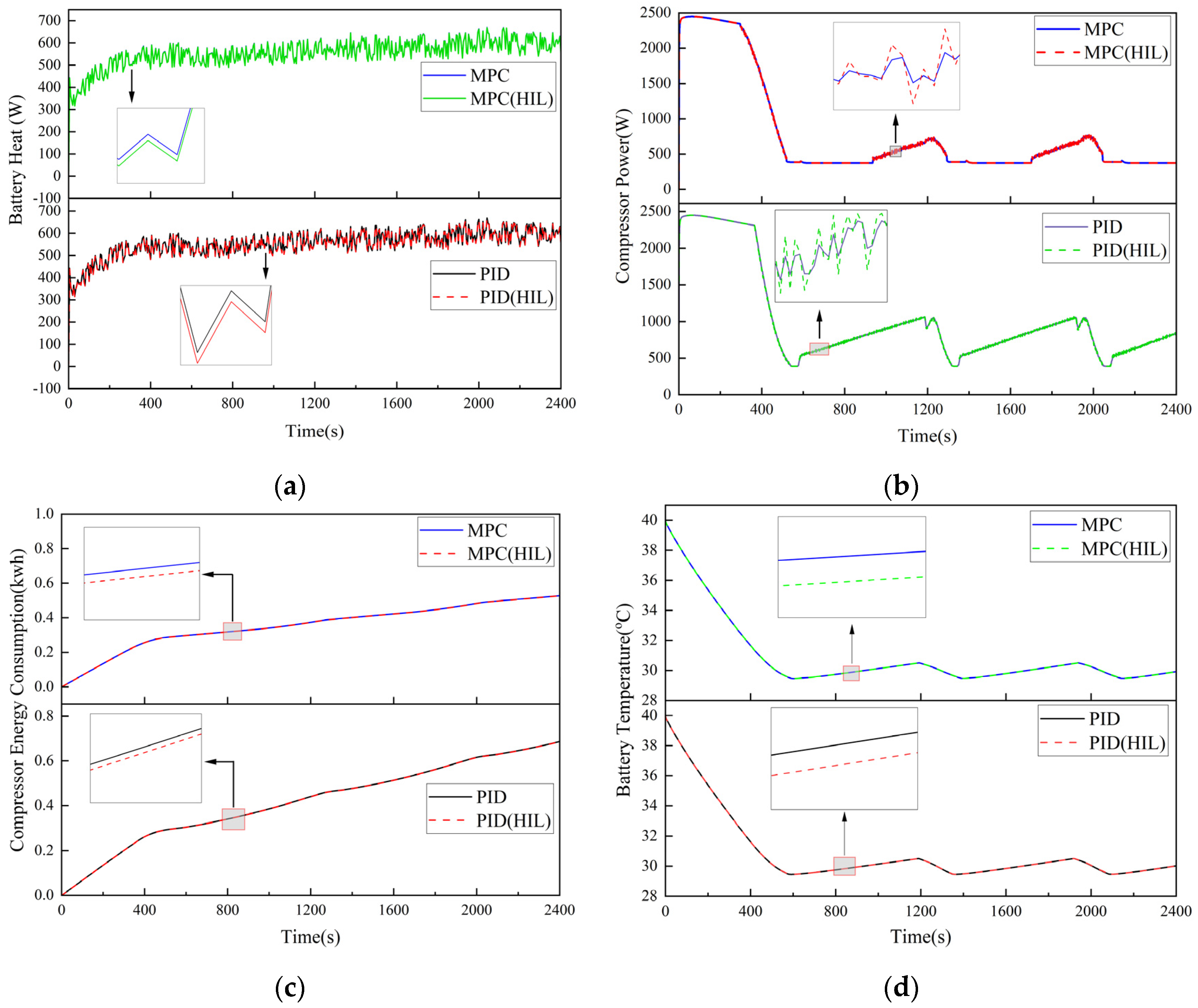
3.2. Hardware-in-the-Loop (HIL) Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NMPC | nonlinear model prediction control |
| PID | proportional integral derivative |
| HIL | hardware-in-the-loop |
References
- Xu, L.; Zhang, J.; Yan, X.; Zhao, S.; Wu, Y.; Liu, M. Review of Research for Agricultural Equipment Electrification Technology. Trans. Chin. Soc. Agric. Mach. 2023, 54, 1–12. [Google Scholar]
- Liu, M.; Lei, S.; Zhao, J.; Meng, Z.; Zhao, C.; Xu, L. Review of Development Process and Research Status of Electric Tractors. Trans. Chin. Soc. Agric. Mach. 2022, 53, 348–364. [Google Scholar]
- Zhang, J.; Zhang, L.; Sun, F.; Wang, Z. An overview on thermal safety issues of lithium-ion batteries for electric vehicle application. IEEE Access 2018, 6, 23848–23863. [Google Scholar] [CrossRef]
- Seong, W.M.; Park, K.Y.; Lee, M.H.; Moon, S.; Oh, K.; Park, H.; Lee, S.; Kang, K. Abnormal self-discharge in lithium-ion batteries. Energy Environ. Sci. 2018, 11, 970–978. [Google Scholar] [CrossRef]
- Tarascon, J.M.; Arman, M. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [Google Scholar] [CrossRef]
- Mali, V.; Saxena, R.; Kumar, K.; Kalam, A.; Tripathi, B. Review on battery thermal management systems for energy-efficient electric vehicles. Renew. Sustain. Energy Rev. 2021, 151, 111611. [Google Scholar] [CrossRef]
- Xiong, P.; Zhang, F.; Zhang, X.; Wang, S.; Liu, H.; Sun, B.; Zhang, J.; Sun, Y.; Ma, R.; Bando, Y.; et al. Strain engineering of two-dimensional multilayered heterostructures for beyond-lithium-based rechargeable batteries. Nat. Commun. 2020, 11, 3297. [Google Scholar] [CrossRef]
- He, L.; Jing, H.; Zhang, Y.; Li, P.; Gu, Z. Review of thermal management system for battery electric vehicle. J. Energy Storage 2023, 59, 106443. [Google Scholar] [CrossRef]
- Goli, P.; Legedza, S.; Dhar, A.; Salgado, R.; Renteria, J.; Balandin, A.A. Graphene-enhanced hybrid phase change materials for thermal management of Li-ion batteries. J. Power Sources 2014, 248, 37–43. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, J.; Pan, W. A review of battery thermal management systems about heat pipe and phase change materials. J. Energy Storage 2023, 62, 106827. [Google Scholar] [CrossRef]
- Wang, H.; Tao, T.; Xu, J.; Mei, X.; Liu, X.; Gou, P. Cooling capacity of a novel modular liquid-cooled battery thermal management system for cylindrical lithium ion batteries. Appl. Therm. Eng. 2020, 178, 115591. [Google Scholar] [CrossRef]
- Fathoni, A.M.; Putra, N.; Mahlia, T.I. A systematic review of battery thermal management systems based on heat pipes. J. Energy Storage 2023, 73, 109081. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Kalogiannis, T.; Jaguemont, J.; Jin, L.; Behi, H.; Karimi, D.; Beheshti, H.; Van Mierlo, J.; Berecibar, M. A comparative study between air cooling and liquid cooling thermal management systems for a high-energy lithium-ion battery module. Appl. Therm. Eng. 2021, 198, 117503. [Google Scholar] [CrossRef]
- Basu, S.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Sohn, D.K.; Yeo, T. Coupled electrochemical thermal modelling of a novel Li-ion battery pack thermal management system. Appl. Energy 2016, 181, 1–13. [Google Scholar] [CrossRef]
- Troncon, D.; Alberti, L. Case of study of the electrification of a tractor: Electric motor performance requirements and design. Energies 2020, 13, 2197. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, G.; Yan, X.; He, Y.; Liu, M.; Xu, L. Cooperative control method considering efficiency and tracking performance for unmanned hybrid tractor based on rotary tillage prediction. Energy 2024, 288, 129874. [Google Scholar] [CrossRef]
- Zeng, W.; Ma, C.; Hu, S.; Li, S.; Zhang, Y. The performance investigation and optimization of reciprocating flow applied for liquid-cooling-based battery thermal management system. Energy Convers. Manag. 2023, 292, 117378. [Google Scholar] [CrossRef]
- Zuo, W.; Li, D.; Li, Q.; Cheng, Q.; Zhou, K.; Jiaqiang, E. Multi-objective optimization of multi-channel cold plate under intermittent pulsating flow by RSM and NSGA-Ⅱ for thermal management of electric vehicle lithium-ion battery pack. Energy 2023, 283, 129085. [Google Scholar] [CrossRef]
- Fayaz, H.; Afzal, A.; Samee, A.M.; Soudagar, M.E.; Akram, N.; Mujtaba, M.A.; Jilte, R.D.; Islam, M.T.; Ağbulut, Ü.; Saleel, C.A. Optimization of thermal and structural design in lithium-ion batteries to obtain energy efficient battery thermal management system (BTMS): A critical review. Arch. Comput. Methods Eng. 2022, 29, 129–194. [Google Scholar] [CrossRef]
- Ali, Z.M.; Jurado, F.; Gandoman, F.H.; Ćalasan, M. Advancements in battery thermal management for electric vehicles: Types, technologies, and control strategies including deep learning methods. Ain Shams Eng. J. 2024, 15, 102908. [Google Scholar] [CrossRef]
- Dai, W.; Lai, H. Comparative study of flow-channel layout schemes in liquid cooling plates of a prismatic battery module. Appl. Therm. Eng. 2024, 236, 121501. [Google Scholar] [CrossRef]
- Ma, K.; Wang, J.; Wang, Q.; Mao, Q. Numerical simulation of battery thermal management based on ring microchannel cold plate. Int. J. Therm. Sci. 2025, 210, 109563. [Google Scholar] [CrossRef]
- Wang, Z.; Guan, Q.; Zhang, H.; Wu, X.; Yu, D. Optimized design of liquid-cooled plate structure for flying car power battery system. J. Energy Storage 2024, 97, 112720. [Google Scholar] [CrossRef]
- Jahanpanah, J.; Soleymani, P.; Karimi, N.; Babaie, M.; Saedodin, S. Transient cooling of a lithium-ion battery module during high-performance driving cycles using distributed pipes—A numerical investigation. J. Energy Storage 2023, 74, 109278. [Google Scholar] [CrossRef]
- Cen, J.; Jiang, F. Li-ion power battery temperature control by a battery thermal management and vehicle cabin air conditioning integrated system. Energy Sustain. Dev. 2020, 57, 141–148. [Google Scholar] [CrossRef]
- Shen, M.; Gao, Q. System simulation on refrigerant-based battery thermal management technology for electric vehicles. Energy Convers. Manag. 2020, 203, 112176. [Google Scholar] [CrossRef]
- Lebrouhi, B.E.; Lamrani, B.; Ouassaid, M.; Abd-Lefdil, M.; Maaroufi, M.; Kousksou, T. Low-cost numerical lumped modelling of lithium-ion battery pack with phase change material and liquid cooling thermal management system. J. Energy Storage 2022, 54, 105293. [Google Scholar] [CrossRef]
- Guo, R.; Sun, Z.; Luo, M. Energy-efficient battery thermal management strategy for range extended electric vehicles based on model predictive control and dynamic programming. Energy 2024, 307, 132769. [Google Scholar] [CrossRef]
- Ma, Y.; Ding, H.; Mou, H.; Gao, J. Battery thermal management strategy for electric vehicles based on nonlinear model predictive control. Measurement 2021, 186, 110115. [Google Scholar] [CrossRef]
- Ma, J.; Liu, A.; Zhang, P.; Chen, Y.; Cai, Y. Collaborative thermal management of power battery and passenger cabin for energy efficiency optimization. Energy Convers. Manag. 2023, 293, 117514. [Google Scholar] [CrossRef]
- Liu, Z.; Xiong, C.; Du, X. Research on the optimization control strategy of a battery thermal management system based on serpentine liquid cooling combined with phase change material. J. Power Sources 2025, 630, 236127. [Google Scholar] [CrossRef]
- Huang, D.; Chen, Z.; Zhou, S. Model prediction-based battery-powered heating method for series-connected lithium-ion battery pack working at extremely cold temperatures. Energy 2021, 216, 119236. [Google Scholar] [CrossRef]
- Ma, Y.; Li, J. Iterative dynamic programming strategy for electric vehicle battery thermal management optimization. Adv. Theory Simul. 2022, 5, 2100602. [Google Scholar] [CrossRef]
- Lian, Y.; Ling, H.; Zhu, J.; Lv, J.; Xie, Z. Thermal management optimization strategy of electric vehicle based on dynamic programming. Control Eng. Pract. 2023, 137, 105562. [Google Scholar] [CrossRef]
- Fan, Y.; Zuo, X.; Zhan, D.; Zhao, J.; Zhang, G.; Wang, H.; Tan, X. A novel control strategy for active battery thermal management systems based on dynamic programming and a genetic algorithm. Appl. Therm. Eng. 2023, 233, 121113. [Google Scholar] [CrossRef]
- Song, Z.; Hofmann, H.; Li, J.; Hou, J.; Zhang, X.; Ouyang, M. The optimization of a hybrid energy storage system at subzero temperatures: Energy management strategy design and battery heating requirement analysis. Appl. Energy 2015, 159, 576–588. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, H.; Chen, J.; Ding, R.; Luo, D. Modeling and model predictive control of a battery thermal management system based on thermoelectric cooling for electric vehicles. Energy Technol. 2024, 12, 2301205. [Google Scholar] [CrossRef]
- Varlese, C.; Haslinger, M.; Junger, C.; Konrad, J.; Krizan, R.; Hametner, C.; Hofmann, P. Predictive fuel cell thermal management for fuel cell electric tractors. Appl. Therm. Eng. 2025, 268, 125835. [Google Scholar] [CrossRef]
- Ma, Y.; Ding, H.; Liu, Y.; Gao, J. Battery thermal management of intelligent-connected electric vehicles at low temperature based on NMPC. Energy 2022, 244, 122571. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A general energy balance for battery systems. J. Electrochem. 1985, 132, 5. [Google Scholar] [CrossRef]
- Ma, Y.; Ma, Q.; Liu, Y.; Gao, J.; Chen, H. Two-level optimization strategy for vehicle speed and battery thermal management in connected and automated EVs. Appl. Energy 2024, 361, 122928. [Google Scholar] [CrossRef]
- Zhang, T.; Li, M.; Li, D. The Research of MPC in Secondary Cooling System of Battery. J. Eng. Thermophys. 2023, 45, 13–19. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Xu, R.; Zhang, J.; Yan, X.; Liu, M.; Shi, M. Research on Energy-Saving Control Strategy of Nonlinear Thermal Management System for Electric Tractor Power Battery Under Plowing Conditions. World Electr. Veh. J. 2025, 16, 249. https://doi.org/10.3390/wevj16050249
Guo X, Xu R, Zhang J, Yan X, Liu M, Shi M. Research on Energy-Saving Control Strategy of Nonlinear Thermal Management System for Electric Tractor Power Battery Under Plowing Conditions. World Electric Vehicle Journal. 2025; 16(5):249. https://doi.org/10.3390/wevj16050249
Chicago/Turabian StyleGuo, Xiaoshuang, Ruiliang Xu, Junjiang Zhang, Xianghai Yan, Mengnan Liu, and Mingyue Shi. 2025. "Research on Energy-Saving Control Strategy of Nonlinear Thermal Management System for Electric Tractor Power Battery Under Plowing Conditions" World Electric Vehicle Journal 16, no. 5: 249. https://doi.org/10.3390/wevj16050249
APA StyleGuo, X., Xu, R., Zhang, J., Yan, X., Liu, M., & Shi, M. (2025). Research on Energy-Saving Control Strategy of Nonlinear Thermal Management System for Electric Tractor Power Battery Under Plowing Conditions. World Electric Vehicle Journal, 16(5), 249. https://doi.org/10.3390/wevj16050249




