Evaluation of Empirical Reference Evapotranspiration Models Using Compromise Programming: A Case Study of Peninsular Malaysia
Abstract
1. Introduction
2. Study Area and Data
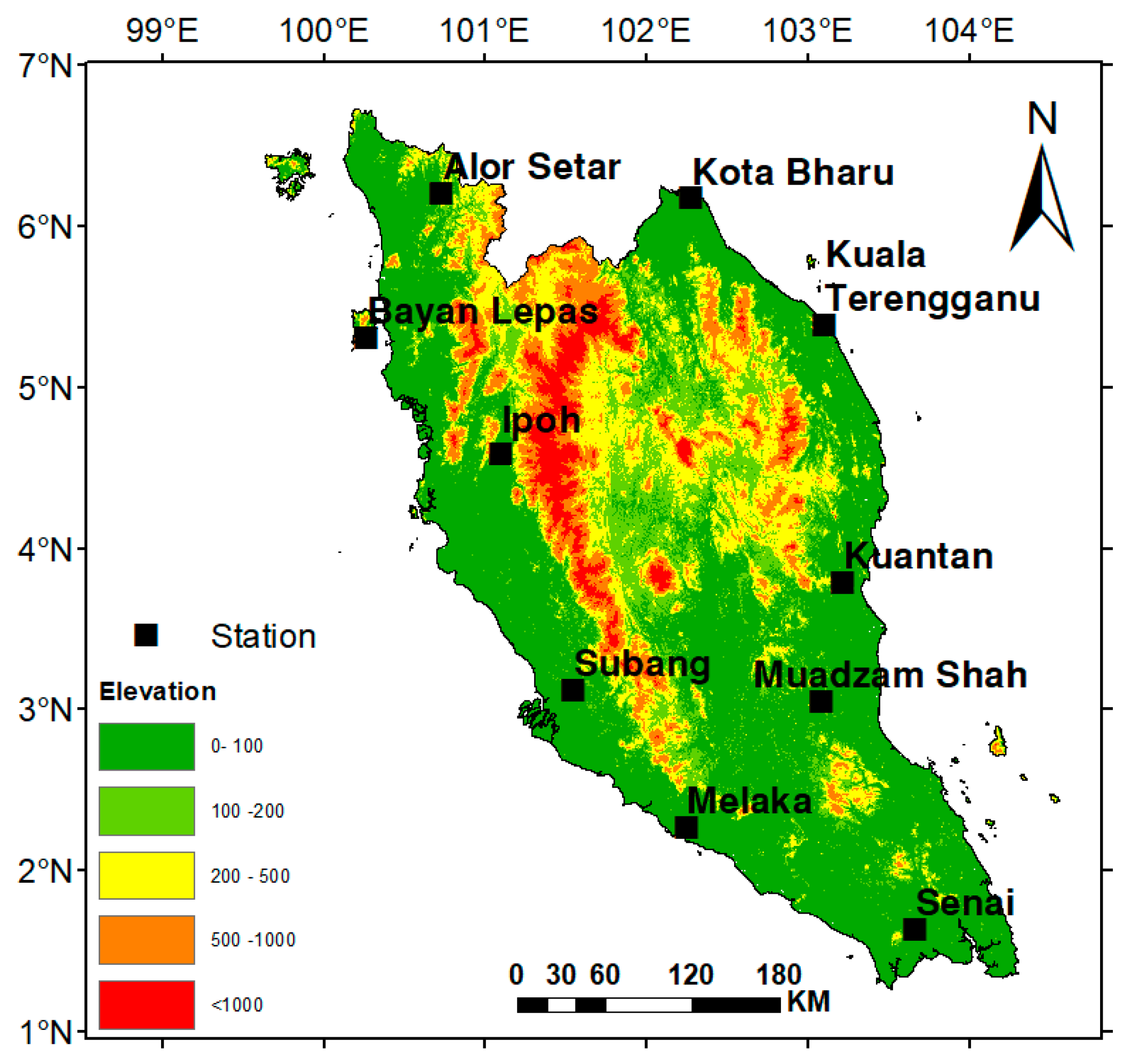
2.1. Geography and Climate of Peninsular Malaysia
2.2. Data and Sources of Information
3. Methodology
- ETo was estimated by the empirical models using the metrological variables.
- Four statistical metrics were used to estimate the capability of different empirical ETo models to estimate different properties of observed ETo at each station.
- CP was used to integrate the results of statistical metrics and rank the ETo models at each station.
- GDM, an information accumulation method, was deployed to rank the empirical models for the entire Peninsula.
3.1. Empirical ETo Models
3.2. Statistical Indices
3.3. Compromise Programming
3.4. Ranking the Empirical ETo Models
- The empirical models were ranked at station level using their CPI (from 1 to 31, the lowest CPI was ranked 1st).
- The frequency of occurrence () of each model of getting a certain rank at all stations was calculated through a 31 × 31 matrix.
- The rank positions were given weight as the inverse of the rank .
- The frequency of occurrence of a model at a certain rank, obtained in Step 2, was multiplied by the weight of the rank, obtained in Step 3.
- The overall score of each ETo model () was estimated by adding the output of Step 4 as presented in Equation (6).
- The empirical models were ranked according to the calculated overall weight, where the highest weighted model was ranked top (1st position).
4. Results
4.1. Evaluation Using Statistical Metrics
4.2. Compromise Programming
4.3. Ranking the Empirical ETo Models
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shahid, S. Impact of climate change on irrigation water demand of dry season boro rice in northwest Bangladesh. Clim. Chang. 2011, 105, 433–453. [Google Scholar] [CrossRef]
- Jun, W.X.; Yun, Z.J.; Hua, W.J.; Min, H.R.; Elmahdi, A.; Hua, L.J.; Gong, W.X.; King, D.; Shahid, S. Climate Change and Water Resources Management in Tuwei River Basin of Northwest China. Mitig. Adapt. Strateg. Glob. Chang. 2012, 19, 107–120. [Google Scholar]
- Wigmosta, M.S.; Vail, L.W.; Lettenmaier, D.P. A distributed hydrology-vegetation model for complex terrain. Water Resour. Res. 1994, 30, 1665–1679. [Google Scholar] [CrossRef]
- Salem, G.; Kazama, S.; Shahid, S.; Dey, N. Impacts of Climate Change on Groundwater Level and Irrigation Cost in A Groundwater Dependent Irrigated Region. Agric. Water Manag. 2018, 208, 33–42. [Google Scholar] [CrossRef]
- Mohsenipour, M.; Shahid, S.; Chung, E.S.; Wang, X.J. Changing pattern of droughts during cropping seasons of Bangladesh. Water Resour. Manag. 2018, 32, 1555–1568. [Google Scholar] [CrossRef]
- Ismail, T.; Harun, S.; Zainudin, Z.M.; Shahid, S.; Fadzil, A.B.; Sheikh, U.U. Development of an optimal reservoir pumping operation for adaptation to climate change. KSCE J. Civ. Eng. 2017, 21, 467–476. [Google Scholar] [CrossRef]
- Fisher, J.B.; Malhi, Y.; Bonal, D.; Da Rocha, H.R.; De Araujo, A.C.; Gamo, M.; Goulden, M.L.; Hirano, T.; Huete, A.R.; Kondo, H. The land—Atmosphere water flux in the tropics. Glob. Chang. Biol. 2009, 15, 2694–2714. [Google Scholar] [CrossRef]
- Shiru, M.S.; Shahid, S.; Alias, N.; Chung, E.-S. Trend analysis of droughts during crop growing seasons of Nigeria. Sustainability 2018, 10, 871. [Google Scholar] [CrossRef]
- Djaman, K.; Komlan, K.; Ganyo, K. Trend analysis in annual and monthly pan evaporation and pan coefficient in the context of climate change in togo. J. Geosci. Environ. Prot. 2017, 5, 41–56. [Google Scholar] [CrossRef]
- Hadi Pour, S.; Abd Wahab, A.K.; Shahid, S.; Wang, X. Spatial pattern of the unidirectional trends in thermal bioclimatic indicators in Iran. Sustainability 2019, 11, 2287. [Google Scholar] [CrossRef]
- Tukimat, N.N.A.; Harun, S.; Shahid, S. Modeling irrigation water demand in a tropical paddy cultivated area in the context of climate change. J. Water Resour. Plan. Manag. 2017, 143, 05017003. [Google Scholar] [CrossRef]
- Irmak, S.; Allen, R.; Whitty, E. Daily grass and alfalfa-reference evapotranspiration estimates and alfalfa-to-grass evapotranspiration ratios in Florida. J. Irrig. Drain. Eng. 2003, 129, 360–370. [Google Scholar] [CrossRef]
- Tukimat, N.N.A.; Harun, S.; Shahid, S. Comparison of different methods in estimating potential evapotranspiration at muda irrigation scheme of Malaysia. J. Agric. Rural Dev. Trop. Subtrop. 2012, 113, 77–85. [Google Scholar]
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D.M. A comparison of six potential evapotranspiration methods for regional use in the southeastern United States 1. JAWRA J. Am. Water Resour. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Djaman, K.; Balde, A.B.; Sow, A.; Muller, B.; Irmak, S.; N’Diaye, M.K.; Manneh, B.; Moukoumbi, Y.D.; Futakuchi, K.; Saito, K. Evaluation of sixteen reference evapotranspiration methods under sahelian conditions in the senegal river valley. J. Hydrol. Reg. Stud. 2015, 3, 139–159. [Google Scholar] [CrossRef]
- Hasenmueller, E.A.; Criss, R.E. Multiple sources of boron in urban surface waters and groundwaters. Sci. Total Environ. 2013, 447, 235–247. [Google Scholar] [CrossRef] [PubMed]
- Roudier, P.; Ducharne, A.; Feyen, L. Climate change impacts on runoff in West Africa: A review. Hydrol. Earth Syst. Sci. 2014, 18, 2789–2801. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Chung, E.S.; Ismail, T.; Wang, X.J. Spatial distribution of secular trends in annual and seasonal precipitation over Pakistan. Clim. Res. 2017, 74, 95–107. [Google Scholar] [CrossRef]
- Jerszurki, D.; Souza, J.L.M.; Silva, L.C.R. Expanding the geography of evapotranspiration: An improved method to quantify land-to-air water fluxes in tropical and subtropical regions. PLoS ONE 2017, 12, e0180055. [Google Scholar] [CrossRef][Green Version]
- Gocic, M.; Trajkovic, S. Analysis of trends in reference evapotranspiration data in a humid climate. Hydrol. Sci. J. 2014, 59, 165–180. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Pereira, A.R.; Villa Nova, N.A.; Sediyama, G.C. Evapo(transpi)ração; FEALQ: Piracicaba, Brazil, 1997; p. 183. [Google Scholar]
- Hamza, M.; Shahid, S.; Bin Hainin, M.R.; Nashwan, M.S. Construction labour productivity: Review of factors identified. Int. J. Constr. Manag. 2019, 19, 1–13. [Google Scholar] [CrossRef]
- Lang, D.; Zheng, J.; Shi, J.; Liao, F.; Ma, X.; Wang, W.; Chen, X.; Zhang, M. A comparative study of potential evapotranspiration estimation by eight methods with fao penman—Monteith method in southwestern china. Water 2017, 9, 734. [Google Scholar] [CrossRef]
- Song, X.; Lu, F.; Xiao, W.; Zhu, K.; Zhou, Y.; Xie, Z. Performance of twelve reference evapotranspiration estimation methods to penman-monteith method and the potential influences in northeast china. Meteorol. Appl. 2019, 26, 83–96. [Google Scholar] [CrossRef]
- Tabari, H.; Grismer, M.; Trajkovic, S. Comparative analysis of 31 reference evapotranspiration methods under humid conditions. Irrig. Sci. 2011, 31, 107–117. [Google Scholar] [CrossRef]
- Hosseinzadeh Talaei, P.; Tabari, H.; Abghari, H. Pan evaporation and reference evapotranspiration trend detection in western Iran with consideration of data persistence. Hydrol. Res. 2014, 45, 213–225. [Google Scholar] [CrossRef]
- Bogawski, P.; Bednorz, E. Comparison and validation of selected evapotranspiration models for conditions in Poland (central europe). Water Resour. Manag. 2014, 28, 5021–5038. [Google Scholar] [CrossRef]
- Lee, T.; Najim, M.; Aminul, M. Estimating evapotranspiration of irrigated rice at the west coast of the peninsular of Malaysia. J. Appl. Irrig. Sci. 2004, 39, 103–117. [Google Scholar]
- Ali, M.H.; Lee, T.; Kwok, C.; Eloubaidy, A.F. Modelling evaporation and evapotranspiration under temperature change in Malaysia. Pertanika J. Sci. Technol. 2000, 8, 191–204. [Google Scholar]
- Ali, M.H.; Shui, L.T. Potential evapotranspiration model for muda irrigation project, Malaysia. Water Resour. Manag. 2008, 23, 57. [Google Scholar] [CrossRef]
- Muniandy, J.M.; Yusop, Z.; Askari, M. Evaluation of reference evapotranspiration models and determination of crop coefficient for momordica charantia and capsicum annuum. Agric. Water Manag. 2016, 169, 77–89. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-guidelines for computing crop water requirements-fao irrigation and drainage paper 56. FaoRome 1998, 300, D05109. [Google Scholar]
- Doorenbos, J.; Pruitt, W. Crop Water Requirements. FAO Irrigation and Drainage Paper 24; Land and Water Development Division, FAO: Rome, Italy, 1977. [Google Scholar]
- Nashwan, M.S.; Shahid, S.; Wang, X. Assessment of satellite-based precipitation measurement products over the hot desert climate of Egypt. Remote Sens. 2019, 11, 555. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shamsuddin, S.; Wang, X.-J. Uncertainty in estimated trends using gridded rainfall data: A case study of Bangladesh. Water 2019, 11, 349. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S. Symmetrical uncertainty and random forest for the evaluation of gridded precipitation and temperature data. Atmos. Res. 2019, 230, 104632. [Google Scholar] [CrossRef]
- Zeleny, M. Compromise Programming, Multiple Criteria Decision-Making. In Multiple Criteria Decision Making; University of South Carolina Press: Columbia, SC, USA, 1973; pp. 263–301. [Google Scholar]
- Rezaei, F.; Ahmadzadeh, M.R.; Safavi, H.R. Som-drastic: Using self-organizing map for evaluating groundwater potential to pollution. Stoch. Environ. Res. Risk Assess. 2017, 31, 1941–1956. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Al-Abadi, A.M.; Wang, X.-J.; Chung, E.-S. Selection of gridded precipitation data for iraq using compromise programming. Measurement 2019, 132, 87–98. [Google Scholar] [CrossRef]
- Chen, W.; Wiecek, M.M.; Zhang, J. Quality utility—A compromise programming approach to robust design. J. Mech. Des. 1999, 121, 179–187. [Google Scholar] [CrossRef]
- Srinivasa Raju, K.; Sonali, P.; Nagesh Kumar, D. Ranking of CMIP5-based global climate models for India using compromise programming. Theor. Appl. Climatol. 2017, 128, 563–574. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S. Spatial distribution of unidirectional trends in climate and weather extremes in Nile river basin. Theor. Appl. Climatol. 2019, 137, 1181–1199. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S.; Abd Rahim, N. Unidirectional trends in annual and seasonal climate and extremes in Egypt. Theor. Appl. Climatol. 2019, 136, 457–473. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Ismail, T.; Ahmed, K. Non-stationary analysis of extreme rainfall in peninsular Malaysia. J. Sustain. Sci. Manag. 2019, 14, 17–34. [Google Scholar]
- Nashwan, M.S.; Ismail, T.; Ahmed, K. Flood susceptibility assessment in Kelantan river basin using copula. Int. J. Eng. Technol. 2018, 7, 584–590. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S.; Chung, E.-S.; Ahmed, K.; Song, Y.H. Development of climate-based index for hydrologic hazard susceptibility. Sustainability 2018, 10, 2182. [Google Scholar] [CrossRef]
- Tangang, F.T. Low frequency and quasi-biennial oscillations in the Malaysian precipitation anomaly. Int. J. Climatol. 2001, 21, 1199–1210. [Google Scholar] [CrossRef]
- Brouwer, C.; Heibloem, M. Irrigation Water Management: Irrigation Water Needs. Training Manual; FAO: Rome, Italy, 1986; Volume 3. [Google Scholar]
- DID. Evaporation in Peninsular Malaysia, 1st ed.; Department of Irrigation and Drainage (DID) Malaysia: Kuala Lumpur, Malaysia, 1976; Volume 5.
- Romanenko, V. Computation of the autumn soil moisture using a universal relationship for a large area. Proc. Ukr. Hydrometeorol. Res. Inst. 1961, 3, 12–25. [Google Scholar]
- Hamon, W.R. Computation of direct runoff amounts from storm rainfall. Int. Assoc. Sci. Hydrol. Publ. 1963, 63, 52–62. [Google Scholar]
- Papadakis, J. Crop Ecologic Survey in Relation to Agricultural Development of Western Pakistan; Draft Report; FAO: Rome, Italy, 1965. [Google Scholar]
- Schendel, U. Vegetations wasserverbrauch und-wasserbedarf. Habilitation, Kiel, 1967; 137p. [Google Scholar]
- Linacre, E.T. A simple formula for estimating evaporation rates in various climates, using temperature data alone. Agric. Meteorol. 1977, 18, 409–424. [Google Scholar] [CrossRef]
- Kharrufa, N. Simplified equation for evapotranspiration in arid regions. Beiträge Hydrol. 1985, 5, 39–47. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Trajkovic, S. Hargreaves versus penman-monteith under humid conditions. J. Irrig. Drain. Eng. 2007, 133, 38–42. [Google Scholar] [CrossRef]
- Ravazzani, G.; Corbari, C.; Morella, S.; Gianoli, P.; Mancini, M. Modified hargreaves-samani equation for the assessment of reference evapotranspiration in alpine river basins. J. Irrig. Drain. Eng. 2011, 138, 592–599. [Google Scholar] [CrossRef]
- Makkink, G. Testing the penman formula by means of lysimeters. J. Inst. Water Eng. 1957, 11, 277–288. [Google Scholar]
- Turc, L. Water Requirements Assessment of Irrigation, Potential Evapotranspiration: Simplified and Updated Climatic Formula; Annales Agronomiques: Paris, France, 1961; pp. 13–49. [Google Scholar]
- Jensen, M.E.; Haise, H.R. Estimating evapotranspiration from solar radiation. Proc. Am. Soc. Civ. Eng. J. Irrig. Drain. Div. 1963, 89, 15–41. [Google Scholar]
- Priestley, C.H.B.; Taylor, R. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- McGuinness, J.L.; Bordne, E.F. A Comparison of Lysimeter-Derived Potential Evapotranspiration with Computed Values; U.S. Department of Agriculture: Washington, DC, USA, 1972.
- Caprio, J.M. The solar thermal unit concept in problems related to plant development and potential evapotranspiration. In Phenology and Seasonality Modeling; Springer: Berlin/Heidelberg, Germany, 1974; pp. 353–364. [Google Scholar]
- Jones, J.W.; Ritchie, J.T. Crop growth models. In Management of Farm Irrigation Systems; Hoffman, G.J., Howel, T.A., Solomon, K.H., Eds.; ASAE: Washington, DC, USA, 1990; pp. 63–69. [Google Scholar]
- Abtew, W. Evapotranspiration measurements and modeling for three wetland systems in south Florida. J. Am. Water Resour. Assoc. 1996, 32, 465–473. [Google Scholar] [CrossRef]
- Dalton, J. Experimental essays on the constitution of mixed gases; on the force of steam or vapor from water and other liquids in different temperatures, both in a torricellian vacuum and in air; on evaporation and on the expansion of gases by heat. Mem. Lit. Philos. Soc. Manch. 1802, 5, 535–602. [Google Scholar]
- Trabert, W. Neue beobachtungen über verdampfungsgeschwindigkeiten [new observations on evaporation rates]. Met. Z. 1896, 13, 261–263. [Google Scholar]
- Meyer, A. Über einige zusammenhänge zwischen klima und boden in Europa. ETH Zur. 1926, 2, 209–347. [Google Scholar]
- Rohwer, C. Evaporation from Free Water Surfaces; US Department of Agriculture: Washington, DC, USA, 1931.
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. London Ser. A Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar]
- Albrecht, F. Die methoden zur bestimmung der verdunstung der natürlichen erdoberfläche. Arch. Meteorol. Geophys. Und Bioklimatol. Ser. B 1950, 2, 1–38. [Google Scholar] [CrossRef]
- Brockamp, B.; Wenner, H. Verdunstungsmessungen auf den Steiner see bei münster. Dt Gewässerkundl Mitt 1963, 7, 149–154. [Google Scholar]
- Gangopadhyaya, M. Measurement and Estimation of Evaporation and Evapotranspiration; WMO: Geneva, Switzerland, 1966. [Google Scholar]
- Mahringer, W. Verdunstungsstudien am neusiedler see. Arch. Meteorol. Geophys. Und Bioklimatol. Ser. B 1970, 18, 1–20. [Google Scholar] [CrossRef]
- Szasz, G. A potenciális párolgás meghatározásának új módszere. Hidrol. Közlöny 1973, 10, 435–442. [Google Scholar]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and nse performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Gorantiwar, S.; Smout, I.K. Multicriteria Decision Making (Compromise Programming) for Integrated Water Resources Management in an Irrigation Scheme; Loughborough University Institutional Repository: Leicestershire, UK, 2010. [Google Scholar]
- Perez-Verdin, G.; Monarrez-Gonzalez, J.C.; Tecle, A.; Pompa-Garcia, M. Evaluating the multi-functionality of forest ecosystems in northern Mexico. Forests 2018, 9, 178. [Google Scholar] [CrossRef]
- Tecle, A.; Shrestha, B.P.; Duckstein, L. A multiobjective decision support system for multiresource forest management. Group Decis. Negot. 1998, 7, 23–40. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Sachindra, D.A.; Nawaz, N.; Chung, E.-S. Fidelity assessment of general circulation model simulated precipitation and temperature over Pakistan using a feature selection method. J. Hydrol. 2019, 573, 281–298. [Google Scholar] [CrossRef]
- Srinivasa Raju, K.; Nagesh Kumar, D. Ranking general circulation models for India using topsis. J. Water Clim. Chang. 2015, 6, 288–299. [Google Scholar] [CrossRef]






| Station Name | Station No | Elev. (m) | Time Period | Tmax (°C) | Tmin (°C) | Tmean (°C) | RH (%) | u (m/s) | Rs (MJ/m2) | ETpan (mm/day) |
|---|---|---|---|---|---|---|---|---|---|---|
| Alor Star | 48603 | 3.9 | 1985–2014 | 32.4 | 23.4 | 27.1 | 81.2 | 1.5 | 18.5 | 3.4 |
| Bayan Lepas | 48601 | 2.5 | 1985–2014 | 31.4 | 23.9 | 27.2 | 80.4 | 1.8 | 17.9 | 2.9 |
| Kota Bharu | 48615 | 4.4 | 2000–2014 | 31.2 | 23.5 | 26.9 | 80.6 | 2.3 | 18.9 | 3.2 |
| Ipoh | 48625 | 40.1 | 1985–2014 | 33.0 | 23.3 | 27.0 | 81.3 | 1.4 | 17.7 | 3.1 |
| Kuala Terengganu | 48618 | 5.2 | 2005–2008 | 31.4 | 23.8 | 27.0 | 82.4 | 1.9 | 17.5 | 3.3 |
| Subang | 48647 | 16.6 | 1985–2014 | 32.4 | 23.2 | 26.9 | 79.6 | 1.5 | 16.5 | 3.2 |
| Kuantan | 48657 | 15.2 | 1999–2014 | 31.7 | 22.9 | 26.2 | 84.1 | 1.7 | 17.0 | 2.9 |
| Muadzam Shah | 48649 | 33.3 | 1985–2014 | 32.1 | 22.7 | 26.3 | 84.7 | 0.9 | 16.3 | 2.5 |
| Melaka | 48665 | 9.0 | 1999–2010 | 31.9 | 23.2 | 26.8 | 80.1 | 1.7 | 17.0 | 3.3 |
| Senai | 48679 | 37.8 | 1985–2010 | 31.8 | 22.5 | 26.0 | 85.7 | 1.4 | 15.1 | 2.7 |
| No | Model | Input Parameter | Equation |
|---|---|---|---|
| Temperature-based | |||
| 1 | Ivanov [51] | Tmean, RH | ETo = |
| 2 | Hamon [52] | Tmean | ETo = RHOSAT × KPEC RHOSAT = ESAT = |
| 3 | Papadakis [53] | Tmean, RH | ETo = |
| 4 | Schendel [54] | Tmean, RH | ETo = |
| 5 | FAO Blaney-Criddle [34] | Tmean | ETo = |
| 6 | Linacre [55] | Tmean | ETo = |
| 7 | Kharrufa [56] | Tmean | ETo = |
| 8 | Hargreaves et al. [57] | Tmean, Tmin, Tmax, Ra | ETo = |
| 9 | Trajkovic [58] | Tmean, Tmin, Tmax, Ra | ETo = |
| 10 | Ravazzani et al. [59] | Tmean, Tmin, Tmax, Ra | ETo = |
| Radiation-based | |||
| 11 | Makkink [60] | Tmean, Rs | ETo = |
| 12 | Turc [61] | Tmean, Rs, RH | ETo = |
| 13 | Jensen et al. [62] | Tmean, Rs | ETo = |
| 14 | Priestley et al. [63] | Tmean, Rs, RH | ETo = |
| 15 | McGuinness et al. [64] | Tmean, Rs | ETo = |
| 16 | Caprio [65] | Tmean, Rs | ETo = |
| 17 | Jones et al. [66] | Tmin, Tmax, Rs | ETo = |
| 18 | Abtew [67] | Tmean, Rs | ETo = |
| 19 | Irmak et al. [12] -Rs | Tmean, Rs | ETo = |
| 20 | Irmak et al. [12] -Rn | Tmean, Rs, RH | ETo = |
| Mass transfer-based | |||
| 21 | Dalton [68] | Tmean, RH, u | ETo = |
| 22 | Trabert [69] | Tmean, RH, u | ETo = |
| 23 | Meyer [70] | Tmean, RH, u | ETo = |
| 24 | Rohwer [71] | Tmean, RH, u | ETo = |
| 25 | Penman [72] | Tmean, RH, u | ETo = |
| 26 | Albrecht [73] | Tmean, RH, u | ETo = |
| 27 | Brockamp et al. [74] | Tmean, RH, u | ETo = |
| 28 | WMO [75] | Tmean, RH, u | ETo = |
| 29 | Mahringer [76] | Tmean, RH, u | ETo = |
| 30 | Szasz [77] | Tmean, RH, u | ETo = |
| Combination-based | |||
| 31 | FAO Penman-Monteith [33] | Tmean, Rs, RH, u, es | ETo = |
| Metric Equation | Range | Optimum Value | |
|---|---|---|---|
| (1) | 0 to +∞ | 0 | |
| (2) | −∞ to +∞ | 0 | |
| (3) | 0 to 1 | 1 | |
| (4) | −∞ to 1 | 1 |
| Model | Wm | Final Rank | Model | Wm | Final Rank |
|---|---|---|---|---|---|
| FAO Penman-Monteith | 6.08 | 1 | Papadakis | 0.58 | 17 |
| Priestley-Taylor | 3.54 | 2 | WMO | 0.57 | 18 |
| Dalton | 2.86 | 3 | Caprio | 0.55 | 19 |
| Meyer | 2.72 | 4 | Irmak-Rs | 0.55 | 20 |
| Makkink | 2.50 | 5 | Jensen and Haise | 0.51 | 21 |
| Rohwer | 2.40 | 6 | Hargreaves and Samani | 0.45 | 22 |
| McGuinness and Bordne | 1.98 | 7 | Penman | 0.44 | 23 |
| Trabert | 1.85 | 8 | Linacre | 0.41 | 24 |
| Mahringer | 1.79 | 9 | Ritchie | 0.41 | 25 |
| Ivanov | 1.62 | 10 | Schendel | 0.38 | 26 |
| Albrecht | 1.59 | 11 | Ravazzani | 0.38 | 26 |
| Brockamp and Wenner | 1.26 | 12 | Trajkovic | 0.36 | 28 |
| Irmak-Rn | 1.05 | 13 | Hamon | 0.35 | 29 |
| Abtew | 0.98 | 14 | Kharuffa | 0.33 | 30 |
| Turc | 0.74 | 15 | FAO Blaney-Criddle | 0.32 | 31 |
| Szasz | 0.71 | 16 | - | - | - |
| Model | p = 1 | p = 2 | p = ∞ | Model | p = 1 | p = 2 | p = ∞ |
|---|---|---|---|---|---|---|---|
| FAO Penman-Monteith | 1 | 1 | 1 | Papadakis | 17 | 17 | 17 |
| Priestley-Taylor | 2 | 2 | 2 | WMO | 18 | 18 | 18 |
| Dalton | 3 | 5 | 4 | Caprio | 19 | 19 | 19 |
| Meyer | 4 | 4 | 3 | Irmak-Rs | 20 | 20 | 20 |
| Makkink | 5 | 3 | 5 | Jensen and Haise | 21 | 21 | 21 |
| Rohwer | 6 | 6 | 8 | Hargreaves and Samani | 22 | 23 | 22 |
| McGuinness and Bordne | 7 | 9 | 7 | Penman | 23 | 22 | 23 |
| Trabert | 8 | 7 | 6 | Linacre | 24 | 25 | 24 |
| Mahringer | 9 | 8 | 9 | Ritchie | 25 | 24 | 25 |
| Ivanov | 10 | 11 | 12 | Schendel | 26 | 27 | 27 |
| Albrecht | 11 | 10 | 10 | Ravazzani | 26 | 24 | 26 |
| Brockamp and Wenner | 12 | 12 | 11 | Trajkovic | 28 | 28 | 28 |
| Irmak-Rn | 13 | 20 | 15 | Hamon | 29 | 29 | 29 |
| Abtew | 14 | 14 | 13 | Kharuffa | 30 | 30 | 30 |
| Turc | 15 | 15 | 14 | FAO Blaney-Criddle | 31 | 31 | 31 |
| Szasz | 16 | 16 | 15 | - | - | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhammad, M.K.I.; Nashwan, M.S.; Shahid, S.; Ismail, T.b.; Song, Y.H.; Chung, E.-S. Evaluation of Empirical Reference Evapotranspiration Models Using Compromise Programming: A Case Study of Peninsular Malaysia. Sustainability 2019, 11, 4267. https://doi.org/10.3390/su11164267
Muhammad MKI, Nashwan MS, Shahid S, Ismail Tb, Song YH, Chung E-S. Evaluation of Empirical Reference Evapotranspiration Models Using Compromise Programming: A Case Study of Peninsular Malaysia. Sustainability. 2019; 11(16):4267. https://doi.org/10.3390/su11164267
Chicago/Turabian StyleMuhammad, Mohd Khairul Idlan, Mohamed Salem Nashwan, Shamsuddin Shahid, Tarmizi bin Ismail, Young Hoon Song, and Eun-Sung Chung. 2019. "Evaluation of Empirical Reference Evapotranspiration Models Using Compromise Programming: A Case Study of Peninsular Malaysia" Sustainability 11, no. 16: 4267. https://doi.org/10.3390/su11164267
APA StyleMuhammad, M. K. I., Nashwan, M. S., Shahid, S., Ismail, T. b., Song, Y. H., & Chung, E.-S. (2019). Evaluation of Empirical Reference Evapotranspiration Models Using Compromise Programming: A Case Study of Peninsular Malaysia. Sustainability, 11(16), 4267. https://doi.org/10.3390/su11164267









