Speed Optimization vs Speed Reduction: the Choice between Speed Limits and a Bunker Levy

Abstract

“Speed optimization and speed reduction” are included in the set of candidate short-term measures under discussion at the International Maritime Organization (IMO), in the quest to reduce greenhouse gas (GHG) emissions from ships. However, there is much confusion on what either speed optimization or speed reduction may mean, and some stakeholders have proposed mandatory speed limits as a measure to achieve GHG emissions reduction. The purpose of this paper is to shed some light into this debate, and specifically examine whether reducing speed by imposing a speed limit is better than doing the same by imposing a bunker levy. To that effect, the two options are compared. The main result of the paper is that the speed limit option exhibits a number of deficiencies as an instrument to reduce GHG emissions, at least vis-à-vis the bunker levy option.

1. Introduction

International shipping is currently at a crossroads. The decision of the 72nd session of the Marine Environment Protection Committee (MEPC 72) of the International Maritime Organization (IMO) in April 2018 to adopt an initial strategy for the reduction of maritime green house gas (GHG) emissions [1] epitomizes the last among a series of recent developments in regards to sustainable shipping. It also sets the scene on what may happen in the future. The IMO initial strategy is in the form of Resolution MEPC.304(72), and includes, among others, the following elements: (a) The vision, (b) the levels of ambition, (c) the guiding principles, (d) a list of short-term, medium-term and long-term candidate measures with a timeline, and (e) miscellaneous other elements, such as follow up actions and others.

As regards the levels of ambition, we highlight two important targets: (i) To peak GHG emissions from international shipping as soon as possible and to reduce the total annual GHG emissions by at least 50% by 2050 compared to 2008 and (ii) to reduce CO₂ emissions per transport work, as an average across international shipping, by at least 40% by 2030, pursuing efforts towards 70% by 2050, compared to 2008.

Among the set of candidate short-term measures, those that are to be finalized and agreed to between 2018 and 2023, one can find the following:

“Consider and analyze the use of speed optimization and speed reduction as a measure, taking into account safety issues, distance travelled, distortion of the market or trade and that such measure does not impact on shipping’s capability to serve remote geographic areas”

The rationale for the measure is very simple. Given the non-linear (at least cubic) relationship between ship speed and fuel consumption (and hence emissions, GHG, and other), reducing ship speed looks like a very promising alternative. So “speed reduction” comes naturally as an obvious candidate GHG reduction measure.

It is actually not that simple. In the debate at the IMO prior to MEPC 72, some countries in South America (and most notably Chile and Peru) objected to the use of the term “speed reduction” as a possible measure, on the ground that this may constitute a barrier to their exports to Asia (and particularly to those that involve perishable products such as agricultural products and others). They suggested the use of “speed optimization” instead. In a compromise solution, at MEPC 72 both wordings were included in the IMO decision text, and hence the above wording. However, what is meant by “speed optimization” in that text is far from clear and hence may be subject to different interpretations.

It turns out that the term “speed reduction” is not well defined either.

In many IMO submissions and in some other documents such as studies, papers, etc. there is widespread confusion on how the term “speed reduction” is interpreted. Sometimes it is interpreted in a literal sense that is reducing speed, irrespective of how the reduction is achieved. In that sense, it is often used as a synonym for “slow steaming,” which is a voluntary measure. But some other times the term is interpreted as mandating speed limits, another name used being “regulating speed”. In fact, a recurrent measure that has been and is being promoted by various Non-Governmental Organizations (NGOs) is mandating speed limits. Since GHG emissions can be reduced by reducing speed, can we achieve the same desirable outcome by imposing speed limits? This is an argument that is being heard frequently over the last several years. The Clean Shipping Coalition (CSC), an NGO, advocated at IMO in 2010 that “speed reduction should be pursued as a regulatory option in its own right and not only as possible consequences of market-based instruments or the EEDI.” However, that proposal was rejected by the IMO at the time. In spite of this decision, lobbying for speed limits has continued by CSC and other groups, and speed limits have been discussed at IMO/MEPC 72 and have succeeded in being included in the roster of candidate short-term measures of the IMO Initial Strategy.

Thus, even though in the eyes of countries like Chile and Peru policies that involve mandatory speed limits are termed “speed reduction” (or even “slow steaming”), in a literal sense speed reduction may also be (a) the voluntary choice of ship operators as a result of depressed market conditions and/or high fuel prices, or (b) the outcome of other, non-prescriptive policies, such as for instance imposing a bunker levy. Confusion on which of these cases pertains not only may prevent one to examine the pros and cons of the various options, but it may also shift regulatory focus. It is one thing to see how to influence the factors that can lead to a rational speed and hence GHG emissions reduction, and another thing to contemplate a direct prescription of the outcome itself, in this case a specific speed limit. Focusing on speed reduction as an outcome and not on the factors that can cause it makes a rational policy decision on the subject more difficult to achieve.

The purpose of this paper is to shed some light into the speed limit debate, and specifically on whether reducing speed by imposing a speed limit is better than doing the same by imposing a bunker levy. We note here that a bunker levy comes under the umbrella of market based measures (MBMs). MBMs have been discussed at the IMO between 2010 and 2013 but their discussion was suspended in 2013, mainly for political reasons. For a discussion of that debate see Psaraftis [2,3].

MBMs are included in the Initial Strategy as a candidate medium-term measure (those are to be finalized and agreed to between 2023 and 2030), as follows:

“New/innovative emission reduction mechanism(s), possibly including Market-based Measures (MBMs), to incentivize GHG emission reduction”

Note the word “possibly”, which means that, as things stand, the fate of MBMs at the IMO is unclear at best. As this paper was being written, two submissions to the IMO have asked for the MBM discussion to reopen: One was by France [4] and the other was by a group of Pacific islands [5]. The French submission did not propose a specific MBM, whereas the Pacific islands proposed a bunker levy. Other than these two submissions, interest on MBMs, at least at the IMO, seems currently slim.

The EU has agreed to align itself with the IMO process, and essentially refrain from taking action on a possible inclusion of shipping into the EU Emissions Trading System (ETS) before seeing what the IMO intends to do on GHGs. ETS is an MBM, and the EU ETS is a major instrument in EU energy policy, covering electricity production and several other major industries (but not shipping). The European Commission will closely monitor the IMO process, starting from what is agreed on the initial strategy in 2018 and all the way to 2023. Whether or not this latest agreement at the EU level might put some pressure on the IMO to resume the suspended discussion on MBMs and adopt a global MBM before the EU moves on ETS is unclear at this time. And even though the ETS looks like the default scenario for the EU if progress at the IMO is not deemed satisfactory, precisely what action the EU will take and when that action will be taken is equally unclear.

Dealing with ship speed is not new in the maritime transportation literature and this body of knowledge is rapidly growing. In Psaraftis and Kontovas [6] some 42 relevant papers were reviewed and a taxonomy of these papers according to various criteria was developed. Many additional papers dealing with ship speed appeared after the above publication. That paper’s Google Scholar citations as of April 2019 stood at 224, and even included papers in seemingly unrelated journals, for instance a paper in “Meat Science” that examined factors that may affect the spoilage of vacuum-packed lamb transported to distant markets [7]. The growing number of references indicates a strong interest of researchers in this topic.

The rest of this paper is organized as follows: Section 2 provides some background and Section 3 presents the arguments put forward by the speed limiters. Section 4 performs a comparative assessment among the two schemes and Section 5 presents the conclusions of the paper.

2. Background

2.1. Definition of “Speed Optimization”

The term “speed optimization” may mean different things to different people. This may create confusion whenever the measure is discussed.

The first confusion is already built-in by the IMO, and comes in the context of the so-called Ship Energy Efficiency Management Plan (SEEMP), the application of which is mandatory for all ships and was adopted by the IMO at the same time as the Energy Efficiency Design Index (EEDI). According to SEEMP [8],

“Speed optimization can produce significant savings. However, optimum speed means the speed at which the fuel used per tonne mile is at a minimum level for that voyage. It does not mean minimum speed; in fact, sailing at less than optimum speed will consume more fuel rather than less. Reference should be made to the engine manufacturer’s power/consumption curve and the ship’s propeller curve. Possible adverse consequences of slow speed operation may include increased vibration and problems with soot deposits in combustion chambers and exhaust systems. These possible consequences should be taken into account.”

Defining the optimum speed as the speed that minimizes fuel used per tonne mile is not very useful. In many cases, minimizing such an objective implies sailing at the minimum permissible speed. In other cases, there is a lower limit to speed reduction as a fuel saving measure, with very low service speeds being associated with high specific fuel oil consumption. Also, the above definition ignores the fact that the speed decision is influenced by a multitude of factors, both technical and commercial, in addition to prevailing weather conditions.

A definition that does not exhibit such deficiencies is the following:

Speed optimization can be defined as the selection of an appropriate speed profile for the ship so as to optimize a specific objective while meeting various requirements (or constraints) on the ship’s operation. The speeds that correspond to the chosen speed profile are called “optimal speeds”.

Given the above definition, what is the objective being optimized, and what are the constraints?

The objective critically depends on who pays for the fuel. If the ship owner pays for the fuel (spot charter scenario in a tramp shipping setting, or ship owner operating his own ships in a liner shipping setting), a typical objective is to maximize average per day profit. If the charterer pays for the fuel (time charter scenario in a tramp shipping setting, or liner operator using chartered vessels), a typical objective is to minimize average per day cost. Of course, it is conceivable that the ship operator may not, for various reasons, act so as to optimize any of the above objectives, or maybe also have additional objectives, secondary or not.

Whereas another conceivable objective (to be minimized) would be GHG emissions, this would be a relevant objective for society, and no private ship operator will necessarily adopt such an objective on a voluntary basis. Note however that this objective is equivalent to minimizing fuel consumption, or fuel costs, so whenever fuel costs are the predominant operational cost component, a solution that minimizes operational costs is close to a solution that minimizes GHG emissions. In this case we may have a win-win scenario, or close to a win-win scenario. By win-win we mean a solution that is optimal both for the ship owner and for society.

Win-win solutions are obviously desirable, however obtaining them may not always be feasible. It is one of the tasks of policy makers, at the IMO and elsewhere, to create the conditions that can make win-win solutions feasible.

Constraints in speed optimization may include specified deadlines or time windows for loading or unloading the cargo, scheduling or timetabling requirements for serving specific ports or meeting feeder connections (liner markets), and maximum and minimum allowable speeds dictated by the maximum power and technology of the main engine. We may also have constraints on maximum allowable hull stress and vertical or transverse accelerations for the safety of the ship and of the cargo and for the comfort of the passengers and the crew. All of these constraints would, in distinct ways, define the feasible envelope for the ship’s speed, and may actually even determine the speed itself.

2.2. Slow Steaming: A Voluntary Practice

Slow steaming is defined as the voluntary practice of sailing slower than a vessel’s design speed. It is typically seen in periods of depressed market conditions and/or high fuel prices. That slow steaming is being practiced in periods of depressed market conditions can be confirmed by the fact that whatever fleet overcapacity existed has been virtually absorbed. Since early 2009, the total containership capacity absorbed due to the longer duration of total roundtrip time for long haul services has reached 1.27 million TEU in October 2013 (taking early 2009 as a starting point), based on Alphaliner’s estimates [9]. More recently (2016), UNCTAD [10] documented a continuing sluggish demand challenged by an accelerated massive global expansion in container supply capacity, estimated at 8% in 2015—its highest level since 2010. Even more recently (2018), the two largest container carriers, Maersk and MSC, have agreed to further slow steam to cut costs, with some speeds as low as 13 knots [11].

Slow steaming is not only practiced in the container market, although it may seem to make more sense there due to the higher speeds of containerships. Slow steaming is reported in every market. On a global scale, and according to the third GHG study of the IMO, the reduction of global maritime CO₂ emissions from 885 million tonnes in 2007 to 796 million tonnes in 2012 is mainly attributed to slow steaming due to the serious slump in the shipping markets after 2008 [12].

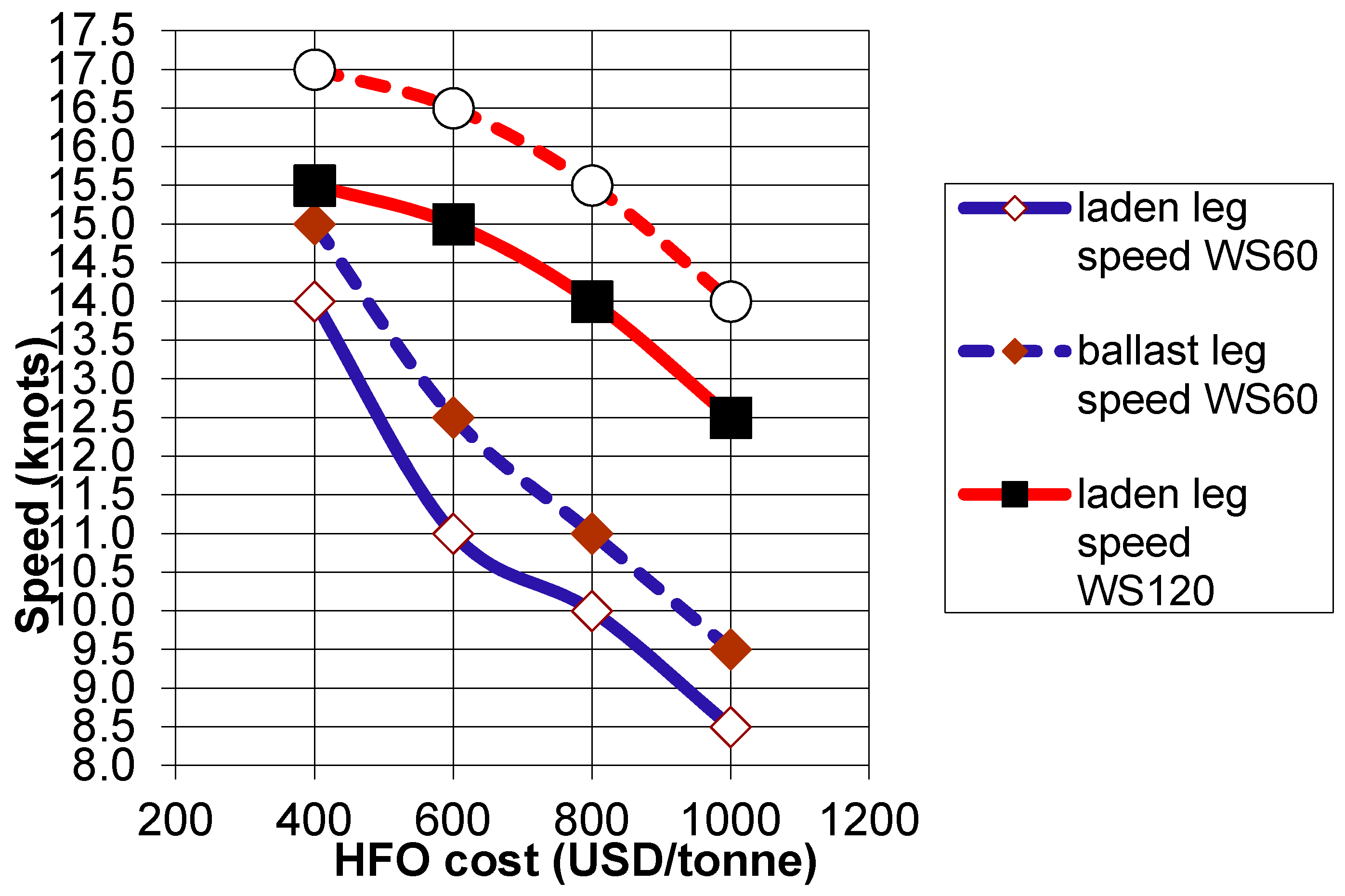
2.3. Factors that May Influence Ship Speed

To understand the main factors that may impact ship speed, Figure 1 captures the impact of both freight rate and bunker price on optimal speed for a specific very large crude carrier (VLCC) trading from the Persian Gulf to Japan. Optimal here means to maximize average per day profit for the ship owner, and speeds are optimized separately in both laden and ballast conditions. Two market conditions are shown for the spot rate, one at Worldscale (WS) 60 and one at WS120 (WS is a nondimensional index measuring the spot rate and is exclusively used in the tanker market). In Figure 1 bunker prices (HFO, Heavy Fuel Oil) range from USD400 to USD1000 per tonne. If both laden and ballast speeds are allowed to vary freely, it can be observed that the impact of both freight rate and bunker price on optimal speed can be quite dramatic, and that the range of optimal speeds can be very broad, depending on the combination of values of these two input parameters. In Figure 1 it can be observed that optimal ballast speeds are typically higher than optimal laden speeds by 1.0 knot in the lower rate scenario and by 1.5 knots in the higher rate scenario.

Figure 2 shows annual CO₂ emissions for the same VLCC as a function of bunker price and spot rate. It can be seen that CO₂ emissions can be reduced significantly if fuel price goes up. This points out to the possible importance of a bunker levy as a tool to reduce CO₂ emissions. The figure also shows that emissions will be reduced (sometimes significantly) whenever fuel prices are up and/or the state of the market is down. Such a reduction is attributed to slow steaming.

Fuel price and the state of the market being the prime factors that influence ship speed, other factors that are important include in-transit inventory costs of the cargo (higher valued cargoes inducing higher speeds), and possible time windows on the pick up and/or delivery of the cargoes. For a discussion of these issues see Psaraftis and Kontovas [6] and Psaraftis [14].

2.4. Other Contexts and Side-Effects

Psaraftis and Kontovas [15] investigated, among other things, the option to slow down in sulfur emissions control areas (SECAs) to reduce the quantity of SO_x produced. Realizing that a reduced speed can not alter the percentage of SOx emissions in a ship’s exhaust, it was shown that if the ship speeds up outside the SECA to make up for lost time within the SECA, more emissions will be produced overall, including SO_x. Fagerholt et al. [16] and Fagerholt and Psaraftis [17] examined route-speed alternatives for ships operating in and out of emissions control areas (ECAs) and Magirou et al. [18] developed stochastic optimal control schemes for speed optimization in a dynamic setting. Giovannini and Psaraftis [19] developed a model for a fixed route liner shipping scenario, which, among other things, considers flexible service frequencies, to be selected among a broader set than the standard assumption of one call per week. The impact of the line’s decisions on CO₂ emissions was also examined.

A possible side-effect of speed reduction concerns possible shifts to other modes of transportation, to the extent these are alternatives to shipping. If ships are made to go slower, shippers may be induced to prefer land-based modes, mostly road, and that may increase overall GHG emissions. Even in long-haul scenarios such as the Far East to Europe trade, some cargoes may be tempted to use the rail alternative (via the Trans Siberian Railway) if the speed of vessels is low enough (see Psaraftis and Kontovas [20] for a discussion). Such considerations may also be relevant in regards to the recent Belt and Road Initiative (BRI), which aims to promote Chinese trade to Europe via a combination of land-based and maritime corridors. It is also noted that in the period 2010 to 2017, 9% to 18% of the Chilean cherry exports to China were carried by airplane [21], meaning that a potential reduction of ship speed may further shift some of these exports to aviation and/or make them less competitive vis-à-vis other cherry producers. This may also increase overall GHG emissions.

In short sea shipping, possible modal shifts due to speed reduction and other measures were investigated by Zis and Psaraftis [22,23] in the context of European SECAs and the Ro/Ro sector. Psaraftis and Kontovas [24], among other things, provided a discussion on the possible impact of slow steaming on port operations. If a port is congested, it would clearly make no sense to sail there at full speed, wasting money on fuel and producing emissions that can be avoided if ship speed were slower. A recent initiative is the so-called ’Virtual Arrival’, which has been used in order to manage the vessels’ arrival time based on the experience of congestion at some discharging ports. At the same time, Californian ports have been offering monetary incentives for ocean going vessels that reduce speed down to 12 knots in the proximity of the port as an emissions reduction measure (Vessel Speed Reduction Programme—VSRP) which has seen great participation rates [25]. In separate but related initiatives, Golias et al. [26] and Du et al. [27] developed models that combined optimizing berth allocation with reducing associated vessel emissions.

3. The Speed Limiters’ Pitch

One of the recent studies that have been used by shipping NGOs like the CSC and others to lobby for speed limits is by CE Delft [28]. An earlier study had the same line of thought, and CSC used that study to propose speed limits to the IMO in 2010, something that was rejected by IMO/MEPC 61. However, it seems that persistence paid off, and speed limits are currently on the table at the IMO as a candidate short-term measure of the initial IMO strategy. Below we comment on the CE Delft study.

The study analyzed two cases of exports from South America to the EU. Even with very conservative assumptions about the impacts, the study claims that the economic impacts of slow steaming are modest: Export values will be reduced by a tenth of a percent at most, and the overall economic impact would be well below a tenth of a percent for the whole of South America.

To calculate the emission reduction potential, the cube law is assumed and calculations are performed on a subset of the world fleet, consisting of containerships, crude oil and product tankers, and bulk carriers. These three types accounted for the majority (actually 52%) of the GHG emissions in 2012. No lifecycle emissions are accounted for (the authors find them to range between 4% and 6% of the emissions reductions achievable by slow steaming, without providing a reference on how this number was computed).

Then the authors proceeded to consider the laid up and idle fleet in these three classes (ranging from 1% for bulkers to 3.5% for containerships, in terms of ship numbers) and consider that this subfleet will take up the reduction of supply ton-miles due to speed reduction. In some of the scenarios examined, they find that this subfleet will not be enough, and additional ships will have to be built to be able to make the projected speed reductions feasible.

What is not mentioned in the study is to what extent the existing fleet is already slow steaming, due to depressed market conditions that prevail in several segments. If a ship is slow steaming, e.g., at 12 knots vs a maximum speed of more than 20 knots, what would be the effect of a speed limit? The latter could very well be superfluous. As slow steaming is being currently practiced in several sectors, this can explain the fact that there is little idle capacity in some market segments.

What is also not mentioned is that freight rates would increase in the short run as a result of the contraction of the supply curve because of the reduced speed. A fortiori, how much the increase is estimated to be is not mentioned either. Such an increase would entail additional costs for the shippers and may very well have impacts on trade which are not examined.

Three speed reduction scenarios, 10%, 20%, and 30% are assumed, and for each scenario, CO₂ emissions reductions are estimated. These range from 13% to 33%.

Then there is a section on the potential impact of speed reduction on trade, which is actually restricted to the examination of the trade of just two (2) products, oilcake and chilled beef, both from Buenos Aires to Rotterdam. In the first case they consider a bulk carrier already slow steaming at 12.2 knots, and in the second a containership whose speed is assumed to be equal to an average speed of 16.3 knots (it is not clear where the average comes from and what is the actual speed in that trade). Using these two examples the authors estimate the costs due to increased sailing time and reach the (general) conclusion that impacts of speed limits on trade are minimal.

In short, and although interesting, this is a study that is full of assumptions, some of which cannot be substantiated. It also fails to address some critical issues, including the practical implementation of the speed limits, including enforcement.

In a more recent document submitted to the IMO [29], CSC made another pitch at the speed limit option, branding it as a measure that can have an immediate impact on reducing GHG emissions, and as a “bridge” measure until more permanent measures are taken.

The way the measure is supposed to work is by limiting what is called the maximum allowable average speed of a vessel, as a function of ship type and size. So called “baseline speeds” could be set on the basis of the average historical operational speeds of each covered ship type and size using historical automatic identification system (AIS) data. Once the baseline speeds are set, target maximum speeds could be arrived at by applying a percentage (%) reduction, to be determined following an impact assessment, below the baseline per covered ship type and size category.

Some of the numbers in that document, in fact along with the whole scheme, are difficult to comprehend. For instance, if a 10% across-the-board speed reduction target is agreed upon and the 2015 speeds are used as baselines, for a 60,000–100,000 DWT bulk carrier the maximum allowable speed would be 10.40 knots, dropping to 9.96 knots for a 100,000–200,000 DWT ship and rising again to 10.64 knots for a ship larger than 200,000 DWT. Why the intermediate size class has to sail slower than the other two is not clear. The equivalent speed limit for the top tier class of containerships (more than 14,500 TEU) is 15.17 knots. There is no benchmarking for other ship types in that document.

The authors also attempt to explicitly address Chile and Peru’s concerns, stating that containerships carrying perishable products would be allowed to not slow down during the export period, so long as they do so in the remainder of the year, on a maximum average per year speed basis. It is clear that such a system would be very difficult to administer and enforce, not to mention the distortions it would create.

For instance, a 15,000 TEU containership in the China to South America trade sailing at (say) 17 knots eastbound and 13 knots westbound (such figures are realistic as will be shown in the next section) would have to slow down only on the eastbound leg, but could, if deemed appropriate, speed up on the westbound leg, up from 13 knots to the designated limit (15.17 knots), except for the “cherry export” periods in which the ship would be allowed to exceed that speed limit altogether, so long as the yearly speed average is at most 15.17 knots. How that yearly average would be computed however is very unclear: Average with respect to time, distance, or other? In the example above, the arithmetic average of 17 and 13 knots is 15 knots, below the 15.17 knots stipulated maximum. Does this mean that sailing one leg at 17 knots and the other at 13 knots would do the trick? If so, then the benefits in terms of GHG emissions reduction would be questionable, since the fuel consumed in a 17/13 knot scenario would surely be higher than those in a 15/15 knot scenario (and so would be the GHG emissions).

The proposers also suggest that specialized reefer ships should be considered to be exempt from ship limits, on the ground that the number of these ships is very small. Again, if this happens, more of these ships (or ships that would label themselves as reefer ships) would be built in the future so as to evade the limit.

There was no analysis of the possible increase of freight rates due to the speed limits, or of the increase in lifecycle GHG emissions due to the construction of new ships so as to cover the required demand throughput, or finally of possible modal shifts due to reduced speed.

4. Comparison between a Bunker Levy and a Speed Limit

4.1. Preamble

As stated earlier, the speed of ships depends on many factors such as fuel price, freight rate, cargo inventory costs, and others, and may actually vary according to the direction of trade. This is especially so in liner trades, the difference reflecting varying ship load factors and values of cargo. Speed directional imbalances have been manifested in several trades worldwide and have been reported in several publications (see for instance Cariou [30], Cheaitou and Cariou [31] and FMC [32], among others). Ongoing research by this author and his colleagues in the context of the ShipCLEAN project, has confirmed that liner cargo from South America to Asia moves at a much slower average speed than cargo in the opposite direction, and that at recent market conditions, slow steaming was being practiced (see also Vilas [33]).

In fact project ShipCLEAN analyzed a Yang-Ming/Cosco transpacific service that includes Chile and Peru (see Figure 3). Observed were an average eastbound speed of 17.5 knots and an average westbound speed as low as 12.5 knots. Both speeds indicate significant slow steaming, especially in the direction from South America to Asia.

The above scenario refers to spring 2018. The situation in the fall of 2018 was not significantly better. A Maersk Line service from Valparaiso, Chile to Yangshan, China for mid-December 2018 (the peak of the cherry export season) would sail the 12,000 nm distance in 35 days, meaning an average speed of 14.3 knots, which is still rather slow (source: Maersk Line).

That speeds are already slow from South America to Asia (and surely also elsewhere) is obviously due to market conditions that have to do with the chronic overcapacity in liner trades worldwide and with other factors that are trade-specific. The speed directional imbalance has surely to do with the imbalances in the values of goods and/or load factors in the two directions. Regardless of what it is, and without any GHG reduction measure being imposed, speed reduction is already there, not as a mandated measure but as a voluntary outcome. The obligatory question is how worse the situation might get by the “speed reduction” that Chile and Peru state that they would like to avoid. It should be noted that for one of the ships of the ShipCLEAN scenario (a 10,114 TEU vessel whose design speed is about 25 knots), a 12.5 knot speed means sailing at 10% of the ship’s maximum continuous rating (MCR), which can achieve significant fuel and GHG emissions savings, and in fact with no externally imposed speed limit.

This difference in average speeds is also manifested in the trades between Asia and Europe, with cargoes from Asia to Europe moving faster than cargoes going in the opposite direction. This imbalance is surely due to commercial considerations that take into account, among other things, the difference in the values of the cargo between the two trade directions and the implied difference in in-transit cargo inventory costs. As ship speeds are the decisions of the carriers and not of the shippers, it is not immediately clear what can be done by countries who want their agricultural or perishable products shipped faster. Shippers associations have been very critical of slow steaming practices, however it is not obvious what they can do to avoid it.

We have seen no comprehensive analysis of the possible market distortions of a speed limit. A discussion of some of the issues is by Devanney [34]. Also we note that Cariou and Cheaitou [35] investigated policy options contemplated by the European Commission and compared speed limits versus a bunker levy as two measures to abate GHGs, with a scenario from the container trades. The paper concluded that the former measure is counterproductive because it may ultimately generate more emissions and incur a cost per tonne of CO₂ which is more than society is willing to pay and because it is sub-optimal as compared to results obtained if an international bunker levy were to be implemented.

4.2. A Rudimentary Example

To shed more light on the issue, in the following we make a rudimentary comparison of a bunker levy vs speed limits. Both measures would cause speed reduction and hence a reduction in CO₂ and other emissions (GHG and non-GHG). A bunker levy would induce speed reduction, and a speed limit would mandate it. Below we attempt to compare the two measures, in terms of emissions reduction and other attributes.

The chosen simple scenario is from the container sector. A generalization to more realistic scenarios or other shipping markets is straightforward and we conjecture that the results would be similar. The example and model below draw from the reference by Psaraftis [14].

A containership of capacity Q (TEU) shuttles between port A and port B, whose interport distance is L (nautical miles—nm). The ship’s speed is v (nm/day), which is within the bracket v_min and v_max. The reason we use nm/day instead of knots in the formulas is to avoid having the number 24 in the equations. However, in the tables and results, knots will be used. The upper bound v_max is dictated by the ship’s MCR, and the lower bound depends essentially on the technology of the engine (older engines typically have a higher v_min than modern, electronically controlled engines, which may also have “slow steaming kits” installed).

Assume that the ship is semi-full in both directions and that the freight rate received by the ship owner is R (USD/TEU), assumed the same in both directions. The assumed load factor of the ship is u (0 ≤ u ≤ 1), again assumed the same in both directions. R is assumed to be on a per laden TEU basis, meaning that if the ship is 75% full (u = 0.75), its per (one way) trip income will be 0.75RQ. Assume that the fuel price is p (USD/tonne) and that the fuel consumption function is FC = kv³ (tonnes/day) with k being a constant. Assume finally that miscellaneous other operating expenses (OPEX) are X (USD/day) and that port turnaround times are ignored. Q, L, R, u, p, k, v_min, v_max and X are assumed known inputs and the sole decision variable is the ship’s speed v.

We also note that this analysis assumes that R is an exogenous variable outside the line’s control and we do not attempt to estimate R as a function of container capacity supply and demand. In that sense, it is expected that slow steaming or speed reduction, if applied for all ships sailing the given route, will generally increase R, however this is not captured in our model.

Table 1. Assumed inputs.

Input	Value
Q	10,000 TEU
L	20,000 nm
R (base case)	1500 USD/TEU
u	0.6
p	500 USD/tonne
vmin	16 knots
vmax	26 knots
X	15,000 USD/day

below shows some hypothetical values for the problem’s inputs.

Finally k is such that FC = 144 tonnes/day when v = 22 knots. The value of k for which this is the case is 9.7827 × 10⁻⁷ (again, v in the formulas is in nm/day).

In this scenario, we can compute various attributes of the round trip, such as

• Round trip time T = 2L/v (days)
• Round trip TEU throughput H = 2uQ (TEU)
• Round trip cost C = T (pkv³ + X) = 2(pkLv² + LX/v) (USD)
• Round trip income I = 2uRQ (USD)
• Round trip profit P = I − C = 2(uRQ − pkLv² − LX/v) (USD)
• Average per day profit P’ = P/T = uRQv/L − pkv³ − X (USD/day)
• Average per day TEU throughput H’ = 2uQ/T= uQv/L (TEU/day)

If the objective of the line is to maximize average per day profit, that is, P’, the optimal speed can be shown to be as follows:

• v_opt = v_min if v_min > v₀
• v_opt = v₀ if v_min ≤ v₀ ≤ v_max
• v_opt = v_max if v_max < v₀

with

v₀ = (uRQ/3pkL)^1/2

(1)

Then CO₂ emissions per unit time (tonnes/day) for this ship are equal to:

CO₂ = fkv_opt³

with f being the carbon coefficient (assumed here equal to 3.11).

For an individual ship,

Table 2. Optimal speed as a function of freight rate R, individual ship.

R (USD/TEU)	500	1000	1500 (Base Case)	1800	2000
vopt (knots)	16.00	18.84	23.07	25.28	26.00
T (days)	104.17	88.47	73.23	65.94	64.10
H (TEU)	12,000	12,000	12,000	12,000	12,000
C (USD)	4,447,589	5,326,987	7,083,480	8,189,078	8,579,871
I (USD)	6,000,000	12,000,000	18,000,000	21,600,000	24,000,000
P (USD)	1,552,451	6,673,013	10,916,520	13,410,922	15,420,129
P’ (USD/day)	14,904	75,430	151,131	203,385	240,554
H’ (TEU/day)	115.20	135.65	166.13	181.99	187.20
CO2 (tonnes/day)	172.27	281.24	516.67	679.18	739.22

below shows the optimal speed and other solution attributes for the above inputs and for selected values of the freight rate R ranging between 500 USD/TEU to 2000 USD/TEU, with a base case value of 1500 USD/tonne.

One can see in general that a higher state of the market (higher R) induces a higher speed and hence higher CO₂ emissions for the ship, and vice versa. It should also be noted that in this particular example and for the two extreme cases R = 500 and 2000 USD/TEU, the optimal speed hits the speed’s lower and upper bounds respectively.

To lower CO₂ emissions, one contemplates either a levy q on fuel, or a speed limit equal to V, with q and V being user inputs. Either of those would generally result in a lower speed. The question is, which of these alternatives achieves lower CO₂ emissions. The answer of course depends on the values of q and V. Depending on these values, and for an individual ship, a levy can achieve lower, the same, or higher CO₂ emissions reductions vis-à-vis those achieved by a speed limit.

Note also that for this comparison to make sense, constant average per day TEU throughput should be maintained, even though speed is reduced. This would necessitate deploying additional ships.

If the initial speed before the levy or the speed limit is v₁ and the final speed after the levy or the speed limit is v₂ (<v₁), we define as the “throughput factor” the ratio r = v₁/v₂ (>1). A ratio r = 1.20 means that r−1 (in this case 20%) more ships should be deployed on the route so as to maintain the same average per day TEU throughput.

To further investigate the issue, we assume that v_min ≤ V ≤ v_max because if V is outside that range, then either the speed limit is superfluous (V > v_max) or the problem is infeasible (V < v_min).

The two cases are compared in

Table 3. Comparison between the speed limit and levy cases, individual ship.

	SPEED LIMIT CASE	LEVY CASE
v0	(uRQ/3pkL)1/2	(uRQ/3 (p + q) kL)1/2
vopt	vopt = vmin if vmin > v0	vopt = vmin if vmin > v0
	vopt = v0 if vmin ≤ v0 ≤ V	vopt = v0 if vmin ≤ v0 ≤ vmax
	vopt = V if V < v0	vopt = vmax if vmax < v0
P’	uRQvopt/L − pkvopt3 − X	uRQvopt/L − (p + q) kvopt3 − X
CO2	fkvopt3	fkvopt3

below as follows.

The superfluous speed limit case occurs if V ≥ (uRQ/3pkL)^1/2, which for our case and for the base case for R means V ≥ 23.07 knots. If this is the case, v_opt is also 23.07 knots.

The non superfluous (binding) speed limit case occurs if V < (uRQ/3pkL)^1/2 = 23.07 knots.

Table 4. Reductions of CO₂ and other attributes as a function of the speed limit V, constant throughput.

V (Knots)	18.00	20.00	22.00
vopt (knots)	18.00	20.00	22.00
T (days)	92.59	83.33	75.76
C (USD)	5,040,279	5,757,889	6,590,909
I (USD)	18,000,000	18,000,000	18,000,000
P (USD)	12,959,721	12,242,111	11,409,091
r	1.28	1.15	1.05
P’ (USD/day)	179,418	169,483	157,951
CO2 (tonnes/day)	314.43	388.18	469.70
ΔCO2 (tonnes/day)	202.24	128.49	46.97
% ΔCO2	39%	25%	9%

shows the results for the base case R, and for selected values of the speed limit V ranging from 18 to 22 knots.

The last two rows in the table show the reductions of CO₂ (in tonnes/day and %) that can be achieved as a function of the speed limit, vis-à-vis the “no speed limit” case (516.67 tonnes/day). Note that the figures for P’, CO₂ and ΔCO₂ have factored in the effect of the throughput factor r.

In turn, we can investigate what happens if we impose a levy q on bunker fuel.

Table 5. Reductions of CO₂ and other attributes as a function of the levy q, constant throughput.

q (USD/Tonne)	100	300	500
vopt (knots)	21.06	18.24	16.32
T (days)	79.13	91.37	102.15
C (USD/rtrip)	7,186,893	7,370,506	7,532,272
I (USD/rtrip)	18,000,000	18,000,000	18,000,000
P (USD/rtrip)	10,813,107	10,629,494	10,467,728
r	1.10	1.27	1.41
P’ (USD/day)	149,723	147,169	144,880
CO2 (tonnes/day)	430.62	322.94	258.27
ΔCO2 (tonnes/day)	86.05	193.73	258.40
% ΔCO2	17%	37%	50%

shows these results (again base case for R) for selected values of q ranging from 100 to 500 USD/tonne.

The first observation from Table 5 is that (by sheer coincidence) a USD 500/tonne levy achieves a 50% reduction in CO₂ emissions. The second observation is that if significant CO₂ emissions reduction is to be achieved via a levy, the levy itself would have to be quite substantial. For a 500 USD/tonne baseline fuel price, a 100 USD/tonne (let alone a 500 USD/tonne) levy is considered substantial and politically very unlikely to be agreed upon. Conversely, a low to modest levy (for instance, up to USD 10/tonne), would not achieve much, in terms of either speed reduction or CO₂ emissions reduction.

We mention the USD 10/tonne figure as this has been used by industry as an unofficial yardstick on what a reasonable bunker levy should be. A rough rationale for such a number is as follows. The United Nations Framework Conference on Climate Change (UNFCCC) wants to raise 100 billion USD per year to combat GHGs globally. If shipping raises 2.2% of that amount (its share in global CO₂), it should raise 2.2 billion USD per year. Assuming 256 million tonnes of marine bunkers per year (796 million tonnes of CO₂ divided by 3.11 [11]), and dividing 2.2 billion USD by 256 million tonnes, gives USD 8.59 /tonne of fuel, which rounds to USD 10/tonne.

Table 4 and Table 5 are not directly comparable, in the sense that from these tables no direct conclusions can be drawn as to what is preferable, a speed limit or a levy. To draw such conclusions, we ask the following question: For a given levy q, what is the value of the speed limit V so that the results are the same in terms of CO₂? And once this happens, what are the other differences between the two cases?

It turns out that for the above scenario the speed limit V for which the optimal speed is the same as that with a levy q is given by:

V = (uRQ/3(p + q)kL)^1/2

Then the optimal speed is equal to V in both cases.

In this case, and for an individual ship, daily CO₂ is also the same and equal to

fkV³ = 2fk (uRQ/3(p + q)kL)^3/2

However, daily profit P’ is different. With a levy q, it is P’ = uRQV/L − (p + q)kV³ − X

With an equivalent speed limit V, and no levy, it is P’’= uRQV/L − pkV³ − X (>P’)

The difference in daily profit is ΔP’ = qkV³

The above are for an individual ship. To maintain the same TEU throughput, the effect of the throughput factor r has also to be taken into account.

This means that for the ship owner, and if the same speed (and hence the same CO₂ emissions) reduction are to be achieved, a speed limit is more profitable than a bunker levy. The ship owner will sail the ship at the same speed as that with a levy, but without paying the levy. This cuts both ways. The difference in daily profit, which is positive for the ship owner, and which possibly reflects an external cost of CO₂ pollution that is not internalized, is a net cost to society. It is money not collected which could be used to achieve out-of-sector emissions reductions (or offsets). These are emissions reductions that can be realized by investing the monies that are collected by a bunker levy into emissions reduction projects outside the maritime sector, for instance by developing a wind farm in New Zealand or a solar farm in Indonesia. The money can also be used for other noble causes (e.g., financial aid to developing countries, research and development, etc.). In that sense, and from a societal point of view, a levy is better than an equivalent speed limit.

4.3. Speed Directional Imbalances

An extension of the above model incorporates different cargo loading factors, different freight rates and different cargo inventory costs in the two directions. To analyze this case, consider that we have:

• Two different load factors, u₁ from A to B, and u₂ from B to A, both in the range 0 to 1.
• Two different freight rates, R₁ from A to B, and R₂ from B to A (both in USD per laden TEU).
• Two different cargo in transit inventory costs, β₁ from A to B, and β₂ from B to A, each expressed in USD per laden TEU per day. Each of the betas is a function of the value of the cargo, according to the formula β_i = CIF_i D/365 (i = 1,2), where CIF_i is the CIF value of the cargo (in USD/TEU) in direction i (i = 1,2) and D is the cargo owner’s cost of capital.
• Two (generally) different speeds, v₁ from A to B and v₂ from B to A.

Note that we continue assuming that daily fuel consumption is equal to kv³, with k being the same in both directions, even though different load factors would generally warrant different values of k. This is tantamount to assuming that for this scenario different load factors would not affect much the immersion of the ship and hence the value of k. We also continue assuming that freight rates are exogenous.

Then it is straightforward to show that the average per pay profit P’ (in USD/day) is given by the following expression:

P’ = −X + {(R₁u₁ + R₁u₂) Q − pkL(v₁² + v₂²) − QL(β₁u₁/v₁ + β₂u₂/v₂)}/L (1/v₁ + 1/v₂)

Looking at this expression, which is to be maximized with respect to both v₁ and v₂, two cases are distinguished:

The first case is if β₁u₁ = β₂u₂. This means that the total value of the cargo is the same in the two directions, even though per laden TEU values of the cargo or load factors may be different. If this is the case, the above expression is symmetric with respect to v₁ and v_2. It can be shown that the optimal solution in this case will have v₁ = v₂, irrespective on whether or not the freight rates R₁ and R₂ or the load factors u₁ and u₂ are different in the two directions. This result is perhaps counter-intuitive as one might expect a higher speed in the direction of the higher freight rate.

In this case one would set v₁ = v₂ = v in the above equation and get:

P’ = −X + (2R₀Q − 2pkLv² − 2QLB₀/v)/2(L/v) = −X − QB₀ + R₀Qv/L − pkv³

where R₀ = 0.5(R₁u₁ + R₁u₂) and B₀ = β₁u₁ = β₂u₂.

This leads to the solution:

• v₁ = v₂ = v_min if v_min > v₀
• v₁ = v₂ = v₀ if v_min ≤ v₀ ≤ v_max
• v₁ = v₂ = v_max if v_max < v₀
• with v₀ = (R₀Q/3pkL)^1/2

which is exactly equivalent to expression (1) (no directional imbalances).

Note that the optimal speed is independent of the in transit inventory costs as the term QB₀ (per day average in transit cargo inventory cost) is a constant. This result is also counter-intuitive. Obviously however the absolute value of the per day profit very much depends on these inventory costs.

The second case is if β₁u₁ ≠ β₂u₂. Assume (without loss of generality) that β₁u₁ > β₂u₂. Then the expression for the per day profit is no longer symmetric with respect to v₁ and v2 and so we can no longer expect that the optimal speeds will be the same in the two directions.

In fact, and after some (rather tedious) algebraic manipulations, we have arrived at this result:

So long as neither speed hits its upper or lower bound, that is, so long as

v_min ≤ v₁ ≤ v_max and v_min ≤ v₂ ≤ v_max,

the following is true:

v₁³ − v₂³ = (β₁u₁ − β₂u₂) Q/2pk

(2)

This expression actually proves that the optimal speeds in the two directions are equal if β₁u₁ = β₂u₂, as mentioned earlier.

In addition, this expression means that the differences of the cubes of the speeds in the two legs are proportional to the difference of the total value of the cargo carried by the ship in the two directions, the ship sailing faster in the direction of the higher value cargo. Also, the lower the fuel price, the higher the speed gap.

The above property is not valid in case either speed reaches its upper or lower bound.

Of course, one cannot solve for the optimal speeds from that equation alone, and it is conceivable that one of the speeds (or even both) hits its upper or lower bounds. To find the actual values of the two optimal speeds, one would have to solve the following constrained non-linear optimization problem (decision variables v₁ and v₂):

Maximize {(R₁u₁ + R₁u₂) Q − pkL(v₁² + v₂²) − QL(β₁u₁/v₁ + β₂u₂/v₂)}/L(1/v₁ + 1/v₂)

Subject to:

• v_min ≤ v₁ ≤ v_max
• v_min ≤ v₂ ≤ v_max

In the ShipCLEAN transpacific scenario, a significant speed difference was observed in the two directions of the Pacific leg: 17.5 knots in the eastbound direction and 12.5 knots in the westbound direction. Shipping companies that we talked to explained that the difference is due to commercial considerations. The above formula provides a justification for such a speed difference.

To gain some insights, if we introduce the two speeds in the above expression, and if we assume a fuel price of 500 USD/tonne and k = 9.7827 × 10⁻⁷, after some arithmetic manipulations we get:

β₁u₁ − β₂u₂ = 4.607 USD/TEU/day

Assuming a 3% interest rate, this translates into a difference of the values of goods of 560,518,000 USD per ship load, or about 56,052 USD/TEU between the two directions. If an average weight of 10 tonnes/TEU is assumed, this also translates into a value difference of about 5605 USD/tonne of cargo. The difference can be due either to higher values of goods, or to higher load factors, eastbound vs westbound, or to both.

Of course, the transpacific route is much more complex than the above simple 2-leg configuration, but this rudimentary analysis may interpret the directional speed imbalance.

4.4. Additional Considerations in the Comparison

We end this section with some additional considerations. As these are only qualitative, they are ultimately subject to quantitative evaluation to draw definite conclusions; this is outside the scope of this paper.

• For ships of different size, a common and uniform levy will result in different optimal speeds. The levy will have to be uniform as it reflects the external cost of GHG emissions, which should be independent of the source of these emissions (not to mention that administering a non-uniform levy would be impossible). However, a larger ship would in general imply a higher optimal speed, everything else being equal. Therefore, achieving equivalence such as the one examined in Section 4.2 by a common and uniform speed limit V would be impossible. To do so, one would have to set size-specific (or maybe also ship type-specific or even route-specific) speed limits. A ship type- and size-specific speed limit has been proposed by CSC in their latest IMO speed-limit paper [29], but it would make the whole exercise an administrative nightmare.
• Conversely, if a common and uniform speed limit V is imposed, the limit may be superfluous for some ship types and sizes and binding for some others, depending on the state of the market, the price of fuel, and a host of other parameters. Having the same speed limit in boom market periods and in depressed market periods could create all sorts of distortions. In depressed market periods the limit may be superfluous, and in boom market periods the limit would force some ships (likely at the high end of the scale) to slow down whereas others do not. A speed limit may also be superfluous in one route direction (e.g., from Europe to the Far East, where ships go slower anyway) and binding in the other direction (ships go faster from the Far East to Europe).
• In addition to not paying the levy, another short-term effect of a speed limit that would be beneficial for ship owners is that freight rates would go up, as the speed limit would effectively shrink the ship transport capacity supply curve. What the freight rate increase will be and who, among ship owners, will be the main beneficiaries of this rate increase would depend (among other things) on the nature and structure of the speed limit in regards to the world fleet. Note that the contraction of the supply curve due to slow steaming because of a bunker levy would also result in a freight rate increase. A comparison of the two outcomes (freight rate increase induced by a speed limit versus freight rate increase induced by a bunker levy) is not straightforward.
• Even though higher freight rates and no payment of a levy may render the speed limit measure preferable to some ship owners versus a levy (let alone versus a “do nothing” option), shippers would be hit twice: They would pay more for their cargo and also suffer increased transit times and increased in-transit inventory costs. Trade may also be affected.
• Another effect of a speed limit, which is more in the long run, is that additional ships will have to be built to sustain ton-mile throughput at lower speeds, particularly if maritime trade is projected to grow. Building these additional ships would produce additional GHG emissions due to shipbuilding and recycling (lifecycle GHG emissions). See Gratsos et al. [36] and Chatzinikolaou and Ventikos [37,38] for more details.
• Building more ships would also take place in the long run if speeds are reduced due to a bunker levy. However, due to the much lower flexibility of a speed limit, it is speculated that lifecycle GHG emissions of the speed limit scenario would be higher, as some ships would have to be built only to sustain a ton-mile throughput that could be met by higher speeds in boom periods (something that would be impossible if a speed limit is instituted). Then in depressed market periods this extra ship capacity would make the fleet overcapacity problem even more acute.
• A speed limit regime would not be compatible with virtual arrival, as the latter scheme requires maximum flexibility on the part of the ship to meet a prescribed port time slot. Flexibility is also a must in cases when schedule disruptions (for instance due to bad weather, port congestion, search and rescue operations, etc.) should be handled. Such flexibility would be reduced by a speed limit.
• The impact of a bunker levy or a speed limit on the economies of LDCs (lesser developed countries) and SIDS (small island developing states) is largely unknown. This may include a decrease of export products competitiveness, an increase of import prices, shifts to other modes of transport, and other side-effects.
• Last but not least, a speed limit would hardly serve as an incentive to economize and improve the energy efficiency of ships. Two ships of the same type and size, one modern and energy efficient and one old and energy inefficient, would have to go at the same speed, and this would offer an unfair advantage to the latter ship and would thus distort competition. In the long run, a speed limit would not incentivize the development of energy efficient technologies that are currently non-viable.

Note that some of the above criteria (for instance amount of GHG reductions, administrative burden, collect money for LDCs or SIDS, incentives to become energy efficient, etc.) are similar to those used by the IMO to compare the MBM proposals (see the reference by Psaraftis [2]).

5. Conclusions

The main result of the paper has been that the speed limit option exhibits a number of deficiencies as an instrument to reduce GHG emissions, at least vis-à-vis the bunker levy option. As this paper was being finalized, the speed limit option was among the set of short-term options being considered by the IMO/MEPC in the quest to reduce maritime GHG emissions, and the fate of this option remained largely unknown.

For the time being, only some NGOs are officially for speed limits, arguing that it is the easiest option to implement so as to reduce GHG emissions, and that it can be used as a “bridge” until longer-term measures can be agreed upon. However, it is clear that as the option may also entail some benefits, others may espouse it too. These include some ship owners who would certainly benefit from the short-term freight rate increase that this measure would bring about. Also, owners of energy-inefficient ships would rather see their energy-efficient competitors being forced to sail at the same reduced speed as they do, than being beaten on speed because of better fuel efficiency. Be that as it may, the principal trade association of global ship owners at the IMO, the International Chamber of Shipping (ICS), does not favor speed limits.

Of course, the real reasons for advocating speed limits are seldom revealed in the public debate, and all promoters typically play the “do-gooder” card, that the option is good for the environment, and in particular vis-à-vis the IMO initial strategy. This paper has shed some light on the pros and cons of this option and in that sense it may contribute to the public debate on this subject.