Energy Management Optimization of Series Hybrid Electric Bus Using an Ultra-Capacitor and Novel Efficiency Improvement Factors
Abstract
1. Introduction
2. SHEB Modeling
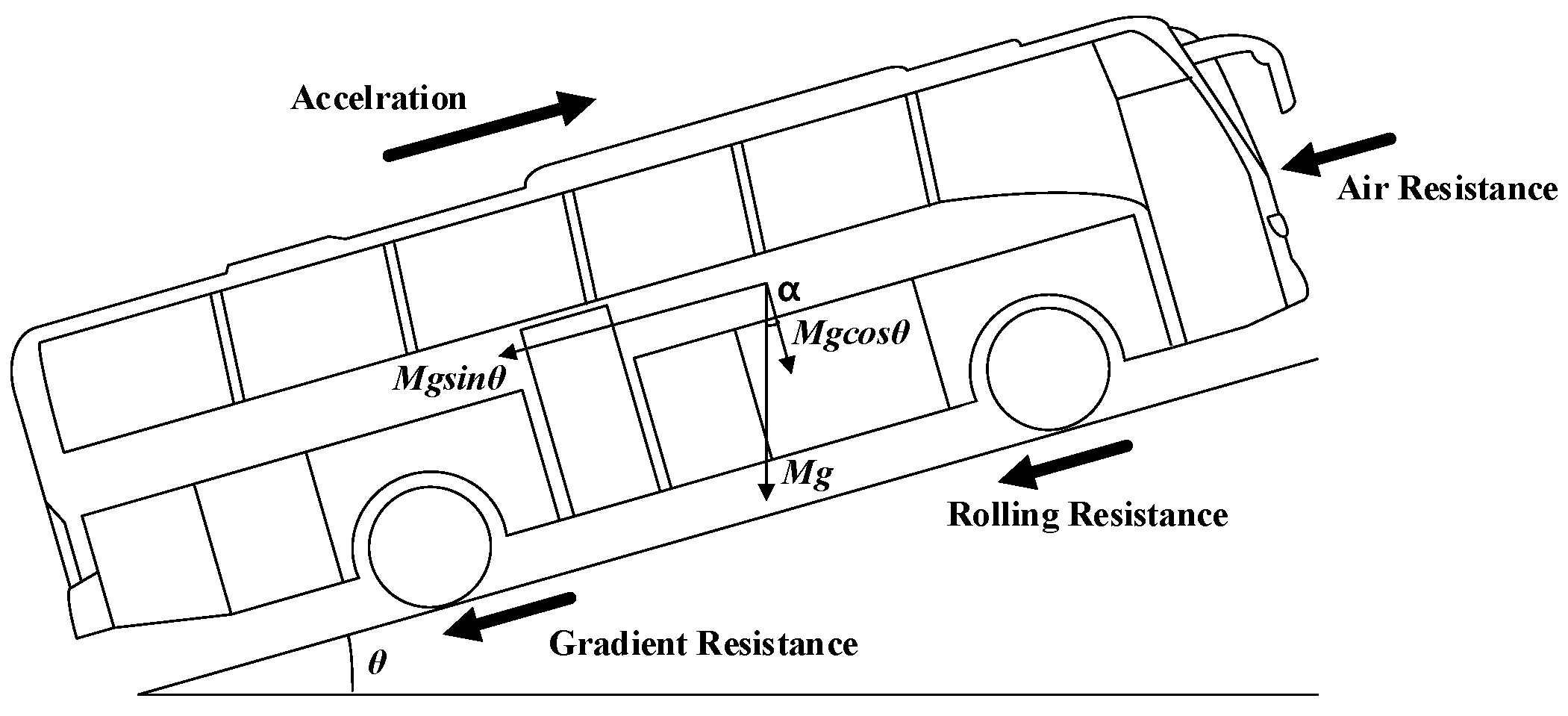
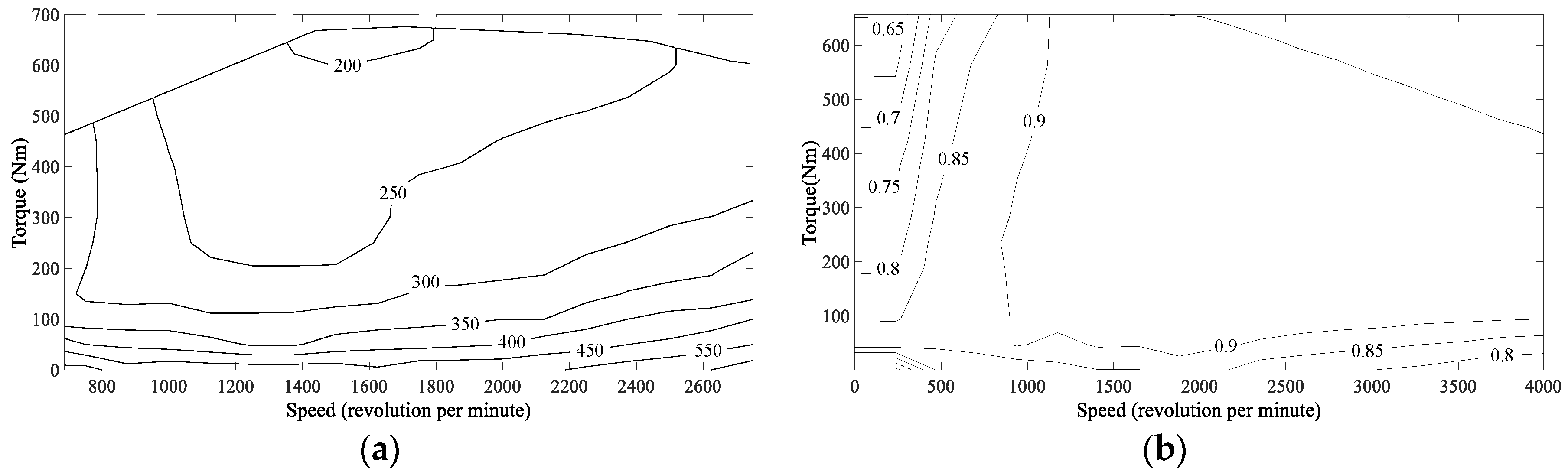
2.1. Powertrain Modeling
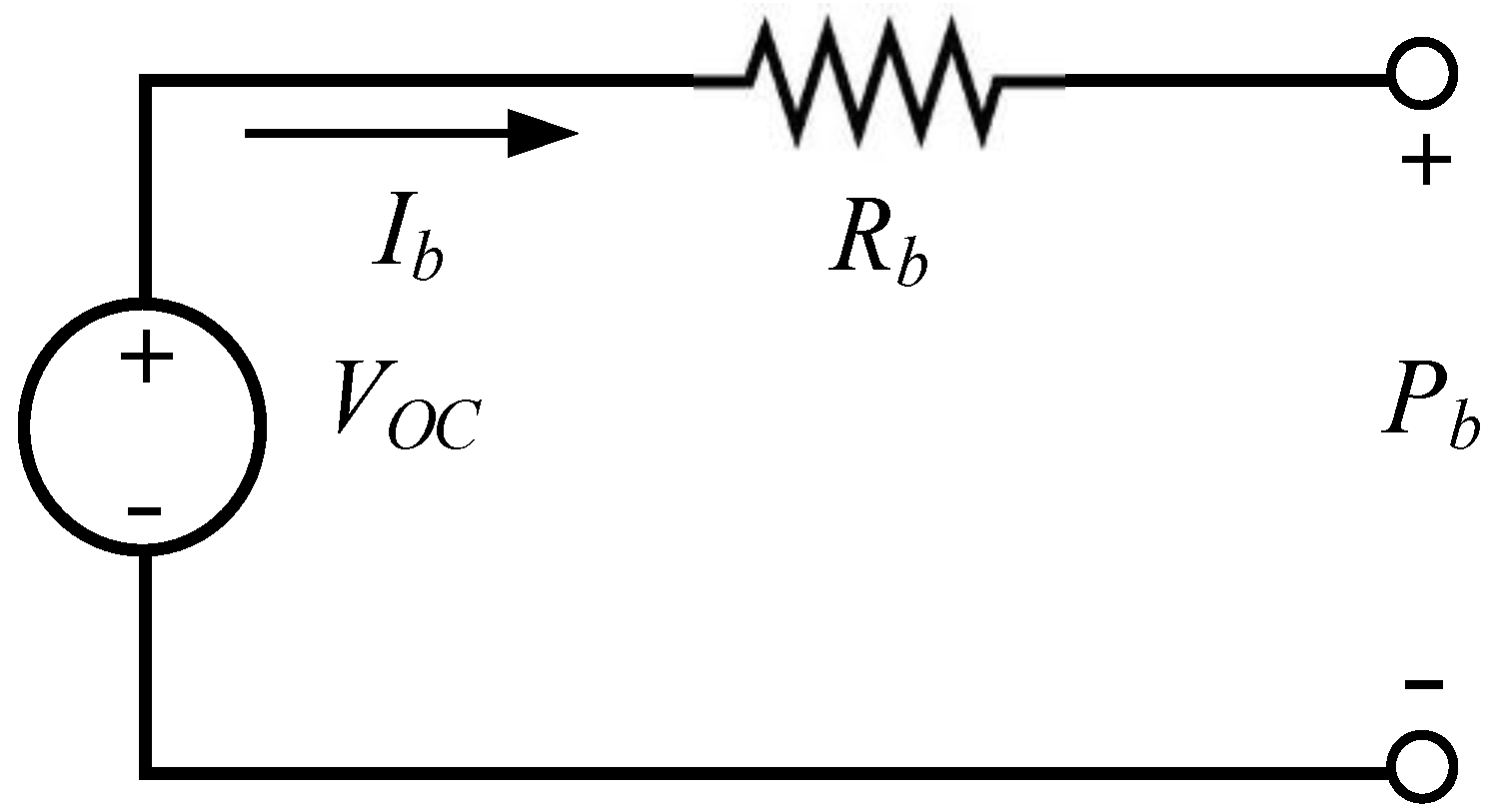
2.2. ESS Modeling
3. Energy Management Strategy
4. Optimization of Efficiency Improvement Factors
4.1. Efficiency Improvement Factors
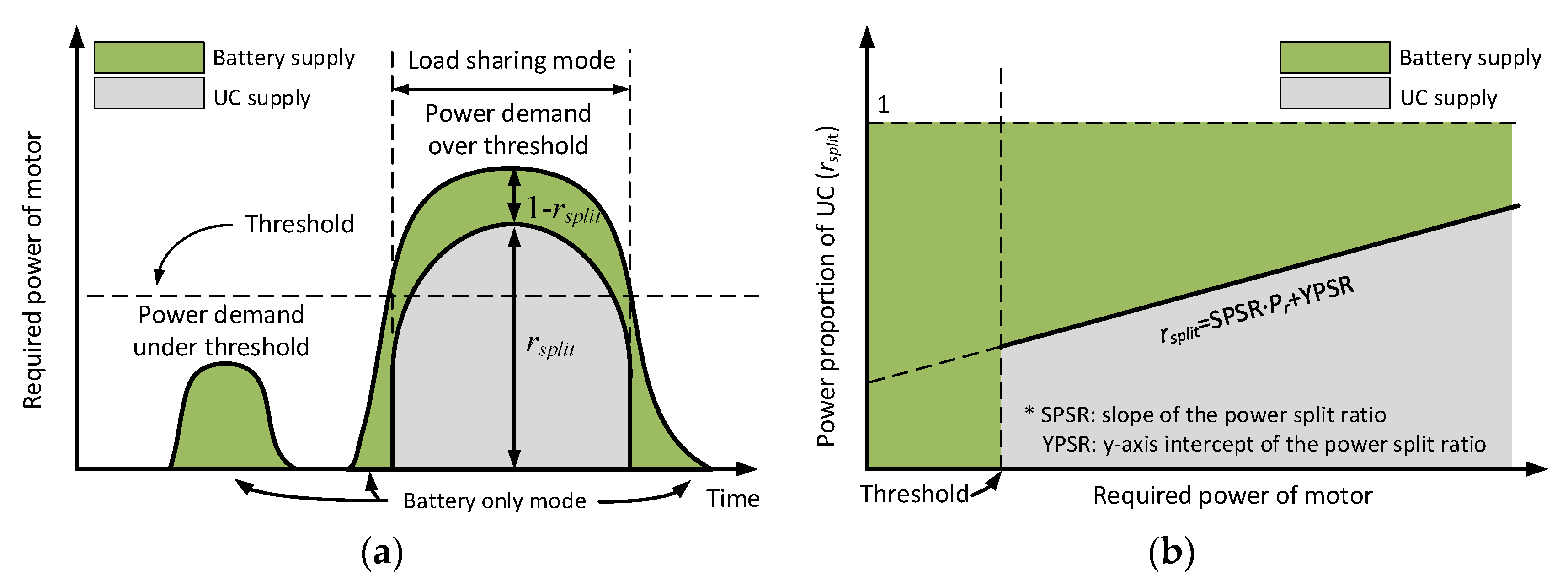
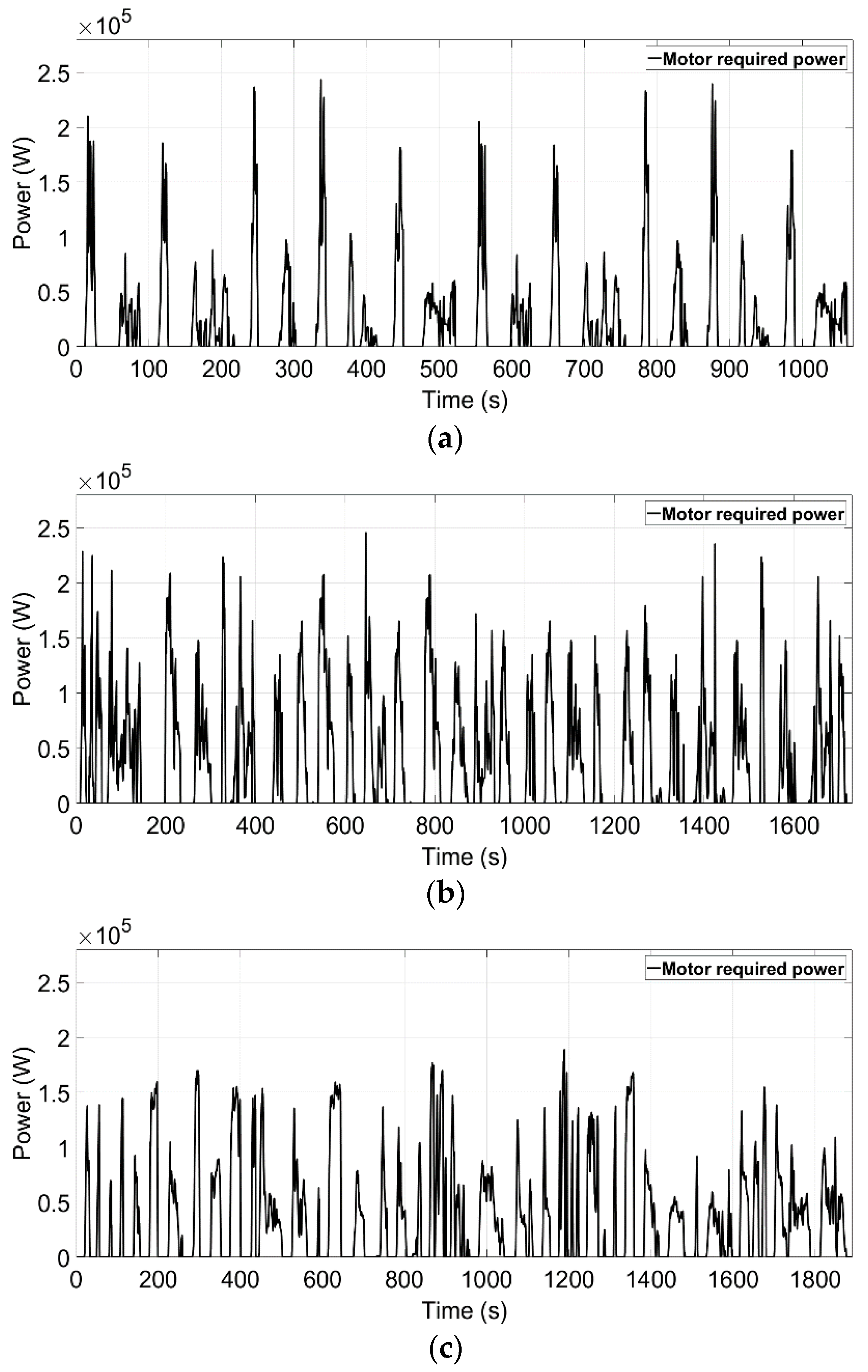
4.1.1. Required Power of the Motor
4.1.2. Power Split Ratio between the ESSs
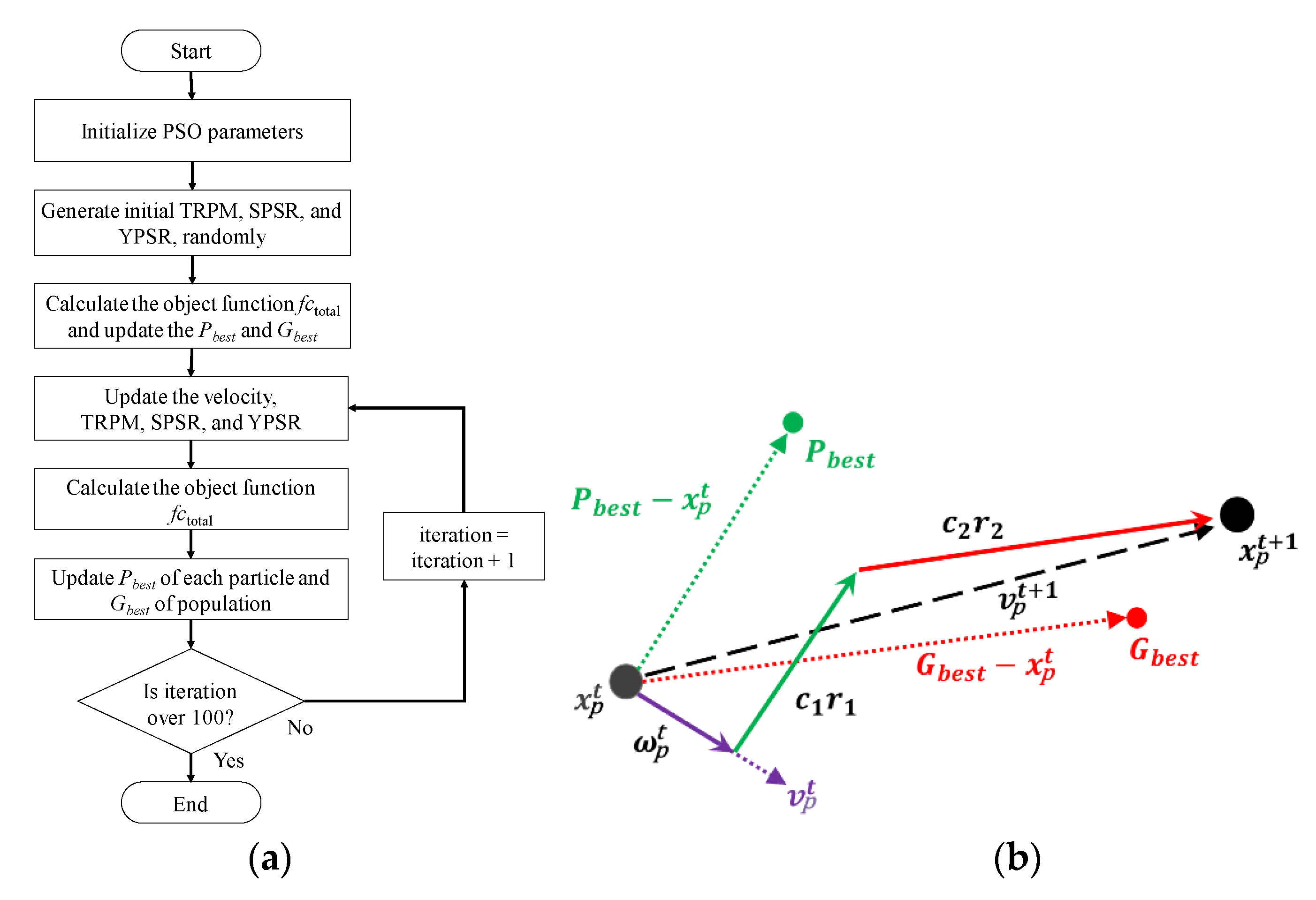
4.2. Particle Swarm Optimization
4.3. Problem Formulation
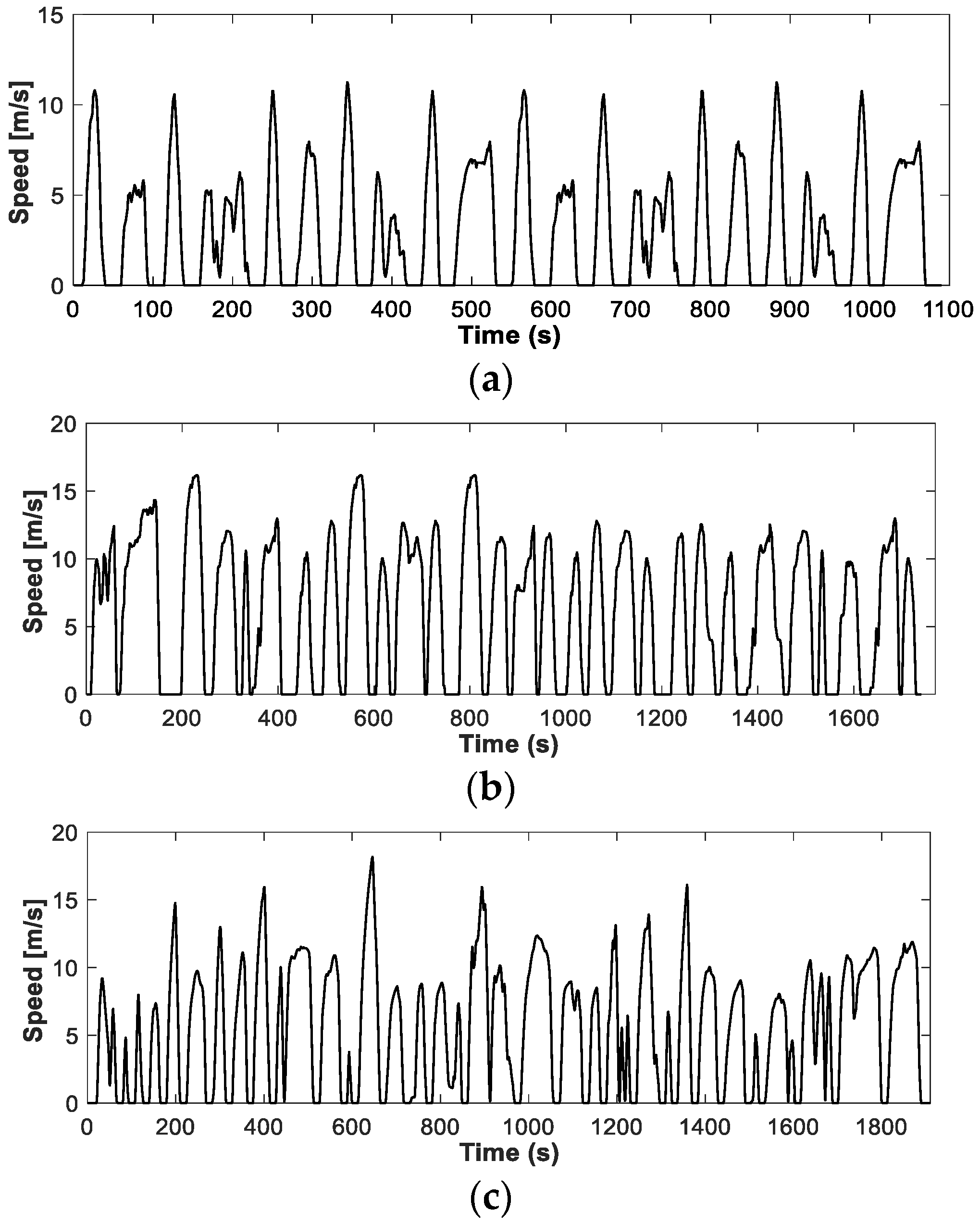
5. Simulation Results and Discussion
5.1. Optimization Results
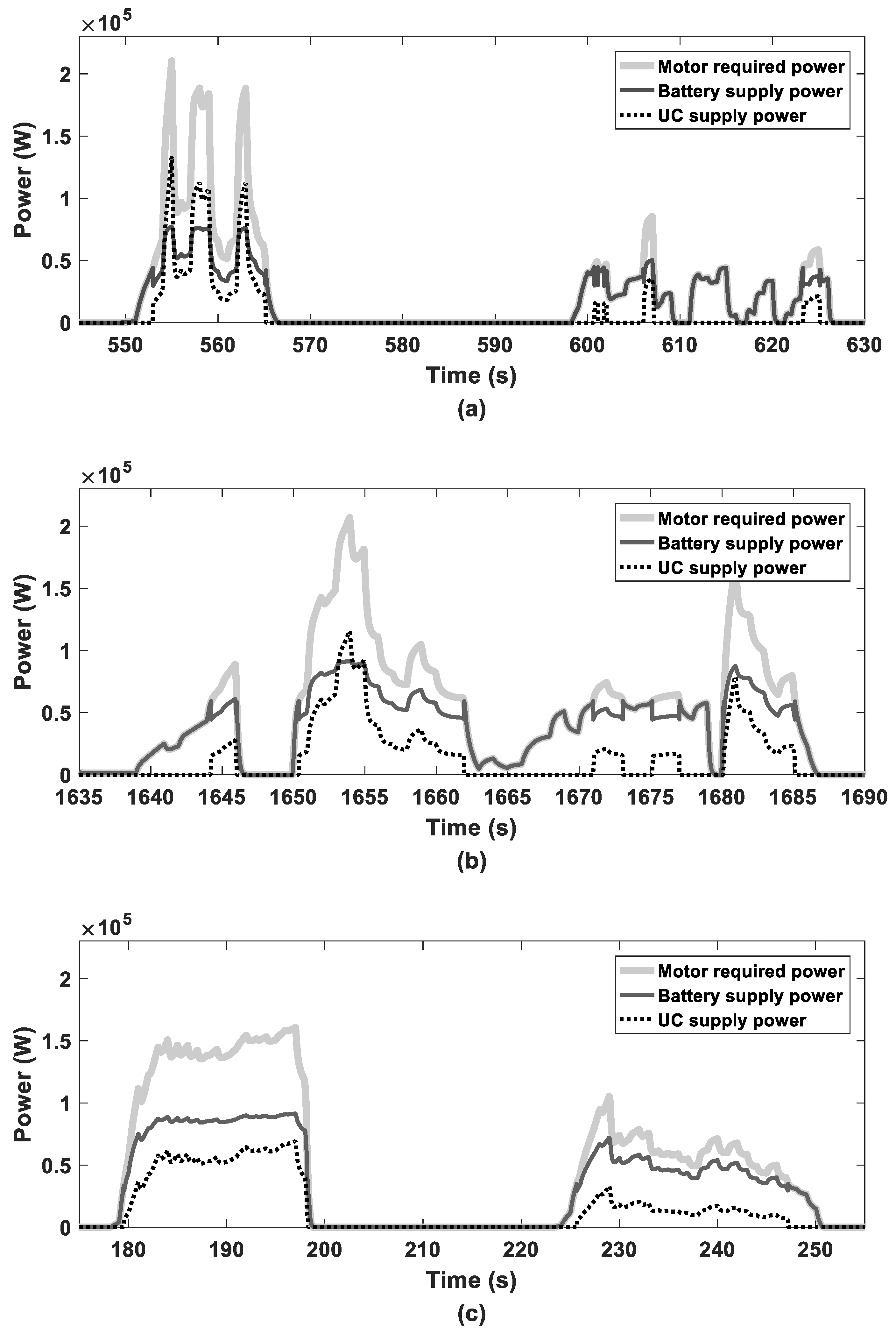
5.2. Power Supply of ESSs
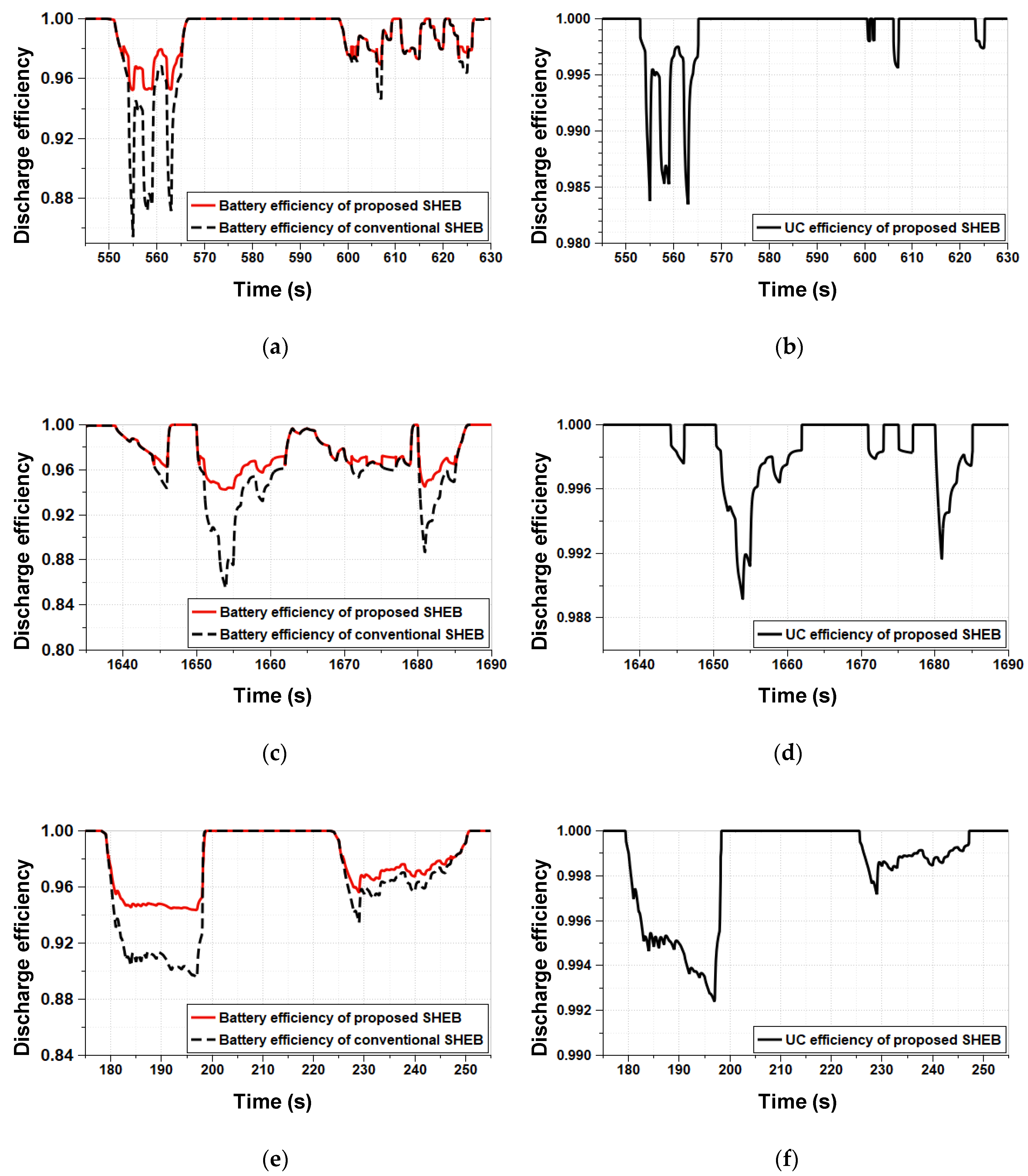
5.3. Battery Efficiency Comparisons
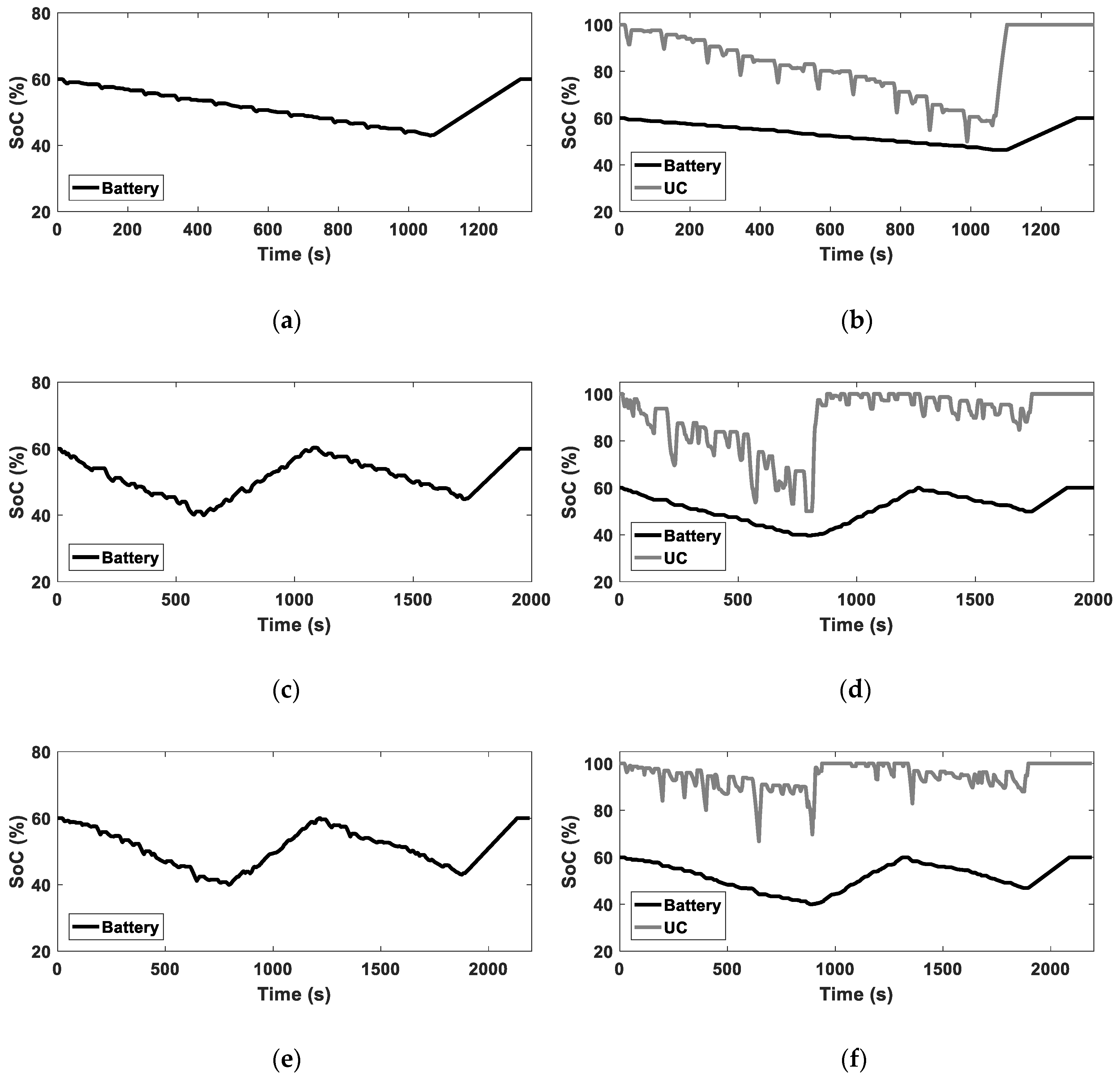
5.4. ESS SOC Comparison
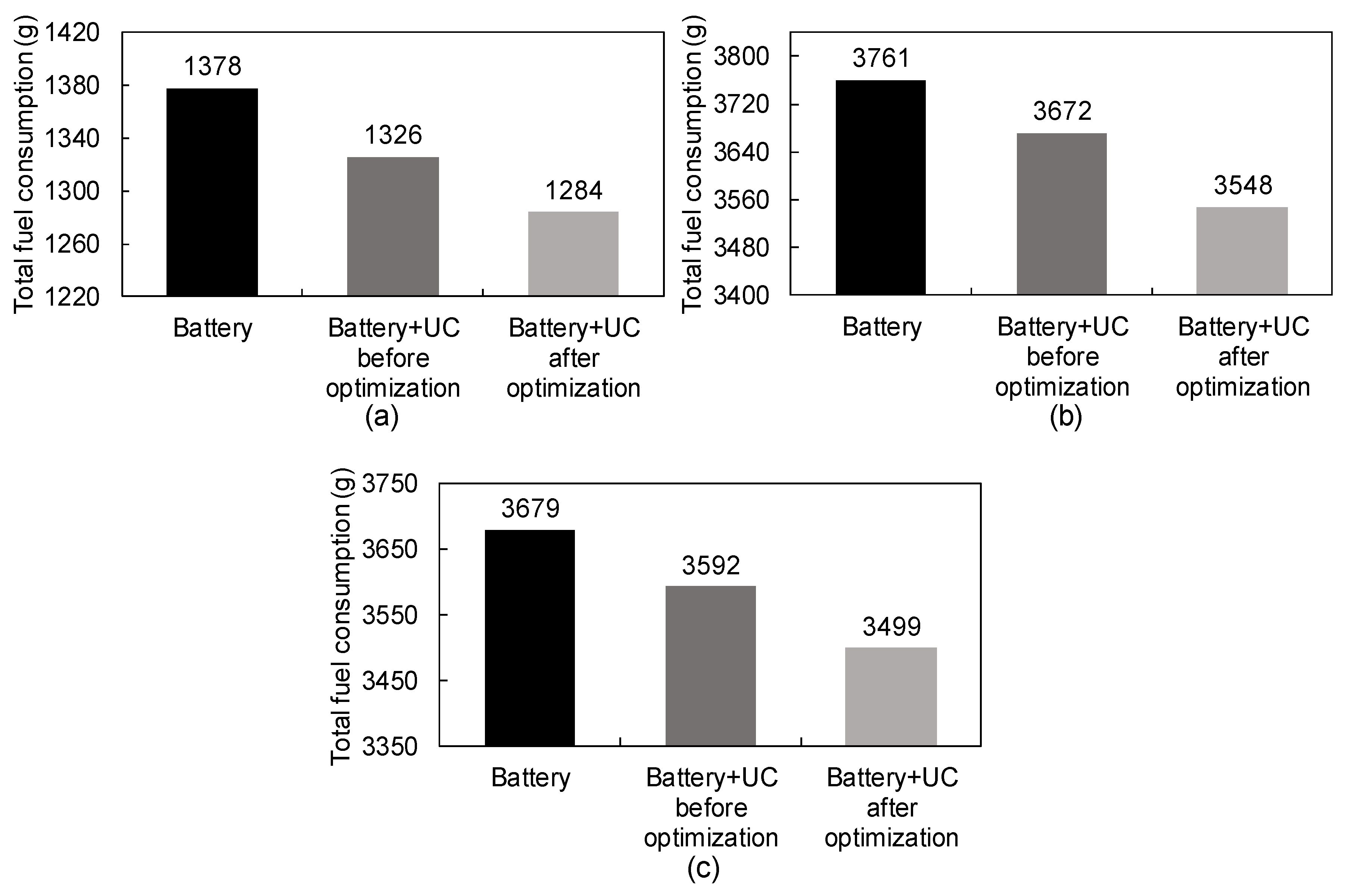
5.5. Comparison of Fuel Efficiency
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sabri, M.; Danapalasingam, K.; Rahmat, M. A review on hybrid electric vehicles architecture and energy management strategies. Renew. Sustain. Energy Rev. 2016, 53, 1433–1442. [Google Scholar] [CrossRef]
- Lukic, S.M.; Wirasingha, S.G.; Rodriguez, F.; Cao, J.; Emadi, A. Power Management of an Ultracapacitor/Battery Hybrid Energy Storage System in an HEV. In Proceedings of the 2006 IEEE Vehicle Power and Propulsion Conference, Windsor, UK, 6–8 September 2006; pp. 1–6. [Google Scholar]
- Li, Y.; Zhang, H.; Liang, X.; Huang, B. Event-triggered-based distributed cooperative energy management for multienergy systems. IEEE Trans. Ind. Inform. 2018, 15, 2008–2022. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, Y.; Sun, H.; Wang, L.; Chow, M.-Y. Distributed Event-Triggered $ H_ {\infty} $ Consensus Based Current Sharing Control of DC Microgrids Considering Uncertainties. IEEE Trans. Ind. Inform. 2019. [Google Scholar] [CrossRef]
- Li, Y.; Gao, D.W.; Gao, W.; Zhang, H.; Zhou, J. Double-Mode Energy Management for Multi-Energy System via Distributed Dynamic Event-Triggered Newton-Raphson Algorithm. IEEE Trans. Smart Grid 2020, 1. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Huang, B.; Han, J. A distributed Newton–Raphson-based coordination algorithm for multi-agent optimization with discrete-time communication. Neural Comput. Appl. 2020, 32, 4649–4663. [Google Scholar] [CrossRef]
- Lee, K. Optimal Power Distribution for Series Hybrid Bus Using Ultracapacitor and Battery; Myongji University: Seoul, Korea, 2018. [Google Scholar]
- Passalacqua, M.; Lanzarotto, D.; Repetto, M.; Vaccaro, L.; Bonfiglio, A.; Marchesoni, M. Fuel economy and energy management system for a series hybrid vehicle based on supercapacitor storage. IEEE Trans. Power Electron. 2019, 34, 9966–9977. [Google Scholar] [CrossRef]
- Schupbach, R.M.; Balda, J.C.; Zolot, M.; Kramer, B. Design methodology of a combined battery-ultracapacitor energy storage unit for vehicle power management. In Proceedings of the IEEE 34th Annual Conference on Power Electronics Specialist, Acapulco, Mexico, 15–19 June 2003; pp. 88–93. [Google Scholar]
- Ostadi, A.; Kazerani, M. A comparative analysis of optimal sizing of battery-only, ultracapacitor-only, and battery–ultracapacitor hybrid energy storage systems for a city bus. IEEE Trans. Veh. Technol. 2014, 64, 4449–4460. [Google Scholar] [CrossRef]
- Wang, G.; Yang, P.; Zhang, J. Fuzzy optimal control and simulation of battery-ultracapacitor dual-energy source storage system for pure electric vehicle. In Proceedings of the 2010 International Conference on Intelligent Control and Information Processing, Dalian, China, 13–15 August 2010; pp. 555–560. [Google Scholar]
- Garcia, F.; Ferreira, A.; Pomilio, J. Control strategy for battery-ultracapacitor hybrid energy storage system. In Proceedings of the 2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 826–832. [Google Scholar]
- Herrera, V.I.; Saez-de-Ibarra, A.; Milo, A.; Gaztañaga, H.; Camblong, H. Optimal energy management of a hybrid electric bus with a battery-supercapacitor storage system using genetic algorithm. In Proceedings of the 2015 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles, Aachen, Germany, 3–5 March 2015; pp. 1–6. [Google Scholar]
- Shen, J.; Khaligh, A. Predictive control of a battery/ultracapacitor hybrid energy storage system in electric vehicles. In 2016 IEEE Transportation Electrification Conference and Expo (ITEC); IEEE: Dearborn, MI, USA, 2016; pp. 1–6. [Google Scholar]
- Shen, J.; Dusmez, S.; Khaligh, A. Optimization of sizing and battery cycle life in battery/ultracapacitor hybrid energy storage systems for electric vehicle applications. IEEE Trans. Ind. Inform. 2014, 10, 2112–2121. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Q.; Zhu, C. Design of Battery and Ultracapacitor Multiple Energy Storage in Hybrid Electric Vehicle. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 1395–1398. [Google Scholar]
- Li, J.-Q.; Sun, F.-C.; Zhang, C.-N.; Li, H.-L. Ultracapacitors parameter matching design and experiment of electric bus. Chin. J. Power Sources 2004, 28, 483–486. [Google Scholar]
- Jeong, J.; Kim, N.; Lim, W.; Park, Y.-I.; Cha, S.W.; Jang, M.E. Optimization of power management among an engine, battery and ultra-capacitor for a series HEV: A dynamic programming application. Int. J. Automot. Technol. 2017, 18, 891–900. [Google Scholar] [CrossRef]
- Zhang, S.; Xiong, R. Adaptive energy management of a plug-in hybrid electric vehicle based on driving pattern recognition and dynamic programming. Appl. Energy 2015, 155, 68–78. [Google Scholar] [CrossRef]
- Buba, A.T.; Lee, L.S. Hybrid Differential Evolution-Particle Swarm Optimization Algorithm for Multiobjective Urban Transit Network Design Problem with Homogeneous Buses. Math. Probl. Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Iliopoulou, C.; Tassopoulos, I.; Kepaptsoglou, K.; Beligiannis, G. Electric transit route network design problem: Model and application. Transp. Res. Rec. 2019, 2673, 264–274. [Google Scholar] [CrossRef]
- Abdelgadir, A.; Alsawalhi, J. Energy management optimization for an extended range electric vehicle. In Proceedings of the 2017 7th International Conference on Modeling, Simulation, and Applied Optimization (ICMSAO), Sharjah, UAE, 4–6 April 2017; pp. 1–5. [Google Scholar]
- Zhang, R.; Tao, J. GA-based fuzzy energy management system for FC/SC-powered HEV considering H 2 consumption and load variation. IEEE Trans. Fuzzy Syst. 2018, 26, 1833–1843. [Google Scholar] [CrossRef]
- Barker, P.P. Ultracapacitors for use in power quality and distributed resource applications. In Proceedings of the Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; pp. 316–320. [Google Scholar]
- Camara, M.B.; Gualous, H.; Gustin, F.; Berthon, A.; Dakyo, B. DC/DC converter design for supercapacitor and battery power management in hybrid vehicle applications—Polynomial control strategy. IEEE Trans. Ind. Electron. 2010, 57, 587–597. [Google Scholar] [CrossRef]
- Amjadi, Z.; Williamson, S.S. Prototype design and controller implementation for a battery-ultracapacitor hybrid electric vehicle energy storage system. IEEE Trans. Smart Grid 2012, 3, 332–340. [Google Scholar] [CrossRef]
- Kim, M.; Jung, D.; Min, K. Hybrid thermostat strategy for enhancing fuel economy of series hybrid intracity bus. IEEE Trans. Veh. Technol. 2014, 63, 3569–3579. [Google Scholar] [CrossRef]
- Gao, J.; Zhu, G.G.; Strangas, E.G.; Sun, F. Equivalent fuel consumption optimal control of a series hybrid electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2009, 223, 1003–1018. [Google Scholar] [CrossRef]
- Ehsani, M.; Gao, Y.; Emadi, A. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles: Fundamentals, Theory, and Design; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Fajri, P.; Ahmadi, R.; Ferdowsi, M. Equivalent vehicle rotational inertia used for electric vehicle test bench dynamic studies. In Proceedings of the IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 4115–4120. [Google Scholar]
- Kugelstadt, T. “Active Filter Design Techniques” in Op Amps for Everyone: Design Reference; Newnes: Boston, MA, USA, 2008; pp. 271–281. [Google Scholar]
- Mahadik, Y.; Vadirajacharya, K. Battery Life Enhancement in a Hybrid Electrical Energy Storage System Using a Multi-Source Inverter. World Electr. Veh. J. 2019, 10, 17. [Google Scholar] [CrossRef]
- Baisden, A.C.; Emadi, A. ADVISOR-based model of a battery and an ultra-capacitor energy source for hybrid electric vehicles. IEEE Trans. Veh. Technol. 2004, 53, 199–205. [Google Scholar] [CrossRef]
- Sun, D.; Lan, F.; Chen, J. Energy management strategy research and performance simulation for electric vehicles based on dual-energy storage system. In Proceedings of the 2013 6th International Conference on Information Management, Innovation Management and Industrial Engineering, Xi’an, China, 23–24 November 2013; pp. 442–445. [Google Scholar]
- Shi, L.; Crow, M. Comparison of ultracapacitor electric circuit models. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–6. [Google Scholar]
- Paladini, V.; Donateo, T.; De Risi, A.; Laforgia, D. Super-capacitors fuel-cell hybrid electric vehicle optimization and control strategy development. Energy Convers. Manag. 2007, 48, 3001–3008. [Google Scholar] [CrossRef]
- Jalil, N.; Kheir, N.A.; Salman, M. A rule-based energy management strategy for a series hybrid vehicle. In Proceedings of the 1997 American Control Conference (Cat. No. 97CH36041), Albuquerque, NM, USA, 6 June 1997; pp. 689–693. [Google Scholar]
- Elsied, M.; Oukaour, A.; Chaoui, H.; Gualous, H.; Hassan, R.; Amin, A. Real-time implementation of four-phase interleaved DC–DC boost converter for electric vehicle power system. Electr. Power Syst. Res. 2016, 141, 210–220. [Google Scholar] [CrossRef]
- Liu, W. Hybrid Electric Vehicle System Modeling and Control; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Song, Z.; Li, J.; Han, X.; Xu, L.; Lu, L.; Ouyang, M.; Hofmann, H. Multi-objective optimization of a semi-active battery/supercapacitor energy storage system for electric vehicles. Appl. Energy 2014, 135, 212–224. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhao, K.; Liu, Z. Energy management strategy research on a hybrid power system by hardware-in-loop experiments. Appl. Energy 2013, 112, 1311–1317. [Google Scholar] [CrossRef]
- Xie, S.; Hu, X.; Lang, K.; Qi, S.; Liu, T. Powering mode-integrated energy management strategy for a plug-in hybrid electric truck with an automatic mechanical transmission based on pontryagin’s minimum principle. Sustainability 2018, 10, 3758. [Google Scholar] [CrossRef]
- Zeng, Y.; Cai, Y.; Kou, G.; Gao, W.; Qin, D. Energy management for plug-in hybrid electric vehicle based on adaptive simplified-ECMS. Sustainability 2018, 10, 2060. [Google Scholar] [CrossRef]
- Rydh, C.J.; Sandén, B.A. Energy analysis of batteries in photovoltaic systems. Part II: Energy return factors and overall battery efficiencies. Energy Convers. Manag. 2005, 46, 1980–2000. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Bai, Q. Analysis of particle swarm optimization algorithm. Comput. Inf. Sci. 2010, 3, 180. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Piscataway, NJ, USA, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Chen, S.-Y.; Wu, C.-H.; Hung, Y.-H.; Chung, C.-T. Optimal strategies of energy management integrated with transmission control for a hybrid electric vehicle using dynamic particle swarm optimization. Energy 2018, 160, 154–170. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Cao, J. Particle swarm optimization-based optimal power management of plug-in hybrid electric vehicles considering uncertain driving conditions. Energy 2016, 96, 197–208. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE international conference on evolutionary computation proceedings. IEEE world congress on computational intelligence (Cat. No. 98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 congress on evolutionary computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; pp. 1945–1950. [Google Scholar]
- Zheng, Y.-L.; Ma, L.-H.; Zhang, L.-Y.; Qian, J.-X. On the convergence analysis and parameter selection in particle swarm optimization. In Proceedings of the 2003 International Conference on Machine Learning and Cybernetics (IEEE Cat. No. 03EX693), Xi’an, China, 5 November 2003; pp. 1802–1807. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Parameter selection in particle swarm optimization. In International Conference on Evolutionary Programming; Springer: Berlin/Heidelberg, Germany, 1998; pp. 591–600. [Google Scholar]
- Li-Ping, Z.; Huan-Jun, Y.; Shang-Xu, H. Optimal choice of parameters for particle swarm optimization. J. Zhejiang Univ. Sci. A 2005, 6, 528–534. [Google Scholar] [CrossRef]
- M’hamdi, B.; Teguar, M.; Mekhaldi, A. Optimal design of corona ring on HV composite insulator using PSO approach with dynamic population size. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1048–1057. [Google Scholar] [CrossRef]
- Xin, J.; Chen, G.; Hai, Y. A particle swarm optimizer with multi-stage linearly-decreasing inertia weight. In Proceedings of the 2009 International Joint Conference on Computational Sciences and Optimization, Sanya, Hainan, China, 24–26 April 2009; pp. 505–508. [Google Scholar]
- Kim, M. Engine torque command handling for a series hybrid electric bus. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 638–652. [Google Scholar] [CrossRef]


| Parameters | Values |
|---|---|
| Weight (ton) | 16 |
| Air Drag Coefficient | 0.6 |
| Air Density (kg/m3) | 1.226 |
| Front Area (m2) | 6.6 |
| Gravitational acceleration (m/s2) | 9.81 |
| Maximum Motor Power (kW) | 240 |
| Maximum Generator Power (kW) | 200 |
| Maximum Engine Power (kW) | 180 |
| Battery Type | Li-ion |
| Battery Internal Resistance (ohm) | 0.17 @ SOC 0.5 |
| Ultra-capacitor (ohm) | 0.022 |
| Parameters | Value |
|---|---|
| Particle number | 10 |
| Maximum iterations | 100 |
| Inertia weight coefficient () | 1 |
| Weight damped coefficient () | 0.4 |
| Cognitive acceleration coefficient (c1) | 1 |
| Social acceleration coefficient (c2) | 1 |
| Random numbers (r1, r2) | [0, 1] |
| Driving cycles | TRPM (kW) | SPSR | YPSR | Total Fuel Consumption (g) |
|---|---|---|---|---|
| Manhattan cycle (initial condition of PSO) | 151.1 | 2.747 × 10−3 | 0.2377 | 1326 |
| Braunschweig cycle (initial condition of PSO) | 139.2 | 2.575 × 10−3 | 0.2592 | 3672 |
| Orange County cycle (initial condition of PSO) | 148.2 | 1.845 × 10−3 | 0.1851 | 3592 |
| Manhattan cycle (result of PSO) | 44.49 | 1.795 × 10−3 | 0.2575 | 1284 |
| Braunschweig cycle (result of PSO) | 59.31 | 2.081 × 10−3 | 0.1284 | 3548 |
| Orange County cycle (result of PSO) | 35.26 | 2.095 × 10−3 | 0.0941 | 3499 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, G.; Lee, K.; Kim, J.; Lee, K.-J.; Lee, S.; Kim, M. Energy Management Optimization of Series Hybrid Electric Bus Using an Ultra-Capacitor and Novel Efficiency Improvement Factors. Sustainability 2020, 12, 7354. https://doi.org/10.3390/su12187354
Hwang G, Lee K, Kim J, Lee K-J, Lee S, Kim M. Energy Management Optimization of Series Hybrid Electric Bus Using an Ultra-Capacitor and Novel Efficiency Improvement Factors. Sustainability. 2020; 12(18):7354. https://doi.org/10.3390/su12187354
Chicago/Turabian StyleHwang, Giyeon, Kyungmin Lee, Jongmyung Kim, Kyu-Jin Lee, Sangyul Lee, and Minjae Kim. 2020. "Energy Management Optimization of Series Hybrid Electric Bus Using an Ultra-Capacitor and Novel Efficiency Improvement Factors" Sustainability 12, no. 18: 7354. https://doi.org/10.3390/su12187354
APA StyleHwang, G., Lee, K., Kim, J., Lee, K.-J., Lee, S., & Kim, M. (2020). Energy Management Optimization of Series Hybrid Electric Bus Using an Ultra-Capacitor and Novel Efficiency Improvement Factors. Sustainability, 12(18), 7354. https://doi.org/10.3390/su12187354





