Maximizing Total Profit of Thermal Generation Units in Competitive Electric Market by Using a Proposed Particle Swarm Optimization
Abstract
:1. Introduction
- (1)
- Propose the effective NCHM for handling constraints.
- (2)
- Propose the high performance PPSO.
- (3)
- Consider valve effects on thermal generation units for the considered problem.
- (1)
- PPSO method has few control parameters, population and the number of iterations. Therefore, the setting of the two parameters is simple.
- (2)
- The process of evaluating solution quality is easily and simply performed by calculating fitness function.
- (1)
- Reach very high success rate with 100%: Implemented methods using NCHM always reaches all successful runs but the same implemented methods without using NCHM must suffer much lower than 100% for success rate.
- (2)
- Converge to high quality solutions: NCHM supports implemented methods to find global optimum solutions with fast speed and reach high stability.
- (3)
- PPSO method always reaches better results than other PSO, SSA, MDE and previous methods.
- (4)
- PPSO method is faster than approximately all other methods for study cases.
- (1)
- The most appropriate values for the population and the number of iterations are not easy to select. In fact, higher values can result in better results but simulation time is still increased correspondingly. If high values are set, all methods have the same best solution and the evaluation is not exactly performed. In this case, real performance of PPSO method cannot be shown.
- (2)
- The procedure of applying PPSO method is a long iterative algorithm. Therefore, the implementation procedure must be careful and verification procedure must be serious.
2. Problem Formulation
2.1. Objective Function
2.2. The Consisdered Constraints
3. Applied PSO Methods
3.1. CF-PSO and IW-PSO
3.2. TVIW-PSO and TVAC-PSO
3.3. PG-PSO
3.4. The Proposed PSO Method
4. Implementation of PPSO Method for the Considered Problem
4.1. The New Constriaint Handling Method for Reseve Power
4.2. Main Steps of the Proposed Method for the Implementation
4.2.1. Selection of Control Variables and Population Initialization
4.2.2. Calculation of Dependent Variables
4.2.3. Correction for Produced Control Variables
4.2.4. Handling Violation of Power Demand and Reserve Demand
4.2.5. Handling Violation of the First Thermal Generating Unit
4.2.6. Fitness Function
4.3. Establishing Limits of Velocity and Producing Initial Velocity
4.4. Termination Criterion for Iterative Algorithm
4.5. The Entire Search Process of PPSO for the Considered Problem
5. Numerical Results
- Test system 1: Three units with convex fuel cost function shown in Equation (1)
- Test system 2: Ten units with convex fuel cost function shown in Equation (1)
- Test system 3: Twenty units with nonconvex fuel cost shown in Equation (2)
- Case 1: Total revenue and total fuel cost are obtained by using Equations (5) and (6)
- Case 2: Total revenue and total fuel cost are obtained by using Equations (7) and (8)
- (1)
- Nop = 5 and Gmax = 5 for test system 1
- (2)
- Nop = 20 and Gmax = 100 for test system 2
- (3)
- Nop = 30 and Gmax = 500 for test systems 3
5.1. The Impact of the Proposed NCHM on Results
- (1)
- Methods using NCHM can reach the highest SR with 100% but SR of the methods without using NCHM is much lower, only from 83.3% to 92.5%.
- (2)
- NCHM can support methods to find the global optimum solutions, high search stability and low possibility to low quality solutions.
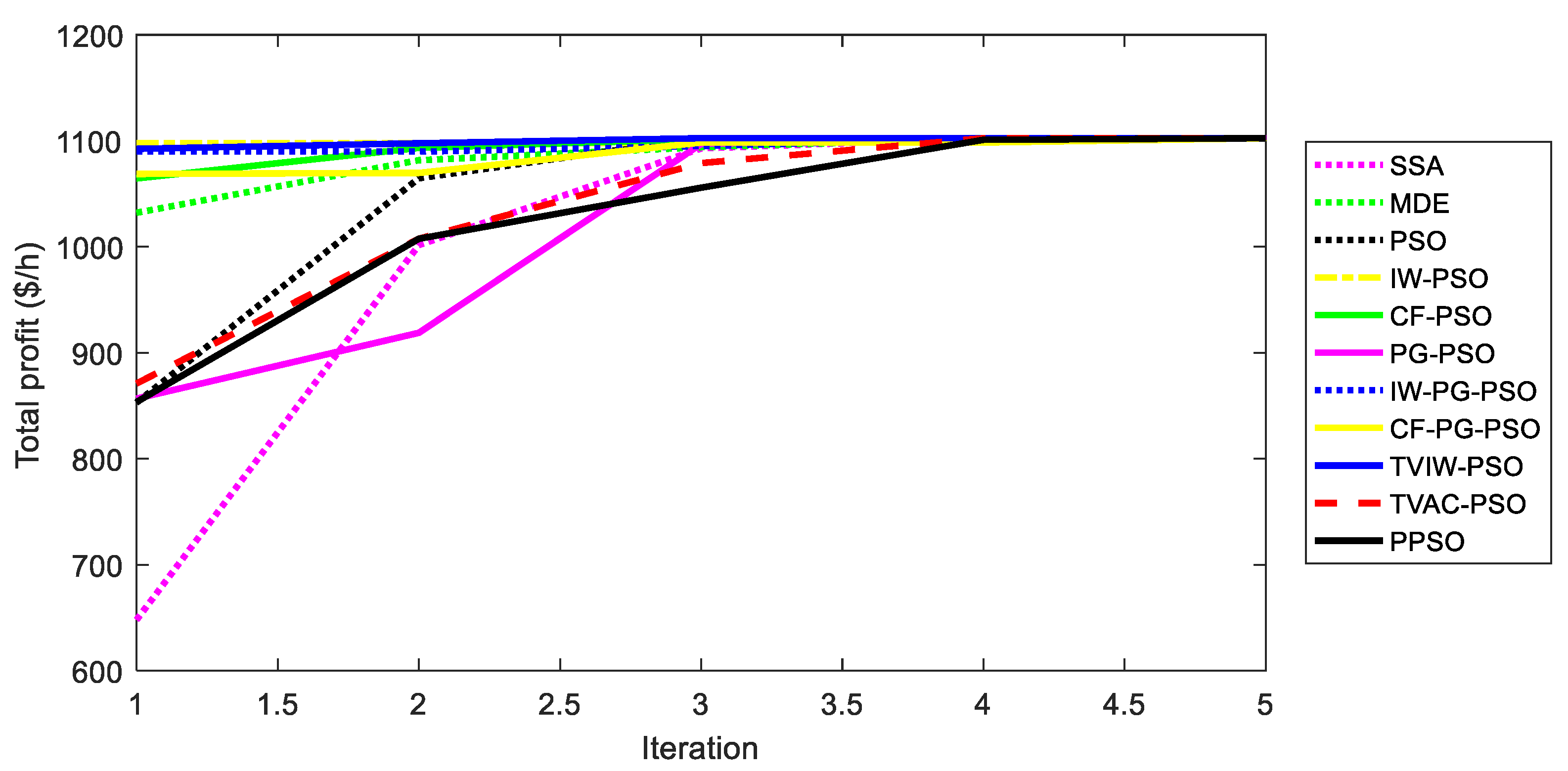
5.2. Comparison for Test System 1
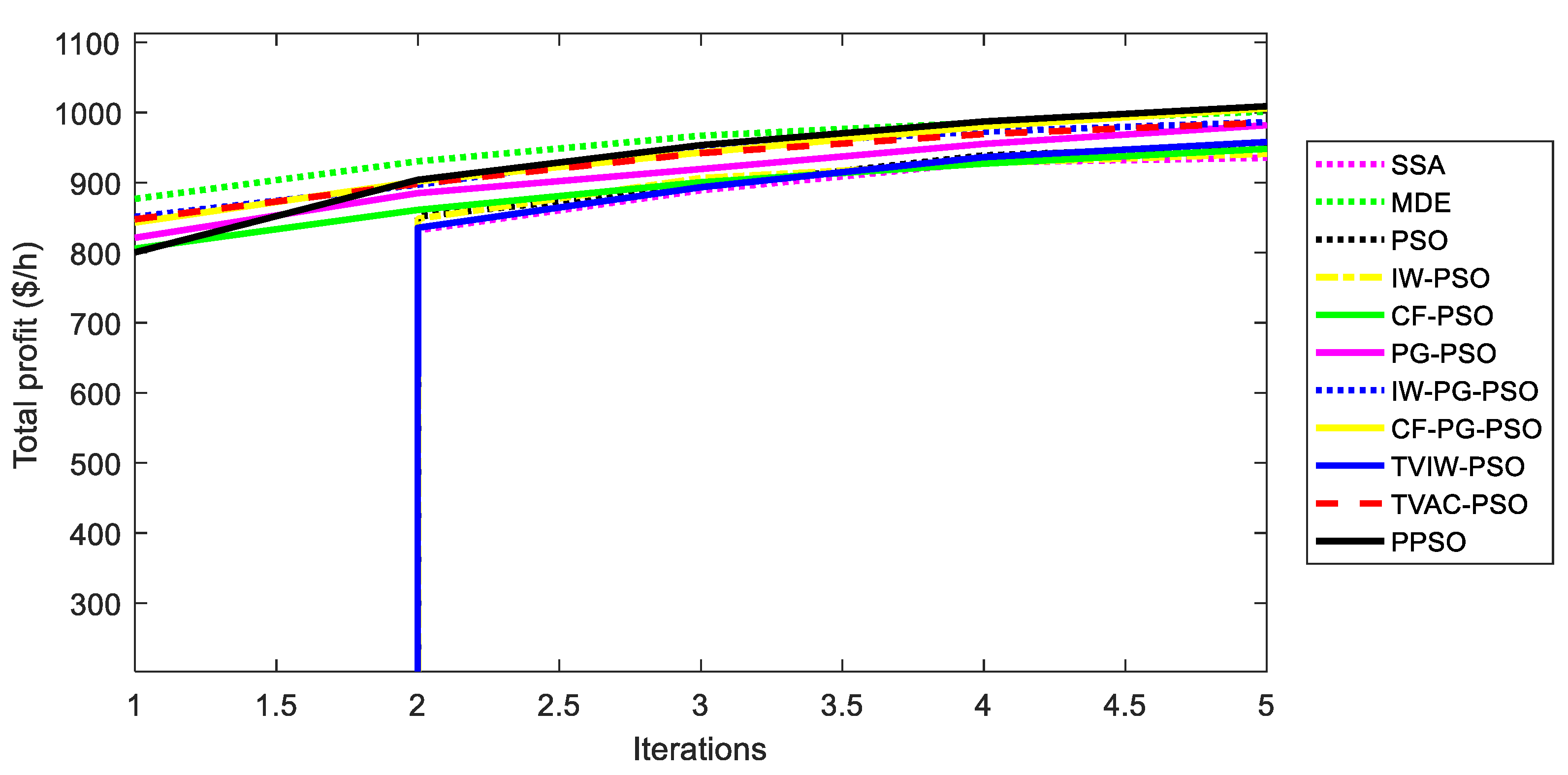
5.3. Comparison for Test System 2
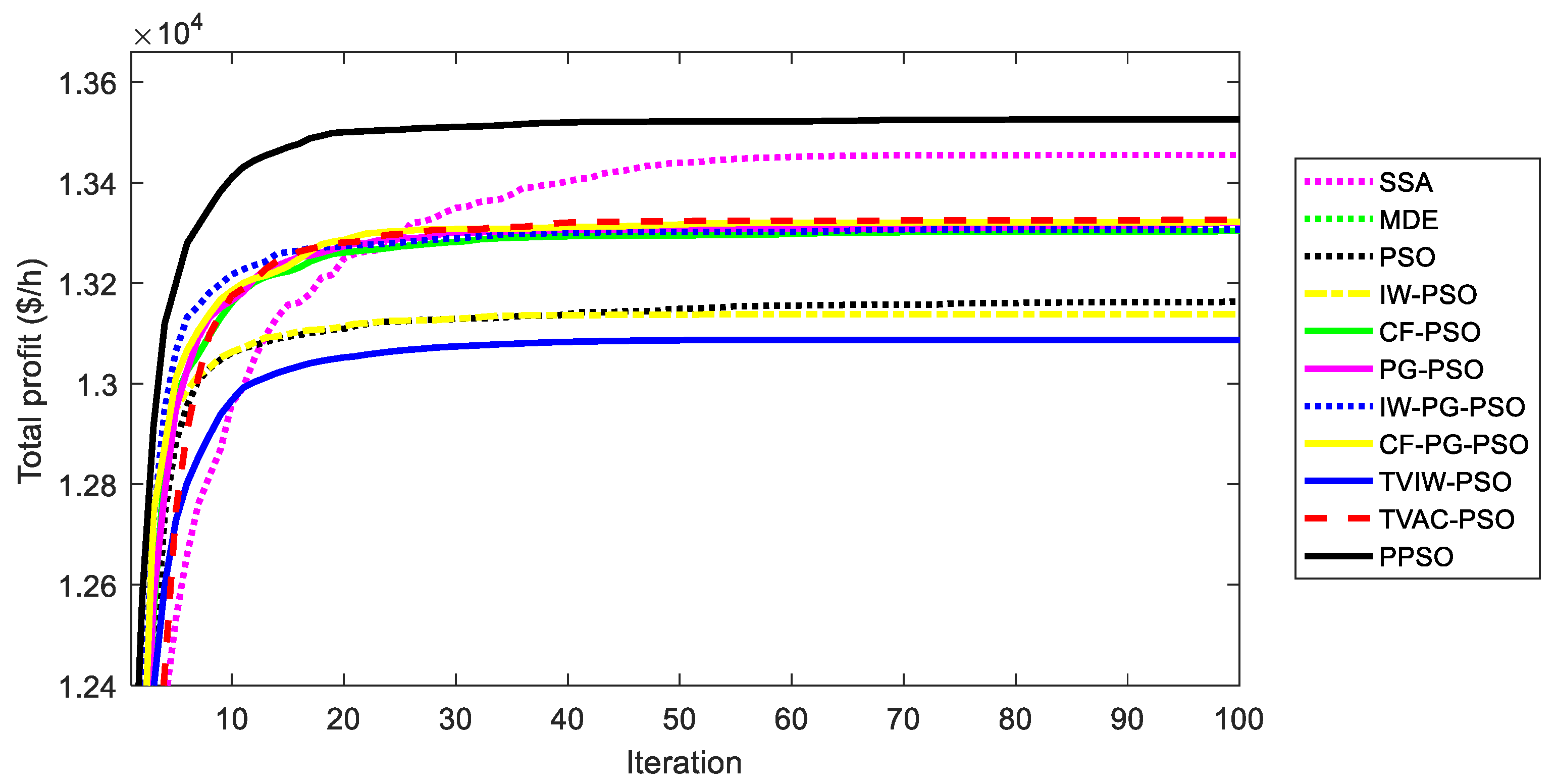
5.4. Comparison for Test System 3
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| IW-PG-PSO | Inertia weight factor and pseudo gradient -based particle swarm optimization |
| CF-PG-PSO | Constriction factor and Pseudo gradient-based particle swarm optimization |
| TVIW-PSO | Time varying inertia weight factor-based particle swarm optimization |
| LF-HLN-EF | Lagrange function-based Hopfield neuron network method with Error function |
| LF-HLN-THF | Lagrange function-based Hopfield neuron network method with hyperbolic tangent function |
| LF-HLN-GdF | Lagrange function-based Hopfield neuron network method with Gudermanian function |
| LF-HLN-GF | Lagrange function-based Hopfield neuron network method with Gompertz function |
| LF-HLN-LF | Lagrange function-based Hopfield neuron network method with Logistic function |
Nomenclature
| Known coefficients of fuel cost function of the nth unit | |
| c1, c2 | Acceleration constants |
| D | Forecasted power demand |
| ΔDp | Penalty term for the violation of power demand corresponding to the pth solution |
| ΔRDp | Penalty term for the violation of reserve demand corresponding to the pth solution |
| ΔPG1,p | Penalty term for the violation of power generation of the first thermal generation unit corresponding to the pth solution |
| ΔRG1,p | Penalty term for the violation of reserve of the first thermal generation unit corresponding to the pth solution |
| ε1, ε2, ε3 | Random numbers generated in range of [0,1] |
| Fp | Fitness function of old position Pop |
| Fitness function of new position | |
| Fn | Fuel cost function of the nth thermal generation unit as producing power only |
| Fuel cost function of the nth thermal generation unit as producing power and reserve | |
| G | Current iteration |
| Gmax | Maximum iteration |
| LBn | Lower bound of generation of the nth thermal generating unit |
| N | Number of thermal generating units |
| n | Unit index |
| Nop | Population size |
| New position and new velocity of the pth particle | |
| The previous position of old position | |
| PGn | Power generation of the nth thermal generating unit |
| PG1 | Power generation of the first thermal generation unit |
| Pobest,p | The so-far best position of the pth particle |
| PoGbest | The so-far best position of all particles |
| RD | Forecasted reserve power demand |
| RGn | Reserve generation of the nth thermal generating unit |
| RG1 | Reserve of the first thermal generation unit |
| TC | Total cost |
| TP | Total profit |
| TR | Total revenue |
| UBn | Upper bound of generation of the nth thermal generating unit |
| VeLB, VeUB | Lower bound and upper bound of velocity |
| Vep, Pop | Old velocity and position of the pth particle |
| ω | Inertia weigh factor |
| ωmin, ωmax | Minimum and maximum value of inertia weigh factor |
Appendix A
| n | (MW) | (MW) | |||
|---|---|---|---|---|---|
| 1 | 0.002 | 10 | 500 | 100 | 600 |
| 2 | 0.0025 | 8 | 300 | 100 | 400 |
| 3 | 0.005 | 6 | 100 | 50 | 200 |
| n | (MW) | (MW) | |||
|---|---|---|---|---|---|
| 1 | 0.0004800 | 16.19 | 1000 | 150 | 455 |
| 2 | 0.0003100 | 17.26 | 970 | 150 | 455 |
| 3 | 0.00200 | 16.60 | 700 | 20 | 130 |
| 4 | 0.0021100 | 16.50 | 680 | 20 | 130 |
| 5 | 0.0039800 | 19.70 | 450 | 25 | 162 |
| 6 | 0.0071200 | 22.26 | 370 | 20 | 80 |
| 7 | 0.0007900 | 27.74 | 480 | 25 | 85 |
| 8 | 0.0041300 | 25.92 | 660 | 10 | 55 |
| 9 | 0.0022200 | 27.27 | 665 | 10 | 55 |
| 10 | 0.0017300 | 27.79 | 670 | 10 | 55 |
| n | (MW) | (MW) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 1000 | 18.19 | 0.00068 | 100 | 0.0840 | 150 | 600 |
| 2 | 970 | 19.26 | 0.00071 | 100 | 0.0840 | 50 | 200 |
| 3 | 600 | 19.8 | 0.00650 | 150 | 0.0630 | 50 | 200 |
| 4 | 700 | 19.1 | 0.00500 | 120 | 0.0770 | 50 | 200 |
| 5 | 420 | 18.1 | 0.00738 | 100 | 0.0840 | 50 | 160 |
| 6 | 360 | 19.26 | 0.00612 | 0 | 0 | 20 | 100 |
| 7 | 490 | 17.14 | 0.00790 | 0 | 0 | 25 | 125 |
| 8 | 660 | 18.92 | 0.00813 | 0 | 0 | 50 | 150 |
| 9 | 765 | 18.27 | 0.00522 | 0 | 0 | 50 | 200 |
| 10 | 770 | 18.92 | 0.00573 | 0 | 0 | 30 | 150 |
| 11 | 800 | 16.69 | 0.00480 | 0 | 0 | 100 | 300 |
| 12 | 970 | 16.76 | 0.00310 | 0 | 0 | 150 | 500 |
| 13 | 900 | 17.36 | 0.00850 | 0 | 0 | 40 | 160 |
| 14 | 700 | 18.7 | 0.00511 | 0 | 0 | 20 | 130 |
| 15 | 450 | 18.7 | 0.00398 | 0 | 0 | 25 | 185 |
| 16 | 370 | 14.26 | 0.07120 | 0 | 0 | 20 | 80 |
| 17 | 480 | 19.14 | 0.00890 | 0 | 0 | 30 | 85 |
| 18 | 680 | 18.92 | 0.00713 | 0 | 0 | 30 | 120 |
| 19 | 700 | 18.47 | 0.00622 | 0 | 0 | 40 | 120 |
| 20 | 850 | 19.79 | 0.00773 | 0 | 0 | 30 | 100 |
| Parameters | System 1 | System 2 | System 3 | |||
|---|---|---|---|---|---|---|
| D (MW) | 1100 | 1100 | 1500 | 1500 | 2500 | 2500 |
| RD (MW) | 100 | 100 | 150 | 150 | 300 | 300 |
| PriceDP ($/MWh) | 11.3 | 11.3 | 31.65 | 31.65 | 31.6 | 30 |
| PriceRP ($/MWh) | 33.9 | 0.0452 | 158.25 | 0.3165 | 158.25 | 0.12 |
| r | 0.005 | 0.005 | 0.05 | 0.005 | 0.05 | 0.005 |
| n | Case 1 | Case 2 | ||
|---|---|---|---|---|
| PGn (MW) | RGn (MW) | PGn (MW) | RGn (MW) | |
| 1 | 324.5042 | 100 | 324.5076 | 100 |
| 2 | 400 | 0 | 400 | 0 |
| 3 | 200 | 0 | 200 | 0 |
| n | Case 1 | Case 2 | ||
|---|---|---|---|---|
| PGn (MW) | RGn (MW) | PGn (MW) | RGn (MW) | |
| 1 | 455 | 0 | 455 | 0 |
| 2 | 455 | 0 | 455 | 0 |
| 3 | 130 | 0 | 130 | 0 |
| 4 | 130 | 0 | 130 | 0 |
| 5 | 162 | 0 | 162 | 0 |
| 6 | 80 | 0 | 80 | 0 |
| 7 | 25 | 60 | 25 | 60 |
| 8 | 42.9997 | 12.0003 | 43 | 12 |
| 9 | 10 | 45 | 10 | 45 |
| 10 | 10 | 32.9997 | 10 | 33 |
| n | Case 1 | Case 2 | ||
|---|---|---|---|---|
| PGn (MW) | RGn (MW) | PGn (MW) | RGn (MW) | |
| 1 | 599.5146 | 0 | 600 | 0 |
| 2 | 50.1367 | 148.7997 | 199.2433 | 0 |
| 3 | 50.0686 | 3.7282 | 50 | 0.0056 |
| 4 | 50 | 0 | 50.6444 | 0 |
| 5 | 92.4212 | 0 | 90.7484 | 13.0514 |
| 6 | 27.7061 | 3.4081 | 20.0254 | 5.194 |
| 7 | 123.4713 | 0 | 125 | 0 |
| 8 | 51.7433 | 29.7412 | 50.5536 | 0 |
| 9 | 140.986 | 0 | 107.5 | 0 |
| 10 | 30 | 0.249 | 50.4308 | 0 |
| 12 | 278.2058 | 0 | 300 | 0 |
| 13 | 463.971 | 0 | 401.3243 | 0 |
| 14 | 139.3174 | 0 | 110.9913 | 0 |
| 15 | 20 | 36.7794 | 67.3715 | 0.0325 |
| 16 | 185 | 0 | 57.1231 | 0 |
| 17 | 40.4855 | 0 | 35.2791 | 0.0142 |
| 18 | 35.6628 | 18.5147 | 30 | 0.2627 |
| 19 | 30 | 0 | 44.9579 | 0.7649 |
| 20 | 54.6993 | 0.0504 | 78.7799 | 0.8343 |
References
- Nguyen, T.T. Solving economic dispatch problem with piecewise quadratic cost functions using lagrange multiplier theory. In International Conference on Computer Technology and Development, 3rd ed.; ASME Press: New York, NY, USA, 2011; pp. 359–363. [Google Scholar] [CrossRef]
- Xu, J.; Yan, F.; Yun, K.; Su, L.; Li, F.; Guan, J. Noninferior Solution Grey Wolf Optimizer with an Independent Local Search Mechanism for Solving Economic Load Dispatch Problems. Energies 2019, 12, 2274. [Google Scholar] [CrossRef] [Green Version]
- Su, C.T.; Chiang, C.L. Nonconvex power economic dispatch by improved genetic algorithm with multiplier updating method. Electr. Power Compon. Syst. 2004, 32, 257–273. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Quynh, N.V.; Van Dai, L. Improved firefly algorithm: A novel method for optimal operation of thermal generating units. Complexity 2018. [Google Scholar] [CrossRef] [Green Version]
- Raja, M.A.Z.; Ahmed, U.; Zameer, A.; Kiani, A.K.; Chaudhary, N.I. Bio-inspired heuristics hybrid with sequential quadratic programming and interior-point methods for reliable treatment of economic load dispatch problem. Neural Comput. Appl. 2019, 31, 447–475. [Google Scholar] [CrossRef]
- Roy, S. The maximum likelihood optima for an economic load dispatch in presence of demand and generation variability. Energy 2018, 147, 915–923. [Google Scholar] [CrossRef]
- Xiong, G.; Shi, D. Hybrid biogeography-based optimization with brain storm optimization for non-convex dynamic economic dispatch with valve-point effects. Energy 2018, 157, 424–435. [Google Scholar] [CrossRef]
- Pham, L.H.; Duong, M.Q.; Phan, V.D.; Nguyen, T.T.; Nguyen, H.N.A. High-Performance Stochastic Fractal Search Algorithm for Optimal Generation Dispatch Problem. Energies 2019, 12, 1796. [Google Scholar] [CrossRef] [Green Version]
- Kien, L.C.; Nguyen, T.T.; Hien, C.T.; Duong, M.Q. A Novel Social Spider Optimization Algorithm for Large-Scale Economic Load Dispatch Problem. Energies 2019, 12, 1075. [Google Scholar] [CrossRef] [Green Version]
- Khan, K.; Kamal, A.; Basit, A.; Ahmad, T.; Ali, H.; Ali, A. Economic Load Dispatch of a Grid-Tied DC Microgrid Using the Interior Search Algorithm. Energies 2019, 12, 634. [Google Scholar] [CrossRef] [Green Version]
- Lin, A.; Sun, W. Multi-Leader Comprehensive Learning Particle Swarm Optimization with Adaptive Mutation for Economic Load Dispatch Problems. Energies 2019, 12, 116. [Google Scholar] [CrossRef] [Green Version]
- Das, D.; Bhattacharya, A.; Ray, R.N. Dragonfly Algorithm for solving probabilistic Economic Load Dispatch problems. Neural Comput. Appl. 2019, 1–17. [Google Scholar] [CrossRef]
- Singh, D.; Dhillon, J.S. Ameliorated grey wolf optimization for economic load dispatch problem. Energy 2019, 169, 398–419. [Google Scholar] [CrossRef]
- Richter, C.W.; Sheble, G.B. A profit-based unit commitment GA for the competitive environment. IEEE Trans. Power Syst. 2000, 15, 715–721. [Google Scholar] [CrossRef]
- Kong, X.Y.; Chung, T.S.; Fang, D.Z.; Chung, C.Y. An power market economic dispatch approach in considering network losses. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 16 June 2005; pp. 208–214. [Google Scholar] [CrossRef]
- Shahidehpour, M.; Marwali, M. Maintenance Scheduling in Restructured Power Systems; Springer Science Business Media: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Hermans, M.; Bruninx, K.; Vitiello, S.; Spisto, A.; Delarue, E. Analysis on the interaction between short-term operating reserves and adequacy. Energy Policy 2018, 121, 112–123. [Google Scholar] [CrossRef]
- Allen, E.H.; Ilic, M.D. Reserve markets for power systems reliability. IEEE Trans. Power Syst. 2000, 15, 228–233. [Google Scholar] [CrossRef]
- Attaviriyanupap, P.; Kita, H.; Tanaka, E.; Hasegawa, J. A hybrid LR-EP for solving new profit-based UC problem under competitive environment. IEEE Trans. Power Syst. 2003, 18, 229–237. [Google Scholar] [CrossRef]
- Ictoire, T.A.A.; Jeyakumar, A.E. Unit commitment by a tabu-search-based hybrid-optimisation technique. IEE Proc. Gener. Transm. Distrib. 2005, 152, 563–574. [Google Scholar] [CrossRef]
- Chandram, K.; Subrahmanyam, N.; Sydulu, M. New approach with muller method for profit based unit commitment. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 1–8 July 2008. [Google Scholar] [CrossRef]
- Dimitroulas, D.K.; Georgilakis, P.S. A new memetic algorithm approach for the price based unit commitment problem. Appl. Energy 2011, 88, 4687–4699. [Google Scholar] [CrossRef]
- Columbus, C.C.; Simon, S.P. Profit based unit commitment: A parallel ABC approach using a workstation cluster. Comput. Electr. Eng. 2012, 38, 724–745. [Google Scholar] [CrossRef]
- Columbus, C.C.; Chandrasekaran, K.; Simon, S.P. Nodal ant colony optimization for solving profit based unit commitment problem for GENCOs. Appl. Soft Comput. 2012, 12, 145–160. [Google Scholar] [CrossRef]
- Sharma, D.; Trivedi, A.; Srinivasan, D.; Thillainathan, L. Multi-agent modeling for solving profit based unit commitment problem. Appl. Soft Comput. 2013, 13, 3751–3761. [Google Scholar] [CrossRef]
- Singhal, P.K.; Naresh, R.; Sharma, V. Binary fish swarm algorithm for profit-based unit commitment problem in competitive electricity market with ramp rate constraints. IET Gener. Trans. Distrib. 2015, 9, 1697–1707. [Google Scholar] [CrossRef]
- Sudhakar, A.V.V.; Karri, C.; Laxmi, A.J. A hybrid LR-secant method-invasive weed optimisation for profit-based unit commitment. Int. J. Power Energy Convers. 2018, 9, 1–24. [Google Scholar] [CrossRef]
- Reddy, K.S.; Panwar, L.K.; Panigrahi, B.K.; Kumar, R. A New Binary Variant of Sine–Cosine Algorithm: Development and Application to Solve Profit-Based Unit Commitment Problem. Arab. J. Sci. Eng. 2018, 43, 4041–4056. [Google Scholar] [CrossRef]
- Reddy, K.S.; Panwar, L.; Panigrahi, B.K.; Kumar, R. Binary whale optimization algorithm: A new metaheuristic approach for profit-based unit commitment problems in competitive electricity markets. Eng. Optim. 2019, 51, 369–389. [Google Scholar] [CrossRef]
- Vo, D.N.; Ongsakul, W.; Nguyen, K.P. Augmented Lagrange Hopfield network for solving economic dispatch problem in competitive environment. AIP Conf. Proc. 2012, 1499, 46–53. [Google Scholar] [CrossRef]
- Duong, T.L.; Nguyen, P.D.; Phan, V.D.; Vo, D.N.; Nguyen, T.T. Optimal Load Dispatch in Competitive Electricity Market by Using Different Models of Hopfield Lagrange Network. Energies 2019, 12, 2932. [Google Scholar] [CrossRef] [Green Version]
- Citizens Power. The USPower Markel: Restrucluring and Risk Manage-Metit; Risk Publications: London, UK, 1997. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- Esmin, A.A.A.; Lambert-Torres, G.; Zambroni de Souza, A.C. A hybrid particle swarm optimization applied to loss power optimization. IEEE Trans. Power Syst. 2005, 2, 866–895. [Google Scholar] [CrossRef]
- Shunmugalatha, A.; Slochanal, M.R.S. Application of hybrid multiagent-based particle swarm optimization to optimal reactive power dispatch. Electr. Power Compon. Syst. 2008, 36, 788–800. [Google Scholar] [CrossRef]
- Polprasert, J.; Ongsakul, W.; Dieu, V.N. Optimal reactive power dispatch using improved pseudo-gradient search particle swarm optimization. Electr. Power Compon. Syst. 2016, 44, 518–532. [Google Scholar] [CrossRef]
- Mohammadi-Ivatloo, B.; Moradi-Dalvand, M.; Rabiee, A. Combined heat and power economic dispatch problem solution using particle swarm optimization with time varying acceleration coefficients. Electr. Power Syst. Res. 2013, 95, 9–18. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vo, D.N. Improved particle swarm optimization for combined heat and power economic dispatch. Sci. Iran. 2016, 23, 1318–1334. [Google Scholar] [CrossRef] [Green Version]
- Clerc, M. The swarm and the queen: Towards a deterministic and adaptive particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 Juny 1999; pp. 1951–1957. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y.H. Comparing inertia weights and constriction factors in particle swarm optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 Juny 2000; pp. 84–88. [Google Scholar] [CrossRef]
- Vo, D.N.; Schegner, P.; Ongsakul, W. A newly improved particle swarm optimization for economic dispatch with valve point loading effects. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 1–8 July 2011. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 Juny 1999; pp. 1945–1950. [Google Scholar] [CrossRef]
- Ratnaweera, A.; Halgamuge, S.K.; Watson, H.C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients. IEEE Trans. Evol. Comput. 2004, 8, 240–255. [Google Scholar] [CrossRef]
- Coxe, R.; Ilić, M. System planning under competition. In Power Systems Restructuring; Springer: Boston, MA, USA, 1998; pp. 283–333. [Google Scholar]
- Mohammadi, F.; Nazri, G.A.; Saif, M. An Improved Mixed AC/DC Power Flow Algorithm in Hybrid AC/DC Grids with MT-HVDC Systems. Appl. Sci. 2020, 10, 297. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, F.; Nazri, G.A.; Saif, M. A Bidirectional Power Charging Control Strategy for Plug-in Hybrid Electric Vehicles. Sustainability 2019, 11, 4317. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, F.; Zheng, C. Stability Analysis of Electric Power System. In Proceedings of the 4th National Conference on Technology in Electrical and Computer Engineering, Tehran, Iran, 27 December 2018. [Google Scholar]
- Mohammadi, F.; Nazri, G.A.; Saif, M. An Improved Droop-Based Control Strategy for MT-HVDC Systems. Electronics 2020, 9, 87. [Google Scholar] [CrossRef] [Green Version]
- Tan, C.W.; Varaiya, P. Interruptible electric power service contracts. J. Econ. Dyn. Control 1993, 17, 495–517. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Dinh, B.H.; Nguyen, T.T. New Solutions to Modify the Differential Evolution Method for Multi-objective Load Dispatch Problem Considering Quadratic Fuel Cost Function. In AETA 2016: Recent Advances in Electrical Engineering and Related Sciences; AETA 2016. Lecture Notes in Electrical Engineering; Springer: Cham, Switherland, 2016; p. 415. [Google Scholar] [CrossRef]






















| Method | Case 1 | Case 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Higher MTP | Higher ATP | Higher MTP | Higher ATP | |||||
| In $/h | In % | In $/h | In % | In $/h | In % | In $/h | In % | |
| PSO | 1.45 | 0.13 | 130.40 | 15.85 | 1.23 | 0.11 | 236.62 | 30.86 |
| IW-PSO | 0.23 | 0.02 | 146.86 | 18.49 | 0.60 | 0.05 | 193.05 | 22.92 |
| CF-PSO | 0.33 | 0.03 | 114.68 | 13.76 | 0.65 | 0.06 | 151.21 | 17.39 |
| PG-PSO | 0.10 | 0.01 | 125.65 | 14.67 | 1.45 | 0.13 | 194.86 | 23.19 |
| IW-PG-PSO | 0.23 | 0.02 | 76.28 | 8.38 | 0.40 | 0.04 | 178.47 | 20.32 |
| CF-PG-PSO | 0.75 | 0.07 | 88.61 | 9.66 | 0.54 | 0.05 | 142.25 | 15.82 |
| TVIW-PSO | 0.13 | 0.01 | 168.25 | 21.31 | 1.02 | 0.09 | 314.01 | 42.90 |
| TVAC-PSO | 0.37 | 0.03 | 179.72 | 22.30 | 0.90 | 0.08 | 261.25 | 33.78 |
| PPSO | 0.02 | 0.00 | 69.06 | 7.35 | 0.45 | 0.04 | 199.24 | 23.04 |
| Method | Case 1 | Case 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Higher MTP | Higher ATP | Higher MTP | Higher ATP | |||||
| In $/h | In % | In $/h | In % | In $/h | In % | In $/h | In % | |
| PSO | 391.03 | 2.76 | 3580.52 | 34.21 | 196.80 | 1.46 | 4146.69 | 45.99 |
| IW-PSO | 787.98 | 5.72 | 3300.27 | 31.08 | 115.63 | 0.86 | 4766.99 | 52.09 |
| CF-PSO | 938.57 | 6.89 | 4026.77 | 40.35 | 114.78 | 0.85 | 4932.34 | 54.35 |
| PG-PSO | 53.79 | 0.37 | 2694.35 | 23.64 | 75.03 | 0.55 | 2667.70 | 23.35 |
| IW-PG-PSO | 275.97 | 1.93 | 2893.48 | 25.89 | 160.95 | 1.19 | 3027.44 | 27.41 |
| CF-PG-PSO | 178.00 | 1.24 | 3533.46 | 33.79 | 79.73 | 0.59 | 3137.16 | 28.90 |
| TVIW-PSO | 331.59 | 2.33 | 4117.14 | 41.75 | 124.70 | 0.92 | 4838.27 | 52.94 |
| TVAC-PSO | 414.13 | 2.93 | 3291.83 | 30.42 | 114.91 | 0.85 | 3335.88 | 30.96 |
| PPSO | 39.15 | 0.27 | 1741.05 | 13.98 | 11.13 | 0.08 | 1343.79 | 10.46 |
| Method | Case 1 | Case 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Higher MTP | Higher ATP | Higher MTP | Higher ATP | |||||
| In $/h | In % | In $/h | In % | In $/h | In % | In $/h | In % | |
| PSO | 20.24 | 0.10 | 2263.72 | 12.56 | 281.76 | 1.95 | 2277.23 | 19.11 |
| IW-PSO | 28.26 | 0.14 | 2173.71 | 12.07 | 146.23 | 1.01 | 2376.21 | 20.24 |
| CF-PSO | 425.54 | 2.09 | 2155.86 | 11.89 | 174.51 | 1.21 | 1852.81 | 14.95 |
| PG-PSO | 241.38 | 1.17 | 1302.57 | 6.84 | 146.42 | 1.01 | 919.01 | 6.87 |
| IW-PG-PSO | 296.20 | 1.44 | 1070.75 | 5.62 | 286.23 | 1.97 | 612.94 | 4.47 |
| CF-PG-PSO | 30.34 | 0.15 | 834.64 | 4.29 | 124.28 | 0.85 | 850.62 | 6.40 |
| TVIW-PSO | 357.07 | 1.75 | 2101.92 | 11.59 | 73.69 | 0.51 | 628.74 | 4.68 |
| TVAC-PSO | 315.84 | 1.54 | 2078.20 | 11.34 | 209.16 | 1.44 | 1286.83 | 9.85 |
| PPSO | 83.30 | 0.40 | 611.88 | 3.07 | 83.32 | 0.57 | 670.91 | 4.81 |
| Method | MTP ($/h) | ATP ($/h) | STD | Gmax | Nop | Cpu Time (s) |
|---|---|---|---|---|---|---|
| LF-HLN-EF [31] | 1102.45 | 1102.45 | - | - | - | 0.017 |
| LF-HLN-THF [31] | 1102.45 | 1102.45 | - | - | - | 0.02 |
| LF-HLN-GdF [31] | 1102.45 | 1102.45 | - | - | - | 0.06 |
| LF-HLN-GF [31] | 1102.45 | 1102.449 | - | - | - | 0.062 |
| LF-HLN-LF [31] | 1102.45 | 1102.45 | - | - | - | 0.069 |
| PSO [31] | 1102.45 | 938.8674 | - | 500 | 5 | 0.383 |
| CSA [31] | 1102.45 | 1099.229 | - | 500 | 5 | 0.765 |
| DE [31] | 1102.45 | 635.3542 | - | 500 | 5 | 0.808 |
| ELF-HNM [30] | 1102.45 | - | - | - | - | 0.16 |
| SSA | 1102.45 | 935.3537 | 193.9 | 5 | 5 | 0.0055 |
| MDE | 1102.45 | 1001.462 | 108.5 | 5 | 5 | 0.0235 |
| PSO | 1102.024 | 953.201 | 186.4 | 5 | 5 | 0.0027 |
| IW-PSO | 1102.45 | 941.067 | 183.6 | 5 | 5 | 0.0027 |
| CF-PSO | 1102.45 | 948.201 | 176.9 | 5 | 5 | 0.0023 |
| PG-PSO | 1102.444 | 981.901 | 190.7 | 5 | 5 | 0.0052 |
| IW-PG-PSO | 1102.367 | 986.454 | 101.6 | 5 | 5 | 0.0051 |
| CF-PG-PSO | 1102.442 | 1006.033 | 195.4 | 5 | 5 | 0.0054 |
| TVIW-PSO | 1102.449 | 957.905 | 196.7 | 5 | 5 | 0.0028 |
| TVAC-PSO | 1102.45 | 985.487 | 185.1 | 5 | 5 | 0.0026 |
| PPSO | 1102.451 | 1008.994 | 96.4 | 5 | 5 | 0.0051 |
| Method | MTP ($/h) | ATP ($/h) | STD | Gmax | Nop | Cpu Time (s) |
|---|---|---|---|---|---|---|
| LF-HLN-EF [31] | 1095.648 | 1095.648 | - | - | - | 0.07 |
| LF-HLN-THF [31] | 1095.647 | 1095.647 | - | - | - | 0.1 |
| LF-HLN-GdF [31] | 1095.61 | 1095.61 | - | - | - | 0.18 |
| LF-HLN-GF [31] | 1095.589 | 1095.589 | - | - | - | 0.185 |
| LF-HLN-LF [31] | 1095.59 | 1095.59 | - | - | - | 0.32 |
| PSO [31] | 1095.648 | 943.7049 | - | 500 | 5 | 0.77 |
| CSA [31] | 1095.648 | 1088.329 | - | 500 | 5 | 0.82 |
| DE [31] | 1095.648 | 745.1618 | - | 500 | 5 | 0.95 |
| ELF-HNM [30] | 1095.648 | - | - | - | - | 0.16 |
| SSA | 1094.993 | 950.3221 | 190.3 | 5 | 5 | 0.0043 |
| MDE | 1095.412 | 872.2816 | 212.5 | 5 | 5 | 0.0238 |
| PSO | 1095.624 | 1003.32 | 185.1 | 5 | 5 | 0.0022 |
| IW-PSO | 1095.648 | 1035.424 | 115 | 5 | 5 | 0.0053 |
| CF-PSO | 1095.648 | 1020.58 | 170.1 | 5 | 5 | 0.0029 |
| PG-PSO | 1095.648 | 1035.26 | 141.9 | 5 | 5 | 0.0045 |
| IW-PG-PSO | 1095.648 | 1056.866 | 123.1 | 5 | 5 | 0.0043 |
| CF-PG-PSO | 1095.647 | 1041.161 | 142.2 | 5 | 5 | 0.0058 |
| TVIW-PSO | 1095.648 | 1045.962 | 110.1 | 5 | 5 | 0.0025 |
| TVAC-PSO | 1095.648 | 1034.671 | 120.3 | 5 | 5 | 0.0025 |
| PPSO | 1095.648 | 1063.955 | 97.3 | 5 | 5 | 0.0049 |
| Method | MTP ($/h) | ATP ($/h) | STD | Gmax | Nop | Cpu Time (s) |
|---|---|---|---|---|---|---|
| LF-HLN-EF [31] | 14,564.73 | 14,564.73 | - | 194 | - | 0.08 |
| LF-HLN-THF [31] | 14,564.73 | 14,564.73 | - | 225.6 | - | 0.1 |
| LF-HLN-GdF [31] | 14,564.72 | 14,564.72 | - | 256.81 | - | 0.11 |
| LF-HLN-GF [31] | 14,564.71 | 14,564.71 | - | 195 | - | 0.08 |
| LF-HLN-LF [31] | 14,564.71 | 14,564.71 | - | 279.57 | - | 0.22 |
| PSO [31] | 14,182.19 | 9771.186 | - | 500 | 5 | 1.5 |
| CSA [31] | 14,564.05 | 14,101.86 | - | 500 | 5 | 1.7 |
| DE [31] | 14,053.03 | 8416.163 | - | 500 | 5 | 1.9 |
| ELF-HNM [30] | 14,564.73 | - | 5000 | - | 0.18 | |
| SSA | 14,370.95 | 14,128.56 | 237.1 | 100 | 20 | 0.1537 |
| MDE | 14,527.64 | 14,041.82 | 240.4 | 100 | 20 | 0.8143 |
| PSO | 14,563.76 | 14,046.23 | 411.4 | 100 | 20 | 0.0224 |
| IW-PSO | 14,563.73 | 13,918.55 | 417.3 | 100 | 20 | 0.0119 |
| CF-PSO | 14,563.77 | 14,007.25 | 381.5 | 100 | 20 | 0.0124 |
| PG-PSO | 14,563.74 | 14,091.15 | 416.1 | 100 | 20 | 0.019 |
| IW-PG-PSO | 14,563.74 | 14,071.23 | 398.1 | 100 | 20 | 0.0189 |
| CF-PG-PSO | 14,563.76 | 13,992.12 | 617.6 | 100 | 20 | 0.0207 |
| TVIW-PSO | 14,563.77 | 13,977.68 | 299.4 | 100 | 20 | 0.0133 |
| TVAC-PSO | 14,563.41 | 14,111.44 | 357.5 | 100 | 20 | 0.0122 |
| PPSO | 14,564.74 | 14,193.08 | 236.9 | 100 | 20 | 0.0148 |
| Method | MTP ($/h) | ATP ($/h) | STD | Gmax | Nop | Cpu Time (s) |
|---|---|---|---|---|---|---|
| LF-HLN-EF [31] | 13,635.11 | 13,635.11 | - | 187 | - | 0.08 |
| LF-HLN-THF [31] | 13,635.11 | 13,635.11 | - | 227.56 | - | 0.1 |
| LF-HLN-GdF [31] | 13,635.11 | 13,635.11 | - | 270.48 | - | 0.12 |
| LF-HLN-GF [31] | 13,635.11 | 13,635.11 | - | 195 | - | 0.09 |
| LF-HLN-LF [31] | 13,635.11 | 13,635.11 | - | 278.86 | - | 0.22 |
| PSO [31] | 13,158.07 | 9824.841 | - | 500 | 5 | 1.6 |
| CSA [31] | 13,635.11 | 13,448.05 | - | 500 | 5 | 1.7 |
| DE [31] | 13,093.19 | 8346.24 | - | 500 | 5 | 2 |
| ELF-HNM [30] | 13,635.11 | - | - | 5000 | - | 0.18 |
| SSA | 13,597.06 | 13,454.77 | 109.8 | 100 | 20 | 0.1535 |
| MDE | 13,626.02 | 13,353.64 | 515.4 | 100 | 20 | 0.84575 |
| PSO | 13,634.83 | 13,163.26 | 528 | 100 | 20 | 0.0138 |
| IW-PSO | 13,603.95 | 13,138.09 | 605.7 | 100 | 20 | 0.0172 |
| CF-PSO | 13,635.02 | 13,303.35 | 359.9 | 100 | 20 | 0.0119 |
| PG-PSO | 13,635.00 | 13,319.49 | 351.4 | 100 | 20 | 0.021 |
| IW-PG-PSO | 13,635.04 | 13,306.97 | 386.6 | 100 | 20 | 0.0251 |
| CF-PG-PSO | 13,635.02 | 13,321.75 | 348.8 | 100 | 20 | 0.0292 |
| TVIW-PSO | 13,618.66 | 13,086.99 | 591.6 | 100 | 20 | 0.0141 |
| TVAC-PSO | 13,634.92 | 13,326.12 | 315.9 | 100 | 20 | 0.0146 |
| PPSO | 13,635.12 | 13,525.28 | 105.1 | 100 | 20 | 0.0206 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kien, L.C.; Duong, T.L.; Phan, V.-D.; Nguyen, T.T. Maximizing Total Profit of Thermal Generation Units in Competitive Electric Market by Using a Proposed Particle Swarm Optimization. Sustainability 2020, 12, 1265. https://doi.org/10.3390/su12031265
Kien LC, Duong TL, Phan V-D, Nguyen TT. Maximizing Total Profit of Thermal Generation Units in Competitive Electric Market by Using a Proposed Particle Swarm Optimization. Sustainability. 2020; 12(3):1265. https://doi.org/10.3390/su12031265
Chicago/Turabian StyleKien, Le Chi, Thanh Long Duong, Van-Duc Phan, and Thang Trung Nguyen. 2020. "Maximizing Total Profit of Thermal Generation Units in Competitive Electric Market by Using a Proposed Particle Swarm Optimization" Sustainability 12, no. 3: 1265. https://doi.org/10.3390/su12031265
APA StyleKien, L. C., Duong, T. L., Phan, V.-D., & Nguyen, T. T. (2020). Maximizing Total Profit of Thermal Generation Units in Competitive Electric Market by Using a Proposed Particle Swarm Optimization. Sustainability, 12(3), 1265. https://doi.org/10.3390/su12031265





