Optimal Scheduling of Hydro–Thermal–Wind–Photovoltaic Generation Using Lightning Attachment Procedure Optimizer

Abstract

This paper presents an effective solution for the short-term hydrothermal generation scheduling (STHS) problem using an integration of wind and photovoltaic power (PV) system. Wind and PV power are integrated into the power system to minimize the total fuel cost of thermal units. In this paper, the lightning attachment procedure optimization algorithm (LAPO) is employed to solve the STHS problem using the wind and PV power integration system. The proposed method is applied for solving five test systems with different characteristics, considering the valve-point loading impact of the thermal unit. The first and third test systems include hydro and thermal units only, and the rest of the systems consist of hydro and thermal units with integrating wind and PV power-generating units to inspect the effect of renewable energy sources in the selected test systems. The simulation results are compared with other studied methods. It is found that the proposed method is superior, and it has the ability to obtain the best solutions with respect to other optimization methods that are implemented to solve the STHS problem.

1. Introduction

In recent years, the demand for electric power has increased, and fossil fuel prices have risen rapidly, which has led to growing the energy crisis in the world. Therefore, the world has tended to reduce the use of thermal units by using renewable energy sources to reduce the polluting emissions and harmful gases that are released from thermal units when fossil fuels are burnt. These harmful gases have a negative effect on the environment, and this leads to an increase in the temperature of the planet, which causes global warming. Renewable energy sources, mainly wind and solar, are very cost-effective as well as eco-friendly to the environment. Therefore, the incorporation of the short-term hydrothermal generation scheduling (STHS) problem and renewable energy has great importance in the power system operation. The STHS problem is one of the most important optimization problems in the power system network. The primary goal of the STHS problem is to determine the optimal power-generation schedule of the thermal and hydro units to minimize the total operation cost of the system.

The STHS is subjected to a variety of constraints related to the hydraulic and thermal units, which include power load balance, power-generation limits, reservoir volume limits, and water discharge rate limits. These constraints with the valve-point loading impact make this problem a non-linear and complicated optimization problem. Several analytical optimization methods have been employed such as dynamic programming (DP) [1], mixed-integer linear programming [2], nonlinear programming (NLP) [3], and Lagrange relaxation (LR) [4]. It should be highlighted here that these methods suffer from stagnation, and they are not able to provide the optimal solution due to the nonlinearity and composite constraints of the STHS problem. Thus, several modern heuristic and meta-heuristic optimization methods have been applied to solve the STHS problem to avoid stagnation of the analytical methods, such as the genetic algorithm (GA) [5], differential evolution (DE) [6], particle swarm optimization (PSO) [7], teaching–learning-based optimization (TLBO) [8], and artificial bee colony (ABC) [9]. An improved harmony search (IHS) optimization algorithm has been introduced in [10] to find the optimal solution to the short-term hydrothermal scheduling problem. In this reference, the proposed method has been employed on two test systems with different constraints including the valve-point loading impact and transmission losses. A modified dynamic neighborhood learning-based particle swarm optimization (MDNLPSO) method has been introduced in [11] to solve the STHS problem considering the valve-point loading impact and the power transmission loss. A real-coded genetic algorithm based on the improved Mühlenbein mutation (RCGA-IMM) algorithm has been applied by Nazari-Heris et al. [12] to solve the STHS problem and minimize the total cost of the hydrothermal system. A differential real-coded quantum-inspired evolutionary algorithm (DRQEA) has been introduced in [13] to solve the STHS problem considering the valve-point loading impact and the power transmission loss.

Renewable energy sources such as wind and PV power have a great important role in many countries as these sources have low cost and produce electric power without any harmful emissions. Hence, the integration of renewable energy resources into the electrical grid attracts more attention from researchers.

Few efforts have been presented to study the effect of inclusion of renewable energy sources such as wind and solar energy in a short-term hydrothermal system. Zhang et al. [14] applied a gradient-based multi-objective cultural differential evolution (GDMOCDE) to solve the STHS problem and minimize the generation cost and emission of thermal plants. Banerjee et al. [15] solved the SHTS problem considering the wind power by using the particle swarm optimization technique (PSO). In 2016, Dubey et al. [16] applied the ant lion optimization algorithm (ALO) to solve the short-term hydrothermal scheduling problem considering the wind speed uncertainty.

A hydro–thermal–wind scheduling problem and wind uncertainty were presented in [17]. In this reference, an extended NSGA-III algorithm was proposed to obtain the optimal Pareto solutions of the multi-objective optimization problem. An enhanced multi-objective bee colony optimization algorithm (EMOBCO) has been proposed in [18] to solve short-term hydro–thermal–wind complementary scheduling considering the uncertainty of wind power. Multi-objective complementary scheduling of the hydro–thermal–RE power system has been presented in [19] to solve the STHS problem, taking both cost and emission objectives and considering the uncertainty of wind power, and a multi-objective hybrid grey wolf optimizer was proposed to solve this problem. Table 1 presents the definitions of test systems applied to solve the STHS problem with integration of wind and PV power. Different optimization methods used to solve the STHS problem with integration of wind and photovoltaic power are summarized in Table 2.

Table 1. Definition of test systems applied to solve the STHS problem with integration of wind and PV power.

Test System	Number of Hydrothermal Generation Units
Test System 1	Four cascaded hydropower plants and three thermal plants
Test System 2	Four cascaded hydropower plants, three thermal plants, and one equivalent wind-and-solar-generating unit
Test System 3	Four hydro plants and ten thermal plants
Test System 4	Four cascaded hydropower plants, eight thermal-power plants, and one equivalent wind- and equivalent solar-generating unit
Test System 5	Four cascaded hydropower plants, eight thermal-power plants, and two wind-generating units

Lightning attachment procedure optimization (LAPO) is a novel algorithm proposed by A.F. Nematollahi et al. [20,21]. LAPO has simulated the lightning attachment process in nature. LAPO is based on five steps, which are air breakdown on the cloud edge, downward leader movement toward the ground, branch fading, upward leader propagation, and the strike point, which mimics the optimal solution. LAPO has a high searching capability that has been applied to solve several optimization problems. In [22], LAPO has been applied to determine the optimal siting and sizing of the unified power flow controller in the transmission system. Y. Heba et al. solved the optimal power flow using the LAPO technique [23]. In [24], the LAPO technique was employed to determine the optimal location and size of the distributed generators in the distribution network. W. Lui et al. presented the LAPO to optimize the image segmentation in [25].

Table 2. Summary of the literature review of optimization methods to solve the STHS problem with integration of wind and PV power.

Reference	Method	Year	Test System	Main Consideration
[26]	ALO	2016	Test System 1, Test System 3, Test System 5	Valve-point loading effect (VPE), transmission loss.
[5]	RCGA-RTVM	2014	Test System 1	Valve-point loading effect of thermal units, power transmission loss.
[27]	HMOCA incorporated DE	2011	Test System 1	Minimization of emission issues.
[19]	Multi-objective hybrid grey wolf optimizer	2018	Test System 2	Minimization of operational costs and pollution emissions
[28]	Fast convergence real-coded genetic algorithm	2018	Test System 2	The effect of valve-point loading of thermal generator and transmission loss is taken into consideration
[10]	IHS	2018	Test System 1	Valve-point loading effect of thermal units, power transmission loss of the system.
[29]	Improved DE	2014	Test System 1	Prohibited discharge zones (PDZs) of hydro units, valve-point loading effect, ramp rate limits of thermal generators, transmission losses.
[30]	CPSO	2019	Test System 1	Valve-point loading effect, prohibited discharge zones (PDZs) of hydro units.
[31]	MOABC	2014	Test System 1	Valve-point loading effect, power transmission losses.
[32]	NSGSA-CM	2014	Test System1	Emission of hydrothermal system.
[8]	TLBO	2013	Test System 1	Valve-point effect of thermal plants, prohibited discharge zones (PDZs) of the water reservoir of the hydro units.
[33]	A hybrid CSA and PSO	2013	Test System 1	Economic emission, power transmission loss, valve-point effect.
[34]	EP	2004	Test System 1	Valve-point loading effect.
[11]	MDNLPSO	2015	Test System 1	Prohibited discharge zones (PDZs) of the water reservoir of the hydro units, valve-point loading effect, transmission losses.
[35]	RCGA-AFSA	2014	Test System 1	Valve-point loading effect, transmission losses, prohibited discharge zones (PDZs), ramp rate limits.
[36]	TLPSOS	2017	Test System 1	Valve-point loading effect.

Table 2. Summary of the literature review of optimization methods to solve the STHS problem with integration of wind and PV power.

Reference	Method	Year	Test System	Main Consideration
[26]	ALO	2016	Test System 1, Test System 3, Test System 5	Valve-point loading effect (VPE), transmission loss.
[5]	RCGA-RTVM	2014	Test System 1	Valve-point loading effect of thermal units, power transmission loss.
[27]	HMOCA incorporated DE	2011	Test System 1	Minimization of emission issues.
[19]	Multi-objective hybrid grey wolf optimizer	2018	Test System 2	Minimization of operational costs and pollution emissions
[28]	Fast convergence real-coded genetic algorithm	2018	Test System 2	The effect of valve-point loading of thermal generator and transmission loss is taken into consideration
[10]	IHS	2018	Test System 1	Valve-point loading effect of thermal units, power transmission loss of the system.
[29]	Improved DE	2014	Test System 1	Prohibited discharge zones (PDZs) of hydro units, valve-point loading effect, ramp rate limits of thermal generators, transmission losses.
[30]	CPSO	2019	Test System 1	Valve-point loading effect, prohibited discharge zones (PDZs) of hydro units.
[31]	MOABC	2014	Test System 1	Valve-point loading effect, power transmission losses.
[32]	NSGSA-CM	2014	Test System1	Emission of hydrothermal system.
[8]	TLBO	2013	Test System 1	Valve-point effect of thermal plants, prohibited discharge zones (PDZs) of the water reservoir of the hydro units.
[33]	A hybrid CSA and PSO	2013	Test System 1	Economic emission, power transmission loss, valve-point effect.
[34]	EP	2004	Test System 1	Valve-point loading effect.
[11]	MDNLPSO	2015	Test System 1	Prohibited discharge zones (PDZs) of the water reservoir of the hydro units, valve-point loading effect, transmission losses.
[35]	RCGA-AFSA	2014	Test System 1	Valve-point loading effect, transmission losses, prohibited discharge zones (PDZs), ramp rate limits.
[36]	TLPSOS	2017	Test System 1	Valve-point loading effect.

In this paper, the authors present the lightning attachment procedure optimization (LAPO) technique to find the hourly optimal power generation of thermal units and hydropower units to minimize the total fuel cost and the total emissions. The effect of wind and photovoltaic generation systems is taken into consideration to find the optimal solution of the STHS optimization problem. To evaluate the performance of the developed algorithm, it is applied to five test systems including four hydropower plants with three thermal units, four cascaded hydropower plants with three thermal plants and one equivalent wind-and-solar-generating unit, four hydro plants with ten thermal units, four cascaded hydropower plants and eight thermal-power plants and one equivalent wind and equivalent solar-generating unit, and four hydro plants with eight thermal units and two wind generation units.

The main contributions of this paper can be depicted as follows:

• The hydro–thermal generation scheduling problem is solved for small and large test systems.
• The renewable energy resources including the wind and PV generation systems are considered in the STHS problem.
• The economic issues are considered with cost reduction in the STHS problem.
• Application of efficient optimizer called LAPO to solve the STHS problem with renewable energy resources.

The rest of this paper is organized as follows: The problem formulation of hydrothermal generation scheduling with a wind and PV power integration system is introduced in Section 2. The lightning attachment procedure optimization algorithm (LAPO) method is illustrated in Section 3. The simulation results are represented in Section 4. Finally, the conclusion is explained in Section 5.

2. Problem Formulation of Hydrothermal Generation Scheduling with Wind and PV Power Integration System

The objective of the STHS problem with integration of wind and PV power is to minimize the total fuel cost as well as emission caused by thermal plants considering the cost of wind and PV power while satisfying various constraints. The objective function of the STHS problem with the wind and PV power integration system considering the different constraints is expressed as follows:

2.1. The Cost Minimization

$$F_{1 }={\displaystyle \sum }_{t=1}^T\left\{{\displaystyle \sum }_{i=1}^{N_s}{f}_{si}^t\left(P_{si}^t\right)+{\displaystyle \sum }_{k=1}^{N_w}{f}_{wk}^t\left(P_{wk}^t\right)+{\displaystyle \sum }_{m=1}^{N_{pv}}{f}_{pvm}^t\left(P_{pvm}^t\right)\right\}$$

(1)

where $F_{1 }$ is the total operating cost of thermal, wind, and PV power-generating units. $f_{si}^t$ is the total fuel cost of thermal units. $f_{wk}^t$ is the total cost of wind-generating units. $f_{pvm}^t$ is the total cost of PV-generating units. The total number of thermal, wind, and PV power-generation units are $N_s$, $N_w,$ and $N_{pv}$, respectively. $T$ is the length of the total scheduling period. The output power generation from thermal, wind, and PV power-generation units are $P_{si}^t$, $P_{wk}^t$, and $P_{pvm}^t,$ respectively.

The fuel cost of the thermal unit at a time $t$ taking into consideration the valve-point loading effect (VPLE) is represented as follows:

$$f_{it}\left(P_{sit}\right)=min{\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{i=1}^{N_s}\left\{a_{i }+b_i{P}_{si}^t+c_i{\left(P_{si}^t \right)}^2+\left|d_{i}sin\left[e_i\left(P_{si}^{min}-P_{si}^t\right)\right]\right| \right\}$$

(2)

where, $a_{i }$, $b_{i }$, $c_{i }$, $d_{i },$ and $e_{i }$ are the cost coefficients of the thermal unit, and $P_{si}^{min}$ is the minimum power-generation limit of the thermal unit.

2.2. The Emission Rate Minimization

The STHS problem with integration of wind and PV power aims to minimize the total amount of emissions that are released from thermal units due to the burning of fossil fuels used to produce electricity. The function of the emission rate can be represented as the sum of a quadratic and an exponential function [37]. The total emission produced by thermal units in the system can be expressed as follows:

$$F_{2 }=min{\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{i=1}^{N_s}\{{\alpha }_{i }+{\beta }_i{P}_{si}^t+{\gamma }_i{\left(P_{si}^t \right)}^2+{\eta }_i\exp \left({\delta }_i{P}_{si}^t\right)\}$$

(3)

where $F_{2 }$ is the total amount of emissions. ${\alpha }_{i }$, ${\beta }_{i }$, ${\gamma }_i$, ${\eta }_i,$ and ${\delta }_{i }$ are the emission coefficients of the thermal unit.

2.3. Constraints

The STHS problem with a wind and PV power integration system should satisfy the following equality and inequality constraints.

(1) power balance constraints

$${\displaystyle \sum }_{i=1}^{N_s}{P}_{si}^t + {\displaystyle \sum }_{j=1}^{N_h}{P}_{hj}^t+{\displaystyle \sum }_{k=1}^{N_w}{P}_{wk}^t+{\displaystyle \sum }_{m=1}^{N_{pv}}{P}_{pvm}^t- P_L^t= P_D^t . t ϵ T$$

(4)

where $N_h$ is the number of hydropower units. $P_D^t$ is the power load demand. $P_{hj}^t$ is the output power of the hydro unit. $P_L^t$ is the transmission loss of the system.

The power generation of hydropower units $P_{hj}^t$ can be represented as

$$P_{hj}^t=C_{1j}{\left(V_{hj}^t\right)}^2+C_{2j}{\left(Q_{hj}^t\right)}^2+C_{3j} V_{hj}^t Q_{hj }^t+C_{4j} V_{hj}^t+ C_{5j} Q_{hj}^t+C_{6j} jϵ N_{h }. t ϵ T$$

(5)

where $C_{1j}$, $C_{2j}$, $C_{3j}$, $C_{4j}$, $C_{5j}$, and $C_{6j}$ represent the coefficients of the hydropower-generating units, respectively. $V_{hj }^t$ and $Q_{hj }^t$ represent the reservoir volume and water release of the hydro unit, respectively.

The power transmission loss $P_{L }^t$ can be represented as follows:

$$P_{L }^t= {\displaystyle \sum }_{i=0}^{N_h+N_s}{\displaystyle \sum }_{j=0}^{N_h+N_s}{P}_{i }^t{B}_{ij} P_{j }^t+{\displaystyle \sum }_{i=0}^{N_h+N_s}{B}_{oi} P_{i }^j+B_{oo}$$

(6)

where, $B_{ij} , B_{oi}, \mathrm{and} B_{oo}$ represent the coefficients of transmission power loss.

(2) Water balance constraint

$$V_{hj}^t= V_{hj}^{t-1}+ I_{hj}^t- Q_{hj}^t-S_{hj}^t+{\displaystyle \sum }_{l=1}^{R_{uj}} \left( Q_{hl}^{t-d_{lj}}+S_{hl}^{t-d_{lj}} \right) .jϵ N_{h }. tϵ T .$$

(7)

where $I_{hj}^t$ and $S_{hj}^t$ represent the water inflow and spillage of the hydro plant. $R_{uj}$ is the number of upstream hydropower-generating units above the reservoir.

(3) Initial and terminal reservoir storage volumes and water discharge rate limits

$$V_{hj}^{min} \le V_{hj }^t\le V_{hj}^{max} ,j ϵ N_{h }, t ϵT$$

(8)

$$Q_{hj}^{min} \le Q_{hj }^t\le Q_{hj}^{max} ,j ϵ N_{h }, t ϵT$$

(9)

where $V_{hj}^{min}$ and $V_{hj}^{max}$ are the minimum and maximum reservoir storage volumes of hydro units. $Q_{hj}^{min}$ and $Q_{hj}^{max}$ are the minimum and maximum water discharge rates of hydro units.

(4) Power generation limits

Each power-generation unit has minimum and maximum output limits.

$$P_{hj}^{min}\le P_{hj}^t\le P_{hj}^{max} .j ϵN_h. tϵ T$$

(10)

$$P_{si}^{min} \le P_{si}^t\le P_{si}^{max} .i ϵN_s. tϵ T.$$

(11)

$$P_{wk}^{min} \le P_{wk}^t\le P_{wk}^{max} .k ϵN_w. tϵ T.$$

(12)

$$P_{pvm}^{min} \le P_{pvm}^t\le P_{pvm}^{max} .m ϵN_{pv}. tϵ T.$$

(13)

2.4. Modeling of Wind and PV Power Generation

The output power of wind unit [26] for a given wind speed at time $t$ is expressed as follows:

$$f_{wk}^t\left(P_{wk}^t\right)={\displaystyle \sum }_{k=1}^{N_w}{K}_{wk}{P}_{wk}^t$$

$$P_{wk}^t=\left\{\begin{array}{cc}0& for v_w^t<v_{in}, v_w^t>v_{out}\\ P_{wrk}^t\ast \left(\frac{v_w^t-v_{in}}{v_r-v_{in}}\right)& for v_{in}\le v_w^t\le v_r\\ P_{wrk}^t& for v_r\le v_w^t\le v_{out}\end{array}\right\}$$

where $v_{in }$, $v_{out} ,$ and $v_r$ are the cut-in, cut-out, and rated wind speeds, respectively.$P_{wrk}^t$ is the rated power of the wind unit.

The output power of PV unit [28] at time $t$ is expressed as follows:

$$f_{pvm}^t\left(P_{pvm}^t\right)= {\displaystyle \sum }_{m=1}^{N_{pv}}{P}_{pvm}^t{K}_{sm}$$

(14)

$$P_{pvm}^t=\left\{\begin{array}{c}{P}_{sr} \left(\frac{G^2}{G_{std } R_C}\right) for 0<G<R_C\\ P_{sr}\left(\frac{G^2}{G_{std }}\right) for G>R_C \end{array}\right\}$$

(15)

where G denotes the forecast solar radiation at a time $t$. $G_{std}$ is the solar radiation in the standard environment set as 1000 $\mathrm{w}/{\mathrm{m}}^2$. $R_C$ is a certain radiation point set as 150 $\mathrm{w}/{\mathrm{m}}^2$. $P_{sr}$ denotes the rated power output of the PV unit.

3. Lightning Attachment Procedure Optimization (LAPO)

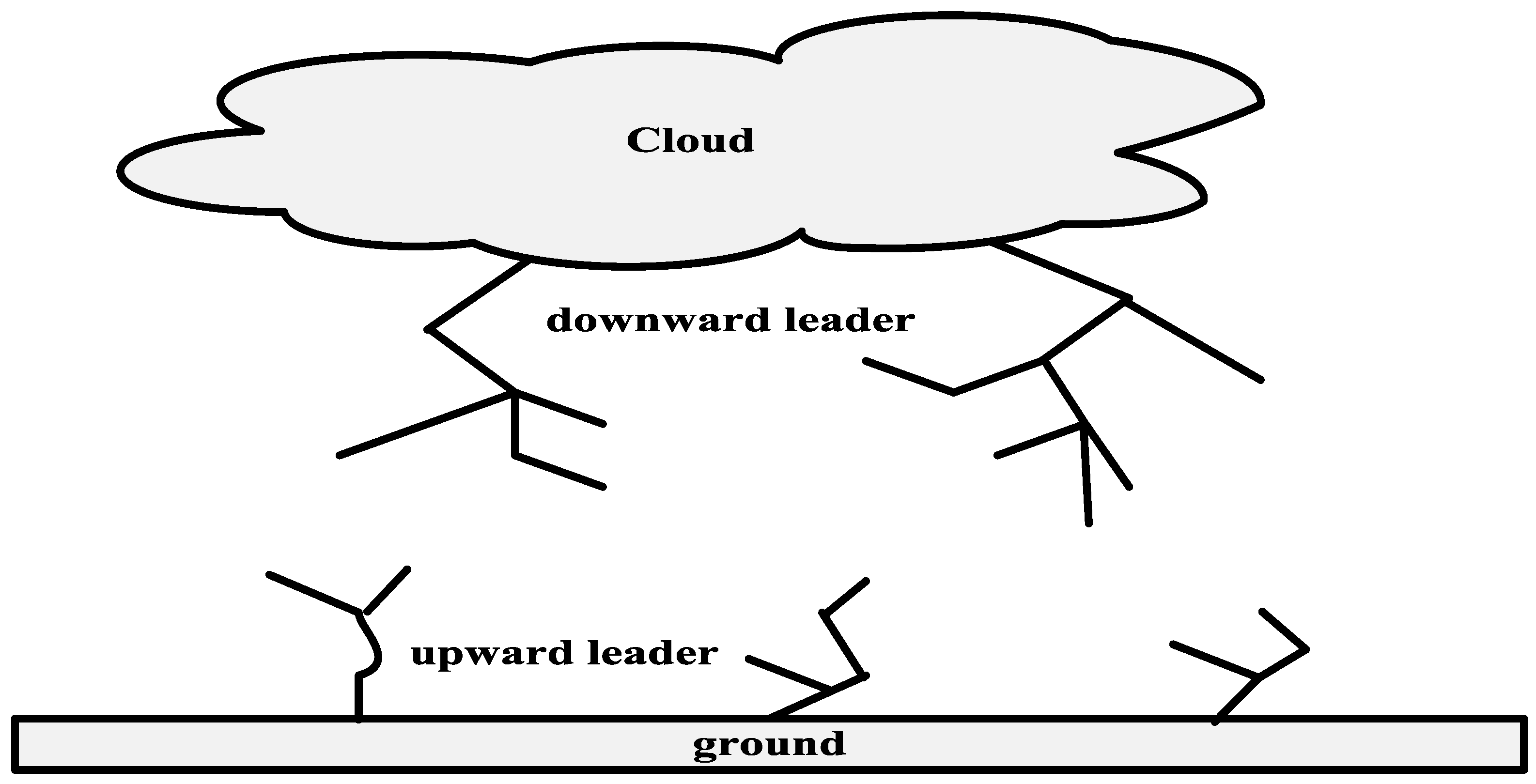
Lightning attachment procedure optimization (LAPO) is a new efficient optimization algorithm that mimics the lightning phenomena procedure in nature. The lightning is formed due to the cumulation of a high number of charges in the clouds. The continuous increase in the number of charges leads to an increase in the electrical strength and breakdown of air; consequently, several downloaders are formed, starting from the downside of the cloud, as shown in Figure 1. The down leaders are combined with the upward leaders at the strike point from the lightning.

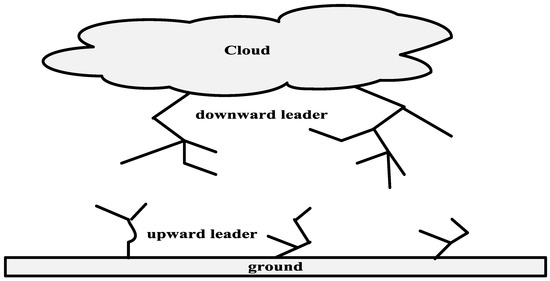
Figure 1. The charge distribution in a cloud.

LAPO is based on five step ladders including (1) air breakdown that closed to the cloud surface (2), the orientation of the lightning downward leaders, (2) branch fading, (3) extension of the upward leaders (4), and strike point position (5).

Mathematical Model of LAPO

• Step 1: Trail spots

The trial spots are the initial downward leaders’ starting points, which are evaluated as follows:

$$X_s^h=X_{min}^h+rand\times \left(X_{max}^h-X_{min}^h\right)$$

(16)

where $X_s^h$ represents the initial position of the downward leader or the trial spot. $X_{min}$ denotes the minimum limit of the control variable, while $X_{max}$ denotes the maximum value. $rand$ represents a random number within range [26]. The objective functions of the initial positions are evaluated as follows.

$$F_s^h=Fitness\left(X_s^h\right)$$

(17)

• Step 2: The next jumping of the initial points

All initial trial spots are averaged, and their objective function is determined:

$$X_r=mean \left(X_s^h\right)$$

(18)

$$F_r=Fitness\left(X_r\right)$$

(19)

$X_r$ is the averaged point. $F_r$ denotes the fitness function of the mean point. It is well-known that the lightning has many paths to jump to the next location where the lightning will go to a high-voltage point.

To update the point i, a random solution j is selected where i ≠ j. The updated point is jumped to the new location as follows:

$$X_{s\_new}^h=X_s^h+rand\times \left(X_r+X_S^j\right) IF F_j>F_r$$

(20)

$$X_{s\_new}^i=X_s^i-rand\times \left(X_r+X_S^j\right) IF F_j<F_r$$

(21)

• Step 3: Branch fading

The downward leader will be faded if the critical point is more than the electric field of the new point in terms of the objective function value; otherwise, it remains continuous; this fading can be mathematically represented as follows:

$$X_s^h=X_{s\_new}^h IF F_{s\_new}^h<F_s^h$$

(22)

$$\mathrm{Otherwise} X_{s\_new}^i=X_s^i$$

(23)

• Step 4: Upward leader movement

In this stage, the points move up, which simulates the orientation of the upward leaders, which are distributed exponentially along the channels, which can be modeled as follows:

$$A=1-\left(\frac{t}{t_{max}}\right)\times exp\left(-\frac{t}{t_{max}}\right)$$

(24)

where $A$ is an exponent operator. $t$ and $t_{max}$ are the iteration number and the maximum number of iterations. The updated point based on the upward motion is given as follows:

$$X_{s\_new}^h=X_{s\_new}^h+rand\times A\times \left(X_{best}^h-X_{worst}^h\right)$$

(25)

where $X_{best}^h$ and $X_{worst}^h$ denote the best and the worse points among the other points.

• Step 5: The strike point

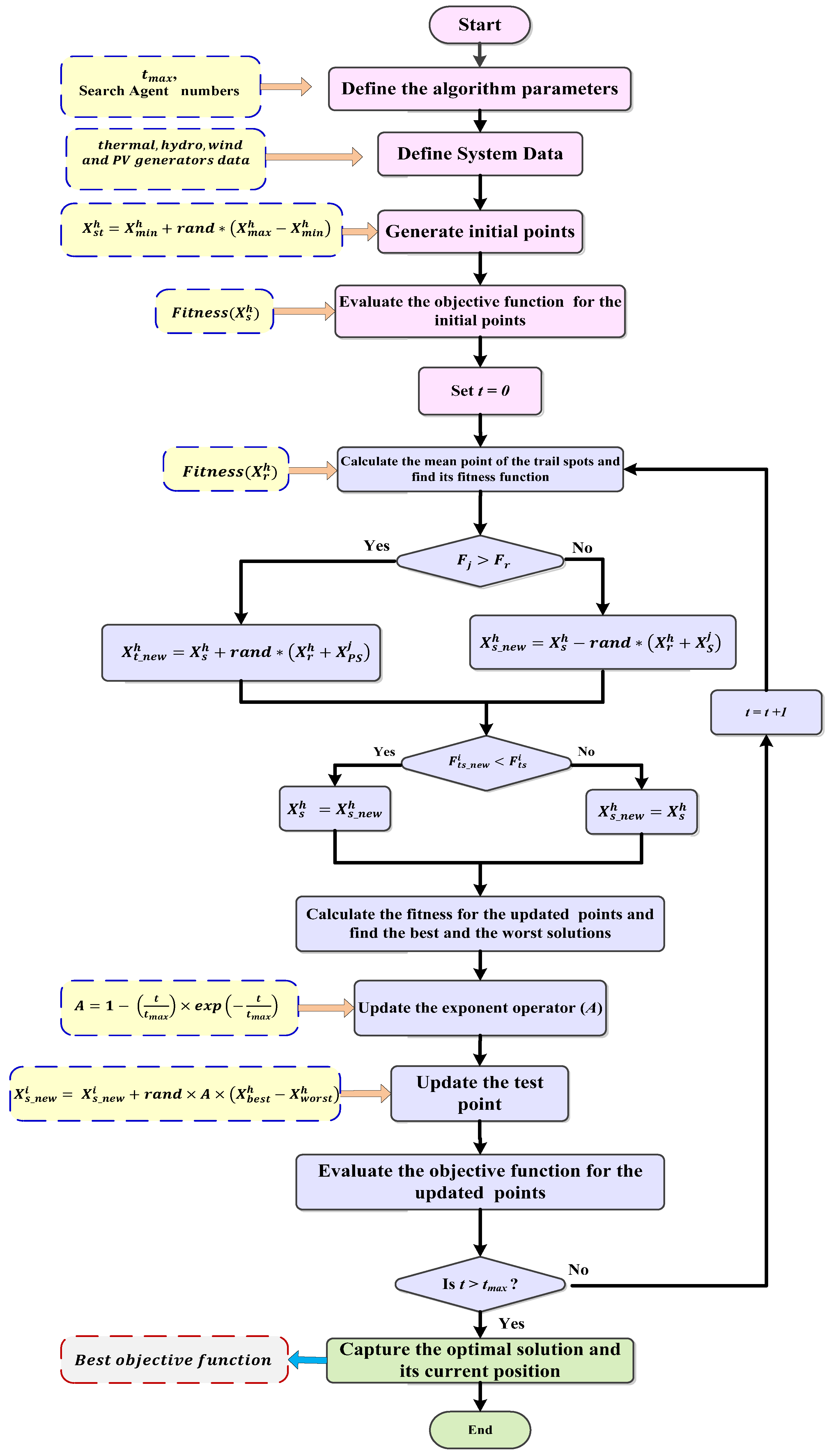
The lightning operation pauses when the down leader and the up leader gather each other, and the striking point is assigned. The flowchart of the LAPO algorithm for obtaining the optimal solution is shown in Figure 2.

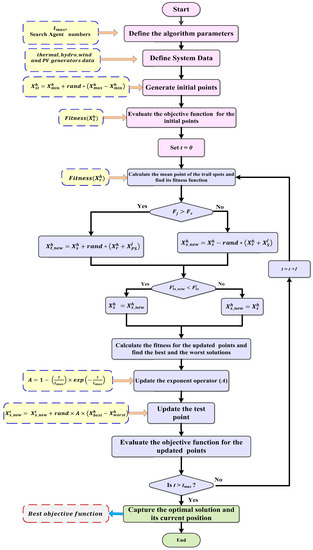
Figure 2. Schematic diagram for STHS problem with wind and PV power integration system using the LAPO algorithm.

4. Simulation Results and Discussion

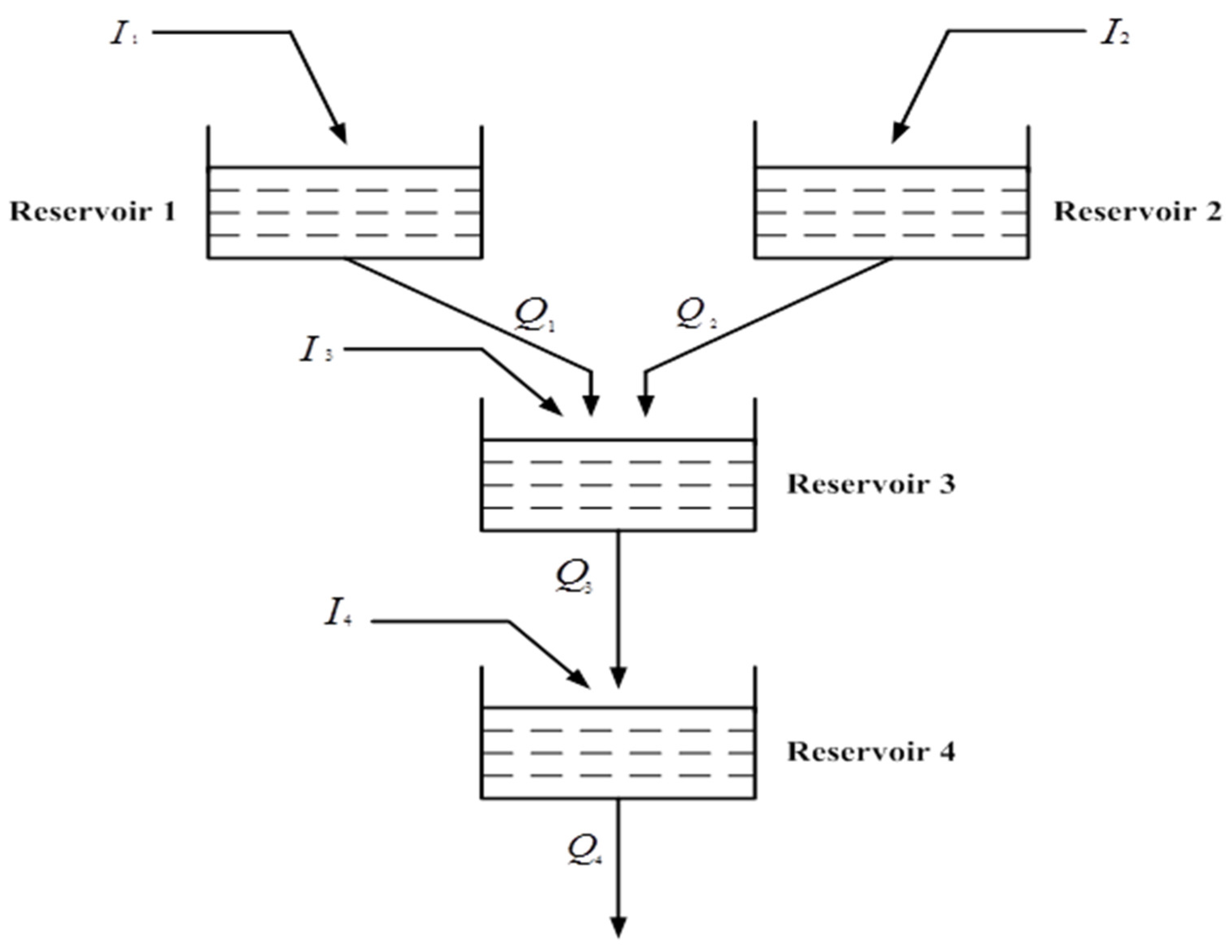
The LAPO algorithm is applied to five hydro–wind–PV–thermal power-generation scheduling test systems to verify the feasibility and effectiveness of the LAPO algorithm to solve the STHS problem with the integration of renewable energy sources. The first test system includes four hydro and three thermal units to obtain the optimal solution to the STHS problem without considering the effect of renewable energy sources. The second test system contains a multi-chain cascade of four hydropower-generating units, three thermal units, a single wind farm, and a single solar-power-generating unit. The third test system consists of a multi-chain cascade of four hydro and ten thermal-power-generating units. The fourth test system consists of a multi-chain cascade of four hydro, eight thermal-power-generating units, one equivalent wind farm, and one equivalent PV power-generation unit. Finally, the fifth test system consists of a multi-chain cascade of four hydro units, eight thermal-power-generating units, and two wind-farm generating units. There are two objectives in this system. The first objective function is the operation cost of thermal-power generation with consideration of the valve-loading-point impact, as in (1). Moreover, the total emission caused by thermal units is considered the second objective function. The hydraulic network of these test systems is demonstrated in Figure 3. The entire scheduling period is 1 day that is divided into 24 intervals. The test systems have been explained in detail and the results have been described below.

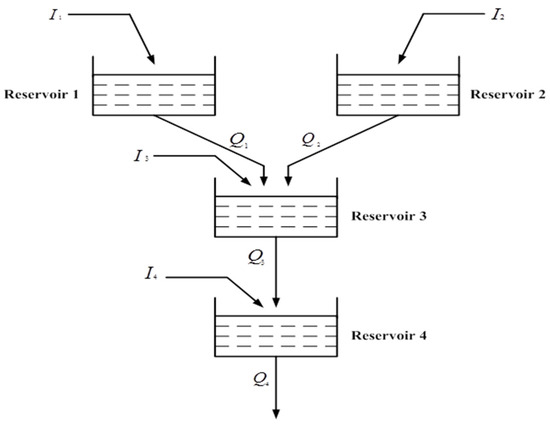
Figure 3. Hydraulic system network.

4.1. Test System 1

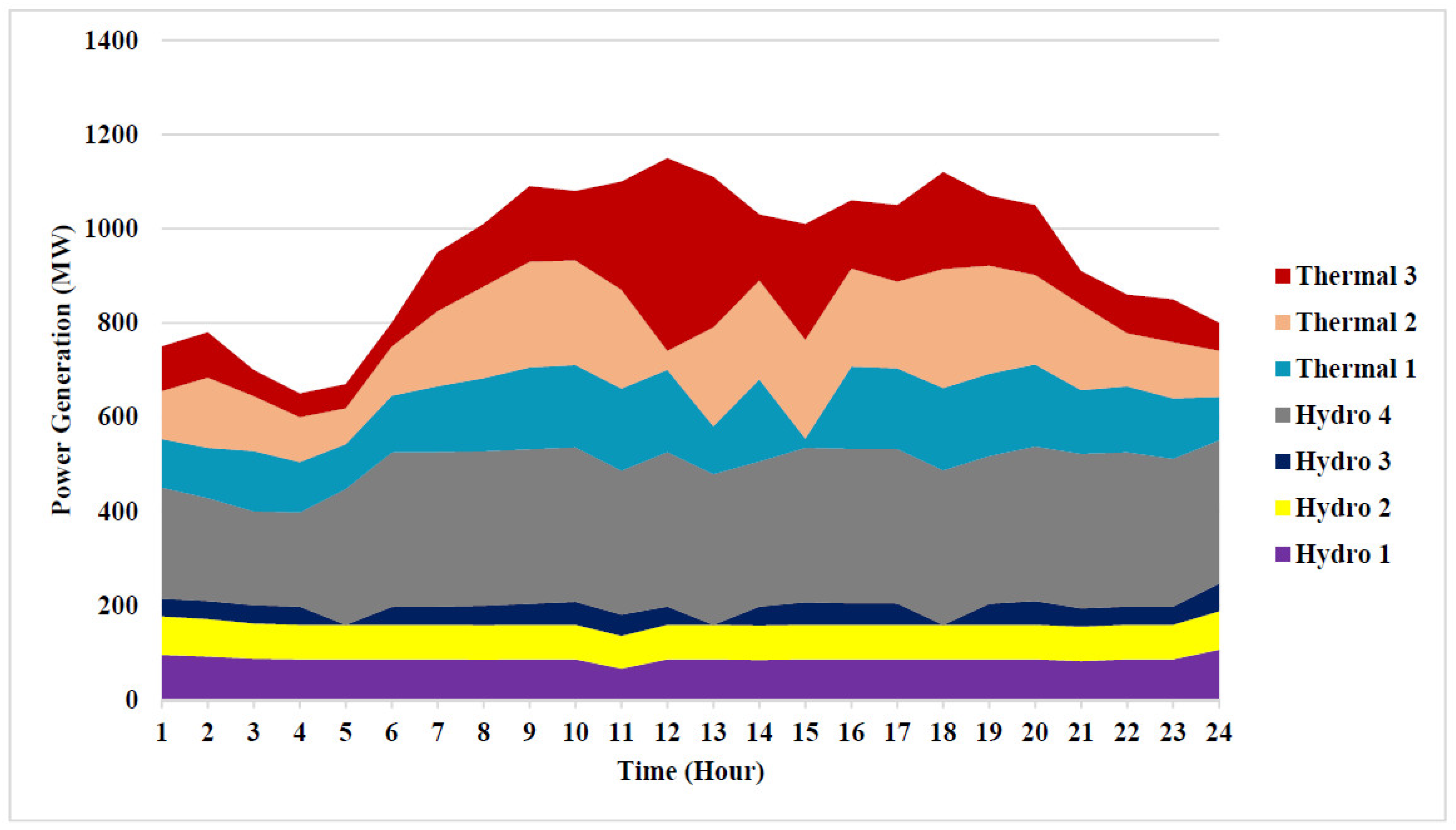
In this system, the LAPO algorithm can be used to obtain the optimal solution to the STHS problem without considering the effect of renewable energy sources. The valve-point loading impact of thermal-power plants is considered. All data details of the hydrothermal system are adopted from [38], while the emission coefficients of the thermal unit are given in [34]. The LAPO algorithm is optimal to solve the STHS problem by finding the minimum total fuel cost and reducing the emission rate of the thermal units with efficiency. The minimum cost that can be found by the LAPO algorithm is $38,800.75. The optimal power generation of the hydro, thermal units, and water discharges of each hour to minimize the fuel cost are shown in Table 3. The optimal results obtained by the LAPO method are compared to heuristic methods in Table 4. The minimum emission that can be found by LAPO is 17,347.325 Ib. The optimal power generation of four hydro units acquired from that LAPO method to minimize the fuel cost is shown in Figure 4. The optimal power generation of four hydro units acquired from the LAPO method to minimize the emission rate is shown in Figure 5.

Table 3. Optimal power generation of thermal and hydro units and water discharge of hydropower units for Test System 1 to minimize cost.

Hours (h)	$\mathbf{Water} \mathbf{Discharge} \mathbf{Rates} ({10}^4 {\mathbf{m}}^3/\mathbf{s})$				Hydro Power (MW)				Thermal Power (MW)			Total Load (MW)
	Qh1	Qh2	Qh3	Qh4	Ph1	Ph2	Ph3	Ph4	Ps1	Ps2	Ps3	PD
1	11.881	14.880	17.128	10.441	92.37	83.227	29.169	177.984	102.638	124.877	139.724	750
2	5.299	6.082	22.175	17.215	55.483	46.549	4.485	216.396	102.675	124.887	229.522	780
3	13.802	13.592	11.488	23.312	95.463	78.521	38.674	207.574	20.012	209.757	50.007	700
4	14.552	14.352	27.639	24.236	91.949	75.821	0	199.121	102.669	40.001	139.801	650
5	5.8224	14.9813	25.821	15.967	56.246	72.473	0	258.852	102.664	40.0032	139.766	670
6	14.999	13.753	10.080	24.148	87.053	70.288	38.070	325.225	99.596	40	139.778	800
7	14.061	14.363	22.972	24.989	86.437	71.486	0	327.820	20.148	124.834	319.271	950
8	13.674	8.094	29.754	24.582	86.147	48.528	0	326.620	20.004	209.427	319.263	1010
9	14.951	12.124	10.746	14.313	86.628	65.992	38.504	262.311	102.671	124.897	409.013	1090
10	12.068	14.793	22.851	16.660	83.597	72.197	0	282.772	102.626	40.000	498.795	1080
11	10.949	12.881	29.978	22.735	81.118	68.188	0	319.873	102.653	209.805	318.360	1100
12	12.959	14.548	12.827	23.469	85.279	71.807	43.305	322.807	102.587	294.706	229.505	1150
13	7.645	6.000	23.631	17.610	66.860	37.085	0	290.082	102.277	294.397	319.2940	1110
14	12.479	12.934	10.477	23.523	86.153	68.327	38.361	323.010	154.915	40.0035	319.270	1030
15	5.250	10.724	10.642	23.184	51.663	61.030	38.454	321.706	102.663	294.730	139.783	1010
16	14.999	14.999	14.427	24.872	89.021	72.499	36.103	313.277	20.000	209.811	319.274	1060
17	14.489	11.211	16.659	24.999	86.612	62.890	30.688	327.847	102.638	209.830	229.509	1050
18	14.999	14.990	10.003	20.425	86.620	72.486	38.052	308.464	174.906	209.925	229.517	1120
19	11.788	9.4846	28.025	24.983	82.931	55.652	0	327.803	164.339	209.750	229.523	1070
20	14.671	6.787	12.142	24.791	86.640	41.686	42.707	327.2481	102.671	40.000	409.035	1050
21	6.073	14.969	29.999	24.984	55.318	72.457	0	327.806	20.000	294.674	139.751	910
22	14.999	13.959	12.685	18.017	86.620	70.717	38.253	293.043	102.663	40.007	228.700	860
23	8.985	9.7949	10.115	22.697	72.635	57.085	38.099	319.711	102.658	209.802	50.007	850
24	10.875	14.999	16.860	24.925	95.751	80.948	54.837	303.378	174.997	40.096	50.000	800

Table 4. Comparison of the simulation results for Test System 1.

Algorithm	Minimum Cost ($)	Average Cost ($)	Maximum Cost ($)
LAPO	38,800.75	38,915.23	39,520
MDNLPSO [11]	40,179	40,637	41,182
CPSO [30]	40,204.32	40,592.73	40,831.55
TLPSOS [36]	40,298.28	40,298.28	40,298.28
ALO [26]	40,780.05	41,094.3414	40,905.8259
ORCCRO [39]	40,936.65	41,127.6819	40,944.2938
MCDE [6]	40,945.75	41,380.54	41,977.04
ACABC [9]	41,074.42	NA	NA
RCCRO [39]	41,497.85	41,502.3669	41,498.2129
DGSA [40]	41,751.15	41,989.02	41,821.49
CSA [41]	42,244.057	NA	NA
MDE [42]	42,611.14	NA	NA
PSO [43]	44,740	NA	NA
DE [42]	44,526.10	NA	NA
EP [34]	45,063.004	NA	NA

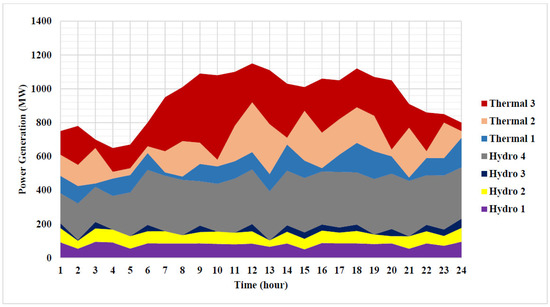
Figure 4. Optimal power generation of thermal and hydro units for Test System 1 to minimize cost.

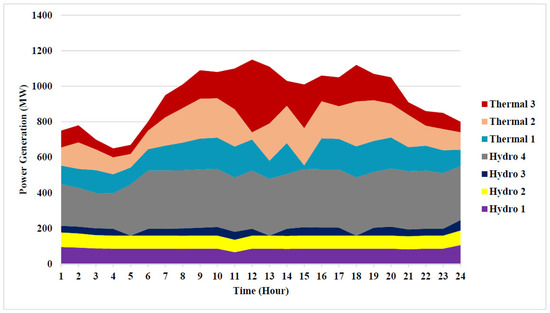
Figure 5. Optimal power generation of thermal and hydro units for Test System 1 to minimize emission.

4.2. Test System 2

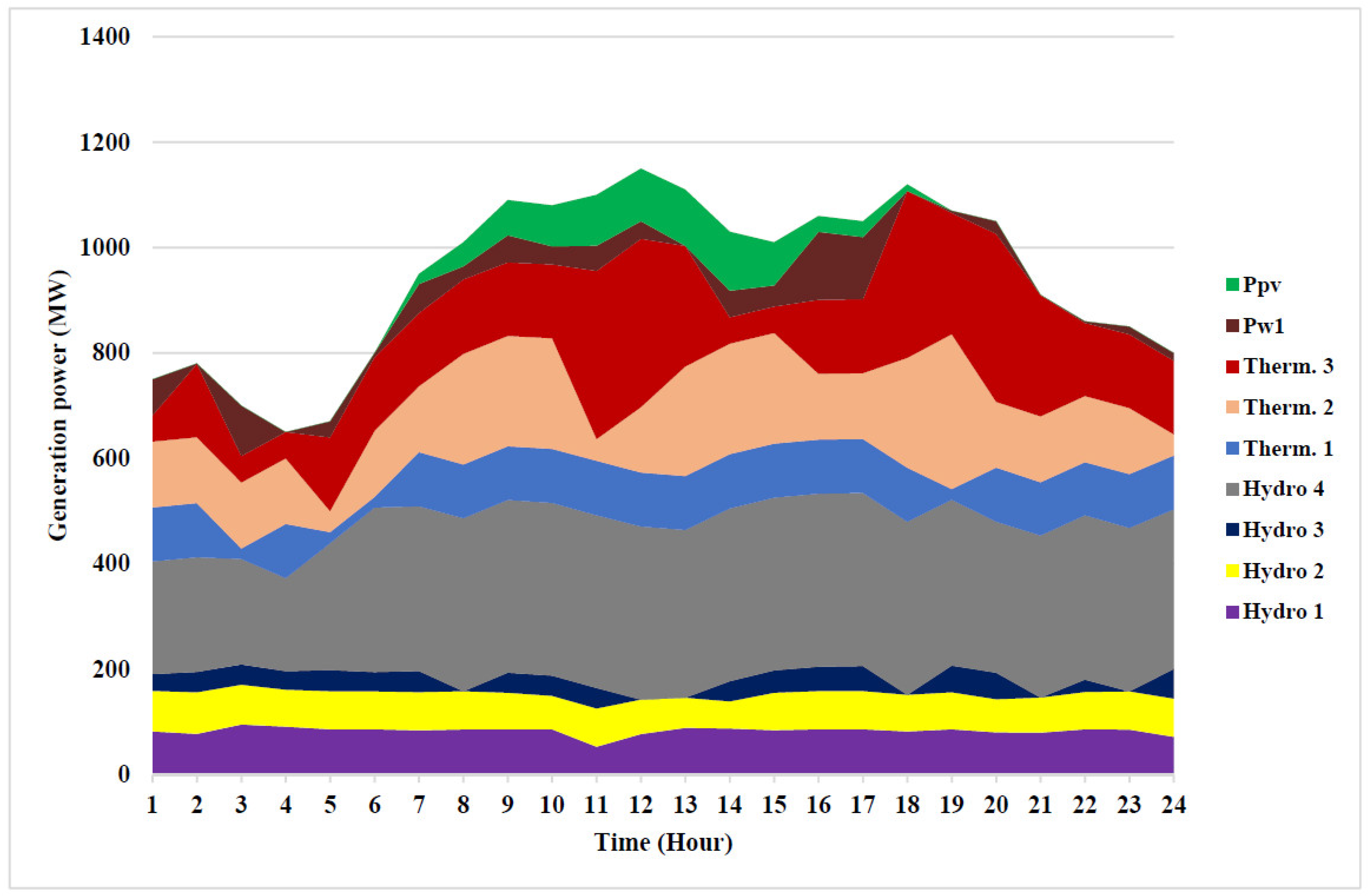
To analyze the effect of renewable energy sources, this system consists of four hydropower units, three thermal-power units, one equivalent wind-power unit, and one equivalent PV-generating unit, but this system is more complex than Test System 1 due to the constraints of the wind and PV-generating units. The rating of the wind-power-generating unit is $P_{wr}=150 \mathrm{MW}$. The cut in, cut out, and rated wind speeds are $v_{in}=4 \mathrm{m}/\mathrm{s}$, $v_o=25 \mathrm{m}/\mathrm{s},$ and $v_r=15 \mathrm{m}/\mathrm{s},$ respectively. The cost coefficient for the wind-power-generating unit is $k_w=3.25$. The cost coefficient for the PV power-generating unit is $k_s=3.5$, The rating of the PV-power-generating unit is $P_{pvr}=150 \mathrm{MW}$. The data details of renewable energy can be found in [28]. With the integration of renewable energy, the total cost obtained by using the LAPO algorithm can be reduced to $38,210.073, which helps in saving $590.68/day. The total cost that can be saved in the year is $215,597. The optimal power generation for hydro–thermal–wind–PV-generating units and water discharge rate obtained by the LAPO algorithm to minimize the fuel cost is shown in Table 5. The optimal power generation of hydropower-generating units for the provided optimal solution to Test System 2 to minimize the cost is shown in Figure 6. The minimum emission obtained by LAPO is 14,921.908 Ib. It is obvious that the emission rate can be reduced to 2425.42 Ib/day by integrating renewable energy. The optimal power generation of hydropower-generating units for the provided optimal solution to Test System 2 to minimize the emission rate is shown in Figure 7.

Table 5. Optimal water discharge of hydropower units and optimal power generation of hydro–thermal–wind–PV generating units for Test System 2 to minimize cost.

Hours (h)	$\mathbf{Water} \mathbf{Discharge} \mathbf{Rates} ({10}^4 {\mathbf{m}}^3/\mathbf{s})$				Hydro Power (MW)				Thermal Power (MW)			RE (MW)
	Qh1	Qh2	Qh3	Qh4	Ph1	Ph2	Ph3	Ph4	Ps1	Ps2	Ps3	PW	PPV
1	9.214	11.549	17.709	14.811	82.387	76.720	32.173	213.054	102.571	124.750	50.023	68.322	0.000
2	8.346	13.687	11.911	18.839	77.682	78.995	38.624	216.981	102.667	125.000	139.579	0.471	0.000
3	14.193	13.851	12.169	24.678	95.500	75.487	38.541	199.442	20.039	124.891	50.611	95.489	0.000
4	14.220	12.885	14.895	16.886	91.504	69.912	35.216	176.028	102.677	124.414	50.187	0.062	0.000
5	13.870	14.851	10.651	16.432	86.411	72.285	40.201	239.963	21.040	40.048	139.760	30.292	0.000
6	14.899	14.466	14.094	20.989	86.636	71.666	36.656	311.552	20.139	125.324	139.808	8.219	0.000
7	12.497	14.848	12.257	21.012	84.489	72.280	40.319	311.675	102.908	124.833	139.044	55.117	19.335
8	13.760	14.968	27.689	24.915	86.222	72.455	0.000	327.607	101.950	209.887	141.301	24.918	45.660
9	14.102	13.266	12.985	24.794	86.461	69.171	38.014	327.257	102.080	209.225	139.617	51.327	66.849
10	14.698	11.287	12.181	24.731	86.642	63.165	38.536	327.070	102.492	209.928	139.937	34.530	77.700
11	5.568	14.985	11.813	24.755	53.512	72.479	38.646	327.140	103.595	40.865	319.245	47.760	96.758
12	9.268	11.928	24.017	24.962	77.378	65.369	0.000	327.743	102.440	124.195	319.332	33.382	100.160
13	13.923	9.859	24.269	22.203	89.011	57.372	0.000	317.535	102.291	208.071	228.475	0.699	106.545
14	14.015	8.542	13.182	24.768	87.832	51.307	38.563	327.178	102.924	209.795	50.003	50.578	111.820
15	12.347	14.105	14.311	24.698	84.717	71.007	42.464	326.969	102.577	210.031	50.059	40.255	81.921
16	14.169	14.878	12.355	24.979	86.496	72.325	46.364	327.792	102.600	124.843	140.478	128.744	30.358
17	14.169	14.878	12.355	24.979	86.496	72.325	47.449	327.792	102.600	124.843	140.478	117.659	30.358
18	11.599	13.383	29.762	24.953	82.442	69.451	0.000	327.717	102.436	208.437	316.964	0.000	12.578
19	14.358	13.659	10.378	23.671	86.575	70.083	50.714	314.179	20.040	293.928	229.887	4.596	0.000
20	10.979	11.158	14.787	17.918	80.634	62.695	50.447	285.915	102.682	124.674	318.791	24.162	0.000
21	10.802	12.270	29.105	22.065	80.059	66.442	0.000	306.975	101.140	124.853	230.298	0.233	0.000
22	14.492	13.813	18.592	20.909	86.613	70.416	23.588	311.124	101.058	125.484	138.634	3.084	0.000
23	13.513	14.921	28.134	22.546	85.989	72.388	0.000	309.510	102.278	125.034	139.843	14.959	0.000
24	7.005	11.643	10.194	24.448	72.180	72.364	56.414	302.196	102.296	40.040	139.651	14.859	0.000
Total cost = $38,210.073

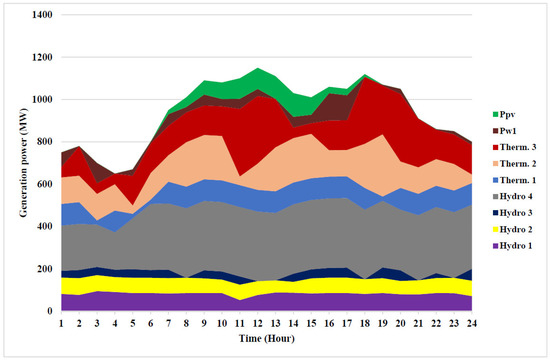
Figure 6. Optimal power generation of thermal and hydro units for Test System 2 to minimize cost.

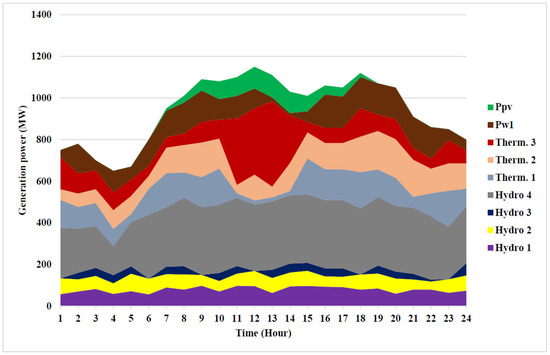
Figure 7. Optimal power generation of thermal and hydro units for Test System 2 to minimize emission.

4.3. Test System 3

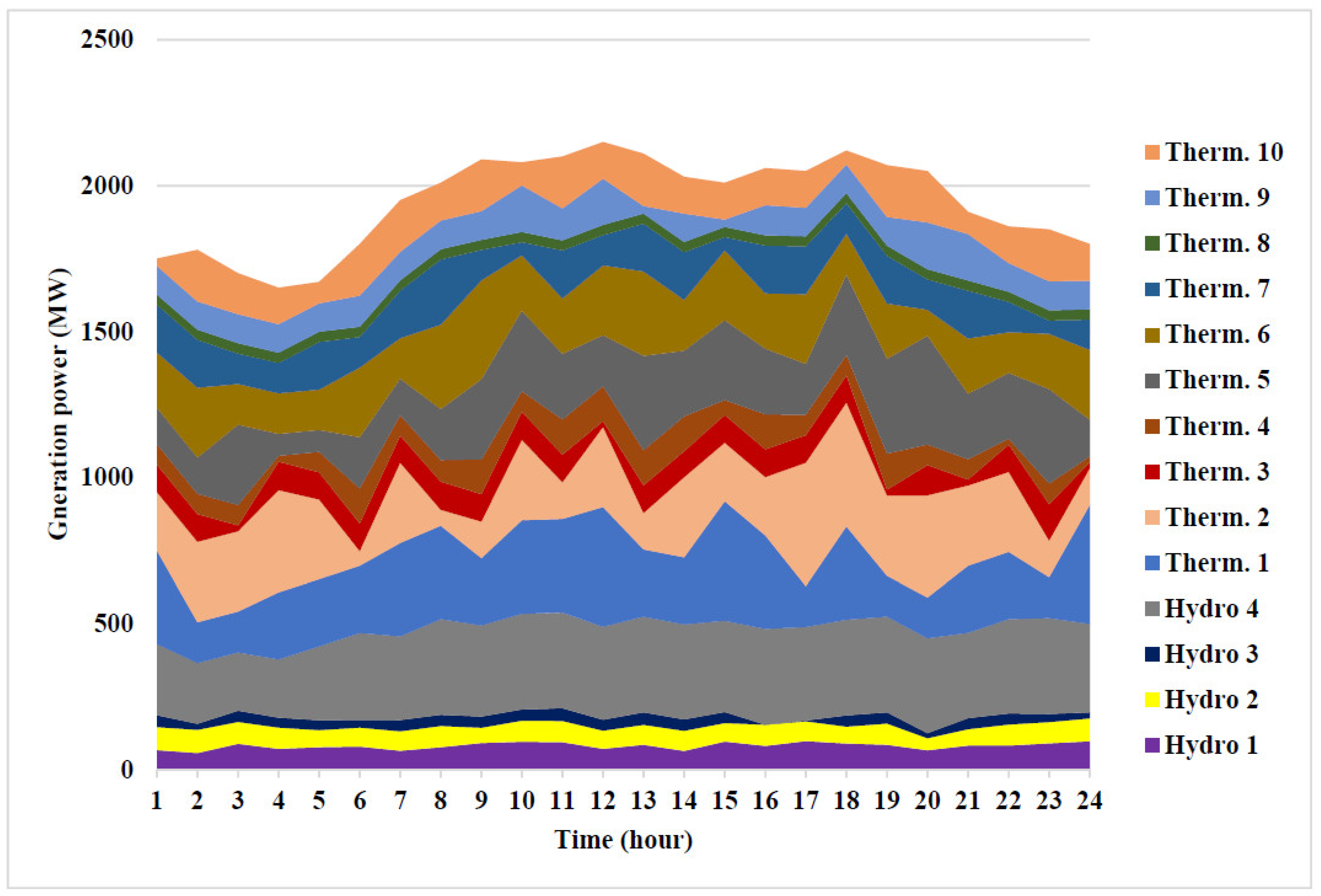
This system is larger than Test Systems 1 and 2. The hydrothermal system comprises four hydro and ten thermal-power-generating units. The system data are adopted from [43]. The optimal fuel cost that can be achieved by the LAPO algorithm is $161,746.4. Table 6 and Table 7 show the optimal variables for the given optimal water-discharge-, hydro-, and thermal-power generation. It is clear that the scheduling results that can be found by the LAPO method satisfy all hydraulic and electric system constraints. The simulation results of the LAPO method are compared to different methods in Table 8. Figure 8 shows the optimal power generation of thermal and hydro-generating units for Test System 3 to minimize cost.

Table 6. Optimal power generation and water discharge of hydropower units for Test System 3.

Hours (h)	$\mathbf{Water} \mathbf{Discharge} \mathbf{Rates} ({10}^4 {\mathbf{m}}^3/\mathbf{s})$				Hydro Power (MW)
	Qh1	Qh2	Qh3	Qh4	Ph1	Ph2	Ph3	Ph4
1	6.760	12.010	12.396	22.714	67.493	78.042	41.173	243.511
2	5.446	13.840	19.180	19.813	57.668	78.867	20.980	208.461
3	10.334	13.490	11.538	24.814	89.058	74.456	38.675	199.517
4	7.351	14.801	15.407	24.734	71.952	72.209	34.096	199.474
5	8.261	9.964	15.398	18.032	77.287	57.842	34.118	253.373
6	8.672	11.778	17.941	24.901	79.209	64.875	26.228	298.063
7	6.503	12.264	10.376	17.186	65.189	66.423	38.296	286.888
8	8.208	14.965	12.397	24.995	77.135	72.450	38.434	327.835
9	11.174	8.820	12.778	21.182	91.325	52.392	38.185	312.563
10	13.096	14.794	12.438	24.982	95.848	72.199	38.411	327.800
11	12.535	14.764	11.850	24.920	94.370	72.152	44.236	327.621
12	7.391	10.933	13.414	22.485	71.490	61.845	37.576	318.797
13	9.678	12.937	11.354	24.851	85.353	68.334	42.941	327.424
14	6.230	13.024	14.458	24.132	64.456	68.563	39.095	325.170
15	11.994	11.273	10.280	24.888	96.367	63.117	38.229	312.290
16	8.689	14.972	29.838	24.968	81.714	72.461	0.000	327.758
17	13.171	12.519	22.438	24.287	98.328	67.179	2.786	320.525
18	10.784	9.906	12.669	24.989	89.995	57.582	38.265	327.789
19	10.022	14.670	11.550	24.924	85.627	72.005	38.674	327.634
20	6.862	6.643	19.986	23.930	66.834	40.874	17.696	324.478
21	9.640	9.382	10.295	17.871	82.517	55.943	38.240	291.995
22	9.895	14.454	12.722	23.527	82.935	71.647	38.227	323.023
23	12.989	14.809	17.387	24.938	90.712	72.221	28.280	327.675
24	11.357	13.412	24.417	24.699	97.803	77.733	20.806	302.835

Table 7. Optimal thermal generation for Test System 3.

Hours (h)	Thermal Power (MW)
	Ps1	Ps2	Ps3	Ps4	Ps5	Ps6	Ps7	Ps8	Ps9	Ps10
1	319.329	199.965	94.364	69.818	124.796	189.692	163.440	35.028	97.976	25.372
2	139.517	274.234	94.918	69.222	124.509	239.416	163.417	35.178	97.002	176.611
3	139.796	274.419	20.186	70.102	274.449	139.641	104.040	35.776	99.753	140.134
4	229.711	348.804	97.751	20.379	74.830	139.648	103.858	35.280	97.494	124.515
5	229.529	272.246	93.673	69.654	74.655	138.513	163.450	35.160	96.971	73.529
6	229.672	50.164	94.925	119.624	174.692	239.511	104.444	35.055	106.832	176.706
7	319.227	274.170	93.270	69.887	124.561	139.562	162.999	35.113	98.052	176.350
8	319.290	54.043	96.594	74.199	174.471	289.433	223.111	35.412	98.156	129.437
9	229.428	124.793	94.384	119.194	274.256	339.054	103.626	35.125	98.252	177.423
10	319.774	274.655	96.785	69.947	275.943	189.591	45.030	35.188	159.733	79.095
11	320.048	125.074	95.298	120.330	224.733	190.024	163.817	35.057	109.062	178.176
12	409.140	274.323	20.044	119.761	174.385	239.579	103.397	35.210	158.384	126.070
13	229.535	124.644	95.479	119.631	323.491	289.222	163.452	35.028	25.489	179.978
14	229.384	274.084	89.611	119.352	224.457	174.504	163.176	35.168	97.131	125.850
15	409.015	199.616	95.678	51.038	273.530	239.439	45.090	35.136	25.152	126.305
16	319.914	199.477	95.586	119.724	224.602	189.559	163.545	35.197	103.567	126.894
17	139.667	421.838	94.528	69.850	174.330	239.204	163.314	35.054	97.669	125.727
18	318.913	424.026	94.116	69.549	274.606	139.759	104.756	35.200	98.136	47.307
19	139.699	274.526	20.807	122.996	324.556	189.534	163.479	35.001	98.366	177.097
20	139.766	349.273	103.877	69.888	372.111	89.593	104.221	35.029	160.000	176.360
21	229.409	274.535	20.314	69.546	224.309	189.571	163.589	35.073	159.362	75.598
22	229.553	273.538	94.161	20.283	224.512	139.818	103.896	35.057	97.956	125.394
23	139.979	124.657	125.709	69.682	323.970	189.614	45.162	35.250	99.308	177.770
24	408.281	124.712	20.438	20.042	124.704	239.473	104.203	35.046	97.895	125.940

Table 8. Comparison of simulation results for Test System 3.

Algorithm	Minimum Cost ($)	Average Cost ($)	Maximum Cost ($)
LAPO	161,746.4	160,445.4	161,935.4
ORCCRO [39]	163,066.0337	163,068.7739	163,134.5391
RCCRO [39]	164,138.6517	164,140.3997	164,182.3520
SPPSO [44]	167,710.56	168,688.92	170,879.30
SPSO [44]	189,350.63	190,560.31	191,844.28
MDE [44]	177,338.60	179,676.35	182,172.01
DE [44]	170,964.15	NA	NA
MCDE [6]	165,331.7	166,116.4	167,060.6
IDE [29]	170,576.5	170,589.6	170,608.3

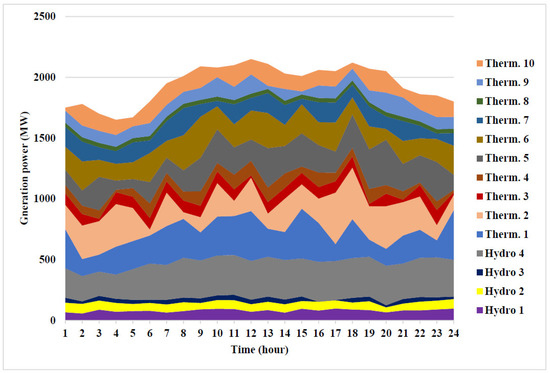
Figure 8. Optimal power generation of thermal and hydro units for Test System 3 to minimize cost.

4.4. Test System 4

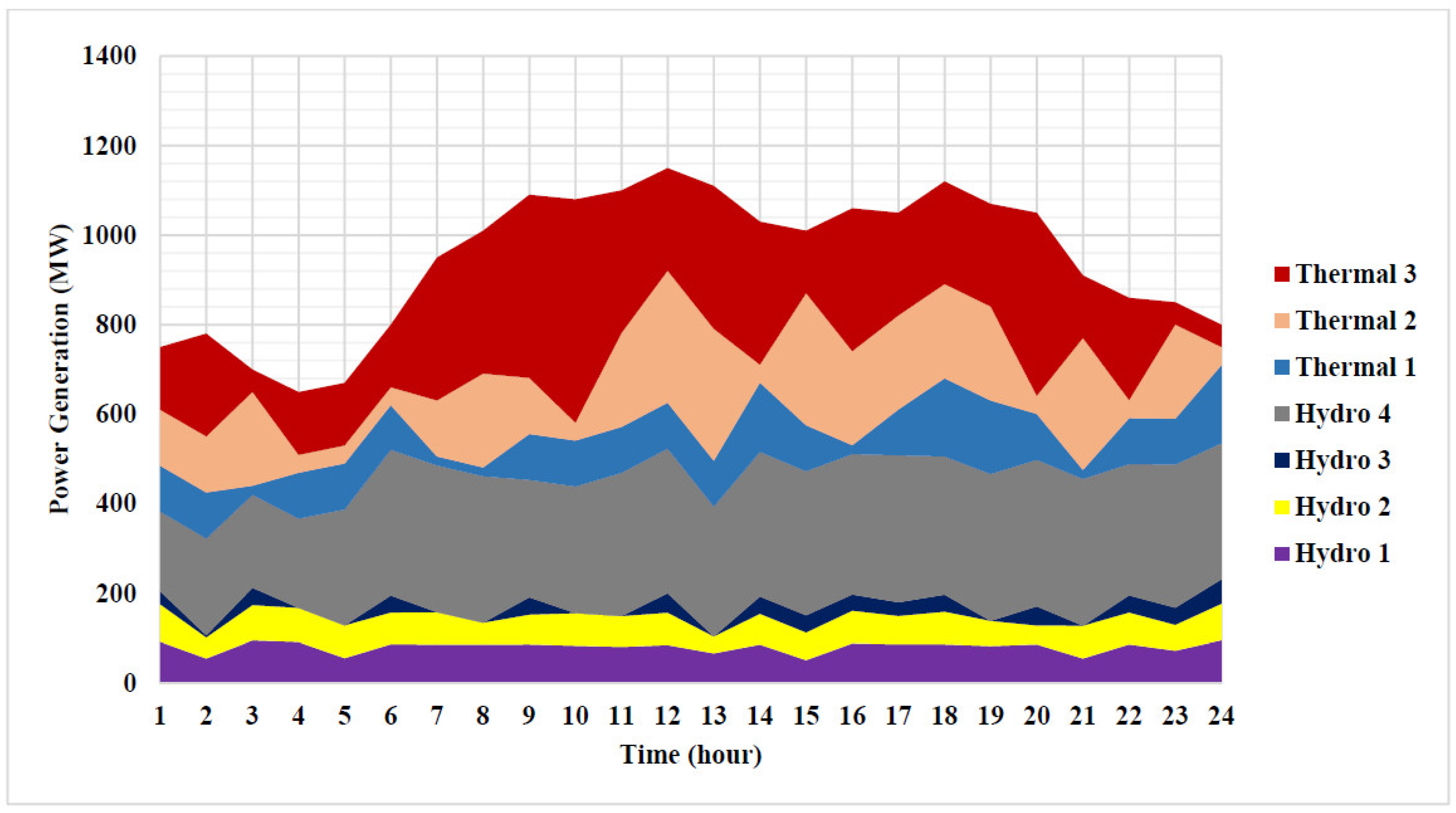
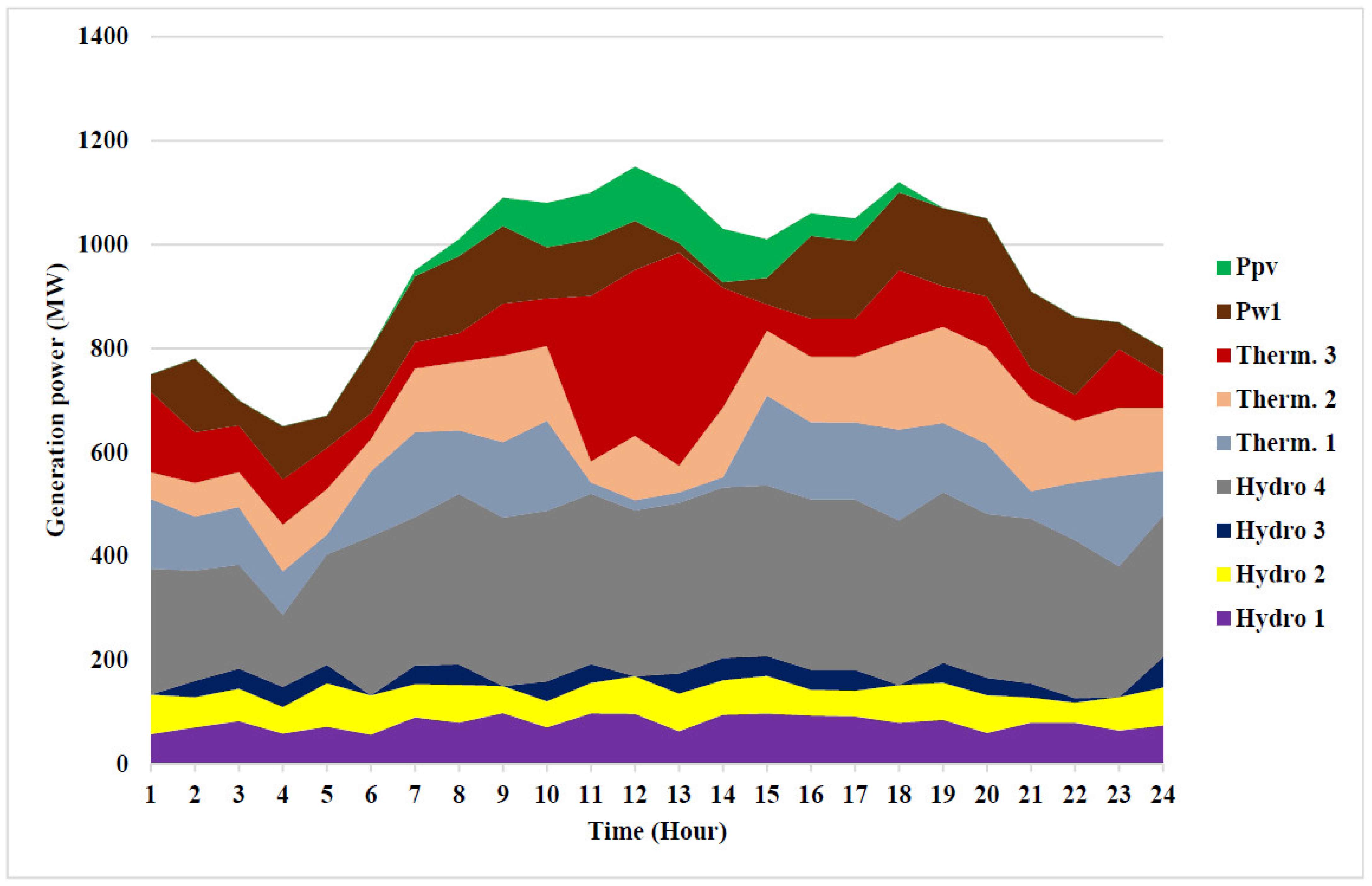
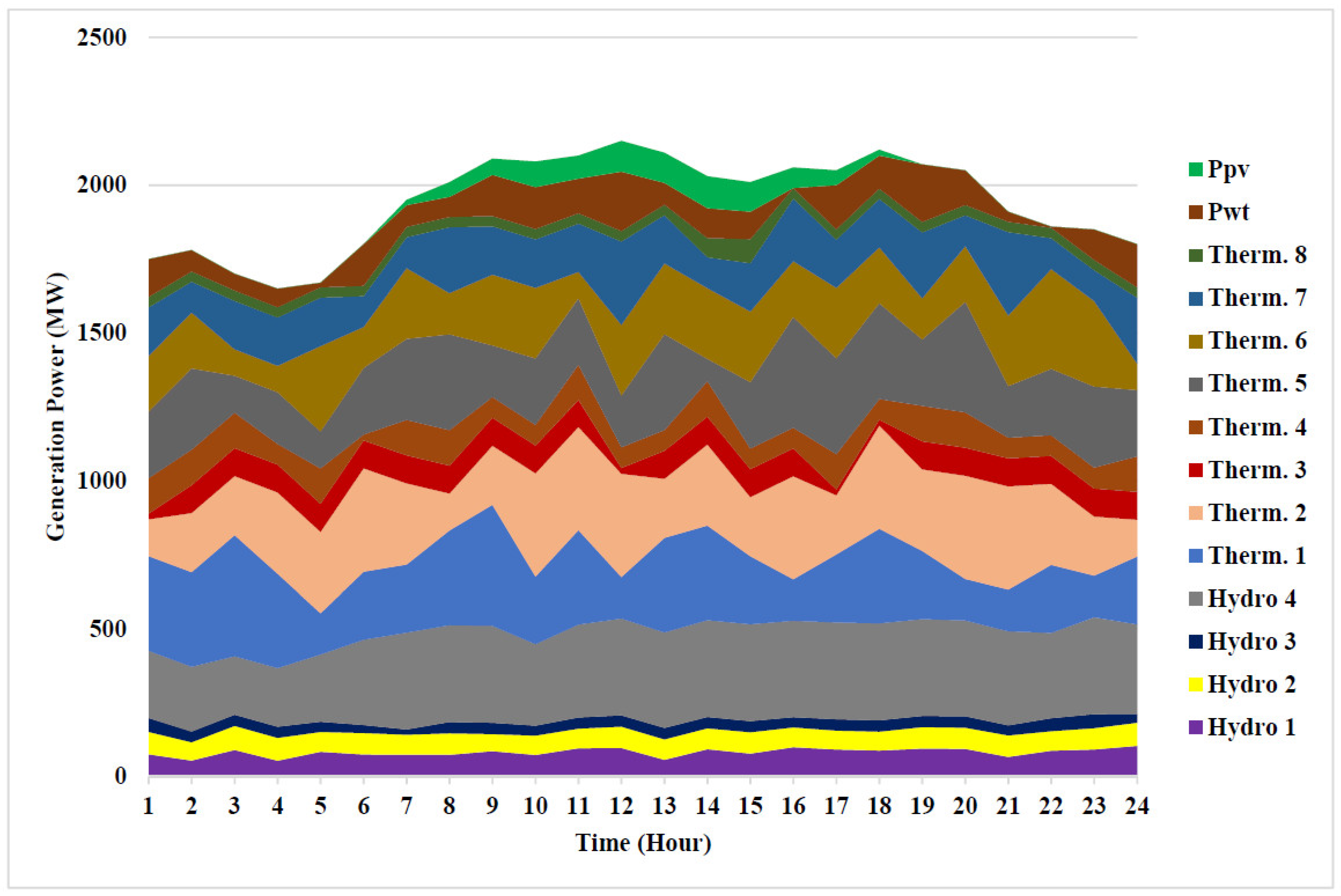
Test System 4 is similar to Test System 3, but two thermal-power-generating units are replaced by wind and PV power units. The optimal cost obtained by the LAPO method to solve the STHS problem with wind and PV power integration system is $158,572.8. The value of fuel cost that is saved by integrating renewable energy is $3173.6/day. In other words, the total annual saving is $1,158,364. The data for renewable energy are similar to Test System 2. The optimal hydropower generation and water discharge are presented in Table 9. The thermal-power generation, wind, and PV-power units for this test system are listed in Table 10. Hourly hydro- and thermal-power generation of the optimal solution for Test System 4 is shown in Figure 9.

Table 9. Optimal power generation and water discharge of hydropower units for Test System 4.

Hours (h)	$\mathbf{Water} \mathbf{Discharge} \mathbf{Rates} ({10}^4 {\mathbf{m}}^3/\mathbf{s})$				Hydro Power (MW)
	Qh1	Qh2	Qh3	Qh4	Ph1	Ph2	Ph3	Ph4
1	7.925	11.136	15.490	17.354	75.249	75.421	47.159	227.490
2	5.078	8.343	14.311	21.083	54.305	61.768	36.305	219.114
3	10.601	14.585	12.904	23.173	89.848	80.999	38.084	197.853
4	5.035	14.937	10.163	23.248	53.819	76.729	38.139	197.966
5	9.371	12.213	14.935	20.424	83.602	66.927	35.134	227.198
6	7.893	14.849	17.662	18.952	74.767	72.282	27.285	288.448
7	7.700	12.670	19.807	24.977	73.598	67.610	17.971	327.784
8	7.617	14.965	12.444	24.949	73.424	72.450	38.407	327.706
9	9.724	9.908	11.767	24.971	85.735	57.592	38.654	327.768
10	7.420	11.803	15.315	15.756	73.029	64.957	34.309	275.292
11	11.805	12.253	13.303	21.505	95.566	66.390	37.699	314.207
12	12.573	14.425	10.641	24.884	96.840	71.595	38.454	327.518
13	5.281	13.149	10.977	23.574	56.699	68.882	38.593	323.198
14	10.655	13.712	11.106	24.824	92.592	70.199	38.628	327.344
15	7.839	14.589	12.495	24.839	77.490	71.875	38.378	327.389
16	12.480	12.249	14.955	24.290	99.433	66.379	35.094	325.690
17	10.413	11.508	10.692	24.870	91.299	63.953	38.479	327.478
18	9.809	11.459	12.541	24.985	87.891	63.780	38.350	327.809
19	11.788	14.915	12.980	24.958	94.466	72.379	38.018	327.731
20	12.334	14.378	11.587	23.847	93.418	71.513	38.825	324.188
21	6.813	14.810	15.299	22.369	66.486	72.223	34.345	318.285
22	10.775	12.098	13.103	17.363	87.322	65.910	44.132	288.231
23	12.974	14.599	12.428	24.829	91.633	71.891	47.674	327.360
24	13.248	13.390	22.845	24.330	103.979	77.677	30.710	301.884

Table 10. Optimal power generation of thermal, wind, and PV power generation for Test System 4.

Hours (h)	Thermal Power (MW)								RE (MW)
	Ps1	Ps2	Ps3	Ps4	Ps5	Ps6	Ps7	Ps8	PW	PPV
1	318.954	124.729	20.295	119.772	224.470	189.373	163.447	35.046	128.594	0.000
2	319.204	199.490	94.699	119.729	274.595	189.569	104.305	35.018	71.901	0.000
3	409.050	199.469	94.804	119.806	124.718	89.731	163.589	35.039	57.009	0.000
4	318.863	274.326	94.814	69.773	174.555	89.699	163.398	35.030	62.889	0.000
5	139.716	274.361	94.885	119.779	124.720	289.084	163.466	35.030	16.097	0.000
6	229.527	349.173	94.792	20.002	224.382	139.288	104.094	35.211	140.749	0.000
7	229.463	274.415	94.673	119.744	274.411	239.455	104.165	35.050	74.084	17.578
8	319.457	124.946	94.690	119.736	324.078	139.814	222.600	35.001	68.185	49.506
9	408.844	199.612	94.827	69.784	174.546	239.541	163.433	35.007	139.598	55.060
10	227.804	349.206	94.654	69.714	224.281	239.431	163.565	35.096	141.773	86.892
11	319.096	348.906	91.073	119.106	224.369	89.717	163.312	35.053	117.605	77.900
12	139.747	348.787	20.258	69.993	174.635	239.439	281.758	35.280	201.329	104.366
13	319.311	199.617	94.858	70.001	324.266	239.510	163.518	35.198	73.874	102.474
14	319.276	273.995	94.863	119.828	74.873	239.589	104.270	65.497	100.768	108.276
15	229.371	199.615	94.800	69.740	224.442	239.345	163.326	81.612	92.618	100.000
16	139.556	348.993	94.357	69.838	374.046	189.469	211.563	35.222	0.359	70.000
17	229.473	199.584	20.049	119.624	323.928	238.441	162.997	35.007	149.688	50.000
18	319.281	349.163	20.012	69.952	323.873	189.469	163.467	35.010	111.943	20.000
19	229.989	275.560	94.824	119.889	224.421	139.663	222.982	35.115	194.962	0.000
20	139.536	349.005	94.735	119.753	373.954	188.513	104.283	35.036	117.229	0.000
21	139.913	349.328	94.877	69.823	174.495	239.085	281.896	35.002	34.240	0.000
22	229.447	274.283	94.236	69.878	224.328	338.203	104.277	35.295	4.457	0.000
23	140.274	199.654	94.907	70.537	274.360	289.342	104.221	35.010	103.137	0.000
24	229.062	124.378	94.552	119.675	224.191	89.683	222.729	35.001	146.479	0.000
Total cost = $158,572.8

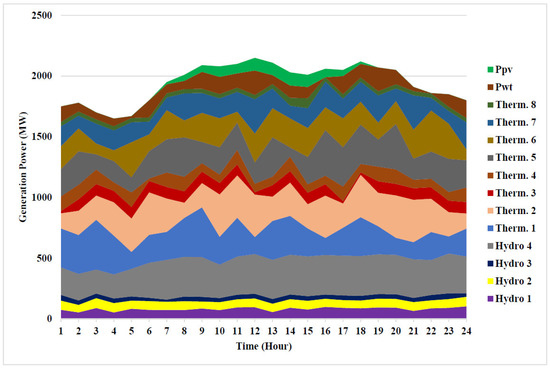
Figure 9. Optimal power generation of thermal and hydro units for Test System 4 to minimize cost.

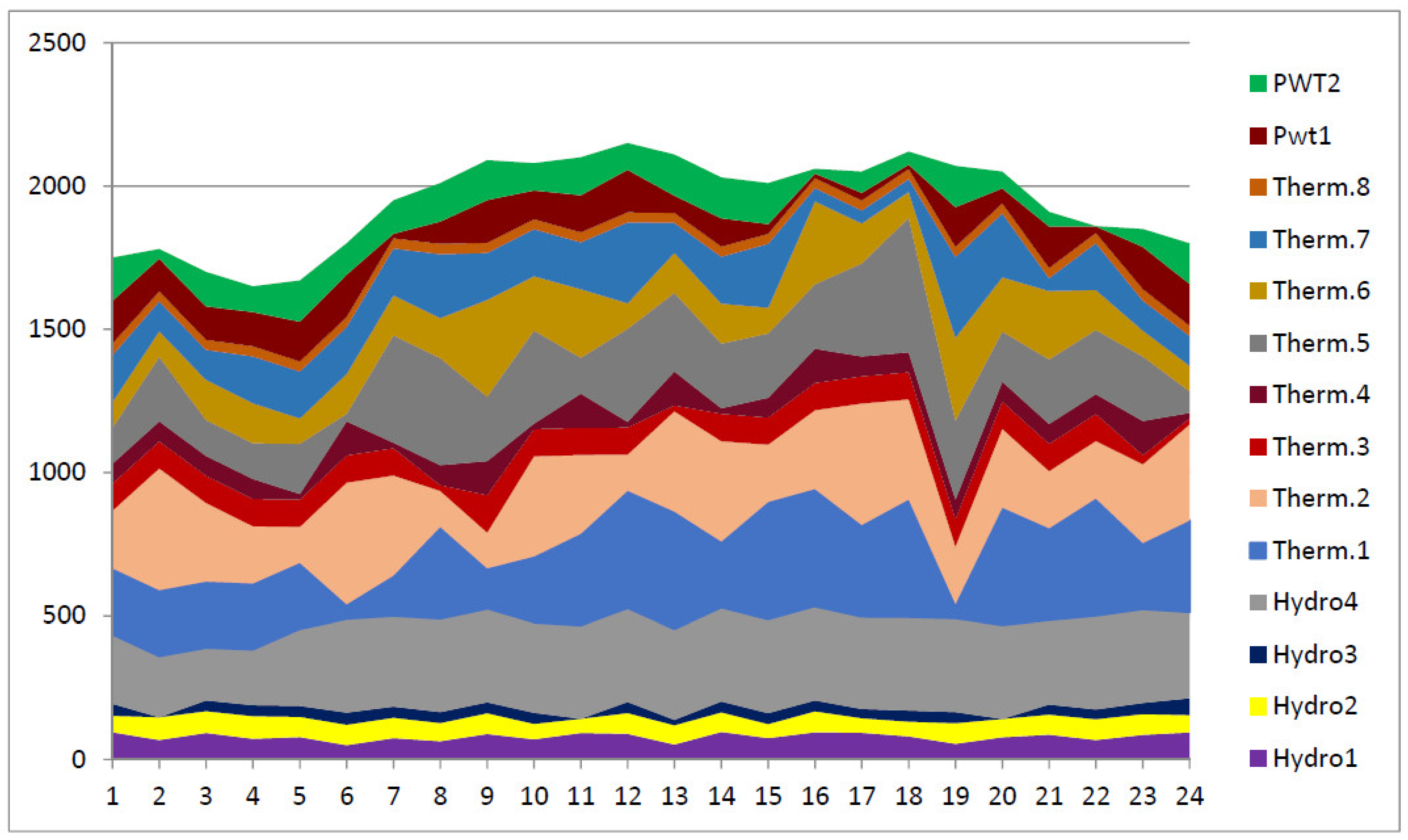
4.5. Test System 5

Test System 5 is similar to Test System 3, but two thermal-power-generating units are replaced by two wind-power-generating units. The optimal cost of Test System 5, which is obtained by LAPO method is $158,342.4, which is reduced to $3404/day when compared to Test System 3 by utilizing renewable energy sources. The total annual saving is $1,242,460. The hourly water discharge of hydro units and hydropower generation are illustrated in Table 11. The optimal solution to thermal, wind, and PV units are listed in Table 12. Figure 10 shows the optimal power generation of thermal and hydro units for Test System 5 to minimize cost.

Table 11. Optimal water discharge and power generation of hydropower units for test system5.

Hours (h)	$\mathbf{Water} \mathbf{Discharge} \mathbf{Rates} ({10}^4 {\mathbf{m}}^3/\mathbf{s})$				Hydro Power (MW)
	Qh1	Qh2	Qh3	Qh4	Ph1	Ph2	Ph3	Ph4
1	13.316	7.132	11.064	22.027	95.066	57.177	41.893	242.550
2	7.040	12.185	28.964	24.946	68.327	79.129	0.000	213.308
3	12.744	11.740	13.309	18.662	92.605	75.627	37.694	184.675
4	7.893	14.223	11.299	21.508	72.162	78.542	38.663	194.459
5	9.245	12.197	13.519	24.784	78.394	69.949	38.921	268.703
6	5.009	13.766	12.985	24.913	50.562	70.315	42.524	327.603
7	8.443	14.087	11.702	24.675	74.779	70.971	38.663	316.807
8	6.605	11.315	10.069	24.565	63.751	63.267	38.061	326.566
9	11.825	14.696	10.162	24.809	89.352	72.046	38.138	326.801
10	7.516	9.069	12.159	24.439	70.567	53.646	38.545	315.488
11	12.529	8.077	27.485	24.431	92.583	49.146	0.000	326.146
12	11.663	14.945	11.957	24.967	89.493	72.422	38.612	327.758
13	5.014	12.388	19.548	22.084	52.444	66.798	19.242	316.991
14	14.496	12.684	10.880	24.986	96.493	67.650	38.560	327.810
15	7.929	8.042	10.029	24.885	74.595	48.980	38.026	327.522
16	13.486	14.917	11.407	24.948	95.129	72.381	38.672	327.704
17	13.720	8.489	15.930	23.143	93.003	50.665	32.787	321.546
18	9.791	8.562	11.804	24.508	80.948	51.054	38.647	326.388
19	5.540	14.547	11.370	24.852	54.812	71.805	38.670	327.425
20	9.321	11.304	27.960	24.982	77.946	63.228	0.000	327.798
21	14.980	13.563	14.761	18.274	86.624	69.868	35.484	294.858
22	8.133	14.743	15.343	24.659	68.189	72.121	34.245	326.854
23	13.571	14.905	12.201	24.985	86.048	72.364	38.527	327.807
24	10.661	8.840	13.440	23.732	94.775	60.017	58.977	300.161

Table 12. Optimal power generation of thermal, wind, and PV power generation for Test System 5.

Hours (h)	Thermal Power (MW)								RE (MW)
	Ps1	Ps2	Ps3	Ps4	Ps5	Ps6	Ps7	Ps8	Pw1	Pw2
1	229.470	200.541	94.834	69.932	124.742	89.819	163.333	40.792	149.957	149.893
2	229.372	424.056	94.811	69.837	224.497	89.886	104.258	35.106	114.686	32.727
3	229.408	274.023	94.608	69.772	125.020	140.117	104.394	35.091	117.125	119.842
4	229.556	199.458	94.795	70.084	124.289	139.960	163.541	35.001	120.003	89.516
5	229.573	124.768	94.967	20.454	174.602	89.435	163.262	35.319	138.316	143.336
6	50.013	423.522	94.707	119.846	25.694	139.591	163.490	35.107	148.381	108.650
7	139.689	348.771	94.750	20.077	373.974	139.828	163.447	35.406	16.111	116.728
8	319.273	124.802	20.187	69.665	373.877	139.759	222.815	35.842	78.357	133.777
9	139.862	124.489	129.846	119.580	224.469	338.231	163.540	35.338	149.816	138.490
10	229.500	348.828	94.542	20.257	324.220	189.585	163.835	35.098	100.698	95.192
11	319.215	274.427	94.590	119.622	124.736	239.498	163.479	35.000	129.460	132.100
12	408.940	125.014	94.794	20.024	324.234	89.837	282.152	35.000	148.813	92.900
13	409.009	349.392	20.119	119.363	273.819	139.680	104.233	35.161	60.566	143.185
14	229.555	349.032	95.603	20.047	224.895	139.826	163.484	35.249	99.160	142.637
15	408.708	199.218	94.793	69.507	223.647	90.048	222.821	35.035	34.289	142.813
16	409.009	274.461	94.783	120.265	224.447	289.530	46.073	35.050	16.403	16.093
17	319.324	423.606	94.803	69.505	324.296	139.724	45.118	35.004	27.117	73.502
18	409.174	349.304	94.776	69.594	469.443	89.984	45.043	35.066	15.594	44.985
19	50.019	199.425	94.995	70.084	274.228	289.226	282.004	35.074	138.649	143.550
20	409.072	274.738	94.801	69.838	174.355	189.540	222.792	35.243	52.524	58.134
21	319.252	198.770	95.208	69.919	224.434	239.368	45.052	35.022	145.296	50.771
22	408.780	199.649	94.587	69.719	223.288	139.596	163.533	35.074	23.587	0.814
23	229.948	274.441	31.281	119.662	224.488	90.843	104.347	40.366	147.501	62.377
24	319.176	334.651	20.783	20.084	74.685	89.384	104.262	35.038	146.505	141.502
Total cost = $158,342.4

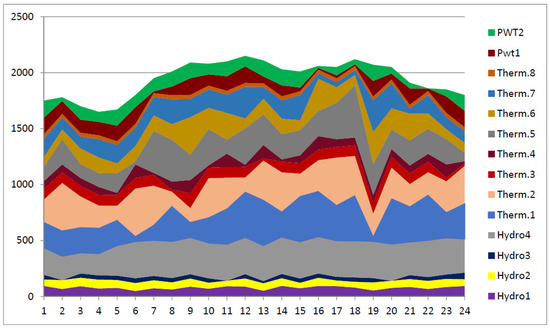
Figure 10. Optimal power generation of thermal and hydro units for Test System 5 for cost-minimizing.

5. Conclusions

This study has presented short-term hydrothermal generation scheduling (STHS) with a wind and photovoltaic power integration system using the LAPO algorithm. To examine the effectiveness of the proposed method, five systems comprising a multi-chain cascade of hydropower, different thermal units, wind units, and PV units have been used to analyze the effect of renewable energy sources in solving the STHS problem with wind and PV power integration system. In Test System 2 with the presence of wind and PV, the minimum fuel cost value reduced by $590.68/day compared to Test System 1. Moreover, total emissions reduced by 2425.42 Ib/day compared to Test System 1. In Test System 4, the minimum fuel cost reduced by $3173.6/day compared to Test System 3. In Test System 5, the minimum fuel cost reduced by $3404/day compared to Test System 3. The simulation results obtained by the LAPO method prove the efficacy and superiority of the proposed method. In the future, the short-term hydrothermal generation scheduling with integration of renewable energy considering uncertainty using different efficient and recent multi-objective optimization algorithms could be considered.