Abstract
This paper uses a standard non-cooperative sequential game with two homogeneous players to analyze investment options of groundwater development project in South Korea’s Jeju island. The model is constructed as an option game taking the uncertainty of water price and the irreversibility of investment into account. The results show that the threshold water price of follower increases with the investment scale of both the leader and the follower while the threshold water price for the leader decreases as the investment scale of the leader increases. This makes the leader choose strategies to maximize the amount of groundwater extraction regardless of the follower’s strategy. Based on the results, it is recommended for policymakers to manage sustainable use of groundwater based on the policy measures such as the groundwater extraction quota system.
1. Introduction
Jeju is a volcanic island located in the southwest of South Korea. The island is isolated from the Korean peninsula, but is about a one-hour distance by flight from Seoul (see Figure 1). Designated as a special autonomy province that maintains unique history and culture distinctive from those of the inland of South Korea (hereafter referred to as Korea), Jeju island attracts many tourists worldwide. With the attraction of volcanic mountain views, clement weather, and beaches, the number of visitors, in particular, from China and Japan is growing. The average number of visitors to Jeju is estimated to be approximately 13.6 million annually.
Figure 1.
Location of Jeju Island and the study area.
The island with subtropical weather normally records abundant annual rainfall that is about 1.5 times larger than that on the inland. However, because of the lack of perennial rivers, the island is vulnerable to water shortage problems. The water resource on the island is mainly collected mostly beneath the ground due to its unique geological property with permeable basalts into which rain and stream waters easily percolate to accumulate and move slowly in accessible and exploitable aquifers. This results in a lack of perennial streams [1]. As there are limited perennial rivers and streams, groundwater is nearly the sole source of water supply. While Jeju, isolated from the inland, has to meet the water demand by itself, the demand for water is expected to increase due to the increasing population and tourists.
There are vast amounts of literature discussing the economics of water resources for agriculture, livestock, and other uses [2,3,4,5,6,7,8,9,10,11]. Since Rubio and Castro [4] and Fisher and Rubio [5] introduced the real options approach to water resources, there has been an ongoing expansion of the application including economic evaluation of irrigation [11,12,13], water infrastructure investment projects (e.g., dams and hydroelectric power generation [14,15,16,17,18,19]), and water supply projects [20,21,22,23,24,25]. Most of the previous studies focus on the economical evaluation of infrastructure investment and water supply project under the assumption of a single player, e.g., supplier, investor, or government.
However, competition among the agents is inevitable given that water resources is limited at least for a given period of time. For example, de Sivla and Hussein [26] focused on the water competition in South America over the La Plata River Basin and Guarani Aquifer System, and examined the conflicts and resolutions from a water politics perspective. Cascão [27] defined the competition for water resources in the Nile River Basin as a hegemonic competition caused by asymmetric power, and proposed non-hegemonic riparians for sustainable and equitable use of water. Lankford and Watson [28] developed the river basic game between Tanzania and Nigeria to resolve the conflicts on water uses in Africa.
Although a large body of the literature was devoted to analyzing water resources, only a few studies were built on a real options game approach. Laukkanen et al. [29] developed a real options game model to analyze the optimal extraction of groundwater among heterogeneous farmers while taking the uncertainty of rainfall into account. The heterogeneous farmers differ in terms of their choice of irrigation technology, which results in different farmer-specific impacts on the aquifer recharge rate. Bhaduri et al. [30,31,32] use a stochastic Stackelberg differential game to examine sustainable transboundary water sharing, the case of water distribution in the Volta Basin of West Africa between Burkina Faso and Ghana.
In this paper, we build on the real options game model to examine the investor’s optimal strategy on groundwater development project, which could provide implications for policymakers to manage sustainable use of groundwater. Specifically, we develop a standard non-cooperative sequential game with two homogeneous players [33] in the context of the groundwater development project in Jeju Island. The model is presented as an option game to invest in water development project, which takes the uncertainty of water price and the irreversibility of investment into account. By combining irreversible investment under uncertainty with non-cooperative sequential game, this paper integrates the two bodies of the literature, i.e., real options and game theory. Real options models have been used to explain uncertainty and irreversibility of investment in a number of contexts, but often times in monopolistic or perfectly competitive framework. On the other hand, games of entry and exit have been studied mostly in a deterministic framework.
2. Methods
2.1. Model
In this paper, we present a standard non-cooperative sequential game with two homogenous players. The game is presented as an option game where two players sequentially make decisions on groundwater extraction investment under water price uncertainty. The resulting equilibrium is a Markov perfect equilibrium, in which each player’s strategy consists of the current state variables. The Markov perfect equilibrium is derived by assuming that each player exercises a Markov strategy based on the other player’s best response, which follows a Markov strategy as well. In Section 3, we use the model to examine a groundwater development project in Jeju Island where water resource management is an important issue because groundwater is nearly the sole source of water supply while the availability of groundwater is limited.
We now introduce the model. Two players are indexed by leader (l) and follower (f). Under the profit maximization, the value function can be written as
where the subscript i = l and f denotes the leader and follower, respectively. In Equation (1), qi is the amount of groundwater extraction of the corresponding player. p(t) is the price of water. The cost C is a function of L and h(t), where L denotes the surface elevation and h(t) denotes the groundwater level, both are measured in meters. Lastly, p is the discount rate and E is the expectation operator.
Water price p(t) evolves exogenously and stochastically according to a geometric Brownian motion (GBM) with drift given by the following expression [12,13,20,21,34]:
where μ is a drift rate and σ is a volatility rate. dz is the increment of a standard Wiener’s process satisfying E(dz) = 0 and E(dz2) = dt.
We specify the cost C(L, h)(t)) as follows:
where c1 denotes charges for utilization of water, which is imposed to players by local government, c(h(t)) cost for groundwater extraction depending on groundwater level h(t), and c3 maintenance cost including costs for meeting water quality requirements and periodic inspections. Let γ denote the marginal cost of groundwater extraction per cubic meter of groundwater from depth of one meter. Thus, L − h(t) represents the depth from which groundwater has to be extracted, and the marginal cost of groundwater extraction per cubic meter can be written as
Groundwater reservoir (S(t)) is assumed to be a single cell [35], which allows us to calculate S(t) as the area of aquifer (m) multiplied by the groundwater level (h(t)).
where S(t) and h(t) evolves according to
where N denotes the natural recharge which is calculated as
In Equation (8), α and r denote natural recharge rate and total precipitation, respectively. In the simulation, total precipitation is assumed to be fixed at the average precipitation for 30 years.
We now rewrite the value function and constraints as follows.
Using Ito’s Lemma and the property that dt2 → 0, dtdz → 0 and dz2 → dt, the following Hamilton–Jacobi–Bellman (HJB) equation is obtained [36]:
which are linear and differentiable with respect to ql and qf. In this model, the optimal quantity of extraction(qopt) follows the bang-bang solution where if p < V (p), then qopt = qmax, and if p > V (p), then qopt = 0 [34,37]. We can get Vl,h = m (p − c1 − c(h) − c3) and Vf,h = m (p − c1 − c(h) − c3) by differentiating Equations (11) and (12) with respect to ql and qf, respectively. By substituting these first order conditions into the Equations (11) and (12), the following constrained HJB is obtained:
2.2. The Follower’s Problem
Since the model is solved backwards, we first solve the optimization problem of the follower. The option value function and the solution for the value function are written as
where the superscript 1 denotes after the investment is made. In equation (15), β > 0 should be satisfied. In Equations (15) and (16), the two unknowns are the threshold water price (p*f) and the option constant term (Af,1), which are determined by imposing the value matching and smooth pasting conditions. While the value matching condition (F (p) = V (p) − If) imposes that the net benefit from the investment should exceed the investment cost, the smooth pasting condition (∂F (p)/∂p = ∂V (p)/∂p) imposes that the marginal net benefit and the marginal investment cost should be equal at the threshold water price. If denotes the initial irreversible investment cost of the follower.
The p*f and Af,1 are obtained as follows.
Equation (17) shows that an increase in groundwater extraction cost and discount rate increase the threshold water price, which delays the follower’s investment. On the other hand, an increase in groundwater level decreases the threshold water price. β/(β−1), the option multiplier, represents hysteresis in the real options literature, i.e., the optimal investment threshold under uncertainty should exceed the threshold point without uncertainty.
2.3. The Leader’s Problem
The leader’s problem is analyzed for the two regimes, i.e., the regime before the follower makes the investment decision and the regime after the follower makes the investment decision.
Equation (19) includes an option-like term, which anticipates the negative effects of the follower’s investment on the leader’s expected payoff. It is not actually the value of the investment option to be exercised by the leader, but the value of the future investment induced by the follower to the leader [33]. Al,1 can be obtained as follows.
Fudenberg and Tirole [38] state that the expected payoff of the two players must be equal at the leader’s investment point. For two player preemption games, Fudenberg and Tirole [38] show that there exists a symmetric mixed strategy equilibrium that involves rent equalization, which means that in equilibrium, the expected value of the first mover equals that of the second mover. If it were not the case, one player would have an incentive to deviate and the proposed outcome could not be an equilibrium. In our model, this can be written as follows:
Since there is no closed form solution for Equation (21), in the next section, the numerical analysis is used to solve for pl by using MATLAB. The solution from the Equations (17) and (21) provides the Markov perfect equilibrium.
3. Simulation
3.1. Data
We consider the case of groundwater facility located in the east of Jeju Island (Figure 1). The area of aquifer (m) is 150,682,797 m2. Topographic elevation of the facility is 342.6EL. m, with depth of 490 m, and the average groundwater level (h) of 250.75 m in 2015 [39]. The average precipitation (r) of the region is 1,923 mm [40] and the natural recharge rate (α) is 0.431 [41].
The drift rate (μ) and the volatility rate (σ) of the water price (p) that follows the gBm process are estimated using the data obtained from the annual statistics of Jeju Special Self-Governing Province [42]. When we define y(t) = log(p(t) − log(p(t−1)) and denote Δ the time interval, it can be shown that y(t) follows the normal distribution, where the mean and variance of y (t) are written as E(y(t)) = (μ − σ2/2)/Δ and Var(y(t)) = σ2Δ, where μ = ӯ/Δ + sy2/2Δ and σ = sy-√Δ can be obtained from the sample mean (ӯ) and the standard deviation (sy) of y(t) [43]. The price parameters are calculated as μ = 0.0436 and σ = 0.1009.
Cost parameters are assumed as follows. Charges for utilization of water (c1) is derived as 0.071 US$ /m3 [39]. In general, the marginal cost of groundwater extraction, could vary depending on the fuel cost or depth of water [44,45]. However, this paper assumes that the marginal cost of groundwater extraction (γ) is constant at 0.00038 US$/m3·m based on [11]. We also assume the constant maintenance cost (c3) at 0.041 US$/m3 based on [46]. The maintenance cost should not be constant especially if there exists the saltwater intrusion problem, as the intrusion of saltwater would increase the maintenance cost. However, as [46] discussed, desalination is not a significant issue on Jeju island. Based on [47,48], investment cost for leader (Il) is calculated as US$9108,333. Assuming that investment cost for follower is lower than that for leader, we simply multiply Il by 0.9 to calculate investment cost for follower (If). Finally, we take the discount rate p = 0.054, which is the average yield of AA- and BBB- grade corporate bonds in 2015 [34].
3.2. Results
Using the parameter values in Table 1, the threshold water price is calculated for three scenarios, the follower’s groundwater extraction is set as (i) 80% of qmax, (ii) equal to qmax, and (iii) 120% of qmax. The scenarios allow us to investigate the optimal extraction of the leader (ql) in response to the possible investment scale of the follower. The scenarios also analyze the threshold water prices corresponding to the investment scale.

Table 1.
Parameters for simulation.
Table 2 presents the threshold water price of the leader p*l and the follower (p*f) for each of the three scenarios. For example, p*l and p*f are estimated as 0.1239 US$/m3 and 0.2593 US$/m3 for scenario 2, respectively. While p*f increases with the investment scale of both the leader and the follower, p*l decreases as the investment scale of the leader increases. Moreover, for each scenario of the investment scale of the leader, p*l is highest when the investment scale of the follower is equal to qmax. Table 2 suggests that the leader selects the strategy to increase ql to lower the p*l and raise p*f regardless of the follower’s strategy. The follower chooses the strategy to decrease qf to lower p*f. Therefore, scenario 3 for the leader and scenario 1 for the follower is the strategic dominance, i.e., (p*l/p*f) = (0.6950, 0.2660), where the ratio of threshold (p*f/p*l) is highest with 2.61 as shown in Table 3. The results can be summarized that the leader chooses the strategy to maximize the amount of her groundwater extraction regardless of the follower’s strategy.

Table 2.
Investment threshold price by scenario (unit: US$/m3).

Table 3.
Ratio (p*f/p*l) of investment threshold price by scenario.
We now perform the sensitivity analysis of the investment threshold price over the range of the variables. Figure 2 shows the sensitivity of the threshold water price (p*f) with respect to the volatility (σ) and the investment cost of follower (If). While an increase in both σ and If increases p*f, Figure 2 shows that p*f is more sensitive to the initial investment cost If than the uncertainty σ.
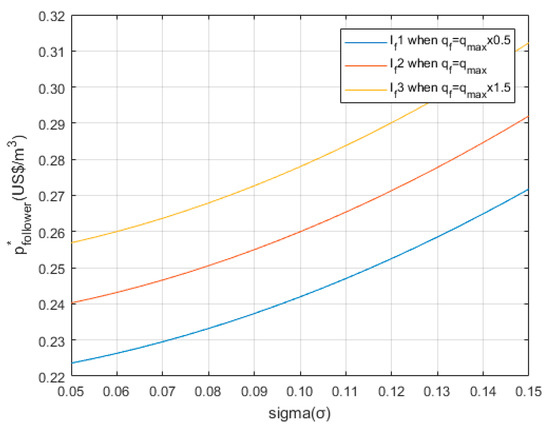
Figure 2.
Sensitivity analysis of p*f with respect to σ and If.
Figure 3 shows the effects of the groundwater extraction of the leader (ql1) and the follower (qf) on the threshold water price of the follower (p*f). p*f increases as ql1 and qf increases, and is more responsive to ql1 compared with qf. It implies that the leader can defer the entry of the follower by increasing ql1 and therefore increasing p*f, which enables the leader to collect monopolistic profits until the follower enters into the market.
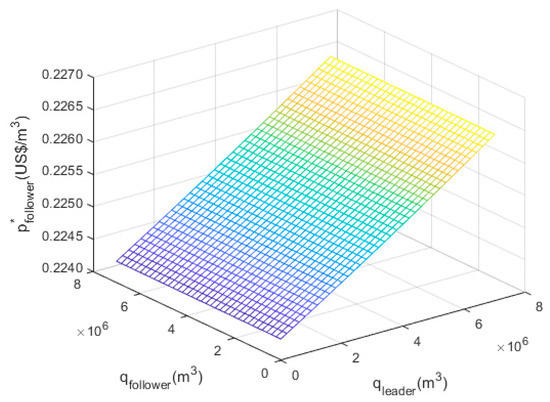
Figure 3.
Sensitivity analysis of p*f with respect to ql and qf.
We now examine dynamics of the extraction cost c(h(t)) in Equation (4) and the groundwater level h(t) in Equation (7). We investigate three scenarios where the total groundwater extraction qtotal is equal to (i) qmax × 1.5, (ii) qmax × 2.0, and (iii) qmax × 2.5.
Figure 4 presents the dynamics of the groundwater extraction cost. As [49] pointed out, late entry of the follower allows the leader to extract the groundwater at a lower cost. Since the leader collects monopolistic profits from preemption, the leader is likely to extract more than the efficient amount. Finally, Figure 5 presents the dynamics of the groundwater level. If the groundwater recharge is greater than the groundwater extraction, the groundwater level will rise, and the positive slope in Figure 5 shows that the recharge is greater than the extraction under all scenarios. On the other hand, it can be shown that the competition between the two players decreases the groundwater level in case of duopoly.
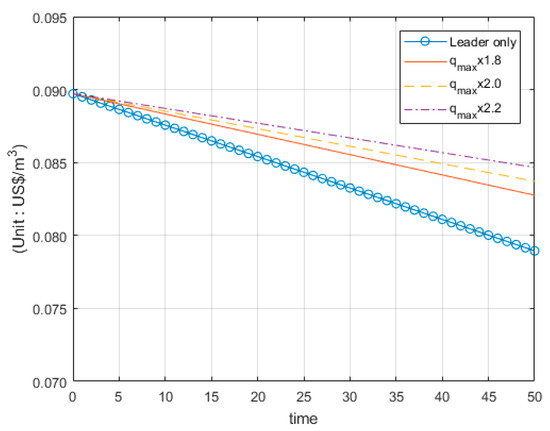
Figure 4.
Dynamics of the groundwater extraction cost c(h(t)).
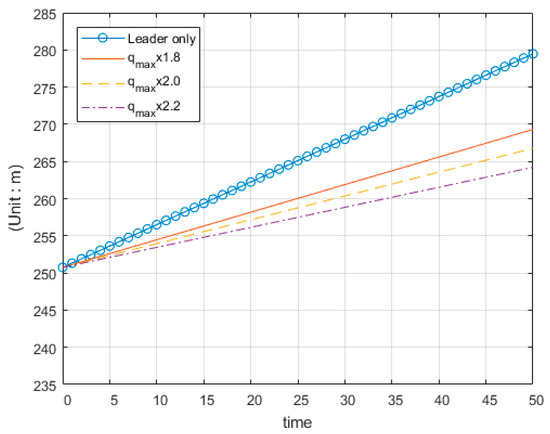
Figure 5.
Dynamics of the groundwater level h(t).
4. Conclusions
In this paper, we developed a model of standard non-cooperative sequential game with two homogeneous players to analyze investment decisions on groundwater development project on South Korea’s Jeju island. The model was presented as an option game, which allowed us to take the uncertainty of water price and the irreversibility of investment into account.
The results show that the threshold water price of the follower increased with the investment scale of both the leader and the follower while the threshold water price of leader decreased as the investment scale of the leader increased. This made the leader choose the strategy to maximize the amount of her groundwater extraction regardless of the follower’s strategy, which allowed the leader to collect monopolistic profits by deferring the entry of the follower. Based on the results, it is recommended for policymakers to manage sustainable use of groundwater based on the policy measures such as the groundwater extraction quota system.
Future research can be extended to several directions. First, our model could be extended to incorporate precipitation uncertainty. Second, it would be interesting to model the conjunctive use of surface water and groundwater. Third, this paper was built on the single-cell aquifer model, which assumed that an aquifer responded uniformly and instantly to groundwater pumping. However, as Brozovic [50] pointed out, our results could be misleading especially if the magnitude of the groundwater pumping externality is large. This should be demonstrated in the future research. Fourth, it is also important to incorporate emerging issues including climate change, ecosystem projection and groundwater quality. Finally, a possible extension could be to develop a model with heterogeneous groundwater developers.
Author Contributions
Conceptualization, J.L.; methodology, J.L.; software, J.L.; validation, J.L.; formal analysis, J.L; investigation, J.L.; data curation, J.L.; writing—original draft preparation, J.L. and H.J.; writing—review and editing, H.J.; visualization, J.L.; supervision, H.J.; project administration, J.L. and H.J. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
We thank two anonymous referees for their helpful comments and suggestions. This article developed a part of the first author’s doctoral dissertation ‘Stochastic dynamic management of groundwater using real options approach with uncertainty of price’, and we would like to express great gratitude to advisor Hojeong Park.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Won, J.H.; Lee, J.Y.; Kim, J.W.; Koh, G.W. Groundwater occurrence on Jeju Island, Korea. Hydrogeol. J. 2006, 14, 532–547. [Google Scholar] [CrossRef]
- Burt, O.R. Optimal resource use over time with an application to ground water. Manag. Sci. 1964, 11, 80–93. [Google Scholar] [CrossRef]
- Knapp, K.C.; Olson, L.J. The economics of conjunctive groundwater management with stochastic surface supplies. J. Environ. Econ. Manag. 1995, 28, 340–356. [Google Scholar] [CrossRef]
- Rubio, S.J.; Castro, J.P. Long-run groundwater reserves under uncertainty. Investig. Econ. 1996, 20, 71–88. [Google Scholar]
- Fisher, A.C.; Rubio, S.J. Adjusting to climate change: Implications of increased variability and asymmetric adjustment costs for investment in water reserves. J. Environ. Econ. Manag. 1997, 34, 207–227. [Google Scholar] [CrossRef]
- Tsur, Y. The economics of conjunctive ground and surface water irrigation systems: Basic principles and empirical evidence from Southern California. In Decentralization and Coordination of Water Resource Management; Springer Science & Business Media: New York, NY, USA, 1997. [Google Scholar]
- Winter, T.C.; Harvery, J.W.; Franke, O.L.; Alley, W.M. Ground Water and Surface Water: A Single Resource; U.S. Department of the Interior Bruce Babbitt, Secretary: Denver, CO, USA, 1998. [Google Scholar]
- Mikhail, M.; Fencl, A.; Naruchaikusol, S.; Kemp-Benedict, E. Innovation and Diffusion of Sustainable Agricultural Water Resource Management in a Changing Climate: A Case Study in Northeast. Thailand; Stockholm Environment Institute: Stockholm, Sweden, 2010. [Google Scholar]
- Evans, W.R.; Evans, R.S.; Holland, G.F. Conjunctive Use and Management of Groundwater and Surface Water within Existing Irrigation Commands: The Need for a New Focus on an Old Paradigm; Groundwater Governance: Sydney, Australia, 2011.
- Douxchamps, S.; Augustine, A.; Jennie, B. Evolution of Agricultural Water Management in Rainfed Crop-Livestock Systems of the Volta Basin; CGIAR Challenge Program on Water and Food: Colombo, Sri Lanka, 2012. [Google Scholar]
- Nasim, S.; Helfand, S. Optimal Groundwater Management in Pakistan’s Indus Water Basin; International Food Policy Res Institute: San Francisco, CA, USA, 2016. [Google Scholar]
- Seo, S.T. A real options approach to the investment analysis of irrigation systems. Korean J. Agric. Econ. 2006, 47, 31–50. [Google Scholar]
- Seo, S.T.; Segarra, E.; Mitchell, P.D.; Leatham, D.J. Irrigation technology adoption and its implication for water conservation in the Texas High Plains: A real options approach. Agric. Econ. 2007, 38, 47–55. [Google Scholar] [CrossRef]
- Mittal, G. Real Options Approach to Capacity Planning under Uncertainty. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2004. [Google Scholar]
- Michailidis, A.; Mattas, K. Using real options theory to irrigation dam investment analysis: An application of binomial option pricing model. Water Resour. Manag. 2007, 21, 1717–1733. [Google Scholar] [CrossRef]
- Wang, T.; De Neufville, R. Building Real Options into Physical Systems with Stochastic Mixed-Integer Programming; Massachusetts Institute of Technology: Cambridge, MA, USA, 1997. [Google Scholar]
- Kjaerland, F. A real option analysis of investments in hydropower—The case of Norway. Energy Policy 2007, 35, 5901–5908. [Google Scholar] [CrossRef]
- Erfani, T.; Pachos, K.; Harou, J. Real-options water supply planning: Multistage scenario trees for adaptive and flexible capacity expansion under probabilistic climate change uncertainty. Water Resour Res. 2018, 54, 5069–5087. [Google Scholar] [CrossRef]
- Kind, J.M.; Baayen, J.H.; Botzen, W.W. Benefits and limitations of real options analysis for the practice of river flood risk management. Water Resour Res. 2018, 54, 3018–3036. [Google Scholar] [CrossRef]
- Clark, E.; Mondello, G. Resource management and the mayor’s guarantee in French water allocation. Environ. Resour. Econ. 2000, 15, 103–113. [Google Scholar] [CrossRef]
- Clark, E.; Mondello, G. Regulating natural monopolies: The case of drinking water in France. J. Contemp. Water Res. Educ. 2002, 121, 72–78. [Google Scholar]
- Brown, C.; Carriquiry, M. Managing hydroclimatological risk to water supply with option contracts and reservoir index insurance. Water Resour. Res. 2007, 43, W11423. [Google Scholar] [CrossRef]
- Gersonius, B.; Ashley, R.; Pathirana, A.; Zevenbergen, C. Climate change uncertainty: Building flexibility into water and flood risk infrastructure. Clim. Chang. 2013, 116, 411–423. [Google Scholar] [CrossRef]
- Yu, S.Y.; Unger, A.J.A.; Kim, T.H. Applicability of the real option valuation method to the economic analysis of water resources supply projects. Econ. Environ. Geol. 2008, 41, 551–562. [Google Scholar]
- Jeong, I.C. An Evaluation of the Economic Value of Outsourcing of Water Supply Services Considering Uncertainty of Water Price. Master’s Thesis, Korea University, Seoul, Korea, 2014. [Google Scholar]
- da Silva, L.P.B.; Hussein, H. Production of scale in regional hydropolitics: An analysis of La Plata River Basin and the Guarani Aquifer System in South America. Geoforum 2019, 99, 42–53. [Google Scholar] [CrossRef]
- Cascão, A.E. Ethiopia–challenges to Egyptian hegemony in the Nile Basin. Water Policy 2008, 10, 13–28. [Google Scholar] [CrossRef]
- Lankford, B.; Watson, D. Metaphor in natural resource gaming: Insights from the RIVER BASIN GAME. Simul. Gaming 2007, 38, 421–442. [Google Scholar] [CrossRef]
- Laukkanen, M.; Koundouri, P. Competition versus Cooperation in Groundwater Extraction: A Stochastic Framework with Heteregoneous Agents; MPRA: München, Germany, 2006. [Google Scholar]
- Bhaduri, A.; Manna, U.; Barbier, E.B.; Liebe, J. Cooperation in Transboundary Water Sharing under Climate Change; ZEF Bonn: Bonn, Germany, 2009. [Google Scholar]
- Bhaduri, A.; Manna, U.; Barbier, E.B.; Liebe, J. Climate change and cooperation in transboundary water sharing: An application of stochastic Stackelberg differential games in Volta river basin. Nat. Resour. Model. 2011, 24, 409–444. [Google Scholar] [CrossRef]
- Bhaduri, A.; Nicostrato, P.; Liebe, J. Scope and Sustainability of Cooperation in Transboundary Water Sharing of the Volta River; ZEF Bonn: Bonn, Germany, 2008. [Google Scholar]
- Weeds, H. Strategic delay in a real options model of R&D competition. Rev. Econ. Stud. 2002, 69, 729–747. [Google Scholar]
- Lee, J.H. Real options analysis of groundwater extraction and management with water price uncertainty. Rev. Environ. Econ. Policy 2018, 27, 639–666. [Google Scholar]
- Gisser, M.; Sanchez, D.A. Competition versus optimal control in groundwater pumping. Water Resour Res. 1980, 16, 638–642. [Google Scholar] [CrossRef]
- Dixit, A.K.; Pindyck, R.S. Investment under Uncertainty; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Park, H.J. A real option approach to optimal use of natural resource: Revisiting the least cost principle. Korea Energy Econ. Rev. 2004, 3, 47–69. [Google Scholar]
- Fudenberg, D.; Tirole, J. Preemption and rent equalization in the adoption of new technology. Rev. Econ. Stud. 1985, 52, 383–401. [Google Scholar] [CrossRef]
- MOLIT; K-Water. National Groundwater Monitoring Network in Korea—Annual Report 2016; Ministry of Land, Infrastructure and Transport & K-Water: Gwacheon, Korea, 2016.
- Korean Meteorological Administration. 1981~2010 Climatological Normals of Korea; Korean Meteorological Administration: Seoul, Korea, 2011.
- Jeju Special Self-Governing Province. Investigation of Hydrological and Geological Resources of Jeju Island (III); Jeju Special Self-Governing Province: Jeju, Korea, 2013.
- Jeju Special Self-Governing Province. Jeju Special Self-Governing Province Annual Statistics; Jeju Special Self-Governing Province: Jeju, Korea, 2019.
- Tsay, R.S. Analysis of Financial Time Series; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Pfeiffer, L.; Lin, C.-Y.C. Does efficient irrigation technology lead to reduced groundwater extraction? Empirical evidence. J. Environ. Econ. Manag. 2014, 67, 189–208. [Google Scholar] [CrossRef]
- Hendricks, N.P.; Peterson, J.M. Fixed effects estimation of the intensive and extensive margins of irrigation water demand. J. Agric. Resour. Econ. 2012, 37, 1–19. [Google Scholar]
- Kim, S.G.; Kim, G.B. Preliminary study on the comparison of water supply costs between groundwater and surface water. J. Geol. Soc. Korea 2016, 52, 457–464. [Google Scholar] [CrossRef]
- Jeju Special Self-Governing Province. Estimation of the Cost of the Ground Water Cost of Jeju Special Self-Governing Province and Improvement of the Charging System; Jeju Special Self-Governing Province: Jeju, Korea, 2012.
- Jeju Special Self-Governing Province. Jeju Special Self-Governing Province Groundwater Regulation; Jeju Special Self-Governing Province: Jeju, Korea, 2016.
- Hartwick, J.M.; Olewiler, N.D. The Economics of Natural Resource Use; Harper & Row Publishers Inc.: New York, NY, USA, 1986. [Google Scholar]
- Brozovic, N. Optimal Extraction of a Path-Dependent, Spatially Heterogeneous Resource; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2002. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).