Optimal Design of an Isolated Hybrid Microgrid for Enhanced Deployment of Renewable Energy Sources in Saudi Arabia

Abstract

Hybrid microgrids are presented as a solution to many electrical energetic problems. These microgrids contain some renewable energy sources such as photovoltaic (PV), wind and biomass, or a hybrid of these sources, in addition to storage systems. Using these microgrids in electric power generation has many advantages such as clean energy, stability in supplying power, reduced grid congestion and a new investment field. Despite all these microgrids advantages, they are not widely used due to some economic aspects. These aspects are represented in the net present cost (NPC) and the levelized cost of energy (LCOE). To handle these economic aspects, the proper microgrids configuration according to the quantity, quality and availability of the sustainable source of energy in installing the microgrid as well as the optimal design of the microgrid components should be investigated. The objective of this paper is to design an economic microgrid system for the Yanbu region of Saudi Arabia. This design aims to select the best microgrid configuration while minimizing both NPC and LCOE considering some technical conditions, including loss of power supply probability and availability index. The optimization algorithm used is Giza Pyramids Construction (GPC). To prove the GPC algorithm’s effectiveness in solving the studied optimization problem, artificial electric field and grey wolf optimizer algorithms are used for comparison purposes. The obtained results demonstrate that the best configuration for the selected area is a PV/biomass hybrid microgrid with a minimum NPC and LCOE of $319,219 and $0.208/kWh, respectively.

1. Introduction

The depletion of fuel, environmental problems and the danger of nuclear use oblige the international community to adopt renewable energy resources, mainly the isolated mode in the non-electrified areas where the extension of the grid is costly, and the power losses are very high. Otherwise, the intermittence of the renewable resources is managed using hybrid systems such as PV and wind, which are considered complementary.

The hybrid microgrid systems (HMGs) become essential electrification of rural areas. The hybrid renewable energy system (HRES) is investigated and proposed in many studies (e.g., [1,2,3,4,5,6,7]), which introduce all necessary information to design isolated HRES. The authors of [1] presented the design and financing of a microgrid on a small Koh Jik Island in Thailand. HOMER is used to provide techno-economic insights. Likewise, a comparison of lead-acid and lithium-ion battery technologies and their impact on LCOE and the renewable fraction is investigated. On the other hand, the authors of [2] presented a review of the energy system model characteristics and the existing tools to optimize the multi-energy system. The authors of [3] presented a review of the recent optimization approaches to resolving the operation cost and reducing the total network losses. The authors of [4] outlined a review of the system optimization and energy management strategies taking into account the sources of PV, wind turbine and fuel cell. In another research [5], a survey of the microgrid development in the seaport areas is outlined. Similarly, the authors of [6] presented a review of the major issues in the adoption of HRES, as well as a survey of the different renewable sources which can be integrated for both isolated and grid-connected modes. In addition, the authors of [7] presented a review containing the optimization tools, constraints and battery types in the HRES design.

The desert of Saudi Arabia is a crucial region for these kinds of projects. Saudi Arabia has excellent meteorological conditions, which explains the important number of studies in this country. In [8], a recent methodology is developed based on social spider optimizer (SSO). The goal is to determine the optimal sizing of a microgrid containing PV, wind, diesel and battery in Aljouf Region. The study focused on three configurations: PV/battery/diesel, wind/battery/diesel and PV/wind/battery/diesel. In addition, several algorithms are used to optimize the cost of energy, respecting the Loss of Power Supply Probability (LPSP) as a technical factor. In [9], the PV/FC/battery system design and a sensitivity analysis study are presented. The project is to feed a small community of the city NEOM in Saudi Arabia. In Yanbu [10], the wind/PV microgrid is analyzed, and the cost of energy is investigated. The technical and economic aspects analyses are performed using HOMER software, considering both the unmet electric load and the excess electricity. In [11], four cities in the Kingdom of Saudi Arabia (Riyadh, Hafar Albatin, Sharurah and Yanbu) are selected for a study which aims to feed a community load demand. The proposed system is a grid-connected PV/wind, where the design is investigated using HOMER software considering technical and economic analyses.

The design of HMGs-renewable energy systems needs to define the suitable configuration for each localization. In [12], three configurations are proposed, namely PV/wind/diesel/battery, PV/tidal/biomass/battery and PV/biomass, in seven areas in Morocco. Barbaro et al. [13] proposed an optimized design of a system containing wind, PV, geothermal, battery and diesel generators as backup. The project considered the technical and financial feasibility for Faial Island in the Azores archipelago. The PV/wind/battery/diesel HMG system is still the most adapted in the world for its power synergy, as well as the use of the battery and diesel as a back-up [14,15,16,17]. The authors of [14] proposed this HMG in Rabat. The authors of [15] presented the same microgrid to feed a residential area in Kasuga City, Fukuoka, Japan. The authors of [16] proposed the same HMG design in Rabat, Morocco and Baghdad, Iraq. The project systems were compared by their levelized cost of energy. In Benin country [17], it was found that PV/diesel/battery microgrid system is the more suitable for feeding off-grid rural communities. An investigation of the economic feasibility of the microgrid based on renewable sources to avoid the strong dependency on fossil fuel on the Lampedusa island in Italy is proposed and investigated in [18]. At the same time, the authors of [19] presented several technologies to integrate the micro resources and the storage systems. Moreover, new DC-bus signaling is proposed and implemented to control the distributed decentralized systems. The authors of [20] presented a study to identify the optimal configuration of components on Pantelleria Island and the sizing and operating schedule that minimize the annual cost. The authors of [21] presented techno-economic feasibility of the renewable energy systems using HOMER Pro, which consider hydrogen as a storage energy system. The authors of [22] proposed an efficient approach to simulate a DC-DC converter that is connected to the PV device.

Many difficulties and challenges in the RES design and sizing need to be balanced between the economic and technical aspects. The literature presents many traditional and recent algorithms to reach these objectives, which proved to provide their feasibility to find the optimal solution. Khan and Javaid [23] proposed a hybrid algorithm named the JLBO composed of Jaya and teaching–learning-based optimization (TLBO), dedicated to finding optimal PV/WT/battery sizing for a microgrid system. Makhdoomi and Askarzadeh [24] proposed a hybrid of CSA and the adaptive chaotic awareness probability algorithms called CSAAC-AP to optimize PV/diesel/PHS microgrid system operation. Kharrich et al. [25] proposed an improvement of the Bonobo Optimizer (BO), using the quasi-oppositional technique for resolving the microgrid design problem that is based on PV, wind, battery, diesel and biomass, with four configurations, and the case study was Aswan, Egypt. The algorithm is compared with BO, Harris Hawks Optimization (HHO), Algorithm of Artificial Electric Field (AEFA) and IWO algorithms. Abo-Elyousr and Nozhy [26] developed a bi-objective ant colony algorithm (BOACA) for the optimal size of several configurations of hybrid microgrids. A comprehensive summary of previous work considering microgrid design and operation is listed in Table 1.

Table 1. Summary of previous work.

Reference	Year	Microgrid System	Location	Algorithm/Tool	Objective Function	Strength	Weakness
Fathy et al. [8]	2020	PV/wind/battery/diesel	Sakaka, Aljouf, Saudi Arabia	-SSO-WOA-ALO -MVO-GWO	COE	Detailed study.	The constraint factors are limited
Rezk et al. [9]	2020	PV/FC/battery	NEOM, Saudi Arabia	HOMER	-NPC -COE	Present the effect of tilt angle and derating factor variation on COE	The study should be enhanced by a comparison of HOMER with other algorithms
Ramli et al. [10]	2016	wind/PV	Yanbu, Saudi Arabia	HOMER	-NPC-COE-unmet demand of the electric load-excess electricity	Consider the unmet electric load demand and the excess electricity	The study does not take the reliability factor as an objective or constraint
Alharthi el al. [11]	2018	PV/wind/grid-connected	-Yanbu, Saudi Arabia -Hafar Albatin, Saudi Arabia -Sharurah, Saudi Arabia -Riyadh, Saudi Arabia	HOMER	-NPC -COE	Provide a general overview of microgrid systems in Saudi Arabia.	In the study, no technical factors are declared
Kharrich et al. [12]	2021	PV/wind/diesel/battery	Dakhla, Morocco	-HHO-AEFA-GWO -STOA-EO	NPC	Apply a new meta-heuristic algorithm	The study does not consider uncertainty
Barbaro et al. [13]	2019	PV/wind/geothermal/diesel	Faial Island, Portugal	Unit Commitment (UC) algorithm	NPV	Develop a new simulation model	The power management is not shown
Yoshida, and Farzaneh [15]	2020	PV/wind/battery/diesel	Kasuga, Japan	PSO	Total cost of system	Use the least-cost perspective approach	The convergence curve of the minimization of the objective function is not presented
Elkadeem et al. [16]	2019	-PV/WT/DG1/DG2/battery -PV/WT/DG1/battery -PV/DG1/DG2/battery -WT/DG1/DG2/battery -DG1/DG2	Dongola, Sudan	HOMER Pro	NPC	Provide a comprehensive feasibility analysis to feed the electricity of agricultural and irrigation areas.	A meta-heuristic algorithm Is not applied and compared to HOMER Pro
Odou et al. [17]	2019	PV/diesel/battery	Alibori, Benin	HOMER software	NPC	Analyze the techno-economic feasibility of hybrid system with case study in rural electrification	The results are obtained by HOMER only and not compared with any other algorithm
Khan and Javaid [23]	2020	PV/wind/battery	Rafsanjan, Iran	-Jaya-TLBO-JLBO -GA	TAC	Propose a hybrid JLBO	The renewable fraction is not considered as an objective function or constraints
Makhdoomi and Askarzadeh [24]	2020	PV/diesel/PHS	Adrar, Algeria	-GA-PSO-CSA -CSAAC-AP	Fuel consumption	Propose modified version of the crow search optimization algorithm	The operation time of the study is only 24 h
Kharrich et al. [25]	2020	-PV/wind/diesel/battery -PV/biomass -PV/diesel/battery -wind/diesel/battery	Aswan, Egypt	-QOBO-BO -HHO-AEFA-IWO	NPC	Propose an algorithm: Quasi-Oppositional BO (QOBO)	The uncertainty of the renewable sources is not considered
Abo-Elyousr and Nozh [26]	2018	PV/wind/biomass/NGFC/NGT	Kharga, Egypt Saint Katherine, Egypt Qussair, Egypt	-BOACA-GA -PSO-HOMER	-COE -GHG	Develop the BOACA algorithm to find optimal HMG	LPSP results are not presented
Heydari and Askarzadeh [27]	2016	PV/biomass	Kerman, Iran	HSA	NPC	Show the limits of HOMER compared to meta-heuristic algorithm	It does not provide a comparison of the HS algorithm
Guangqian et al. [28]	2018	-PV/diesel/battery -Wind/diesel/battery -Wind/PV/diesel/battery	Khorasan, Iran	-HSA-SAA -HHSSAA	LCC	Propose hybrid meta-heuristic algorithm to size a grid-independent system	The reliability is not considered
Sawle et al. [29]	2018	-PV/biomass/diesel/battery -PV/diesel/battery -Wind/biomass/diesel/battery -Wind/diesel/battery -PV/wind/diesel/battery -PV/wind/biomass/diesel/battery	Barwani, India	-GA-PSO-BFPSO -TLBO	Sum of several objectives	Consider the social aspect	Uncertainty is not considered
Ramli et al. [30]	2018	PV/wind/diesel/battery		MOSaDE	-COE-LPSP	Clear study	There is not comparison with a multi-objective algorithm

In this paper, microgrid design and power management are investigated for two configurations, PV/biomass and PV/wind/diesel/battery, to feed an isolated area in the Yanbu region of Saudi Arabia. The main objective of this paper is minimizing NPC, considering technical factors. The optimization is applied using many meta-heuristic algorithms such as the Giza Pyramids Construction (GPC), AEFA and Grey Wolf Optimizer (GWO). In summary, the paper presents four contributions:

• Optimal design of the microgrid system feeding a load in the Yanbu region in Saudi Arabia
• Proposing and analyzing two configurations of microgrid systems considering their technical and operational features
• Presenting the optimal design operation of the hybrid renewable microgrid system by selecting suitable renewable sources to meet the required objectives and constraints
• Investigation and implementation of a recent GPC optimization algorithm and compared it with other algorithms

The mathematical modeling of renewable systems (PV and wind), conventional diesel and battery systems are presented in Section 2. Section 3 presents the mathematical formulation of the objective function. Section 4 presents the mathematical modeling of GPC optimization algorithm. Section 5 presents the case study. Section 6 presents the results and discussions. Finally, Section 7 presents the main conclusions.

2. Mathematical Modeling

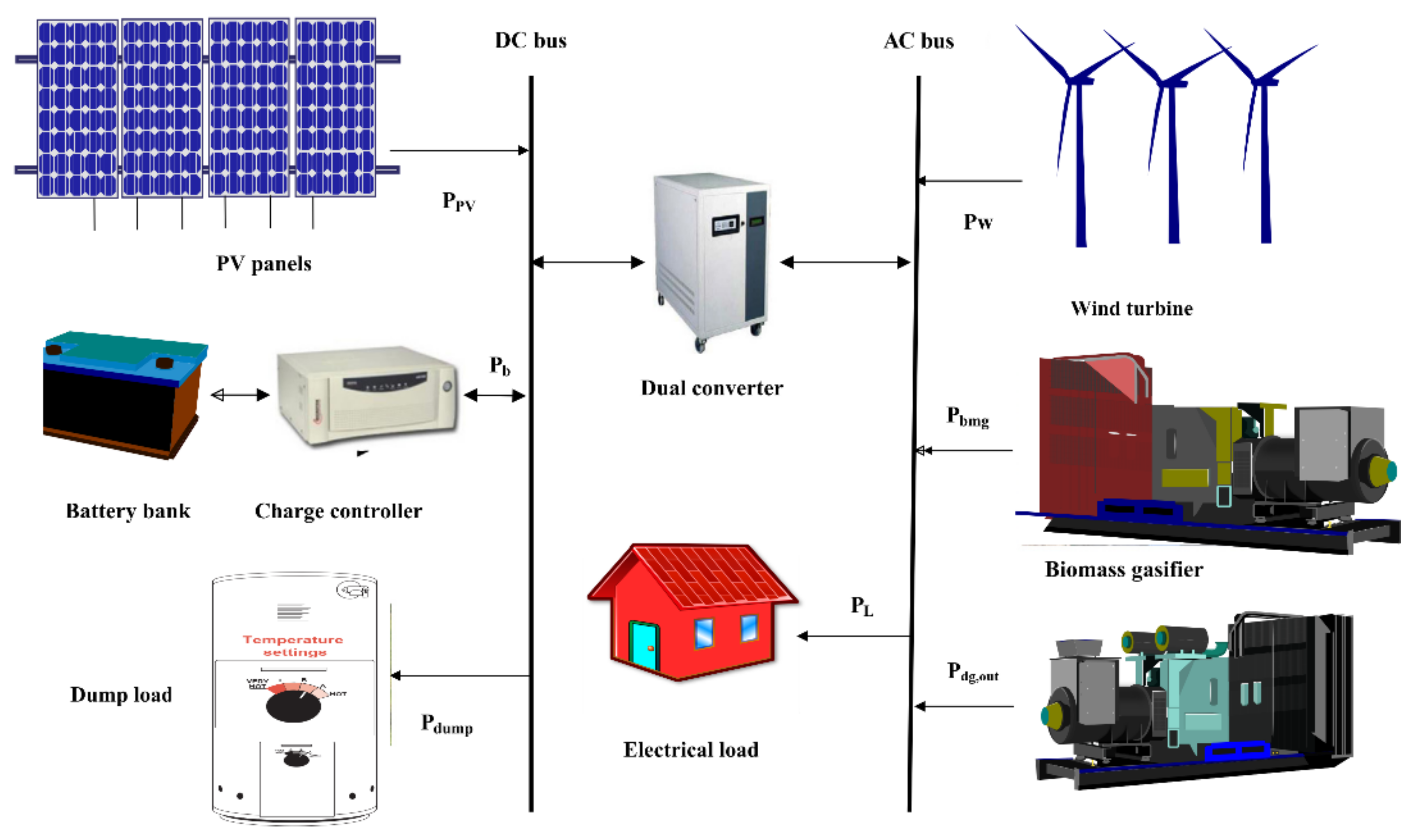
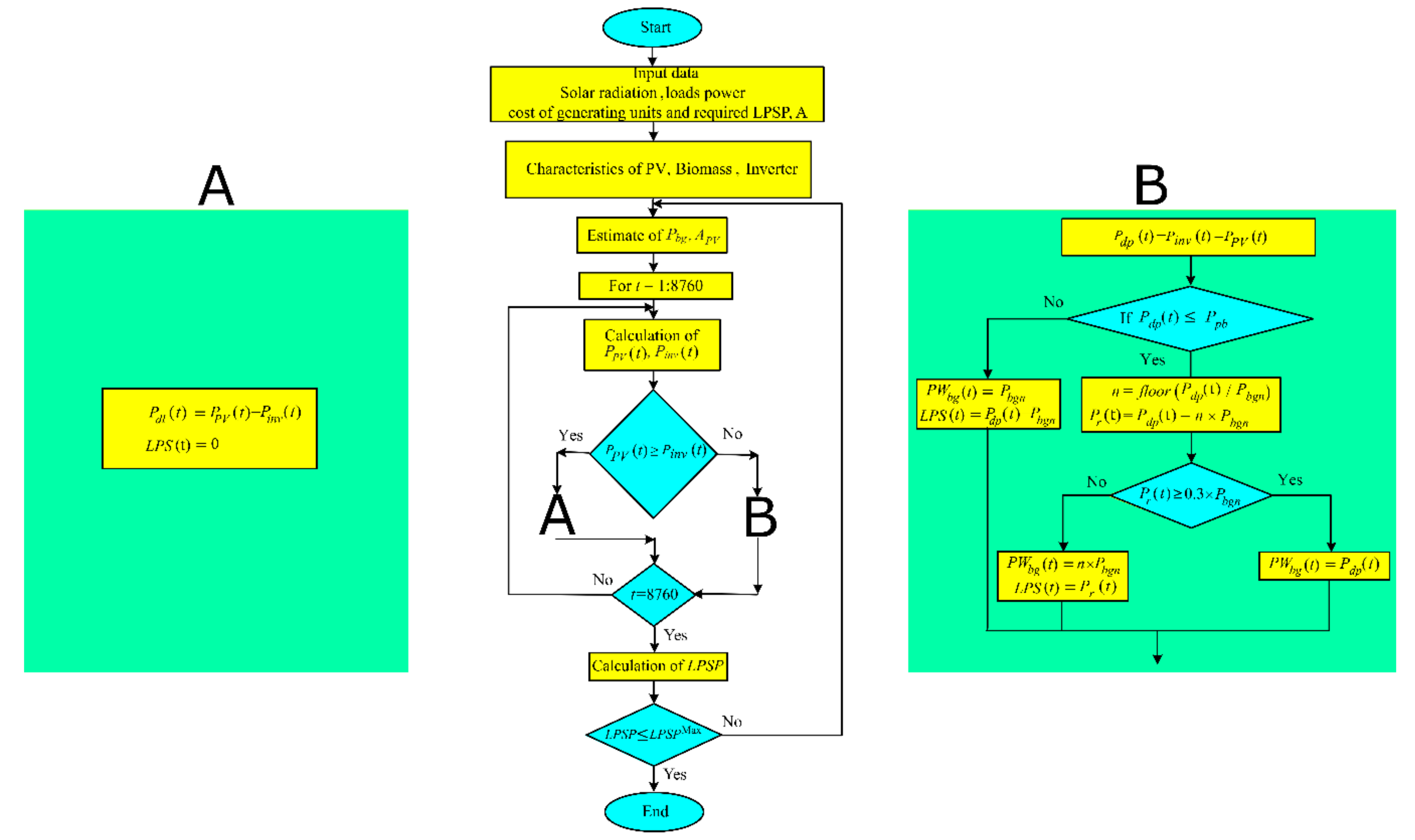
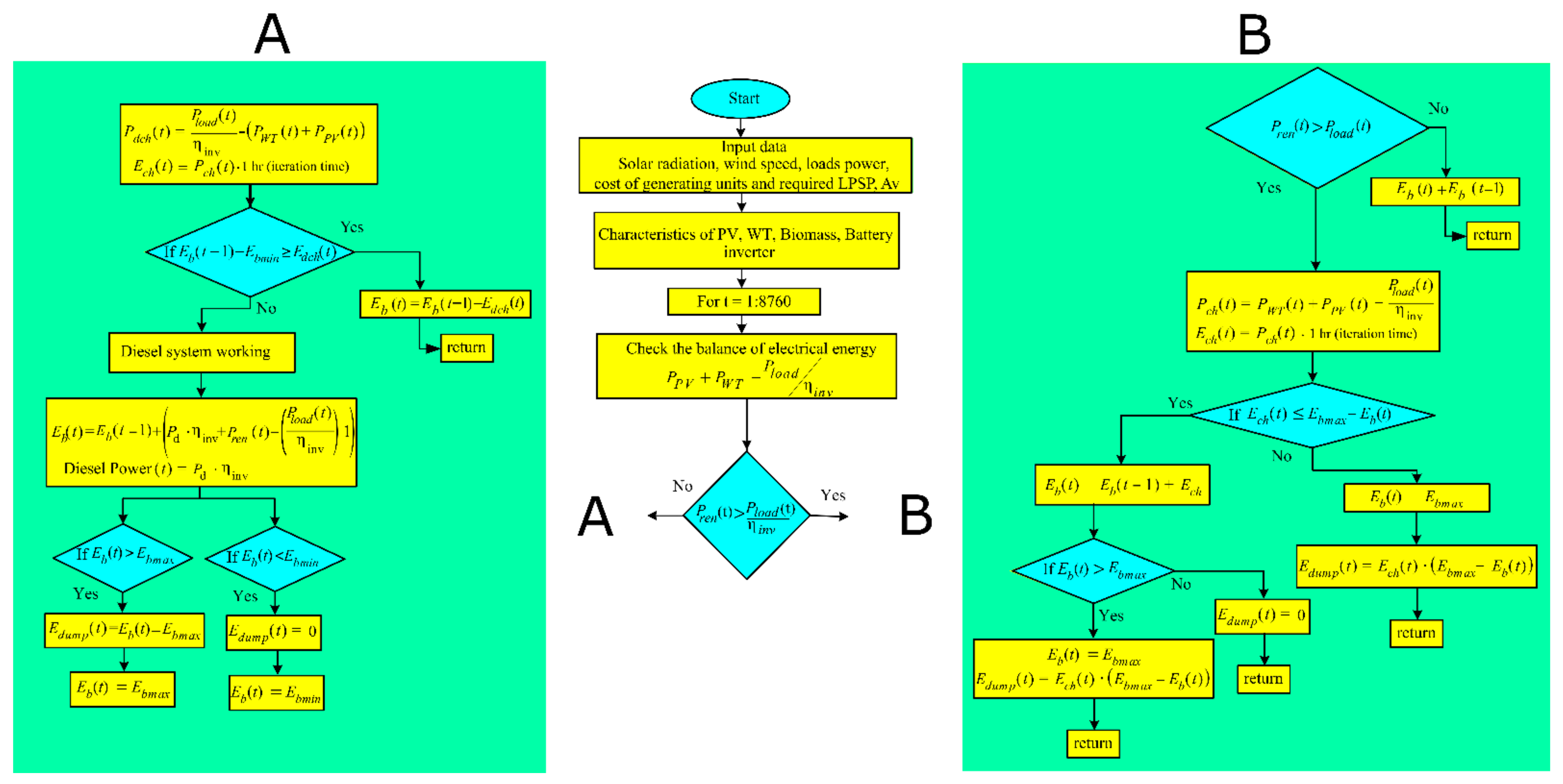
In this case study, two configurations of the HMG systems are presented. The systems are composed of PV, wind, diesel, biomass and battery systems, as presented in Figure 1. The first configuration considers the PV/biomass microgrid system with the power management strategy presented in Figure 2. The second configuration considers the PV/wind/diesel/battery system with the power management shown in Figure 3. The main sequence of the microgrid operation is as follows:

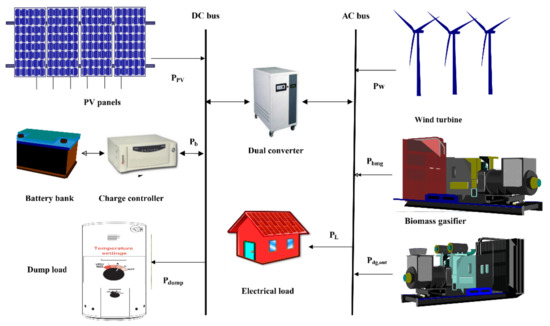
Figure 1. Components of the microgrid systems.

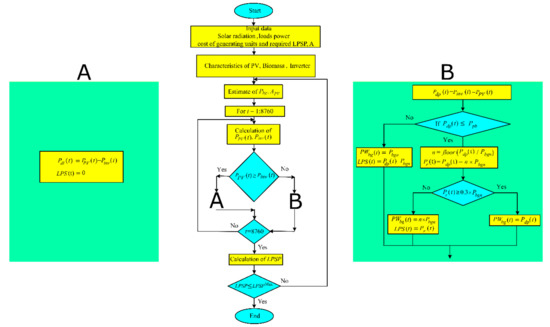
Figure 2. Management strategy of the PV/biomass system.

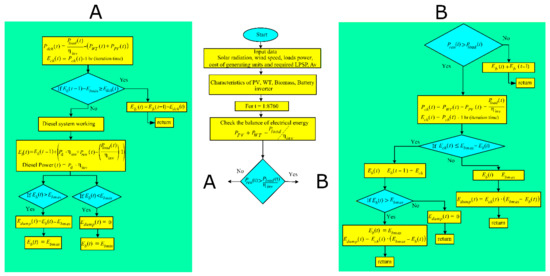
Figure 3. Management strategies of the PV/wind/diesel/battery microgrid system.

• The PV and wind turbine supply energy as a pillar of the system.
• The battery operates when there is a shortage of power from renewable sources.
• The diesel generator works and supplies power when the battery is at its min SOC.

2.1. PV Modeling

The power of the PV panel can be represented as [27]:

$$P_{pv}=I\left(t\right)\times {\eta }_{pv}<t>\times A_{pv}$$

(1)

where $I$ represents solar irradiation, $A_{pv}$ represents the area of PV panel and ${\eta }_{pv}$ represents the efficiency of the PV system, which is calculated by:

$${\eta }_{pv}\left(t\right)={\eta }_r\times {\eta }_t\times \left[1-\beta \times \left(T_a<t>-T_r\right)-\beta \times I<t>\times \left(\frac{NOCT-20}{800}\right)\times \left(1-{\eta }_r\times {\eta }_t\right)\right]$$

(2)

where $NOCT$ represents nominal operating of the cell temperature (°C), ${\eta }_r$ represents the reference efficiency, ${\eta }_t$ represents MPPT equipment efficiency, $\beta$ is temperature coefficient, $T_a$ represents ambient temperature (°C) and $T_r$ represents cell reference temperature (°C).

2.2. Wind Generator Modeling

The wind power depends on wind speed, which can be presented as [28]:

$$P_{wind}=\left\{\begin{array}{ll}& 0,V<t>\le V_{ci}, V<t>\ge V_{co}\\ \hfill a\times V{<t>}^3-b\times & P_r, V_{ci}<V<t><V_r\\ & P_r, V_r\le V<t><V_{co}\end{array}\right.$$

(3)

where $V$ represents wind speed; $P_r$ represents wind rated power; $V_{ci}$, $V_{co}$ and $V_r$ are cut-in, cut-out and rated wind speeds, respectively; and a and b represent two constants that are calculated as:

$$\left\{\begin{array}{c}a=P_r/\left(V_r{}^3-V_{ci}{}^3\right)\\ b=V_{ci}{}^3/\left(V_r{}^3-V_{ci}{}^3\right)\end{array}\right.$$

(4)

The rated power of wind is calculated as:

$$P_r=\frac{1}{2}\times \rho \times A_{wind}\times C_p\times V_r{}^3$$

(5)

where $\rho$ represents the air density, $A_{wind}$ represents the wind turbine swept area and $C_p$ represents the max power coefficient, which is limited between 0.25% and 0.45%.

2.3. Biomass System Modeling

The biomass produces power as [29]:

$$P_{BM}=\frac{Tota{l}_{bio}\times 1000\times C{V}_{bio}\times {\eta }_{bio}}{8760\times O_{time}}$$

(6)

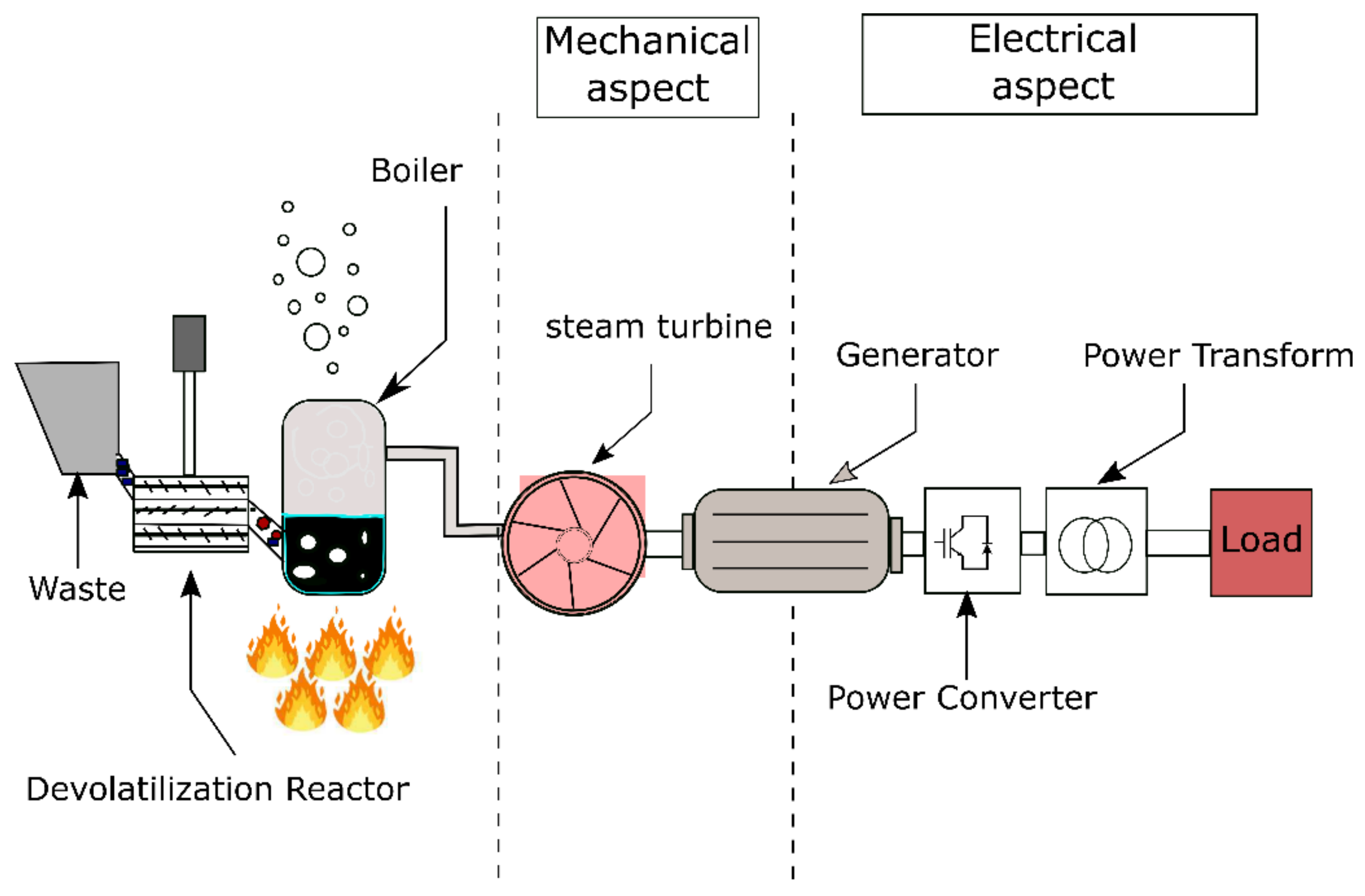
where $Tota{l}_{bio}$ is the total organic material of biomass which is from the date palm waste, $C{V}_{bio}$ represents the calorific value of the organic material (≈20 MJ/kg), ${\eta }_{bio}$ is the biomass efficiency and $O_{time}$ is the operating hour for each day. The procedure of converting the biomass to electricity is presented in Figure 4.

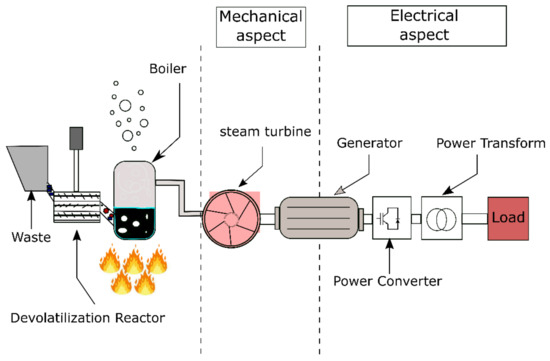
Figure 4. Energy conversion procedure of the biomass system.

2.4. Diesel Generator System Modeling

The rated power of diesel generator ($P_{dg}$) is represented as [30]:

$$P_{dg}=\frac{F_{dg}<t>-A_g\times P_{dg,out}}{B_g}$$

(7)

where $F_{dg}$ is fuel consumption, $P_{dg,out}$ is the output power and $A_g$ and $B_g$ are two constants that represent the linear curve of the fuel consumption.

2.5. Battery Energy Storage System Modeling

The battery is an essential element in isolated microgrid systems. The battery capacity (kWh) can be expressed as [30]:

$$C_{bat}=\frac{E_l\times AD}{DOD\times {\eta }_{inv}\times {\eta }_b}$$

(8)

where $E_l$ represents the total energy load that should be transferred to the HRES; $AD$ represents the battery autonomy; $DOD$ is the depth of discharge (%), which should avoid dominating the storage to the minimum state of the battery; and ${\eta }_{inv}$ and ${\eta }_b$ are the efficiency of inverter and battery (%), respectively, which consider the losses in the transfer of energy.

3. Mathematical Formulation of the Objective Function

3.1. Net Present Cost

The objective preserved in this paper is to minimize the Net Present Cost (NPC), which represents the total investment project cost. It contains the sum of all systems capital $\left(C\right)$, operation and maintenance $\left(OM\right)$ and replacement $\left(R\right)$ costs, as well as the fuel cost of the diesel $\left(F{C}_{dg}\right)$ when it is added to the system. This paper also considers the interest rate ($i_r$), inflation rate ($\delta$), escalation rate ($\mu$) and the project lifetime (N). In summary, the NPC can be calculated as follows [31]:

$$NPC=C+OM+R+F{C}_{dg}$$

(9)

3.1.1. Costs of PV and Wind

The concept of cost calculation for PV and WT is generally similar. Their capital costs are based on the initial cost (${\lambda }_{PV,WT}$) and the area ($A_{PV,WT}$). The capital cost of PV and/or wind is calculated as [32]:

$$C_{PV,WT}={\lambda }_{PV,WT}\times A_{PV,WT}$$

(10)

The $OM$ costs are [32]:

$$O{M}_{PV,WT}={\theta }_{PV,WT}\times A_{PV,WT}\times \sum _{i=1}^N{\left(\frac{1+\mu }{1+i_r}\right)}^i$$

(11)

where ${\theta }_{PV,WT}$ represents the annual operation and maintenance cost.

3.1.2. Costs of Diesel Generation

The diesel generator costs are calculated as [31]:

$$C_{dg}={\lambda }_{dg}\times P_{dg}$$

(12)

$$O{M}_{dg}={\theta }_{dg}\times N_{run}\times \sum _{i=1}^N{\left(\frac{1+\mu }{1+i_r}\right)}^i$$

(13)

$$R_{diesel}=R_{dg}\times P_{dg}\times \sum _{i=7,14\dots }{\left(\frac{1+\delta }{1+i_r}\right)}^i$$

(14)

$$C_f\left(t\right) = p_f\times F_{dg}<t>$$

(15)

$$F{C}_{dg}=\sum _{t=1}^{8760}{C}_f<t>\times \sum _{i=1}^N{\left(\frac{1+\delta }{1+i_r}\right)}^i$$

(16)

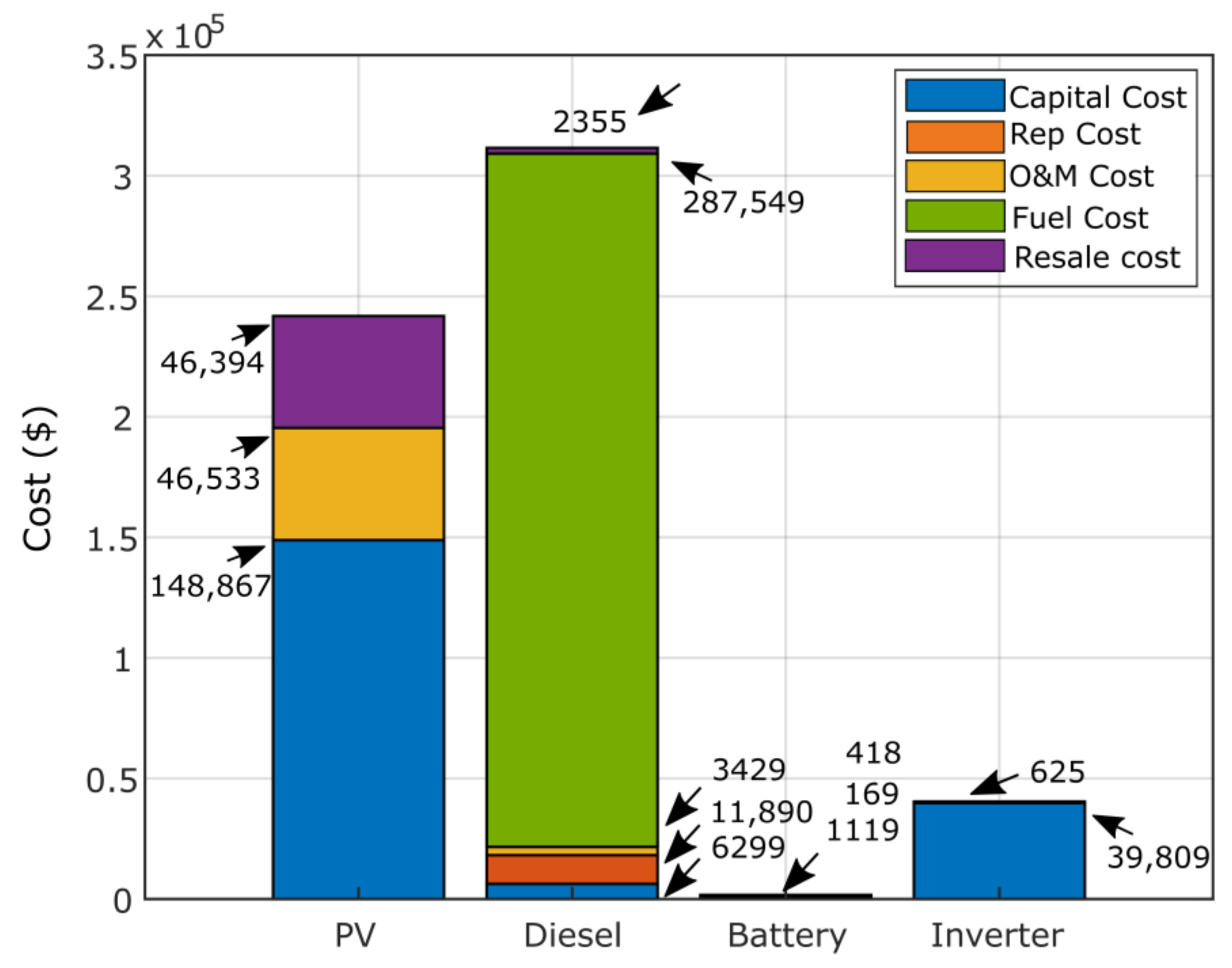
where $C_{dg}$ is capital cost, ${\lambda }_{dg}$ represents initial cost of the diesel for each KW, $O{M}_{dg}$ is the actual O&M cost, ${\theta }_{dg}$ represents annual O&M cost, $N_{run}$ represents operating hours number of diesel generator per year, $R_{diesel}$ is the diesel generator replacement cost, $R_{dg}$ is annual replacement cost, $p_f$ represents the fuel cost, $F_{dg}$ is annual fuel consumption and $F{C}_{dg}$ represents total fuel cost.

3.1.3. Costs of Battery System

The capital with OM (which contains the replacement) costs of battery are as follows [32]:

$$C_{BESS}={\lambda }_{bat}\times C_{bat}$$

(17)

$$O{M}_{BESS}={\theta }_{bat}\times C_{bat}\times \sum _{i=1}^{T_B}{\left(\frac{1+\mu }{1+\delta }\right)}^{\left(i\_1\right)N_{bat}}$$

(18)

where ${\lambda }_{bat}$ is the battery initial cost and ${\theta }_{bat}$ represents battery annual O&M cost.

3.1.4. Costs of Biomass System

The biomass costs are calculated as [27]:

$$C_{bg}={\lambda }_{bg}\times P_{bg}$$

(19)

$$O{M}_{bg}={\theta }_1\times P_{bg}\times \sum _{i=1}^N{\left(\frac{1+\mu }{1+i_r}\right)}^i+{\theta }_2\times P_w\times \sum _{i=1}^N{\left(\frac{1+\mu }{1+i_r}\right)}^i$$

(20)

where ${\lambda }_{bg}$ represents initial cost of biomass, ${\theta }_1$ is annual fixed O&M cost, ${\theta }_2$ represents variable O&M cost and $P_w$ is the annual generated energy (kWh/Year).

3.1.5. Costs of Inverter

The capital and O&M costs of the inverter are calculated as [31]:

$$C_{inv}={\lambda }_{inv}\times P_{inv}$$

(21)

$$O{M}_{Inv}={\theta }_{Inv}\times \sum _{i=1}^N{\left(\frac{1+\mu }{1+i_r}\right)}^i$$

(22)

where ${\lambda }_{inv}$ is the inverter initial cost and ${\theta }_{Inv}$ is annual O&M cost of inverter.

3.2. Levelized Cost of Energy

The Levelized Cost of Energy (LCOE) is calculated as follows [30]:

$$LCOE=\frac{NPC\times CRF}{{\sum }_{t=1}^{8760} P_{load}<t>}$$

(23)

where $P_{load}$ is the load demand and $CRF$ is the capital recovery factor that converts the initial to annual capital cost, which is calculated as follows:

$$CRF\left(ir,R\right)=\frac{i_r\times {\left(1+i_r\right)}^R}{{\left(1+i_r\right)}^R-1}$$

(24)

where $R$ represents the lifetime of the project.

3.3. Loss of Power Supply Probability

The loss of power supply probability represents the reliability of microgrid system. LPSP is calculated as [30]:

$$LPSP=\frac{{\sum }_{t=1}^{8760}\left(P_{load}<t>-P_{pv}<t>-P_{wind}<t>+P_{dg,out}<t>+P_{SOC, bmin}\right)}{{\sum }_{t=1}^{8760}{P}_{load}<t>}$$

(25)

where $P_{SOC,bmin}$ is the minimum state of charge of battery.

3.4. Availability Index

The availability index (A) is calculated to confirm the ability of the designed system as follows [32]:

$$A=1-\frac{DMN}{{\sum }_{t=1}^{8760}{P}_{load}<t>}$$

(26)

$$DMN=P_{bmin}<t>-P_b<t>-\left(P_{pv}<t>+P_{wind}<t>+P_{dg,out}<t>-P_{load}<t>\right)\times u<t>$$

(27)

where $P_b$ represent the battery power. u is equal to 1 if the load is not satisfied; otherwise, it is equal to 0.

4. Optimization Algorithm

The HMG design needs an efficient meta-heuristic algorithm that can help to resolve the system’s complex operations. In a recent paper, we proposed a new optimization algorithm called Giza Pyramids construction. The effeteness of GPC is investigated through the hybrid microgrid design of two scenarios: PV/biomass and PV/wind/diesel/battery. Moreover, the GPC is compared with two other optimization algorithms to prove its ability to find the optimal solutions.

Harifi et al. [33] initially proposed the GPC algorithm, simulating the building process of the pyramids in Giza. The GPC optimization is a new population-based metaheuristic optimization algorithm that is inspired by the movement of workers and stone blocks during the pyramid building. The GPC is dedicated to several areas, including engineering applications.

To prove the effectiveness of the GPC, it is compared with two other algorithms, AEFA and GWO, which are presented in Appendix A.1 and Appendix A.2, respectively. Appendix A.3 represents the parameters of the algorithms declared above.

The GPC pseudocode is listed in Algorithm 1.

Algorithm 1: Giza Pyramids construction [33]

Step 1:

Initialize a set of random stone block or workers $X_w^i=\left(X_w^1,X_w^2,\dots ,X_w^N\right)$ within the limits $X_{min}^i\le X_B^i\le X_{max}^i$. Initialize the GPC parameters.

Evaluate the objective function of all populations.

Step 2: for iter = 1 to Max_iter, do

Step 3: for i = 1 to N do Calculate the amount of stone block displacement.

Calculate the amount of worker movement. Estimate new positions of stone blocks and workers. Investigate the possibility of substituting workers. Determine new position and new fitness.

if new_fitness < Pharaoh’s agent cost then     set new_fitness as Pharaoh’s agent cost.   end if end Sort solution for next iteration. end

5. Yanbu Case Study of the Hybrid Microgrid System

The case study is proposed for the Yanbu region of Saudi Arabia, as shown Figure 5. The project is dedicated to feed a domestic load with the coordinate latitude 24.265° and longitude 38.06°. A heat dump system is used to dump power.

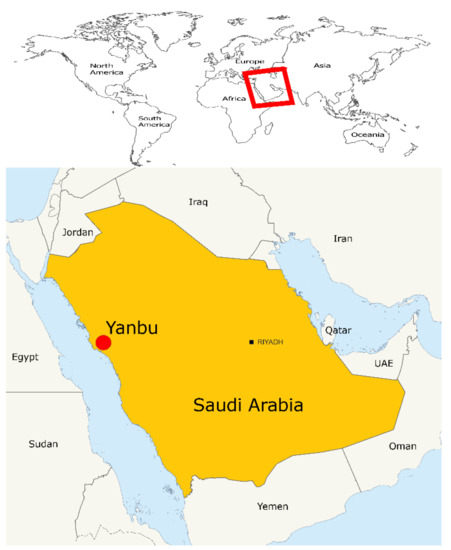
Figure 5. Map of Yanbu microgrid project.

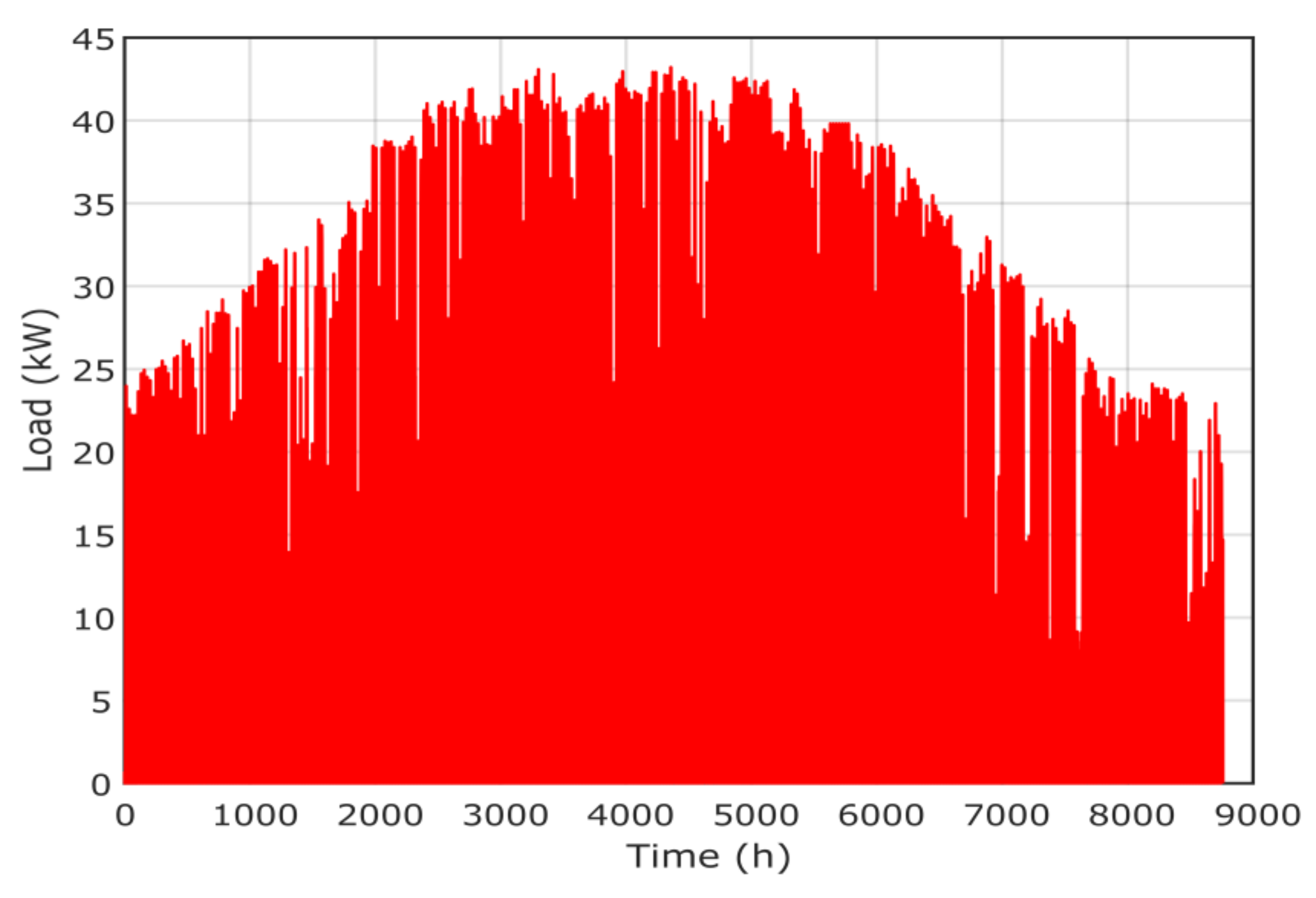
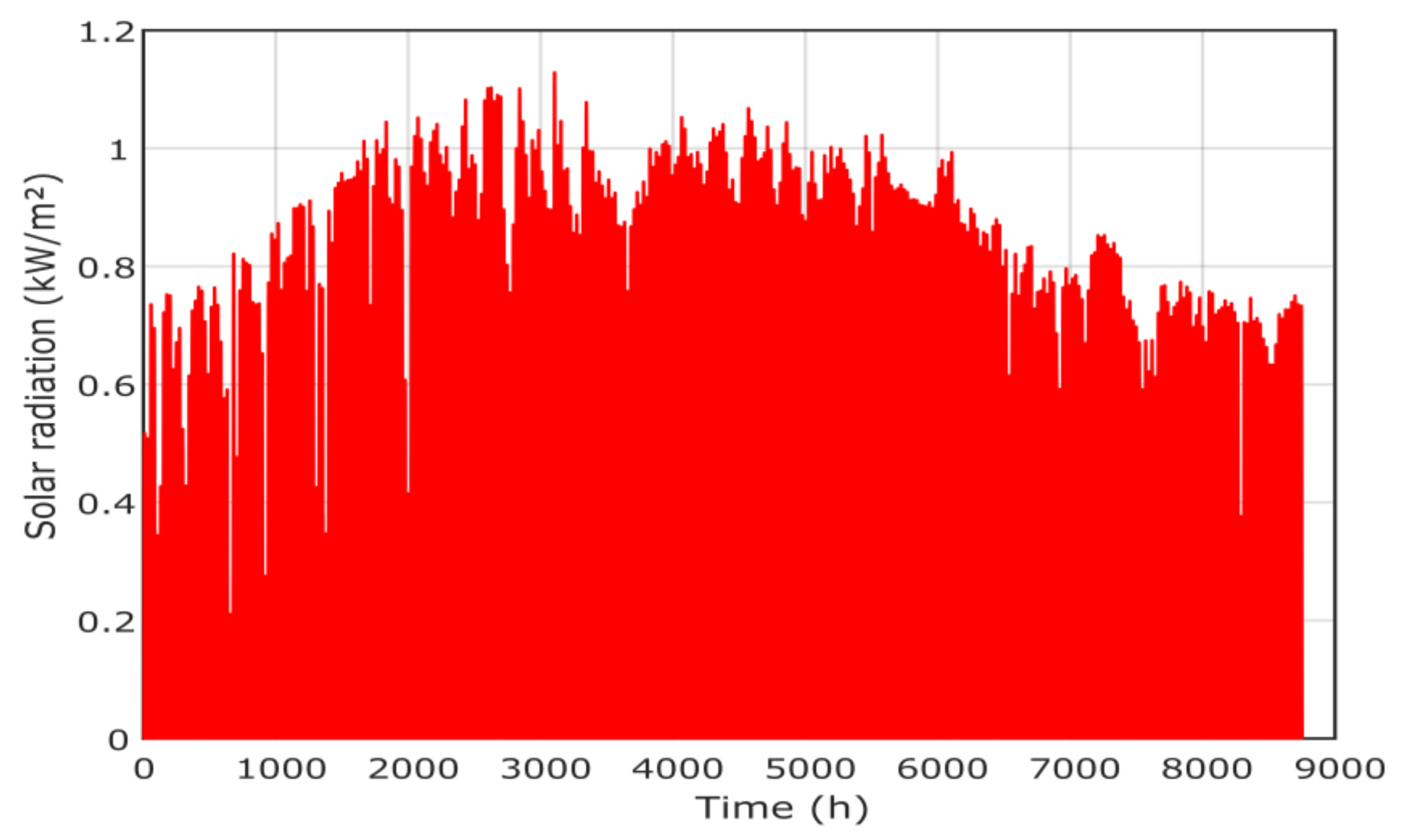
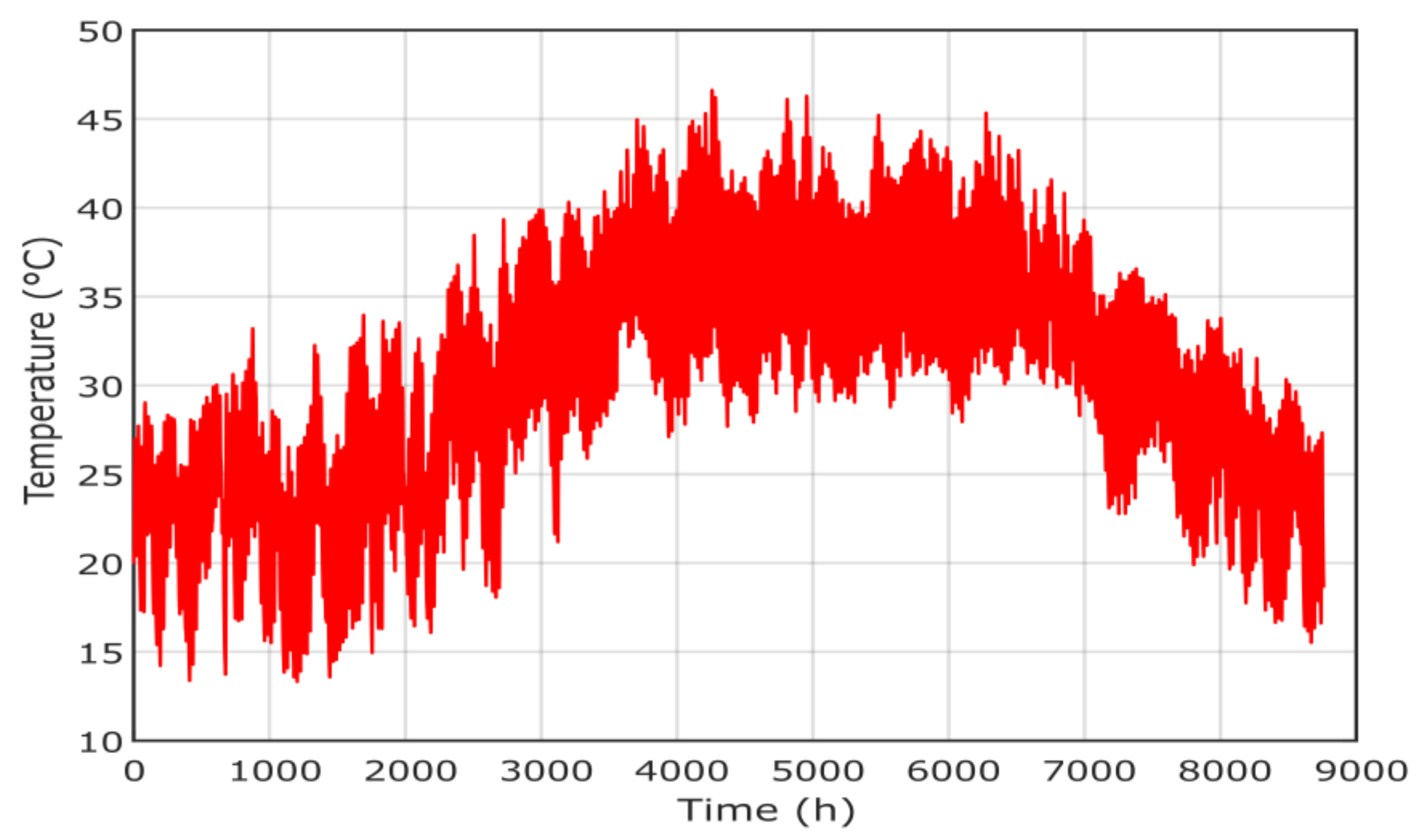
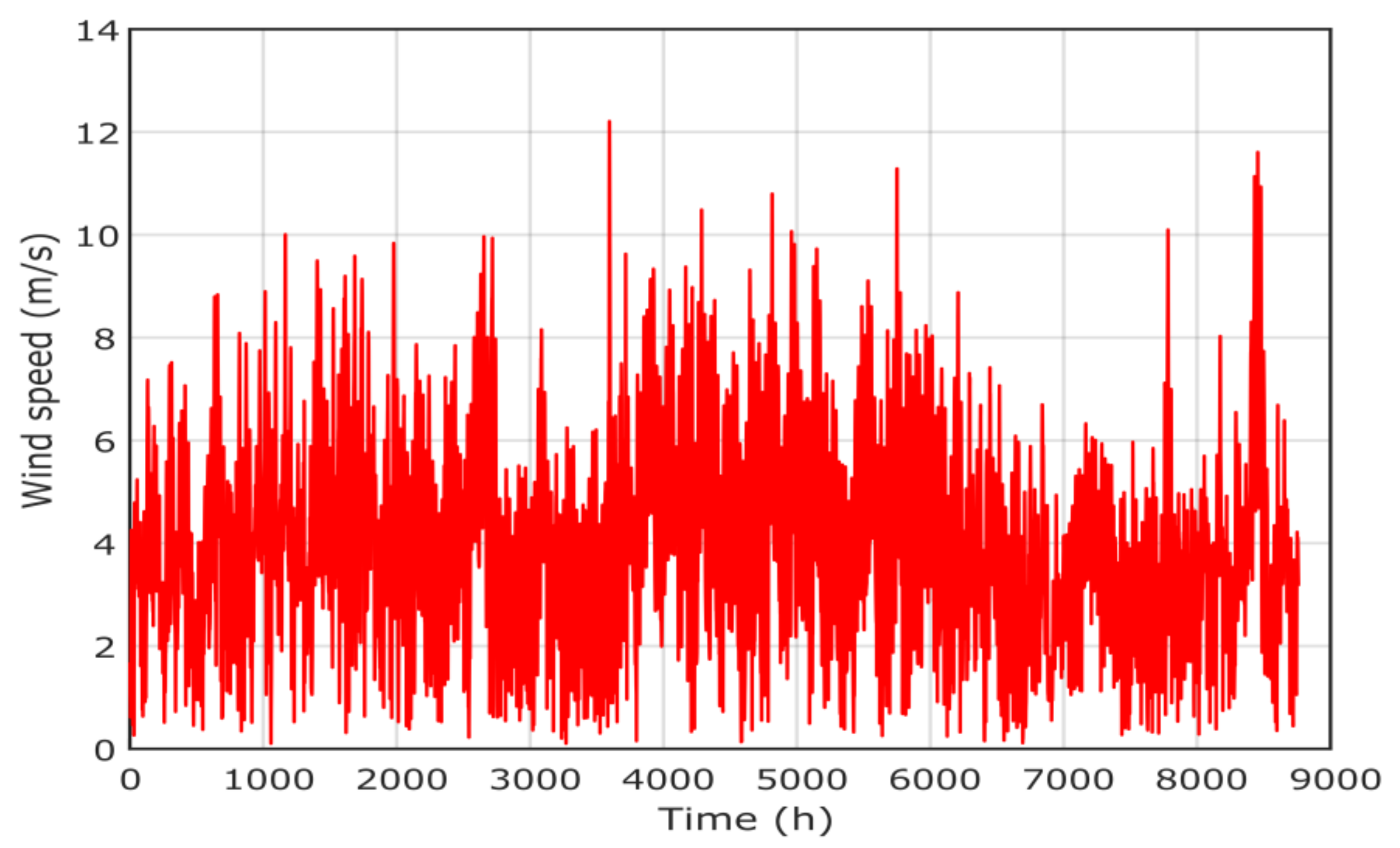
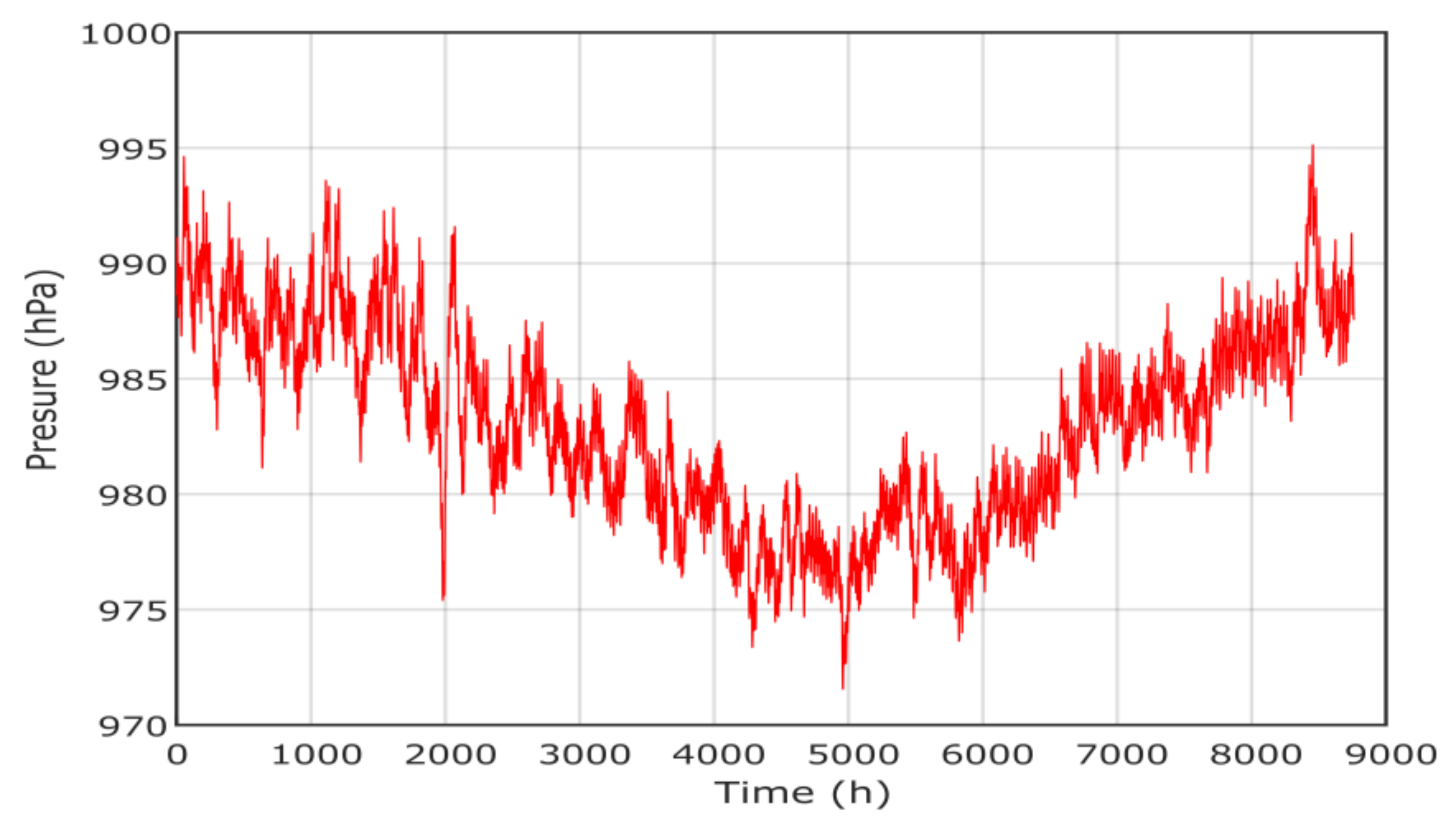
The hourly load demand is presented in Figure 6 where the peak is about 43 kW. The metrological data [34], including solar radiation, temperature, wind speed and pressure, are presented in Figure 7, Figure 8, Figure 9 and Figure 10, respectively. The project economic and technical data are presented in Table 2 for PV, wind, biomass, diesel and battery systems.

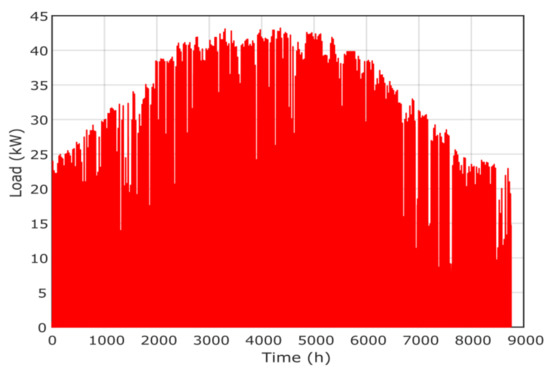
Figure 6. Annual power load of the project.

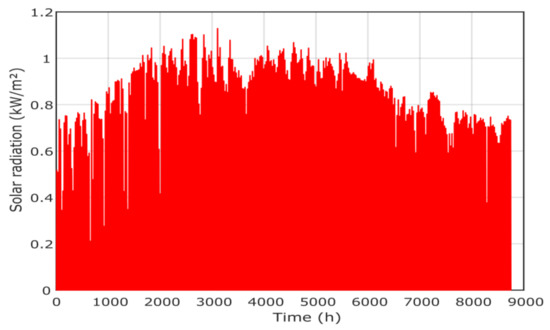
Figure 7. Solar radiation of the project location in Yanbu region.

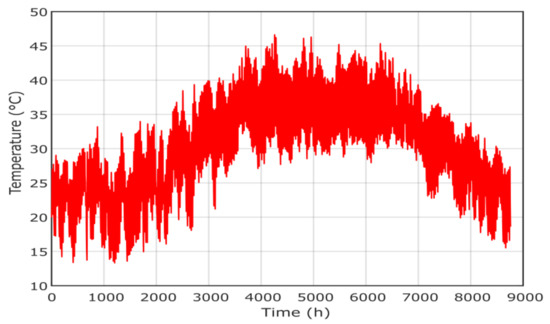
Figure 8. Temperature of the project location in Yanbu region.

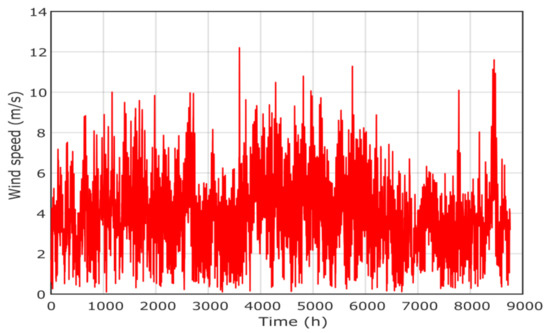
Figure 9. Wind speed of project location in Yanbu region.

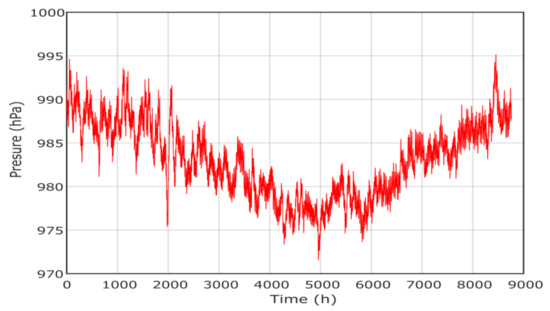
Figure 10. Annual pressure of project in Yanbu region.

Table 2. The project data: economic and technical [27,30,31,32].

Symbol	Indix	Quantity
N	Microgrid project lifetime	20 years
$i_r$	Interest rate index	0.882%
$\mu$	Escalation rate index	5%
$\delta$	Inflation rate index	2%
PV system
${\lambda }_{pv}$	initial cost of PV	$400/m2
${\theta }_{pv}$	Annual cost of PV O&M	$\$0.01\times {\lambda }_{pv}$/m2/year
${\eta }_r$	Reference efficiency of PV	25%
${\eta }_t$	MPPT Efficiency	100%
$T_r$	reference temperature of cell PV	25 °C
$\beta$	Temperature coefficient	0.005 °C
NOCT	Nominal operating temperature cell	47 °C
$N_{pv}$	PV system lifetime	20 years
WT system
${\lambda }_{wind}$	Wind initial cost	$125/m2
${\theta }_{wind}$	Annual O&M cost of wind	$\$0.01\times {\lambda }_{wind}$/m2/year
$C_{p\_wind}$	Maximum power coefficient	48%
$V_{ci}$	Cut-in wind speed	2.6 m/s
$V_{co}$	Cut-out wind speed	25 m/s
$V_r$	Rated wind speed	9.5 m/s
$N_{wind}$	Wind system lifetime	20 years
Diesel generator
${\lambda }_{dg}$	Diesel initial cost	$250/kW
${\theta }_{dg}$	Annual O&M cost of diesel	$0.05/h
$R_{dg}$	Replacement cost	$210/kW
$p_f$	Fuel price in Egypt	$0.43/L
$N_{diesel}$	Diesel system lifetime	7 years
BESS
${\lambda }_{bat}$	Initial cost of battery	$100/kWh
${\theta }_{bat}$	Annual O&M cost of the battery	$\$0.03\times {\lambda }_{bat}$/m2/year
$DOD$	Depth of discharge	80%
${\eta }_b$	Battery efficiency	97%
$SO{C}_{min}$	Minimum state of charge	20%
$SO{C}_{max}$	Maximum state of charge	80%
$N_{bat}$	Battery system lifetime	5 years
Inverter
${\lambda }_{inv}$	Inverter initial cost	$400/kW
${\theta }_{inv}$	Annual O&M cost of inverter	$20/year
${\eta }_{inv}$	Inverter efficiency	97%

6. Results and Discussions

In this paper, GPC is chosen and implemented to design an HMG system. PV, wind turbine, biomass system, diesel generator and battery storage system are used for two scenarios:

(A)

PV/biomass hybrid microgrid system

(B)

PV/wind/diesel/battery microgrid system

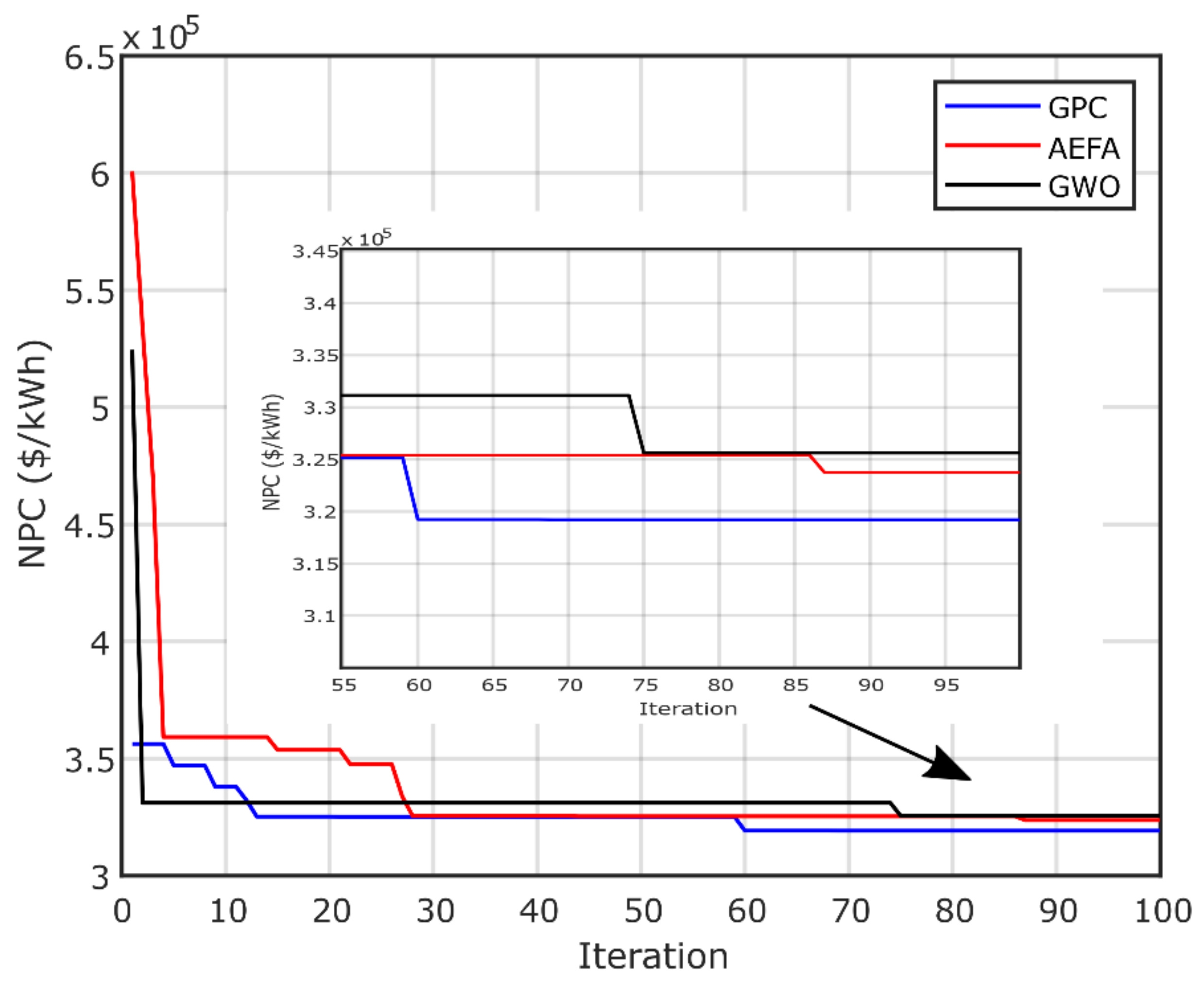
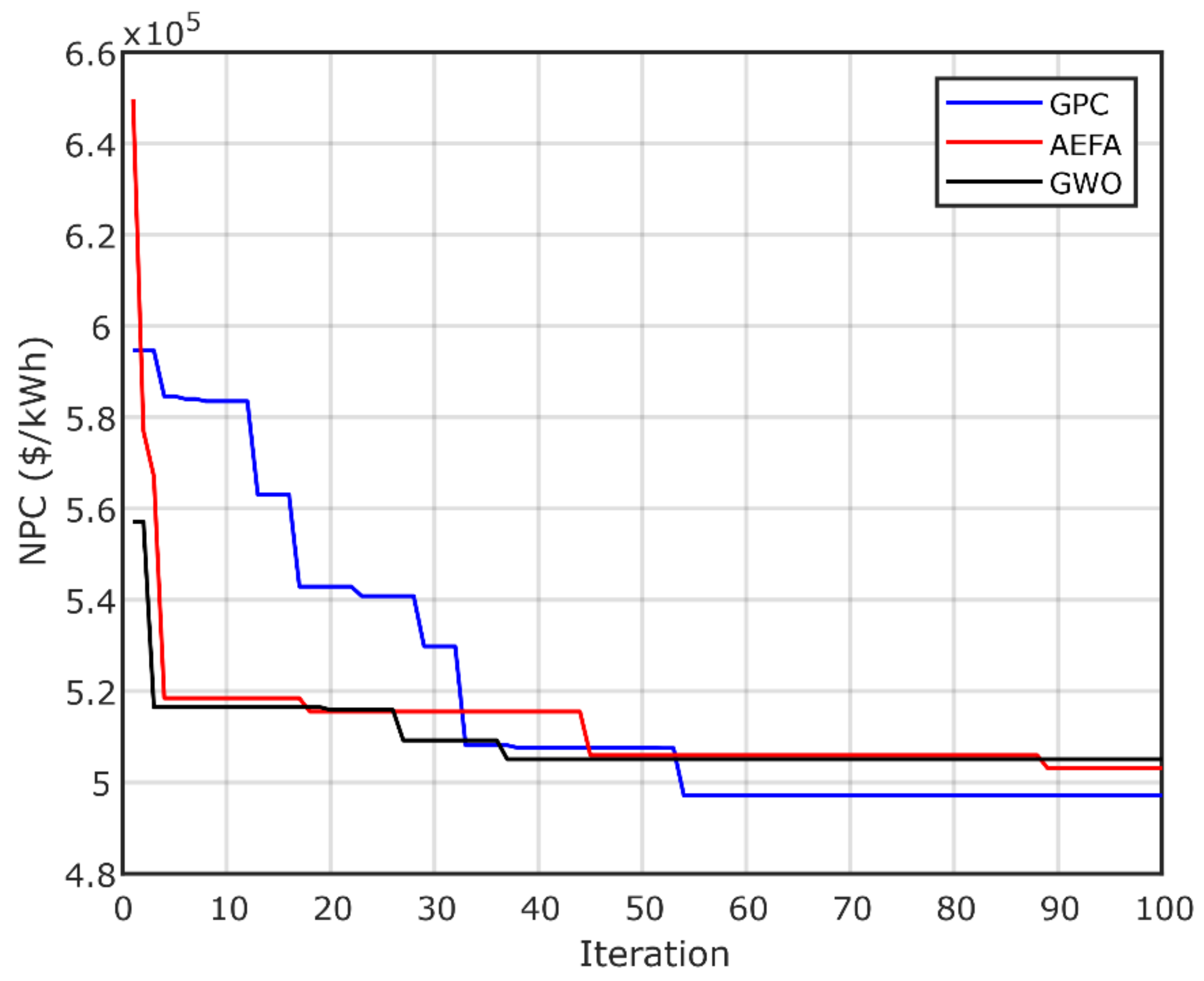
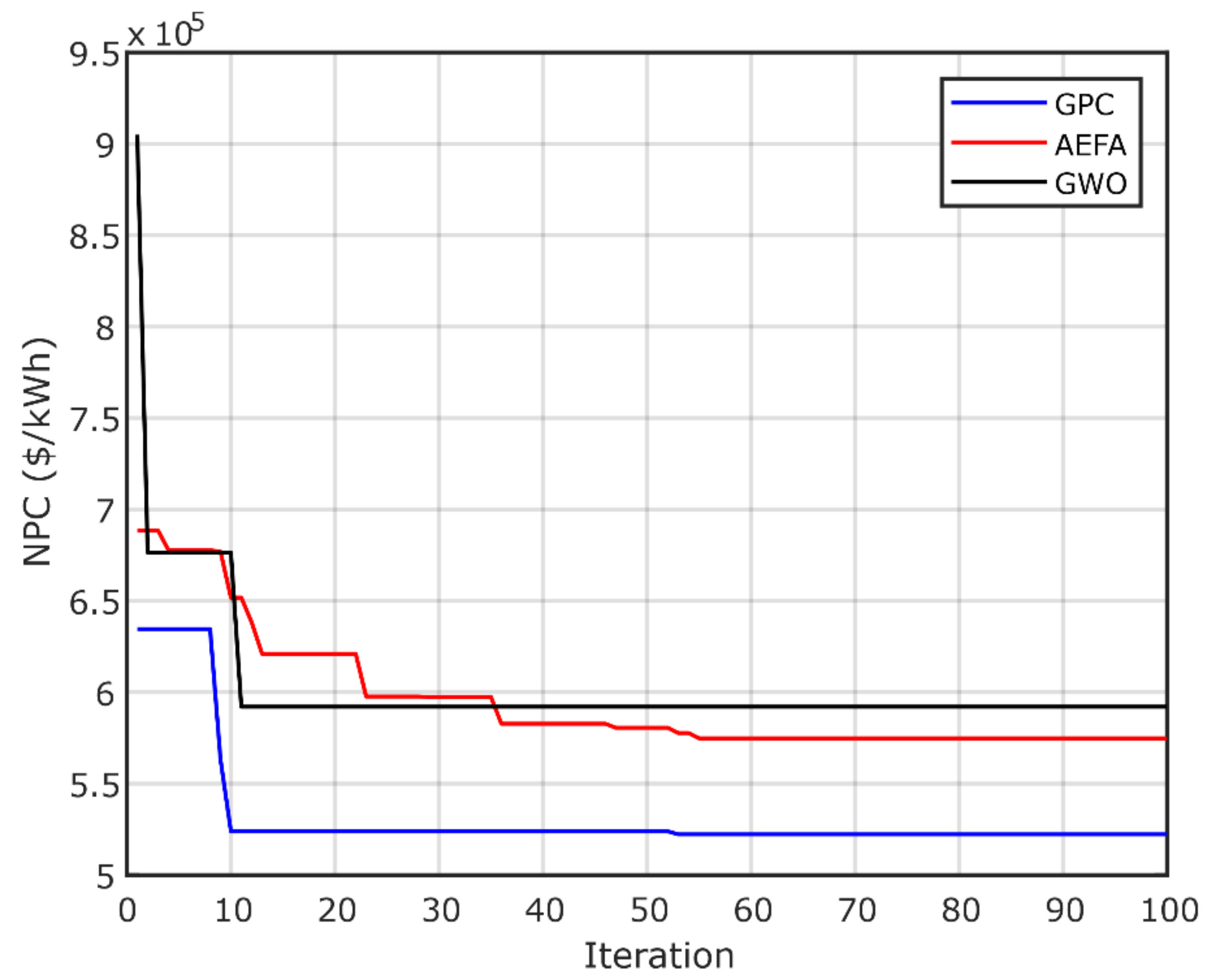
The results obtained by GPC are compared with those of the AEFA and GWO algorithms to validate its ability and effectiveness in achieving the best optimal design with high reliability and minimum investment costs. The simulations were performed using MATLAB editor R2018a. The convergence of the three optimization algorithms (GPC, AEFA and GWO) are shown in Figure 11, Figure 12 and Figure 13, which display the convergence curves of all algorithms. It is clear that the GPC algorithm achieves the best optimal designs for both configurations. Figure 11 presents the PV/biomass system convergence curves, which show that the GPC has the best results compared to those of the AEFA and GWO algorithms. Figure 12 presents the convergence curve of PV/diesel/battery system, using GPC, AEFA and GWO. Figure 13 presents the convergence of PV/wind/diesel/battery system, proving that GPC is the best algorithm. Thus, GPC needs less computational time to find the optimal system, which reduces the computer source usage, as well as reduces the system cost. The AEFA and GWO algorithms need more time for convergence. The best value of convergence is found in Iterations 59 (GPC), 87 (AEFA) and 75 (GWO) for the first PV/biomass microgrid system. For the second system, the best value is found at Iterations 54(GPC), 88 (AEFA) and 47 (GWO). For the third configuration, the optimal is found at Iterations 53 (GPC), 55 (AEFA) and 12 (GWO). Typically, in microgrid design problems, 100 iterations are sufficient.

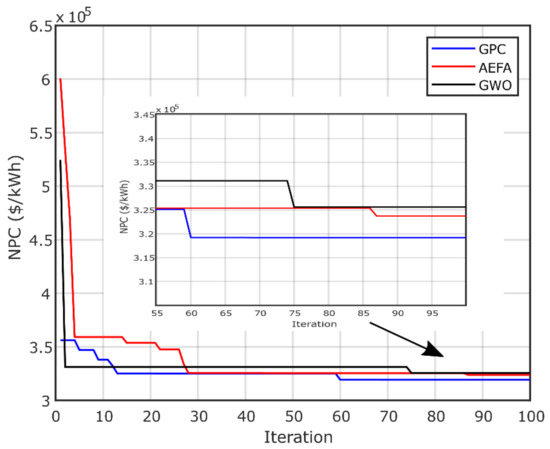
Figure 11. NPC convergence of PV/biomass system.

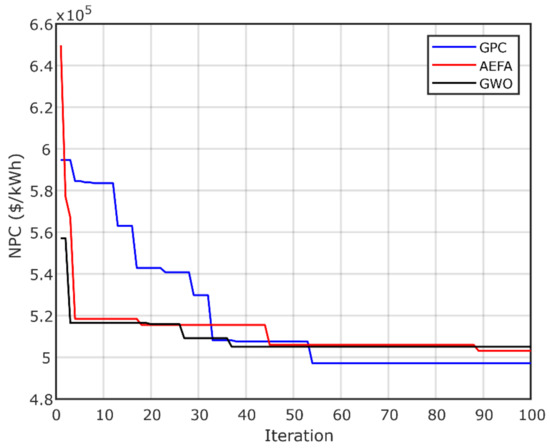
Figure 12. NPC convergence of PV/diesel/battery system.

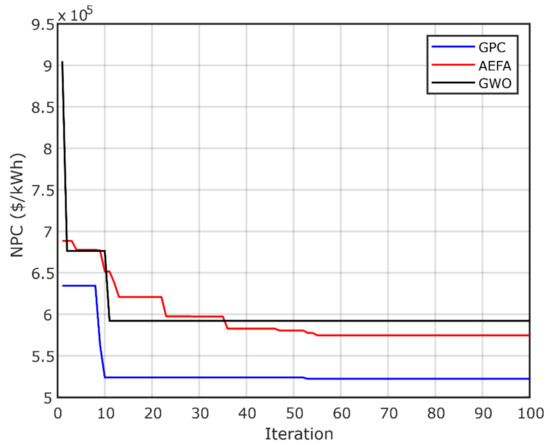
Figure 13. NPC convergence of PV/wind/diesel/battery system.

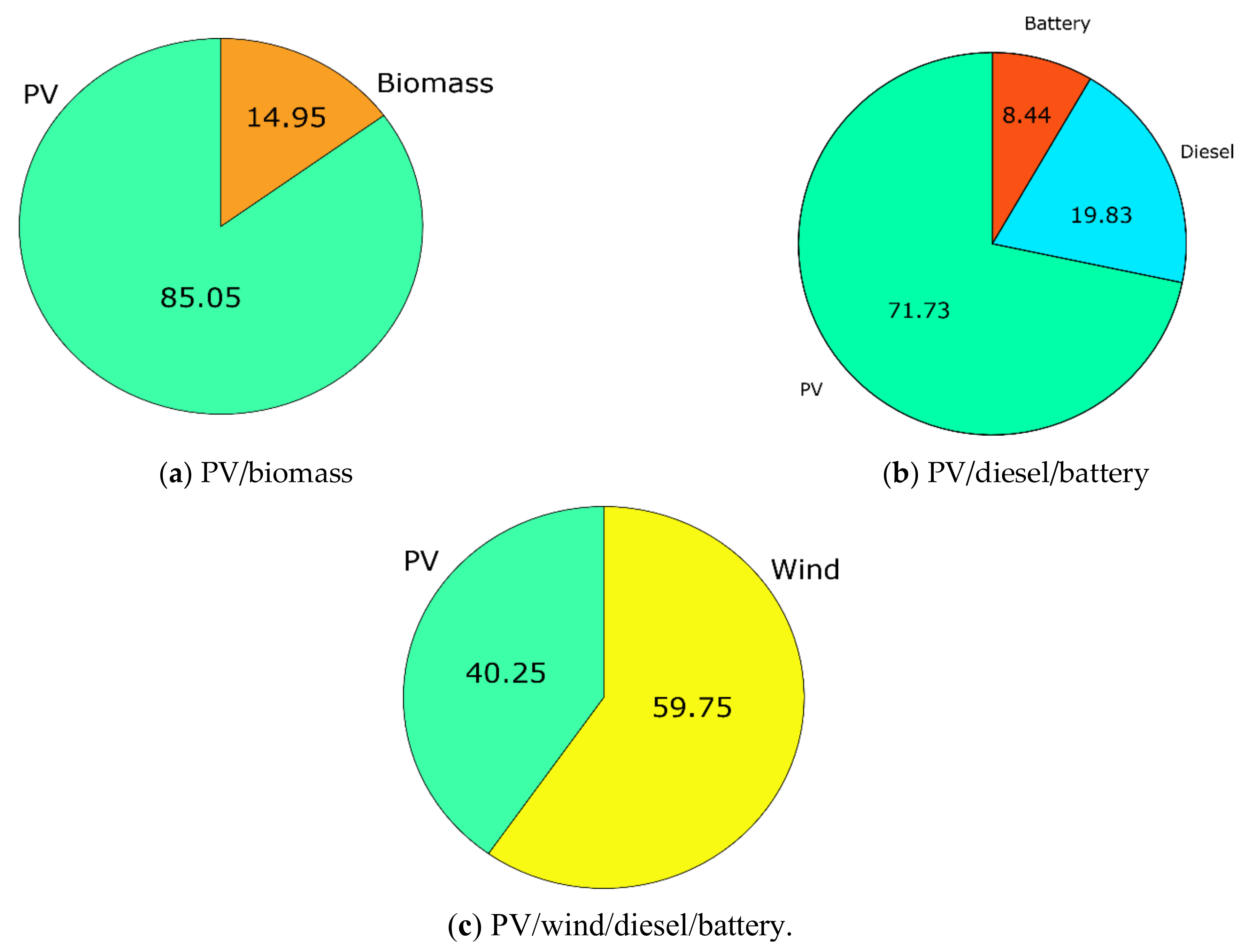
The objective functions (NPC) and other technical and economical calculated parameters for both hybrid microgrid systems are listed in Table 3. From the obtained results, the best optimal microgrid design in this study is found for the first scenario of PV/biomass system with NPC of $319,219 and LCOE of $0.208/kWh for cost of energy. The associated LPSP limit is 0.049 and the availability is about 96%. The optimal results are obtained using the GPC algorithm in both configurations, where the computational time of GPC is the shortest compared with those of AEFA and GWO as shown in Table 4. This project’s optimal microgrid system is to install 265,870 m² of PV panel with a 1000 ton/year biomass generator.

Table 3. Economic and technical factor results for all configurations.

Microgrid System	Algorithm	NPC ($)	LCOE ($/kWh)	LPSP (%)	A (%)	AD (Day)
PV/biomass	GPC	319,219	0.208	0.049	96.409	--
	AEFA	323,724	0.211	0.046	96.450	--
	GWO	325,612	0.213	0.048	96.527	--
PV/diesel/BESS	GPC	497,124	0.325	0.045	99.825	0.9
	AEFA	503,112	0.328	0.041	99.736	2.2
	GWO	505,078	0.329	0.039	99.858	0.7
PV/WT/diesel/BESS	GPC	522,290	0.341	0.05	95	0
	AEFA	574,806	0.375	0.045	98.826	2
	GWO	592,074	0.386	0.046	98.705	2.09

Table 4. Design results of PV/biomass and PV/wind/diesel/battery systems using GPC, AEFA and GWO optimization methods.

Microgrid System	Algorithm	PV (m2)	Wind (m2)	Diesel (kW)	Battery (kWh)	Biomass (Ton/Year)	Time(s)
PV/biomass	GPC	265.870	--	--	--	1000	46,291
	AEFA	295.263	--	--	--	995.954	82,420
	GWO	305.290	--	--	--	981.023	161,439
PV/diesel/BESS	GPC	372.168	--	25.199	11.195	--	229,861
	AEFA	360.071	--	25.969	28.247	--	50,794
	GWO	390.121	--	25.279	8.866	--	87,471
PV/WT/diesel/BESS	GPC	535	2000	0	0	--	53,392
	AEFA	191	1837	34	26	--	338,099
	GWO	284	1741	31	26	--	592,074

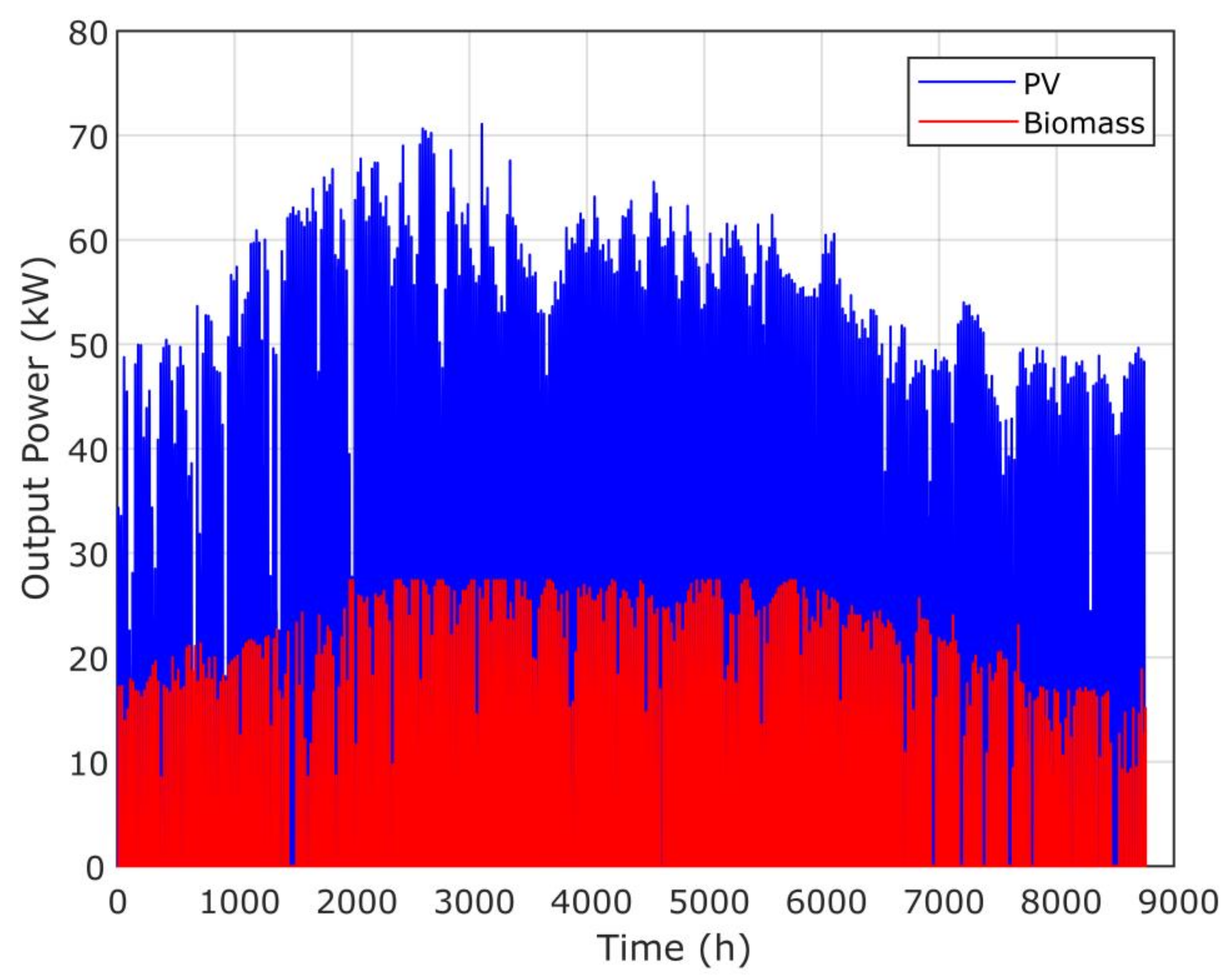
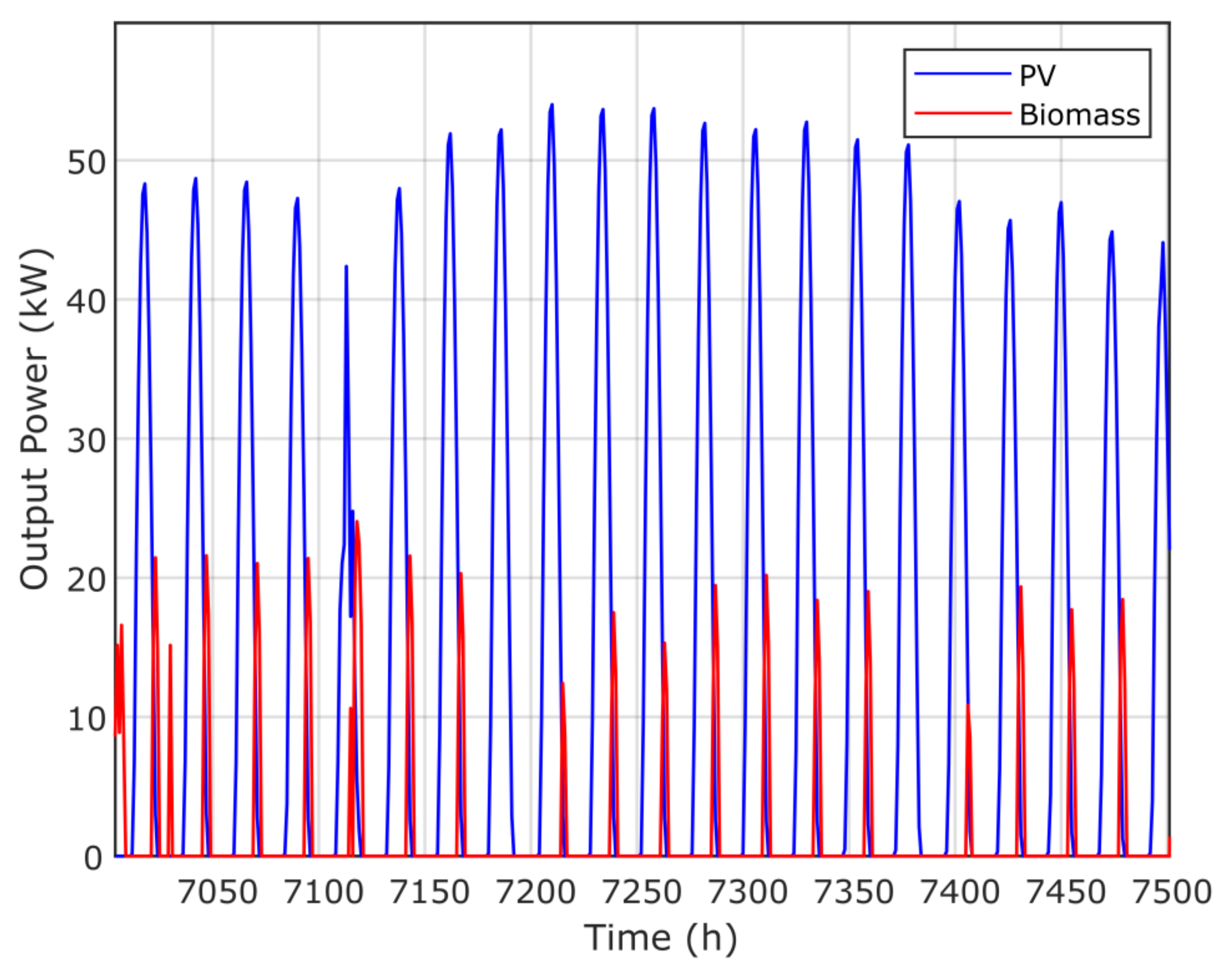
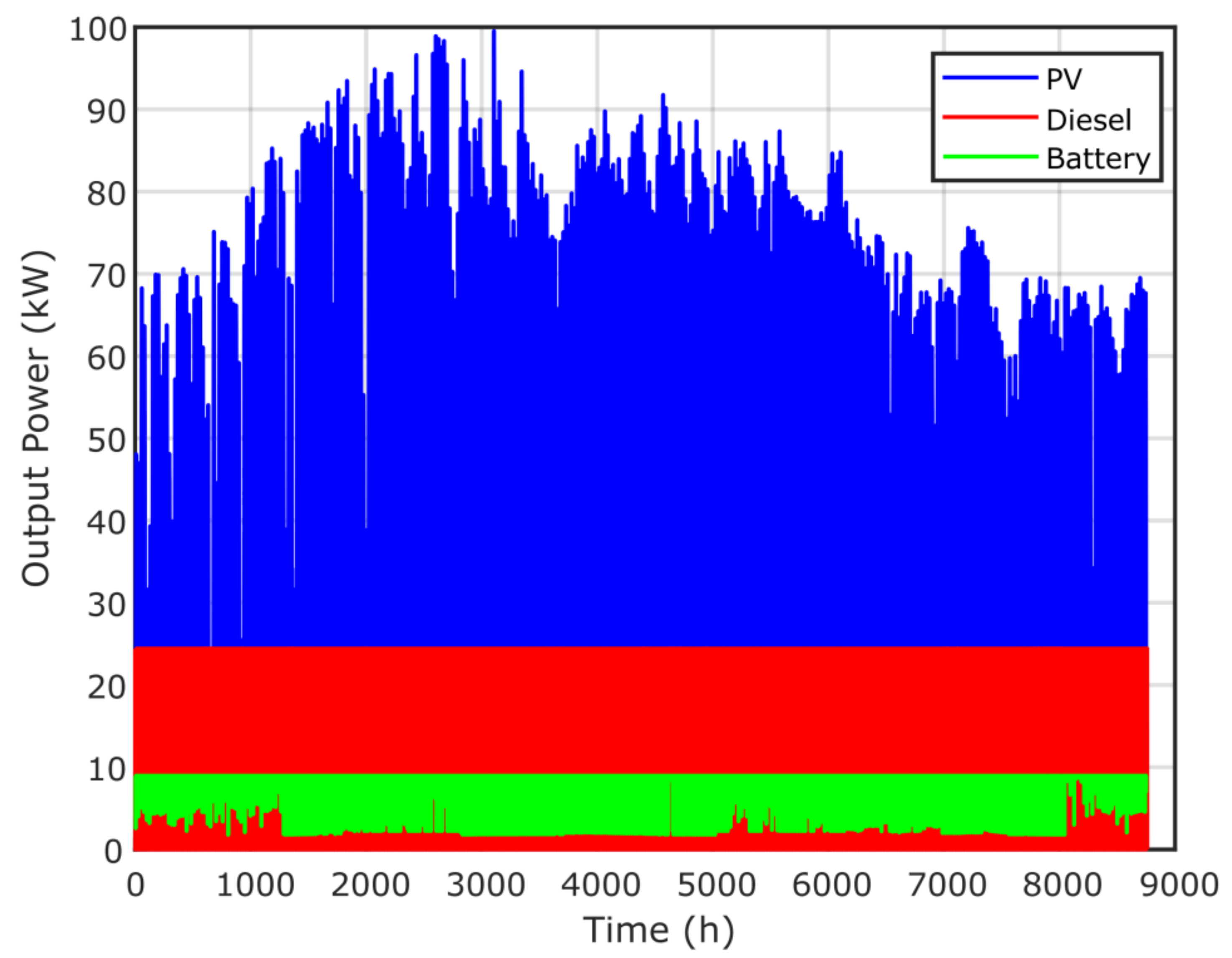
Figure 14 presents the annual contribution of the optimal microgrid system using the proposed GPC algorithm, while Figure 15 presents the time response of PV and biomass. Figure 16 and Figure 17 present the annual contribution and the time response of PV/diesel/battery. Figure 18 presents the annual contribution of PV/wind/diesel/battery using the GPC algorithm, while Figure 19 presents the time response of the PV and wind systems.

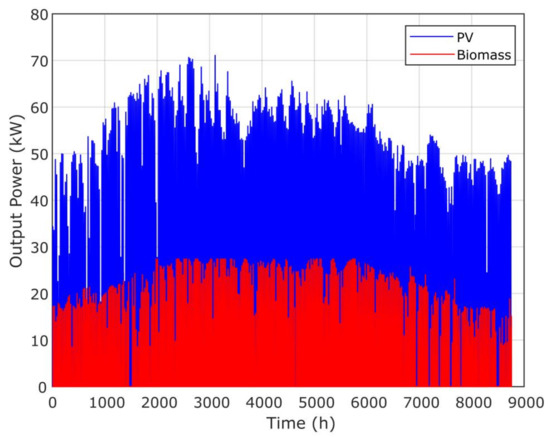
Figure 14. Annual contribution of PV/biomass system using the GPC algorithm.

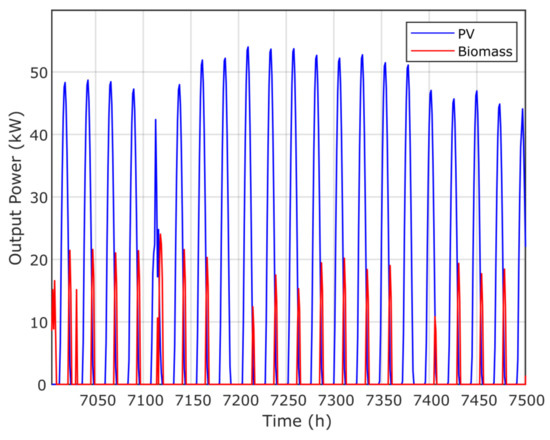
Figure 15. Time–response of the PV and biomass system via the GPC algorithm.

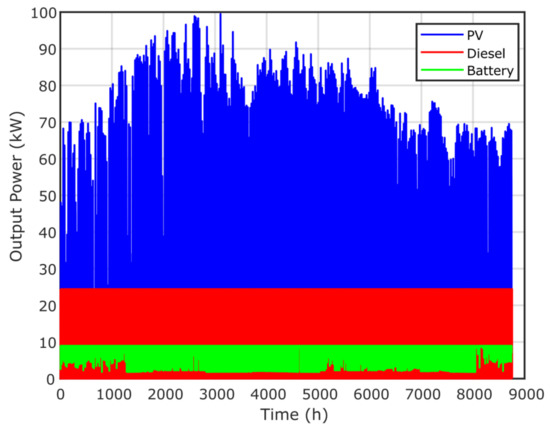
Figure 16. Annual contribution of PV/diesel/battery system using the GPC algorithm.

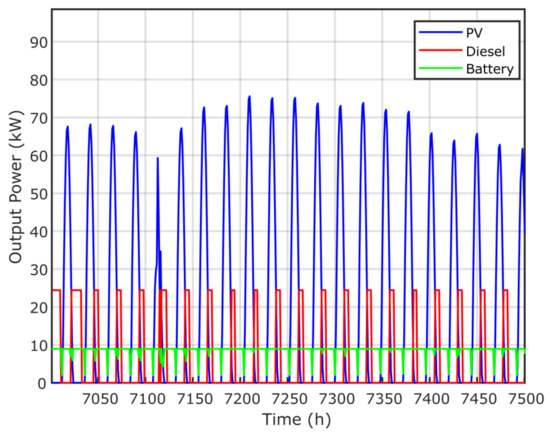
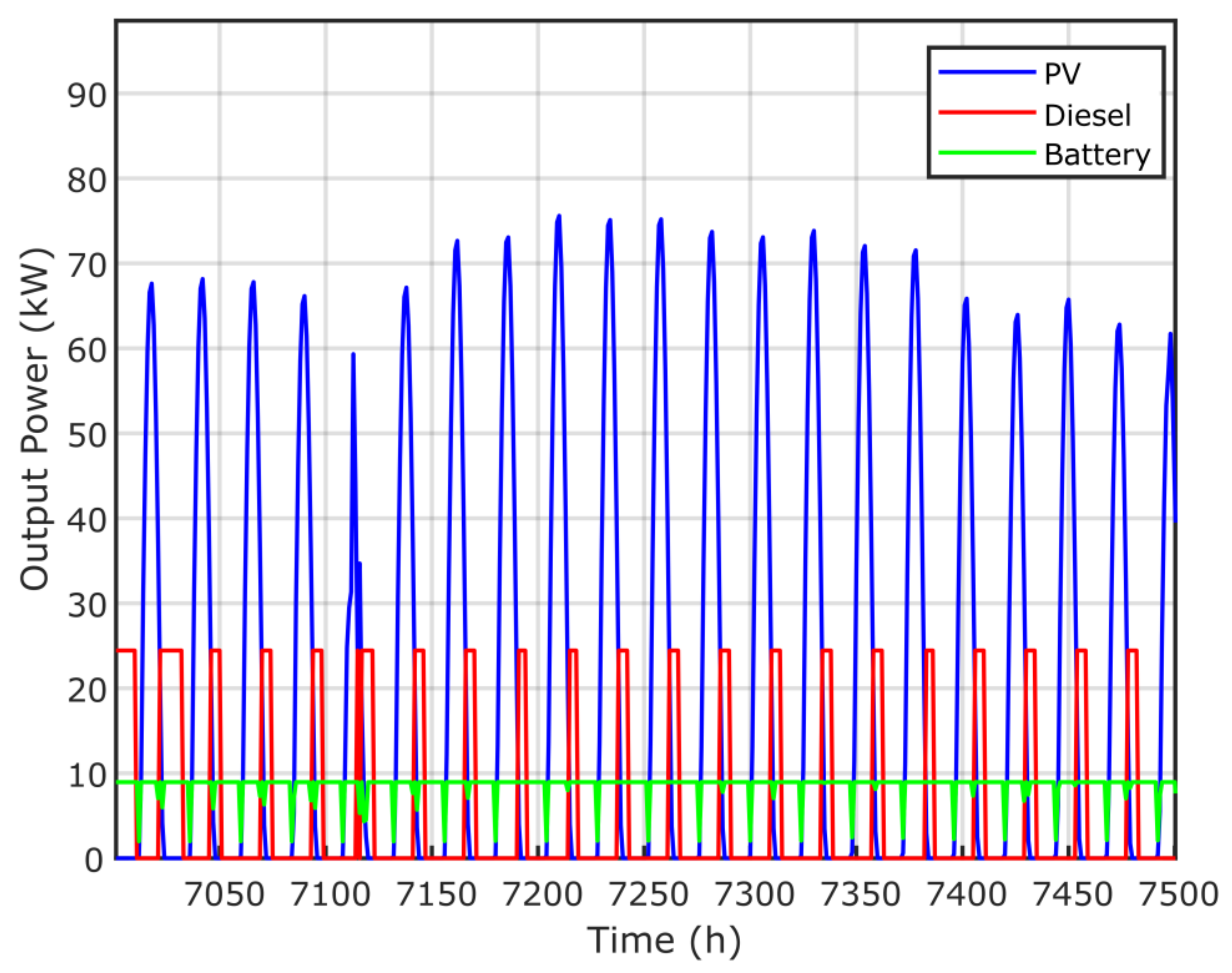
Figure 17. Time–response of the PV, diesel and battery generator via the GPC algorithm.

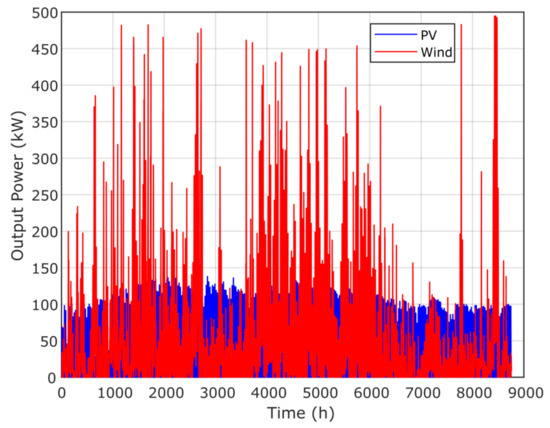
Figure 18. Annual contribution of PV/wind/diesel/battery using the GPC algorithm.

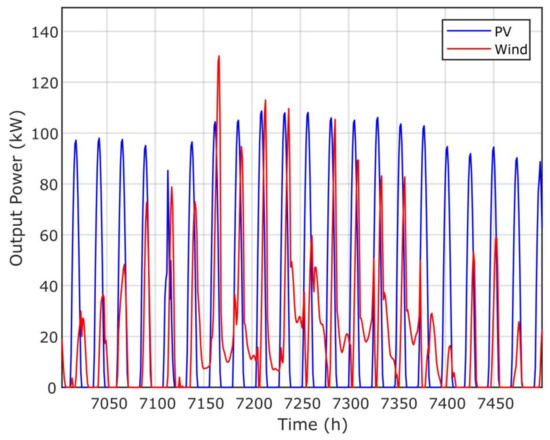
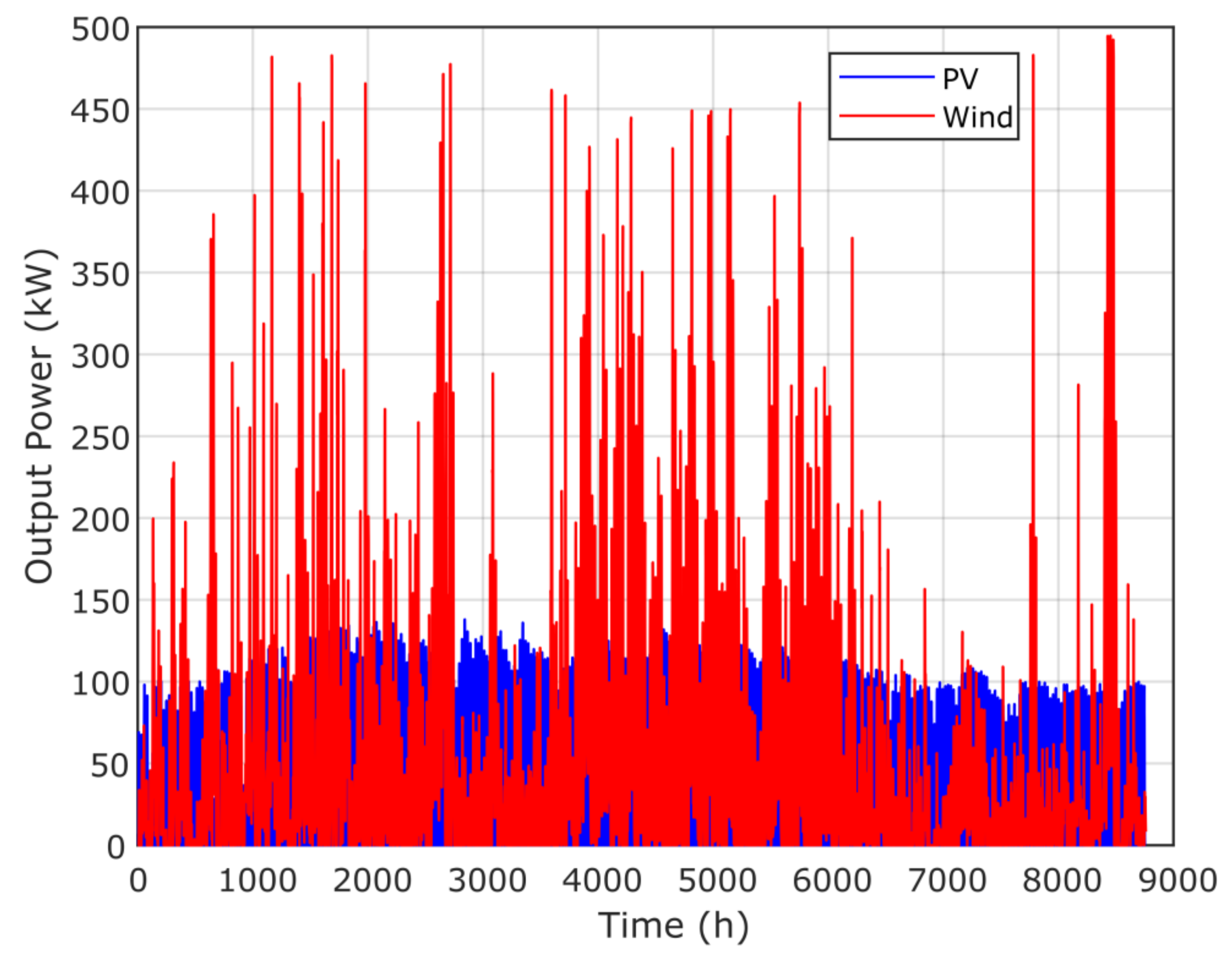
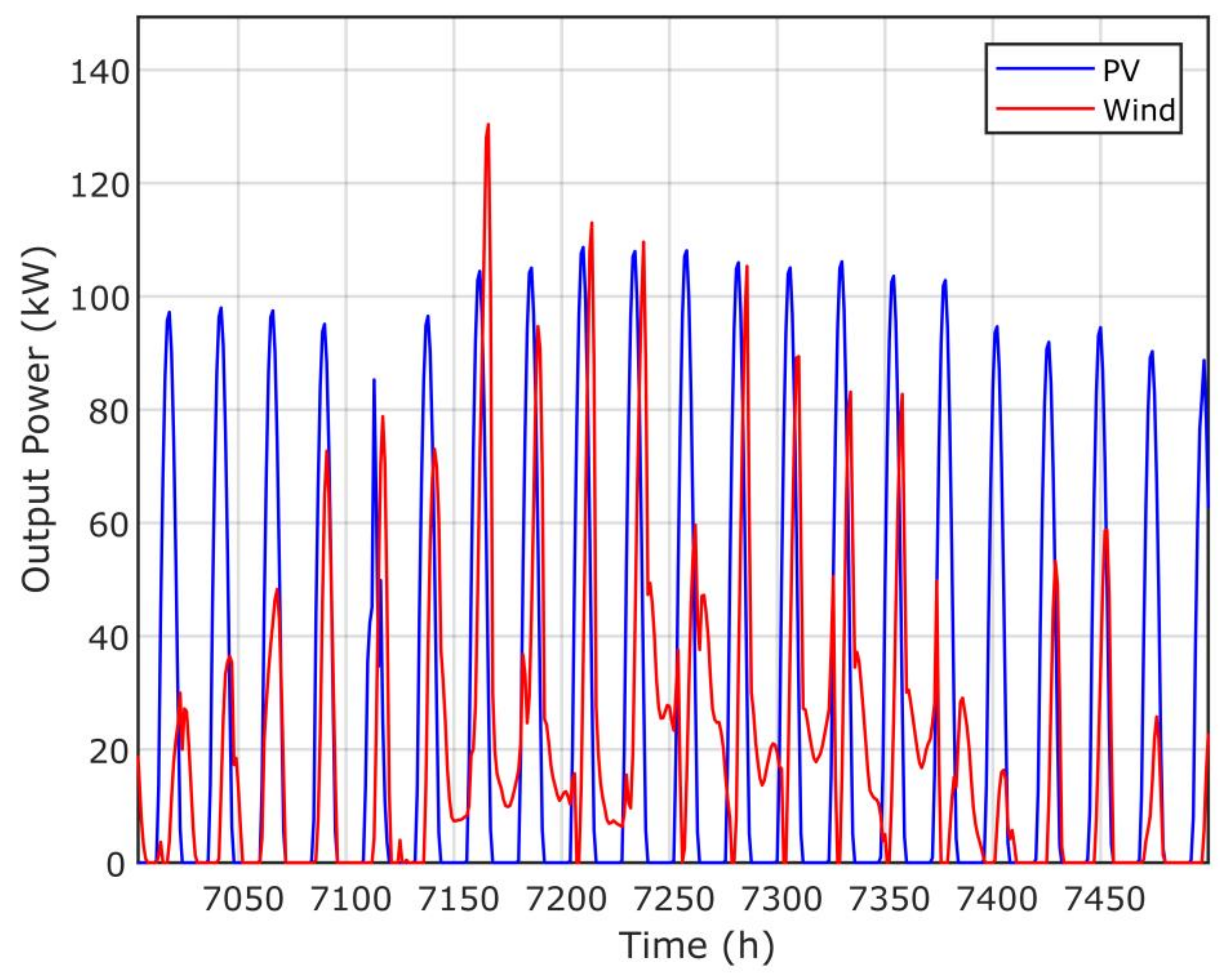
Figure 19. Time–response of PV and wind via the GPC algorithm.

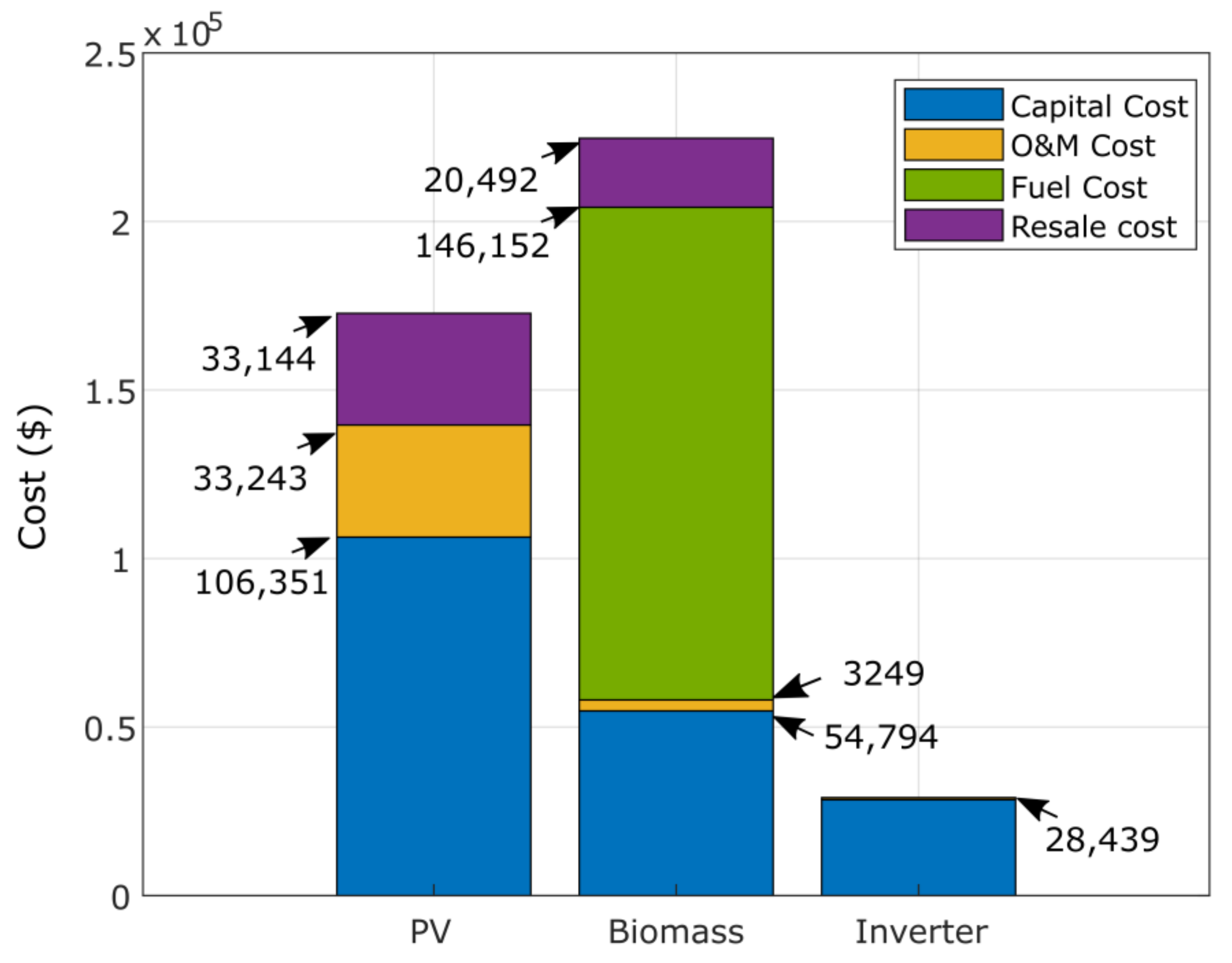
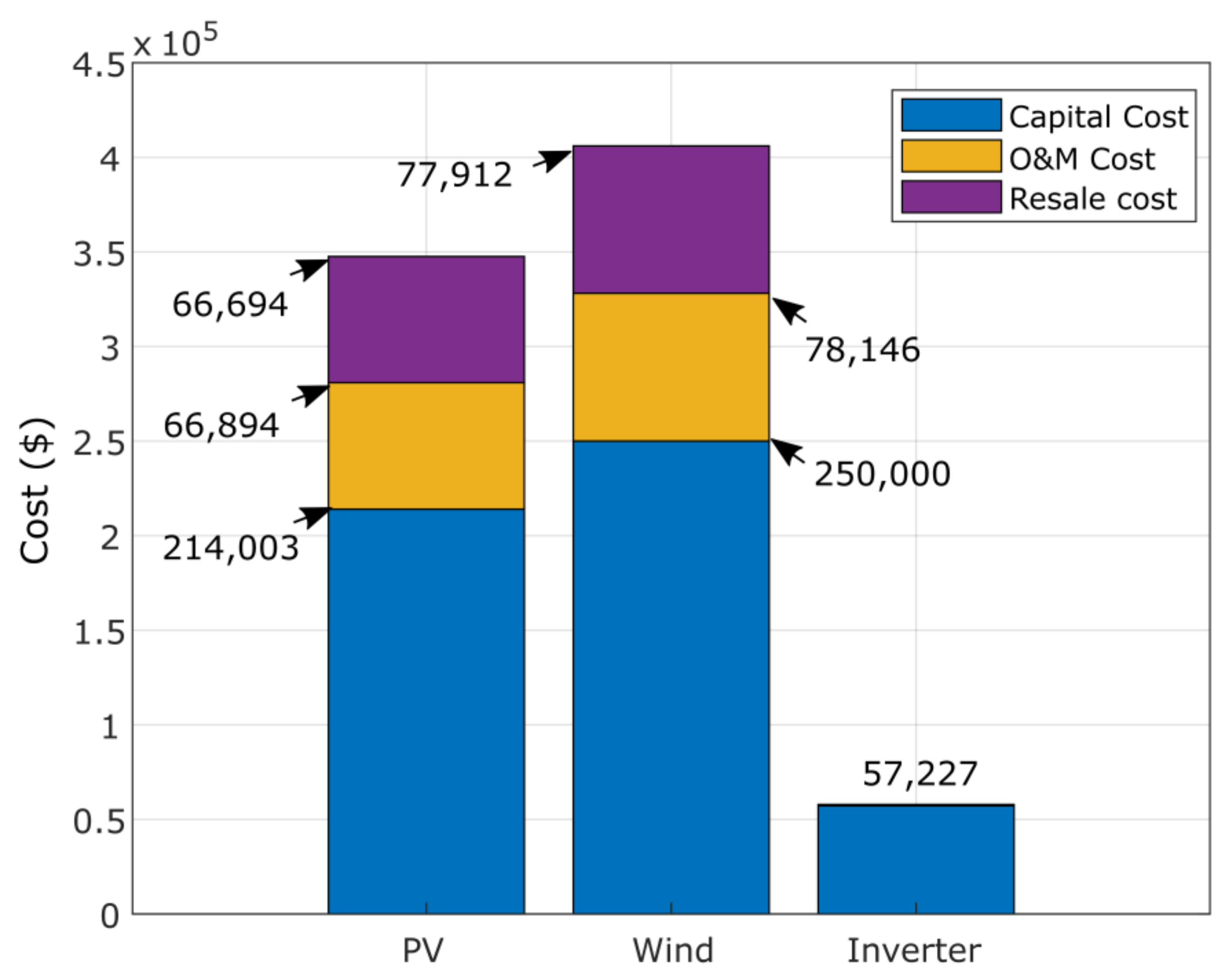
Figure 20 shows the required costs of PV, biomass and inverter, considering the capital, operation/maintenance, replacement and resale costs. All costs are expressed in dollars. Figure 21 and Figure 22 show the detailed costs of the two studied configurations, PV/diesel/battery and PV/wind/diesel/battery, respectively, where PV is the least expensive in both configurations. The cost of fuel is the highest during the project lifetime at $287,549 in the second configuration. Figure 23 presents the percent of total annual contribution, of which PV is the first contributor with 85%; similarly, PV represents 71.73% in the second configuration. The wind is the most important contributor in the PV/wind/diesel/battery with 59.75%.

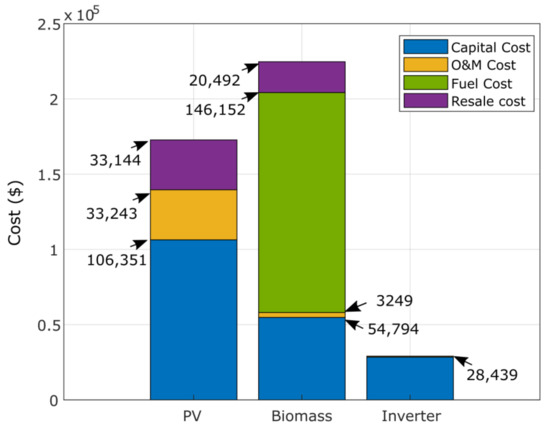
Figure 20. Detailed cost results ($) of the optimal PV/biomass system obtained using GPC algorithm.

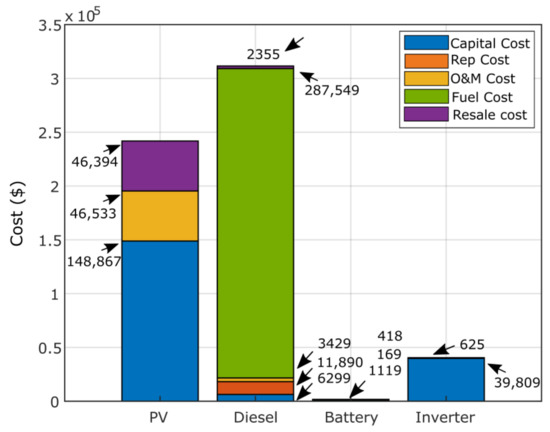
Figure 21. Detailed cost results ($) of the optimal PV/diesel/battery system obtained using GPC algorithm.

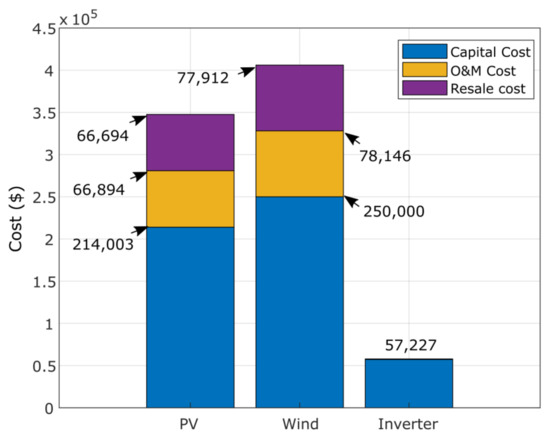
Figure 22. Detailed costs results ($) of the optimal PV/wind/diesel/battery system obtained using GPC algorithm.

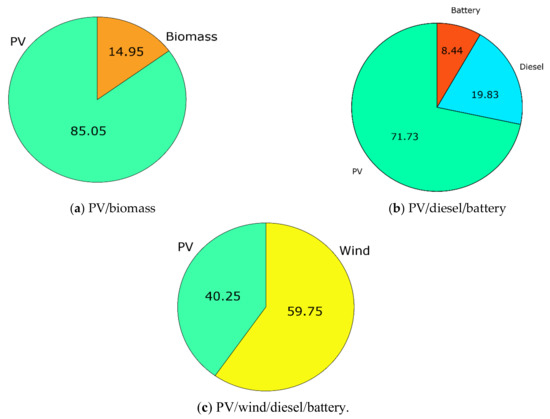
Figure 23. Power contribution percent of microgrid systems using the GPC algorithm: (a) PV/biomass; (b) PV/diesel/battery; and (c) PV/wind/diesel/battery.

7. Conclusions

The hybrid microgrid isolated systems is a cost-effective system, especially in Saudi Arabia, where solar radiation is significant. The paper presents the design of three hybrid microgrid systems in Yanbu region. The minimum cost of investment is obtained using the PV/biomass system by applying the recent GPC optimization algorithm. The developed algorithm is compared with the AEFA and GWO algorithms. The objective function is to minimize the net present cost respecting some technical constraints. The best optimal system has 265,870 m² of PV and 1000 ton/year biomass generator. The NPC is $319,219 and LCOE is $0.208/kWh. In future work, the proposal and implementation of new optimization algorithms and new microgrid system configurations will be the main focus. A new framework containing an efficient algorithm and a good power management helps to find a cost-effective microgrid system.

Appendix A.1. Algorithm of Artificial Electric Field

Anita and Yadav [35] were inspired by physical theorem, especially from the Coulomb’s law in the electrostatic force, to propose a recent algorithm called the artificial electric field. The concepts of the electric field and charged particles give us a theory of attraction and repulsion between the charged particles. The AEFA algorithm is presented in Algorithm A1.

Algorithm A1: AEFA [35]

Initialize a random population $X_B^i=\left(X_B^1,X_B^2,\dots ,X_B^N\right)$ of N size, within the limits $X_{min}^i\le X_B^i\le X_{max}^i$. Initialize velocity with a random value.

Evaluate the fitness of all populations.

Set iteration count to zero. Reproduction and Updating.

While the criteria are not satisfied do

Calculate K (t), best (t) and worst (t)

for i = 1: N do    Evaluate fitness values.    Calculate the total force of each direction.    Calculate acceleration.    ${\mathrm{V}}_i$(t + 1) = rand () × ${\mathrm{V}}_i$(t) +${\mathrm{a}}_i$(t)   ${\mathrm{X}}_i$(t + 1) = ${\mathrm{X}}_i$(t) + ${\mathrm{V}}_i$(t + 1)

end for

end while

Appendix A.2. Algorithm of Grey Wolf Optimizer

Mirjalili et al. [36] proposed the grey wolf optimizer, which mimics the leadership hierarchy and hunting mechanism of grey wolves in nature. The four types of grey wolves are alpha, beta, delta, and omega. All types are employed to simulate the leadership hierarchy. Three essential steps of hunting are implemented: searching prey, encircling prey, and attacking prey. The pseudo-code of GWO algorithm is presented in Algorithm A2.

Algorithm A2: GWO [36]

Initialize a set of grey wolf population $X_p^i=\left(X_p^1,X_p^2,\dots ,X_p^N\right)$ within the limits $X_{min}^i\le X_p^i\le X_{max}^i$. Initialize the parameters $a,A,\mathrm{and}C$ Calculate the fitness of all population. $X_{\alpha }=bestsearchagent$ $X_{\beta }=secondbestsearchagent$ $X_{\delta }=hirdbestsearchagent$

While (iter < $ite{r}_{max}$)

for i = 1: N do

Update the position of the current search agent    end for   Update a, A and C   Calculate the fitness of the whole population   Update $X_{\alpha }$, $X_{\beta }$ and $X_{\delta }$   iter = iter + 1 end while return $X_{\alpha }$

Appendix A.3. Algorithm Parameters

Algorithms	Parameters
GPC	Gravity = 9.8; Angle of Ramp = 30; Minimum Friction = 1; Maximum Friction = 10; Substitution Probability = 0.5.
AEFA	$K_0$ = 500; ⍺ = 30; Population size = 10; Maximum iteration = 100
GWO	a = Linear reduction from 2 to 0; Search agents = 10; Maximum iteration = 100