Online Retailer’s Contingent Free-Shipping Decisions under Large-Scale Promotions Considering Delayed Delivery
Abstract
:1. Introduction
2. Literature Review
2.1. The CFS Policy
2.2. Demand Postponement Strategy
2.3. Firms’ Operational Decisions during Price Promotions
3. Model
3.1. Notations and Assumptions
3.2. The Basic Model
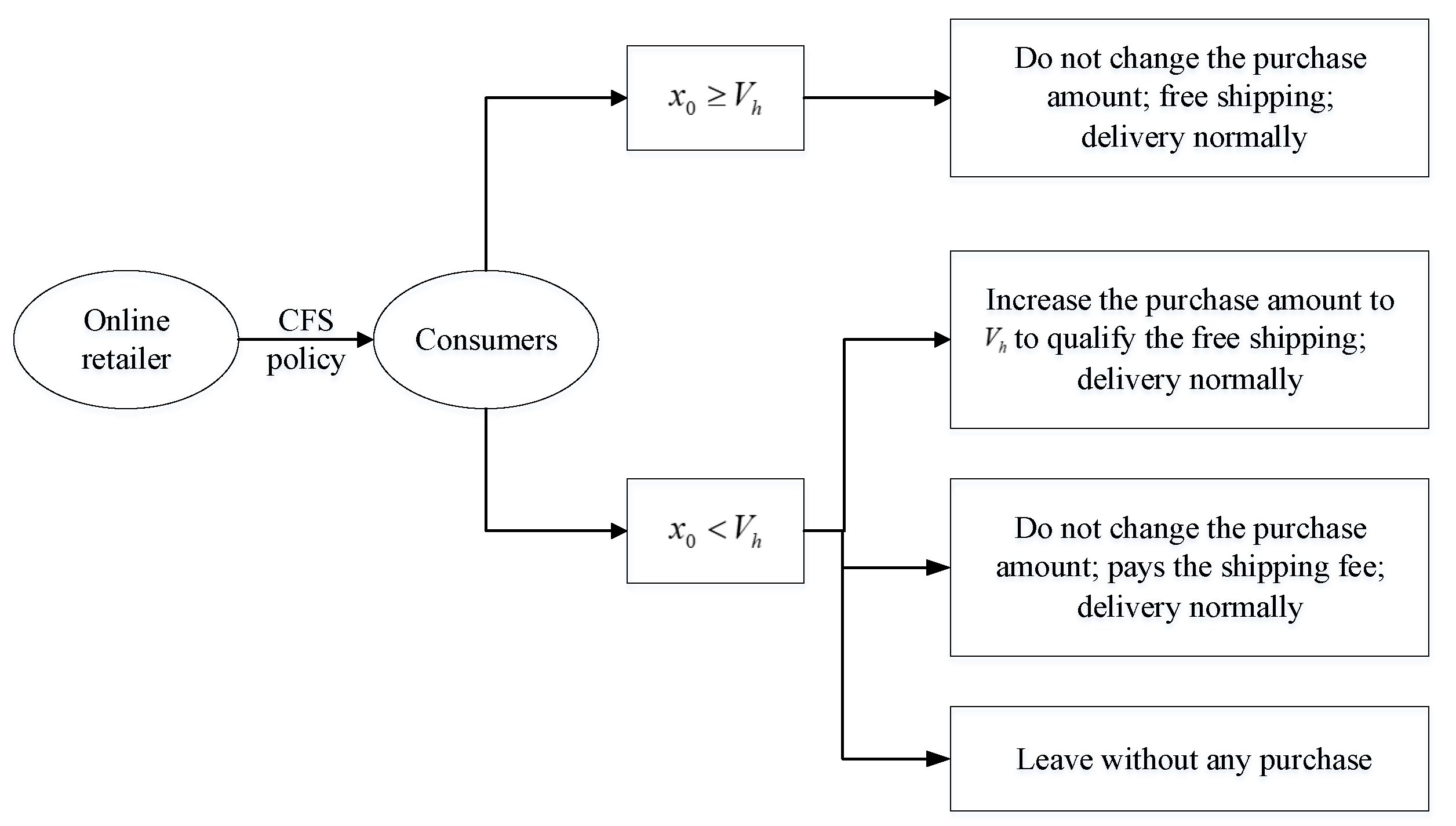
3.2.1. Consumer’s Purchasing Decision
3.2.2. Online Retailer’s Decision
3.3. The Developed Model with Delayed Delivery
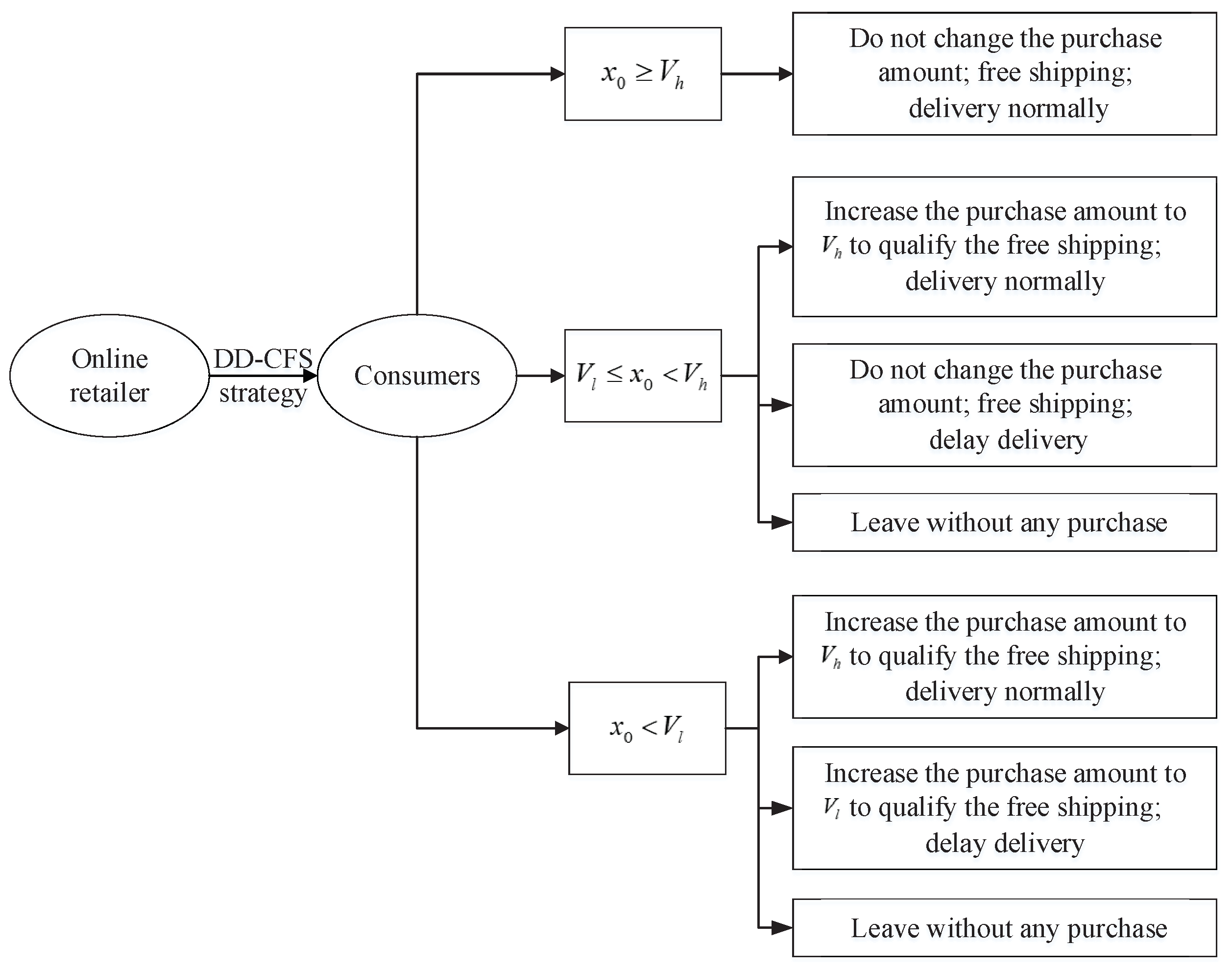
3.3.1. Consumer’s Purchasing Decision
3.3.2. Online Retailer’s Decision
4. Numerical Example
4.1. Numerical Results
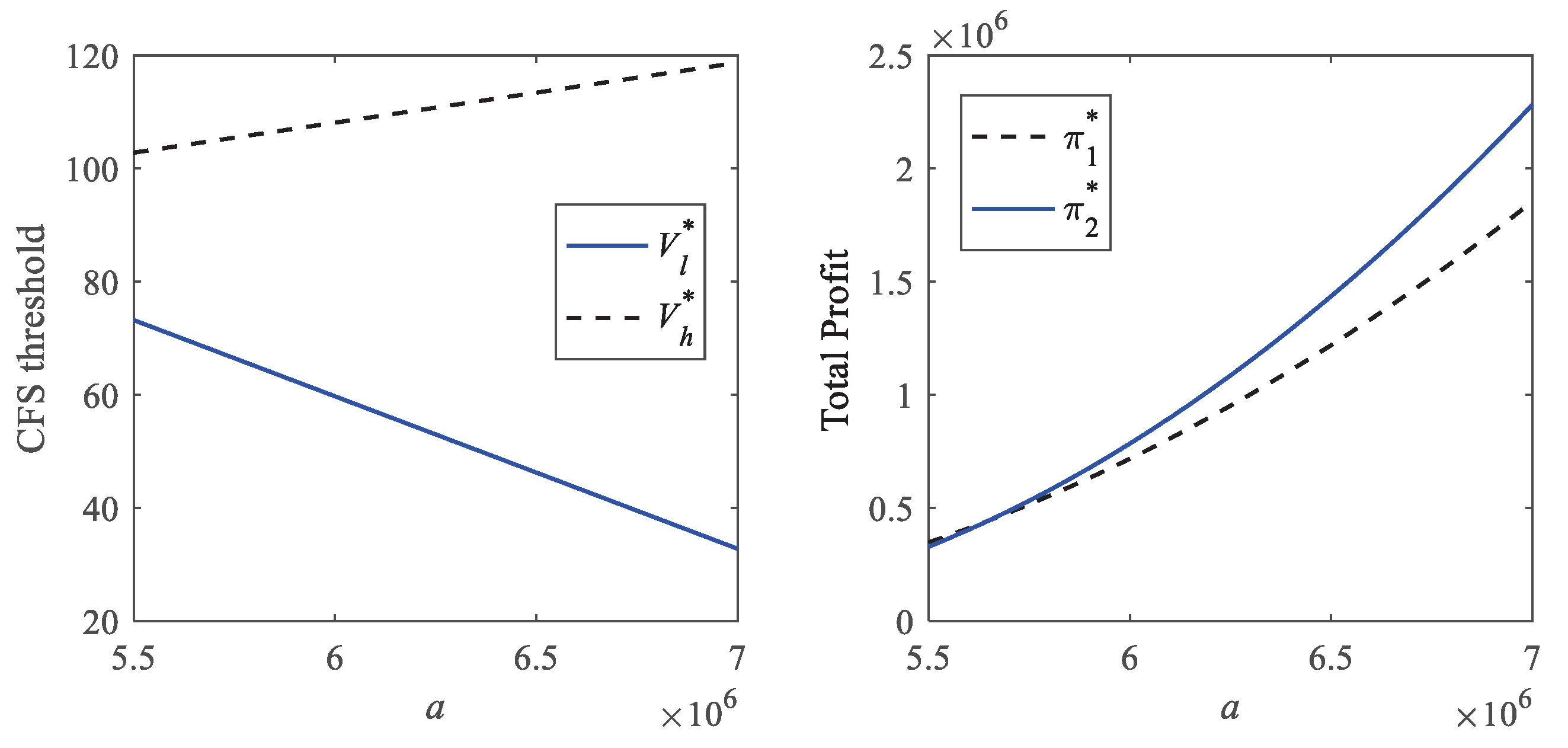
4.2. Sensitivity Analysis
4.2.1. The Impact of T
4.2.2. The Impact of C
4.2.3. The Impact of
4.2.4. The Impact of
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cyber Monday: Brisk Sales, Fewer Discounts and Plenty of Out-of-Stock Problems. Available online: https://edition.cnn.com/2021/11/30/business/cyber-monday-sales-total-2021/index.html (accessed on 30 November 2021).
- Alibaba Posts Record Sales for Singles Day, but Growth Is Slowing. Available online: https://edition.cnn.com/2021/11/10/business/china-singles-day-intl-hnk/index.html (accessed on 12 November 2021).
- Shu, L.; Wu, F.; Chu, L.K. Risk-averse procurement strategy under large-scale promotion online considering strategic customer. Comput. Ind. Eng. 2017, 112, 576–585. [Google Scholar] [CrossRef]
- Fang, Z.; Ho, Y.; Tan, X.; Tan, Y. Show Me the Money: The Economic Impact of Membership-based Free Shipping Programs on e-Tailers. Inform. Syst. Res. 2021, 32, 1115–1127. [Google Scholar] [CrossRef]
- Lewis, M. The effect of shipping fees on customer acquisition, customer retention, and purchase quantities. J. Retail. 2006, 82, 13–23. [Google Scholar] [CrossRef]
- Lewis, M.; Singh, V.; Fay, S. An Empirical Study of the Impact of Nonlinear Shipping and Handling Fees on Purchase Incidence and Expenditure Decisions. Market. Sci. 2006, 25, 51–64. [Google Scholar] [CrossRef]
- Koukova, N.T.; Srivastava, J.; Steul-Fischer, M. The effect of shipping fee structure on consumers’ online evaluations and choice. J. Acad. Market. Sci. 2012, 40, 759–770. [Google Scholar] [CrossRef]
- Huang, W.; Cheng, Y. Threshold free shipping policies for internet shoppers. Transport. Res. A Pol. 2015, 82, 193–203. [Google Scholar] [CrossRef]
- Huang, W.H.; Shen, G.C.; Liang, C.L. The effect of threshold free shipping policies on online shoppers’ willingness to pay for shipping. J. Retail. Consum. Serv. 2019, 48, 105–112. [Google Scholar] [CrossRef]
- Jiang, Y.; Shang, J.; Liu, Y. Optimizing shipping-fee schedules to maximize e-tailer profits. Int. J. Prod. Econ. 2013, 146, 634–645. [Google Scholar] [CrossRef]
- Zhou, B.; Michael, N.K.; Zhao, Y. Managing stochastic inventory systems with free shipping option. Eur. J. Oper. Res. 2009, 196, 186–197. [Google Scholar] [CrossRef]
- Kwon, K.; Cheong, T. A minimax distribution-free procedure for a newsvendor problem with free shipping. Eur. J. Oper. Res. 2014, 232, 234–240. [Google Scholar] [CrossRef]
- Leng, M.; Parlar, M. Free shipping and purchasing decisions in B2B transactions: A game-theoretic analysis. IIE. Trans. 2005, 37, 1119–1128. [Google Scholar] [CrossRef]
- Hua, G.; Wang, S.; Cheng, T.C.E. Optimal order lot sizing and pricing with free shipping. Eur. J. Oper. Res. 2012, 218, 435–441. [Google Scholar] [CrossRef]
- Leng, M.; Becerril-Arreola, R. Joint Pricing and Contingent Free-Shipping Decisions in B2C Transactions. Prod. Oper. Manag. 2010, 19, 390–405. [Google Scholar] [CrossRef]
- Boone, T.; Ganeshan, R. Exploratory analysis of free shipping policies of online retailers. Int. J. Prod. Econ. 2013, 143, 627–632. [Google Scholar] [CrossRef]
- Becerril-Arreola, R.; Leng, M.; Parlar, M. Online retailers’ promotional pricing, free-shipping threshold, and inventory decisions: A simulation-based analysis. Eur. J. Oper. Res. 2013, 230, 272–283. [Google Scholar] [CrossRef]
- Song, J.; Yin, Y.; Huang, Y. A coordination mechanism for optimizing the contingent-free shipping threshold in online retailing. Electron. Commer. Res. Appl. 2017, 26, 73–80. [Google Scholar] [CrossRef]
- Iyer, A.V.; Wu, D.Z. A Postponement Model for Demand Management. Manag. Sci. 2003, 49, 983–1002. [Google Scholar] [CrossRef]
- Wu, Z.; Wu, J. Price Discount and Capacity Planning under Demand Postponement with Opaque Selling. Decis. Support. Syst. 2015, 76, 24–34. [Google Scholar] [CrossRef]
- Alim, M.; Beullens, P. Joint inventory and distribution strategy for online sales with a flexible delivery option. Int. J. Prod. Econ. 2020, 222, 1–12. [Google Scholar] [CrossRef]
- Shin, Y.; Lee, S.; Moon, I. Robust multiperiod inventory model with a new type of buy one get one promotion: “My Own Refrigerator”. Omega 2021, 99, 102170. [Google Scholar] [CrossRef]
- Papanastasiou, Y.; Savva, N. Dynamic Pricing in the Presence of Social Learning and Strategic Consumers. Manag. Sci. 2017, 63, 919–939. [Google Scholar] [CrossRef]
- Dong, J.; Wu, D.D. Two-period pricing and quick response with strategic customers. Int. J. Prod. Econ. 2019, 215, 165–173. [Google Scholar] [CrossRef]
- Chen, K.; Zha, Y.; Alwan, L.C.; Zhang, L. Dynamic pricing in the presence of reference price effect and consumer strategic behaviour. Int. J. Prod. Res. 2020, 58, 546–561. [Google Scholar] [CrossRef]
- Chen, P.; Zhao, R.; Yan, Y.; Li, X. Promotional pricing and online business model choice in the presence of retail competition. Omega 2020, 94, 102085. [Google Scholar] [CrossRef]
- Li, C.; Chu, M.; Zhou, C.; Zhao, L. Two-period discount pricing strategies for an e-commerce platform with strategic consumers. Comput. Ind. Eng. 2020, 147, 106640. [Google Scholar] [CrossRef]
- Maihami, R.; Karimi, B. Optimizing the pricing and replenishment policy for non-instantaneous deteriorating items with stochastic demand and promotional efforts. Comput. Oper. Res. 2014, 51, 302–312. [Google Scholar] [CrossRef]
- Zhang, J.L.; Chen, J.; Lee, C.Y. Joint optimization on pricing, promotion and inventory control with stochastic demand. Int. J. Prod. Econ. 2008, 116, 190–198. [Google Scholar] [CrossRef]
- Chen, Z. Optimization of production inventory with pricing and promotion effort for a single-vendor multi-buyer system of perishable products. Int. J. Prod. Econ. 2018, 203, 333–349. [Google Scholar] [CrossRef]
- Tsao, Y.C.; Sheen, G.J. Dynamic pricing, promotion and replenishment policies for a deteriorating item under permissible delay in payments. Comput. Oper. Res. 2008, 35, 3562–3580. [Google Scholar] [CrossRef]
- Lin, Z. Price promotion with reference price effects in supply chain. Transp. Res. E 2016, 85, 52–68. [Google Scholar] [CrossRef]
- Su, Y.; Geunes, J. Price promotions, operations cost, and profit in a two-stage supply chain. Omega 2012, 40, 891–905. [Google Scholar] [CrossRef]
- Kurata, H.; Liu, J. Optimal promotion planning-depth and frequency-for a two-stage supply chain under Markov switching demand. Eur. J. Oper. Res. 2007, 177, 1026–1043. [Google Scholar] [CrossRef]
- Wu, F.; Shu, L.; Zhao, S.S.; Jiang, B. Risk-Averse Portfolio Procurement Strategy Under Large-Scale Promotion Online. IEEE. Trans. Eng. Manag. 2022, 69, 1252–1261. [Google Scholar] [CrossRef]
- Zeng, M.; Cao, H.; Chen, M.; Li, Y. User behaviour modeling, recommendations, and purchase prediction during shopping festivals. Electron. Market. 2019, 29, 263–274. [Google Scholar] [CrossRef]
- Xu, X.; Li, Q.; Peng, L.; Hsia, T.L.; Huang, C.J.; Wu, J.H. The impact of informational incentives and social influence on consumer behavior during Alibaba’s online shopping carnival. Comput. Hum. Behav. 2017, 76, 245–254. [Google Scholar] [CrossRef]
- Xu, X.; Wang, L.; Zhao, K. Exploring Determinants of Consumers’ Platform Usage in “Double Eleven” Shopping Carnival in China: Cognition and Emotion from an Integrated Perspective. Sustainability 2020, 12, 2790. [Google Scholar] [CrossRef]
- Yu, H.; Zeng, A.Z.; Zhao, L. Single or dual sourcing: Decision-making in the presence of supply chain disruption risks. Omega 2009, 37, 788–800. [Google Scholar] [CrossRef]
- Khouja, M.; Pan, J.; Ratchford, B.T. Analysis of free gift card program effectiveness. J. Retail. 2011, 87, 444–461. [Google Scholar] [CrossRef]








| Notations | |
|---|---|
| m | The online retailer’s profit margin |
| C | The shipping fee of the unit order |
| T | The length of the delivery delay time |
| a | Potential market size |
| Consumer sensitivity to the shipping fee | |
| Consumer sensitivity to CFS threshold | |
| The demand for consumer orders in the basic model | |
| The demand for consumer orders in the developed model | |
| The consumer’s planned purchase amount (in dollars), which follows the uniform distribution | |
| v | Consumer’s marginal utility when the real purchase amount is less than the planned purchase amount, |
| d | Consumer’s marginal utility when the real purchase amount is not less than the planned purchase amount, |
| Indicator of consumers’ negative attitude toward the shipping fee, | |
| Indicator of consumers’ negative attitude toward the delayed delivery time, which follows the uniform distribution | |
| k | The discount on the shipping fee for the delayed delivery |
| R | The total shipping fees |
| E | The total expected revenues |
| The online retailer’s total expected profit | |
| Subscript | |
| n | The shipping-fee-sensitive consumer |
| s | The on-time delivery required consumer |
| Decision variables | |
| x | Consumer’s real purchase amount (in dollars) |
| The high CFS threshold value | |
| The low CFS threshold value |
| CFS Threshold | Demand | The Expected Profit | |
|---|---|---|---|
| The basic model | |||
| The developed model |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Bian, W.; Yang, X.; Niu, S.; Cai, Y.; Guan, J.; Wang, W. Online Retailer’s Contingent Free-Shipping Decisions under Large-Scale Promotions Considering Delayed Delivery. Sustainability 2022, 14, 10773. https://doi.org/10.3390/su141710773
Ma X, Bian W, Yang X, Niu S, Cai Y, Guan J, Wang W. Online Retailer’s Contingent Free-Shipping Decisions under Large-Scale Promotions Considering Delayed Delivery. Sustainability. 2022; 14(17):10773. https://doi.org/10.3390/su141710773
Chicago/Turabian StyleMa, Xiaxia, Wenliang Bian, Xiqing Yang, Shengnan Niu, Yongming Cai, Jie Guan, and Wenbin Wang. 2022. "Online Retailer’s Contingent Free-Shipping Decisions under Large-Scale Promotions Considering Delayed Delivery" Sustainability 14, no. 17: 10773. https://doi.org/10.3390/su141710773
APA StyleMa, X., Bian, W., Yang, X., Niu, S., Cai, Y., Guan, J., & Wang, W. (2022). Online Retailer’s Contingent Free-Shipping Decisions under Large-Scale Promotions Considering Delayed Delivery. Sustainability, 14(17), 10773. https://doi.org/10.3390/su141710773







