Remaining Fatigue Life Predictions of Railway Prestressed Concrete Sleepers Considering Time-Dependent Surface Abrasion
Abstract
:1. Introduction
2. Theoretical Life-Cycle Assessment Method of Prestressed Concrete Sleepers
2.1. Damage Accumulation Method
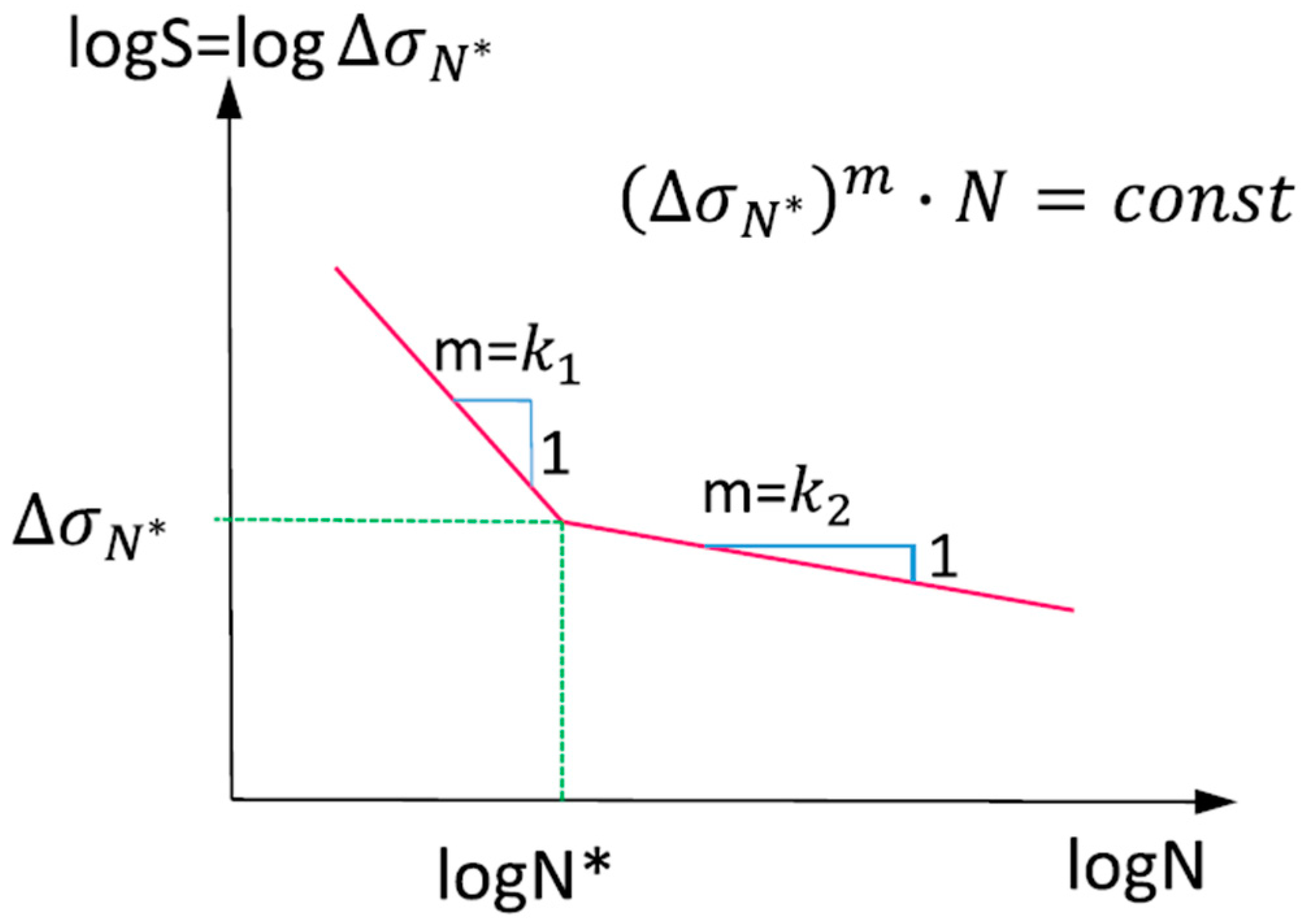
2.2. Material Properties of Fatigue
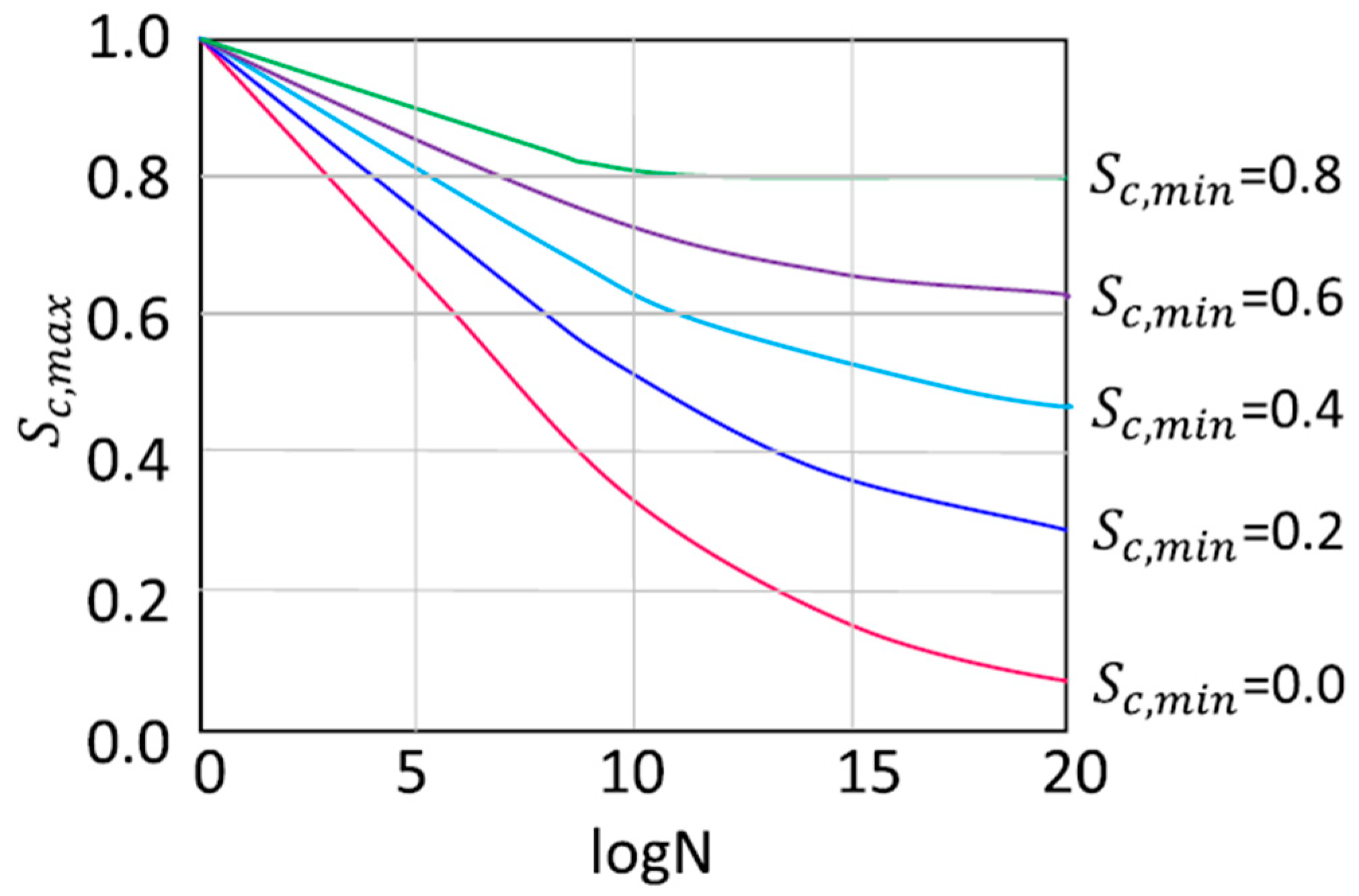
2.3. Fatigue Life Assessment
3. Numerical Life-Cycle Assessment Method of Prestressed Concrete Sleepers
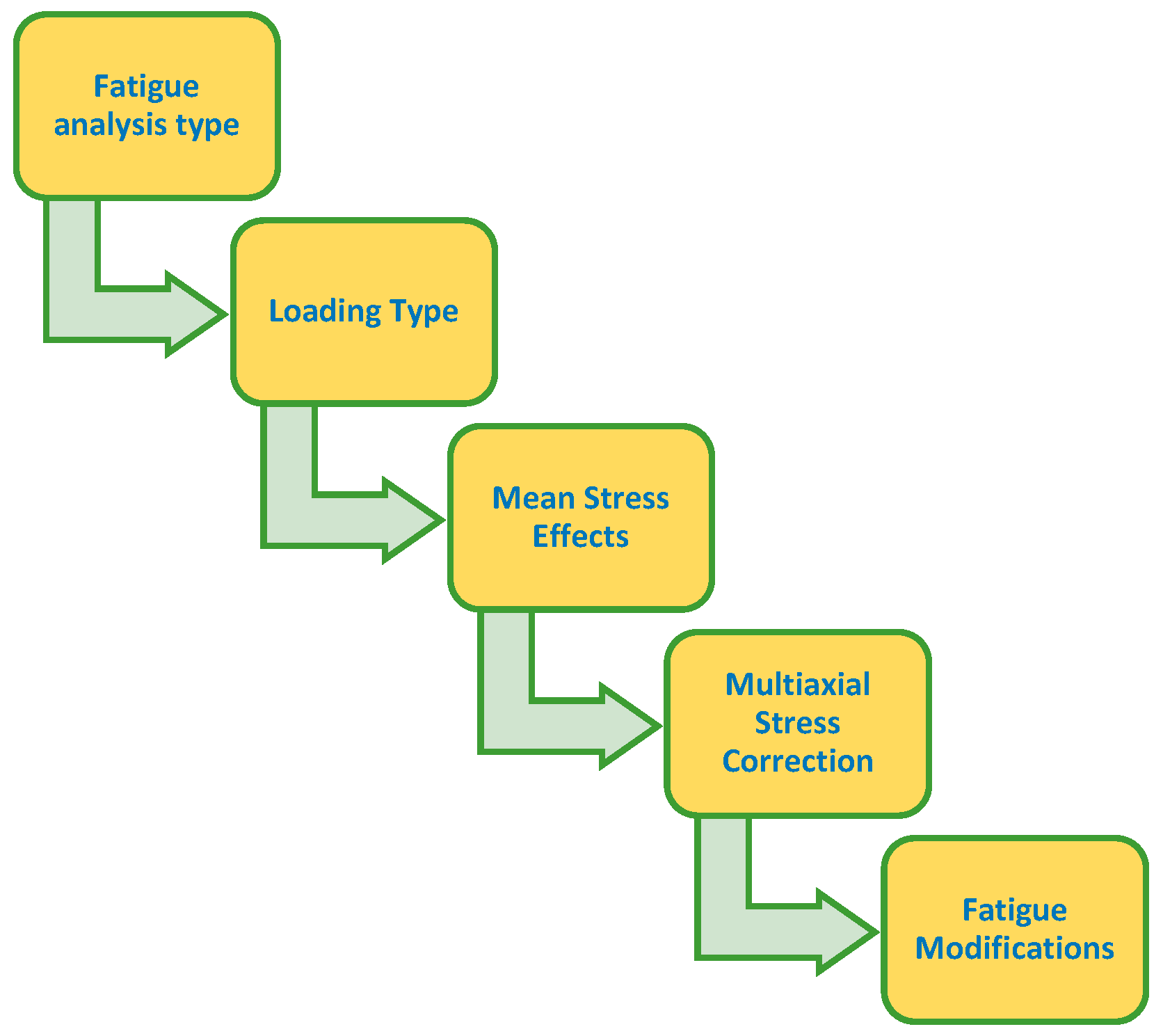
3.1. Fatigue Analysis Decisions
3.2. Types of Cyclic Loading
- Constant amplitude, proportional loading;
- Constant amplitude, non-proportional loading;
- Non-constant amplitude, proportional loading;
- Non-constant amplitude, non-proportional loading.
3.3. Fatigue Life Results
4. Prestressed Concrete Sleeper Modelling
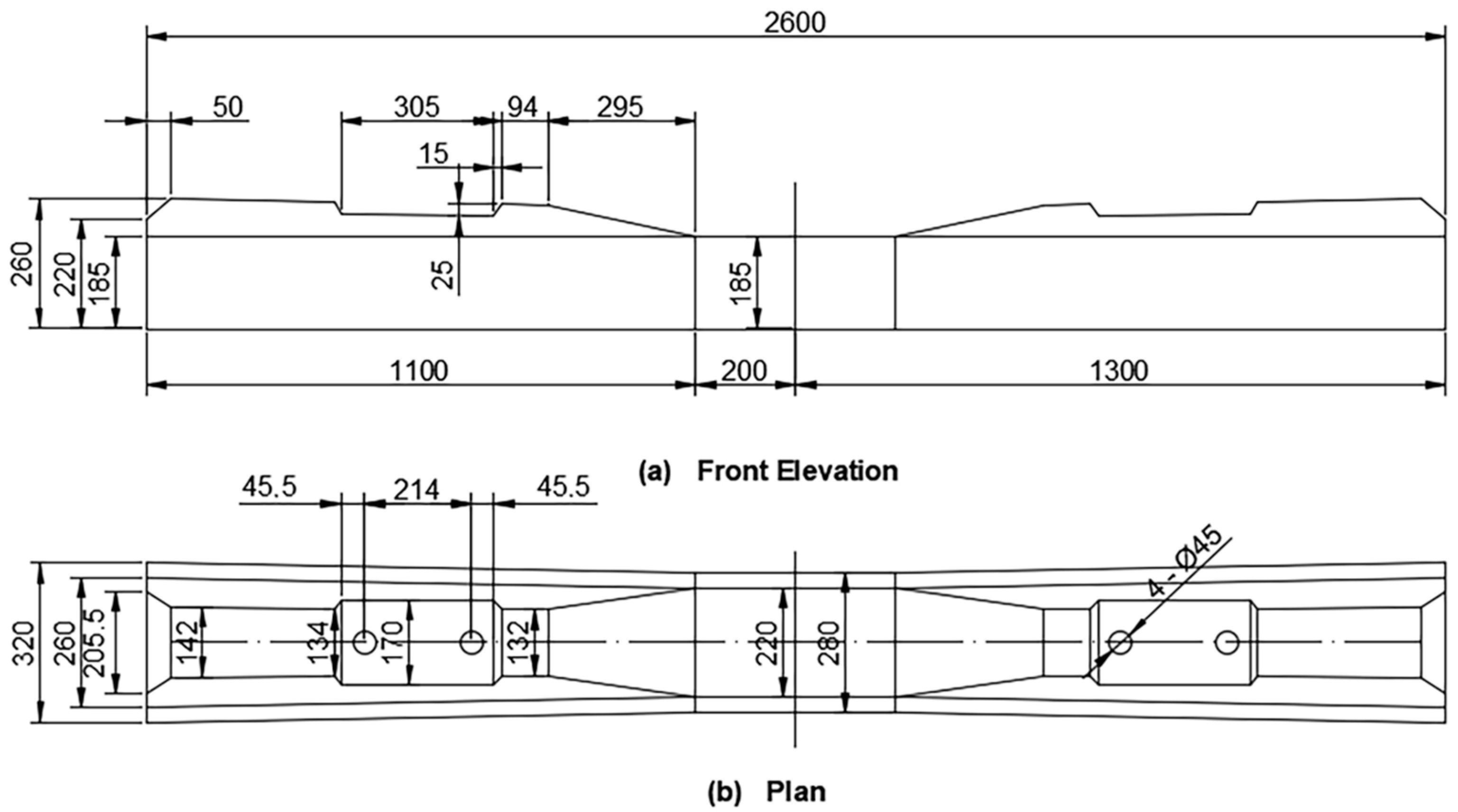
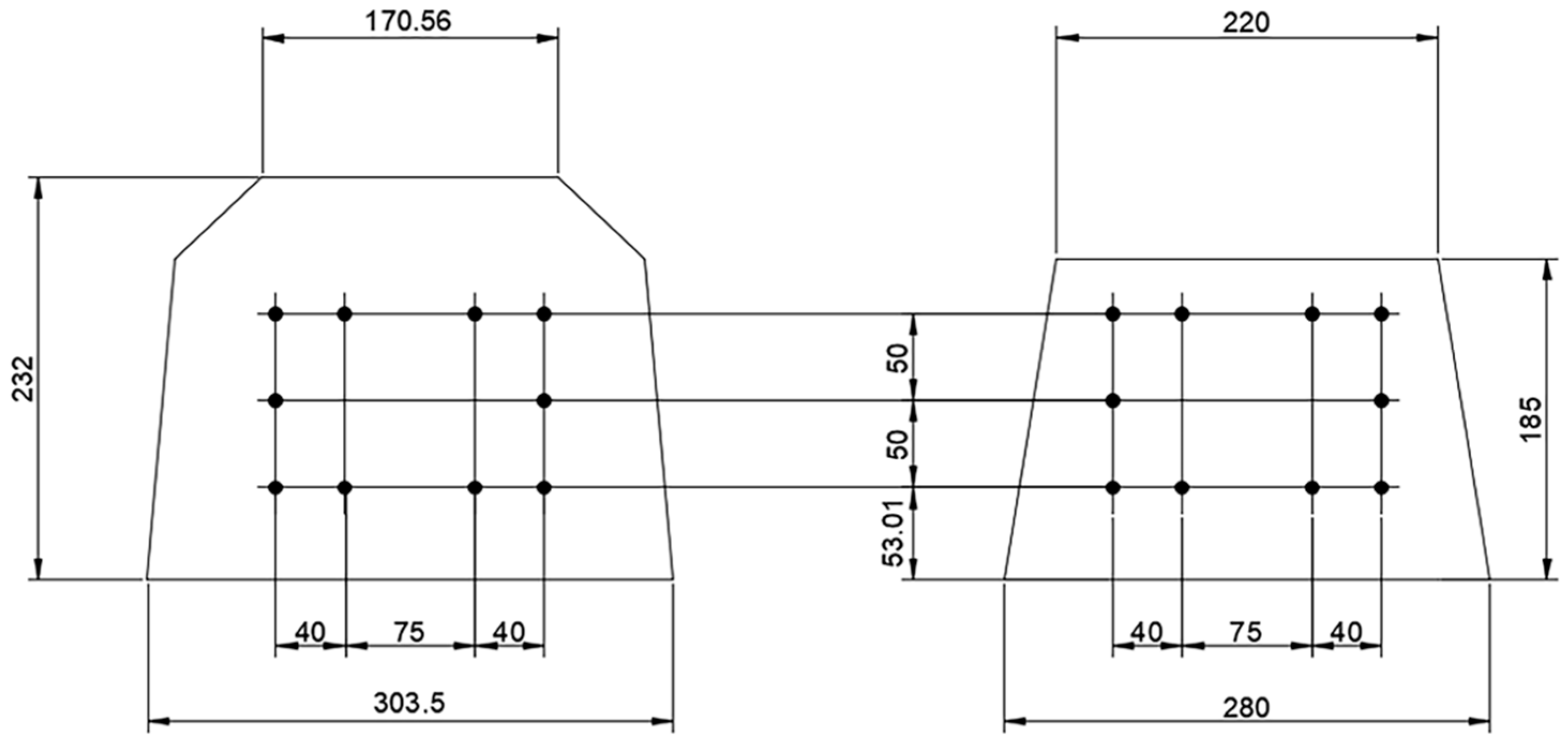
4.1. Properties of the Railway Sleeper
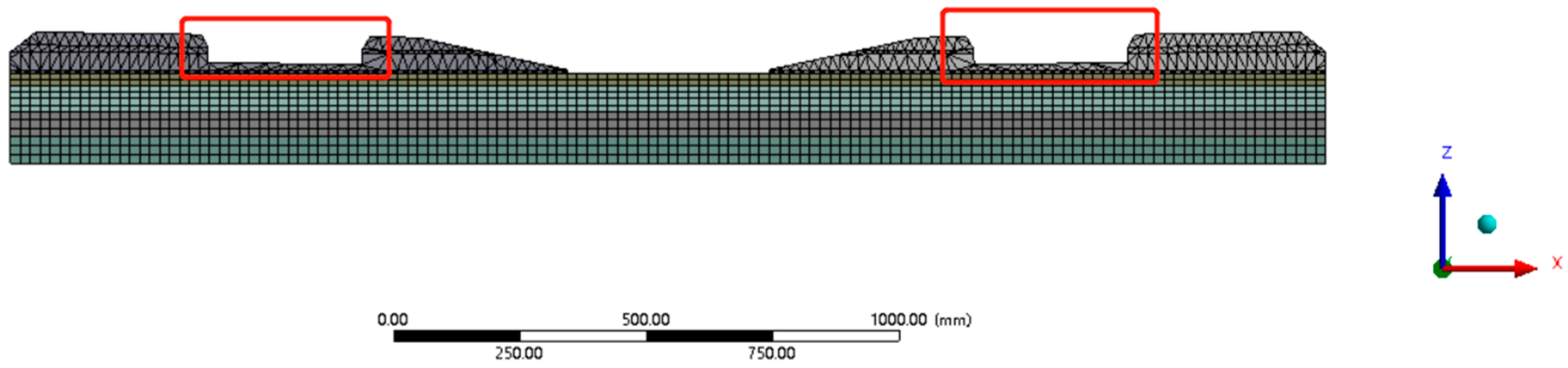
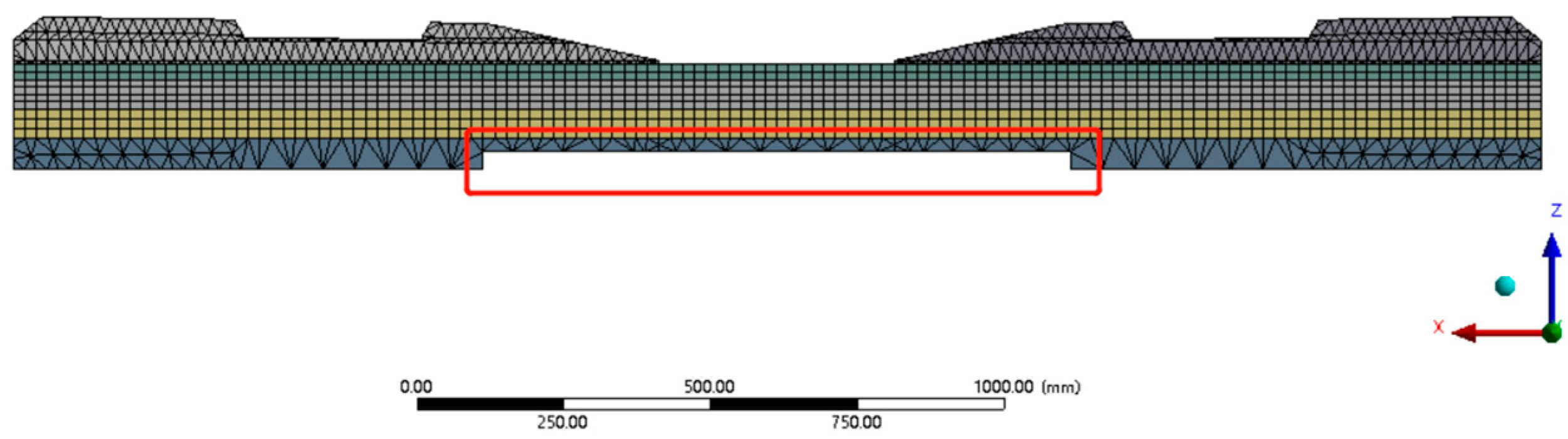
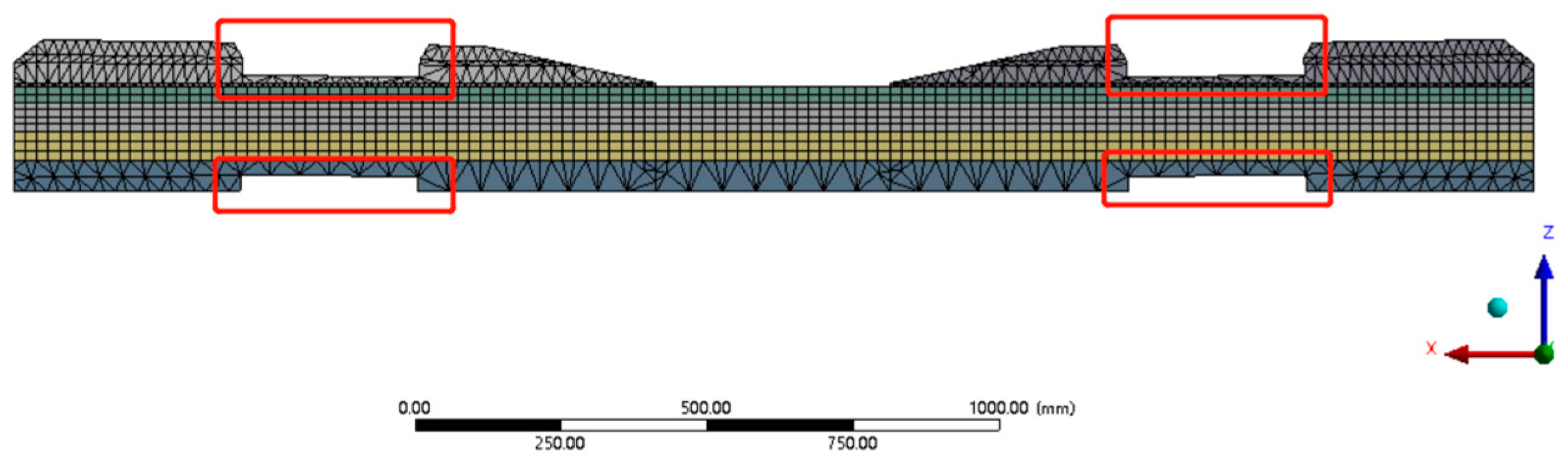
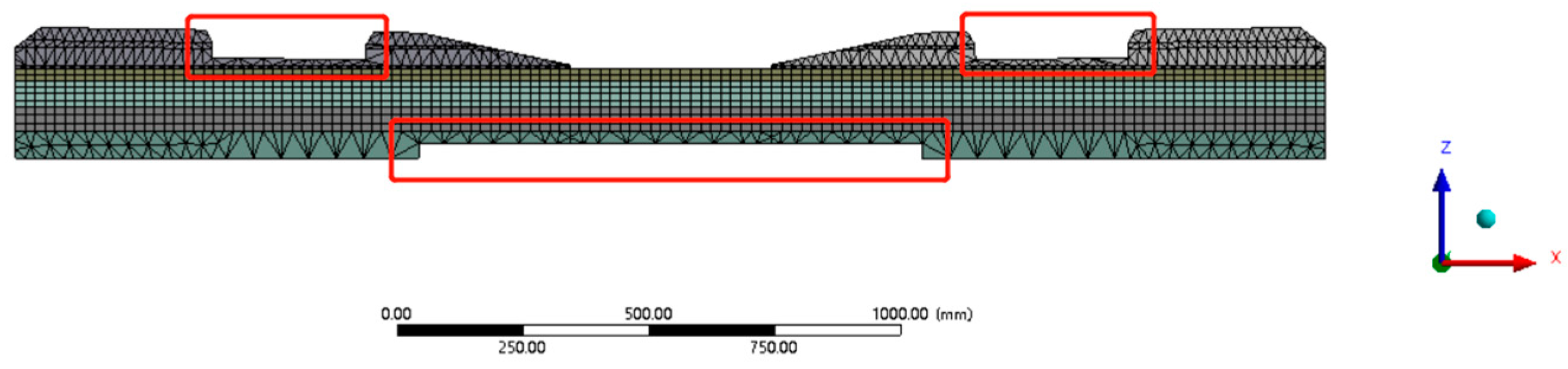
4.2. Finite Element Model
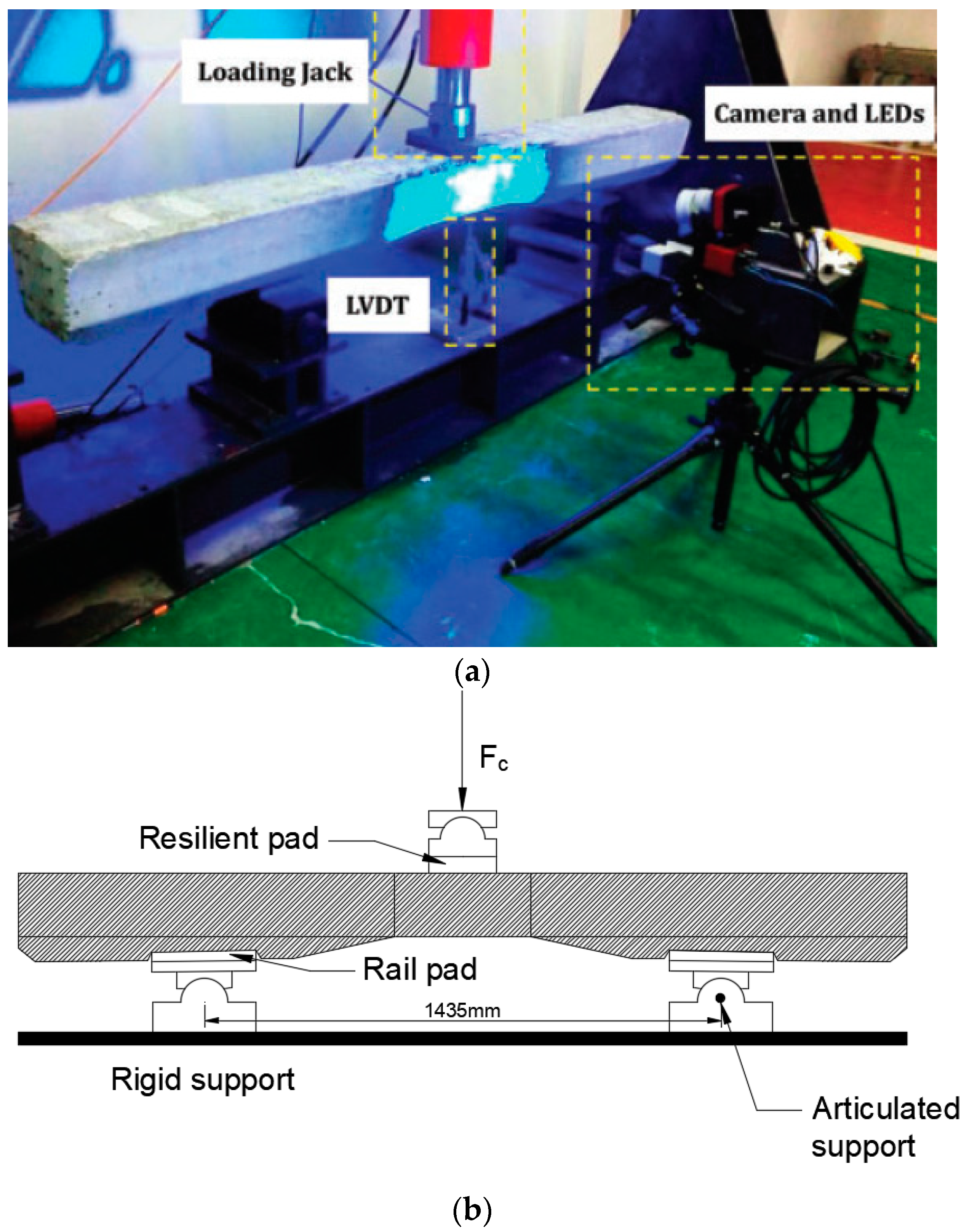
4.3. Experimental Program
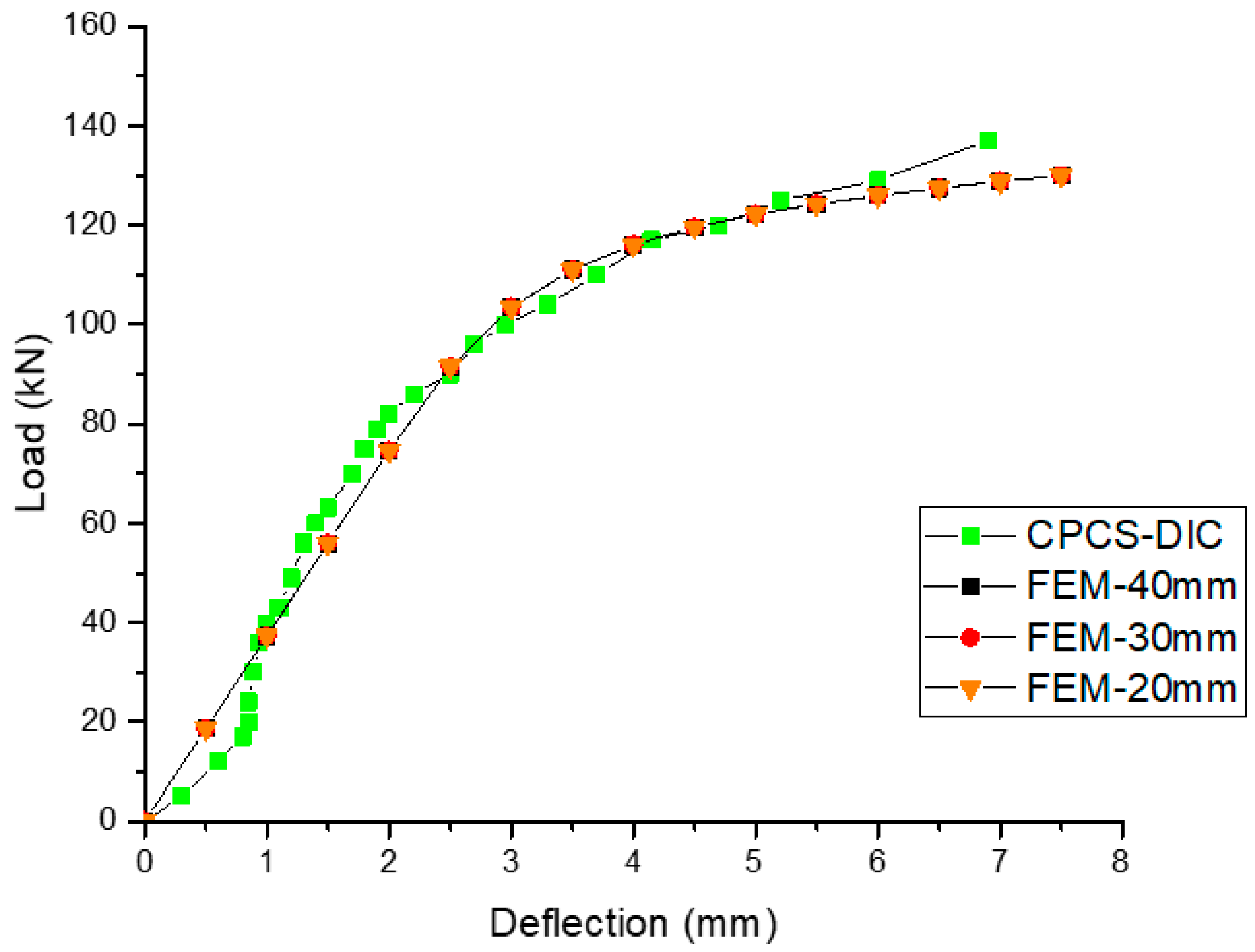
4.4. FE Sleeper Model Validation
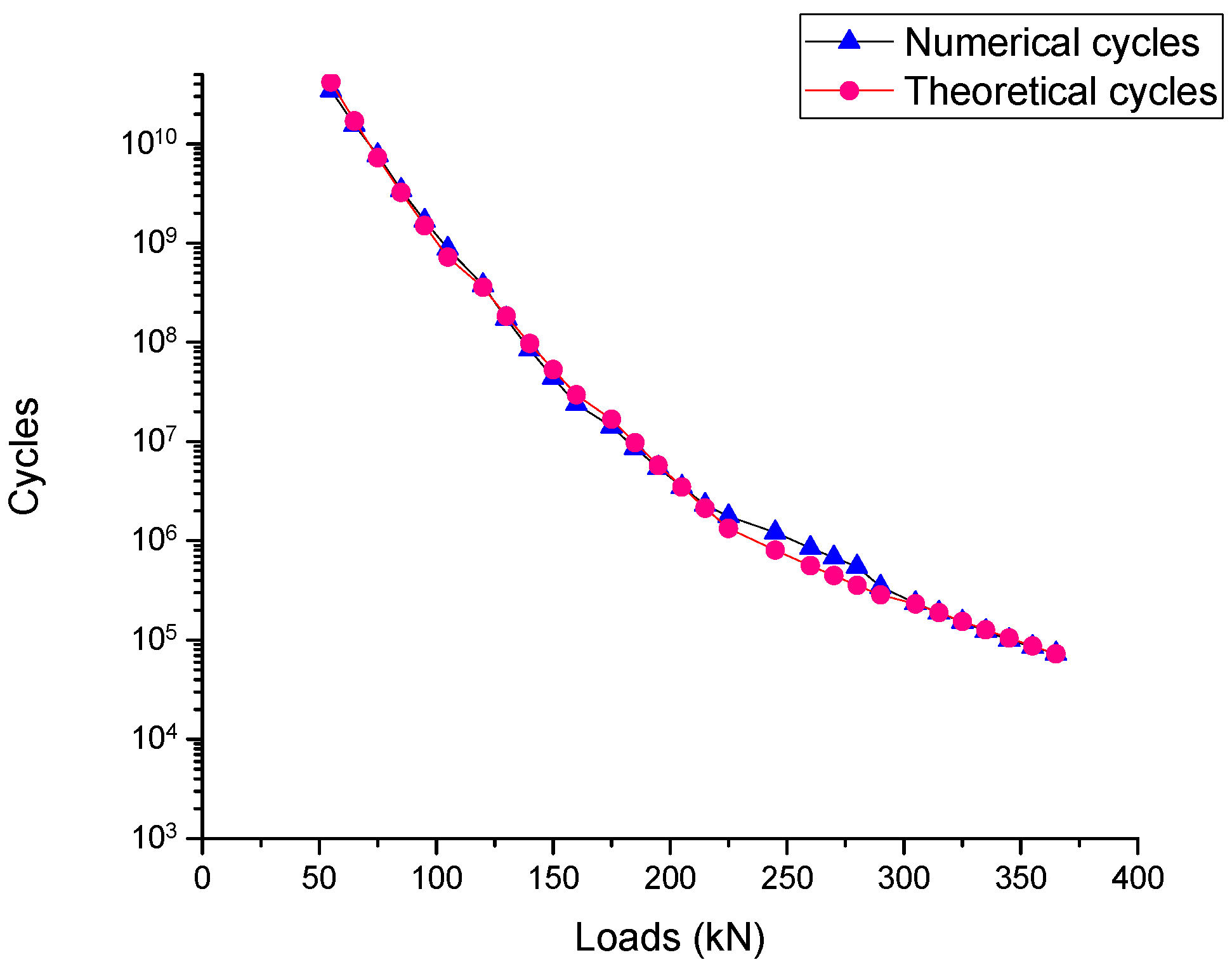
4.5. Fatigue Model Validation
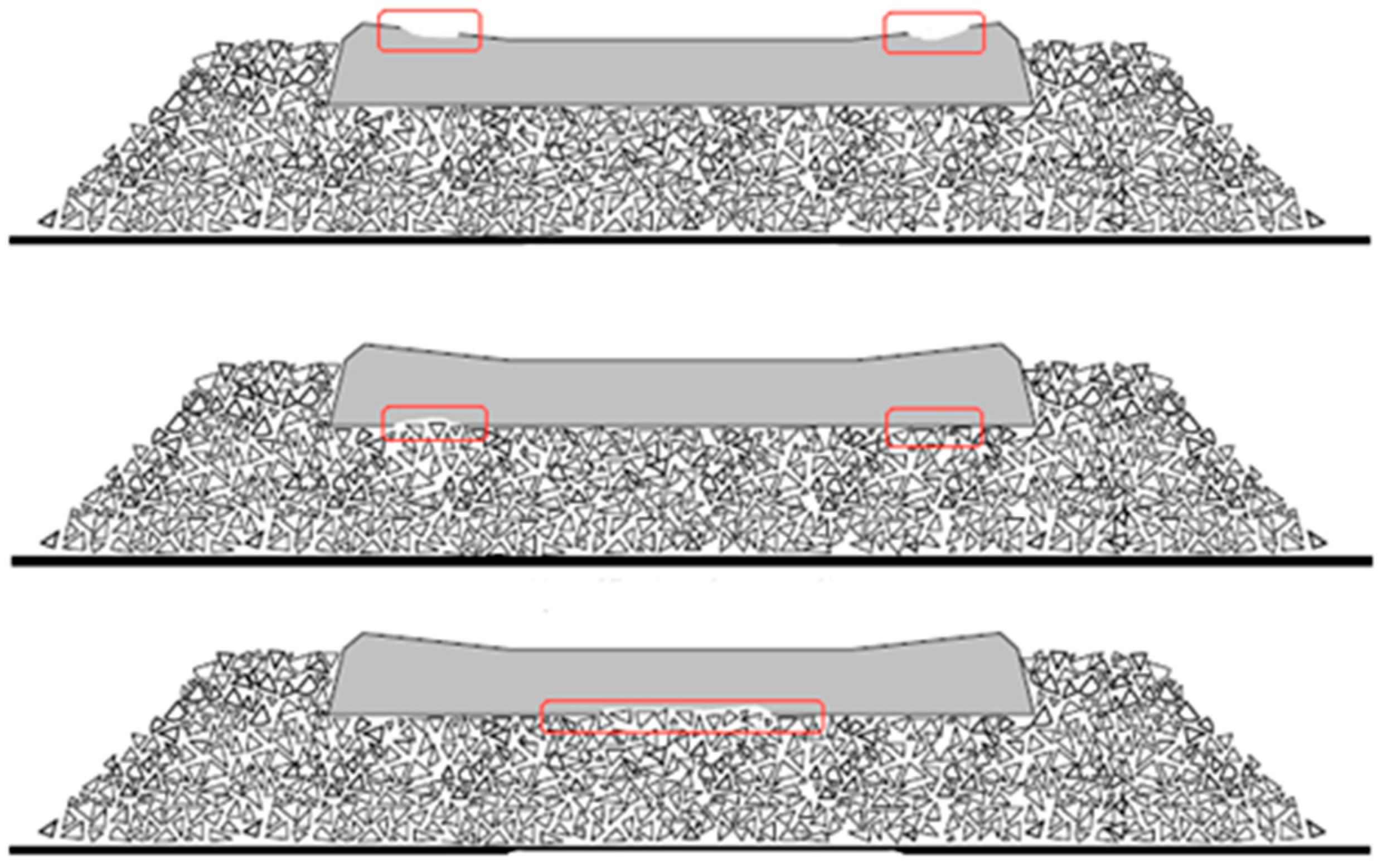
5. Influence of Surface Abrasions on Fatigue Life
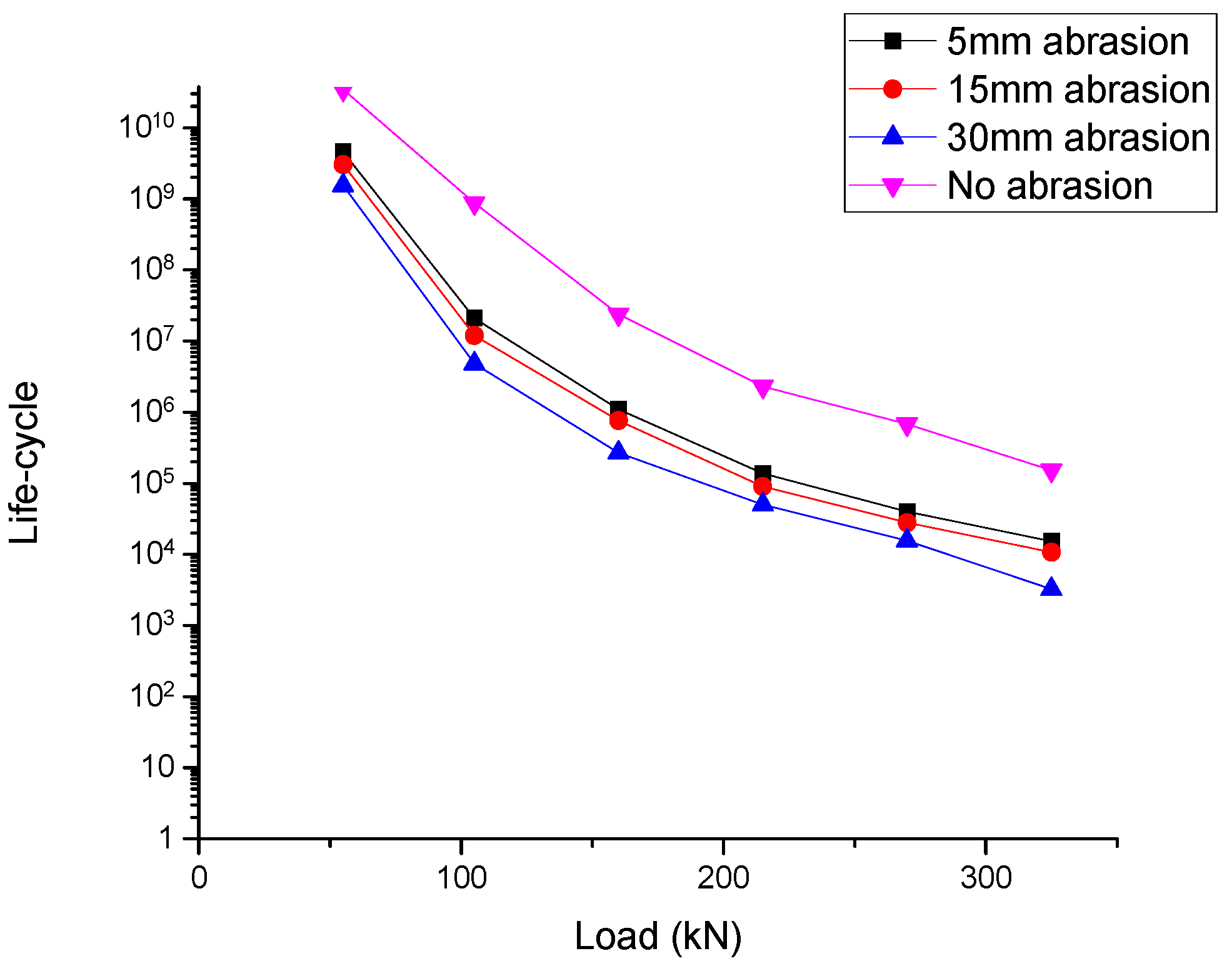
5.1. Rail-Seat Abrasion Results
5.2. Soffit Abrasion at Rail-Seat Results
5.3. Soffit Abrasion at Midspan Results
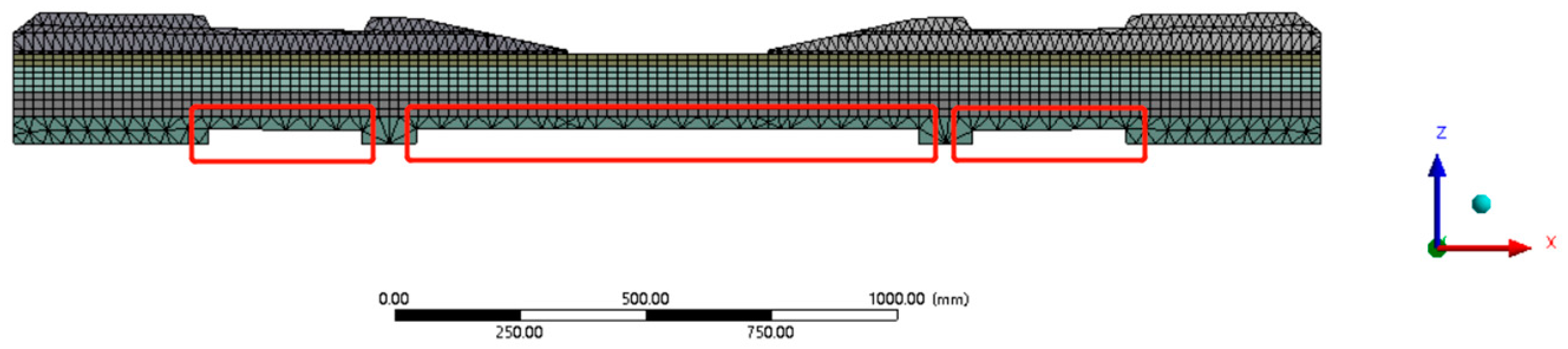
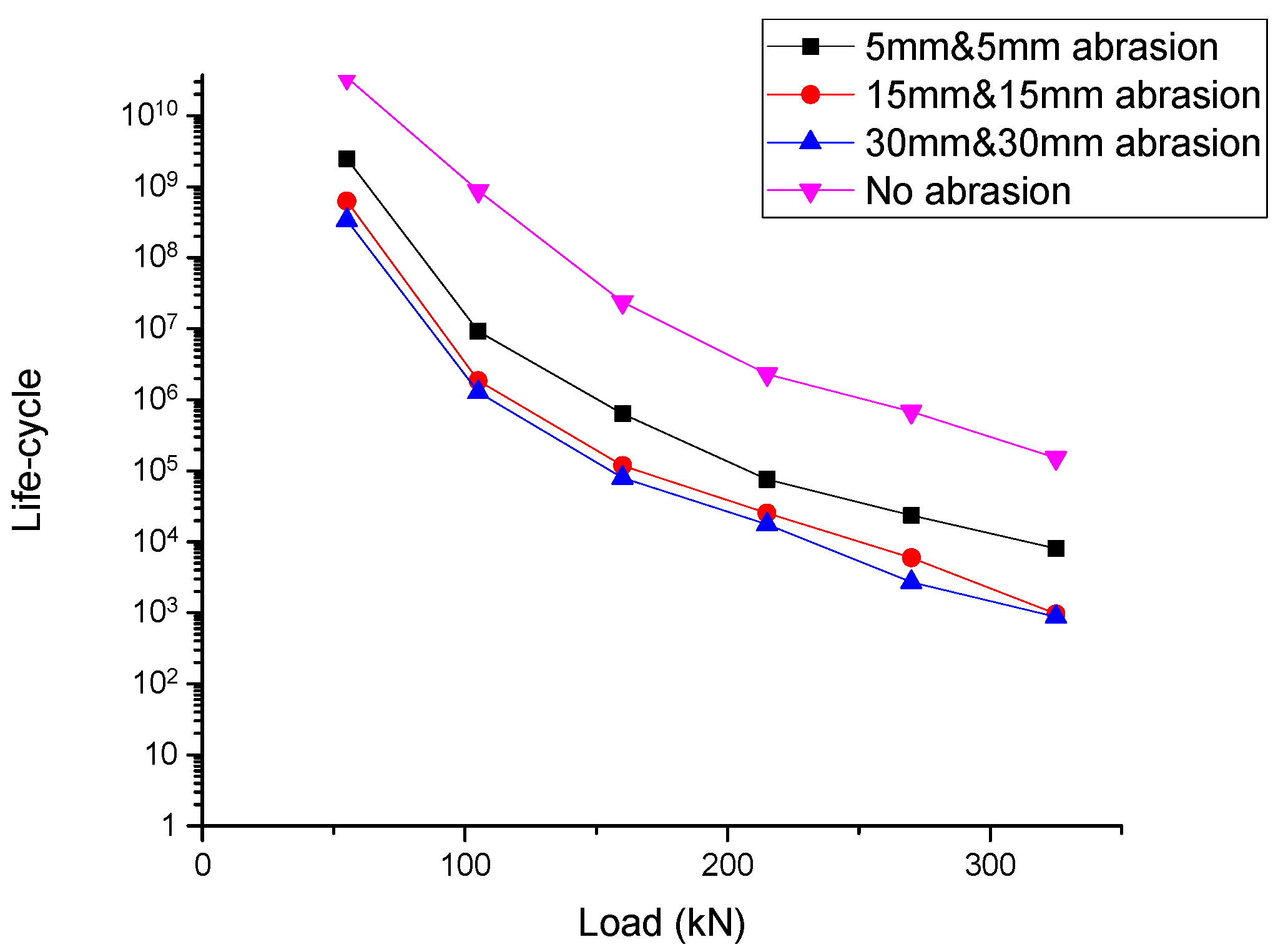
5.4. Rail-Seat Abrasion and Soffit Abrasion at Rail Seat Results
5.5. Rail-Seat Abrasion and Soffit Abrasion at Midspan Results
5.6. Soffit Abrasion at Rail Seat and Soffit Abrasion at Midspan Results
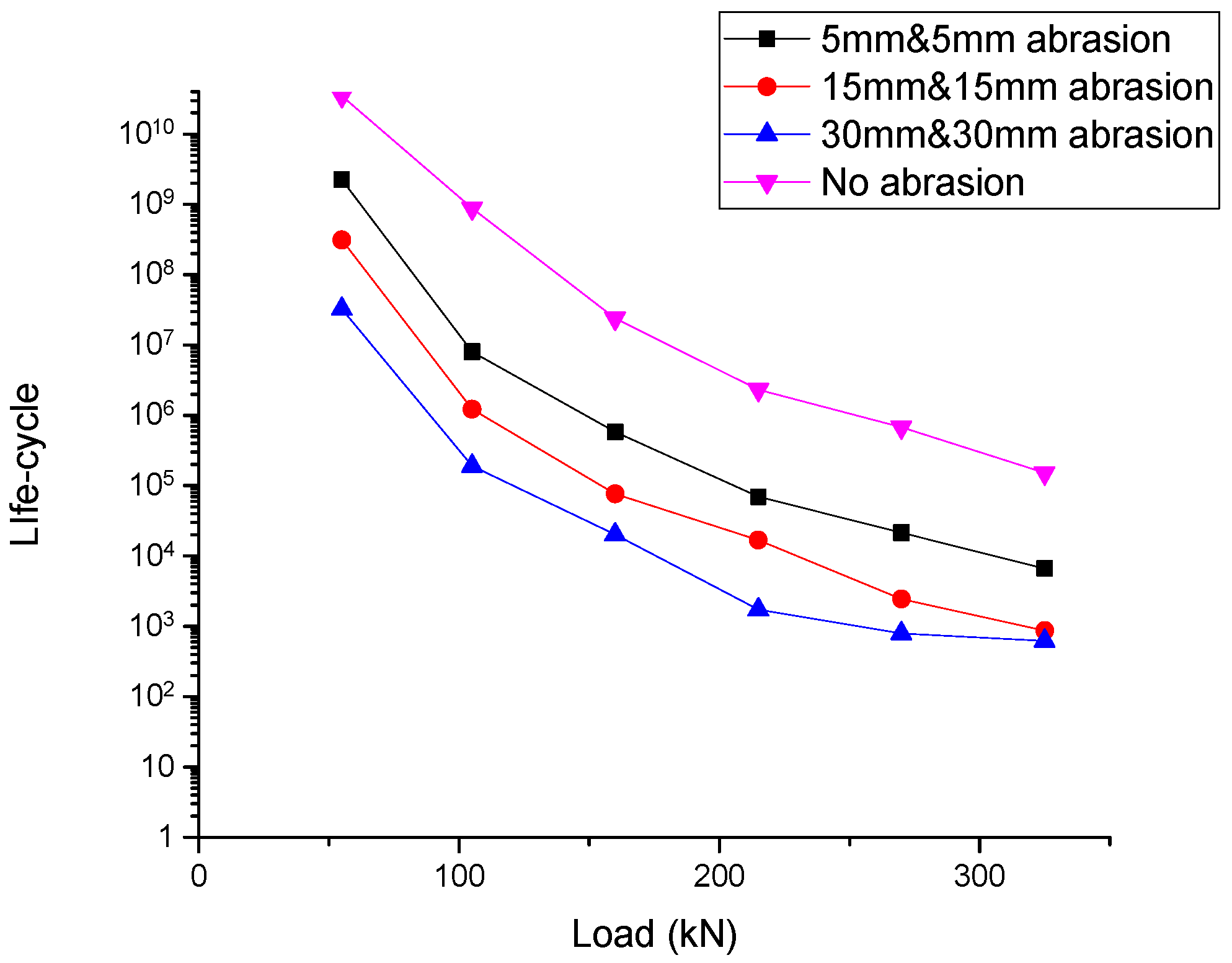
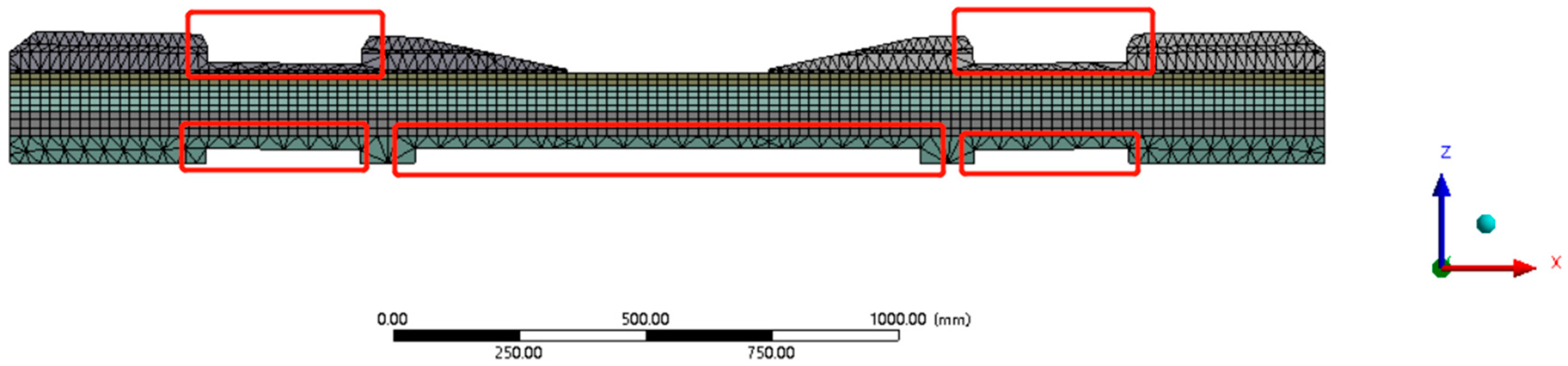
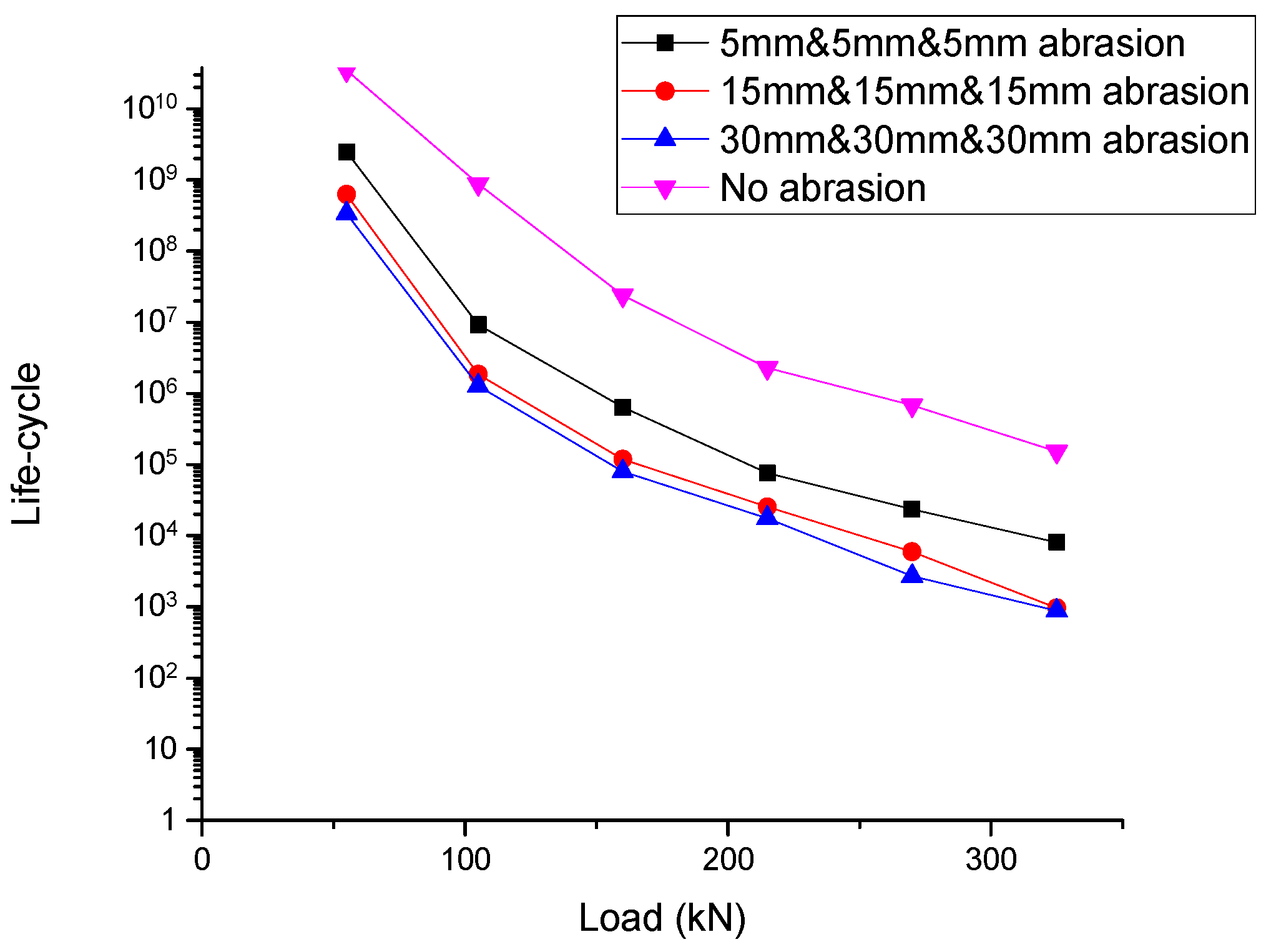
5.7. Rail-Seat Abrasion, Soffit Abrasion at Rail Seat, and Soffit Abrasion at Midspan Results
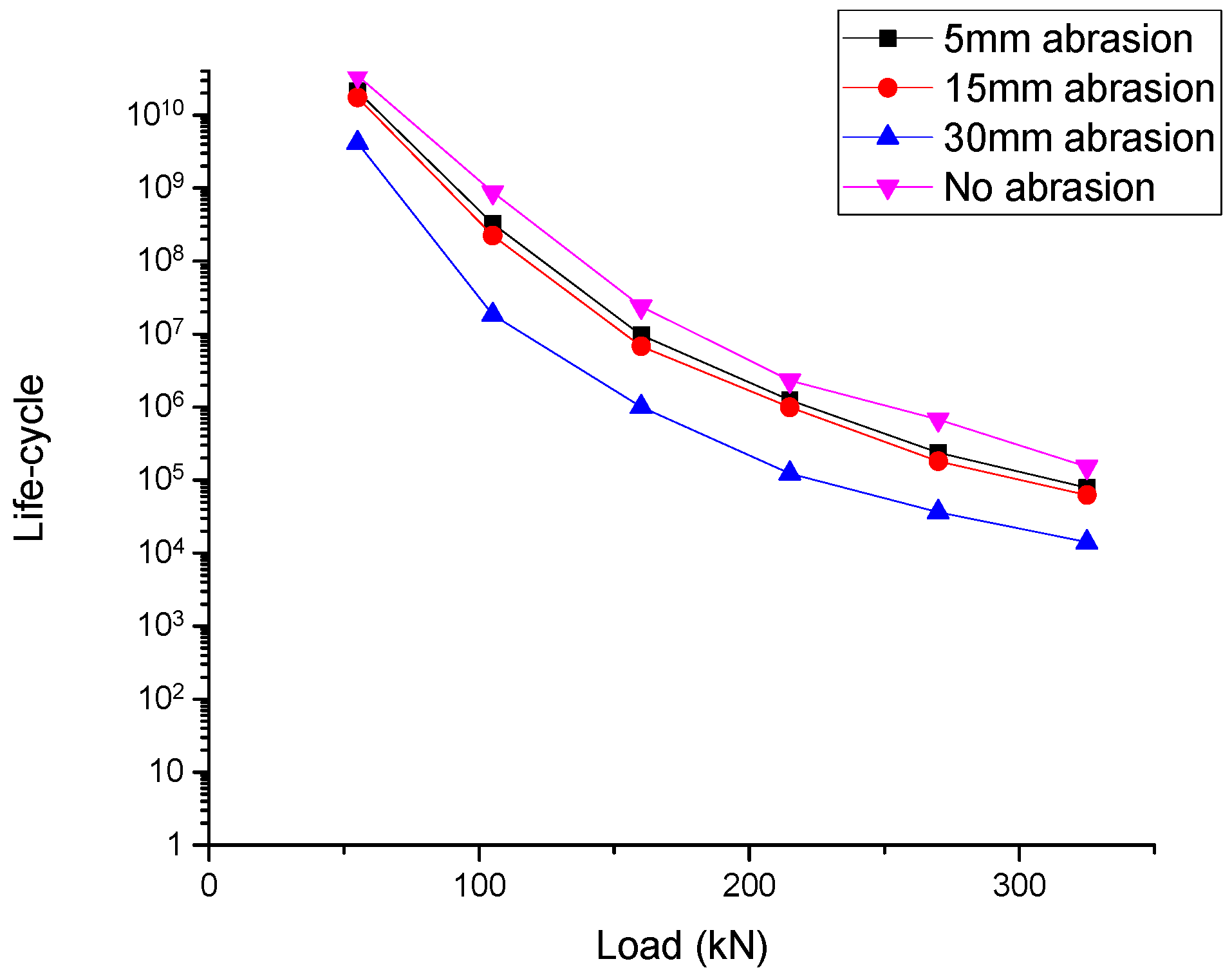
5.8. Discussions
6. Conclusions
- Surface abrasion significantly influences the structural performance of prestressed concrete sleepers. From the results, undamaged sleepers have much more service life than worn sleepers. Therefore, track maintenance should be carried out regularly to prevent loss of life-cycle from surface abrasion;
- Rail-seat abrasion has a relatively low influence on railway sleepers in comparison with soffit abrasion. Soffit abrasion at the rail seat can critically reduce the life-cycle;
- The risk of more than one abrasion pattern happening in the railway sleeper is far greater than a single abrasion pattern;
- In this study, the life-cycle was found to largely depend on the magnitude of the dynamic load and abrasion depth. Both large dynamic loads and abrasion depths can result in serious decreases in life-cycle.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Steffens, D.M. Identification and Development of a Model of Railway Track Dynamic Behaviour. Ph.D. Thesis, Queensland University of Technology, Brisbane City, QLD, Australia, 2005. [Google Scholar]
- Taherinezhad, J.; Sofi, M.; Mendis, P.; Ngo, T. A review of behaviour of prestressed concrete sleepers. Electron. J. Struct. Eng. 2013, 13, 1–16. [Google Scholar] [CrossRef]
- Esveld, C.; Esveld, C. Modern Railway Track; MRT-Productions: Zaltbommel, The Netherland, 2001; Volume 385. [Google Scholar]
- Kaewunruen, S.; Remennikov, A.M. Impact capacity of railway prestressed concrete sleepers. Eng. Fail. Anal. 2009, 16, 1520–1532. [Google Scholar] [CrossRef]
- Remennikov, A.; Murray, M.H.; Kaewunruen, S. Reliability-based conversion of a structural design code for railway prestressed concrete sleepers. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2012, 226, 155–173. [Google Scholar] [CrossRef]
- Van Dyk, B.J.; Dersch, M.S.; Edwards, J. International Concrete Crosstie and Fastening System Survey–Final Results; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2012. [Google Scholar]
- Ferdous, W.; Manalo, A. Failures of mainline railway sleepers and suggested remedies–review of current practice. Eng. Fail. Anal. 2014, 44, 17–35. [Google Scholar] [CrossRef]
- Van Dyk, B.J.; Edwards, J.R.; Dersch, M.S.; Ruppert, C.J., Jr.; Barkan, C.P. Evaluation of dynamic and impact wheel load factors and their application in design processes. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 33–43. [Google Scholar] [CrossRef]
- Remennikov, A.M.; Kaewunruen, S. A review of loading conditions for railway track structures due to train and track vertical interaction. Struct. Control Health Monit. Off. J. Int. Assoc. Struct. Control Monit. Eur. Assoc. Control Struct. 2008, 15, 207–234. [Google Scholar] [CrossRef]
- Li, D.; You, R.; Kaewunruen, S. Mechanisms and Evolution of Cracks in Prestressed Concrete Sleepers Exposed to Time-Dependent Actions. Appl. Sci. 2022, 12, 5511. [Google Scholar] [CrossRef]
- Remennikov, A.; Kaewunruen, S. Determination of dynamic properties of rail pads using an instrumented hammer impact technique. Acoust. Aust. 2005, 33, 63–67. [Google Scholar]
- Kaewunruen, S.; Remennikov, A. On the residual energy toughness of prestressed concrete sleepers in railway track structures subjected to repeated impact loads. Electron. J. Struct. Eng. 2013, 13, 41–61. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Remennikov, A.M.; Murray, M.H. Introducing a new limit states design concept to railway concrete sleepers: An Australian experience. Front. Mater. 2014, 1, 8. [Google Scholar] [CrossRef]
- Chen, Z.; Shin, M.; Wei, S.; Andrawes, B.; Kuchma, D.A. Finite element modeling and validation of the fastening systems and concrete sleepers used in North America. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2014, 228, 590–602. [Google Scholar] [CrossRef]
- César Bastos, J.; Dersch, M.S.; Edwards, J.R. Degradation Mechanisms of Concrete Due to Water Flow in Cracks of Prestressed Railroad Sleepers under Cyclic Loading. J. Mater. Civ. Eng. 2022, 34, 04022025. [Google Scholar] [CrossRef]
- Parvez, A.; Foster, S.J. Fatigue of steel-fibre-reinforced concrete prestressed railway sleepers. Eng. Struct. 2017, 141, 241–250. [Google Scholar] [CrossRef]
- Riding, K.A.; Peterman, R.J.; Guthrie, W.S.; Brueseke, M.; Mosavi, H.; Daily, K. A Study of Environmental and Track Factors That Contribute to Abrasion Damage of Concrete Ties; Department of Transportation, Federal Railroad Administration: Washington, DC, USA, 2019.
- Kernes, R.G.; Shurpali, A.A.; Edwards, J.R.; Dersch, M.S.; Lange, D.A.; Barkan, C.P. Investigation of the mechanics of rail seat deterioration and methods to improve the abrasion resistance of concrete sleeper rail seats. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2014, 228, 581–589. [Google Scholar] [CrossRef]
- Ngamkhanong, C.; Li, D.; Remennikov, A.M.; Kaewunruen, S. Dynamic capacity reduction of railway prestressed concrete sleepers due to surface abrasions considering the effects of strain rate and prestressing losses. Int. J. Struct. Stab. Dyn. 2019, 19, 1940001. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Ngamkhanong, C.; Lim, C.H. Damage and failure modes of railway prestressed concrete sleepers with holes/web openings subject to impact loading conditions. Eng. Struct. 2018, 176, 840–848. [Google Scholar] [CrossRef]
- You, R.; Goto, K.; Ngamkhanong, C.; Kaewunruen, S. Nonlinear finite element analysis for structural capacity of railway prestressed concrete sleepers with rail seat abrasion. Eng. Fail. Anal. 2019, 95, 47–65. [Google Scholar] [CrossRef]
- Li, D.; Ngamkhanong, C.; Kaewunruen, S. Influence of surface abrasion on creep and shrinkage of railway prestressed concrete sleepers. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017. [Google Scholar]
- Li, D.; Kaewunruen, S.; You, R. Time-dependent behaviours of railway prestressed concrete sleepers in a track system. Eng. Fail. Anal. 2021, 127, 105500. [Google Scholar] [CrossRef]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Union: Maastricht, The Netherlands, 2004.
- Nussbaumer, A. EN1993-1-9: A code for fatigue design. In Proceedings of the Conference Fatigue Design, Denver, CO, USA, 17–21 July 2005. [Google Scholar]
- Rao, V.; Talukdar, S. Prediction of fatigue life of a continuous bridge girder based on vehicle induced stress history. Shock Vib. 2003, 10, 325–338. [Google Scholar] [CrossRef]
- Kaewunruen, S. Monitoring structural deterioration of railway turnout systems via dynamic wheel/rail interaction. Case Stud. Nondestruct. Test. Eval. 2014, 1, 19–24. [Google Scholar] [CrossRef]
- Nielsen, J.C.; Li, X. Railway track geometry degradation due to differential settlement of ballast/subgrade–numerical prediction by an iterative procedure. J. Sound Vib. 2018, 412, 441–456. [Google Scholar] [CrossRef]
- You, R.; Li, D.; Ngamkhanong, C.; Janeliukstis, R.; Kaewunruen, S. Fatigue life assessment method for prestressed concrete sleepers. Front. Built Environ. 2017, 3, 68. [Google Scholar] [CrossRef]
- You, R.; Kaewunruen, S. Evaluation of remaining fatigue life of concrete sleeper based on field loading conditions. Eng. Fail. Anal. 2019, 105, 70–86. [Google Scholar] [CrossRef]
- Béton, C.E.-I.d. CEB-FIP Model Code 1990: Design Code; Thomas Telford Publishing: London, UK, 1993. [Google Scholar]
- Browell, R.; Hancq, A. Calculating and Displaying Fatigue Results; Ansys Inc.: Canonsburg, PA, USA, 2006; p. 2. [Google Scholar]
- EN 13230-2; Railway Applications-Track-Concrete Sleepers and Bearers Part 2: Prestressed Monoblock Sleepers. Standardization, E.C.f., 2009. Available online: https://standards.iteh.ai/catalog/standards/cen/afc7f289-4b2c-4620-9849-1b5e6a7b865b/en-13230-2-2016 (accessed on 2 August 2022).
- Sadeghi, J.; Barati, P. Comparisons of the mechanical properties of timber, steel and concrete sleepers. Struct. Infrastruct. Eng. 2012, 8, 1151–1159. [Google Scholar] [CrossRef]
- Jing, G.; Yunchang, D.; You, R.; Siahkouhi, M. Comparison study of crack propagation in rubberized and conventional prestressed concrete sleepers using digital image correlation. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 236, 350–361. [Google Scholar] [CrossRef]
- Parvez, A.; Foster, S.J. Fatigue behavior of steel-fiber-reinforced concrete beams. J. Struct. Eng. 2015, 141, 04014117. [Google Scholar] [CrossRef]
- Li, D.; Kaewunruen, S.; You, R.; Liu, P. Fatigue life modelling of railway prestressed concrete sleepers. Structures 2022, 41, 643–656. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Sussman, J.M.; Matsumoto, A. Grand challenges in transportation and transit systems. Front. Built Environ. 2016, 2, 4. [Google Scholar] [CrossRef] [Green Version]






| Main Causes | Problems | Worldwide Response 1 |
|---|---|---|
| Lateral load |
| 3.15 |
| 5.5 | |
| Vertical dynamic load |
| 5.21 |
| 4.57 | |
| 5.36 | |
| Manufacturing and maintenance defects |
| 6.14 |
| 4.09 | |
| Environmental considerations |
| 4.67 |
| S–N Curve of Prestressing Steel Used for | Stress Exponent | |||
|---|---|---|---|---|
| Pre-Tensioning | 106 | 5 | 9 | 185 |
| Material Properties | Basic Variables | Value |
|---|---|---|
| Concrete |
| 65 MPa |
| 33 GPa | |
| 1570 MPa | |
| Prestressed wire |
| 200 GPa |
| 420 kN |
| Specimen ID | Failure Cycles | Average | Standard Deviation |
|---|---|---|---|
| SF2-a | 773,793 | 896,290 | 173,236 |
| SF3-a | 1,018,787 |
| Failure Cycles | ||||
|---|---|---|---|---|
| Experimental Result | Theoretical Result | Deviation Ratio% | Numerical Result | Deviation Ratio% |
| 896,290 | 889,577 | 0.75 | 849,000 | 5.28 |
| Load (kN) | No Abrasion | 5 mm Rail-Seat Abrasion | 15 mm Rail-Seat Abrasion | 30 mm Rail-Seat Abrasion |
|---|---|---|---|---|
| 55 | 3.47 × 1010 | 2.12 × 1010 | 1.75 × 1010 | 4.15 × 109 |
| 105 | 8.79 × 108 | 3.27 × 108 | 2.23 × 108 | 1.83 × 107 |
| 160 | 2.39 × 107 | 9.68 × 106 | 6.81 × 106 | 1.01 × 106 |
| 215 | 2.30 × 106 | 1.25 × 106 | 9.90 × 105 | 1.23 × 105 |
| 270 | 6.79 × 105 | 2.38 × 105 | 1.82 × 105 | 36,627 |
| 325 | 1.52 × 105 | 78,521 | 62,593 | 14,068 |
| Load (kN) | No Abrasion | 5 mm Soffit Abrasion at Rail Seat | 15 mm Soffit Abrasion at Rail Seat | 30 mm Soffit Abrasion at Rail Seat |
|---|---|---|---|---|
| 55 | 3.47 × 1010 | 2.85 × 109 | 1.08 × 109 | 5.04 × 108 |
| 105 | 8.79 × 108 | 1.10 × 107 | 2.99 × 106 | 1.63 × 106 |
| 160 | 2.39 × 107 | 7.19 × 105 | 1.87 × 105 | 1.02 × 105 |
| 215 | 2.30 × 106 | 85,372 | 36,816 | 22,380 |
| 270 | 6.79 × 105 | 26,466 | 11,413 | 4527 |
| 325 | 1.52 × 105 | 10,165 | 1673 | 936 |
| Load (kN) | No Abrasion | 5 mm Soffit Abrasion at Midspan | 15 mm Soffit Abrasion at Midspan | 30 mm Soffit Abrasion at Midspan |
|---|---|---|---|---|
| 55 | 3.47 × 1010 | 4.59 × 109 | 3.04 × 109 | 1.54 × 109 |
| 105 | 8.79 × 108 | 2.09 × 107 | 1.20 × 107 | 4.81 × 106 |
| 160 | 2.39 × 107 | 1.10 × 106 | 7.61 × 105 | 2.68 × 105 |
| 215 | 2.30 × 106 | 1.37 × 105 | 90,168 | 50,015 |
| 270 | 6.79 × 105 | 39,963 | 27,953 | 15,505 |
| 325 | 1.52 × 105 | 15,349 | 10,736 | 3250 |
| Load (kN) | No Abrasion | 5 mm & 5 mm | 15 mm & 15 mm | 30 mm & 30 mm |
|---|---|---|---|---|
| 55 | 3.47 × 1010 | 2.25 × 109 | 3.12 × 108 | 3.25 × 107 |
| 105 | 8.79 × 108 | 8.01 × 106 | 1.22 × 106 | 1.90 × 105 |
| 160 | 2.39 × 107 | 5.80 × 105 | 76,391 | 20,139 |
| 215 | 2.30 × 106 | 69,485 | 16,878 | 1728 |
| 270 | 6.79 × 105 | 21,541 | 2455 | 792 |
| 325 | 1.52 × 105 | 6630 | 871 | 621 |
| Load (kN) | No Abrasion | 5 mm & 5 mm | 15 mm & 15 mm | 30 mm & 30 mm |
|---|---|---|---|---|
| 55 | 3.47 × 1010 | 2.73 × 109 | 1.33 × 109 | 7.74 × 108 |
| 105 | 8.79 × 108 | 1.04 × 107 | 3.95 × 106 | 2.12 × 106 |
| 160 | 2.39 × 107 | 6.91 × 105 | 2.31 × 105 | 1.39 × 105 |
| 215 | 2.30 × 106 | 82,248 | 44,032 | 28,812 |
| 270 | 6.79 × 105 | 25,498 | 13,650 | 7828 |
| 325 | 1.52 × 105 | 9557 | 2466 | 998 |
| Load (kN) | No Abrasion | 5 mm & 5 mm | 15 mm & 15 mm | 30 mm & 30 mm |
|---|---|---|---|---|
| 55 | 3.47 × 1010 | 2.49 × 109 | 6.26 × 108 | 3.37 × 108 |
| 105 | 8.79 × 108 | 9.23 × 106 | 1.86 × 106 | 1.28 × 106 |
| 160 | 2.39 × 107 | 6.38 × 105 | 1.19 × 105 | 79,896 |
| 215 | 2.30 × 106 | 76,113 | 25,415 | 17,652 |
| 270 | 6.79 × 105 | 23,596 | 5963 | 2706 |
| 325 | 1.52 × 105 | 8078 | 966 | 881 |
| Load (kN) | No Abrasion | 5 mm & 5 mm & 5 mm | 15 mm & 15 mm & 15 mm | 30 mm & 30 mm & 30 mm |
|---|---|---|---|---|
| 55 | 3.47 × 1010 | 2.49 × 109 | 6.26 × 108 | 3.37 × 108 |
| 105 | 8.79 × 108 | 9.23 × 106 | 1.86 × 106 | 1.28 × 106 |
| 160 | 2.39 × 107 | 6.38 × 105 | 1.19 × 105 | 79,896 |
| 215 | 2.30 × 106 | 76,113 | 25,415 | 17,652 |
| 270 | 6.79 × 105 | 23,596 | 5963 | 2706 |
| 325 | 1.52 × 105 | 8078 | 966 | 881 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Kaewunruen, S.; You, R. Remaining Fatigue Life Predictions of Railway Prestressed Concrete Sleepers Considering Time-Dependent Surface Abrasion. Sustainability 2022, 14, 11237. https://doi.org/10.3390/su141811237
Li D, Kaewunruen S, You R. Remaining Fatigue Life Predictions of Railway Prestressed Concrete Sleepers Considering Time-Dependent Surface Abrasion. Sustainability. 2022; 14(18):11237. https://doi.org/10.3390/su141811237
Chicago/Turabian StyleLi, Dan, Sakdirat Kaewunruen, and Ruilin You. 2022. "Remaining Fatigue Life Predictions of Railway Prestressed Concrete Sleepers Considering Time-Dependent Surface Abrasion" Sustainability 14, no. 18: 11237. https://doi.org/10.3390/su141811237
APA StyleLi, D., Kaewunruen, S., & You, R. (2022). Remaining Fatigue Life Predictions of Railway Prestressed Concrete Sleepers Considering Time-Dependent Surface Abrasion. Sustainability, 14(18), 11237. https://doi.org/10.3390/su141811237









