1. Introduction
Over the years, the demand for mobility and transportation has evolved significantly. As per reports, the number of vehicles on the road in 2015 was 1.1 billion cars and 377 million trucks [
1], and this is expected to increase to as much as two billion by the year 2040 [
2]. Due to the increasing number of vehicles, the governments of most countries have implemented various vehicle regulations and guidelines to reduce fuel consumption and the greenhouse effect [
3]. Automobile industries have begun contributing towards the same by shifting a portion of the manufacturing momentum towards electric vehicles (EVs) [
3]. As a result, the market demand for EVs has increased rapidly over the past several years. It has been observed in [
4] that the EV stock will likely increase by as much as 120 million over the next ten years as consumers shift to EVs over internal combustion vehicles. Especially in smart cities, the adoption of EVs has increased tremendously in recent years due to the high cost, high maintenance, and low energy efficiency of fossil fuel vehicles [
5].
As per the UK government’s decision, petrol vehicles are going to be phased out by 2030 in keeping with environmentally friendly planning [
6]. However, the growth in the number of EVs requires the installation of a large amount of charging station (CS) infrastructure in order to enable efficient charging of EVs. The increase in demand for EVs is likely to overburden the request for charging points (CPs) at the CS [
7]. Thus, it is necessary to efficiently acquire coordination policies for scheduling EVs at the CS without any conflicts. Many researchers worldwide have discussed various coordination schemes to schedule EVs for charging while ignoring the charging demand uncertainty and arrival time in real time [
8]. However, these factors can make the CS less reliable for EVs, which can demotivate EV charging at that particular CS, leading to a loss for the CS [
9]. To address the issues mentioned above, researchers around the world have tried to resolve them by implementing different coordination algorithms for EVs [
10,
11]. For example, Alvarez et al. [
12] presented a hybrid artificial bee colony incorporated with local search algorithms to schedule EVs for charging. Qarebagh et al. [
13] discussed a simulated annealing heuristic algorithm to resolve the position allocation problem for EV charging. To resolve the security and privacy issues in [
13], Chamola et al. [
14] investigated an internet of things (IoT) and edge computing-based architecture for secure and optimal EV charging scheduling. Similarly, Kumar et al. [
15] adopted an IoT technology approach to secure EV scheduling using a Match Market and cryptography-based algorithm. Moreover, the authors of [
16] designed an IoT-based efficient coordination mechanism between the EVs and CS using a Concurrent Transmission (CT)-based mechanism to schedule EVs in a reliable way.
In [
17], Venkatakirthiga et al. formulated an optimization algorithm to schedule EVs for residential consumers in the form of a linear programming model. The authors in [
18] discussed EV charging scheduling in residential networks with a two-step non-linear optimization approach. Lu et al. [
19] proposed a decentralized price coordination algorithm for EV charging at a CS. They mainly focused on securing EV charging against adversarial and external attacks. Many researchers have suggested different coordination algorithms for EV scheduling [
20,
21]. However, most of these do not address scheduling of EVs at the CS or consider factors such as wait times, increased charging demand, conflict resolution, or IPFS bandwidth. Furthermore, there is little discussion in the literature of security and privacy issues arising in the context of EV scheduling. Several authors [
14,
15,
16] have incorporated IoT-based frameworks for secure charging scheduling, although monitoring communications between EVs for charging can encounter various security attacks such as single-point-of-failure, eavesdropping, etc. [
22]. Motivated by this apparent research gap, we introduce a novel blockchain and IoT-based consensus mechanism with an IPFS protocol to effectively monitor and schedule EVs at the CS. Moreover, the integration of blockchain technology with IPFS in the proposed
COME mechanism overcomes the security and trust issues of IoT technology in order to further provides trustable and cost-efficient charging scheduling for EVs with minimal required bandwidth. Blockchain is becoming a disruptive technology in many industrial and service sectors [
23]. To understand the utilization of blockchain in other industrial sectors, Agrawal et al. [
24] carried out a case study on a blockchain-based framework for supply chain traceability to establish trust between supply chain participants in the network. Chiacchio et al. [
25] proposed a non-fungible token solution to strengthen the tracking and tracing capability of the pharmaceutical supply chain utilizing blockchain technology. Auer et al. [
26] presented a case study on blockchain and IoT-based shared mobility for car sharing and leasing to provide secure and authentic data storage for users. Furthermore, considering the modernization of the transportation system, the authors of [
27] studied the use of a blockchain for data collection in the automotive industry sector in order to address challenges such as scalability, costs, privacy, security attacks, etc. Thus, the security advantages and applications of blockchain technology in varied industrial sectors motivates us to incorporate it into our proposed optimized consensus mechanism for EV scheduling.
The mechanism is designed to support the convenient charging of EVs while avoiding any financial loss on the part of the CS. The proposed mechanism aims to schedule arriving EVs for the multiple CPs available at a CS. It is applied to ensure that EVs do not need to search for another CS due to higher wait times, otherwise a particular CS may suffer from loss. This approach makes the mechanism reliable for both EVs and CS.
Many researchers have suggested solutions to coordinate EV scheduling at the CS, however, they have not discussed scenarios involving security when a large number of EVs simultaneously arrive at the CS. For example, in [
12,
14,
15,
17], the authors primarily emphasized scheduling EVs for charging. However, they did not explore which EV (emergency, low-energy, and sufficient energy EVs) should be allocated to each CP available at the CS. Furthermore, the adoption of IoT [
14,
15] does not provide a promising solution to mitigate the privacy issues involved in EV scheduling. Motivated by this, we introduce a blockchain and IoT-based consensus mechanism integrated with the IPFS to allocate CPs for EV charging at the CS. As a decentralized and transparent network, a blockchain can facilitate enhanced security and privacy in EV scheduling for the CPs at the CS. The main aim when integrating blockchain with IoT in the proposed consensus mechanism is to overcome the secure data storage issues of IoT for EV scheduling at the CS. Our approach ensures that data transactions added to the blockchain network cannot be altered or changed, which prevents data manipulation, data spoofing, Man-in-the-Middle (MITM), and other kinds of security attacks from disrupting the network. IPFS ensures low-cost transactions between EV and CS for efficient scheduling with the minimum bandwidth. The consensus mechanism is applicable based on the arrival of a number of EVs less than or up to a threshold number and whether there is any emergency situation or high authority EV arriving for charging at a particular CS. Moreover, EVs do not have to wait in the queue to charge, and the CS can benefit when the number of EVs arriving exceeds the threshold, which is resolved using the FCFS scheduling algorithm and coalition game theory approach in scenario 3. Thus, there is a need to introduce a blockchain-based consensus mechanism to schedule EVs to reach the CP on time within the threshold waiting time, leading to a benefit to the CS. We simulate the performance of the blockchain and IoT-based consensus mechanism considering different scenarios based on the arrival of a number of EVs (less, up to, or more than the threshold number) and in an emergency situation. All scenarios are simulated in the Remix IDE (Integrated Development Environment) using Solidity high-level language written as a self-executable code while fully considering various performance parameters.
In brief, the research contribution of this paper are as follows:
We propose a novel blockchain and IoT-based consensus mechanism called COME for scheduling and monitoring EV use of available CPs at a CS. This approach is designed considering multiple scenarios based on the type and number of EVs arriving at the CS.
We integrate IPFS with blockchain to attain minimum bandwidth and cost efficiency for communication between the EVs and CS during charging.
We employ various scheduling algorithms and coalition game theory to resolve conflicts between EVs arriving at the CS.
We evaluate the performance of the proposed COME consensus mechanism by considering various performance parameters, including wait time, conflict resolution, charging demand, scalability, and IPFS bandwidth.
The rest of this paper is organized as follows.
Section 2 describes the operation of the consensus mechanisms considering different scenarios.
Section 3 presents the experimental results. Finally, the paper is concluded in
Section 4.
2. Preliminaries
Before discussing the optimized blockchain and IoT-based consensus mechanism for EV charging, we need to generalize the consensus mechanism by which the blockchain maintains data integrity and confidentiality in the network. Blockchain, as a distributed ledger technology, facilitates data storage in the form of a chain of blocks in a distributed manner without the involvement of any centralized authority [
28]. Each block in the blockchain consists of data that is verified, validated, and appended to the next block to form a secure and preserved network. Therefore, a blockchain network proves to be entirely secure and transparent, adding transactions which are unalterable and thereby ensuring the confidentiality and verifiability of the network. The security of a blockchain network is due to the introduced consensus protocol, which ensures that all the participants or nodes agree on the validity of all transactions in order to prevent any malicious or adversarial attacks [
29]. For example, if a transaction requested is added to the blockchain network, then all of the nodes in the network should be in consensus to add it to the network. Various consensus algorithms such as Proof of Work (PoW), Proof of Stake (PoS), Proof of Burn (PoB), and others can be used to facilitate security and data integrity in the blockchain network [
30].
Here, we propose a blockchain-based consensus mechanism to schedule EVs for CPs at the CS. With the increasing number of EVs, it is becoming difficult to schedule them at the CS. The difficulty of the problem depends on the number and type of arriving EVs. For example, if the number of EVs arriving at the CS is the same as the number of CPs, then the EVs can each be directly allocated to a CP based on the FCFS algorithm. However, if the number of EVs arriving at the CS is more than the number of CPs, we need to consider different scenarios based on the type of EVs, i.e., emergency or high-authority vehicles, in order to coordinate them efficiently. This raises the need for the EVs and CS to be in consensus in order for them to be efficiently scheduled among the CPs. The CS avoids loss because adding data transactions to the blockchain network ensures that consensus between the EVs and CS is established securely and efficiently.
3. Consensus Mechanism
The blockchain and IoT-based
COME consensus mechanism comprises various members, including different EVs and CS designed based on different scenarios. Blockchain as a decentralized and immutable framework is used to secure transactions between the EVs and CS for the purposes of charging.
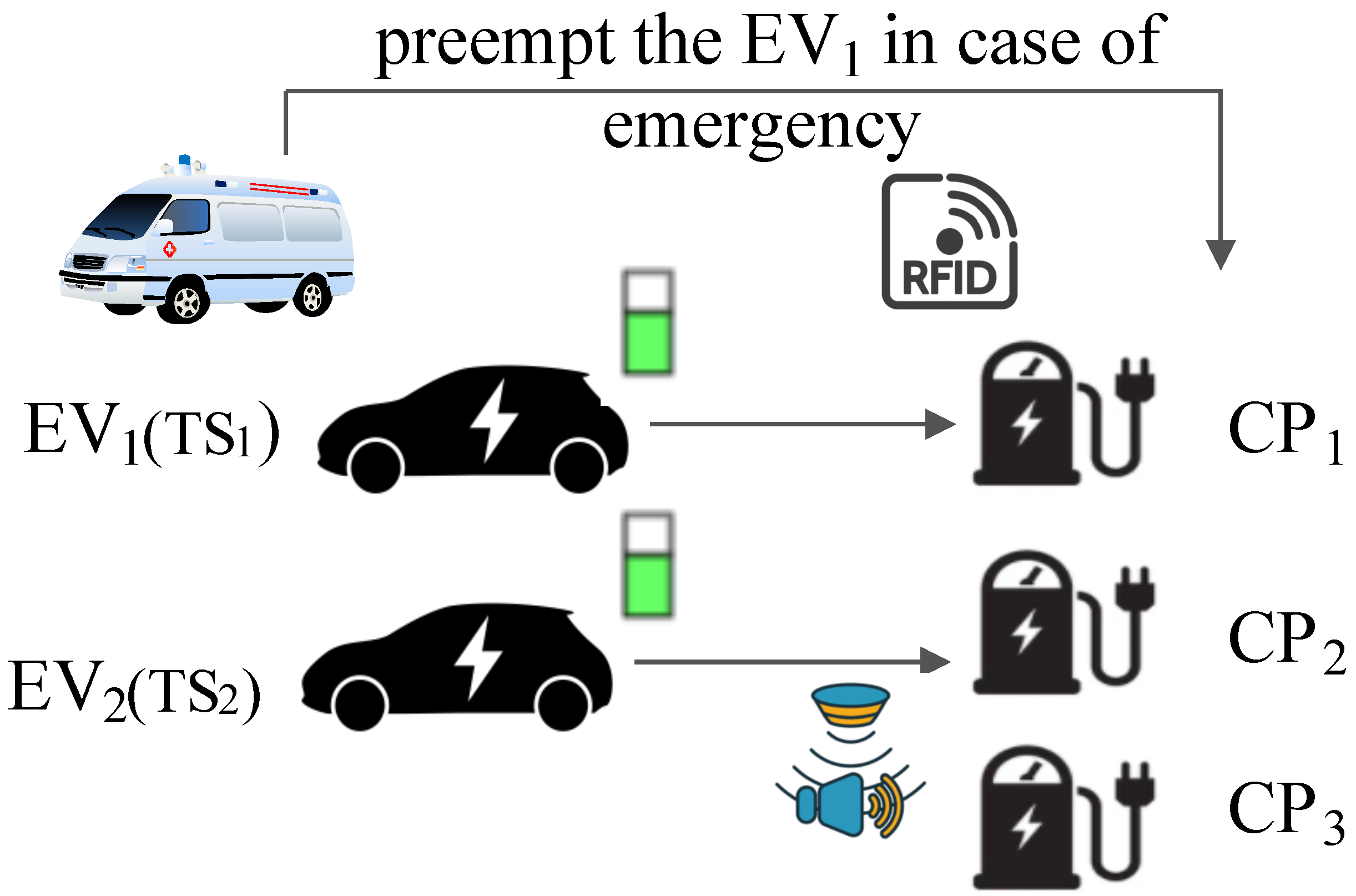
Figure 1 shows the scheduling of
m number of EVs, i.e., {
} ∈
arriving for charging at
n number of installed CPs, i.e., {
} ∈
at a CS embedded with the IoT devices, i.e., sound sensors to detect emergency vehicles (
) arriving at the CS. Here,
can be of two types: an emergency situation such as an ambulance, police vehicle, or fire brigade, and a less severe situation such as arrival of high-authority vehicle. The CS is equipped with RFID sensors to monitor and manage the energy (
) of EVs at the time of their arrival. EVs with a timestamp order
, i.e.,
,
, and burst time (
) need to be scheduled at the CS;
for EVs can be written in ascending order in the form of
:
Furthermore, we consider different scenarios for scheduling the number of arriving EVs at a CS with the assumption that the nodes, i.e., the EV and CS involved in the network, are responsive and honest, which prevents any malicious activity from disrupting the network. Moreover, it ensures reliable and secure coordination between the EV and CS in the network.
3.1. Scenario 1: Number of EVs Arriving Is Less Than the Number of CPs
In the first scenario, when the number of EVs arriving is less than or equal to the number of CPs at the CS, the EVs can be scheduled for charging in an optimal way using the First-Come First-Served (FCFS) algorithm. Arriving EVs can be scheduled directly at the CP based on their timestamp order
. However,
Figure 2 shows that if there are
EVs arriving at the CS, the EV that arrives first can search for another CP and
can be allocated to the CP with priority. In case of an emergency situation, the EVs can be scheduled with the help of the execution time
and turnaround time
of
using parameters
and (
). The FCFS algorithm to allocate the EVs at a given CP can be defined as follows:
Definition 1. FCFS is a scheduling algorithm that schedules EVs for charging at the CS based on their timestamp order . It schedules EVs based on parameters such as the execution time () and turn-around time () of , which can be expressed as follows: As per Definition 1,
can be calculated using
and
. The other parameter,
, can be evaluated using
and
, as shown in Equation (
2). As discussed earlier, fewer EVs request to access the CS. For this reason, we implement the FCFS algorithm for scheduling EVs. However, if an EV arrives with for an emergency, the EV that arrives first can leave the CP to search for another slot at the CS. In this case, the emergency EV crew does not have to wait to before having their vehicle charged. The aforementioned parameters for scheduling EVs can be represented as follows:
where
signifies the number of arriving EVs associated with a timestamp order, execution time, burst time, and turnaround time for charging,
denotes the EVs allocated for charging at the CPs based on the FCFS algorithm with the help of
, and
signifies the
allocated to
number of CPs in the case of an emergency.
Algorithm 1 shows the detailed procedure for scheduling
m number of EVs at
n number of CPs with the time complexity of
and
.
| Algorithm 1 FCFS algorithm for scheduling fewer EVs than CPs at CS |
Input: Output: EV schedule with wait time for charging in case of emergency Initialization: e = 1, s = 1 - 1:
procedureSchedule_EVs() - 2:
When arriving are less than CPs at a CS - 3:
for do - 4:
for do - 5:
if then - 6:
- 7:
- 8:
- 9:
else - 10:
- 11:
end if - 12:
end for - 13:
end for - 14:
end procedure
|
3.2. Scenario 2: Number of EVs arriving up to a Threshold Number
In the proposed consensus mechanism, the second scenario can be considered when the number of EVs entering with
for charging is greater than the number of CPs. It is necessary to check the energy
of the EVs, i.e., whether they arrive with energy lower than the threshold energy value for charging (
). If the number of EVs arriving is up to a particular threshold number, i.e.,
, then EVs can be scheduled using the LRTF scheduling algorithm based on the parameter
. The number of EVs arriving within
can be scheduled based on the
, which can be represented as follows:
Definition 2. LRTF can be defined as a preemptive scheduling algorithm to schedule EVs based on their and energy . LRTF works on the principle that the EVs arriving with along with energy less than the receive priority for charging over other EVs with available energy greater than . It can be defined as As discussed in Definition 2, EVs with available energy less than have the chance to charge their vehicles first. Due to the preemptive nature of the scheduling algorithm, it executes for a fixed amount of time T. After that, if EVs arrive with less available energy, they preempt the other EVs for charging.
There can be a case in which EVs arriving at the CS all have energy greater than ; in this case, EVs are scheduled based on their , i.e., the EVs that arrive first receive access to the CP first.
However,
Figure 3 shows that if an emergency vehicle (
) such as an ambulance arrives at the CS, it can preempt other EVs. Similarly, if all the EVs arriving at the CS are emergency vehicles, they are scheduled based on their
. The LRTF scheduling algorithm relies on parameters including the waiting time of EVs (
) with energy
, which can be calculated using the turnaround time (
) of EVs with energy
and execution time (
) of EVs with energy
. The waiting time of
is less than the waiting time of other EVs, as
are preferred first for charging, i.e., {
}. Thus, emergency vehicles with the highest priority can be scheduled for charging by preempting other EVs. Then, EVs with energy
have to wait for charging, meaning that EVs with energy
can charge their vehicle based on the LRTF algorithm as shown in Algorithm 2. These parameters can be interpreted using
and (
), which are represented as follows:
where
denotes the number of EVs along with their timestamp order, execution time, burst time, waiting time, turnaround time, and available energy for charging,
signifies the allocation of EVs to
number of CPs based on
, and
shows the allocation of
to CP at a CS. We use a Longest Remaining Time First (LRTF) scheduling algorithm instead of the FCFS algorithm due to the increase in the number of EVs up to a threshold number compared to the number of CPs. EVs can be scheduled according to their emergency status and energy requirements. Algorithm 2 shows the procedure for scheduleing
m number of EVs at
n number of CPs with time complexity
and
.
| Algorithm 2 LRTF algorithm for scheduling EVs arrived up to a threshold number |
Input: Output: EVs schedule with waiting time for charging Initialization: e = 1, s = 1 - 1:
procedureSchedule_EVs() - 2:
When arriving are up to a threshold number - 3:
for do - 4:
for do - 5:
if then - 6:
- 7:
else - 8:
- 9:
- 10:
- 11:
- 12:
end if - 13:
end for - 14:
end for - 15:
end procedure
|
3.3. Scenario 3: Number of EVs Arriving Exceeds the Threshold Number
In the third scenario, the number of EVs arriving at the CS crosses a particular threshold value , leading to a higher number of EVs than the number of CPs. Now, there can be a number of possible ways to schedule the arriving EVs in case of emergency or energy less than the threshold value. We consider an arrival queue (()) for EVs, which is divided into two more queues, i.e., a normal queue (()) and priority queue (()); () contains EVs with energy greater than and () consists of a low-energy queue (()()), i.e., EVs with energy less than . An emergency queue (()()), i.e., EVs , consists of emergency vehicles with the highest priority. Now, we need to consider the scheduled EVs at the CS with their timestamp order based on which EVs can be scheduled. We consider a linked list which contains the scheduled EVs, i.e., charging at the CPs with the assumption of energy greater than . The cases based on the arriving EVs for charging can be defined as follows:
3.3.1. Case 1: When Priority Queue Is Empty
In case 1, we consider an empty priority queue. This means that all the EVs arriving at the CS have energy
(
), as mentioned in the previous scenario for the arrival of EVs up to a threshold number. However, as we are considering an assumption for
of energy
(
), the arriving EVs can be scheduled for charging based on their timestamp order
using the FCFS algorithm. This means that the EVs arriving with the minimum timestamp order (
) receive preference for charging. Thus,
Figure 4 shows that the EV with the minimum timestamp order has to wait for a particular time
T to allow the scheduled EVs to charge their vehicles. Thus, EVs arriving with a minimum timestamp order can be allocated for charging with a waiting time of
evaluated using execution time (
) and turnaround time (
) of the scheduled EV which has been charged vehicle first in the linked list
using
and (
). The following associations to schedule EVs can be represented as follows:
where
l represents the number of arriving EVs waiting to be scheduled based on the execution and turnaround times with the minimum timestamp and
denotes the scheduling of EVs to
k number of CPs on the basis of
.
Algorithm 3 shows the detailed procedure to allocate
m number of EVs in the normal queue to
n number of CPs with time complexity
and
.
| Algorithm 3 Algorithm to schedule arriving EVs exceeding the threshold number |
Input: Output: Arrived EVs exceeding the threshold number scheduled for CP with waiting time , , and Initialization: e = 1, s = 1 - 1:
procedureSchedule_EVs() - 2:
When arriving are less than CPs at CS - 3:
for do - 4:
for do - 5:
if ( then - 6:
- 7:
- 8:
- 9:
- 10:
else if (()()) then - 11:
- 12:
- 13:
- 14:
else - 15:
- 16:
- 17:
- 18:
end if - 19:
end for - 20:
end for - 21:
end procedure
|
3.3.2. Case 2: Emergency Queue Is Empty
We consider this case to schedule EVs for charging when all of the arrived EVs belong to the normal queue and low energy queue, i.e., the emergency queue is empty. Thus, we want to schedule EVs arriving with energy
(
) and
(
) present in the low energy queue and normal queue for charging at the CS with the assumption that all scheduled EVs are of energy
(
). EVs can be scheduled for charging using the FCFS algorithm by assigning priority to EVs. The assigned priority can be expressed as {
>
}, in which higher priority is assigned to EVs with energy
less than
over EVs which already have sufficient energy. Thus,
Figure 5 shows that when EVs with higher priority arrive at the CS, the vehicle can be allocated charging priority. However, if EVs arrive with the same priority, we can consider the previous case to schedule EVs using the FCFS algorithm based on their timestamp order. EVs with higher priority can replace the scheduled EV with the minimum timestamp order in a preemptive way. According to the assumption, all the EVs present in the linked list
have energy greater than
. Thus, a scheduled EV that is been replaced has to be inserted in the waiting queue
.
As discussed, a higher priority is assigned to EVs in the low energy queue; they can directly preempt scheduled EVs based on their timestamp order. The wait time
associated with the EVs present in the low energy queue can be evaluated using the preemption time (
) and scheduling time (
) while preempting the scheduled EV with the minimum timestamp order. As the scheduled EV that has been replaced has to wait in the wait queue
, the high priority EV provides the replaced EV with a reward (
). The parameters for scheduling a high priority EV can be represented as follows:
where
denotes the number of EVs waiting to be scheduled for charging based on the wait time calculated using
and
and
shows the number of EVs with energy less than the threshold value associated with
number of CPs for charging.
Algorithm 3 shows the procedure to schedule m number of EVs present in the normal queue and low energy queue at n number of CPs with time complexity and .
3.3.3. Case 3: When EVs in the Priority Queue and Normal Queue Exceed the Threshold Number
EVs are scheduled for charging with a certain assigned priority. In the previous case, EVs arrive with energy () and (). However, if an emergency vehicle arrives at the CS, the priority order can be arranged further, i.e., {>>}. Having already scheduled EVs with energy less than the threshold value in the previous case, in this case we consider the assumption that the linked list contains EVs with energy ().
Here,
Figure 6 shows that the arrival of EVs
in case of emergency with the highest priority can be scheduled by preempting the EV with the lowest priority, i.e., EVs with energy
greater than
based on their timestamp order. This means the EV with the highest priority can charge its vehicle by replacing the scheduled EV with the lowest priority, i.e.,
(
), present in the linked list
. Similarly, when EVs with the same priority arrive, we can consider the previous case, i.e., Case 1, to schedule EVs based on their timestamp order. The waiting time
involved in scheduling
in case of emergency can be evaluated using the preemption time (
) and allocation time (
) required to schedule the EV with the highest priority. Now, a reward
is transferred to the sacrificing scheduled EV, i.e.,
of energy
(
). Similarly,
has to wait in the waiting queue
with the lowest priority, as we mentioned in the previous case. Algorithm 3 shows the procedure to schedule
m number of EVs in normal and priority queue at
n number of CPs with time complexity
and
. The associations required for scheduling can be represented as follows.
where
o indicates the number of EVs in case of emergency waiting to be scheduled for charging and
denotes the number of EVs associated with
number of CPs for charging.
In this scenario, after EVs are scheduled in an emergency, the next EV with higher priority and energy () can be scheduled similarly, as mentioned in the previous case. However, now there is an emergency EV scheduled in the linked list that cannot be preempted, as it has the highest priority. Thus, the EV with energy () again has to wait for charging.
Here, we have observed from all the cases that there can be an issue of starvation for EVs with energy (), i.e., greater than the threshold value. As in Case 2 and Case 3, EVs with energy () with the lowest priority must remain in the wait queue to charge their vehicles. If the waiting time for EVs with energy () considering the different cases exceeds the particular threshold time (), it is necessary to introduce a game theory approach to ensure that these vehicles are able to charge.
3.3.4. When the Waiting Time of EVs Exceeds the Threshold Time
We have discussed various scenarios to schedule EVs based on several different cases. However, in Case 3 the number of EVs with energy
(
) waiting in the queue reaches the threshold waiting time. This leads to the issue of starvation for EVs waiting to have their vehicles charged. Thus, we introduce a game theoretical approach for EVs waiting in the queue with the assumption that they receive the opportunity to charge when there is an emergency vehicle in less severe condition. To thid end, we divide emergencies into two categories: first, a critical situation such as an ambulance, fire brigade, or police vehicle, and second, a less severe condition such as the arrival of a high-authority vehicle. Thus, we can consider that if there is no emergency, EVs with energy
(
) can waiting in the queue for their chance to charge their vehicle based on the timestamp order
according to the available charging slots. This can be represented as follows.
Here, we adapt a coalition game theory approach by which EVs waiting in the can form a coalition with in case of a less severe emergency. We use the idea of transferable utility (TU) to transfer a reward to the cooperating EV. The coalition and TU can be represented as follows.
Coalition Game: the coalition game
comprises of a set
, where
P denotes the number of players
, which is P =
, and
is the coalition function mapped as a real valued number
and can be computed as the maximum output to each coalition
[
31,
32].
TU Game: We use the concept of the TU game in which
is a real-valued function for coalition
formed among EVs who agree to form a coalition with EVs
waiting in the queue for charging to transfer the reward to the contributing EV
in case of no severe emergency. We use the Shapley value as a solution to provide EVs cooperating in a coalition with rewards. The Shapley value (
) works on the principle that a reward is transferred to the contributing EV based on their forming of a coalition
. The reward transferred for player
considering the Shapley value for coalition
can be interpreted as follows [
31]:
s.t.
The cooperative game consists of N players, i.e.,
, in which players
and
both try to charge their vehicles prior to others. Both players decide on a strategy to achieve the same by maximizing their priority, i.e.,
and
. We can represent the strategy (
) as follows:
Thus, players try to charge their vehicle before others with the help of strategy . However, if this strategy is followed, then EVs waiting in the queue for a long time do not have the chance to charge. This leads to a loss for the CS if they decide to search for another CS to have their vehicle charged.
Therefore, EVs waiting in the queue can form a coalition with arriving emergency vehicle with no severity. This means that EVs have the opportunity to charge in case of the arrival of
with no severe condition. In return, the EV that has the opportunity to charge has to transfer a reward to the contributing
. This condition forms a Nash Equilibrium in which EVs waiting in the queue can receive the chance to charge and contributing EVs receive a reward
calculated using the Shapley value for the same, leading to benefit for both EVs and the CS in the coalition. Algorithm 4 shows the procedure for scheduling
m number of EVs with energy
(
) waiting in the queue at
n number of CPs using coalition game theory with time complexity
and
. This can be represented as follows:
where
f denotes the scheduling of EVs waiting in the queue at
number of CPs at the CS.
| Algorithm 4 Algorithm to schedule EVs for charging when waiting time exceeds the threshold value |
Input: Output: EVs waiting in the queue scheduled for charging Initialization: e = 1, s = 1 - 1:
procedureSchedule_EVs() - 2:
When waiting time for exceeds the threshold value - 3:
if then - 4:
for do - 5:
- 6:
end for - 7:
for each {} do - 8:
- 9:
end for - 10:
for do - 11:
for do - 12:
- 13:
- 14:
end for - 15:
end for - 16:
end if - 17:
end procedure
|
Thus far, we have considered different scenarios to perform EV scheduling at a CS with the help of a blockchain network incorporating IPFS. Scheduling is based on different scenarios involving the arrival of emergency, low-energy, and sufficient-energy EVs. The blockchain network keeps track of the users, i.e., EVs and CS, during scheduling. Thus, even if a malicious EV tries to access the CS, it is only charged based on its requirements. In this way, the blockchain can deny the request of a particular EV for charging to ensure that other EVs are not delayed. The introduction of the blockchain network ensures that EVs are scheduled in a secure and trusted manner based on the discussed scenarios.
5. Discussion and Conclusions
5.1. Discussion
A rapid surge in EVs can overburden the limited number of CPs at the CS, necessitating a coordination algorithm to optimally schedule EVs at the CS for charging. For example, the arrival of EVs (both emergency and non-emergency vehicles) at the CS requires a procedure by which the scheduling of EVs can be prioritized for charging and to prevent delay or dissatisfaction among EVs while charging. Various advanced optimization algorithms such as heuristics, metaheuristics, and hybrid algorithms have been explored to perform EV scheduling in different domains such as online learning, transportation, healthcare, multi-objective optimization, data classification, etc. The research works include Dulebenets’ [
34] proposal of a diploid evolutionary algorithm to enable sustainable cross-docking management for truck scheduling, which showed improved performance compared to a conventional evolutionary algorithm. The authors of [
35] studied a berth scheduling case study with the help of an applied linear programming model based on the self-adaptive parameter control strategy. Later, [
36] extended the previous work in [
34] to perform adaptive and low service cost truck scheduling at a cross-docking terminal utilizing the Polyploid Memetic Algorithm. However, the above-mentioned research works do not focus on performance parameters such as wait time, conflict resolution, charging demand, scalability, and IPFS bandwidth analysis with the increase in the number of EVs for charging. Therefore, considering that the increasing number of EVs can overburden charging infrastructure, it is necessary to manage this issue. Thus, we have proposed a blockchain and IoT-driven consensus mechanism for optimal EVs scheduling at the CS. We have presented different scenarios for optimal allocation of EVs for charging, which are designed by utilizing scheduling algorithms and a coalition game theory approach based on the number of EVs, i.e., whether the number exceeds the threshold or not. If the number of EVs arriving is less than the number of CPs, then the FCFS scheduling algorithm is utilized to allocate the EVs to CPs for charging, as discussed in scenario 1. Scenario 2 involves a number of EVs arriving up to a threshold number. In this scenario, we check their available energy to enable efficient scheduling at the CS using the LRTF algorithm. Finally, scenario 3 involves a number of EVs that exceeds the threshold number. In scenario 3, different cases are considered based on the arrival of emergency vehicles or the available energy associated with the EVs for allocation to a CS with the help of the scheduling algorithms and the coalition game theory approach. Hence, we have specified several scenarios to enable optimized and efficient coordination between nodes, i.e., the EVs and CS, involved in the blockchain network. Therefore, the proposed consensus mechanism,
COME, is designed utilizing several algorithms which ensure that the participating nodes in the network are in consensus, with the assumption that only honest and responsive nodes are involved. Finally, the blockchain-based proposed consensus mechanism is simulated in Remix IDE considering the designed scenarios in terms of parameters, i.e., wait time, conflict resolution, charging demand, scalability, and IPFS bandwidth analysis. In future work, the performance of the proposed blockchain-based consensus mechanism can be improved by considering a scenario that lessens the effect of any involvement of dishonest or non-responsive nodes, which can interrupt the scheduling of EVs at the CS.
5.2. Conclusions
This paper has proposed an optimized blockchain and IoT-based consensus mechanism, COME, to schedule EVs for charging at a CS. With the increase in the number of EVs, it is becoming difficult to coordinate them efficiently at a CS, especially in case of emergency EVs or high-authority vehicles. We explored various traditional consensus protocols and obtained insights into their charging demand, wait time, scalability, and IPFS bandwidth issues. The aforementioned challenges can discourage EVs from charging, leading to a loss for the CS. Therefore, we applied different scheduling algorithms such as FCFS, LRTF, and coalition game theory over diverse scenarios to resolve conflicts between EVs and the CS. Scenarios were considered based on the number of EVs arriving at the CS and the emergency situation. For example, if the number of EVs arriving at the CS is less than or up to a threshold number, scheduling can be resolved using the FCFS and LRTF scheduling algorithms considered in scenario 1 and scenario 2. Moreover, if EVs arriving at the CS exceed the threshold number, the different cases considered here for EV scheduling using FCFS and the coalition game theory approach can be relied on. Finally, the performance of the proposed consensus mechanism has been simulated by executing the smart contracts in Remix IDE implemented using Solidity high-level language and considering performance metrics such as charging demand, wait time, conflict resolution, scalability, and IPFS bandwidth in comparison with the traditional pBFT consensus protocol. The comparisons shows that the proposed COME mechanism outperforms the traditional system in terms of security, reliability, and conflict resolution.
In the future, the performance of the proposed consensus mechanism can be optimized in case of the arrival of a number of EVs when the wait time exceeds the threshold time by using different game theory approaches in dynamic real-time scenarios. Moreover, several advanced optimization algorithms, i.e., heuristics, metaheuristics, and hybrid algorithms, can be explored in different domains, such as transportation, healthcare, multi-objective optimization, data classification, etc., to improve the applicability of the proposed mechanism. Additionally, we intend to consider the scenario in which any dishonest or non-responsive nodes (i.e., the EVs and CS) involved in the network are observed and prevented from disrupting the scheduling through any malicious attack.