Multi–Disciplinary Optimizations of Small-Scale Gravitational Vortex Hydropower (SGVHP) System through Computational Hydrodynamic and Hydro–Structural Analyses
Abstract
:1. Introduction
Literature Survey
- To optimize the geometrical parameters of the basin, and notch and conical angles to obtain maximum tangential velocity.
- Understanding the physical principle behind the vortex flow field and thereby impact on hydro-rotors, which are essential when considering energy extraction.
- Optimizing the geometry and size of turbine blades to extract more power from the maximum vortex strength (rotational energy).
- To do the numerical investigation on GVHP with different turbine blade profiles and its construction materials through HSI (Hydro–Structural Interaction) analysis in order to obtain the optimum blade design and suitable lightweight material which agrees with the maximum vortex velocity structure and also it will contribute to the maximum power output [1,2,3,4,5,6,7,8,9,10].
2. Proposed Methodology—Computational Hydrodynamic Analysis
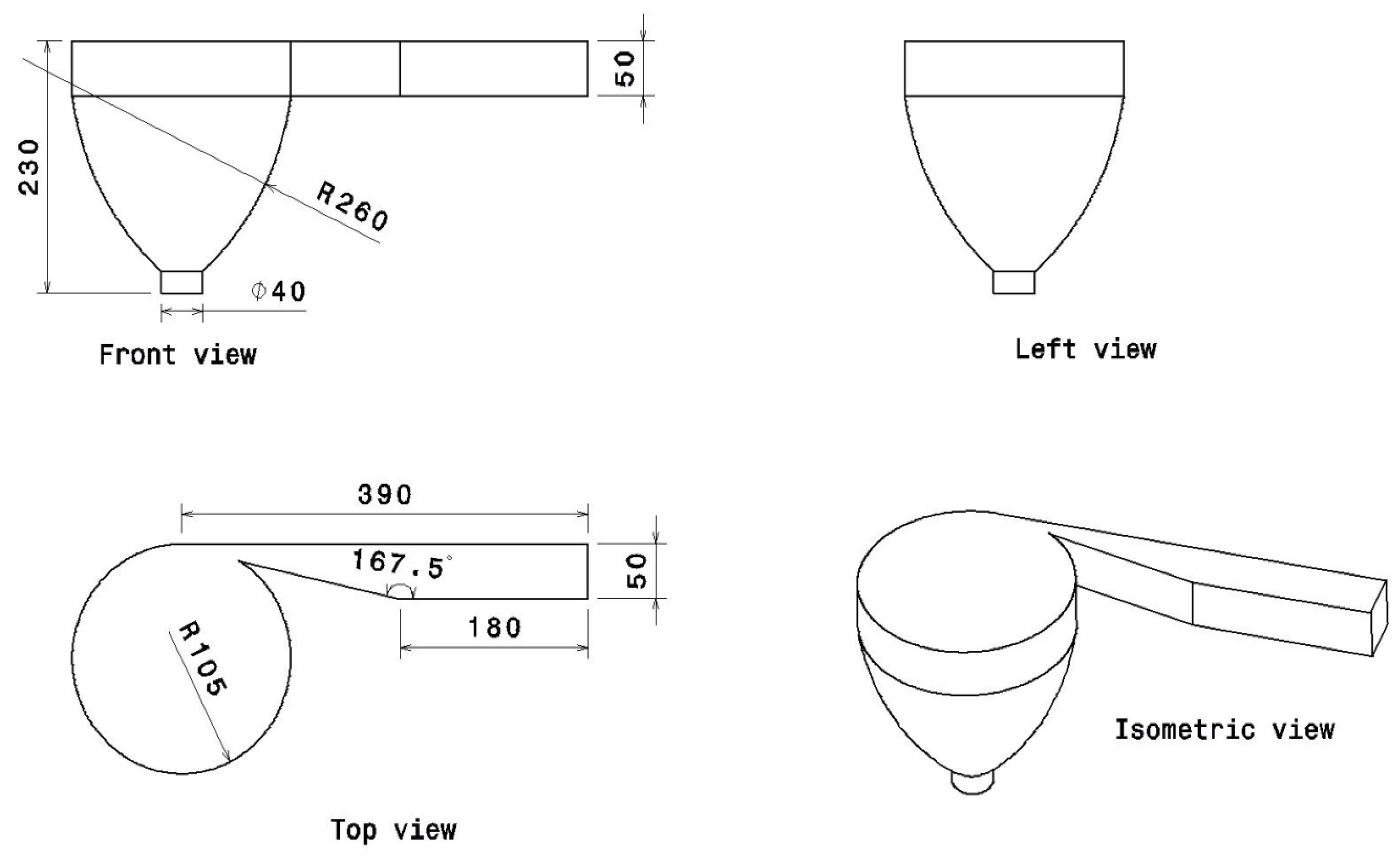
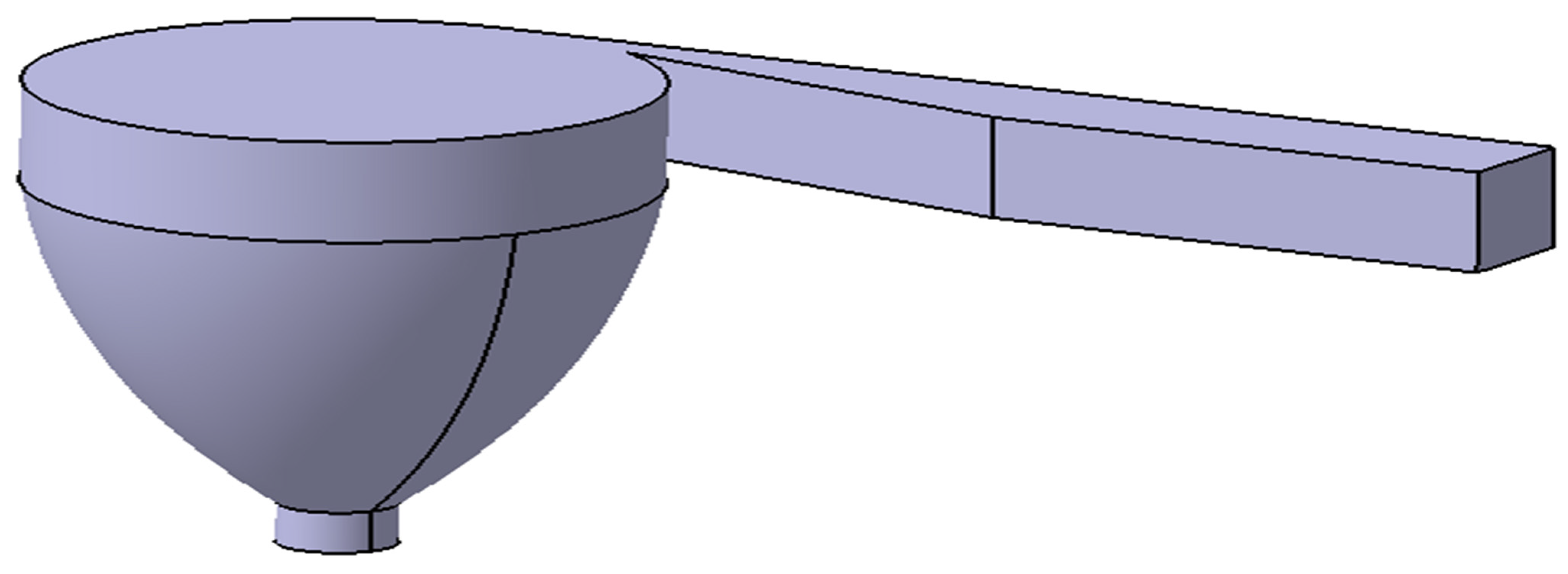
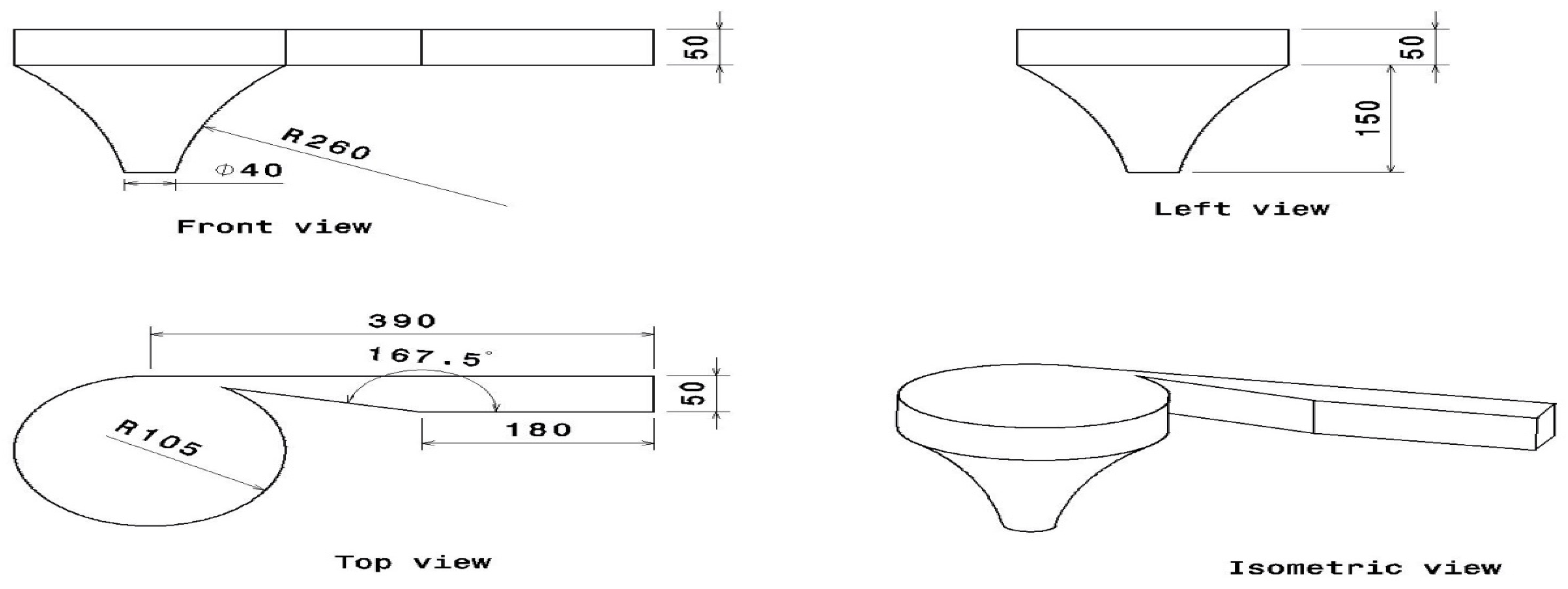
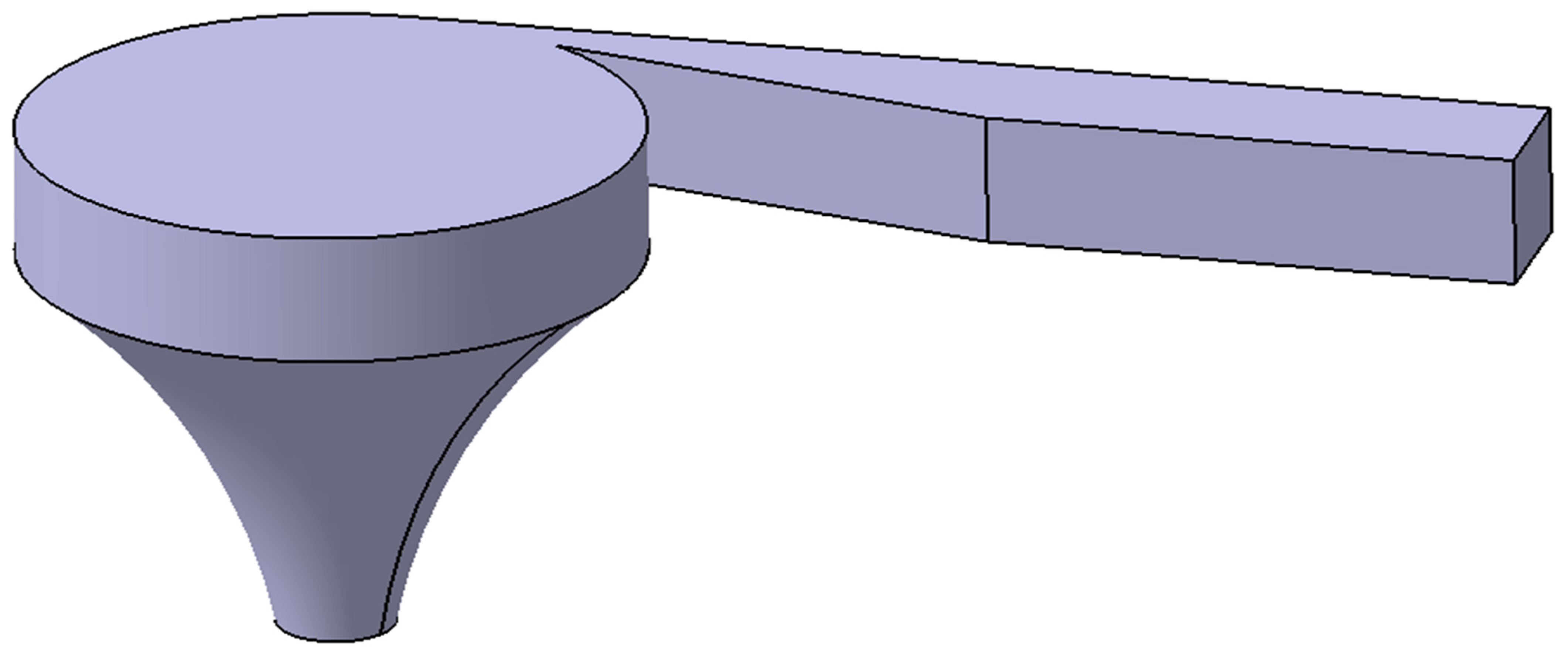
2.1. Conceptual Design
2.1.1. Symbols and Notations
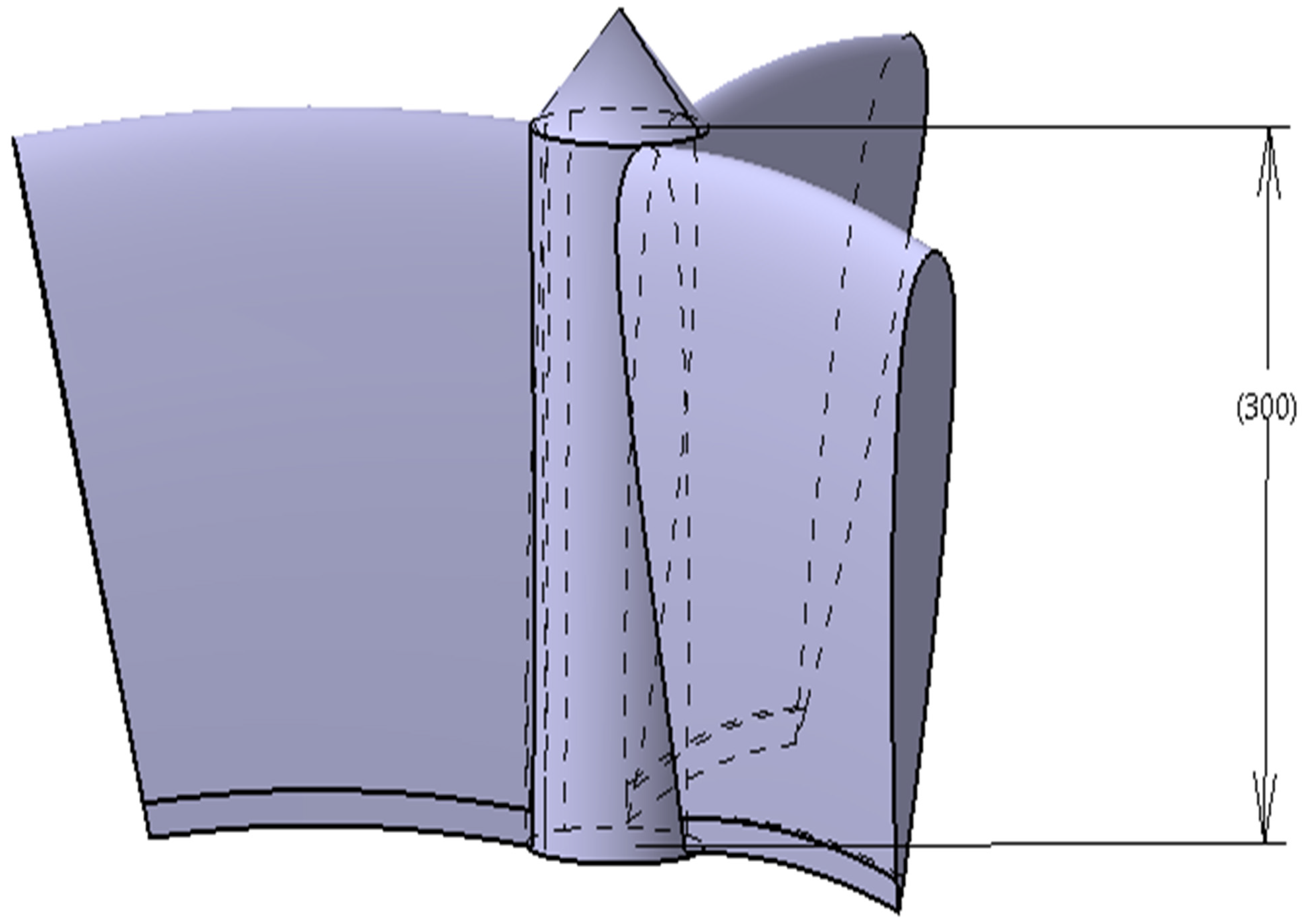
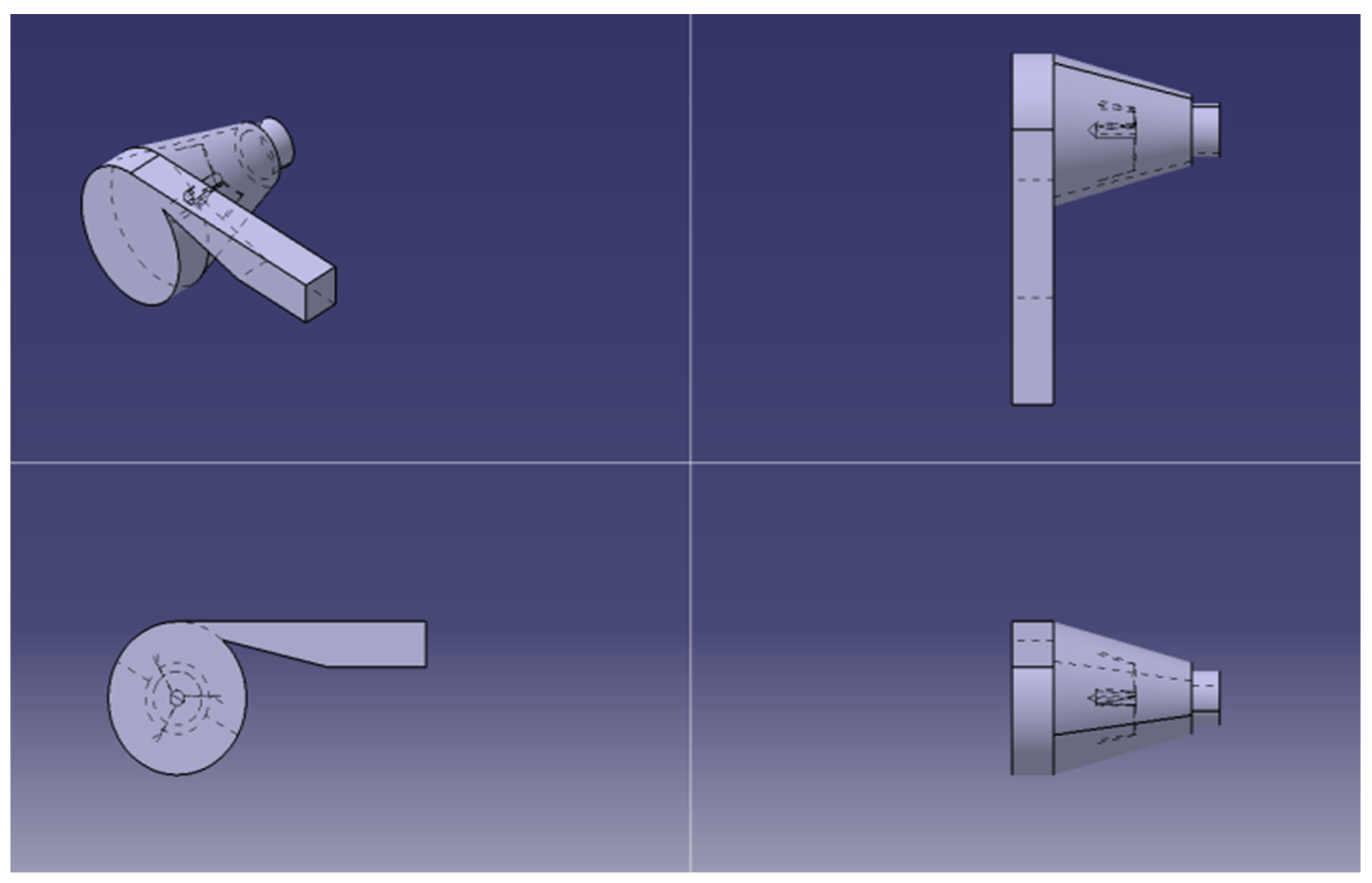
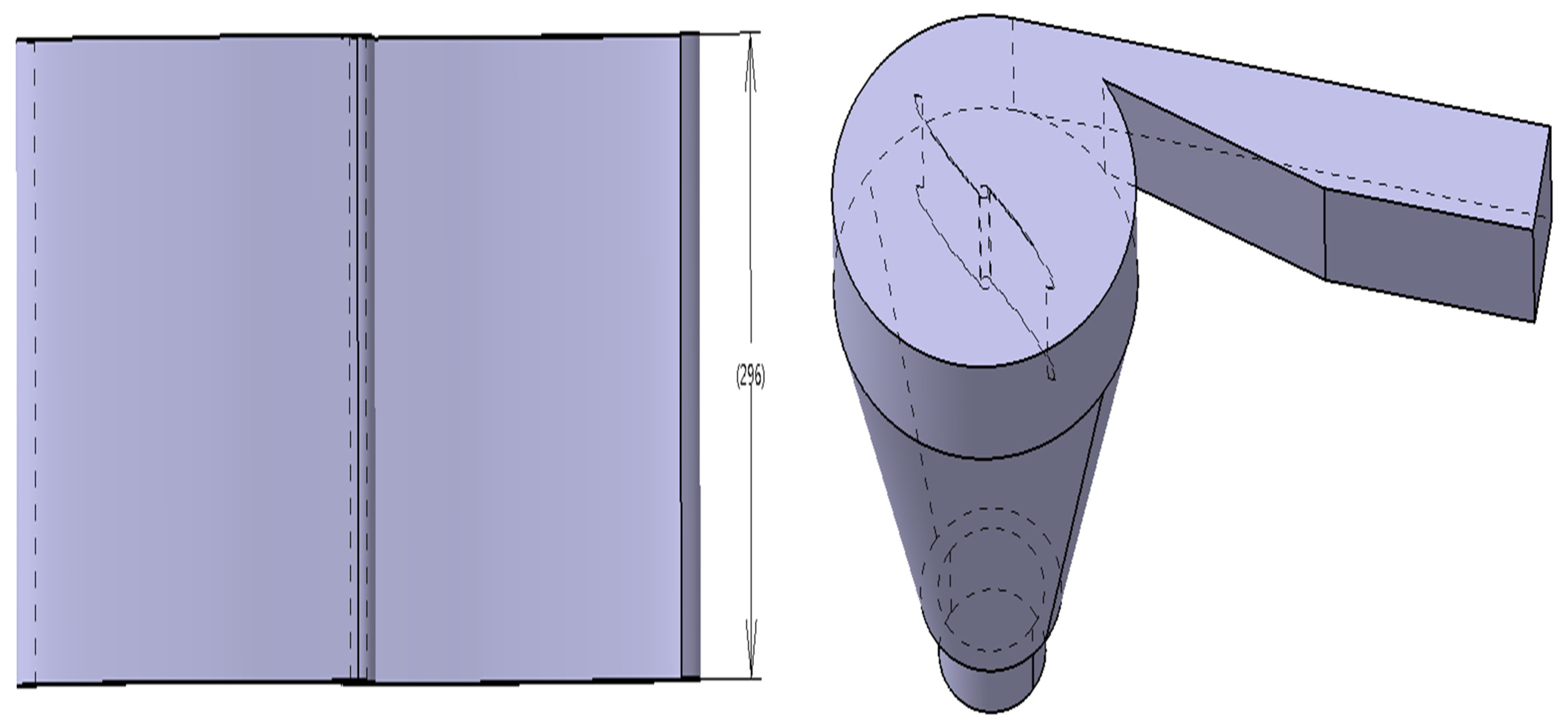
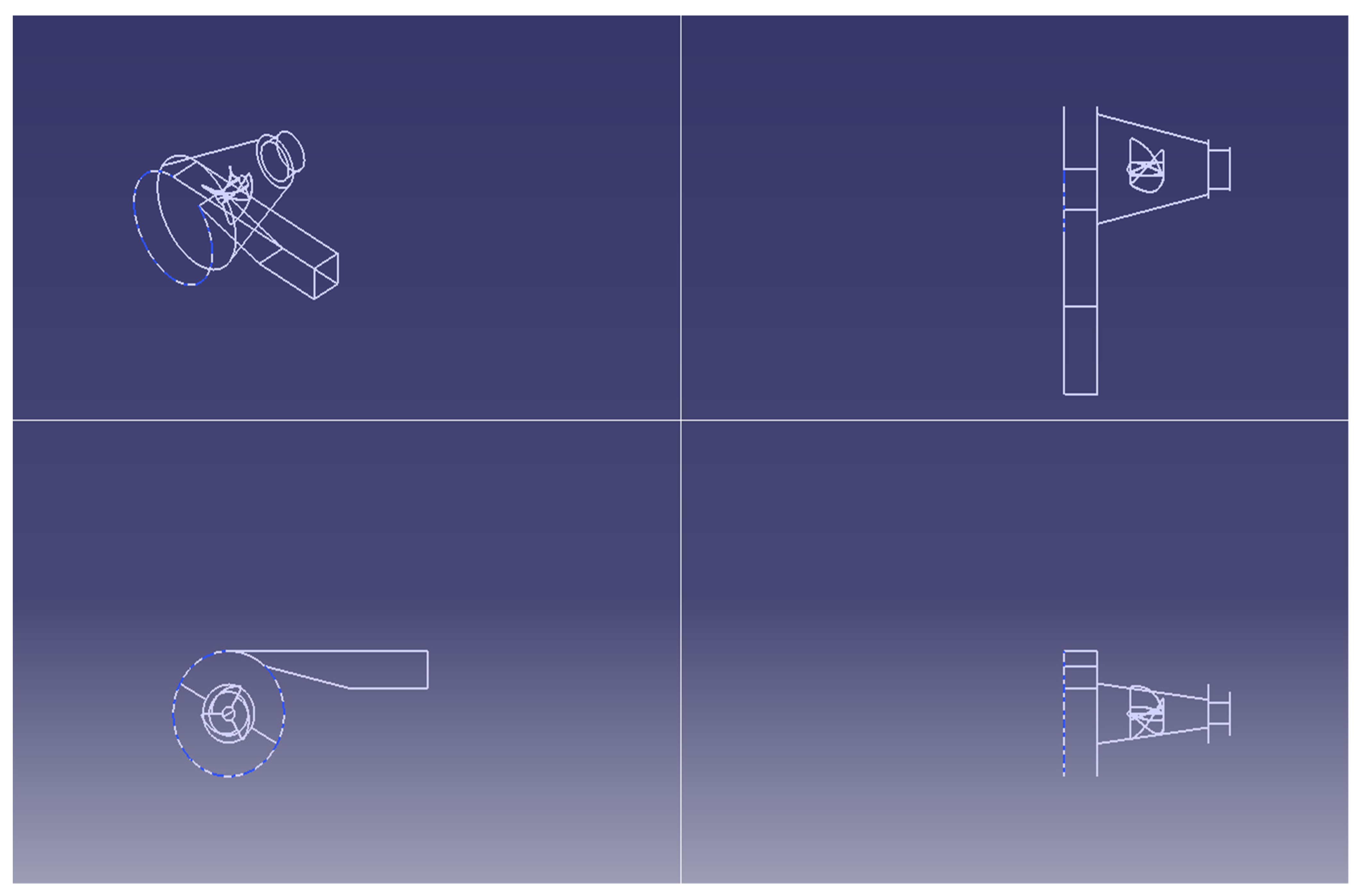
2.1.2. Hydro-Rotor–I
2.1.3. Hydro-Rotor II
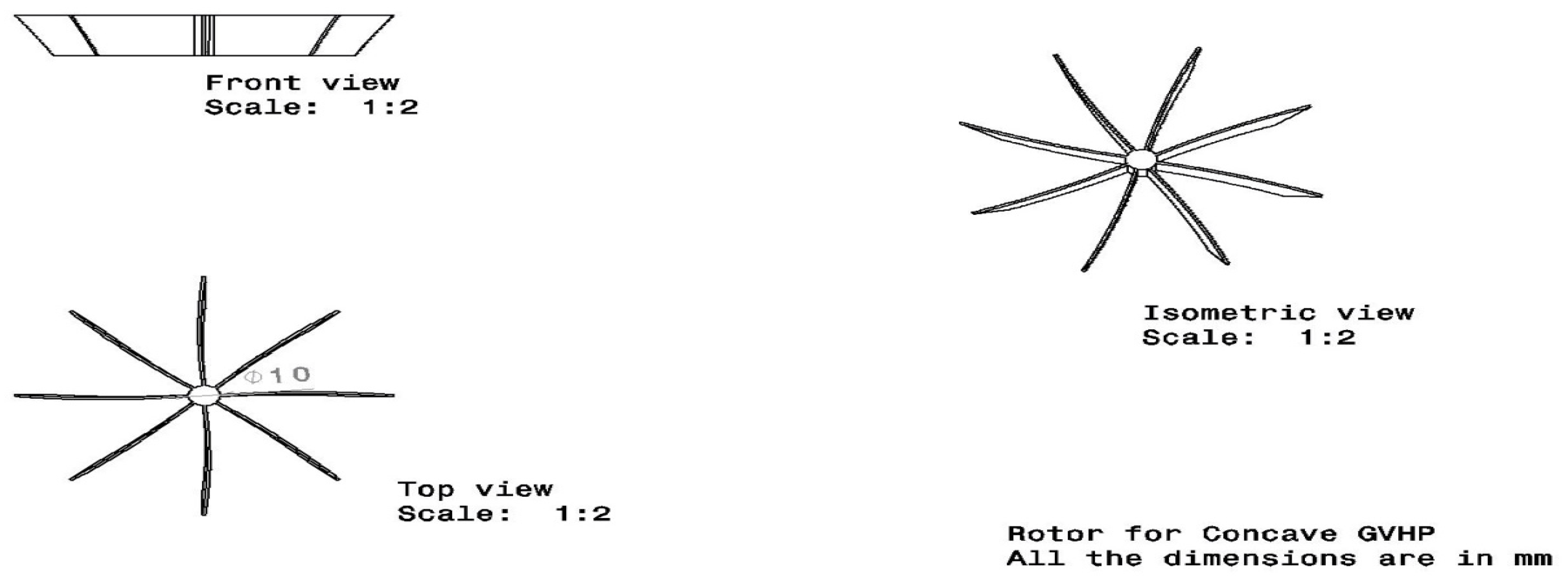
2.1.4. Hydro-Rotor III
2.1.5. Hydro-Rotor–IV
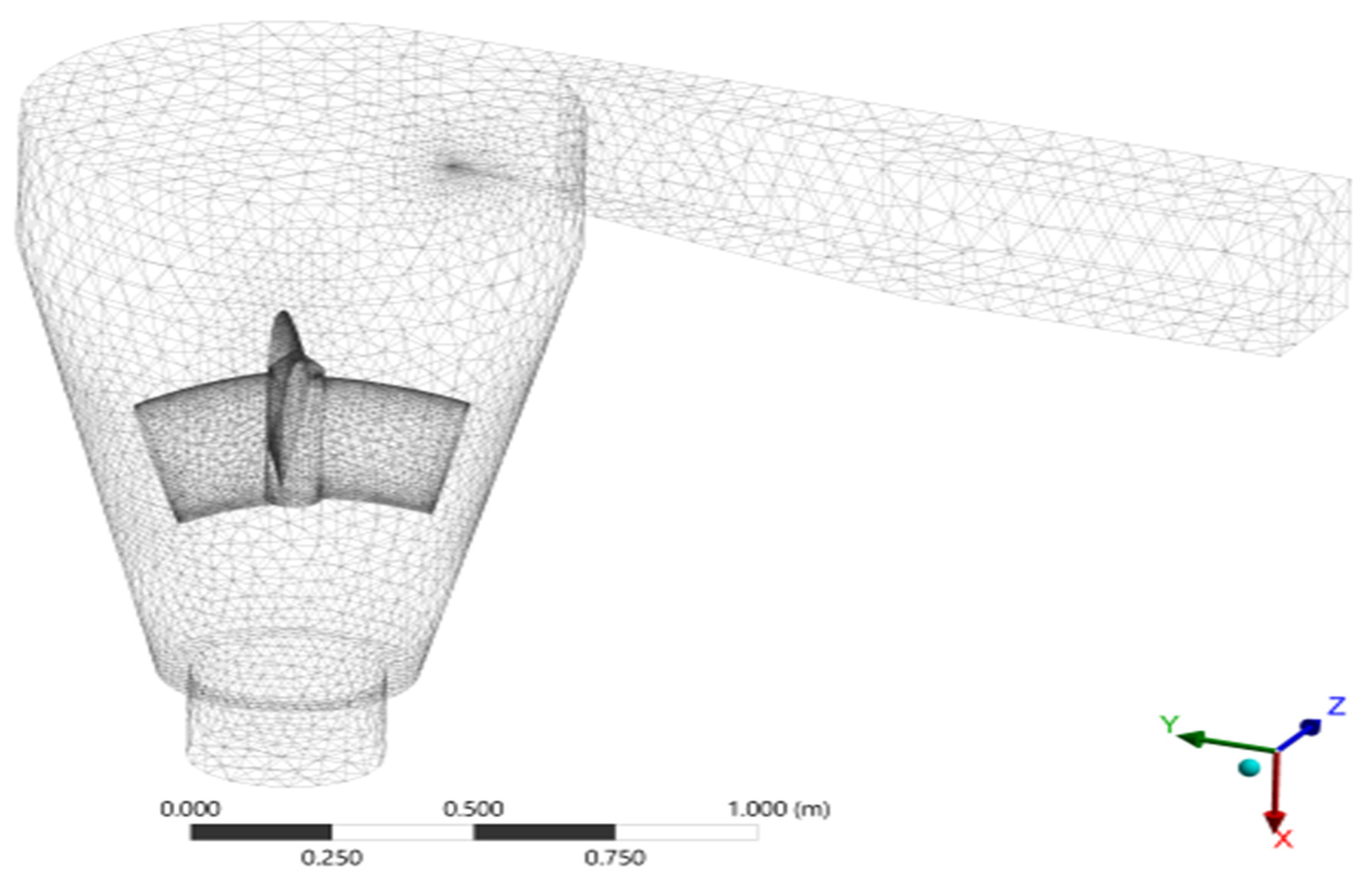
2.2. Computational Model and Discretization Process
2.3. Boundary Conditions
2.4. Details about the Hydrodynamic Analysis
2.5. Governing Equations for Hydrodynamic Analysis
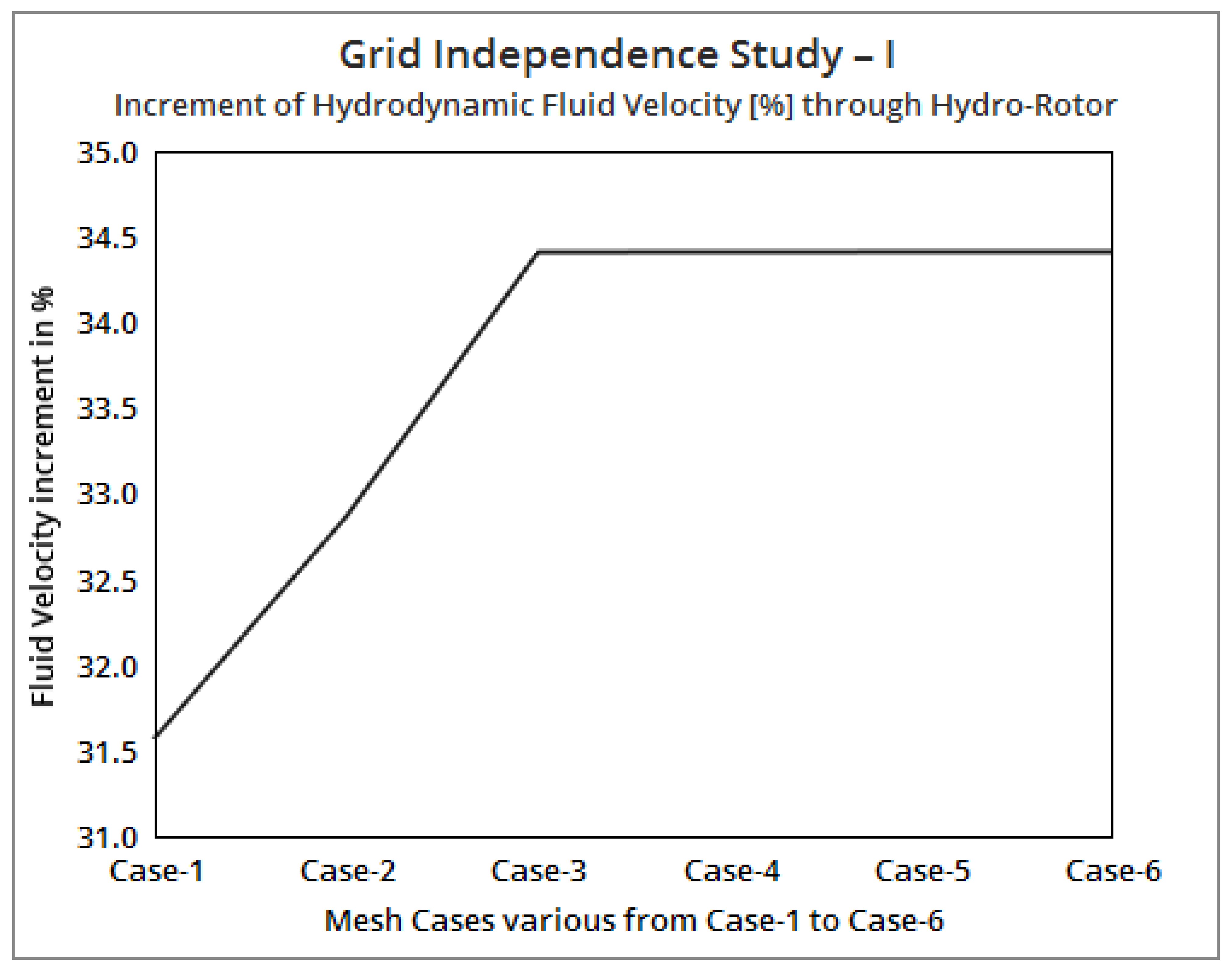
2.6. Grid Convergence Study
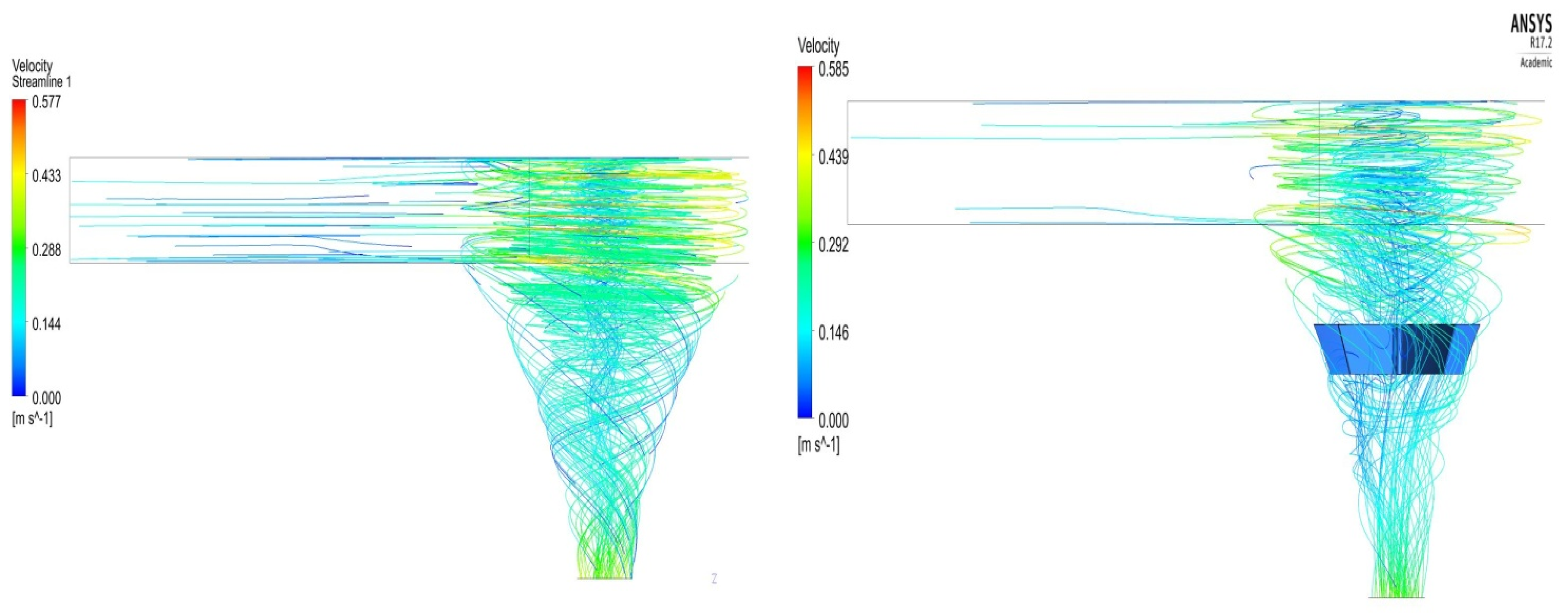
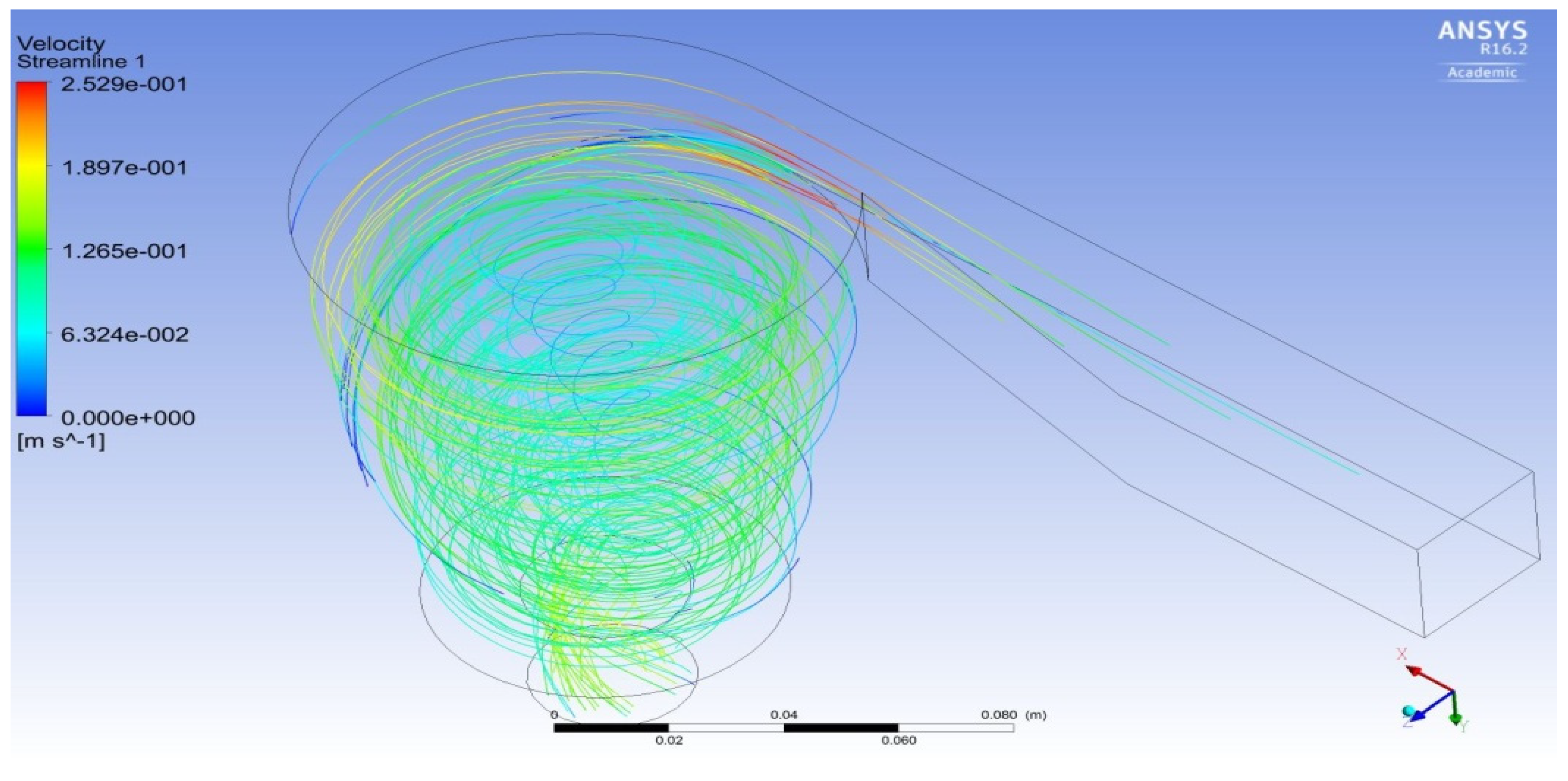
2.7. Validation Study of Proposed Methodology
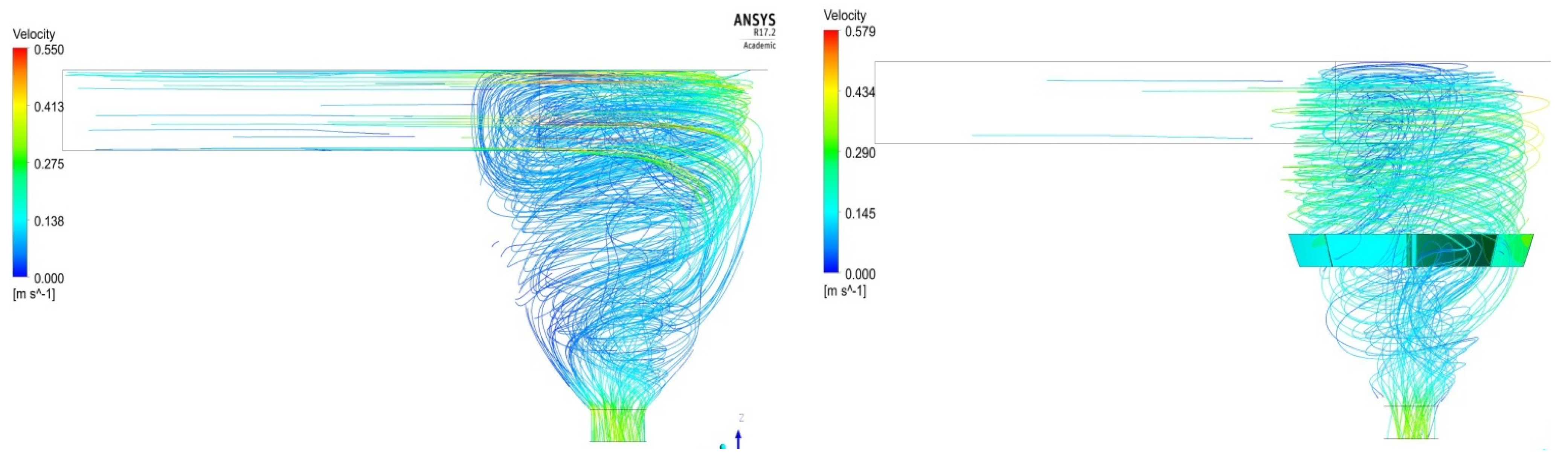
3. Computational OptimizationResults and Discussions—I
3.1. Optimization of Design Based on Shape through CHA
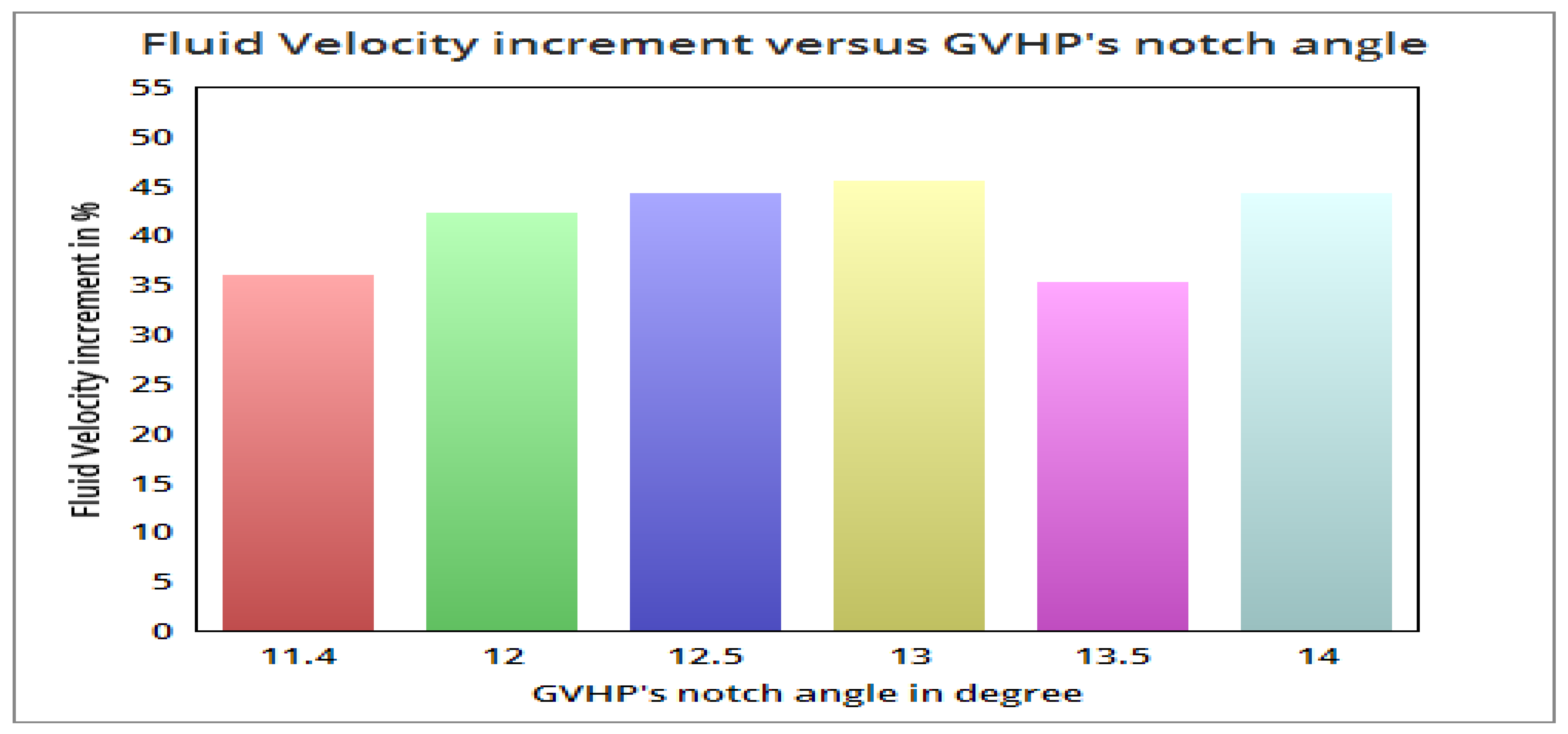
3.2. Optimization of Design Based on SGVHP’s Notch Angle
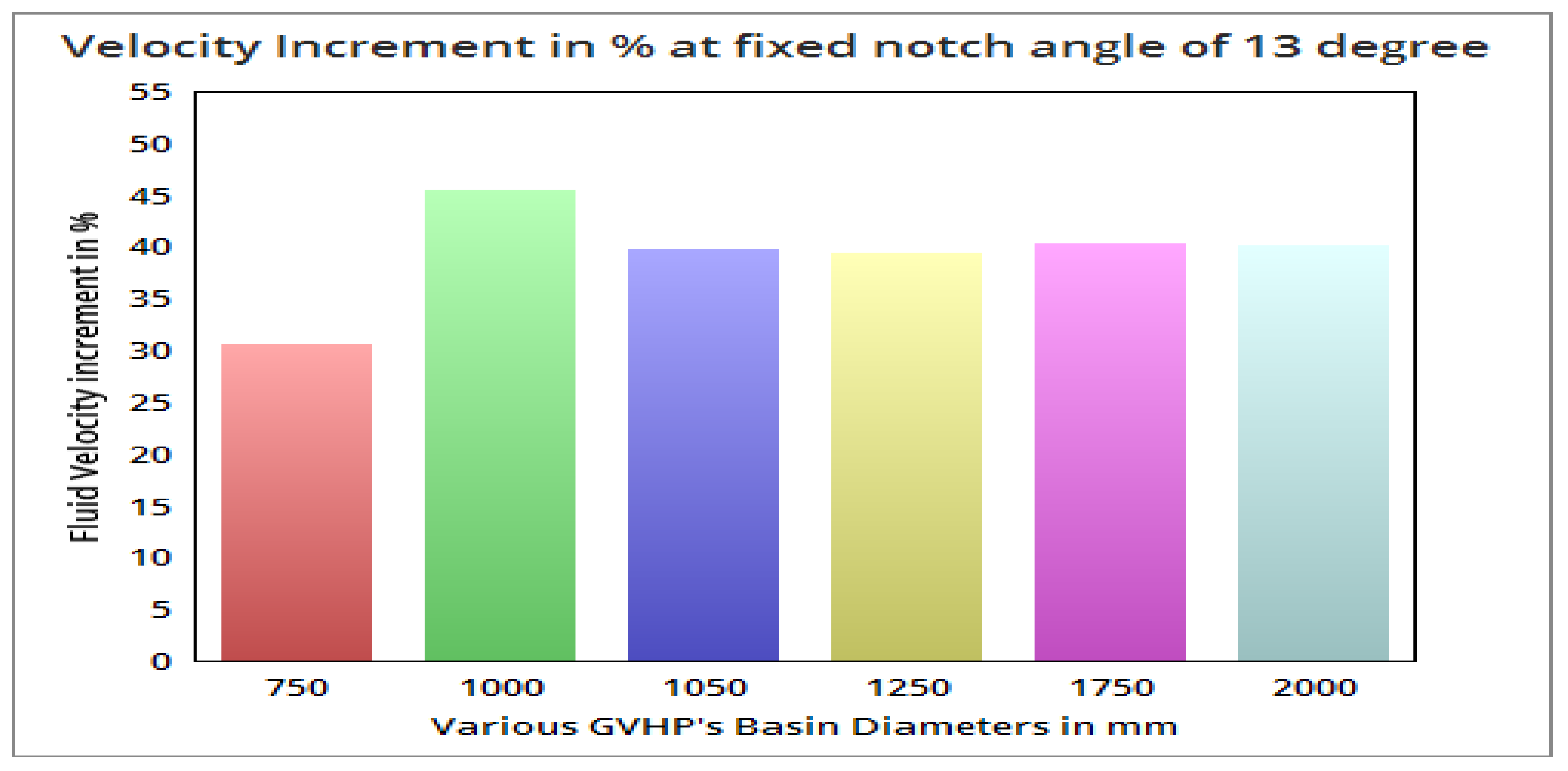
3.3. Optimization of Design Based on SGVHP’s Basin Diameter
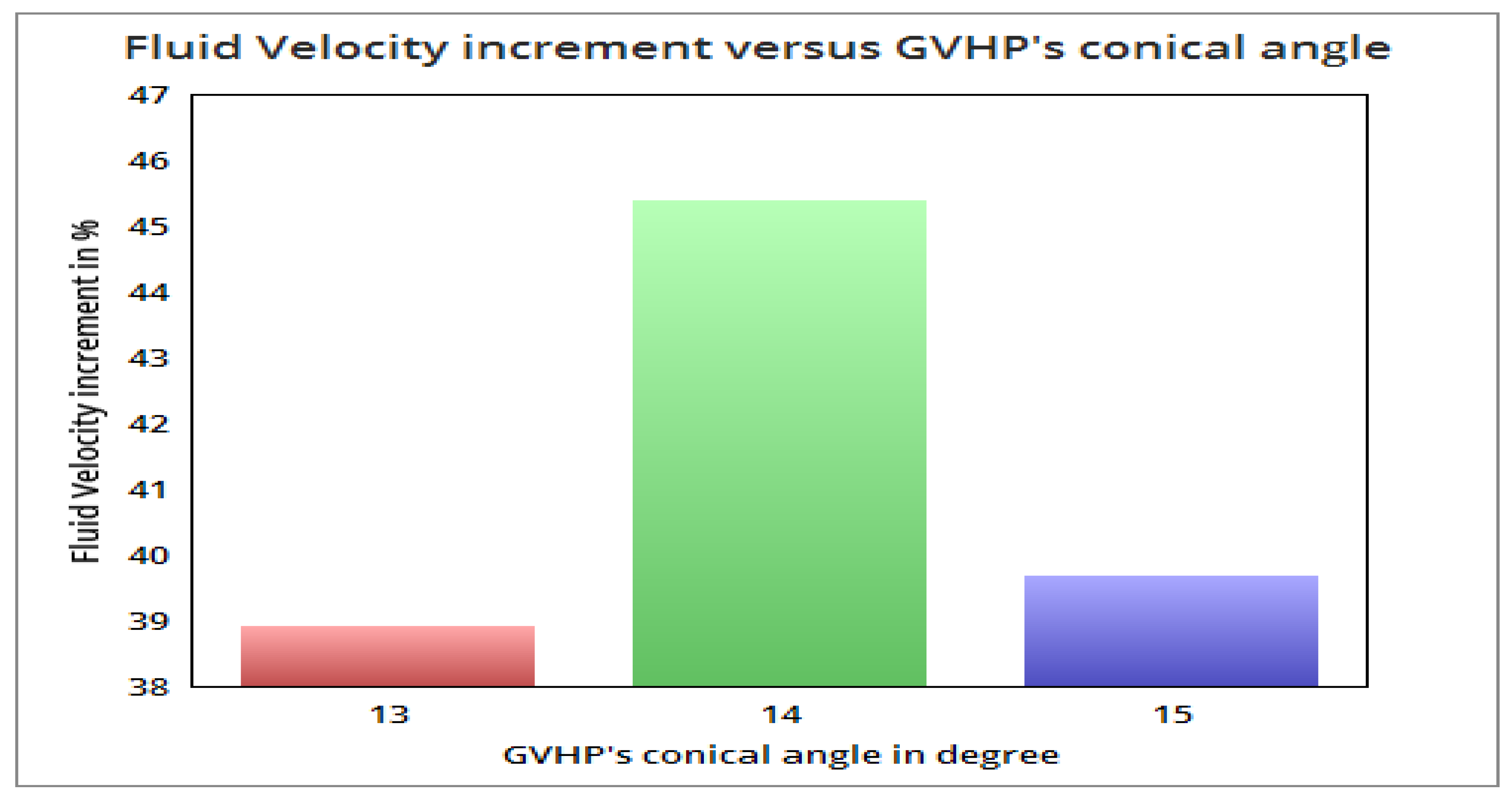
3.4. Optimization of Design Based on SGVHP’s Conical Angle
4. Computational Optimization Results and Discussions—II
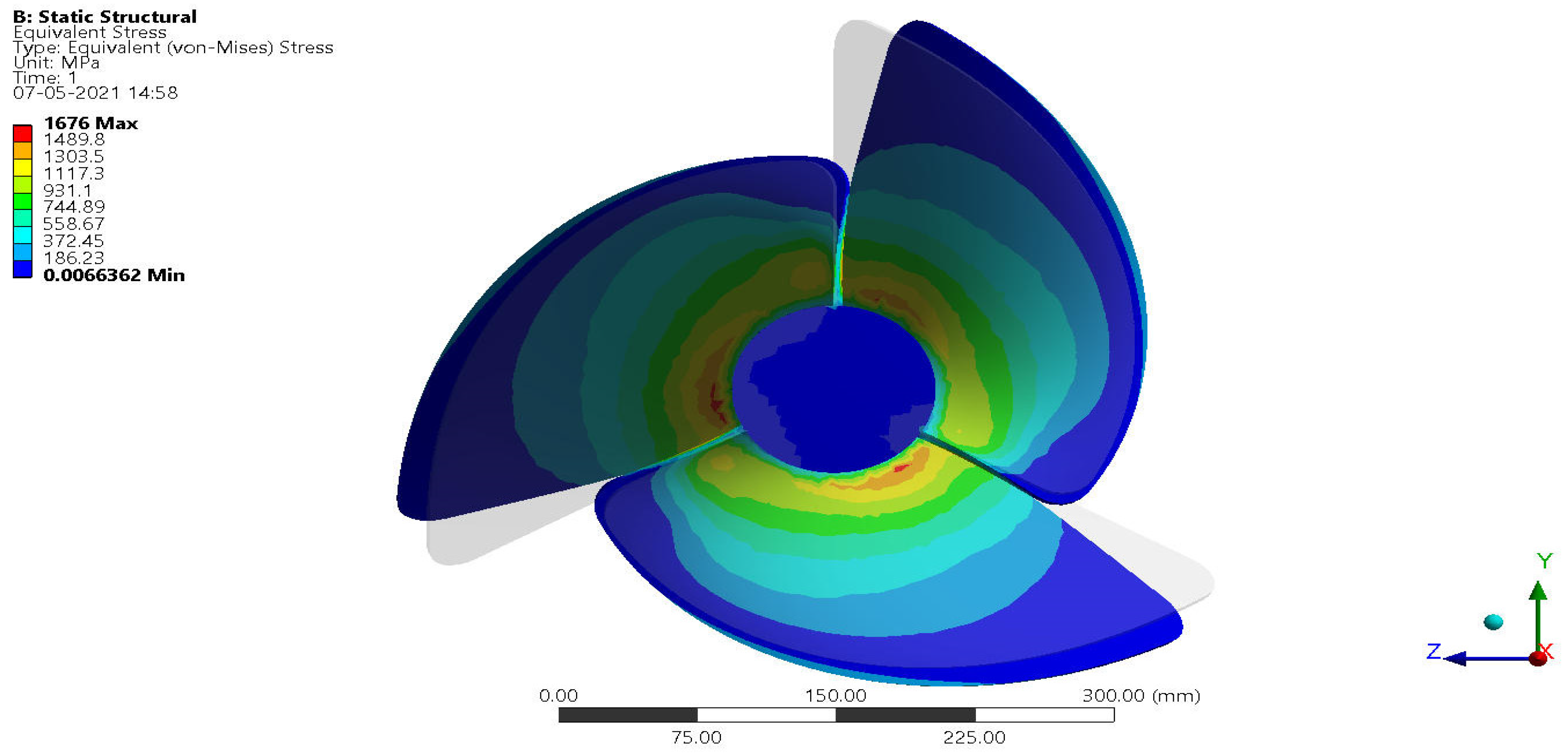
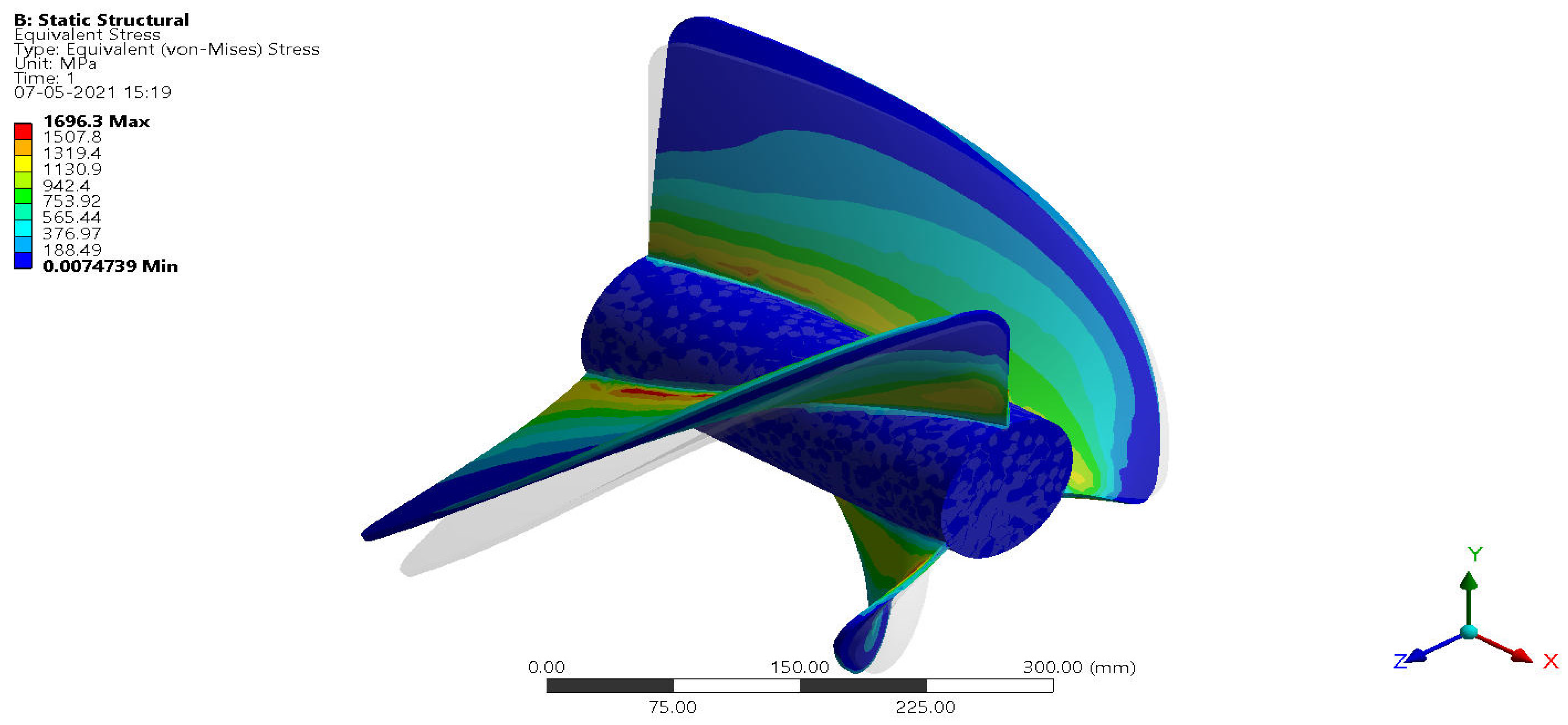
4.1. Optimization of Lightweight for GVHP Rotors
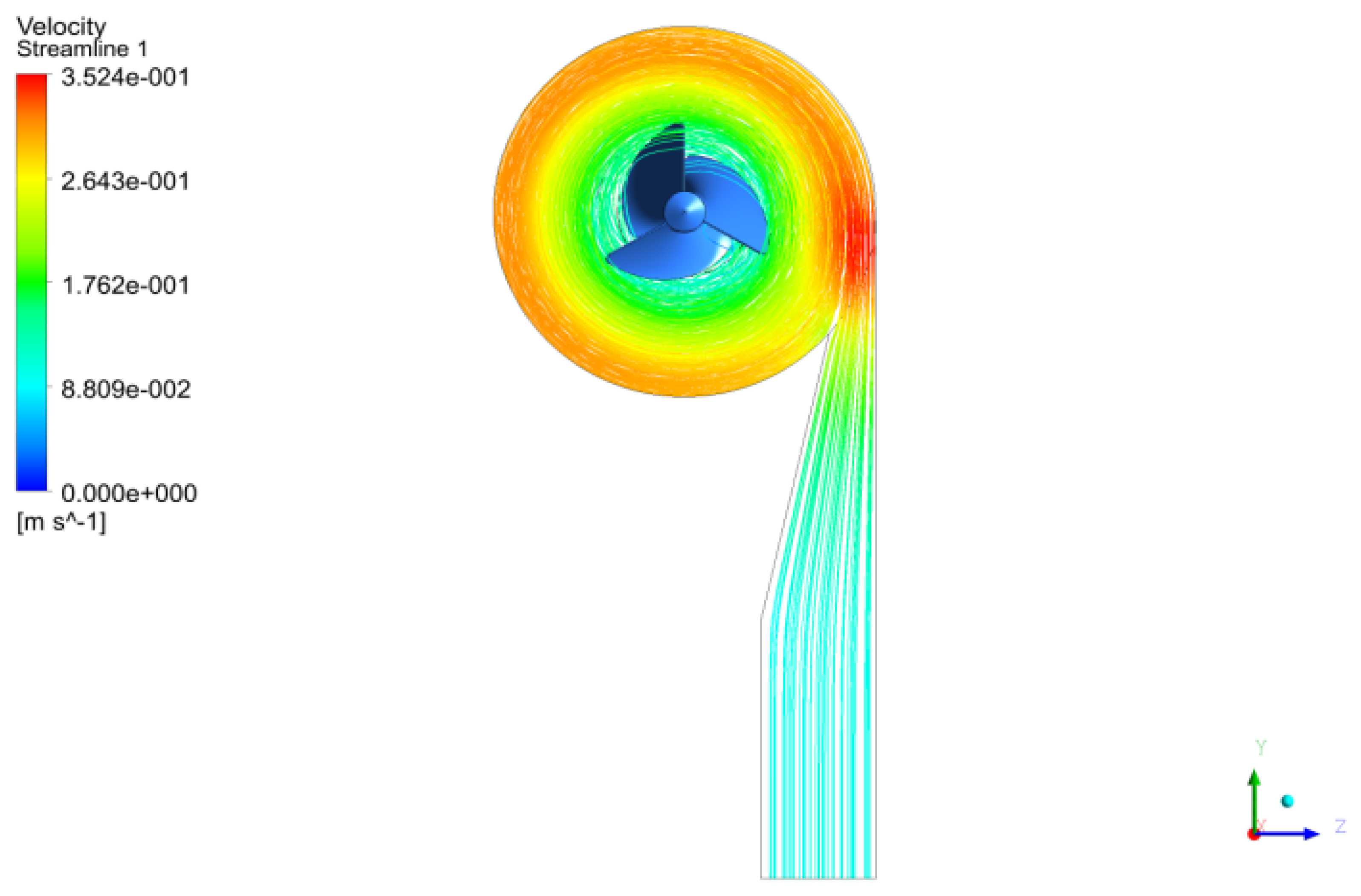
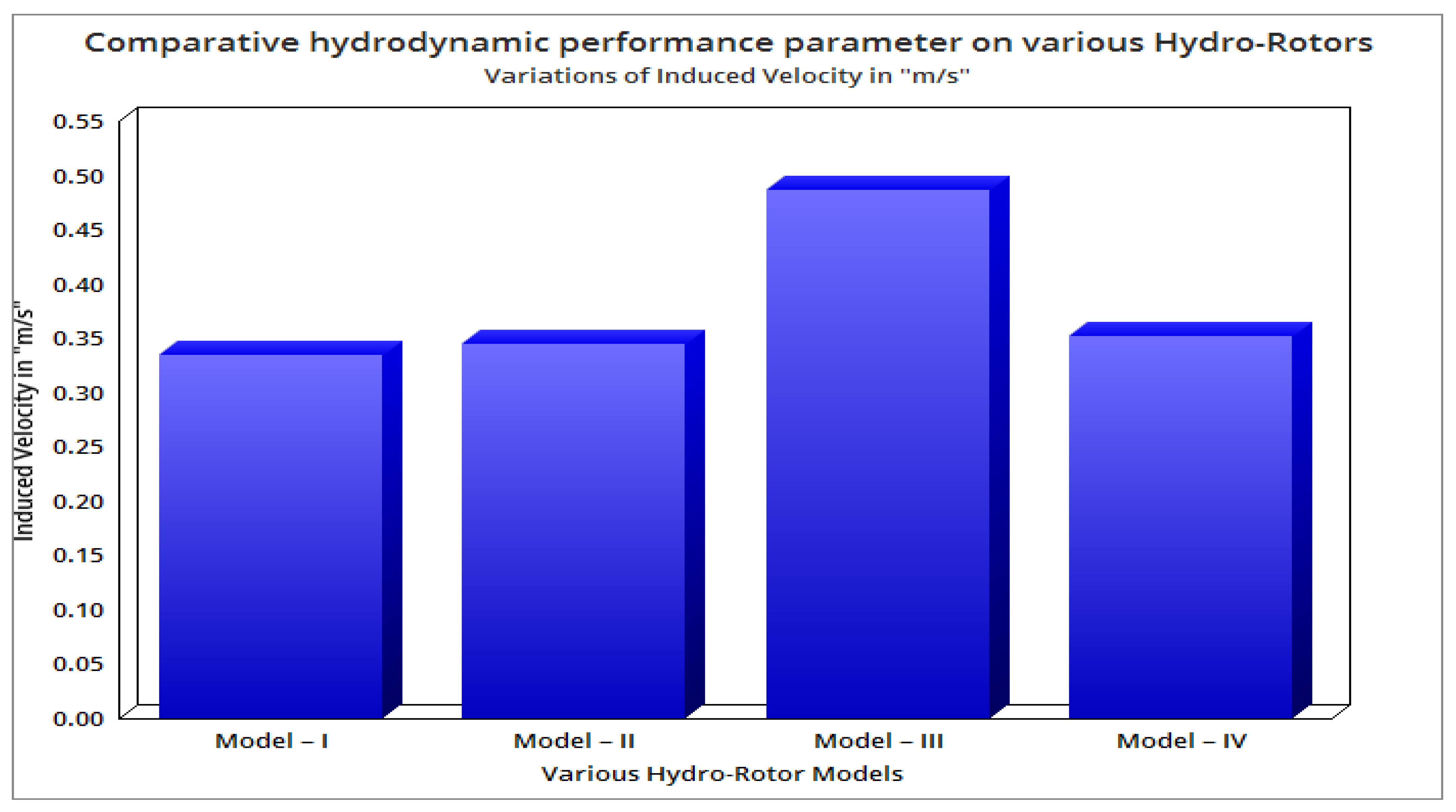
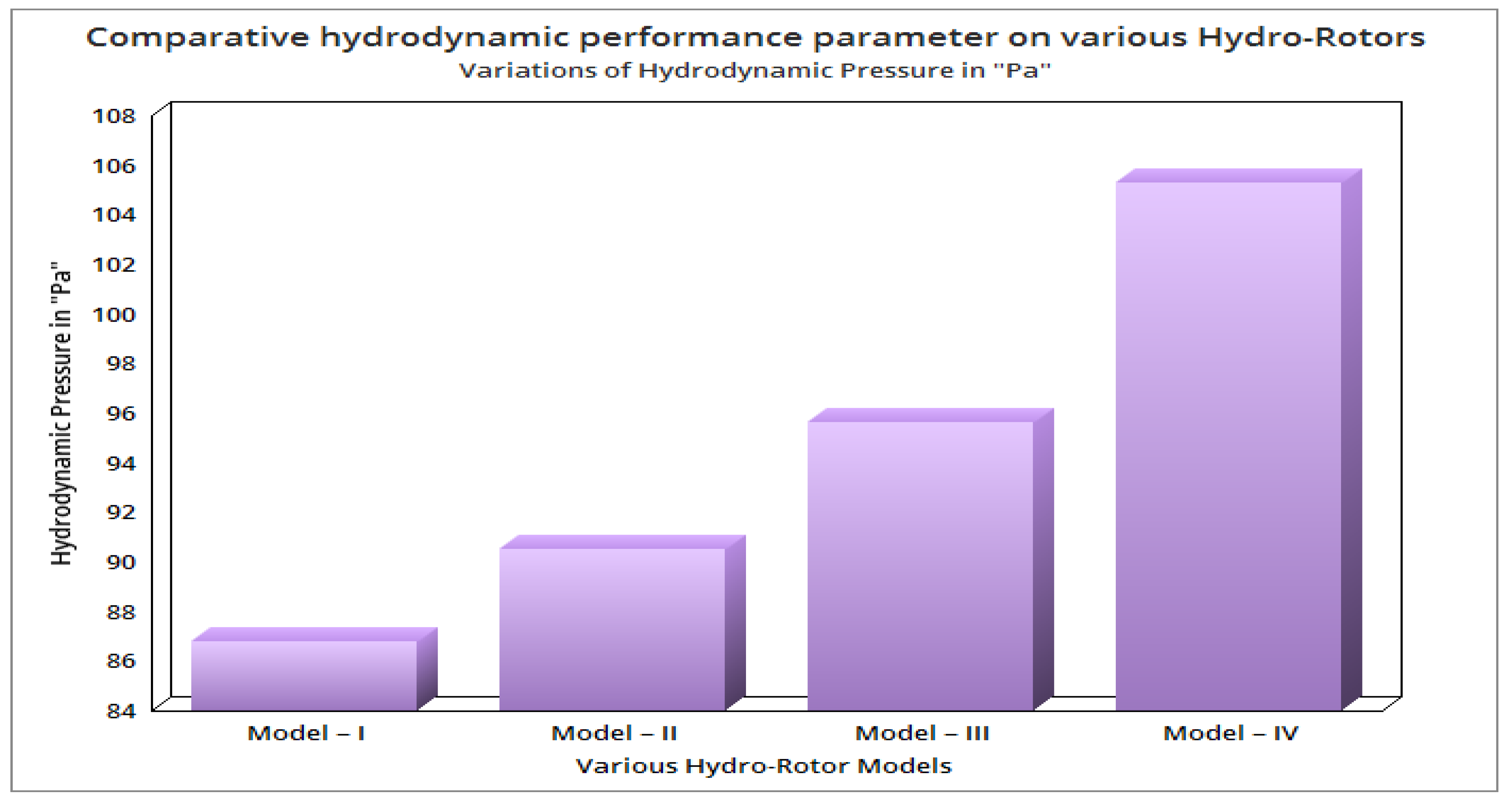
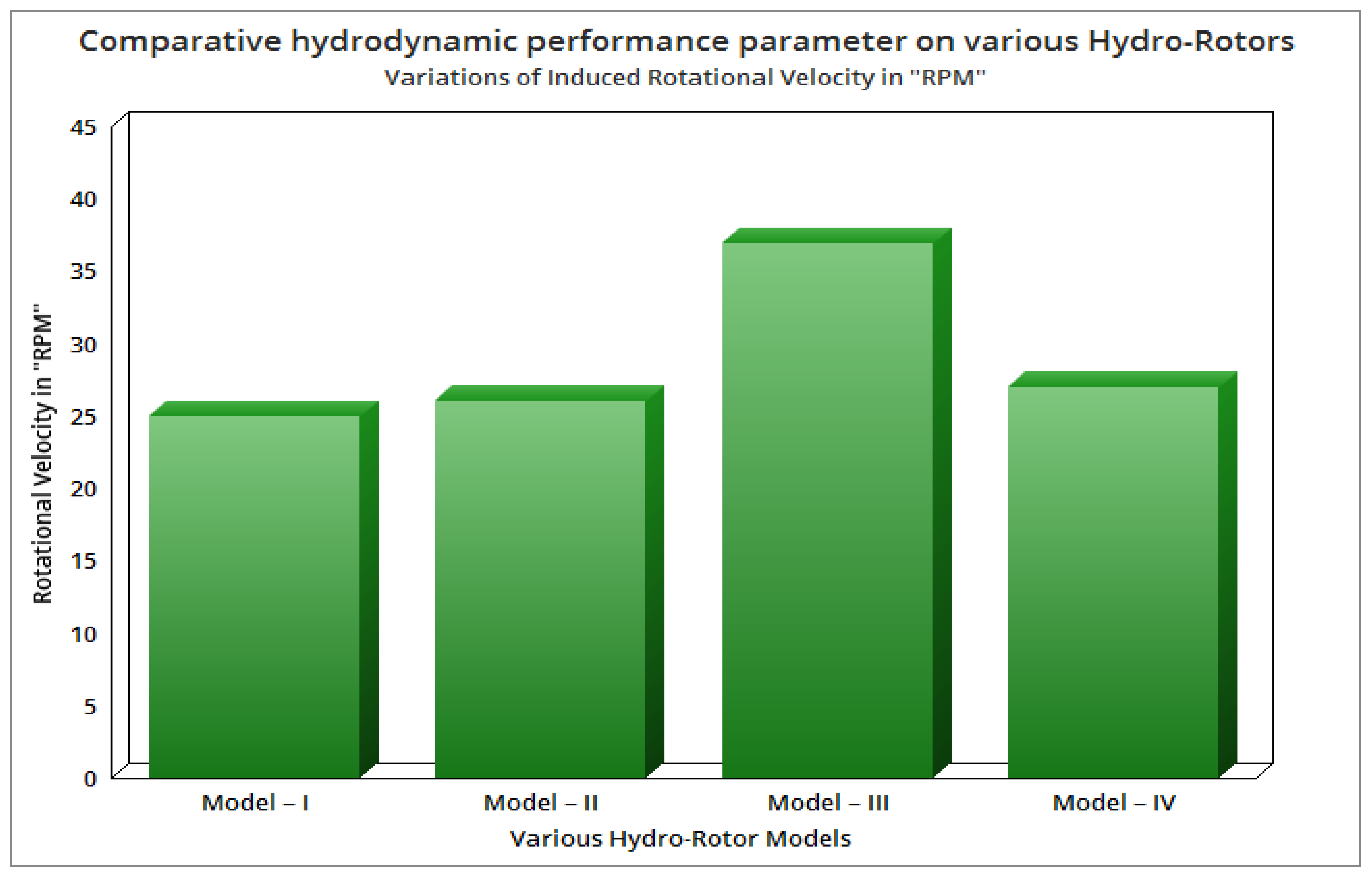
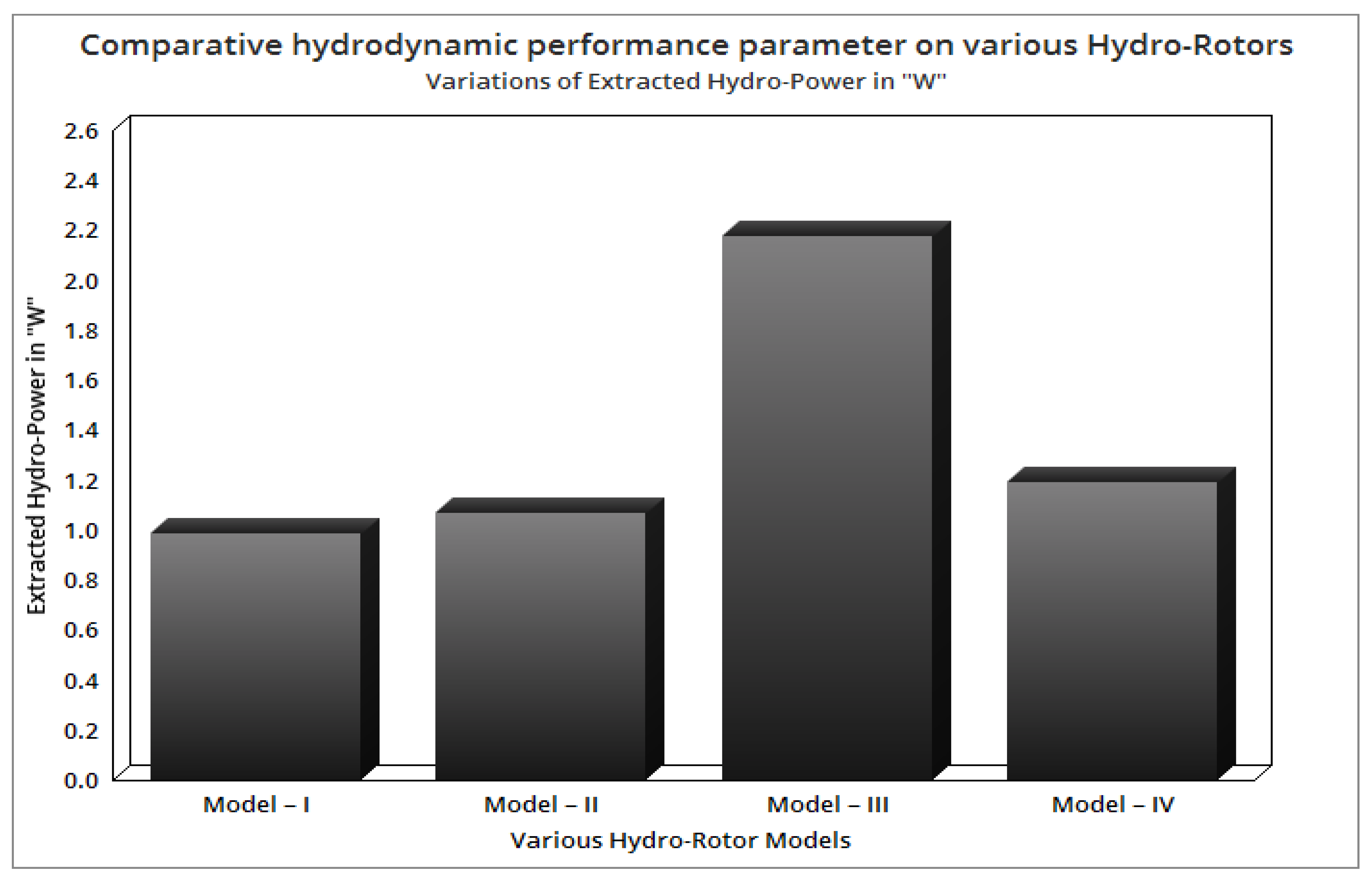
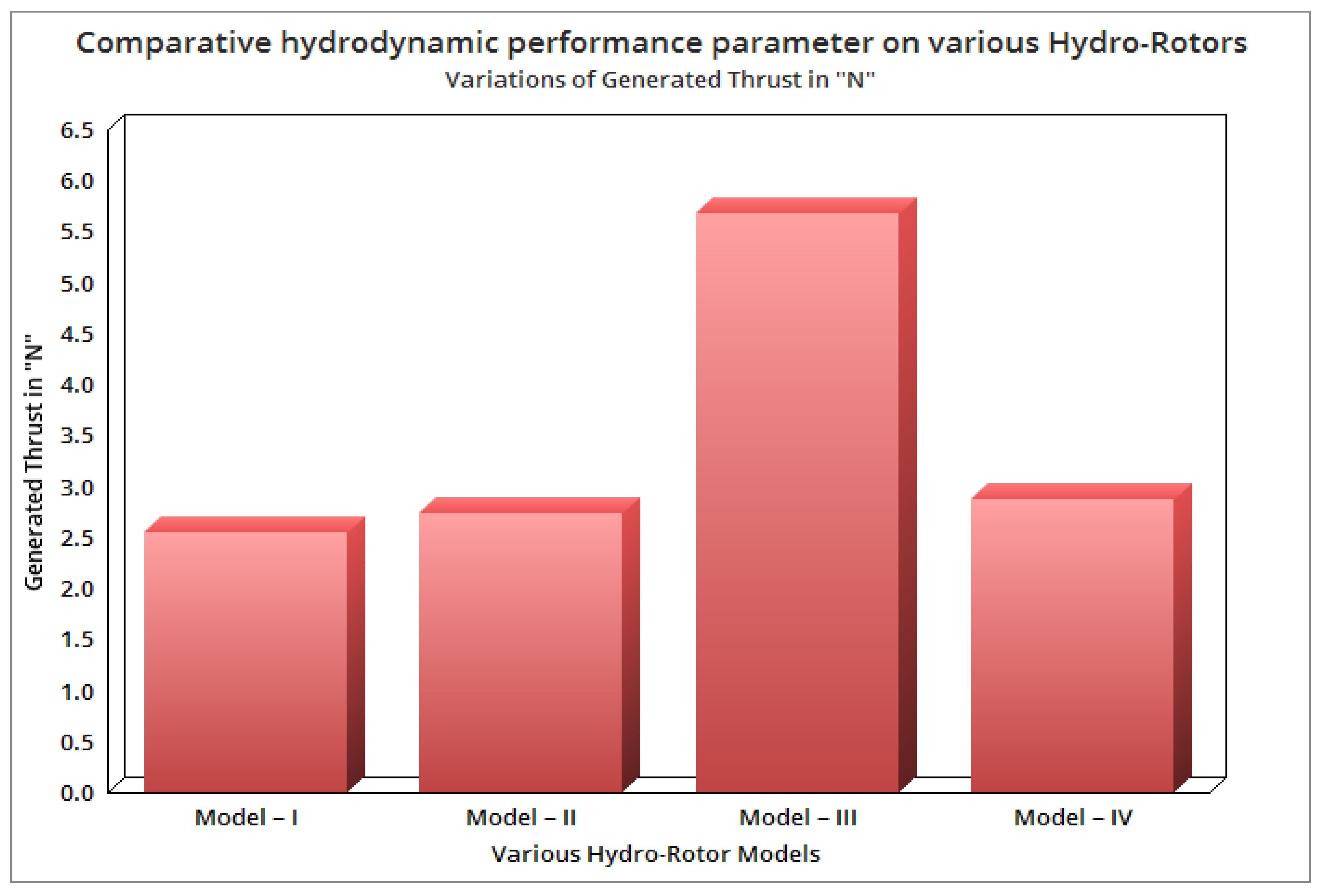
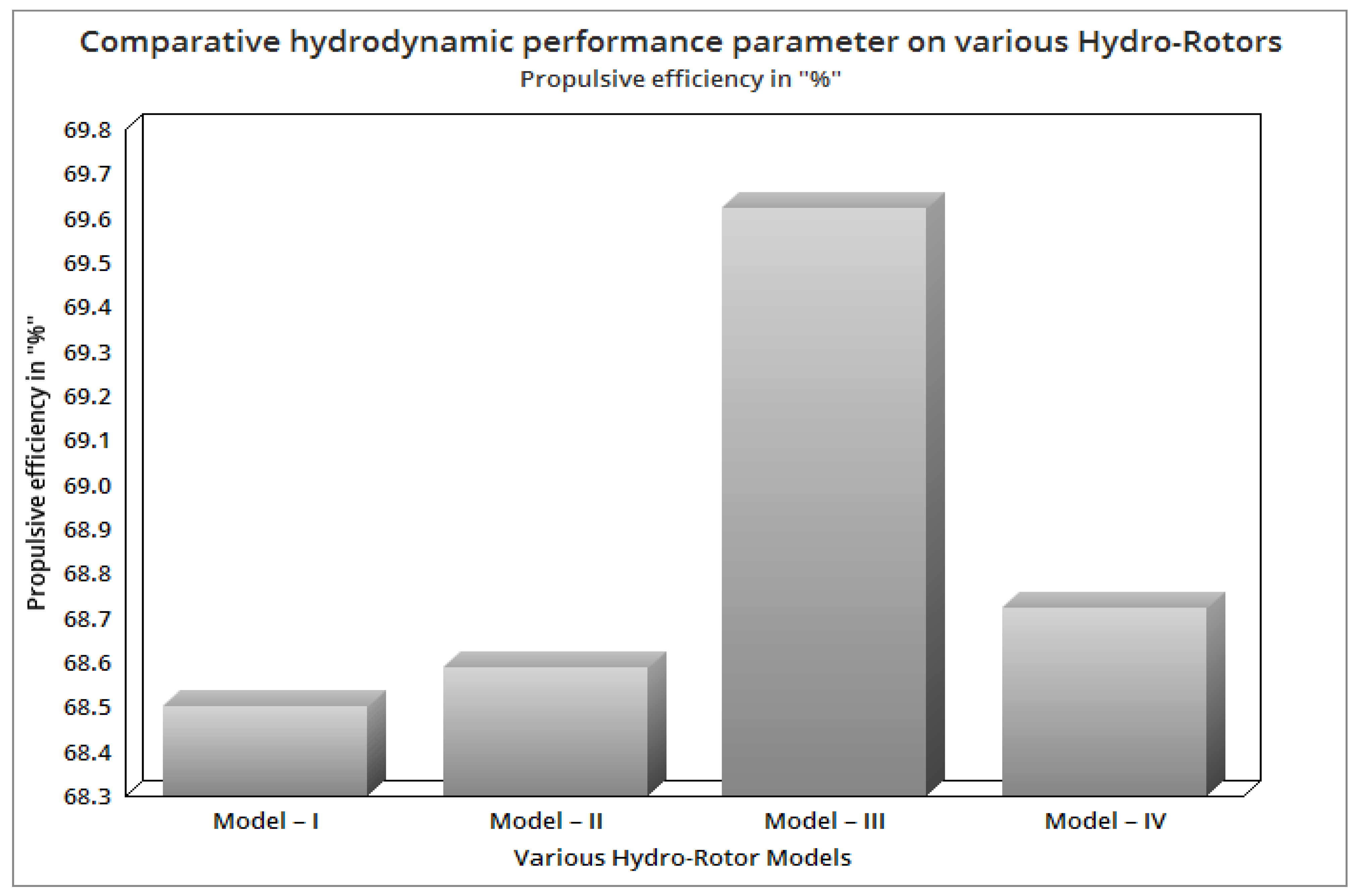
4.2. Optimization of Hydro-RotorsBased on High-Performance Factors
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jha, A.K.; Subedi, D.U.; Timilsina, A.B. Assessment of Gravitational Water Vortex Hydropower Plant in Nepal. Int. Res. J. Eng. Technol. 2018, 5, 2679–2691. [Google Scholar]
- Sánchez, A.R.; Del Rio, J.A.S.; Muñoz, A.J.G.; Montoya, J.A.P. Numerical and Experimental Evaluation of Concave and Convex Designs for Gravitational Water Vortex Turbine. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 64, 160–172. [Google Scholar]
- Thapa, D.; Mishra, A.; Sarath, K.S. Effect of inlet geomentory in the Quality of vortex formed using Vortex flow channel. Int. J. Mech. Eng. Technol. 2017, 8, 515–524. [Google Scholar]
- Power, C.; McNabola, A.; Coughlan, P. A Parametric Experimental Investigation of the Operating Conditions of Gravitational Vortex Hydropower (GVHP). J. Clean Energy Technol. 2015, 4, 112–119. [Google Scholar] [CrossRef] [Green Version]
- Sreerag, S.R.; Raveendran, C.K.; Jinshah, B.S. Effect of Outlet Diameter on the Performance of Gravitational Vortex Turbine with Conical Basin. Int. J. Sci. Eng. Res. 2016, 7, 457–463. [Google Scholar]
- Dhakal, S.; Nakarmi, S.; Pun, P.; Thapa, A.B.; Bajracharya, T.R. Development and Testing of Runner and Conical Basin for Gravitational Water Vortex Power Plant. J. Inst. Eng. 2014, 10, 140–148. [Google Scholar] [CrossRef] [Green Version]
- Wanchat, S.; Suntivarakorn, R.; Wanchat, S.; Tonmit, K.; Kayanyiem, P. A Parametric Study of a Gravitation Vortex Power Plant. Adv. Mater. Res. 2013, 805–806, 811–817. [Google Scholar] [CrossRef]
- Anjali Mohanan, M. Power Generation with Simultaneous Aeration using a Gravity Vortex Turbine. Int. J. Sci. Eng. Res. 2016, 7, 19–24. [Google Scholar]
- Arul Prakash, R.; Vijayanandh, R. Design Optimization of Convergent—Divergent Nozzle Using Computational Fluid Dynamics Approach. Int. J. Mech. Prod. Eng. Res. Dev. 2019, 9, 220–232. [Google Scholar]
- Shabaraa, H.M.; Yaakoba, O.B.; Yasser, M.; Ahmeda, Y.M.; Elbatrana, A.H. CFD Simulation of Water Gravitation Vortex Pool Flow for Mini Hydropower Plants. J. Sci. Eng. 2015, 74, 77–81. [Google Scholar]
- Rahman, M.M.; Tan, J.H.; Fadzlita, M.T.; Wan KhairulMuzammil, A.R. A Review on the Development of Gravitational Water Vortex Power Plant as Alternative Renewable Energy Resources. In Proceedings of the international Conference on Materials Technology and Energy, Materials Science and Engineering, Miri, Malaysia, 20–21 April 2017; p. 217. [Google Scholar]
- Yaakob, O.; Ahmed, Y.; Elbatran, A.H.; Shabara, H.M. A Review on Micro Hydro Gravitational Vortex Power and Turbine Systems. J. Teknol. 2014, 69. [Google Scholar] [CrossRef] [Green Version]
- Dhakal, S.; Timilsina, A.B.; Dhakal, R.; Fuyal, D.; Bajracharya, T.R.; Pandit, H.P. Effect of Dominant Parameters for Conical Basin: Gravitational Water Vortex Power Plant. In Proceedings of the International Conference on Technology and Innovation Management & IOE Graduate Conference, Kathmandu, Nepal, 4 October 2014. [Google Scholar] [CrossRef]
- Ersoy, S. Vortex with the Formation of Electricity Generation and System Modelling. Int. J. Environ. Sci. Dev. 2014, 5, 152–154. [Google Scholar] [CrossRef] [Green Version]
- Müller, S.; Cleynen, O.; Hoerner, S.; Lichtenberg, N.; Thévenin, D. Numerical analysis of the compromise between power output and fish-friendliness in a vortex power plant. J. Ecohydraulics 2018, 3, 86–98. [Google Scholar] [CrossRef]
- Kueh, T.C.; Beh, S.L.; Ooi, Y.S.; Rilling, D.G. Experimental study to the influences of rotational speed and blade shape on water vortex turbine performance. J. Phys. Conf. Ser. 2017, 822, 12066. [Google Scholar] [CrossRef] [Green Version]
- Nishi, Y.; Inagaki, T. Performance and Flow Field of a Gravitation Vortex Type Water Turbine. Int. J. Rotating Mach. 2017, 2017, 2610508. [Google Scholar] [CrossRef]
- Vijayakumar, M.; Vijayanandh, R.; Ramesh, M.; Senthil Kumar, M.; Raj Kumar, G.; Sivaranjani, S.; Jung, D.W. Conceptual Design and Numerical analysis of an Unmanned Amphibious Vehicle. In Proceedings of the AIAA Scitech2021 Forum, Online, 11–15 & 19–21 January 2021. [Google Scholar]
- Salazar-Marín, E.A.; Rodríguez-Valencia, A.F. Design, assembly and experimental tests of a Savonius type wind turbine. Sci. Technol. 2019, 24, 397–407. [Google Scholar] [CrossRef]
- Kumar, M.S.; Krishnan, A.S.; Vijayanandh, R. Computational, Experimental and Surface Characterisation of Glass Fibre Reinforced Plastic Composite for Wind Turbine Blade Application. J. Environ. Prot. Ecol. 2021, 22, 602–616. [Google Scholar]
- Carlton, J.S. Marine Propellers and Propulsion, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2007; Volume 12, pp. 435–458. ISBN 978-07506-8150-6. [Google Scholar]
- Vijayanandh, R.; Kumar, M.S.; Rahul, S.; Thamizhanbu, E.; Jafferson, M.D.I. Conceptual Design and Comparative CFD Analyses on Unmanned Amphibious Vehicle for Crack Detection. Int. Conf. Unmanned Aer. Syst. Geomat. 2020, 51, 133–149. [Google Scholar] [CrossRef]
- Praveen Kumar, V.; Kishor Kumar, S.; Sankaresh Pandian, K.R.; Ashraf, E.; Thanga Tamil Selvan, K.; Vijayanandh, R. Conceptual Design And Hydrodynamic Research On Unmanned Aquatic Vehicle. Int. J. Innov. Technol. Explor. Eng. 2019, 8 (Suppl. 11), 121–127. [Google Scholar] [CrossRef]
- Vijayanandh, R.; Kiran, P.; Prasanth, S.I.; Kumar, G.R.; Balaji, S. Conceptual Design and Optimization of Flexible Landing Gear for Tilt-Hexacopter Using CFD; Springer: Cham, Switzerland, 2020; pp. 151–174. [Google Scholar] [CrossRef]
- Raja, V.; Solaiappan, S.K.; Rajendran, P.; Madasamy, S.K.; Jung, S. Conceptual Design and Multi-Disciplinary Computational Investigations of Multirotor Unmanned Aerial Vehicle for Environmental Applications. Appl. Sci. 2021, 11, 8364. [Google Scholar] [CrossRef]
- Vijayanandh, R.; Venkatesan, K.; Kumar, R.R.; Kumar, M.S.; Jagadeeshwaran, P. Theoretical and Numerical Analyses on Propulsive Efficiency of Unmanned Aquatic Vehicle’s Propeller. J. Phys. Conf. Ser. 2020, 1504, 12004. [Google Scholar] [CrossRef]



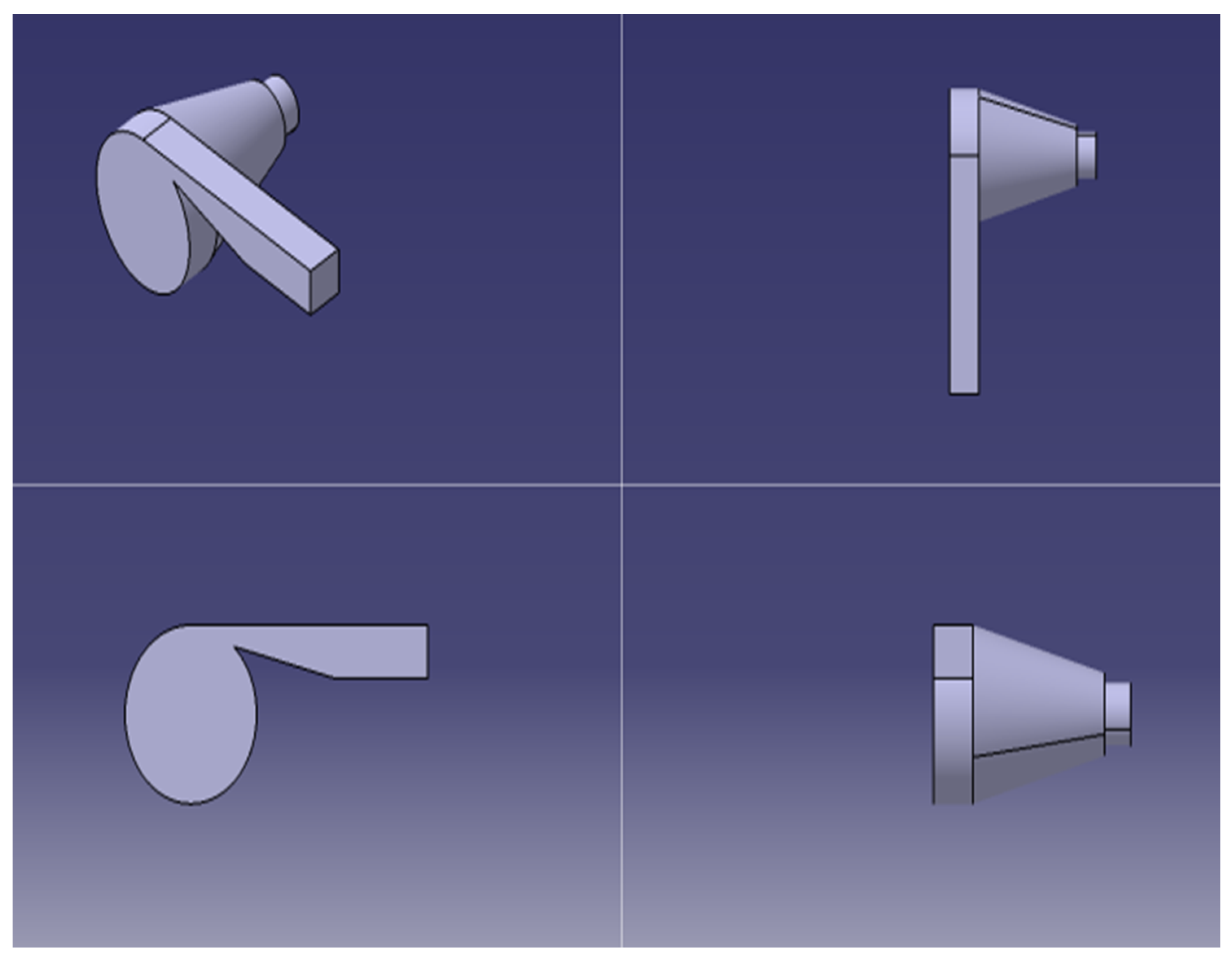
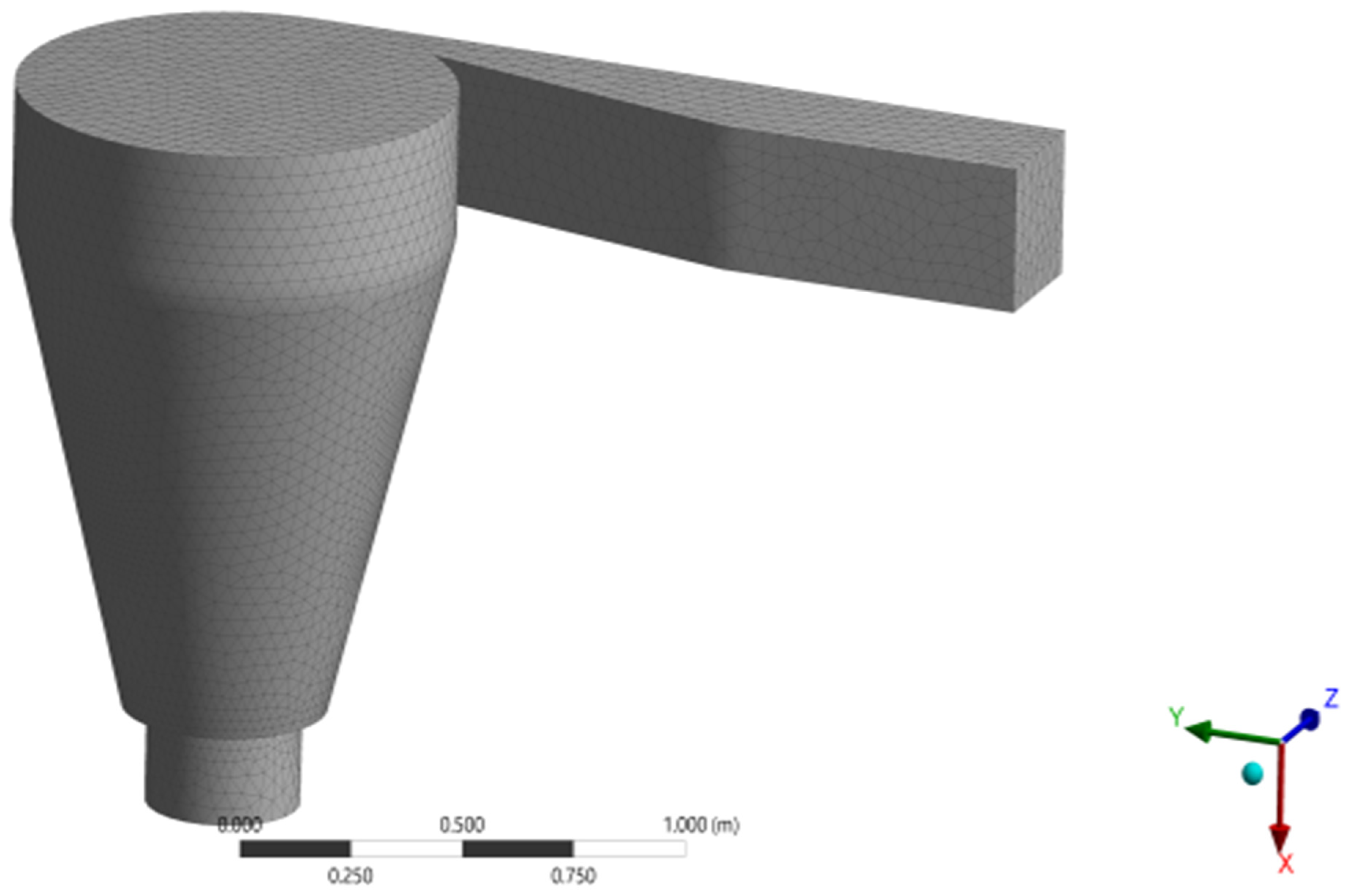
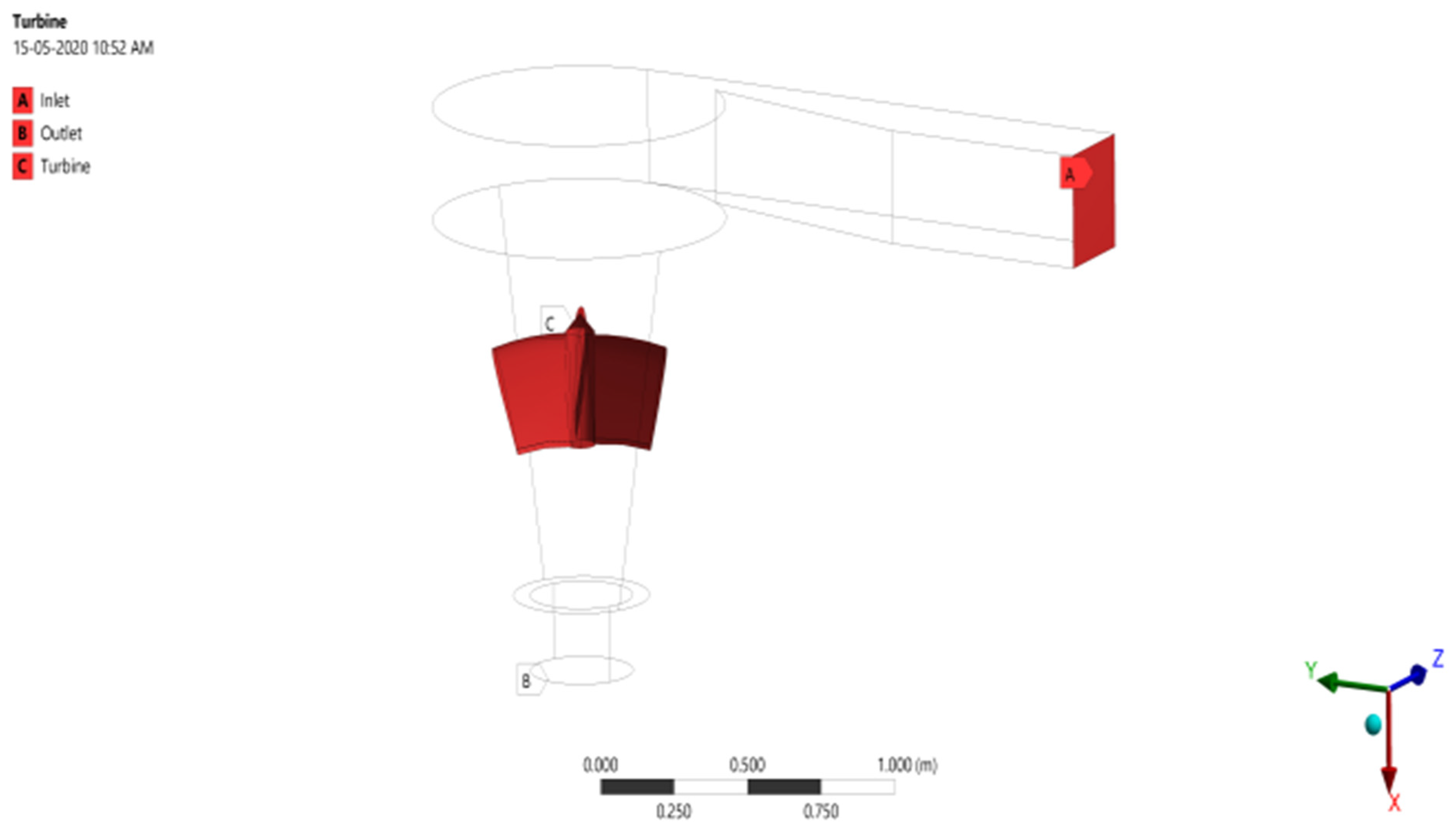
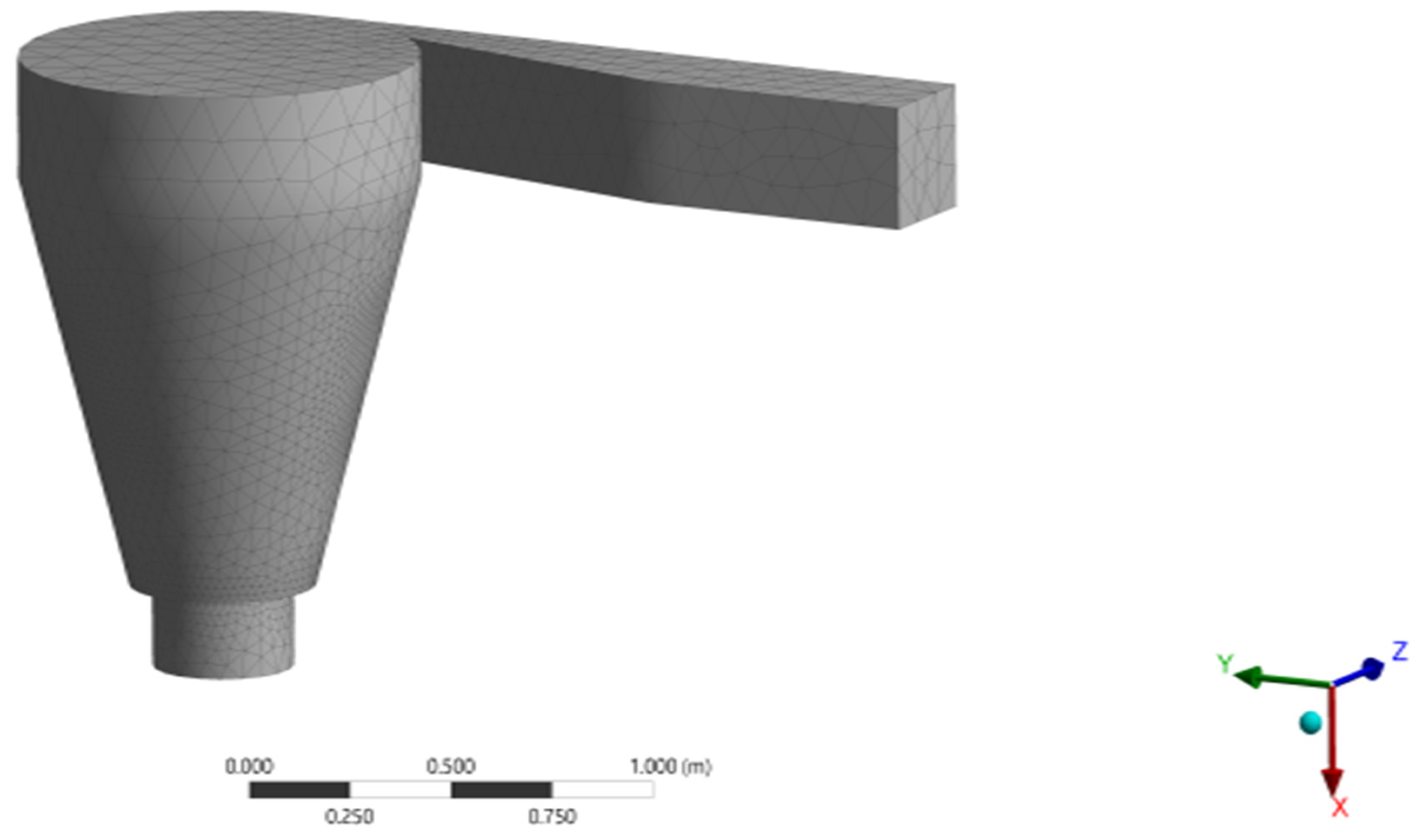







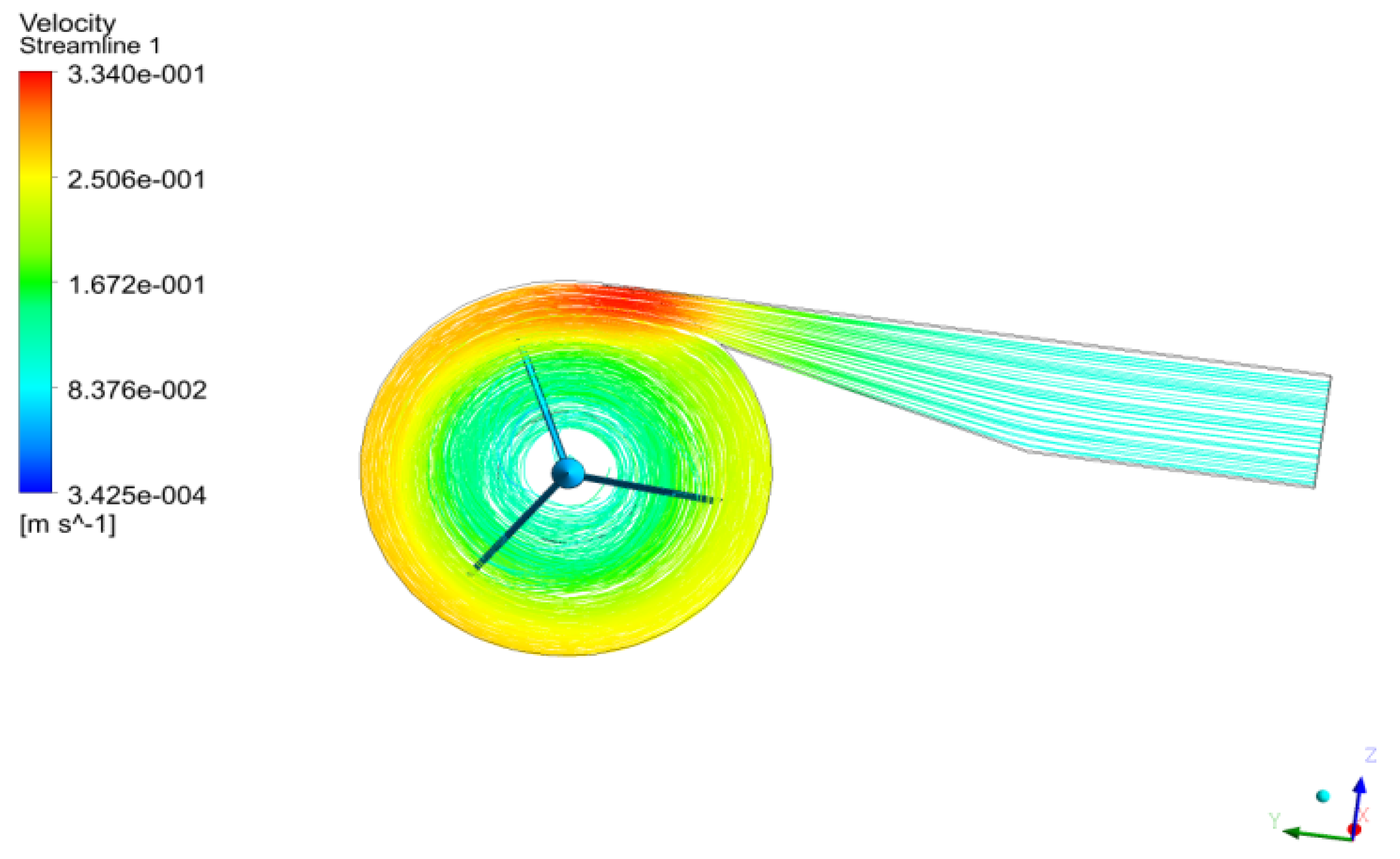
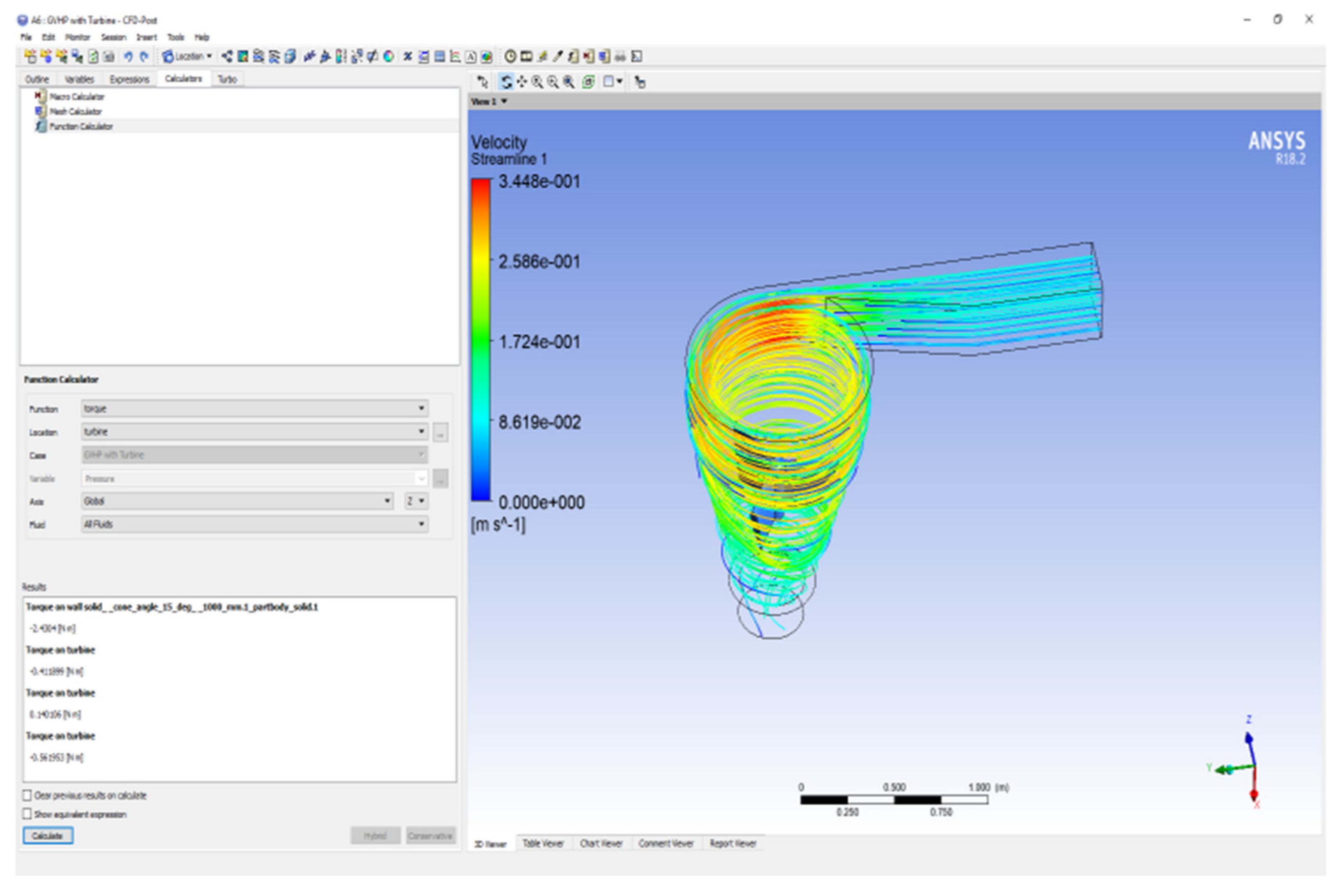

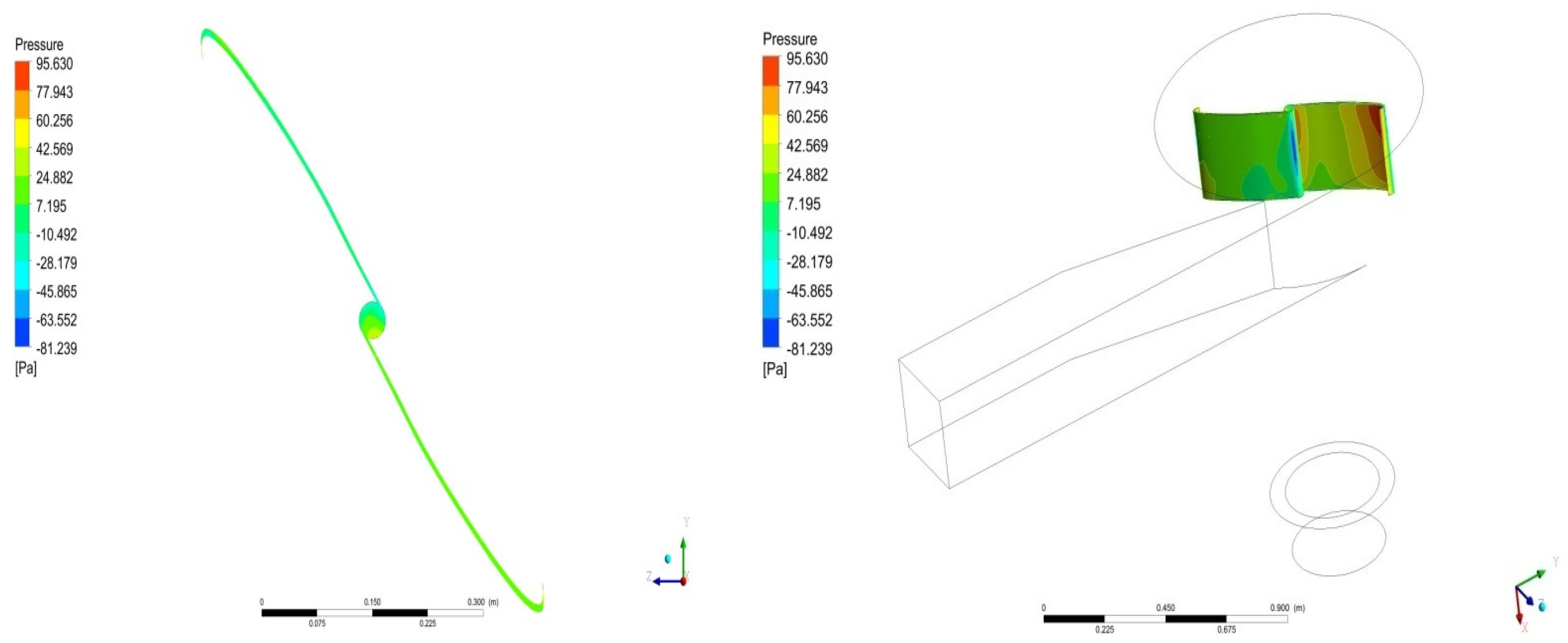
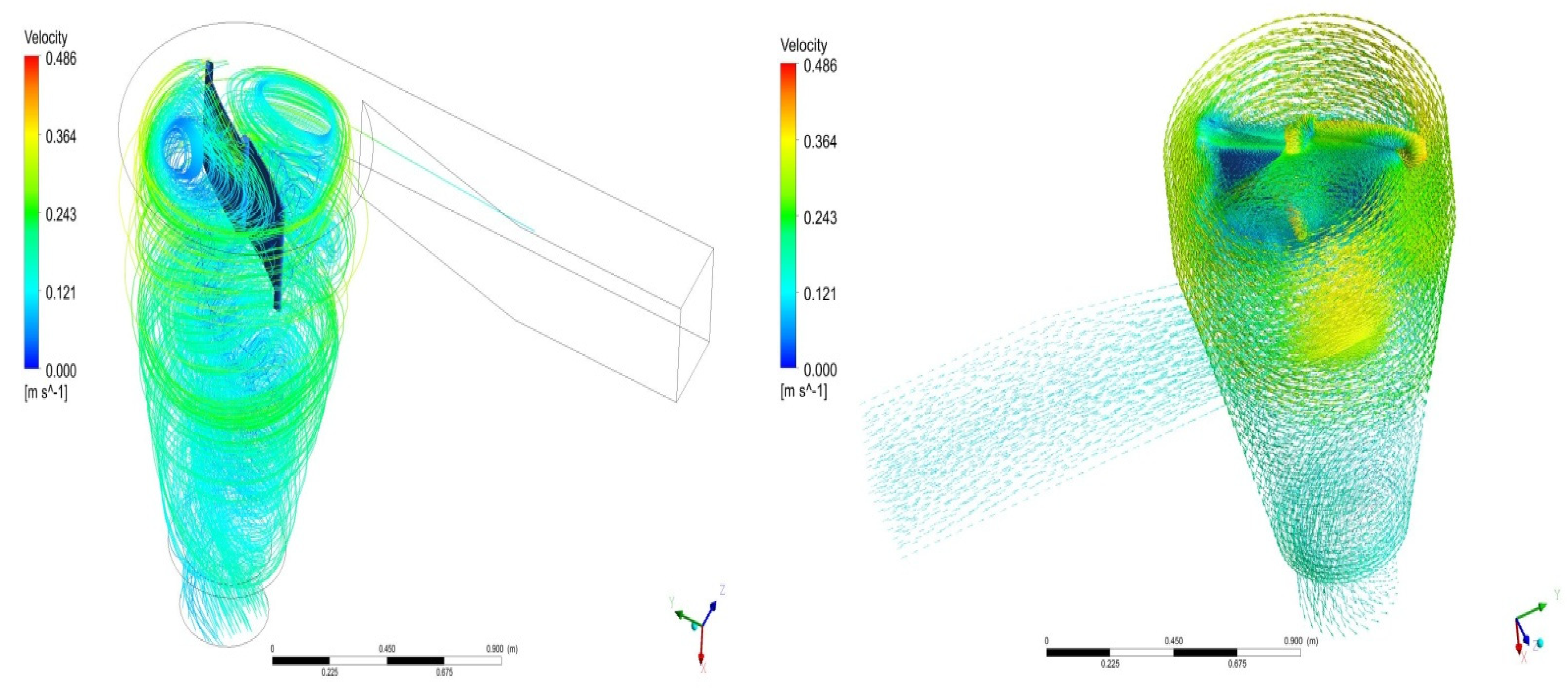


| Symbol | Meaning |
|---|---|
| Hydrostatic velocity (m/s) | |
| D | Diameter of the hydro-rotor (m) |
| r | Radius of the hydro-rotor (m) |
| Sectional radius of the hydro-rotor (m) | |
| Pitch of the hydro-rotor (m) | |
| Pitch angle (degree) | |
| Coefficient of lift of hydro-rotor (no unit) | |
| b | Chord length of the hydro-rotor (m) |
| N | Angular velocity (RPM) |
| Q | Torque of the rotor (Nm) |
| P | Power extracted by the rotor (watts) |
| T | Thrust force (Newtons) |
| A | Area of the hydro-rotor (m2) |
| ρ | Density of ocean water (1025 kg/m3) |
| Induced velocity (m/s) | |
| PDeliver | Delivered power (watts) |
| Vmsa | Mean speed of advance (m/s) |
| Bp | Power coefficient (no unit) |
| λOptimum | Hydro-rotor speed coefficient(no unit) |
| DOptimum | Optimum diameter of the hydro-rotor (m) |
| n | Number of blades in hydro turbine (no unit) |
| Expanded area ratio (no unit) | |
| Tip ratio (no unit) | |
| αA | Angle of attack (degree) |
| Rotational velocity (rad/s) | |
| e | Overlap distance (m) |
| d | Diameter of the single blade (m) |
| h | Height of the hydro-rotor (m) |
| Endplate diameter (m) | |
| PH | Hydropower (watts) |
| AS | Swept area of the Savonius hydro-rotor (m2) |
| Mesh Cases | Type of Mesh | Nodes | Elements |
|---|---|---|---|
| 1 | Coarse | 82,391 | 452,032 |
| 2 | Medium | 86,525 | 473,892 |
| 3 | Fine | 94,475 | 514,421 |
| 4 | Fine with face mesh on turbine | 95,894 | 514,665 |
| 5 | Fine with inflation on turbine | 123,100 | 985,742 |
| 6 | Fine with face mesh and inflation on turbine | 187,542 | 1,412,566 |
| Design Details | Experimental Result | Computational Result | Error Percentage |
|---|---|---|---|
| Convex–GVHP | 0.23 W | 0.2421 | 4.99 |
| Concave–GVHP | 0.37 W | 0.371737 | 0.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Raji, A.P.; Raja, V.; Wang, F.; AL-bonsrulah, H.A.Z.; Murugesan, R.; Ranganathan, S. Multi–Disciplinary Optimizations of Small-Scale Gravitational Vortex Hydropower (SGVHP) System through Computational Hydrodynamic and Hydro–Structural Analyses. Sustainability 2022, 14, 727. https://doi.org/10.3390/su14020727
Jiang Y, Raji AP, Raja V, Wang F, AL-bonsrulah HAZ, Murugesan R, Ranganathan S. Multi–Disciplinary Optimizations of Small-Scale Gravitational Vortex Hydropower (SGVHP) System through Computational Hydrodynamic and Hydro–Structural Analyses. Sustainability. 2022; 14(2):727. https://doi.org/10.3390/su14020727
Chicago/Turabian StyleJiang, Yingzi, Arul Prakash Raji, Vijayanandh Raja, Fuzhang Wang, Hussein A. Z. AL-bonsrulah, Ramesh Murugesan, and Sudhakaran Ranganathan. 2022. "Multi–Disciplinary Optimizations of Small-Scale Gravitational Vortex Hydropower (SGVHP) System through Computational Hydrodynamic and Hydro–Structural Analyses" Sustainability 14, no. 2: 727. https://doi.org/10.3390/su14020727
APA StyleJiang, Y., Raji, A. P., Raja, V., Wang, F., AL-bonsrulah, H. A. Z., Murugesan, R., & Ranganathan, S. (2022). Multi–Disciplinary Optimizations of Small-Scale Gravitational Vortex Hydropower (SGVHP) System through Computational Hydrodynamic and Hydro–Structural Analyses. Sustainability, 14(2), 727. https://doi.org/10.3390/su14020727









