Study of Transformer Harmonic Loss Characteristic in Distribution Network Based on Field-Circuit Coupling Method

Abstract

One of the primary causes of additional losses in dry-type distribution transformers is harmonic disturbances in the distribution network. It is critical to investigate the change law of trans-former losses under harmonic conditions. The effect of harmonics on transformer core losses and winding losses is first investigated in this paper. The field-circuit coupling method is then used to create a finite element model of a three-phase phase dry type distribution transformer. Finally, the relationship between core loss and harmonic voltage, winding loss and harmonic current is calculated and analyzed for each harmonic frequency. The AC resistance factor model is found to be more accurate than the conventional model in calculating transformer harmonic winding losses. This paper’s findings have significant theoretical implications for the analysis of harmonic losses and loss reduction in distribution networks.

1. Introduction

The transformer is an important piece of transmission and distribution equipment in the power system, and there is a significant amount of loss. Transformer losses account for approximately 8% of total power generation capacity in China’s power grids. Dry type distribution transformer losses account for 60% to 80% of total distribution network losses [1,2,3]. The efficiency of the transformer is directly related to the efficiency of the grid’s power conversion and is an important economic indicator for electrical energy transmission. The power characteristics of distributed power generation and the diversity of loads in the new type of distribution network can cause power quality pollution in the distribution network, such as harmonics, three-phase voltage imbalance, voltage fluctuations, and flicker. Distributed power generation degrades distribution network power quality and increases distribution network losses [4]. As a result, an in-depth examination of transformer loss calculation under power quality disturbance is extremely useful in reducing network losses and optimizing distribution network structure. The abbreviations involved in this paper are shown in Table 1.

Table 1. An explanation of the parameters and variables used in this paper.

Abbreviation	Transformer Parameters (Nameplate Value)
PTL	Total theoretical transformer losses
PNL	No-load core loss
PLL	Load winding losses
$B_m$	Working flux density amplitude of silicon steel sheet
n	Hysteresis coefficient, generally 2 to 2.5
t	Thickness of silicon steel sheet
G	Core quality
$p_F$	Additional losses in the iron core
$P_{I^{2}R}$	Transformer winding resistance losses
$P_{EC}$	Eddy current losses in windings
$P_{OSL}$	Additional losses due to winding skin effect and proximity effect
$K_h$	Hysteresis loss factor
$K_c$	Eddy current loss factor
Em	Transformer induced electromotive force amplitude
N	Number of winding turns
A	Effective cross-sectional area of the iron core
h	Number of harmonics
Rdc	Windings DC resistance
${\delta }_h$	$\mathrm{hth}\mathrm{harmonic}\mathrm{winding}\mathrm{skin}\mathrm{depth},{\delta }_h=\sqrt{2/{\omega }_h\mu \sigma }$
$\sigma$	Electrical conductivity of copper conductors
$\mu$	Copper conductor magnetic permeability
${\omega }_h$	Angular frequency of the hth harmonic
P	Number of winding layers
d	Thickness of each layer of silicon steel sheet
A	Vector magnetic position
JS	Source current density
v	Magnetoresistivity
S	Cross-sectional area of windings
h	Coil tangent direction unit vector
$\mathsf{\Omega }$	Three-phase transformer core area

The equivalent model method, the parametric method, and the harmonic factor method are the three main analytical methods for calculating transformer harmonic losses. This paper [5] compares six commonly used transformer harmonic equivalent models and validates the applicability of the currently used transformer harmonic simplification models. In the literature [6], a transformer harmonic loss model based on circuit theory was developed to derive a formula for calculating transformer harmonic loss. However, the harmonic winding resistance model $\sqrt{h}{R}_{dc}$ in this model has errors at high frequency harmonics. In the IEEE Std C57.110 standard [7] the correction method for eddy current losses and additional losses in transformer windings under harmonics is proposed. In this standard the concept of harmonic lead-in is introduced, but harmonic winding ohmic losses are not corrected. In the literature [8], the concept of AC resistance factor $1+\frac{\mathsf{\Psi }}{3}{\Delta }^4$ is proposed for improving the harmonic winding AC resistance formula, the accuracy of which is yet to be verified.

Numerical models are frequently used to solve such problems in order to obtain an accurate model for calculating transformer losses under harmonic conditions. In terms of the means and accuracy with which the problem can be solved, the numerical method outperforms the analytical method. Because of its high computational accuracy and ability to adapt to various complex shapes, the finite element method has become a proven analytical tool in engineering. Several researchers used the finite element method of field-path coupling to model the two-dimensional structure of the transformers used. In the literature [9,10], researchers have analysed the leakage field distribution and the influence of harmonic currents on harmonic losses. The Finite element analysis software ANSYS was used to build a simplified two-dimensional simulation model of the leakage field of the transformer, but the two-dimensional model simulation is subject to some errors with respect to the actual operating conditions [11]. A 3D simulation model of the transformer electric-magnetic-structural force field was established in [12], which basically matched the simulation results with the test data to verify the effectiveness of the 3 D finite element method. The Steinmetz model was used in [13] to investigate the magnetic loss characteristics of transformers. The effect of harmonic characteristic quantities on the core loss characteristics was investigated using the generalised Steinmeth model, and the simulation results demonstrated that the method has a high degree of computational accuracy. Furthermore, using the field-circuit coupling method and a finite element model, the loss characteristics of a high-voltage DC converter transformer, a filter transformer, a harmonic filter distribution transformer, and a high-speed permanent magnet generator were simulated. The method’s validity was established [14,15,16,17,18,19,20]. Kamran Dawood et al. [21] proposed a method for determining the leakage impedance in the tap winding using finite elements. For all cases, the difference between the finite element models and the experimental short-circuit test was less than 1%. A design method for economical, low harmonic loss distribution transformers is presented in the paper [22]. Yazdani-Asrami et al. [23] used the finite element method (FEM) to simulate and analyze the effect of non-sinusoidal voltages on distribution transformer no-load losses. The simulation results show that increasing the THD of distorted voltage will significantly increase the transformer’s no-load loss. In literature [24], an analytical algorithm for calculating the hysteresis losses of three-phase HTS transformer windings in the presence of harmonic loads is presented and the results show that this algorithm is highly accurate. Susnjic et al. [25] used 3D FE analysis to calculate eddy current losses in power transformers generated in yoke ply-wood and unshielded tank walls. A numerical study of copper losses in three-phase transformers with different geometrical designs was carried out using the finite element method by Chiu et al. [26]. The results show that the eddy currents in the windings cause additional losses. The non-sinusoidal AC losses of coils have been studied using the finite element method by M. Yazdani–Asrami et al. [27]. The results of the study have important implications for the design of HTS transformers and HTS power cables.

The effect of harmonic voltage and harmonic current on the iron and copper losses of transformers is investigated in this paper. An analytical calculation model for transformer iron and copper losses under harmonic action is developed. A three-phase 10 kV transformer model is created using a field-circuit coupled model and a finite element simulation model to calculate transformer core and winding losses, and the effects of harmonic voltages and currents are quantified.

2. Transformer Loss Model

The losses in transformers can be divided into: iron losses, copper losses, dielectric losses and miscellaneous losses. In this paper the losses in the transformer core and windings under harmonic action are discussed. According to the Steinmetz empirical formula and the IEEE Std C57.110 standard, the total losses of a transformer can be expressed as the sum of the transformer no-load core losses and the load winding losses, as shown in Equation (1).

$$P_{TL}=\underset{P_{NL}}{\underbrace{(k_{1}f{B}_m^n+k_2{f}^2{B}_m^2{t}^2)\cdot G+p_F}}+\underset{P_{LL}}{\underbrace{P_{I^{2}R}+P_{EC}+P_{OSL}}}$$

(1)

where P_TL is the total theoretical loss of transformer, including no-load core loss P_NL and P_LL. f is the current frequency. B_m is the silicon core working flux density amplitude. n is hysteresis coefficient which equals to 2~2.5. t is silicon wafer thickness. k₁ and k₂ depend on the characteristics of silicon steel, which can be obtained from experiments [13]. G is the core mass. $k_{1}f{B}_m^n$ is the unit core magnetic loss. $k_2{f}^2{B}^2{t}^2$ is the unit core vortex loss. p_F is core additional loss and its’ proportion is relatively small. P_EC is the transformer winding resistance loss and P_OSL is the additional loss caused by winding skin effect and adjacent effect.

2.1. Transformer Core Harmonic Loss

According to Equation (1), the unit core loss part of the transformer can be characterized as:

$$P_{NL}=k_{1}f{B}_m^n+k_2{f}^2{B}_m^2{t}^2+{p^{\prime }}_F$$

(2)

where, k₁ and k₂ can be characterized by the core hysteloss coefficient Kh and the core vortex loss coefficient K_c, respectively, which are only dependent on the core material. n is the hysteresis coefficient, generally taken as 2, ${p^{\prime }}_F$ unit additional core loss.

Because:

$$B_m=\frac{E_m}{4.44fNA}$$

(3)

where, E_m is the induced motive potential amplitude of transformer, which is positively correlated with the primary side voltage of the transformer. N is winding turns. A is effective cross-sectional area of the transformer core.

The unit core loss of a transformer under single harmonics can be calculated according to the following formula [28]:

$$P_{NL}=\frac{E_{mh}^2}{{4.44}^2{N}^2{A}^2}(\frac{K_h}{f}+K_c{t}^2)+{p^{\prime }}_F$$

(4)

Then, the unit core loss of the transformer under multiple harmonics can be carried out as [29]:

$$P_{NLh}=\frac{1}{{4.44}^2{N}^2{A}^2}{\displaystyle \sum _{h=2}^{h_{\max }}{E}_{mh}^2(\frac{K_h}{f}+K_c{t}^2)}+{p^{\prime }}_F$$

(5)

According to Equation (5), the transformer core hysteresis loss increases with the increase of the primary harmonic voltage content and decrease with the increase of the harmonic frequency. The vortex loss also increases with the primary harmonic voltage content. As the additional losses are relatively small and do not affect the trend of no-load losses with frequency, they are treated as constant values that do not vary with frequency in the theoretical calculations in this paper.

2.2. The Winding Harmonic Loss

The T-type equivalent model is often used to simulate the transformer working principle when analyzing the transformer winding harmonic loss, and the transformer harmonic winding resistance is usually equivalent to $\sqrt{h}$R_dc (h is the harmonic order, R_dc is the winding DC resistance) in order to calculate the transformer winding resistance loss $P_{I_h{}^{2}R}$ and vortex loss $P_{ECh}$. The external power supply can be regarded as the superposition of independent sources of different harmonic components when calculating the transformer loss by using T-type equivalent model, as shown in Figure 1.

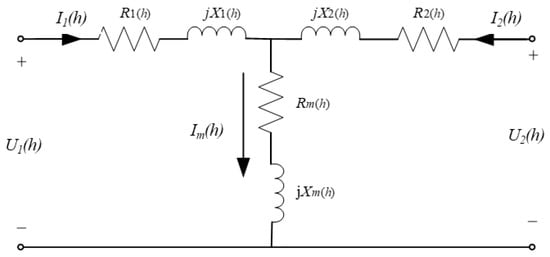
Figure 1. A T-type equivalent circuit model.

In Figure 1, h is the harmonic order and I_1(h) is the primary side harmonic current. I_2(h) is the harmonic current on the secondary side of the transformer. R_1(h) and X_1(h) are the transformer primary side winding resistance and leakage resistance under the h-th harmonic action. R_2(h) and X_2(h) are the resistance and reactance of the secondary side winding of the transformer under the h-th harmonic. R_m(h) and X_m(h) are the excitation impedance and excitation resistance of the transformer under the h-th harmonic.

When using the T-transformer equivalent loss model equivalent circuit, R_(h) is calculated using $\sqrt{h}$R_dc for equivalence. Harmonic reactance is a quantity proportional to frequency, so it is easy to obtain jX_(h) = jhX₍₁₎. The active power loss of the transformer primary side harmonic winding can be calculated as:

$$P_{LLh1}={\displaystyle \sum _{h=2}^{h_{\max }}{\left|\frac{{\stackrel{·}{U}}_{1(h)}-{\stackrel{·}{I}}_{m(h)}(R_{m(h)}+j{X}_m{}_{(h)})}{R_{1(h)}+j{X}_{1(h)}}\right|}^2{R}_{1(h)}}={\displaystyle \sum _{h=2}^{\infty }{I}_{1(h)}^2{R}_{1(h)}}$$

(6)

Similarly, the active power loss of the secondary side harmonic winding is:

$$P_{LLh2}={\displaystyle \sum _{h=2}^{h_{\max }}{\left|\frac{\frac{1}{k}{\stackrel{·}{I}}_{m(h)}(R_{m(h)}+j{X}_{m(h)})-{\stackrel{·}{U}}_{2(h)}}{R_{2(h)}+j{X}_{2(h)}}\right|}^2{R}_{2(h)}}={\displaystyle \sum _{h=2}^{\infty }{I}_{2(h)}^2{R}_{2(h)}}$$

(7)

$$k=\frac{N_1}{N_2}$$

(8)

where, N₁ and N₂ are the number of primary and secondary turns of the transformer respectively. k is the ratio of turns. Then the calculation relation of harmonic winding loss of three-phase transformer is as follows:

$$P_{Th}=3(P_{LLh1}+P_{LLh2})$$

(9)

Equations (6) and (9) shows that when the harmonic voltage acts on the transformer the excitation reactance of the transformer increases, so the current value ${\stackrel{·}{I}}_{m(h)}$ value is very small. Therefore this item ${\stackrel{·}{I}}_{m(h)}(R_{m(h)}+j{X}_m{}_{(h)})$ can be neglected. The harmonic current produces harmonic losses directly in the winding resistance, which increases the winding losses. Therefore, the transformer harmonic winding losses are mainly related to the harmonic current.

However, the $\sqrt{h}$R_dc model does not consider the loss $P_{OSL}$ resulting from the winding skin effect and the proximity effect on the winding resistance. The AC resistance coefficient $1+(\mathsf{\Psi }/3){\Delta }^4$ model was proposed in [7] to accurately express the transformer harmonic winding loss.

$$R_{(h)}=(1+\frac{\mathsf{\Psi }}{3}{\Delta }^4)R_{dc}$$

(10)

$$\mathsf{\Psi }=\frac{5p^2-1}{15}$$

(11)

where, R_(h) is the h-th harmonic winding AC resistance, and R_dc is the winding DC resistance. $\Delta =d/{\delta }_h$ ${\delta }_h=\sqrt{2/{\omega }_h\mu \sigma }$ is the skin effect depth of the h-th harmonic winding. Σ and μ are the electrical conductivity and magnetic conductivity of the copper wire, respectively. p is the number of winding layers. D is the thickness of each silicon steel sheet and ω_h is the angular frequency of the h-th harmonic.

Then, the modified three-phase transformer is as follows:

$$P_{Th}=3{\displaystyle \sum _{h=2}^{h_{\max }}{\left|\frac{\stackrel{·}{U_{1(h)}}}{(1+\frac{\mathsf{\Psi }}{3}{\Delta }^4)R_{dc}+jhX}\right|}^2(1+\frac{\mathsf{\Psi }}{3}{\Delta }^4)R_{dc}}={\displaystyle \sum _{h=2}^{\infty }{I}_{1(h)}^2(1+\frac{\mathsf{\Psi }}{3}{\Delta }^4)R_{dc}}$$

(12)

An actual 630 kVA transformer is used as an example [30]. The transformer has a winding layer of 36, a silicon steel sheet thickness of 1.2 mm and a transformer winding DC resistance of 0.91 Ω. The resistive frequency characteristics of the transformer’s harmonic winding model are shown in Figure 2.

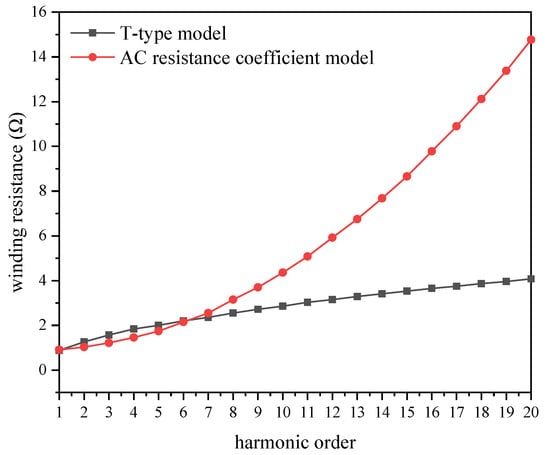
Figure 2. Winding harmonic resistance characteristics.

When the harmonic frequencies are very low, the angular frequency values ${\omega }_h$ of the harmonics are very low. From equations ${\delta }_h=\sqrt{2/{\omega }_h\mu \sigma }$ and $\Delta =d/{\delta }_h$, the value of $\Delta$ is very small. Therefore the value of ${\Delta }^4$ is negligible. The h-th harmonic winding AC resistance R_(h) is very close to $\sqrt{h}$R_dc. At low frequencies the skin effect and the proximity effect on the AC resistance are negligible, so it can be seen from 2 that the two resistance models are a good fit at this time. However, as the frequency increases, the value of ${\Delta }^4$ increases very significantly. $\sqrt{h}$R_dc more slowly as the frequency increases. The effect of the skin effect and the proximity effect caused by the leakage field on the harmonic resistance of the winding becomes progressively greater, and the size of the harmonic resistance of the winding as characterised by the two models appears to vary considerably. It is easy to see from Equation (12) that the two models will produce a large difference in the calculation of the transformer’s harmonic current winding losses.

3. The Field-Circuit Coupling Model

In order to analyze the accuracy of the transformer model described above, the field-road coupling theory is applied to establish the transformer finite element model and solve the transformer loss by numerical method. Vector magnetic position A and scalar potential Φ are introduced to the Maxwell equations to form independent electric field and magnetic field partial differential equations:

$$\left\{\begin{array}{l}B=\nabla \times A\\ E=-\nabla \varphi \end{array}\right.$$

(13)

Taking the equation into the Maxwell equations yields the independent magnetic field and electric field partial differential equations:

$$\left\{\begin{array}{l}{\nabla }^{2}A-\mu \epsilon \frac{{\partial }^{2}A}{\partial t^2}=-\mu J_S\\ {\nabla }^2\varphi -\mu \epsilon \frac{{\partial }^2\varphi }{\partial t^2}=-\frac{\rho }{\epsilon }\end{array}\right.$$

(14)

Matrix form of the field control equations for in 3 D transient field-circuit coupling calculation is shown in Equation (15) [31].

$$v\nabla \times \nabla \times A+v\nabla ·\nabla ·A+\sigma \nabla \varphi +\frac{\partial A}{\partial t}\sigma -J_S=0$$

(15)

where, A is vector magnetic position. $J_S$ is source current density. $v$ is reluctivity.

The calculation of $J_S$ can be based on the following formula:

$$J_S=\frac{N}{S}i(t)\cdot h$$

(16)

where, N is number of turns of winding. S is the cross section of the winding. h is unit vector along the coil tangent direction.

The equivalent model by coupling calculation of the circuit and the electromagnetic field is shown in Figure 3. R_e characterizes the core vortex loss, and the hysteresis loop characterizes the hysteresis loss generated during the change of the core magnetic field.

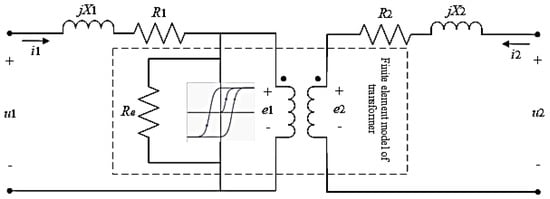
Figure 3. An equivalent circuit diagram of the field−coupling model.

The circuit control equation is:

$$u=iR+L\frac{di}{dt}+e$$

(17)

$$e=\frac{N}{S}\frac{\partial }{\partial t}{\displaystyle {\int }_{\mathsf{\Omega }}Ahd\mathsf{\Omega }}$$

(18)

where, Ω is the core area of three-phase transformer.

By solving the differential equation of Equations (15)–(19), the field-circuit coupling calculation of the three-dimensional model can be realized.

4. Simulation and Discussion

The three-dimensional transformer core and winding finite element model is established based on the SCB10-630/10 step-down dry-type transformer commonly used in the distribution network to simulate and calculate the internal electromagnetic process of the transformer. An external circuit is set up to implement the calculation of the coupling between the circuit and the magnetic field. The model does not take into account the losses in the pull plates, clamps and leads. It is also assumed that the dry type distribution transformer consists of the core, yoke, high and low voltage windings, insulating resin and surrounding air.

A schematic diagram of the transformer is shown in Figure 4.

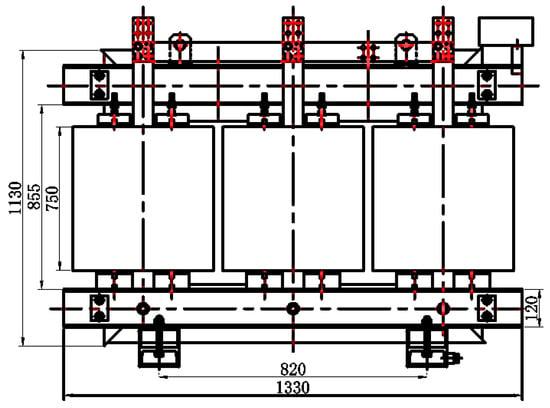
Figure 4. A schematic diagram of a 630/10 transformer (unit: mm).

To obtain the transformer parameters, a three-dimensional finite element model of the transformer is established based on the transformer data (Table 2). To ensure that the transformer leakage field is included in the simulation, the simulation space boundary exceeds 50% of the transformer’s 3D model. Each simulation’s finite element values do not exceed 5% of the actual values. The simulation step size is set to one-twentieth of the excitation source period, and the simulation stop time is set to ensure that all parameters converge.

Table 2. The transformer parameters.

Parameter	Transformer Parameters (Nameplate Value)	Finite Element Simulation Values
capacity	630 kV·A	625.39 kV·A
Rated voltage	10/0.4 kV	9.83/0.388 kV
Connection group number	Yyn0	Yyn0
No-load loss	≤1.36 kW	1.01 kW
Load loss (120 °C)	≤5.88 kW	5.43 kW
Short-circuit impedance voltage Uk%	4.0%	4.3%

Figure 5 shows the 3D finite element simulation model of the transformer, and Table 2 shows the transformer parameters.

Figure 5. A 3D finite element model of the transformer (unit: mm).

The finite element model is a more idealised approximate model. Because the no-load loss of the model only considers the core eddy current loss and hysteresis loss, and ignores the silicon steel sheet interlayer loss. There are some errors with the actual transformer nameplate losses, but the short-circuit impedance is close to the real transformer. Therefore, the simulation results of the model have some reference value.

4.1. Transformer No-Load Loss Analysis

Simulated no-load tests are carried out on a finite element transformer model using a field-circuit coupled model, and no-load test simulation results are obtained. The secondary side of the transformer is disconnected and the primary side of the transformer is added to inject the fundamental rated voltage and the 5th harmonic respectively. The time domain waveforms of the fundamental no-load loss and 5th harmonic no-load loss of the transformer obtained from the simulation are shown in Figure 6.

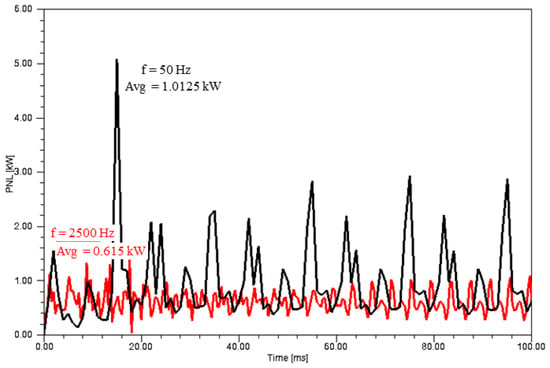
Figure 6. The time domain waveform plot of transformer no-load loss.

From Figure 6, the average value of the 5th harmonic no-load loss is less than that of the fundamental no-load loss, which is in accordance with the analysis result in Section 2.1. Since the no-load loss is mainly the core loss, the transformer core loss density distribution map obtained according to the field-circuit coupling method simulation is shown in Figure 7.

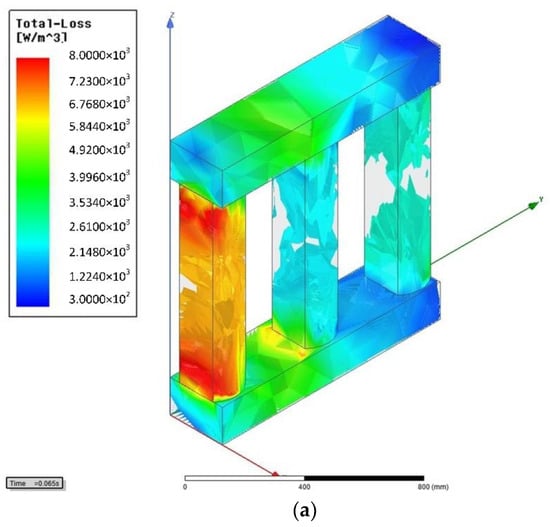
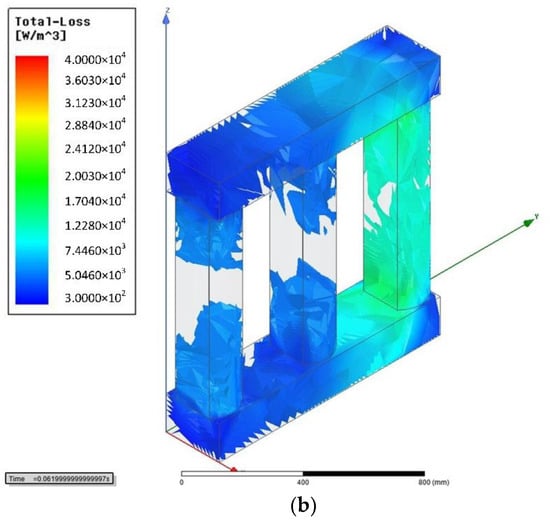
Figure 7. (a) Fundamental harmonic core loss density distribution map; (b) 5th harmonic core loss density distribution. Transformer no-load loss density distribution.

Figure 7a shows the fundamental harmonic core loss density distribution map and 7b shows the 5th harmonic core loss density distribution, respectively. It can be seen that when one transformer phase is at the peak voltage, the loss density of the transformer core acting under the fundamental harmonic voltage is greater than that of under 5th harmonic.

By varying the frequency of harmonics, the average core loss under the 5th, 7th, 11th, 13th, 17th, and 19th harmonic obtained by the field-circuit coupling method are shown in Table 3. The hysteresis loss and eddy current loss in Table 3 are plotted and are shown in Figure 8.

Table 3. The average core loss under harmonic voltage (kW).

h	Hysteresis Loss	Eddy Current Loss	Total Core Loss
Fundamental	0.4844	0.4031	1.013
5	0.1102	0.3825	0.615
7	0.0629	0.3769	0.562
11	0.0403	0.3714	0.537
13	0.0336	0.3651	0.521
17	0.0249	0.3597	0.503
19	0.0199	0.3525	0.484

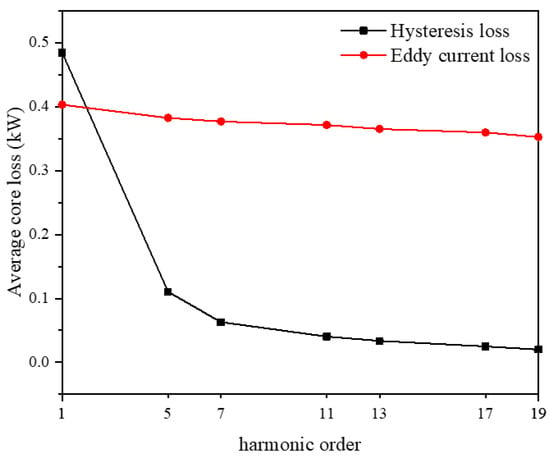
Figure 8. The core loss harmonic.

Figure 8 shows that the simulated core hysteresis loss decreases as the no-load voltage frequency increases, while the core eddy current loss varies only slightly with frequency. The movement of the magnetic do-mains in the core material causes hysteresis losses in the core. The core hysteresis losses from the 5th, 7th, 11th, 13th, 17th, and 19th harmonics are all smaller than the fundamental core hysteresis losses, as shown in Figure 8. The hysteresis loss decreases as the frequency of the no-load voltage increases, demonstrating that the losses caused by magnetic domain movement are inversely proportional to the frequency of change of the magnetic field inside the transformer core. The core eddy current losses are mainly dependent on the magnitude of the induced electric potential, which varies very little with frequency.

Equation (5) is used to calculate the theoretical transformer core loss and is compared to the simulated value as shown in Table 4 and Figure 9.

Table 4. A comparison of calculated and simulated results at no load and errors. (Absolute values).

h	Calculation Result	Simulation Result	Error
Fundamental	1.237	1.013	22.4%
3	0.895	0.808	8.7%
5	0.553	0.615	6.2%
7	0.519	0.562	4.3%
9	0.490	0.550	6%
11	0.472	0.537	6.2%
13	0.464	0.521	5.7%
15	0.454	0.509	5.5%
17	0.449	0.484	3.5%

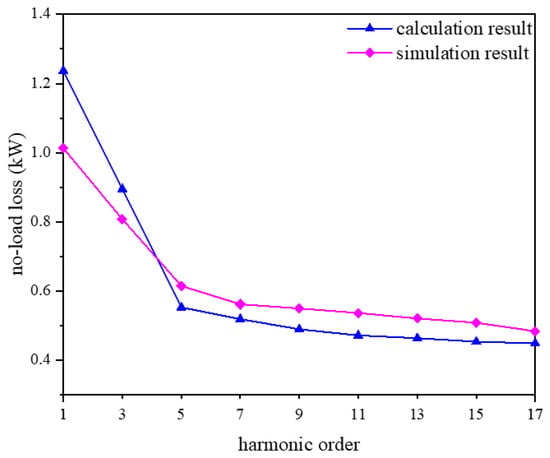
Figure 9. A no-load loss simulation and calculation value comparison.

The comparison between the calculated values and the simulation results in Figure 9 shows that the results of Equation (5) are consistent with the trend of the simulation results. The error is mainly due to the inaccurate calculation of the additional losses. The reasonableness of Equation (5) is verified.

4.2. Transformer Load Loss Analysis

Transformer load losses are mainly those generated by transformer windings. The first and second side currents of the transformer are maintained at the rated current, and the distribution of the transformer winding losses under the fundamental wave and the harmonic current is simulated, and the result is shown in Figure 10.

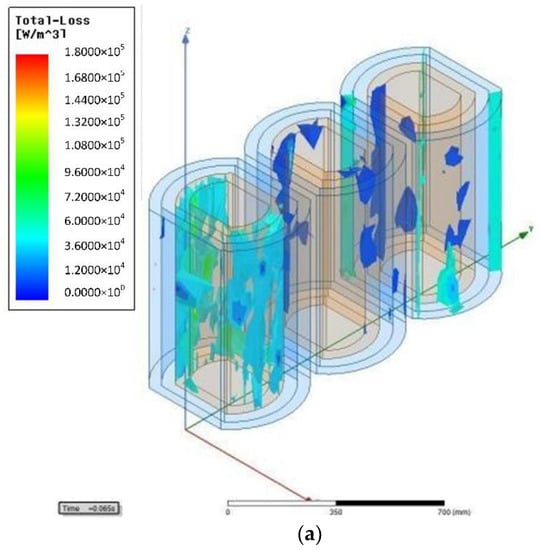
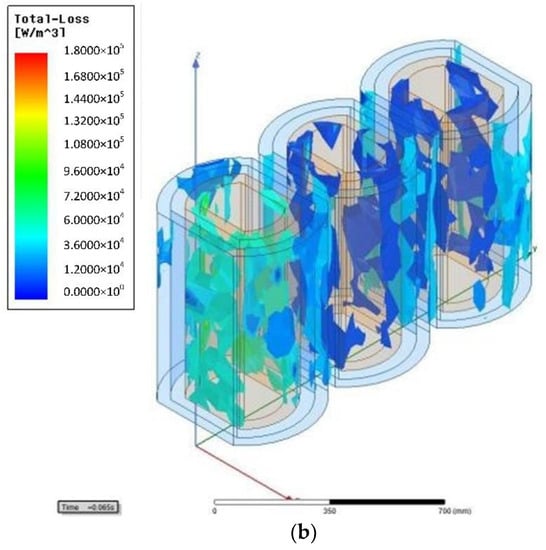
Figure 10. (a) Fundamental wave winding loss density distribution; (b) 5th harmonic winding loss density distribution. Transformer load loss density distribution.

It can be seen that when the transformer is at peak voltage in the same phase, the loss density of the transformer winding produced under the fundamental wave is less than the loss density under the 5th harmonic current. This means that harmonic currents can increase the loss value of the transformer windings.

According to the allowable values of harmonic currents specified in GB/T 14549-1993, harmonic currents with contents of 5%, 7% and 9% are injected into the primary side of the transformer respectively. The average values of the transformer harmonic winding losses for the 5th, 7th, 11th, 13th, 17th and 19th transformers without and after taking into account the skin effect are obtained by the field-coupling method respectively as shown in the Table 5 and Table 6.

Table 5. The average value of winding losses with different harmonic content (kW) (before considering the skin effect).

h	5%	7%	9%
Fundamental	4.42	4.42	4.42
5	4.88	5.07	5.30
7	4.97	5.23	5.44
11	5.14	5.41	5.73
13	5.19	5.50	5.79
17	5.26	5.62	5.91
19	5.30	5.69	5.99

Table 6. The average value of winding losses with different harmonic content (kW) (after considering the skin effect).

h	5%	7%	9%
Fundamental	4.42	4.42	4.42
5	4.98	5.09	5.37
7	5.12	5.33	5.59
11	5.59	6.05	6.66
13	5.97	6.56	7.05
17	6.56	7.14	7.26
19	7.43	7.91	8.34

Table 5 and Table 6 are plotted as a trend graph to obtain Figure 11 and Figure 12.

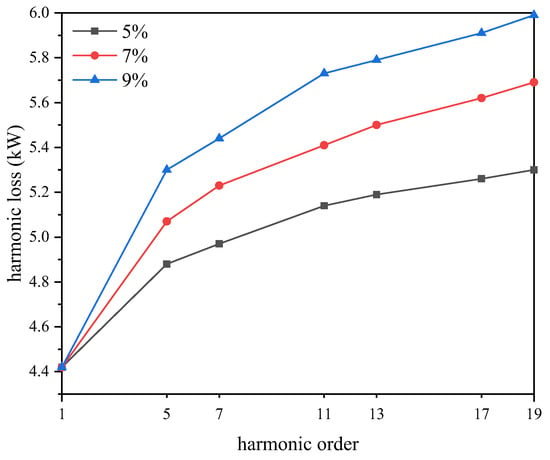
Figure 11. Winding loss under harmonic (cell splitting).

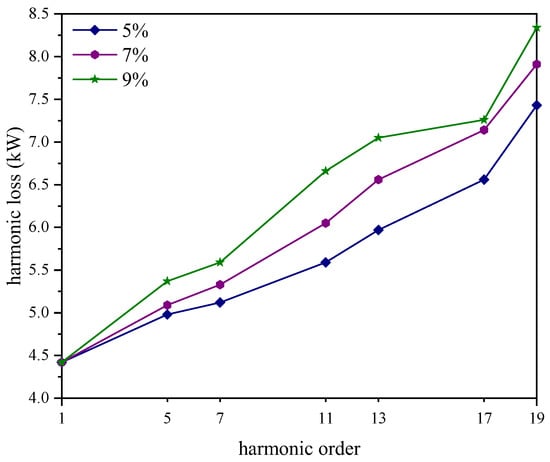
Figure 12. Winding loss under harmonic (skin depth profiling).

Figure 11 and Figure 12 show that the higher the content of harmonic currents in the transformer winding, the greater the value of harmonic losses. At the same time, the harmonic loss value grows in proportion to the number of harmonics. When the skin effect is taken into account for the same harmonic current content, the losses of each harmonic are higher than when it is not. The skin effect on winding in the harmonic case is taken into account in the model shown in Figure 12. The skin effect losses are also accounted for in the winding losses, so the higher values are reasonable.

Figure 11 shows that the harmonic characteristics of the simulated winding losses are consistent with the harmonic resistance characteristics of the $\sqrt{h}$R_dc model in Figure 2 when the skin effect is ignored. The harmonic characteristics of the winding losses obtained after accounting for the skinning depth of δ_h are consistent with the harmonic characteristics of the AC resistance factor $1+\frac{\mathsf{\Psi }}{3}{\Delta }^4$ of Figure 2, as shown in Figure 12.

The winding losses at 5% harmonic current content are calculated using the two models separately and compared with the simulated values after the skinning effect is added to obtain Figure 13.

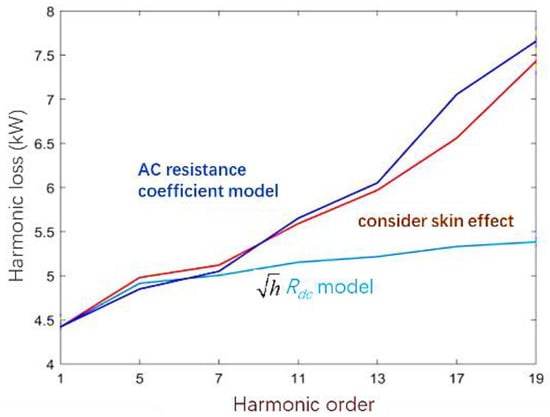
Figure 13. Winding loss simulation and calculation value comparison.

Figure 13 shows that after accounting for the skin effect on winding losses, harmonic additional losses increase with the number of harmonics. At the same time, the higher harmonic additional losses significantly increase. The finite element simulation results fit well with the calculated values of the high harmonic winding losses after the AC resistance factor correction, with small errors.

Table 7 displays the error results. Except for the 17th harmonic, the absolute value of error for the AC resistance factor model is less than 5%, whereas the $\sqrt{h}$R_dc model exceeds 25% as the number of harmonics increases. In calculating higher harmonic losses in transformer windings, the AC resistance coefficient model is thus more accurate than the conventional model.

Table 7. The error between calculated and simulated values of harmonic losses for different models (absolute values).

h	$\sqrt{\mathit{h}}{\mathit{R}}_{\mathit{dc}}\mathbf{Model}$	AC Resistance Coefficient Model
Fundamental	0	0
5	1.8%	3.8%
7	2.9%	2.0%
11	9.7%	1.3%
13	15.6%	1.4%
17	20.1%	7.8%
19	28.1%	3.2%

5. Conclusions

Based on the field-circuit coupling method, a three-dimensional model of a three-phase coherent distribution transformer is established in this paper. The harmonic loss change law of the transformer is simulated and analyzed by using the finite element method. The following conclusions are obtained:

(1)

As the voltage frequency increases, the hysteresis loss of the core of the three-phase coherent distribution trans-former decreases. As a result, when eliminating the line harmonic voltage in the transformer’s long-term no-load or light-load distribution line, the low harmonic voltage should be prioritized.

(2)

By the finite element method of field-path coupling, the AC resistance coefficient $1+\frac{\mathsf{\Psi }}{3}{\Delta }^4$ model is more accurate than the conventional harmonic winding resistance model $\sqrt{h}$ R_dc when calculating the high harmonic resistance of the winding of a three-phase dry-type distribution transformer due to skin and proximity effects. By using the AC resistance factor model, the accuracy of the calculation of high harmonic losses in transformer windings can be significantly improved. The errors in the 7th, 11th, 13th, 17th and 19th harmonic losses calculated using the AC resistance coefficient model are reduced by 31%, 87%, 91%, 61% and 89% respectively compared to the $\sqrt{h}$ R_dc model.

(3)

Harmonic additional winding losses increase as harmonic currents increase. The more harmonic currents there are, the greater the harmonic additional losses. The extra losses are most noticeable at higher harmonic currents. Higher harmonic currents should be monitored more closely in distribution lines where transformers are heavily loaded or overloaded in order to reduce harmonic load losses in the transformer.

A partial simplification of the transformer model has been made when using finite element simulation. For example, the losses in the pull plates, clips and leads are ignored. Further deepening and extension studies will be carried out in future work.