Detecting Discontinuities in Steel Wire Ropes of Personal Lifts Based on the Analysis of Their Residual Magnetic Field
Abstract
:1. Introduction, Aim, and Scope
1.1. Use of Steel Wire Ropes
1.2. Magnetic Methods to Diagnose Steel Wire Rope Damage
1.3. Other Methods of Diagnosing Steel Wire Rope Damage
1.4. Problems with the Diagnosis of Steel Wire Rope Damage
1.5. Aim of the Work
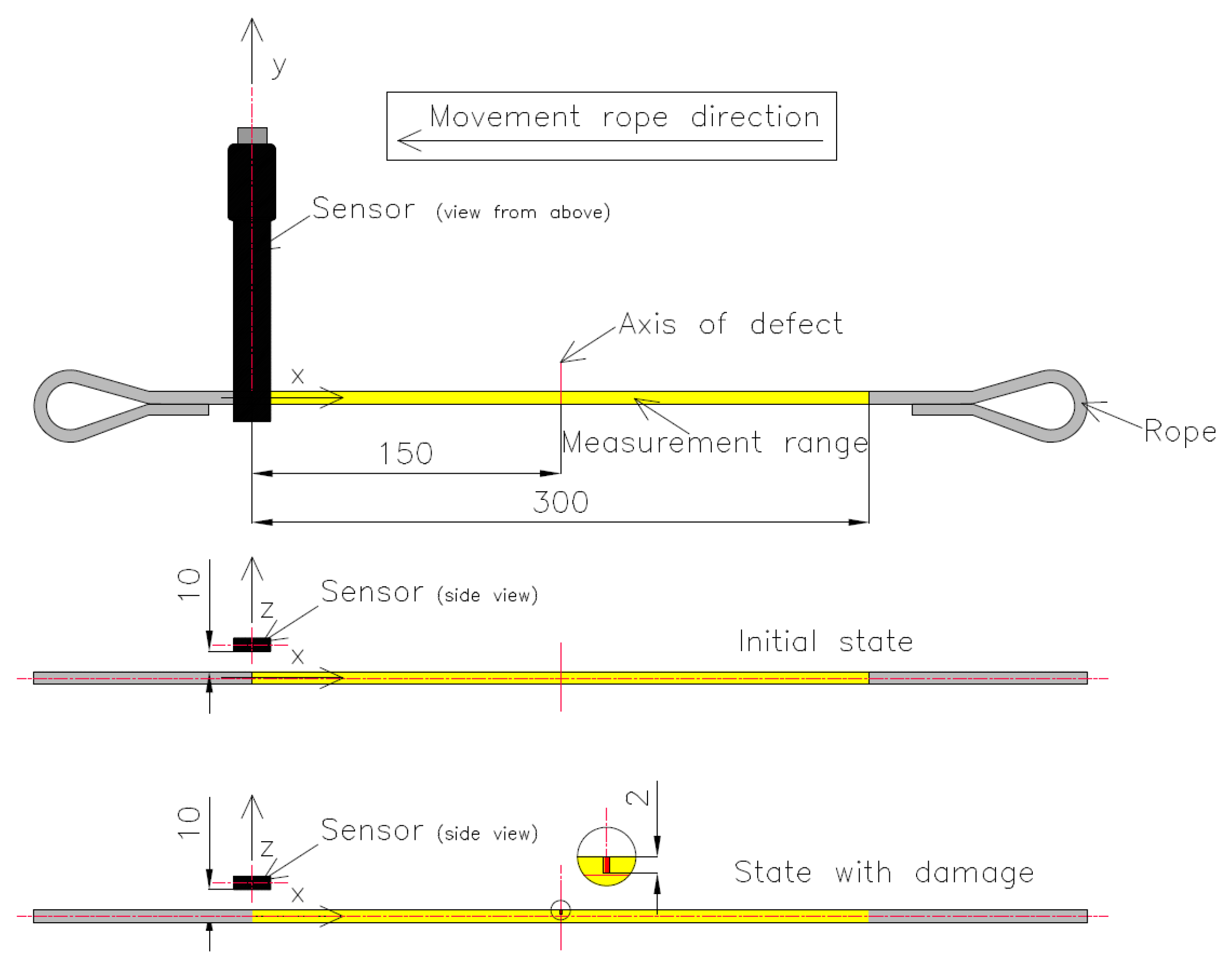
2. Experimental Details
2.1. Examined Object: Steel Wire Ropes
2.2. Measurement Details
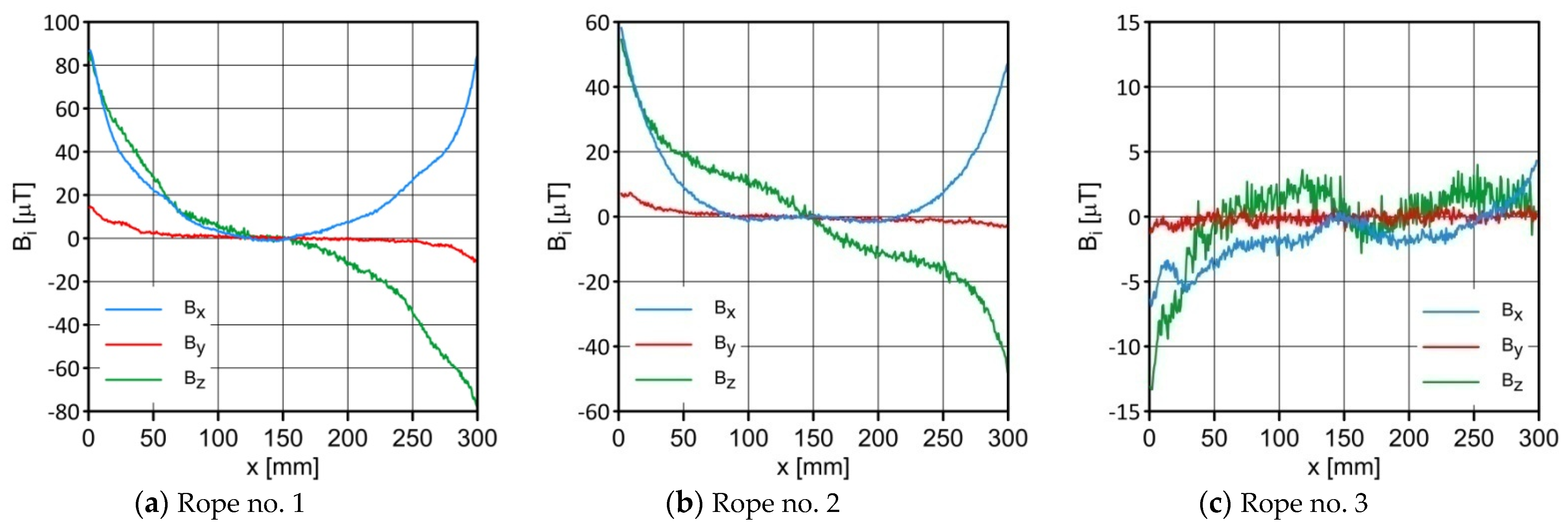
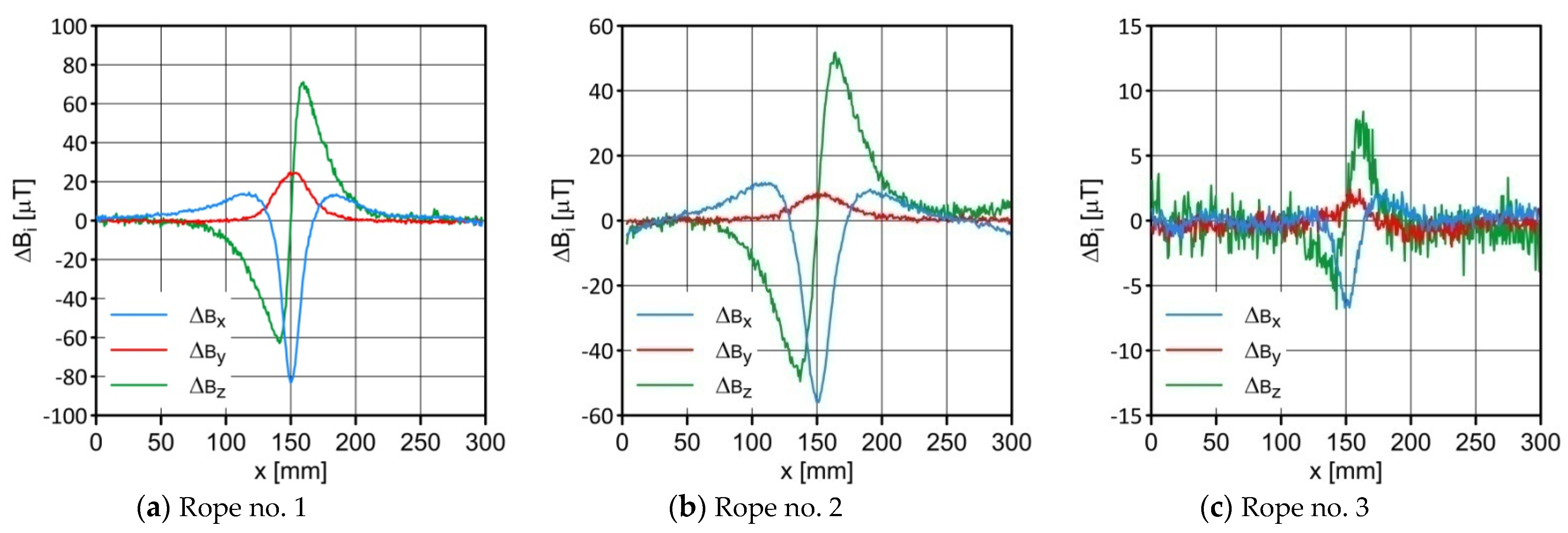
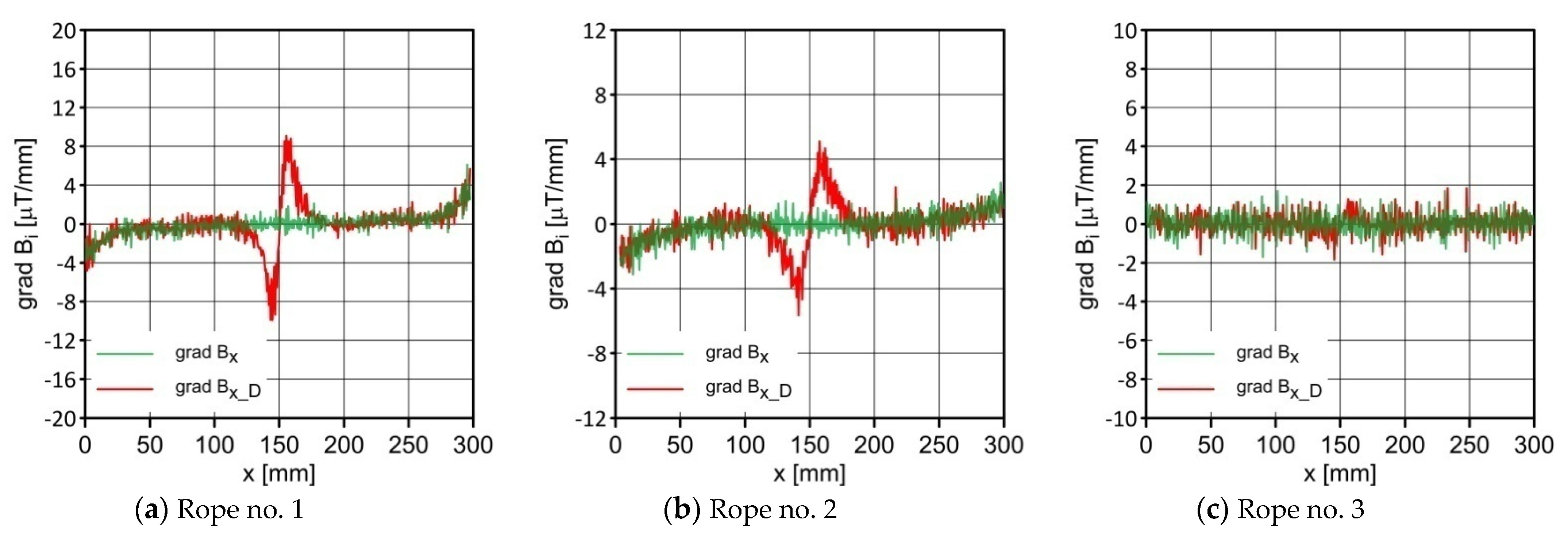
3. Results
4. Discussion
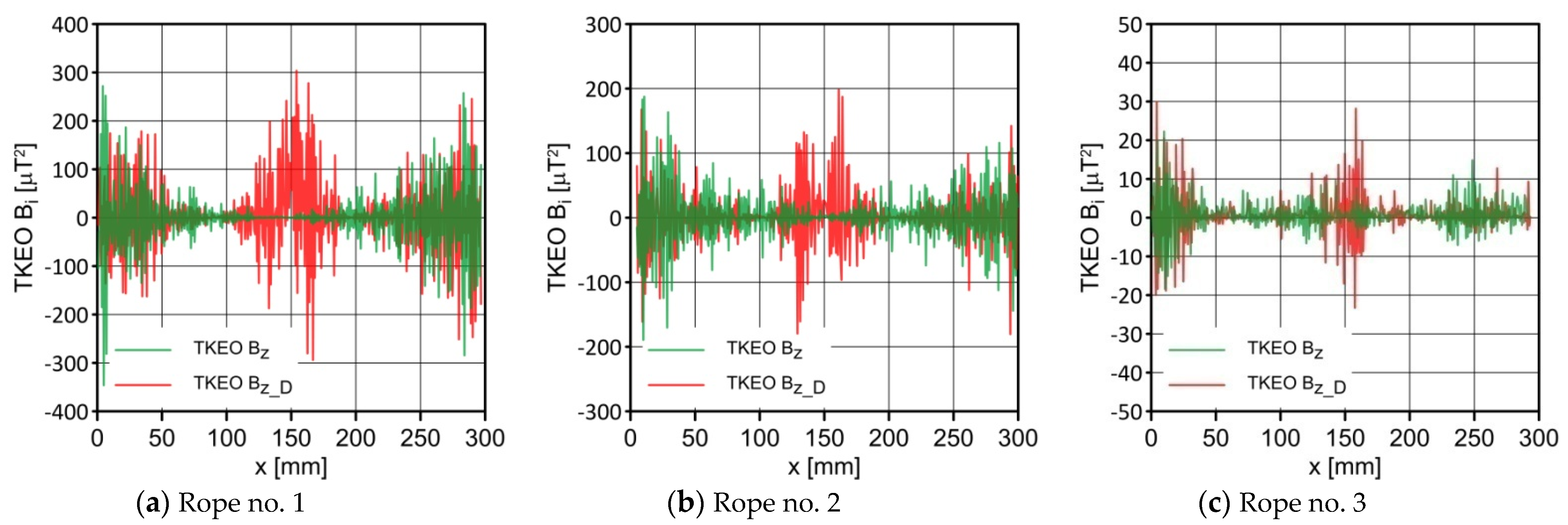
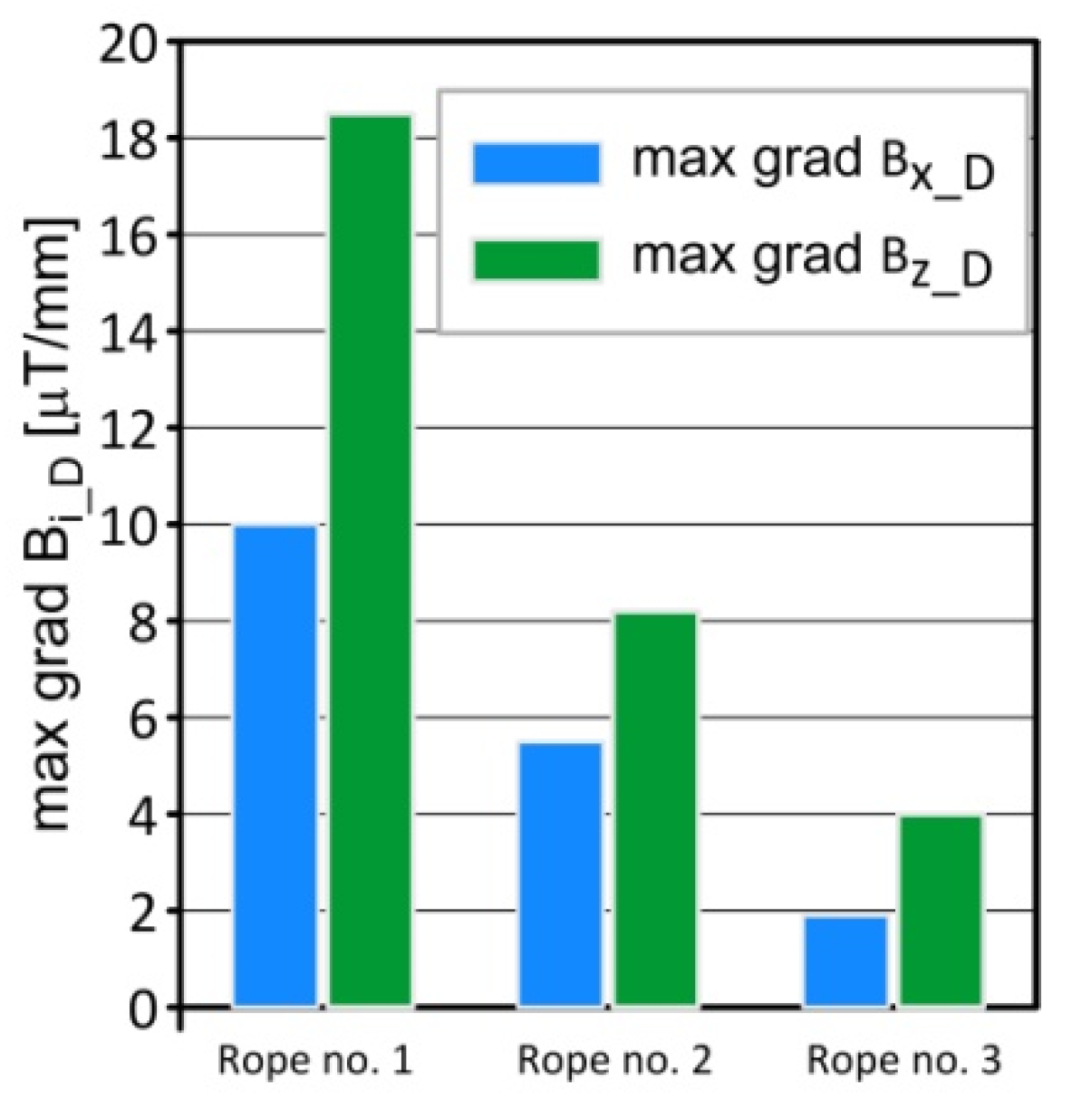
4.1. Interpretation of Charts
4.2. Analysis of the Results
5. Conclusions
- The use of the phenomenon of tunneling magnetoresistance in diagnosing the technical condition of wire ropes is promising. Passive magnetic diagnostics is much more energy-efficient than active techniques. It does not require generating an external magnetic field and consuming energy. Reduced energy consumption leads to environmental sustainability.
- The induction component distributions along the rope length were measured with and without a defect. Comparing the obtained results showed that the difference in the values near the defect for almost every component was apparent. This confirmed the results presented in [6]. Even without knowing the initial state, the magnetic anomaly caused by the discontinuity of the material gave a sufficiently strong diagnostic signal to enable its detection.
- We found that the values of the induction components were an important diagnostic parameter. Visible changes were observed in the induction gradient for the x and z components. Additionally, there was a clear peak in the TKEO analysis for the Bx_D signal.
- We introduced the product of the magnetic field induction components measured on the rope surface , which was an excellent diagnostic signal, giving a clear image of the discontinuity in the signal distribution.
- A comprehensive approach using many features of the diagnostic signal is the basis for developing a new passive magnetic method for evaluating the defectoscopic condition of steel ropes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Giglio, M.; Manes, A. Life prediction of a wire rope subjected to axial and bending loads. Eng. Fail. Anal. 2005, 12, 549–568. [Google Scholar] [CrossRef]
- Chaplin, C. Interactive Fatigue in Wire Rope Applications. In Proceedings of the Symposium on mechanics of slender structures (MoSS 2008), Baltimore, MD, USA, 23–25 July 2008. [Google Scholar]
- El Barkany, A.; Benali, A.; El Ghorba, M.; Chergui, M.H.; Choukir, A. Nondestructive evaluation methods of broken wire ropes of lifting. Int. J. Constr. Educ. Res. 2012, 2, 154–162. [Google Scholar]
- Sukhorukov, V.; Slesarev, D.; Vorontsov, A. Electromagnetic Inspection and Diagnostics of Steel Ropes: Technology, Effectiveness and Problems, ET’. Undefined. 2014. Available online: https://www.semanticscholar.org/paper/Electromagnetic-Inspection-and-Diagnostics-of-Steel-Sukhorukov-Slesarev/fdc1c06b5bca1285f93c83dc5f611174629f911f (accessed on 27 June 2022).
- Seelam, A.B.; Jawed, M.S.; Krishanmurthy, S.H. Design and analysis of elevator wire ropes. Int. J. Simul. Multidiscip. Des. Optim. 2021, 12, 20. [Google Scholar] [CrossRef]
- Mazurek, P.; Roskosz, M.; Kwasniewski, J. Novel diagnostic of steel wire rope with passive magnetic methods. IEEE Magn. Lett. 2021, 13, 1–5. [Google Scholar] [CrossRef]
- Houda, M.; Abdellah, E.B.; Ahmed, E.B. Steel wire ropes failure analysis: Experimental study. Eng. Fail. Anal. 2018, 91, 234–242. [Google Scholar]
- Liu, S.; Sun, Y.; Jiang, X.; Kang, Y. Comparison and analysis of multiple signal processing methods in steel wire rope defect detection by hall sensor. Measurement 2021, 171, 108768. [Google Scholar] [CrossRef]
- Mouhib, N.; Wahid, A.; Sabah, F.; Chakir, H.; ELghorba, M. Experimental characterization and damage reliability analysis of central core strand extracted from steel wire rope. Eng. Fail. Anal. 2021, 120, 105103. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, E.; Jia, F. Study on bending fatigue failure behaviors of end-fixed wire ropes. Eng. Fail. Anal. 2022, 135, 106172. [Google Scholar] [CrossRef]
- Milone, A.; Landolfo, R.; Berto, F. Methodologies for the fatigue assessment of corroded wire ropes: A state-of-the-art review. Structures 2022, 37, 787–794. [Google Scholar] [CrossRef]
- Dai, L.; Zhao, M.; Tang, B.; Yang, N.; Xiao, Y.; Wu, T. Signal acquisition system for broken wire of elevator wire rope based on TMR sensor. J. Phys. Conf. Ser. 2021, 2010, 012113. [Google Scholar] [CrossRef]
- Xia, H.; Yan, R.; Wu, J.; He, S.; Zhang, M.; Qiu, Q.; Zhu, J.; Wang, J. Visualization and Quantification of Broken Wires in Steel Wire Ropes Based on Induction Thermography. IEEE Sens. J. 2021, 21, 18497–18503. [Google Scholar] [CrossRef]
- Pan, F.; Ren, L.; Zhou, J.; Liu, Z. Fault classification based on computer vision for steel wire ropes. J. Phys. Conf. Ser. 2022, 2184, 012035. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, D.; Zhu, X. Tension Monitoring and Defect Detection by Magnetostrictive Longitudinal Guided Wave for Fine Wire Rope. IEEE Trans. Instrum. Meas. 2021, 70, 6003707. [Google Scholar] [CrossRef]
- Zhou, J.; Ren, L.; Liu, Z. Instantaneous lift-off distance estimation in magnetic flux leakage testing of steel wire ropes. J. Phys. Conf. Ser. 2022, 2184, 012051. [Google Scholar] [CrossRef]
- Ruta, H.; Krakowski, T.; Lonkwic, P. Optimisation of the Magnetic Circuit of a Measuring Head for Diagnostics of Steel-Polyurethane Load-Carrying Belts Using Numerical Methods. Sustainability 2022, 14, 2711. [Google Scholar] [CrossRef]
- Yaghmaei Poudeh, A.; Dehghanbanadaki, A.; Golpazir, I. Reuse of elevator wire rope waste to improve the tensile strength of plain concrete. Innov. Infrastruct. Solut. 2021, 7, 70. [Google Scholar] [CrossRef]
- Xue, Z.; Chang, X.; Feng, S.; Fang, L.; Liu, Y. Research on test method of elevator wire rope under special environment. J. Phys. Conf. Ser. 2021, 1748, 052039. [Google Scholar] [CrossRef]
- Sheinker, A.; Frumkis, L.; Ginzburg, B.; Salomonski, N.; Kaplan, B.-Z. Magnetic Anomaly Detection Using a Three-Axis Magnetometer. IEEE Trans. Magn. 2009, 45, 160–167. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, X.; Zheng, P. Non-Destructive Detection of Wire Rope Discontinuities from Residual Magnetic Field Images Using the Hilbert-Huang Transform and Compressed Sensing. Sensors 2017, 17, 608. [Google Scholar] [CrossRef] [Green Version]
- Mazurek, P.; Kwaśniewski, J.; Roskosz, M.; Siwoń-Olszewski, R. The use of a magnetic flux leakage in the assessment of the technical state of a steel wire rope subjected to bending. J. Konbin 2018, 48, 493–513. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Zhang, E.; Pan, S.; Yan, X.; Gao, W. Fast Quantitative Method to Detect the Cross-Sectional Loss of Wire Rope Defects. IEEE Trans. Instrum. Meas. 2021, 70, 6004411. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, P.; Tan, X. Recognition of Broken Wire Rope Based on Remanence using EEMD and Wavelet Methods. Sensors 2018, 18, 1110. [Google Scholar] [CrossRef] [PubMed]
- Mazurek, P.; Roskosz, M. Influence of the Earth’s magnetic field on the diagnosis of steel wire rope by passive magnetic methods. J. Magn. Magn. Mater. 2021, 547, 168802. [Google Scholar] [CrossRef]
- Mouradi, H.; El Barkany, A.; Biyaali, A. Investigation on the main degradation mechanisms of steel wire ropes: A literature review. J. Eng. Appl. Sci. 2016, 11, 1206–1217. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, S.; Xie, C.; Bai, G. Non-Invasive Force Measurement Based on Magneto-Elastic Effect for Steel Wire Ropes. IEEE Sens. J. 2021, 21, 8979–8987. [Google Scholar] [CrossRef]
- Pineda-Sanchez, M.; Puche-Panadero, R.; Riera-Guasp, M.; Perez-Cruz, J.; Roger-Folch, J.; Pons-Llinares, J.; Climente-Alarcon, V.; Antonino-Daviu, J.A. Application of the Teager–Kaiser Energy Operator to the Fault Diagnosis of Induction Motors. IEEE Trans. Energy Convers. 2013, 28, 1036–1044. [Google Scholar] [CrossRef]
- SpinMeter-3D USB 3 Axis Magnetometer—Software Installation and User Guide. Available online: http://www.micromagnetics.com/product_page_spinmeter3.html (accessed on 20 August 2022).
- Gao, J.; Wang, J.; Zhang, L.; Yu, Q.; Huang, Y.; Shen, Y. Magnetic Signature Analysis for Smart Security System Based on TMR Magnetic Sensor Array. IEEE Sens. J. 2019, 19, 3149–3155. [Google Scholar] [CrossRef]
- Khan, M.A.; Sun, J.; Li, B.; Przybysz, A.; Kosel, J. Magnetic sensors-A review and recent technologies. Eng. Res. Express 2021, 3, 022005. [Google Scholar] [CrossRef]
- Yan, S.; Zhou, Z.; Yang, Y.; Leng, Q.; Zhao, W. Developments and applications of tunneling magnetoresistance sensors. Tsinghua Sci. Technol. 2022, 27, 443–454. [Google Scholar] [CrossRef]










| No. of the Rope | 1 | 2 | 3 |
|---|---|---|---|
| Cross section | 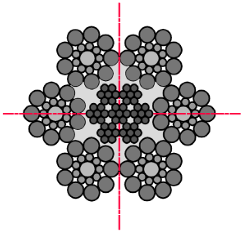 |  |  |
| Diameter | ø6.0 mm | ø6.5 mm ø5.0 mm (metalic part) | ø5.1 mm ø4.0 mm (metalic part) |
| Construction | 6 × 19S + IWRC(7 × 7) | 7 × 19W + IWRC(7 × 7) coated | 6 × 19S + IWRC(7 × 7) coated |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazurek, P.; Roskosz, M.; Kwaśniewski, J.; Wu, J.; Schabowicz, K. Detecting Discontinuities in Steel Wire Ropes of Personal Lifts Based on the Analysis of Their Residual Magnetic Field. Sustainability 2022, 14, 14641. https://doi.org/10.3390/su142114641
Mazurek P, Roskosz M, Kwaśniewski J, Wu J, Schabowicz K. Detecting Discontinuities in Steel Wire Ropes of Personal Lifts Based on the Analysis of Their Residual Magnetic Field. Sustainability. 2022; 14(21):14641. https://doi.org/10.3390/su142114641
Chicago/Turabian StyleMazurek, Paweł, Maciej Roskosz, Jerzy Kwaśniewski, Jianbo Wu, and Krzysztof Schabowicz. 2022. "Detecting Discontinuities in Steel Wire Ropes of Personal Lifts Based on the Analysis of Their Residual Magnetic Field" Sustainability 14, no. 21: 14641. https://doi.org/10.3390/su142114641
APA StyleMazurek, P., Roskosz, M., Kwaśniewski, J., Wu, J., & Schabowicz, K. (2022). Detecting Discontinuities in Steel Wire Ropes of Personal Lifts Based on the Analysis of Their Residual Magnetic Field. Sustainability, 14(21), 14641. https://doi.org/10.3390/su142114641








