A Machine Learning Method for the Risk Prediction of Casing Damage and Its Application in Waterflooding
Abstract
:1. Introduction
2. Methodology
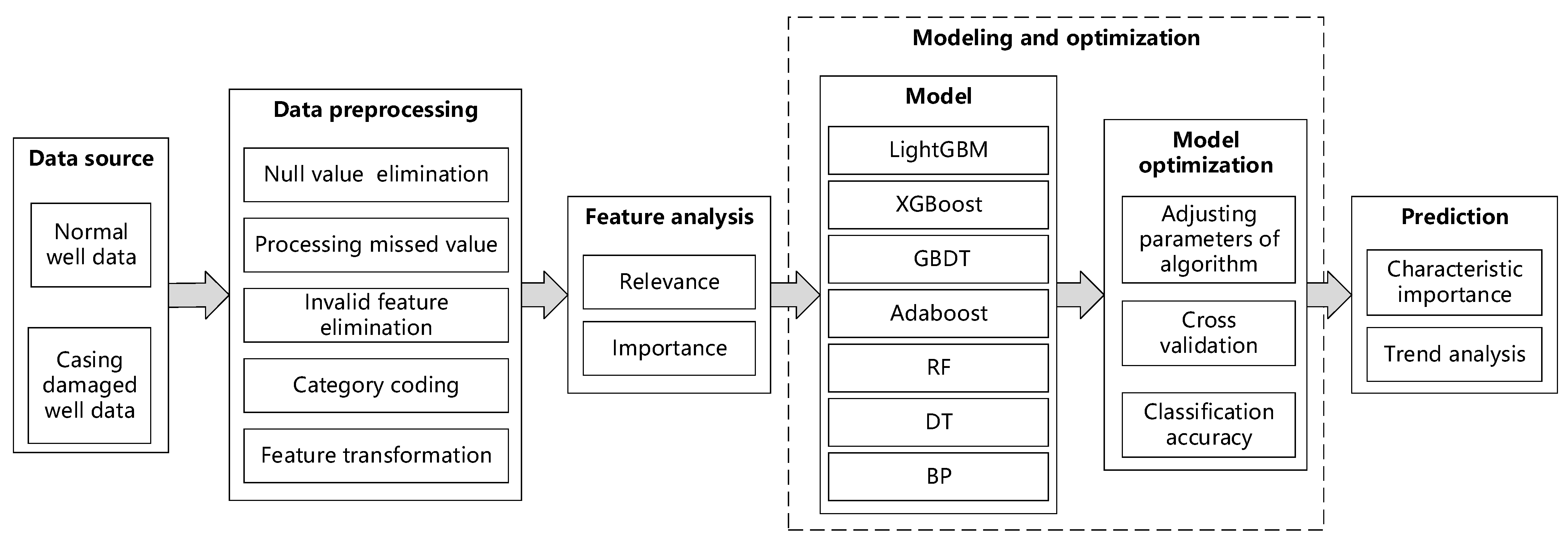
2.1. Technical Concept
- (1)
- Collect data for normal and casing-damaged wells, such as sublayer data, perforation data, casing data, and production data.
- (2)
- Preprocess the collected data through null-value elimination, missed-value processing, invalid-feature elimination, and category coding. Aggregate and construct new parameters based on the original data, and preliminarily determine the data items having a strong correlation with casing damage.
- (3)
- Adopt a box plot, F-test, and mutual information, among other methods, to analyze the correlation between factor characteristics and casing damage.
- (4)
- Use seven common machine learning classification algorithms to build the casing damage prediction model and adjust the main parameters of the algorithms. Then verify the model adopting five-fold cross-validation. Evaluate the accuracy of the model using five indicators, namely the accuracy, precision, recall, F1-score, and AUC. Finally, obtain the optimal model in terms of these errors.
- (5)
- Apply the optimal model to predict the probability of casing damage in wells.
2.2. Feature Analysis
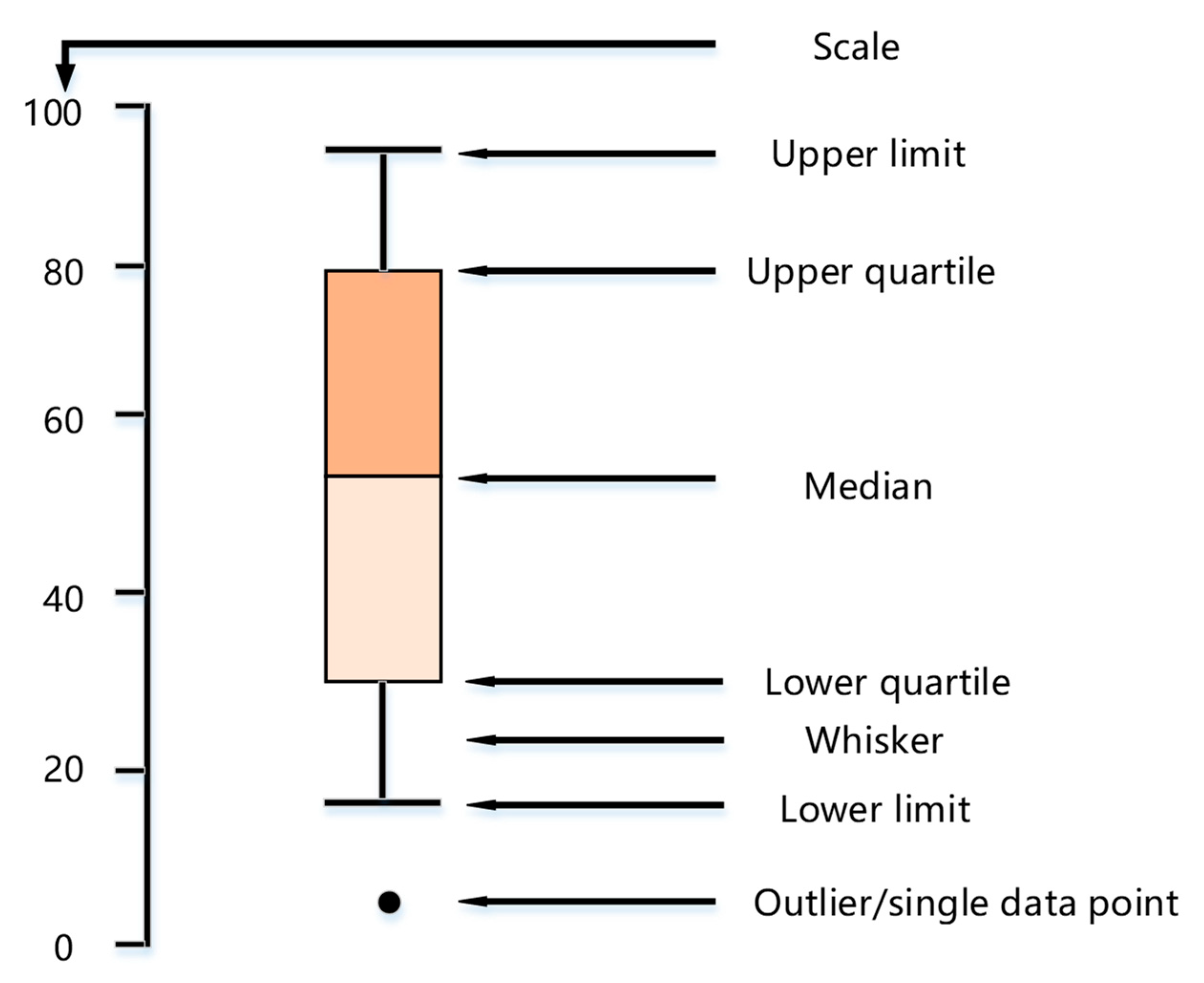
- (1)
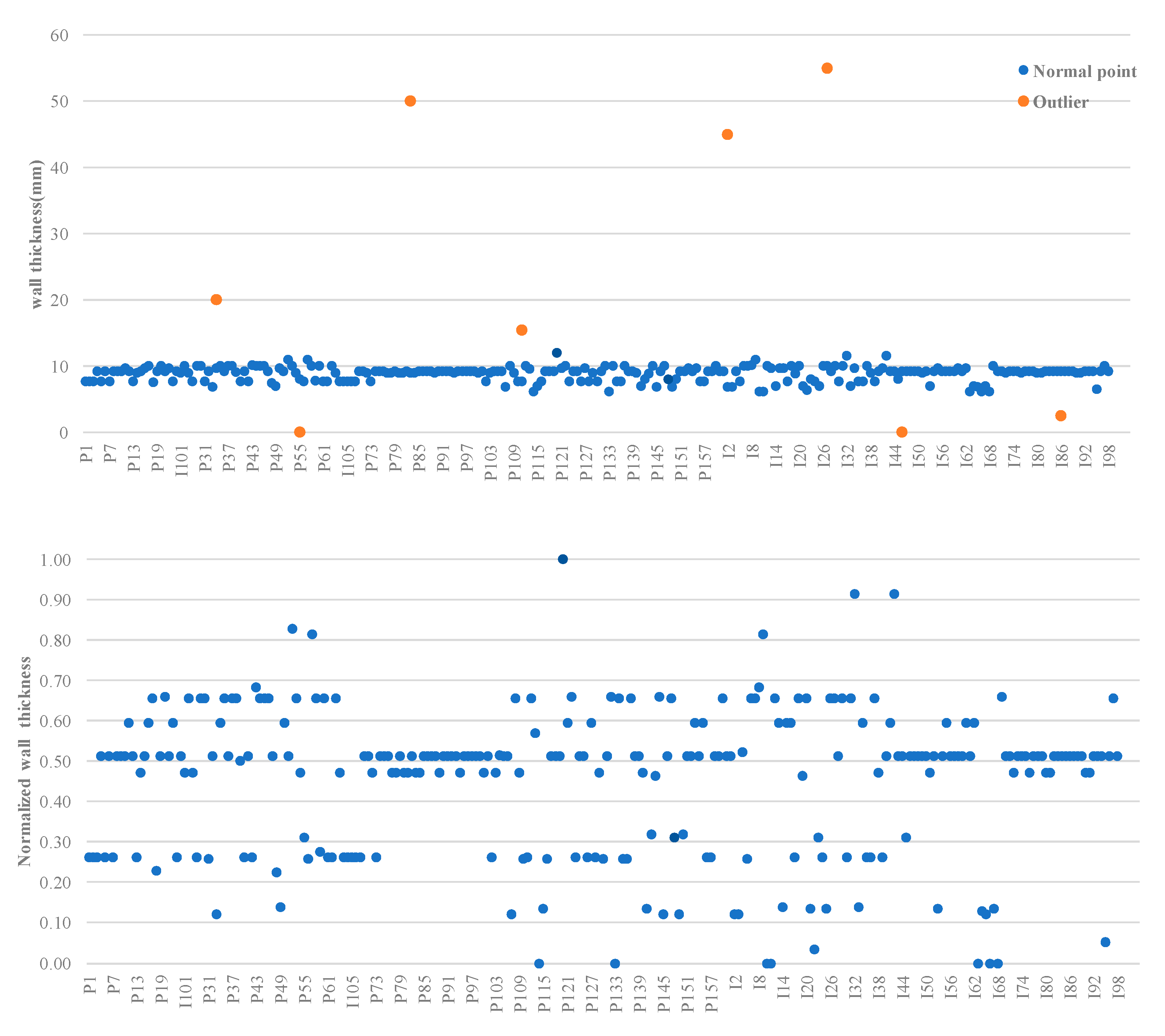
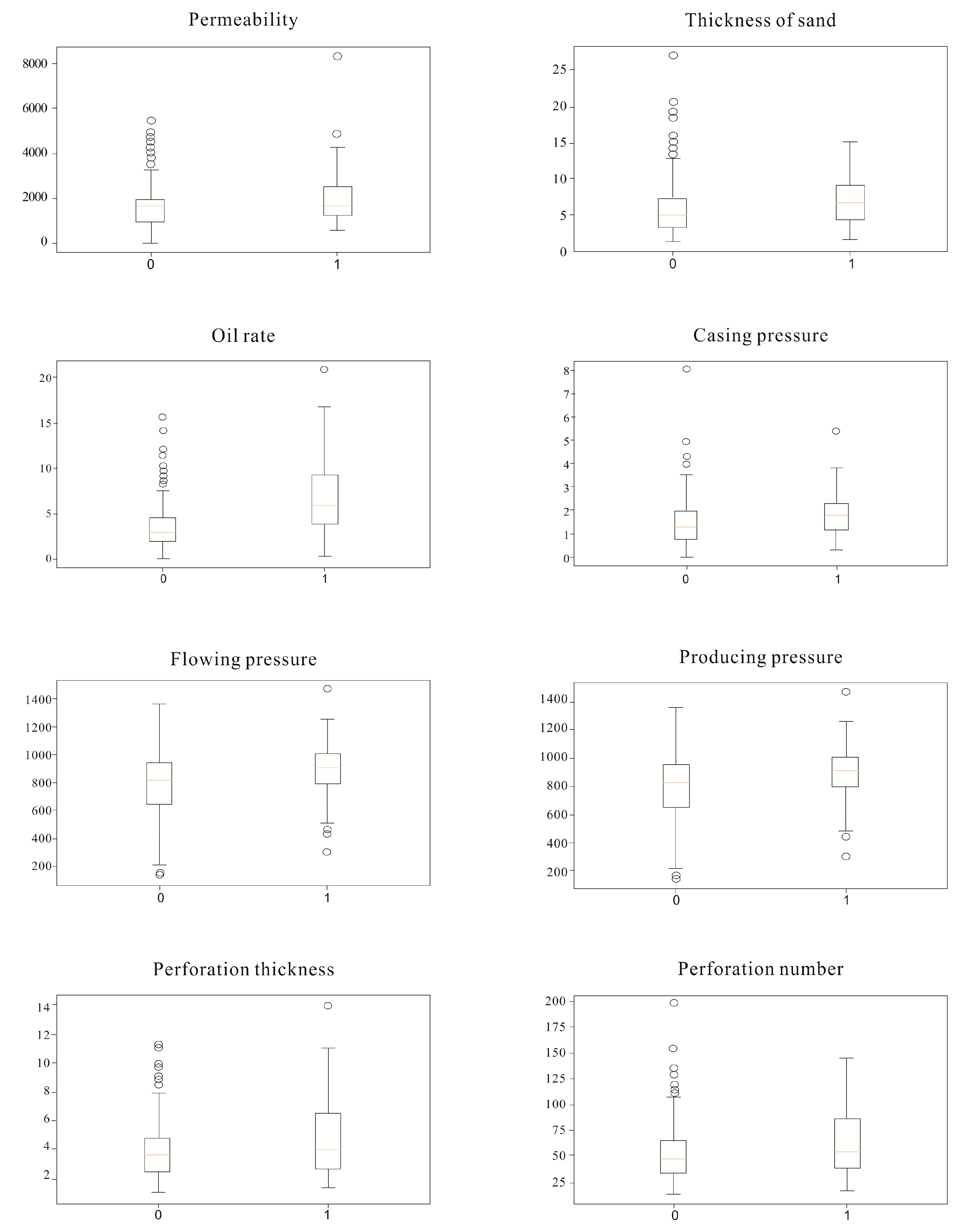
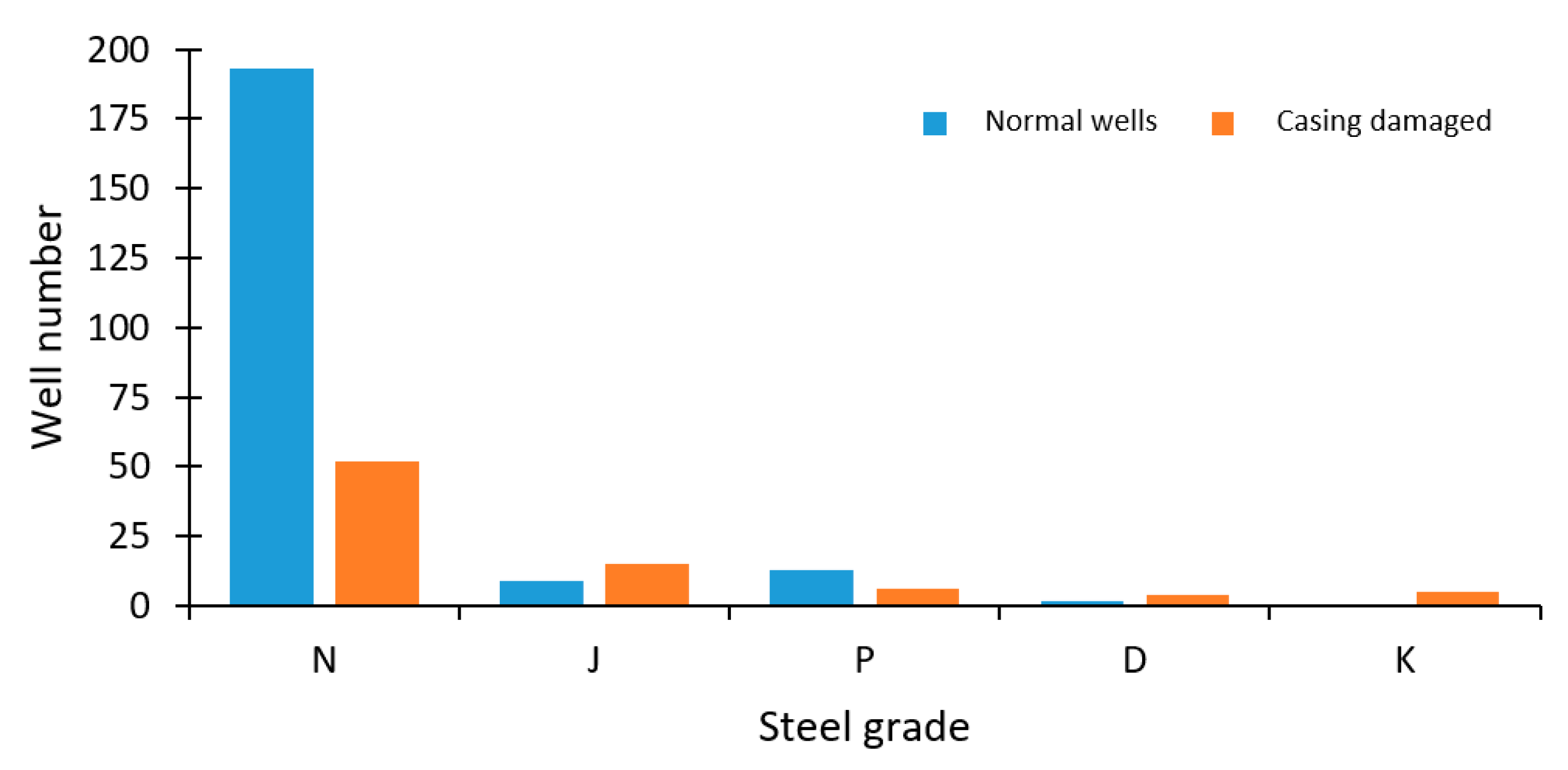
- Box-plot visualization: A data distribution can be visualized using five statistical values of the data, namely the minimum, upper quartile, median, lower quartile, and maximum, as shown in Figure 2. This box-plot visualization is unaffected by outliers and shows whether the data are roughly symmetry, accurately and stably describes the discrete distribution of the data, especially for the comparison of several types of samples, and is conducive to data cleaning.
- (2)
- F-test: The F-test is a filtering method used to capture the linear relationship between each feature and label. The F-test is adopted to analyze the test data, test whether the average values of multiple normal populations with equal variances are equal and judge the importance of the effects of various factors on the test indicators.
- (3)
- Calculation of mutual information: Mutual information is an information measure used in information theory to estimate the correlation between category features and labels. Mutual information takes a non-negative value. Mutual information is equal to zero if and only if the two features are independent and have a higher value for higher dependency. Mutual information can be regarded as the amount of information about another random variable contained in one random variable or the decrease in uncertainty of a random variable due to knowing another random variable.
2.3. Model Establishment
- (1)
- Modeling algorithms
- (2)
- Parameter optimization
- (3)
- Effect verification
- (4)
- Model accuracy evaluation
- (5)
- Model application
3. Application
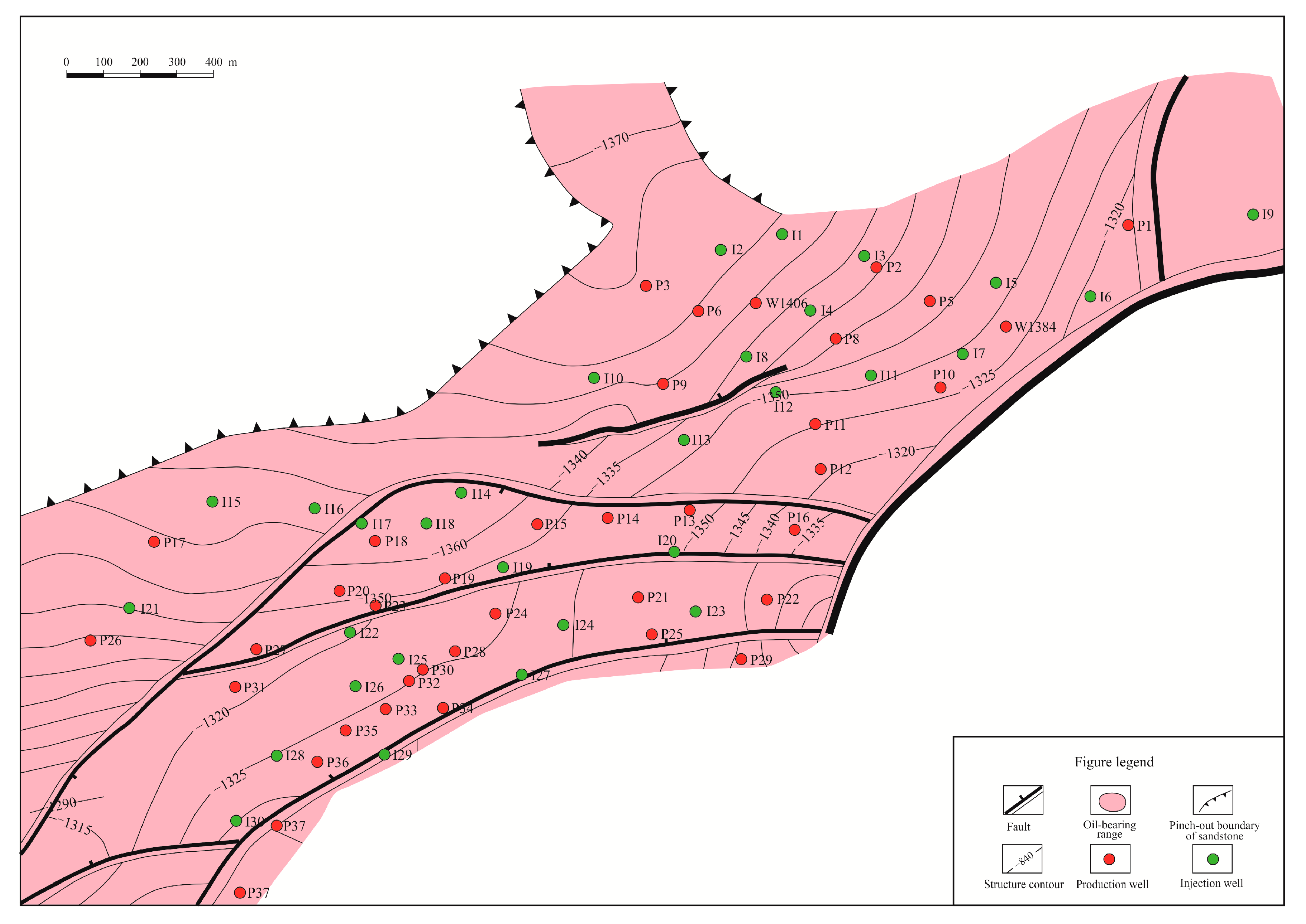
3.1. Overview of the Block
3.2. Data Processing
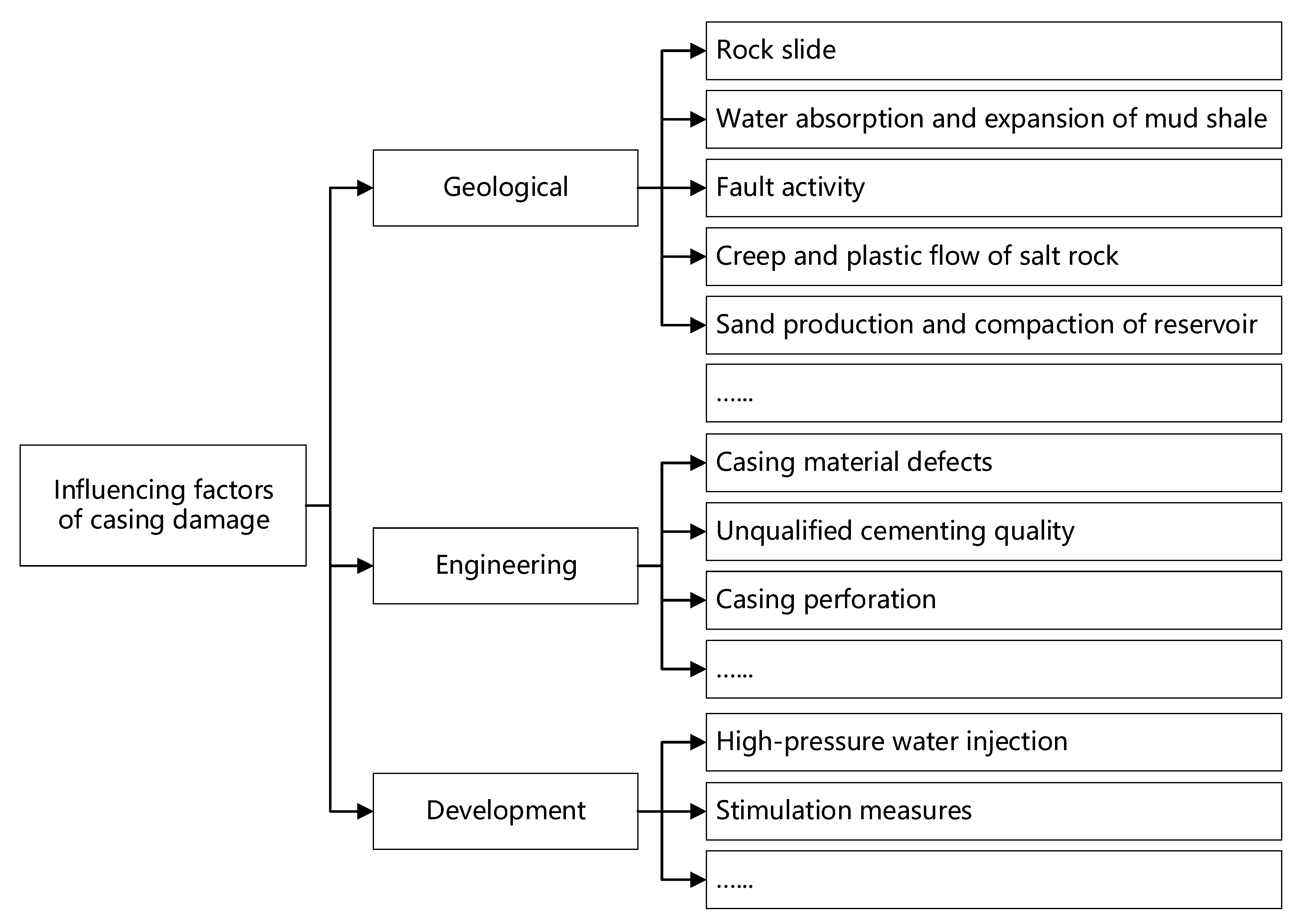
3.3. Analysis of Main Control Factors
- (1)
- Univariate analysis based on box plots and bar charts
- (2)
- Multivariate quantitative study adopting the F-test and mutual information
3.4. Establishment of the Prediction Model
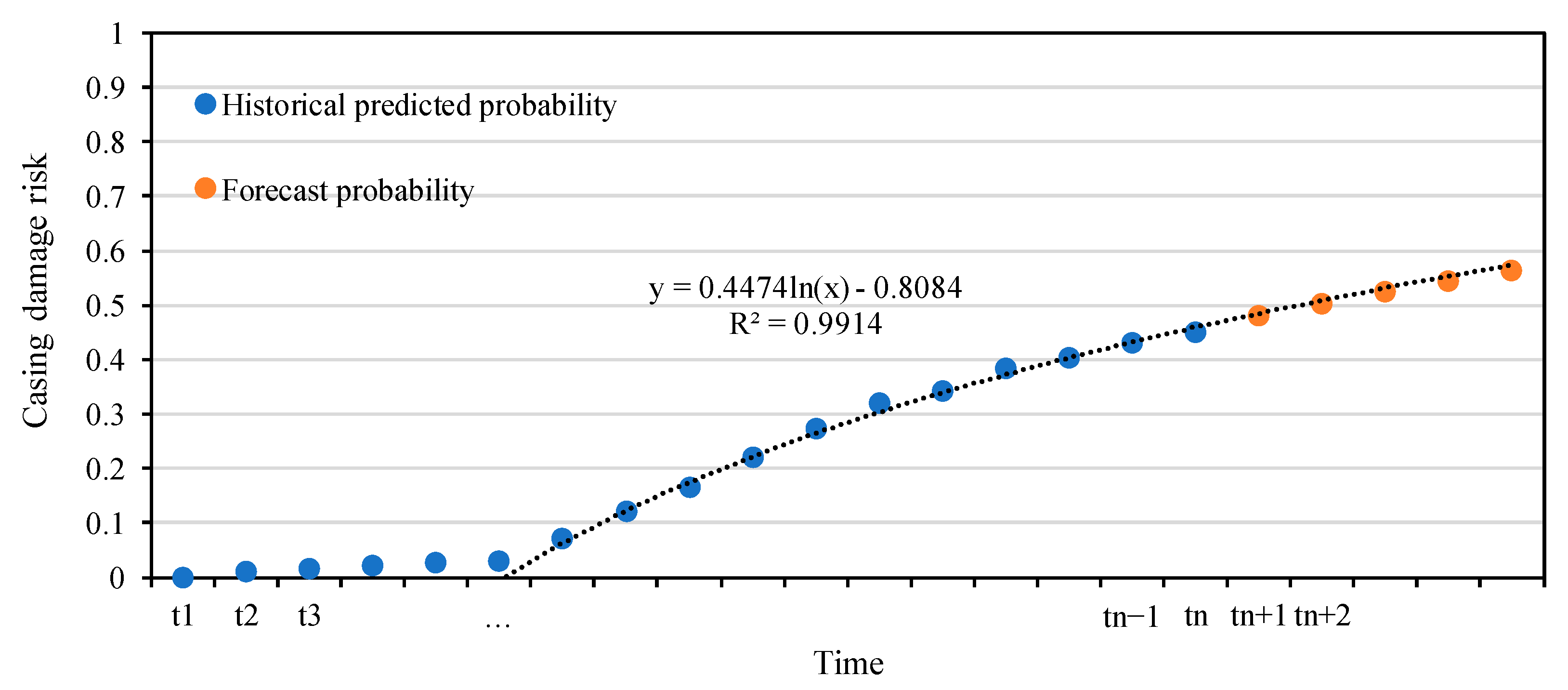
3.5. Results
4. Research Limitations
- (1)
- The identification of damaged wells faced the common modeling problem of insufficient failure data to find a correct solution.
- (2)
- Although two schemes based on well and well-layer granularities were proposed and well-layer granularity was adopted to build the model, there were incomplete sub-layer data to support our recommendations.
- (3)
- There remain instabilities in the prediction model. The precision, recall, and F1 standard deviations of the validation set and the test set were large because different data divisions led to different training data distributions learned by the model, and the prediction law learned by the model was thus unstable. This situation can be improved by expanding the volume of data, especially for casing-failure wells.
5. Conclusions
- (4)
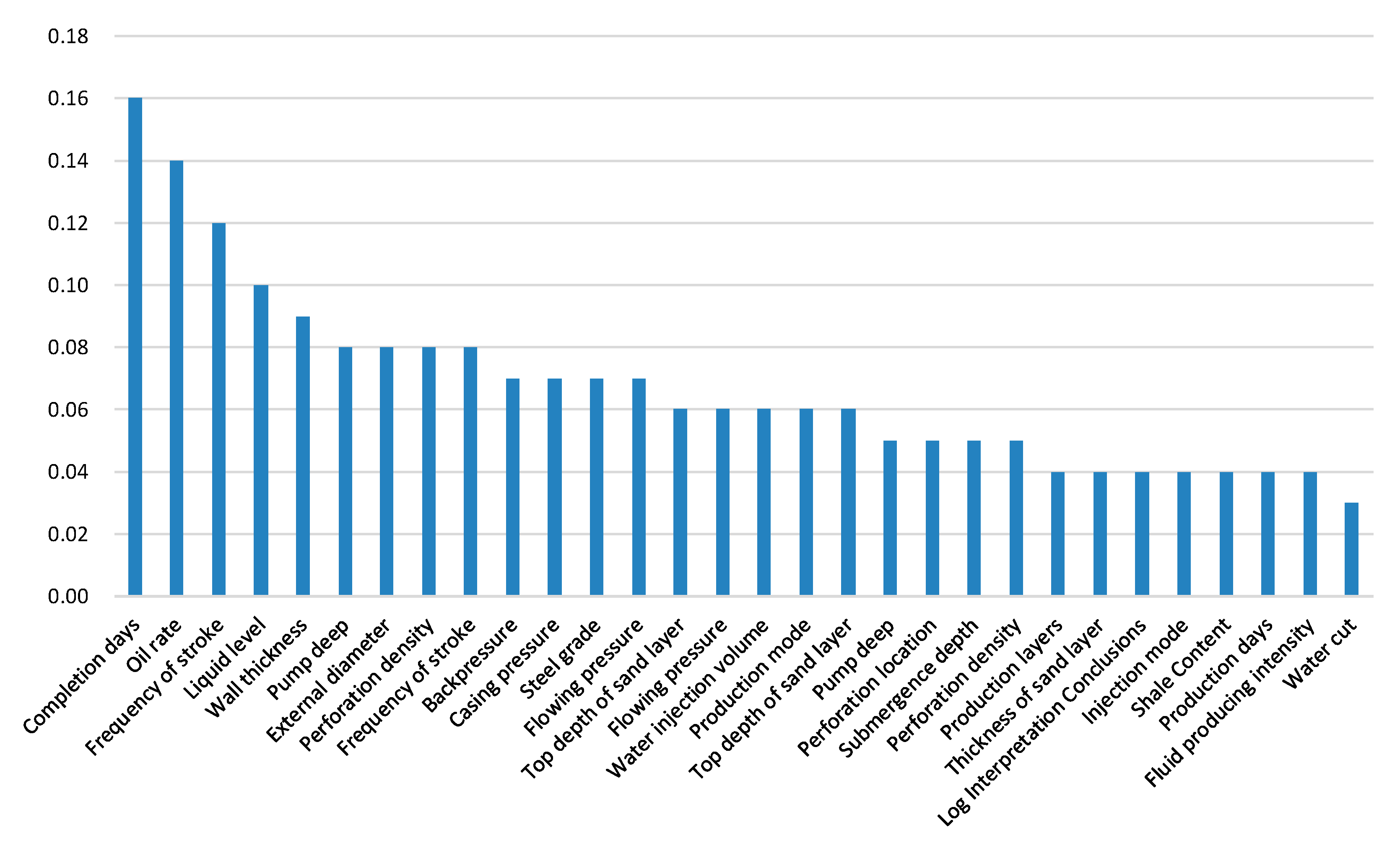
- The study considered 295 factors in four areas (geology, engineering, development, and production) and adopted the F-test and mutual information to demonstrate and determine the main control factors, such as the completion days, oil rate, and wall thickness.
- (5)
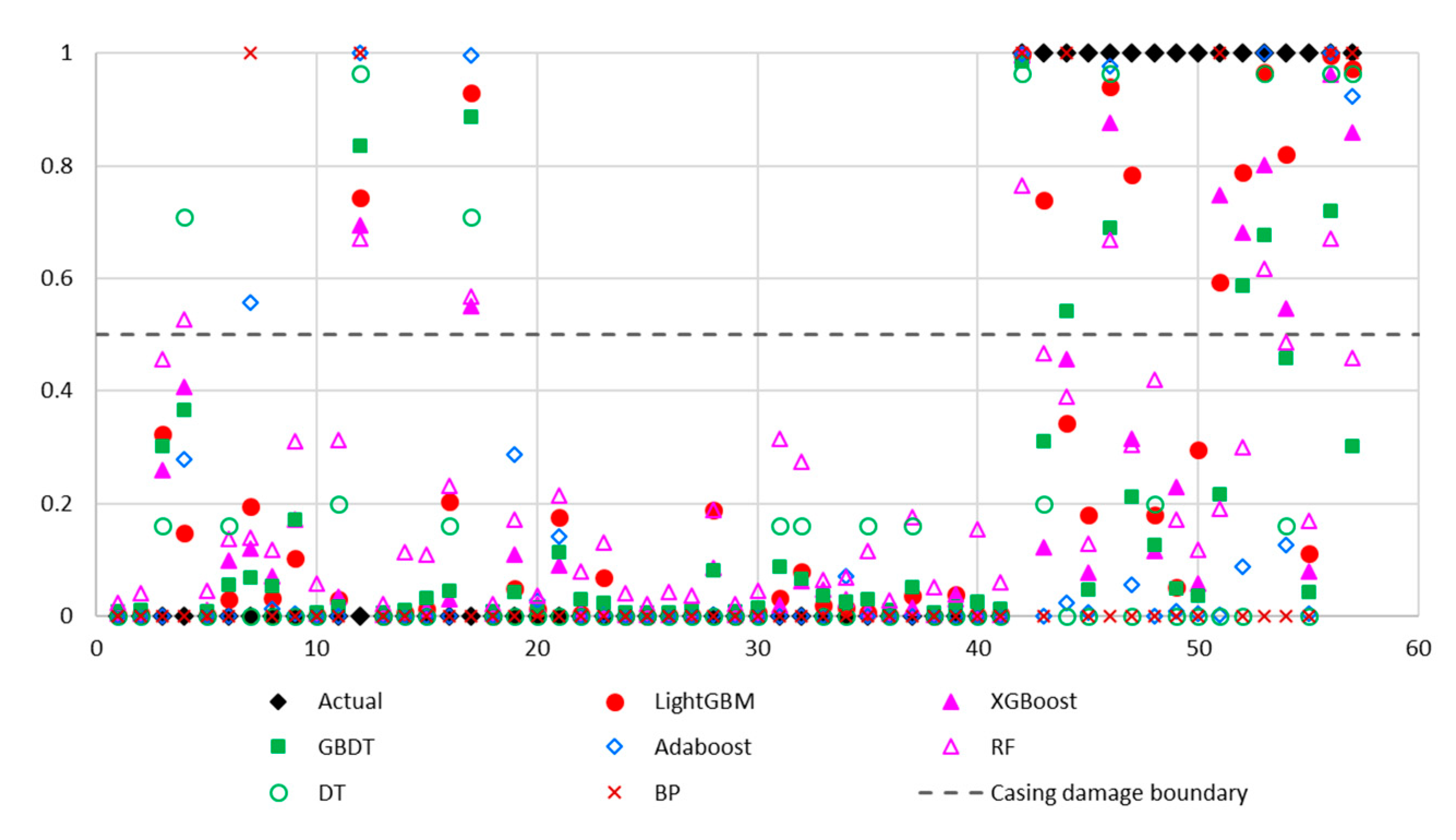
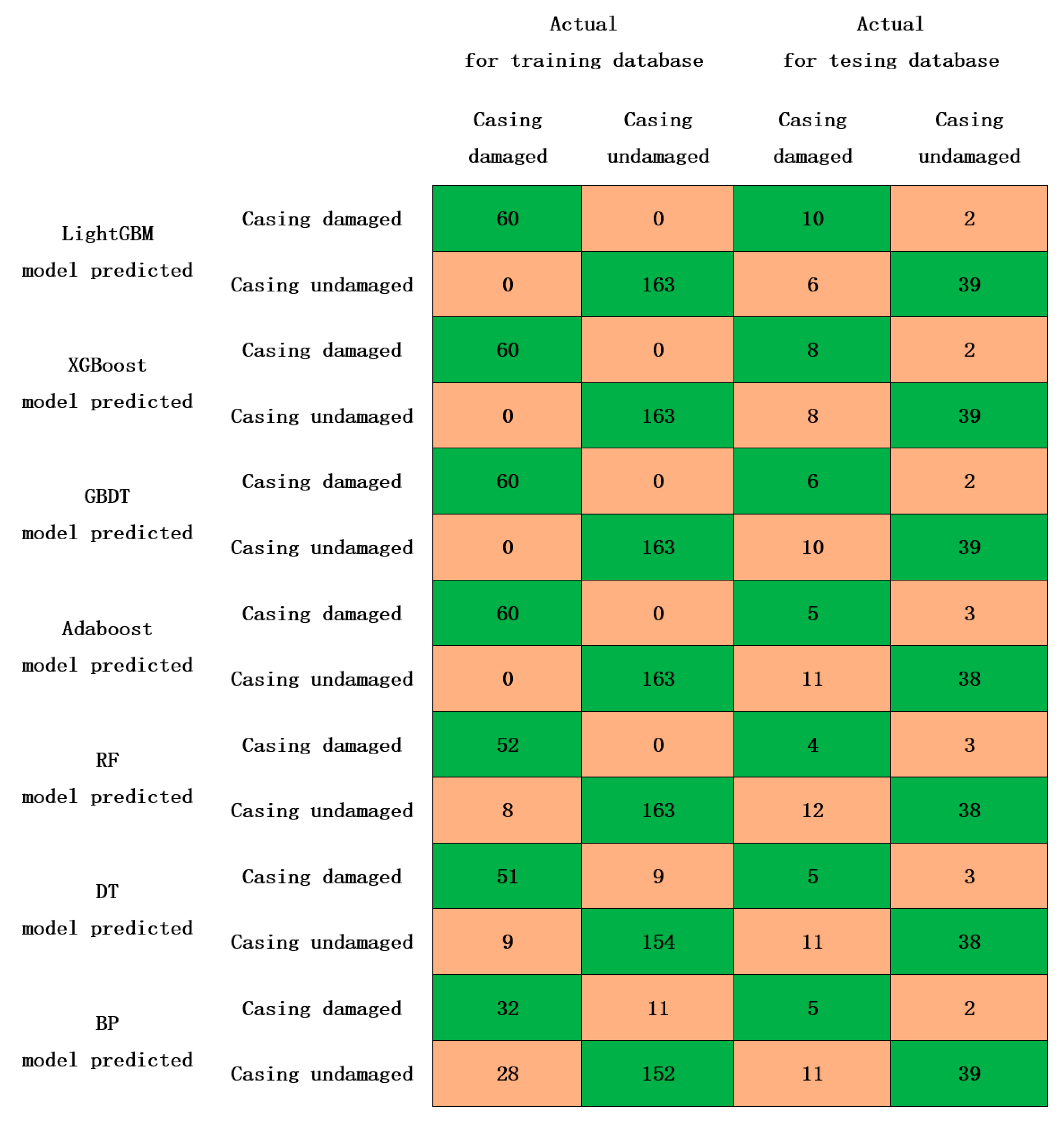
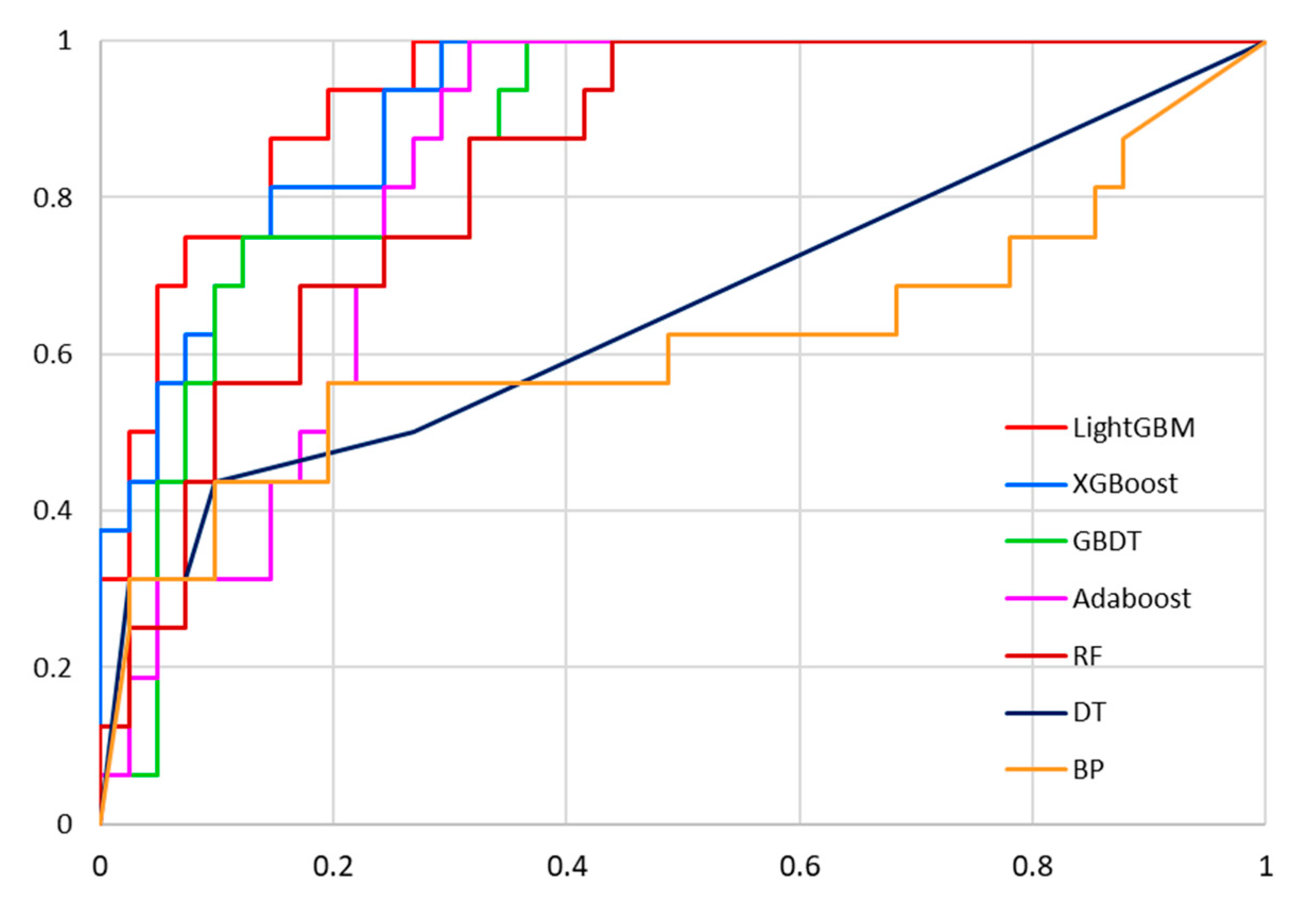
- The study investigated and established a casing damage prediction model based on the LightGBM algorithm using the top 30 controlling factors as the input data, following a comprehensive comparison of seven algorithms, namely the decision tree, RF, AdaBoost, GBDT, XGBoost, LightGBM, and backpropagation neural network algorithms, in terms of five evaluation indices.
- (6)
- The study used different modeling schemes at well and well-layer granularity. The prediction accuracy was higher for the well granularity scheme, with a precision exceeding 80% and recall exceeding 70%.
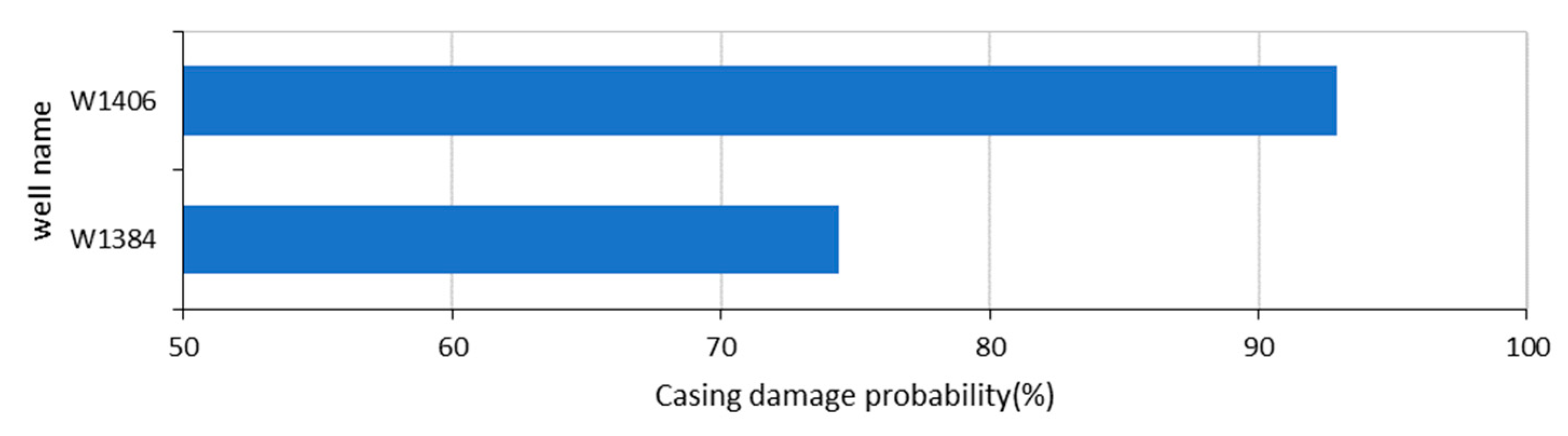
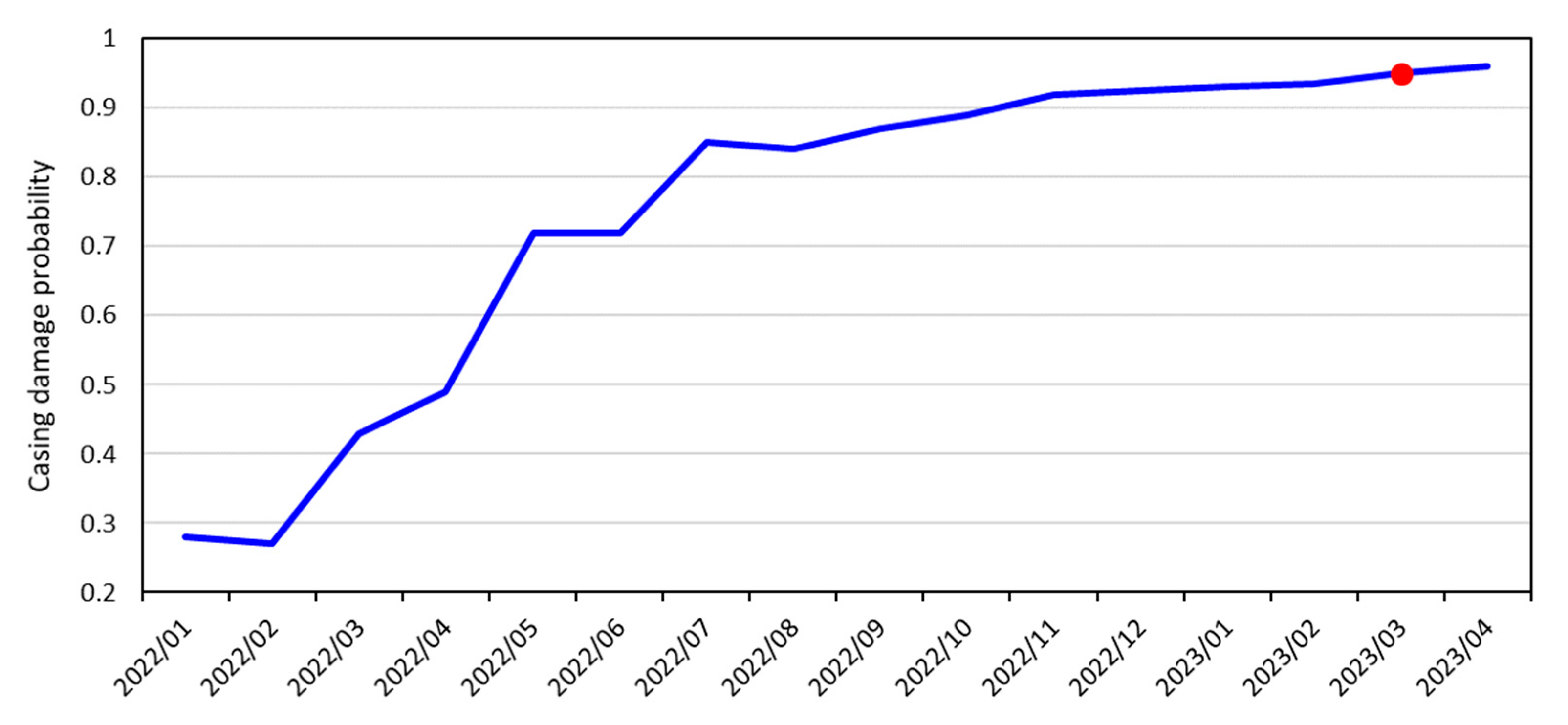
- (7)
- Oilfield data showed that the results of the prediction model are in good agreement with actual casing damage. The prediction model can effectively guide the daily production of an oilfield, extend the life cycles of oil and water well casings, and improve the efficiency of oilfield development.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Noshi, C.I.; Amani, M. Casing string fatigue: No more. In Proceedings of the Presented at Offshore Technology Conference, Houston, TX, USA, 2 May 2022. [Google Scholar] [CrossRef]
- Li, M. Study on Creep Casing Failure Mechanism of Mudstone in Shallow Formation. Master’s Thesis, Northeast Petroleum University, Daqing, China, 2021. [Google Scholar]
- Zhang, X.; Wang, L.; Meng, F. Bayesian neural network approach to casing damage forecasting. Prog. Geophys. 2018, 33, 1319–1324. Available online: https://kns.cnki.net/kcms/detail/11.2982.P.20180122.1050.050.html (accessed on 9 March 2018).
- Fang, J.; Yue, B.; Zhao, H. Analysis of surface loading on casing and cement sheath under nonuniform geologic stress. J. China Univ. Pet. 1997, 21, 46–48. [Google Scholar]
- Fang, J.; Gu, Y.; Mi, F. A numerical analysis of casing collapse under nonuniform load. China Pet. Mach. 1999, 27, 34–37. [Google Scholar]
- Zhang, G.; Liu, C. Effect of creep of surrounding rocks on deformation of oil well casing. Chin. J. Rock Mech. Eng. 2000, 19, 971–975. [Google Scholar]
- Diao, S.; Yang, C.; Liu, J. Mechanism of seepage induced casing damage and numerical simulation. Rock Soil Mech. 2008, 29, 327–332. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, S.; Wang, Z. Evaluating method of the geological-factor risks of the casing damage based on the certainly factors. Pet. Geol. Oilfield Dev. Daqing 2016, 35, 104–108. [Google Scholar]
- Fu, L.; Ma, L.; Wang, W. Cause and repair & maintenance measures of casing in oil and water well. Pet. Drill. Tech. 2002, 30, 53–56. [Google Scholar]
- Xiao, Y. Research on Casing Damage Mechanism, Detection Method and Casing Damage Prediction. Master’s Thesis, Daqing Petroleum Institute, Daqing, China, 2007. [Google Scholar]
- Wang, T.; Yang, S.; Zhu, W. Law and countermeasures for the casing damage of oil production wells and water injection wells in tarim oilfield. Pet. Explor. Dev. 2011, 38, 352–361. [Google Scholar] [CrossRef]
- Fang, X. Casing damage analysis and preventing measures under complex conditions. Pet. Geol. Recovery Effic. 2013, 20, 94–98+101. [Google Scholar] [CrossRef]
- Zhang, J. Study on Casing Damage Causes and Prediction Methods in Complex Faulted Basins. Doctoral Thesis, Ocean University of China, Qingdao, China, 2014. [Google Scholar]
- Zheng, X. Discussion on damage and prevention of oil well casing under complex conditions. Chem. Eng. Equip. 2019, 76+90. [Google Scholar] [CrossRef]
- Lian, Z.; Zhao, G.; Zhang, X. Analysis of computer simulation of three-dimension loads acting on casing. J. Southwest Pet. Univ. Sci. Technol. Ed. 1995, 17, 101–108. [Google Scholar]
- Meng, F.; Zhang, J.; Yang, C.; Yu, W.; Chen, Y. Three-dimensional finite element numerical simulation and physical experiment for magnetism-stress detecting in oil casing. J. Ocean. Univ. China 2015, 14, 669–674. [Google Scholar] [CrossRef]
- Deng, J.; Liu, S.; Shi, D. Calculation of elastoplastic deformation of wellbore in soft mudstone using lagrangian method. J. Geomech. 1999, 5, 35–39. [Google Scholar]
- Han, L.; Yin, F.; Yang, S.; Liu, W.; Deng, Y. Coupled seepage-mechanical modeling to evaluate formation deformation and casing failure in waterflooding oilfields. J. Pet. Sci. Eng. 2019, 180, 124–129. [Google Scholar] [CrossRef]
- Xie, R.; Liu, J.; Zhang, Y. Detecting casing damages with electromagnetic defect detection log and its applications. Well Logging Technol. 2003, 27, 242–245. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Zhao, G. Prediction of casing damage through sequential fussy synthetic evaluation. J. Southwest Pet. Inst. 1996, 18, 77–80. [Google Scholar]
- Zhao, P.; Li, C.; Lu, J. Modeling for a class of nonlinear system and its application in predicting the casing failure trend. Pet. Explor. Dev. 1997, 24, 86–89. [Google Scholar]
- Cheng, L.S.; Luo, Y.; Ding, Z.P. Fuzzy comprehensive evaluation model for estimating casing damage in heavy oil reservoir. Pet. Sci. Technol. 2013, 31, 1092–1098. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, L.; Hu, J. Real-time risk assessment of casing-failure incidents in a whole fracturing process. Process Saf. Environ. Prot. 2018, 120, 206–214. [Google Scholar] [CrossRef]
- Zhou, Y.; Jia, J. Research on new method for predicting of casing damage. Drill. Eng. 2009, 36, 230–234. [Google Scholar]
- Zhou, Y.; Jia, J.; Li, R. Dynamic prediction method of casing damage based on rough set theory and support vector machine. J. China Univ. Pet. 2010, 34, 71–75. [Google Scholar]
- Yan, X.; Xu, Z.; Yang, X. Life prediction analysis of gas well casing string under complex conditions based on support vector machine. In Proceedings of the 8th National MTS Material Testing Academic Conference, Tainan, China, 24–25 September 2010; pp. 560–564. [Google Scholar]
- Zhao, Y.; Jiang, H.; Li, H. Research on predictions of casing damage based on machine learning. J. China Univ. Pet. 2020, 44, 57–67. [Google Scholar]
- Zhu, J.; Wang, S.; Liu, H.; Wang, J. Multi-factor evaluation technology for casing damaged wells. In Proceedings of the International Oil & Gas Conference and Exhibition in China, Beijing, China, 5 December 2006. [Google Scholar]
- Huang, J.; Meng, F.; Zhang, X.; Yang, G. Application of genetic neural network based on pca in prediction of casing damage. J. Xi’an Shiyou Univ. Nat. Sci. Ed. 2018, 33, 84–89. [Google Scholar]
- Wang, L.; Meng, F.; Zhang, X. Application of bayesian neural network based on hmc algorithm in casing damage forecast. Inn. Mong. Petrochem. Ind. 2020, 46, 9–12. [Google Scholar]
- Noshi, C.I.; Noynaert, S.F.; Schubert, J.J. Failure predictive analytics using data mining: How to predict unforeseen casing failures? In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 12 November 2018. [Google Scholar]
- Noshi, C.; Noynaert, S.; Schubert, J. Data mining approaches for casing failure prediction and prevention. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 22 March 2019. [Google Scholar]
- Song, M.; Zhou, X. A casing damage prediction method based on principal component analysis and gradient boosting decision tree algorithm. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 15 March 2019. [Google Scholar]
- Tang, Q.; Wu, H.; Teng, G.; Bu, H.; Tan, C.; Liu, J.; Zhang, X.; Zhang, Y.; Yan, W.; Deng, J. Prediction of casing damage in unconsolidated sandstone reservoirs using machine learning algorithms. In Proceedings of the 2019 IEEE International Conference on Computation, Communication and Engineering, Fujian, China, 8–10 November 2019. [Google Scholar]
- Tan, C.; Wu, H.; Liu, J.; Yan, W.; Deng, J.; Zhang, Y.; Tang, Q.; Bu, H. A novel data mining approach in preventing casing damage of oil production wells. In Proceedings of the 2019 IEEE Eurasia Conference on IOT, Communication and Engineering, Yunlin, Taiwan, 3–6 October 2019. [Google Scholar]
- Carpenter, C. Data mining effective for casing-failure prediction and prevention. J. Pet. Technol. 2019, 71, 55–56. [Google Scholar] [CrossRef]
- Xue, J. Casing damage classification method using random forest algorithms. J. Phys. Conf. Ser. 2020, 1437, 012131. [Google Scholar] [CrossRef]
- Li, T. Research on the method of applying machine learning to predict casing damage. Master’s Thesis, China University of Petroleum, Beijing, China, 2020. [Google Scholar]
- Noshi, C.I.; Amani, M. Data driven physics-guided casing fatigue life estimation. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 4 May 2022. [Google Scholar] [CrossRef]
| Scheme | Function | Database | Advantage | Disadvantage |
|---|---|---|---|---|
| Well granularity | Predict casing damage for a single well | Single well data | Easy to prepare data | Geological layer, perforation, and other related data need to be aggregated upward, resulting in information loss |
| Well-layer granularity | Predict casing damage for each well layer | Sub-layer data | Fully use of geology and engineering layer information | Difficult to prepare data, and the production data of sub-layers often needs to be obtained by other technical means |
| Predicted Class | |||
|---|---|---|---|
| Class = Casing Damaged Well | Class = Normal Well | ||
| Actual class | Class = casing damaged well | True positives (TP) | False negatives (FN) |
| Class = normal well | False positives (FP) | True negatives (TN) | |
| Evaluation Indicator | Definition | Calculation Method |
|---|---|---|
| Accuracy | The proportion of correctly predicted samples to total samples | |
| Precision | The proportion of samples predicted to be positive and actually positive in the number of samples detected | |
| Recall | The proportion of samples predicted to be positive and actually positive in the number of samples actually positive | |
| F1-score | Harmonic average of precision and recall | |
| AUC (Area Under Curve) | It is an evaluation indicator of the merit of a binary classification model and indicates the probability that a positive case of prediction will rank ahead of a negative case. |  |
| Data Categories | Granularity | Samples Records | Main Features |
|---|---|---|---|
| Basic data | Well | 446 | Wellname, block, completion date, current well type, etc. |
| Sub-layer data | Well layer | >60,000 | Wellname, layer, sand layer depth, porosity, permeability, oil saturation, lithology, casing state, etc. |
| Casing data | Casing interval | >3000 | Wellname, steel grade, ID, OD, wall thickness, cement depth, etc. |
| Perforation data | Perforation interval | >10,000 | Wellname, perforation method, perforation depth, perforation density, perforation number, etc. |
| Production data | Well | Oil wells: >74,000 | Wellname, daily oil rate, daily liquid rate, monthly oil rate, monthly liquid rate, cumulative oil production, cumulative liquid production, water cut, oil pressure, casing pressure, etc. |
| Water well: >37,000 | Wellname, daily water injection, monthly water injection, cumulative water injection, oil pressure, casing pressure, etc. | ||
| Well layer | Oil well: >1,000,000 | Wellname, layer, daily oil rate, daily liquid rate, monthly oil rate n, monthly liquid rate, cumulative oil production, cumulative liquid production, water cut, etc. | |
| Water well: >500,000 | Wellname, layer, daily water injection, monthly water injection, cumulative water injection, etc. |
| No. | Steel Grades | Category Code | Normalized Values |
|---|---|---|---|
| 1 | J55 | 1 | 0 |
| 2 | N80 | 2 | 0.25 |
| 3 | P110 | 3 | 0.5 |
| 4 | K55 | 4 | 0.75 |
| 5 | D40 | 5 | 1 |
| Factors | F_Value | p_Value | Factors | Mi |
|---|---|---|---|---|
| Oil rate | 57.61 | 0.00 | Completion days | 0.16 |
| Frequency of stroke | 33.51 | 0.00 | Oil rate | 0.14 |
| Steel grade | 22.09 | 0.00 | Frequency of stroke | 0.12 |
| Submergence depth | 20.98 | 0.00 | Liquid level | 0.10 |
| Liquid level | 18.23 | 0.00 | Wall thickness | 0.09 |
| Production layers | 18.09 | 0.00 | Pump depth | 0.08 |
| Wall thickness | 16.78 | 0.00 | External diameter | 0.08 |
| Perforation location | 16.17 | 0.00 | Perforation density | 0.08 |
| Log Interpretation Conclusions | 15.21 | 0.00 | Frequency of stroke | 0.08 |
| Backpressure | 14.56 | 0.00 | Backpressure | 0.07 |
| Perforation thickness | 11.73 | 0.00 | Casing pressure | 0.07 |
| Water injection volume | 10.79 | 0.00 | Steel grade | 0.07 |
| Pump deep | 10.53 | 0.00 | Flowing pressure | 0.07 |
| Displacement | 10.22 | 0.00 | Top depth of sand layer | 0.06 |
| Water cut | 8.24 | 0.00 | Flowing pressure | 0.06 |
| Production layer | 7.84 | 0.01 | Water injection volume | 0.06 |
| Pump diameter | 7.53 | 0.01 | Production mode | 0.06 |
| Completion days | 7.50 | 0.01 | Top depth of sand layer | 0.06 |
| Fluid producing intensity | 7.05 | 0.01 | Pump deep | 0.05 |
| Casing pressure | 6.63 | 0.01 | Perforation location | 0.05 |
| Injection mode | 6.02 | 0.01 | Submergence depth | 0.05 |
| Top height of cement ring | 5.59 | 0.02 | Perforation density | 0.05 |
| Perforation density | 5.27 | 0.02 | Production layers | 0.04 |
| Top depth of sand layer | 4.80 | 0.03 | Thickness of the sand layer | 0.04 |
| Thickness of the sand layer | 4.34 | 0.04 | Log interpretation conclusions | 0.04 |
| Production days | 4.14 | 0.04 | Injection mode | 0.04 |
| Shale Content | 3.86 | 0.05 | Shale Content | 0.04 |
| Flowing pressure | 3.60 | 0.06 | Production days | 0.04 |
| Producing pressure difference | 3.54 | 0.06 | Fluid producing intensity | 0.04 |
| Oil pressure | 3.16 | 0.08 | Water cut | 0.03 |
| Algorithm | Decision Tree (DT) | Random Forest (RF) | AdaBoost | GBDT | XGBoost | LightGBM | Neural Network (BP) |
|---|---|---|---|---|---|---|---|
| Major parameters | Max_depth | max_depth | max_depth | max_depth | max_dept | max_dept | hidden_layer_ |
| Max features | n_estimators | n_estimators | n_estimators | n_estimators | n_estimators | sizes, activation | |
| max_samples | max_features | subsample | subsample | subsample | |||
| max_features | max_features | colsample_bytree | colsample_bytree |
| Algorithm | Accuracy (%) | Precision (%) | Recall (%) | F1 (%) | AUC (%) |
|---|---|---|---|---|---|
| LightGBM | 87.50 ± 3.15 | 75.29 ± 8.80 | 78.33 ± 9.50 | 76.38 ± 6.17 | 91.73 ± 3.27 |
| XGBoost | 87.49 ± 4.20 | 81.91 ± 13.13 | 70.0 ± 18.26 | 73.69 ± 8.86 | 88.11 ± 3.99 |
| GBDT | 84.48 ± 3.90 | 74.54 ± 13.24 | 66.67 ± 11.79 | 68.97 ± 5.38 | 89.89 ± 2.04 |
| Adaboost | 87.07 ± 2.67 | 84.19 ± 10.94 | 65.00 ± 20.75 | 71.02 ± 8.66 | 87.69 ± 5.59 |
| RF | 87.06 ± 4.10 | 80.86 ± 14.84 | 71.67 ± 19.18 | 73.46 ± 8.33 | 90.45 ± 2.72 |
| DT | 84.91 ± 4.02 | 70.80 ± 8.08 | 71.67 ± 12.64 | 70.77 ± 9.11 | 81.84 ± 5.92 |
| BP | 67.66 ± 5.62 | 37.97 ± 8.58 | 41.67 ± 16.67 | 39.09 ± 12.03 | 58.24 ± 9.06 |
| Algorithm | Accuracy (%) | Precision (%) | Recall (%) | F1 (%) | AUC (%) |
|---|---|---|---|---|---|
| LightGBM | 89.84 ± 10.29 | 69.72 ± 31.12 | 67.50 ± 14.25 | 66.85 ± 23.29 | 84.11 ± 13.61 |
| XGBoost | 90.14 ± 6.92 | 69.21 ± 29.89 | 60.0 ± 16.3 | 62.15 ± 19.72 | 82.21 ± 10.76 |
| GBDT | 87.05 ± 9.51 | 57.56 ± 32.92 | 62.5 ± 19.76 | 57.86 ± 24.59 | 82.35 ± 17.53 |
| Adaboost | 91.37 ± 5.27 | 72.48 ± 26.17 | 55.0 ± 16.77 | 61.96 ± 20.0 | 8 7.69 ± 5.59 |
| RF | 87.68 ± 8.69 | 64.0 ± 35.78 | 42.5 ± 18.96 | 48.65 ± 23.68 | 77.6 ± 10.05 |
| DT | 89.21 ± 4.47 | 82.0 ± 30.33 | 32.5 ± 14.25 | 42.33 ± 15.88 | 65.63 ± 13.87 |
| BP | 90.44 ± 4.12 | 81.71 ± 30.94 | 37.5 ± 8.84 | 50.37 ± 13.59 | 76.41 ± 5.14 |
| Granularity | Accuracy (%) | Precision (%) | Recall (%) | F1 (%) | AUC (%) |
|---|---|---|---|---|---|
| Well | 87.29 ± 3.77 | 80.69 ± 9.40 | 71.31 ± 11.38 | 74.99 ± 8.06 | 91.86 ± 3.77 |
| Well-layer | 92.45 ± 2.36 | 79.79 ± 13.43 | 60.81 ± 14.20 | 67.79 ± 11.27 | 93.95 ± 3.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wu, L.; Jia, D.; Wang, L.; Chang, J.; Li, X.; Cui, L.; Shi, B. A Machine Learning Method for the Risk Prediction of Casing Damage and Its Application in Waterflooding. Sustainability 2022, 14, 14733. https://doi.org/10.3390/su142214733
Zhang J, Wu L, Jia D, Wang L, Chang J, Li X, Cui L, Shi B. A Machine Learning Method for the Risk Prediction of Casing Damage and Its Application in Waterflooding. Sustainability. 2022; 14(22):14733. https://doi.org/10.3390/su142214733
Chicago/Turabian StyleZhang, Jiqun, Li Wu, Deli Jia, Liming Wang, Junhua Chang, Xianing Li, Lining Cui, and Bingbo Shi. 2022. "A Machine Learning Method for the Risk Prediction of Casing Damage and Its Application in Waterflooding" Sustainability 14, no. 22: 14733. https://doi.org/10.3390/su142214733






