The One E-Ticket Customized Bus Service Mode for Passengers with Multiple Trips and the Routing Problem

Abstract

To alleviate the problems of traffic congestion, excessive energy consumption, and the environmental pollution caused by private cars, it is essential to use public transportation (PT). However, passengers making multiple trips in a short time period must repeatedly make travel mode choices, purchase tickets, and wait for buses for each trip, which may negatively affect their preference for PT. In order to improve the attractiveness of PT, especially for passengers requiring multiple trips in a short time period, this paper proposes the one e-ticket customized bus service mode for passengers with multiple trips (OECBSM-PMT) by customized buses (CBs). Besides, a CB-routing optimization model for the OECBSM-PMT is also developed in this paper, formulated as a mixed-integer linear programming based on a vehicle routing problem with pickup and delivery and time windows (VRPPDTW). The model aims to maximize the profit and minimize the costs of operation with considering passengers with multi-trip requests, homogeneous CB fleets with pickup/delivery-time-window constraints, and mixed loads. A service effectiveness identification procedure based on genetic algorithm (GA) is proposed to cope with the calculation considering the characteristics of passengers with multiple trips. Finally, the proposed model and algorithm are verified and analyzed using the case of the 2022 Beijing Winter Olympic Games. It can be found from the results that the method can provide an optimized CB route plan and timetable, and the algorithm GA-I obtains better solutions than other solving strategies in most instances. The proposed OECBSM-PMT and corresponding optimized method can better adapt to diverse travel demands, significantly improve the convenience for passengers, especially those making multiple trips in a short time period and will eventually promote a higher level of public transport service.

1. Introduction

1.1. Background

The rapid development of urbanization in China has diversified travel into aspects such as traveling for commuting, business, sightseeing, and shopping reasons, which has led to an increase in the average number of daily passenger trips. For example, the number of daily trips per capita in private cars in Beijing reached 3.33 on weekdays and 3.20 on weekends in 2019, both of which were significantly higher than in previous years [1]. The increase in passengers making multiple trips in a short time period has created higher demand for more flexible and convenient travel modes, possibly reinforcing the reliance on private cars. According to the Ministry of Transport of the People’s Republic of China, there were 27.53 million newly registered cars in 2021, and car ownership was up to 297 million as of September 2021 [2]. Such a large number of private cars has caused serious traffic congestion and accelerated energy consumption. Meanwhile, excessive exhaust emissions have caused environmental pollution and global warming, making it difficult for the global Paris Agreement, aimed at controlling the rate of increase in global temperatures, to be achieved.

To sustainably handle these challenges, a higher use of public transportation (PT) has been proposed. However, traditional PT, with fixed stations, routes, and schedules, struggles to provide flexible and convenient services for passengers, especially those making multiple trips. Fortunately, the combination of information technology, artificial intelligence, and cloud computing has been reshaping PT systems. The customized bus (CB), as a new type of PT system, can provide flexible and efficient transit services for passengers with similar travel demands [3], and thereby better encourage passengers to shift from private cars to buses.

1.2. Literature Review

Evolved from the ‘subscription bus’ phenomenon [4], the CB has the advantages of reducing environmental pollution, improving daily trip structure, and alleviating traffic congestion [5], thus attracting much attention in recent years. However, considering the higher operating costs of CBs compared to traditional PT, the absence of a suitable CB service mode based on the characteristics of passenger-diversified travel demands will make it difficult for it to survive in the competitive market and lead to a substantial waste of resources and the disappointment of many loyal passengers [6].

Some scholars have studied CBs from the perspective of service mode. Liu et al. [7] summarized the application of various CB service modes in 30 Chinese cities from the perspective of service design and operational processes. Wang et al. [8] investigated the indicators of the CB service mode in Beijing and analyzed the traffic adaptation management of CB services. Wang et al. [9] analyzed the key determinants of passenger loyalty toward CBs based on the historical purchase behavior and personal attributes of users. Wang et al. [10] promoted the idea of the use of the CB service mode during the COVID-19 pandemic to prevent cross-infection on the way to work in Shenzhen, Jinan, and Beijing. He et al. [11] proposed a commuter-oriented CB service mode based on the travel behavior characteristics of commuters under COVID-19.

For the CB operation process, it is essential to solve the CB routing problem and obtain optimized CB schedules to provide a high level of service by considering operating costs and service efficiency [12]. Specifically, the objective functions mainly focus on minimizing operating costs and route length or maximizing operating profit and the number of satisfied passengers [13,14,15,16]. Ma et al. [17] proposed a methodological framework for CB network design based on passengers’ travel needs, collected through Internet questionnaires. Cao et al. [18] characterized passenger assignment on CBs by minimizing average travel time, waiting time, penalty for delay, and ticket price. Tong et al. [19] proposed a CB service design problem under space-time and formulated an optimization model to determine the CB service dispatch strategy. Guo et al. [12] proposed a mixed-integer programming model that simultaneously determined station location and route design. Chen et al. [20] studied the CB route design problem by allowing CBs to perform multiple trips. Even though an increasing amount of research has explored the CB operation problem, each passenger has been assumed to have a single travel need, with all travel needs independent. No previous studies have considered the scenario whereby a passenger may have multiple travel needs and how to describe the demand satisfaction of passengers making multiple trips.

The CB routing problem can be modeled mathematically by one of the well-known optimization problems: the vehicle routing problem (VRP). The classical VRP introduced by Dantzig and Ramser [21] has been studied intensively. Angelelli et al. [22] introduced a new type of problem scenario: the VRP with pickup and delivery and time windows (VRPPDTW). The objective of the VRP varies from one study to another based on the focus of the problem. Some objective functions observed in the literature include but are not limited to minimization of total route length, travel and vehicle usage cost, passengers’ inconvenience, and their combination [23,24,25]. Chen et al. [20] proposed a CB route design model based on the VRPPDTW with simultaneous optimization of operating cost and passenger benefit. In order to solve the VRP, several algorithms have been suggested in the extant literature. Fan et al. [25] maximized customer satisfaction and minimized total cost simultaneously based on a classical tabu search. Baldacci et al. [26] proposed an exact algorithm based on a set-partitioning formulation to minimize total routing costs. Yanik et al. [23] used a genetic algorithm (GA) to fix the status of the vendor used for the assignment decisions. In a clustering algorithm proposed by Hame et al. [27], the solution considers a recursive single-vehicle algorithm based on the passenger-to-vehicle assignment from the first clustering stage.

Previous studies have made important contributions to the CB service mode and organizational optimization by studying the CB routing problem. However, as mentioned before, previous studies assume that each collected request contains only one trip and so no models or algorithms can be applied directly to handle the scenario whereby a passenger’s request contains multiple trips. To satisfy the travel demand of these passengers with multiple trips, this paper proposes the one e-ticket customized bus service mode for passengers with multiple trips (OECBSM-PMT), which can overcome the shortcomings of traditional CB services, such as the need to repeatedly make travel mode choices, purchase tickets, and wait for buses for each trip. Besides, the CB routing problem of the OECBSM-PMT is modeled mathematically based on the VRPPDTW, and the corresponding algorithm considering the characteristics of multiple trips is proposed based on a GA strategy. Finally, the model and algorithm are verified and analyzed using the case of the 2022 Beijing Winter Olympic Games.

1.3. Contributions

The contributions of this study can be summarized as follows. Firstly, rather than treating each trip independently as in the traditional CB service, this paper proposes the OECBSM-PMT, which can satisfy the travel request of a passenger who may need to make several trips in a short time period. A passenger with multiple trips can enjoy the CB service for each trip by simply sending his/her travel request once in the OECBSM-PMT. Secondly, to provide high-level CB services for passengers with multiple trips, the CB routing problem of the OECBSM-PMT is modeled mathematically based on the VRPPDTW considering the characteristics of multiple trips. Thirdly, this paper proposes a service effectiveness identification procedure based on GA with optimization time difference insertion heuristics (OTDIH) to cope with the calculation under the characteristics of passengers with multiple trips. The service effectiveness identification procedure can help the GA to obtain better solutions in an acceptable computational time.

The remainder of this paper is organized as follows. Section 2 provides a detailed description of the OECBSM-PMT and presents an example and relevant notation. In Section 3, the mathematical foundation of the CB routing problem of the OECBSM-PMT is introduced. Section 4 proposes the OTDIH-based GA used to cope with the problem. Section 5 further tests the model using the case of the 2022 Beijing Winter Olympic Games. Section 6 provides concluding remarks and suggested future research.

2. Description of the OECBSM-PMT, Illustrative Example and Notation

2.1. The OECBSM-PMT

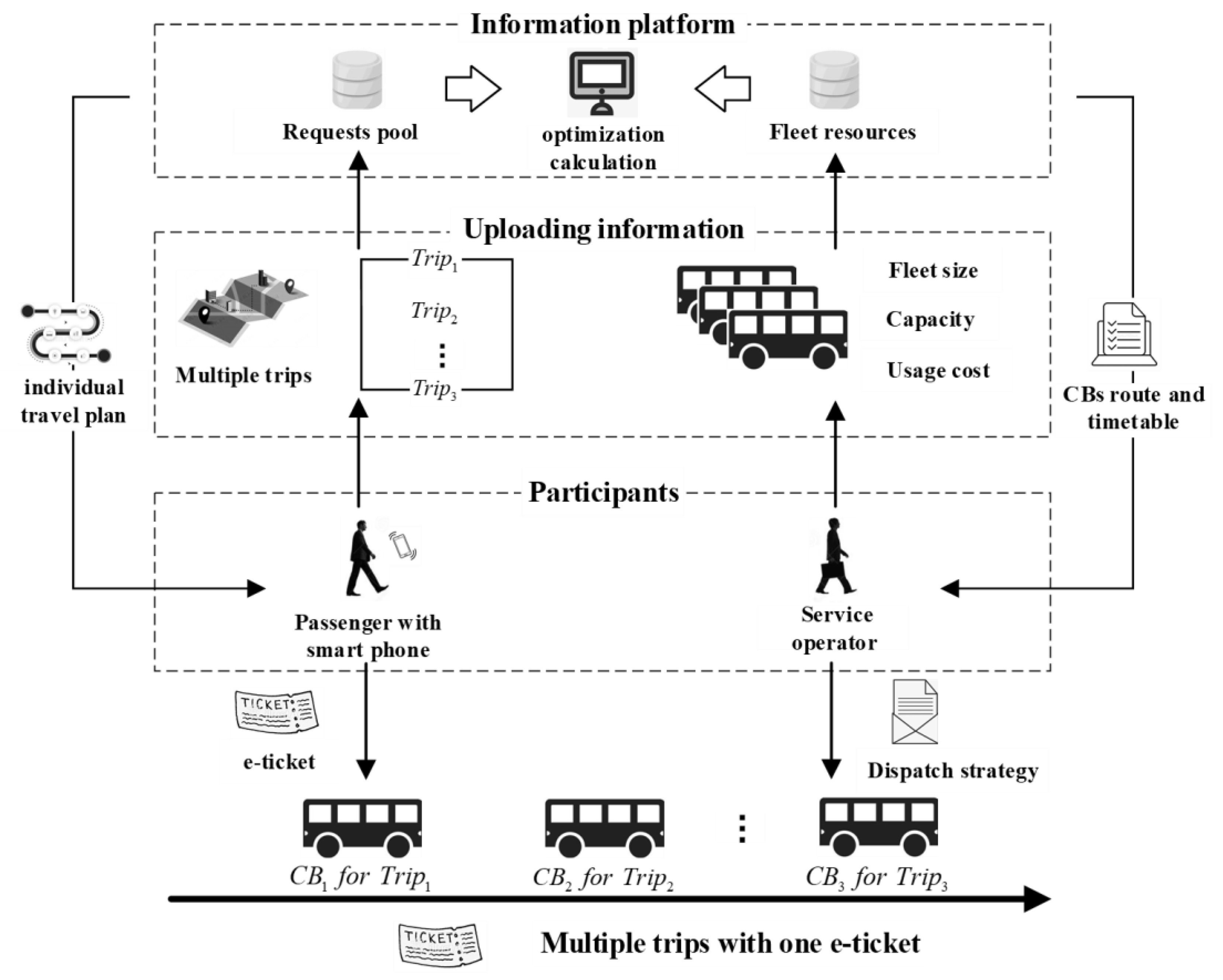
The OECBSM-PMT is based on an information platform built with computer and communication technologies to optimize the organization of CBs, with operational data derived from the passengers and operators participating in the mode, as shown in Figure 1. Each passenger sends a service request containing either a single trip or several trips to the requests pool on the platform, specifically including information on the origin and destination, and time window for boarding and alighting. Meanwhile, the operators provide fleet resource information, such as fleet size, capacity, and usage costs to the fleet resource pool on the platform. Then, optimization calculations from the perspectives of both passengers and operators are carried out based on the above information to obtain the CB schedule: from the perspective of the passengers, the criterion for an effective service is that each trip in his/her multi-trip request is satisfied; from the perspective of the operators, the objective is to maximize the service profit and minimize the CB usage and travel costs. With an optimized CB schedule, the information platform sends individual travel tickets to passengers electronically, including information on boarding and alighting times and the corresponding CB schedules. Meanwhile, the service operators are provided with a CB dispatch strategy for determining the routing plan of the CBs and corresponding timetable. The OECBSM-PMT enables passengers with multiple trips to complete their travel needs with only one personalized e-ticket.

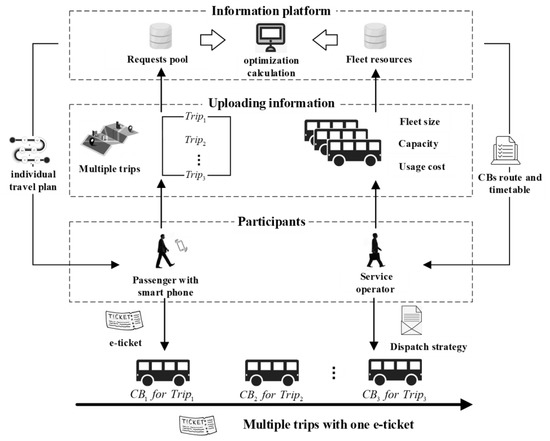
Figure 1. The components and relationships of the OECBSM-PMT service mode.

2.2. An Illustrative Example

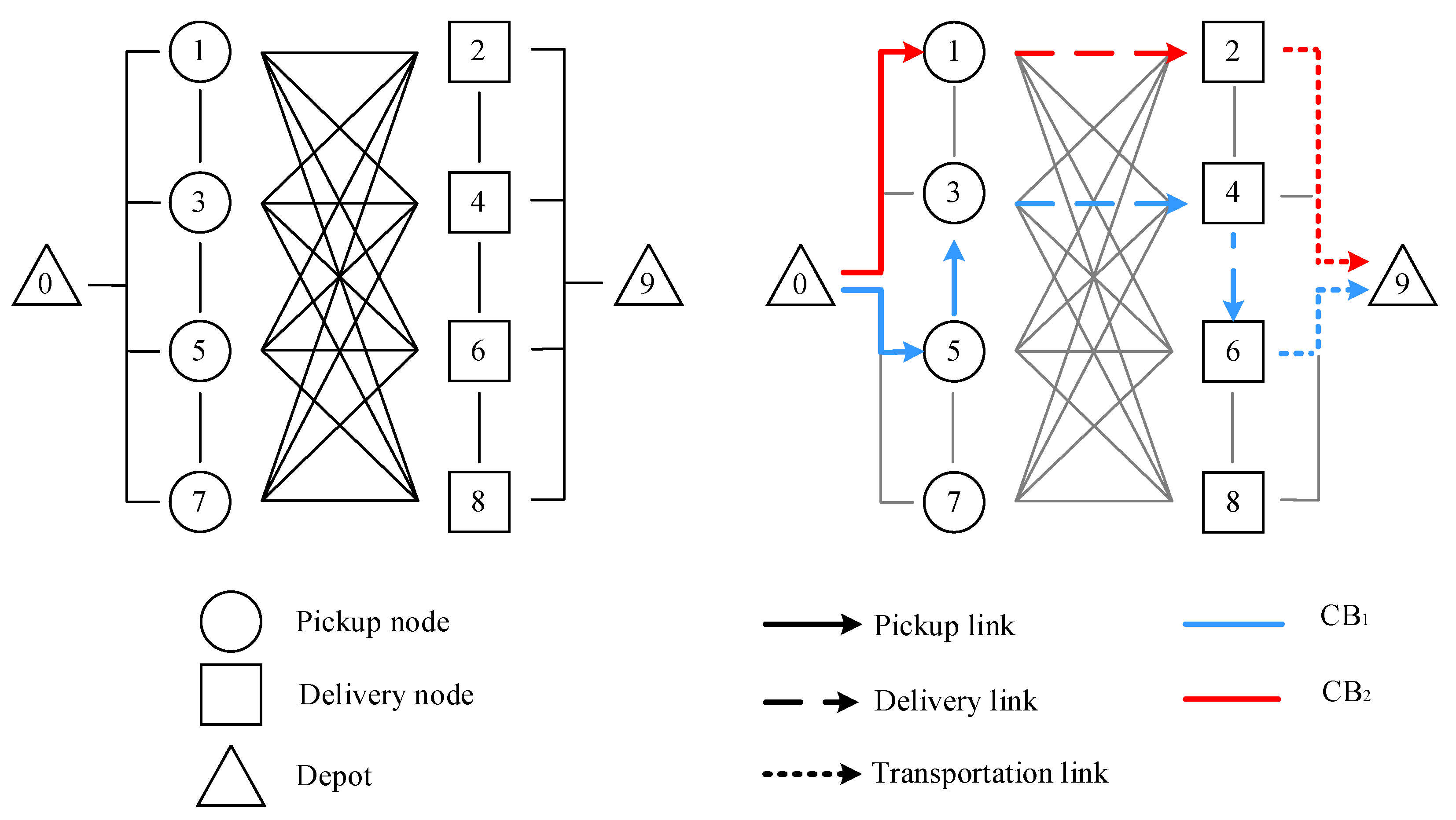
Consider a transportation network including two depots and eight nodes (four pickup nodes and four delivery nodes), as shown in Figure 2. Table 1 lists the travel times between nodes. Suppose there are three passengers, A, B, and C. Passenger A sends a request to the platform including two trips [(1,2), (3,4)], which means Passenger A needs to travel from node 1 to node 2 first and then from node 3 to node 4. Both Passenger B and Passenger C send requests to the platform including only one trip, [(5,6)] and [(7,8)], respectively. The time window of each pickup/delivery node is shown in Table 2, where $a_i$ and $b_i$ represent the earliest and latest times, respectively. Meanwhile, the operators provide fleet resource information to the platform. Suppose there are two CBs with capacity assumed to be 2.

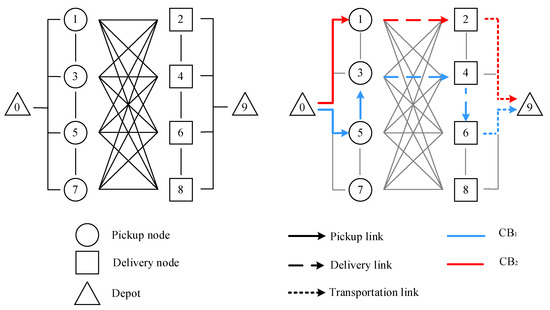
Figure 2. The network and shortest path combination of the customized buses.

Table 1. Travel times (h:min) between nodes.

Dep. Arr.	1	2	3	4	5	6	7	8	9
0	0:20	\	0:25	\	0:25	\	0:10	\	\
1	\	1:30	2:50	0:50	2:50	3:30	1:00	0:45	\
2	0:00	\	2:10	0:45	2:10	1:00	3:30	2:50	0:10
3	1:00	2:10	\	0:30	0:00	3:30	2:50	0:45	\
4	0:40	0:40	1:30	\	1:30	0:50	0:45	1:30	0:10
5	1:00	2:10	0:00	0:30	\	3:30	2:50	0:45	\
6	0:50	\	2:57	1:10	2:57	\	1:20	2:06	0:10
7	0:30	0:30	\	0:45	1:20	1:30	\	2:10	\
8	2:30	2:30	0:30	\	0:30	2:10	1:25	\	0:20

Table 2. Time windows of pickup/delivery nodes.

Node	1	2	3	4	5	6	7	8
$a_i$	9:35	11:20	14:40	15:55	14:40	16:30	15:35	16:40
$b_i$	10:35	12:20	15:40	16:05	15:40	17:30	16:35	17:40

Based on the optimization objective, the CB dispatch strategy is calculated considering the time window constraint, load constraint, and travel times between nodes. Specifically, from Table 1 and Table 2, it can be found that the time windows of pickup nodes 3 and 5 are the same and the travel time between these two nodes is zero. It can be deduced that the second trip of the request of Passenger A and the request of Passenger B start from the same location. Therefore, these two trips can be allocated to one CB under time and load constraints, i.e., CB₁ can operate along the following route: 0→5→3→4→6→9. For the request of Passenger C, service is infeasible with the given timetable. This is because the earliest arrival time at node 8 from node 7 is 17:45 which is later than the latest requested delivery time to node 8 of 17:40. Considering the time window and load constraints, CB₂ can be dispatched to satisfy the first trip of the request of Passenger A. Therefore, the optimized CB dispatch strategy consists of CB₁ and CB₂ respectively operating along the following two routes: 0→5→3→4→6→9 and 0→1→2→9, as shown in Figure 2. Finally, the passengers whose requests can be satisfied will receive e-tickets: Passenger A receives an e-ticket containing trips (1,2) and (3,4), and Passenger B receives an e-ticket containing trip (5,6).

Based on the above observations, the request of each passenger may contain one or several trips, and each trip has its own origin/destination and time window requirements. One of the key issues in the OECBSM-PMT is to identify the satisfaction of a passenger’s request, especially when the request contains several trips. In other words, the platform should identify whether all trips in a passenger’s request can be served, which would be considered an effective service.

3. The CB Routing Optimization Model of the OECBSM-PMT

In order to optimize the CB schedule, this paper models the CB routing problem of the OECBSM-PMT mathematically based on one of the well-known optimization problems: the VRPPDTW. The objective of the problem is to maximize the service profit and minimize the costs of operation, including CB usage and driving. Furthermore, passengers with multiple trips, mixed loads, and homogeneous fleets with pickup and delivery time windows are considered. In our proposed model, an effective service means all the given requests of a passenger with multiple trips are satisfied, with each request accessed at most once.

3.1. Notation

Table 3 lists the notation used in this study.

Table 3. Sets, indices, and parameters used for model formulation.

Notation	Definition
$\overline{C}$	Set of all passengers’ requests
$C$	$\mathrm{Set} \mathrm{of} \mathrm{all} \mathrm{trips} \mathrm{in} \mathrm{the} \mathrm{request}, C\in \overline{C}$
$P$	Set of pickup nodes
$D$	Set of delivery nodes
$N$	$\mathrm{Set} \mathrm{of} \mathrm{nodes} (\mathrm{pickup} \mathrm{nodes} \mathrm{and} \mathrm{delivery} \mathrm{nodes}) N=P\cup D$
$L$	Set of links
$K$	Set of customized buses
$t_w$	$\mathrm{Trip} \mathrm{in} \mathrm{request} C$$, t_w\in C, C\in \overline{C}$
$N_C$	$\mathrm{Number} \mathrm{of} \mathrm{trips} \mathrm{in} \mathrm{request} C$
$i,j$	$\mathrm{Index} \mathrm{of} \mathrm{nodes}, i,j\in N$
$(i,j)$	$\mathrm{Index} \mathrm{of} \mathrm{indices}, (i,j)\in L$
$o/d$	Index of departure/arrival depots
$k$	$\mathrm{Index} \mathrm{of} \mathrm{customized} \mathrm{buses}, k\in K$
$d_{i,j}$	$\mathrm{Travel} \mathrm{cost} \mathrm{from} \mathrm{node} i$$\mathrm{to} \mathrm{node}j$$, i,j\in N$
$S_i$	$\mathrm{Service} \mathrm{time} \mathrm{at} \mathrm{node} i$$, i\in N$
$t_{i,j,k}$	$\mathrm{Travel} \mathrm{time} \mathrm{between} \mathrm{nodes} i$$\mathrm{and} j$$\mathrm{by} \mathrm{vehicle} k$$, i,j\in N, k\in K$
$[a_i,b_i]$	$\mathrm{Time} \mathrm{window} \mathrm{of} \mathrm{node} i$$, \mathrm{where} a_i$$\mathrm{is} \mathrm{the} \mathrm{earliest} \mathrm{service} \mathrm{time} \mathrm{and} b_i$$\mathrm{is} \mathrm{the} \mathrm{latest} \mathrm{service} \mathrm{time}, i\in N$
$q^C$	$\mathrm{The} \mathrm{service} \mathrm{profit} \mathrm{of} \mathrm{request} C$
${\alpha }_k$	$\mathrm{The} \mathrm{usage} \cos \mathrm{t} \mathrm{of} \mathrm{CB} k$
$l_{i,k}$	$\mathrm{The} \mathrm{demand} \mathrm{of} \mathrm{pickup}/\mathrm{delivery} \mathrm{node} i$$\mathrm{by} \mathrm{vehicle} k$
$C_k$	$\mathrm{Capacity} \mathrm{of} \mathrm{vehicle} k,\begin{array}{c}\end{array}k\in K$
$\epsilon /M$	A sufficiently small / large positive number
${\alpha }_i^C$	$1 \mathrm{if} \mathrm{request} C,C\in \overline{C}$$, \mathrm{contains} \mathrm{pickup} \mathrm{node} i, i\in P$ and 0 otherwise
$x_{i,j,k}$	$1 \mathrm{if} \mathrm{customized} \mathrm{bus} k$$\mathrm{travels} \mathrm{from} \mathrm{node} i$$\mathrm{to} \mathrm{node} j$$\mathrm{and} 0 \mathrm{otherwise}, i,j\in N,k\in K$.
$Z^C$	$1 \mathrm{if} \mathrm{request} C,C\in \overline{C}$ is satisfied, and 0 otherwise
$T_{i,k}$	$\mathrm{Time} \mathrm{when} \mathrm{vehicle} k$$\mathrm{starts} \mathrm{service} \mathrm{at} \mathrm{node} i$$, i\in N,k\in K$
$L_{i,k}$	$\mathrm{Load} \mathrm{of} \mathrm{vehicle} k$$\mathrm{after} \mathrm{service} \mathrm{at} \mathrm{node} i$$, i\in N,k\in K$

3.2. The Optimization Model

The mathematical representation of the OECBSM-PMT can be described as follows. Let $\overline{C}$ be the set of all passengers’ requests $\overline{C}=\left\{C|C\in \overline{C}\right\}$, and let each request $C=\left\{t_w|t_w\in C\right\}=\left\{t_1,t_2,\dots ,t_{N_C}\right\}$ contain one or several trips, where $N_C$ is the total number of trips in request $C\in \overline{C}$. Let $P$ and $D$ denote the sets of pickup nodes and delivery nodes, respectively. Then, we get $N=P\cup D$, which contains all pickup and delivery nodes, where each node in set N can be modeled as a virtual node in the transportation network. Furthermore, trip $t_w\in C,C\in \overline{C}$ can be denoted by $\left(i,j\right), i\in P, j\in D$, where i and j are the pickup node and delivery node, respectively. It should be noted here that, as nodes represent requests, different nodes in the transportation network may represent the same geographical location. Let $K$ be the set of all CBs and $C_k$ be the capacity of CB k. Each bus $k,k\in K$, starts from departure depot $o$, then visits a sequence of nodes to transport passengers, before returning to arrival depot $d$. The depot can be a CB depot, event venue, or regular bus parking area.

To identify the satisfaction of a passenger’s request in the OECBSM-PMT, especially when the request contains several trips, this paper introduces a binary decision variable $Z^C$ to describe whether all trips in request $C\in \overline{C}$ are served,

$$Z^C=\{\begin{array}{cc}1& \mathrm{if}{\displaystyle \sum _{i\in P}^{}}{\displaystyle \sum _{j\in N}^{}}{\displaystyle \sum _{k\in K}^{}}{\alpha }_i^C{x}_{i,j,k}^{}=N_C\hfill \\ 0& \mathrm{otherwise}\hfill \end{array},C\in \overline{C}$$

(1)

$${\alpha }_i^C=\{\begin{array}{cc}1& \mathrm{if} \mathrm{request} C \mathrm{contains} \mathrm{node} i\\ 0& \mathrm{otherwise}\hfill \end{array} ,i\in P,C\in \overline{C}$$

(2)

Again, if and only if each trip in a request with multiple trips is served can the passenger be defined as being served effectively. Besides, each CB starts its route from the depot and visits a sequence of nodes to transport passengers. Each visited node ($i\in N$) along the route in the constructed request network is recognized by the pickup/delivery node. Although the nodes in the request network have no geographical significance, they are all generated by realistic passenger requests. Therefore, the timetable attribute of each node in the request network corresponds to the following practical features:

Feature 1. If the travel time between two nodes is zero, these two nodes are generated from the same physical location.

Feature 2. The time windows of the trips in a request do not overlap, and the arrival location of the previous trip can be the departure location of the next trip.

Feature 3. The travel time of the directed link $(i,j)\in L$ is related to the real road network, which is influenced by the outbound and inbound directions.

With the above considerations, the CB routing optimization model of the OECBSM-PMT is formulated as follows:

$$Max{\displaystyle \sum _{C\in \overline{C}}{q}^C{Z}^C}-{\displaystyle \sum _{j\in P}{\displaystyle \sum _{k\in K}{\alpha }_k{x}_{o,j,k}}}-{\displaystyle \sum _{i\in N\cup o}{\displaystyle \sum _{j\in N\cup d}{\displaystyle \sum _{k\in K}{d}_{i,j}{x}_{i,j,k}}}}$$

(3)

$${\displaystyle \sum _{j\in P\cup d}{x}_{o,j,k}}=1\begin{array}{cc}& \forall k\in K\end{array}$$

(4)

$${\displaystyle \sum _{i\in D\cup o}{x}_{i,d,k}}=1\begin{array}{cc}& \forall k\in K\end{array}$$

(5)

$${\displaystyle \sum _{i\in N\cup o}{x}_{i,j,k}}-{\displaystyle \sum _{i\in N\cup d}{x}_{j,i,k}}=0\begin{array}{cc}& \forall j\in N\end{array},\forall k\in K$$

(6)

$${\displaystyle \sum _{j\in N}{\displaystyle \sum _{k\in K}{x}_{i,j,k}} \le 1}\begin{array}{cc}& \forall i\in P\end{array}$$

(7)

$${\displaystyle \sum _{j\in N}{x}_{i,j,k}}-{\displaystyle \sum _{j\in N}{x}_{j,n+i,k}}=0\begin{array}{cc}& \forall i\in P\end{array},\forall k\in K$$

(8)

$$a_i\le T_{i,k}\le b_i\begin{array}{cc}& \forall i\in N\end{array},\forall k\in K$$

(9)

$$T_{i,k}+S_i+t_{i,j,k}\le T_{j,k}+M\begin{array}{cc}\left(1-x_{i,j,k}\right)& \begin{array}{cc}\forall i,j\in N,\forall k\in K& \end{array}\end{array}$$

(10)

$$T_{i,k}+S_i+t_{i,n+i,k}\le T_{n+i,k}\begin{array}{cc}& \begin{array}{cc}\forall i\in P,\forall k\in K& \end{array}\end{array}$$

(11)

$$L_{i,k}-l_{j,k}\le L_{j,k}+M\begin{array}{cc}\left(1-x_{i,j,k}\right)& \begin{array}{cc}\forall i\in N,\forall j\in D,\forall k\in K& \end{array}\end{array}$$

(12)

$$L_{i,k}+l_{j,k}\le L_{j,k}+M\begin{array}{cc}\left(1-x_{i,j,k}\right)& \begin{array}{cc}\forall i\in N,\forall j\in P,\forall k\in K& \end{array}\end{array}$$

(13)

$$l_{i,k}\le L_{i,k}\le C_k\begin{array}{cc}& \begin{array}{cc}\forall i\in P,\forall k\in K& \end{array}\end{array}$$

(14)

$$0\le L_{i,k}\le C_k-l_{i,k}\begin{array}{cc}& \begin{array}{cc}\forall i\in D,\forall k\in K& \end{array}\end{array}$$

(15)

$$L_{o,k}=0\begin{array}{cc}& \begin{array}{cc}\forall k\in K& \end{array}\end{array}$$

(16)

$$M(Z^C-1)\le {\displaystyle \sum _{i\in P^C}{\displaystyle \sum _{j\in N}{\displaystyle \sum _{k\in K}{x}_{i,j,k}-N_C } }}\le Z^C-\epsilon \begin{array}{l}\hfill \end{array}\forall C\in \overline{C}$$

(17)

$$x_{i,j,k} binary \forall i,j\in N,\forall k\in K$$

(18)

$$Z^C binary \forall C\in \overline{C}$$

(19)

The objective of the model is to maximize the operational profit and minimize the costs of CB usage and travel, as shown in function (3), where $q^C$ denotes the service profit associated with the demand of request $C$, ${\alpha }_k$ is the usage cost of CB $k$, and $d_{i,j}$ is the travel cost when the CB visits the link $(i,j)$, which is related to the travel time. Constraints (4) and (5) restricts each CB to depart from depot $o$ and then visit a series of nodes ($j\in N$) according to flow balance constraint (6) before terminating its route at depot $d$. Next, constraints (7) and (8) dictate that each node is served no more than once, and each trip can only be served by one CB. Constraint (9) presents the time window constraints. Clearly, the constraint restricts the arrival time $T_{i,k}$ of CB $k$ at node $i$ to fall within time window $[a_i,b_i]$. Constraints (10) and (11) restrict the time sequence of access to the nodes and force the CB to visit the pickup node before the corresponding delivery node, where $S_i$ denotes the service time at node $i$ and $t_{i,j,k}$ the travel time between nodes $i$ and $j$ for CB $k$, and $M$ denotes a sufficiently large positive number. For the sake of considering loading constraints, it is noted that, when a CB carries out trips, the loading state $L_{i,k}\forall i\in N,\forall k\in K$ should be updated based on the demand $l_{i,k}$ of the corresponding pickup/delivery node $i$, which is formulated by constraints (12) and (13). Furthermore, constraints (14)–(16) ensure that the load of the CB does not exceed its capacity, and that its loading state when leaving the depot is empty. Constraint (17) defines that the binary decision variables $Z^C$ equal 1 if all trips in request $C$ are served, and 0 otherwise, where $\epsilon$ denotes a sufficiently small positive number. Finally, the binary requirements are given by (18) and (19).

4. Solution Framework

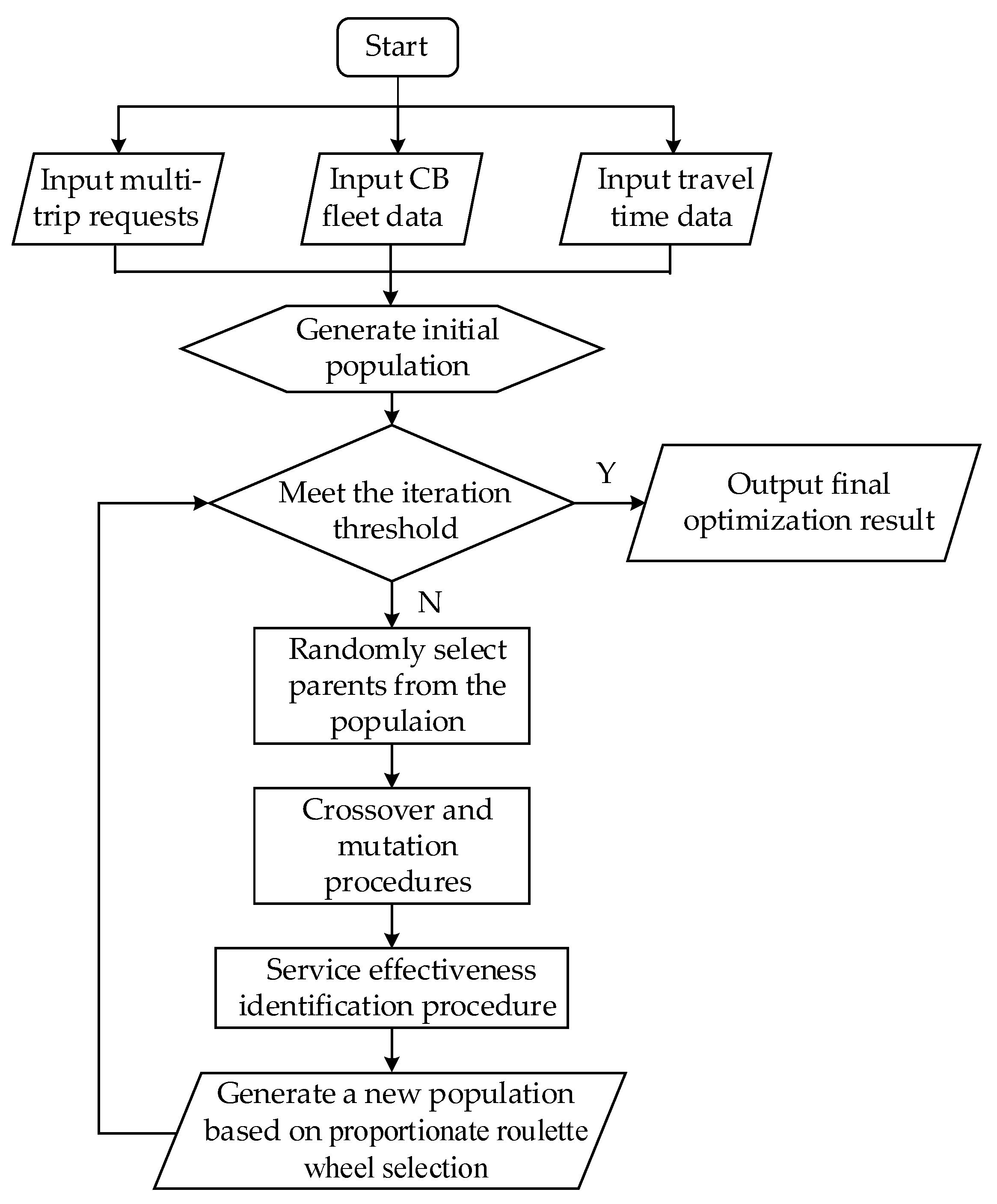
The CB routing problem for the OECBSM-PMT service is a typical NP-hard problem. To ensure the efficiency and accuracy of the calculation, this paper develops a solution algorithm based on the GA, which is an algorithm commonly used to address the routing problem due to its performance in terms of efficiency and flexibility. Meanwhile, considering the characteristics of effective service in the OECBSM-PMT, the algorithm also needs to identify the multiple trips of each passenger to guarantee they can occur with one e-ticket service under the loading and time window constraints. Furthermore, in searching for the optimal solution under the time window constraints, the OTDIH is used in the insertion procedure for efficient and accurate calculations. The basic flow diagram of the algorithm is shown in Figure 3.

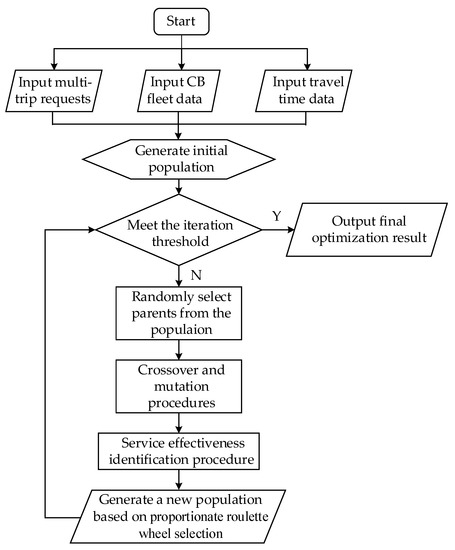
Figure 3. The basic flow diagram of genetic algorithm.

4.1. Chromosome Coding and Insertion Procedure

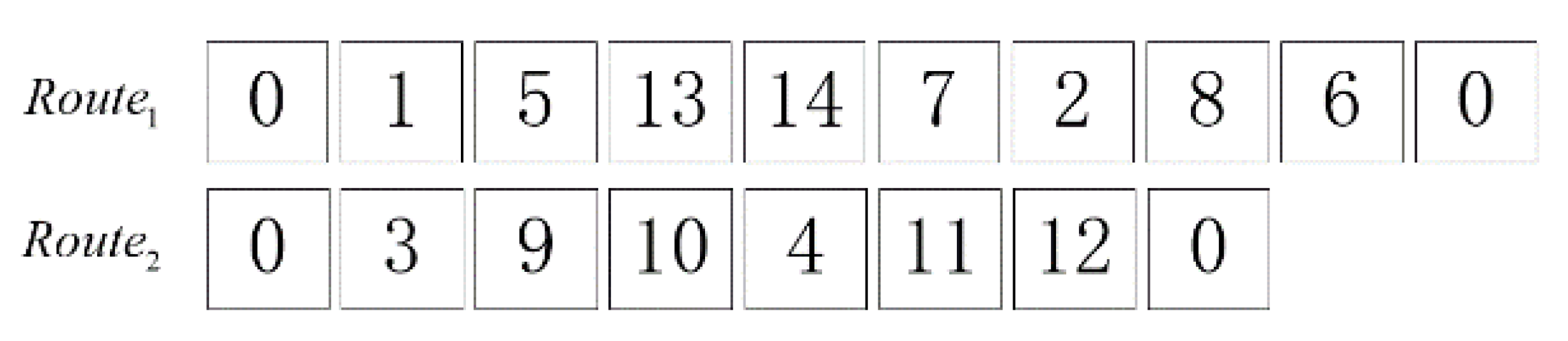
Each solution is represented by the form of the chromosome, which is a permutation of nodes. The solution indicates the order in which the vehicle fleet visits the pickup/delivery nodes and depots. The encoding for the VRPPDTW-based CB routing problem is more complicated, since the chromosome not only needs to represent the sequence visited by the vehicle but also requires the sequence of pickups and deliveries for each request. Considering the above, this study sets the odd number $i$ as the pickup node, and $i+1$ as the corresponding delivery node. Meanwhile, node “0” represents the departure and arrival depot. Figure 4 represents the solution under the form of the chromosome, where each route is carried out by a CB.

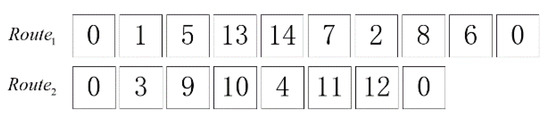
Figure 4. Chromosome coding of GA for CB routing problem of OECBSM-PMT service.

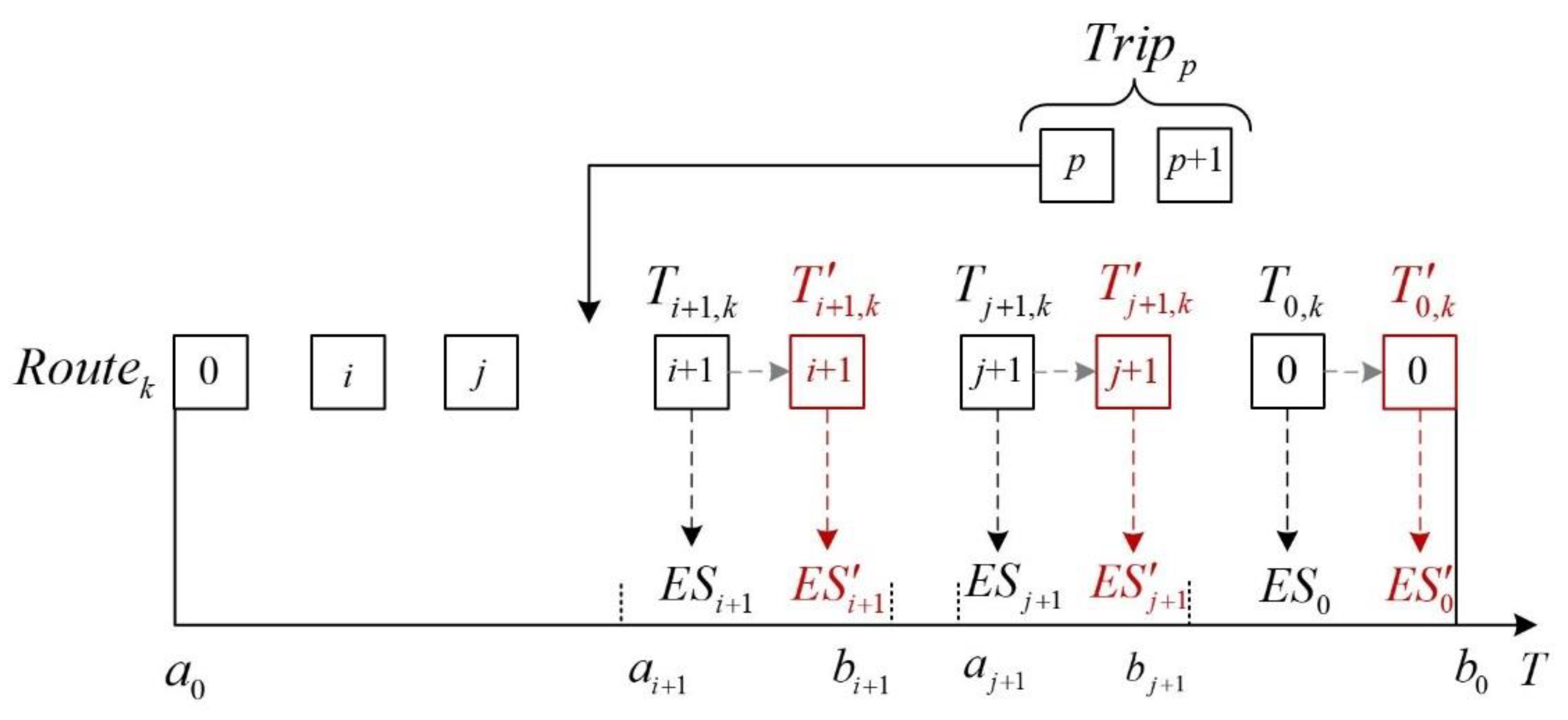
From the perspective of the coding feasibility of the chromosome, it is necessary to ensure that the pickup node $i$ is always before the corresponding delivery node $i+1$. Meanwhile, the coding also needs to follow the capacity constraint and time window constraint in the insertion procedure. Specifically, the capacity constraint is there to detect whether the maximum load of the CB exceeds its capacity, which is relatively easy to determine. However, the time window constraint is more complicated during the insertion of a new request since the actual arrival time may change when a new request is inserted into the current route. Fortunately, the constraint can be handled by the OTDIH [28], proposed based on the push forward insertion detection method, as shown in Figure 5. It can be seen from the figure that there is an attempt to insert a trip $(p,p+1)$ into a feasible route $Rout{e}_k(0,\alpha ,\beta ,\alpha +1,\beta +1,0)$. Meanwhile, $T_{i+1,k}$ and $T_{j+1,k}$ are the original arrival times for delivery nodes $i+1$ and $j+1$. When pickup node $p$ is inserted into the position between nodes $j$ and $i+1$, the arrival time of nodes $i+1$, $j+1$, and 0 will change to ${T^{\prime }}_{i+1,k}$, ${T^{\prime }}_{j+1,k}$, and ${T^{\prime }}_{0,k}$.

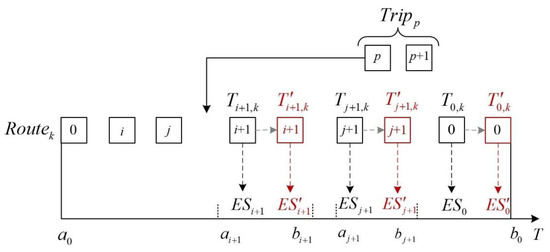
Figure 5. The process of inserting a new request into the route of CB $k$.

Specifically, inserting a new request into the current route will cause the arrival time of each node after the insert position to change. Considering the possibility that ${T^{\prime }}_{i+1,k}$, ${T^{\prime }}_{j+1,k}$ or ${T^{\prime }}_{0,k}$ may not be in the corresponding time window, it is essential to check the feasibility of the route after the insertion. Let us set up a feasible route $Rout{e}_k(0,\alpha ,\beta ,\alpha +1,\beta +1,0)$ as an example. $Tri{p}_p$ denotes the trip $(p,p+1)$ to be inserted into the current route. $w_j$ is the waiting time at node $j$. $E{F}_j$ is the earliest time the vehicle can finish its service at node $j$. $E{S}_i$ is the earliest time the vehicle can arrive at node $i$, and $L{S}_i$ is the latest time the vehicle can arrive at node $i$. The above variables can be illustrated as follows:

$$w_j=\max \{0,a_j-(T_{i,k}{+s}_i+t_{i,j,k})\} \forall (i,j)\in Rout{e}_k,\forall k\in K$$

(20)

$$E{F}_j=\max \{a_j+s_j,E{F}_i+t_{i,j,k}+s_j\} \forall (i,j)\in Rout{e}_k,\forall k\in K$$

(21)

$$E{S}_i=E{F}_i-s_i \forall i\in Rout{e}_k,\forall k\in K$$

(22)

$$L{S}_i=\min \{b_i,L{S}_j-t_{i,j,k}-s_i\} \forall (i,j)\in Rout{e}_k,\forall k\in K$$

(23)

Accordingly, for any two adjacent nodes $i,j$ along the route, the time interval between the two nodes is $T{D}_{i,j}$, calculated as

$$T{D}_{i,j}=L{S}_j-E{F}_i \forall (i,j)\in Rout{e}_k,\forall k\in \mathrm{K}$$

(24)

The constraints for determining whether random node $l$ can be inserted between two nodes $i$ and $j$ on route $k$ are

$$E{S}_l\le b_l \forall l\in Tri{p}_p$$

(25)

$$T{D}_{i,j}\ge t_{i,l,k}+s_l+t_{l,j,k}+w_l \forall (i,j)\in Rout{e}_k,\forall l\in Tri{p}_p\forall k\in \mathrm{K}$$

(26)

Compared with the traditional time window constraint detection method, the advantage of the OTDIH is the use of pre-insertion detection instead of post-insertion detection. Clearly, since the insertion is performed after the detection, infeasible insertions will be avoided, so that limited computing resources will not be wasted on updating the time window and loading information for infeasible solutions. Accordingly, the computational efficiency of the algorithm is improved. The pre-insertion detection also improves the flexibility of the programming. Based on the OTDIH, the pseudo-code of the insertion procedure is as Algorithm 1:

Algorithm 1: OTDIH Based Inserted Operator
1:	Initialize parameters. Route $Rout{e}_k(0,i,j,\dots i+1,\dots j+1,0)$; Set of trip requests waiting to be inserted ($Tri{p}_p$); Set of feasible insertion options ${Set}_f=\{Ø\}$;
2:	Calculate the earliest finish time $E{F}_i$ and the latest arrival time $L{S}_i$ for each node in route $Rout{e}_k$;
3:	Select a new trip request: $(p,p+1) \leftarrow Tri{p}_p$;
4:	Insert node $p$$\mathrm{from} \mathrm{the} \mathrm{first} \mathrm{possible} \mathrm{insertion} \mathrm{position} (0,i)$ in route $Rout{e}_k$;
5:	Calculate the time difference $T{D}_{0,i}$ and earliest arrival time $E{S}_p$
6:	If (the insert satisfies the constraint (25)(26))
7:	Update $E{F}_i$, $L{S}_i$ and $L_{i,k}$ of each node behind the insertion position;
8:	Enter row 11;
9:	else
10:	Try to insert the node $p$ into the next position;
11:	Insert node $p+1$ from the position behind node $p$;
12:	Calculate the time difference $T{D}_{p,i}$ and earliest arrival time $E{S}_{p+1}$
13:	If (the insert satisfies the constraint (25)(26))
14:	Update $E{F}_i$, $L{S}_i$ and $L_{i,k}$ of each node behind the insertion position;
15:	Record the insertion option of trip request $(p,p+1)$ in ${Set}_f$;
16:	Calculate the corresponding objective value of the inserted route $Rout{e}_k$;
17:	Search for other feasible insertion options for trip request $(p,p+1)$$\mathrm{on} \mathrm{route} Rout{e}_k$ until all the positions have been calculated;
18:	else
19:	Try to insert the node $p$ into the next position;
20:	Select the feasible solution with the largest objective value and update $Rout{e}_k$.
21:	End;

4.2. Crossover and Mutation Procedures

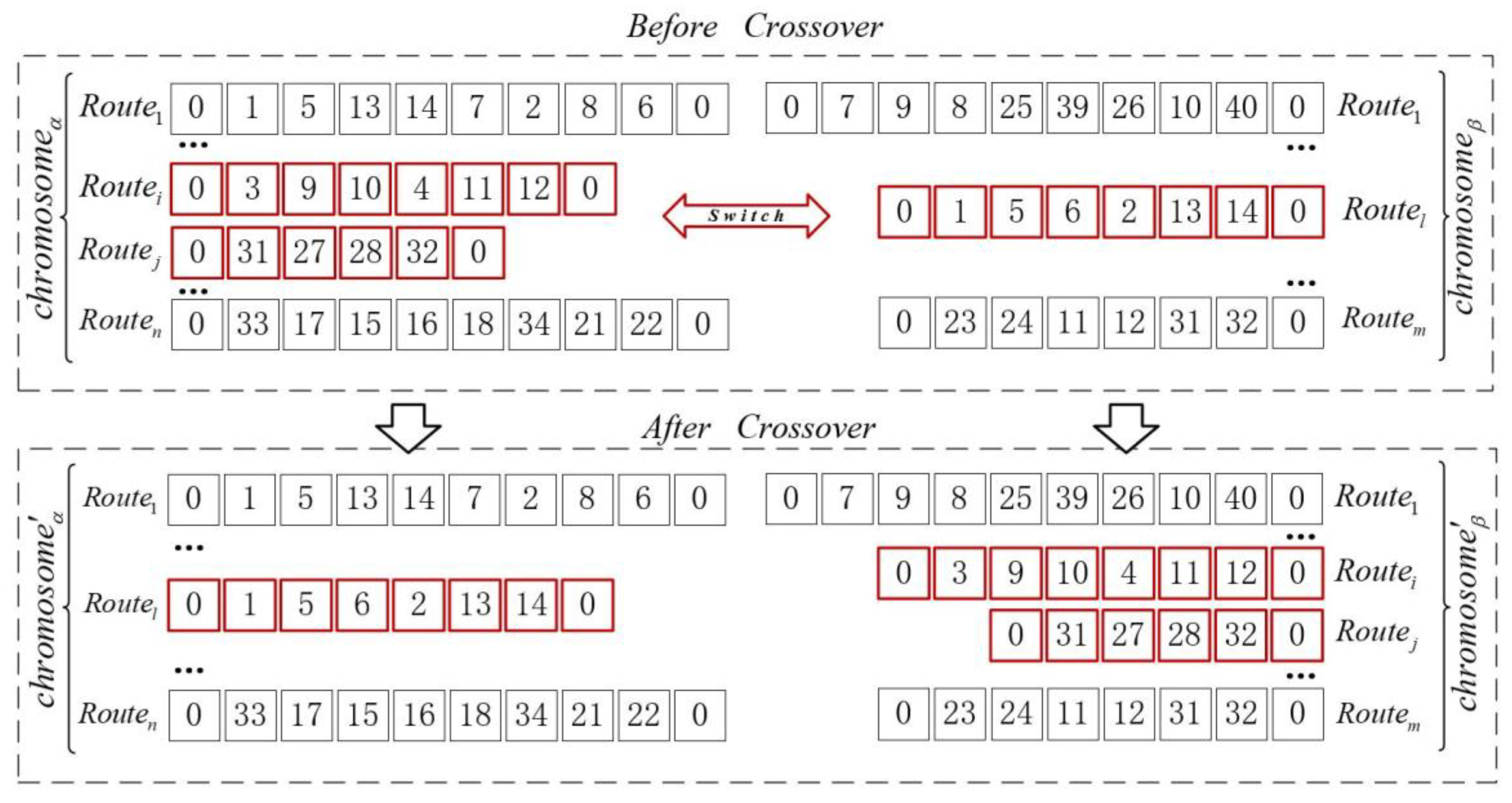
The crossover procedure for solving the CB routing problem for the OECBSM-PMT service needs to ensure that the pickup node of each request is always before the corresponding delivery node after the crossover. Meanwhile, the time window and loading constraints also need to be met. Accordingly, the unit of chromosome segment exchange in the crossover procedure is route $(0,i,j,\dots i+1,\dots j+1,0)$. This paper proposes a random matching crossover method to increase the changes in the crossover procedure to enhance its effectiveness and flexibility:

Step 1: Select solutions $chromosom{e}_{\alpha }$ and $chromosom{e}_{\beta }$ from the parent group, and randomly select 1–2 routes from these solutions to exchange, as shown in Figure 6.

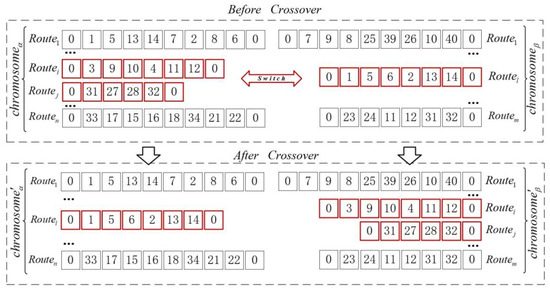
Figure 6. Random matching crossover procedure for solving CB routing problem for OECBSM-PMT service.

Step 2: Identify the repeated requests caused by the crossover and delete these requests in the corresponding solution $chromosom{e^{\prime }}_{\alpha }$ or $chromosom{e^{\prime }}_{\beta }$.

Step 3: It is essential to reinsert the missing requests caused by the crossover into the solution based on the insertion procedure. If the insertion is unfeasible, generate an empty route at the end of the solution in which to insert the request.

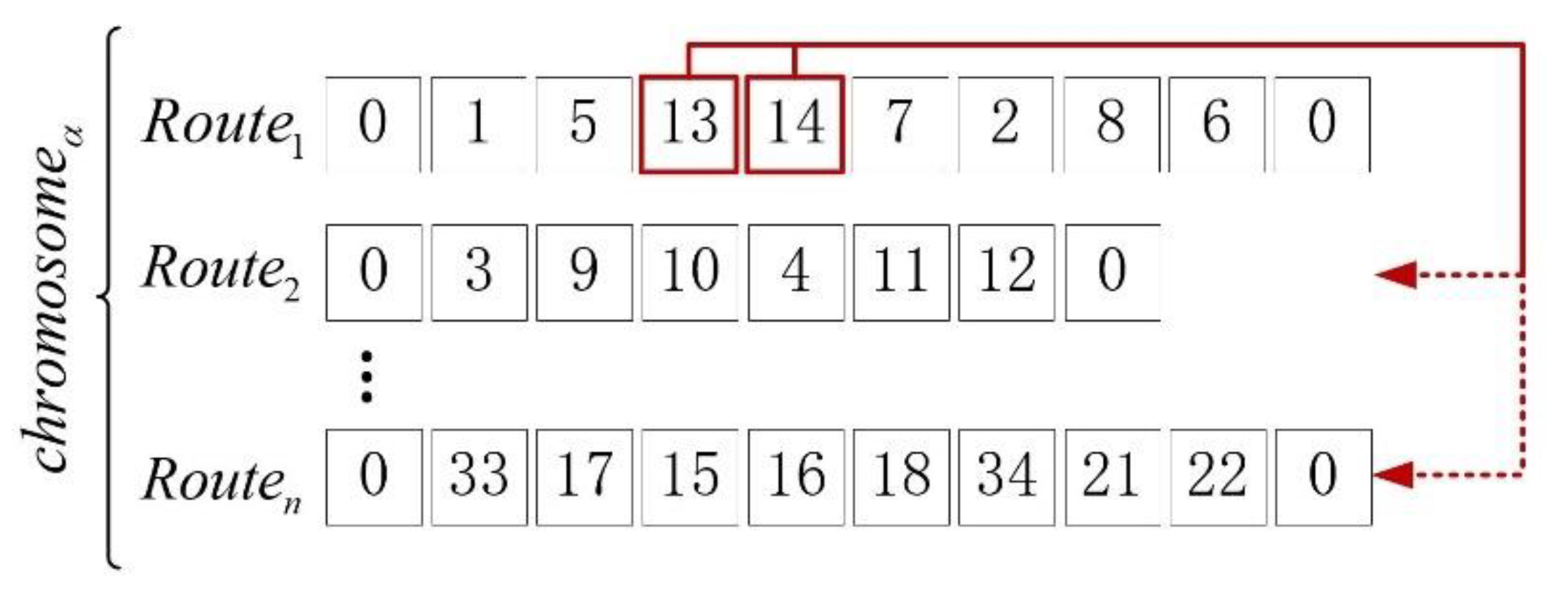
The mutation procedure of the algorithm also needs to ensure that the order of pickup and delivery is correct. The time window and loading constraints also need to be met. Accordingly, the unit of chromosome segment that is mutated in the mutation process is request $(p,p+1)$. The specific steps are as follows:

Step 1: Randomly select a request $(p,p+1)$ from the parent solution $chromosom{e}_{\alpha }$.

Step 2: Delete pickup node $p$ and delivery node $p+1$ from their original positions.

Step 3: According to the constraint considered in the insertion procedure, carry out the insertion based on a randomly selected route, as shown in Figure 7. If the insertion cannot be performed, generate an empty route at the end of the solution in which to insert the request.

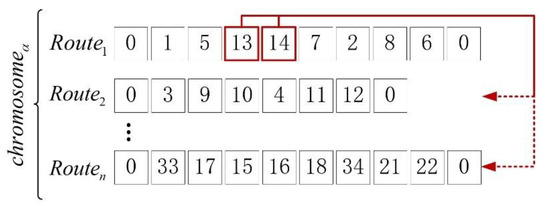
Figure 7. Mutation procedure for solving CB routing problem for OECBSM-PMT service.

4.3. Service Effectiveness Identification Procedure

The most important feature of the CB routing problem for the OECBSM-PMT service is delivering effective service for passengers with multiple trips. In order to use limited fleet resources to provide a more effective service, this paper proposes a service effectiveness identification procedure. Specifically, the procedure identifies the completeness of the service for each request in the offspring solution generated by the crossover and mutation procedures. When not all trips in a request are satisfied, the procedure tries to insert the missing trips into the solution. If no insertion attempts are feasible, the request is removed from the solution to free up fleet resources to service other requests.

By adopting the identification procedure, the fleet resources are efficiently utilized to serve more requests effectively under the time window and load constraints, and a better solution with a higher objective value is obtained within the limited calculation time. A comparison of the solutions calculated with and without the identification procedure is provided in detail in the case study section.

5. Case Study

The OTDIH-based GA solving the CB routing problem of the OECBSM-PMT service is coded using JAVA. A Windows-based 3.0 GHz Intel Core i5 processor-based system with 16 GB of RAM is used to perform cases of different scales based on the Beijing 2022 Winter Olympic Games. The Olympic Winter Games of 2022 will be the first ever multi-regional Winter Olympic Games. There are a total of 13 event venues located in Beijing, Zhangjiakou, and Yanqing, creating a large number of requests for multiple trips between venues from spectators who wish to attend several events in a day. This paper sets up different scenarios based on the actual events schedules for 8 and 16 February 2022. Passengers with similar travel plans are aggregated into the same request, and the service profit of request is $q^C=\xi d_C$, where $d_C$ denotes the demand of request $C$ and $\xi =100$. Meanwhile, a limited fleet of CBs with 40 seats is provided to serve passengers with the usage cost ${\alpha }_k=100,k\in K$, and the travel time is based on real road traffic conditions which is equal to travel cost in minutes [29]. The service time is set to 5 min at each pickup/delivery node.

A small-scale case is set up based on a partial events schedule for 8 February 2022, which is shown in Table 4. Specifically, there are 12 requests with multiple trips for that day and the total number of passengers are 171. The requests, each containing one or two trips, along with origin, destination, and corresponding time windows, are shown in Table 5.

Table 4. Event arrangements for Beijing 2022 Winter Olympic Games on 8 February 2022.

Start Time	End Time	Event Category	Event Venue	Hosting Area
09:15	10:30	Figure skating	Capital Indoor Stadium	Beijing
10:00	11:25	Freestyle skiing	Big Air Shougang	Beijing
10:40	12:15	Snowboarding	Genting Snow Park	Zhangjiakou
12:10	14:30	Ice hockey	Wukesong Gymnasium	Beijing
18:30	20:00	Speed skating	National Speed Skating Oval	Beijing
19:50	21:10	Skeleton	National Snowmobile Sled Center	Yanqing
21:10	23:30	Ice hockey	Wukesong Gymnasium	Beijing

Table 5. Spectators’ multi-trip requests.

Multi-Trip ID	Demand	Departure Venue	Arrival Venue	Boarding Time (Start)	Boarding Time (End)	Drop-Off Time (Start)	Drop-Off Time (End)
1	9	8	5	10:30	11:30	14:40	15:40
		5	2	19:00	20:00	20:10	21:10
2	5	6	5	11:25	12:25	15:40	16:40
		5	2	19:00	20:00	20:10	21:10
3	11	3	5	14:30	15:30	15:40	16:40
		5	2	19:00	20:00	20:10	21:10
4	10	8	5	12:15	13:15	15:40	16:40
…	…	…	…	…	…	…	…

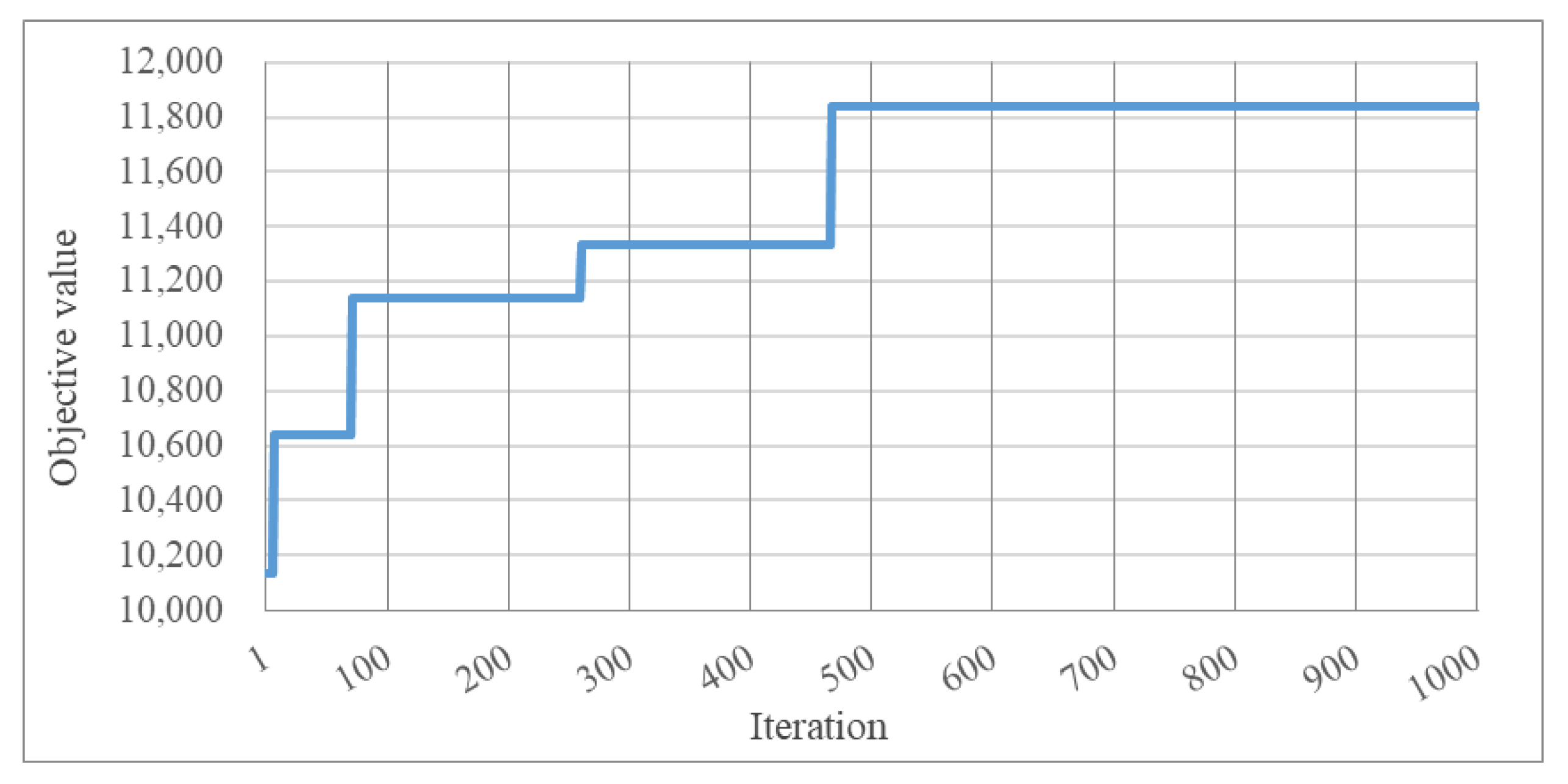
The GA-I algorithm proposed in this paper was able to complete the computation in 6.15 s after 1000 iterations, with crossover parameter $P_c=0.7$ and mutation parameter $P_m=0.2$ at a population size of 500. The calculation process is shown in Figure 8, where the search achieves a large increase in the objective value in the first 100 iterations, and then the optimization nearly converges to 11,842 after approximately 500 iterations. The result shows that the algorithm is able to achieve optimization within an acceptable computational time and obtains the optimal solution efficiently.

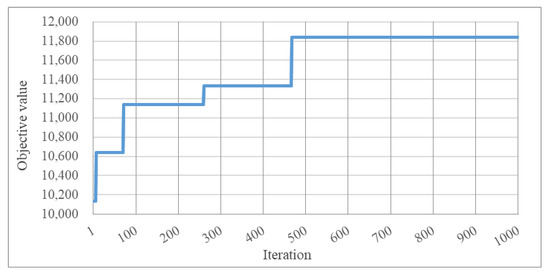
Figure 8. The iteration process for the OECBSM-PMT.

Furthermore, a comparison of GA-I to different solving strategies is implemented based on the same case. Specifically, GA-II is set to randomly select an offspring solution from all feasible options during the crossover and mutation procedure, instead of choosing the optimal solution based on the objective value. Based on GA-II, GA-III does not further optimize the offspring using the service effectiveness identification procedure, but directly treats the offspring generated from the crossover and mutation procedure as the parent of the next generation. As can be seen from Table 6, the selection strategy of GA-II increases the stochasticity and flexibility of the offspring and generates a better solution than GA-I in the instances with $P_c=0.7$, $P_m=0.1$ and $P_c=0.9$, $P_m=0.3$. However, the difference between the objective values of these two solutions is not large, while GA-I generates better solutions in the remaining instances and is thus more stable in obtaining high-quality solutions in almost all instances. Meanwhile, there is a much larger gap between GA-I and GA-III, since GA-III does not identify the completion of the serviced requests using the identification procedure, so some of the serviced requests are incomplete after the optimized crossover and mutation procedure. As a result, the limited fleet resources are wasted on incomplete services to some extent, resulting in a failure to provide a more effective service and leading to a much lower objective value than the other two solving strategies. In summary, the comparison shows that the GA-I used in this paper is able to obtain the optimal solution efficiently and accurately in most instances.

Table 6. Comparison between different solving strategies with multiple combinations of crossover and mutation parameters.

Parameters		GA-I	GA-II	GA-III
Crossover	Mutation
0.70	0.10	11,331	11,332	11,145
	0.20	11,842	11,840	11,147
	0.30	11,842	11,142	11,147
0.80	0.10	11,841	11,339	11,145
	0.20	11,334	11,334	11,145
	0.30	11,841	11,333	11,147
0.90	0.10	11,844	11,333	11,147
	0.20	11,336	11,333	11,145
	0.30	11,334	11,335	11,146

A larger-scale case based on the events to be held on 16 February 2022 is next established to test the performance of GA-I when considering different combinations of the crossover and mutation parameters and three different sizes of population pools. Specifically, a case with 96 requests involving multiple trips and a total demand of 1414 is set up based on the schedule shown in Table 7.

Table 7. Event arrangements for Beijing 2022 Winter Olympic Games on 16 February 2022.

Start Time	End Time	Event Category	Event Venue	Hosting Area
09:05	11:00	Curling	The National Aquatics Centre	Beijing
10:15	12:15	Alpine skiing	National Alpine Skiing Center	Yanqing
12:10	13:25	Ice hockey	National Indoor Stadium	Beijing
13:45	14:30	Alpine skiing	National Alpine Skiing Center	Yanqing
14:00	15:10	Ice hockey	Wukesong Gymnasium	Beijing
14:05	15:20	Curling	The National Aquatics Centre	Beijing
15:45	16:55	Biathlon	National Winter Biathlon Center	Zhangjiakou
16:40	19:00	Ice hockey	The National Stadium	Beijing
17:00	18:00	Cross-country skiing	National Cross Country Skiing Center	Zhangjiakou
19:00	21:55	Cross-country skiing	National Cross Country Skiing Center	Zhangjiakou
19:00	20:15	Freestyle skiing	Genting Snow Park	Zhangjiakou
19:30	21:20	Skeleton	Wukesong Gymnasium	Beijing
19:30	21:05	Short track speed skating	Capital Indoor Stadium	Beijing
19:30	21:15	Short track speed skating	Capital Indoor Stadium	Beijing
20:05	21:00	Curling	The National Aquatics Centre	Beijing
21:30	22:30	Ice hockey	National Indoor Stadium	Beijing

The calculated results based on different combinations of parameters after 5000 iterations are presented in Table 8, showing that the convergence speed is related to the size of the population pool, and that different combinations of crossover and mutation parameters can affect the solution quality. The calculation time is relatively short when the population size is small, but the quality cannot be guaranteed. Meanwhile, the quality of the solution is not entirely proportional to the size of the population and can be optimized with different combinations of parameters. The best solution, with objective value of 81,273, is calculated with $P_c=0.7$, $P_m=0.1$ and a population size of 1000.

Table 8. Comparison between different crossover and mutation parameters and population sizes.

Parameters		Population Size	Objective Value	Computational Time (s)
Crossover	Mutation
0.70	0.10	500	80,096	1670
		800	78,276	2644
		1000	78,097	3327
0.70	0.20	500	79,899	1694
		800	77,586	2642
		1000	77,000	3405
0.70	0.30	500	78,490	1740
		800	79,989	2753
		1000	79,186	3509
0.80	0.10	500	78,105	1859
		800	80,182	2928
		1000	78,910	3843
0.80	0.20	500	78,997	1894
		800	79,606	2993
		1000	76,914	3927
0.80	0.30	500	77,621	1920
		800	78,600	3056
		1000	81,273	3887
0.90	0.10	500	80,078	2045
		800	77,512	3333
		1000	76,066	4208
0.90	0.20	500	76,997	2121
		800	77,302	3310
		1000	78,110	4301
0.90	0.30	500	78,977	2208
		800	76,409	3397
		1000	77,098	4547

6. Conclusions

This paper proposed a one e-ticket customized bus service mode for passengers with multiple trips (OECBSM-PMT), which can provide flexible, convenient, and high-level mobile services for passengers who need to travel multiple times in a short period of time. The service mode can improve the quality of PT services in terms of reducing the complexity of multiple travel decisions, repeated ticket purchases, and waiting for buses for each trip, thereby encouraging passengers to switch from private cars to buses, which can reduce energy consumption and exhaust emissions, and alleviate traffic congestion.

The CB routing optimization model for the OECBSM-PMT is modeled mathematically by considering the effective service of each request, and mix-load, time window, and loading constraints. An optimized CB routing schedule which maximizes the service profit and minimizes the costs of CB usage and travel can be calculated.

An OTDIH-based GA is proposed to handle the optimization of CB routing in cases of different scales. Furthermore, taking the criterion for effective service into account, a service effectiveness identification procedure is developed in the GA to efficiently utilize the fleet resources, and the results show that this GA (GA-I) obtains better solutions than other solving strategies in most instances.

As an innovative mode of travel, the CB service has undergone rapid growth in the past decade. There is much work still to be done in this field. To further investigate the OECBSM-PMT, the key factors affecting the setting of a CB line need to be considered, and other constraints and goals need to be considered from a realistic perspective, such as multiple depots and the travel preferences of different types of passengers. Furthermore, based on the big data of mobile terminals and traffic systems, developing an interactive efficient information platform for the OECBSM-PMT, for passengers, drivers, and operators, will be an important future research direction.