A Review on State Estimation Techniques in Active Distribution Networks: Existing Practices and Their Challenges

Abstract

This paper provides a comprehensive review of distribution system state estimation in terms of basic definition, different methods, and their application. In the last few years, the operation of distribution networks has been influenced by the installation of distributed generations. In order to control and manage an active distribution network’s performance, distribution system state estimation methods are introduced. A transmission system state estimation cannot be used directly in distribution networks since transmission and distribution networks are different due to topology configuration, the number of buses, line parameters, and the number of measurement instruments. So, the proper state estimation algorithms should be proposed according to the main distribution network features. Accuracy, computational efficiency, and practical implications should be considered in the designing of distribution state estimation techniques since technical issues and wrong decisions could emerge in the control center by inaccurate distribution state estimation results. In this study, conventional techniques are reviewed and compared with data-driven methods in order to highlight the pros and cons of different techniques. Furthermore, the integrated distribution state estimation methods are compared with the distributed approaches, and the different criteria, including the level of area overlapping execution time and computing architecture, are elaborated. Moreover, mathematical problem formulation and different measuring methods are discussed.

1. Introduction

Real-time monitoring, energy management, and control of active distribution networks (ADNs) are critical due to the limited number of smart measuring devices, radial or weakly meshed distribution system configurations, and high penetration of stochastic and non-stochastic distributed generations (DGs) [1]. State estimation approaches have been introduced to determine the current operation of distribution networks. State estimation (SE) techniques make a link between measurement devices and control centers to present and monitor all the electrical quantities in ADNs. State estimation approaches have been applied in transmission grids from many years ago, but these techniques are not applicable directly in the distribution grids. An appropriate technique should be realized according to the features of distribution networks. Transmission and distribution grids differ significantly in the following cases [2,3,4,5]: One—the measurement instruments are usually installed in a limited bus, unlike the transmission ones that all buses are monitored by measurements devices. Two—the distribution grids are mostly configured in the radial or weakly meshed networks, but the topology of transmission grids is highly meshed. Three—the high number of buses and imbalanced configuration in distribution networks make them different from the balanced structure of transmission grids. Four—due to the low X/R ratios in the distribution networks, decoupled SE algorithms for transmission networks are not possible in the distribution grids. Therefore, appropriate state estimation methods should be provided to make a link between measurement devices and a control center to identify the performance of ADNs The first distribution system state estimation (DSSE) method was reported in 1990 when supervisory control and data acquisition (SCADA) systems were introduced [6,7]. DSSE plays a crucial role in the management of ADNs since bad data and error detection in the measurements is also possible from the DSSE results. Highly accurate estimation of a system’s states depends on the accuracy and the number of real measurements obtained from measuring devices, including SCADA, phasor measurement unit (PMU) [8], micro PMU (μPMU), etc. [9,10]. However, installing the measuring devices at all the buses is not practical due to economic constraints [11]. Therefore, the number of real measurements needed to estimate the states of ADNs is not always adequate. To overcome this inadequacy, pseudo-measurements are introduced, which can be generated from historical data [12]. In addition to real- and pseudo-measurements, virtual measurements are also used for the DSSE approaches [13]. Virtual measurement or zero injection node is defined when the bus power injection is zero, and this type of measurement is more accurate than pseudo-measurement. So, DSSE techniques should be adjusted according to the requirements of distribution grids while the accuracy and time efficiency of DSSE results are improved [14]. The needs of the three-phase DSSE approach are studied in [15,16]. The conventional WLS method is changed for unbalanced three-phase distribution grids [17]. Power flow methods are also introduced in three-phase distribution grids to meet the requirements of these networks [18,19]. Since the conventional power flow methods in transmission grids cannot be used, a new method should be designed to satisfy the requirements for distribution management systems. In [20,21], the new mathematical three-phase power flow calculations are studied in order to model DGs in distribution grids. The overview of state estimation in the distribution system is shown in Figure 1. Real-, pseudo-, and virtual-measurements, along with network data, are the inputs of the DSSE algorithm. The DSSE block estimates the states of the system, and the estimated states are then sent to the control and management center for further processing, such as bad data detection [22], system topology identification [23,24], and state prediction. In the recent review papers [25,26,27,28], problems of distribution networks and different methods of DSSE are considered. However, the implementation of the distributed state estimation approach has not been reviewed completely. In this study, the necessity of reviewing the concept of distributed state estimation in the distribution grids are discussed. Model-based and data-based DSSE methods are also analyzed. The most comprehensive reference guide to DSSE algorithms is proposed in this paper.

In this paper, we review the approaches and methodologies of DSSE. In Section 2, we explain model-based integrated techniques for DSSE. Section 3 reviews distributed approaches for DSSE. Section 4 evaluates the implementation of artificial neural networks (ANNs) for DSSE. Section 5 describes the general consideration of distribution system state estimation approaches, and finally, Section 6 draws the conclusions and future research direction.

2. Distribution State Estimation: Model-Based Approaches

The concept of state estimation was introduced by Schweppe in power networks [29,30,31]. The vector of voltage magnitudes and phase angles at grid buses is defined as the state of a power grid by Schweppe. State estimation techniques are non-linear mathematical algorithms to estimate the states of a system using available raw measurements, which are combined with noise, as well as the parameters of the system. Bad data and measurement errors are also detected during this process. The estimated states are used to evaluate the system performance and evaluate its reliability [32]. SE techniques are widely developed and applied in transmission networks, but the application of these methods is limited in distribution grids because of some constraints. As an example, decoupled state estimation approaches in transmission grids [33] cannot be used in a similar way in distribution grids. This is because of the three-phase and imbalance configuration of distribution networks. This structure will become even more complicated when the single-phase grid of small renewable energy resources is connected to distribution grids [34].

Model-based techniques are mainly used for state estimation where the physical model of the system is known. One of the most common model-based state estimation methods is the weighted least square (WLS) method, where the weighted sum of the errors (residual values) between the estimated and the actual values (obtained from power flow calculations [35]) are minimized [36]. Weighted least absolute value estimator (WLAV) is another estimator that is applied in the distribution grid. WLAV estimator is solved by minimization of the $L_1$ norm of weighted measurement residuals. The Schweppe Huber Generalized M (SHGM) estimator is another estimator that combines both WLS and WLAN methods. The solution of this estimator is solved by the iteratively reweighted least-squares (IRLS) method [37].

Table 1. Conventional Distribution State Estimation Algorithms [38,39].

Method	General Formulation	Definition
WLS	${}_x{}^{minimize} J\left(x\right)={\displaystyle \sum _{i=1}^m}{y}_i^2\left(x\right)$	$y_i\left(x\right)=w_i(h_i\left(x\right)-z_i)$ $x\in {ℝ}^{n\times 1}$: state vector $J\left(x\right)$: objective function $h\left(x\right)\in {ℝ}^{m\times 1}$: the vector of measurement function $w\in {ℝ}^{m\times 1}$: weighting vector of measurementz z $\in {ℝ}^{m\times 1}$: measurement vector $\alpha$: tuning parameter
LAV	${}_x{}^{minimize} J\left(x\right)={\displaystyle \sum _{i=1}^m}\left|y_i\left(x\right)\right|$
WLAV	${}_x{}^{minimize} J\left(x\right)={\displaystyle \sum _{i=1}^m}{w}_i\left|y_i\left(x\right)\right|$
SHGM	${}_x{}^{minimize} J\left(x\right)={\displaystyle \sum _{i=1}^m}\left|s_i\left(x\right)\right|$ $s_i\left(x\right)=\left\{\begin{array}{c}\frac{y_i^2\left(x\right) }{2} if \left|y_i\left(x\right)\right|\le \alpha w_i\\ \alpha w_i\left|y_i\left(x\right)\right|-\frac{1}{2}{\alpha }^2{w}_i^2 otherwise\end{array}\right\}$

gives the mathematical expression for these algorithms.

The performance of the SHGM estimator depends on the weight factor ${\omega }_i$ and tuning parameter $\alpha$. In [38], the performance of WLS, WLAV, and SHGM estimators are evaluated in the bias, consistency, and quality criteria. It is shown that the WLS algorithm has the better performance in these three criteria, and it is an appropriate estimator in the distribution grids.

The state vector of the power grid can be defined as a set of variables; when the state variables are calculated, other electric power quantities can be computed from these states [40,41]. Voltage magnitudes and phase angles are usually defined as a state vector in distribution grids, and it is recognized as the node voltage distribution system state estimation (NV-DSSE). The main advantages of NV-DSSE are that a constant number of state variables can be computed, and this approach is not sensitive to the radial or weakly meshed structure of the power grid.

In the NV-DSSE method, the state vector includes bus voltage magnitudes and phases [42]. State vector can be represented in polar coordination for three-phases as $x=\left[{\delta }_{2\varnothing },\dots ,{\delta }_{N\varnothing },V_{1\varnothing },\dots ,V_{N\varnothing }\right]$, where ${\delta }_{N\varnothing }$ is voltage phase and $V_{N\varnothing }$ is voltage magnitude for three phases $\varphi =\left\{A,B,C\right\}$, and N is the number of buses. It is assumed that there are no measuring devices installed in the slack bus and only conventional measurements are available in distribution grid. The voltage magnitude and phase angle of the slack bus is 1 p.u. and zero (${\delta }_{1\varnothing }=0$) (or ±${120}^{°}$, if three-phase DSSE is considered), respectively. If there is a measuring device at the slack bus, the state vector will be defined as $x=\left[{\delta }_{1\varnothing },\dots ,{\delta }_{N\varnothing },V_{1\varnothing },\dots ,V_{N\varnothing }\right]$, where the phase angle ${\delta }_{1\varnothing }$ is not zero [43,44,45]. There are two main differences between the traditional (non-PMU) configuration and the configuration in which a PMU is placed at the slack bus. First, the definition of the mathematical equation relating measurements to physical parameters of the distribution grids is altered. Second, the Jacobian matrix has a different structure. State variables in NV-DSSE can also be represented in the rectangular form as $x=\left[V_{1,r}^{\varnothing },V_{2,r}^{\varnothing },\dots ,V_{N,r}^{\varnothing },V_{2,x}^{\varnothing },\dots ,V_{N,x}^{\varnothing }\right]$, when only traditional measurements are available in distribution grid. When PMU is placed in the slack, the state vector is defined as $x=[V_{1,r}^{\varnothing },V_{2,r}^{\varnothing },\dots ,V_{N,r}^{\varnothing },$ $V_{1,x}^{\varnothing },V_{2,x}^{\varnothing },\dots ,V_{N,x}^{\varnothing }]$ [46]. $V_{N,r}^{\varnothing }$ is the real part and $V_{N,x}^{\varnothing }$ is the imaginary part of node voltages on each phase. Many available measurements such as the power injections of loads or generators that is known as pseudo-measurements can be implemented more simply in the rectangular form compare to polar coordination definition.

Another method for DSSE is the branch current distribution system state estimation method (BC-DSSE), introduced by Baran and Kelly in 1995 [47]. The main purpose of the Branch Current estimator is to make simpler and more efficient state estimation calculations in the radial or weakly meshed structure of distribution grids. In early studies, power and current measurements are used in the branch current state estimation calculations. In the BC-DSSE method, the states are expressed in rectangular form as $x=\left[i_{1,r_{Nb}}^{\varnothing },\cdots ,i_{N,r_{Nb}}^{\varnothing },i_{1,x_{Nb}}^{\varnothing },\cdots ,i_{N,x_{Nb}}^{\varnothing }\right]$, where $i_{N,r_{Nb}}^{\varnothing }$ is the real part and $i_{N,x_{Nb}}^{\varnothing }$ is the imaginary part of branch currents on each phase, and $N$ is the number of branches. In this definition, power injections on distribution grid buses as the most available pseudo-measurements and current magnitude measurements could be implemented easily [48]. The state vector is also defined in polar form as $x=\left[i_1^{\varnothing },\dots ,i_N^{\varnothing },{\theta }_1^{\varnothing },\dots ,{\theta }_N^{\varnothing }\right]$, where $i_N^{\varnothing }$ is the current magnitude in every branch on each phase $(\varphi )$, ${\theta }_N^{\varnothing }$ is the current angle and $N$ is the number of branches. In [49], the formulation of BC-DSSE in polar and rectangular formations is completely considered. A new BC-DSSE method in weakly meshed distribution networks is proposed in [50]. Since nodal voltage analysis in ADNS is so critical in a control center, the new BC-DSSE model is proposed in [51] to include the slack bus voltage in the state vector. This state vector is expressed as $\left[V_S^{\varnothing },i_{1,r_{Nb}}^{\varnothing },\cdots ,i_{N,r_{Nb}}^{\varnothing },i_{1,x_{Nb}}^{\varnothing },\cdots ,i_{N,x_{Nb}}^{\varnothing }\right]$, where $V_S^{\varnothing }$ is the voltage magnitude of the slack bus and $i_{N,r_{Nb}}^{\varnothing }$ is the real part and $i_{N,x_{Nb}}^{\varnothing }$ is the imaginary part of branch currents on each phase ($\varphi =\left\{A,B,C\right\}$), and $N$ is the number of branches. The overall information about voltage profile of distribution grids could be possible by the inclusion of voltage magnitude on the slack bus in the state vector. The state vector in BC-DSSE is defined in rectangular formulation as $x=\left[v_{s,r}^{\varnothing },v_{s,x}^{\varnothing },i_{1,r_{Nb}}^{\varnothing },\cdots ,i_{N,r_{Nb}}^{\varnothing },i_{1,x_{Nb}}^{\varnothing },\cdots ,i_{N,x_{Nb}}^{\varnothing }\right]$, where a PMU is located at the slack node [52]. $i_{N,r_{Nb}}^{\varnothing }$ is the real part and $i_{N,x_{Nb}}^{\varnothing }$ is the imaginary part of branch currents on each phase; $v_{s,r}^{\varnothing }$ is real and $v_{s,x}^{\varnothing }$ is imaginary parts of the slack bus voltage. The state vector is also shown in the polar structure as $x=\left[v_{s,r}^{\varnothing },v_{s,x}^{\varnothing }, i_1^{\varnothing },\dots ,i_N^{\varnothing },{\theta }_1^{\varnothing },\dots ,{\theta }_N^{\varnothing }\right]$ if PMU is placed at the slack bus. Where $v_{s,r}^{\varnothing }$ is real and $v_{s,x}^{\varnothing }$ is imaginary parts of the slack; $i_N^{\varnothing }$ is the current magnitude in every branch on each phase $(\varphi )$, ${\theta }_N^{\varnothing }$ is the current angle and $N$ is the number of branches. In [53], BC-DSSE method is considered in the presence of PMU measurements. Computation time and efficiency of polar and rectangular coordination are compared. Some properties of NV-DSSE and BC-DSSE methods are summarized in

Table 2. Properties of NV-DSSE and BC-DSSE Approaches, [28,54,55].

	NV-DSSE	BC-DSSE
Property	1— High computational complexity, 2— It is for meshed network, 3— It is sensitive to measurement weights, 4— Straightforward procedure to estimation the voltage magnitude and angle,	1— Simple computation due to inclusion current measurements, 2— It is for radial or weakly meshed structure, 3— Inclusion of PMU measurement is simple, 4— Sparse Measurement Matrixes

.

3. Distribution State Estimation: Distributed Approach

Some issues in ADNS are not addressed by integrated DSSE approaches: One—the robustness and accuracy of integrated DSSE methods are influenced by the lack of real measurements. Two—computational complexity will be increased in the unbalanced three-phase distribution grids. Three—a reliable communication infrastructure is required to collect data and send them to a control center to perform SE calculations [56]. Four—the performance of distribution grids will be impacted more by the large penetration of DGs. As a result, distributed methods are introduced in distribution grids to deal with the aforementioned issues. Distributed approaches have been used in transmission grids from several years ago [57,58]. However, new methods are required in distribution grids due to differences between transmission and distribution grids. In the distribution system distributed state estimation (DS-DSE), the network is divided into several areas. Topology and geography information [59,60], clustering [61], heuristic [62] algorithms, and graph theory [63] are studied to split distribution power networks into several areas. In [64], the new approach based on the community detection method [65] is studied to divide imbalance three-phase distribution grids into areas. The state estimation calculation is performed in each area locally, which differs from the integrated DSSE algorithms that are performed centrally for the whole network. DS-DSE can be classified by different criteria such as, level of area overlapping execution time, and computing architecture [66].

a.

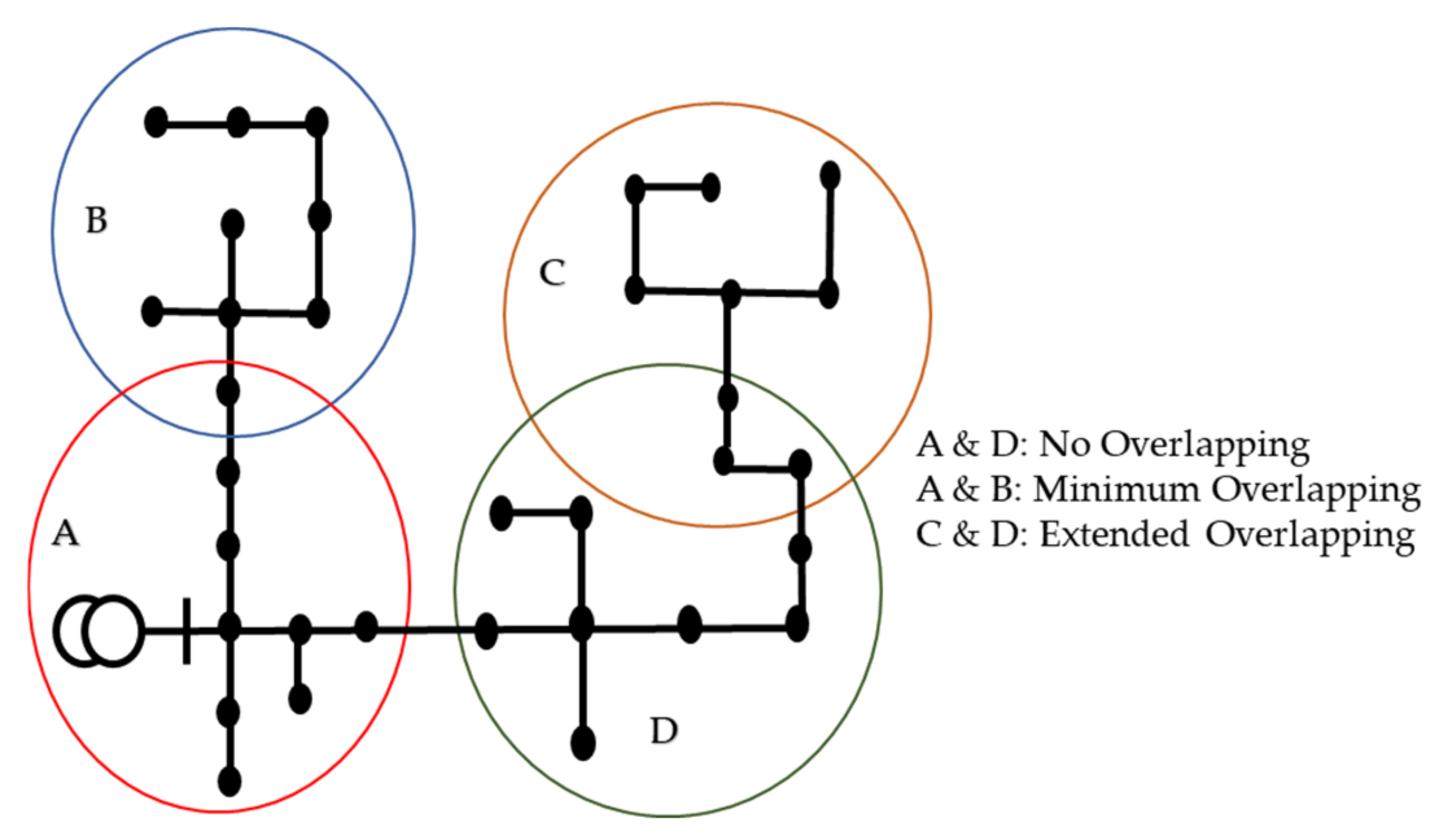
Level of Area Overlapping: Figure 2 shows the different configurations of area overlapping: 1—No overlapping, 2—Minimum overlapping, 3—the extended overlapping.

1-

No overlapping: there is no common node, as seen between areas A and D. State estimation calculation in each area is autonomous. The accuracy of the results from each area can be improved in the integrated step by considering the border from the adjacent area.

2-

Minimum overlapping: there is only one common node, as seen between areas A and B. The benefit of this configuration is the ability to install one measuring device at the common boundary bus to guarantee the observability of both areas.

3-

Extended overlapping: there are two or more common nodes, as seen between areas C and D, where there are three common nodes. As the number of common nodes increases, state estimation algorithms in each area may become more complex in terms of computation. In this configuration, areas communicate and exchange information with their neighboring areas in order to update the results of the state estimation algorithms.

Figure 2. Different Area Configurations in DS-DSE.

Figure 2. Different Area Configurations in DS-DSE.

b.

Execution time: The second criterion is the execution time of the state estimation process, which should be considered in DS-DSE. There are two approaches for performing local state estimation: series and parallel implementation [67,68,69]. Each approach differently addresses the common issues, including lack of measurements, communication rates, and execution time.

Series implementation: the estimated states from each area are sent to the adjacent area sequentially. As seen in Figure 3, area 1 sends its estimated states (SE1) to area 2, then area 2 performs distributed DSSE locally and sends its estimated states (SE2) to area 3, and this process continues to cover all the areas. In this method, each area can only communicate with its direct neighbor. Therefore, the communication costs are low. However, the execution time is relatively high in comparison with integrated state estimation.

Parallel implementation: As seen in Figure 3, the state estimation algorithm is performed in each area separately without exchanging any information with neighboring areas. The estimated states within each area are then sent to the integration step. In the integration step, the results from each area are combined to improve the overall accuracy. In a parallel configuration, the communication costs rely on the integration step. The execution time is low since there is not any communication among neighboring areas.

The parallel and series configurations can be used together to leverage both structures. A hybrid structure can improve the communication rate among areas and the accuracy of the final estimated states.

Figure 3. Execution of the Estimation Process.

Figure 3. Execution of the Estimation Process.

c.

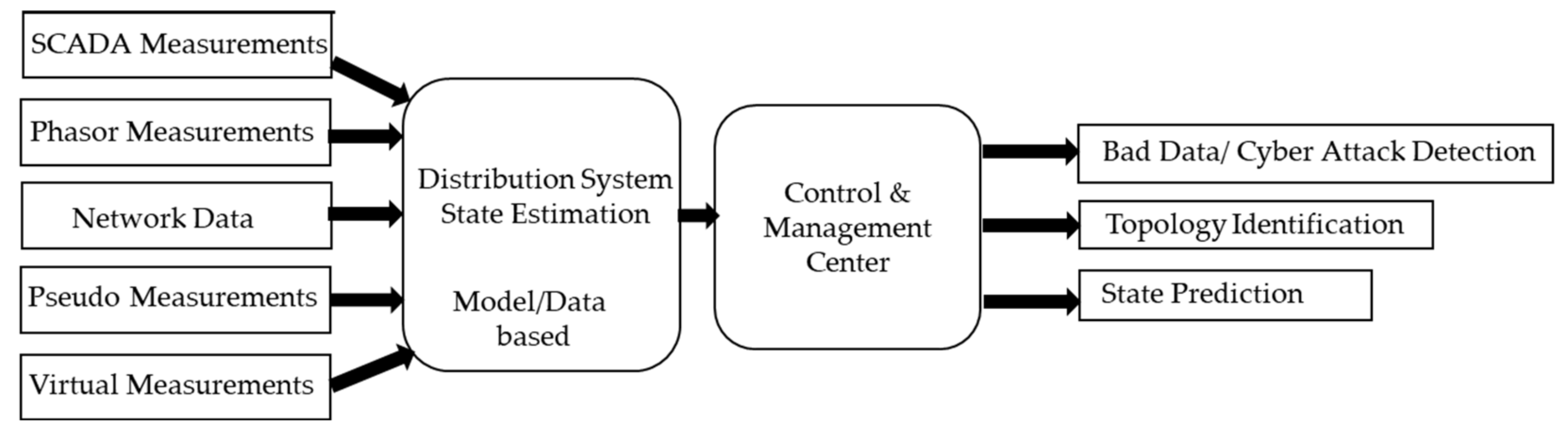
Computing Architecture: In the DS-DSE approach, the architecture of collecting data and the estimated states are important [70]. There are two forms of communication, namely centralized and decentralized, shown in Figure 4. In the decentralized form, each area has its own control center to process local data to perform the state estimation algorithm [71]. In addition, there is a central control center that receives the results from the state estimator of each area to synchronize them and monitor the performance of the whole network. In the centralized architecture, as shown in Figure 4, there is only a central control center that processes the network data and the measurements from each area [72]. The data from each area is sent to the main control center and state estimation calculation is performed centrally. The rate of communication and computation in the centralized architecture are faster than in the decentralized architecture, since there is no communication among the areas, except in the overlapping areas [73].

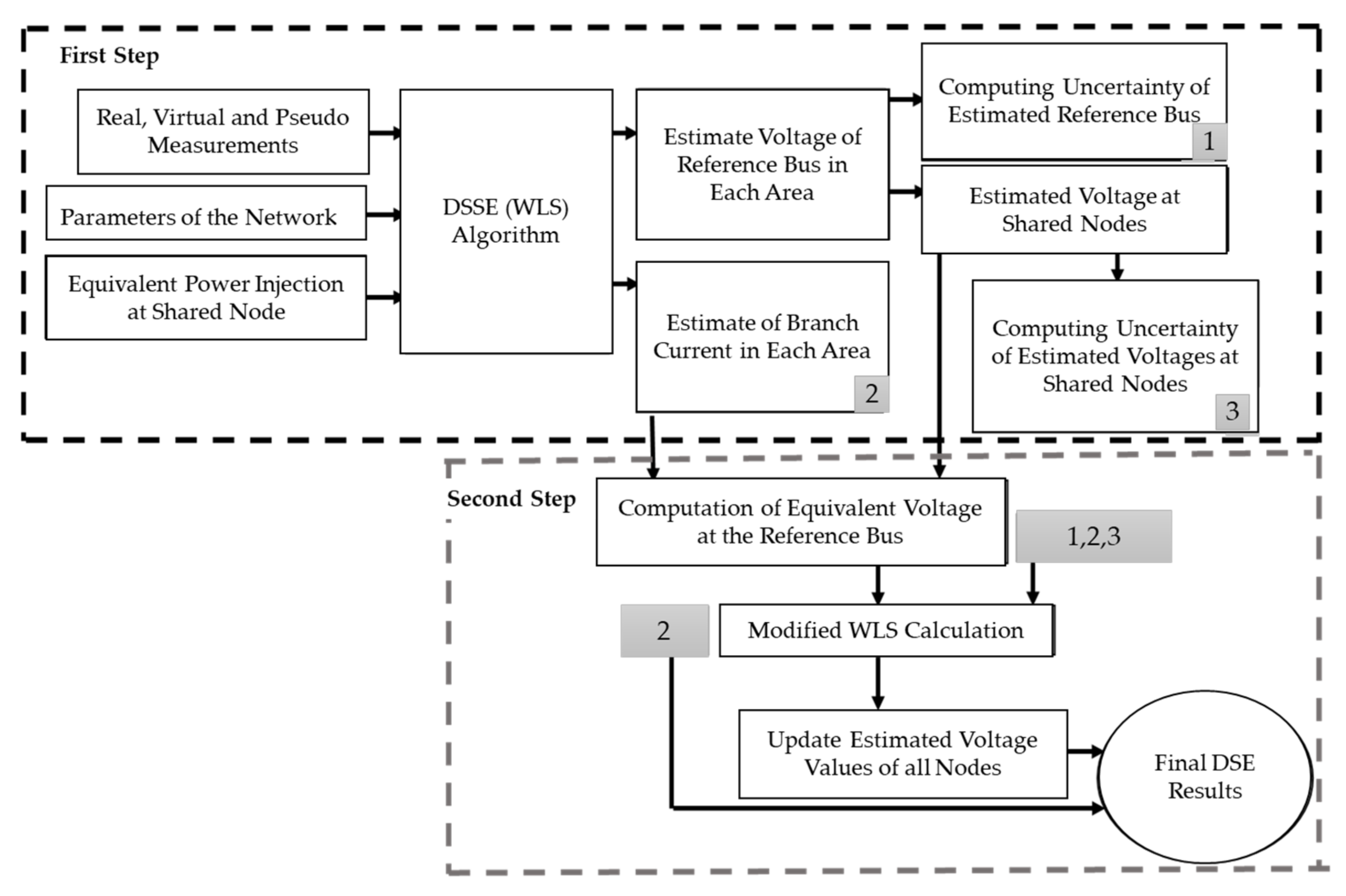
DS-DSE Procedures

A two-steps algorithm was proposed in [74] for solving the DS-DSE, where state estimation is performed locally in each area in the first step, and the estimated results are improved and refined in the second step (integration step). In order to estimate the states of each area locally, the network parameters and available measurements are used as input signals to the DS-DSE algorithm. Figure 5 shows a three-area system with common node ‘s’ between areas A and B. It is assumed that a measuring device is placed at the shared node s, and the voltage of this node as well as the currents of all connected branches are measured. The equivalent injection real and reactive power measurements on the outer branches, which converged to the shared node, are shown as $P_{eq}$ and $Q_{eq}$ in Figure 5. These equivalent measurements will also be a part of the available measurements in the shared nodes. In each area, the state vector is defined as: $x=\left[v_{ref}^r,v_{ref}^x,i_{b{r}_1}^r,\dots ,i_{b{r}_{\mathrm{N}}}^r,i_{b{r}_1}^x,\dots ,i_{b{r}_1}^x\right]$. $v_{ref}^r,v_{ref}^x$ are the real and imaginary parts of the voltage of the reference bus in each area, respectively. The reference bus is usually considered at the overlapping node where a measuring device is placed. $i_{b{r}_{\mathrm{N}}}^r,$ $i_{b{r}_{\mathrm{N}}}^x$ are the real and imaginary parts of the branch current and N is the number of branches. In each area, another indirect value, i.e., the estimated voltage at the shared nodes, is calculated from the actual (direct) state vector values [73]. The uncertainty of the direct and indirect values is also calculated and is used for further processing in the second step.

In the second step, the estimated voltage of the nodes in the overlapping areas, along with the local voltage estimations from the first step, are merged to improve the final state estimation results. The equivalent voltage at the reference bus in each area is recalculated from the estimated branch currents and node voltages from the first step. When PMU measurements are available at the shared node, the voltage angle can be acquired directly. When conventional measurements are available at the shared nodes, the voltage angles and their voltage magnitudes which are estimated at the shared nodes from the first step, are used to calculate an equivalent voltage phasor. Sharing the real measurements among the areas creates some correlations among the estimated states in different areas, which are needed in the second step calculations. These correlations can be defined as the covariance terms in the weighting matrix of the WLS method in the second step. As shown in Figure 6, the uncertainty of the estimated voltage at the reference buses, the estimated branch current values, and the uncertainty of the estimated voltage at the shared nodes, along with the equivalent voltage at the reference buses, are used as the inputs for the WLS calculation. In the second step, since the off-diagonal terms of the weighting matrix in the WLS method are not zero, the method is named the ‘modified WLS’ technique in Figure 6. In this figure, the procedures of the first step and the second step are shown.

Another method to solve the DS-DSE is based on exchanging data among the adjacent areas at the iteration level until the convergence condition is satisfied. After each iteration of performing local SE, the information on boundary nodes is shared among adjacent areas until the convergence criteria are satisfied for each estimator. Due to the high number of iterations, this method is time-consuming and has a high computation burden.

Table 3. DS-DSE Approach Summary.

Reference	LO	ET	SPSE	DS-DSE Procedures	Pros and Cons
[60]	NO, EO	P, S	C	IL	(+) execution time and computational complexity are improved, fast convergence rate, (−) high data rate communication,
[66]	MO, EO	P	C	IL	(+) computational time is decreased, imbalanced three-phase DS-DSE calculation is considered, (−) high data rate communication, only conventional measurements are included,
[75]	EO	P	D	IL	(+) fast convergence rate, high estimation accuracy in presence of DGs, three-phase state estimation calculation, (−) only traditional measurements are included, only voltage magnitude estimation is performed,
[76]	MO	P	D	SEL	(+) PMU-based method is proposed for DS-DSE calculation, computational requirement of DS-DSE method is decreased, (−) PMU-based method is not practical in the large scale of distribution grids because PMU is costly, high data rate communication,
[59,77]	MO	P	D	SEL	(+) minimum communication cost, considering correlation among the local estimations, computational complexity is improved, high robustness is achieved, (−) the passive distribution network is considered,
[74,78]	MO	P	D	IL, SEL	(+) different measurement configurations are considered in the overlapping nodes, voltage profile estimation is improved, (−) high data rate communication,
[79]	MO	P	D	IL	(+) fast convergence rate, computational complexity is decreased, (−) high data rate communication,
[80]	NO	P	D	IL	(+) conventional and PMU measurement are included, fast convergence rate, accuracy is improved, (−) high data rate communication,
[81]	MO	P, S	D	IL	(+) voltage estimation result is improved, fast convergence rate, (−) high data rate communication

LO: Level of Overlapping (NO: No Overlapping, MO: Minimum Overlapping, EO: Extended Overlapping). ET: Execution Time (S: Series, P: Parallel); SPSE: Structure of Performing State Estimation (C: Centralized, D: Decentralized); DS-DSE Procedures (IL: Iteration Level, SEL: State Estimation Level).

provides an overview of the DS-DSE methods presented in the literature. The pros and cons of each method are also studied in this table.

A new gradient-based method for DS-DSE is proposed in [75], and the results are compared with the Gauss–Newton method. It shows that the proposed method is more suitable for a large system. A new DSE-DSSE approach is proposed in [59]. WLS is performed in parallel and decentralized structures in each area. Then, the correlations among the states in the overlapping areas are modeled in the integration step. It is shown that the accuracy of the final results is improved by applying these correlations. The impact of no overlapping and minimum overlapping areas on the DS-DSE results is investigated in [60]. In [76], the impact of the required number of PMUs is evaluated on the accuracy of the DS-DSE method. Minimum overlapping and parallel configuration are considered in this study. It is shown that in the case of no-overlapping, the overall cost of installing measuring devices is increased compared with the minimum overlapping case. Reference [77] performed local state estimation in each area by considering the minimum overlapping between adjacent areas. Then, the provided data by adjacent areas are shared among other areas to improve the accuracy of final DS-DSE results. A bi-directional communication algorithm between areas is proposed in [79] to exchange the obtained information at the boundary buses to achieve the overall convergence.

The following benefits can be maintained by the DSE method:

1-

Since SE calculation is performed in each area parallelly, the execution time of SE processing decreases significantly.

2-

DS-DSE accuracy is determined after each step based on the measurement precision. So, uncertainty evaluation [82] of SE results is also possible when more complicated measurement functions are available.

3-

Since SE calculation is performed independently in each area, different SE algorithms can be used in each area.

4-

The communication capacity requirement, the necessary computation, and the storage requirement are divided into among areas.

4. Distribution State Estimation: Data-Driven Approaches

Due to the high penetration of non-stochastic renewable energy resources, highly variable loads in the power grid, and the integration of electric vehicles to the grid, the conventional DSSE methods fail to address the high uncertainty and monitor every change and topology configuration [83,84]. Furthermore, conventional pseudo-measurement generating methods that are used to tackle the lack of real measurements suffers from high uncertainty levels in ADNs with high penetration of DGs. Moreover, the conventional DSSE approaches, which depend on parameters and models of distribution networks, are complicated, time-consuming, and very sensitive to initial conditions [85]. To overcome these issues, intelligent, data-driven, and model-free state estimation algorithms based on artificial intelligence (AI) and machine learning (ML) have been introduced in recent years, which reduce the computation time and increase the accuracy of the results. There are different ML approaches such as supervised, unsupervised, and reinforcement learning [86]. In the supervised learning approaches, input data and their corresponding output (label) are available [87]. In the training phase, the relation between inputs and outputs is defined as a function. Regression and classification methods are two examples of supervised learning. In unsupervised learning, there is no output corresponding to the input data [88]. Clustering and dimensionality reduction algorithms are two examples of unsupervised learning methods. Finding patterns of energy consumption is an unsupervised learning problem that can be categorized by clustering analysis. Reinforcement learning is another machine learning algorithm that seeks to take suitable action to maximize reward in a particular situation [89]. All these mentioned methods are summarized in Figure 7.

Table 4. Data-driven methods Application in DSSE.

Application	Reference	Method
DSSE	[84] [85] [90] [91] [92] [93] [94]	Deep Neural Network (DNN) ANN (Model-based + Data-based) Artificial Neural Network (ANN)DNN (Model-based + Data-based) Graph-Pruned Neural Network Regression+ Long Short-term Memory+ Sparse Bayesian Learning DNN + Random Forest Classifier Artificial Neural Network (ANN)

provides an overview of the application of data-driven approaches in DSSE.

Data-based state estimation can be efficiently used in large and unbalanced distribution networks. Reference [84] proposes a DNN method based on a supervised regression algorithm to estimate the magnitude of voltage or branch current in ADNs. Lack of measurements is properly addressed by considering different switch statuses to generate input data for the training phase. This method is efficient in large distribution networks with high penetration of DGs. Reference [85] considers the sensitivity of the conventional DSSE approaches to initial states using a shallow neural network. It is shown that by combining the model-based and data-driven methods, the computation time is decreased, and the accuracy and robustness are improved. Unlike other existing models, the proposed method is robust enough under non-Gaussian noise as well. In [90], the supervised regression method is used to estimate phasor measurements. The proposed method is evaluated by real data, and it is shown that the bias of the error is decreased. Reference [91] proposes a hybrid model-based and DNN approach applied to state prediction in large ADNs. The results from the DNN model are used as initial guesses for model-based DSSE. An evaluation of this model on two large ADNs shows that the proposed approach reduces computation time and is suitable for active distribution networks. In [92], the structure of the distribution network is designed based on the Graph Conventional NN (GCNN). This topology is considered as one of the inputs of the training model. The method decreases the complexity and overparameterization of the state estimation training model. Moreover, the proposed method is robust against cyber-attacks. Reference [93] uses regression learning, long short-term memory (LSTM), and sparse Bayesian learning (SBL) to perform power flow, load forecasting, and state estimation, respectively. Data obtained from smart meters and distribution-level PMUs are used as inputs to train the state estimation model. The effectiveness of the proposed model is tested in different ADNs. In [94], both model-based and data-based methods are combined to gain the benefits of SCADA and advanced measurement infrastructure (AMI) with different time scales. When SCADA measurements are available, the DNN method and random forest classifier (FRC) are combined to perform state estimation and topology detection. When both SCADA and AMI measurements are available at the same time, an only model-based method is used. The effectiveness of the proposed method against topology changes and errors is evaluated on the standard 33-bus distribution networks. Reference [95] implemented a new learning approach based on the parallel distributed processing (PDP) method to predict the hourly active and reactive power of medium voltage ADNs. The data-driven distributed state estimation (DD-DSE) approach is introduced in distribution networks in the last few years to improve the efficiency and robustness of the SE results. The concept of DS-DSE technique (as it is expressed in part 3) is completely applicable in DD-DSE. In [96], 123-IEEE power network is divided into several areas, and an ANN method is performed in each area parallelly. Then, the results of state estimation in each area are more processed in the second step. The final results are compared to the integrated WLS method, and it is shown that execution time and computational complexity are improved in a data-based SE method. In [97], a novel machine learning-based distributed state estimation is proposed. Mathematical formulations of a data which exchanged in the boundary area are analyzed, and a new machine learning-based supervised learning is designed. Convergence and accuracy are improved in this method.

5. General Consideration of Distribution System State Estimation Approaches

DSSE methods are introduced to monitor the performance of ADNs. Transmission SE methods are changed to make them performable in distribution grids. Integrated WLS methods are widely used in distribution grids. The nodal voltage and branch current are commonly considered as the state vector in this method. Because of the lack of measurements in distribution grids, pseudo-measurements from loads and generators are considered to make a distribution grid observable. Because conventional SE methods are not practical in a large scale of distribution grids, DS-DSE methods are introduced to address some problems with the integrated DSSE method. The computational efficiency and reducing time consumption are the main benefits of DS-DSE compared to an integrated DSSE method. Data-based estimators are considered to improve the time consumption and results compared to model-based algorithms in ADNs. Data-based methods rely on measurements data, unlike model-based methods. Model-based models depend on the relationship between measurements and physical parameters. Model-based and data-based techniques are combined in some studies to improve SE results across different time scales. The main purposes of SE methods are to improve SE results and time efficiency and decrease computational complexity.

6. Conclusions and Future Work

In this paper, we have provided a critical review of the existing methods of distribution grid state estimation. Both conventional model-based and novel data-driven algorithms have been explored, providing their pros and cons. Furthermore, the concept of distributed state estimation methods and their application to distribution networks is overviewed in detail. Finally, research gaps, challenges, and potential solutions have been provided. Based on the survey, the recent works more focused on data-based methods or hybrid algorithms consisting of data-based and modified conventional state estimation approaches in order to enhance the accuracy. It is highlighted that by increasing the installation of smart measuring devices in distribution networks with high penetration of renewable energy resources, the state estimation techniques will result in better performance, and as a result, the system observability will be improved. Furthermore, the distributed state estimation algorithms show better performance in terms of robustness compared with the integrated state estimation algorithms.

Although both conventional and data-based distribution state estimation approaches have been successful to estimate the states of the system precisely, there are still many interesting topics that need to be investigated, such as: One—explore the best hybrid scheme including both model- and data-based approaches for different time scales to leverage from both approaches. Two—investigate the distribution state estimation techniques in case of occurrence of an extreme event. System observability needs to be examined in case of losing measuring devices due to cyber-attacks, or natural disasters. Three—network topology changes should be detected in case of an extreme event. Machine learning-based algorithms will need to be studied deeply for this application.