Effect of Fluid Contact Angle of Oil-Wet Fracture Proppant on the Competing Water/Oil Flow in Sandstone-Proppant Systems
Abstract
:1. Introduction
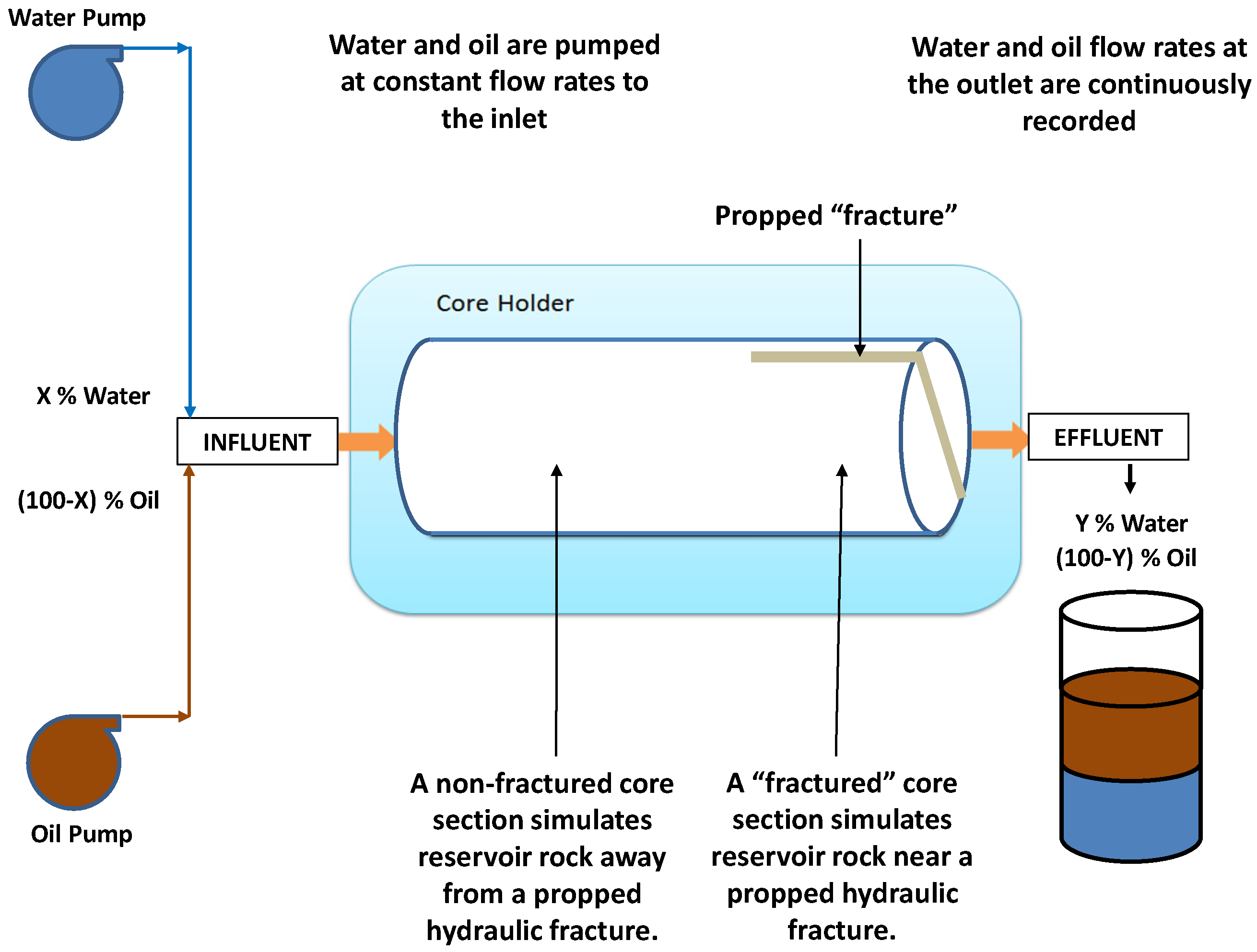
2. Experimental Design
- Measure the dimension and dry weight of a sandstone core sample.
- Remove the air in the core sample by vacuum in a water chamber.
- Measure the wet weight of the core sample, calculate pore volume (PV) and core sample porosity.
- Transfer the wet core sample into the core holder, seal the core with confining pressure, inject water through the core, and calculate core permeability.
- Inject oil (43° API) into the core until the desired water saturation (45% to 50%) is reached.
- Remove the core sample from the core holder and cut a 6-inch-long (0.1 inch and 0.2 inches wide) “fracture” along the diameter of the core.
- Fill the “fracture” with proppant particles, transfer the core sample into the core holder, and seal the core with confining pressure.
- Inject water and oil with deigned water-cut 40% at 5 cc/min through the core and record water and oil-flow volumes every one minute at the outlet.
- Stop fluid injection when the effluent water-cut reaches the influent water-cut.
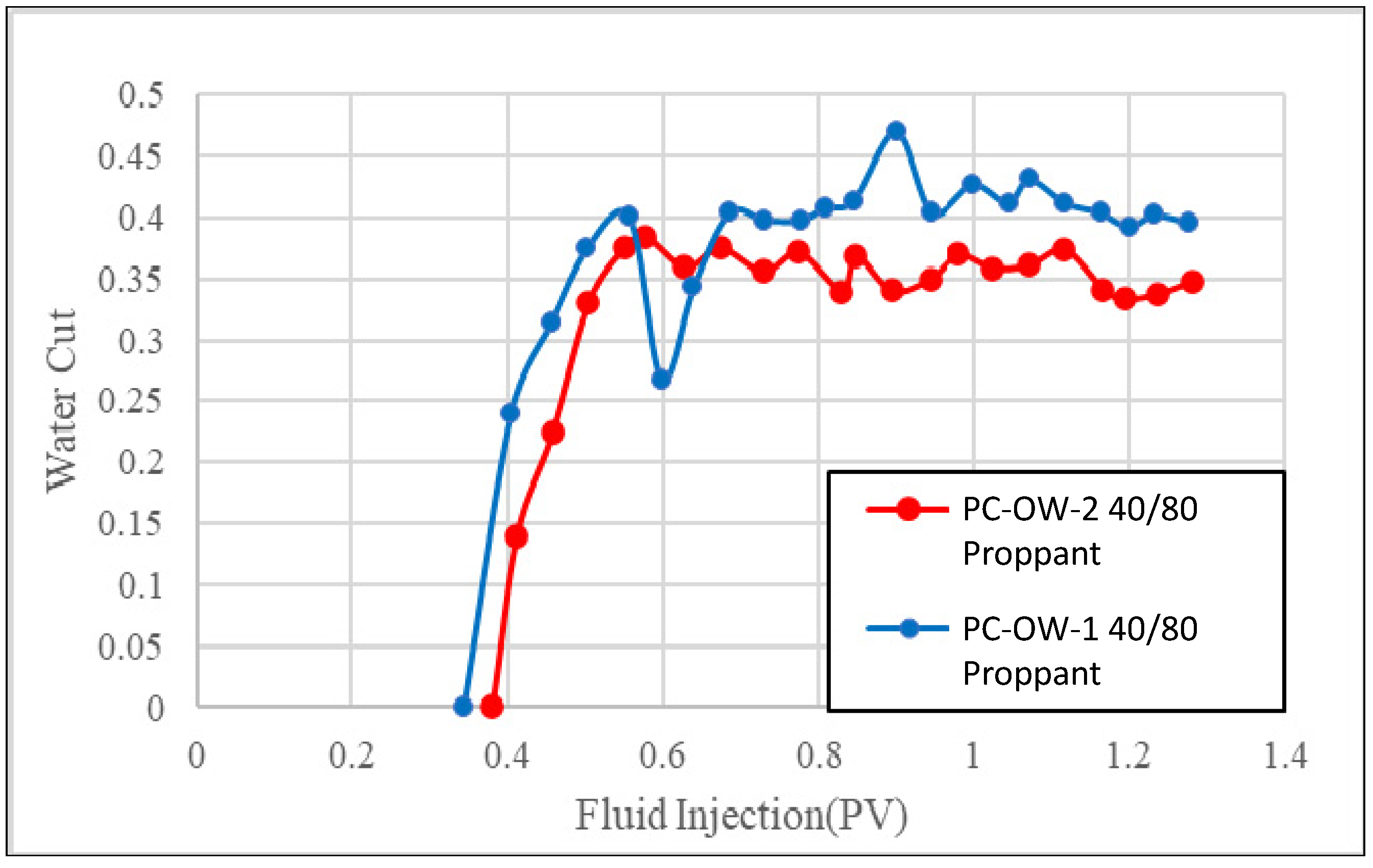
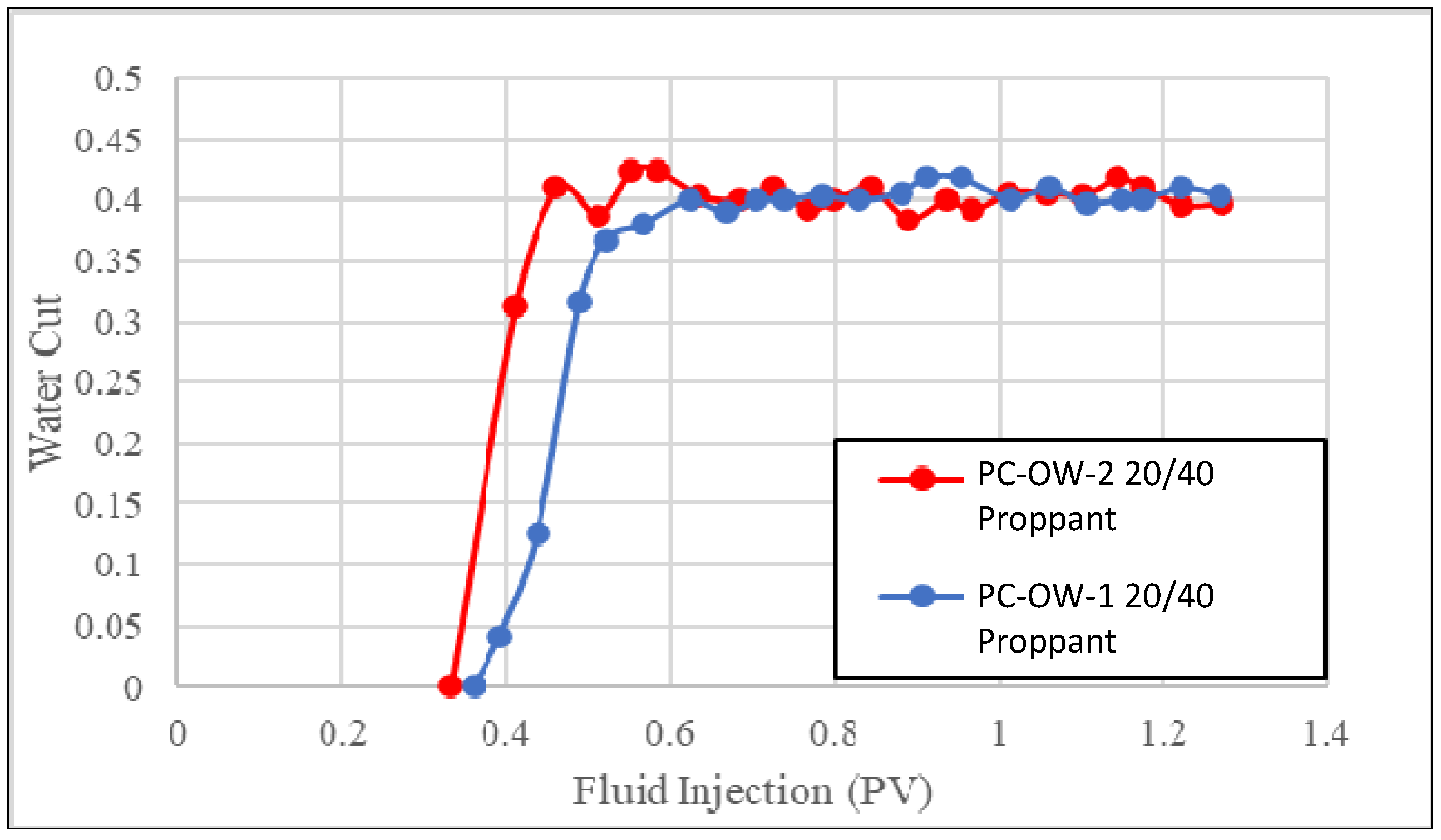
3. Experimental Result
4. Conclusions
- The newly developed method for determining the contact angle of fracture proppant pack gives a similar result for the water–stainless steel 304 system given in the literature with a difference of 3%. It gives a similar result for the water–copper system given by the literature with a difference of 3.5%. Therefore, the new method is considered valid for determining liquid contact angle on the smooth surfaces of solid particles. However, no data are found from the literature to validate the new method in determining the liquid contact angle on the surface of proppant packs.
- The PC fracture proppant packs with water contact angles greater than 90° and oil contact angles significantly less than 90° can be considered as oil-wet proppants. The experimental result from testing with two sandstones and two fracture widths indicates that reducing the oil contact angle of oil-wet proppants can improve the AORW performance of proppant packs through increasing capillary force and thus promoting oil imbibition into the proppant packs.
- The PC fracture proppant packs with water contact angles less than 90° and oil contact angles less than 90° may be considered as mixed-wet proppants. Their AORW performance depends on water and oil viscosities and should be tested in laboratories before the proppant is considered for well fracturing operations.
- The new method for contact angle measurement was developed based on the assumption that the liquid droplet on the surface of the proppant pack assumes a shape of a truncated sphere. This assumption may not be valid for large droplets where gravitational force makes the droplets flat. It is worthwhile to investigate the critical size of droplets below which the assumption of sphere truncation is valid. A potential means of evaluating the critical size of the droplet is to perform analysis with Eötvös number (Eo) or Bond number (Bo), which is a dimensionless number measuring the importance of gravitational forces compared to surface tension forces to characterize the shape of bubbles or drops moving in a surrounding fluid. This is to be investigated in future studies. The new method may not be accurate for situations where the proppant size is large or the contact angle is very small. In these conditions, the liquid would sink into the proppant pack quickly without forming a stable droplet. The critical proppant size and the minimum permissible contact angle should be investigated in future studies.
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of an Equation for Determining Contact Angle on the Basis of Droplet Measurement


References
- Mao, D.; Miller, D.S.; Karanikas, J.M.; Lake, E.A.; Fair, P.S.; Liu, X. Influence of Finite Hydraulic-Fracture Conductivity on Unconventional Hydrocarbon Recovery with Horizontal Wells; Society of Petroleum Engineers: Rechardson, TX, USA, 2017. [Google Scholar] [CrossRef]
- Longoria, R.A.; Liang, T.; Huynh, U.T.; Nguyen, Q.P.; DiCarlo, D.A. Water Blocks in Tight Formations: The Role of Matrix/Fracture Interaction in Hydrocarbon-Permeability Reduction and Its Implications in the Use of Enhanced Oil Recovery Techniques; Society of Petroleum Engineers: Rechardson, TX, USA, 2017. [Google Scholar] [CrossRef]
- Le, T.D.; Murad, M.A.; Pereira, P.A. A New Matrix/Fracture Multiscale Coupled Model for Flow in Shale-Gas Reservoirs; Society of Petroleum Engineers: Rechardson, TX, USA, 2017. [Google Scholar] [CrossRef] [Green Version]
- Safari, R.; Lewis, R.; Ma, X.; Mutlu, U.; Ghassemi, A. Infill-Well Fracturing Optimization in Tightly Spaced Horizontal Wells; Society of Petroleum Engineers: Rechardson, TX, USA, 2017. [Google Scholar] [CrossRef]
- Zhang, F.; Zhu, H.; Zhou, H.; Guo, J.; Huang, B. Discrete-Element-Method/Computational-Fluid-Dynamics Coupling Simulation of Proppant Embedment and Fracture Conductivity after Hydraulic Fracturing; Society of Petroleum Engineers: Rechardson, TX, USA, 2017. [Google Scholar] [CrossRef]
- Zhu, H.; Shen, J.; Zhang, F. A fracture conductivity model for channel fracturing and its implementation with Discrete Element Method. J. Pet. Sci. Eng. 2018, 172, 149–161. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Senetakis, K. A micromechanical study of shale rock-proppant composite interface. J. Pet. Sci. Eng. 2020, 184, 106542. [Google Scholar] [CrossRef]
- Mehmood, F.; Liao, J.; Hou, M.Z.; Zahoor, M.K.; Xiong, Y. Optimization of hydraulic fracturing with rod-shaped proppants for improved recovery in tight gas reservoirs. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 38. [Google Scholar] [CrossRef]
- Shaibu, R.; Guo, B.; Wortman, P.; Lee, J. Stress-Sensitivity of Fracture Conductivity of Tuscaloosa Marine Shale cores. J. Pet. Sci. Eng. 2022, 210, 110042. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Y.; Teng, Y.; Peng, S. Experiment study on the evolution of permeability and heat recovery efficiency in fractured granite with proppants. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 3. [Google Scholar] [CrossRef]
- Dong, K. Effect of Ceramic Proppant Surface Wettability on Oil Flow Efficiency in Hydraulic-Fractured Wells. Int. J. Eng. Res. Dev. 2018, 14, 13–22. [Google Scholar]
- Dong, K.; Wang, M.; Zhang, C. Effect of wettability of ceramic proppant surface in guar gum solution on the oil flow efficiency in fractures. Pet. J. 2018, 5, 388–396. [Google Scholar] [CrossRef]
- Dong, K.; He, W.; Wang, M. Effect of surface wettability of ceramic proppant on oil flow performance in hydraulic fractures. Energy Sci. Eng. 2019, 7, 504–514. [Google Scholar] [CrossRef] [Green Version]
- Washburn, E.W. The dynamics of capillary flow. Phys. Rev. 1921, 17, 273. [Google Scholar] [CrossRef]
- Xiao, D.; Wang, M.; Guo, B.; Weng, D. Effect of surface wetting behavior of ceramic proppant on the two-phase flow across the interface of sandstone and fracture. Energy Sci. Eng. 2020, 8, 1330–1336. [Google Scholar] [CrossRef]
- Dove, J.W.; Buckton, G.; Doherty, C. A comparison of two contact angle measurement methods and inverse gas chromatography to assess the surface energies of theophylline and caffeine. Int. J. Pharm. 1996, 138, 199–206. [Google Scholar] [CrossRef]
- Awasthi, A.; Bhatt, Y.J.; Garg, S.P. Measurement of contact angle in systems involving liquid metals. Meas. Sci. Technol. 1996, 7, 753. [Google Scholar] [CrossRef]
- Hung, Y.L.; Chang, Y.Y.; Wang, M.J.; Lin, S.Y. A simple method for measuring the superhydrophobic contact angle with high accuracy. Rev. Sci. Instrum. 2010, 81, 065105. [Google Scholar] [CrossRef] [PubMed]
- Meiron, T.S.; Marmur, A.; Saguy, S. Contact angle measurement on rough surfaces. Rev. Sci. Instrum. 2004, 274, 637–644. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.; Binks, B.P.; Clint, J.H. Determination of contact angles on microporous particles using the thin-layer wicking technique. Langmuir 2005, 21, 8319–8325. [Google Scholar] [CrossRef] [PubMed]
- Iliev, S.; Pesheva, N. Nonaxisymmetric drop shape analysis and its application for determination of the local contact angles. J. Colloid Interface Sci. 2006, 301, 677–684. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.L.; Kim, C.J.C. Contact Angle Measurement of Small Capillary Length Liquid in Super-repelled State. Sci. Rep. 2017, 7, 740. [Google Scholar] [CrossRef] [PubMed]
- Chini, S.F.; Amirfazli, A. A method for measuring contact angle of asymmetric and symmetric drops. Rev. Sci. Instrum. 2011, 388, 29–37. [Google Scholar] [CrossRef]
- Parmar, J.S.; Dehghanpour, H.; Kuru, E. Unstable Displacement: A Missing Factor in Fracturing Fluid Recovery. In Proceedings of the SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October–1 November 2012. SPE 162649. [Google Scholar]
- Moajil, A.A.; Alghizzi, A.; Alsalem, A.; AlDarweesh, A. Advanced HSP Ceramic Proppants—An Evaluation and Effect of Fines on Proppant Pack Conductivity. In Proceedings of the SPE Trinidad and Tobago Section Energy Resources Conference, Port of Spain, Trinidad and Tobago, 25–26 June 2018. SPE-191182-MS. [Google Scholar]
- Al-Boghail, F.; Moajil, A.A.; Al-Arawi, A.; Al-Darwish, S. Direct Approach for Contact Angle Measurement of Neutral Wet HSP Proppants. In Proceedings of the SPE Asia Pacific Oil & Gas Conference and Exhibition, Perth, Australia, 20–22 October 2020. SPE-202287-MS. [Google Scholar]
- FTA (FIRST TENANGSTROMS). Contact Angle and Surface Energy Measurements on Steel. 19 July 2003. Available online: https://www.firsttenangstroms.com/ (accessed on 10 January 2022).
- KSI (KINO Scientific Instrument Inc.). Contact Angle of Water on Smooth Surfaces and Wettability. 2022. Available online: http://www.uskino.com/articleshow_113.html (accessed on 10 January 2022).
- Evgeniya, O.; Feoktistov, D.; Kuznetsov, G. Investigation of drop dynamic contact angle on copper surface. In Proceedings of the EPJ Web Conference, Paris, France, 20 August 2015; Volume 82, p. 01053. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Guo, B.; Liu, N. Numerical Simulation of CO2 Migration into Cement Sheath of Oil/Gas Wells. J. Nat. Gas Sci. Eng. 2021, 94, 104085. [Google Scholar] [CrossRef]



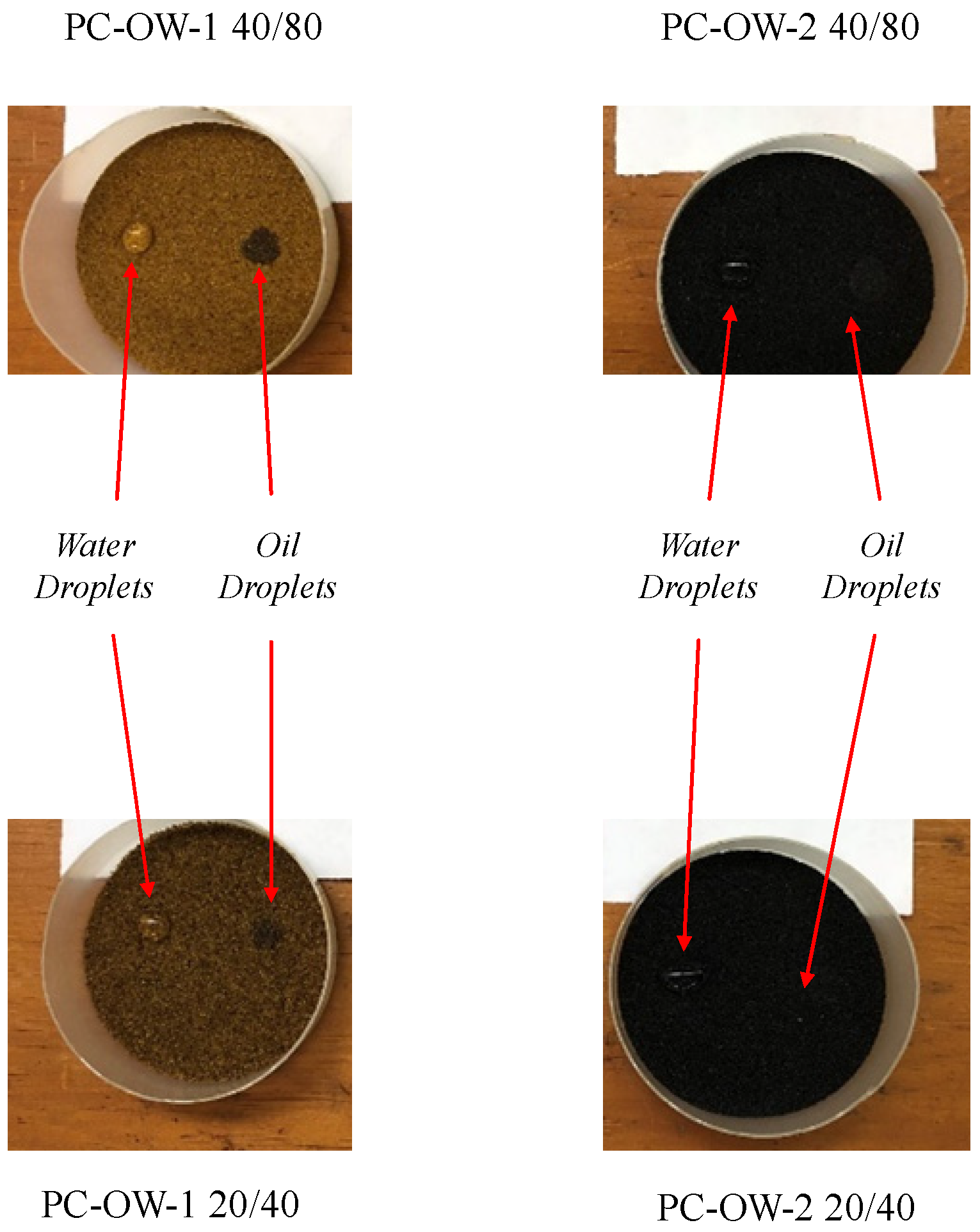





| Petrophysical Properties | PB-SS | UGB-SS | ||||
|---|---|---|---|---|---|---|
| Core 1 | Core 2 | Core 1 | Core 2 | Core 3 | Core 4 | |
| Porosity (%) | 16.19 | 15.81 | 19.2 | 19.25 | 19.27 | 19.06 |
| Water Permeability (md) | 8 | 9 | 68 | 68 | 52 | 49 |
| Water Saturation (%) | 50.2 | 50.1 | 45.4 | 45.3 | 45.4 | 45.5 |
| Proppant Sample | Droplet Volume (cc) | Droplet Diameter (cm) | Calculated Contact Angle (deg) | |||
|---|---|---|---|---|---|---|
| Water | Oil | Water | Oil | Water | Oil | |
| PC-OW-1 40/80 | 0.045 | 0.025 | 0.4313 | 0.515 | 114.91 | 75.58 |
| PC-OW-2 40/80 | 0.045 | 0.025 | 0.534 | 0.777 | 94.47 | 29.63 |
| PC-OW-1 20/40 | 0.045 | 0.025 | 0.459 | 0.551 | 109.01 | 67.08 |
| PC-OW-2 20/40 | 0.045 | 0.025 | 0.701 | 0.857 | 61.45 | 22.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Guo, B. Effect of Fluid Contact Angle of Oil-Wet Fracture Proppant on the Competing Water/Oil Flow in Sandstone-Proppant Systems. Sustainability 2022, 14, 3766. https://doi.org/10.3390/su14073766
Wang M, Guo B. Effect of Fluid Contact Angle of Oil-Wet Fracture Proppant on the Competing Water/Oil Flow in Sandstone-Proppant Systems. Sustainability. 2022; 14(7):3766. https://doi.org/10.3390/su14073766
Chicago/Turabian StyleWang, Ming, and Boyun Guo. 2022. "Effect of Fluid Contact Angle of Oil-Wet Fracture Proppant on the Competing Water/Oil Flow in Sandstone-Proppant Systems" Sustainability 14, no. 7: 3766. https://doi.org/10.3390/su14073766






