Modular Regulators of Water Level in Ditches of Subirrigation Systems
Abstract
:1. Introduction
2. Materials and Methods
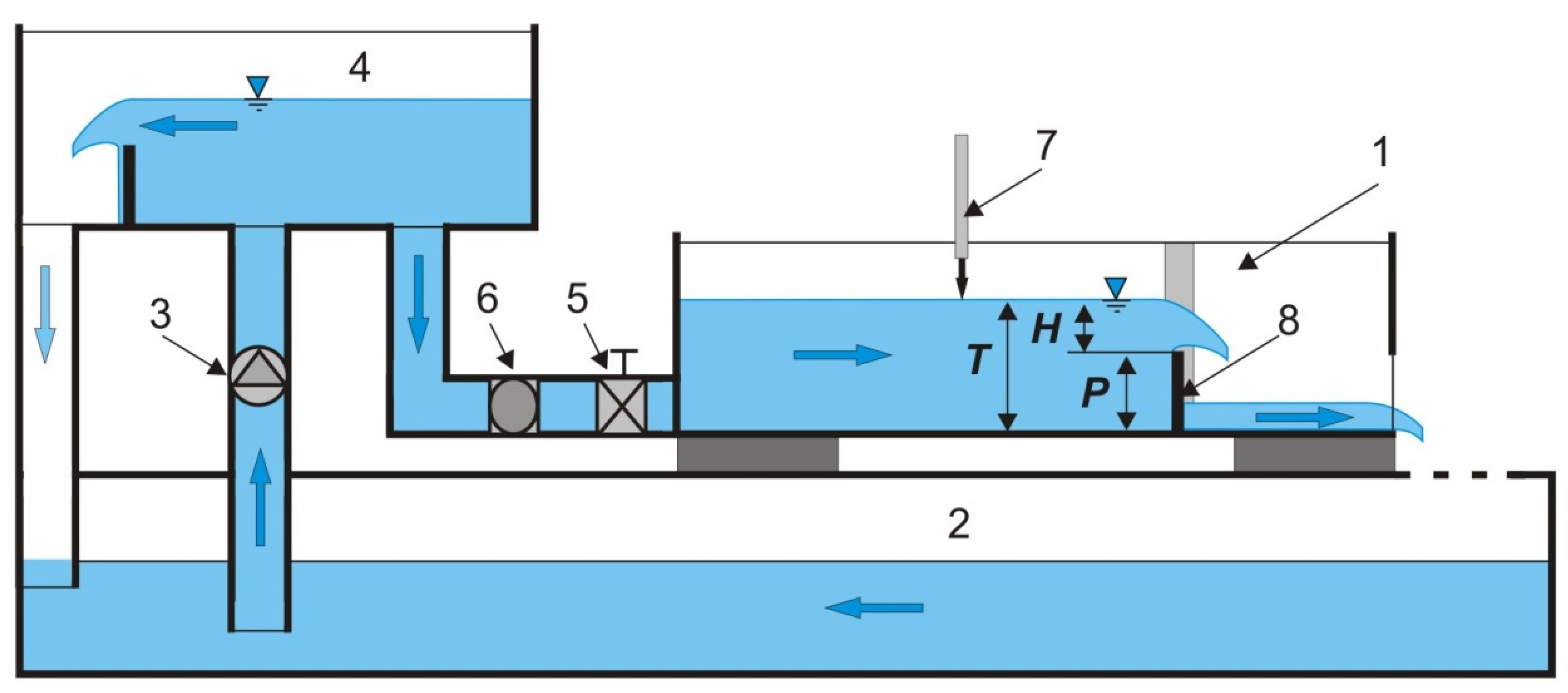
2.1. Regulators
2.2. Laboratory Experiment
2.3. Study Models
3. Laboratory Test Results
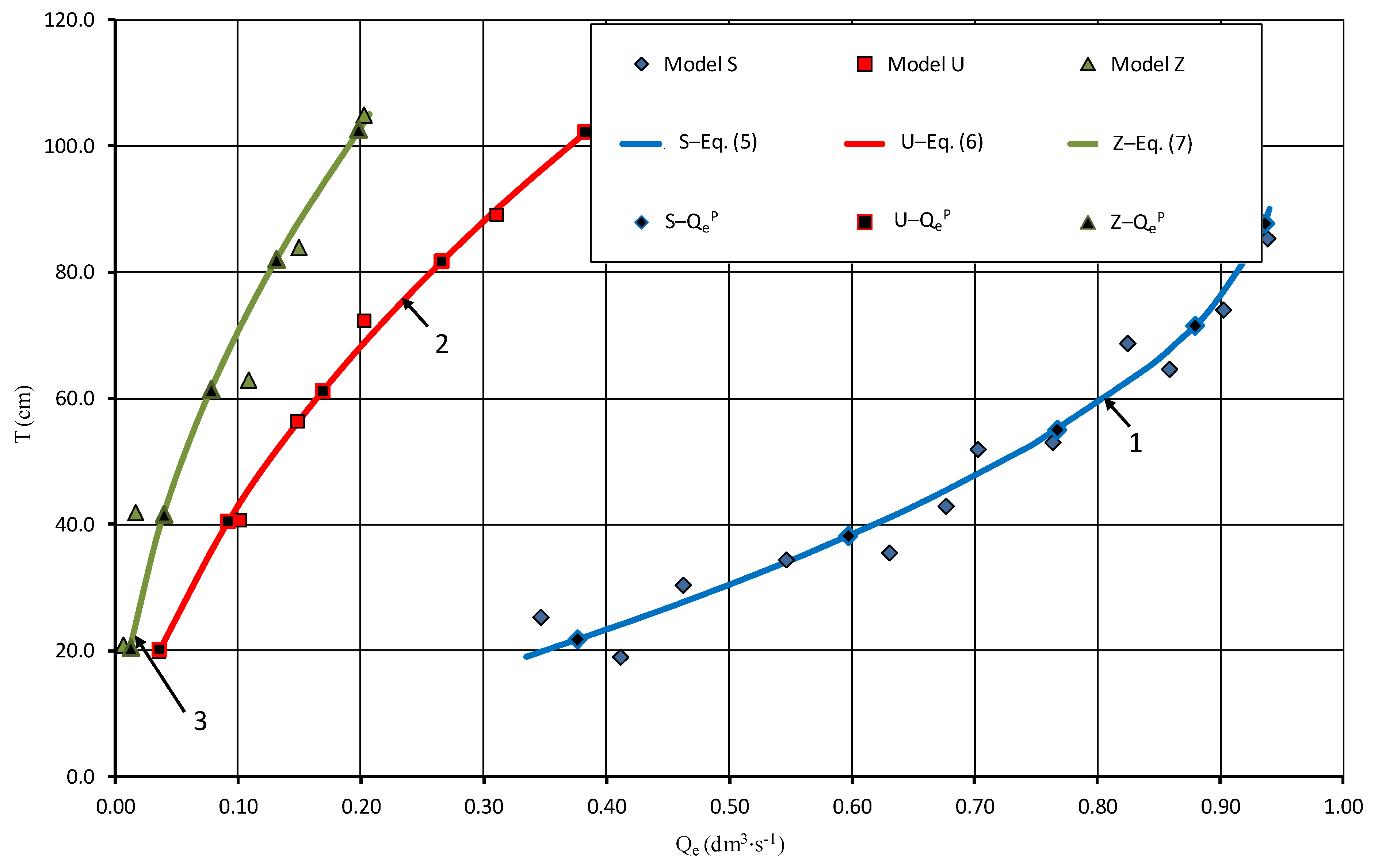
3.1. Effective Flow Qe
- S model, the scope of formula validity 19.1 cm ≤ H ≤ 85.4 cm:
- U model, the scope of formula validity 20.0 cm ≤ H ≤ 89.2 cm:
- Z model, the scope of formula validity 21.0 cm ≤ H ≤ 105.0 cm:
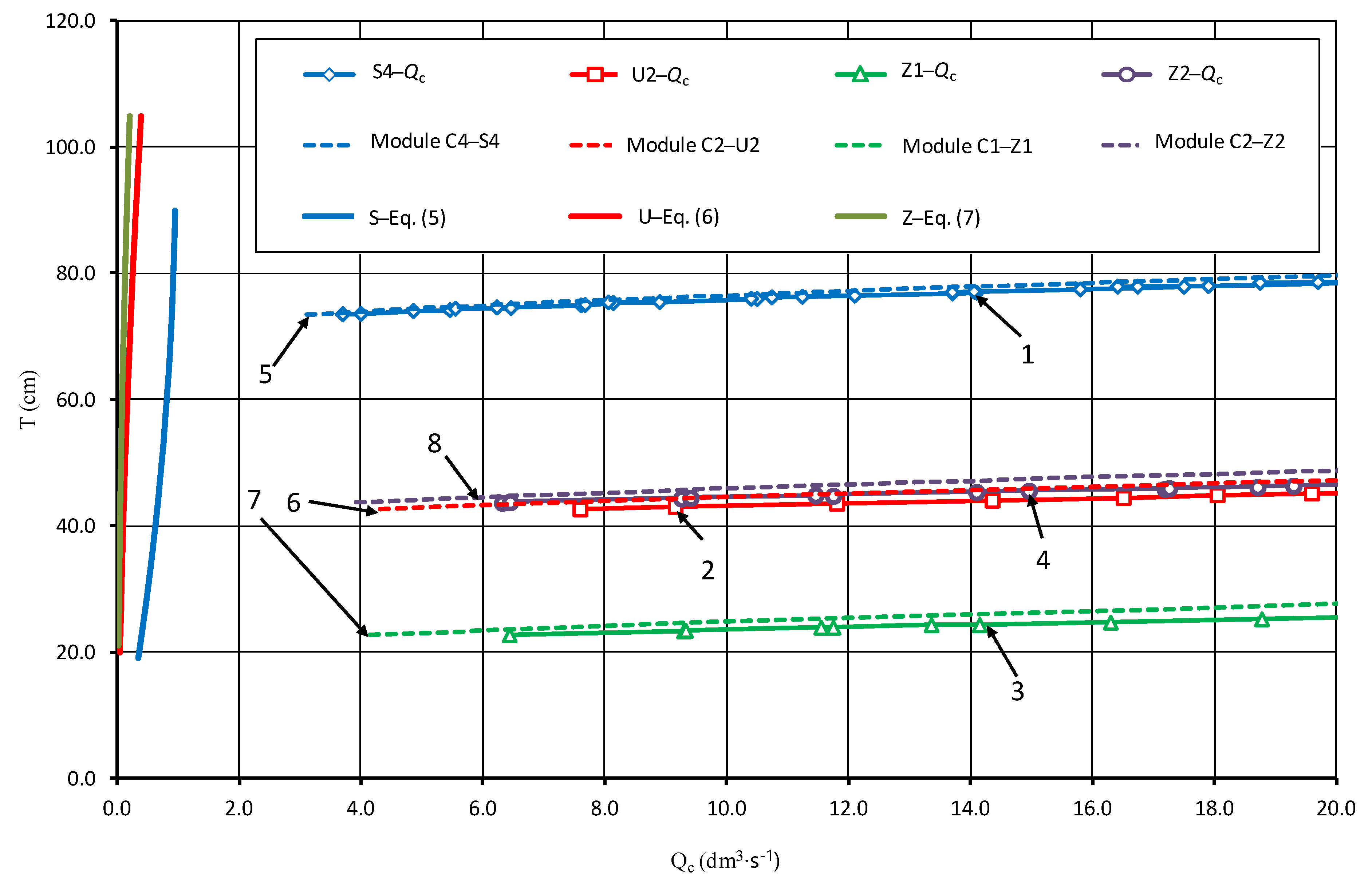
3.2. Total Flow Qc
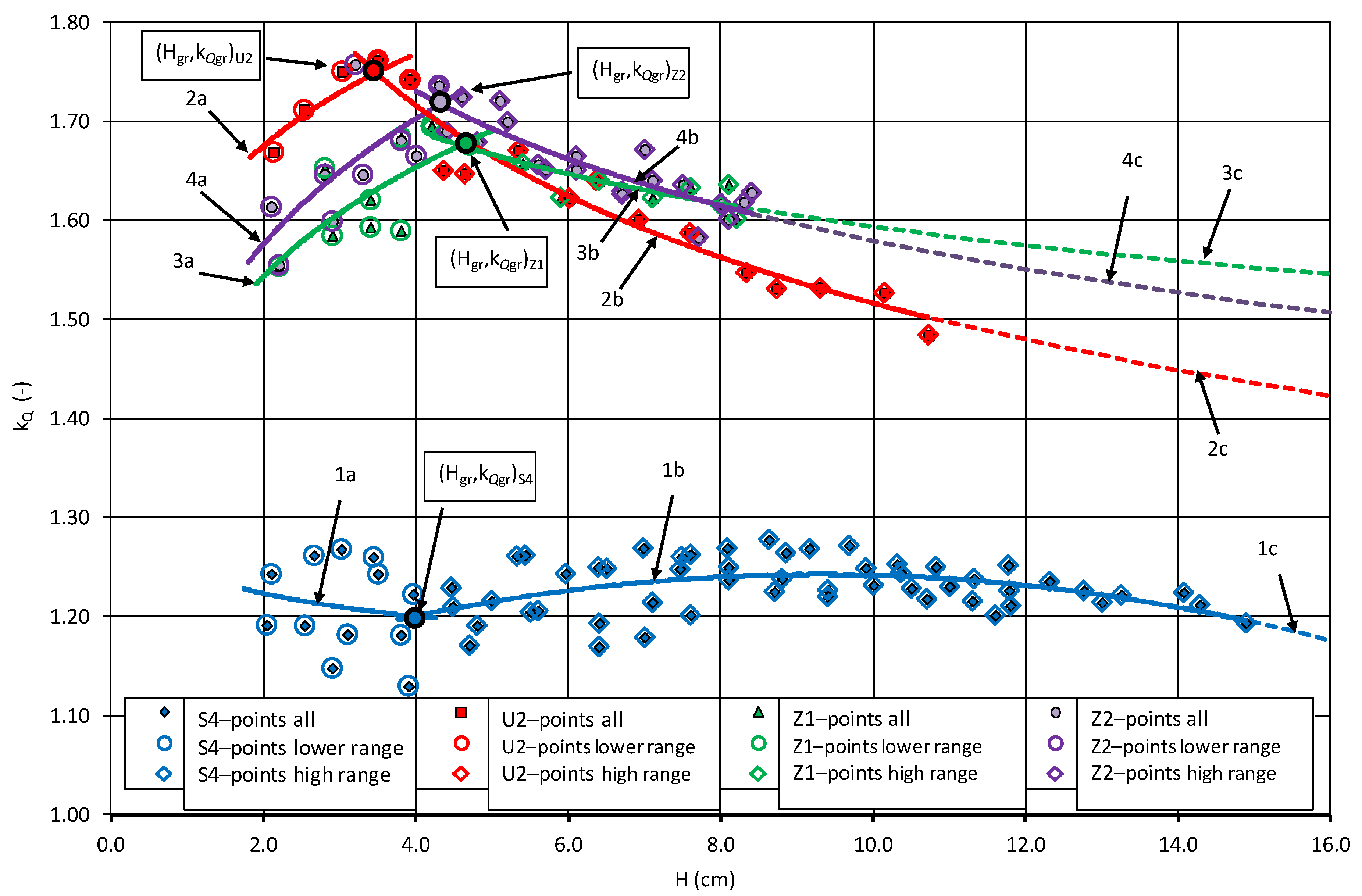
4. Discussion
5. Conclusions
- The tested regulators are suitable for damming water in drainage ditches with flows equal to or greater than the effective flow. The S regulator with straight beams, which are mounted in side recesses without special locks, has the highest effective flow.
- The S rectilinear regulator is characterized by the lowest value of modular flow coefficient taking into account the shape of the overflow edge profile compared to other regulators.
- The capacity of regulators with beams with a developed shape in the plan depends on the shape of the overflow plan described by the type of U and Z beams, the height of the sill P, and the height of the elevation of the upper water above the overflow H (Figure 8). With water depth above the control overflow crest up to 4.0 cm, the flow increase for the U beams in the plan is greater than that for the Z beams with a refracted shape in the plan (curve 2a compared to curves 3a and 4a in Figure 8).
- At the same sill height P, for fillings smaller than 4.0 cm, curvilinear U beams have a higher value of modular flow coefficient than the Z beams with a refracted shape. With fillings greater than 4.0 cm, the opposite relationship occurs (curve 2 compared to curve 3 in Figure 8). The height of the overflow sill for the same beam shape in the plan (Z1 and Z2 variants) changes the value of the modular flow coefficient (curve 3 compared to curve 4 in Figure 8).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Climate Change 2014 Synthesis Report, IPICC, 2015, Switzerland. Available online: https://www.ipcc.ch/site/assets/uploads/2018/02/SYR_AR5_FINAL_full.pdf (accessed on 11 February 2022).
- PGWP 2019. Projekt Plan Przeciwdziałania Skutkom Suszy (PPSS). Państwowe Gospodarstwo Wody Polskie, Warszawa, Sierpień 2019. Available online: https://www.wody.gov.pl/nasze-dzialania/stop-suszy (accessed on 11 February 2022). (In Polish)
- Przybyła, C.Z.; Szafrański, C.Z. Water management problems in agriculture in Wielkopolska. Water Environ. Rural Areas 2004, 4, 25–38. [Google Scholar]
- Wilderer, P.A. Applying Sustainable Water Management Concepts in Rural and Urban Areas: Some Thoughts About Reasons, Means and Needs. Water Sci. Technol. 2004, 49, 8–16. [Google Scholar] [CrossRef] [PubMed]
- Ankum, P.; Renault, D. Modernization of Irrigation Systems–Technical Modules; FAO Land & Water Division, Masscote: Rome, Italy, 2008; pp. 1–32. [Google Scholar]
- Machiels, O.; Erpicum, S.; Dewals, B.J.; Archambeau, P.; Pirotton, M. Piano Key Weirs: The experimental study of an efficient solution for rehabilitation. WIT Trans. Ecol. Environ. 2010, 133, 95–106. [Google Scholar] [CrossRef] [Green Version]
- Oleszczuk, R.; Stocka, I.; Urbański, J.; Hewelke, E. Ocena stanu technicznego budowli wodno-melioracyjnych na obiekcie nawodnień podsiąkowych Solec. Wiadomości Melior. I Łąkarskie 2016, 2, 72–76. (In Polish) [Google Scholar]
- Oleszczuk, R.; Stocka, I.; Urbański, J.; Hewelke, E. Stan techniczny budowli piętrzących na przykładzie wybranego systemu nawodnień podsiąkowych. Water Environ. Rural Areas 2017, 17, 89–100. (In Polish) [Google Scholar]
- Schuurmans, J.; Hof, A.; Dijkstra, S.; Bosgra, O.H.; Brouwer, R. Simple Water Level Controller for Irrigation and Drainage Canals. J. Irrig. Drain. Eng. 1999, 125, 189–195. [Google Scholar] [CrossRef]
- Popek, Z.; Bajkowski, S.; Siwicki, P.; Urbański, J. Laboratory Tests of New Groundwater Table Level Regulators in Subsurface Drainage Systems. Water 2021, 13, 631. [Google Scholar] [CrossRef]
- Skaggs, R.W.; Fausey, N.R.; Evans, R.O. Drainage water management. J. Soil Water Conserv. 2012, 67, 167A–172A. [Google Scholar] [CrossRef] [Green Version]
- Smedema, L.K.; Vlotman, W.F.; Rycroft, D.W. Modern Land Drainage: Planning, Design and Management of Agricultural Drainage Systems; CRC Press: Abingdon, UK, 2004; p. 449. [Google Scholar] [CrossRef]
- Szejba, D.; Bajkowski, S. Determination of Tile Drain Discharge under Variable Hydraulic Conditions. Water 2019, 11, 120. [Google Scholar] [CrossRef] [Green Version]
- Bajkowski, S. Discharge coefficients of the horizontal vortex chamber. Sci. Pap. Univ. Agric. Krakow Environ. Engineer. Ser. 2001, 21, 673–681. (In Polish) [Google Scholar]
- Subhash, C.; Jain, M. Free-surface swirling flows in vertical dropshaft. J. Hydraul. Eng. 1987, 113, 1277–1289. [Google Scholar]
- Bajkowski, S. Hydraulic properties of horizontal vortex chamber. Adv. Hydro-Sci. Eng. 2002, 150, 47–58. (In Polish) [Google Scholar]
- Bos, M.G. Discharge Measurement Structures. International Institute for Land Reclamation and Improvement, 3rd ed.; International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1989; p. 402. [Google Scholar]
- Bajkowski, S. Submerged sharp-crested morning-glory-spillway criteria of submergence and the discharge coefficients. Model. Investig. Hydro-Eng. 1987, 51, 5–15. [Google Scholar]
- Harada, M. The Society of Instrument and Control Engineers. In Fluid Control and Measurement; Pergamon Press: Tokyo, Japan, 1986; Volume 1, p. 587. [Google Scholar]
- Voron, B. Regulation and management of water in irrigation canals and water saving irrigation methods and technologies. La Houille Blanche 1995, 4, 72–81. [Google Scholar] [CrossRef] [Green Version]
- Frankenberger, J.; Kladivko, E.; Sands, G.; Jaynes, D.; Fausey, N.; Helmers, M.; Brown, L. Drainage Water Management for the Midwest: Questions and Answers about Drainage Water Management for the Midwest; Purdue Extension: West Lafayette, IN, USA, 2006; 8p. [Google Scholar]
- Jaynes, D.B. Changes in yield and nitrate losses from using drainage water management in central Iowa. J. Soil Water Conserv. 2012, 67, 485–494. [Google Scholar] [CrossRef] [Green Version]
- Sunohara, M.D.; Gottschall, N.; Craiovan, E.; Wilkes, G.; Topp, E.; Frey, S.K.; Lapen, D.R. Controlling tile drainage during the growing season in Eastern Canada to reduce nitrogen, phosphorus, and bacteria loading to surface water. Agric. Water Manag. 2016, 178, 159–170. [Google Scholar] [CrossRef]
- Sojka, M.; Kozłowski, M.; Stasik, R.; Napierała, M.; Kęsicka, B.; Wróżyński, R.; Jaskuła, J.; Liberacki, D.; Bykowski, J. Sustainable Water Management in Agriculture—The Impact of Drainage Water Management on Groundwater Table Dynamics and Subsurface Outflow. Sustainability 2019, 11, 4201. [Google Scholar] [CrossRef] [Green Version]
- Brandyk, A.; Kaca, E.; Oleszczuk, R.; Urbański, J.; Jadczyszyn, J. Conceptual Model of Drainage-Sub Irrigation System Functioning-First Results from a Case Study of a Lowland Valley Area in Central Poland. Sustainability 2021, 13, 107. [Google Scholar] [CrossRef]
- Pietrucha, J.; Gralewski, J.; Kolasiński, D. Device for Water Level Control. Patent Office of the Republic of Poland Patent 237597, 2021. [Google Scholar]
- Żbikowski, A.; Bajkowski, S.; Batijewski, W.; Dąbkowski, L.; Kubrak, J.; Lipka, W. Wytyczne wymiarowania przelewów i ich kanałów odprowadzających w budowlach wodnomelioracyjnych. In Obliczenia Hydrauliczne Przelewów Budowli Wodno-Melioracyjnych; Okruszko, H., Ed.; BiblioteczkaWiadomości IMUZ: Warsaw, Poland, 1986; Volume 67, pp. 9–93. (In Polish) [Google Scholar]
- Bekheet, A.A.; AboulAtta, N.M.; Saa, N.Y.; El-Molla, D.A. Effect of the shape and type of piano key weirs on the flow efficiency. Ain Shams Eng. J. 2022, 13, 1–15. [Google Scholar] [CrossRef]
- Nezami, F.; Farsadizadeh, D.; Nekooie, M.A. Discharge coefficient for trapezoidal side weir. Alexandria University. Alex. Eng. J. 2015, 54, 595–605. [Google Scholar] [CrossRef] [Green Version]
- Emiroglu, M.E.; Kaya, N.; Agaccioglu, H. Discharge Capacity of Labyrinth Side Weir Located on a Straight Channel. J. Irrig. Drain. Eng. 2010, 136, 37–46. [Google Scholar] [CrossRef]
- Sadeghian, H.; Parvaneh, A.; Nekooie, M.A.; Parvaneh, M. Discharge characteristics of triangular labyrinth side weirs (with inclined bed) located on a straight channel. In Proceedings of the 38th Iahr World Congress, Panama City, Panama, 1–6 September 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Ikinciogullari, E.; Emiroglu, M.E. Estimation of triangular labyrinth side weir discharge capacity using schmidt approach. Sigma J. Eng. Nat. Sci. 2019, 37, 289–303. [Google Scholar]
- Khalili, M.; Honar, T. Discharge Coefficient of Semi-Circular Labyrinth Side Weir in Subcritical Flow. WSA 2017, 43, 433. [Google Scholar] [CrossRef] [Green Version]
- Dursun, O.F.; Kaya, N.; Firat, M. Estimating Discharge Coefficient of Semi-Elliptical Side Weir Using ANFIS. J. Hydrol. 2012, 426–427, 55–62. [Google Scholar] [CrossRef]

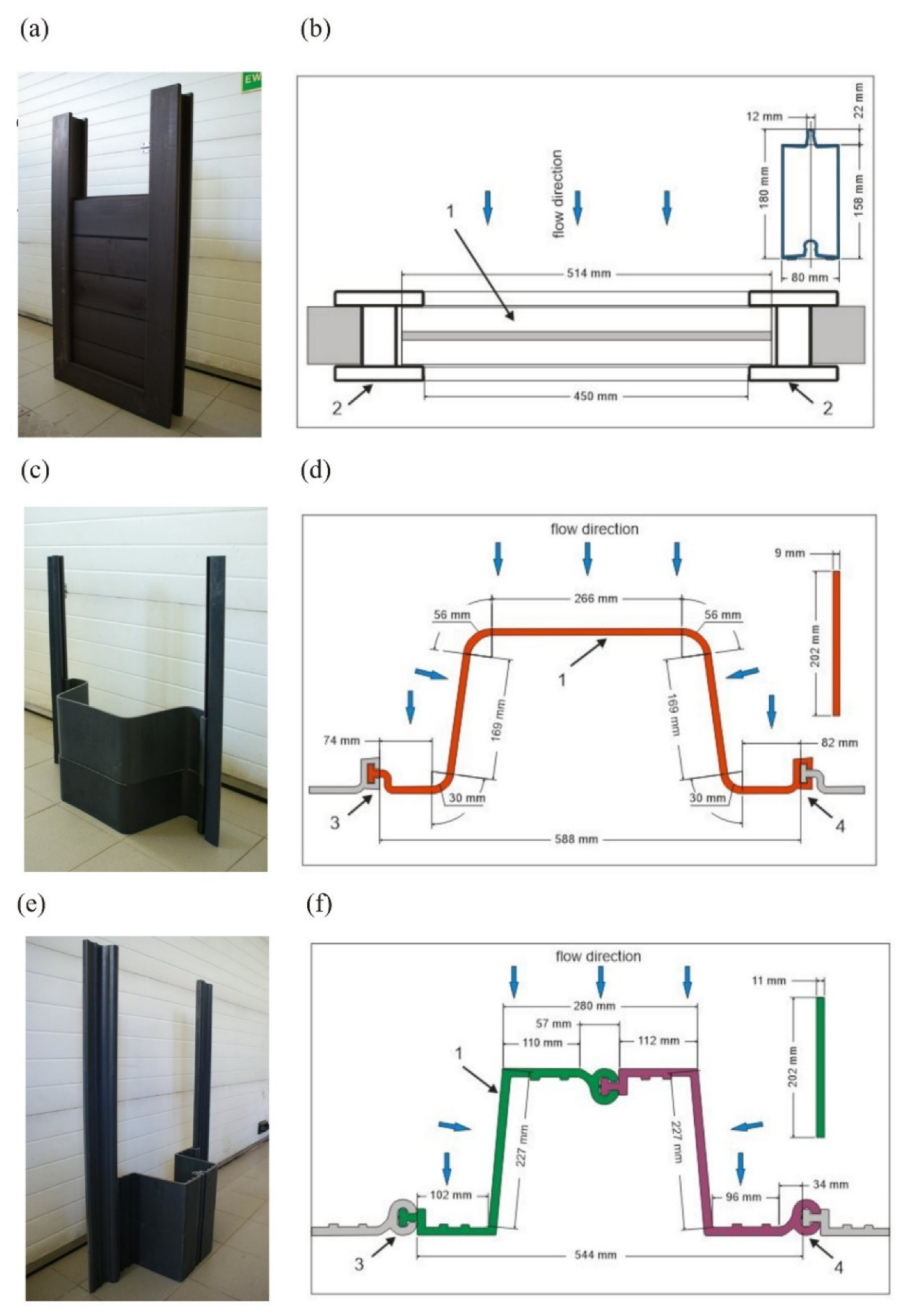
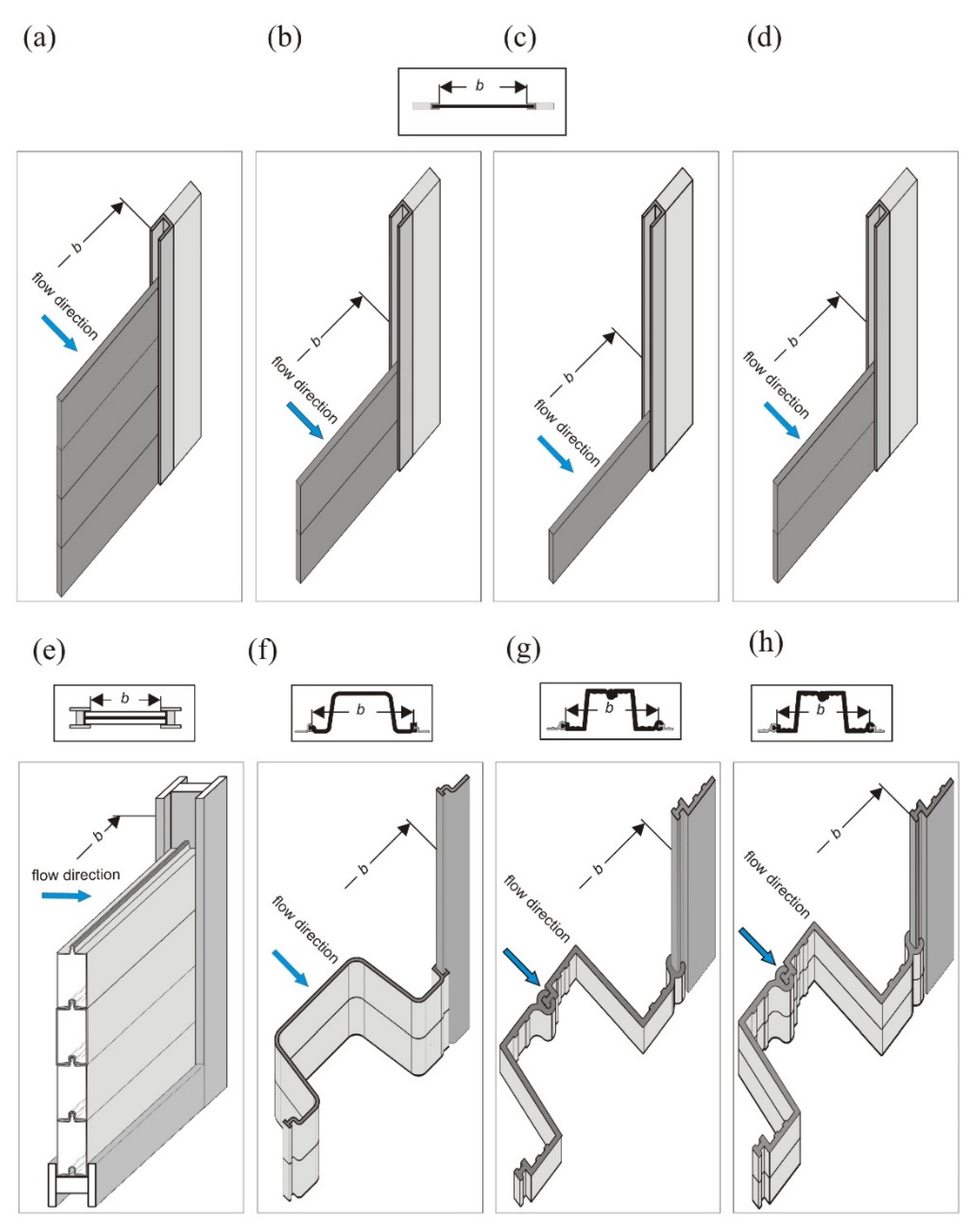

| No. | Model | Module | b (m) | Lp (m) | Lk (cm) | kr | Variant | P (cm) | Qe (dm3·s−1) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1. | C (sharp-crested)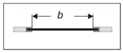 | M45 | 0.450 | 0.450 | 1.2 | C4–S4 | 71.5 | ||
| 2. | M59 | 0.588 | 0.588 | 0.9 | 1.00 | C2–U2 | 40.5 | ||
| 3. | M54 | 0.544 | 0.544 | 1.1 | C1–Z1 | 20.5 | |||
| 4. | M54 | 0.544 | 0.544 | 1.1 | C2–Z2 | 41.6 | |||
| 5. | S (rectilinear)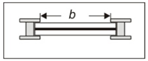 | S5 | 87.7 | 0.937 | |||||
| 6. | S4 | 71.5 | 0.879 | ||||||
| 7. | M45 | 0.450 | 0.450 | 1.2 | 1.00 | S3 | 55.0 | 0.767 | |
| 8. | S2 | 38.2 | 0.597 | ||||||
| 9. | S1 | 21.8 | 0.376 | ||||||
| 10. | S0 | 6.8 | 0.000 | ||||||
| 11. | U (labyrinth)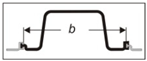 | U5 | 102.2 | 0.383 | |||||
| 12. | U4 | 81.7 | 0.266 | ||||||
| 13. | M59 | 0.588 | 0.935 | 0.9 | 1.58 | U3 | 61.2 | 0.169 | |
| 14. | U2 | 40.5 | 0.092 | ||||||
| 15. | U1 | 20.2 | 0.036 | ||||||
| 16. | U0 | 0.0 | 0.000 | ||||||
| 17. | Z (compound)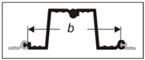 | Z5 | 102.6 | 0.198 | |||||
| 18. | Z4 | 82.0 | 0.131 | ||||||
| 19. | M54 | 0.544 | 0.967 | 1.1 | 1.74 | Z3 | 61.4 | 0.078 | |
| 20. | Z2 | 41.6 | 0.040 | ||||||
| 21. | Z1 | 20.5 | 0.013 | ||||||
| 22. | Z0 | 0.0 | 0.000 |
| No. | Variant | Variable | Qc (dm3·s−1) | T (cm) | H (cm) | Re | H/P | H/Lk | H/B |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | S4 (rectilinear)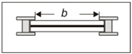 | max | 55.90 | 86.39 | 14.89 | 1.56 × 105 | 0.21 | 12.34 | 0.139 |
| 2 | average | 24.39 | 79.34 | 7.84 | 7.43 × 104 | 0.11 | 6.50 | 0.073 | |
| 3 | min | 3.70 | 73.54 | 2.04 | 1.33 × 104 | 0.03 | 1.69 | 0.019 | |
| 4 | U2 (labyrinth)  | max | 57.36 | 51.22 | 10.72 | 1.55 × 105 | 0.26 | 12.60 | 0.100 |
| 5 | average | 29.13 | 46.59 | 6.09 | 7.10 × 104 | 0.15 | 7.16 | 0.057 | |
| 6 | min | 7.20 | 42.63 | 2.13 | 1.36 × 104 | 0.05 | 2.50 | 0.020 | |
| 7 | Z1 (compound)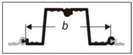 | max | 39.28 | 28.70 | 8.20 | 1.05 × 105 | 0.40 | 7.67 | 0.077 |
| 8 | average | 20.98 | 25.51 | 5.01 | 5.51 × 104 | 0.24 | 4.68 | 0.047 | |
| 9 | min | 6.44 | 22.70 | 2.20 | 1.43 × 104 | 0.11 | 2.06 | 0.021 | |
| 10 | Z2 (compound) | max | 40.85 | 50.00 | 8.40 | 1.07 × 105 | 0.20 | 7.86 | 0.079 |
| 11 | average | 23.25 | 47.02 | 5.42 | 6.53 × 104 | 0.13 | 5.07 | 0.051 | |
| 12 | min | 6.31 | 43.70 | 2.10 | 1.43 × 104 | 0.05 | 1.97 | 0.020 |
| No. | Parameter | S4 | U2 | Z1 | Z2 |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 |
| Curve in Figure 7 | 1 | 2 | 3 | 4 | |
| 1 | a1 | 1.0 | 0.1871 | 0.2798 | 0.2408 |
| 2 | b1 | 1.5 | 2.0 | 2.0 | 2.0 |
| 3 | a2 | 0.0 | 3.4250 | 2.5577 | 2.8244 |
| 4 | b2 | 0.0 | 1.0 | 1.0 | 1.0 |
| 5 | c1 = Qe (dm3·s−1) | 0.8794 | 0.0917 | 0.0126 | 0.0397 |
| 6 | r | 0.9956 | 0.9983 | 0.9984 | 0.9985 |
| 7 | R2 | 0.9987 | 0.9990 | 0.9987 | 0.9978 |
| 8 | N | 65 | 17 | 18 | 28 |
| No. | Parameter | S4 | U2 | Z1 | Z2 |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 |
| Lower zone | |||||
| 1 | Curve in Figure 8 | 1a | 2a | 3a | 4a |
| 2 | Hmin (cm) | 2.04 | 2.13 | 2.20 | 2.10 |
| 3 | Qmin (dm3·s−1) | 3.70 | 7.20 | 6.44 | 6.31 |
| 4 | a3 | 1.2473 | 1.5871 | 1.4413 | 1.4589 |
| 5 | b3 | −0.0280 | 0.0779 | 0.0991 | 0.1115 |
| 6 | a4, b4, c2 | 0.0 | 0.0 | 0.0 | 0.0 |
| 7 | r | −0.1810 | 0.8327 | 0.7692 | 0.7092 |
| 8 | R2 | 0.0272 | 0.7675 | 0.5976 | 0.5229 |
| 9 | N | 12 | 5 | 10 | 9 |
| Border point | |||||
| 10 | Hgr (cm) | 3.98 | 3.48 | 4.58 | 4.32 |
| 11 | kQgr (dm3·s−1) | 1.20 | 1.75 | 1.68 | 1.72 |
| Upper zone | |||||
| 14 | Curve in Figure 8 | 1b | 2b | 3b | 4b |
| 15 | a3 | −0.0015 | 2.0691 | 1.8489 | 1.9885 |
| 16 | b3 | 2.0 | −0.1350 | −0.0646 | −0.1001 |
| 17 | a4 | 0.0279 | 0.0 | 0.0 | 0.0 |
| 18 | b4 | 1.0 | 0.0 | 0.0 | 0.0 |
| 19 | c2 | 1.113 | 0.0 | 0.0 | 0.0 |
| 20 | r | 0.0268 | −0.9549 | −0.8671 | −0.8683 |
| 21 | R2 | 0.2071 | 0.9318 | 0.7917 | 0.7719 |
| 22 | N | 53 | 14 | 10 | 20 |
| 23 | Hmax (cm) | 14.89 | 10.72 | 8.20 | 8.40 |
| 24 | Qmax (dm3·s−1) | 55.90 | 57.36 | 39.28 | 40.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bajkowski, S.; Urbański, J.; Oleszczuk, R.; Siwicki, P.; Brandyk, A.; Popek, Z. Modular Regulators of Water Level in Ditches of Subirrigation Systems. Sustainability 2022, 14, 4103. https://doi.org/10.3390/su14074103
Bajkowski S, Urbański J, Oleszczuk R, Siwicki P, Brandyk A, Popek Z. Modular Regulators of Water Level in Ditches of Subirrigation Systems. Sustainability. 2022; 14(7):4103. https://doi.org/10.3390/su14074103
Chicago/Turabian StyleBajkowski, Sławomir, Janusz Urbański, Ryszard Oleszczuk, Piotr Siwicki, Andrzej Brandyk, and Zbigniew Popek. 2022. "Modular Regulators of Water Level in Ditches of Subirrigation Systems" Sustainability 14, no. 7: 4103. https://doi.org/10.3390/su14074103
APA StyleBajkowski, S., Urbański, J., Oleszczuk, R., Siwicki, P., Brandyk, A., & Popek, Z. (2022). Modular Regulators of Water Level in Ditches of Subirrigation Systems. Sustainability, 14(7), 4103. https://doi.org/10.3390/su14074103






