Dynamic Behavior of the Transition Zone of an Integral Abutment Bridge
Abstract
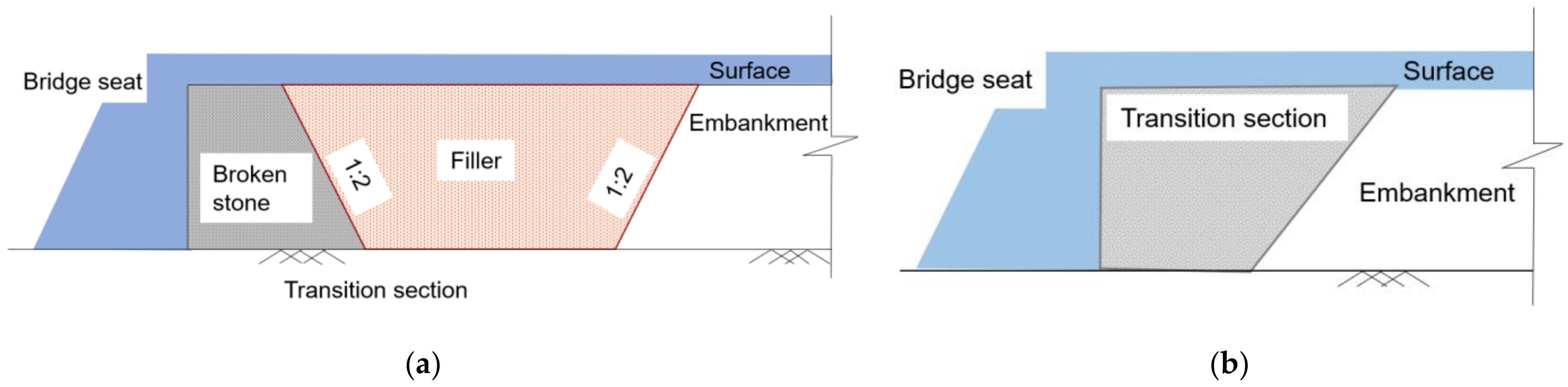
:1. Introduction
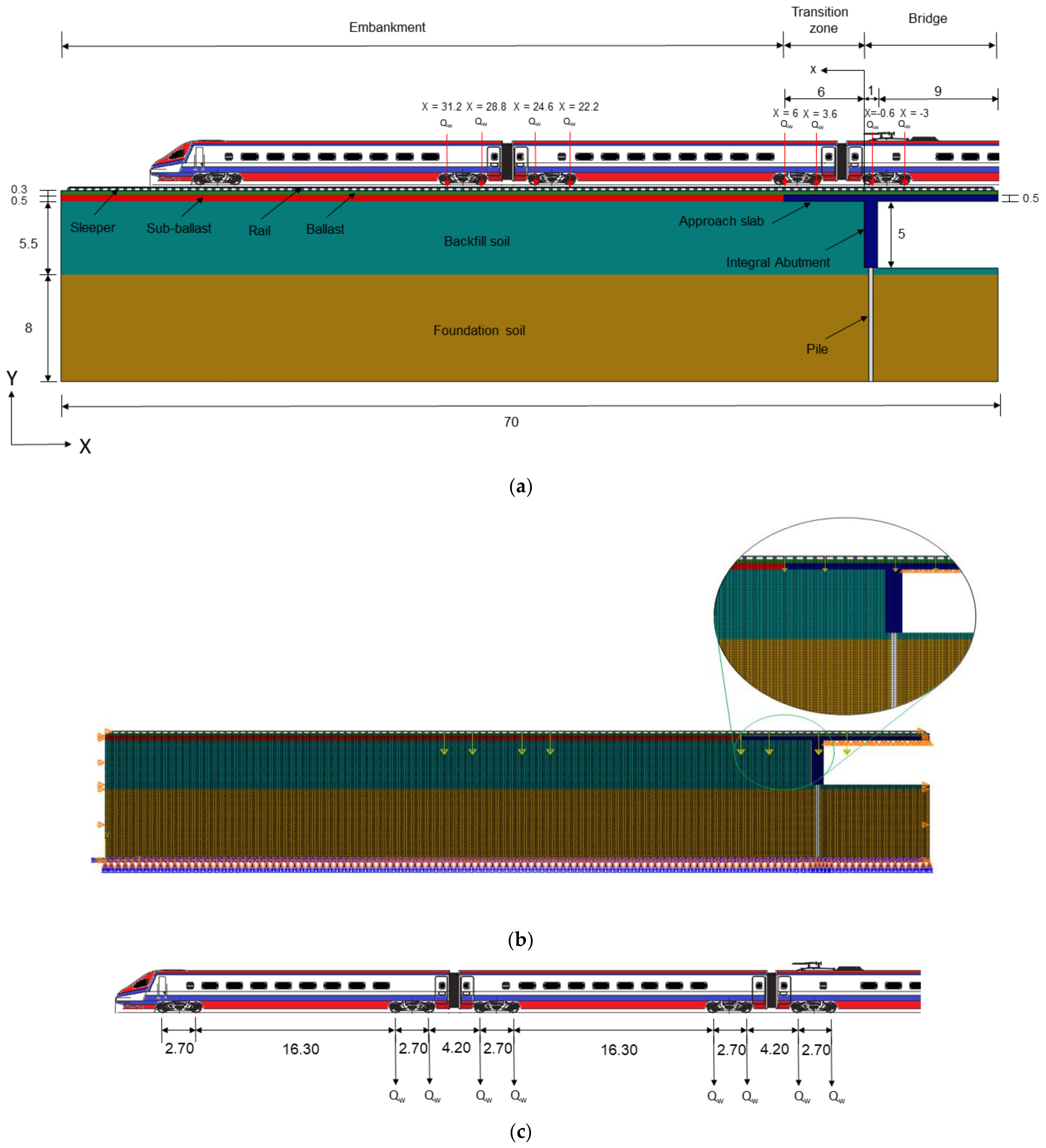
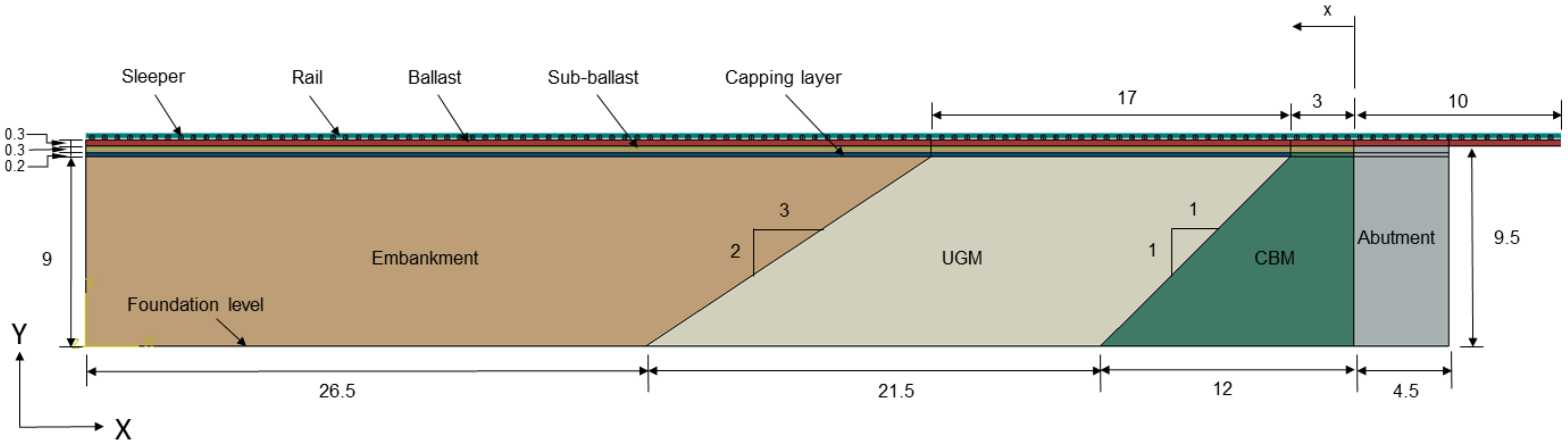
2. Numerical Model of the Integral Abutment Bridge
Boundary and Loading Conditions
3. Parametric Study
3.1. Variation of the Length of the Transition Zone
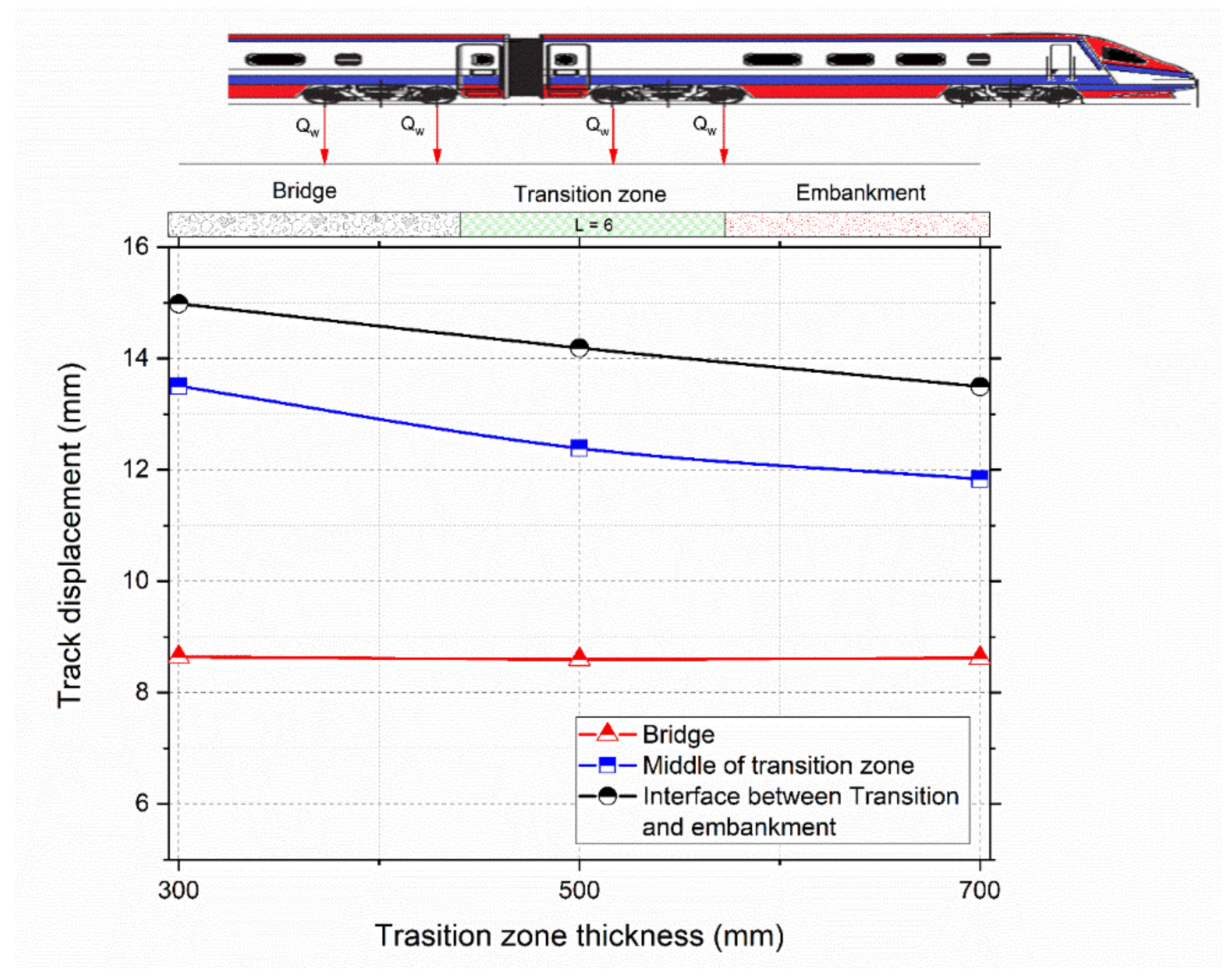
3.2. Variation of the Transition Zone Thickness
3.3. Variation of Backfill Soil Density
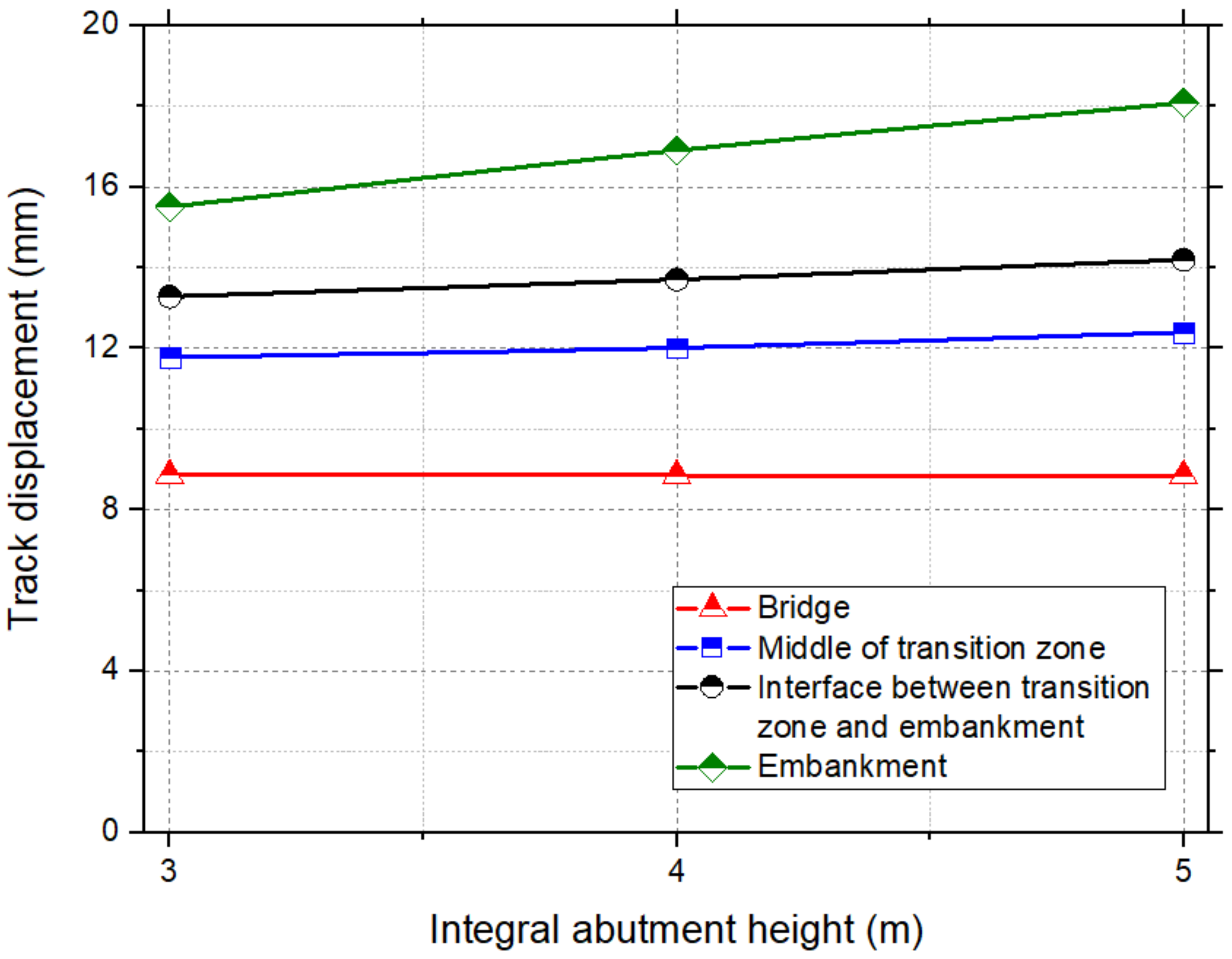
3.4. Variation of Height of the Integral Abutment
3.5. Variation of Inclination of Transition Zone
4. Dynamic Loading: Simulation and Results
Variation in Thickness and Fall in Inclination of the Approach Slab
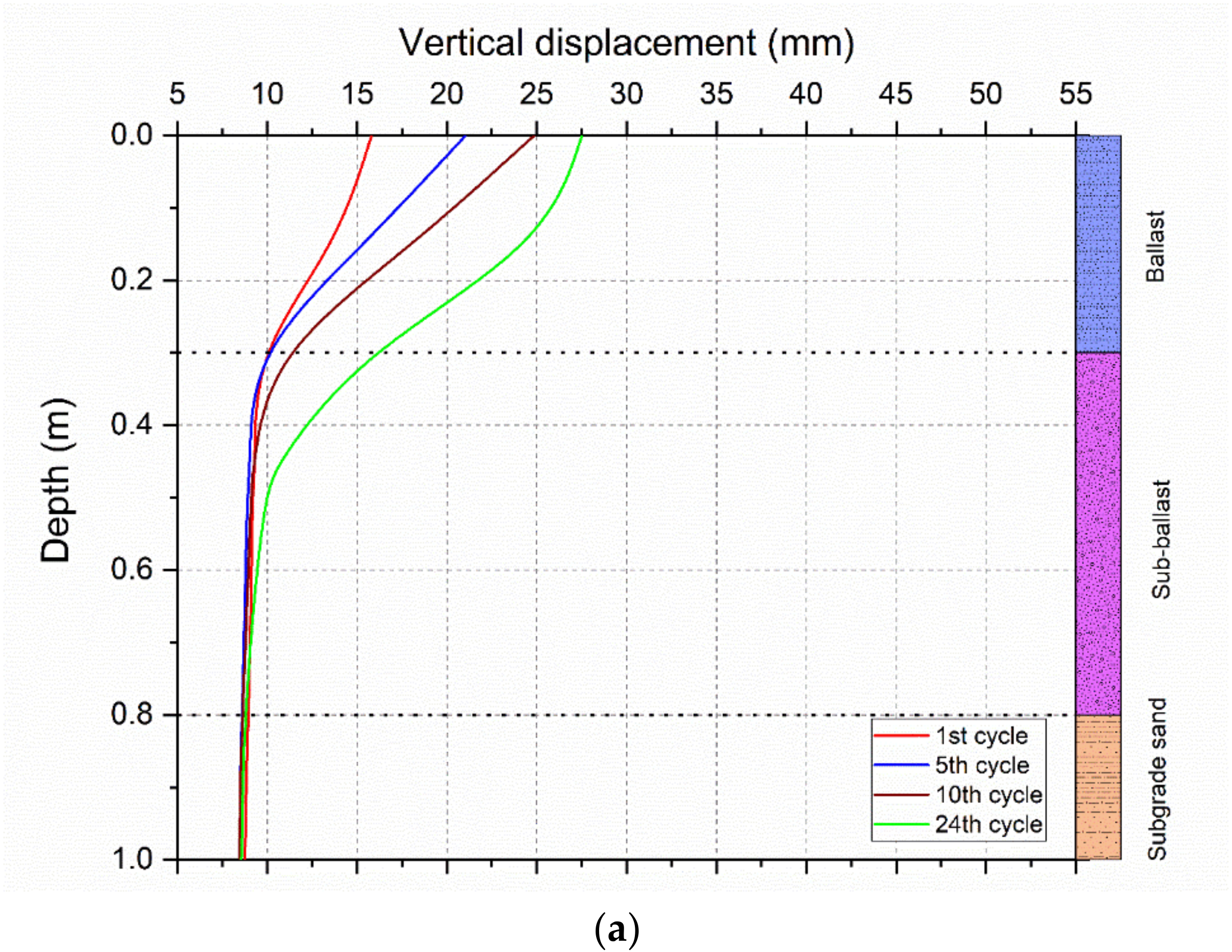
5. Cyclic Loading
6. Model Validation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Banimahd, M. Advanced Finite Element Modelling of Coupled Train-Track Systems: A Geotechnical Perspective; Heriot-Watt University: Edinburgh, UK, 2008. [Google Scholar]
- Shan, Y.; Albers, B.; Savidis, S.A. Influence of different transition zones on the dynamic response of track–subgrade systems. Comput. Geotech. 2013, 48, 21–28. [Google Scholar] [CrossRef]
- Giannakos, K.; Tsoukantas, S. Transition Zone between Ballastless and Ballasted Track: Influence of Changing Stiffness on Acting Forces. Procedia Soc. Behav. Sci. 2012, 48, 3548–3557. [Google Scholar] [CrossRef] [Green Version]
- Banimahd, M.; Woodward, P.K.; Kennedy, J.; Medero, G.M. Behaviour of train-track interaction in stiffness transitions. Proc. Inst. Civ. Eng.—Transp. 2012, 165, 205–214. [Google Scholar] [CrossRef]
- Dahlberg, T. Railway track stiffness variations—Consequences and countermeasures. Int. J. Civ. Eng. 2010, 8, 1–12. [Google Scholar]
- Li, D.; Davis, D. Transition of railroad bridge approaches. J. Geotech. Geoenviron. Eng. 2005, 131, 1392–1398. [Google Scholar] [CrossRef]
- Sañudo, R.; dell’Olio, L.; Casado, J.A.; Carrascal, I.A.; Diego, S. Track transitions in railways: A review. Constr. Build. Mater. 2016, 112, 140–157. [Google Scholar] [CrossRef]
- Paixão, A.; Fortunato, E.; Calçada, R. Transition zones to railway bridges: Track measurements and numerical modelling. Eng. Struct. 2014, 80, 435–443. [Google Scholar] [CrossRef]
- Alves Ribeiro, C.; Paixão, A.; Fortunato, E.; Calçada, R. Under sleeper pads in transition zones at railway underpasses: Numerical modelling and experimental validation. Struct. Infrastruct. Eng. 2015, 11, 1432–1449. [Google Scholar] [CrossRef]
- Paixão, A.; Fortunato, E.; Calçada, R. Design and construction of backfills for railway track transition zones. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2015, 229, 58–70. [Google Scholar] [CrossRef]
- Wilk, S.T.; Stark, T.D.; Rose, J.G. Evaluating tie support at railway bridge transitions. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 1336–1350. [Google Scholar] [CrossRef]
- Liu, K.; Su, Q.; Ni, P.; Zhou, C.; Zhao, W.; Yue, F. Evaluation on the dynamic performance of bridge approach backfilled with fibre reinforced lightweight concrete under high-speed train loading. Comput. Geotech. 2018, 104, 42–53. [Google Scholar] [CrossRef]
- Wang, H.; Markine, V. Corrective countermeasure for track transition zones in railways: Adjustable fastener. Eng. Struct. 2018, 169, 1–14. [Google Scholar] [CrossRef]
- Shi, C.; Zhao, C.; Zhang, X.; Andersson, A. Analysis on dynamic performance of different track transition forms using the discrete element/finite difference hybrid method. Comput. Struct. 2020, 230, 106187. [Google Scholar] [CrossRef]
- Al-qarawi, A.; Leo, C.; Liyanapathirana, D.S. Effects of Wall Movements on Performance of Integral Abutment Bridges. Int. J. Geomech. 2020, 20, 4019157. [Google Scholar] [CrossRef]
- Kunin, J.; Alampalli, S. Integral Abutment Bridges: Current Practice in United States and Canada. J. Perform. Constr. Facil. 2000, 14, 104–111. [Google Scholar] [CrossRef]
- Lovell, M.D. Long Term Behavior of Integral Abutment Bridges; ProQuest Dissertations Publishing: Ann Arbor, MI, USA, 2010. [Google Scholar]
- Talbott, A.M. Earthquake Resistance of Integral Abutment Bridges; ProQuest Dissertations Publishing: Ann Arbor, MI, USA, 2008. [Google Scholar]
- Pak, D.; Bigelow, H.; Feldmann, M. Design of composite bridges with integral abutments. Steel Constr. 2017, 10, 23–30. [Google Scholar] [CrossRef] [Green Version]
- Nimbalkar, S.; Indraratna, B.; Dash, S.K.; Christie, D. Improved Performance of Railway Ballast under Impact Loads Using Shock Mats. J. Geotech. Geoenviron. Eng. 2012, 138, 281–294. [Google Scholar] [CrossRef]
- Thiagarajan, G.; Gopalaratnam, V.; Halmen, C.; Ajgaonkar, S.; Ma, S.; Gudimetla, B.; Chamarthi, R. Bridge Approach Slabs for Missouri DOT Looking at Alternative and Cost Efficient Approaches; Report No.-OR 11.009; Missouri Department of Transportation: Jefferson City, MO, USA, 2010. Available online: https://rosap.ntl.bts.gov/view/dot/18591 (accessed on 20 January 2022).
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil Mechanics in Engineering Practice, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Farooq, M.A.; Nimbalkar, S.; Fatahi, B. Three-dimensional finite element analyses of tyre derived aggregates in ballasted and ballastless tracks. Comput. Geotech. 2021, 136, 104220. [Google Scholar] [CrossRef]
- Li, L.; Nimbalkar, S.; Zhong, R. Finite element model of ballasted railway with infinite boundaries considering effects of moving train loads and Rayleigh waves. Soil Dyn. Earthq. Eng. 2018, 114, 147–153. [Google Scholar] [CrossRef]
- Kramer, S.L. Geotechnical Earthquake Engineering; Pearson Education India: New Delhi, India, 1996. [Google Scholar]
- Shi, X. Structural Performance of Approach Slab and Its Effect on Vehicle Induced Bridge Dynamic Response. Ph.D. Thesis, Louisiana State University, Baton Rouge, LA, USA, 2006. Available online: https://digitalcommons.lsu.edu/gradschool_dissertations/2752 (accessed on 20 January 2022).
- Coelho, B.; Hölscher, P.; Priest, J.; Powrie, W.; Barends, F. An assessment of transition zone performance. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2011, 225, 129–139. [Google Scholar] [CrossRef]
- Shin, E.C.; Kim, D.H.; Das, B.M. Geogrid-reinforced railroad bed settlement due to cyclic load. Geotech. Geol. Eng. 2002, 20, 261–271. [Google Scholar] [CrossRef]








| Transition Zone Configuration | Methodology | Conclusion | Reference |
|---|---|---|---|
| Two sections included in the transition zone: a soft and a stiff section. | Finite Element (FE) modeling to check for a smooth stiffness transition with and without USP. | Reduction in rail–track contact force, especially on using USP. | Dahlberg [5] |
| Variation of dynamic transition properties for different lengths using Finite Element Method (FEM). |
| Shan et al. [2] |
| USP provided in wedge-shaped backfill consisting of UGM, CBM and 5% binder content. | Numerical modelling of the transition section, including the USP. | Less track stiffness and minor changes at the rail track entry and exit considering the direction of the train movement. | Alves Ribeiro et al. [9] |
| A wedge-shaped backfill with two zones: UGM and CBM | FEM to check stiffness transition and long-term behavior of the transition zone | Wedge-shaped backfill is suitable to minimize the effects of stiffness variation. | Paixão et al. [8] |
| Poor/well-supported bridge transition sections. | Experimental analysis on the bridge transition sections to evaluate track performance using tie supports. | Well-supported bridge transition zones show better performance. | Wilk et al. [12] |
| Addition of Fibre Reinforced Light Weight Concrete (FRLWC) to the transition zone. | FEM for comparing the dynamic response of the FRLWC backfill section with a typical transition section. | Elevated acceleration attained on the track using inverted trapezoidal shape with FRLWC backfill material delivered better performance. | Liu et al. [13] |
| Two transition sections: embankment–slab track and slab track–embankment. | Field tests and numerical analysis to check for the adjustable fastener in the transition zone. |
| Wang and Markine [14] |
| Evaluated the design of different transition zones using the discrete element method for better dynamic performance. |
| Shi et al. [11] |
| Material | Constitutive Model | Density, ρ (kg/m3) | Young’s Modulus, E (MPa) | Poisson’s Ratio, υ | Friction Angle, ϕ’ | Dilation Angle, ψ | Cohesion, c’ (kPa) | Rayleigh Coefficients | |
|---|---|---|---|---|---|---|---|---|---|
| α | β | ||||||||
| Rail 3 | Elastic | 7700 | 206,000 | 0.3 | - | - | - | - | - |
| Sleepers 3 | Elastic | 2350 | 25,500 | 0.2 | - | - | - | - | - |
| Ballast 1 | DP 4 | 1600 | 110 | 0.3 | 40 | 5 | 1 | 8.52 | 0.0004 |
| Sub-Ballast 1 | DP 4 | 2220 | 400 | 0.25 | 35 | 2 | 1 | 8.52 | 0.0004 |
| Backfill soil 2 | MC 5 | 1835 | 35 | 0.35 | 38 | 8 | 6 | ||
| Foundation soil 2 | MC 5 | 1682 | 30 | 0.3 | 20 | 1 | 20 | 1.355 | 0.001 |
| Integral abutment (Concrete) 2 | Elastic | 2385 | 30,000 | 0.25 | - | - | - | - | - |
| HP pile 2 | Elastic | 7951 | 200,000 | 0.3 | - | - | - | - | - |
| Approach slab 2 | Elastic | 2385 | 30,000 | 0.25 | - | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakhare, A.; Farooq, H.; Nimbalkar, S.; Dodagoudar, G.R. Dynamic Behavior of the Transition Zone of an Integral Abutment Bridge. Sustainability 2022, 14, 4118. https://doi.org/10.3390/su14074118
Sakhare A, Farooq H, Nimbalkar S, Dodagoudar GR. Dynamic Behavior of the Transition Zone of an Integral Abutment Bridge. Sustainability. 2022; 14(7):4118. https://doi.org/10.3390/su14074118
Chicago/Turabian StyleSakhare, Akshay, Hafsa Farooq, Sanjay Nimbalkar, and Goudappa R. Dodagoudar. 2022. "Dynamic Behavior of the Transition Zone of an Integral Abutment Bridge" Sustainability 14, no. 7: 4118. https://doi.org/10.3390/su14074118
APA StyleSakhare, A., Farooq, H., Nimbalkar, S., & Dodagoudar, G. R. (2022). Dynamic Behavior of the Transition Zone of an Integral Abutment Bridge. Sustainability, 14(7), 4118. https://doi.org/10.3390/su14074118







