Sustainable Improvement of Planting Quality for a Planar 5R Parallel Transplanting Mechanism from the Perspective of Machine and Soil Interaction

Abstract

The poor shape of the cavity formed by the planar 5R parallel transplanting mechanism will cause Salvia miltiorrhiza seedlings to tilt while transplanting them. In order to improve the quality of the cavity in Salvia miltiorrhiza planting, this paper analyzed the structural composition and working principle of a planar 5R parallel transplanting mechanism for Salvia miltiorrhiza and established the bidirectional coupling model between the transplanting mechanism and the soil. Based on the model, a regression analysis model and the influence of three factors and five levels were obtained by using the experimental optimization design method, which reflected the relationship between the parameters of the mechanism on the parameters of the cavity. In terms of the optimization objective and regression model, the optimal parameter combination of the transplanting mechanism was obtained by multi-objective parameter optimization. A virtual test of cavity formation was conducted on the transplanting mechanism for Salvia miltiorrhiza with an optimal parameter combination. The results proved that the parameters of cavity output via the regression model and the measurement from the bidirectional coupling model were basically consistent, which verifies the accuracy of our parameter optimization for the transplanting mechanism. This paper provides a new approach to the sustainable improvement of a Salvia miltiorrhiza transplanting mechanism from the perspective of the interaction between the machine and the soil.

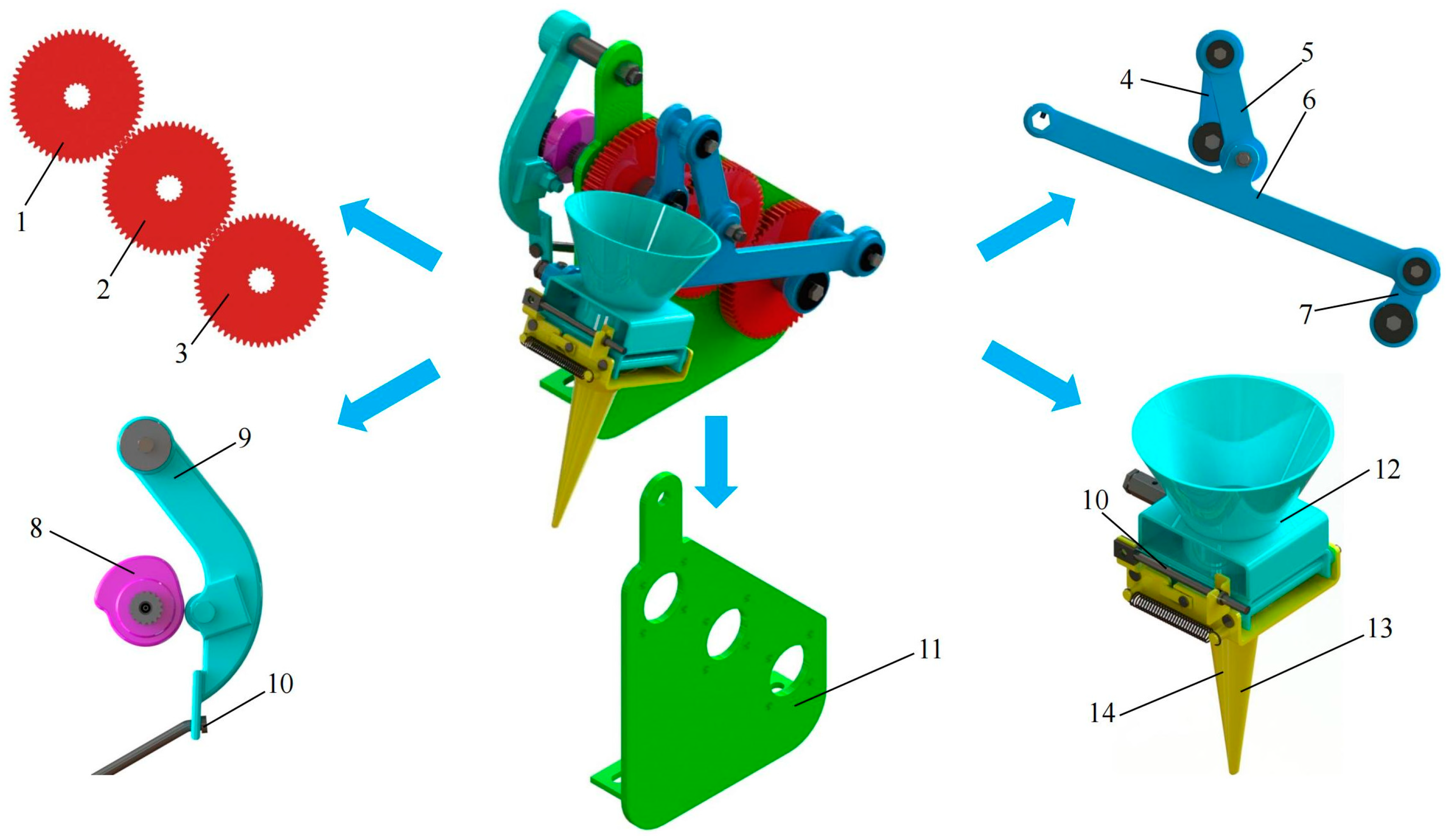
1. Introduction

Salvia miltiorrhiza is commonly used in China as a medicinal material for treating cardiovascular and cerebrovascular diseases. The planting method for Salvia miltiorrhiza involves naked root transplanting [1,2]. The agronomy for planting Salvia miltiorrhiza seedlings requires a transplanting spacing of 150 mm, a transplanting depth of 150–160 mm, and an angle between the seedlings and the ridge surface of no less than 80° [3,4]. Therefore, the length and depth for transplanting Salvia miltiorrhiza seedlings are significantly greater than those of vegetables and other similar crops. In order to realize the mechanical transplanting of Salvia miltiorrhiza seedlings, based on the kinematic model of mechanisms, the project designed a kind of planar 5R parallel transplanting mechanism to meet the agronomic requirements of Salvia miltiorrhiza seedling transplanting, which takes the posture and trajectory of the planter for the transplanting mechanism as the design objectives [5,6,7].

As the planar 5R parallel transplanting mechanism plants Salvia miltiorrhiza seedlings, the planter interacts with the soil to form the cavity and then opens, which allows the Salvia miltiorrhiza seedlings to fall into the formed cavity [8]. On the one hand, the naked root seedlings of Salvia miltiorrhiza have no substrate as a support, and the seedlings lean against the side of the cavity under the action of the soil backflow after transplanting, which ensures the upright degree of the naked seedlings by relying on the contour of the duckbill [9]. On the other hand, the process of transplanting Salvia miltiorrhiza seedlings on mulch film is carried out by the planter piercing the mulch film to plant the Salvia miltiorrhiza seedlings, and the size of the hole for the cavity determines the damaged degree of the mulch film [10]. Therefore, a larger size hole will lead to a greater degree of tear for the mulch film, and the greater the degree of a tear in the mulch film, the lesser effect the mulch film will have on heat preservation, moisture retention, and weed growth inhibition [11].

Many scholars have made profound studies on the problems of the formation of a cavity in terms of the duckbill transplanting mechanism. Yu et al. [12] designed a planetary gear train transplanting mechanism from the perspective of mechanism kinematics, which was used for the transplantation of vegetable pot seedlings with a large planting spacing for the cavity. Ji et al. [13] designed a planetary gear train slip-type pot seedling transplanting mechanism for the transplanting of tomato pot seedlings into the cavity and optimized the parameters through the mechanism kinematics model; Hu et al. [14] used a planetary gear transplanting mechanism to achieve the vertical planting of pot seedlings into a cavity and optimized the kinematic parameters of the mechanism; Hwang et al. [15] designed a multi-linkage mechanism for transplanting vegetable pot seedlings into a cavity and optimized the kinematic parameters of the mechanism; Zhou et al. [16] designed a rotary transplanting mechanism for vegetable pot seedlings to achieve a series of operations, such as seedling picking, transporting, and mulch film penetration, forming, and planting, which optimized the parameters of the mechanism through mechanism synthesis; Iqbal et al. [17] designed a planetary cylindrical gear mechanism for transplanting the tomato pot seedlings into a cavity. Han et al. [18] used the discrete element method to simulate a cavity-forming process for a device and analyzed the influence of the structural and kinematic parameters of the planter on the parameters of a cavity. Wu et al. [19] studied the effects of the structural and operating parameters of a planter for a rape pot seedling transplanter on formation quality through discrete element simulation and the soil bin test. Yang et al. [20] used the RecurDyn-EDEM bidirectional coupling technology to analyze the dynamic behavior changes of soil particles under the action of hanging cups and studied the influence of the structural and kinematic parameters of hanging cups on the parameters of cavities.

In accordance with the agronomic requirements of crops, most studies on the mechanism of cavity formation during transplanting have focused on the design and optimization of the mechanism’s parameters from the perspective of mechanism kinematics. Some studies focused on the influence law for the parameters of a transplanting mechanism on the parameters of a cavity, which optimized the parameters of the transplanting mechanism in cavity formation. However, there are no studies on the influence law for the parameters of the Salvia miltiorrhiza transplanting mechanism on the parameters of a cavity.

In view of the above situation, this paper took the planar 5R parallel transplanting mechanism for Salvia miltiorrhiza as the research object, analyzed the composition and working principle, and established a multi-body dynamics and discrete element two-way coupling model of the transplanting mechanism and the soil. Based on the coupling model, the regression equation for the parameters of the transplanting mechanism on the parameters of a cavity was established via an experimental design method using quadratic orthogonal rotation center combination, which was used to optimize the transplanting mechanism from the perspective of the quality of cavity formation. The trend and interaction of the parameters of the transplanting mechanism on the parameters of a cavity were obtained using a response surface, which analyzed the formation mechanism of the transplanting mechanism for Salvia miltiorrhiza.

2. Materials and Methods

2.1. Composition and Working Principle for Planar 5R Parallel Mechanism

A structural diagram of the planar 5R parallel transplanting mechanism is shown in Figure 1. The mechanism is mainly composed of a straight, cylindrical geared mechanism, a 5R parallel mechanism, a frame for the planar 5R parallel mechanism, a cam-pull arm opening and closing control mechanism, and a duckbill planter. Numbers 1, 2, and 3 are the straight-tooth cylindrical gears, respectively, which constitute the spur gear mechanism. Numbers 4, 5, 6, and 7 are crank 1, connecting rod 1, connecting rod 2, and crank 2, respectively, which constitute the 5R parallel mechanism. Numbers 8, 9, and 10 are the cam, the pull arm, and the stay wire, respectively, which constitute the cam-pull arm opening and closing control mechanism. Number 11 is the frame of the 5R parallel mechanism. Numbers 12, 13, and 14 are the upper frame, the right and left duckbills, respectively, which constitute the duckbill planter.

The working principle of the planar 5R parallel transplanting mechanism is shown in Figure 2. During operation, the power of uniform rotation is transmitted to straight-tooth cylindrical gear 2. The spur gear mechanism transmits uniform velocity rotation to crank 1 and crank 2 of the planar 5R parallel mechanism. Crank 1 drives connecting rod 1 to oscillate at a constant velocity, and crank 2 drives connecting rod 2 to oscillate at a constant velocity. Connecting rod 2 oscillates under the compound motion of connecting rod 1 and crank 2. The duckbill planter is fixedly connected to connecting rod 2, and oscillates under the drive of connecting rod 2 in order to insert into and withdraw from the soil.

During the process of inserting into and withdrawing from the soil, the cam is fixedly connected to the straight-tooth cylindrical gear and rotates with the spur gear. It pushes the pull arm to rotate back and forth. The end of the stay wire is respectively connected to the pull arm and left duckbill of the duckbill planter. The pull arm drives the stay wire to control the opening and closing of the left and right duckbills. As the duckbill planter reaches the lowest position, the left and right duckbill open under the action of the stay wire, and the Salvia miltiorrhiza seedlings fall into the cavity that was formed by the duckbill planter.

The shape of the cavity, which was formed by the planar 5R parallel transplanting mechanism, is approximately conical; the depth of the cavity is 150–160 mm, and the included angle between the center line of the cavity and the ridge should be as close as 90°, and the diameter of the hole for the cavity should be as small as possible. The depth of the cavity is 150–160 mm, and the length of the rhizome for Salvia miltiorrhiza seedlings is about 150 mm, which can completely cover the rhizome of Salvia miltiorrhiza seedlings with soil and promote its growth. Due to the geotropism of rhizome plant growth [21], the included angle between the center line of the cavity and the ridge is close to 90°, which increases the rooting depth of Salvia miltiorrhiza after transplanting, and it can improve the roughness of rhizome during the growth of Salvia miltiorrhiza. Based on the above measures, the yield of Salvia miltiorrhiza can be increased by about 10% [22].

2.2. Establishment of Bidirectional Coupling Model for Planar 5R Parallel Transplanting Mechanism Based on DEM and MBD

The bidirectional coupling of the discrete element method and multi-body dynamics is an effective way to simulate the interaction between the complicated mechanism and the discrete element particles, which has been widely applied in the field of agricultural machinery [23,24], e.g., the formation process of a cavity for the duckbill planter under the action of the planar 5R parallel transplanting mechanism involved the bidirectional interaction between the mechanism and the soil. Therefore, the method of bidirectional coupling for DEM and MBD was used to analyze the formation process of the mechanism [25,26].

2.2.1. Multi-Body Dynamics Model

The multi-body dynamics model of the planar 5R parallel transplanting mechanism was established in the Recurdyn software (DEM Solutions Ltd., Edinburgh, Scotland, UK), and the kinematic pairs between the components are set as per

Table 1. Kinematic pair configuration table of multi-body dynamics model.

No.	Part 1	Part 2	Kinematic Pair
1	Frame	Ground	Moving pair
2	Spur gear 1	Frame	Rotary pair
3	Spur gear 3	Frame	Rotary pair
4	Crank 1	Linkage 1	Rotary pair
5	Crank 2	Linkage 2	Rotary pair
6	Spur gear 1	Spur gear 2	Contact pair
7	Spur gear 2	Spur gear 3	Contact pair
8	Spur gear 1	Crank 1	Fixed coupling pair
9	Spur gear 3	Crank 2	Fixed coupling pair
10	Upper frame	Linkage 2	Fixed coupling pair
11	Upper frame	Right duckbill	Rotary pair
12	Upper frame	Left duckbill	Rotary pair
13	Left duckbill	Right duckbill	Contact pair

.

In the model, the forward velocity of the mechanism was set as 0.25 m/s, the rotary velocity of the spur gear was set as 30 r/min, and the rotary displacement of the right duckbill was set as STEP (Time, 0.85, 0, 0.9, 0.1) + STEP (Time, 1.4, 0, 1.5, −0.1).

2.2.2. Discrete Element Modeling

Soil Particle Model

To enhance the authenticity of the model, the basic structure of soil particles primarily consisted of block-shaped particles, core-shaped particles, sheet-shaped particles, and column-shaped particles due to the looseness and macropores of the topsoil layer after tillage. The different combinations of spherical particles in the discrete element software were used to replace the different types of soil particles to simulate soil aggregates. The spherical, linear, triangular, and tetrahedral combinations were established to represent (approximately) block, nuclear, sheet, and columnar soil particles [27,28], as shown in Figure 3.

The parameters of the soil model are seen in

Table 2. Parameters of the soil model.

Particle Model		Radius	Contact Radius	Co-Ordinate Position
				X	Y	Z
Spherical		5	5	0	0	0
Linear	Particle 1	5	5	−4	0	0
	Particle 2	5	5	0	0	0
	Particle 3	5	5	4	0	0
Triangular	Particle 1	5	5	0	2.2	0
	Particle 2	5	5	−2.2	−1.5	0
	Particle 3	5	5	2.2	−1.5	0
Tetrahedron	Particle 1	5	5	0	0	2.45
	Particle 2	5	5	0	2.6	−2.45
	Particle 3	5	5	−3	−2.6	−2.45
	Particle 4	5	5	3	−2.6	−2.45

[29,30]. In accordance with the relevant literature [31,32], the basic parameters of the selected discrete element model are shown in

Table 3. Basic parameters of the discrete element model.

Items	Parameters	Value
Topsoil layer	Poisson’s ratio for soil	0.38
	Soil particle density/(kg·m−3)	2040
	Shear modulus of soil particles/MPa	6
Upper soil layer	Poisson’s ratio for soil	0.38
	Soil particle density/(kg·m−3)	2260
	Shear modulus of soil particles/MPa	6
Subsoil layer	Poisson’s ratio for soil	0.38
	Soil particle density/(kg·m−3)	2500
	Shear modulus of soil particles/MPa	6
Bottom soil layer	Poisson’s ratio for soil	0.38
	Soil particle density/(kg·m−3)	2650
	Shear modulus of soil particles/MPa	6
Interactions between soil particles	Coefficient of restitution between soil particles	0.6
	Coefficient of static friction factor between soil particles	0.541
	Coefficient of rolling friction factor between soil particles	0.31
Planter	Poisson’s ratio for steel	0.3
	Density of steel/(kg·m−3)	7850
	Shear modulus of steel	7.9 × 1010
	Coefficient of restitution between soil and implements	0.6
	Coefficient of static friction between soil and implements	0.6
	Coefficient of dynamic friction between soil and implements	0.6

.

Soil Particle Contact Model

Due to the low soil moisture content in the planting environment for the transplanting mechanism, the duckbill planter could cause soil backflow while interacting with the soil, which made it impossible to observe the profile of the cavity. Therefore, two different types of soil contact model parameters were set in the EDEM (engineering discrete element method) 2020 (DEM Solutions Ltd., Edinburgh, Scotland, UK). The first was the Edinburgh elasto-plastic adhesion contact model, which could achieve the different plasticity and viscosity of particles in order to present the profile of a cavity formed by the planter. The second was the Hertz-Mindlin with bonding contact model, which could simulate the transporting behavior of soil particles during the actual transplanting process by the transplanting mechanism by setting the force of soil particles based on the actual soil moisture content.

According to the related literature [33,34] on the discrete element parameter calibration of the physical characteristics of similar soil, the parameters of the contact model for the soil particles are shown in

Table 4. Contact model parameters of soil.

Contact Model	Parameters	Value
Edinburgh elasto-plastic Adhesion contact model	Constant pull-off force/(N)	0
	Surface energy/(J/m2)	15.6
	Contact plasticity ratio	0.36
	Slope exp	1.5
	Tensile exp	4.24
	Tangential stiff multiplier	0.52
Hertz-Mindlin with bonding contact model	Normal stiffness per unit area/(N/m3)	19,000
	Shear stiffness per unit area/(N/m3)	14,000
	Critical normal stress/(Pa)	55,000
	Critical shear stress/(Pa)	29,000
	Bonded disk radius/(mm)	1.2

.

2.2.3. Establishment of Multi-Body Dynamics Discrete Element Bidirectional Coupling Model for a Transplanting Mechanism

Based on the multi-body dynamics model of a transplanting mechanism and the discrete element model of soil, the bidirectional coupling model of Recurdyn-EDEM for the transplanting mechanism was constructed. The simplified model is shown in Figure 4.

2.3. Experimental Design and Optimization

In this section, through the multi-body dynamics discrete element bidirectional coupling model between the transplanting mechanism and the soil, we took the parameters of the transplanting mechanism as the variables and took the parameters of the cavity formed by the transplanting mechanism as the response indicators. In combination with the design of rotation-regression-orthogonal combination, the optimal parameter combination of the transplanting mechanism was determined.

2.3.1. Determination of Factor Level

The selected factors were the various parameters of the planar 5R parallel transplanting mechanism that affected the parameters of the cavity. The main factor affecting the parameters of the cavity was the length of crank 1, the length of crank 2, and the difference in the installation angle between crank 1 and crank 2. Therefore, according to the value range of the constraint conditions for the planar 5R parallel mechanism, the level of the factor was determined to be five, and the test factor codes are shown in

Table 5. Experimental variables and levels.

	Factors
	x1	x2	x3
Codes	Length of Crank 1/mm	Length of Crank 2/mm	Difference in the Installation Angles between Crank 1 and Crank 2/°
−1.682	78	48	11.5
−1	85	55	15
0	95	65	20
1	105	75	25
1.682	112	82	28.5

.

2.3.2. Determination of Response Indicators

In terms of the analysis of the working process for the planar 5R parallel transplanting mechanism, the response index was determined as the vertical distance between the lowest point of the cavity and the ridge surface y₁, the included angle between the line that connects the top midpoint to the lowest point of the cavity and the ridge y₂, and the distance of the hole on the top of the cavity y₃.

2.3.3. Test Results and Analysis

The test scheme and results are shown in

Table 6. Experimental plan and results.

No.	Factors			Indexes
	x1	x2	x3	y1/mm	y2/(°)	y3/mm
1	−1(85)	−1(55)	−1(15)	136.1	90.9	49.2
2	1(105)	−1(55)	−1(15)	173.2	85.9	61.6
3	−1(85)	1(75)	−1(15)	111.3	99.5	65.7
4	1(105)	1(75)	−1(15)	154.6	93.9	67.8
5	−1(85)	−1(55)	1(25)	134.1	90.1	53.3
6	1(105)	−1(55)	1(25)	175.2	82.7	59.5
7	−1(85)	1(75)	1(25)	113.4	103.1	76.0
8	1(105)	1(75)	1(25)	152.3	89.2	53.3
9	−1.682(78)	0(65)	0(20)	115.5	99.5	55.4
10	1.682(112)	0(65)	0(20)	181.4	87.3	53.4
11	0(95)	−1.682(48)	0(20)	170.0	82.7	63.6
12	0(95)	1.682(82)	0(20)	125.8	97.5	69.8
13	0(95)	0(65)	−1.682(11.5)	142.3	92.4	63.6
14	0(95)	0(65)	1.682(28.5)	148.4	91.8	53.3
15	0(95)	0(65)	0(20)	142.3	91.7	51.2
16	0(95)	0(65)	0(20)	140.5	91.6	50.2
17	0(95)	0(65)	0(20)	144.8	92.4	52.4
18	0(95)	0(65)	0(20)	142.2	92.5	57.2
19	0(95)	0(65)	0(20)	146.3	92.4	51.1
20	0(95)	0(65)	0(20)	140.3	92.5	53.2
21	0(95)	0(65)	0(20)	144.2	90.8	50.2
22	0(95)	0(65)	0(20)	142.2	91.6	50.8
23	0(95)	0(65)	0(20)	145.5	91.3	49.4

, the analysis of variance for each response index is shown in

Table 7. Variance analysis of the regression model.

Testing Indicators	Sources of Variation	Sum of Squares	Freedom	F	p
y1	Model	7329.41	9	89.35	<0.0001 **
	x1	5386.73	1	590.60	<0.0001 **
	x2	1905.93	1	208.97	<0.0001 **
	x3	7.41	1	0.81	0.3838
	x1x2	2.00	1	0.22	0.6473
	x1x3	0.02	1	0.0022	0.9634
	x2x3	0.005	1	0.0055	0.9817
	x12	16.54	1	2.14	0.1676
	x22	10.83	1	1.45	0.2498
	x32	0.092	1	0.0022	0.9884
	Residual	118.57	13
	Sum	7453.17	22
y2	Model	509.06	9	86.21	<0.0001 **
	x1	201.19	1	306.66	<0.0001 **
	x2	272.38	1	415.17	<0.0001 **
	x3	2.73	1	4.17	0.0621
	x1x2	6.30	1	9.60	0.0085 **
	x1x3	14.31	1	21.81	0.0004 **
	x2x3	1.05	1	1.60	0.2278
	x12	4.83	1	7.37	0.0177 *
	x22	6.01	1	9.16	0.0097 **
	x32	0.13	1	0.20	0.6582
	Residual	8.53	13
	Sum	517.55	22
y3	Model	1096.70	9	10.91	<0.0001 **
	x1	2.11	1	0.19	0.6712
	x2	180.34	1	16.15	0.0015 **
	x3	27.91	1	2.50	0.1380
	x1x2	192.08	1	17.20	0.0011 **
	x1x3	120.12	1	10.76	0.0006 **
	x2x3	4.80	1	0.43	0.5233
	x12	16.99	1	1.52	0.2393
	x22	460.36	1	41.22	<0.0001 **
	x32	96.61	1	8.65	0.0115 **
	Residual	145.20	13
	Sum	1241.90	22

Notes: ** indicates that the difference is extremely significant (p < 0.01); * indicates that the difference is significant (0.01 ≤ p ≤ 0.05).

, and x₁, x₂, and x₃ are the values of the factor codes.

Multiple regression fitting and variance analysis were carried out on the experimental data using the Design-Expert 8.0 software (Stat-Ease Ltd., Minneapolis, MN, USA). Under the conditions that the model was significant and that the misfit terms were not significant, the insignificant regression terms were excluded. The regression equation between the index and the factor was obtained:

$$y_1=144.53+19.86x_1-11.81x_2+0.74x_3$$

(1)

$$y_2=91.92-3.84x_1+4.47x_2-0.89x_1{x}_2-1.34x_1{x}_3+0.55x_1^2-0.62x_2^2$$

(2)

$$y_3=51.73-0.39x_1+3.63x_2-1.43x_3-4.90x_1{x}_2-3.87x_1{x}_3+5.38x_2^2+2.47x_3^2$$

(3)

In order to analyze the impact of the experimental factors on the response indicators, the response surface was obtained by using the Design-Expert 8.0 software, as shown in Figure 5.

Figure 5a illustrates the influence of the length of crank 1 and crank 2 on the vertical distance at the zero level of other factors. The vertical distance exhibits a positive correlation with both the length of crank 1 and the length of crank 2. However, the impact of the length of crank 1 on the vertical distance is significantly greater than that of crank 2.

Figure 5b illustrates the influence of the lengths of crank 1 and crank 2 on the included angle at the zero level of the other factors. The length of crank 1 is positively correlated with the included angle, while the length of crank 2 is negatively correlated with it.

Figure 5c illustrates the impact of the length of crank 2 and the variance in installation angles between crank 1 and crank 2 on the included angle at the zero level of the other factors. When the length of crank 2 is below the zero level, the included angle demonstrates a positive correlation with the difference in installation angles between crank 1 and crank 2. Alternatively, when the length of crank 2 is above the zero level, the included angle displays a negative correlation with the difference in installation angles between crank 1 and crank 2.

The difference in the installation angles between crank 1 and crank 2 is below the zero level, and the included angle is negatively correlated with the length of crank 2. The difference in the installation angles between crank 1 and crank 2 is above the zero level, and the included angle is negatively correlated with the length of crank 2. The influence of negative correlation for the latter was significantly larger than that of the former.

Figure 5d is the influence that the length of crank 1 and crank 2 have on the distance of the hole on the top of the cavity at the zero level of the other factors. The length of crank 2 is below the zero level, and the distance of the hole is positively correlated with the length of crank 1. The length of crank 2 is above the zero level, and the included angle is in a negative correlation with the length of crank 1.

The length of crank 1 is above the zero level, and the distance of the hole is negative first and then in a positive correlation with the length of crank 2. The length of crank 1 is below the zero level, and the distance of the hole is in a negative correlation with the length of crank 2.

Figure 5e is the influence of the length of crank 1 and the difference in the installation angles between crank 1 and crank 2 on the distance of the hole on the top of the cavity at the zero level of the other factors. The length of crank 1 is below the zero level, and the distance of the hole is in a positive correlation with the difference in the installation angles between crank 1 and crank 2. The length of crank 1 is above the zero level, and the distance of the hole is in a negative correlation with the difference in the installation angles between crank 1 and crank 2.

The difference in the installation angles between crank 1 and crank 2 is above the zero level, and the distance of the hole is negatively correlated with the length of crank 1. The difference in the installation angles between crank 1 and crank 2 is below the zero level, and the distance of the hole is positively correlated with the length of crank 1.

2.3.4. Parameter Optimization

In order to achieve the best combination of experimental factors, a mathematical model for optimizing the parameters was established. The optimal evaluation index was determined based on the requirements for the planar 5R parallel transplanting mechanism, which included a depth of 150–160 mm, an included an angle of 90° between the center line of the cavity and the ridge of approach and a minimal distance between the hole on the top of the cavity. In order to obtain the optimal parameters for the transplanting mechanism’s working performance, an optimal model was established, with the objective function and constraint conditions as follows:

$$\left\{\begin{array}{l}150\mathsf{mm}\le y_1\le 160\mathsf{mm}\\ {85}^{\circ }\le y_2\le {95}^{\circ }\\ \min y_3\\ \mathsf{s}.\mathsf{t}.\left\{\begin{array}{l}75\mathsf{m}\mathsf{m}\le x_1\le 112\mathsf{m}\mathsf{m}\\ 48\mathrm{mm}\le x_2\le 82\mathrm{mm}\\ {11.5}^{\circ }\le x_3\le {28.5}^{\circ }\end{array}\right.\end{array}\right.$$

(4)

By utilizing the optimization module of the Design-Expert 8.0 software, the optimized parameters for the planar 5R parallel transplanting mechanism were determined: the length of crank 1 was 101.3 mm; the length of crank 2 was 64.8 mm; the difference in the installation angles between crank 1 and crank 2 was 25.3°. Based on the regression equation, the vertical distance between the lowest point of the cavity and the ridge surface y₁ was 155.3 mm, the included angle between the line connecting the top midpoint to the lowest point of the cavity and the ridge y₂ was 89.6°, and the distance of the hole on the top of the cavity y₃ was 50.9 mm.

3. Results and Analysis

3.1. Analysis of Formation Process for Transplanting Mechanism

The bidirectional coupling model of Recurdyn and EDEM was used to simulate the formation process of the transplanting mechanism, as shown in Figure 6. The planter is driven by the transplanting mechanism as it inserts into the soil, forms the cavity, and then withdraws from the cavity.

Figure 6a shows the process of the duckbill planter starting to insert into the soil until reaching the lowest point. The duckbill planter inserts into the soil at a certain angle of 74°, which is tilted to the right with the ridge. After inserting into the soil, the duckbill planter is gradually tilted to the left until being perpendicular to the ridge, which is driven by the planar 5R parallel mechanism. Then, the duckbill planter reaches the lowest point in the status of maintaining perpendicularity to the ridge and eventually forms the cavity for planting Salvia miltiorrhiza seedlings.

The size of the hole formed by the planar 5R parallel transplanting mechanism is controlled by the attitude of the duckbill planter, which has a conical shape with a decreasing diameter in the downward direction. This means that, although the planter is inserted into the soil at a certain angle with the ridge surface, the hole formed is smaller than the width of the planter’s upper end. As the depth of the duckbill planter inserted into the soil increases, its posture gradually becomes perpendicular to the ridge. The hole formed by the lower end of the duckbill planter is covered by the upper end, and eventually, the contour of the formed cavity closely matches that of the duckbill planter.

Figure 6b illustrates the process of the duckbill planter withdrawing from the soil at its lowest point. The duckbill planter moves upwards with a status of maintaining perpendicularity to the ridge, which is driven by the planar 5R parallel mechanism. As the duckbill planter exits above the cavity, it tilts to the right. With the complete withdrawal from the cavity, the posture of the duckbill planter tilts 83° to the right.

The duckbill planter remains perpendicular to the ridge in the first half of the withdrawal from the cavity, which has little effect on the contour of the cavity. In the second half of withdrawal from the cavity, the duckbill planter tilts to the right under the drive of the planar 5R parallel mechanism. At this point, the upper end of the duckbill planter has been removed from the cavity, and the tilted lower end of the planter does not touch the soil particles, which will not affect the contour of the cavity.

The contour of the cavity and the size of the hole of the cavity are determined by the changes in the posture of the duckbill planter as it moves through the soil. The angle of the planter’s posture ranges from [74°, 90°] to [90°, 83°] while operating in the soil.

During the interaction between the duckbill planter and the soil, the planter is driven by the planar 5R parallel transplanting mechanism to reach its lowest point. Then, the left and right duckbills open, which changes the shape of the hole from circular to approximately elliptical, as shown in Figure 7a,b. The sectional shape of the cavity is depicted in Figure 7c.

The measuring tools in the EDEM software (DEM Solutions Ltd., Edinburgh, Scotland, UK) were used to measure the parameters of the cavity, as shown in

Table 8. The parameters of cavity output using the regression model, measured using the EDEM software.

	y1/mm	y2/(°)	y3/mm
Parameters of the cavity output by regression model	155.3	89.6	50.9
Parameters of the cavity measured in EDEM software	156.8	90.4	51.5

. The vertical distance between the lowest point of the cavity and the ridge surface y₁ is 156.8 mm, the included angle between the line, which connects the top midpoint to the lowest point of the cavity and the ridge y₂ is 90.4°, and the distance of the hole on the top of the cavity y₃ is 51.5 mm.

A comparison between the parameters of the cavity (the output by the regression model and the values measured in the EDEM software) was basically consistent, which verified the accuracy of this parameter optimization for the planar 5R parallel transplanting mechanism.

3.2. Transport Behavior of Soil Particles under the Action of the Transplanting Mechanism

In order to simulate the actual operation process of the transplanting mechanism with parameter optimization, the contact model of soil was set as the Hertz-Mindlin with bonding contact model in EDEM, and the parameters of the Hertz-Mindlin with bonding contact model can be seen in Table 8.

After setting the parameters in EDEM, by using the bidirectional coupling model of the transplanting mechanism and soil, the vector graphics of the soil particles under the action of the transplanting mechanism were obtained, as shown in Figure 8.

As shown in Figure 8a, while being inserted into the soil, the duckbill planter drives the soil particles downwards towards the contour of the planter. As the duckbill planter is about to open, the left and right duckbills rapidly compress the soil particles on both sides, which causes an instantaneous increase in velocity. At this point, the maximum velocity of the soil particles is 0.726 m/s.

As shown in Figure 8b, while the duckbill planter opens, the soil particles at the front and back of the planter move back and fill the transplanting cavity from top to bottom. At this point, the maximum velocity of the soil particles is 0.814 m/s. Once the left and right duckbill planters have fully opened, they will continue to move upwards, driven by the transplanting mechanism, and gradually leave the soil behind. Throughout this process, the quality of the soil particles moving back in the front and back of the duckbill planter gradually deteriorates, and the velocity of the soil particles also decreases gradually.

4. Conclusions

Based on multi-body dynamics and discrete element bidirectional coupling technology, this study optimized the parameters of a planar 5R parallel transplanting mechanism for Salvia miltiorrhiza and analyzed the process of cavity formation and the actual transplanting operation. The following conclusions were reached:

• Based on an analysis of the composition and working principle, a bidirectional coupling model of multi-body dynamics and the discrete element method was established for the planar 5R parallel transplanting mechanism and soil;
• Through the bidirectional coupling model, the experimental design method was used to obtain a regression equation between the parameters of the planar 5R parallel transplanting mechanism and the parameters of the cavity. The influence of the parameters of the planar 5R parallel transplanting mechanism on the parameters of the cavity was analyzed by using the response surface method;
• In terms of the regression equation, the optimized parameters of the planar 5R parallel transplanting mechanism were obtained using the multi-objective function optimization: the length of crank 1 was 101.3 mm, the length of crank 2 was 64.8 mm, and the difference in the installation angles between crank 1 and crank 2 was 25.3°;
• After analyzing the formation process and transport behavior of soil particles using the optimized parameters on the planar 5R parallel mechanism, the variations in the attitude angle of the duckbill planter in the soil were determined to range from [74°, 90°] to [90°, 83°]. Furthermore, the transport law for soil particles under the influence of a duckbill planter was confirmed.

Therefore, this study optimizes the parameters of the transplanting mechanism from the perspective of the interaction between the machines and the soil. In the future, the prototype of the transplanting mechanism will be developed, and it will be used to study the actual planting quality of the transplanting mechanism in field experiments.