Measurement and Analysis of the Influence Factors of Tractor Tire Contact Area Based on a Multiple Linear Regression Equation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment Materials
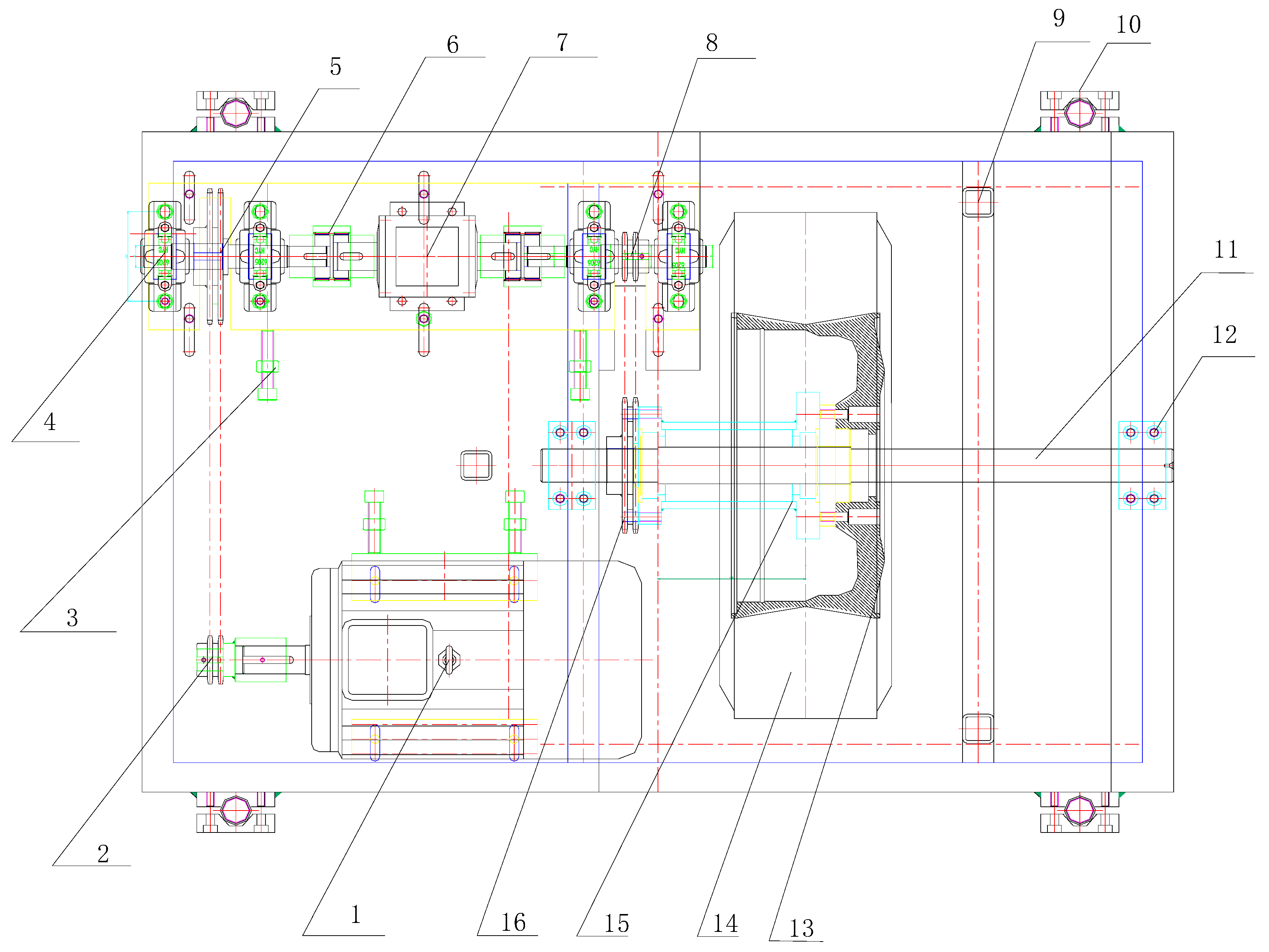
2.1.1. A Soil-Bin Testing Facility
2.1.2. Laser Profiler
2.2. Experiment Method
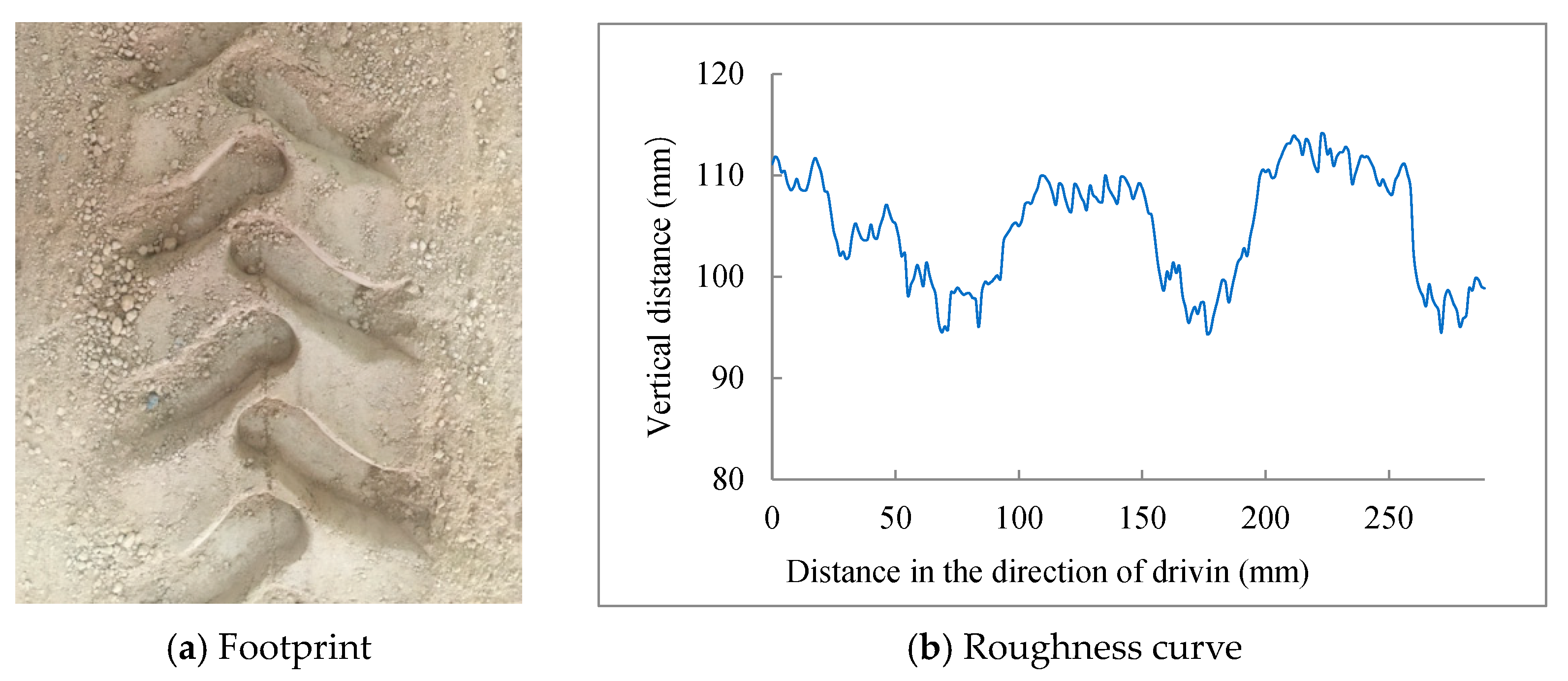
2.2.1. Roughness after Rutting
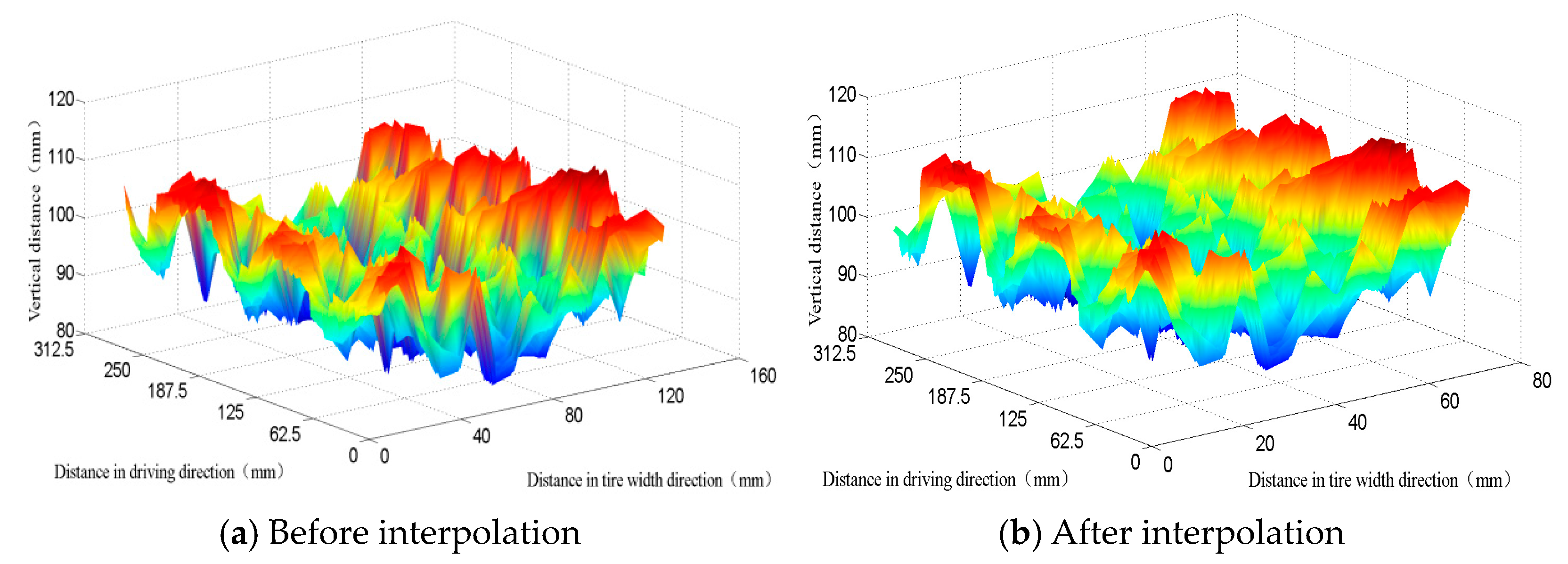
2.2.2. Fractal Interpolation Theory
2.2.3. Roentgen Formula to Calculate the 3D Contact Area
2.2.4. Multiple Linear Regression
3. Results and Discussion
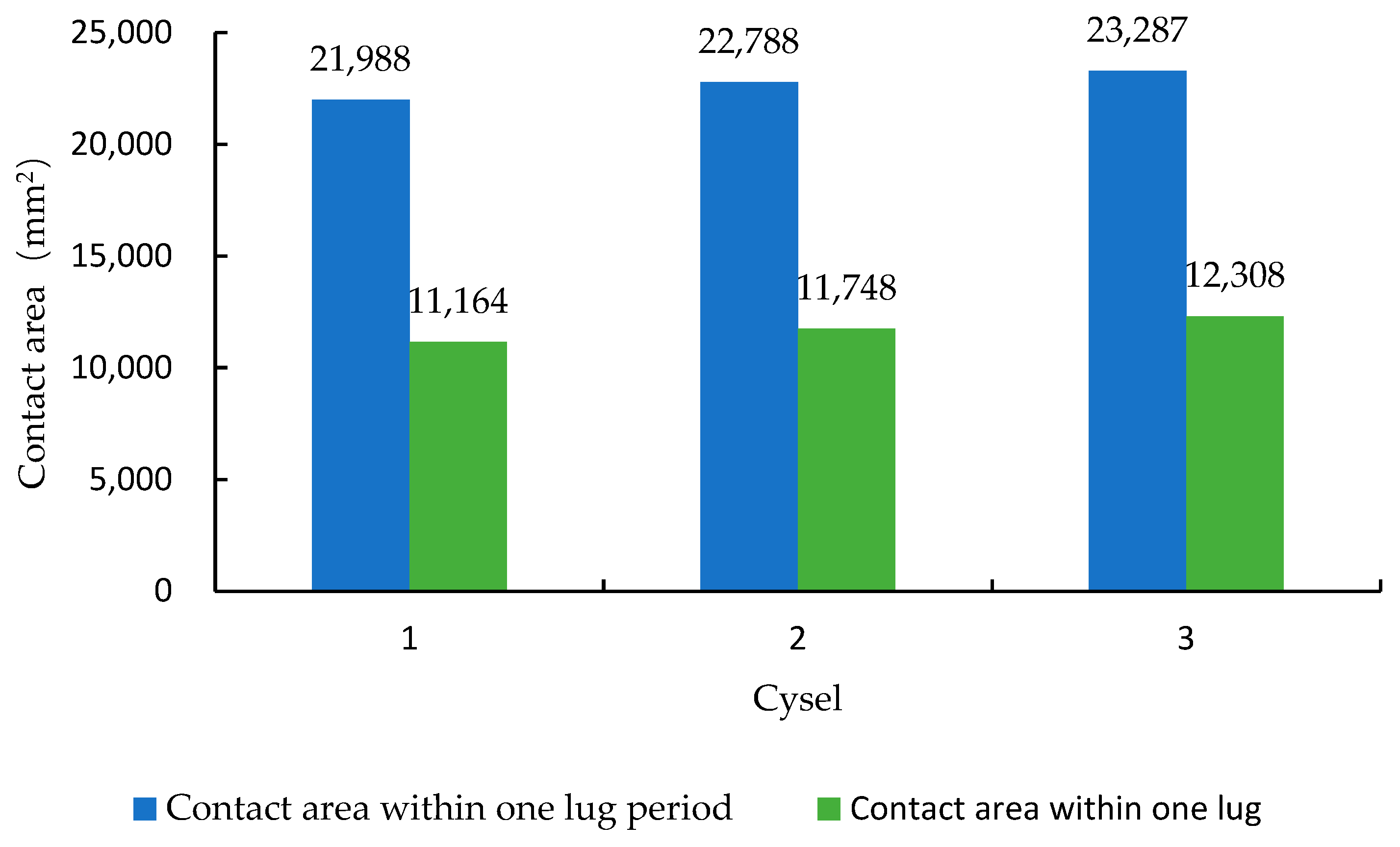
3.1. The Distribution Rule of Contact Area under the Same Tire Pattern Cycle
3.2. Fractal Dimension
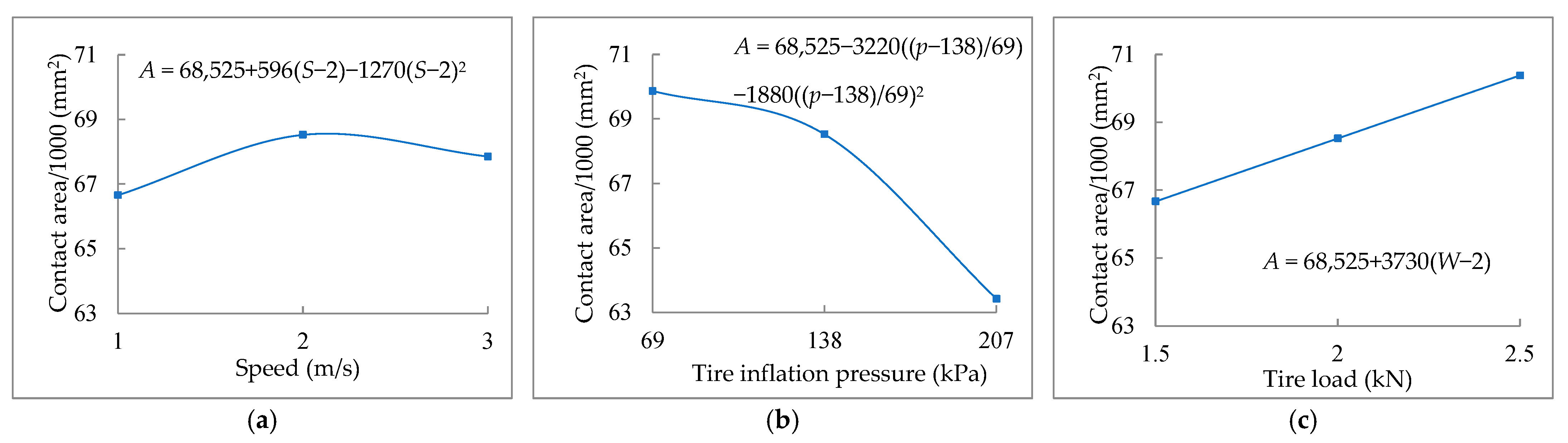
3.3. Empirical Equation for Contact Area
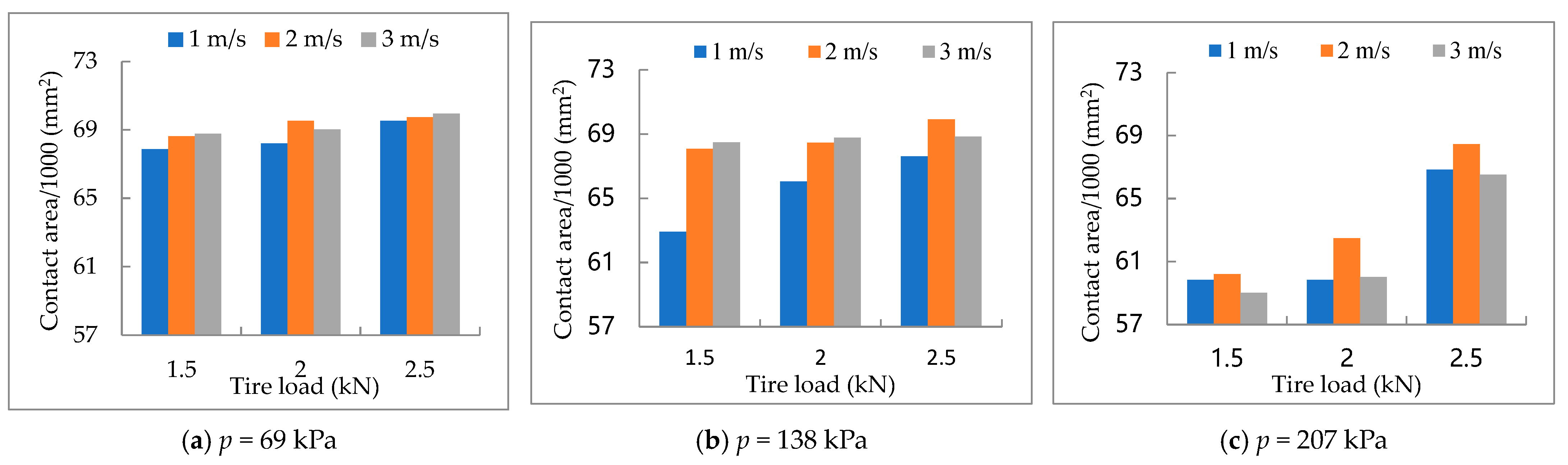
3.4. Combination Influence of Influence Factors
4. Conclusions
- The width of a chevron tread pattern in the tire was obviously less than the width of the tread, but the contact area of a single chevron tread pattern was more than half of the contact area within a cycle. That was to say, the contact area of a chevron tread pattern was slightly larger than the area of the tread because of the height of the chevron tread pattern.
- The empirical Equations (12)–(14) demonstrated that the contact area varied in a quadratic manner with speed at a given inflation pressure and tire load and varied in a quadratic manner with inflation pressure at a given speed and tire load and varied linearly with the tire load for a given speed and inflation pressure.
- The combination of high speed (S = 3 m/s), low inflation pressure (69 kPa), and high tire load (W = 2.5 kN) led to the biggest contact area (A = 69,934 mm2) and possibly severe soil compact and unsustainable development of agriculture. Therefore, this combination of speed, inflation pressure, and tire load is not recommended for the soil conditions used in this study.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Teimourlou, R.F.; Taghavifar, H. Determination of the Super-Elliptic Shape of Tire-Soil Contact Area Using Image Processing Method. Cercet. Agron. Mold. 2015, 48, 5–14. [Google Scholar] [CrossRef]
- Kokieva, E.G.; Troyanovskaya, I.P.; Orekhovskaya, A.A.; Kalimullin, M.N.; Dzjasheev, A.-M.S.; A Ivanov, A.; A Sokolova, V. Research of soil compaction process in area of contact with a wheel mover. J. Phys. Conf. Ser. 2021, 2094, 042003. [Google Scholar] [CrossRef]
- Lu, J.; Cheng, M.; Zhao, C.; Li, B.; Peng, H.; Zhang, Y.; Shao, Q.; Hassan, M. Application of lignin in preparation of slow-release fertilizer: Current status and future perspectives. Ind. Crops Prod. 2021, 176, 114267. [Google Scholar] [CrossRef]
- Yue, K.; Fornara, D.A.; Heděnec, P.; Wu, Q.; Peng, Y.; Peng, X.; Ni, X.; Wu, F.; Peñuelas, J. No tillage decreases GHG emissions with no crop yield tradeoff at the global scale. Soil Tillage Res. 2023, 228, 105643. [Google Scholar] [CrossRef]
- Memon, M.S.; Guo, J.; Tagar, A.A.; Perveen, N.; Ji, C.; Memon, S.A.; Memon, N. The effects of tillage and straw incorporation on soil organic carbon status, rice crop productivity, and sustainability in the rice-wheat cropping system of eastern China. Sustainability 2018, 10, 961. [Google Scholar] [CrossRef] [Green Version]
- Farhadi, P.; Golmohammadi, A.; Malvajerdi, A.S.; Shahgholi, G. Finite element modeling of the interaction of a treaded tire with clay-loam soil. Comput. Electron. Agric. 2019, 162, 793–806. [Google Scholar] [CrossRef]
- Batey, T. Soil compaction and soil management—A review. Soil Use Manag. 2009, 25, 335–345. [Google Scholar] [CrossRef]
- Júnnyor, W.D.S.G.; Diserens, E.; De Maria, I.C.; Araujo-Junior, C.F.; Farhate, C.V.V.; de Souza, Z.M. Prediction of soil stresses and compaction due to agricultural machines in sugarcane cultivation systems with and without crop rotation. Sci. Total Environ. 2019, 681, 424–434. [Google Scholar] [CrossRef]
- Augustin, K.; Kuhwald, M.; Brunotte, J.; Duttmann, R. Wheel Load and Wheel Pass Frequency as Indicators for Soil Compaction Risk: A Four-Year Analysis of Traffic Intensity at Field Scale. Geosciences 2020, 10, 292. [Google Scholar] [CrossRef]
- Wulfsohn, D. Soil-Tire Contact area. In Advances in Soil Dynamics; Upadhyaya, S.K., Chancellor, W.J., Perumpral, J.V., Wulfsohn, D., Way, T.R., Eds.; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2009; Volume 3, p. 59. [Google Scholar]
- Wong, J. Theory of Ground Vehicles; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Upadhyaya, S.; Wolf, D.; Chancellor, W.J.; Shmulevich, I.; Hadas, A. Traction-Soil Compaction Tradeoffs as a Function of Dynamic Soil-Tire Interation Due to Varying Soil and Loading Conditions; United States Department of Agriculture: Washington, DC, USA, 1995. [Google Scholar] [CrossRef]
- Grečenko, A. Tyre footprint area on hard ground computed from catalogue values. J. Terramech. 1995, 32, 325–333. [Google Scholar] [CrossRef]
- Schjønning, P.; Lamandé, M.; Tøgersen, F.A.; Arvidsson, J.; Keller, T. Modelling effects of tyre inflation pressure on the stress distribution near the soil–tyre interface. Biosyst. Eng. 2007, 99, 119–133. [Google Scholar] [CrossRef]
- Arvidsson, J.; Keller, T. Soil stress as affected by wheel load and tyre inflation pressure. Soil Tillage Res. 2007, 96, 284–291. [Google Scholar] [CrossRef]
- Diserens, E. Calculating the contact area of trailer tyres in the field. Soil Tillage Res. 2009, 103, 302–309. [Google Scholar] [CrossRef]
- Zhang, J.; Kong, X.; Obrien, E.J.; Peng, J.; Deng, L. Noncontact measurement of tire deformation based on computer vision and Tire-Net semantic segmentation. Measurement 2023, 217, 113034. [Google Scholar] [CrossRef]
- Taghavifar, H.; Mardani, A. Potential of functional image processing technique for the measurements of contact area and contact pressure of a radial ply tire in a soil bin testing facility. Measurement 2013, 46, 4038–4044. [Google Scholar] [CrossRef]
- Cueto, O.G.; Coronel, C.E.I.; Bravo, E.L.; Morfa, C.A.R.; Suárez, M.H. Modelling in FEM the soil pressures distribution caused by a tyre on a Rhodic Ferralsol soil. J. Terramech. 2016, 63, 61–67. [Google Scholar] [CrossRef]
- Michael, M.; Vogel, F.; Peters, B. DEM–FEM coupling simulations of the interactions between a tire tread and granular terrain. Comput. Methods Appl. Mech. Eng. 2015, 289, 227–248. [Google Scholar] [CrossRef]
- Botta, G.; Becerra, A.T.; Tourn, F.B. Effect of the number of tractor passes on soil rut depth and compaction in two tillage regimes. Soil Tillage Res. 2009, 103, 381–386. [Google Scholar] [CrossRef]
- Kenarsari, A.E.; Vitton, S.J.; Beard, J.E. Creating 3D models of tractor tire footprints using close-range digital photogrammetry. J. Terramech. 2017, 74, 1–11. [Google Scholar] [CrossRef]
- Farhadi, P.; Golmohammadi, A.; Sharifi, A.; Shahgholi, G. Potential of three-dimensional footprint mold in investigating the effect of tractor tire contact volume changes on rolling resistance. J. Terramech. 2018, 78, 63–72. [Google Scholar] [CrossRef]
- Jiang, C.; Lu, Z.; Upadhyaya, S.K.; Memon, M.S. Measurement and Analysis of the Vertical Stress Distribution within a Cultivated Soil Volume under Static Conditions. Trans. ASABE 2019, 62, 1035–1043. [Google Scholar] [CrossRef]
- Barnsley, M.F. Fractal functions and interpolation. Constr. Approx. 1986, 2, 32–303. [Google Scholar] [CrossRef]
- Yadav, R.; Raheman, H. Development of an artificial neural network model with graphical user interface for predicting contact area of bias-ply tractor tyres on firm surface. J. Terramech. 2023, 107, 1–11. [Google Scholar] [CrossRef]
- Ptak, W.; Czarnecki, J.; Brennensthul, M.; Lejman, K.; Małecka, A. Evaluation of Tire Footprint in Soil Using an Innovative 3D Scanning Method. Agriculture 2023, 13, 514. [Google Scholar] [CrossRef]





| Depth (cm) | Mean Dry Bulk Density (g/cm3) | Mean Soil Moisture Content (Wet Basis) w (%) | Soil Mechanical Composition/% | Mean Soil Compactness (kPa) | ||||
|---|---|---|---|---|---|---|---|---|
| Depth | ||||||||
| <0.002 mm | 0.002–0.5 mm | >0.5 mm | 100 mm | 200 mm | 300 mm | |||
| 0–5 | 1.29 | 17.65 | 21.67 | 35.89 | 42.44 | 21 | 177 | 414 |
| Level | Factor | ||
|---|---|---|---|
| Tire Load (kN) | Inflation Pressure (kPa) 1 | Speed (m/s) | |
| 1 | 1.5 | 207 (slightly overinflated) | 1 |
| 2 | 2 | 138 (slightly underinflated) | 2 |
| 3 | 2.5 | 69 (seriously underinflated) | 3 |
| Parameters | Coded Values | ||||
|---|---|---|---|---|---|
| S (m/s) | p (kPa) | W (kN) | x1 | x2 | x3 |
| 1 | 69 | 1.5 | −1 | −1 | −1 |
| 2 | 138 | 2 | 0 | 0 | 0 |
| 3 | 207 | 2.5 | 1 | 1 | 1 |
| Variable | Parameter Estimate | Standard Error | Pr Value |
|---|---|---|---|
| Intercept | 68,525 | 13,213 | <0.0001 |
| x1 | 596 | 3.33 | 0.083 |
| x2 | −3220 | 97 | <0.0001 |
| x3 | 1865 | 33 | <0.0001 |
| x12 | −1270 | 5 | 0.0362 |
| x22 | −1880 | 11 | 0.0034 |
| x2x3 | 1568 | 15 | 0.0008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, C.; Lu, Z.; Dong, W.; Cao, B.; Shin, K. Measurement and Analysis of the Influence Factors of Tractor Tire Contact Area Based on a Multiple Linear Regression Equation. Sustainability 2023, 15, 10017. https://doi.org/10.3390/su151310017
Jiang C, Lu Z, Dong W, Cao B, Shin K. Measurement and Analysis of the Influence Factors of Tractor Tire Contact Area Based on a Multiple Linear Regression Equation. Sustainability. 2023; 15(13):10017. https://doi.org/10.3390/su151310017
Chicago/Turabian StyleJiang, Chunxia, Zhixiong Lu, Wenbin Dong, Bo Cao, and Kyoosik Shin. 2023. "Measurement and Analysis of the Influence Factors of Tractor Tire Contact Area Based on a Multiple Linear Regression Equation" Sustainability 15, no. 13: 10017. https://doi.org/10.3390/su151310017
APA StyleJiang, C., Lu, Z., Dong, W., Cao, B., & Shin, K. (2023). Measurement and Analysis of the Influence Factors of Tractor Tire Contact Area Based on a Multiple Linear Regression Equation. Sustainability, 15(13), 10017. https://doi.org/10.3390/su151310017






