Spatial Distribution of Water Risk Based on Atlas Compilation in the Shaanxi Section of the Qinling Mountains, China

Abstract

Global climate change and rapid socio-economic development have increased the uncertainty in water resource systems and the complexity of water risk issues. Analyzing water risk and its spatial distribution is integral to the attainment of Sustainable Development Goal (SDG) 6, as this contributes to effective water resource partition management. In this paper, a compiling method of risk atlas with multiple layers is proposed, and the water risk system is divided into five sub-systems including the risk of resource, management, engineering, quality, and disaster. The information used for the risk atlas is calculated by a risk evaluation model based on a Pressure–State–Response (PSR) framework, hierarchical cluster, and set pair analysis (SPA). Risks in the Qinling Mountains of Shaanxi (as a case study) are evaluated and visualized. The results show that grades IV and V of engineering, disaster, and resource risk exceed 40%, indicating that they require prior control. The quality and management risks are not major, but there is still room for improvement. Overall, the risk atlas can effectively and objectively reflect the spatial distribution of water risk and provide a basis for the layout of water risk control measures.

1. Introduction

Since the 21st century, the rapid growth of population and water consumption has led to a prominent contradiction between water supply and demand [1,2]. The excessive exploitation of water resources has brought pressure on the ecological environment and caused its deterioration [3]. With economic development, accelerating urbanization, and future changes to the hydrological cycle caused by climate change, the imbalance between the supply and demand of water resources will continue to expand, which will lead to an increase in the risk of future water resources [4,5,6]. The formulation of Sustainable Development Goal (SDG) 6—Ensure availability and sustainable management of water and sanitation for all—in the 2030 Agenda for Sustainable Development represents the emphasis of the United Nations on sustainable water security issues [7]. How to analyze and curb water risk in accordance with SDG 6 targets becomes an important measure of ensuring the sustainable use and management of water resources [8].

The comprehensive analysis and assessment of risk is an essential part of the whole risk management concept, with the purpose of establishing where risk is excessively high so that early mitigation actions can be taken [9]. Hall and Borgomeo [10] pointed out that although risk is forward-looking and often considered to be future-oriented, past sequences of events and their impacts could provide some evidence about risks and monitoring variables associated with risk would assist in risk assessment. Semi-quantitative evaluations based on the construction of indicator systems have thus gained widespread attention [11,12,13,14,15], with a focus on the selection of indicators and ranking methods [16,17]. To select the most relevant indicators, researchers typically start by specifying a logical framework. Based on the Pressure–State–Response (PSR) or Driver–Pressure–State–Impact–Response (DPSIR) framework, Hammond et al. [18], Deng et al. [19], and Gomez et al. [20] constructed the evaluation model of flood risk, drought risk, and water environment risk, respectively. Moreover, composite index methods, such as the weighted composite method [21,22,23] and the fuzzy comprehensive evaluation method [15,24], were commonly used in risk assessment practice. These methods belong to the category of linear weighted evaluation methods, whereas the nature of the risk assessment process is nonlinear [25]. Therefore, some nonlinear assessment approaches, such as set pair analysis (SPA) [14,26], machine learning [27], and function models [28], have been used for risk evaluation to better cope with that. Among them, the SPA method can analyze the fuzzy uncertainty relationship between the sample, subsystem, index values, and criteria in three aspects—the identity, the discrepancy, and the contradistinction—and is, therefore, more suitable for water risk assessment problems with uncertainty and complexity [29,30].

Although many attempts have been made in extant studies to address water-related issues, they have largely focused on one specific aspect of water risk. The study of regional water risk, as a complex system engineering, encompasses diverse challenges for water accessibility, water quality, water availability, and natural disasters [31,32]. Single-perspective analysis severs the complex coupling within a water resource system and is inadequate to deal with complex water risk issues. A more integrated and systematic assessment approach to water risk is one requirement to address diverse water challenges and ensure sustainable development. The five outcome-based targets of SDG 6 embody a broad spectrum of water risk, including resource risk (target 6.1), quality risk (targets 6.3 and 6.6), management risk (targets 6.4 and 6.5), engineering risk (targets 6.1 and 6.4), and disaster risk (target 6.6), which provides the direction for integrated water risk assessment. Moreover, the diversity of impacting factors ensures water risk has significant regional differences. Determining the spatial distribution of risk is the precondition for realizing water resource partition management, and it also helps greatly during planning document making [33]. Digital maps are important interactive tools to visualize and compare spatial distributions. As a perceptible way of presenting risks, risk maps enable authorities, citizens, and the media to be aware of the levels and spatial distribution of risks to which their city is exposed intuitively. With the progress and development in science, risk maps have been extensively developed, especially in the field of natural hazards such as drought, flood, and landslide [34,35,36]. However, there are few reports on the study of maps that integrate multiple types and multiple layers of water risk information.

Consequently, the aim of this study is to develop a framework for integrated water risk assessment based on SDG 6 and its targets, as well as to propose a method for water risk atlas compilation using geospatial technology, which helps us to clarify the spatial distribution of water risk, to realize water resource partition management according to local conditions, and to provide important scientific support for the layout of water risk control measures, allowing for an integrated and systematic response to diverse water challenges.

2. Materials and Methods

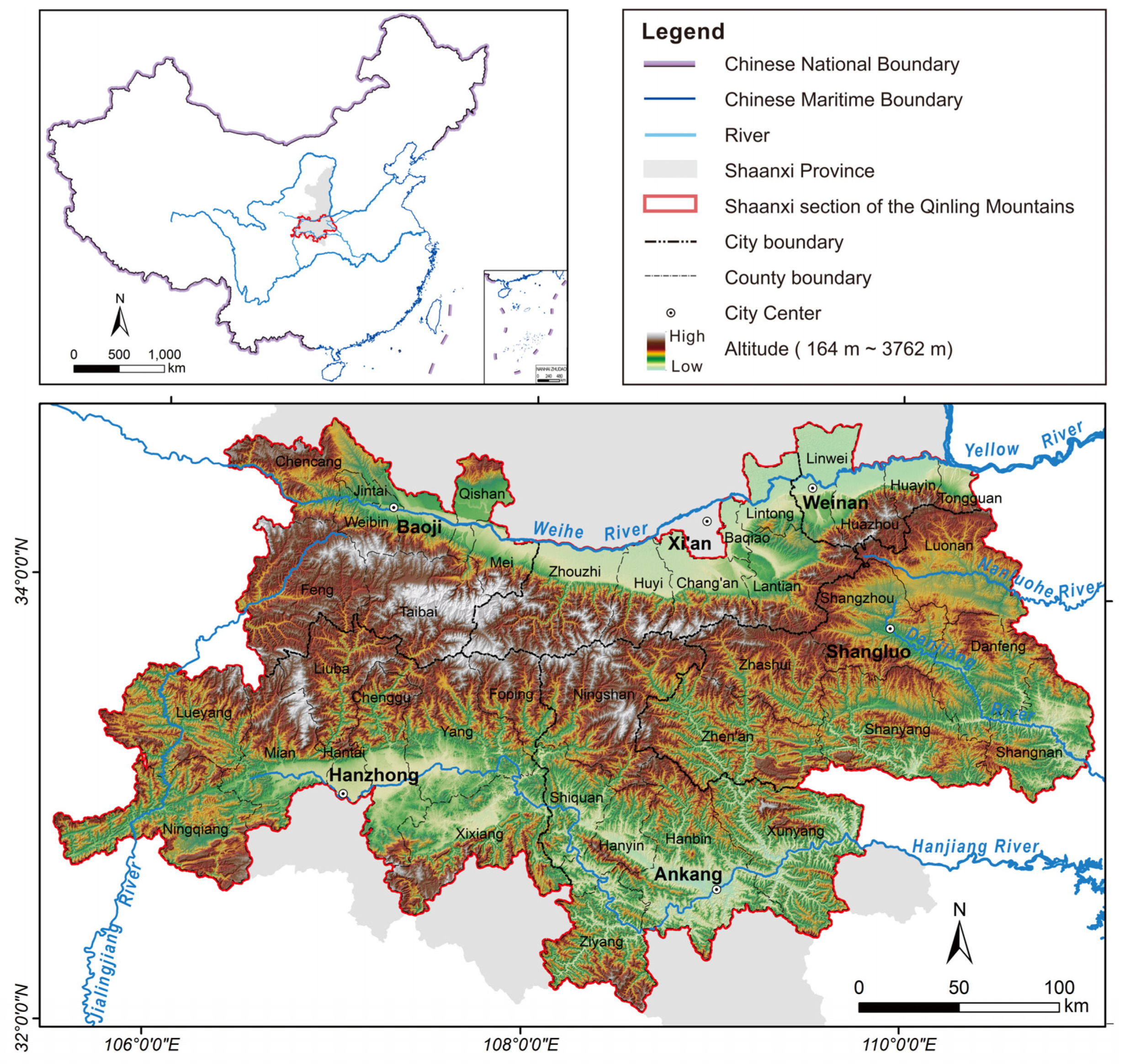
2.1. Study Area

The Shaanxi section of the Qinling Mountains (32°07′–34°47′ N, 105°29′–111°02′ E) is located in the southern part of Shaanxi Province, China. There are 39 counties, including Baqiao, Lintong, Chang’an, Lantian, Zhouzhi, Huyi, Weibin, Chencang, Jintai, Qishan, Meixian, Fengxian, Taibai, Linwei, Huazhou, Tongguan, Huayin, Hantai, Chenggu, Yangxian, Xixiang, Mianxian, Ningqiang, Lueyang, Liuba, Foping, Hanbin, Hanyin, Shiquan, Ningshan, Ziyang, Xunyang, Shangzhou, Zhashui, Luonan, Danfeng, Shanyang, Shangnan, and Zhen’an, which belong to the 6 cities of Xi’an, Hanzhong, Ankang, Baoji, Weinan, and Shangluo (Figure 1).

As an important boundary between north and south China, the Qinling Mountains are roughly in line with the 800 mm rainfall contours and 0 °C isothermal curve in January. As a result of the influences of the special topography and climate, precipitation is characterized by an asymmetry in temporal and spatial distribution. The Guanzhong region on the northern slope of the Qinling Mountains is the political and economic center of Shaanxi Province. However, the amount of water resources per capita is less than 400 m³, which is 1/4 of that in China and 1/15 of that in the world, and is still on a decreasing trend [37]. Moreover, along with the rapid development of population and industrial agglomeration, water pollution and over-exploitation are becoming increasingly serious problems, which hinder the sustainable development of the economy and society [38]. The Hanjiang Valley on the southern slope has abundant water resources, but the effective regulation and storage capacity only accounts for 11.9% of the average annual surface water resources, which is 1/3 of that in China. Most of the self-produced water flows out of the boundaries without being used, resulting in a prominent contradiction between water supply and demand. Although water efficiency has improved in recent years due to the implementation of the “Three Red Lines” water policy, there is still room for improvement compared to other Chinese regions [39]. In addition, the Shaanxi section of the Qinling Mountains is located in the province with the most serious soil and water loss in China. The ecological environment is fragile and disasters such as droughts and floods occur frequently, all of which threaten the sustainable use of water resources and the coordinated development of the economy and society.

2.2. Data Source

The data used in this research include spatial data and statistical data. Spatial data including administrative divisions, a digital elevation model (DEM), and a normalized difference vegetation index (NDVI) are mainly derived from the Geospatial Data Cloud (GDC, http://www.gscloud.cn, last access date: 25 April 2023) and the Resource and Environment Science and Data Center (RESDC, http://www.resdc.cn, last access date: 25 April 2023). Statistical data including water-related data and socio-economic data are mainly derived from the “Shaanxi Statistics Yearbook (2015–2019)” and the “Water Resources Bulletin (2015–2019)”.

2.3. Conceptual Framework

The water risk atlas is a generic term of a series of figures that reflect the type and magnitude of water risk distribution characteristics based on spatial data and statistics, oriented by the SDGs and supported by risk theory and geographic information technology. The principle is to evaluate risks and their regional differences based on the natural environmental elements and socio-economic conditions of the study area.

According to different risk sources, the water risk atlas can be divided into five layers: resource, management, engineering, quality, and disaster. The risk of resource (R) arises from a quantitative shortage of water resources, i.e., water consumption exceeds water availability, essentially a conflict between limited and spatially and temporally unevenly distributed water resources and the water demands of a growing population. High resource risk would lead to lower output and reduced food production, which becomes a primary constraint on regional economic development and social stability [40]. The risk of management (M) describes the degree of water development and the efficiency of water utilization, used to analyze whether a region is experiencing an avoidable increase in water demand due to a lack of water saving. High management risks would induce water scarcity and thus hinder sustainable economic and social development. The risk of engineering (E) refers to the imbalance in the spatial–temporal deployment of water resources and weak disaster-defense capacity due to the lag of hydraulic engineering construction, which would not only cause a shortage of water supply but also pose a threat to people’s lives and property [41]. The risk of quality (Q) describes the deterioration of water quality brought on by the release of contaminants, which prevents water resources from being able to meet production demands. The deterioration of the water environment due to water quality risks would also increase the cost of consumption for water users, which indirectly limits economic and social development [42]. The risk of disaster (D) describes the possibility of disasters, such as soil erosion and flood, that would adversely affect water quality, quantity, and human life and property. The framework shown in Figure 2 illustrates the compiling process of the water risk atlas, consisting of the following six main steps:

• Database construction: preparation of the datasets, which should include spatial and statistical data;
• Indicator selection: with the risk conception as a reference, the three aspects of the PSR model should be logically analyzed for each risk layer to select and formulate appropriate indicators, thereby constructing a multidimensional risk assessment indicator system;
• Weight assignment: using the Criteria Importance Through Inter-criteria Correlation (CRITIC) method, the objective weight of each indicator could be assigned by taking into account both contrast intensity and conflicting character;
• Standard classification: based on the features of the study area, a clustering algorithm could be used to determine the threshold for each indicator with reference to the accepted criteria that exist;
• Risk rank judgement: according to the indicator system, weights, and standard established, the risk evaluation value and grade could be calculated employing the SPA method from three aspects—the identity, the discrepancy, and the contradistinction;
• Atlas compilation: based on the risk evaluation value and grade obtained, a sunburst, a heatmap and a spatial distribution map could be produced for each risk layer to generate a regional water risk atlas.

2.4. Model Development

As shown in Figure 2, the evaluation model for water risk consists of four important components: the selection of indicators, classification of standards, assigning of weights to selected indicators, and ranking algorithm. This section presents the details on the selected research methods in this work.

2.4.1. Indicator Selection and Standard Classification

The selection of the assessment indicators is the basis of water risk assessment. A rational indicator system is expected to contain features of a dynamic bidirectional transmission mechanism and feedback besides assuring the broad coverage of indicators [43]. As a well-accepted method to assess resilience, the PSR framework [44] not only has obvious advantages in reflecting dynamic assessment processes [45,46] but also has conceptual coherence with the substance of risk—a product of the combination of a risk source and a risk-bearing entity [25]. In integrated water risk assessments, the pressure indicators answer the question of “why such a change happened” from the viewpoint of the risk source; the state and response indicators answer the questions of “what has changed” and “what should be done” from the viewpoint of the risk-bearer [47].

Cluster analysis is a method often used for classifying samples or variables including three types: k-means cluster, two-step cluster, and hierarchical cluster [11]. Applying cluster analysis to the classification of standards can overcome the subjective uncertainty of manually setting thresholds. Compared with the natural breaks method [48,49,50,51,52] and the numerical equalization method [53], it is also more scientific and reasonable. Both the k-means cluster and hierarchical cluster can be applied to numerical variables, and the latter has been proven to have a potential advantage [54] and is therefore used in this study. The principle of the hierarchical cluster is that the nearest samples are clustered into clusters first, and then the distant samples are clustered into clusters. This process continues, and each sample eventually can be gathered in the appropriate class [55]. Researchers can use the Euclidean distance to calculate the sample distance to measure their similarity [56]. The equation for calculating the binary Euclidean distance is as follows:

$$d(x_i,x_j)={\left[{\displaystyle {\sum }_{k=1}^p{\left(x_{ik}-x_{jk}\right)}^2}\right]}^{1/2}$$

(1)

Let $d_{ij}=d\left(x_i,x_j\right)$, ${D={(d}_{ij})}_{p\times p}$, form a distance matrix:

$$\left[\begin{array}{cc}\begin{array}{cc}0& d_{12}\\ d_{21}& 0\end{array}& \begin{array}{cc}\cdots & d_{1n}\\ \dots & d_{2n}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ d_{1n}& d_{2n}\end{array}& \begin{array}{cc}⋮& ⋮\\ \dots & 0\end{array}\end{array}\right]$$

(2)

where $d_{ij}$ and $d_{ji}$ are the distance between variables i and j.

According to the nearest distance matrix, the two samples with the closest distance are combined into one class, and clustering is performed using the Ward’s method. When $G_p$ and $G_q$ are merged into $G_r$, the recursive equation for the distance to other $G_k$ is

$$D_{rk}^2=\frac{n_k+n_p}{n_r+n_k}{D}_{pk}^2+\frac{n_k+n_q}{n_r+n_k}{D}_{qk}^2-\frac{n_k}{n_r+n_k}{D}_{pq}^2$$

(3)

where $n_k$, $n_p$, $n_r$ and $n_q$ are the number of samples of $G_p$, $G_k$, $G_r$ and $G_q$, respectively.

2.4.2. Weight Assignment

The weight is the physical quantity that measures the contribution of each evaluation indicator to the target [57], which holds an important place in an evaluation system. The weight analysis method can be usually divided into subjective and objective weighting methods. The subjective methods require the domain expert’s knowledge and vision. These techniques are often biased and do not capture the essence of the data [58]. Criteria Importance Through Inter-criteria Correlation (CRITIC), as a commonly used objective weighting method proposed by Diakoulaki et al. [59], can determine weights by considering both data volatility and correlations, unlike some methods that consider only one aspect [60]. The CRITIC method takes sample indicator values as input. The indicator value of each sample, which should be normalized to a [0, 1] interval, computes the standard deviation σ_j and the correlation coefficient to measure the contrast intensity and the conflicting character. Then, the indicator (C), which integrates the contrast intensity and the conflicting character, can be calculated using Equation (4):

$$C_j={\sigma }_j{\displaystyle \sum _{i=1}^m(1-r_{ij})}$$

(4)

where C_j is the information given by the j-th indicator, and r_ij is the linear correlation between indicators i and j. The weights are computed by Equation (5):

$${\omega }_j=\frac{{\mathrm{C}}_j}{{\displaystyle {\sum }_{j=1}^n{\mathrm{C}}_j}}$$

(5)

where ω_j is the weight of the j-th indicator using the CRITIC method.

2.4.3. Set Pair Analysis (SPA) Method for Risk Rank Judgement

The essence of risk events is uncertainty [61]. SPA is a method to analyze the internal uncertainty of a given system from three aspects: the identity, the discrepancy, and the contradistinction [62]. Assume sample indicator value x_t as set A_t, where t = 1, 2, …, T, and T is the number of assessment indicators. Further, assume the corresponding assessment standard as set B_k, where k = 1, 2, …, K, and K is the number of assessment grades. Then, the sets A_t and B_k can form a set pair W (A_t, B_k). For the set pair W (A_t, B_k), S is the number of the identical terms of the characteristic, which means indicator value x_t and its k-th standard are in the same grade. F₁, F₂, and F_K-2 are the number of the discrepant terms of the characteristic, which means indicator value x_t and its k-th standard are different by one, two, and K − 2 grades. P is the number of contradictory terms of the characteristic, which means indicator value x_t and its k-th standard are different by K − 1 grades [63]. According to the principle of SPA theory, the connection degree of W (A_t, B_k) can be described as

$${\mu }_k=\frac{S}{N}+\frac{F_1}{N}{i}_1+\frac{F_2}{N}{i}_2+\dots +\frac{F_{k-2}}{N}{i}_{k-2}+\frac{P}{N}j$$

(6)

Here, a = S/N is called the identity degree, b = F/N the discrepancy degree, and c = P/N the contradictory degree. Then, Equation (6) can be rewritten as

$${\mu }_k=a+b_1{i}_1+b_2{i}_2+\dots +b_{k-2}{i}_{k-2}+cj$$

(7)

Where i is the uncertainty coefficient of discrepancy, which has different values [−1, 1] in different conditions, and j is the uncertainty coefficient of the contradictory, which has a value of −1 [64].

For the indicator which is more superior when it is smaller, the connection degree μ_st between the sample value x_t and its grade standard can be defined as follows:

$${\mu }_{st}=\left\{\begin{array}{ll}1+0i_1+0i_2+\dots +0i_{k-2}+0j,\hfill & \hfill x_t\le S_1\hfill \\ \frac{S_2-x_t}{S_2-S_1}+\frac{x_t-S_1}{S_2-S_1}{i}_1+0i_2+\dots +0i_{k-2}+0j,\hfill & \hfill S_1\le x_t\le S_2\hfill \\ 0+\frac{S_3-x_t}{S_3-S_2}{i}_1+\frac{x_t-S_2}{S_3-S_2}{i}_2+\dots +0i_{k-2}+0j,\hfill & \hfill S_2\le x_t\le S_3\hfill \\ \cdots \hfill & \hfill \hfill \\ 0+0i_1+0i_2+\dots +\frac{S_K-x_t}{S_K-S_{K-1}}{i}_{k-2}+\frac{x_t-S_{K-1}}{S_K-S_{K-1}}j,\hfill & \hfill S_{K-1}\le x_t\le S_K\hfill \\ 0+0i_1+0i_2+\dots +0i_{k-2}+1j,\hfill & \hfill x_t>S_K\hfill \end{array}\right.$$

(8)

For the indicator which is more superior when it is bigger, the connection degree μ_st between the sample value x_t and its grade standard can be defined as follows:

$${\mu }_{st}=\left\{\begin{array}{ll}1+0i_1+0i_2+\dots +0i_{k-2}+0j,\hfill & \hfill x_t\ge S_1\hfill \\ \frac{x_t-S_2}{S_1-S_2}+\frac{S_1-x_t}{S_1-S_2}{i}_1+0i_2+\dots +0i_{k-2}+0j,\hfill & \hfill S_2\le x_t\le S_1\hfill \\ 0+\frac{x_t-S_3}{S_2-S_3}{i}_1+\frac{S_2-x_t}{S_2-S_3}{i}_2+\dots +0i_{k-2}+0j,\hfill & \hfill S_3\le x_t\le S_2\hfill \\ \cdots \hfill & \hfill \hfill \\ 0+0i_1+0i_2+\dots +\frac{x_t-S_K}{S_{K-1}-S_K}{i}_{k-2}+\frac{S_{K-1}-x_t}{S_{K-1}-S_K}j,\hfill & \hfill S_K\le x_t\le S_{K-1}\hfill \\ 0+0i_1+0i_2+\dots +0i_{k-2}+1j,\hfill & \hfill x_t<S_K\hfill \end{array}\right.$$

(9)

where S₁, S₂, S₃, …, S_K-1, and S_K are the threshold values of 1, 2, 3, …, K-1, and K grades, respectively, x_t is the sample indicator value of each sample, s is the s-th sample, and t is the t-th indicator.

Combining the calculation result of the indicator weight based on the CRITIC method, the K-element connection degree μ of set pair W (A, B) can be defined as

$$\mu (A,B)={\displaystyle \sum _{t=1}^T{\omega }_t{\mu }_{st}}={\displaystyle \sum _{t=1}^T{\omega }_t{a}_t}+{\displaystyle \sum _{t=1}^T{\omega }_t{b}_{t,1}}{i}_1+\cdots +{\displaystyle \sum _{t=1}^T{\omega }_t{b}_{t,K-2}}{i}_{k-2}+{\displaystyle \sum _{t=1}^T{\omega }_t{c}_t}j$$

(10)

where ω_t is the weight of t-th indicator.

Let $f_1={\displaystyle \sum _{t=1}^T{\omega }_t{a}_t} , f_2={\displaystyle \sum _{t=1}^T{\omega }_t{b}_{t,1}}, \cdots , f_{K-1}={\displaystyle \sum _{t=1}^T{\omega }_t{b}_{t,K-2}}, f_K={\displaystyle \sum _{t=1}^T{\omega }_t{c}_t}$, the evaluation value G_s of a given sample s can be defined as follows:

$$G_s=f_1\times 1+f_2\times 2+\cdots +f_{K-1}\times (K-1)+f_K\times K$$

(11)

The following confidence criterion is defined:

$$h_k=(f_1+f_2+\cdots +f_k)>\lambda ,\lambda \in [0.5,0.7]$$

(12)

where λ is the confidence degree. When λ approaches 0.7, the assessment result tends to be conservative and reliable. When λ is given, h_k can be determined by Equation (11). The assessment grade k can be also obtained from h_k. Then, the ranking value of a given sample can be judged as the k-th grade.

Using set pair analysis, the indicator set based on the PSR framework can be closely combined with the standard set based on the hierarchical cluster. This combination reduces the influence of the researcher’s subjective consciousness on the evaluation results, while fully exploiting the hidden information in the data. The fuzzy uncertainty relationship between evaluation samples, evaluation indicator values, and evaluation criteria is also well characterized. According to the indicator system, weights, and standard established above, the evaluation value and evaluation grade of each sample under different risk types can be calculated, which lays the data foundation for the risk atlas. After that, the evaluation results can be visualized as a spatial atlas with geographic information technology.

3. Results

3.1. Determination of Indicator and Standard

Based on the PSR framework and the features of water resources in the study area, the assessment indicator system has been established by extracting 25 indicators of water risk, as shown in

Table 1. The assessment indicator system and grading standards of water risk.

Subsystem	Indicator		Grade I	Grade II	Grade III	Grade IV	Grade V	Weight
			Very Low	Low	Moderate	High	Very High
R	R1	Natural population growth rate (‰)	<1.5	[1.5, 3.0)	[3.0, 4.5)	[4.5, 5.5]	>5.5	0.055
	R2	Annual precipitation (mm)	>1100	[840, 1100]	[670, 840)	[570, 670)	<570	0.033
	R3	Water yield coefficient	>0.55	[0.44, 0.55]	[0.33, 0.44)	[0.23, 0.33)	<0.23	0.033
	R4	Water yield modulus (104 m3/km2)	>58	[42, 58]	[27, 42)	[18, 27)	<18	0.028
	R5	Water resources per capita (m3)	>5000	[2000, 5000]	[1000, 2000)	[500, 1000)	<500	0.051
M	M1	Surface water resource utilization ratio (%)	<10	[10, 20)	[20, 30)	[30, 40]	>40	0.035
	M2	Water consumption per unit of GDP (m3/CNY 104)	<20	[20, 50)	[50, 80)	[80, 120]	>120	0.054
	M3	Water consumption per mu of irrigated farmland (m3/mu)	<250	[250, 450)	[450, 650)	[650, 850]	>850	0.042
	M4	Daily domestic water consumption per capita (m3)	<70	[70, 90)	[90, 110)	[110, 130]	>130	0.037
	M5	Water consumption per CNY 10,000 of industrial added value (m3/CNY 104)	<15	[15, 27)	[27, 50)	[50, 73]	>73	0.031
Q	Q1	Compliance rate of section water quality (%)	>90	[80, 90]	[70, 80)	[60, 70)	<60	0.054
	Q2	Wastewater emissions per unit of GDP (tons/CNY 104)	<5	[5, 8)	[8, 10)	[10, 13]	>13	0.031
	Q3	Ratio of wastewater to runoff (%)	<1	[1, 4)	[4, 10)	[10, 20]	>20	0.024
	Q4	Fertilizer use per unit area (tons/hm2)	<0.2	[0.2, 0.4)	[0.4, 0.6)	[0.6, 0.8]	>0.8	0.033
	Q5	Ratio of treated sewage (%)	>95	[90, 95]	[85, 90)	[80, 85)	<80	0.057
D	D1	NDVI	>0.80	[0.60, 0.80]	[0.45, 0.60)	[0.35, 0.45)	<0.35	0.045
	D2	Soil and water loss rate (%)	<16	[16, 31)	[31, 44)	[44, 55]	>55	0.034
	D3	Frequency of rainfall > 25 mm (%)	<1.36	[1.36, 1.57)	[1.57, 1.99)	[1.99, 2.36]	>2.36	0.056
	D4	Elevation (m)	>1100	[900, 1100]	[725, 900)	[550, 725)	<550	0.027
	D5	Per capita GDP (CNY 104)	>8.0	[6.5, 8.0]	[4.8, 6.5)	[3.7, 4.8)	<3.7	0.039
E	E1	Storage coefficient (%)	>50	[30, 50]	[20, 30)	[8, 20)	<8	0.026
	E2	Proportion of standard dikes (%)	>90	[75, 90]	[60, 75)	[45, 60)	<45	0.043
	E3	Proportion of water investment (%)	>2.0	[1.6, 2.0]	[1.2, 1.6)	[0.9, 1.2)	<0.9	0.074
	E4	Effective irrigation rate (%)	>90	[70, 90]	[50, 70)	[35, 50)	<35	0.035
	E5	Per unit area storage capacity (104 m3/km2)	>30	[20, 30]	[15, 20)	[10, 15)	<10	0.023

. For indicator R₁, M₁, M₂, M₃, M₄, M₅, Q₂, Q₃, Q₄, D₂, and D₃, the efficiency of the indicator is superior when the indicator value is smaller. For indicator R₂, R₃, R₄, R₅, Q₁, Q₅, D₁, D₄, D₅, E₁, E₂, E₃, E₄, and E₅, the efficiency of the indicator is superior when the indicator value is bigger. The assessment standard grades of water risk are divided into five classes, namely very low (grade I), low (grade II), medium (grade III), high (grade IV), and very high (grade V). Table 1 also shows the weights of indicators determined by the CRITIC method and the threshold of the indicators determined by the hierarchical cluster based on the sample data of 39 counties in the Shaanxi section of the Qinling Mountains from 2015 to 2019.

3.2. Evaluation Results of Water Risk Based on SPA

According to Equations (8) and (9) in Section 2.4.3, the connection degree between every individual indicator value x_t and the corresponding first standard can be calculated. For indicator R₁, M₁, M₂, M₃, M₄, M₅, Q₂, Q₃, Q₄, D₂, and D₃, μ_st can be calculated with Equation (8). For indicator R₂, R₃, R₄, R₅, Q₁, Q₅, D₁, D₄, D₅, E₁, E₂, E₃, E₄, and E₅, μ_st can be calculated with Equation (9). Then, the connection degree μ(A, B) of set pair W (A, B), in which set A is sample indicator values and set B is the first assessment grade standards, can be acquired by Equation (10). According to the connection degree μ(A, B) of each sample and confidence criterion with λ = 0.6, the evaluation value and the risk grade of all types and the corresponding integrated risk grade can be identified by using Equations (11) and (12).

3.3. Spatial Atlas of Water Risk in the Shaanxi Section of the Qinling Mountains

Based on the results of the risk evaluation, a sunburst, a heatmap, and a spatial distribution map could be produced for each subsystem to generate a regional water risk atlas, thereby exploring the spatial characteristics and corresponding causes of water resource risks in the study area. The sunburst shows the overall performance of the study area in each category of risk by depicting the proportions of different risk grades and details the composition of areas with very high risk through a hierarchical structure. The heatmap displays the distribution of the grades of the indicators in the counties with very high risk, assisting decision-makers in intuitively determining the course of action for risk mitigation from a holistic perspective. The spatial distribution map illustrates the spatial distribution of risks and provides a detailed and visual representation of the risk indicator grades for each high-risk county, which can help with localization decisions. The water resource risk atlas constructed by combining these three visualization techniques can help to understand all aspects of risk data from multiple perspectives and explore the information behind the data as fully as possible. The combination of the three achieves the stratification and visualization of water risk perception.

As shown in Figure 3, the risk of resource shows a decreasing trend from the eastern part of the northern slope to the western part of the southern slope of the Qinling Mountains. The risk of grade V accounts for 21.7%, which is concentrated in Baqiao, Lintong, Chang’an, Huyi, Lantian, Zhouzhi, Linwei, Huazhou, Tongguan, Huayin, Danfeng, and Shangnan, belonging to Xi’an, Weinan, and Shangluo, respectively. The resource risk subsystem describes the magnitude of the supporting forces underpinning the sustainable utilization of regional water resources in terms of the supply and demand gap in water quantity. As the dividing line between China’s warm-temperate and subtropical zones, the Qinling Mountains are generally consistent with the 800 mm rain isolines. This climatic difference makes the southern slope of the Qinling Mountains warmer and wetter, while the northern slope is relatively dry, which explains the imbalance of water resources between the north and the south of the Qinling Mountains to a certain extent. Figure 3b shows that 10/12 counties are at risk grade V for the water resources per capita indicator (R₅). Combined with Figure 3c, it can be seen that these 10 counties with small R₅ are all located on the northern slope, i.e., Guanzhong region. As the core area of the Belt and Road construction, the Guanzhong region has an increasing population due to the economic development and urban expansion, which is an important reason for the imbalance between water supply and demand. In addition, the warm and humid air brought by the southwest monsoon gradually weakens in the northeast when it reaches the southwest of the study area, due to the blockage of the Qinling Mountains, and is prone to produce precipitation in the southwestern part of the study area, i.e., Hanzhong and Baoji [65], which contributes to the very high risk in the northeastern cities of Xi’an and Weinan and explains the decreasing risk in the study area from the northeast to the southwest. Danfeng and Shangnan counties on the southern slope both have water resources per capita shares of over 1000 m³, which is a respectable amount. However, the water yield coefficients and moduli in these two counties are relatively small, indicating a spatial scarcity of water resources and a weak capacity to convert precipitation into water resources. Thus, these two counties are also considered to be at very high resource risk.

The overall distribution of management risk shows that the risk of management in the western part of the southern slope is higher than those in other regions, and the counties with risk grade of V are Baqiao, Foping, Hantai, and Mian County, accounting for 5.7% (Figure 4). The management risk subsystem describes the extent of water resource development, effectiveness, and efficiency of utilization. Figure 4b shows that for the counties with a very high risk of management, the performance of the indicators is relatively balanced, with no particularly dangerous indicators, suggesting that the reasons for presenting management risks are not quite the same across these counties. As shown in Figure 4c, for Baqiao District on the northern slope, the risk mainly stems from the high surface water utilization ratio (M₁), high domestic water consumption (M₄), and high industrial water consumption (M₅). As an old industrial base in Xi’an City, Baqiao District is dominated by the textile industry. This industry has a poor rate of water recycling, low product profitability, and high water consumption, all of which contribute to the high water consumption per CNY 10,000 of industrial added value [66]. Moreover, as the main urban area of Xi’an City, Baqiao District has an urbanization rate of over 95%. According to the “Shaanxi Province Industry Water Consumption Quotas (DB61/T 943-2020)”, the water consumption quota for urban residents in Xi’an is twice as high as that for rural residents. In this sense, the high domestic water consumption in Baqiao District is justifiable. The three counties with very high risk on the southern slope are all located in Hanzhong City and have an inefficient utilization of water for agriculture (M₃) in common. Two reasons for this situation: one is the lack of water-saving irrigation facilities in Hanzhong City; the second is the weak awareness of farmers to save water [67]. Hantai District, similar to Baqiao District, has a high degree of surface water utilization and low domestic water utilization efficiency, which is inevitable in its role as the main urban area of the city. Mian and Foping counties have low surface water utilization ratios, but both counties have much room for improvement in water utilization effectiveness and efficiency in all industries.

The risk of engineering is mainly concentrated in the Danjiang River Basin, Jialingjiang River Basin, and the middle mountainous area. The risk of grade V accounts for 73.5%, involving 25 counties in 5 cities including Xi’an, Baoji, Shangluo, Hanzhong, and Ankang (Figure 5). The engineering risk subsystem describes the construction of water projects in terms of flood control, water storage, and irrigation. Figure 5b shows that all 25 counties with a very high risk of engineering have low storage capacity per unit area, and 18 of them have low storage capacity coefficients, implying weak reservoir regulation capacity. A comparison of Figure 1 and Figure 5c shows that most of the counties with a very high risk of engineering are located in mountainous areas with high altitudes. According to the principles of protection priority and ecological priority in the “Qinling Ecological Protection Regulations of Shaanxi Province”, the development of areas with an elevation of more than 1500 m is restricted, which might be the reason for their lack of engineering construction. Reservoir silting due to soil erosion also contributes to the low storage coefficient [68]. Furthermore, Shangluo City, as a typical mountainous agricultural city with many slopes and few flats, is significantly short of irrigation projects due to objective conditions [69].

The risk of water quality is mainly concentrated in the lower reaches of the Weihe River in the eastern part of the northern slope of the Qinling Mountains, and the areas with a risk grade of V are Baqiao, Linwei, and Huazhou, accounting for 3.4% (Figure 6). It is obvious that the risk of water quality in the Shaanxi section of the Weihe River increases from west to east, reaching its peak in Linwei District, Weinan City. The water quality risk subsystem describes the sustainability of conservation water resources in the study area in terms of pollutant treatment, discharge, and water quality status. Figure 6b shows that the three counties with a very high risk of quality suffer from high wastewater emissions and fertilizer use. The Weihe River is the largest tributary of the Yellow River. Xi’an and Weinan, the cities with the most developed economy, densest population, most concentrated industry, and largest pollutant discharge in the Guanzhong area of Shaanxi Province, are located on the lower reaches of the Weihe River, and the water quality of the Weihe River is greatly influenced by domestic sewage and industrial and agricultural waste from these cities [70]. In 2018, the wastewater emissions of Linwei, Baqiao, and Huazhou were 15.62 tons/CNY 10,000, 17.62 tons/CNY 10,000, and 19.73 tons/CNY 10,000, respectively, which were 2.44~3.09 times that found in the Shaanxi section of the Qinling Mountains. Although the water quality of the Weihe River has continued to improve over the past ten years, which is related to the strict policy on water pollution control, the Weihe River is still the most important potential source of pollution in the Yellow River. The restoration and maintenance of Weihe River health remain important goals of Weihe River Basin management and conservation.

The risk of disaster is mainly concentrated in the eastern part of the northern slope and the Hanjiang River Basin of the southern slope, and the counties with risk grade of V are Mei, Lintong, Chang’an, Lantian, Zhouzhi, Huazhou, Tongguan, Huayin, Hanbin, Ziyang, Xixiang, Ningqiang, and Foping, accounting for 30.4% (Figure 7). This disaster risk subsystem is described from the perspective of disaster sensitivity and anti-disaster ability. Among the above extremely high-risk areas, most of the counties on the northern slope are located in the transitional area from the Qinling Mountains to the plain, with large terrain fall and low vegetation coverage, which are vulnerable to disasters. On the southern slope, the upper Han River has a large curvature, many tributaries, and abundant water. In case of heavy or prolonged rain, the water collection speed is too fast for it to be discharged in time, which makes the river flood-prone. Moreover, the soil and water loss rates of Chang’an, Lantian, Ziyang, Mei, Huayin, and Tongguan are more than 60%, with fragile ecological environments. The per capita GDP of Huazhou, Ningqiang, Lantian, Zhouzhi, and Tongguan counties is less than CNY 30,000, indicating a poor ability for disaster prevention and reduction. According to the Flash Flood Investigation and Evaluation Dataset of Shaanxi Province and historical disaster statistics provided by the emergency management bureaus, all of the above 13 counties with very high risk have been flooded in recent years, and Ziyang County has been flooded more than 45 times.

Figure 8a,c reflects the integrated water risk from five aspects: endowment conditions, development and utilization efficiency, engineering construction, water quality, and the probability of disasters. The results show that the integrated water risk covers four grades: II, III, IV, and V. The proportion of risk for grade III is the largest (around 45%), followed by grade II (around 36%). The risk of grade V accounts for 14.8%, mainly concentrated in the eastern part of the northern slope of the Qinling Mountains. The above risk evaluation results of different types and layers are summarized and compared in Figure 8b. The boxplot showed that the mean evaluation values of the risk of engineering, disaster, and resource are 3.69, 3.62, and 3.20, respectively, which are higher than that of the integrated water risk of 2.81. The median evaluation values of these three types of risk were also higher than that of the integrated risk. The proportion of risk for grades IV and V of engineering, disaster, and resource exceed 40%, which means that these three risks need prior control. The resource risk assessment value has the largest range, indicating that the results have a high degree of dispersion and obvious spatial differences. The average and median evaluation values of quality and management risk are lower than others, and the evaluation value of these two risks are mostly less than 3, which shows that the water quality and management risks in the Shaanxi section of the Qinling Mountains are not major, but there is still room for improvement.

4. Discussion

Generally, risk mitigation and management can be divided into three phases: (1) evaluation and analysis; (2) the implementation of mitigation and preventive measures based on the understanding of the spatial distribution of risk; and (3) the design of the plan to reduce and control risk [71]. The purpose of this work is to propose a tool for the integrated and systematic evaluation and analysis of the spatial distribution of water risk, under the guidance of SDG 6. The results contribute to the first phase of risk management by providing evidence to local authorities to develop preventive measures to reduce future water risk. For different risk sources, risks can be controlled through the appropriate adjustment of corresponding factors.

In high-risk areas of resource, the conflict stems from the mismatch between the limited amount of natural water resources and the water demands of a growing population. Controlling population growth may relieve the pressure on water resources, but it will also bring new social problems and is not conducive to sustainable development [72]. Encouraging the utilization of unconventional water resources, such as reclaimed wastewater, brackish water, and rainwater, is a viable way to control resource risk [73]. Formulating corresponding preferential policies in terms of water prices and finances can help promote the utilization of reclaimed water [74]. In high-risk areas of management, the different sources of conflict require different responses. For example, counties with low water use benefits should try to adjust their industrial structure [75], while counties with low agricultural water use efficiency should promote water-saving irrigation technology according to local conditions and increase water-saving publicity [76]. The core of these measures is the constraint of water consumption, including strengthening water resource management and improving the efficiency of water resource use, which contributes to the construction of a water-saving society. In high-risk areas of engineering, improvement in the regulation and storage capacity of water resources requires both the construction of storage projects and a focus on reservoir dredging [77]. In high-risk areas of quality, strengthening the supervision of pollution discharge and developing sewage purification technology can reduce the concentration of pollutants discharged. In high-risk areas of disasters, risk mitigation measures include improving hazard-resistance by structural measures, building resilient cities through non-structural measures, and restoring ecological vulnerability by expanding forest areas and controlling soil erosion [78].

The contributions of this work, compared to previous studies, are as follows: (1) Guided by the targets of SDG 6, an integrated water risk assessment framework was constructed including five dimensions: resource, quality, management, engineering, and disaster. (2) The combination of the PSR framework, CRITIC method, hierarchical cluster, and SPA method reduced the influence of subjective consciousness on the evaluation results, while fully exploiting the hidden information in the data, and uncertainties in risk assessment were well characterized. (3) A compiling method of spatial atlas of water resource risk was proposed, which achieved the stratification and visualization of water risk perception, helped indicate the primary localities for the application of mitigation measures and the general direction of risk control, and provided a reference for the layout of risk control measures. In order to improve the effectiveness of the prevention and control measures, research on the main influencing factors that contributed to the high risk under different risk types deserves to be further promoted. Additionally, compared to using water resource regionalization as the study unit, using counties as the study unit can lessen the difficulty of obtaining some data and assist in the implementation of the policy. However, it would destroy the integrity of the watershed and cannot characterize regional water resources well, which is also the direction of the optimization of future research.

5. Conclusions

In this work, the definition and framework of the water risk atlas were proposed under the guidance of SDG 6 first. A multidimensional water risk assessment model based on the PSR framework, CRITIC method, hierarchical cluster, and SPA theory was established by classifying water risks into five categories, i.e., the risk of resource, management, engineering, quality, and disaster. Then, a compiling method of water risk atlas, consisting of sunbursts, heatmaps, and risk spatial distribution maps was proposed. Risks in the Shaanxi section of the Qinling Mountains, as a case study were evaluated under the different types by using the constructed model, which laid the data foundation for the water risk atlas. The main conclusions are as follows:

• The integrated water risk is significantly higher in the northern Qinling Mountains than in the southern part. The mean and median evaluation values of the risk of engineering, disaster, and resource are higher than that of integrated water risk, and their proportion of risk for grades IV and V exceeds 40%, which means that these three risks are the main causes of water risk in the study area and need to be controlled as a priority.
• The multidimensional water risk atlas proposed in this paper can effectively help users to visualize the types and spatial distribution of risks faced by the region and provide a reference for the layout of risk control measures.
  • The risk of resource shows a decreasing trend from the eastern part of the northern slope to the western part of the southern slope of the Qinling Mountains. The encouragement of the use of unconventional water sources is a practical strategy to reduce resource risk in high-risk locations. In order to encourage the use of reclaimed water, suitable preferential policies with regard to water prices and finances can be developed.
  • Counties with high risks of management are concentrated in the western part of the southern slope and need to adjust their industrial structure or promote water-saving irrigation technology, according to local conditions, to improve the efficiency of water use.
  • The risk of engineering is mainly concentrated in the Danjiang River Basin, Jialingjiang River Basin, and the middle mountainous area. The construction of storage projects and reservoir dredging could help to improve the regulation and storage capacity of water resources.
  • Counties with high risks of water quality are mainly concentrated on the lower reaches of the Weihe River in the eastern part of the northern slope of the Qinling Mountains and should reduce the concentration of pollutants discharged by improving wastewater purification technology and pollution discharge monitoring.
  • The risk of disaster is mainly concentrated in the eastern part of the northern slope and the Hanjiang River Basin of the southern slope. Structural measures, non-structural measures, and ecological vulnerability protection measures could all help reduce disaster risk.