Sustainable Seismic Design of Triple Steel Structures
Abstract
:1. Introduction
- The sequential failures of the constituent ERSs affect the behavior of the combined structure.
- The use of REDDs changes the stress–strain relationships of individual members and of the entire system.
- The high rigidity of the HRRC forces the entire structure to respond as a Single Degree of Freedom (SDOF) system.
- The lateral load distribution follows the same profile as the uniform drift of the prototype.
- The proposed combination can prevent physical collapse and provide self-centering.
- The use of more than one ductile ERS with different Yield Drift Ratios (YDR) increases the global ductility of the system.
1.1. Constructional Issues
- Industrialization: the mass production of identical beams, braces, connections, splices, and REDD parts.
- Avoiding counterproductive details and introducing purpose-specific arrangements [25].
- Column length and section selection for the minimum number of splices.
- The utilization of locally available means and methods of construction.
- The practicality of disassembly, reassembly, and realignment for PERR.
1.2. Structural Issues
- 7.
- Beam sizing for maximum lateral resistance under combined seismic and gravity forces.
- 8.
- The elimination/reduction of P-delta and residual effects, and similar issues.
- 9.
- 10.
- Drift control and the imposition of uniform drift along the height of the structure [16].
- 11.
- The elimination/reduction of higher modes of vibration.
- 12.
- The limitation of damage to replaceable energy-dissipating items [30].
- 13.
- The imposition of SDOF responses for all loading combinations.
- 14.
- The estimation of YDR for beams and MFs of uniform strength [31].
- 15.
- The determination of the strength–stiffness YDR relationship for MFs equipped with REDDs.
1.3. Environmental Issues
1.4. Repairs and Recentering Issues
- 19.
- 20.
- The provision of built-in force-generating sources for realignment and static stability during stiffness reduction operations.
- 21.
- The provision of replaceable optional FS devices to prevent premature failure during PERR.
- 22.
- The provision of alternative sources of energy in case of power outages.
2. Theoretical Background and Development
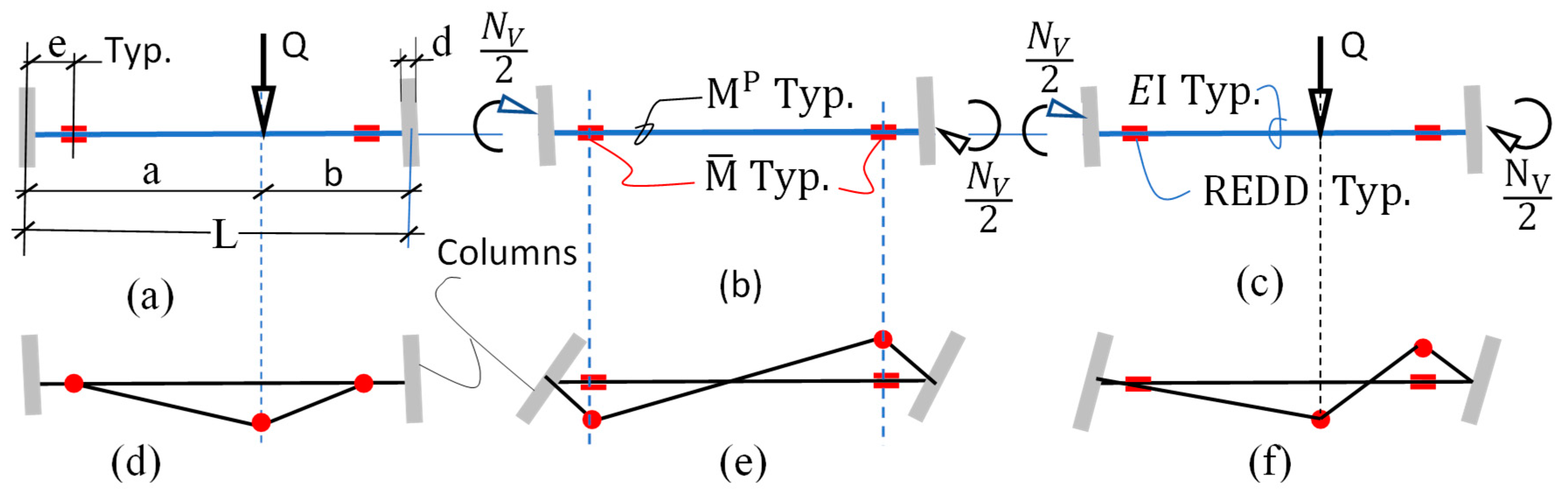
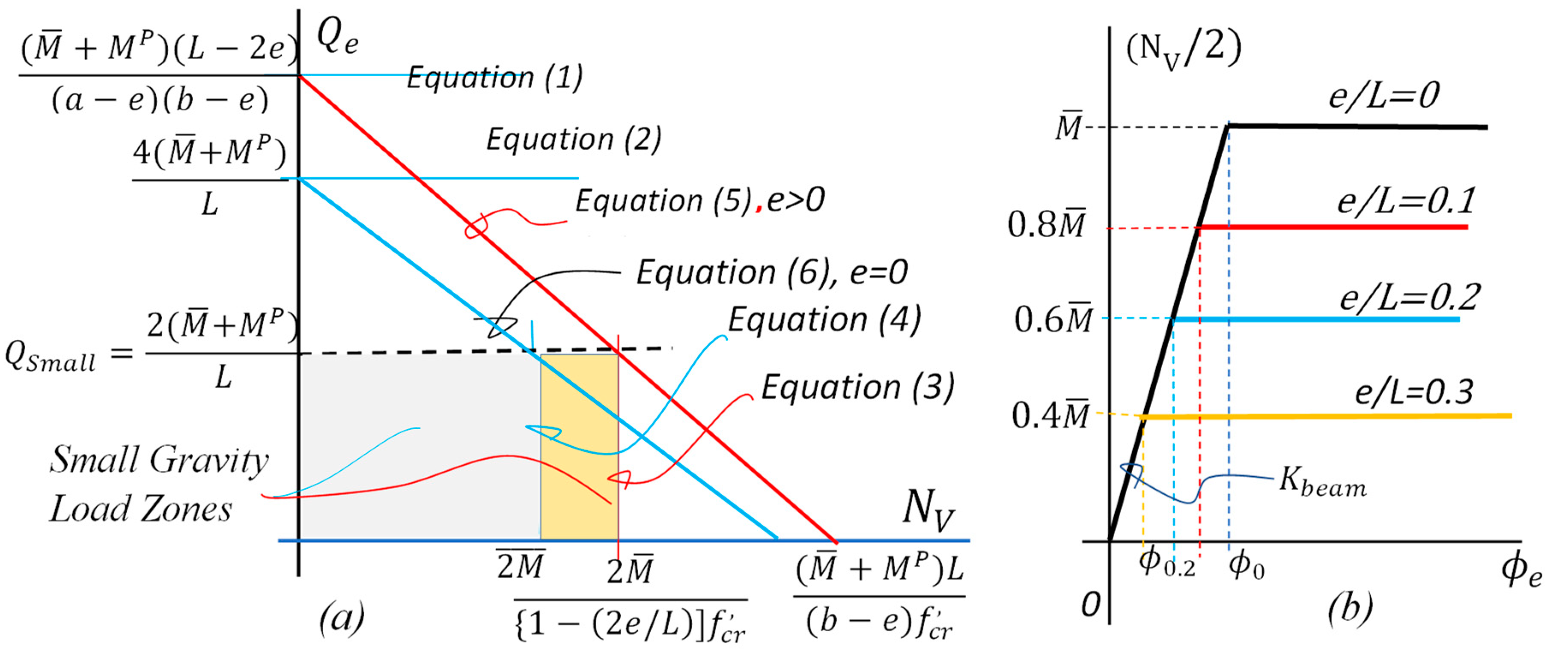
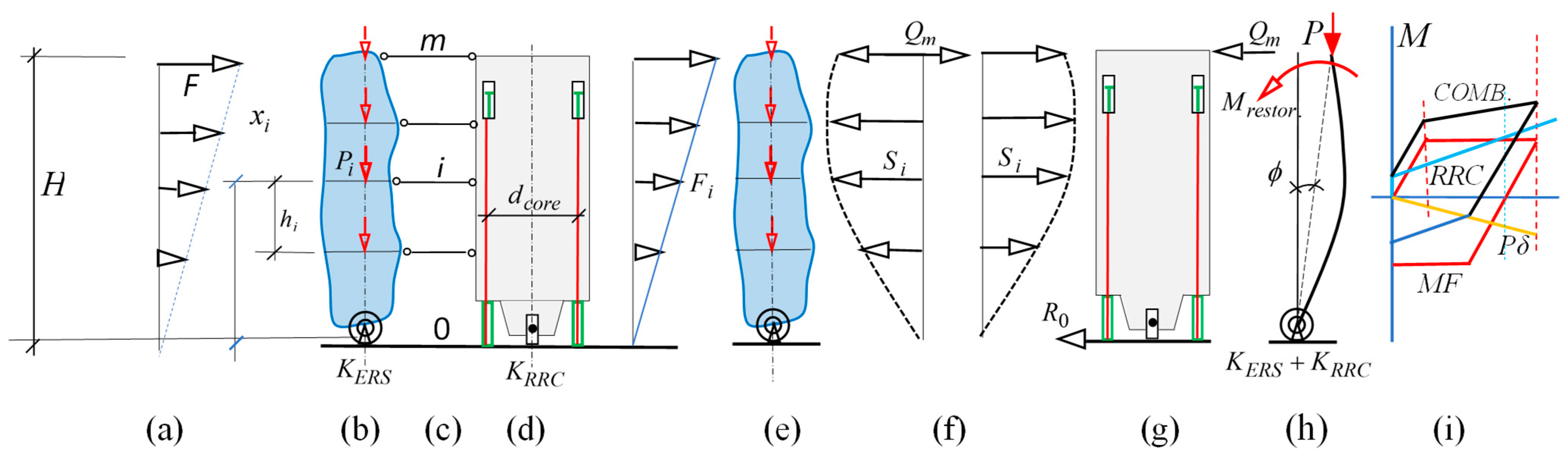
2.1. The Small Gravity Load Concept
2.2. Strength–Stiffness Relationship of REDD-Equipped Beams
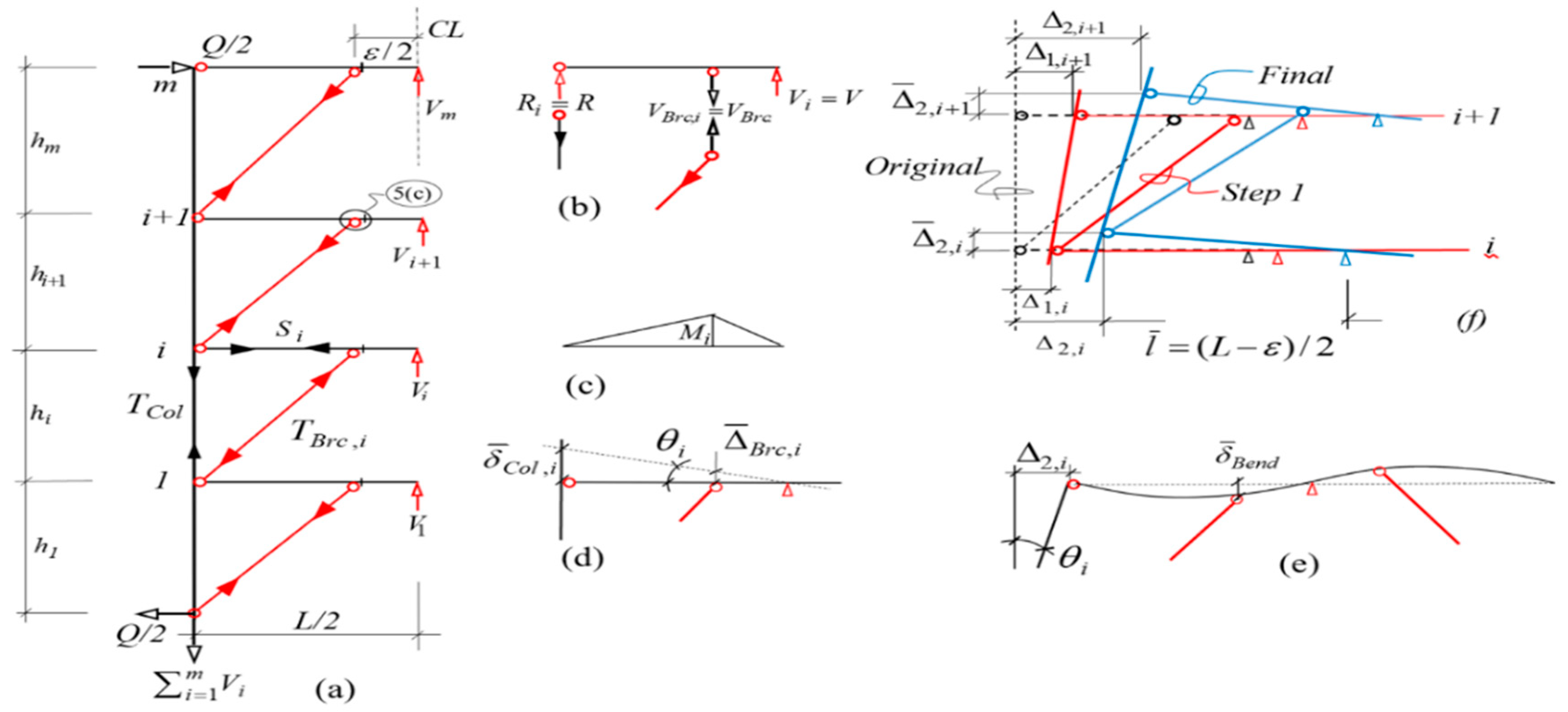
3. Moment Frame of Uniform Strength
3.1. MF Design Strategies
- Select so that automatically satisfies the code requirement .
- Select the ratio as a constant and work out for each beam. This option is rather efficient for small variations in L.
- Keep and e constant, and work out for each bay.
- Keep and e constant, and work out .
- For small variations in story heights, select the end column properties, half of those for inner bays.
- For small variations in story heights, select the roof- and grade-level beam properties, half of those for other levels.
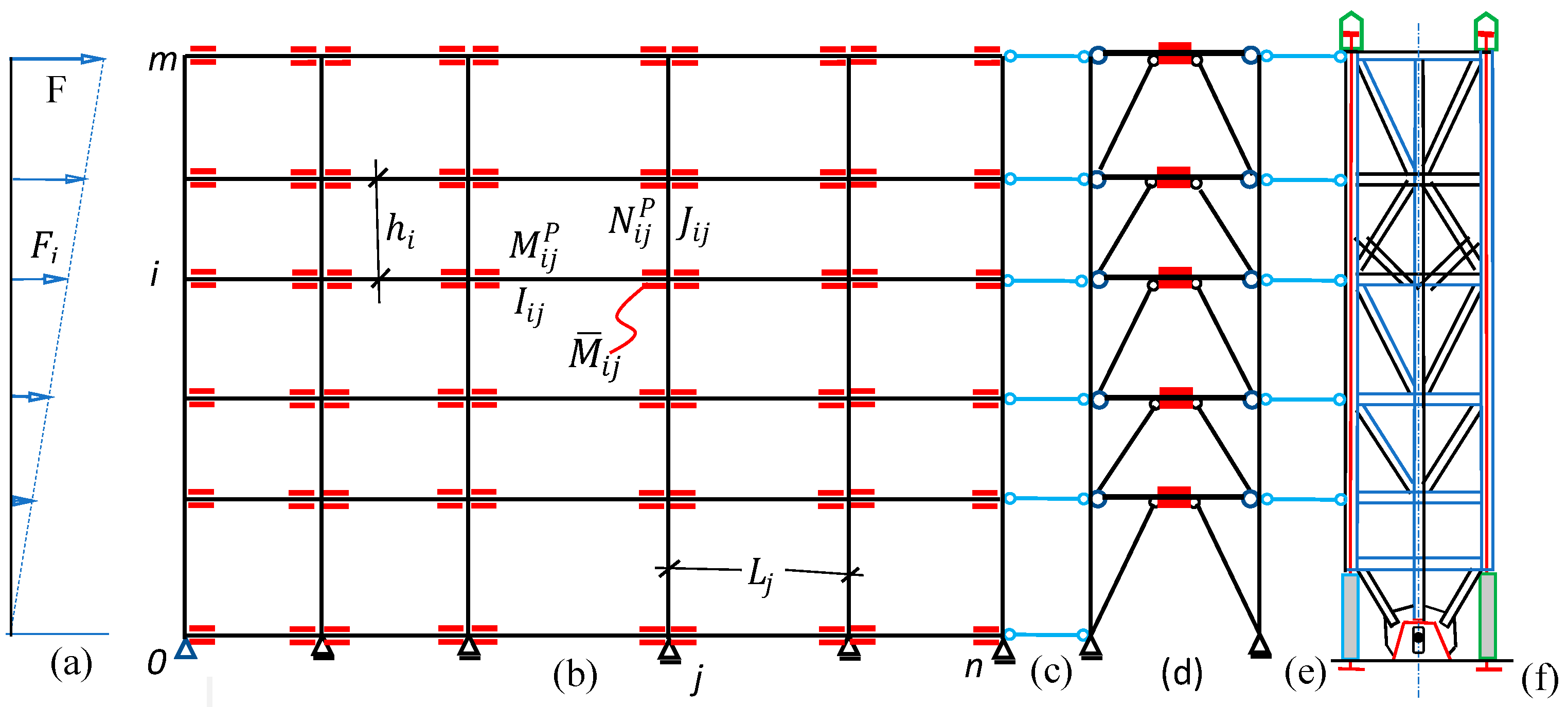
4. Development of a Generic Sustainable Triple System
4.1. Case Study 1
4.2. Case Study 2
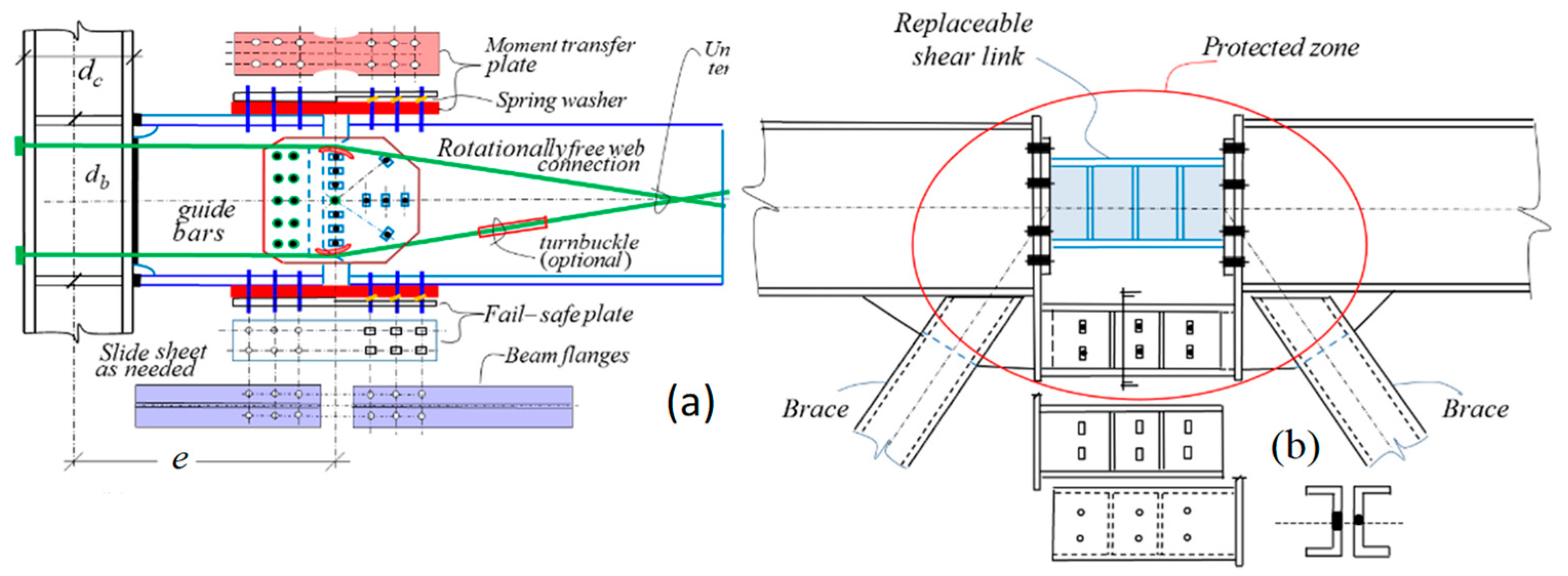
5. EBF of Uniform Strength as Part of Triple ERS
6. The Hybrid Rigid Rocking Core
Case Study 4
7. The Analysis and Design of the Archetype
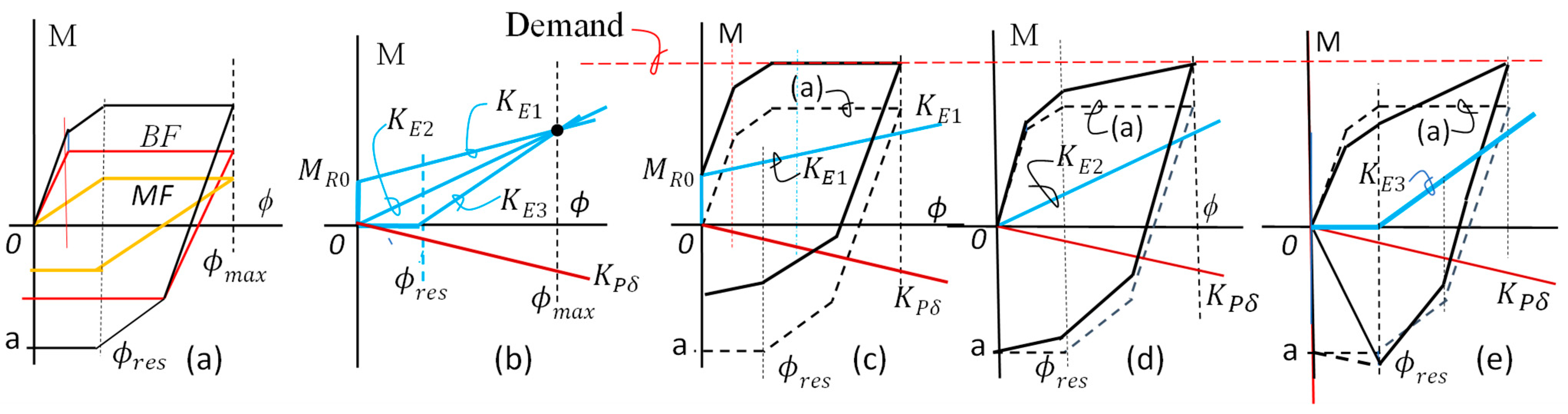
7.1. Seismic Resistance
- First, the EBF will fail by forming a stable failure mechanism while supporting the P-delta system and leaning on the MF.
- Next, the MF will undergo a plastic failure mechanism while leaning on the HRRC.
- The HRCC will remain intact and elastic, even beyond , while supporting the damaged RRCs and the undamaged gravity systems.
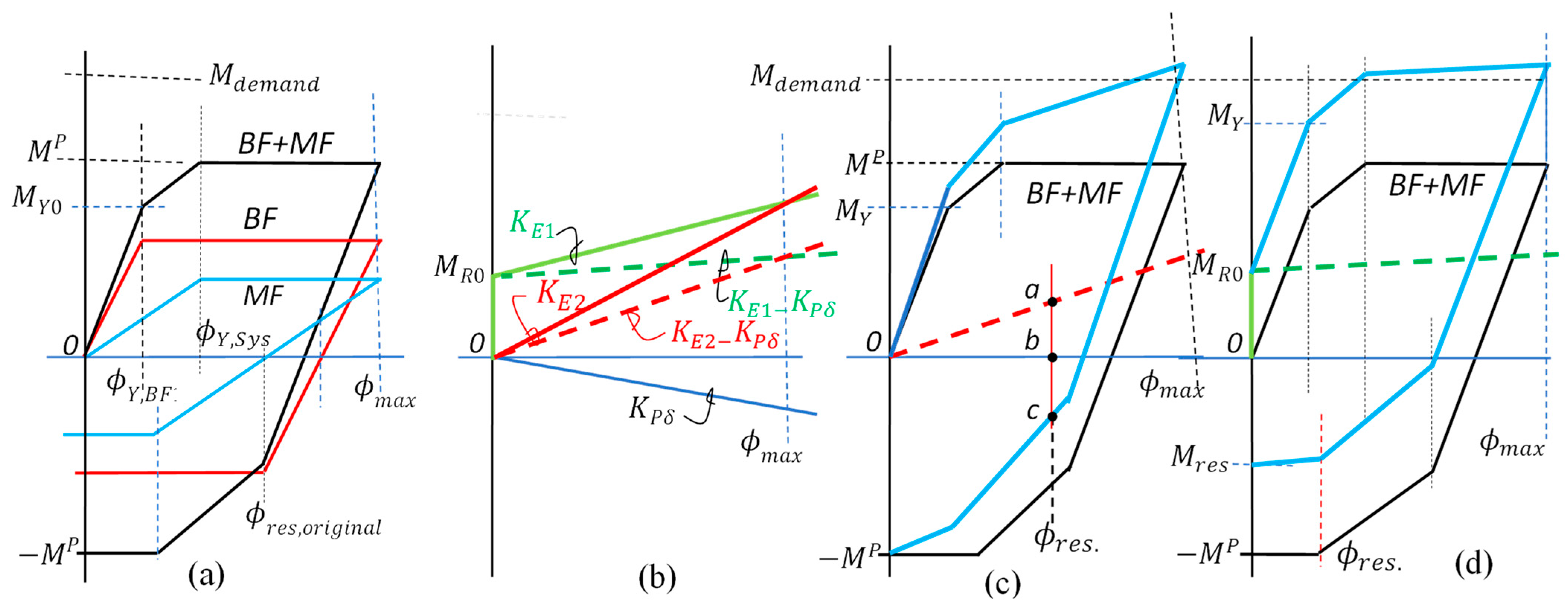
7.2. Post-Earthquake Realignment and Repair
- Option (Figure 8c): Forced recentering is achieved with a reduced residual moment (0a − ), which is not as satisfactory as , and requires storing a large preload within the structure. Recentering is materialized because the ordinance of the restoring effect is larger than that of the combined system at , i.e., the restoring force is sufficient to overcome the plastic resistance of the system at that point.
- Option (Figure 8d): Full recentering is not achieved. The restoring ordinance is less than that of the plastic resistance at . The total residual moment 0a is not satisfactory either, since .
- Option (Figure 8e): Neither forced recentering nor residual moment reduction can be achieved due to a lack of stored energies at the early stages of loading. This case is ideally suited for GSR + RFA treatment. Line suggests a possible load path for GSR. It also implies that no premature slackening of the tendons can be allowed for cases and , unless GSR + RFA is also envisaged.
7.3. GSR and the Single Vector Concept
8. Conclusions
- Constructional issues, as presented in Section 1.1.
- Structural issues, as listed in Section 1.2.
- Environmental issues, as referred to in Section 1.3.
- Recentering and repair issues pointed out in Section 1.4.
- Theoretical and conceptual issues, as discussed within the text.
- The small gravity load concept presented in Section 2.1.
- The strength–stiffness relationship of REDD-equipped beams, discussed in Section 2.2.
- MFs of uniform strength as part of triple ERSs, as reported under Section 3.
- The development of a generic sustainable triple system outlined, in Section 4.
- The analysis of EBFs of uniform strength as part of a triple ERS, outlined in Section 5.
- The hybrid rigid rocking core as part of a triple ERS introduced in Section 6.
- GSR and the single vector concept, as described under Section 7.3.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Eurocode-8; Design of Structures for Earthquake Resistance. European Standards: Brussels, Belgium, 1998.
- Priestly, M.J.N. Performance-based seismic design. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- ASCE/SEI 7-2016; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. ASCE: Reston, VA, USA, 2016.
- Krawinkler, H.; Deierlein, G.G. Challenges towards achieving earthquake resilience through Performance-Based Earthquake Engineering. In Performance-Based Seismic Engineering: Vision for an Earthquake Resilient Society; Fischinger, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 3–26. [Google Scholar]
- Aukeman, L.J. Evaluation of the ASCE7-05 Design Rule for Relative Strength in a Tall Buckling-Restrained Braced Frame Dual System. Master’s Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2011. [Google Scholar]
- Grigorian, M.; Sedighi, S.; Targhi, M.A. Sustainable Earthquake-Resistant Mixed Multiple Seismic Systems. J. Struct. Eng. 2023, 149, 3. [Google Scholar] [CrossRef]
- Gilmore, A.T. Options for sustainable earthquake-resistant design of concrete and steel buildings. Earthquakes Struct. 2012, 3, 783–804. [Google Scholar] [CrossRef]
- MacRae, G.A.; Kimura, Y.; Roeder, C. Effect of Column Stiffness on Braced Frame Seismic Behavior. J. Struct. Eng. 2004, 130, 381–391. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Borchers, E.; Pena, A. Design and Behavior of Steel Shear Plates with Openings as Energy Dissipating Fuses; Technical Report 173; John, A., Ed.; Blume Earthquake Engineering Center: Stanford, CA, USA, 2011. [Google Scholar]
- Hajjar, F.; Sesen, A.; Jampole, E.; Wetherbee, A. A Synopsis of Sustainable Structural Systems with Rocking, Self-Centering, and Articulated Energy-Dissipating Fuses; Department of Civil and Environmental Engineering Reports, Report No. NEU-CEE2013-01; Northeastern University: Boston, MA, USA, 2013. [Google Scholar]
- Grigorian, M.; Grigorian, C.E. Performance Control: New Elastic-Plastic Design Procedure for Earthquake Resisting Moment Frames. J. Struct. Eng. 2012, 138, 812–821. [Google Scholar] [CrossRef]
- Wiebe, L.; Christopoulos, C. Controlled rocking systems for enhanced seismic resilience: State of the art. In Sustainable Development of Critical Infrastructure; Liu, X., Ang, A.H.-S., Eds.; ASCE: Reston, VA, USA, 2014; pp. 496–503. [Google Scholar]
- Pessiki, S. Sustainable Seismic Design. Procedia Eng. 2017, 171, 33–39. [Google Scholar] [CrossRef]
- Gebelein, J.; Barnard, M.; Burton, H.; Cochran, M.; Haselton, C.; McLellan, R.; Porter, K. Considerations for a framework of resilient structural design for earthquakes. In Proceedings of the SEAOC Convention, San Diego, CA, USA, 12–15 September 2017. [Google Scholar]
- Fang, C.; Wang, W.; Qiu, C.; Hu, S.; MacRae, G.A.; Eatherton, M.R. Eatherton Seismic resilient steel structures: A review of research, practice, challenges and opportunities. J. Constr. Steel Res. 2022, 191, 107172. [Google Scholar] [CrossRef]
- Wada, A.; Mori, N. Seismic Design for the Sustainable City: A Report on Japanese Practice. In Structures Congress 2008: Crossing Borders; ASCE: Reston, VA, USA, 2008. [Google Scholar] [CrossRef]
- Deierlein, G.G.; Ma, X.; Eatherton, M. Collaborative research on development of innovative steel braced on mitigation of drift frame systems with controlled rocking and replaceable fuses. In Proceedings of the 6th International Conference on Urban Earthquake Engineering, Tokyo, Japan, 3–4 March 2009. [Google Scholar]
- ASCE. Sustainability, ASCE/SEI Sustainability Committee; ASCE: Reston, VA, USA, 2014; Available online: http://www.asce.org/sustainability/ (accessed on 6 April 2023).
- EC (European Commission). Seismic Performance Assessment Addressing Sustainability and Energy Efficiency; Publications Office of the EU: Brussels, Belgium, 2014. [Google Scholar]
- Lu, Y.; Panagiotou, M. Earthquake damage resistant multistory buildings using 7 combination of base isolation and rocking core walls. In Proceedings of the 1st Huixian International Forum on Earthquake Engineering, Harbin, China, 16–19 August 2014. [Google Scholar]
- Naeim, F. The Seismic Design Handbook; Kluwer Academic Publishers: Norwell, MA, USA, 2001. [Google Scholar]
- Kam, W.Y.; Jury, R. Performance–based seismic assessment: Myths and fallacies. In Proceedings of the NZSEE Conference, Wellington, New Zealand, 10–12 April 2015; pp. 673–687. [Google Scholar]
- Astaneh-Asl, A. Seismic Design of Steel Column-Tree Moment-Resisting Frames; Structural Steel Educational Council: Lafayette, CA, USA, 1997. [Google Scholar]
- Astaneh, A.; Call, S.M.; McMullin, K.M. Design of single plate shear connections. Eng. J. 1989, 26, 21–32. [Google Scholar] [CrossRef]
- Chancellor, N.B.; Eatherton, M.R.; Roke, D.A.; Akbaş, T. Self-Centering Seismic Lateral Force Resisting Systems: High Performance Structures for the City of Tomorrow. Buildings 2014, 4, 520–548. [Google Scholar] [CrossRef] [Green Version]
- Grigorian, M.; Moghadam, A.S.; Kamizi, M. On repairable earthquake resisting archetypes with a view to resiliency objectives and assisted self-centering. Struct. Des. Tall Spéc. Build. 2019, 28, e1603. [Google Scholar] [CrossRef]
- Fahnestock, R.; Sause, J.; Ricles, B.; Simpson, M.; Kurata, T.; Okazaki, Y.; Kawamata, Z.; Tao, J.; Duke, D.; Rivera, B.; et al. US-Japan collaboration for shake table testing of a frame-spine system with force-limiting connections. In Proceedings of the 17th World Conference on Earthquake Engineering, online, Japan, 27 September–2 October 2021. [Google Scholar]
- Eatherton, M.R.; Ma, X.; Krawinkler, H.; Deierlein, G.G.; Hajjar, J.F. Quasi-Static Cyclic Behavior of Controlled Rocking Steel Frames. J. Struct. Eng. 2014, 140, 11. [Google Scholar] [CrossRef]
- Grigorian, M.; Kamizi, M.; Sedighi, S. A basis for developing sustainable earthquake-resisting structures. In Proceedings of the Institution of Civil Engineers-Structures and Buildings; ICE: London, UK, 2021; Volume 174, pp. 516–533. [Google Scholar] [CrossRef]
- Karavasilis, T.; Blakeborough, T.; Williams, M.S. Development of nonlinear analytical model and seismic analyses of a steel frame with self-centering devices and viscoelastic dampers. Comput. Struct. 2011, 89, 1232–1240. [Google Scholar] [CrossRef] [Green Version]
- Grigorian, M.; Grigorian, C. Lateral Displacements of Moment Frames at incipient collapse. J. Eng. Struct. 2012, 44, 174–185. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, H. High Performance Damage-Resistant Seismic Resistant Structural Systems for Sustainable and Resilient City: A Review. Shock Vib. 2018, 2018, 8703697. [Google Scholar] [CrossRef] [Green Version]
- Grigorian, M.; Moghadam, A.S.; Sedighi, S. Sustainable seismic design and health monitoring. Struct. Control Health Monit. 2022, 29, e3058. [Google Scholar] [CrossRef]
- Janhunen, B.; Tipping, S.; Wolfe, J.; Mar, D. Seismic retrofit of a 1960s steel moment-frame high-rise using a pivoting spine. In Proceedings of the 2012 Annual Meeting of the Los Angeles Tall Buildings Structural Design Council, Los Angeles, CA, USA, 4 May 2012. [Google Scholar]
- Pollino, M.; Slovenec, D.; Qu, B.; Mosqueda, G. Seismic Rehabilitation of Concentrically Braced Frames Using Stiff Rocking Cores. J. Struct. Eng. 2017, 143, 9. [Google Scholar] [CrossRef]
- Neal, B.G. The Plastic Methods of Structural Analysis; Chapman and Hall: London, UK, 1963. [Google Scholar]
- Hayman, J. Plastic Design of Frames; Cambridge University Press: Cambridge, UK, 1971. [Google Scholar]
- Foulkes, J. Minimum weight design and the theory of plastic collapse. Q. Appl. Math. 1953, 10, 347–358. [Google Scholar] [CrossRef] [Green Version]
- Brandt, A. Criteria and Methods of Structural Optimization; Kluwer Academic Publications: New York, NY, USA, 1978. [Google Scholar]
- Grigorian, M.; Grigorian, C. Performance control for seismic design of moment frames. J. Constr. Steel Res. 2011, 67, 1106–1114. [Google Scholar] [CrossRef]
- Taranth, B.S. Sustainable earthquake-resisting system. J. Struct. Div. 1998, 144, 04017199. [Google Scholar]
- Shen, Y.; Christopoulos, C.; Mansour, N.; Tremblay, R. Seismic Design and Performance of Steel Moment-Resisting Frames with Nonlinear Replaceable Links. J. Struct. Eng. 2011, 137, 1107–1117. [Google Scholar] [CrossRef]
- Bozkurt, M.B.; Topkaya, C. Replaceable links with gusseted brace joints for eccentrically braced frames. Soil Dyn. Earthq. Eng. 2018, 115, 305–318. [Google Scholar] [CrossRef]
- Qu, B.; Guo, X.; Chi, H.; Pollino, M. Probabilistic evaluation of effect of column stiffness on seismic performance of steel plate shear walls. Eng. Struct. 2012, 43, 169–179. [Google Scholar] [CrossRef]
- Ajrab, J.; Pekcan, G.; Mander, J. Rocking wall–frame structures with supplemental tendon systems. J. Struct. Eng. 2004, 130, 895–903. [Google Scholar] [CrossRef]
- Akbari, A.; Massumi, A.; Grigorian, M. Seismic performance evaluation of steel moment frames with mid-span rigid rocking cores. Steel Compos. Struct. 2023, 46, 5. [Google Scholar]
- Mahin, S. Resilience by design: A structural engineering perspective. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Grigorian, M.; Moghadam, A.S.; Mohammadi, H.; Kamizi, M. Methodology for developing earthquake-resilient structures. Struct. Des. Tall Spéc. Build. 2018, 28, e1571. [Google Scholar] [CrossRef]
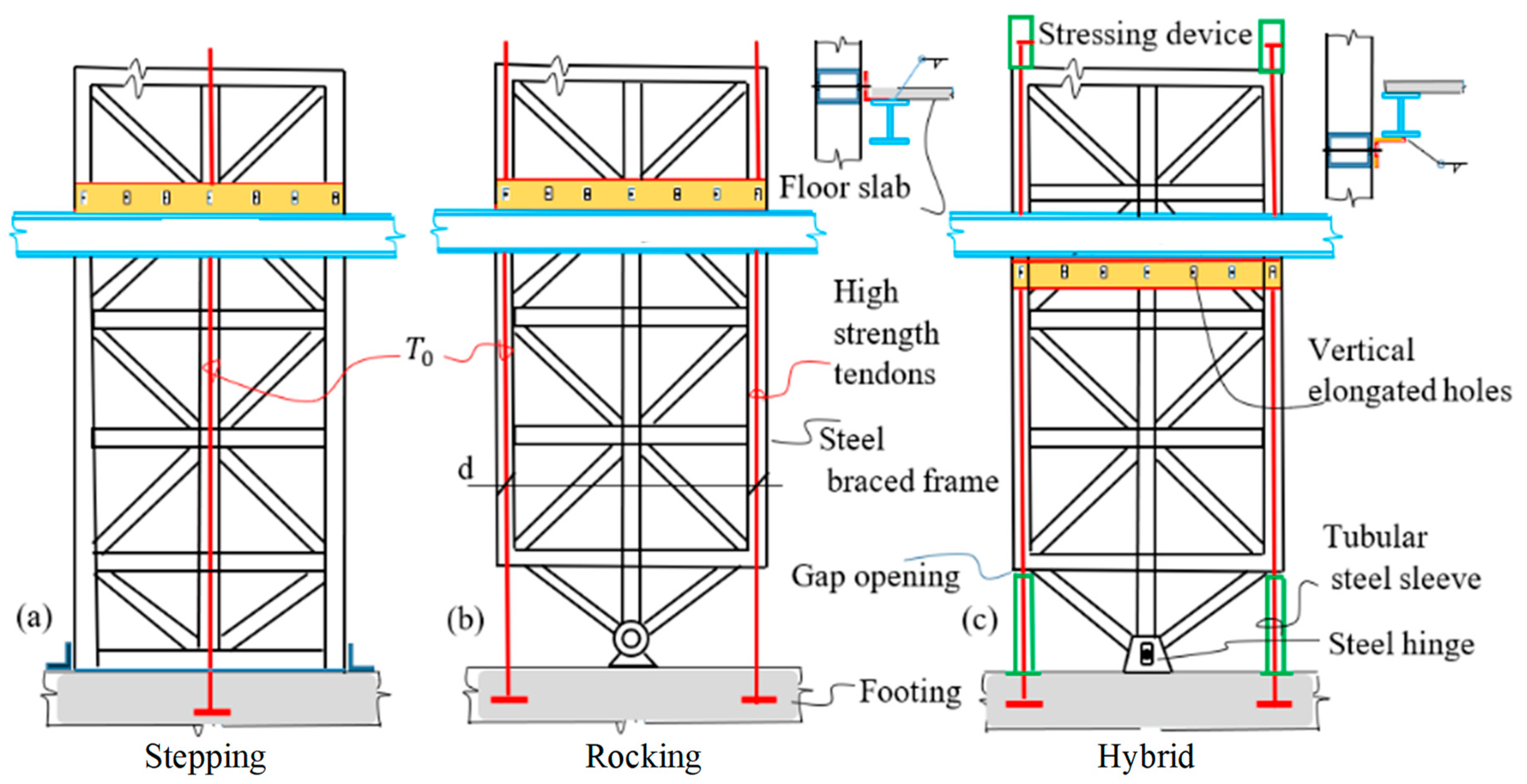
| Status | Rigid Stepping Core | Rigid Rocking Core | Hybrid Rocking Core | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Tc | Mc | T1 | Tr | Mc | T1 | Tr | Mc | C1 | Cr | |
| At rest | T0 | - | T0 | T0 | - | T0 | T0 | - | T0 + P/2 | |
| No gap | T + T0 | (T + T0 + P)d/2 | T + T0 | T0 − T | Td | T + T0 | T0 − T | (T + T0 + P)d/2 | T0 − T + P/2 | T0 − T + P/2 |
| Gap | T + T0 | (T + T0 + P)d/2 | T + T0 | 0 | (T + T0)d/2 | T + T0 | 0 | (T + T0 + P)d/2 | 0 | T0 − T + P/2 |
| Opng | T ≥ (T0 + P) | T ≥ T0 | T ≥ (T0 + P/2) | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grigorian, M.; Moghadam, A.S.; Massumi, A. Sustainable Seismic Design of Triple Steel Structures. Sustainability 2023, 15, 10336. https://doi.org/10.3390/su151310336
Grigorian M, Moghadam AS, Massumi A. Sustainable Seismic Design of Triple Steel Structures. Sustainability. 2023; 15(13):10336. https://doi.org/10.3390/su151310336
Chicago/Turabian StyleGrigorian, Mark, Abdolreza S. Moghadam, and Ali Massumi. 2023. "Sustainable Seismic Design of Triple Steel Structures" Sustainability 15, no. 13: 10336. https://doi.org/10.3390/su151310336








