Reconstruction of Fault Architecture in the Natural Thermal Spring Area of Daruvar Hydrothermal System Using Surface Geophysical Investigations (Croatia)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Geological and Hydrogeological Settings
2.2. Methods
2.2.1. Electrical Resistivity Tomography
2.2.2. Seismic Investigations
3. Results
3.1. Electrical Resistivity Tomography (ERT)
3.2. Seismic Investigations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- EU CORDIS; European Climate Infrastructure and Environment Executive Agency (CINEA). CORDIS Results Pack on Geothermal Energy—Supporting the Development of Europe’s Geothermal Energy Sector; Publications Office of the European Union: Luxembourg, 2022. [Google Scholar]
- Fetting, C. The European Green Deal; ESDN Report; ESDN Office: Vienna, Austria, 2020. [Google Scholar]
- Moeck, I.S. Catalog of Geothermal Play Types Based on Geologic Controls. Renew. Sustain. Energy Rev. 2014, 37, 867–882. [Google Scholar] [CrossRef] [Green Version]
- Moeck, I.; Hinz, N.; Faulds, J.; Bell, J.; Kell-Hills, A.; Louie, J. 3D Geological Mapping as a New Method in Geothermal Exploration: A Case Study from Central Nevada. GRC Trans. 2010, 34, 807–812. [Google Scholar]
- Pola, M.; Cacace, M.; Fabbri, P.; Piccinini, L.; Zampieri, D.; Torresan, F. Fault Control on a Thermal Anomaly: Conceptual and Numerical Modeling of a Low-Temperature Geothermal System in the Southern Alps Foreland Basin (NE Italy). J. Geophys. Res. Solid Earth 2020, 125, e2019JB017394. [Google Scholar] [CrossRef]
- Siler, D.L.; Faulds, J.E.; Hinz, N.H.; Dering, G.M.; Edwards, J.H.; Mayhew, B. Three-Dimensional Geologic Mapping to Assess Geothermal Potential: Examples from Nevada and Oregon. Geotherm. Energy 2019, 7, 2. [Google Scholar] [CrossRef] [Green Version]
- Torresan, F.; Piccinini, L.; Cacace, M.; Pola, M.; Zampieri, D.; Fabbri, P. Numerical Modeling as a Tool for Evaluating the Renewability of Geothermal Resources: The Case Study of the Euganean Geothermal System (NE Italy). Environ. Geochem. Health 2022, 44, 2135–2162. [Google Scholar] [CrossRef]
- Maitra, A.; Singh, A.; Keesari, T.; Sharma, S.P.; Gupta, S. Elevated Equilibrium Geotherm in Stable Continental Shield: Evidence From Integrated Structural, Hydrological, and Electromagnetic Studies on Nonvolcanic Hot Springs in the Eastern Ghats Belt, India. J. Geophys. Res. Solid Earth 2020, 125, e2019JB017747. [Google Scholar] [CrossRef]
- Fulignati, P.; Marianelli, P.; Sbrana, A.; Ciani, V. 3D Geothermal Modelling of the Mount Amiata Hydrothermal System in Italy. Energies 2014, 7, 7434–7453. [Google Scholar] [CrossRef] [Green Version]
- Torresan, F.; Piccinini, L.; Pola, M.; Zampieri, D.; Fabbri, P. 3D Hydrogeological Reconstruction of the Fault-Controlled Euganean Geothermal System (NE Italy). Eng. Geol. 2020, 274, 105740. [Google Scholar] [CrossRef]
- Faulds, J.E.; Hinz, N.H.; Dering, G.M.; Siler, D.L. The Hybrid Model—The Most Accommodating Structural Setting for Geothermal Power Generation in the Great Basin, Western USA. Trans.-Geotherm. Resour. Counc. 2013, 37, 3–10. [Google Scholar]
- Curewitz, D.; Karson, J.A. Structural Settings of Hydrothermal Outflow: Fracture Permeability Maintained by Fault Propagation and Interaction. J. Volcanol. Geotherm. Res. 1997, 79, 149–168. [Google Scholar] [CrossRef]
- Cacace, M.; Blöcher, G.; Watanabe, N.; Moeck, I.; Börsing, N.; Scheck-Wenderoth, M.; Kolditz, O.; Huenges, E. Modelling of Fractured Carbonate Reservoirs: Outline of a Novel Technique via a Case Study from the Molasse Basin, Southern Bavaria, Germany. Environ. Earth Sci. 2013, 70, 3585–3602. [Google Scholar] [CrossRef]
- Pola, M.; Gandin, A.; Tuccimei, P.; Soligo, M.; Deiana, R.; Fabbri, P.; Zampieri, D. A Multidisciplinary Approach to Understanding Carbonate Deposition under Tectonically Controlled Hydrothermal Circulation: A Case Study from a Recent Travertine Mound in the Euganean Hydrothermal System, Northern Italy. Sedimentology 2014, 61, 172–199. [Google Scholar] [CrossRef]
- Faulkner, D.R.; Jackson, C.A.L.; Lunn, R.J.; Schlische, R.W.; Shipton, Z.K.; Wibberley, C.A.J.; Withjack, M.O. A Review of Recent Developments Concerning the Structure, Mechanics and Fluid Flow Properties of Fault Zones. J. Struct. Geol. 2010, 32, 1557–1575. [Google Scholar] [CrossRef]
- Caine, J.S.; Evans, J.P.; Forster, C.B. Fault Zone Architecture and Permeability Structure. Geology 1996, 24, 1025–1028. [Google Scholar] [CrossRef]
- Bense, V.F.; Gleeson, T.; Loveless, S.E.; Bour, O.; Scibek, J. Fault Zone Hydrogeology. Earth-Sci. Rev. 2013, 127, 171–192. [Google Scholar] [CrossRef]
- Bruhn, D.; Manzella, A.; Vuataz, F.; Faulds, J.; Moeck, I.; Erbas, K. Exploration Methods. In Geothermal Energy Systems; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2010; pp. 37–112. ISBN 9783527408313. [Google Scholar]
- Singh, A.; Sharma, S.P. Identification of Different Geologic Units Using Fuzzy Constrained Resistivity Tomography. J. Appl. Geophys. 2018, 148, 127–138. [Google Scholar] [CrossRef]
- Chandra, P.C. Groundwater Geophysics in Hard Rock; CRC Press: Boca Raton, FL, USA, 2015; ISBN 9780429062605. [Google Scholar]
- Yáñez, G.; Perez-Estay, N.; Araya-Vargas, J.; Sanhueza, J.; Figueroa, R.; Maringue, J.; Rojas, T. Shallow Anatomy of the San Ramón Fault (Chile) Constrained by Geophysical Methods: Implications for Its Role in the Andean Deformation. Tectonics 2020, 39, 2020TC006294. [Google Scholar] [CrossRef]
- Lévy, L.; Maurya, P.K.; Byrdina, S.; Vandemeulebrouck, J.; Sigmundsson, F.; Árnason, K.; Ricci, T.; Deldicque, D.; Roger, M.; Gibert, B.; et al. Electrical Resistivity Tomography and Time-Domain Induced Polarization Field Investigations of Geothermal Areas at Krafla, Iceland: Comparison to Borehole and Laboratory Frequency-Domain Electrical Observations. Geophys. J. Int. 2019, 218, 1469–1489. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Estay, N.; Molina-Piernas, E.; Roquer, T.; Aravena, D.; Araya Vargas, J.; Morata, D.; Arancibia, G.; Valdenegro, P.; García, K.; Elizalde, D. Shallow Anatomy of Hydrothermal Systems Controlled by the Liquiñe-Ofqui Fault System and the Andean Transverse Faults: Geophysical Imaging of Fluid Pathways and Practical Implications for Geothermal Exploration. Geothermics 2022, 104, 102435. [Google Scholar] [CrossRef]
- Richards, K.; Revil, A.; Jardani, A.; Henderson, F.; Batzle, M.; Haas, A. Pattern of Shallow Ground Water Flow at Mount Princeton Hot Springs, Colorado, Using Geoelectrical Methods. J. Volcanol. Geotherm. Res. 2010, 198, 217–232. [Google Scholar] [CrossRef]
- Di Napoli, R.; Martorana, R.; Orsi, G.; Aiuppa, A.; Camarda, M.; De Gregorio, S.; Gagliano Candela, E.; Luzio, D.; Messina, N.; Pecoraino, G.; et al. The Structure of a Hydrothermal System from an Integrated Geochemical, Geophysical, and Geological Approach: The Ischia Island Case Study. Geochem. Geophys. Geosyst. 2011, 12, Q07017. [Google Scholar] [CrossRef]
- Mandal, A.; Basantaray, A.K.; Chandroth, A.; Mishra, U. Integrated Geophysical Investigation to Map Shallow Surface Alteration/Fracture Zones of Atri and Tarabalo Hot Springs, Odisha, India. Geothermics 2019, 77, 24–33. [Google Scholar] [CrossRef]
- Chalikakis, K.; Plagnes, V.; Guerin, R.; Valois, R.; Bosch, F.P. Contribution of Geophysical Methods to Karst-System Exploration: An Overview. Hydrogeol. J. 2011, 19, 1169–1180. [Google Scholar] [CrossRef]
- Molli, G.; Doveri, M.; Manzella, A.; Bonini, L.; Botti, F.; Menichini, M.; Montanari, D.; Trumpy, E.; Ungari, A.; Vaselli, L. Surface-Subsurface Structural Architecture and Groundwater Flow of the Equi Terme Hydrothermal Area, Northern Tuscany Italy. Ital. J. Geosci. 2015, 134, 442–457. [Google Scholar] [CrossRef]
- Rolia, E.; Sutjiningsih, D. Application of Geoelectric Method for Groundwater Exploration from Surface (A Literature Study). AIP Conf. Proc. 2018, 1977, 020018. [Google Scholar]
- Sikah, J.N.; Aning, A.A.; Danuor, S.K.; Manu, E.; Okrah, C. Groundwater Exploration Using 1D and 2D Electrical Resistivity Methods. J. Environ. Earth Sci. 2016, 6, 55–63. [Google Scholar]
- Briški, M.; Stroj, A.; Kosović, I.; Borović, S. Characterization of Aquifers in Metamorphic Rocks by Combined Use of Electrical Resistivity Tomography and Monitoring of Spring Hydrodynamics. Geosciences 2020, 10, 137. [Google Scholar] [CrossRef] [Green Version]
- Mishra, U.; Mohapatra, A.K.; Mandal, A.; Singh, A. Identification of Potential Artificial Groundwater Recharge Sites in an Alluvial Setting: A Coupled Electrical Resistivity Tomography and Sediment Characterization Study. Groundw. Sustain. Dev. 2023, 20, 100875. [Google Scholar] [CrossRef]
- Pradhan, R.M.; Singh, A.; Ojha, A.K.; Biswal, T.K. Structural Controls on Bedrock Weathering in Crystalline Basement Terranes and Its Implications on Groundwater Resources. Sci. Rep. 2022, 12, 11815. [Google Scholar] [CrossRef]
- Reynolds, J.M. An Introduction to Applied and Environmental Geophysics; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Yamanaka, H.; Takemura, M.; Ishida, H.; Niwa, M. Characteristics of Long-Period Microtremors and Their Applicability in Exploration of Deep Sedimentary Layers. Bull.-Seismol. Soc. Am. 1994, 84, 1831–1841. [Google Scholar] [CrossRef]
- Mele, M.; Bersezio, R.; Bini, A.; Bruno, M.; Giudici, M.; Tantardini, D. Subsurface Profiling of Buried Valleys in Central Alps (Northern Italy) Using HVSR Single-Station Passive Seismic. J. Appl. Geophys. 2021, 193, 104407. [Google Scholar] [CrossRef]
- EskIşar, T.; Özyalin, Ş.; Kuruoǧlu, M.; Yilmaz, H.R. Microtremor Measurements in the Northern Coast of İzmir Bay, Turkey to Evaluate Site-Specific Characteristics and Fundamental Periods by H/V Spectral Ratio Method. J. Earth Syst. Sci. 2013, 122, 123–136. [Google Scholar] [CrossRef]
- Giustini, F.; Brilli, M.; Carlucci, G.; Ciotoli, G.; Gaudiosi, I.; Mancini, M.; Simionato, M. Geophysical and Geochemical Multi-Method Investigations for Reconstructing Subsurfaces, Alluvial Sedimentology, and Structural Geology (Tiber Valley, Rome). Int. J. Earth Sci. 2023, 112, 197–216. [Google Scholar] [CrossRef]
- Agostini, L.; Boaga, J.; Galgaro, A.; Ninfo, A. HVSR Technique in Near-Surface Thermal-Basin Characterization: The Example of the Caldiero District (North-East Italy). Environ. Earth Sci. 2015, 74, 1199–1210. [Google Scholar] [CrossRef]
- Borović, S.; Marković, I. Utilization and Tourism Valorisation of Geothermal Waters in Croatia. Renew. Sustain. Energy Rev. 2015, 44, 52–63. [Google Scholar] [CrossRef]
- Marković, T.; Borović, S.; Larva, O. Geochemical Characteristics of Thermal Waters of Hrvatsko Zagorje. Geol. Croat. 2015, 68, 67–77. [Google Scholar] [CrossRef]
- Horváth, F.; Musitz, B.; Balázs, A.; Végh, A.; Uhrin, A.; Nádor, A.; Koroknai, B.; Pap, N.; Tóth, T.; Wórum, G. Evolution of the Pannonian Basin and Its Geothermal Resources. Geothermics 2015, 53, 328–352. [Google Scholar] [CrossRef]
- Mraz, V. Izvještaj o Hidrogeološkim Istražnim Radovima Na Području Daruvarskih Toplica II. Faza (Report on Conducted Hydrogeological Research in Daruvar Spa—Phase II); Geološki zavod Zagreb: Zagreb, Croatia, 1983. [Google Scholar]
- Borović, S.; Pola, M.; Bačani, A.; Urumović, K. Constraining the Recharge Area of a Hydrothermal System in Fractured Carbonates by Numerical Modelling. Geothermics 2019, 82, 128–149. [Google Scholar] [CrossRef]
- Šimunić, A. Geotermalne i Mineralne Vode Republike Hrvatske; Hrvatski Geološki Institut: Zagreb, Croatia, 2008; ISBN 978-953-6907-14. [Google Scholar]
- Jamičić, D.; Vragović, M.; Matičec, D. Osnovna Geološka Karta SFRJ 1:100,000. Tumač Za List Daruvar (Basic Geological Map of SFRJ 1:100,000. Explanatory Notes for Sheet Daruvar); Savezni geološki zavod Beograd; Geološki zavod Zagreb: Beograd, Serbia, 1989. [Google Scholar]
- Prelogović, E.; Saftić, B.; Kuk, V.; Velić, J.; Dragaš, M.; Lučić, D. Tectonic Activity in the Croatian Part of the Pannonian Basin. Tectonophysics 1998, 297, 283–293. [Google Scholar] [CrossRef]
- Saftić, B.; Velić, J.; Sztanó, O.; Juhász, G.; Ivković, Ž. Tertiary Subsurface Facies, Source Rocks and Hydrocarbon Reservoirs in the SW Part of the Pannonian Basin (Northern Croatia and South-Western Hungary). Geol. Croat. 2003, 56, 101–122. [Google Scholar] [CrossRef]
- Tomljenović, B.; Csontos, L. Neogene-Quaternary Structures in the Border Zone between Alps, Dinarides and Pannonian Basin (Hrvatsko Zgorje and Karlovac Basins, Croatia). Int. J. Earth Sci. 2001, 90, 560–578. [Google Scholar] [CrossRef]
- Lučić, D.; Saftić, B.; Krizmanić, K.; Prelogović, E.; Britvić, V.; Mesić, I.; Tadej, J. The Neogene Evolution and Hydrocarbon Potential of the Pannonian Basin in Croatia. Mar. Pet. Geol. 2001, 18, 133–147. [Google Scholar] [CrossRef]
- Handy, M.R.; Ustaszewski, K.; Kissling, E. Reconstructing the Alps–Carpathians–Dinarides as a Key to Understanding Switches in Subduction Polarity, Slab Gaps and Surface Motion. Int. J. Earth Sci. 2015, 104, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Jamičić, D. The Role of Sinistral Strike-Slip Faults in the Formation of the Structural Fabric of the Slavonian Mts. (Eastern Croatia). Geol. Croat. 1995, 48, 155–160. [Google Scholar]
- Babić, Ž.; Šikić, V.; Mraz, V. Hidrogeološka Istraživanja Termomineralnih Vrela Kupališnog Lječilišta Daruvar (Hydrogeological Research of Thermomineral Springs at Daruvar Spa); Institut za Geološka Istraživanja Zagreb: Zagreb, Croatia, 1971. [Google Scholar]
- Borović, S. Integrirani Hidrogeološko—Hidrogeokemijski Model Daruvarskog Geotermalnog Vodonosnika. Integrated Hydrogeological-Hydrogeochemical Model of Daruvar Geothermal Aquifer. Ph.D. Thesis, University of Zagreb, Zagreb, Croatia, 2015. [Google Scholar]
- KARST, d.o.o. Pivovara Daruvar—Izrada Istražne Bušotine Uz Spremnik Za Mazut (Pivovara Daruvar—Construction of an Exploratory Well next to a Tank); KARST d.o.o.: Zagreb, Croatia, 2021. [Google Scholar]
- Ratkaj, I.; Kinjerovac, Z. Završno Izvješće Vodoistražni Radovi Na Prodručiu Daruvara—Izrada Istražne Bušotine Dar-1 (Final Report on the Hydrogeological Investigations in the Area of Daruvar—Construction of the Exploration Well Dar-1); CROSCO, Naftni servisi d.o.o.: Zagreb, Croatia, 2009. [Google Scholar]
- Brlek, M.; Iveša, L.; Brčić, V.; Santos, A.; Ćorić, S.; Milošević, M.; Avanić, R.; Devescovi, M.; Pezelj, Đ.; Mišur, I.; et al. Rocky-Shore Unconformities Marking the Base of Badenian (Middle Miocene) Transgressions on Mt. Medvednica Basement (North Croatian Basin, Central Paratethys). Facies 2018, 64, 25. [Google Scholar] [CrossRef]
- Urumović, K.; Terzić, J.; Kopić, J.; Kosović, I. Identification of Aquifer and Pumped Well Parameters Using the Data Hidden in Non-Linear Losses. Sustainability 2023, 15, 11170. [Google Scholar] [CrossRef]
- Loke, M.H.; Chambers, J.E.; Rucker, D.F.; Kuras, O.; Wilkinson, P.B. Recent Developments in the Direct-Current Geoelectrical Imaging Method. J. Appl. Geophys. 2013, 95, 135–156. [Google Scholar] [CrossRef]
- Yoshino, T. Electrical Properties of Rocks. In Encyclopedia of Solid Earth Geophysics; Gupta, H.K., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 339–344. ISBN 978-3-030-58631-7. [Google Scholar]
- Fikos, I.; Vargemezis, G.; Zlotnicki, J.; Puertollano, J.R.; Alanis, P.B.; Pigtain, R.C.; Villacorte, E.U.; Malipot, G.A.; Sasai, Y. Electrical Resistivity Tomography Study of Taal Volcano Hydrothermal System, Philippines. Bull. Volcanol. 2012, 74, 1821–1831. [Google Scholar] [CrossRef]
- Chabaane, A.; Redhaounia, B.; Gabtni, H. Combined Application of Vertical Electrical Sounding and 2D Electrical Resistivity Imaging for Geothermal Groundwater Characterization: Hammam Sayala Hot Spring Case Study (NW Tunisia). J. Afr. Earth Sci. 2017, 134, 292–298. [Google Scholar] [CrossRef]
- Pavić, M.; Kosović, I.; Pola, M.; Urumović, K.; Briški, M.; Borović, S. Multidisciplinary Research of Thermal Springs Area in Topusko (Croatia). Sustainability 2023, 15, 5498. [Google Scholar] [CrossRef]
- Hermawan, O.R.; Eka Putra, D.P. The Effectiveness of Wenner-Schlumberger and Dipole-Dipole Array of 2D Geoelectrical Survey to Detect The Occurring of Groundwater in the Gunung Kidul Karst Aquifer System, Yogyakarta, Indonesia. J. Appl. Geol. 2016, 1, 71. [Google Scholar] [CrossRef] [Green Version]
- Zhou, B.; Dahlin, T. Properties and Effects of Measurement Errors on 2D Resistivity Imaging Surveying. Near Surf. Geophys. 2003, 1, 105–117. [Google Scholar] [CrossRef] [Green Version]
- Loke, M.H.; Barker, R.D. Rapid Least-Squares Inversion of Apparent Resistivity Pseudosections by a Quasi-Newton Method. Geophys. Prospect. 1996, 44, 131–152. [Google Scholar] [CrossRef]
- Seaton, W.J.; Burbey, T.J. Evaluation of Two-Dimensional Resistivity Methods in a Fractured Crystalline-Rock Terrane. J. Appl. Geophys. 2002, 51, 21–41. [Google Scholar] [CrossRef]
- Loke, M.H.; Petersen, K.D. Rapid 2-D Resistivity & IP Inversion Using the Least-Squares Method (Res2DInv Manual); Seequent 2023, Ed.; Seequent: Arhus, Denmark, 2023. [Google Scholar]
- Loke, M.H.; Acworth, I.; Dahlin, T. A Comparison of Smooth and Blocky Inversion Methods in 2D Electrical Imaging Surveys. Explor. Geophys. 2003, 34, 182–187. [Google Scholar] [CrossRef] [Green Version]
- Galgaro, A.; Boaga, J.; Rocca, M. HVSR Technique as Tool for Thermal-Basin Characterization: A Field Example in N-E Italy. Environ. Earth Sci. 2014, 71, 4433–4446. [Google Scholar] [CrossRef]
- Mitjanas, G.; Ledo, J.; Macau, A.; Alías, G.; Queralt, P.; Bellmunt, F.; Rivero, L.; Gabàs, A.; Marcuello, A.; Benjumea, B.; et al. Integrated Seismic Ambient Noise, Magnetotellurics and Gravity Data for the 2D Interpretation of the Vallès Basin Structure in the Geothermal System of La Garriga-Samalús (NE Spain). Geothermics 2021, 93, 102067. [Google Scholar] [CrossRef]
- Cheng, F.; Xia, J.; Ajo-Franklin, J.B.; Behm, M.; Zhou, C.; Dai, T.; Xi, C.; Pang, J.; Zhou, C. High-Resolution Ambient Noise Imaging of Geothermal Reservoir Using 3C Dense Seismic Nodal Array and Ultra-Short Observation. J. Geophys. Res. Solid Earth 2021, 126, e2021JB021827. [Google Scholar] [CrossRef]
- Nakamura, Y. What Is the Nakamura Method? Seismol. Res. Lett. 2019, 90, 1437–1443. [Google Scholar] [CrossRef]
- Park, C.B.; Miller, R.D.; Xia, J. Multichannel Analysis of Surface Waves. Geophysics 1999, 64, 800–808. [Google Scholar] [CrossRef] [Green Version]
- Xia, J.; Miller, R.D.; Park, C.B. Estimation of Near-Surface Shear-Wave Velocity by Inversion of Rayleigh Waves. Geophysics 1999, 64, 691–700. [Google Scholar] [CrossRef] [Green Version]
- Konno, K.; Ohmachi, T. Ground-Motion Characteristics Estimated from Spectral Ratio between Horizontal and Vertical Components of Microtremor. Bull. Seismol. Soc. Am. 1998, 88, 228–241. [Google Scholar] [CrossRef]
- Yue, W.Z.; Tao, G. A New Non-Archie Model for Pore Structure: Numerical Experiments Using Digital Rock Models. Geophys. J. Int. 2013, 195, 282–291. [Google Scholar] [CrossRef] [Green Version]
- Glover, P.W.J. A Generalized Archie’s Law for n Phases. Geophysics 2010, 75, E247–E265. [Google Scholar] [CrossRef] [Green Version]
- Glover, P.W.J. Archie’s Law—A Reappraisal. Solid Earth 2016, 7, 1157–1169. [Google Scholar] [CrossRef] [Green Version]
- Asquith, G.; Krygowski, D.; Henderson, S.; Hurley, N. Basic Relationships of Well Log Interpretation. In Basic Well Log Analysis; American Association of Petroleum Geologists: Tulsa, OK, USA, 2019; pp. 1–20. [Google Scholar] [CrossRef]
- Hamada, G.M.; Almajed, A.A.; Okasha, T.M.; Algathe, A.A. Uncertainty Analysis of Archie’s Parameters Determination Techniques in Carbonate Reservoirs. J. Pet. Explor. Prod. Technol. 2013, 3, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Fetter, C.W. Applied Hydrogeology; Waveland Press: Long Grove, IL, USA, 2018. [Google Scholar]

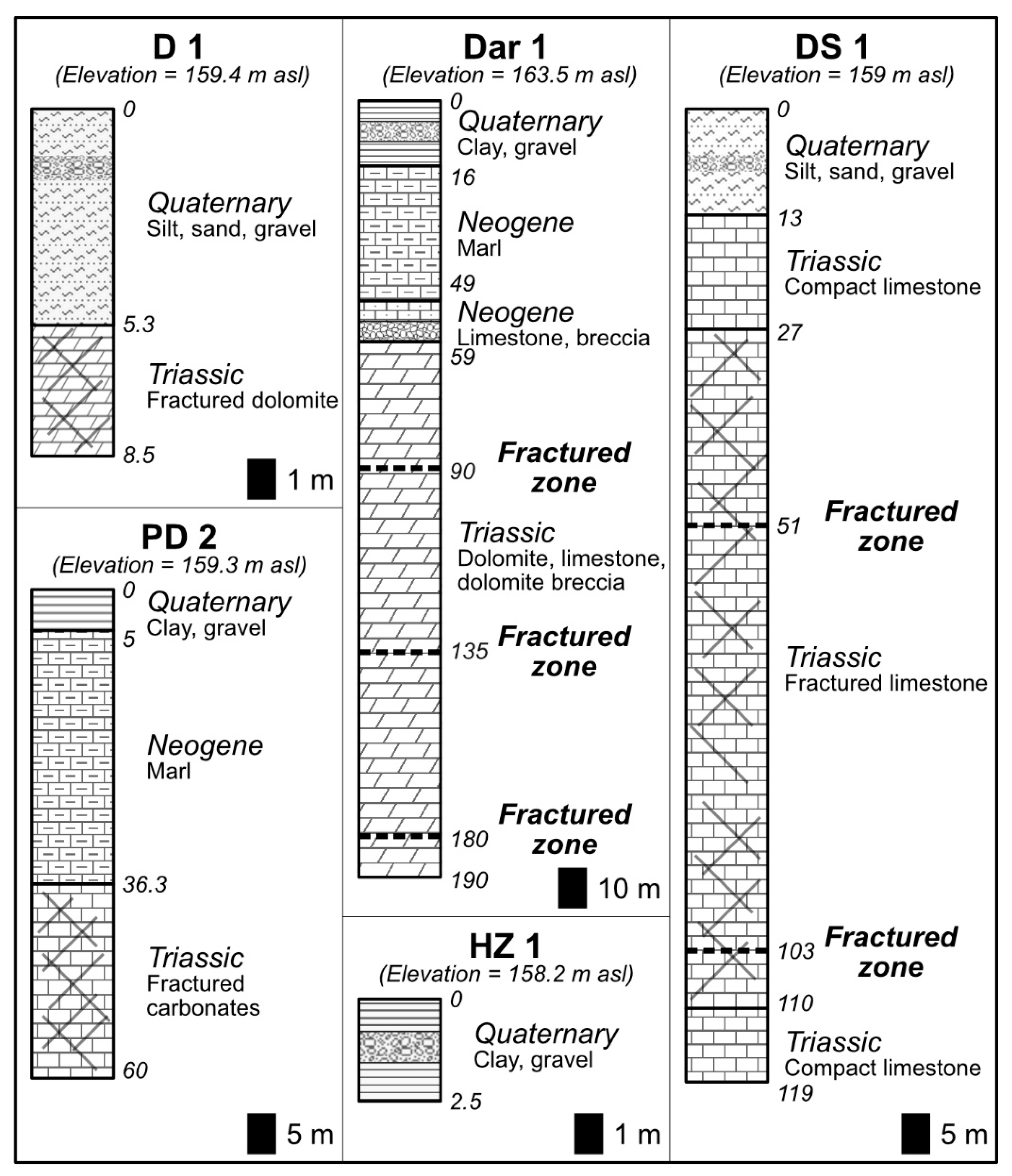


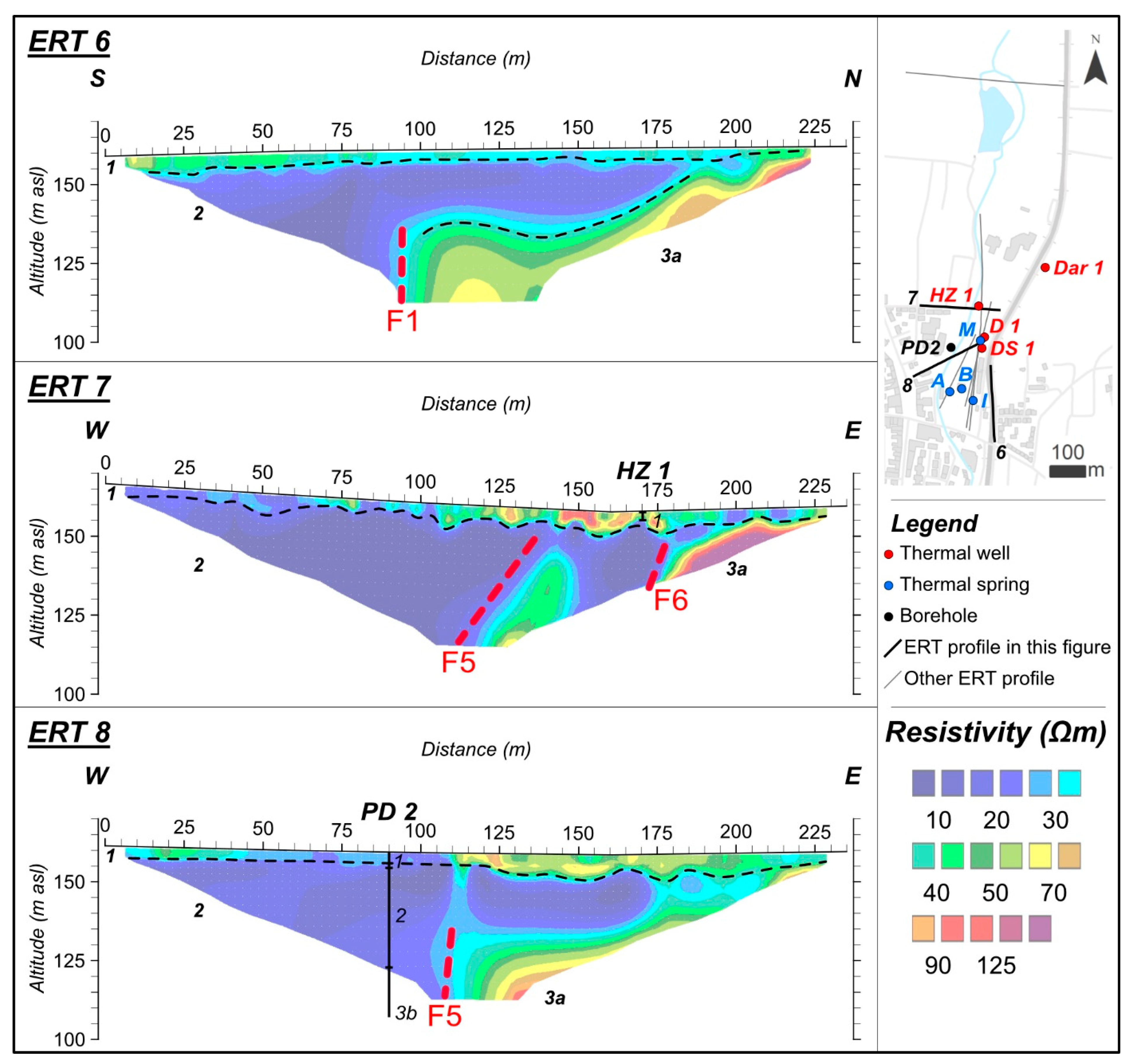
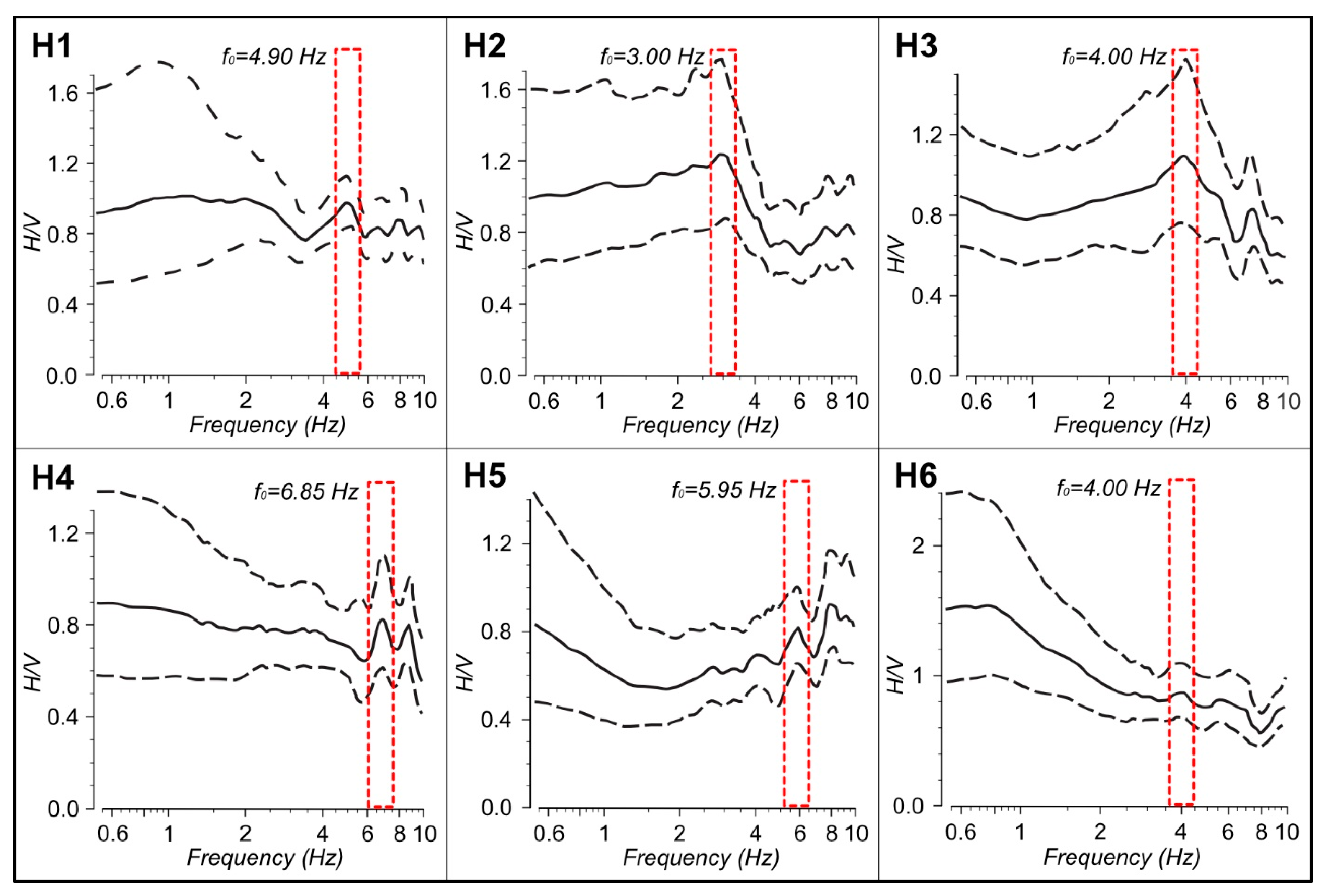

| Profile | Coordinates | Azimuth | Number of Electrodes | Electrode Distance | Length of Profile | |
|---|---|---|---|---|---|---|
| Beginning | End | (°N) | (m) | (m) | ||
| ERT 1 | 17°13′33.7″ E; 45°35′32.86″ N | 17°13′35.4″ E; 45°35′53.2″ N | 3 | 64 | 10 | 630 |
| ERT 2 | 17°13′46.78″ E; 45°36′5.14″ N | 17°13′25.6″ E; 45°36′6.53″ N | 275 | 48 | 10 | 470 |
| ERT 3 | 17°13′33.14″ E; 45°35′35.14″ N | 17°13′36.78″ E; 45°35′44.96″ N | 14 | 48 | 5 | 235 |
| ERT 4 | 17°13′33.3″ E; 45°35′33.14″ N | 17°13′35.01″ E; 45°35′40.67″ N | 9 | 48 | 5 | 235 |
| ERT 5 | 17°13′29.74″ E; 45°35′34.98″ N | 17°13′34.67″ E; 45°35′41.89″ N | 26 | 64 | 5 | 315 |
| ERT 6 | 17°13′37.05″ E; 45°35′31.77″ N | 17°13′36.61″ E; 45°35′39.02″ N | 357 | 48 | 5 | 235 |
| ERT 7 | 17°13′27.18″ E; 45°35′44.67″ N | 17°13′38″ E; 45°35′44.16″ N | 93 | 48 | 5 | 235 |
| ERT 8 | 17°13′26.23″ E; 45°35′37.99″ N | 17°13′35.96″ E; 45°35′41.36″ N | 63 | 48 | 5 | 235 |
| HVSR/MASW | Coordinates | |
|---|---|---|
| E | N | |
| H1 | 17°13′31.40″ | 45°35′35.06″ |
| H2 | 17°13′33.06″ | 45°35′37.42″ |
| H3 | 17°13′35.37″ | 45°35′40.33″ |
| H4 | 17°13′37.46″ | 45°35′44.42″ |
| H5 | 17°13′41.38″ | 45°35′53.77″ |
| H6 | 17°13′44.83″ | 45°35′48.19″ |
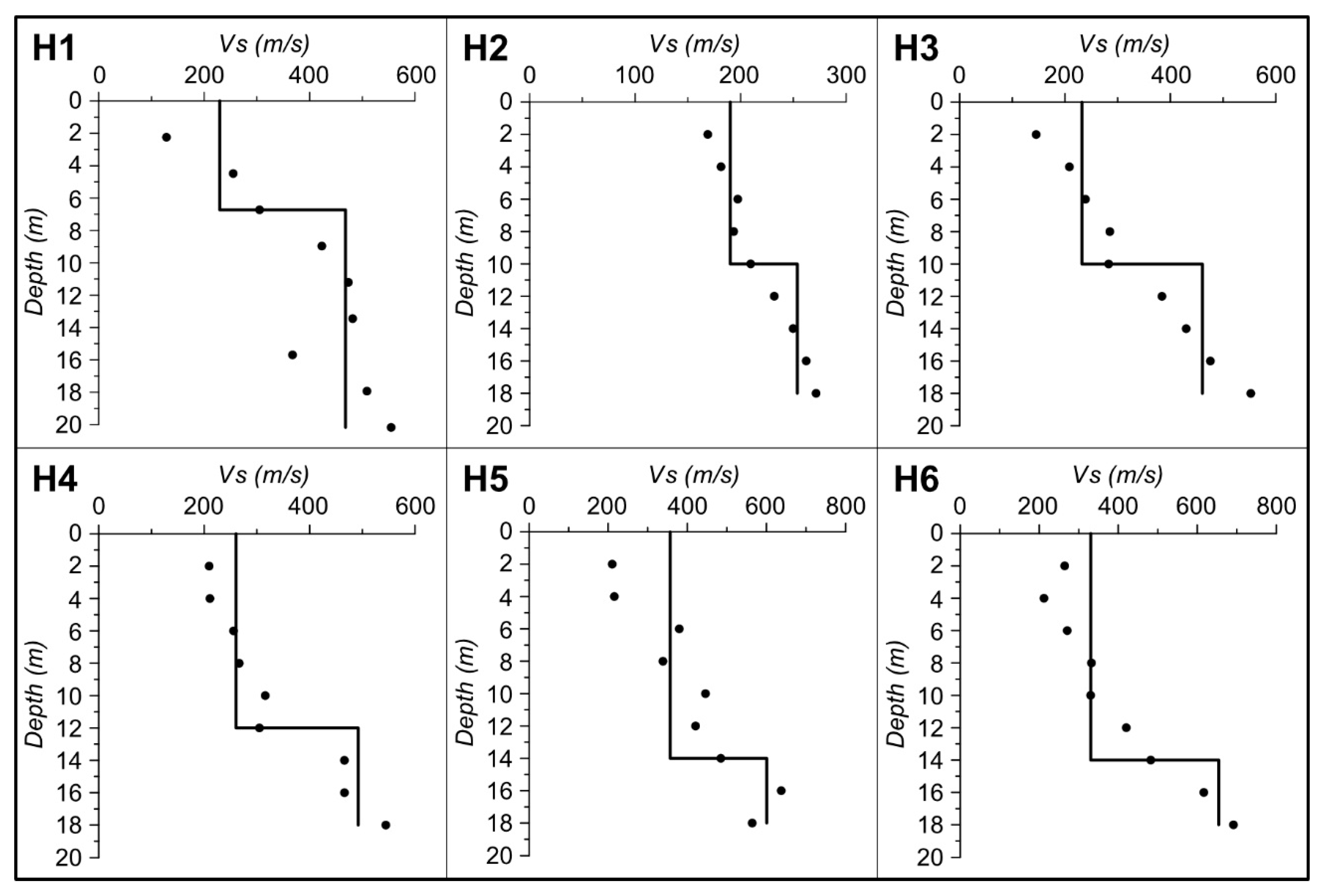
| f0 | Vs | h | |
|---|---|---|---|
| (Hz) | (m/s) | (m) | |
| H1 | 4.90 | 229.5 | 11.71 |
| H2 | 3.00 | 190.14 | 15.85 |
| H3 | 4.00 | 232.06 | 14.5 |
| H4 | 6.85 | 260.52 | 9.51 |
| H5 | 5.95 | 356.49 | 14.98 |
| H6 | 4.00 | 330.3 | 20.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kosović, I.; Briški, M.; Pavić, M.; Padovan, B.; Pavičić, I.; Matoš, B.; Pola, M.; Borović, S. Reconstruction of Fault Architecture in the Natural Thermal Spring Area of Daruvar Hydrothermal System Using Surface Geophysical Investigations (Croatia). Sustainability 2023, 15, 12134. https://doi.org/10.3390/su151612134
Kosović I, Briški M, Pavić M, Padovan B, Pavičić I, Matoš B, Pola M, Borović S. Reconstruction of Fault Architecture in the Natural Thermal Spring Area of Daruvar Hydrothermal System Using Surface Geophysical Investigations (Croatia). Sustainability. 2023; 15(16):12134. https://doi.org/10.3390/su151612134
Chicago/Turabian StyleKosović, Ivan, Maja Briški, Mirja Pavić, Božo Padovan, Ivica Pavičić, Bojan Matoš, Marco Pola, and Staša Borović. 2023. "Reconstruction of Fault Architecture in the Natural Thermal Spring Area of Daruvar Hydrothermal System Using Surface Geophysical Investigations (Croatia)" Sustainability 15, no. 16: 12134. https://doi.org/10.3390/su151612134
APA StyleKosović, I., Briški, M., Pavić, M., Padovan, B., Pavičić, I., Matoš, B., Pola, M., & Borović, S. (2023). Reconstruction of Fault Architecture in the Natural Thermal Spring Area of Daruvar Hydrothermal System Using Surface Geophysical Investigations (Croatia). Sustainability, 15(16), 12134. https://doi.org/10.3390/su151612134






