Abstract
As particulate organic carbon (POC) from lakes plays an important role in lake ecosystem sustainability and carbon cycle, the estimation of its concentration using satellite remote sensing is of great interest. However, the high complexity and variability of lake water composition pose major challenges to the estimation algorithm of POC concentration in Class II water. This study aimed to formulate a machine-learning algorithm to predict POC concentration and compare their modeling performance. A Convolutional Neural Network–Long Short-Term Memory (CNN–LSTM) algorithm based on spectral and time sequences was proposed to construct an estimation model using the Sentinel 2 satellite images and water surface sample data of Chaohu Lake in China. As a comparison, the performances of the Backpropagation Neural Network (BP), Generalized Regression Neural Network (GRNN), and Convolutional Neural Network (CNN) models were evaluated for remote sensing inversion of POC concentration. The results show that the CNN–LSTM model obtained higher prediction precision than the BP, GRNN, and CNN models, with a coefficient of determination (R2) of 0.88, a root mean square error (RMSE) of 3.66, and residual prediction deviation (RPD) of 3.03, which are 6.02%, 22.13%, and 28.4% better than the CNN model, respectively. This indicates that CNN–LSTM effectively combines spatial and temporal information, quickly captures time-series features, strengthens the learning ability of multi-scale features, is conducive to improving estimation precision of remote sensing models, and offers good support for carbon source monitoring and assessment in lakes.
1. Introduction
Particulate organic carbon (POC) in lake water is a category of carbon that is unable to be dissolved in water but is instead suspended in the water column as an organic particulate matter [1]. This involves phytoplankton, zooplankton cells, and the associated non-living debris, terrestrial organic particulate matter, etc. POC, a crucial component of the carbon cycle in lakes, regulates the behavior of dissolved organic carbon, colloidal organic carbon, and dissolved inorganic carbon in the water column and is closely linked to biological life processes and primary productivity [2]. It additionally performs a crucial role in the substance transformation and energy flow of ecosystems. In recent years, studies of lake eutrophication have shown that terrestrial inputs are an important source of organic carbon in lakes and rivers. The organic carbon, about 37% is mineralized as CO2 and CH4, 16% is input to the oceans by riverine transport and atmospheric deposition, and the remaining 47% is buried in sediments [3,4]. To understand the movement and transformation of particulate carbon and investigate control strategies for lake eutrophication, it is crucial to investigate the geographical and temporal properties of POC quantities in water bodies.
Satellite remote sensing monitoring of POC concentration distribution in surface water can provide an effective method for quantifying the long-term trend of POC in lakes, which can support lake biogeochemical cycle and ecosystem research. Due to the selective absorption and scattering of POC in visible and near-infrared bands, the increase in the concentration of POC will lead to a decrease in the propagation distance of light and an increase in the decay rate, and the intensity of light is closely related to the concentration and physical properties of particulate matter [5]. At the same time, the different proportions of organic particles and inorganic particles in the particles have different absorption and reflection characteristics for different wavelengths of light [6]. Therefore, the visible light and near-infrared reflection spectra of water can reflect the inherent optical properties of particulate organic carbon, including the scattering, absorption, and reflection characteristics among different particles. By analyzing the characteristic sensitive bands of particulate organic carbon, many scholars extracted different characteristic information to invert POC content, such as the blue-green band ratio [7], Maximum Normalized Difference Carbon Index (MNDCI) [8], Three-band combination based on the bio-optical model [9], POC-source color index [10], etc. Meanwhile, they have found that POC has a close correlation with other water quality parameters, such as Chl-a [11], suspended particulate matter (SPM) [12], turbidity [13], etc. The models built using these features often have the characteristics of high accuracy, wide mobility, and specificity to the study region, and promote the application of remote sensing and spectroscopy in the quantitative analysis of POC in the ocean [14].
However, influenced by exogenous river input, surface runoff, and human activities in inland lake water, the changes in the concentration and composition of water components have resulted in the high complexity and diversity of water optics [15]. We only rely on a single sensitive feature band or bio-optical characteristics, whether empirical, semi-analytical, or analytical methods, which are difficult to have good adaptability in complex aquatic environments [16]. In recent years, with the rapid development of artificial intelligence technology, many scholars have used machine-learning algorithms and trained many data to try to find out the characteristic signals of POC in visible and near-infrared spectra to predict the concentrations of different forms of carbon in water bodies [17,18,19]. Machine-learning models have powerful feature learning capabilities, can automatically learn complex spatial and spectral features from satellite remote sensing data, and effectively capture nonlinear relationships through multi-level data transformation and feature extraction, thus improving the performance of classification and identification, which has become a hot spot in the research of remote sensing inversion of water quality parameters, such as partial least squares regression (PLSR) [20], artificial neural networks (ANN) [21], support vector machines (SVM) [22], and convolutional neural network (CNN) [23], which have good performance in predicting the concentration of POC in water.
These machine-learning algorithms provide beneficial exploration for predicting the concentration of POC in water bodies. However, the machine-learning models are subject to the effects of the particular environmental conditions in the lakes because they lack physical mechanical qualities [24]. In the estimation of POC, relevant feature vectors need to be extracted, but in lakes, the complexity of water bodies may make it difficult to fully mine the key information of these features. Traditional spectral and spatial information is often faced with the difficulty of insufficient information and difficult to capture features [25]. As a result, it is necessary to further assess the potential of various machine-learning algorithms for lake waters. With the continuous development of machine learning, especially deep learning, we have added time-dimensional information to the deep learning algorithm, captured the time-dependent relationship signal of lake water in time series from the perspective of space–time multi-dimensionality, and integrated time-series features to model [26]. This method has been studied in the field of water color remote sensing, but in complex lake water, the estimation of POC concentration by this method has rarely been reported. CNN–LSTM is a hybrid model combining CNN and LSTM. LSTM network can effectively process time-series data and capture time-series features. Combined with the efficient extraction ability of spatial and spectral features of the CNN model, the hybrid model can learn and extract multi-dimensional scale feature information [27], which is conducive to improving the inversion precision of POC concentration.
In the present study, we used Sentinel 2 satellite imagery and water sample data to evaluate the performance of machine-learning algorithms in predicting POC concentrations in lake water. The main objectives of the study are: (i) to formulate a machine-learning algorithm including time dimension to evaluate the predicted precision of POC concentration in lake water; (ii) to evaluate the performance of satellite remote sensing based on improved algorithms in mapping the spatial distribution and quantitative estimating the long-term trend of POC in lakes.
2. Materials and Methods
2.1. Study Area
As one of the five major freshwater lakes in China, Chaohu Lake is situated in the southern portion of Hefei City in central Anhui Province, near the middle and lower reaches of the Yangtze River. The lake is a shallow, artificially controlled body of water with an overall “long and narrow” shape and is 55 km long from east to west, 21 km wide from north to south, 176 km surrounding its perimeter, an average depth of 2.89 m, a storage capacity of 20.7 × 108 m3 and an area of 780 square kilometers. Nine major rivers enter and exit the lake, with the Hangbu River having the greatest input, with approximately 60% of the total water entering the lake, and most of the lake’s water flows into the Yangtze River through the Yuxi River in the east. The overall management of Chaohu Lake has risen recently, and the lake’s ecosystem and water quality have both significantly improved. However, the endogenous lake has an elevated level of nutrients, the water is still eutrophic, and there are occasional outbreaks of cyanobacterial blooms [25]. As a result, synthetic management and scientific control strategies need to be strengthened. Figure 1 shows the study area and the locations of the sampling sites.
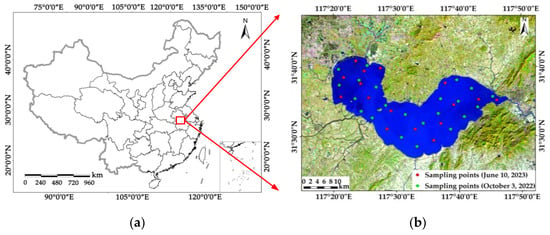
Figure 1.
(a) Location of study area; (b) Sampling points of Chaohu Lake.
2.2. Data Acquisition and Pre-Processing
2.2.1. Water Sampling and Laboratory Analysis
A total of 38 water samples were taken in the lake as part of the field water sample collection on 3 October 2022 and 10 June 2023. A water sampler was used to collect water samples from 30 cm to 50 cm below the water’s surface during the sampling procedure. The obtained water samples were stored in 500 mL sampling vials, each one bearing a unique number, and kept at a temperature between 2 and 4 °C. Then they were tested to determine the mass concentration of POC. The water samples were filtered with GF/F, and the filtered samples were subsequently cauterized for four hours at 450 °C in a muffle furnace. To eliminate inorganic carbon, the samples were subsequently acidified in strong hydrochloric acid for 12 h. After being acidified, the samples were dried for 24 h at 60 °C in an oven before being weighed and packaged. The POC concentration at each location was then estimated after the percentage carbon content of the sample was determined by an elemental analyzer (EA3000) [28,29]. The statistical description of the POC concentration of the water samples is shown in Table 1.

Table 1.
Statistical characteristics of the POC concentration of the water samples.
2.2.2. Remote Sensing Data
Remote sensing data were obtained from current Sentinel-2A MSI images from the European Space Agency (https://scihub.copernicus.eu (accessed on 20 June 2023)), which were acquired on 3 October 2022 and 10 June 2023, respectively. The inversion of POC concentration is based on the data from 3 October 2023. The image files are at the L2A level and have been pre-processed by radiometric calibration and atmospheric correction. In this study, all bands of the images were resampled to a spatial resolution of 10 m using the SNAP 7.0 software officially recommended by the European Space Agency and were imported into the ENVI 5.3 software for mosaic and cropping. Finally, ArcGIS 10.6 software was used to extract the multi-band remote sensing reflectance of 38 sample points on two different date images.
2.2.3. Data Pre-Processing
The sensitive band was chosen following the correlation coefficient by examining the correlation between the single-band reflectance, the combination of band reflectance, and the POC concentration of the sample locations. Then, to determine which waveband combination had the strongest connection with POC concentration, the wavebands with the highest POC correlation were ultimately selected and merged. The correlation coefficient is expressed as.
where R is the correlation coefficient and and are the mean values of the variables x and y, respectively [30].
Finally, a matrix with a sample matrix of 38 × 10 is obtained. Among them, 38 is the number of sample points, and 10 is the number of wavebands and waveband combinations.
The resulting band reflectance is normalized, which is beneficial to reduce the influence of environmental factors on spectral reflectance and avoid the noise generated by spectral reflectance by other interference factors. The calculation formula is as follows:
In Equation (2), X is the band reflectance, Xmin is the minimum band reflectance, Xmax is the maximum band reflectance, and Y is the normalized band reflectance [31].
2.3. Methods
2.3.1. Backpropagation Neural Network (BP)
BP is a commonly used artificial neural network model, mainly for solving classification and regression problems. It consists of three layers: input, hidden, and output layers, each of which consists of multiple neuron nodes. By creating weighted connections between nodes, the network may transfer signals and compute outcomes [32].
The training process of the BP neural network is based on a backpropagation algorithm. The network is initially supplied with input samples, and then forward propagation is used to generate the outputs. After that, a distinction between the output and the true value is determined, and the difference is given back to the hidden and input layers through backpropagation layer by layer to reduce the error. This procedure is repeated until the error converges or a preset training target is attained. Through iterative optimization, it has been determined that the number of layers in the BP neural network is 6, and the number of neurons in the fully connected layer is 100 [33].
2.3.2. Generalized Regression Neural Network (GRNN)
GRNN is a modification of Radial Basis Function Neural Network (RBF) with a four-layer neural network structure, usually divided into an input layer, a pattern layer, a summation layer, and an output layer. GRNN can build generalized regression neural networks with radial basis neurons and linear neurons, which are suitable for function approximation. Radial basis functions and competing neurons can build probabilistic neural networks, which are commonly used in nonlinear regression methods and have a wide range of applications in problems such as prediction and classification [34].
The output layer’s function is to transfer the input sample data directly to the pattern layer, and its number of neurons is equal to the number of dimensions of the input samples. A Gaussian function is utilized as the activation function in the mode layer, which has the same amounts of neurons as the input layer. Equation (2) is used to determine the transfer function for each neuron i. Equations (3) and (4) describe the two different types of neurons in the summation layer, respectively. Equation (5) is used to calculate the number of neurons in the output layer, which is equal to the output vector’s dimensionality for the sample data [35]. As GRNN only needs to adjust a single parameter, the optimal value can be determined through simple experimentation and adjustment. In this case, the value of SPREAD is set to 0.50.
where Xi in Equation (2) is the input sample data corresponding to neuron i (where i is 1, 2, …, n). is a smoothing parameter, and the choice of is closely related to the accuracy of the model, when is set small tends to 0, the model prediction value is close to the training sample value, resulting in poor generalization ability of the model; when is set larger, the predicted value is close to the mean of all samples; Yi in Equations (3) and (4) is the i-th sample predicted value. Y in Equation (5) is the output variable with maximum probability [36].
2.3.3. Convolutional Neural Network (CNN)
A Convolutional Neural Network is a feed-forward neural network that consists of an input layer, a convolutional layer, a pooling layer, a fully connected layer, and an output layer. CNN processes data with a grid structure through convolutional operations, extracting local features and using pooling layers to reduce the feature dimensionality. The main advantage is the sharing of weights, which can reduce the number of parameters, simplify the model, and reduce the computational burden [37].
The main difference between CNN and traditional neural networks is the convolutional and pooling layers. The convolutional layer effectively extracts the data features by convolving all the input information. The pooling layer compresses the input features to simplify the computational complexity of the network. This feature extractor, consisting of a convolutional layer and a pooling layer, maximizes the potential information of the input values and reduces the bias that can be introduced by human extraction of the data. For low-dimensional data, one-dimensional convolution is often used, and its output for sequence feature extraction is:
where Y is the extracted feature; is the sigmoid activation function; W is the weight matrix; X is the time series; and b is the bias vector [38].
2.3.4. Convolutional Neural Network–Long Short-Term Memory (CNN–LSTM)
Long Short-Term Memory (LSTM) is a temporal recurrent neural network specifically designed to solve the long-term dependency problem that exists in Recurrent Neural Networks (RNN). All RNNs consist of repeating neural network modules that form a chain structure. LSTM networks are an improvement on RNNs by introducing a gate structure that includes forgetting gates, input gates, and output gates. The forgetting gate determines which information in the cellular memory cell needs to be forgotten, the input gate determines which new information needs to be added to the cellular memory cell, and the output gate determines how the information in the cellular memory cell is passed on to the next step. The LSTM network model can be trained by a temporal backpropagation algorithm to the LSTM network as a means of determining the relevant parameters of the LSTM [39].
The cellular memory unit in the LSTM network gives it good memory capability and is widely used in fields such as time-series prediction. Its specific formula is:
where Wf, Wi, Wc, Wo are the weight matrices; bf, bi, bc, bo are the corresponding bias vectors; tanh is the hyperbolic tangent function; is the dot product; ht−1 is the output at the previous moment; ft is the retained degree value; Ct−1 is the memory state at the previous moment; it is the added degree value of the state at the current moment; is the intermediate state; Ct is the current state; ot is the output degree value; ht is the output at the current moment; xt is the input at the current moment [27].
Figure 2 depicts the CNN–LSTM structure, which combines CNN and LSTM to create a new network structure. Data exceptions like data noise and jumps are removed through processing and optimization of the incoming data. From the time-series data of the unit operation-related parameters, CNN is utilized to extract features. The CNN algorithm is used to extract the relationships between the data in the parameters, reduce noise, and make the sequence features of each parameter more obvious, to obtain the data sequence features of the parameters related to the unit operation. The LSTM network is then used to extract the time-series features of the reconstructed data, and the regularization method is added after the LSTM network to lessen the overfitting phenomenon. To complete the prediction, inverse normalization is applied to the LSTM network’s output data [40].
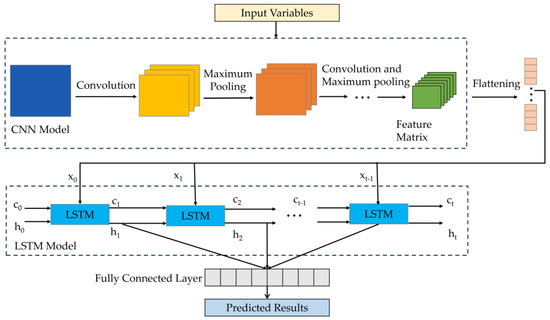
Figure 2.
CNN–LSTM network structure.
In deep learning models such as CNN and LSTM, some hyperparameters need to be set for model training. Among them, the number of epochs represents the number of iterations of learning the entire training dataset, and the batch size represents the number of samples used in each training iteration. Due to the possibility of neural networks overfitting, we introduce dropout and early stopping strategies and choose the Adam algorithm to optimize the learning rate. Regarding activation functions, we adopt the ReLU function [26]. In this study, the main model structure consists of a ten-dimensional input, one-dimensional output, three convolutional layers, and two long LSTM layers. The convolutional layers perform deep feature extraction using a kernel size of 3 × 1 and a “Same” padding strategy. The pooling layers then perform sampling on the data from the convolutional layers using a kernel size of 2 × 1 and a “Same” padding strategy. The Flatten layer transforms all the features into a one-dimensional form. For the CNN, we set the number of epochs to 800, mini-batch size to 16, dropout rate to 0.3, and learning rate to 0.001.
2.4. Model Evaluation
The model is assessed by the coefficient of determination (R2), root mean squared error (RMSE), and residual prediction deviation (RPD) metrics. R2 serves as the primary indicator of the degree of correlation between various variables; the higher the correlation coefficient, the more significant the correlation. A measurement of the mean error in the data is the RMSE. The RMSE is capable of demonstrating how variable the data are, and the lower it is, the more accurate the model’s forecast is. A statistical metric called RPD is used to evaluate the effectiveness of models for quantitative analysis. When RPD ≤ 1.5, the model results are poor, and accurate values cannot be obtained; when 1.5 < RPD < 2 the model is considered moderately effective and when RPD ≥ 2 the model has excellent predictive power [41].
where is the predicted value of the i-th sample, yi is the measured value of the i-th sample, is the mean value, n is the total number of samples and SD is the standard deviation.
2.5. Modeling
Using Sentinel-2A remote sensing images and water surface sample point data, four machine-learning models were applied to a remote sensing inversion model of the POC concentration in Chaohu Lake. For modeling, the waveband reflectance datasets and water surface data of 38 sample points were used as input datasets, and the datasets were randomly divided into training datasets and test datasets, of which the training datasets were 26 groups and the test datasets were 12 groups, as shown in Table 2. The range of POC content in the training set included the range of the validation set, which ensured the applicability of the established models to the validation set. The best prediction model for POC concentration was selected and comparatively analyzed by revealing the effect of different feature variations on the accuracy of the four models. The POC concentration prediction process is shown in Figure 3.

Table 2.
Descriptive statistics of sample sets.
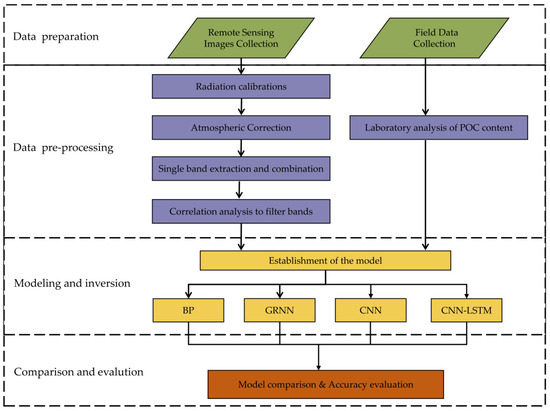
Figure 3.
Flow chart for POC concentration prediction.
3. Results and Discussion
3.1. Relevant Analysis
In the remote sensing inversion of water quality parameters, the magnitude of Pearson’s correlation coefficient is usually used as an evaluation index. The optimal band is selected from the different combination forms of remote sensing image bands for modeling, and the correlation coefficients are calculated for the different band combination forms. Band1, Band5, Band6, Band7, Band8, Band9, and Band11 of Sentinel-2A images are selected and the image spectra of sampling points are collected for further analysis. The correlation coefficient matrix between single-band reflectance and POC concentration is given in Figure 4, labeling the areas of higher correlation coefficients between band combinations and POC concentration. It can be seen that the single bands are positively correlated with the POC concentration and have a good correlation, with Band 6 having the highest correlation with the POC concentration (0.626). After conducting band combination and correlation coefficient analysis, we can use the exhaustive method to select the best band combination and perform operations such as summing, differencing, ratioing, and ratio combination (ri + rj)/(ri − rj) on the spectral values of Sentinel-2A imagery. Here, ri and rj represent the reflectance of the i-th and j-th bands (i ≠ j) [42]. It shows that there is a high correlation among the variables when different bands are combined, with correlation coefficients ranging from −0.500 to 0.677. Sensitivity analysis helps us identify variables that have a significant impact on the model’s output, enabling us to recognize the key variables that affect the model’s performance. Multiple experimental results have shown that the model based on sensitive spectral variables and POC concentration, as shown in Table 3, has an R2 of 0.60 to 0.90. The sensitive spectral variables used for modeling include B5, B6, B7, B8, B9, B9/B1, B9/B11, B11-B9, *B1, and *B2. This involved a total of ten band combinations participating in the BP, GRNN, and CNN–LSTM algorithms to construct a remote sensing prediction model for POC in Lake Chaohu.
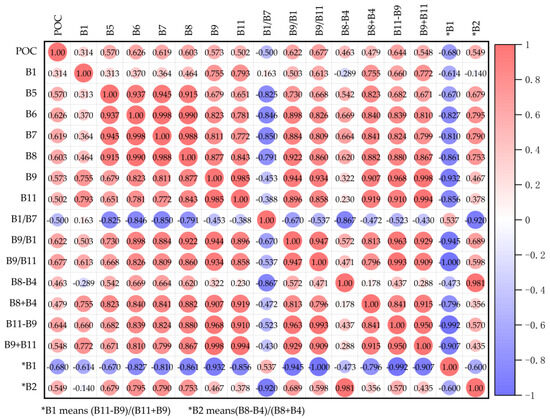
Figure 4.
Pearson-based correlation analysis between MSI bands and POC.

Table 3.
Precision Analysis of different POC models.
3.2. Model Analysis of POC Prediction
From Table 3 and Figure 5, the prediction results of the four models of BP, GRNN, CNN, and CNN–LSTM were compared, and CNN–LSTM has a good predictive value in predicting POC concentrations. By comparing the training set and validation set, the BP model performs the worst in terms of performance indicators, with a weaker ability to fit the data and a lower degree of agreement between predicted results and measured values. The R2 values are 0.76 and 0.61, the RMSE values are 6.17 and 7.38, and the RPD values are 2.09 and 1.50, respectively. The GRNN model has shown some improvements in performance indicators on both the training set and validation set, with R2 values of 0.82 and 0.75, RMSE values of 5.70 and 5.57, and RPD values of 2.26 and 1.99, respectively. Compared to them, the CNN model has significantly improved predictive indicators, performing well on both the training set and validation set, with R2 values of 0.87 and 0.83, RMSE values of 4.84 and 4.70, and RPD values of 2.67 and 2.36, respectively. Finally, the CNN–LSTM model, as the optimization of the CNN, has the best prediction effect with R2, RMSE, and RPD of 0.88, 3.66, and 3.03, respectively, with 6.02% and 28.4% improvement in R2 and RPD over the CNN, and 22.13% decrease in RMSE.
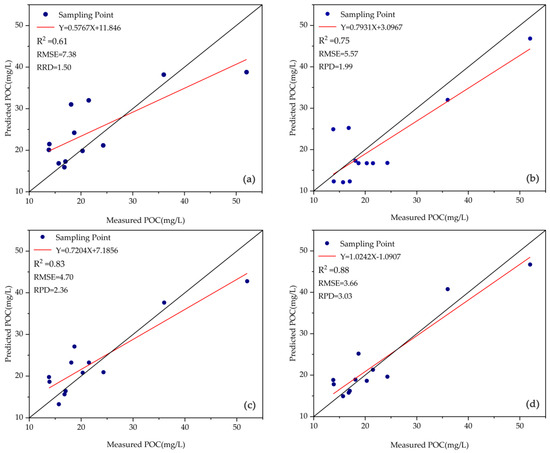
Figure 5.
Predictions from four different models: (a) BP, (b) GRNN, (c) CNN, (d) CNN–LSTM. The measured and predicted values are represented as POC concentrations and model predictions, respectively. The black line indicates a 1:1 relationship and the red line indicates the trend of the model.
3.3. Inversion Results and Analysis
For the four models, the distribution of POC concentrations was calculated in the research region, respectively. As shown in Figure 6, the CNN–LSTM inversion results show that the mean POC concentration in the lake area is 22.88 mg/L, with a standard deviation of 10.19 mg/L, a maximum of 49.2 mg/L, and a minimum of 20.81 mg/L. This is consistent with the trend of the mean concentration of 22.34 mg/L, a standard deviation of 11.09 mg/L at the sample points. POC concentration is lower in the lake’s eastern and central regions and higher in the western section of the lake, demonstrating a trend of spreading from west to east. In addition, because of shipping and human activities near the islands in the lake, the POC concentration is higher near the shipping line extending to the islands.
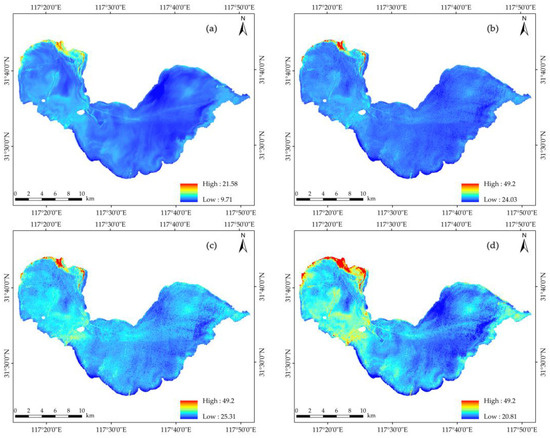
Figure 6.
Prediction of inversion results of different models (a) BP, (b) GRNN, (c) CNN, (d) CNN–LSTM.
The main reasons for the spatial distribution of POC may be a mix of factors including water quality, plant development, bottom sediment, and pollutant input, according to the lake’s spatial distribution of POC concentration. In some regions of the western shore, due to the high terrain, large lake runoff, plentiful aquatic plant and herbaceous plants along the coast, high concentration of pollution particles, and organic carbon being stirred and transported, facilitating the transmission and diffusion of pollutants, these result in high POC content in some areas of the west bank. In the center and the eastern half of the lake, the water quality is higher, and the water flow is less erratic, which favors the deposition of organic carbon and has a lower POC content. Along the coastal area around the lake and some of the lake inlet areas, several rivers converge into the lake, including the Nanfei River, Fifteen Mile River, Pai River, Shuangqiao River, and Yuxi River. Due to the influence of rivers and lakes, the intake of organic matter from land-based sources has increased the input and output of pollutants, resulting in high POC content.
4. Discussion
CNN–LSTM is a high-performance spatiotemporal deep learning model with strong feature extraction and model expression capabilities. However, establishing a POC concentration inversion model with high applicability and predictive accuracy remains challenging in complex lake water bodies. In this study, we used the CNN–LSTM model to investigate the performance of POC concentration inversion based on Sentinel-2 multispectral satellite data.
Through a comparison of four models, we found that the CNN–LSTM model outperformed the BP, GRNN, and CNN models in estimating POC concentration in lakes. The R2 and RPD values of the CNN–LSTM model increased by 44.26% and 102.0% compared to those of the BP model, 17.33% and 52.26% than those of the GRNN model, and 6.02% and 28.39% than these of the CNN model. Moreover, the RMSE values decreased by 50.41%, 34.29%, and 22.13%, respectively for the BP, GRNN, and CNN models. CNN–LSTM uses time-series modeling to learn and extract multi-scale features in the spatiotemporal dimension, effectively capturing nonlinear relationships in spatiotemporal data, which is the key to good prediction [43]. This is consistent with the findings of Baek [26] and Yang [44], indicating that the CNN–LSTM model demonstrates good performance in terms of inversion accuracy and model stability. It suggests that the CNN–LSTM model is feasible and has high accuracy for remote sensing modeling and prediction of POC concentration.
From the perspective of model prediction results, the BP model performs poorly in terms of accuracy and stability. It is sensitive to initial weights and tends to become stuck in local optima. The GRNN model, on the other hand, generally performs well. GRNN is a sample-based non-parametric regression algorithm that learns quickly, but it is not sensitive to original parameters and may not perform well with complex temporal data in large datasets. CNN can achieve good performance in predicting POC concentration, but convolution often searches for patterns from high-dimensional data, and the size of the kernel limits the search for spectral representation. Additionally, CNN requires a large training dataset and computational capabilities [37]. The CNN–LSTM model is a hybrid model that effectively reduces the number of training parameters. It can extract high-dimensional features and time-series features from data. Using activation functions, it can create a nonlinear mapping relationship between optimal characteristics and POC concentration, demonstrating strong generalization ability and effectively improving the accuracy and stability of POC prediction [27].
This study also validated the feasibility of CNN–LSTM on a small sample dataset. The results showed the predicted value of the model had an R2 value of 0.88, an RMSE value of 3.66, and an RPD value of 3.03. This has been confirmed by El Bilali [45] and Talukdar [46], who effectively improved the accuracy of model prediction using the Deep Dense Neural Network model with 20–60 small sample datasets. Their results showed high Nash Sutcliff-Efficiency values up to 0.91 and an R2 value of 0.98. The CNN–LSTM model uses a small sample dataset to achieve efficient feature extraction and time-series modeling in a short training time, avoiding high noise and excessive details in large datasets during training, and reducing overfitting risks. Additionally, the model can accurately and quickly capture spatiotemporal multi-scale features from limited data, make accurate feature discrimination, and improve the performance of the model in small sample environments [47].
There are also limitations in using small sample datasets. First, a small sample dataset may not fully cover the various complex water environments in lakes, making it difficult to learn the potential structures and features in the samples. This can limit the algorithm’s ability to generalize. The randomness and incompleteness exhibited by small sample datasets make the model more sensitive to slight variations in the input data, potentially affecting the stability of the model. Second, the spectral resolution of Sentinel-2 satellite multispectral data is limited, and a small number of band sequences may result in the loss of some spectral feature details. The accuracy and robustness of model predictions need further testing [48].
5. Conclusions
Taking Chaohu Lake as an example, the predictive performance of machine-learning algorithms is explored for estimating POC concentration using Sentinel-2A satellite and measurement data from water samples. A CNN–LSTM model is presented for estimating the POC concentration of Class II water in lakes by comparing BP, GRNN, and CNN. A thematic map of the spatial distribution of POC concentration is presented through model prediction. The following are the primary conclusions:
- (1)
- The BP, GRNN, and CNN models for POC in Class II water have good prediction ability, with R2 above 0.6, RSME 3.66~7.38 mg/L, in which the CNN model has better performance with R2 0.83, RSME 4.7 mg/L, and RPD 2.36, indicating that CNN has strong feature learning and nonlinear modeling ability, and can better simulate the spatial characteristics of POC in complex water bodies.
- (2)
- When time dimension information is incorporated into the CNN model, CNN–LSTM uses a gating mechanism with higher memory and generalization capabilities and has good prediction ability, stability, and robustness with R2 0.88, RMSE 3.66 mg/L, and RPD 3.03, which is 6.02% and 28.4% higher than CNN’s R2 and RPD, and 22.13% lower than RMSE. This is in a good performance range, indicating that the CNN–LSTM model can better predict the temporal and spatial characteristics of POC in lake water.
- (3)
- According to Sentinel 2 satellite inversion results, the average POC concentration was 22.88 mg/L, with a standard deviation of 10.19 mg/L in Chaohu Lake. POC concentrations were significantly greater in the western region of the lake and lower in the lake’s central and eastern regions, indicating a spreading situation from west to east.
As can be seen, the CNN–LSTM model for POC remote sensing assessment of Class II lake water can be used as a reference method for the quick acquisition of POC data on the lake water surface. This will significantly provide real-time data support for the dynamic management of the ecological environment in the lake basin. However, the prediction of POC concentration in water usually requires many continuous and complete time-series data. A small sample dataset may lead to insufficient training of the model [49]. As spectral and time-series dimensional information increases and the sample dataset continues to expand, the predictive performance of the model needs further testing in the future. Meanwhile, the POC concentration in water may be affected by multiple environmental factors, such as surface environment variables, water flow speed, meteorological conditions, etc. These factors may result in features not being fully captured, and the adaptability of the model to the new environmental variables needs to be further evaluated [50].
Author Contributions
Conceptualization and writing original draft preparation: B.P. and H.Y.; methodology, supervision, project administration, funding acquisition, B.P. and F.X.; field test: S.C. and M.Z.; data analysis: J.D., H.Y. and H.C.; writing—review and editing supported by B.P. and S.D. All authors have read and agreed to the published version of the manuscript.
Funding
The author gratefully acknowledges the financial support from National Natural Science Foundation of China (42277075), Anhui Natural Science Research Foundation (2208085US14, 1708085MD90), Anhui University Collaborative Innovation Fund (GXXT-2019-047), Natural Science Foundation of colleges and universities in Anhui Province (KJ2020JD07, KJ2020JD09).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Matsuoka, A.; Babin, M.; Vonk, J.E. Decadal trends in the release of terrigenous organic carbon to the Mackenzie Delta (Canadian Arctic) using satellite ocean color data (1998–2019). Remote Sens. Environ. 2022, 283, 113322. [Google Scholar] [CrossRef]
- Yan, R.; Feng, J.; Wang, Y.; Fu, L.; Luo, X.; Niu, L.; Yang, Q. Distribution, Sources, and Biogeochemistry of Carbon Pools (DIC, DOC, and POC) in the Mangrove-Fringed Zhangjiang Estuary, China. Front. Mar. Sci. 2022, 9, 909839. [Google Scholar] [CrossRef]
- Liu, D.; Tian, L.; Jiang, X.; Wu, H.; Yu, S. Human activities changed organic carbon transport in Chinese rivers during 2004–2018. Water Res. 2022, 222, 118872. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.Q.; Yu, Q.; Feig, A.D.; Ye, C.; Blunden, A. Effects of climate and land-surface processes on terrestrial dissolved organic carbon export to major U.S. coastal rivers. Ecol. Eng. 2013, 54, 192–201. [Google Scholar] [CrossRef]
- Rouf, M.A.; Golder, M.R.; Sumana, Z.A. Satellite-based observation of particulate organic carbon in the northern Bay of Bengal. Environ. Adv. 2021, 6, 100124. [Google Scholar] [CrossRef]
- Kratzer, S.; Kyryliuk, D.; Brockmann, C. Inorganic suspended matter as an indicator of terrestrial influence in Baltic Sea coastal areas—Algorithm development and validation, and ecological relevance. Remote Sens. Environ. 2020, 237, 111609. [Google Scholar] [CrossRef]
- Hu, S.B.; Cao, W.X.; Wang, G.F.; Xu, Z.T.; Lin, J.F.; Zhao, W.J.; Yang, Y.Z.; Zhou, W.; Sun, Z.H.; Yao, L.J. Comparison of MERIS, MODIS, SeaWiFS-derived particulate organic carbon, and in situ measurements in the South China Sea. Int. J. Remote Sens. 2016, 37, 1585–1600. [Google Scholar] [CrossRef]
- Son, Y.B.; Gardner, W.D.; Mishonov, A.V.; Richardson, M.J. Multispectral remote-sensing algorithms for particulate organic carbon (POC): The Gulf of Mexico. Remote Sens. Environ. 2009, 113, 50–61. [Google Scholar] [CrossRef]
- Lin, J.; Lyu, H.; Miao, S.; Pan, Y.; Wu, Z.; Li, Y.; Wang, Q. A two-step approach to mapping particulate organic carbon (POC) in inland water using OLCI images. Ecol. Indic. 2018, 90, 502–512. [Google Scholar] [CrossRef]
- Xu, J.; Lei, S.; Bi, S.; Li, Y.; Lyu, H.; Xu, J.; Xu, X.; Mu, M.; Miao, S.; Zeng, S.; et al. Tracking spatio-temporal dynamics of POC sources in eutrophic lakes by remote sensing. Water Res. 2020, 168, 115162. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Stuart, V.; Nair, A.; Oka, K.; Nakane, T.; Bouman, H.; Forget, M.H.; Maass, H.; Platt, T. Carbon-to-chlorophyll ratio and growth rate of phytoplankton in the sea. Mar. Ecol. Prog. Ser. 2009, 383, 73–84. [Google Scholar] [CrossRef]
- Stramski, D.; Constantin, S.; Reynolds, R.A. Adaptive optical algorithms with differentiation of water bodies based on varying composition of suspended particulate matter: A case study for estimating the particulate organic carbon concentration in the western Arctic seas. Remote Sens. Environ. 2023, 286, 113360. [Google Scholar] [CrossRef]
- Zhao, Z.; Huang, C.; Meng, L.; Lu, L.; Wu, Y.; Fan, R.; Li, S.; Sui, Z.; Huang, T.; Huang, C.; et al. Eutrophication and lakes dynamic conditions control the endogenous and terrestrial POC observed by remote sensing: Modeling and application. Ecol. Indic. 2021, 129, 107907. [Google Scholar] [CrossRef]
- Scharnweber, K.; Vanni, M.J.; Hilt, S.; Syväranta, J.; Mehner, T. Boomerang ecosystem fluxes: Organic carbon inputs from land to lakes are returned to terrestrial food webs via aquatic insects. Oikos 2014, 123, 1439–1448. [Google Scholar] [CrossRef]
- Moser, K.A.; Baron, J.S.; Brahney, J.; Oleksy, I.A.; Saros, J.E.; Hundey, E.J.; Sadro, S.; Kopáček, J.; Sommaruga, R.; Kainz, M.J.; et al. Mountain lakes: Eyes on global environmental change. Glob. Planet. Chang. 2019, 178, 77–95. [Google Scholar] [CrossRef]
- Xu, J.; Li, Y.; Lyu, H.; Lei, S.; Mu, M.; Bi, S.; Xu, J.; Xu, X.; Miao, S.; Li, L.; et al. Simultaneous inversion of concentrations of POC and its endmembers in lakes: A novel remote sensing strategy. Sci. Total Environ. 2021, 770, 145249. [Google Scholar] [CrossRef]
- Sauzède, R.; Johnson, J.E.; Claustre, H.; Camps-Valls, G.; Ruescas, A.B. Estimation of Oceanic Particulate Organic Carbon with Machine Learning. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, V-2-2020, 949–956. [Google Scholar] [CrossRef]
- Sadaiappan, B.; Balakrishnan, P.; Vishal, C.R.; Vijayan, N.T.; Subramanian, M.; Gauns, M.U. Applications of Machine Learning in Chemical and Biological Oceanography. ACS Omega 2023, 8, 15831–15853. [Google Scholar] [CrossRef]
- Lee, T.R.; Wood, W.T.; Phrampus, B.J. A Machine Learning (KNN) Approach to Predicting Global Seafloor Total Organic Carbon. Glob. Biogeochem. Cycles 2019, 33, 37–46. [Google Scholar] [CrossRef]
- Toming, K.; Kotta, J.; Uuemaa, E.; Sobek, S.; Kutser, T.; Tranvik, L.J. Predicting lake dissolved organic carbon at a global scale. Sci. Rep. 2020, 10, 8471. [Google Scholar] [CrossRef]
- Liu, H.; Li, Q.; Bai, Y.; Yang, C.; Wang, J.; Zhou, Q.; Hu, S.; Shi, T.; Liao, X.; Wu, G. Improving satellite retrieval of oceanic particulate organic carbon concentrations using machine learning methods. Remote Sens. Environ. 2021, 256, 112316. [Google Scholar] [CrossRef]
- Sun, J.; Dang, W.; Wang, F.; Nie, H.; Wei, X.; Li, P.; Zhang, S.; Feng, Y.; Li, F. Prediction of TOC Content in Organic-Rich Shale Using Machine Learning Algorithms: Comparative Study of Random Forest, Support Vector Machine, and XGBoost. Energies 2023, 16, 4159. [Google Scholar] [CrossRef]
- Kim, J.; Jang, W.; Hwi Kim, J.; Lee, J.; Hwa Cho, K.; Lee, Y.-G.; Chon, K.; Park, S.; Pyo, J.; Park, Y.; et al. Application of airborne hyperspectral imagery to retrieve spatiotemporal CDOM distribution using machine learning in a reservoir. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103053. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, P.; Jamet, C.; Dionisi, D.; Hu, Y.; Lu, X.; Pan, D. Retrieving bbp and POC from CALIOP: A deep neural network approach. Remote Sens. Environ. 2023, 287, 113482. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, X.; Peng, Y.; Wang, H.; Wang, X.; Song, J.; Fei, G. Restoration of aquatic macrophytes with the seed bank is difficult in lakes with reservoir-like water-level fluctuations: A case study of Chaohu Lake in China. Sci. Total Environ. 2022, 813, 151860. [Google Scholar] [CrossRef] [PubMed]
- Baek, S.-S.; Pyo, J.; Chun, J.A. Prediction of Water Level and Water Quality Using a CNN-LSTM Combined Deep Learning Approach. Water 2020, 12, 3399. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, Y.; Huang, H.; Li, A.; Yang, L.; Zhou, C. A CNN-LSTM Model for Soil Organic Carbon Content Prediction with Long Time Series of MODIS-Based Phenological Variables. Remote Sens. 2022, 14, 4441. [Google Scholar] [CrossRef]
- Novak, M.G.; Cetinić, I.; Chaves, J.E.; Mannino, A. The adsorption of dissolved organic carbon onto glass fiber filters and its effect on the measurement of particulate organic carbon: A laboratory and modeling exercise. Limnol. Oceanogr. Methods 2018, 16, 356–366. [Google Scholar] [CrossRef]
- Liu, D.; Sun, Z.; Shen, M.; Tian, L.; Yu, S.; Jiang, X.; Duan, H. Three-dimensional observations of particulate organic carbon in shallow eutrophic lakes from space. Water Res. 2023, 229, 119519. [Google Scholar] [CrossRef]
- Makowski, D.; Ben-Shachar, M.; Patil, I.; Lüdecke, D. Methods and Algorithms for Correlation Analysis in R. J. Open Source Softw. 2020, 5, 2306. [Google Scholar] [CrossRef]
- Singh, D.; Singh, B. Investigating the impact of data normalization on classification performance. Appl. Soft Comput. 2020, 97, 105524. [Google Scholar] [CrossRef]
- Massimo Buscema, D. Back Propagation Neural Networks. Subst. Use Misuse 1998, 33, 233–270. [Google Scholar] [CrossRef] [PubMed]
- Sadrara, M.; Khorrami, M.K. Principal component analysis-multivariate adaptive regression splines (PCA-MARS) and back propagation-artificial neural network (BP-ANN) methods for predicting the efficiency of oxidative desulfurization systems using ATR-FTIR spectroscopy. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2023, 300, 122944. [Google Scholar] [CrossRef] [PubMed]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Ghritlahre, H.K.; Prasad, R.K. Exergetic performance prediction of solar air heater using MLP, GRNN and RBF models of artificial neural network technique. J. Environ. Manag. 2018, 223, 566–575. [Google Scholar] [CrossRef] [PubMed]
- Yue, H.; Bu, L. Prediction of CO2 emissions in China by generalized regression neural network optimized with fruit fly optimization algorithm. Environ. Sci. Pollut. Res. 2023, 30, 80676–80692. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.-C.; Roth, H.R.; Gao, M.; Lu, L.; Xu, Z.; Nogues, I.; Yao, J.; Mollura, D.; Summers, R.M. Deep Convolutional Neural Networks for Computer-Aided Detection: CNN Architectures, Dataset Characteristics and Transfer Learning. IEEE Trans. Med. Imaging 2016, 35, 1285–1298. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Smagulova, K.; James, A.P. A survey on LSTM memristive neural network architectures and applications. Eur. Phys. J. Spec. Top. 2019, 228, 2313–2324. [Google Scholar] [CrossRef]
- Zha, W.; Liu, Y.; Wan, Y.; Luo, R.; Li, D.; Yang, S.; Xu, Y. Forecasting monthly gas field production based on the CNN-LSTM model. Energy 2022, 260, 124889. [Google Scholar] [CrossRef]
- Ding, J.; Yang, A.; Wang, J.; Sagan, V.; Yu, D. Machine-learning-based quantitative estimation of soil organic carbon content by VIS/NIR spectroscopy. PeerJ 2018, 6, e5714. [Google Scholar] [CrossRef] [PubMed]
- Panda, P.K.; Panda, R.B.; Dash, P.K. The Study of Water Quality and Pearson’s Correlation Coefficients among Different Physico-chemical Parameters of River Salandi, Bhadrak, Odisha, India. Am. J. Water Resour. 2018, 6, 146–155. [Google Scholar]
- Bildirici, M.; Ersin, Ö. Forecasting volatility in oil prices with a class of nonlinear volatility models: Smooth transition RBF and MLP neural networks augmented GARCH approach. Pet. Sci. 2015, 12, 534–552. [Google Scholar] [CrossRef]
- Yang, H.; Du, Y.; Zhao, H.; Chen, F. Water Quality Chl-a Inversion Based on Spatio-Temporal Fusion and Convolutional Neural Network. Remote Sens. 2022, 14, 1267. [Google Scholar] [CrossRef]
- El Bilali, A.; Lamane, H.; Taleb, A.; Nafii, A. A framework based on multivariate distribution-based virtual sample generation and DNN for predicting water quality with small data. J. Clean. Prod. 2022, 368, 133227. [Google Scholar] [CrossRef]
- Talukdar, S.; Shahfahad; Ahmed, S.; Naikoo, M.W.; Rahman, A.; Mallik, S.; Ningthoujam, S.; Bera, S.; Ramana, G.V. Predicting lake water quality index with sensitivity-uncertainty analysis using deep learning algorithms. J. Clean. Prod. 2023, 406, 136885. [Google Scholar] [CrossRef]
- Mori, M.; Gonzalez Flores, R.; Suzuki, Y.; Nukazawa, K.; Hiraoka, T.; Nonaka, H. Prediction of Microcystis Occurrences and Analysis Using Machine Learning in High-Dimension, Low-Sample-Size and Imbalanced Water Quality Data. Harmful Algae 2022, 117, 102273. [Google Scholar] [CrossRef]
- Niu, C.; Tan, K.; Jia, X.; Wang, X. Deep learning based regression for optically inactive inland water quality parameter estimation using airborne hyperspectral imagery. Environ. Pollut. 2021, 286, 117534. [Google Scholar] [CrossRef]
- Shang, W.; Jin, S.; He, Y.; Zhang, Y.; Li, J. Spatial–Temporal Variations of Total Nitrogen and Phosphorus in Poyang, Dongting and Taihu Lakes from Landsat-8 Data. Water 2021, 13, 1704. [Google Scholar] [CrossRef]
- Bildirici, M.; Ersin, Ö. Markov-switching vector autoregressive neural networks and sensitivity analysis of environment, economic growth and petrol prices. Environ. Sci. Pollut. Res. 2018, 25, 31630–31655. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).