Optimal Design and Mean Stress Estimation of Modular Metamaterials Inspired by Burr Puzzles
Abstract
:1. Introduction
2. Models and Methods
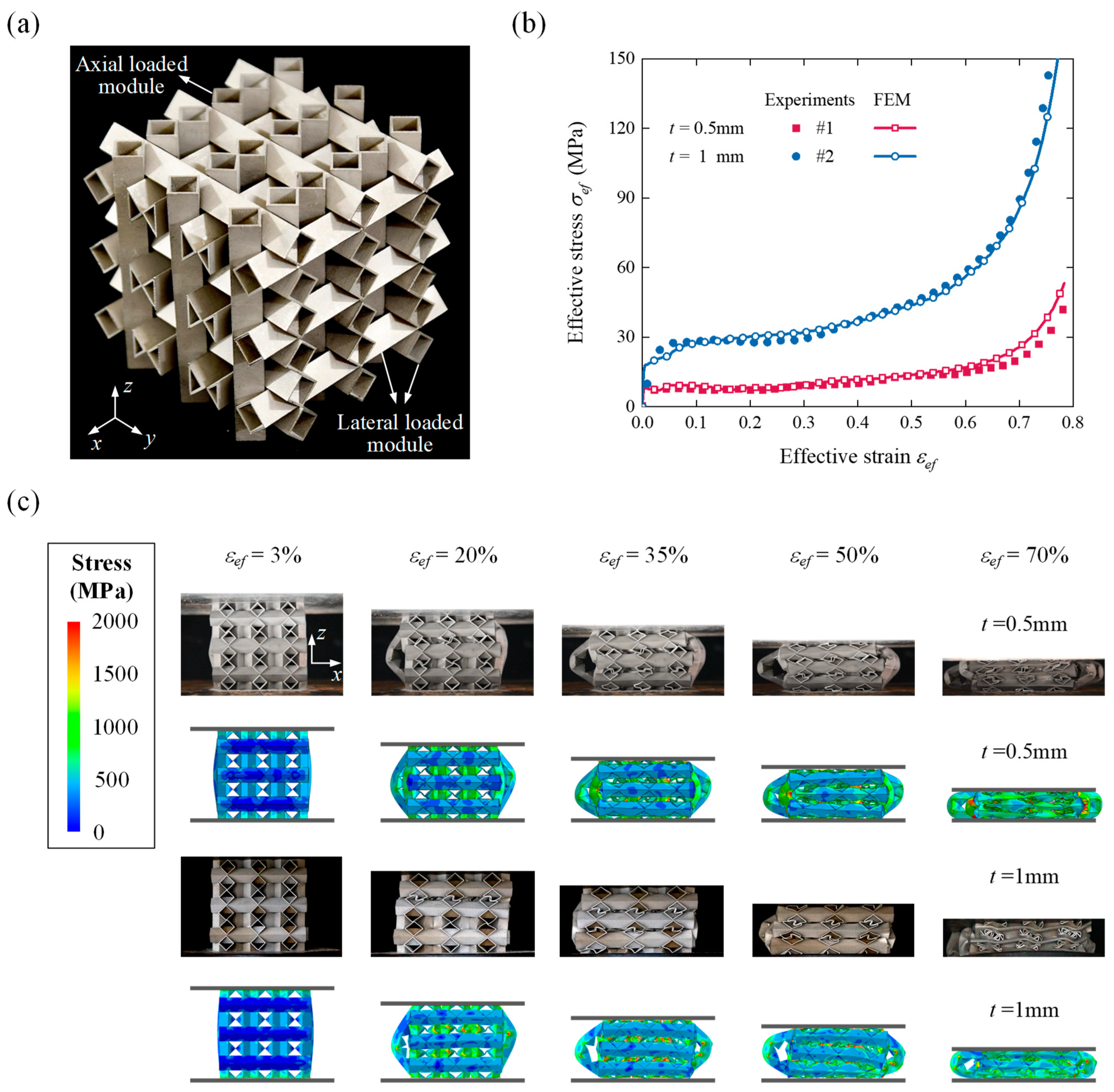
2.1. Models
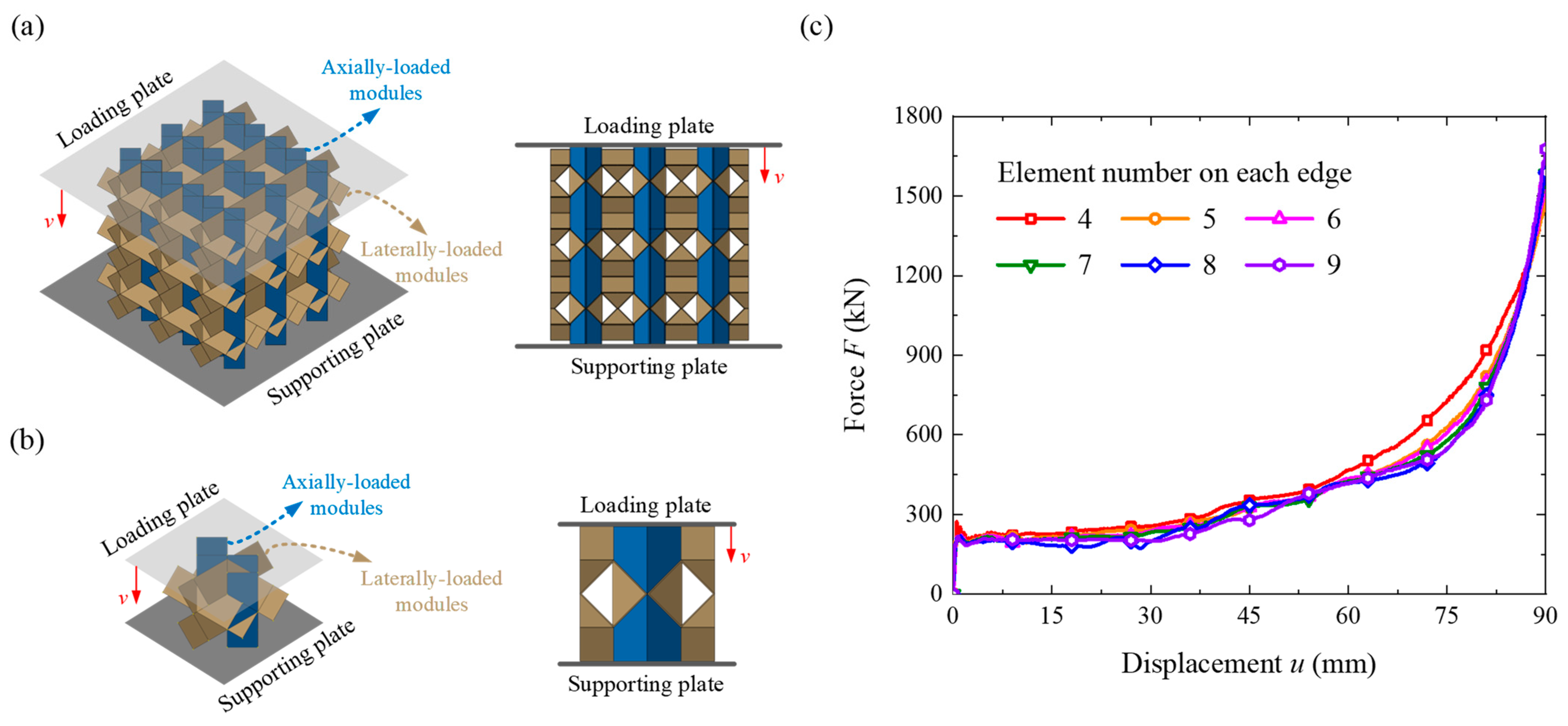
2.2. Experimental Details
2.3. FEM Simulation Details
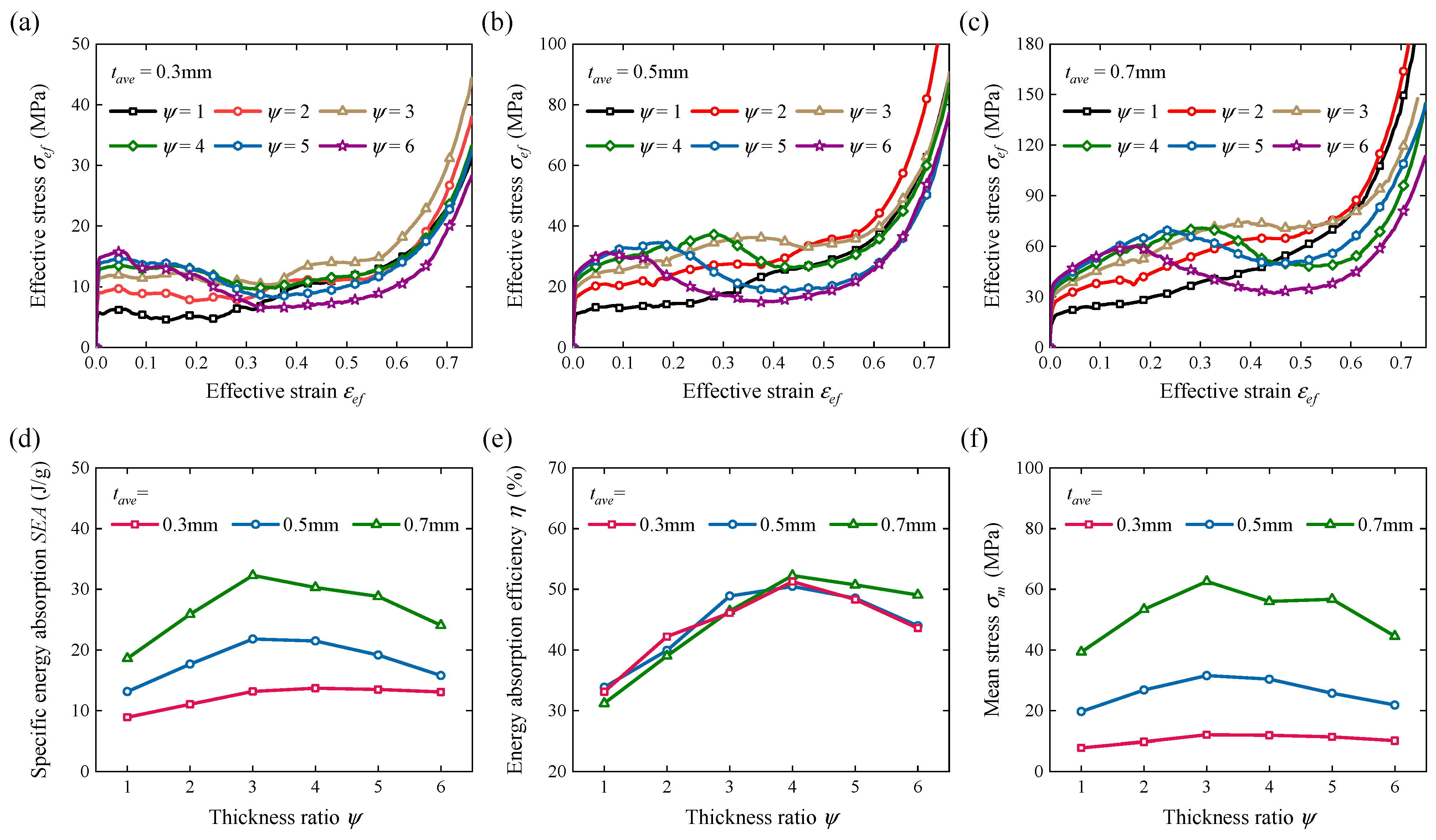
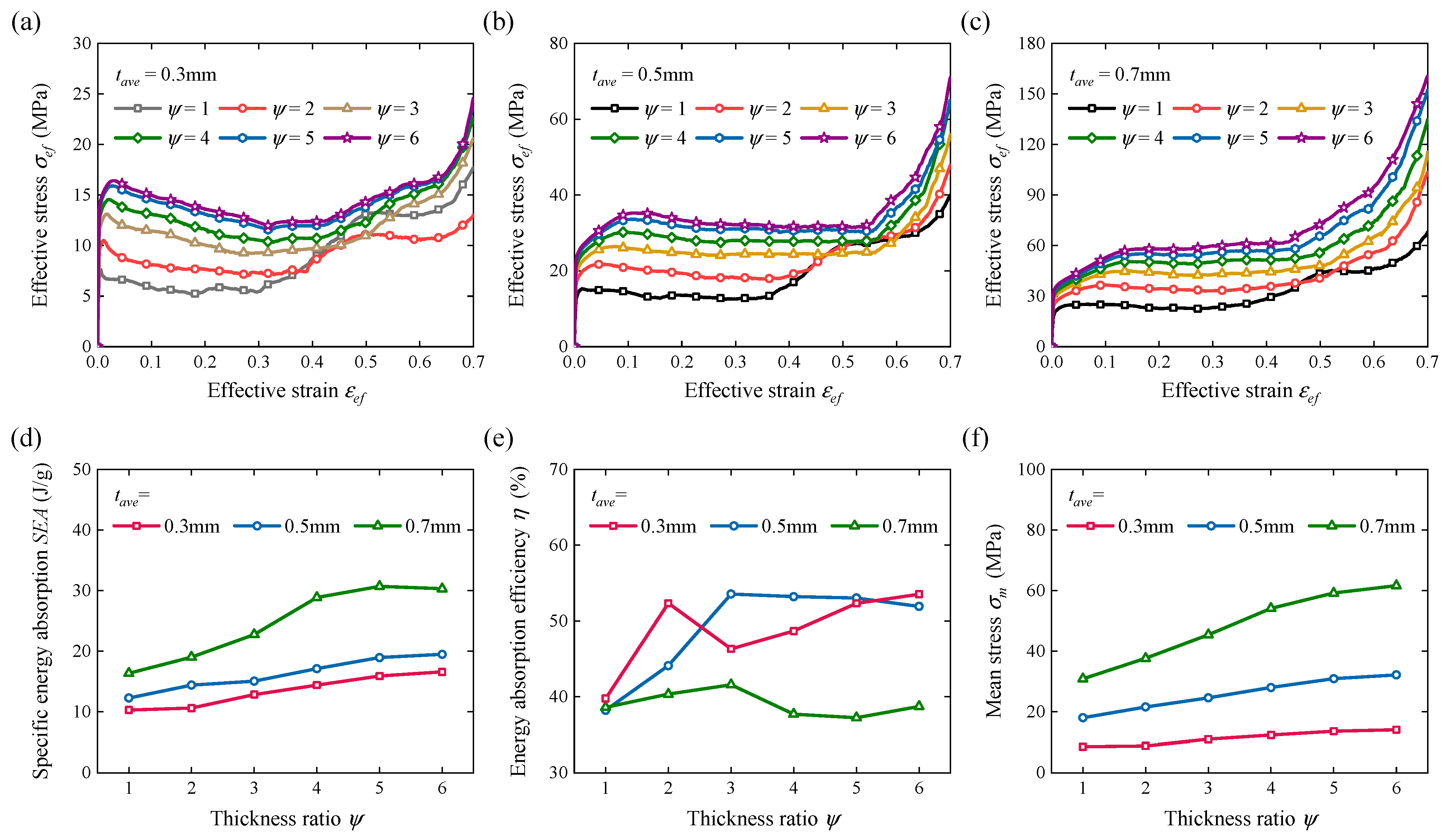
2.4. Key Performance Indicators
3. Results and Discussions
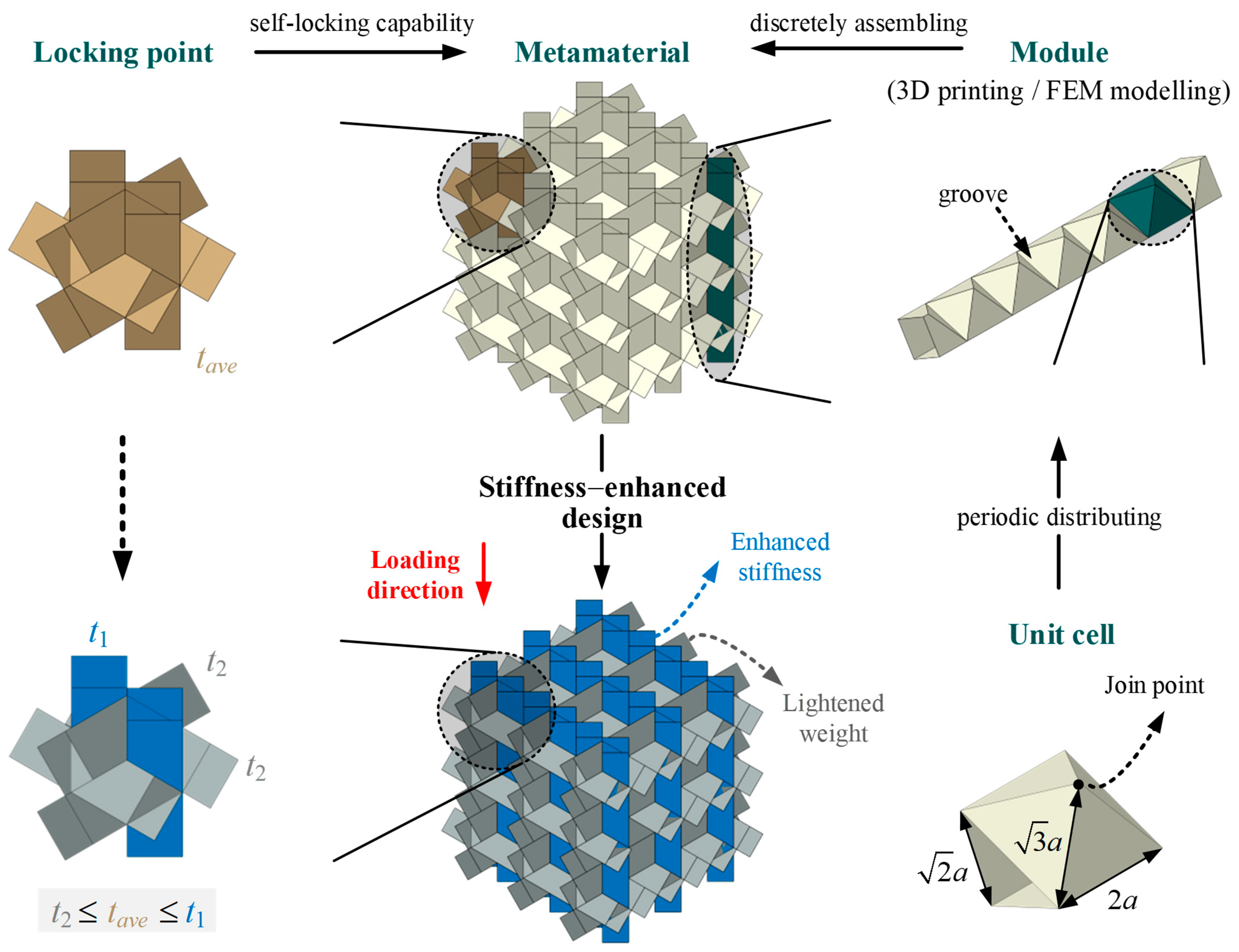
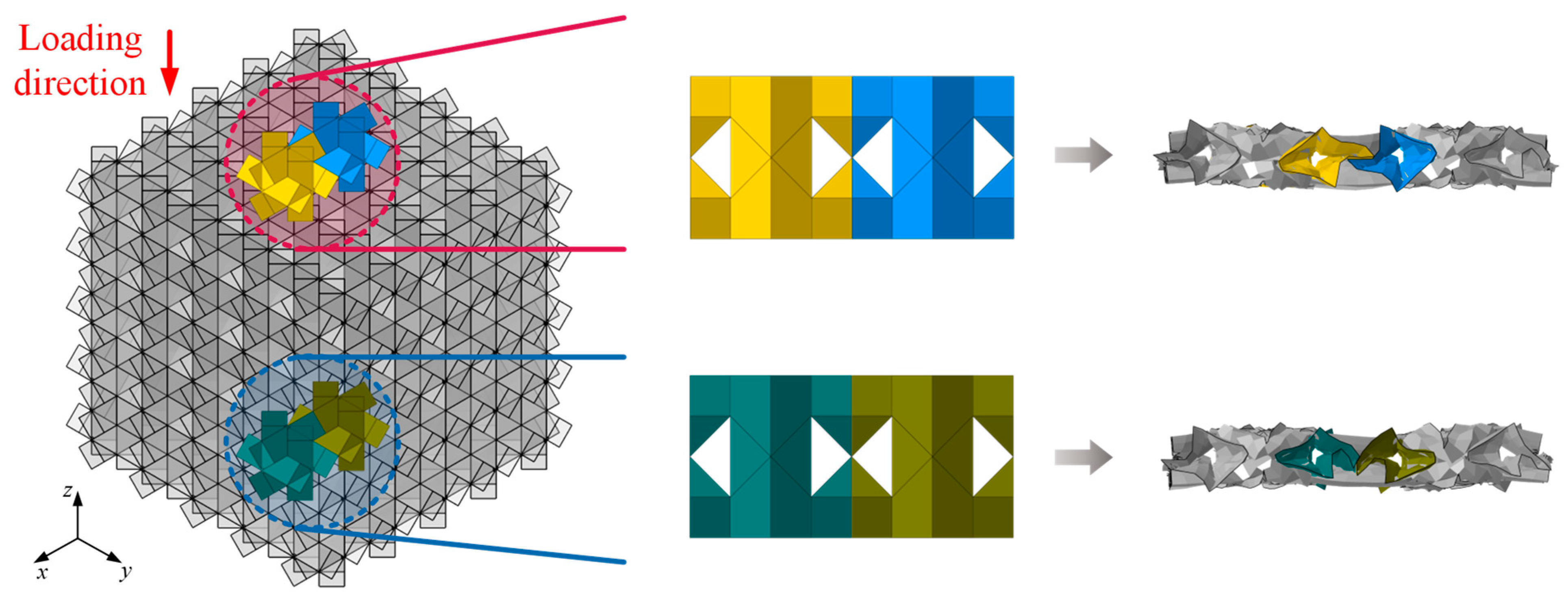
3.1. Modular Metamaterials
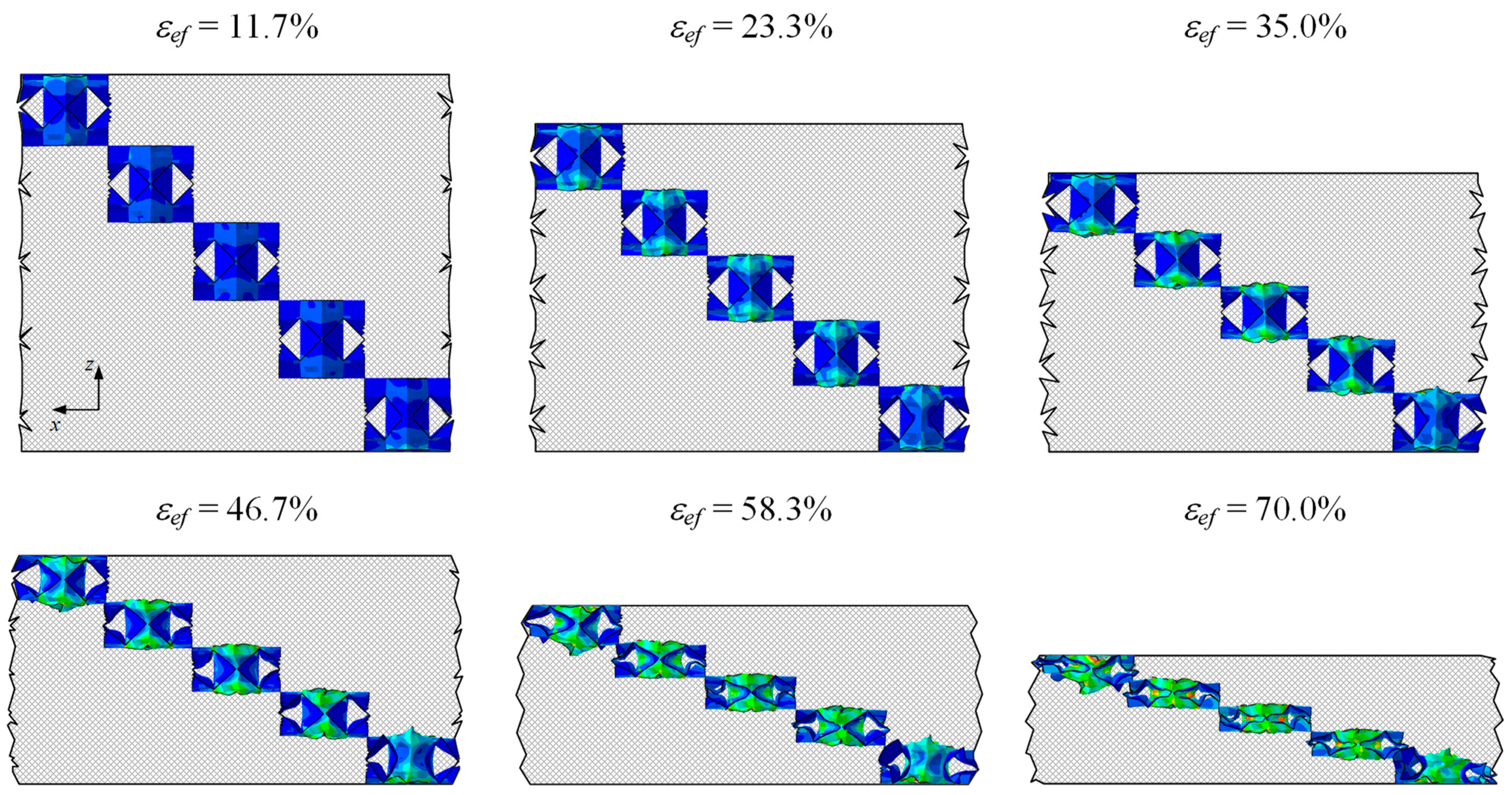
3.2. Locking Points
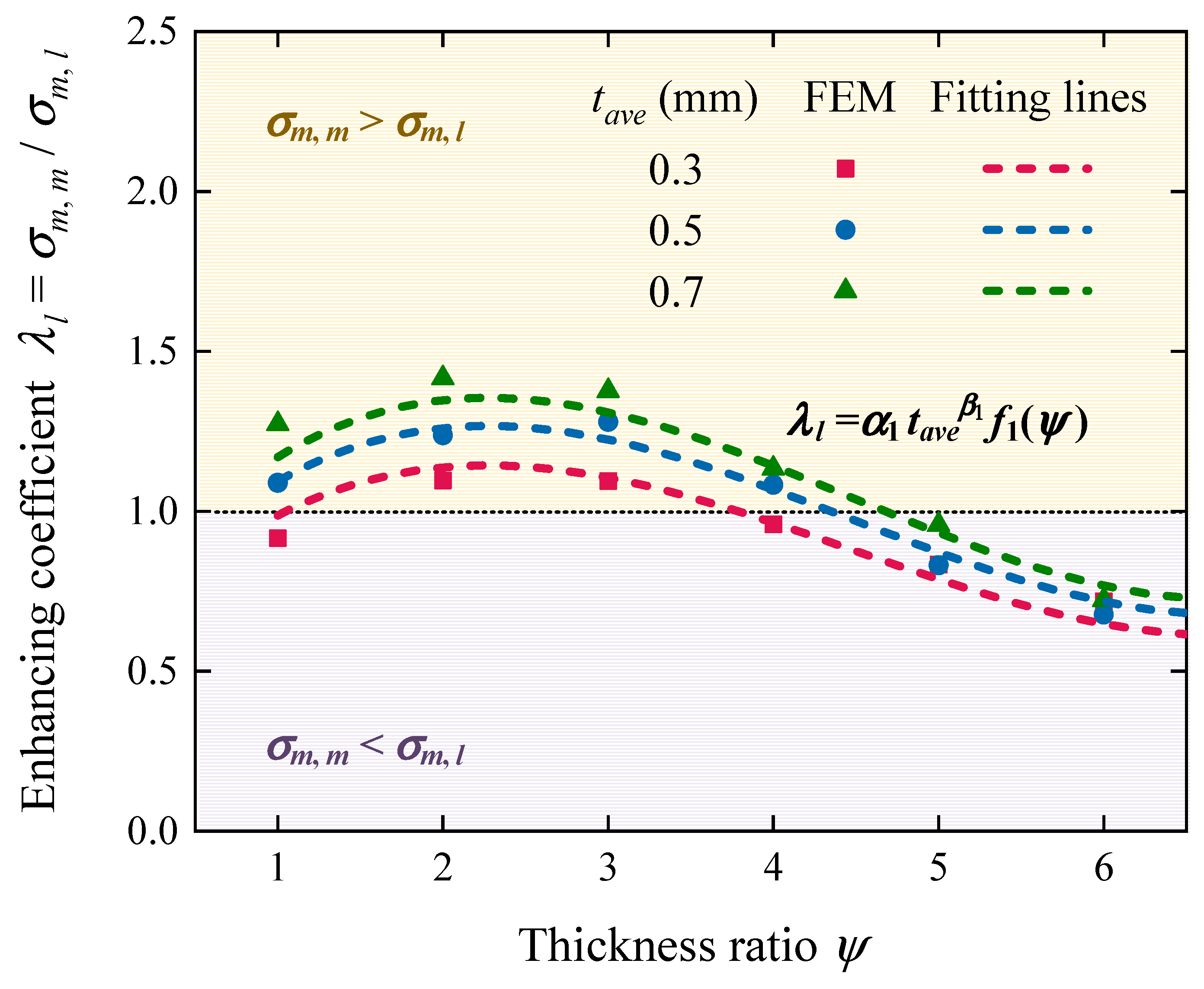
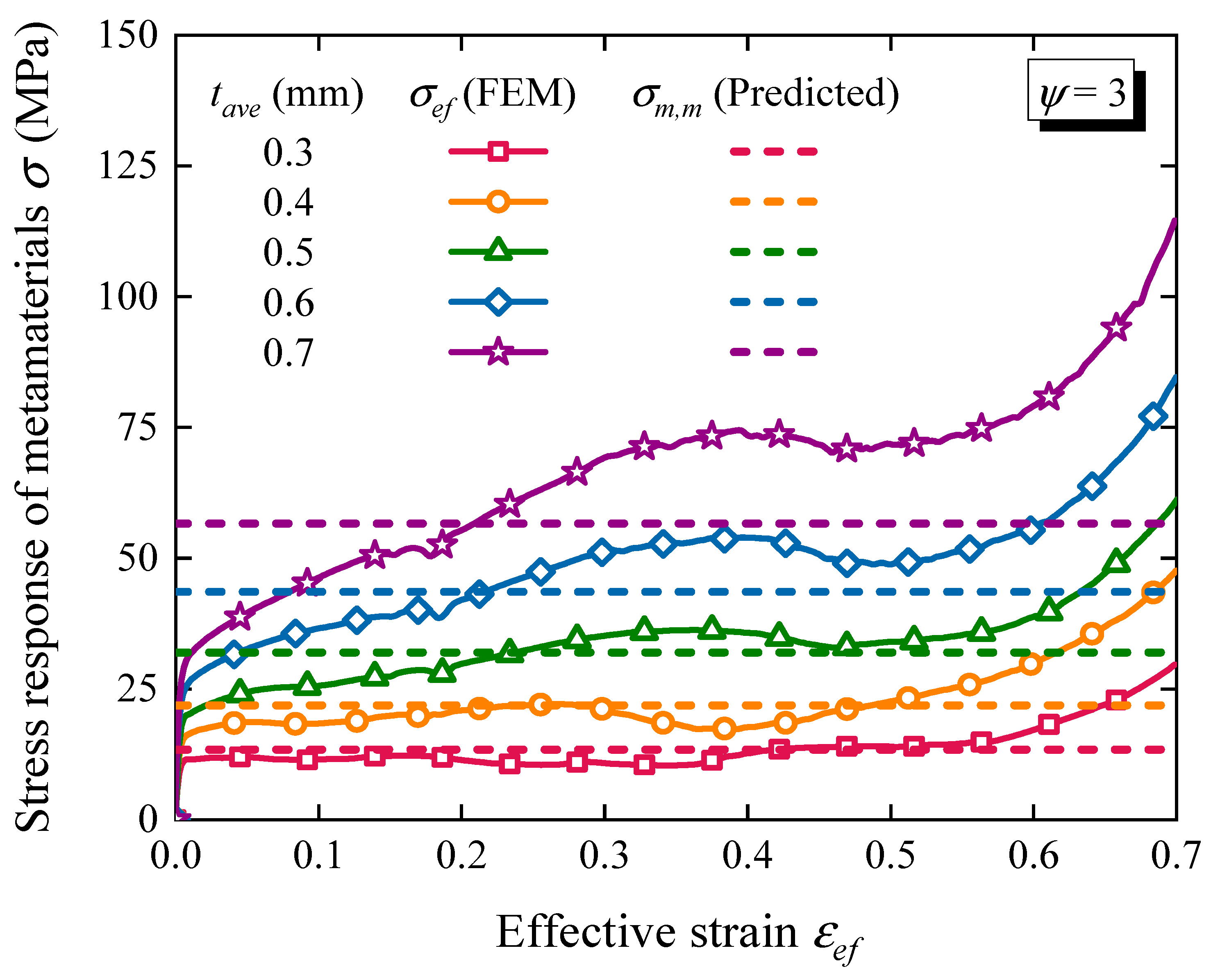
3.3. Estimation of Mean Stress
- (1)
- Select as the optimal thickness ratio, which is obtained by substituting Equation (14) into .
- (2)
- Select the module length and number based on actual storage space.
- (3)
- Select the average thickness tave according to the load characteristics. Increasing tave can significantly enhance the mean stress and specific energy absorption SEA, and decreasing tave can lighten the weight and suitably elongate the effective stroke.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Bearing and Deforming Diagrams of Various Modules in a Single Locking Point
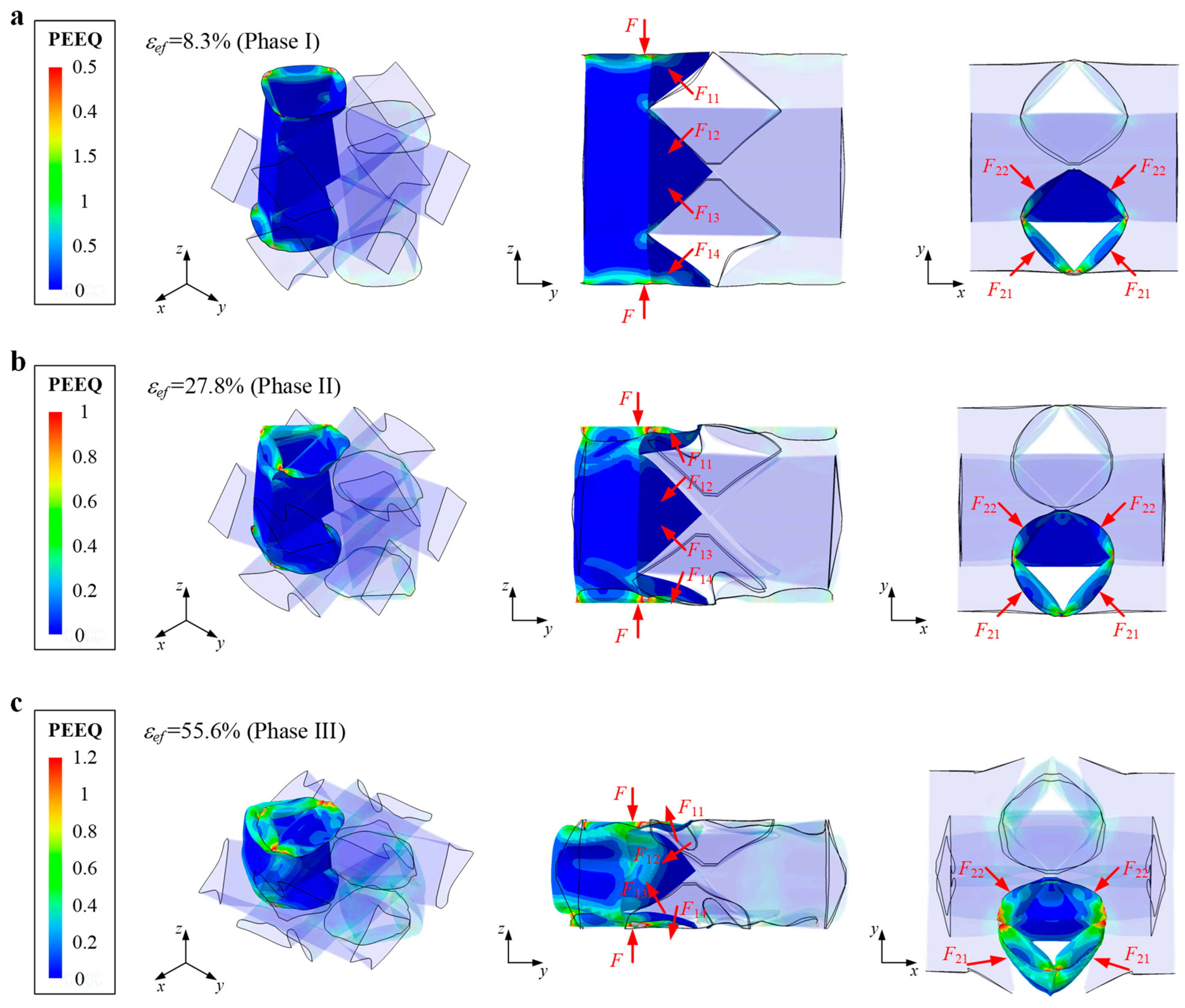

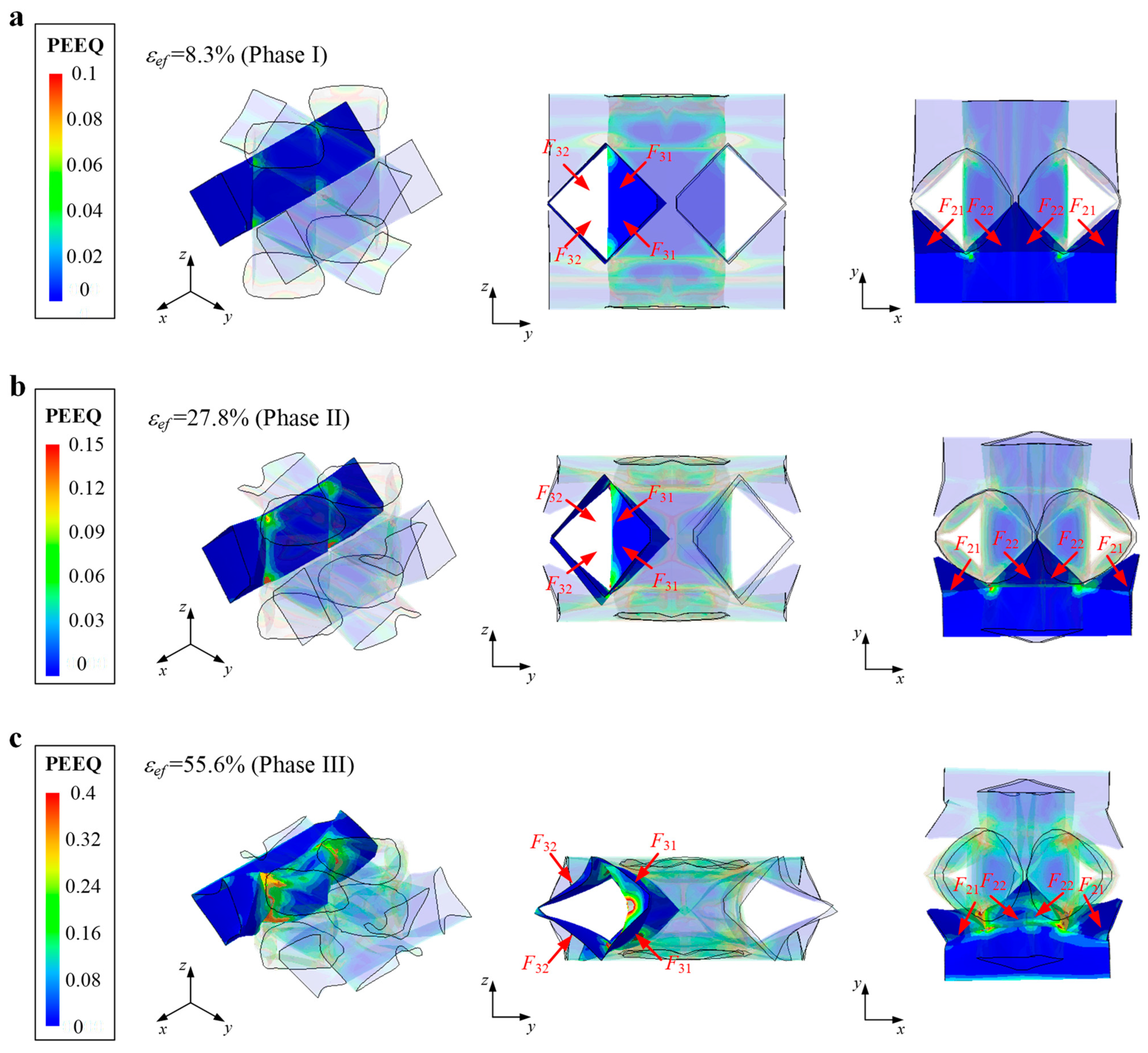
References
- Lu, G.; Yu, T. Energy Absorption of Structures and Materials; Woodhead Publishing Ltd.: Cambridge, UK, 2003. [Google Scholar]
- Alghamdi, A. Collapsible impact energy absorbers: An overview. Thin-Walled Struct. 2001, 39, 189–213. [Google Scholar] [CrossRef]
- Abramowicz, W. Thin-walled structures as impact energy absorbers. Thin-Walled Struct. 2003, 41, 91–107. [Google Scholar] [CrossRef]
- Compton, B.G.; Lewis, J.A. 3D-printing of lightweight cellular composites. Adv. Mater. 2014, 26, 5930–5935. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Yang, K.; Sun, Y.; Yao, Y.; Zhu, W. A universal strategy for flexible, efficient and programmable crashworthiness under quasi-static and dynamic loadings based on plastic deformation of metals. Mater. Des. 2022, 222, 111027. [Google Scholar] [CrossRef]
- Khan, S.Z.; Masood, S.H.; Ibrahim, E.; Ahmad, Z. Compressive behaviour of Neovius Triply Periodic Minimal Surface cellular structure manufactured by fused deposition modelling. Virtual Phys. Prototyp. 2019, 14, 360–370. [Google Scholar] [CrossRef]
- Wierzbicki, T. Crushing analysis of metal honeycombs. Int. J. Impact Eng. 1983, 1, 157–174. [Google Scholar] [CrossRef]
- Hu, L.; He, X.; Wu, G.; Yu, T. Dynamic crushing of the circular-celled honeycombs under out-of-plane impact. Int. J. Impact Eng. 2015, 75, 150–161. [Google Scholar] [CrossRef]
- Yang, K.; Li, Z.; Ge, D. Quasi-static and dynamic out-of-plane crashworthiness of 3D curved-walled mixed-phase honeycombs. Thin-Walled Struct. 2023, 182, 110305. [Google Scholar] [CrossRef]
- Qi, J.; Li, C.; Tie, Y.; Zheng, Y.; Duan, Y. Energy absorption characteristics of origami-inspired honeycomb sandwich structures under low-velocity impact loading. Mater. Des. 2021, 207, 109837. [Google Scholar] [CrossRef]
- Zhang, W.; Yin, S.; Yu, T.; Xu, J. Crushing resistance and energy absorption of pomelo peel inspired hierarchical honeycomb. Int. J. Impact Eng. 2019, 125, 163–172. [Google Scholar] [CrossRef]
- Ruan, D.; Lu, G.; Wang, B.; Yu, T.X. In-plane dynamic crushing of honeycombs—A finite element study. Int. J. Impact Eng. 2003, 28, 161–182. [Google Scholar] [CrossRef]
- Qi, C.; Jiang, F.; Yang, S. Advanced honeycomb designs for improving mechanical properties: A review. Compos. Part B Eng. 2021, 227, 109393. [Google Scholar] [CrossRef]
- Harris, J.A.; McShane, G.J. Metallic stacked origami cellular materials: Additive manufacturing, properties, and modelling. Int. J. Solids Struct. 2020, 185–186, 448–466. [Google Scholar] [CrossRef]
- Niknejad, A.; Abedi, M.M.; Liaghat, G.H.; Nejad, M.Z. Prediction of the mean folding force during the axial compression in foam-filled grooved tubes by theoretical analysis. Mater. Des. 2012, 37, 144–151. [Google Scholar] [CrossRef]
- Zhai, J.; Zhang, D.; Li, M.; Cui, C.; Cai, J. Out-of-plane energy absorption and crush behavior of origami honeycomb. Thin-Walled Struct. 2022, 181, 109966. [Google Scholar] [CrossRef]
- Hu, D.; Wang, Y.; Song, B.; Dang, L.; Zhang, Z. Energy-absorption characteristics of a bionic honeycomb tubular nested structure inspired by bamboo under axial crushing. Compos. Part B Eng. 2019, 162, 21–32. [Google Scholar] [CrossRef]
- Yang, C.; Kyriakides, S. Crushing of low density foams under triaxial loadings. Extrem. Mech. Lett. 2020, 35, 100620. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, D.; Hou, S.; Yang, D.; Nieh, T.G.; Lu, Z. Cellular structure and energy absorption of AlCu alloy foams fabricated via a two-step foaming method. Mater. Des. 2020, 196, 109090. [Google Scholar] [CrossRef]
- Kaczyński, P.; Ptak, M.; Gawdzińska, K. Energy absorption of cast metal and composite foams tested in extremely low and high-temperatures. Mater. Des. 2020, 196, 109114. [Google Scholar] [CrossRef]
- Xue, R.; Cui, X.; Zhang, P.; Liu, K.; Li, Y.; Wu, W.; Liao, H. Mechanical design and energy absorption performances of novel dual scale hybrid plate-lattice mechanical metamaterials. Extrem. Mech. Lett. 2020, 40, 100918. [Google Scholar] [CrossRef]
- Wang, S.; Ma, Y.; Deng, Z. Stretching-dominated truss lattice materials: Elastic anisotropy evaluation, control, and design. Compos. Struct. 2022, 298, 116004. [Google Scholar] [CrossRef]
- Wang, Y.; Ramirez, B.; Carpenter, K.; Naify, C.; Hofmann, D.C.; Daraio, C. Architected lattices with adaptive energy absorption. Extrem. Mech. Lett. 2019, 33, 100557. [Google Scholar] [CrossRef]
- Mao, A.; Zhao, N.; Liang, Y.; Bai, H. Mechanically efficient cellular materials inspired by cuttlebone. Adv. Mater. 2021, 33, 2007348. [Google Scholar] [CrossRef] [PubMed]
- Jenett, B.; Cameron, C.; Tourlomousis, F.; Rubio, A.P.; Gershenfeld, N. Discretely assembled mechanical metamaterials. Sci. Adv. 2020, 6, eabc9943. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Zhang, Y.; Ren, X.; Han, D.; Jiang, W.; Zhang, X.G.; Luo, H.C.; Xie, Y.M. Design and mechanical characteristics of auxetic metamaterial with tunable stiffness. Int. J. Mech. Sci. 2022, 223, 107286. [Google Scholar] [CrossRef]
- Hu, J.; Tan, A.T.L.; Chen, H.; Hu, X. Superior compressive properties of 3D printed plate lattice mechanical metamaterials. Int. J. Mech. Sci. 2022, 231, 107586. [Google Scholar] [CrossRef]
- Tan, X.; Wang, B.; Yao, K.; Zhu, S.; Chen, S.; Xu, P.; Wang, L.; Sun, Y. Novel multi-stable mechanical metamaterials for trapping energy through shear deformation. Int. J. Mech. Sci. 2019, 164, 105168. [Google Scholar] [CrossRef]
- Khajeh-Khalili, F.; Honarvar, M.A.; Limiti, E. A Novel High-Isolation Resistor-Less Millimeter-Wave Power Divider Based on Metamaterial Structures for 5G Applications. IEEE Trans. Compon. Packag. Manuf. Technol. 2021, 11, 294–301. [Google Scholar] [CrossRef]
- Ben-Yelun, I.; Gómez-Carano, G.; Millán, F.J.S.; Sanz, M.Á.; Montáns, F.J.; Saucedo-Mora, L. GAM: General Auxetic Metamaterial with Tunable 3D Auxetic Behavior Using the Same Unit Cell Boundary Connectivity. Materials 2023, 16, 3473. [Google Scholar] [CrossRef]
- Khajeh-Khalili, F.; Honarvar, M.A.; Naser-Moghadasi, M.; Dolatshahi, M. High-gain, high-isolation, and wideband millimetre—Wave closely spaced multiple-input multiple-output antenna with metamaterial wall and metamaterial superstrate for 5G applications. IET Microw. Antennas Propag. 2021, 15, 379–388. [Google Scholar] [CrossRef]
- Gupta, A.; Sharma, R.; Thakur, A.; Gulia, P. Metamaterial foundation for seismic wave attenuation for low and wide frequency band. Sci. Rep. 2023, 13, 2293. [Google Scholar] [CrossRef] [PubMed]
- Lian, J.-W.; Ansari, M.; Hu, P.; Guo, Y.J.; Ding, D. Wideband and High-Efficiency Parallel-Plate Luneburg Lens Employing All-Metal Metamaterial for Multibeam Antenna Applications. IEEE Trans. Antennas Propag. 2023, 71, 3193–3203. [Google Scholar] [CrossRef]
- Pan, F.; Li, Y.; Li, Z.; Yang, J.; Liu, B.; Chen, Y. 3D pixel mechanical metamaterials. Adv. Mater. 2019, 31, 1900548. [Google Scholar] [CrossRef] [PubMed]
- Xin, X.; Liu, L.; Liu, Y.; Leng, J. 4D pixel mechanical metamaterials with programmable and reconfigurable properties. Adv. Funct. Mater. 2022, 32, 2107795. [Google Scholar] [CrossRef]
- Li, J.; Chen, Z.; Li, Q.; Jin, L.; Zhao, Z. Harnessing Friction in Intertwined Structures for High-Capacity Reusable Energy-Absorbing Architected Materials. Adv. Sci. 2022, 9, 2105769. [Google Scholar] [CrossRef]
- Fang, H.; Chu, S.A.; Xia, Y.; Wang, K.-W. Programmable self-locking origami mechanical metamaterials. Adv. Mater. 2018, 30, 1706311. [Google Scholar] [CrossRef]
- Kamrava, S.; Mousanezhad, D.; Ebrahimi, H.; Ghosh, R.; Vaziri, A. Origami-based cellular metamaterial with auxetic, bistable, and self-locking properties. Sci. Rep. 2017, 7, 46046. [Google Scholar] [CrossRef]
- Chen, Y.; Qiao, C.; Qiu, X.; Zhao, S.; Zhen, C.; Liu, B. A novel self-locked energy absorbing system. J. Mech. Phys. Solids 2016, 87, 130–149. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, Q.; Yang, H.; Yang, L.; Xiong, J. A periodic dissipative system with self-locking capacity. Int. J. Impact Eng. 2022, 166, 104233. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, L.; Du, B.; Liu, H.; Chen, B.; Peng, S.; Guo, Y.; Chen, L.; Li, W.; Fang, D. Bidirectional self-locked energy absorbing system: Design and quasi-static compression properties. Thin-Walled Struct. 2019, 144, 106366. [Google Scholar] [CrossRef]
- Liu, Y.; Xiong, F.; Yang, K.; Chen, Y. A novel omnidirectional self-locked energy absorption system inspired by windmill. J. Appl. Mech. 2020, 87, 085001. [Google Scholar] [CrossRef]
- Yang, K.; Rao, L.; Hu, L.; Pan, F.; Yin, Q.; Chen, Y. Flexible, efficient and adaptive modular impact-resistant metamaterials. Int. J. Mech. Sci. 2022, 239, 107893. [Google Scholar] [CrossRef]
- Wang, H.; Yang, J.; Liu, H.; Sun, Y.; Yu, T. Internally nested circular tube system subjected to lateral impact loading. Thin-Walled Struct. 2015, 91, 72–81. [Google Scholar] [CrossRef]
- Ha, N.S.; Pham, T.M.; Tran, T.T.; Hao, H.; Lu, G. Mechanical properties and energy absorption of bio-inspired hierarchical circular honeycomb. Compos. Part B Eng. 2022, 236, 109818. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H. Numerical and theoretical studies on energy absorption of three-panel angle elements. Int. J. Impact Eng. 2012, 46, 23–40. [Google Scholar] [CrossRef]




| Young’s Modulus E (GPa) | Poisson’s Ratio u | Yield Stress σs (MPa) | Hardening Modulus Ep (MPa) | Ultimate Stress σu (MPa) | Density ρs (kg/m3) |
|---|---|---|---|---|---|
| 206 | 0.3 | 360 | 1100 | 664 | 7980 |
| Metamaterial Specimen | tave (mm) | t1 (mm) | t2 (mm) | ψ | a (mm) | n | mmeta (kg) |
|---|---|---|---|---|---|---|---|
| Regular #1 | 0.5 | 0.5 | 0.5 | 1 | 9 | 6 | 1.08 |
| Regular #2 | 1 | 1 | 1 | 1 | 9 | 6 | 2.16 |
| Locking Point Specimen | tave (mm) | t1 (mm) | t2 (mm) | ψ | a (mm) | n | mlock (g) |
|---|---|---|---|---|---|---|---|
| Regular #3 & #4 | 0.5 | 0.5 | 0.5 | 1 | 9 | 2 | 43.84 |
| Regular #5 & #6 | 1 | 1 | 1 | 1 | 9 | 2 | 87.68 |
| Stiffness-enhanced #7 & #8 | 1 | 2 | 0.5 | 4 | 9 | 2 | 87.68 |
| α1 | β1 | a0 | a1 | a2 | a3 | α2 | γ2 |
|---|---|---|---|---|---|---|---|
| 1.15 | 0.2 | 0.644 | 0.616 | −0.182 | 0.014 | 49.17 | 0.37 |
| Average Thickness tave (mm) | Mean Stress of Metamaterials | ||
|---|---|---|---|
| Actual Value | Predicted Value | Relative Error | |
| 0.3 | 12.59 | 13.41 | 6.11% |
| 0.4 | 20.34 | 21.9 | 7.12% |
| 0.5 | 31.55 | 31.95 | 1.25% |
| 0.6 | 45.62 | 43.56 | 4.52% |
| 0.7 | 62.61 | 56.61 | 9.58% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Li, X.; Li, Z.; Zhu, W.; Yao, Y. Optimal Design and Mean Stress Estimation of Modular Metamaterials Inspired by Burr Puzzles. Sustainability 2023, 15, 13963. https://doi.org/10.3390/su151813963
Yang K, Li X, Li Z, Zhu W, Yao Y. Optimal Design and Mean Stress Estimation of Modular Metamaterials Inspired by Burr Puzzles. Sustainability. 2023; 15(18):13963. https://doi.org/10.3390/su151813963
Chicago/Turabian StyleYang, Kuijian, Xiaoxun Li, Zhi Li, Weiyu Zhu, and Yingkang Yao. 2023. "Optimal Design and Mean Stress Estimation of Modular Metamaterials Inspired by Burr Puzzles" Sustainability 15, no. 18: 13963. https://doi.org/10.3390/su151813963





