Sensitivity Analysis of Factors Influencing the Blast Resistance of Reinforced Concrete Columns Based on Grey Relation Degree
Abstract
1. Introduction
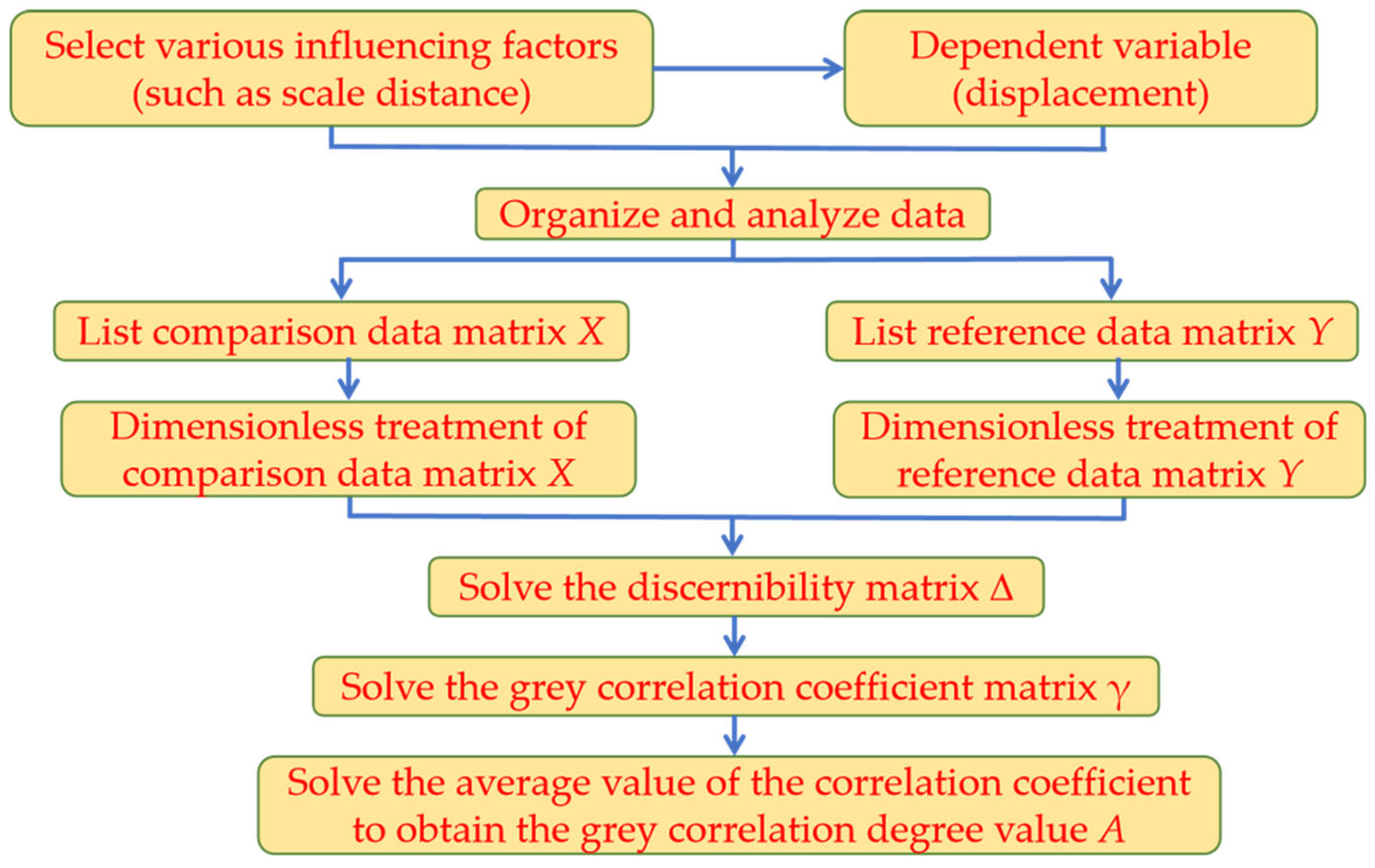
2. Grey Relation Analysis Methods
- List comparison data matrix X and reference data matrix Y.
- 2.
- Dimensionless treatment of comparison data matrix X and reference data matrix Y.
- 3.
- Solve the grey correlation difference information between the comparison data matrix X and the reference data matrix Y.
- 4.
- Solve the grey correlation coefficient matrix .
- 5.
- Solving grey relation degree A.
3. Model Validation for Numerical Simulation
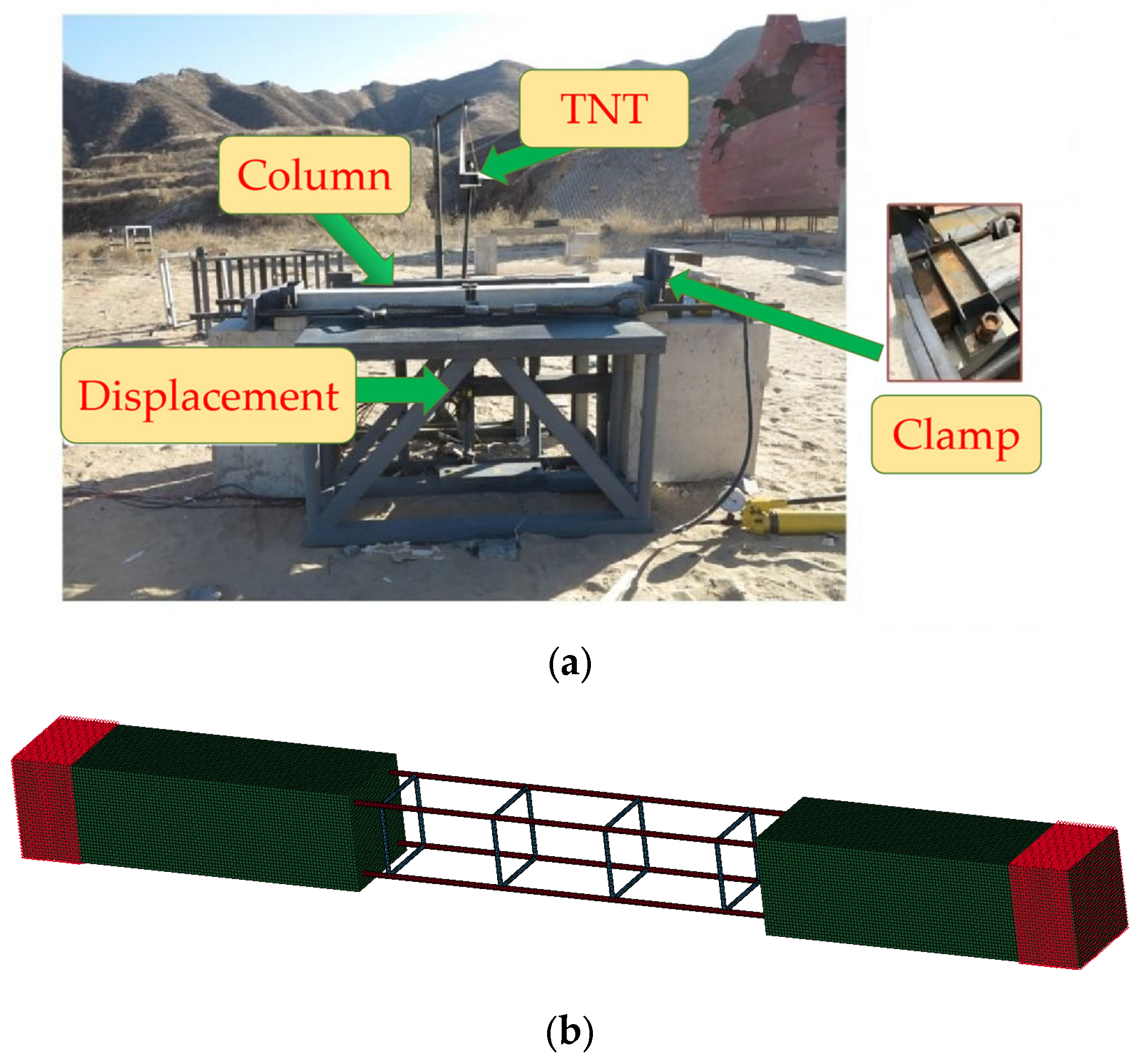
3.1. Introduction of Experiment
3.2. Introduction of Numerical Simulation
3.2.1. Type of Unit
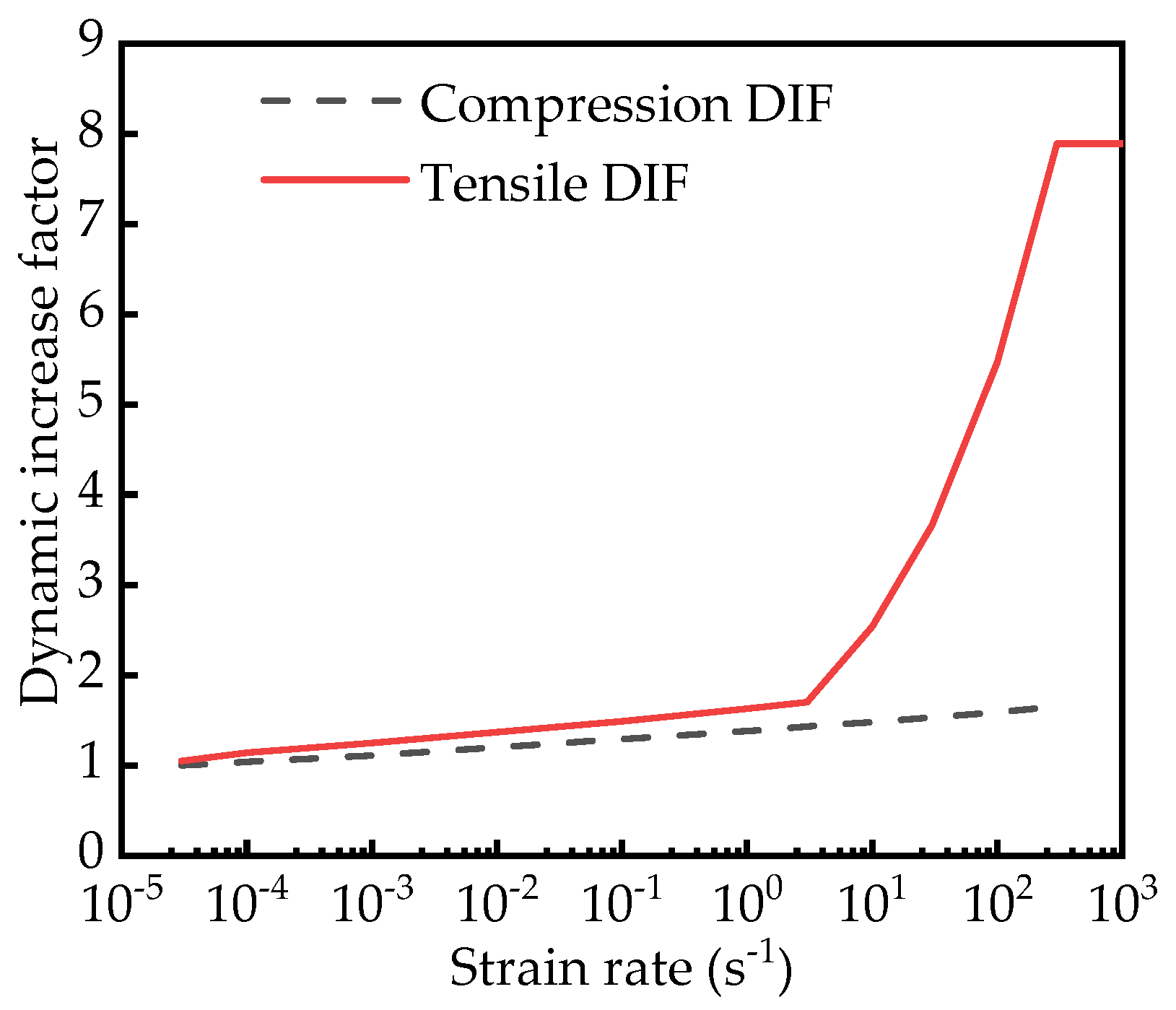
3.2.2. Type of Material
- Reinforcement
- 2.
- Concrete
3.2.3. Boundary Conditions and Blast Loading
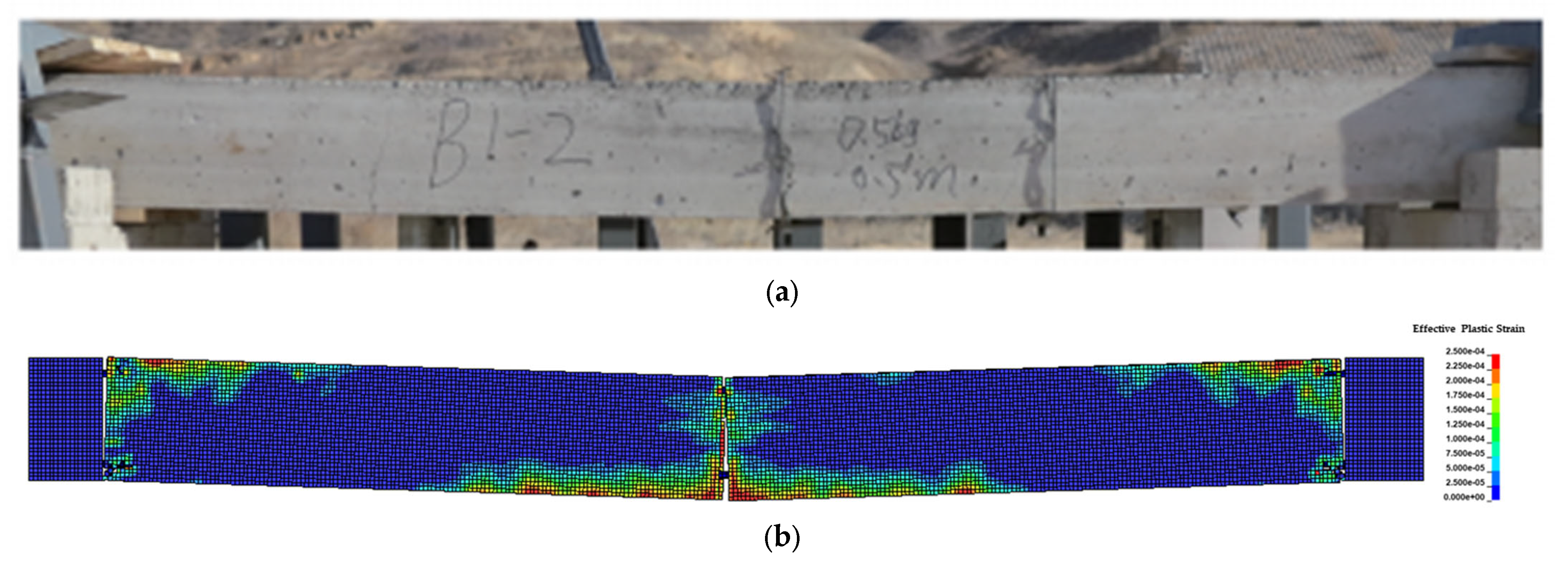
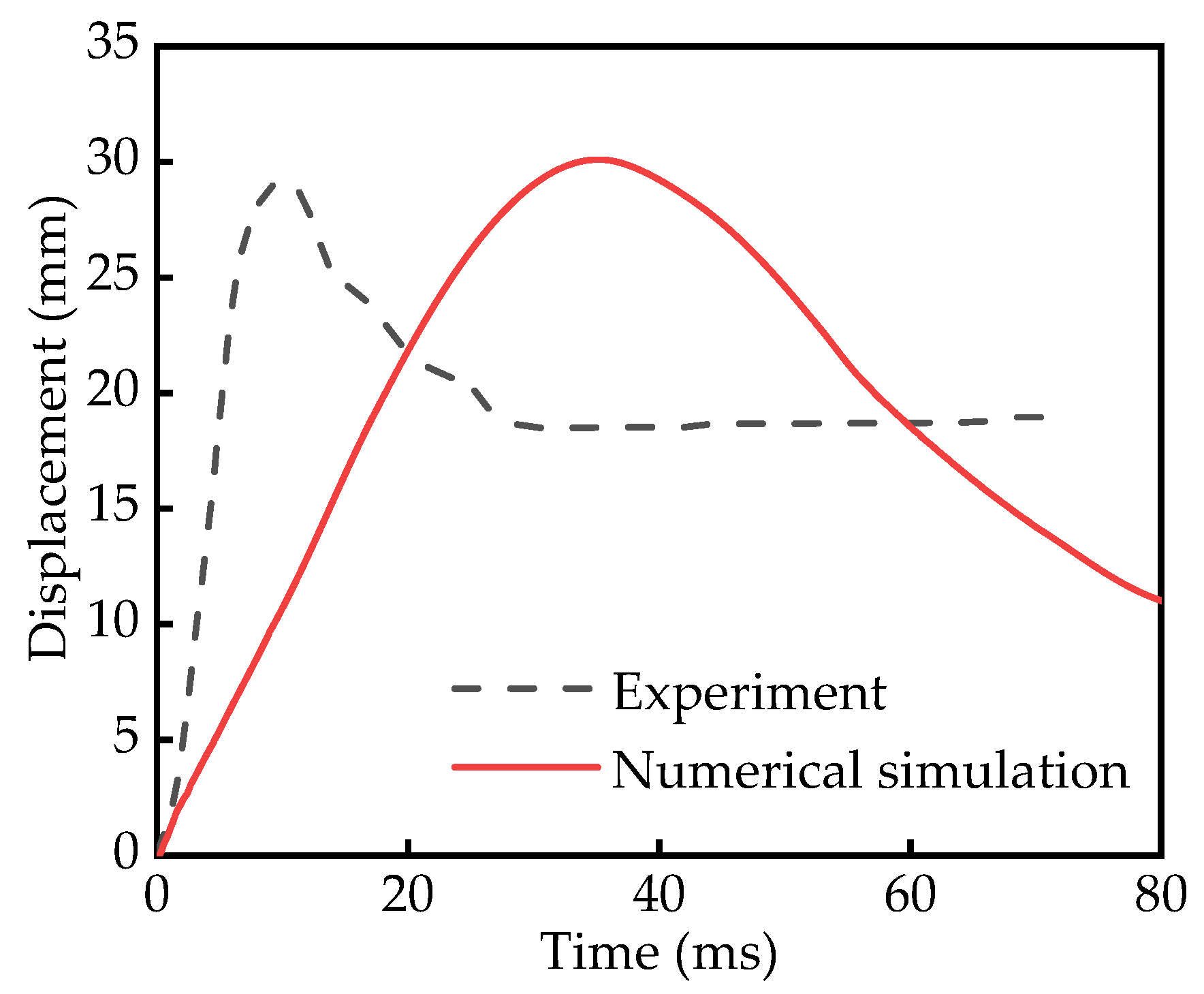
3.3. Model Validation for Numerical Simulation
3.4. Failure Types of RC Columns
4. Numerical Simulation of Dynamic Response of RC Columns under Blast Loading
4.1. Introduction of the Numerical Model
4.2. Working Conditions for Numerical Simulation
5. The Variation Law of Mid-Span Displacement
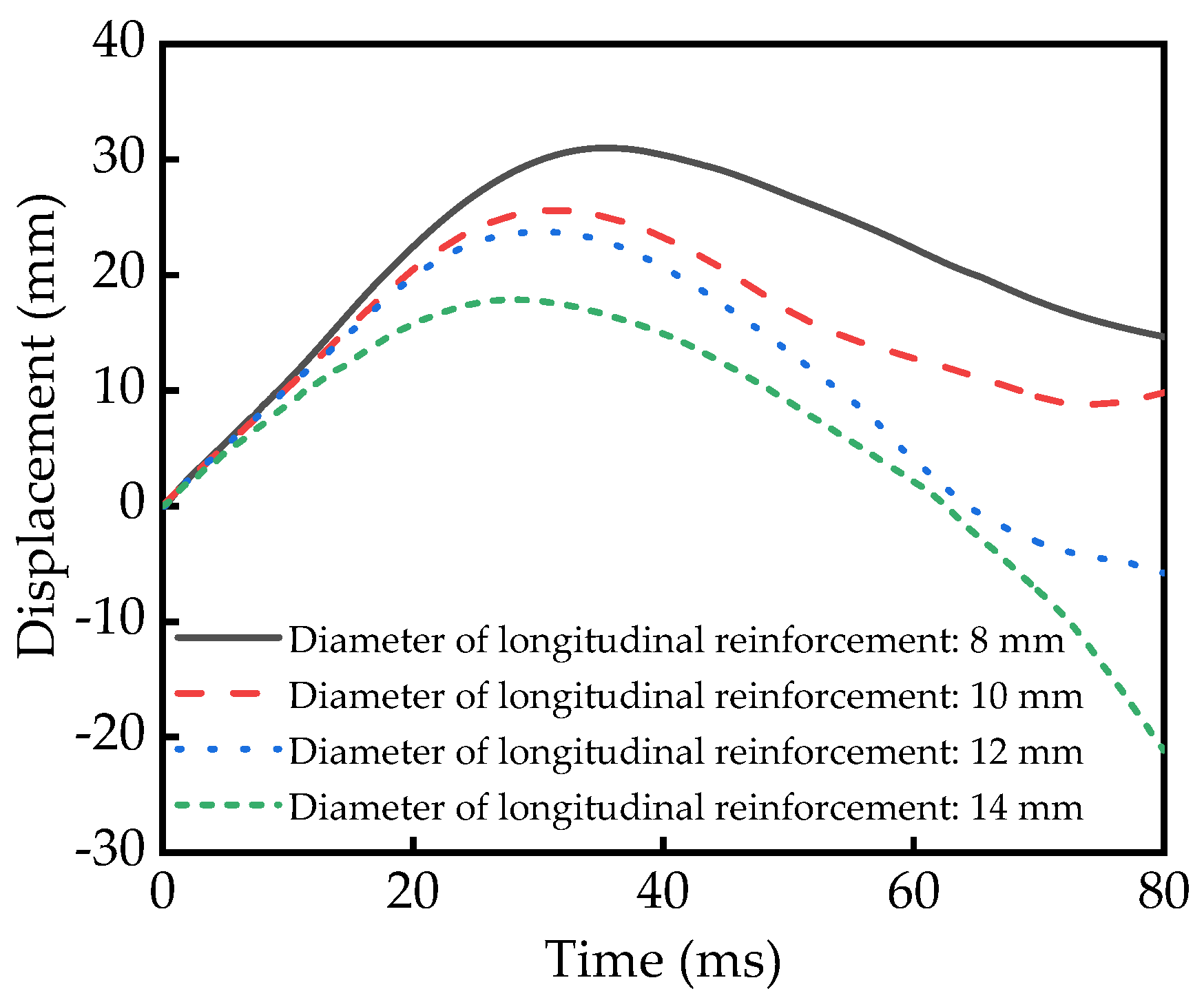
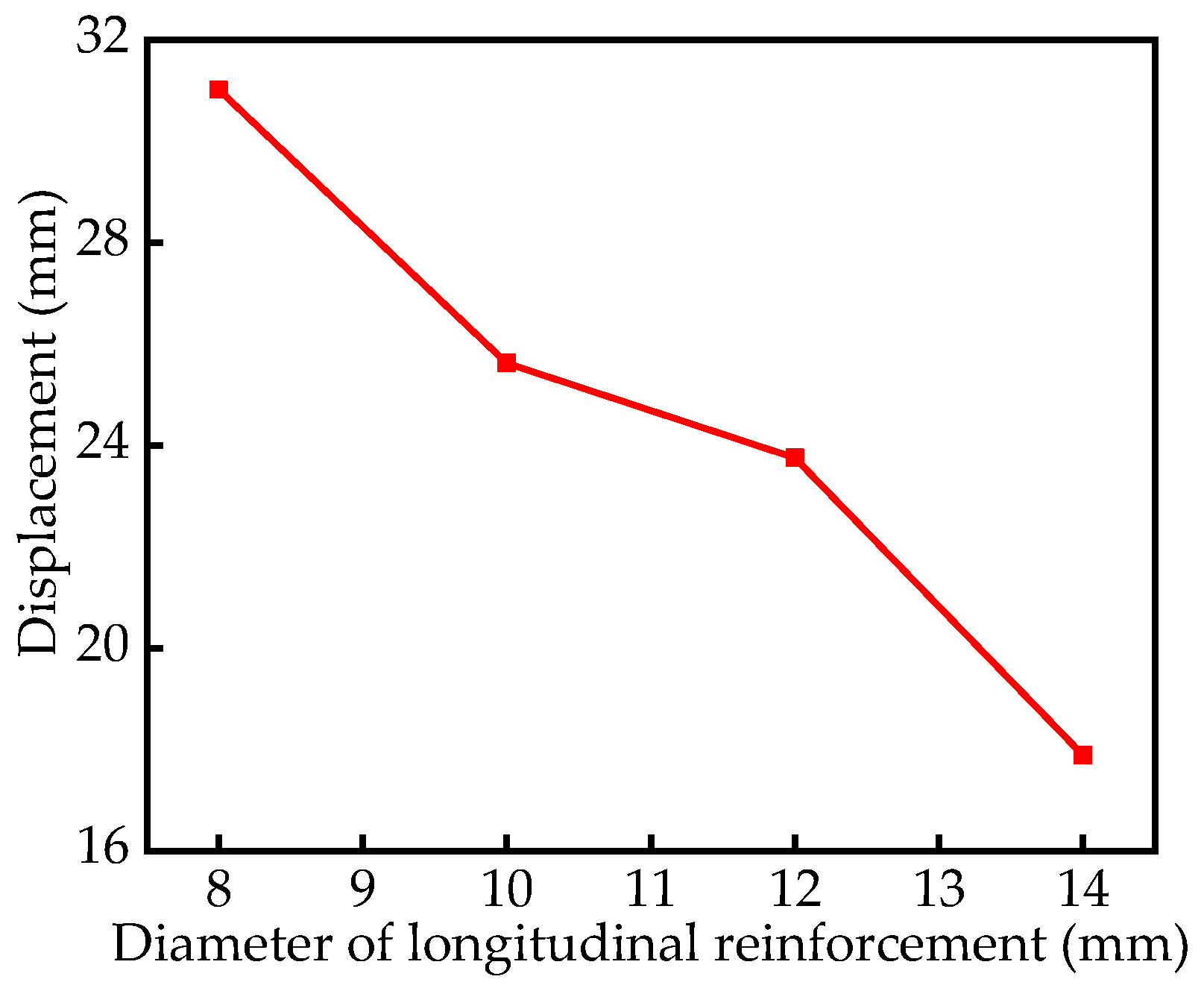
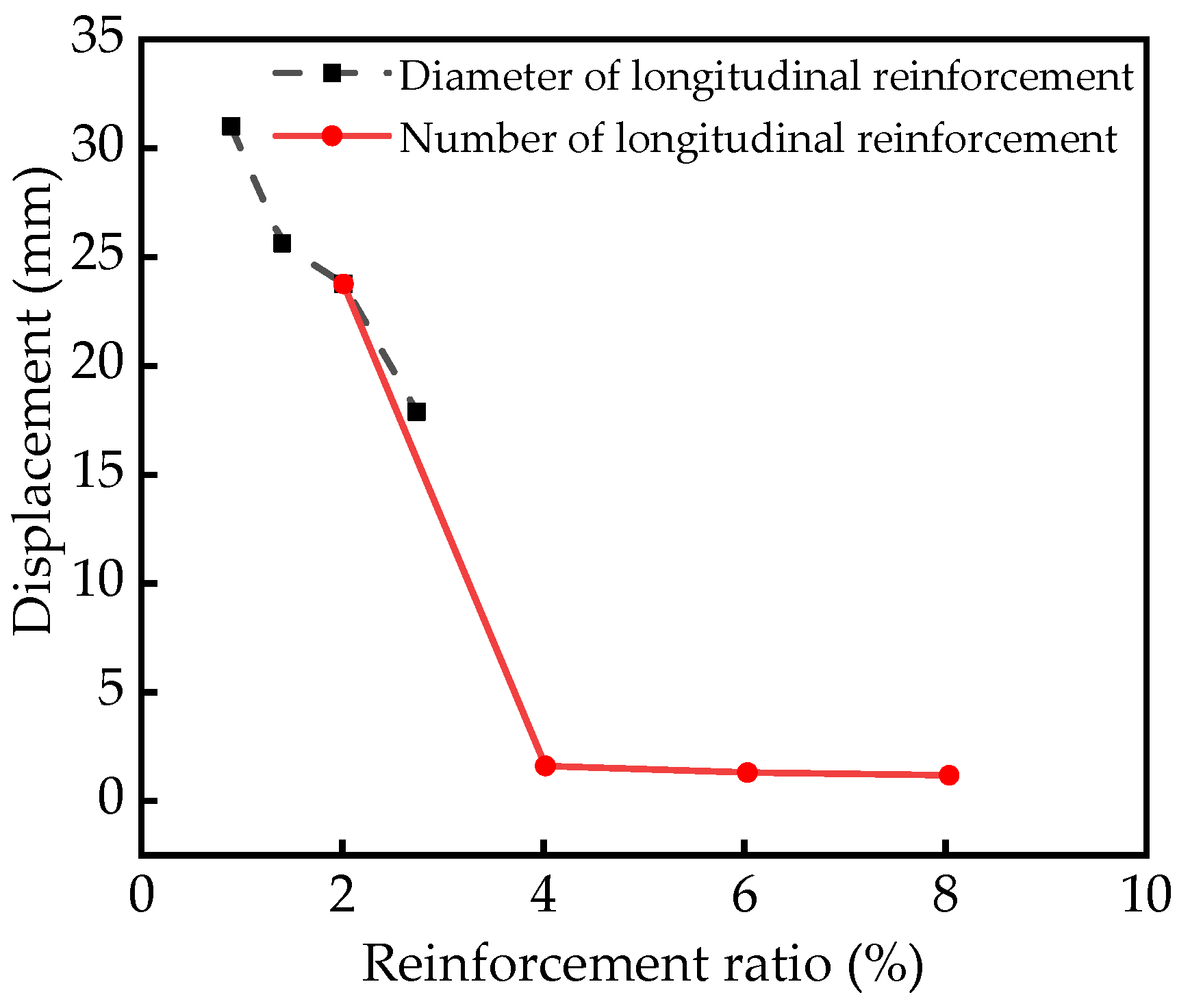
5.1. Reinforcement Ratio Diameter of Longitudinal Reinforcement
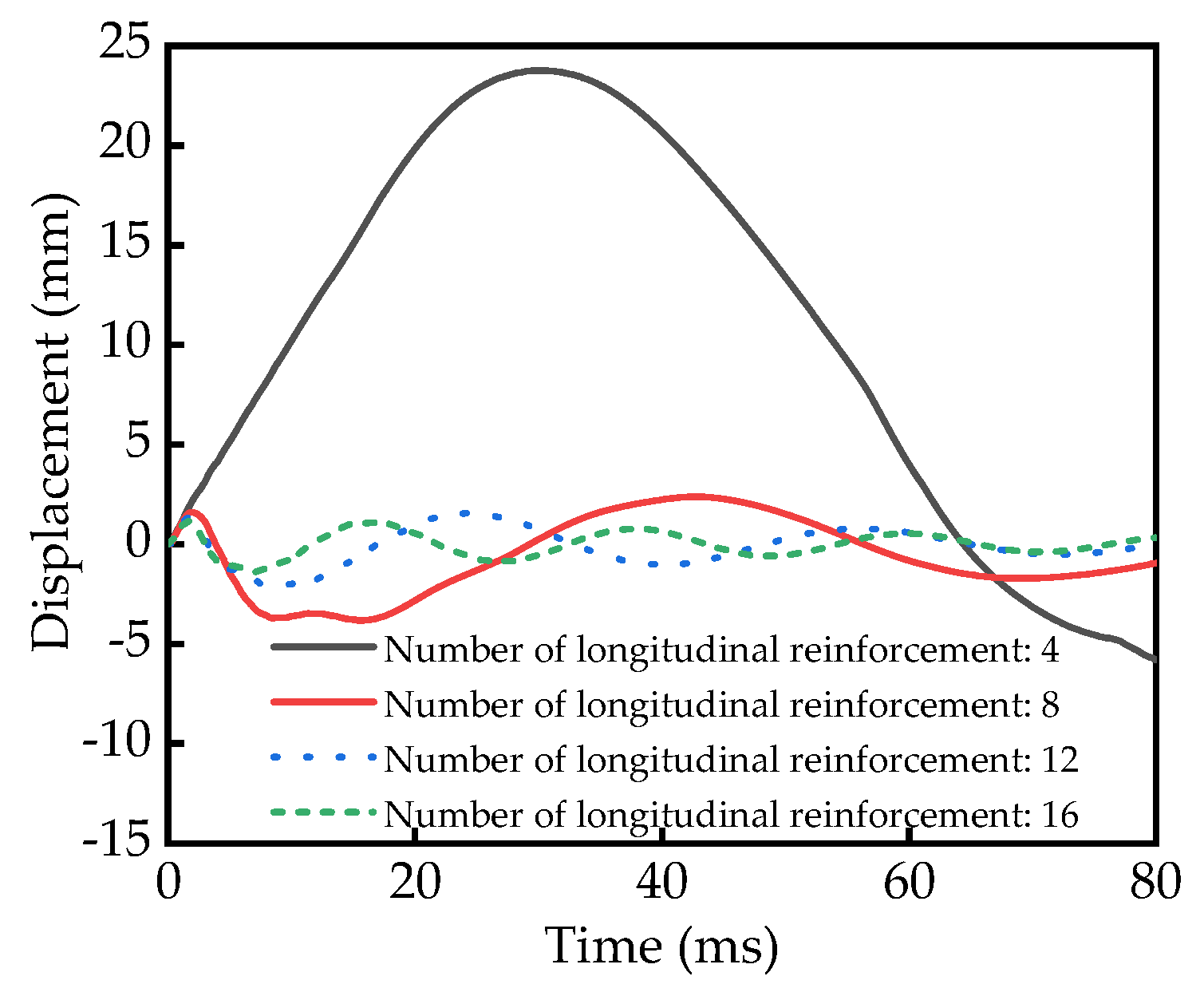
5.2. Reinforcement Ratio Number of Longitudinal Reinforcement
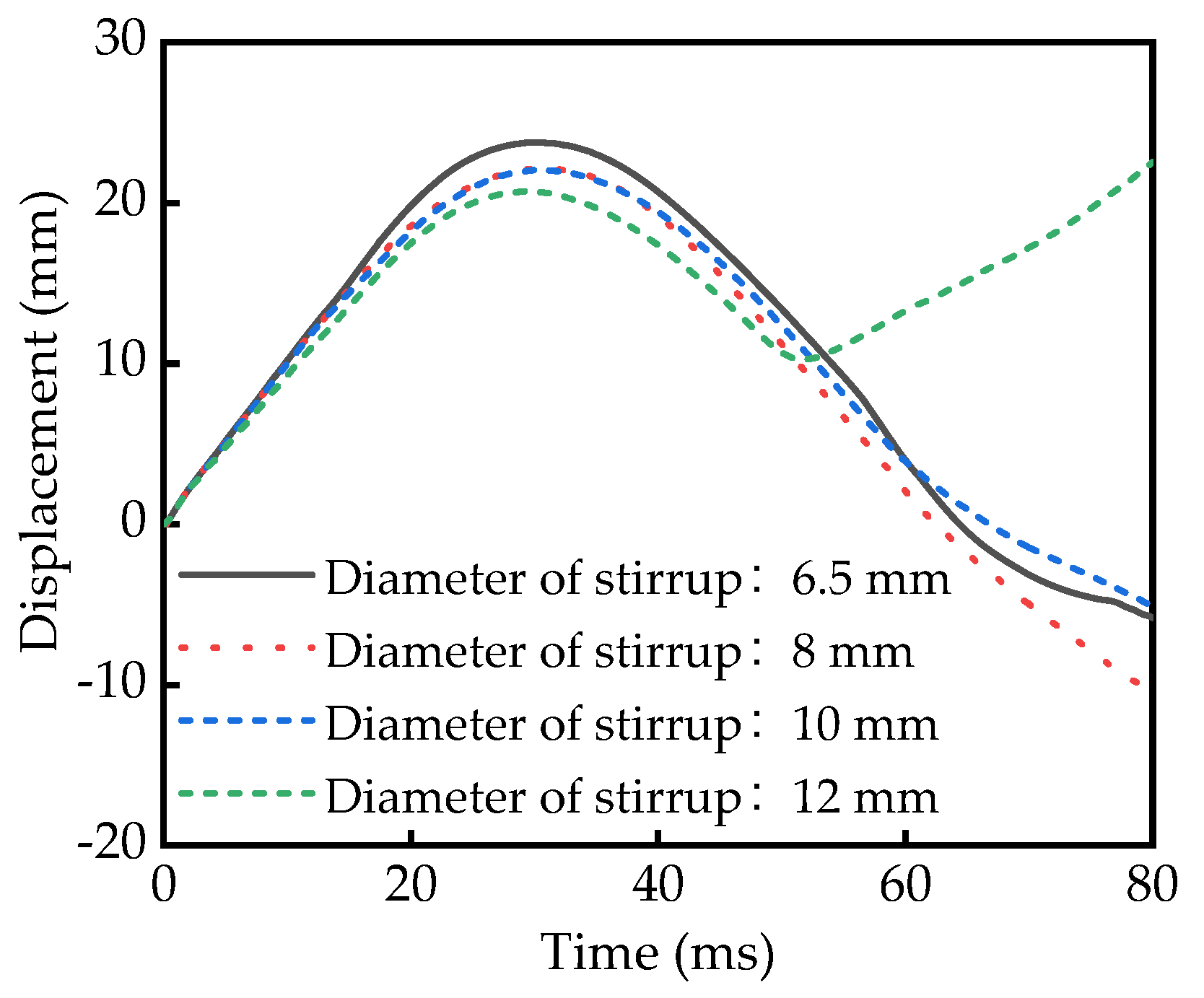
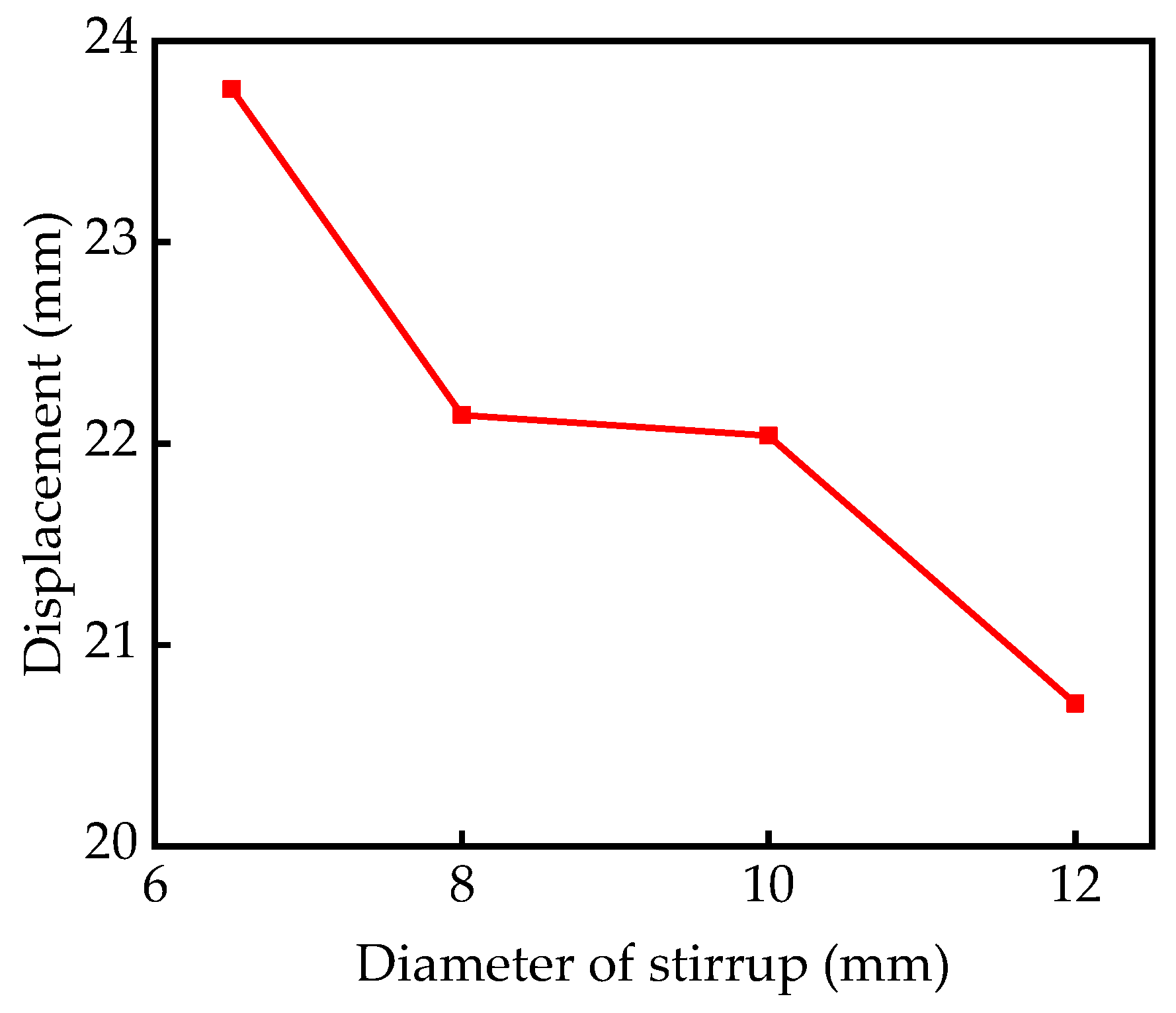
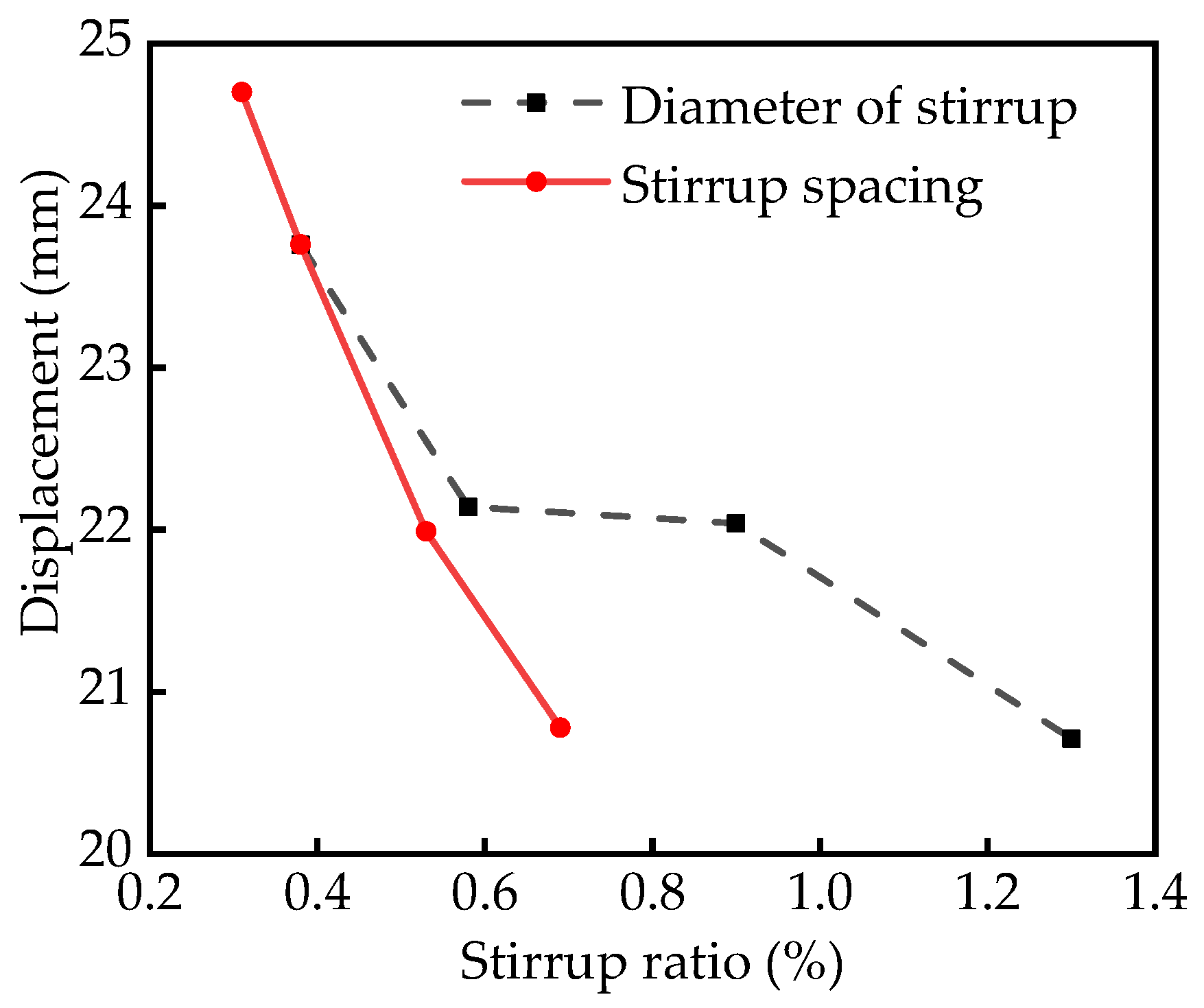
5.3. Stirrup Ratio Diameter of Stirrup
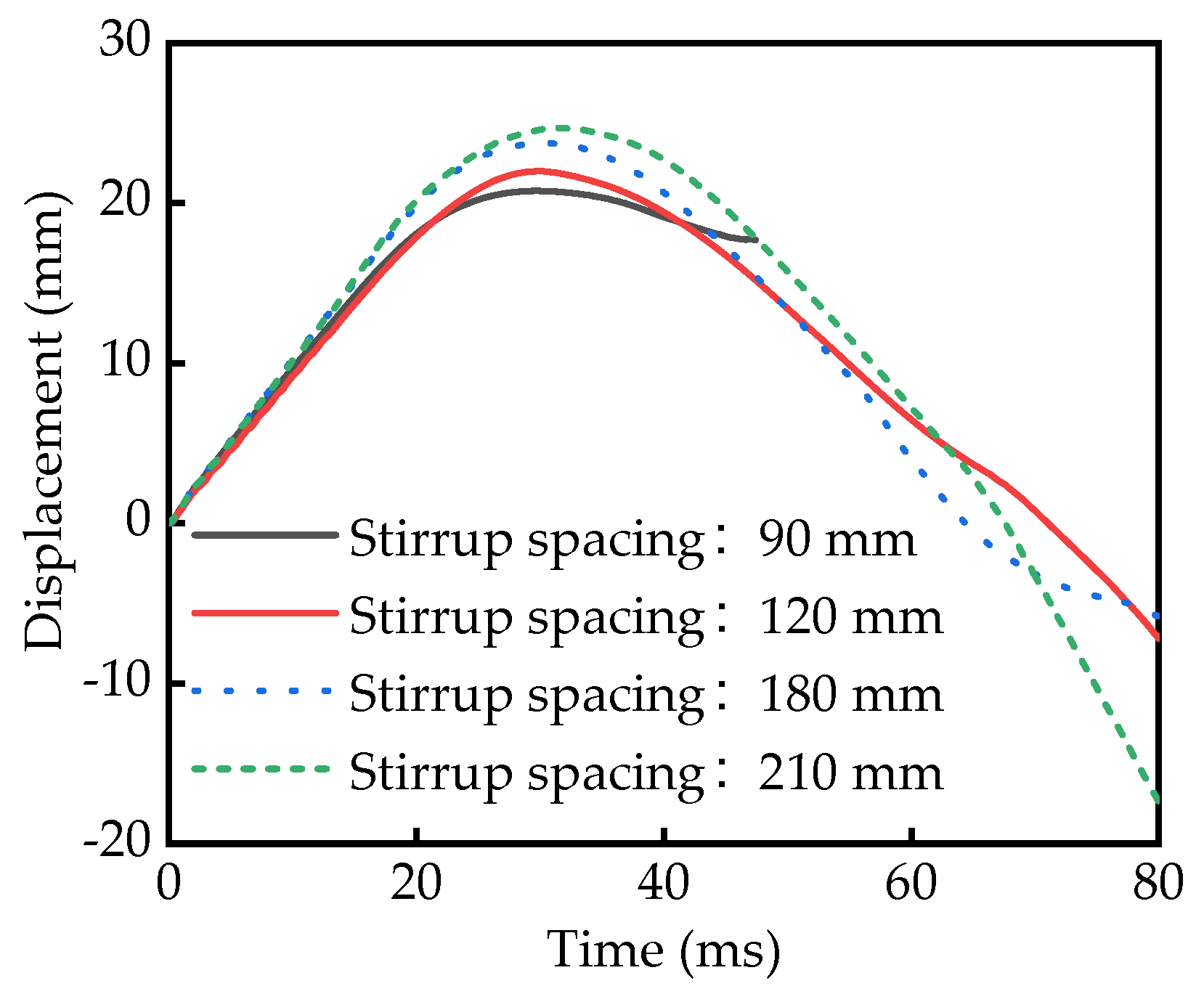
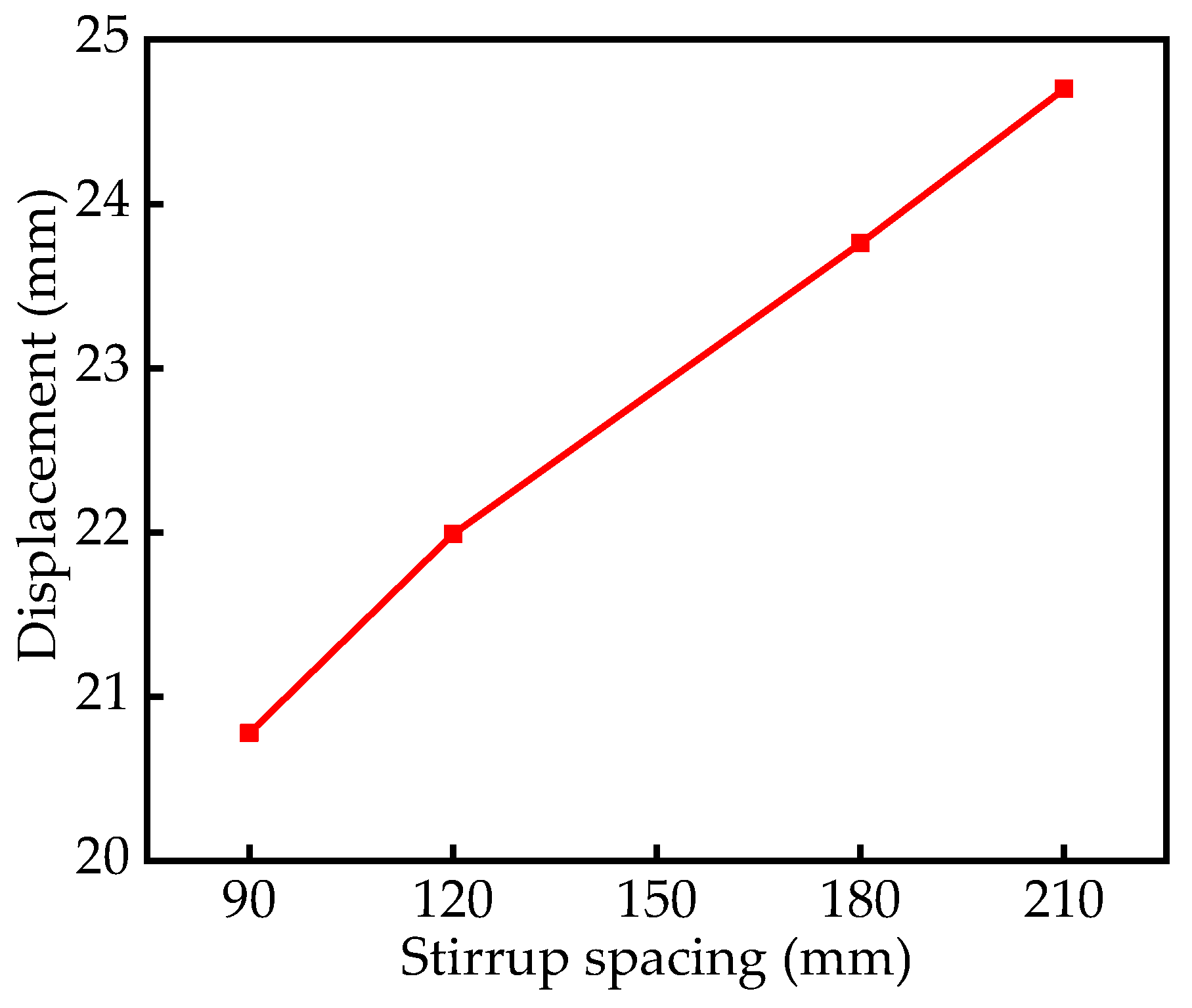
5.4. Stirrup Ratio–Stirrup Spacing
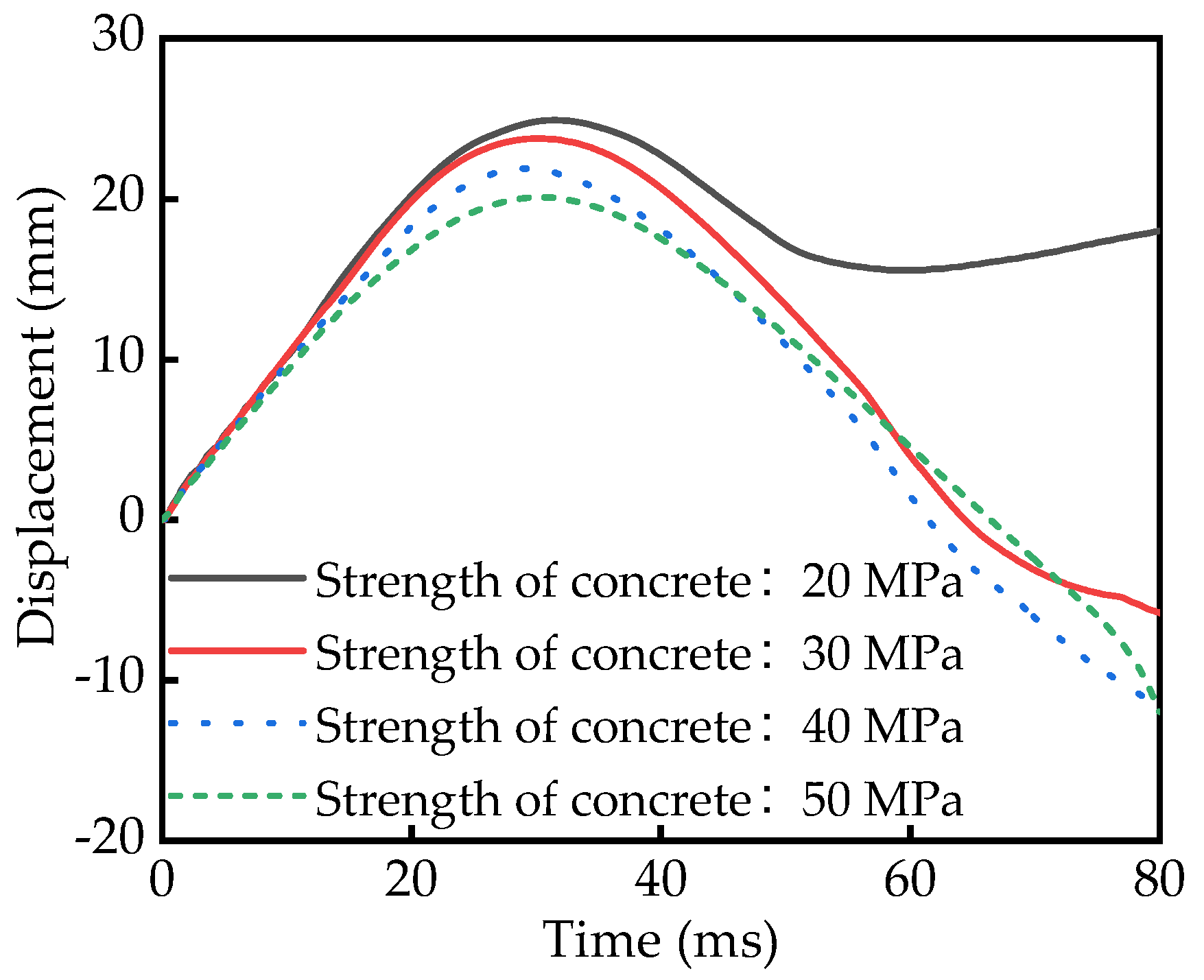
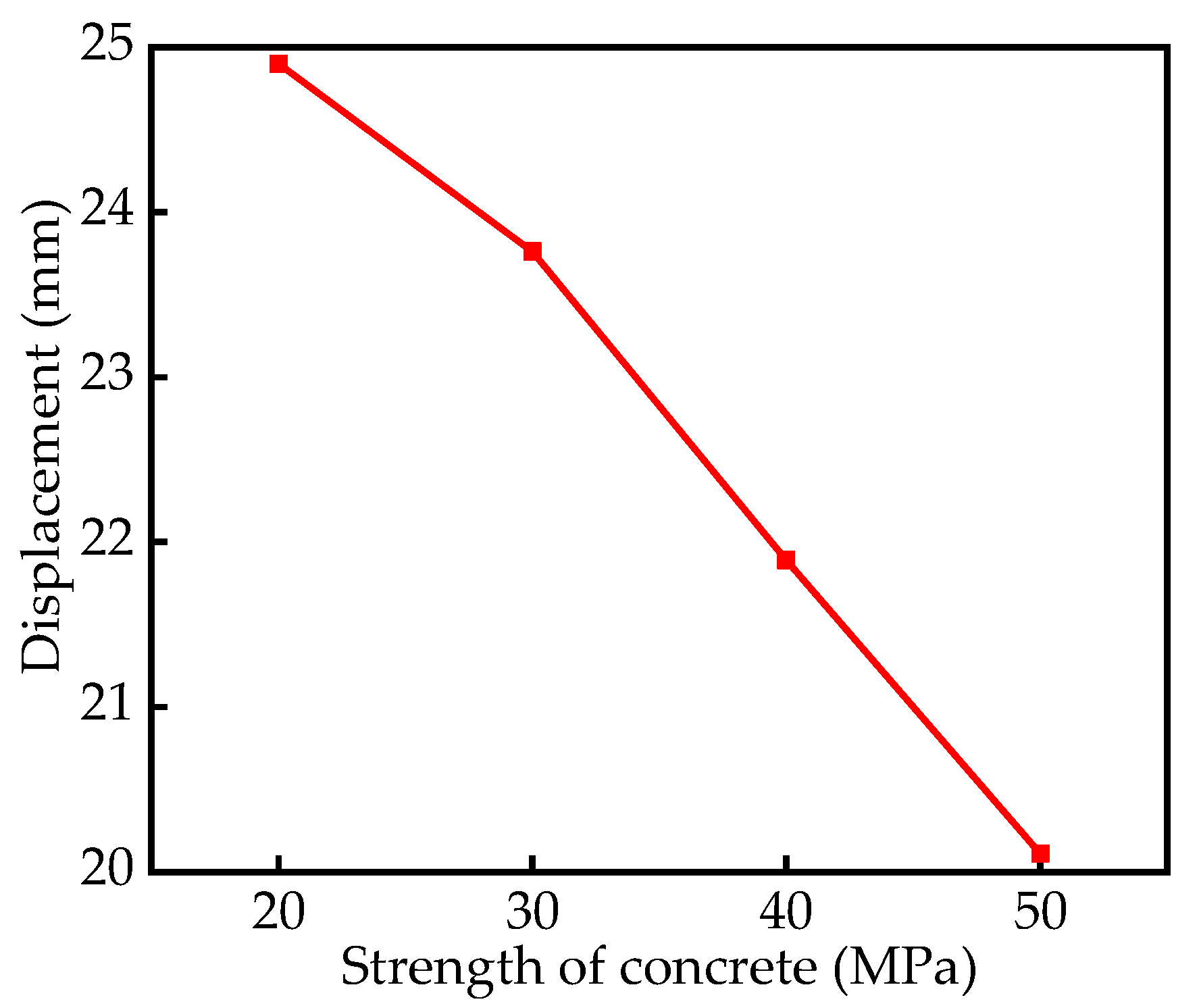
5.5. Strength of Concrete
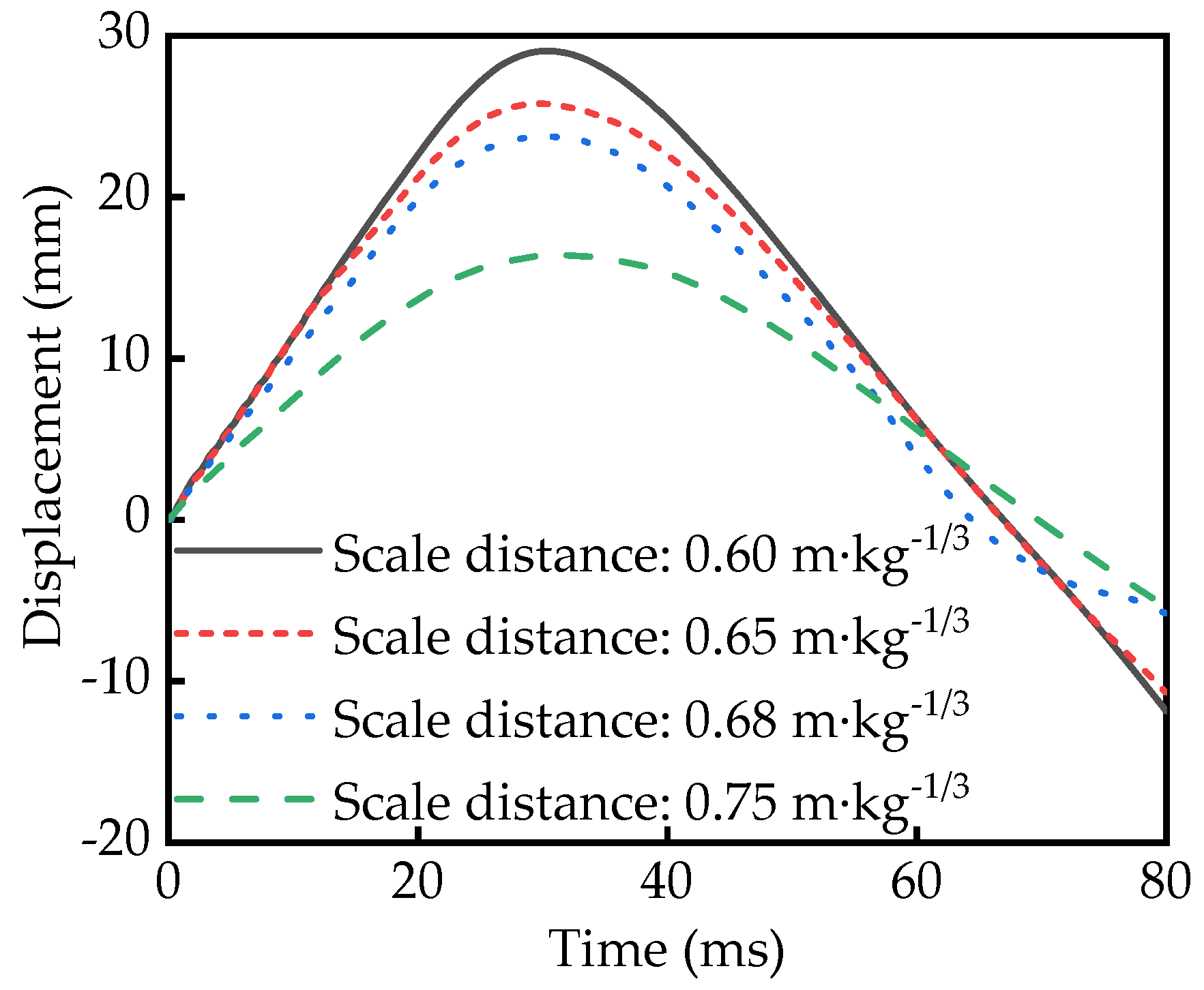
5.6. Scale Distance
5.7. Strength of Longitudinal Reinforcement
6. Sensitivity Analysis of Influencing Factors
7. Discussion
8. Conclusions
- By changing the diameter and number of longitudinal reinforcements, the reinforcement ratio can be changed. However, when the reinforcement ratio is the same, the mid-span peak displacement of the RC column obtained by changing the number of longitudinal reinforcements is smaller than that obtained by changing the diameter of longitudinal reinforcement. When designing and constructing RC structures, controlling the reinforcement ratio by changing the number of longitudinal reinforcements can make the RC structures have better blast resistance;
- By changing the diameter and spacing of the stirrup, the stirrup ratio can be changed. However, when the stirrup ratio is the same, the mid-span peak displacement of the RC column obtained by changing the stirrup spacing is smaller than that obtained by changing the diameter of the stirrup. When designing and constructing RC structures, controlling the stirrup ratio by changing the stirrup spacing can improve the blast resistance of the RC structures;
- The grey relation degree of the influencing factors on the mid-span peak displacement of RC columns are in descending order: stirrup spacing, the diameter of the stirrup, scale distance, diameter of longitudinal reinforcement, number of longitudinal reinforcement, and concrete strength. The spacing and diameter of the stirrup have a significant impact on the mid-span peak displacement of RC columns, with relation degrees of 0.6914 and 0.6660, respectively. By quantitatively expressing the strength of the correlation of influencing factors, more consideration should be given to changing the influencing factors of strong correlation in the design and construction of RC structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, C.; Jia, X.; Huang, Z.; Zhao, L.; Shang, W. Damage of full-scale reinforced concrete beams under contact explosion. Int. J. Impact Eng. 2022, 163, 104180. [Google Scholar] [CrossRef]
- Andreotti, R.; Riganti, G.; Boniardi, M. Numerical simulation of a terrorist attack. Appl. Mech. Mater. 2011, 1381, 308–313. [Google Scholar] [CrossRef]
- Anas, S.; Alam, M.; Umair, M. Experimental and numerical investigations on performance of reinforced concrete slabs under explosive-induced air-blast loading: A state-of-the-art review. Structures 2021, 31, 428–461. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, F.; Zou, J. Numerical simulation of gas extraction in coal seam strengthened by static blasting. Sustainability 2022, 14, 12484. [Google Scholar] [CrossRef]
- Zhang, B.; Zhai, D.; Wang, W. Failure mode analysis and dynamic response of a coal mine refuge chamber with a gas explosion. Appl. Sci. 2016, 6, 145. [Google Scholar] [CrossRef]
- Pak, S.; Jung, S.; Roh, C.; Kang, C. Case Studies for Dangerous Dust Explosions in South Korea during Recent Years. Sustainability 2019, 11, 4888. [Google Scholar] [CrossRef]
- Xue, Y.; Chen, G.; Zhang, Q.; Xie, M.; Ma, J. Simulation of the dynamic response of an urban utility tunnel under a natural gas explosion. Tunn. Undergr. Space Technol. 2021, 108, 103713. [Google Scholar] [CrossRef]
- Cai, P.; Li, M.; Liu, Z.; Li, P.; Zhao, Y.; Zhou, Y. Experimental and numerical study of natural gas leakage and explosion characteristics. ACS Omega 2022, 7, 25278–25290. [Google Scholar] [CrossRef]
- Huang, L.; Pei, S.; Wang, Y.; Zhang, L.; Ren, S.; Zhang, Z.; Xiao, Y. Assessment of flammability and explosion risks of natural gas-air mixtures at high pressure and high temperature. Fuel 2019, 247, 47–56. [Google Scholar] [CrossRef]
- Yang, S.; Ning, J.; Xu, X. Fragment theoretical model of concrete blocks subjected to blast loads. Int. J. Impact Eng. 2023, 176, 104562. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, Q.; Yuan, M.; Qian, X.; Li, M.; Wu, H.; Shen, X.; Liang, Y. Traceability and failure consequences of natural gas explosion accidents based on key investigation technology. Eng. Fail. Anal. 2022, 139, 106448. [Google Scholar] [CrossRef]
- Eskew, E.; Jang, S. Damage assessment of a building subjected to a terrorist attack. Adv. Struct. Eng. 2014, 17, 1693–1704. [Google Scholar] [CrossRef]
- Codina, R.; Ambrosini, D.; Borbon, F. Alternatives to prevent progressive collapse protecting reinforced concrete columns subjected to near field blast loading. Procedia Eng. 2017, 199, 2445–2450. [Google Scholar] [CrossRef]
- Dua, A.; Braimah, A.; Kumar, M. Experimental and numerical investigation of rectangular reinforced concrete columns under contact explosion effects. Eng. Struct. 2020, 205, 109891. [Google Scholar] [CrossRef]
- Abedini, M.; Mutalib, A.; Raman, S.; Baharom, S.; Nouri, J. Prediction of residual axial load carrying capacity of reinforced concrete (RC) columns subjected to extreme dynamic loads. Am. J. Eng. Appl. Sci. 2017, 10, 431–448. [Google Scholar] [CrossRef]
- Yu, J.; Yu, X.; Tang, J.; Deng, Y. Local damage of precast concrete columns with grout sleeve connections under contact detonation. Eng. Struct. 2022, 265, 114499. [Google Scholar] [CrossRef]
- Yao, S.; Zhang, D.; Chen, X.; Lu, F.; Wang, W. Experimental and numerical study on the dynamic response of RC slabs under blast loading. Eng. Fail. Anal. 2016, 66, 120–129. [Google Scholar] [CrossRef]
- Yao, S.; Zhang, D.; Lu, F.; Wang, W.; Chen, X. Damage features and dynamic response of RC beams under blast. Eng. Fail. Anal. 2016, 62, 103–111. [Google Scholar] [CrossRef]
- Conrad, K.; Abass, B. Effects of transverse reinforcement spacing on the response of reinforced concrete columns subjected to blast loading. Eng. Struct. 2017, 142, 148–164. [Google Scholar]
- Hassan, A.; Frederic, P.; Russell, P.; Murat, S. Behavior of ultra-high performance fiber reinforced concrete columns under blast loading. Int. J. Impact Eng. 2015, 80, 185–202. [Google Scholar]
- Li, Z.; Zhang, X.; Shi, Y.; Wu, C.; Li, J. Predication of the residual axial load capacity of CFRP-strengthened RC column subjected to blast loading using artificial neural network. Eng. Struct. 2021, 242, 112519. [Google Scholar] [CrossRef]
- Ushapriya, B.; Kumar, A. Behaviour of raked column subjected to blast loading. J. Build. Pathol. Rehabil. 2023, 8, 19. [Google Scholar] [CrossRef]
- Park, J.; Kim, M.; Scanlon, A.; Choi, H.; Lee, Y. Residual strength of reinforced concrete columns subjected to blast loading. Mag. Concrete Res. 2014, 66, 60–71. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Zhao, Z.; Qiang, H.; Yang, K.; Wang, X. Design and performance evaluation framework for seismically isolated reinforcement concrete columns subjected to blast loads. Structures 2022, 45, 2239–2252. [Google Scholar] [CrossRef]
- Sinha, A.; Kanaujia, S.; Kumar, M.; Sachdeva, A.; Singh, S. Effect of positional eccentricity of blast source on beam–column joint response of framed systems. Innov. Infrastruct. Solut. 2022, 7, 178. [Google Scholar] [CrossRef]
- Abebe, S.; Getachew, S. Numerical study on effect of constant and variable axial loads on RC column subjected to blast load. Heliyon 2022, 8, e11681. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Hu, Y.; Chen, L.; Li, Z.; Xiang, H. Experimental investigation into the close-in blast performance of RC columns with axial loading. Eng. Struct. 2022, 268, 114688. [Google Scholar] [CrossRef]
- Rong, Q.; Zhao, Z.; Hou, X.; Jiang, Z. A P-I Diagram Approach for Predicting Dynamic Response and Damage Assessment of Reactive Power Concrete Columns Subjected to Blast Loading. Buildings 2022, 12, 462. [Google Scholar] [CrossRef]
- Ghasemi, M.; Zhang, C.; Khorshidi, H.; Sun, L. Development of P-I model for FRP composite retrofitted RC columns subjected to high strain rate loads using LBE function. Eng. Struct. 2022, 252, 113580. [Google Scholar]
- Ju, S.; Kwak, H. A FE model to evaluate the resisting capacity of RC beams and columns under blast loading based on P-I diagram. Int. J. Impact Eng. 2022, 161, 104113. [Google Scholar] [CrossRef]
- Li, M.; Xia, M.; Zong, Z.; Wu, G.; Zhang, X. Residual axial capacity of concrete-filled double-skin steel tube columns under close-in blast loading. J. Constr. Steel Res. 2023, 201, 107697. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, H.; Hao, Y. Prediction of blast response of RC columns considering dynamic bond-slip between reinforcement and concrete. Eng. Struct. 2023, 283, 115921. [Google Scholar] [CrossRef]
- Li, Z.; Zhong, B.; Shi, Y.; Yan, J. Nonlocal formulation for numerical analysis of post-blast behavior of RC columns. Int. J. Concr. Struct. M. 2017, 11, 403–413. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, D.; Lu, F.; Wang, S.; Tang, F. Experimental study and numerical simulation of the damage mode of a square reinforced concrete slab under close-in explosion. Eng. Fail. Anal. 2013, 27, 41–51. [Google Scholar] [CrossRef]
- Ma, L.; Wu, H.; Fang, Q. A unified performance-based blast-resistant design approach for RC beams/columns. Int. J. Impact Eng. 2023, 173, 104459. [Google Scholar]
- Welt, T.; Lehman, D.; Lowes, L.; Lafave, J. A constitutive model for confined concrete in slender rectangular RC sections incorporating compressive energy. Constr. Build. Mater. 2018, 193, 344–362. [Google Scholar] [CrossRef]
- Shi, Y.; Hu, Y.; Liu, S.; Cui, J.; Chen, L. Mitigation of the blast load on RC column by hanging granite slabs. Eng. Struct. 2023, 280, 115668. [Google Scholar] [CrossRef]
- Jiang, Z.; Rong, Q.; Hou, X.; Zhao, Z.; Yang, E. Methodology for Predicting the Structural Response of RPC-Filled Steel Tubular Columns under Blast Loading. Appl. Sci. 2022, 12, 9142. [Google Scholar] [CrossRef]
- Mohammed, T.; Abebe, S. Numerical investigation on CFRP strengthening and reinforcement bar detailing of RC columns to resist blast load. Heliyon 2022, 8, e10059. [Google Scholar] [CrossRef]
- Fang, C.; Linzell, D.; Yosef, T.; Rasmussen, J. Numerical modeling and performance assessment of bridge column strengthened by FRP and polyurea under combined collision and blast loading. J. Compos. Constr. 2022, 26, 04022002. [Google Scholar] [CrossRef]
- Fang, C.; Yosef, T.; Linzell, D.; Rasmussen, J. Computational modeling and dynamic response of highway bridge columns subjected to combined vehicle collision and air blast. Eng. Fail. Anal. 2021, 125, 105389. [Google Scholar] [CrossRef]
- Fang, C.; Yosef, T.; Linzell, D.; Rasmussen, J. Residual axial capacity estimates for bridge columns subjected to combined vehicle collision and air blast. J. Bridge Eng. 2021, 26, 04021035. [Google Scholar] [CrossRef]
- Shi, Y.; Sun, X.; Cui, J. Reliability analysis of reinforced concrete columns under combined seismic and blast loads. Sci. China Technol. Sc. 2023, 66, 363–377. [Google Scholar] [CrossRef]
- Lee, J.; Aoude, H.; Yoon, Y.; Mitchell, D. Impact and blast behavior of seismically-detailed RC and UHPFRC-Strengthened columns. Int. J. Impact Eng. 2020, 143, 103628. [Google Scholar] [CrossRef]
- Xu, Z.; Li, J.; Wu, C. A numerical study of blast resistance of fire damaged ultra-high performance concrete columns. Eng. Struct. 2023, 279, 115613. [Google Scholar] [CrossRef]
- Chen, W.; Zhou, Z.; Zou, H.; Guo, Z. Predictions of residual carrying-capacities for fire and near-field blast-damaged reactive powder concrete-filled steel tube columns. Int. J. Prot. Struct. 2018, 9, 525–553. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, W.; Zhang, Y.; Zou, H. Post fire blast-resistances of RPC-FST columns using improved Grigorian model. Int. J. Impact Eng. 2017, 107, 80–95. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Ye, M.; Li, M.; Wu, Y. Blast fragility assessment of aging coastal RC columns exposed to non-uniform CIC attacks using LBE function. J. Build. Eng. 2023, 71, 106510. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, H.; Hao, Y. Blast fragility analysis of RC columns considering chloride-induced corrosion of steel reinforcement. Struct. Saf. 2022, 96, 102200. [Google Scholar] [CrossRef]
- Deng, J. Grey Theory, 1st ed.; Huazhong University of Science and Technology Press: Wuhan, China, 2002; pp. 1–15. [Google Scholar]
- Liu, S.; Guo, T.; Dang, Y. Grey System Theory and Its Application, 2nd ed.; Science Press: Beijing, China, 1999; pp. 1–20. [Google Scholar]
- Wu, Y.; Mu, C.; Zhang, H.; Zhou, H. Sensitivity analysis of influencing factors of underground civil air defense construction vibration under vehicle load. Appl. Sci. 2022, 12, 12361. [Google Scholar] [CrossRef]
- Xie, L.; Wu, C.; Duan, M.; Lyu, N. Analysis of freeway safety influencing factors on driving workload and performance based on the gray correlation method. J. Adv. Transport. 2021, 2021, 6566207. [Google Scholar] [CrossRef]
- Hu, W.; Zhao, Q.; Liu, Y.; Li, Z.; Kong, X. Damage evaluation of the paving around manholes under vehicle dynamic load. Adv. Mater. Sci. Eng. 2020, 2020, 6510439. [Google Scholar] [CrossRef]
- Yan, J.; Liu, Y.; Li, Z.; Xu, Z.; Huang, F. Effects of transverse reinforcement ratio and axial load on the blast response of steel reinforced concrete columns. Acta Armamentarii 2020, 41, 35–43. [Google Scholar]
- Comite Euro-International du Beton. CEB-FIP Model Code 1990, 1st ed.; Thomas Telford: London, UK, 1990. [Google Scholar]
- Malvar, L.; Crawford, J. Dynamic increase factors for concrete. In Proceedings of the Twenty-Eighth DDESB Seminar, Orlando, FL, USA, 18–20 August 1998. [Google Scholar]
- Crawford, J.; Malver, L. User’s and Theoretical Manual for K&C Concrete Model; Technical Report TR-97-53.1; Karagozian & Case: Glendale, CA, USA, 1997. [Google Scholar]
- Li, T. Dynamic Response and Damage Assessment of Reinforced Concrete Slabs Subjected to Blast Loading. Ph.D. Thesis, Chang’an University, Xi’an, China, 2012. [Google Scholar]
- Wang, W. Study on Damage Effects and Assessments Method of Reinforced Concrete Structural Members under Blast Loading. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2012. [Google Scholar]




| Material Type | Young’s Modulus (GPa) | Poisson’s Ratio | Yield Stress (MPa) | Ultimate Strain |
|---|---|---|---|---|
| Longitudinal reinforcement | 207 | 0.3 | 400 | 0.22 |
| Stirrup | 207 | 0.3 | 518 | 0.085 |
| Density (kg·m−3) | Poisson’s Ratio | Strength of Concrete (MPa) |
|---|---|---|
| 2400 | 0.2 | 31.3 |
| Working Conditions | Diameter of Longitudinal Reinforcement (mm) | Number of Longitudinal Reinforcement | Diameter of Stirrup (mm) | Stirrup Spacing (mm) | Strength of Concrete (MPa) | Scale Distance (m·kg−1/3) | Strength of Longitudinal Reinforcement (MPa) |
|---|---|---|---|---|---|---|---|
| 1 | 8/10/12/14 | 4 | 6.5 | 180 | 30 | 0.68 | 400 |
| 2 | 12 | 4/8/12/16 | 6.5 | 180 | 30 | 0.68 | 400 |
| 3 | 12 | 4 | 6.5/8/10/12 | 180 | 30 | 0.68 | 400 |
| 4 | 12 | 4 | 6.5 | 90/120/180/210 | 30 | 0.68 | 400 |
| 5 | 12 | 4 | 6.5 | 180 | 20/30/40/50 | 0.68 | 400 |
| 6 | 12 | 4 | 6.5 | 180 | 30 | 0.6/0.65/0.68/0.75 | 400 |
| 7 | 12 | 4 | 6.5 | 180 | 30 | 0.68 | 300/335/400/500 |
| Diameter of Longitudinal Reinforcement (mm) | Reinforcement Ratio (%) | Displacement (mm) |
|---|---|---|
| 8 | 0.89 | 31.02 |
| 10 | 1.40 | 25.63 |
| 12 | 2.01 | 23.76 |
| 14 | 2.74 | 17.89 |
| Number of Longitudinal Reinforcement (mm) | Reinforcement Ratio (%) | Displacement (mm) |
|---|---|---|
| 4 | 2.01 | 23.76 |
| 8 | 4.02 | 1.62 |
| 12 | 6.03 | 1.31 |
| 16 | 8.04 | 1.18 |
| Diameter of Stirrup (mm) | Stirrup Ratio (%) | Displacement (mm) |
|---|---|---|
| 6.5 | 0.38 | 23.76 |
| 8 | 0.58 | 22.14 |
| 10 | 0.90 | 22.04 |
| 12 | 1.30 | 20.71 |
| Stirrup Spacing (mm) | Reinforcement Ratio (%) | Displacement (mm) |
|---|---|---|
| 90 | 0.69 | 20.78 |
| 120 | 0.53 | 21.99 |
| 180 | 0.38 | 23.76 |
| 210 | 0.31 | 24.70 |
| Strength of Concrete (MPa) | Displacement (mm) |
|---|---|
| 20 | 24.90 |
| 30 | 23.76 |
| 40 | 21.89 |
| 50 | 20.11 |
| Scale Distance (m·kg−1/3) | Displacement (mm) |
|---|---|
| 0.6 | 29.06 |
| 0.65 | 25.80 |
| 0.68 | 23.76 |
| 0.75 | 16.40 |
| Strength of Longitudinal Reinforcement (MPa) | Displacement (mm) |
|---|---|
| 300 | 22.75 |
| 335 | 22.75 |
| 400 | 23.76 |
| 500 | 22.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Xie, Q.; Mu, C. Sensitivity Analysis of Factors Influencing the Blast Resistance of Reinforced Concrete Columns Based on Grey Relation Degree. Sustainability 2023, 15, 12285. https://doi.org/10.3390/su151612285
Wu Y, Xie Q, Mu C. Sensitivity Analysis of Factors Influencing the Blast Resistance of Reinforced Concrete Columns Based on Grey Relation Degree. Sustainability. 2023; 15(16):12285. https://doi.org/10.3390/su151612285
Chicago/Turabian StyleWu, Yangyong, Quanmin Xie, and Chaomin Mu. 2023. "Sensitivity Analysis of Factors Influencing the Blast Resistance of Reinforced Concrete Columns Based on Grey Relation Degree" Sustainability 15, no. 16: 12285. https://doi.org/10.3390/su151612285
APA StyleWu, Y., Xie, Q., & Mu, C. (2023). Sensitivity Analysis of Factors Influencing the Blast Resistance of Reinforced Concrete Columns Based on Grey Relation Degree. Sustainability, 15(16), 12285. https://doi.org/10.3390/su151612285










