System Design, Optimization and 2nd Law Analysis of a 100 MWe Double Reheat s-CO2 Power Plant at Full Load and Part Loads
Abstract
:1. Introduction
- To perform a system design of a 100 MWe coal-fired double reheat recompression s-CO2 system based on the parameters and configurations reported by Chen et al. [22].
- To evaluate its performance at full load as well as at part loads of 80%, 60% and 40% based on 1st and 2nd laws of thermodynamics.
- To optimize the performance based on thermal efficiency (1st law efficiency) at full load.
- Identify the crucial operational parameters that influence thermal efficiency.
- Identify the system components that contribute to high exergy destruction.
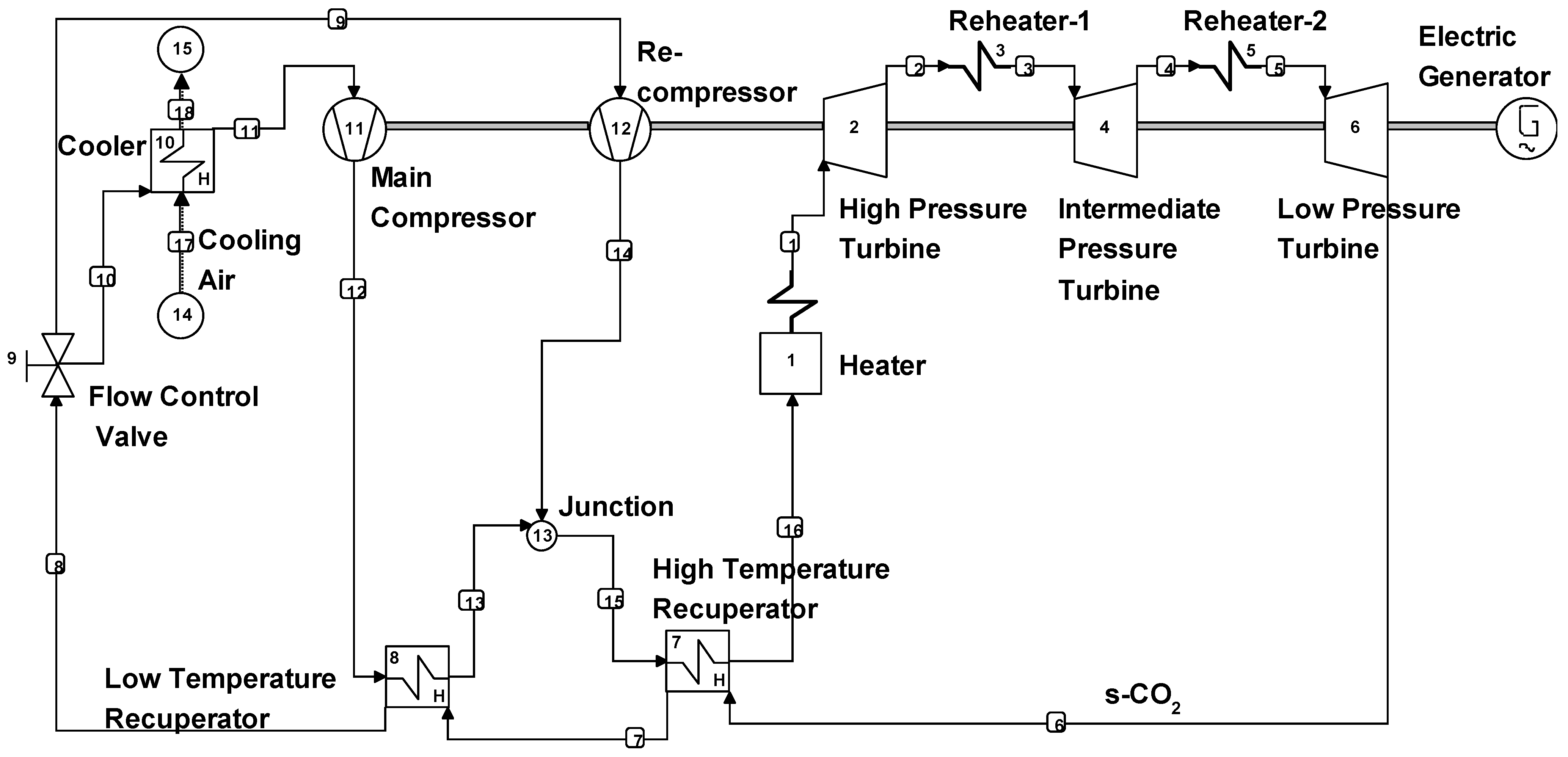
2. System Layout Description
- All components operate at a steady state.
- Changes in kinetic and potential energies are neglected for all fluid streams.
- All components are perfectly insulated and there is no heat exchange with the surroundings.
- The heat exchangers (recuperators and cooler) are the shell and tube type.
- The dead state conditions are taken to be 1 bar and 30 °C.
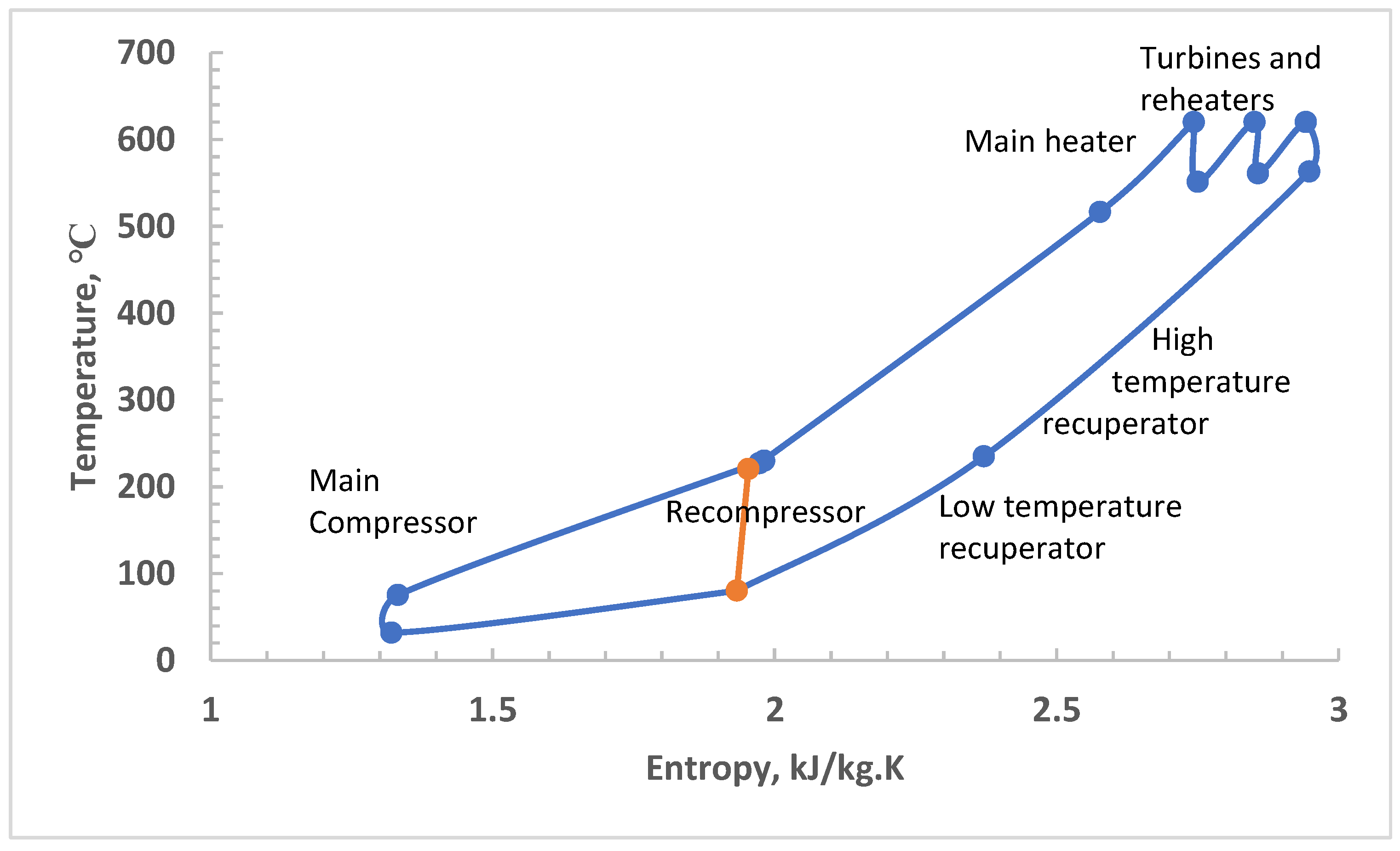
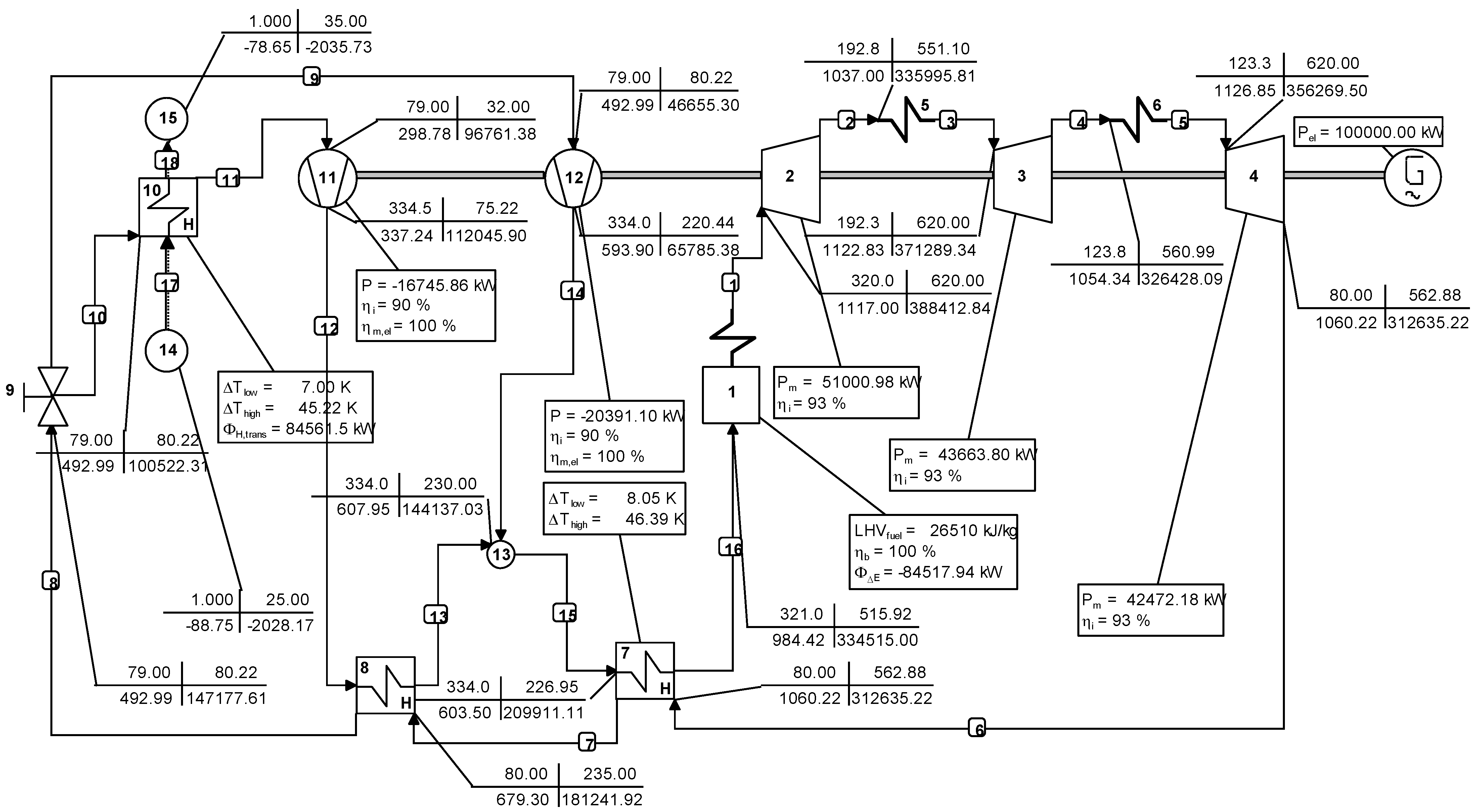
3. Results and Discussion
3.1. Optimization
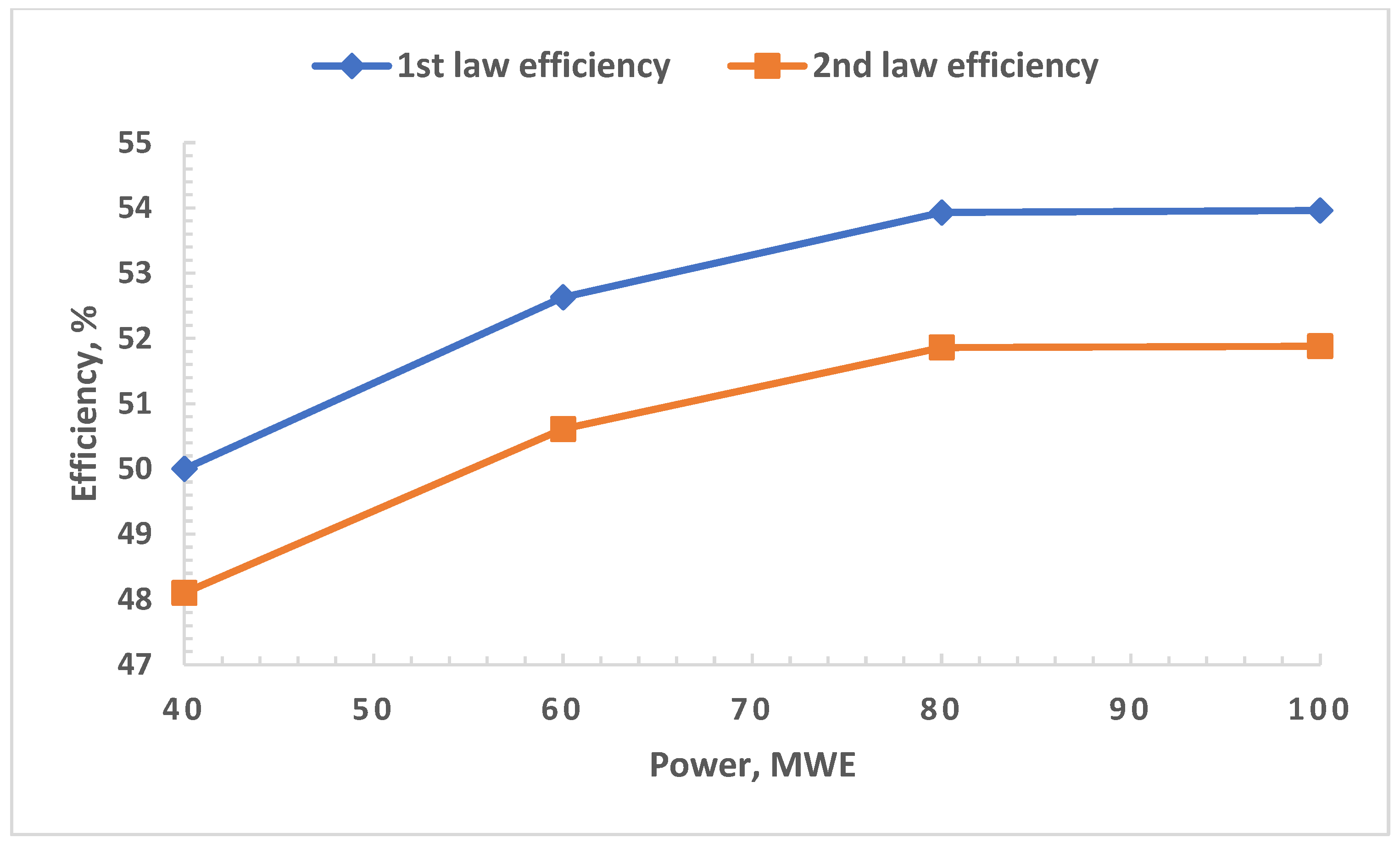
3.2. Part Load Performance
4. Conclusions
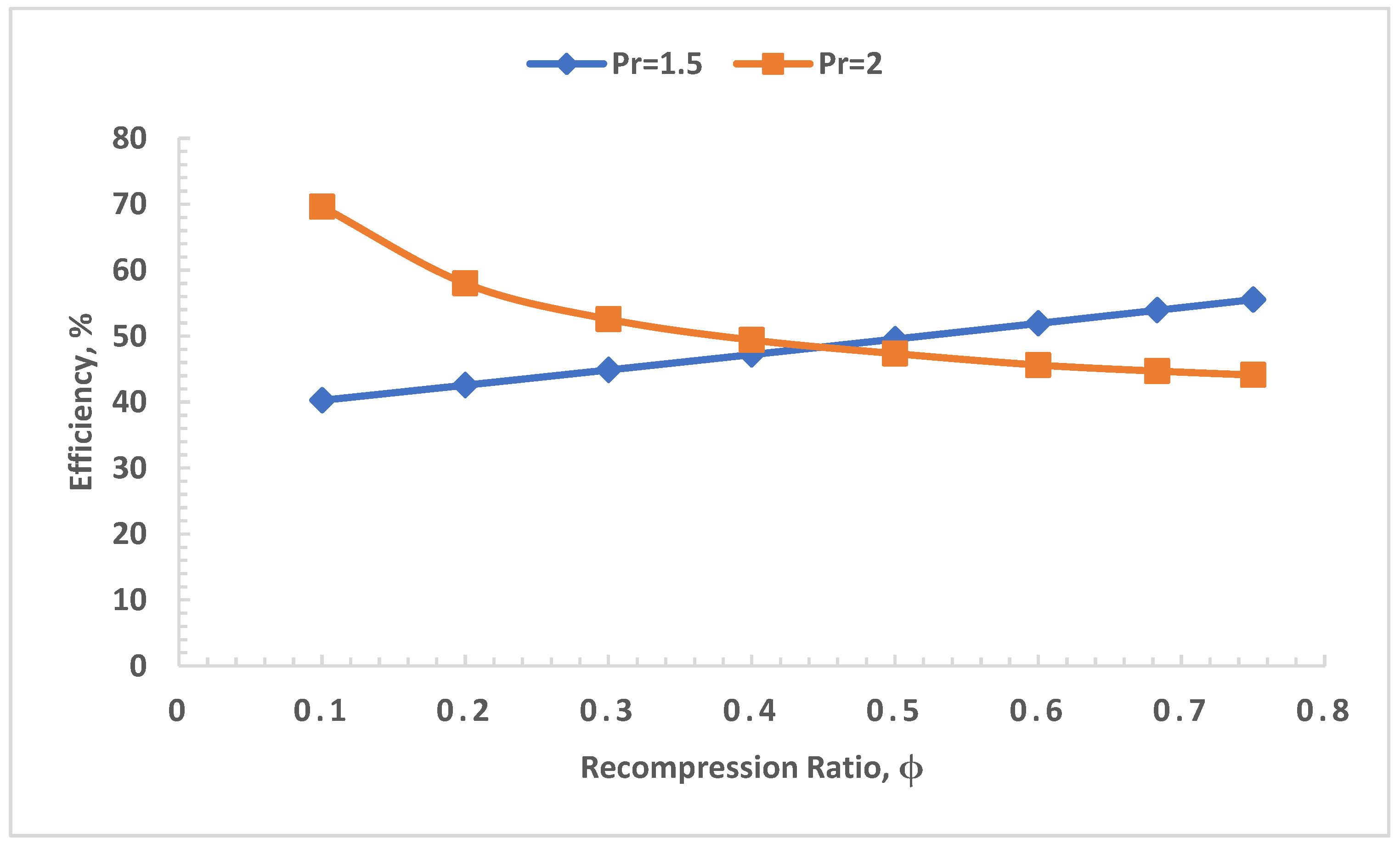
- Recompression ratio and turbine inlet pressures as well as pressure ratios were identified as crucial for improving the performance of the power plant. The power plant at full load was optimized and an estimated 1st law efficiency of 61.7% and 2nd law efficiency of 59.3% were attained.
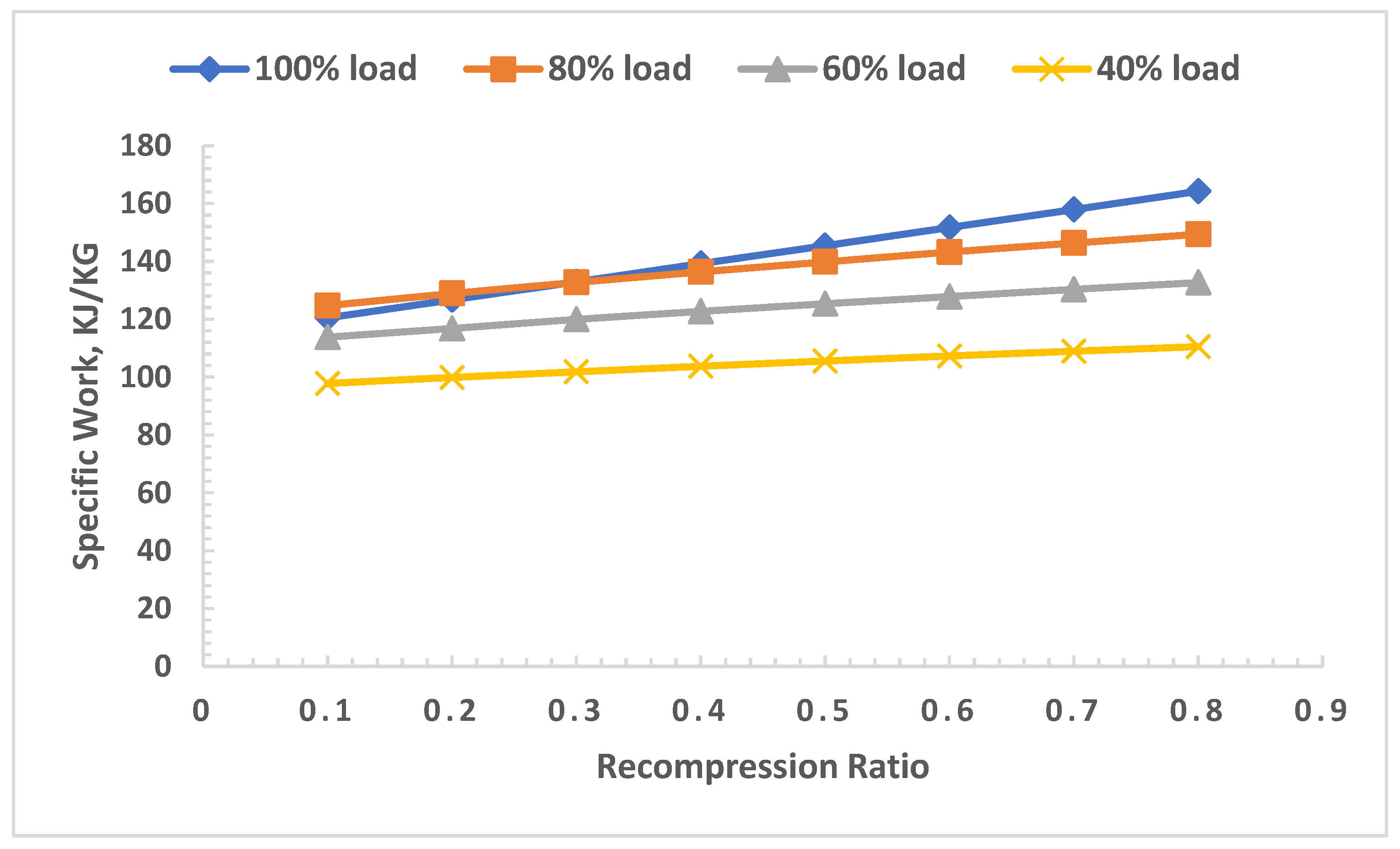
- The specific work was highest (~160 kJ/kg) at full load and almost the same at 80% load, especially at low recompression ratios. It dropped rapidly at lower loads, indicating that the recompression ratio should be kept high at lower loads.
- The power plant operated almost equally well at full load and 80% load while a drastic drop in efficiency was noticed at 60% and 40% loads compared to those at 100% load.
- Operational pressures decreased at part loads while few temperatures, especially at the turbine exit, increased marginally. The mass flow rate reduced at part load when compared to full load.
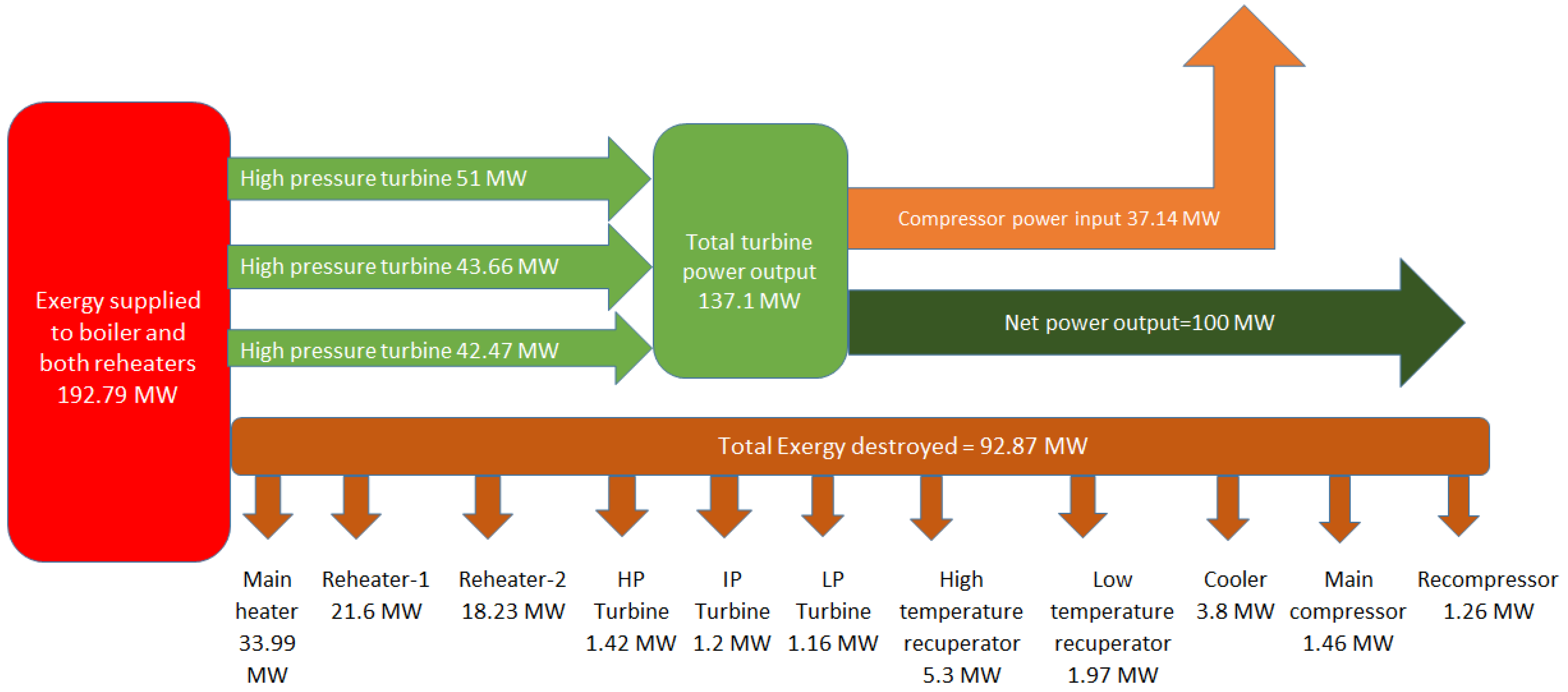
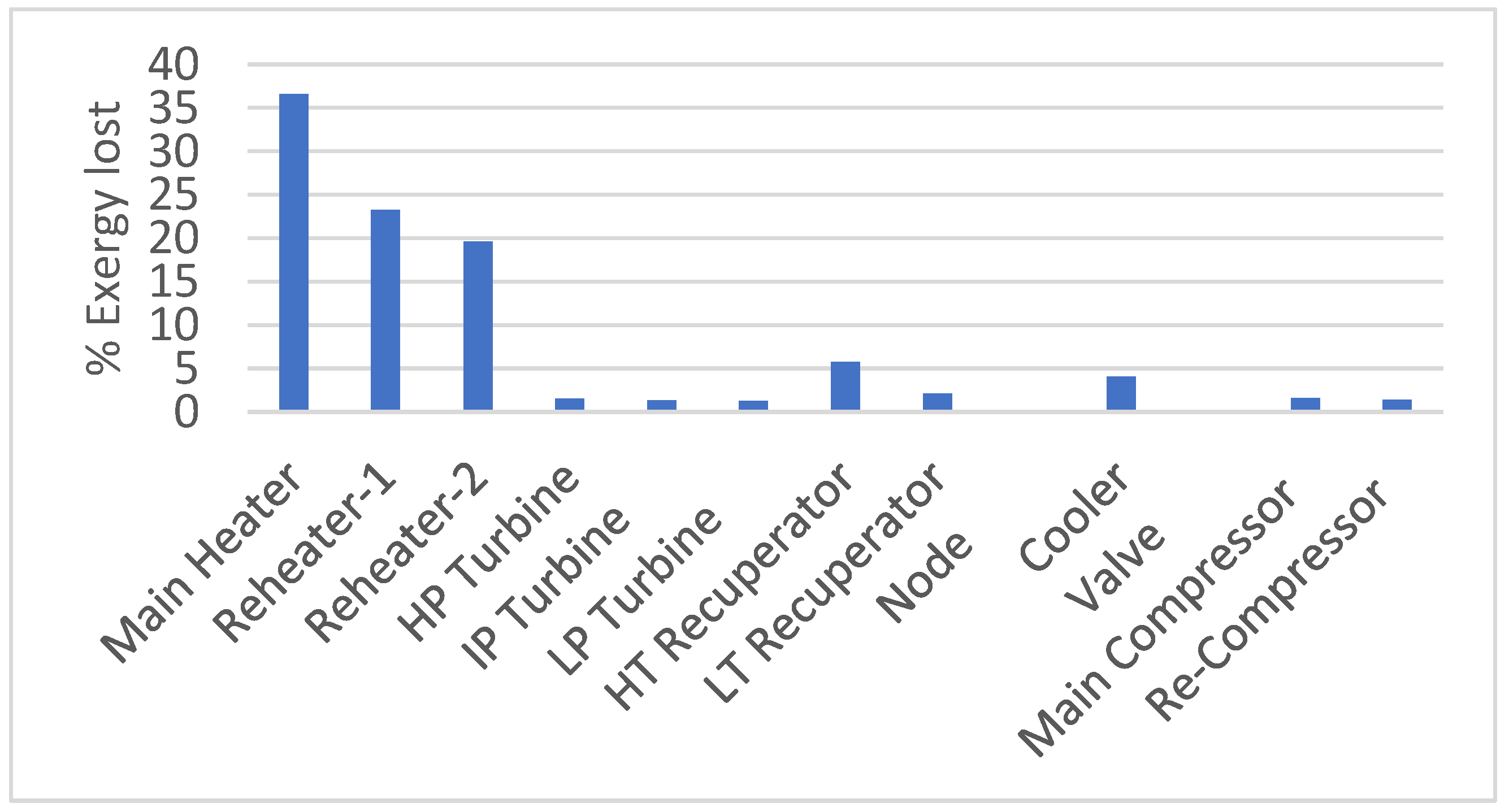
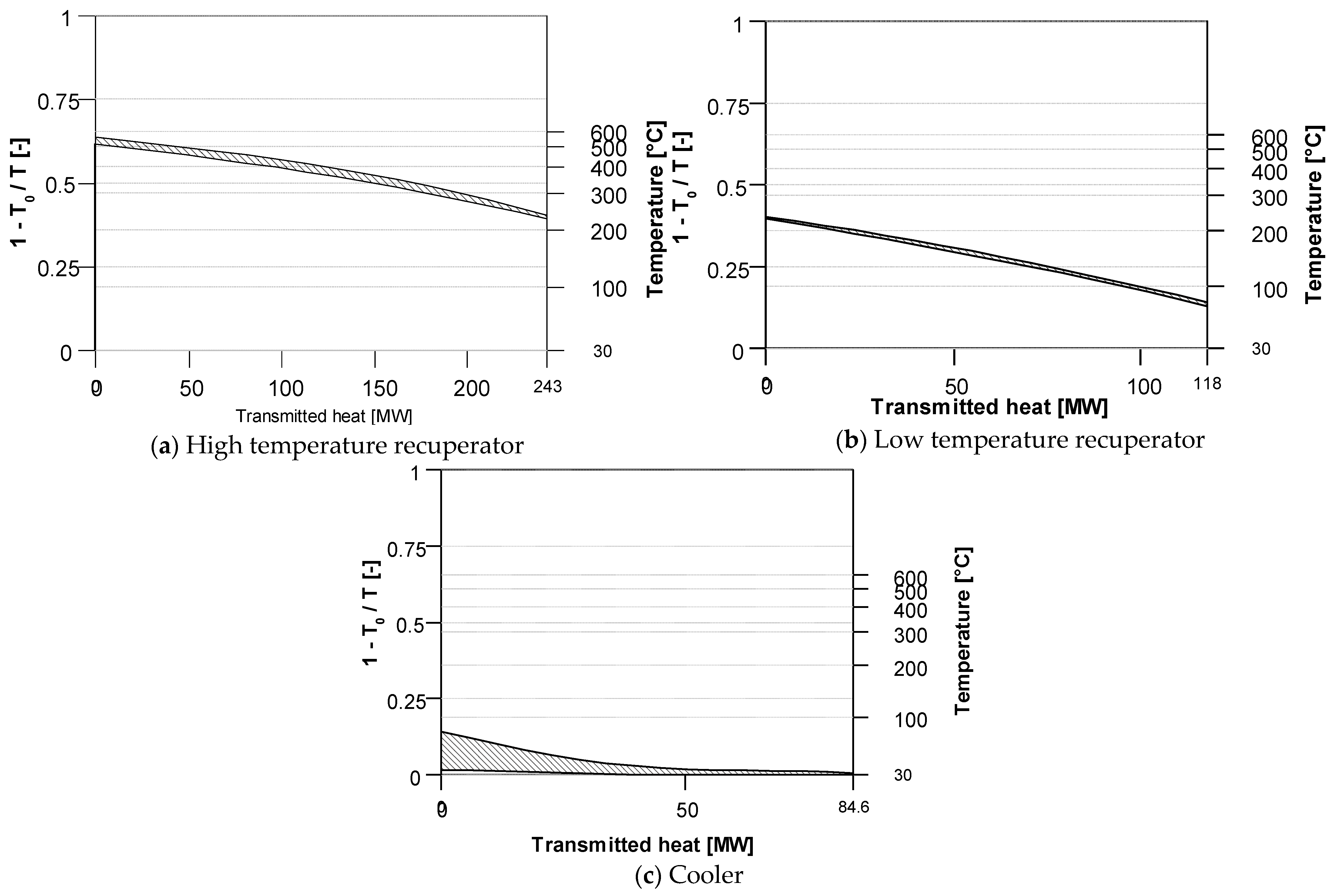
- Most of the exergy is destroyed in the main heater (>35%), re-heater (>20%), followed by the high-temperature recuperator and cooler.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Name |
| Rate of energy transfer, kW | |
| h | Specific enthalpy, kJ/kg |
| h0 | Dead state specific enthalpy, kJ/kg |
| Mass flow rate, kg/s | |
| Rate of heat transfer, kW | |
| S | Specific entropy, kJ/kg-K |
| S0 | Dead state specific entropy, kJ/kg-K |
| Sgen | Entropy generated, kJ/K |
| T | Absolute temperature, K |
| T0 | Dead state temperature, K |
| Rate of work, kW | |
| Rate of Exergy Transfer, kW | |
| Exergy destroyed, kW | |
| ϕ | Recompression ratio, (-) |
References
- Furlan, C.; Mortarino, C. Forecasting the impact of renewable energies in competition with non-renewable sources. Renew. Sustain. Energy Rev. 2018, 81, 1879–1886. [Google Scholar] [CrossRef]
- Javidkia, F.; Hashemi-Tilehnoee, M.; Zabihi, V. A comparison between fossil and nuclear power plants pollutions and their environmental effects. J. Energy Power Eng. 2011, 5, 811–820. [Google Scholar]
- Ryzhkov, A.F.; Bogatova, T.F.; Maslennikov, G.E.; Osipov, P.V.; Nizov, V.A. Creation of energy-efficient and environmentally friendly energy sources on fossil fuels to address global climate issues. J. Physics: Conf. Ser. 2020, 1677, 012115. [Google Scholar] [CrossRef]
- Sreekanth, M.; Kumar, R.R.; Kolar, A.K.; Leckner, B. Estimation of wood char size at the end of devolatilization in a bubbling fluidized bed combustor. Fuel 2008, 87, 3393–3402. [Google Scholar] [CrossRef]
- Yin, C.; Yan, J. Oxy-fuel combustion of pulverized fuels: Combustion fundamentals and modeling. Appl. Energy 2016, 162, 742–762. [Google Scholar] [CrossRef]
- Pragadeesh, K.S.; Regupathi, I.; Sudhakar, D.R. Insitu gasification—Chemical looping combustion of large coal and biomass particles: Char conversion and comminution. Fuel 2021, 292, 120201. [Google Scholar] [CrossRef]
- Yang, M.; Duan, L.; Tong, Y. Design and Performance Analysis of New Ultra-Supercritical Double Reheat Coal-Fired Power Generation Systems. Energies 2021, 14, 238. [Google Scholar] [CrossRef]
- Osman, A.I.; Hefny, M.; Maksoud, M.I.A.A.; Elgarahy, A.M.; Rooney, D.W. Recent advances in carbon capture storage and utilisation technologies: A review. Environ. Chem. Lett. 2021, 19, 797–849. [Google Scholar] [CrossRef]
- Pipitone, G.; Bolland, O. Power generation with CO2 capture: Technology for CO2 purification. Int. J. Greenh. Gas Control. 2009, 3, 528–534. [Google Scholar] [CrossRef]
- Available online: https://www.epa.gov/energy/greenhouse-gases-equivalencies-calculator-calculations-and-references#:~:text=Home%20electricity%20use&text=The%20national%20average%20carbon%20dioxide,EIA%202020b%3B%20EPA%202021 (accessed on 9 February 2023).
- Liao, G.; Liu, L.; Jiaqiang, E.; Zhang, F.; Chen, J.; Deng, Y.; Zhu, H. Effects of technical progress on performance and application of supercritical carbon dioxide power cycle: A review. Energy Convers. Manag. 2019, 199, 111986. [Google Scholar] [CrossRef]
- Ahn, Y.; Bae, S.J.; Kim, M.; Cho, S.K.; Baik, S.; Lee, J.I.; Cha, J.E. Review of supercritical CO2 power cycle technology and current status of research and development. Nucl. Eng. Technol. 2015, 47, 647–661. [Google Scholar] [CrossRef]
- Angelino, G. Carbon Dioxide Condensation Cycles for Power Production. J. Eng. Power 1968, 90, 287–295. [Google Scholar] [CrossRef]
- Feher, E.G. The supercritical thermodynamic power cycle. Energy Convers. 1968, 8, 85–90. [Google Scholar] [CrossRef]
- Marion, J. Mwe Supercritical Carbon Dioxide (sCO2) Pilot Power Plant. December. Available online: https://www.gti.energy/wp-content/uploads/2019/01/STEP-Project-Detailed-Description-Dec2018.pdf (accessed on 9 February 2023).
- Sarkar, J. Review and future trends of supercritical CO2 Rankine cycle for low-grade heat conversion. Renew. Sustain. Energy Rev. 2015, 48, 434–451. [Google Scholar] [CrossRef]
- Crespi, F.; Gavagnin, G.; Sánchez, D.; Martínez, G.S. Supercritical carbon dioxide cycles for power generation: A review. Appl. Energy 2017, 195, 152–183. [Google Scholar] [CrossRef]
- Yin, J.; Zheng, Q.; Peng, Z.; Zhang, X. Review of supercritical CO2 power cycles integrated with CSP. Int. J. Energy Res. 2019, 44, 1337–1369. [Google Scholar] [CrossRef]
- White, M.T.; Bianchi, G.; Chai, L.; Tassou, S.A.; Sayma, A.I. Review of supercritical CO2 technologies and systems for power generation. Appl. Therm. Eng. 2021, 185, 116447. [Google Scholar] [CrossRef]
- Yu, A.; Su, W.; Lin, X.; Zhou, N. Recent trends of supercritical CO2 Brayton cycle: Bibliometric analysis and research review. Nucl. Eng. Technol. 2020, 53, 699–714. [Google Scholar] [CrossRef]
- Sun, E.; Hu, H.; Li, H.; Liu, C.; Xu, J. How to Construct a Combined S-CO2 Cycle for Coal Fired Power Plant? Entropy 2018, 21, 19. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Y.; Zhang, X. Energy and exergy analyses of S–CO2 coal-fired power plant with reheating processes. Energy 2020, 211, 118651. [Google Scholar] [CrossRef]
- Bai, W.; Li, H.; Zhang, L.; Zhang, Y.; Yang, Y.; Zhang, C.; Yao, M. Energy and exergy analyses of an improved recompression supercritical CO2 cycle for coal-fired power plant. Energy 2021, 222, 119976. [Google Scholar] [CrossRef]
- Rogalev, N.; Rogalev, A.; Kindra, V.; Komarov, I.; Zlyvko, O. Structural and Parametric Optimization of S–CO2 Nuclear Power Plants. Entropy 2021, 23, 1079. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, D.; Chacartegui, R.; de Escalona, J.M.; Muñoz, A.; Sánchez, T. Performance analysis of a MCFC & supercritical carbon dioxide hybrid cycle under part load operation. Int. J. Hydrogen Energy 2011, 36, 10327–10336. [Google Scholar]
- Fan, G.; Li, H.; Du, Y.; Chen, K.; Zheng, S.; Dai, Y. Preliminary design and part-load performance analysis of a recompression supercritical carbon dioxide cycle combined with a transcritical carbon dioxide cycle. Energy Convers. Manag. 2020, 212, 112758. [Google Scholar] [CrossRef]
- Yang, J.; Yang, Z.; Duan, Y. Part-load performance analysis and comparison of supercritical CO2 Brayton cycles. Energy Convers. Manag. 2020, 214, 112832. [Google Scholar] [CrossRef]
- Tong, Y.; Duan, L.; Pang, L. Off-design performance analysis of a new 300 MW supercritical CO2 coal-fired boiler. Energy 2020, 216, 119306. [Google Scholar] [CrossRef]
- Lee, S.; Yaganegi, G.; Mee, D.J.; Guan, Z.; Gurgenci, H. Part-load performance prediction model for supercritical CO2 radial inflow turbines. Energy Convers. Manag. 2021, 235, 113964. [Google Scholar] [CrossRef]
- Alfani, D.; Binotti, M.; Macchi, E.; Silva, P.; Astolfi, M. sCO2 power plants for waste heat recovery: Design optimization and part-load operation strategies. Appl. Therm. Eng. 2021, 195, 117013. [Google Scholar] [CrossRef]
- Fan, G.; Dai, Y. Thermo-economic optimization and part-load analysis of the combined supercritical CO2 and Kalina cycle. Energy Convers. Manag. 2021, 245, 114572. [Google Scholar] [CrossRef]
- Fan, G.; Du, Y.; Li, H.; Dai, Y. Off-design behavior investigation of the combined supercritical CO2 and organic Rankine cycle. Energy 2021, 237, 121529. [Google Scholar] [CrossRef]
- Wang, R.; Wang, X.; Shu, G.; Tian, H.; Cai, J.; Bian, X.; Li, X.; Qin, Z.; Shi, L. Comparison of different load-following control strategies of a sCO2 Brayton cycle under full load range. Energy 2022, 246, 123378. [Google Scholar] [CrossRef]
- Xingyan, B.; Wang, X.; Wang, R.; Cai, J.; Tian, H.; Shu, G. Optimal selection of supercritical CO2 Brayton cycle layouts based on part-load performance. Energy 2022, 256, 124691. [Google Scholar] [CrossRef]
- Gini, L.; Maccarini, S.; Traverso, A.; Barberis, S.; Guedez, R.; Pesatori, E.; Bisio, V. A prototype recuperated supercritical CO2 cycle: Part-load and dynamic assessment. Appl. Therm. Eng. 2023, 225, 120152. [Google Scholar] [CrossRef]
- Kotas, T.J. The Exergy Method of Thermal Plant Analysis; Krieger Publishing, Co.: Malabar, FL, USA, 1995. [Google Scholar]
- Sathish, S.; Kumar, P.; Nassar, A. Analysis of a 10 MW recompression supercritical carbon dioxide cycle for tropical climatic conditions. Appl. Therm. Eng. 2020, 186, 116499. [Google Scholar] [CrossRef]
- Adibhatla, S.; Kaushik, S. Energy and exergy analysis of a super critical thermal power plant at various load conditions under constant and pure sliding pressure operation. Appl. Therm. Eng. 2014, 73, 51–65. [Google Scholar] [CrossRef]
 .
.
 .
.
| S. No | Reference | Source of Energy | Type of System | Objective |
|---|---|---|---|---|
| 1 | Sanchez et al. [25] | Natural gas | MCFC and s-CO2 hybrid system | 1st law analysis, inventory control strategy |
| 2 | Fan et al. [26] | Nuclear energy | Combined super critical and trans-critical | 1st and 2nd law analysis, identify a control strategy |
| 3 | Yang et al. [27] | Solar energy | Simple recuperative, reheat, recompression and intercooling cycles studied separately | 1st law analysis, performance comparison between different cycles |
| 4 | Tong et al. [28] | Coal | Single reheat recompression | Focusses on boiler furnace part load performance |
| 5 | Lee et al. [29] | - | - | Focusses on turbine part load performance |
| 6 | Alfani et al. [30] | Waste heat | Simple recuperative, simple recuperative cycle with bypass and turbine split flow configurations | 1st law and Techno-economic analysis and optimization |
| 7 | Fan and Dai [31] | Nuclear energy | Combined s-CO2 and Kalina cycle | 1st and 2nd law analysis, Thermo-economic optimization and evaluate different control strategies |
| 8 | Fan et al. [32] | Nuclear energy | Combined s-CO2 with Organic Rankine Cycle | 1st law and economic analysis |
| 9 | Wang et al. [33] | Fuel oil | Recompression s-CO2 Brayton cycle | Comparison of control strategies |
| 10 | Xingyan et al. [34] | - | Simple recuperated, recompression, single reheat, intercooling cycles considered separately | Performance evaluation based on layout and control strategies |
| 11 | Gini et al. [35] | Molten salt | Simple recuperated s-CO2 cycle | Control strategy development |
| Present work | Coal | Double reheat recompression | System design, 1st and 2nd law analysis and parameter optimization for better efficiency |
| Parameter | Value |
|---|---|
| Lower heating value of coal | 26.51 MJ/kg |
| Exergy of coal | 27.57 MJ/kg |
| Pressure/Temperature of CO2 at HP turbine inlet | 320 bar/620 °C |
| Temperature of CO2 at IP and LP turbine inlet | 620 °C |
| Pressure of CO2 at IP turbine inlet | 192.3 bar |
| Pressure of CO2 at LP turbine inlet | 123.3 bar |
| Pinch points in heat exchangers | 5 °C |
| Turbine isentropic efficiency | 93% |
| Compressor isentropic efficiency | 90% |
| Pressure drop in heater | 1 bar |
| Pressure drop in recuperators | 0.5 bar |
| Recompression ratio | 0.683 |
| Component | Mass Balance | Energy Balance | Exergy Balance |
|---|---|---|---|
| Heater | |||
| High Pressure Turbine | |||
| Reheater-1 | |||
| Intermediate Pressure Turbine | |||
| Reheater-2 | |||
| Low Pressure Turbine | |||
| High Temperature Recuperator | |||
| Low Temperature Recuperator | |||
| Flow Control valve | |||
| Cooler | |||
| Main Compressor | |||
| Re-Compressor | |||
| Junction |
| Temperature, °C | Pressure, bar | Mass Flow Rate, kg/s | |||||||
|---|---|---|---|---|---|---|---|---|---|
| S. No. | Chen et al. [22] | This Work | % Error | Chen et al. [22] | This work | % Error | Chen et al. [22] | This Work | % Error |
| 1 | 620 | 620 | 0 | 320 | 320 | 0 | 39.565 | 40.982 | 3.58 |
| 2 | 550.92 | 550.76 | 0.03 | 192.3 | 192.3 | 0 | 39.565 | 40.982 | 3.58 |
| 3 | 620 | 620 | 0 | 192.3 | 192.3 | 0 | 39.565 | 40.982 | 3.58 |
| 4 | 560.73 | 560.46 | 0.05 | 123.3 | 123.3 | 0 | 39.565 | 40.982 | 3.58 |
| 5 | 620 | 620 | 0 | 123.3 | 123.3 | 0 | 39.565 | 40.982 | 3.58 |
| 6 | 561.9 | 562.88 | 0.17 | 79 | 80 | 1.27 | 39.565 | 40.982 | 3.58 |
| 7 | 235 | 235 | 0 | 79 | 79.5 | 0.63 | 39.565 | 40.982 | 3.58 |
| 8 | 86.73 | 86.73 | 0 | 79 | 79 | 0 | 39.565 | 40.982 | 3.58 |
| 9 | 86.73 | 86.73 | 0 | 79 | 79 | 0 | 27.023 | 27.991 | 3.58 |
| 10 | 32.65 | 32.44 | 0.64 | 79 | 79 | 0 | 27.023 | 27.991 | 3.58 |
| 11 | 80.89 | 77.7 | 3.94 | 334.5 | 334.5 | 0 | 27.023 | 27.991 | 3.58 |
| 12 | 230 | 225.42 | 1.99 | 334 | 334 | 0 | 27.023 | 27.991 | 3.58 |
| 13 | 229.7 | 229.57 | 0.06 | 334 | 334 | 0 | 12.542 | 12.991 | 3.58 |
| 14 | 515.63 | 516.13 | 0.1 | 333.5 | 333.5 | 0 | 39.565 | 40.982 | 3.58 |
| 15 | 543.63 | 545.5 | 0.34 | 1 | 1 | 0 | 5.965 | 6.011 | 0.77 |
| 16 | 506.7 | 512.72 | 1.19 | 1 | 1 | 0 | 5.534 | 5.532 | 0.04 |
| Design | Optimized at Different Recompression Ratio | |||||
|---|---|---|---|---|---|---|
| Recompression ratio, φ | 0.683 | 0.683 | 0.75 | 0.8 | 0.9 | 1 |
| High pressure turbine inlet pressure, bar | 320 | 320 | 320 | 320 | 320 | 320 |
| Intermediate pressure turbine inlet pressure, bar | 192.3 | 206.9 | 206.9 | 206.9 | 206.9 | 206.9 |
| Low pressure turbine inlet pressure, bar | 123.3 | 130.5 | 130.5 | 130.5 | 130.5 | 130.5 |
| 1st law efficiency, ηI, % | 53.92 | 53.94 | 55.57 | 56.77 | 59.2 | 61.7 |
| 2nd law efficiency, ηII, % | 51.85 | 51.87 | 53.42 | 54.59 | 56.94 | 59.3 |
| Net Power (Turbine/Compressor) | Full Load, 100 MW | 80% Load, 80 MW | 60% Load, 60 MW | 40% Load, 40 MW |
|---|---|---|---|---|
| High Pressure Turbine | 51 | 41.7 | 32.8 | 23.34 |
| Intermediate Pressure Turbine | 43.6 | 34.1 | 25.2 | 16.2 |
| Low Pressure Turbine | 42.47 | 29.9 | 19.66 | 10.98 |
| Main Compressor | −16.75 | −11.6 | −7.92 | −4.74 |
| Re-compressor | −20.4 | −14.17 | −9.7 | −5.8 |
| Pipe | 100 MW | 80 MW | 60 MW | 40 MW |
|---|---|---|---|---|
| 1 | 637.5 | 548.69 | 461.9 | 367.97 |
| 2 | 637.5 | 548.69 | 461.9 | 367.97 |
| 3 | 637.5 | 548.69 | 461.9 | 367.97 |
| 4 | 637.5 | 548.69 | 461.9 | 367.97 |
| 5 | 637.5 | 548.69 | 461.9 | 367.97 |
| 6 | 637.5 | 548.69 | 461.9 | 367.97 |
| 7 | 637.5 | 548.69 | 461.9 | 367.97 |
| 8 | 637.5 | 548.69 | 461.9 | 367.97 |
| 9 | 202.1 | 173.94 | 146.4 | 116.65 |
| 10 | 435.4 | 374.76 | 315.48 | 251.33 |
| 11 | 435.4 | 374.76 | 315.48 | 251.33 |
| 12 | 435.4 | 374.76 | 315.48 | 251.33 |
| 13 | 435.4 | 374.76 | 315.48 | 251.33 |
| 14 | 202.1 | 173.94 | 146.4 | 116.65 |
| 15 | 637.5 | 548.69 | 461.9 | 367.97 |
| 16 | 637.5 | 548.69 | 461.9 | 367.97 |
| 17 | 8370.5 | 6836.36 | 5481 | 4093.88 |
| 18 | 8370.5 | 6836.36 | 5481 | 4093.88 |
| Pipe | 100 MW | 80 MW | 60 MW | 40 MW |
|---|---|---|---|---|
| 1 | 320 | 277.3 | 236.7 | 194.3 |
| 2 | 192.8 | 170.9 | 150.3 | 129.4 |
| 3 | 192.3 | 170.4 | 149.8 | 128.9 |
| 4 | 123.8 | 114.2 | 105.6 | 97.27 |
| 5 | 123.3 | 113.7 | 105.1 | 96.77 |
| 6 | 80 | 80 | 80 | 80 |
| 7 | 80 | 80 | 80 | 80 |
| 8 | 79 | 79 | 79 | 79 |
| 9 | 79 | 79 | 79 | 79 |
| 10 | 79 | 79 | 79 | 79 |
| 11 | 79 | 79 | 79 | 79 |
| 12 | 334.5 | 280.8 | 240.2 | 197.8 |
| 13 | 332.5 | 278.8 | 238.2 | 195.8 |
| 14 | 334 | 278.8 | 238.2 | 195.8 |
| 15 | 334 | 278.8 | 238.2 | 195.8 |
| 16 | 333.5 | 278.3 | 237.7 | 195.3 |
| 17 | 1 | 1 | 1 | 1 |
| 18 | 1 | 1 | 1 | 1 |
| Pipe | 100 MW | 80 MW | 60 MW | 40 MW |
|---|---|---|---|---|
| 1 | 620 | 620 | 620 | 620 |
| 2 | 551.1 | 554.4 | 558.75 | 565.4 |
| 3 | 620 | 620 | 620 | 620 |
| 4 | 560.99 | 566.53 | 573.26 | 582.33 |
| 5 | 620 | 620 | 620 | 620 |
| 6 | 562.88 | 573.39 | 583.71 | 594.62 |
| 7 | 235 | 235 | 235 | 235 |
| 8 | 80.22 | 73.73 | 68.32 | 62.03 |
| 9 | 80.22 | 73.73 | 68.32 | 62.03 |
| 10 | 80.22 | 73.73 | 68.32 | 62.03 |
| 11 | 32 | 32 | 32 | 32 |
| 12 | 75.22 | 68.73 | 63.32 | 57.03 |
| 13 | 230 | 230 | 230 | 230 |
| 14 | 220.44 | 192.93 | 169.95 | 142.82 |
| 15 | 227.08 | 217.93 | 210.03 | 200.17 |
| 16 | 516.64 | 522.43 | 529.32 | 536.52 |
| 17 | 25 | 25 | 25 | 25 |
| 18 | 35 | 35 | 35 | 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manavalla, S.; M., F.; Daniel, J.; Ramasamy, S.; Yunus Khan, T.M.; Baig, R.U.; Almakayeel, N.; Voddin Tirumalapur, B.K. System Design, Optimization and 2nd Law Analysis of a 100 MWe Double Reheat s-CO2 Power Plant at Full Load and Part Loads. Sustainability 2023, 15, 14677. https://doi.org/10.3390/su152014677
Manavalla S, M. F, Daniel J, Ramasamy S, Yunus Khan TM, Baig RU, Almakayeel N, Voddin Tirumalapur BK. System Design, Optimization and 2nd Law Analysis of a 100 MWe Double Reheat s-CO2 Power Plant at Full Load and Part Loads. Sustainability. 2023; 15(20):14677. https://doi.org/10.3390/su152014677
Chicago/Turabian StyleManavalla, Sreekanth, Feroskhan M., Joseph Daniel, Sivakumar Ramasamy, T. M. Yunus Khan, Rahmath Ulla Baig, Naif Almakayeel, and Bhanu Kiran Voddin Tirumalapur. 2023. "System Design, Optimization and 2nd Law Analysis of a 100 MWe Double Reheat s-CO2 Power Plant at Full Load and Part Loads" Sustainability 15, no. 20: 14677. https://doi.org/10.3390/su152014677
APA StyleManavalla, S., M., F., Daniel, J., Ramasamy, S., Yunus Khan, T. M., Baig, R. U., Almakayeel, N., & Voddin Tirumalapur, B. K. (2023). System Design, Optimization and 2nd Law Analysis of a 100 MWe Double Reheat s-CO2 Power Plant at Full Load and Part Loads. Sustainability, 15(20), 14677. https://doi.org/10.3390/su152014677









