TCN-Informer-Based Flight Trajectory Prediction for Aircraft in the Approach Phase
Abstract
:1. Introduction
- A temporal convolutional network (TCN)-Informer architecture is proposed for the TP of GA aircraft belonging to medium and long time series data. The dimension is incorporated as three spatial dimensions (latitude, longitude, and altitude). Recording and representing flight trajectory enables the analysis and reconstruction of flight trajectory in a more detailed and accurate manner. It also allows full visualization of the aircraft’s position and flight trajectory.
- The TCN model is used to extract the spatiotemporal features and trends of the long-term sequence of flight trajectory data. The TCN can keep the gradient stable and receive inputs of arbitrary length. The incorporated dilated causal convolutions can better change the receptive field size and better control the memory size of the model.
- Adaptive input embedding in the proposed TP model can take full advantage of the correlation in the time dimension. The integration of the Prob-Sparse self-attention mechanism and the distilling mechanism in the encoder-decoder architecture is superior to the data-driven method.
- By using real flight trajectory data from a variety of time-series network model comparison algorithm validations, the results show that the TCN-Informer architecture has the lowest prediction error in each dimension of the indicators and comprehensive evaluation indicators. The TCN-Informer architecture has high prediction accuracy in time-series prediction. Therefore, the prediction results can be used to identify standard flight trajectory gaps and to provide some assistance in deciding whether the airplane requires a go-around.
2. Literature Review
2.1. State-Space Model Methods
2.2. Data-Driven Methods
3. Methodology
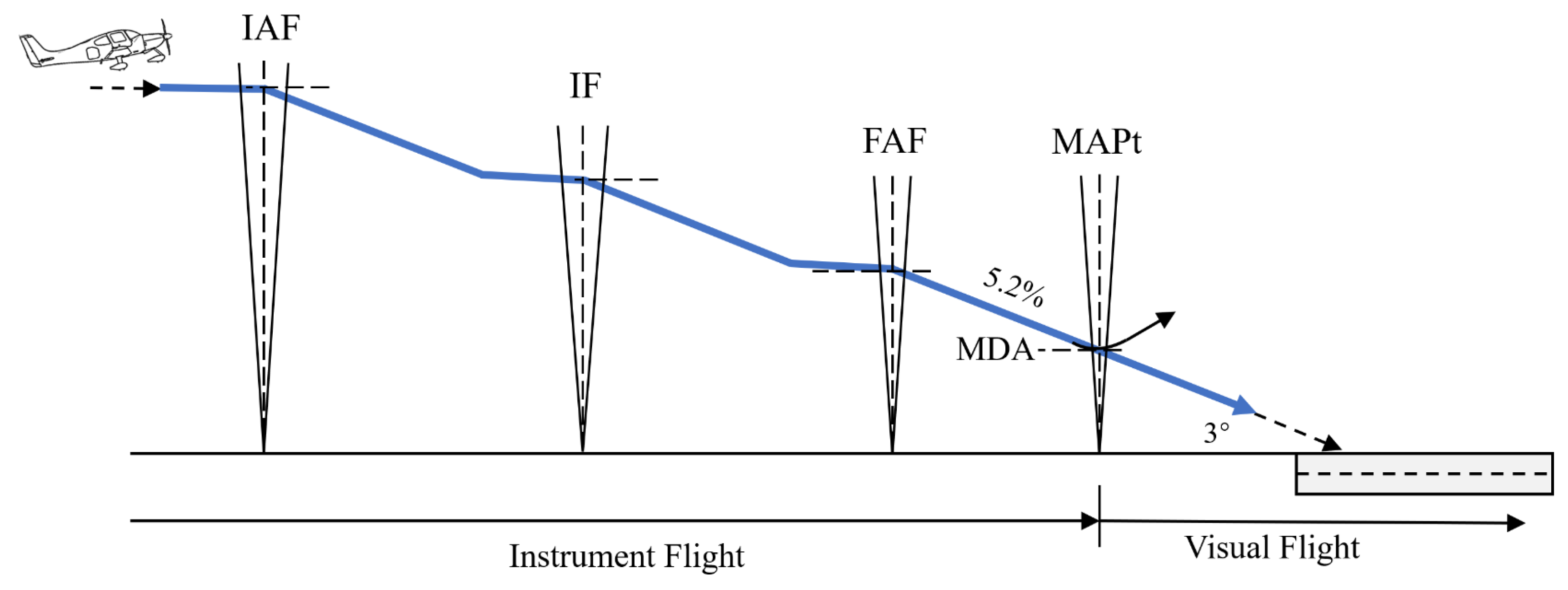
3.1. Problem Formulation
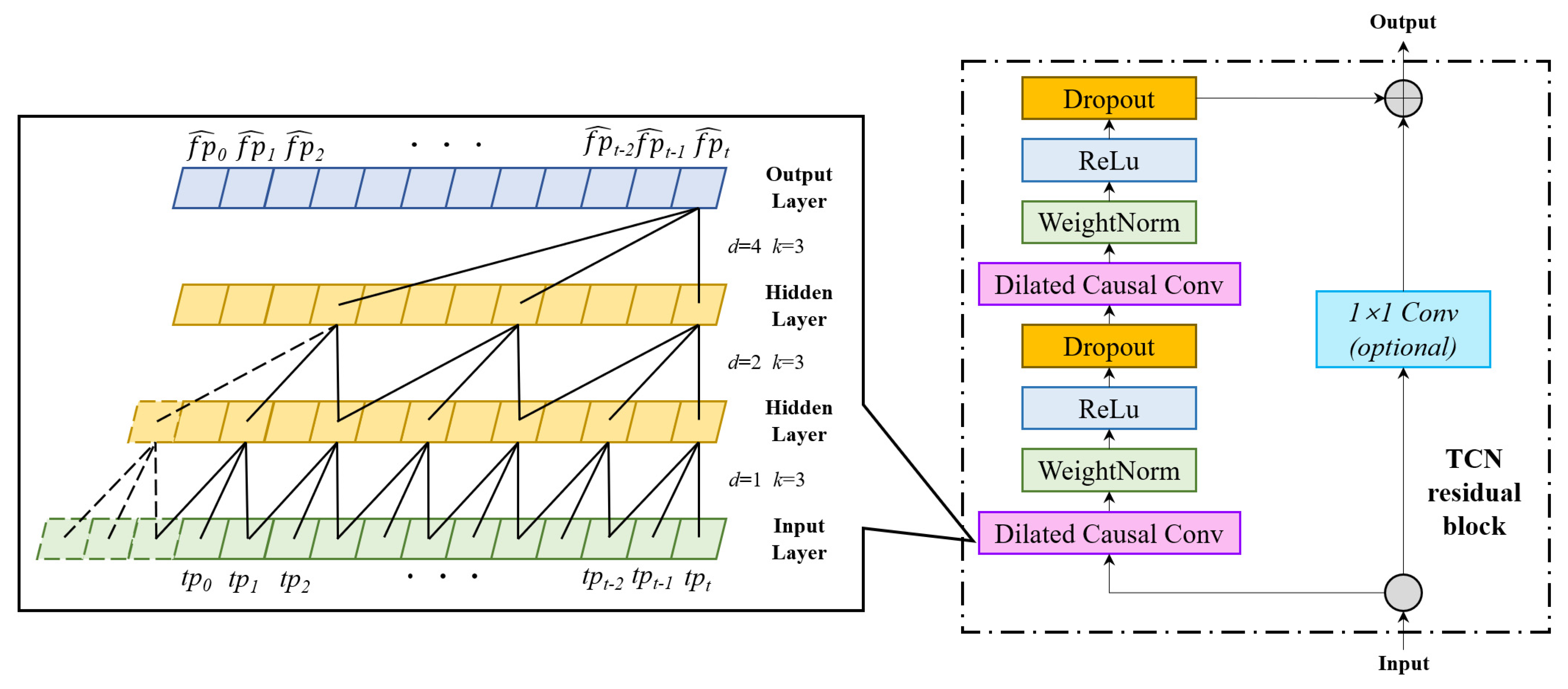
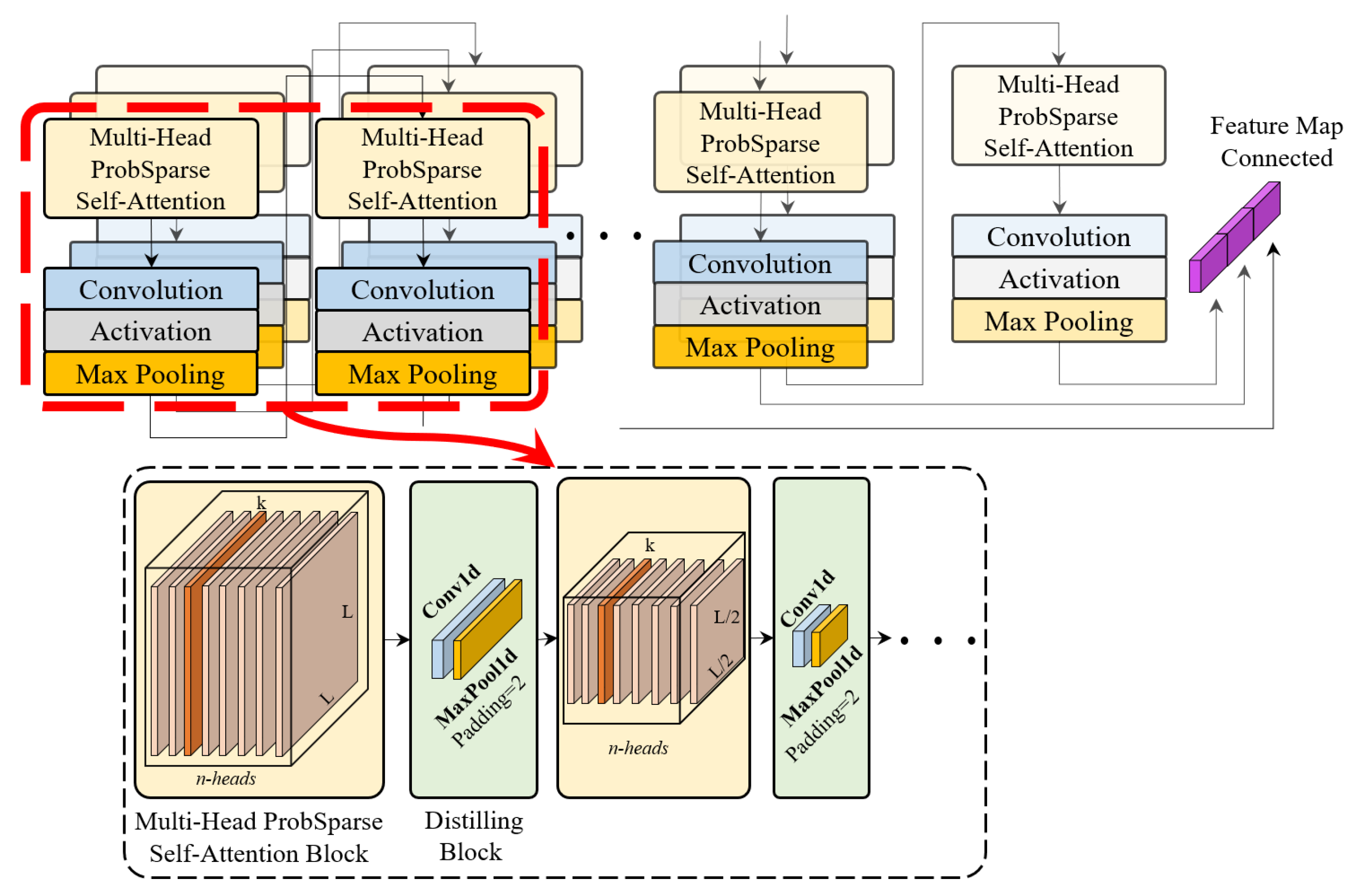
3.2. TCN-Based Feature Extraction
3.3. Informer Based Sequence Prediction
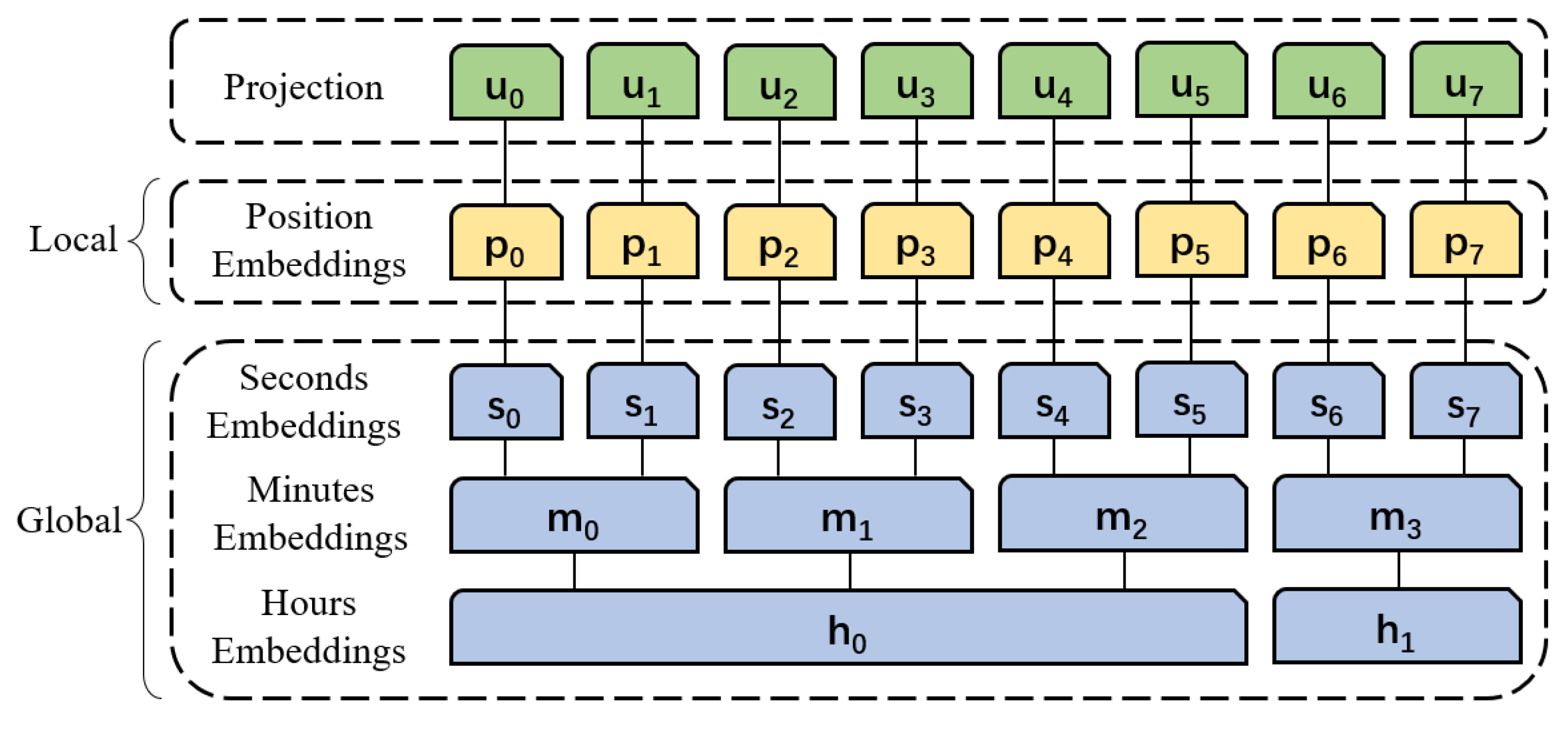
3.3.1. Adaptive Input Embedding
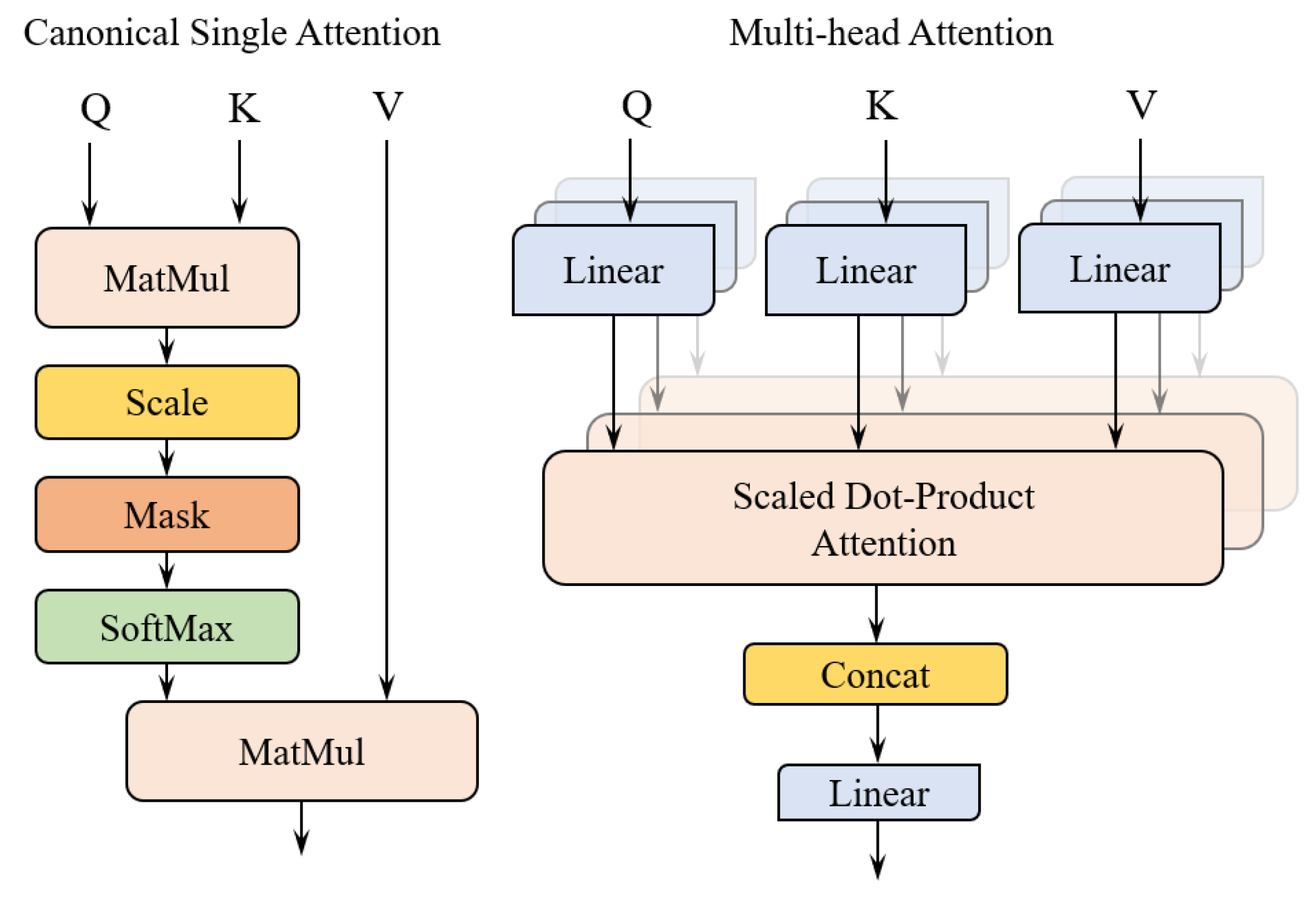
3.3.2. ProbSparse Self-Attention Mechanism
3.3.3. Distilling Mechanism
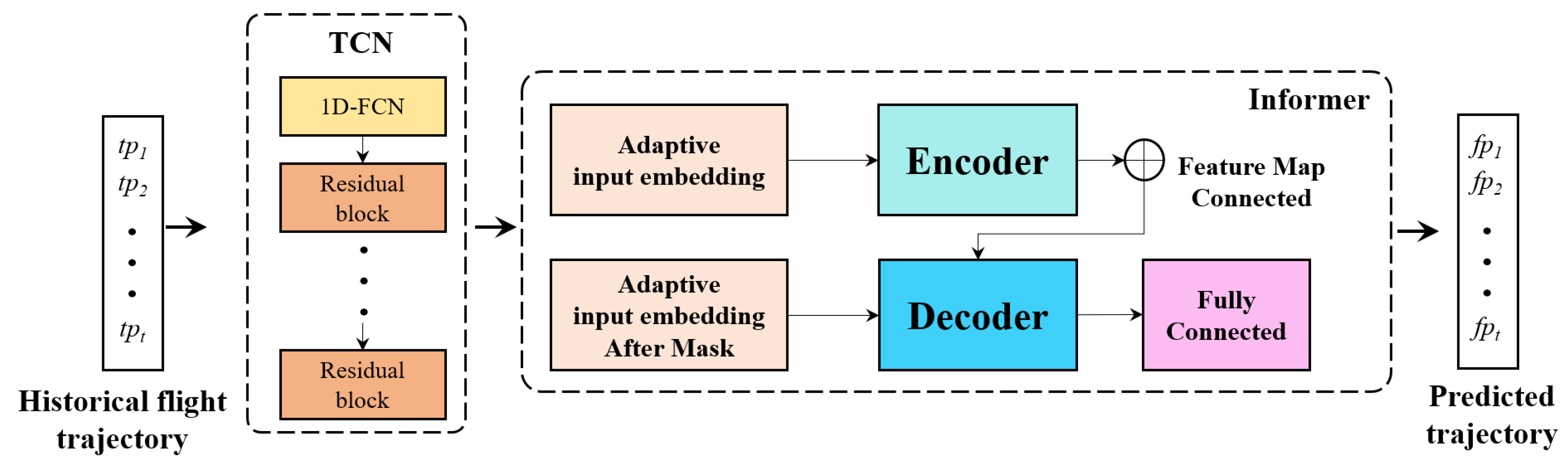
3.4. Hybrid Flight Trajectory Prediction Network
3.4.1. Feature Extraction of the Trajectory Data
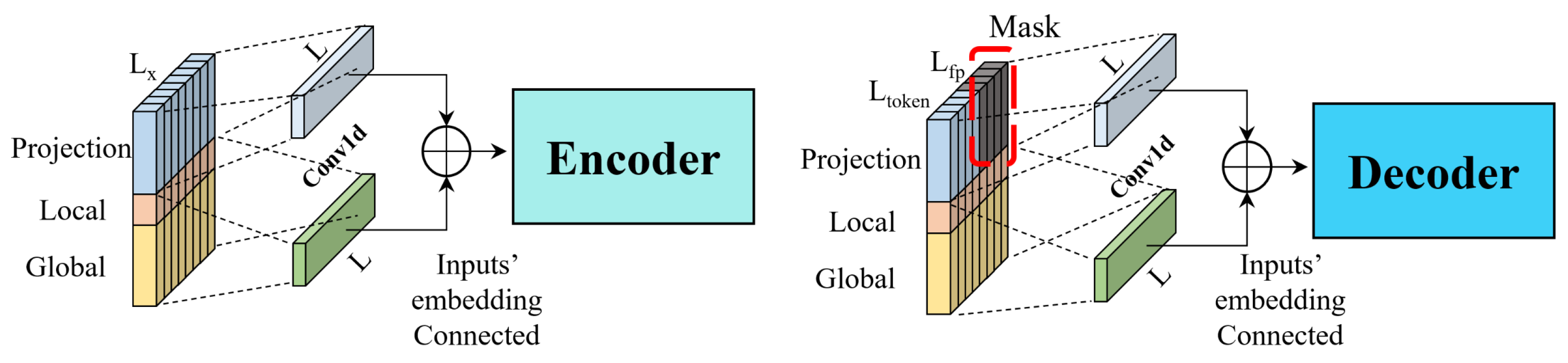
3.4.2. Embedding of the Trajectory Data
3.4.3. Encoder and Decoder of the TP model
4. Experiments
4.1. Data Collection and Preprocessing
4.1.1. Data Collection
4.1.2. Data Preprocessing
- The data files smaller than 50 KB from the collected flight data were removed. This file is typically for short powerups and short shutdowns of the G1000 system after driving. It is not of analytical value.
- If most of the consecutive gaps (consecutive occurrences of more than 30 s) occur at ultralow altitudes in the runway area, then the dataset cannot be used, and the data file is deleted.
- Occasionally, time discontinuities or duplications occur in the data file; thus, it is necessary to add or remove times and fill in the missing values using linear interpolation with Equation (17).
4.2. Experimental Design
4.2.1. Comparison of the Model Structures
- TCN: TCN-based regression networks are less frequently applied to TP tasks, but TCN models significantly outperform generalized recurrent architectures such as LSTM and GRU in some experiments [21]. TCN can be used as a model reference comparison for TP tasks.
- LSTM: Currently, long- and short-term memory networks are applied to TP tasks and optimized on the basis of LSTM to improve the model prediction accuracy [18]. This study uses the most basic LSTM model as a reference comparison.
- Informer: Regarding the underlying transformer model, the Informer is focused on the TP task of dealing with long sequential inputs. This model [24,25,26,27,28] adopts the multi-head attention model with a distilling mechanism as a framework; moreover, the model eliminates the limitations of the recurrent neural network’s long-term dependence and inability to perform parallel computations and utilizes the attention distilling mechanism and generative decoding approach to reduce the complexity of the model and speed up its training and prediction.
4.2.2. Experimental Setup
4.2.3. Evaluation Metrics
4.3. Experimental Results
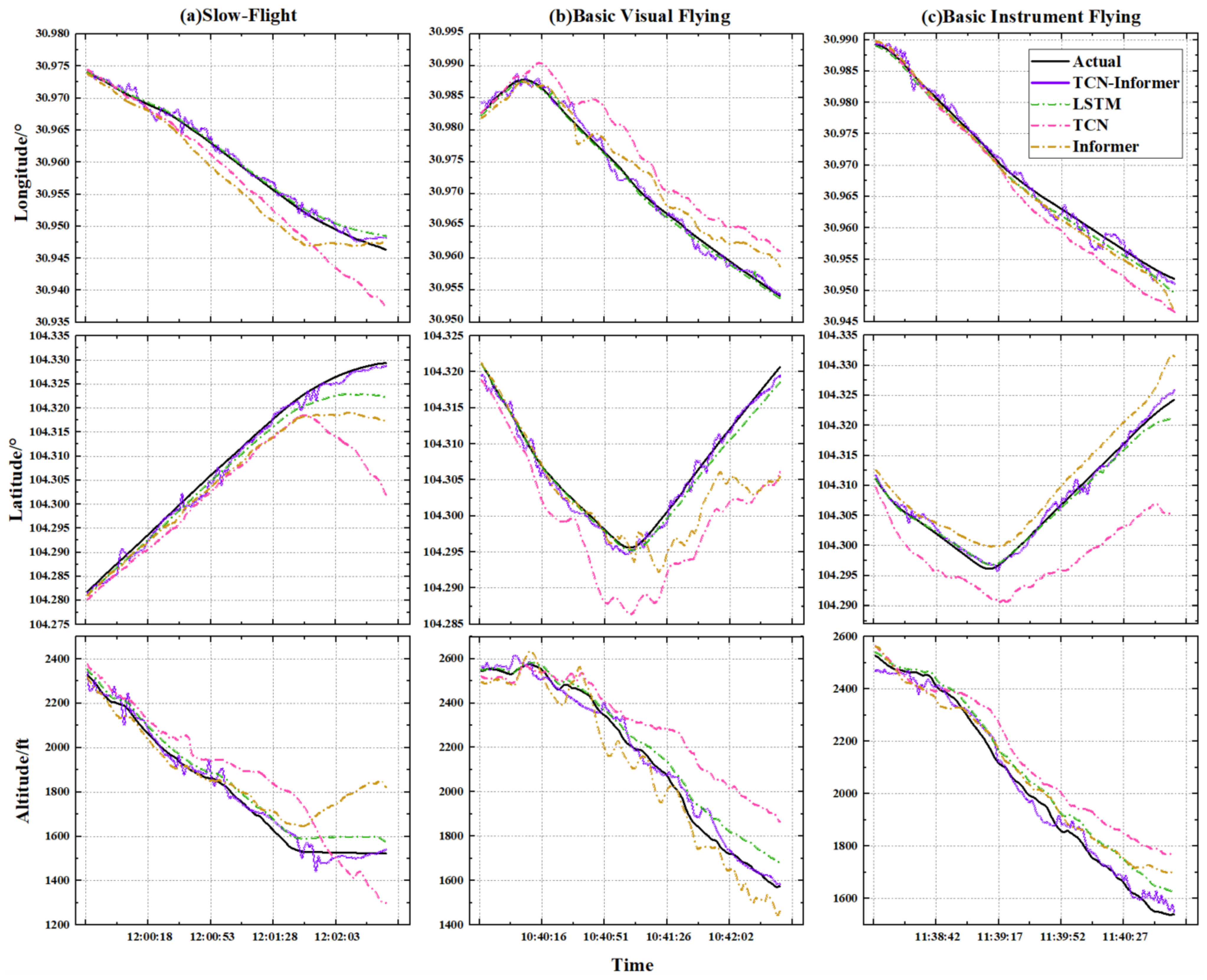
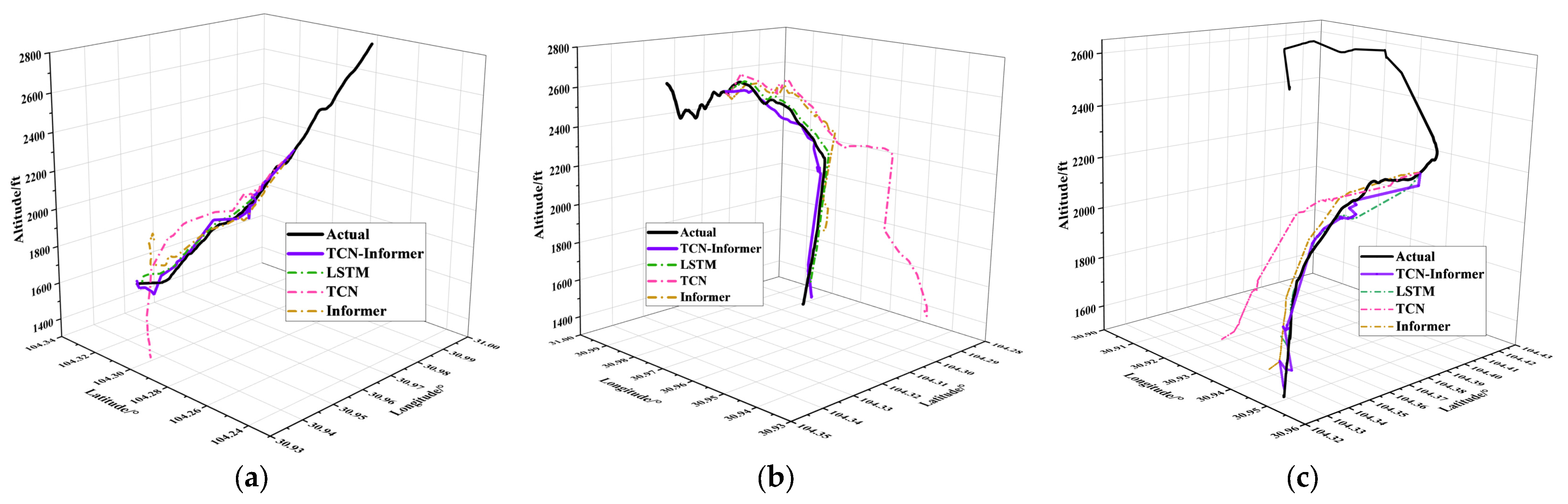
4.3.1. Visualization and Quantitative Analysis
4.3.2. Comparison of the Metric Error Values
4.4. Discussion
5. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Abbreviation in Full | Abbreviation | Abbreviation in Full |
| GA | general aviation | FAF | final approach fix |
| ATC | air traffic control | ILS | instrument landing system |
| LOC | loss of control | MAPt | missed approach point |
| TP | trajectory prediction | TCN | temporal convolutional network |
| QAR | airborne quick access recorder | CNN | convolutional neural network |
| ICAO | International Civil Aviation Organization | LSTM | long short-term memory |
| ADS-B | Automatic Dependent Surveillance-Broadcast | FCN | fully convolutional network |
| VFR | visual flight rules | LSTF | long sequence time series forecasting |
| IFR | instrument flight rules | MAE | mean absolute error |
| QNH | query normal height | RMSE | root mean square error |
| IAF | initial approach fix | MAPE | mean absolute percentage error |
| IF | intermediate approach fix |
References
- Wang, C.; Hu, M.; Yang, L.; Zhao, Z. Prediction of air traffic delays: An agent-based model introducing refined parameter estimation methods. PLoS ONE 2021, 16, e0249754. [Google Scholar] [CrossRef]
- Valasek, J.; Harris, J.; Pruchnicki, S.; McCrink, M.; Gregory, J.; Sizoo, D.G. Derived angle of attack and sideslip angle characterization for general aviation. J. Guid. Control Dyn. 2020, 43, 1039–1055. [Google Scholar] [CrossRef]
- Sailaranta, T.; Siltavuori, A. Stability Study of the Accident of a General Aviation Aircraft. J. Aerosp. Eng. 2018, 31, 06018001. [Google Scholar] [CrossRef]
- Schwarz, C.W.; Fischenberg, D.; Holzäpfel, F. Wake turbulence evolution and hazard analysis for general aviation takeoff accident. J. Aircr. 2019, 56, 1743–1752. [Google Scholar] [CrossRef]
- Fultz, A.J.; Ashley, W.S. Fatal weather-related general aviation accidents in the United States. Phys. Geogr. 2016, 37, 291–312. [Google Scholar] [CrossRef]
- Vilardaga, S.; Prats, X. Operating cost sensitivity to required time of arrival commands to ensure separation in optimal aircraft 4D trajectories. Transp. Res. Part C Emerg. Technol. 2015, 61, 75–86. [Google Scholar] [CrossRef]
- Tian, Y.; He, X.; Xu, Y.; Wan, L.; Ye, B. 4D trajectory optimization of commercial flight for green civil aviation. IEEE Access 2020, 8, 62815–62829. [Google Scholar] [CrossRef]
- Masi, G.; Amprimo, G.; Ferraris, C.; Priano, L. Stress and Workload Assessment in Aviation—A Narrative Review. Sensors 2023, 23, 3556. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.-Y.; Luo, X.; He, L. Research on method of trajectory prediction in aircraft flight based on aircraft performance and historical track data. Math. Probl. Eng. 2021, 2021, 6688213. [Google Scholar] [CrossRef]
- Obajemu, O.; Mahfouf, M.; Maiyar, L.M.; Al-Hindi, A.; Weiszer, M.; Chen, J. Real-time four-dimensional trajectory generation based on gain-scheduling control and a high-fidelity aircraft model. Engineering 2021, 7, 495–506. [Google Scholar] [CrossRef]
- Salahudden, S.; Joshi, H.V. Aircraft trajectory generation and control for minimum fuel and time efficient climb. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 1435–1448. [Google Scholar] [CrossRef]
- Yuan, L.H.; Wang, L.D.; Xu, J.T. Adaptive fault-tolerant controller for morphing aircraft based on the L2 gain and a neural network. Aerosp. Sci. Technol. 2023, 132, 107985. [Google Scholar] [CrossRef]
- Ma, L.; Tian, S. A hybrid CNN-LSTM model for aircraft 4D trajectory prediction. IEEE Access 2020, 8, 134668–134680. [Google Scholar] [CrossRef]
- Shi, Z.; Xu, M.; Pan, Q. 4-D flight trajectory prediction with constrained LSTM network. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7242–7255. [Google Scholar] [CrossRef]
- Guo, D.; Wu, E.Q.; Wu, Y.; Zhang, J.; Law, R.; Lin, Y. Flightbert: Binary encoding representation for flight trajectory prediction. IEEE Trans. Intell. Transp. Syst. 2022, 24, 1828–1842. [Google Scholar] [CrossRef]
- Jia, P.; Chen, H.; Zhang, L.; Han, D. Attention-lstm based prediction model for aircraft 4-d trajectory. Sci. Rep. 2022, 12, 15533. [Google Scholar] [CrossRef]
- Wang, Z.-S.; Zhang, Z.-Y.; Cui, Z. Research on Resampling and Clustering Method of Aircraft Flight Trajectory. J. Signal Process. Syst. 2022, 95, 319–331. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, K. A Fractal Dimension Feature Model for Accurate 4D Flight-Trajectory Prediction. Sustainability 2023, 15, 1272. [Google Scholar] [CrossRef]
- Jin, X.; Yu, X.; Wang, X.; Bai, Y.; Su, T.; Kong, J. Prediction for Time Series with CNN and LSTM. In Proceedings of the 11th International Conference on Modelling, Identification and Control (ICMIC2019), Tianjin, China, 13 July 2019; Springer: Singapore, 2020; pp. 631–641. [Google Scholar]
- Chan, S.; Oktavianti, I.; Puspita, V. A deep learning cnn and ai-tuned svm for electricity consumption forecasting: Multivariate time series data. In Proceedings of the IEEE 10th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 17–19 October 2019; pp. 488–494. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef]
- Yuan, R.; Abdel-Aty, M.; Gu, X.; Zheng, O.; Xiang, Q. A Unified Approach to Lane Change Intention Recognition and Driving Status Prediction through TCN-LSTM and Multi-Task Learning Models. arXiv 2023, arXiv:2304.13732. [Google Scholar]
- Zhou, H.; Li, J.; Zhang, S.; Yan, M.; Xiong, H. Expanding the prediction capacity in long sequence time-series forecasting. Artif. Intell. 2023, 318, 103886. [Google Scholar] [CrossRef]
- Xu, H.; Peng, Q.; Wang, Y.; Zhan, Z. Power-Load Forecasting Model Based on Informer and Its Application. Energies 2023, 16, 3086. [Google Scholar] [CrossRef]
- An, Z.; Cheng, L.; Guo, Y.; Ren, M.; Feng, W.; Sun, B.; Ling, J.; Chen, H.; Chen, W.; Luo, Y.; et al. A novel principal component analysis-informer model for fault prediction of nuclear valves. Machines 2022, 10, 240. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, L.; Li, N.; Tian, J. Time series forecasting of motor bearing vibration based on informer. Sensors 2022, 22, 5858. [Google Scholar] [CrossRef]
- Ma, J.; Dan, J. Long-Term Structural State Trend Forecasting Based on an FFT–Informer Model. Appl. Sci. 2023, 13, 2553. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, S.; Xia, B. Deep learning coupled model based on TCN-LSTM for particulate matter concentration prediction. Atmos. Pollut. Res. 2023, 14, 101703. [Google Scholar] [CrossRef]

| Features | Trajectory Point |
|---|---|
| Longitude/degree | 104.359 |
| Latitude/degree | 30.939 |
| Altitude/feet | 2396.9 |
| Ground speed/knot | 71.03 |
| Heading/degree | −60.4 |
| Parameter | Description | Value |
|---|---|---|
| kernel_size (TCN) | The number of units from the previous layer | 3 |
| nb_filters (TCN) | The number of filters | 64 |
| Activation (TCN) | The function to fully connected layer | ReLU |
| Dilation (TCN) | The size of dilated convolution interval | {1,2,4,8,16} |
| Dropout (TCN) | The rate used in the dropout layer | 0.2 |
| d_model (Informer) | dimension of model | 512 |
| n_heads (Informer) | num of heads | 8 |
| Activation (Informer) | GeLU | |
| e_layers (Informer) | num of encoder layers | 3 |
| d_layers (Informer) | num of decoder layers | 2 |
| Dropout (Informer) | 0 | |
| Batch size | Number of samples passing through to the network at one time | 64 |
| Learning rate | 2 × 10−5 | |
| Optimizer | The function to minimize loss | Adam |
| Loss function | The function to calculate loss | MSE |
| Flight Subject | Model | MAE/° | RMSE/° | MAPE/% |
|---|---|---|---|---|
| Slow-Flight | TCN | 32.1454 | 78.3910 | 7.9654 |
| LSTM | 9.8064 | 25.3971 | 2.9366 | |
| Informer | 20.8752 | 58.0409 | 7.7361 | |
| TCN-Informer | 9.4425 | 20.8853 | 1.3440 × 10−3 | |
| Basic Visual Flying | TCN | 28.5440 | 79.1948 | 2.6529 |
| LSTM | 11.3799 | 29.5784 | 1.2906 | |
| Informer | 18.4654 | 46.3703 | 2.8452 | |
| TCN-Informer | 9.4923 | 25.1775 | 2.0402 × 10−3 | |
| Basic Instrument Flying | TCN | 22.5312 | 55.4356 | 2.8083 |
| LSTM | 11.2161 | 25.8144 | 1.9288 | |
| Informer | 13.1692 | 32.2399 | 2.2530 | |
| TCN-Informer | 7.6254 | 17.3124 | 8.5077 × 10−4 |
| Flight Subject | Evaluation Metrics | Model | Longitude/° | Latitude/° | Altitude/ft |
|---|---|---|---|---|---|
| Slow-Flight | MAE | TCN | 2.9475 × 10−3 | 5.4885 × 10−3 | 138.6668 |
| LSTM | 4.5944 × 10−4 | 1.8136 × 10−3 | 41.5848 | ||
| Informer | 2.5651 × 10−3 | 3.3762 × 10−3 | 82.8541 | ||
| TCN-Informer | 2.2472 × 10−4 | 1.4018 × 10−3 | 37.9198 | ||
| RMSE | TCN | 4.1494 × 10−3 | 8.2815 × 10−3 | 173.5556 | |
| LSTM | 6.8025 × 10−4 | 2.4814 × 10−3 | 46.0996 | ||
| Informer | 3.1418 × 10−3 | 4.6291 × 10−3 | 128.1257 | ||
| TCN-Informer | 2.4666 × 10−4 | 1.8077 × 10−3 | 45.9907 | ||
| MAPE/% | TCN | 9.5224 × 10−3 | 5.2614 × 10−3 | 8.0965 | |
| LSTM | 1.4842 × 10−3 | 1.7386 × 10−3 | 2.4175 | ||
| Informer | 8.2859 × 10−3 | 3.2364 × 10−3 | 5.1675 | ||
| TCN-Informer | 1.3440 × 10−3 | 1.3440 × 10−3 | 1.3440 × 10−3 | ||
| Basic Visual Flying | MAE | TCN | 3.7299 × 10−3 | 6.7160 × 10−3 | 133.7629 |
| LSTM | 5.7556 × 10−4 | 1.1042 × 10−3 | 52.0386 | ||
| Informer | 7.1360 × 10−3 | 5.3758 × 10−3 | 76.0873 | ||
| TCN-Informer | 4.1887 × 10−4 | 1.1028 × 10−3 | 39.3285 | ||
| RMSE | TCN | 4.5117 × 10−3 | 7.9371 × 10−3 | 176.8146 | |
| LSTM | 6.2505 × 10−4 | 1.2624 × 10−3 | 65.9584 | ||
| Informer | 9.7240 × 10−3 | 8.4468 × 10−3 | 101.6972 | ||
| TCN-Informer | 2.5396 × 10−4 | 1.0554 × 10−3 | 55.4143 | ||
| MAPE/% | TCN | 1.2044 × 10−2 | 6.4387 × 10−3 | 7.0794 | |
| LSTM | 1.8584 × 10−3 | 1.0586 × 10−3 | 2.7139 | ||
| Informer | 2.3046 × 10−2 | 5.1537 × 10−3 | 3.7982 | ||
| TCN-Informer | 1.6402 × 10−3 | 1.0402 × 10−3 | 2.0402 × 10−3 | ||
| Basic Instrument Flying | MAE | TCN | 2.1724 × 10−3 | 7.5674 × 10−3 | 102.9894 |
| LSTM | 2.0974 × 10−4 | 2.9056 × 10−4 | 47.8487 | ||
| Informer | 7.0690 × 10−4 | 5.2345 × 10−4 | 56.1740 | ||
| TCN-Informer | 1.6903 × 10−4 | 1.1603 × 10−4 | 28.6839 | ||
| RMSE | TCN | 2.8080 × 10−3 | 9.0990 × 10−3 | 123.4807 | |
| LSTM | 8.2249 × 10−4 | 7.7270 × 10−4 | 57.1074 | ||
| Informer | 1.3013 × 10−3 | 2.9763 × 10−3 | 69.3845 | ||
| TCN-Informer | 1.6903 × 10−4 | 5.1603 × 10−4 | 36.9918 | ||
| MAPE/% | TCN | 7.0166 × 10−3 | 7.2549 × 10−3 | 5.5557 | |
| LSTM | 2.2829 × 10−3 | 5.0181 × 10−4 | 2.5899 | ||
| Informer | 3.2415 × 10−3 | 2.5123 × 10−3 | 3.0203 | ||
| TCN-Informer | 8.5076 × 10−4 | 8.5076 × 10−4 | 8.5076 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; Fan, B.; Li, F.; Xu, X.; Sun, H.; Cao, W. TCN-Informer-Based Flight Trajectory Prediction for Aircraft in the Approach Phase. Sustainability 2023, 15, 16344. https://doi.org/10.3390/su152316344
Dong Z, Fan B, Li F, Xu X, Sun H, Cao W. TCN-Informer-Based Flight Trajectory Prediction for Aircraft in the Approach Phase. Sustainability. 2023; 15(23):16344. https://doi.org/10.3390/su152316344
Chicago/Turabian StyleDong, Zijing, Boyi Fan, Fan Li, Xuezhi Xu, Hong Sun, and Weiwei Cao. 2023. "TCN-Informer-Based Flight Trajectory Prediction for Aircraft in the Approach Phase" Sustainability 15, no. 23: 16344. https://doi.org/10.3390/su152316344
APA StyleDong, Z., Fan, B., Li, F., Xu, X., Sun, H., & Cao, W. (2023). TCN-Informer-Based Flight Trajectory Prediction for Aircraft in the Approach Phase. Sustainability, 15(23), 16344. https://doi.org/10.3390/su152316344







