Thermal Assessment of Dielectric Microspacer Technology Using an Advanced Three-Dimensional Simulation Model
Abstract
1. Introduction
1.1. General Context
1.2. Benchmark Design of the TIPV Converter
2. Methodology
2.1. Model A (Simple Conductive Problem)
2.2. Model B (Inclusion of Radiation/Thermionic Emission across the Electrode Gap)
- (1)
- The net radiative and thermionic emission flux is calculated only between the anode upper and cathode lower surfaces.
- (2)
- Radiation from the cathode to DMS surface and from the DMS to anode is neglected due to the small surface of the DMS with respect to the anode and the cathode.
- (3)
- Radiative and convective losses from the sidewalls are neglected.
- (4)
- The TIPV efficiency is considered equal to zero to study the worst-case scenario in terms of incoming heat flux. However, the UDFs can be used as well in cases where the TIPV efficiency is known.
- (5)
- Contact thermal resistance in the DMS is neglected.
- (6)
- Emissivity values of the anode and cathode sections are included.
- (7)
- Near-field radiation is neglected.
2.3. Geometry and Mesh Layout
2.4. Boundary and Initial Conditions
3. Results and Discussion
3.1. Model A (Conduction)
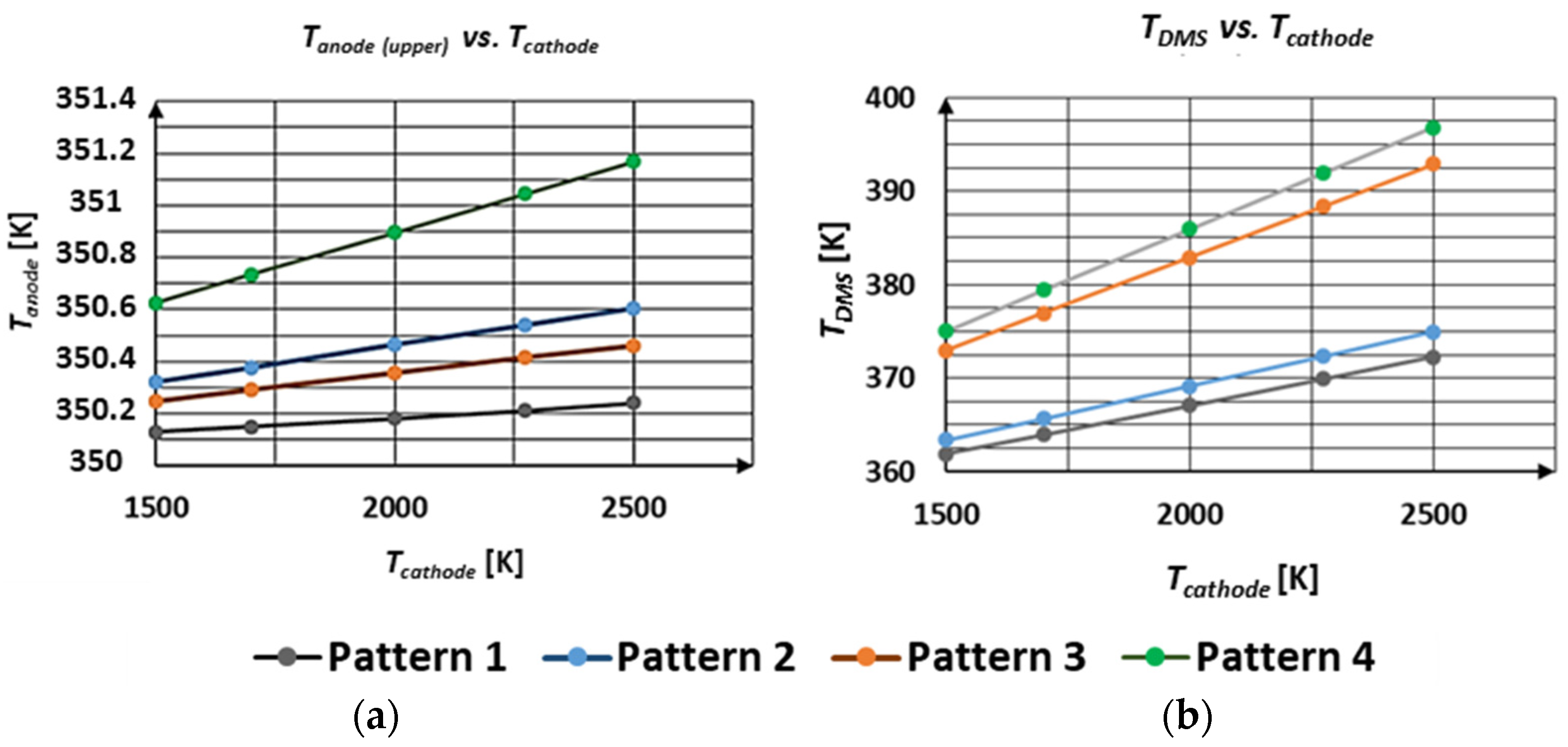
3.1.1. Initial Set of Cases (Patterns 1–4)
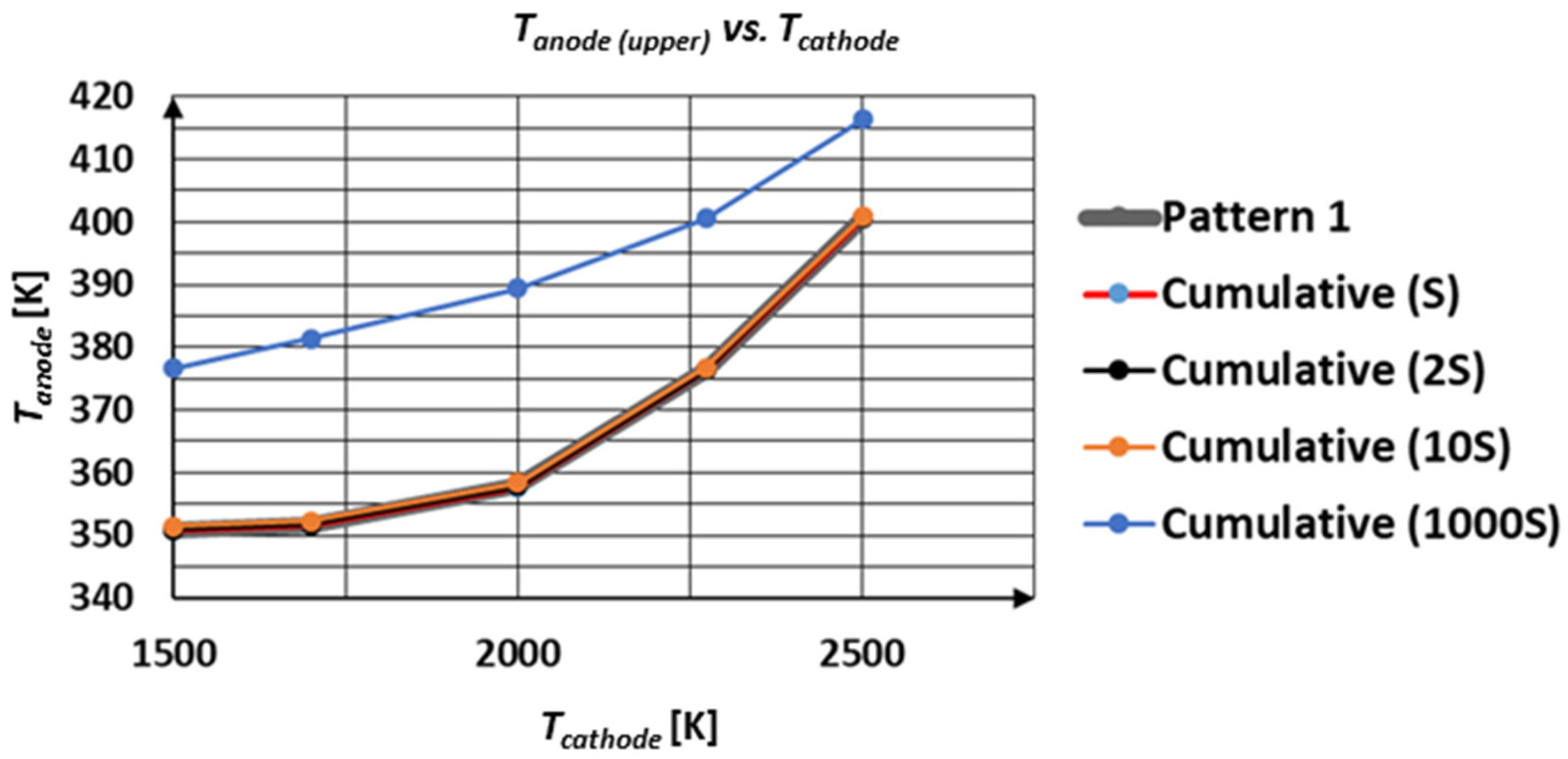
3.1.2. Parametric Study on Different Designs (Cumulative vs. Ring Shape Pattern)
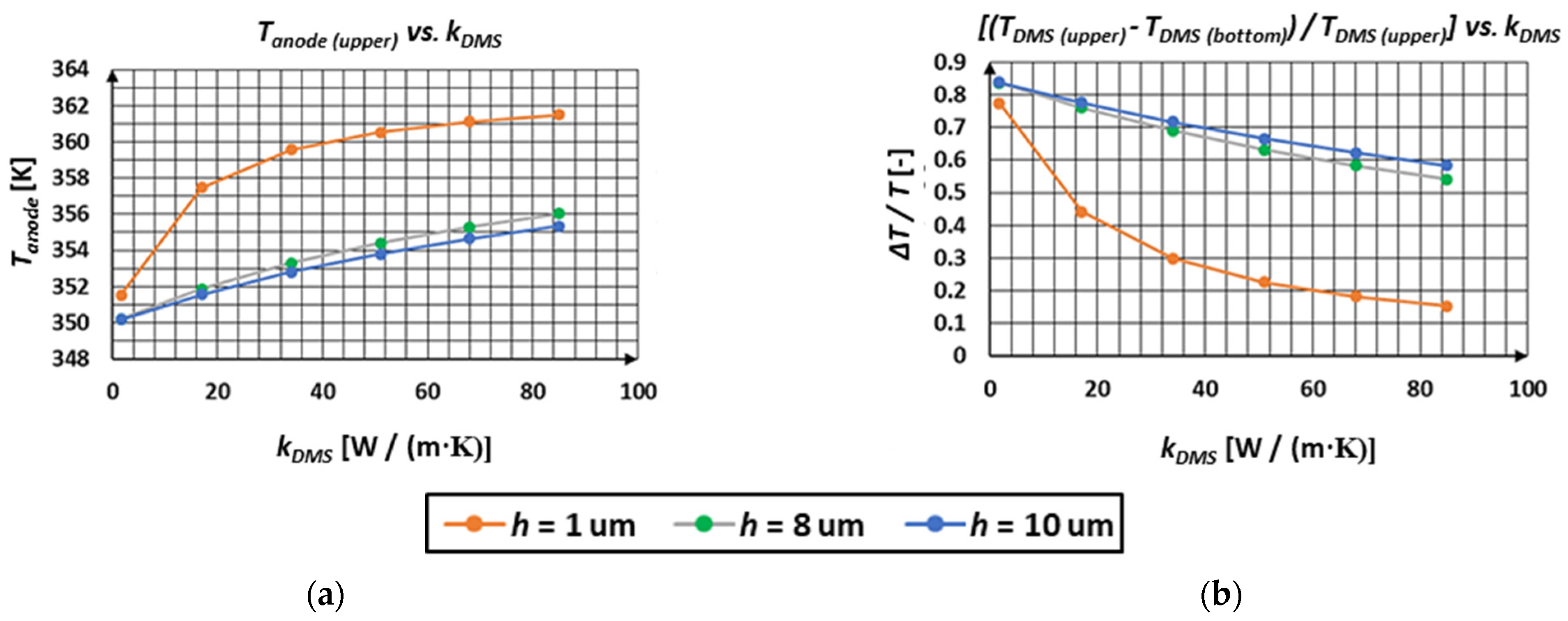
3.1.3. Sensitivity Analysis on Material Properties
3.2. Model B (Inclusion of Radiation/Thermionic Emission)
3.2.1. Patterns 1–4 (Ring Shape)
3.2.2. Cumulative Surface Coverage
3.2.3. Mitigation Risk
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Variables and Parameters | |||
| b | Thickness | SDMS | Surface of the DMS |
| JC | Thermionic current density | T | Temperature |
| k | Thermal conductivity | ε | Material emissivity |
| Qcond | Heat transfer through conduction | ηTIPV | Overall TIPV anode efficiency |
| Qin-anode | Thermal flux heating the anode | ΦC | Material work function |
| Qrad | Net photon flux emitted from the cathode to the anode | Constants | |
| Qrad’ | Net photon flux emitted from the anode back to the cathode | AR* | Richardson constant value |
| QTI | Net electron flux emitted from the cathode to the anode | e | Electric charge |
| QTI’ | Net electron flux emitted from the anode back to the cathode | kB | Boltzmann constant |
| Sanode | Surface of the anode | σ | Stefan–Boltzmann constant |
References
- Schwede, J.W.; Bargatin, I.; Riley, D.C.; Hardin, B.E.; Rosenthal, S.J.; Sun, Y.; Schmitt, F.; Pianetta, P.; Howe, R.T.; Shen, Z.-X.; et al. Photon-Enhanced Thermionic Emission for Solar Concentrator Systems. Nat. Mater. 2010, 9, 762–767. [Google Scholar] [CrossRef] [PubMed]
- Nikolaev, A.L.; Kazmina, M.A.; Lyanguzov, N.V.; Abdulvakhidov, K.G.; Kaidashev, E.M. Synthesis of ZnO Nanorods for Piezoelectric Resonators and Sensors. J. Adv. Dielect. 2022, 12, 2160020. [Google Scholar] [CrossRef]
- Manan, A.; Rehman, M.U.; Ullah, A.; Ahmad, A.S.; Iqbal, Y.; Qazi, I.; Khan, M.A.; Shah, H.U.; Wazir, A.H. High Energy Storage Density with Ultra-High Efficiency and Fast Charging–Discharging Capability of Sodium Bismuth Niobate Lead-Free Ceramics. J. Adv. Dielect. 2021, 11, 2150018. [Google Scholar] [CrossRef]
- Molokov, A.; Sysoeva, A.; Naberezhnov, A.; Kumar, R.; Koroleva, E.; Vakhrushev, S. Effect of Interface Carbonization on Dielectric Properties of Potassium Nitrate Nanocomposite Based on Porous Glasses. J. Adv. Dielect. 2022, 12, 2250013. [Google Scholar] [CrossRef]
- Bellucci, A.; Sabbatella, G.; Girolami, M.; Mastellone, M.; Serpente, V.; Mezzi, A.; Kaciulis, S.; Paci, B.; Generosi, A.; Polini, R.; et al. Dielectric Micro- and Sub-Micrometric Spacers for High-Temperature Energy Converters. Energy Technol. 2021, 9, 2000788. [Google Scholar] [CrossRef]
- Dielectric MicroSpacer Technology. Available online: https://cordis.europa.eu/project/id/754568 (accessed on 22 December 2022).
- Stamatopoulos, P.; Zeneli, M.; Nikolopoulos, A.; Bellucci, A.; Trucchi, D.M.; Nikolopoulos, N. Introducing a 1D Numerical Model for the Simulation of PN Junctions of Varying Spectral Material Properties and Operating Conditions. Energy Convers. Manag. 2021, 230, 113819. [Google Scholar] [CrossRef]
- Zeneli, M.; Bellucci, A.; Sabbatella, G.; Trucchi, D.M.; Nikolopoulos, A.; Nikolopoulos, N.; Karellas, S.; Kakaras, E. Performance Evaluation and Optimization of the Cooling System of a Hybrid Thermionic-Photovoltaic Converter. Energy Convers. Manag. 2020, 210, 112717. [Google Scholar] [CrossRef]
- Bellucci, A.; Linares, P.G.; Villa, J.; Martí, A.; Datas, A.; Trucchi, D.M. Hybrid Thermionic-Photovoltaic Converter with an In0.53Ga0.47As Anode. Sol. Energy Mater. Sol. Cells 2022, 238, 111588. [Google Scholar] [CrossRef]
- Bellucci, A.; García-Linares, P.; Martí, A.; Trucchi, D.M.; Datas, A. A Three-Terminal Hybrid Thermionic-Photovoltaic Energy Converter. Adv. Energy Mater. 2022, 12, 2200357. [Google Scholar] [CrossRef]
- Qiu, H.; Lin, S.; Xu, H.; Hao, G.; Xiao, G. Hybrid Thermionic-Photovoltaic Converter with Graphene-on-Semiconductor Heterojunction Anode for Efficient Electricity Generation. Iscience 2022, 25, 105051. [Google Scholar] [CrossRef] [PubMed]
- Campbell, M.F.; Celenza, T.J.; Schmitt, F.; Schwede, J.W.; Bargatin, I. Progress Toward High Power Output in Thermionic Energy Converters. Adv. Sci. 2021, 8, 2003812. [Google Scholar] [CrossRef] [PubMed]
- Campbell, M.F.; Azadi, M.; Lu, Z.; Eskenazi, A.G.; Jain, A.; Bang, J.W.; Sieg, P.G.; Popov, G.A.; Nicaise, S.M.; Van Houten, K.C.; et al. Nanostructured Spacers for Thermionic and Thermophotovoltaic Energy Converters. J. Microelectromech. Syst. 2020, 29, 637–644. [Google Scholar] [CrossRef]
- Wang, H.; Loveless, A.M.; Darr, A.M.; Garner, A.L. Experimental Studies of Gas Breakdown and Electron Emission for Nanoscale Vacuum Gaps. In Proceedings of the 2022 IEEE International Conference on Plasma Science (ICOPS), Seattle, WA, USA, 22–26 May 2022; pp. 1–2. [Google Scholar] [CrossRef]
- Nicaise, S.M.; Lin, C.; Azadi, M.; Bozorg-Grayeli, T.; Adebayo-Ige, P.; Lilley, D.E.; Pfitzer, Y.; Cha, W.; Van Houten, K.; Melosh, N.A.; et al. Micron-Gap Spacers with Ultrahigh Thermal Resistance and Mechanical Robustness for Direct Energy Conversion. Microsyst. Nanoeng. 2019, 5, 31. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-H.; Bargatin, I.; Melosh, N.A.; Howe, R.T. Optimal Emitter-Collector Gap for Thermionic Energy Converters. Appl. Phys. Lett. 2012, 100, 173904. [Google Scholar] [CrossRef]
- Rahman, E.; Nojeh, A. Interplay between Near-Field Radiative Coupling and Space-Charge Effects in a Microgap Thermionic Energy Converter under Fixed Heat Input. Phys. Rev. Appl. 2020, 14, 024082. [Google Scholar] [CrossRef]
- Jensen, D.; Taufiq Elahi, A.N.M.; Ghashami, M.; Park, K. Submicrometer-Gap Thermionic Power Generation Based on Comprehensive Modeling of Charge and Thermal Transport. Phys. Rev. Appl. 2021, 15, 024062. [Google Scholar] [CrossRef]
- Go, D.B.; Haase, J.R.; George, J.; Mannhart, J.; Wanke, R.; Nojeh, A.; Nemanich, R. Thermionic Energy Conversion in the Twenty-First Century: Advances and Opportunities for Space and Terrestrial Applications. Front. Mech. Eng. 2017, 3, 13. [Google Scholar] [CrossRef]
- CORDIS, European Commission Production Method Of Electrical Energy by Enhanced Thermal Electron Emission by the Use of Superior Semiconductors. Available online: https://cordis.europa.eu/project/id/308975/reporting (accessed on 12 December 2022).
- Ahmad, T.; Plee, S.L.; Myers, J.P. ANSYS Fluent Theory Guide 2013. Available online: http://www.pmt.usp.br/academic/martoran/notasmodelosgrad/ANSYS%20Fluent%20Theory%20Guide%2015.pdf (accessed on 12 December 2022).
- Datas, A. Hybrid Thermionic-Photovoltaic Converter. Appl. Phys. Lett. 2016, 108, 143503. [Google Scholar] [CrossRef]
- Datas, A.; Vaillon, R. Thermionic-Enhanced near-Field Thermophotovoltaics. Nano Energy 2019, 61, 10–17. [Google Scholar] [CrossRef]
- Li, W.; Peng, W.; Yang, Z.; Su, G.; Su, S.; Chen, J. Performance Improvements and Parametric Design Strategies of an Updated Thermionic-Photovoltaic Converter. Phys. Scr. 2020, 95, 035208. [Google Scholar] [CrossRef]
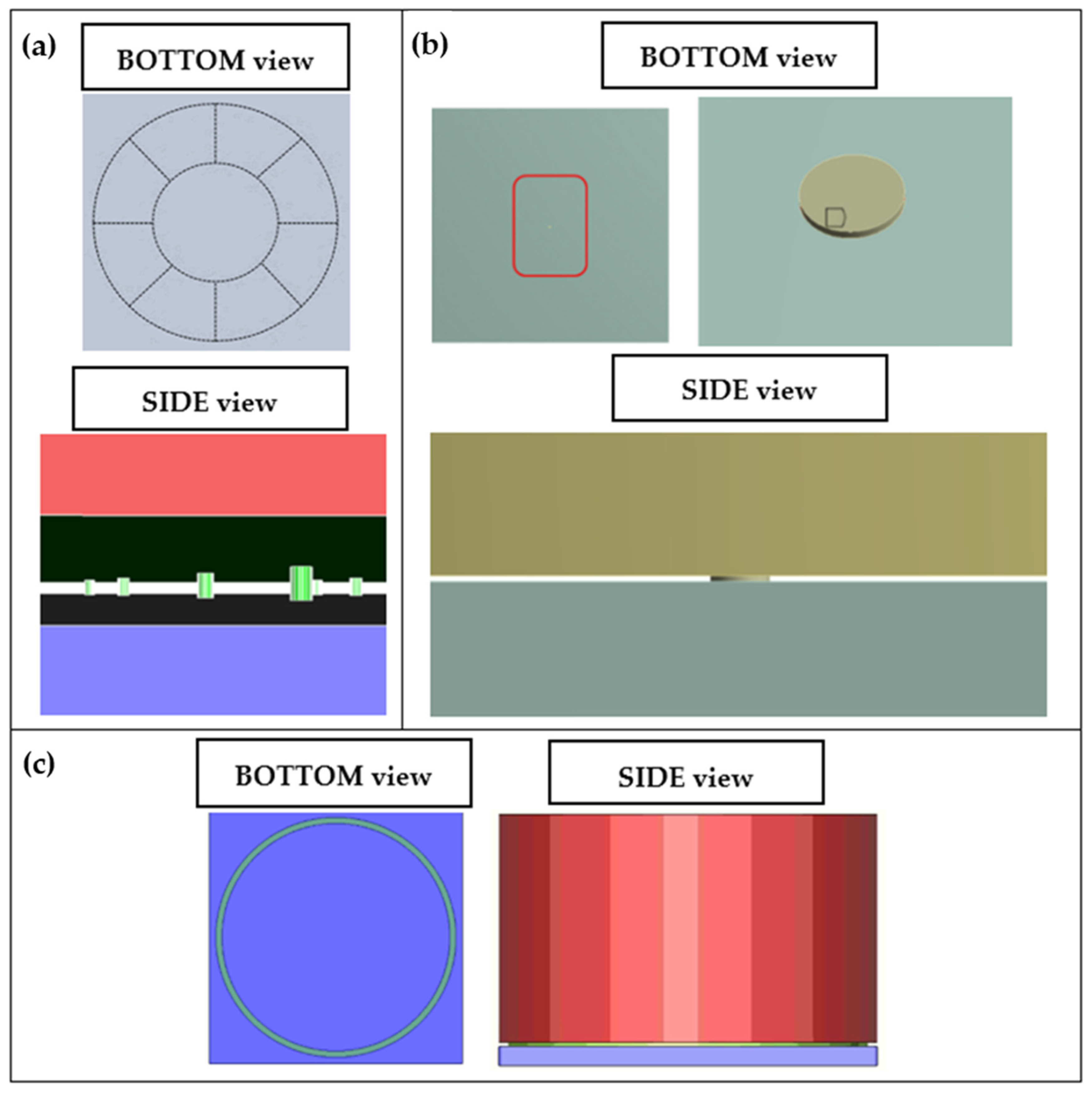













| Pattern Number | Shape | DMS Height (μm) | DMS Diameter (μm) | Number of DMS | SDMS (mm2) | SDMS/Sanode (mm2/mm2) |
|---|---|---|---|---|---|---|
| 1 | Ring | 8 | 5 | 261 | 5.12 × 10−3 | 5.12 × 10−5 |
| 2 | Ring | 8 | 5 | 663 | 1.25 × 10−2 | 1.25 × 10−4 |
| 3 | Ring | 8 | 10 | 126 | 9.89 × 10−3 | 9.89 × 10−5 |
| 4 | Ring | 8 | 10 | 323 | 2.45 × 10−2 | 2.45 × 10−4 |
| 5 | Cumulative | 8 | 80.7 | 1 | 5.12 × 10−3 | 5.12 × 10−5 |
| 6 | Cumulative | 8 | 114 | 1 | 1.02 x 10−2 | 1.02 x 10−4 |
| 7 | Cumulative | 8 | 255 | 1 | 5.12 × 10−2 | 5.12 × 10−4 |
| 8 | Cumulative | 8 | 807 | 1 | 5.12 × 10−1 | 5.12 × 10−3 |
| 9 | Cumulative | 8 | 2553 | 1 | 5.12 | 5.12 × 10−2 (5.12%) |
| 10 | Commercial | 100 | 9500 (Out)/ 9000 (In) | 1 | 7.265 | 7.3 × 10−2 (7.26%) |
| Component | b (mm) | k (W/(m·K)) | ε (-) |
|---|---|---|---|
| Cathode (W) | 6 | 100 | 0.28 |
| DMS (ZrO2) | 8 × 10−3 * | 1.7 ** | - |
| Anode (GaAs) | 0.5 | 46 | 0.6 |
| Pattern Number | 1 | 2 | 3 | 4 | 5–9 | 10 |
|---|---|---|---|---|---|---|
| Number of elements [millions] | 3.3 | 4.7 | 3.73 | 4.06 | 0.5–0.6 | 0.132 |
| Component | BC Type | Parameters | Units | Values |
|---|---|---|---|---|
| Cathode lower | Wall | Qout | W/m2 | * |
| Cathode upper | Wall | T | K | 1500–2500 |
| Anode lower | Wall | T | K | 350 |
| Anode upper | Wall | Qin-anode | W/m2 | * |
| External Walls | Adiabatic walls | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeneli, M.; Bellucci, A.; Sabbatella, G.; Fotopoulou, M.; Apostolopoulos, V.; Stamatopoulos, P.; Trucchi, D.M.; Nikolopoulos, A.; Rakopoulos, D. Thermal Assessment of Dielectric Microspacer Technology Using an Advanced Three-Dimensional Simulation Model. Sustainability 2023, 15, 1786. https://doi.org/10.3390/su15031786
Zeneli M, Bellucci A, Sabbatella G, Fotopoulou M, Apostolopoulos V, Stamatopoulos P, Trucchi DM, Nikolopoulos A, Rakopoulos D. Thermal Assessment of Dielectric Microspacer Technology Using an Advanced Three-Dimensional Simulation Model. Sustainability. 2023; 15(3):1786. https://doi.org/10.3390/su15031786
Chicago/Turabian StyleZeneli, Myrto, Alessandro Bellucci, Gianfranco Sabbatella, Maria Fotopoulou, Vasilis Apostolopoulos, Panagiotis Stamatopoulos, Daniele M. Trucchi, Aristeidis Nikolopoulos, and Dimitrios Rakopoulos. 2023. "Thermal Assessment of Dielectric Microspacer Technology Using an Advanced Three-Dimensional Simulation Model" Sustainability 15, no. 3: 1786. https://doi.org/10.3390/su15031786
APA StyleZeneli, M., Bellucci, A., Sabbatella, G., Fotopoulou, M., Apostolopoulos, V., Stamatopoulos, P., Trucchi, D. M., Nikolopoulos, A., & Rakopoulos, D. (2023). Thermal Assessment of Dielectric Microspacer Technology Using an Advanced Three-Dimensional Simulation Model. Sustainability, 15(3), 1786. https://doi.org/10.3390/su15031786







