Abstract
The transport of dangerous goods by road represents a specific problem, considering that these vehicles can have great negative effects on people and the environment in the event of an accident. In the last few decades, various methods have been defined for risk management in this area. Most of these methods are based on reducing the probability and the consequences of an accident. In a large number of cases, the probability of the occurrence is in much greater focus than the consequences. To fill this gap, we created a new model for assessing the consequences on the population in the event of a fire during gasoline transportation. The model is based on the hypothesis that hazard intensity is directly proportional to the intensity of the heat generated by the fire and inversely proportional to the distance from the accident. The model was implemented through a Belgrade case study with multi-agent simulation. The results of the paper show that there is a 43% probability that there would be between 11 and 28 casualties in the observed location in the event of an accident. This confirms the initial hypothesis and shows that the model can be successfully used to assess the consequences.
1. Introduction
In the last few decades, the safety of the transport of dangerous goods by road, as well as the whole concept of risk management, has been a very popular topic. In 2020, 3.95% of the total transport work in the road freight transport sector in the European Union, i.e., 71.3 billion ton-kilometers, represented dangerous goods [1]. A particular problem is vehicles transporting dangerous goods such as liquid fuels because requests for these types of goods occur daily in the most diverse areas. According to data from the EUROSTAT database, 52% of the total quantity of dangerous goods transported on the territory of the European Union in 2020 were liquid fuels [1]. Therefore, the process of defining the routes for vehicles transporting dangerous goods, as one of the main tools for risk management in urban city areas [2], represents an important strategic task. This concept is primarily presented through two aspects: the reduction in the probability of an accident and the reduction in potential consequences. If the probability of an accident occurring at a certain location is low, and if the consequences for people and the environment are negligible, the location will be considered at a lower risk level. However, the question arises of whether a certain location is considered at a low-risk level if there has never been an accident involving dangerous goods. The problem of the previous question is best described by the situation that happened in 2018 in Bologna. Until that moment, there had never been an accident with dangerous goods at the observed location, and the consequences reached large proportions, with more than 60 casualties. Confirmation that this problem has not occurred in the last few years but has been present for a long time is the scenario from 1978 in the Spanish city of Los Alfaques, where an accident with a tanker transporting liquefied petroleum gas caused 102 casualties and over 140 injuries [3]. Research shows that the number of accidents in the dangerous goods transport sector has displayed an increasing trend during the 20th century and that 63% of those accidents occurred in the road transport sector [4]. In June 2017, an accident with a tanker transporting gasoline caused a fire near the Pakistani city of Ahmedpur Sharkia, in which 217 people died and more than 400 were injured. Accidents of this type are almost by rule most common in developing countries, such as the accident in Congo in 2010 with 230 casualties, the accident in Nigeria in 2012 with 121 casualties, and the accident in Sierra Leone in 2021 with 151 dead and 304 injured [5]. Of course, accidents of this type are not exclusively related to developing countries. In June 2020, an accident involving a tanker on the Shenhai highway in China caused the death of 20 people, 175 injuries, and the destruction of several houses [6]. Similar accidents in Mexico and India at the end of 2020 caused the death of several people [7]. Therefore, the main research question of this paper is how to estimate the number of casualties in locations where there has never been an accident involving a vehicle transporting dangerous goods. In such situations, the assessment of the consequences is of key importance during the risk assessment. Based on this, consequence assessment models must have a significant place in route selection for vehicles transporting dangerous goods, especially in urban city areas. As most of the existing models for risk assessment place a much greater focus on the probability of an accident, the authors of this paper decided to create a new model for consequence assessment. The subject of the paper is the assessment of the consequences on people in the event of an accident, and the paper aims to define a new model for estimating the number of casualties in the event of a fire during an accident with a tanker transporting gasoline. The defined model is based on the hypothesis that the intensity of the hazard is directly dependent on the intensity of the heat emitted by the fire, and is inversely proportional to the distance from the center of the accident. The model is applied in the case study at a specific location in Belgrade, using a multi-agent simulation model. The outcome of the research is a new model that can calculate the number of potential casualties in the event of a fire during an accident with a tanker transporting gasoline.
The rest of the paper is structured as follows. Section 2 includes an overview of relevant literature related to existing models for risk management in terms of assessment and analysis of consequences. Section 3 includes the theoretical setting of the model for assessing the consequences of a fire accident involving a vehicle transporting gasoline, as well as its application steps. Section 4 presents the input data and the setting of the case study for Belgrade, as well as the creation of the simulation model used in this work. Section 5 contains the presentation of the results derived from the previously defined model, while Section 6 contains concluding considerations and potential directions for further research.
2. Literature Review
Risk management in the transport of dangerous goods is a topic that has been relevant for many years. Although the authors have been engaged in research in this field since the 1930s, the first serious research in this area appeared in the late 1980s and early 1990s [7]. The first models related to risk management include qualitative risk analyses based on database searches and statistical analyses to define the basic characteristics of the transport of dangerous goods [8,9,10,11,12]. In this period, the analysis and assessment of consequences, as one of the steps of risk management, was almost completely neglected.
Over time, qualitative analyses have become a basis for the development of quantitative risk management methods that take into account the probability of catastrophic events and the size of the consequences. A large number of authors in these methods use F/N curves that define risk based on two previously specified attributes [13,14,15,16,17]. However, although these methods are theoretically dependent on the probability of an accident and the size of the consequences, the probability of an accident is in much greater focus. Huo Chai states that, although traditional risk management methods are considered biattributive, and depend both on the probability of an accident and the size of consequences, they are actually one-sided and take only the probability of occurrence into account [18]. Even Cassini, which is one of the creators of these models, points out that one of the main problem with risk assessment is the lack of reliable consequence assessment models [14]. All of this indicates a weak application of consequence assessment models in traditional risk management models.
Over time, models for the analysis and assessment of consequences are increasingly being used and have become an integral part of algorithms for route selection and risk assessment. However, in a large number of cases, their application remains limited to the assessment of the size of the impact zone of dangerous goods based on the relevant literature and the assessment of the exposed population. This is confirmed in the review paper by Guo and Luo [7], where they point out several papers in which such models are represented.
With the development of software and computer simulations, the application of models for the analysis of consequences is also increasing. In their work, Kampova et al. model the population consequences of an accident with a gasoline tanker, where the impact of explosion, heat, and poisoning effects are determined using ALOHA, EFFECTSGIS, and TerEx softwares. The results indicate that, for the defined input parameters, a circle of 66 m and 112 persons are affected [19]. Babapoor et al. define a model that simulates the consequences of a fire due to the occurrence of a traffic accident with a vehicle transporting gasoline in a tunnel, in order to design an efficient fire protection system [20]. Tixier et al. present software designed to train firefighters when responding to an accident involving a vehicle transporting dangerous goods. This software, OSIRIS, uses mathematical models to simulate the effects of explosions, fires, and the spread of gases and, as a result, provides numerical values and graphs displayed on a map [21].
Consequence assessment models find application in both research and experimental works. Vianello et al. experiment with small-scale laboratory tunnels simulating the impact of heat caused by fires of different intensities and speeds in order to determine the intensity of the hazard. A series of experiments were conducted simulating an accident between a light vehicle and a vehicle carrying dangerous goods resulting in a fire. The obtained results largely agree with real-world scenarios [22]. As part of his research, Vagiokas presents a methodology for carrying out a study on fire safety during fuel transportation. One of the steps of this study is the presentation of a mathematical model for the analysis of consequences in the event of a fire accident, which is based on the intensity of heat and exposure time [23].
One of the more detailed works in this area, which deals with the assessment of consequences in the true sense of the word, is the work of Marc Assael from 2015. In his work, Assael quantifies the consequences of hazard effects and tests them through various case studies. In one of them, the author determines the probability of an individual suffering based on several different factors, where the most important are exposure time and heat intensity [24].
As can be concluded from the above, models for assessing consequences have extremely modest application in the existing literature and the current risk management methods. The result of this is that, in the majority of the existing models, the analysis of consequences is either completely neglected or limited to defining the impact zone and the exposed population. This is a shortcoming of these models, as the analysis of the consequences, for both people and the environment, is equally important when choosing a route for vehicles transporting dangerous goods, as well as the probability of an accident. For these reasons, the authors of this paper decided to create a new consequence assessment model.
3. Theoretical Setup of the Model
The model defined in this paper was created by combining several different elements, from relevant literature, which have an impact on the magnitude of the consequences. These elements include the calculation of the flame height in the case of fire, the definition of the shape and size of the impact zone depending on the flame height and the intensity of the heat generated by the fire, as well as the calculation of the intensity of the hazard using a modified probit model. The originality of this paper lies in the fact that, for the first time, these elements are integrated into such a model.
The consequence assessment model proposed in this paper consists of two main elements:
- calculation of the shape and size of the impact zone, as well as the size of different segments of the zone depending on the intensity of heat;
- calculation of hazard intensity, precisely, the probability that an individual will be injured or killed in a certain segment of the impact zone.
The shape and size of the impact zone of dangerous goods can depend on many different factors, such as the type and quantity of dangerous goods transported, topographic characteristics of the terrain, climate conditions, and so on [25,26]. Given that the hazard considered in this work is fire, and taking into account an assumption that the heat caused by fire spreads evenly in all directions, a circle of the appropriate radius is defined as the shape of the impact zone. On the other hand, the size of the impact zone is defined by a graphical method, based on the height reached by the flame. For verification of the graphical method, the analytical method proposed by B. Butler [27] was used. Figure 1 shows the heat intensity as a function of the size of the impact zone and the flame height [28].
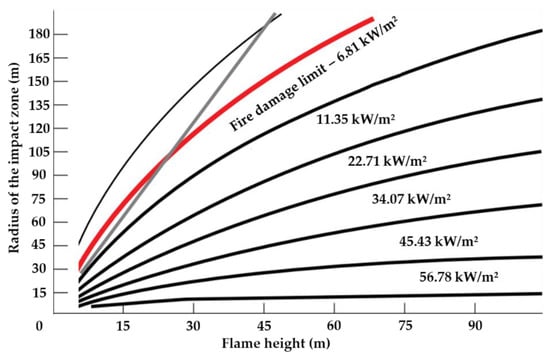
Figure 1.
Heat intensity as a function of the radius of the impact zone and the flame height [28].
The x-axis of the graph shows the flame height expressed in meters, while the y-axis shows the radius of the impact zone. The red curve on the graph represents the limit of fire injury. In other words, when the width of the impact zone, for the corresponding flame height, exceeds this limit, there is no longer any risk of injury to people. Based on this curve, the final limit of the impact zone is determined. The black curves represent the limits for different heat intensities of the fire. These curves will be used later in the model when defining different segments of the impact zone. The grey curve represents “the rule of thumb” that firefighters use to determine the size of the safety zone. The safety zone is in this case equal to four times the flame height.
Therefore, if the flame height is known, it is possible to determine the size of the impact zone. The flame height is determined based on the following equation [29,30]:
In Equation (1), H represents the flame height and D represents the diameter of the area affected by the fire. Given that, at the time of the incident, the largest amount of gasoline is inside the tank, as a suitable value for D, it is necessary to adopt the total length of the cargo area of the tank, considering that this is the maximum length over which the flame can spread at the time of the accident.
After the flame height is calculated, the size of the impact zone is determined by the graphical method according to the following steps:
- On the x-axis of the coordinate system, it is necessary to mark the value of the calculated flame height;
- From this point, a vertical line should be drawn to the intersection with the red curve on the graph;
- From the intersection of each curve, including the red one, a horizontal line should be drawn to the left towards the y-axis;
- The intersection of the horizontal lines and the y-axis of the coordinate system represent the sizes of different segments of the impact zone, where each of them is characterized by a certain intensity of heat.
After the size of the impact zone has been calculated, it is necessary to determine the probability that an individual will be hurt within a certain segment of the impact zone of dangerous goods. As stated in the Introduction, the initial hypothesis is that the intensity of the hazard, and thus the probability that the individual will be hurt, is directly proportional to the intensity of the heat. According to the previous section, the hazard intensity was calculated based on the modification of the probit model adapted to this type of hazard [31,32]:
In Equation (2), Y represents the probit value or the probability measure, C represents the intensity of heat expressed in kW/m2, and T represents the exposure period expressed in minutes. The output values of the probit model represent numerous values that are converted into hazard intensity values based on the probit table [33]. The probit table is presented in Table 1.

Table 1.
Probit table [33].
The values from Table 1 represent the probit values that can be calculated with Equation (2) and are later used when determining the hazard intensity. On the other hand, the values in the first column and the header of the table represent the probability that an individual will get hurt in the event of an accident. This probability is shown in percentage on a scale from 0 to 100. In further analysis, the hazard intensity, which represents this probability expressed on a scale from 0 to 1, will be used. Given that the obtained probit value is usually not identical to the one in the table, but lies between two values, the final value of the hazard intensity must be determined by interpolation according to Equation (3).
When the obtained hazard intensity values for each of the segments of the impact zone are multiplied by the number of people within that segment, it is possible to determine the number of injured people at the observed location.
4. Case Study for the City of Belgrade
4.1. Case Study Setup
The first step when setting up a case study is defining the space and time of the research. The area of research is a specific location on the territory of the city of Belgrade. To select a location for assessing the consequences, it is necessary to define the transport route for the vehicles transporting gasoline. Several steps were used to determine the vehicle route. The first step represents the definition of the starting point of the journey, i.e., the original location. The starting point of the journey represents the location from which the largest amount of gasoline is transported by road to the city of Belgrade. Based on that, the Pančevo refinery [34] was chosen as the starting point of the journey. The second step refers to the choice of roads on which the defined vehicle should move to reach the target location, in terms of physical and regulatory restrictions, as well as the maneuverability of the vehicle. The transportation route was defined based on field research and a review of legal regulations. The criterion for choosing the final route for the tanker is the minimum travel time between the starting point and the destination point. The last step refers to the choice of the final destination of the route. Given that the highest average population density is represented in the central city zones, as a destination, it is necessary to define a location that is located in the central city zone or near the border of the central city zone. The Trg Oslobođenja fuel station, on Bulevar Oslobođenja street, was adopted as the route destination. The place of occurrence of the accident was generated by random selection in the central area of the city on the vehicle route. The location for which the assessment of the consequences will be carried out is located on Bulevar Oslobođenja street near Slavija Square. Figure 2 shows the accident location.
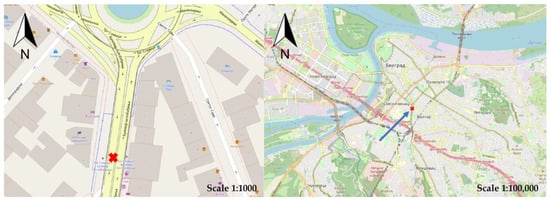
Figure 2.
Accident location.
On the other hand, the research time was defined based on the transport demand for this type of good in the territory of the city of Belgrade, as well as based on legal restrictions regarding the movement of freight vehicles through the central zone of the city [34,35]. As the movement of goods vehicles through Bulevar Oslobođenja street is only allowed after 8:00 p.m., the period between 8:00 p.m. and 9:00 p.m. is defined as the research period.
The decision that regulates the ban on the transportation of goods in certain periods through certain streets on the territory of the city also defines the limit regarding the maximum permissible weight of the vehicle. For this reason, it is necessary to define the representative vehicle. As this decision defines the ban on the movement of freight vehicles whose maximum permitted weight exceeds 12 t in the observed location, a tank with one chamber, a capacity of 6000 L, a payload of 7000 kg, and a total weight of 12,000 kg is adopted as the representative vehicle. Table 2 shows the specifications for the selected vehicle.

Table 2.
Specifications of the selected vehicle.
When the length of the cargo area is known, it is possible to determine the height that the flame reaches in the event of a fire. Based on Equation (1), the calculated flame height is 7.44 m. After that, it is possible to determine the boundaries for each of the segments of the impact zone using the graphic method.
Based on the value of the heat intensity using the probit model, it is possible to determine the hazard intensity for each of the impact zone segments. Heat intensity i.e., the value C in Equation (2), is read from Figure 1 depending on which segment of the zone of influence it is. On the other hand, a period of 9 min is adopted as the value T, given that it is the estimated time that elapses from the moment of the accident to the moment when the fire service arrives at the location from the nearest fire station and starts the sanation process. This value was established after consultation with the fire department of the city of Belgrade and was defined as adequate for the observed location. Table 3 presents the values calculated from the probit model.

Table 3.
Hazard intensity values.
4.2. Simulation Model
The transport system of an urban area is a system in which several different groups of entities function. Each of these entities functions independently and has a direct influence on the others. One of the ways to present the city’s transport system is through a simulation model. As the consequence assessment model implies direct interaction between multiple groups, the authors of this paper created a model in which different autonomous entities interact together. With that in mind, a multi-agent simulation model was created to test the initial hypothesis.
The simulation model defined in this paper was created in NetLogo software. NetLogo is a free software package designed for multi-agent simulations developed in 1999 at Northwestern University. The user can use it to give instructions to hundreds or thousands of agents working independently. In this way, it is possible to investigate the connection between the behavior of individuals at the micro level, as well as the patterns at the macro level that arise from their interaction [36].
The model interface consists of a field in which the simulation takes place, 2 buttons for setting and starting the simulation, 21 sliders used to adjust various model parameters, 15 counters, and 1 graph. The software allows the analyst to create different groups of agents and to define appropriate characteristics and behavior for each of them. A total of six groups of agents are defined within this model:
- tanker;
- passenger cars;
- buses;
- trams;
- cargo vehicles;
- passengers.
In addition to these groups of mobile agents, two groups of fixed agents are also defined, which are not displayed on the interface during the simulation. These are the residents and employees who are located in buildings near the accident site. Although not displayed on the interface, these agents are included in the simulation when estimating casualties. The tanker agent represents a vehicle that carries a potential risk of an incident situation, while the other groups of agents represent potentially exposed people. Essentially, the exposed agents within this model can be divided into four main groups, namely, residents, employees, traffic participants, and users of the public transport system. For each of the mentioned groups, data were collected from different sources and integrated into the model so that the simulation would have the most accurate results. The data used to estimate the number of exposed residents and employed persons are data on the number of residents according to the 2011 census by traffic zones, obtained from the Urban Planning Institute of the City of Belgrade. Data on the passenger cars, buses, trams, and trucks flow were taken from the traffic count conducted in 2015 by the University of Belgrade—Faculty of Traffic and Transport Engineering in 2015 to create the Transport Model for the City of Belgrade. Data on the time spent by public transport vehicles at stops were obtained from vehicle management system reports for stops and lines operating at the observed location. Data on the minimum and maximum vehicle speed, as well as data on the average and maximum occupancy of passenger cars, were taken from the Transport Model of the City of Belgrade. The average and maximum occupancy of public transport vehicles, passenger volume at stops, and the number of passengers at the beginning of the simulation were taken from the passenger counting study conducted by the Center for Urban Development Planning.
After the data have been collected for each of the potential groups of exposed people, all input parameters of the model should be defined. Input parameters of the model are defined based on sliders placed on the interface, where each slider represents one input parameter. All mentioned parameters were defined to adequately simulate the functioning of the transport system of a city. The realistic values of the parameters on the flow and speed of the vehicles show how the transport system at the observed location functions in a given period. On the other hand, data on the average occupancy of vehicles and the number of passengers at bus stops and in public transport vehicles indicate how many people may be exposed to dangerous goods in the event of an accident. Without well-defined parameters and accurate and reliable data adopted as input parameter values, the simulation of the functioning of the city’s transport system, and thus the simulation of the defined model, is not possible. Considering that this is a new model for consequence assessment, all parameters proposed within this model are originally proposed by the authors and are not taken from previous works. The limitation of the model is that it is based exclusively on inputs from the transport system and basic demographic data for the impact zone, but it does not consider the spatial and temporal distribution of people as consequences of their other activities (in-home activities, work, leisure activities, and so on). Therefore, the parameters that describe these activities are not included in this model. However, the authors believe that, for a relative comparison of the estimated number of casualties between multiple locations, these parameters are not of crucial impact. Table 4 shows the model input parameters and their values.

Table 4.
Model input parameters.
After all of the input values have been set, the simulation is set up and started. Agents enter the map and move along defined paths according to their characteristics. The simulation lasts until the moment the tanker arrives at the place of the accident. Upon the arrival of the tanker at the defined location, the movement of other agents stops and the impact zone is defined around the accident site. For each of the segments of the impact zone, the model generates the number of injured and casualties depending on the value of the hazard intensity and the number of people who are in the zone at the time of the accident. The output from the model is a map of the location, with the impact zone drawn and the estimated number of injured in it. Figure 3 shows the results of the simulation model.
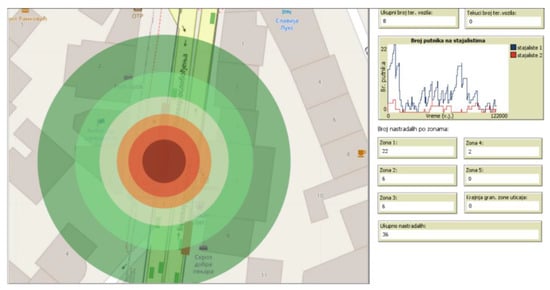
Figure 3.
Output of the simulation model (screenshot from NetLogo).
5. Results and Discussion
The simulation model contains 10 random number generators, which are used to define different patterns for the encounter and movement of different groups of agents within the simulation. For the results of the model to be as realistic as possible, the simulation experiment is performed 30 times, where the values of the random numbers are changed for each simulation run. Table 5 shows the results that represent the number of casualties obtained for each of the 30 performed simulations.

Table 5.
Results of the simulation model.
The arithmetic mean of the number of injured and casualties for the above 30 simulations is 18.83, while the standard deviation and the coefficient of variation are 11.24 and 0.60, respectively.
Based on the previously presented results, it can be concluded that the value of the number of injured and casualties varies from simulation to simulation and that it largely depends on the current circumstances in the system. The high values in certain simulations can be explained by the presence of public transport vehicles near the scene of the incident. Thus, in simulation number 21, in which 51 casualties were estimated, the tram and bus are at stop 1 at the time of the accident. This simulation is also the one with the highest number of injured and casualties recorded.
On the other hand, the slightly lower values in some situations are the consequence of the reduced number of exposed people, the absence of passengers at the stop, the absence of vehicles in the impact zone, and so on. For these reasons, the arithmetic mean alone cannot be a representative indicator of the estimation of the number of injured and casualties at the observed location. Based on that, the estimated data are divided into three groups, where each of the groups is characterized by a certain probability of occurrence and the average value of the number of injured. For the limit values of the groups, the values around which the largest number of simulation results occur are adopted. The first group consists of those simulations where the estimated number of casualties is 28 or more. The second group consists of simulations in which the estimated number of casualties is in the range of 11 to 28, and the third group consists of those simulations in which the estimated number of casualties is 11 or less. The probability of occurrence for each of the groups represents the value obtained by dividing the number of simulations in which the number of casualties is within the range of the group by the total number of simulations. Table 6 shows the defined groups with the mean value of the number of casualties and the probability of occurrence.

Table 6.
Probability of occurrence and an average value of the number of casualties for each group.
Based on the data from Table 6, it can be concluded that the most common simulations are from group 2 and that the highest probability is that between 11 and 28 casualties will occur in a defined location. In second place is group 3 and the probability that less than 11 victims will appear in a defined location is 33%. The last in rank is group 1, where there is a 23% probability that more than 28 victims will be reported at the location in the event of an accident. Based on this, it can be concluded that the highest probability is that between 11 and 28 victims will be reported in the selected location in the event of an accident.
6. Conclusions
Gasoline, as a type of dangerous good with high transport demands, represents a great potential danger to people and the environment. This raises the question of what consequences this type of good can have in the event of an accident. The answer to this question can be obtained by conducting a consequence assessment. Within this paper, a model for assessing the consequences was defined, which takes into account the intensity of the hazard emitted by the fire and the number of exposed people within the impact zone of dangerous goods. The fact that elements such as the calculation of the flame height, the definition of the size and shape of the impact zone, and calculation of the intensity of the hazard are for the first time integrated into a single model makes this model new and original. Moreover, research was conducted based on the application of this model using multi-agent simulation. The model created in this paper has the potential for wide application in dangerous good transport planning, especially in urban areas. By assessing the consequences at specific locations, it is possible to define routes with lower risk levels, in terms of the magnitude of the consequences, and thus reduce the overall risk at that location. However, as the road transport of dangerous goods is a very complex area, the model proposed in this paper covers only a small part of the problem. Therefore, the results obtained from its application cannot be considered outside the comprehensive context. For these reasons, this model should be an integral part of the models for defining the routes for vehicles transporting dangerous goods. Based on the research and application of the simulation model, it is possible to draw the following conclusions.
The results of this paper confirm the initial hypothesis that the intensity of the hazard is directly dependent on the heat emitted by the fire and inversely proportional to the distance from the center of the accident. The results also indicate that agent-based simulations can be used as a suitable tool for modeling the transportation system of a city. Moreover, it has been shown that agent-based simulation is suitable for the implementation of various models in the field of road transport of dangerous goods. The simulation was performed 30 times and the results of all simulations are in accordance with the authors’ expectations.
The results of the model indicate that the number of casualties varies depending on the circumstances in which the accident occurred. If there are one or more public transport vehicles at the scene of the accident, a larger number of passengers at the stop, or a larger number of other traffic participants, the consequences will be greater. On the other hand, if there are no people at the scene of the accident, the consequences will be significantly less. For this reason, the results are divided into three groups, where each of the groups is characterized by the range of the number of casualties and the probability of occurrence of that event. The probability distribution indicates that there is a 43% chance that the number of casualties will be in the range of 11 to 28, a 33% chance that the number of casualties will be less than or equal to 11, and a 23% chance that the number of casualties will be greater than or equal to 28. Based on that, another conclusion of this paper is that the number of casualties largely depends on the number of exposed people. By avoiding areas with a high population density, a high degree of attractiveness for public transport users, and a large number of private car users, the potential consequences can be significantly reduced.
Considering that the assessment of consequences is only one step of the risk management methodology, there are many directions for further research. Further research can be directed towards the application of the conducted research and model on alternative transport routes that connect the observed source and target location to determine the magnitude of the consequences on them. Based on that, it is possible to determine an acceptable transport route between the observed source and target location using a multi-criteria analysis. One of the directions of further research is the definition of a model for determining the probability of an accident. In this way, together with the model for assessing the consequences, it is possible to determine the overall risk for the observed area. Moreover, it is possible to continue the research in terms of defining the measures that represent a response to the previously defined incident situation, that is, defining and implementing the rehabilitation process. The proposed model can also have some policy implications. Currently, in the city of Belgrade, there is not a single regulation that regulates the movement of vehicles that transport dangerous goods in and through the urban city zones. The defined model can represent one of the basic steps of the methodology for defining regulations on restrictions for the movement of vehicles transporting dangerous goods through the urban city zones. Dangerous goods can have major negative effects on people and the environment, especially when transported through the central zone of the city. For this reason, the application of this model is a basic step when defining the level of risk, as well as all further measures aimed to reduce consequences during the transport of this type of good.
Author Contributions
Conceptualization, S.P., B.M., M.Đ., P.Ž., S.B. and S.T.; Methodology, S.P., B.M. and M.Đ.; Software, S.P. and M.Đ.; Validation, S.P., B.M., M.Đ., P.Ž. and S.B.; Investigation, S.P.; Data curation, S.P.; Writing—original draft, S.P., B.M., M.Đ., P.Ž., S.B., S.T. and A.N.; Writing—review & editing, S.P., B.M., M.Đ., P.Ž., S.B., S.T. and A.N.; Visualization, S.P., B.M., M.Đ., P.Ž., S.B. and S.T.; Supervision, B.M., P.Ž. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eurostat–“Eurostat Data Explorer”. Available online: https://appsso.eurostat.ec.europa.eu/nui/submitViewTableAction.do (accessed on 30 August 2022).
- Izdebski, M.; Jacyna-Gołda, I.; Gołda, P. Minimisation of the probability of serious road accidents in the transport of dangerous goods. Reliab. Eng. Syst. Saf. 2022, 217, 108093. [Google Scholar] [CrossRef]
- Arturson, G. The Los Alfaques disaster: A boiling-liquid, expanding-vapour explosion. Burns 1981, 7, 233–251. [Google Scholar] [CrossRef]
- Oggero, A.; Darbra, R.M.; Muñoz, M.; Planas, E.; Casal, J. A survey of accidents occurring during the transport of hazardous substances by road and rail. J. Hazard. Mater. 2006, 133, 1–7. [Google Scholar] [CrossRef]
- Qureshi, O.M.; Hafeez, A.; Kazmi SS, H. Ahmedpur Sharqia oil tanker tragedy: Lessons learnt from one of the biggest road accidents in history. J. Loss Prev. Process Ind. 2020, 67, 104243. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Fan, L.; Shi, S.; Zhang, T.; Qi, M. Research on the prediction of dangerous goods accidents during highway transportation based on the ARMA model. J. Loss Prev. Process Ind. 2021, 72, 104583. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Luo, C. Risk assessment of hazardous materials transportation: A review of research progress in the last thirty years. J. Traffic Transp. Eng. 2022, 9, 571–590. [Google Scholar] [CrossRef]
- Harwood, D.W.; Viner, J.G.; Russell, E.R. Truck Accident Rate Model for Hazardous Materials Routing. Transp. Res. Reco 1990, 1264, 12–23. Available online: http://onlinepubs.trb.org/Onlinepubs/trr/1990/1264/1264-002.pdf (accessed on 19 September 2022).
- Davies, P.A.; Lees, F.P. The assessment of major hazards: The road transport environment for conveyance of hazardous materials in Great Britain. J. Hazard. Mater. 1992, 32, 41–79. [Google Scholar] [CrossRef]
- Hobeika, B.A.G.; Kim, S. Characteristics of hazardous material accidents in Pennsylvania. J. Transp. Eng. 1993, 119, 226–238. [Google Scholar] [CrossRef]
- Vílchez, J.A.; Sevilla, S.; Montiel, H.; Casal, J. Historical analysis of accidents in chemical plants and in the transportation of hazardous materials. J. Loss Prev. Process Ind. 1995, 8, 87–96. [Google Scholar] [CrossRef]
- Montiel, H.; JVílchez, A.; Arnaldos, J.; Casal, J. Historical analysis of accidents in the transportation of natural gas. J. Hazard. Mater. 1996, 51, 77–92. [Google Scholar] [CrossRef]
- Spadoni, G.; Leonelli, P.; Verlicchi, P.; Fiore, R. A numerical procedure for assessing risks from road transport of dangerous substances. J. Loss Prev. Process Ind. 1995, 8, 245–252. [Google Scholar] [CrossRef]
- Cassini, P. Road transportation of dangerous goods: Quantitative risk assessment and route comparison. J. Hazard. Mater. 1998, 61, 133–138. [Google Scholar] [CrossRef]
- Bonvicini, S.; Leonelli, P.; Spadoni, G. Risk analysis of hazardous materials transportation: Evaluating uncertainty by means of fuzzy logic. J. Hazard. Mater. 1998, 62, 59–74. [Google Scholar] [CrossRef]
- Leonelli, P.; Bonvicini, S.; Spadoni, G. Hazardous materials transportation: A risk-analysis-based routing methodology. J. Hazard. Mater. 2000, 71, 283–300. [Google Scholar] [CrossRef]
- Fabiano, B.; Currò, F.; Palazzi, E.; Pastorino, R. A framework for risk assessment and decision-making strategies in dangerous good transportation. J. Hazard. Mater. 2002, 93, 1–15. [Google Scholar] [CrossRef]
- Chai, H.; He, R.C.; Jia, X.Y.; Ma, C.X.; Dai, C.J. Generalized route planning approach for hazardous materials transportation with equity consideration. Arch. Transp. 2018, 46, 33–46. [Google Scholar] [CrossRef]
- Kampova, K.; Makka, K.; Moricova, V. Modeling of the Extraordinary Event Consequences for the Transport of Dangerous Substances. Perner’s Contacts 2018, 13, 28–34. [Google Scholar]
- Babapoor, A.; Bab, V.; Ahamadi Sabegh, M. A New Investigation on Tunnel Pool Fire Phenomenon Using CFD Technique. Iran. J. Chem. Chem. Eng. 2018, 37, 171–182. [Google Scholar]
- Tixier, J.; Dusserre, G.; Rault-Doumax, S.; Ollivier, J.; Bourely, C. OSIRIS: Software for the consequence evaluation of transportation of dangerous goods accidents. Environ. Model. Softw. 2002, 17, 627–637. [Google Scholar] [CrossRef]
- Vianello, C.; Fabiano, B.; Palazzi, E.; Maschio, G. Experimental study on thermal and toxic hazards connected to fire scenarios in road tunnels. J. Loss Prev. Process Ind. 2012, 25, 718–729. [Google Scholar] [CrossRef]
- Nikolaos, V. Fire Hazards Of Transportation Of Fuels. Int. J. Eng. Sci. 2018, 7, 38–48. [Google Scholar] [CrossRef]
- Assael, M.J.; Paschalidis, L.C.; Sakellaropoulos, G.P. Evaluation of the effects of fires and explosions in the transport of hazardous materials. Arch. Transp. 2015, 34, 7–18. [Google Scholar] [CrossRef]
- Milovanović, B.; Jovanović, V. Control and Prevention in the Transportation of Dangerous Goods; University of Belgrade–Faculty of Transport and Traffic Engineering: Belgrade, Serbia, 2016. [Google Scholar]
- Holeczek, N. Analysis of different risk models for the hazardous materials vehicle routing problem in urban areas. Clean. Environ. Syst. 2021, 2, 100022. [Google Scholar] [CrossRef]
- Butler, B.W.; Cohen, J.D. Firefighter Safety Zones: A Theoretical Model Based on Radiative Heating. Int. J. Wildland Fire 1998, 8, 73–77. [Google Scholar] [CrossRef]
- Butler, B.W.; Cohen, J.D. Firefighter safety zones: How big is big enough? Fire Manag. Notes 1998, 58, 13–16. [Google Scholar]
- Zhang, M.; Song, W.; Wang, J.; Chen, Z. Accident consequence simulation analysis of pool fire in fire dike. Procedia Eng. 2014, 84, 565–577. [Google Scholar] [CrossRef]
- Marková, I.; Lauko, J.; Osvaldová, L.M.; Mózer, V.; Svetlík, J.; Monoši, M.; Orinčák, M. Fire size of gasoline pool fires. Int. J. Environ. Res. Public Health 2020, 17, 411. [Google Scholar] [CrossRef]
- The Netherlands Organization of Applied Scientific Research. Methods for the Calculation of Physical Effects (Yellow Book); Public Series on Dangerous Substances No. PSG2; The Netherlands Organization of Applied Scientific Research: The Hague, The Netherlands, 2005; p. 870. [Google Scholar]
- The Norwegian Directorate for Civil Protection (DSB). Guidelines for Quantitative Risk Analysis of Facilities Handling Hazardous Substances; The Norwegian Directorate for Civil Protection (DSB): Tønsberg, Norway, 2019. [Google Scholar]
- Finney, D.J. Probit Analysis; Cambridge University Press: Cambridge, UK, 1952; p. 330. Available online: https://dspace.gipe.ac.in/xmlui/bitstream/handle/10973/36028/GIPE-025784.pdf?sequence=3&isAllowed=y (accessed on 5 July 2021).
- Jovanović, V.; Tica, S.; Milovanović, B.; Živanović, P. Researching and analyzing the features of oil and demand for transporting oil derivates in the area of Belgrade. Transport 2009, 24, 249–256. [Google Scholar] [CrossRef]
- Secretariat for Traffic| Department for the Supply and Movement of Freight Motor Vehicles through the City. Available online: http://bgsaobracaj.rs/sekretarijat/sektor-za-gradsku-logistiku/9/odeljenje-za-poslove-snabdevanja-i-kretanja-teretnih-motornih-vozila-kroz-grad (accessed on 5 July 2021).
- Sklar, E. Software review: NetLogo, a multi-agent simulation environment. Artif. Life 2007, 13, 303–311. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).