Neural Networks Based Dynamic Load Modeling for Power System Reliability Assessment
Abstract
1. Introduction
- Fast dynamics of both mechanical and electrical characteristics, e.g., induction motors
- Significant effects of under-voltage excursions, e.g., discharge lighting
- Insignificant delays and discontinuities in response to voltage faults, e.g., incandescent lighting
- Slow characteristics, e.g., electric heating
2. Standard Loads Model
2.1. Static Load Models
2.2. Dynamic Load Models
2.3. Load Model Calibrations
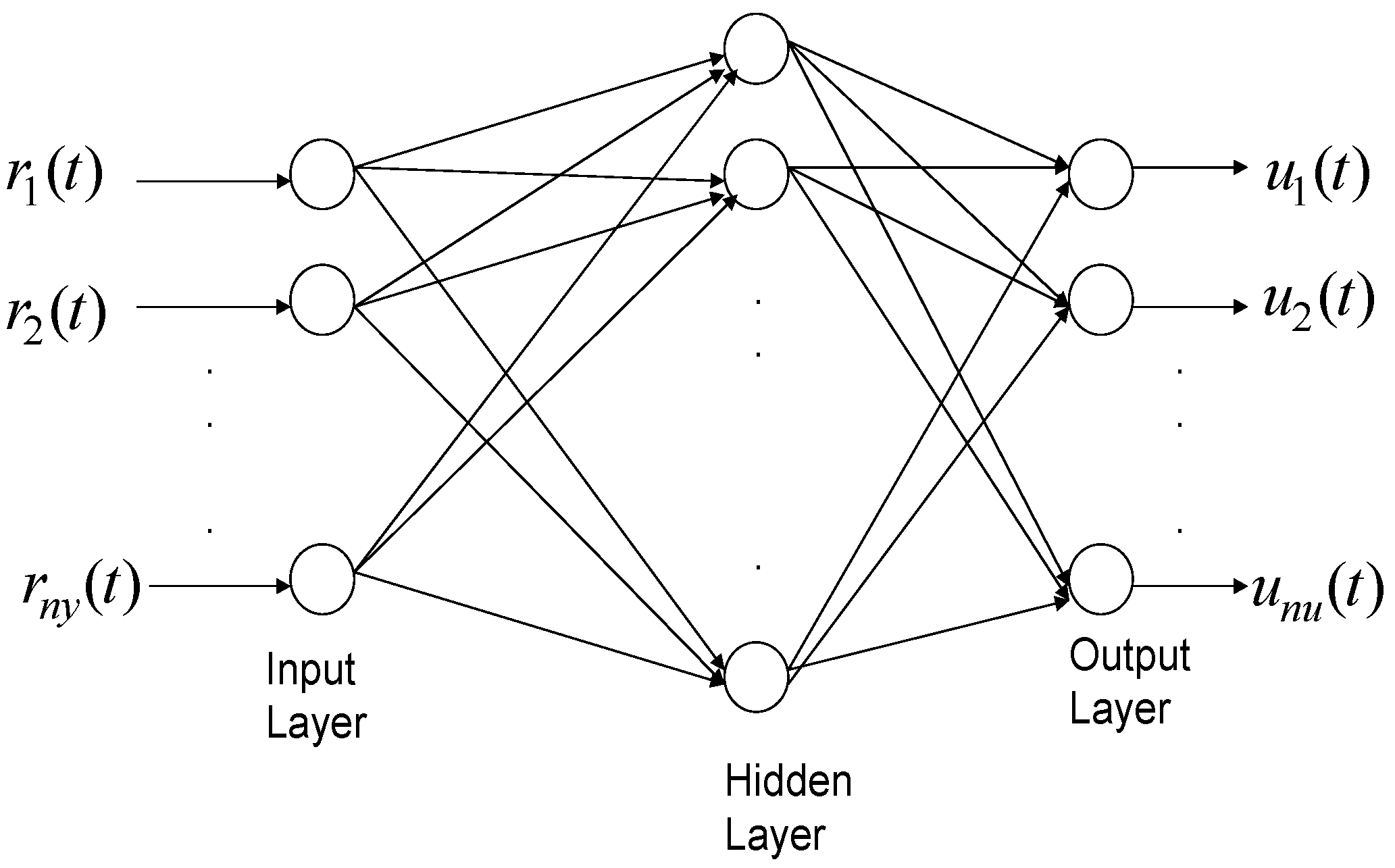
3. Neural Network Based Composite Load Modelling for Reliability Assessment
3.1. Power System Reliability Assessment
3.2. Proposed Neural Network Based Composite Load Modelling
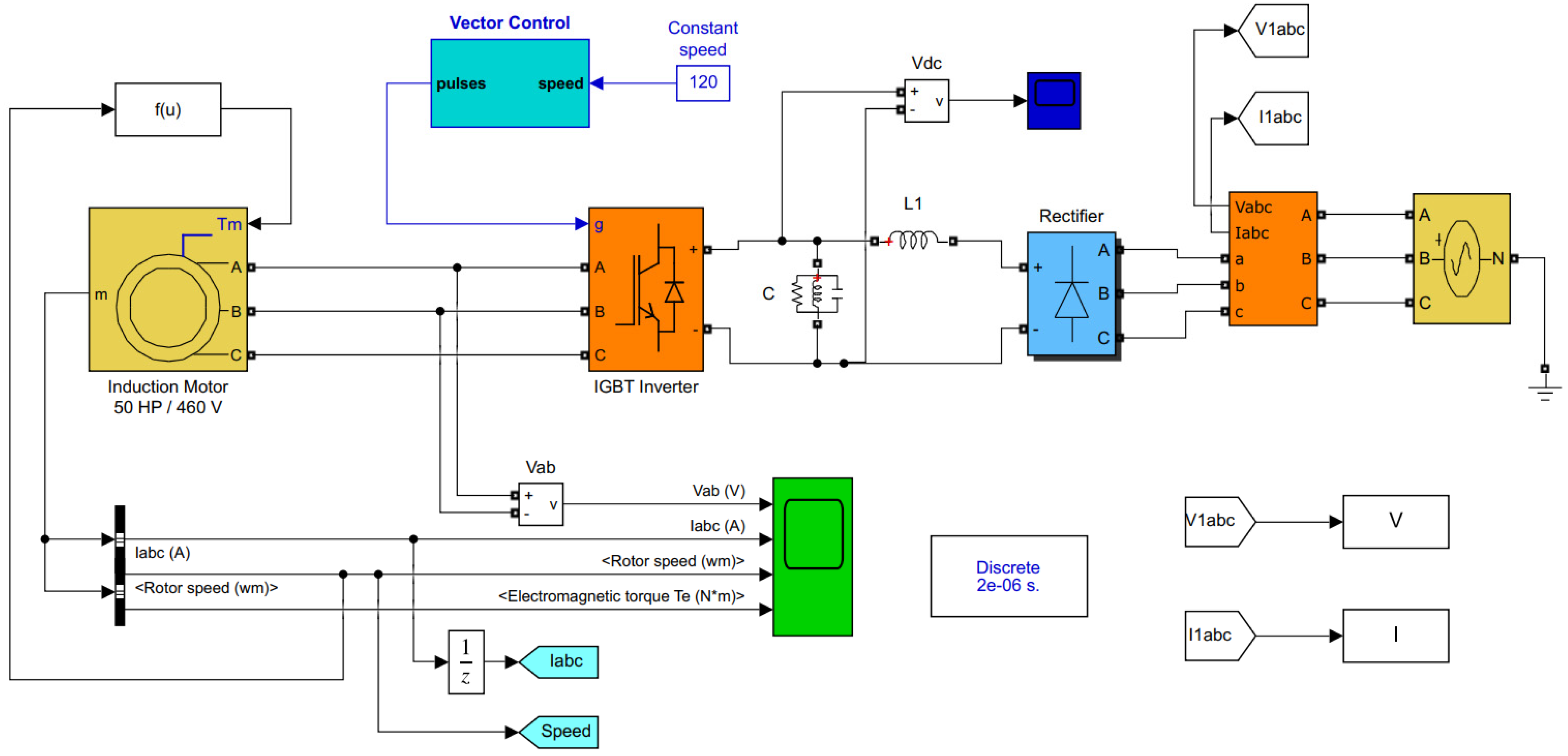
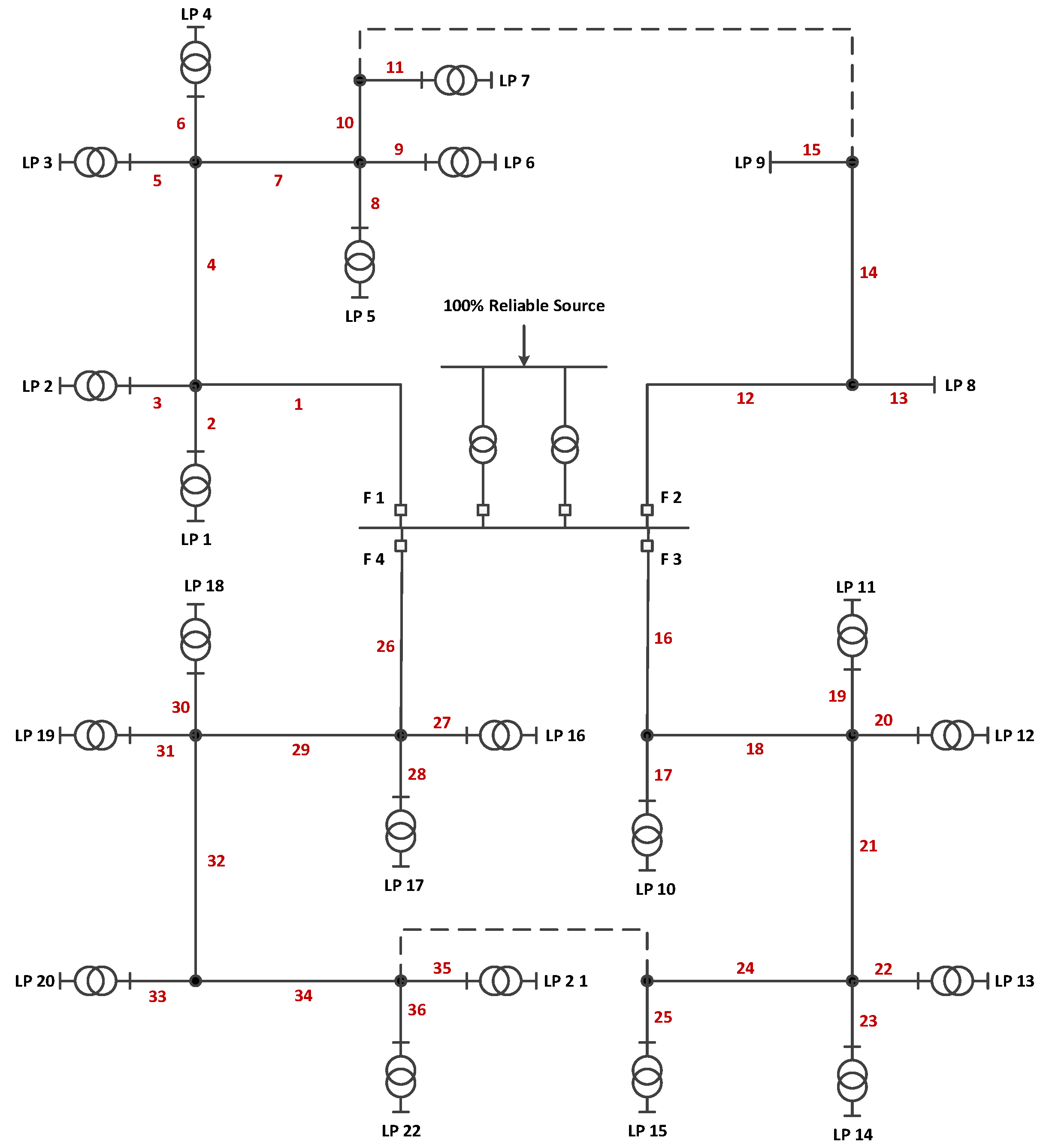
4. Case Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taylor, C. Power System Voltage Stability; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Mitra, A.; Dutta, R.; Gupta, A.; Mohapatra, A.; Chakrabarti, S. A robust data-driven approach for adaptive dynamic load modeling. IEEE Trans. Power Syst. 2022, 37, 3779–3791. [Google Scholar] [CrossRef]
- Paidi, E.; Nechifor, A.; Albu, M.; Yu, J.; Terzija, V. Development and validation of a new oscillatory component load model for real-time estimation of dynamic load model parameters. IEEE Trans. Power Deliv. 2020, 35, 618–629. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Shi, D.; Wang, J.; Wang, Z. Two-stage WECC composite load modeling: A double deep q-learning networks approach. IEEE Trans. Smart Grid 2020, 11, 4331–4344. [Google Scholar] [CrossRef]
- Chávarro-Barrera, L.; Pérez-Londoño, S.; Mora-Flórez, J. An adaptive approach for dynamic load modeling in microgrids. IEEE Trans. Smart Grid 2021, 12, 2834–2843. [Google Scholar] [CrossRef]
- Wang, S.; Huang, R.; Huang, Z.; Fan, R. A robust dynamic state estimation approach against model errors caused by load changes. IEEE Trans. Power Syst. 2020, 35, 4518–4527. [Google Scholar] [CrossRef]
- Keyhani, A.; Lu, W.; Heydt, G.T. Neural Network Based Composite Load Models for Power System Stability Analysis. In Proceedings of the 2005 IEEE International Conference on Computational Intelligence for Measurement Systems and Applications, Messian, Italy, 20–22 July 2005. [Google Scholar]
- Karki, R.; Billinton, R.; Verma, A. Reliability Modeling and Analysis of Smart Power Systems; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Veliz, F.; Borges, C.; Rei, A. A comparison of load models for composite reliability evaluation by nonsequential monte carlo simulation. IEEE Trans. Power Syst. 2010, 25, 649–656. [Google Scholar] [CrossRef]
- Cho, N.; Awodele, K. Comparison of Four Load Models for Reliability Evaluation Considering Reconfiguration Using Monte Carlo Simulation. In Proceedings of the 2012 IEEE International Conference on Power System Technology (POWERCON), Auckland, New Zealand, 30 October–2 November 2012. [Google Scholar] [CrossRef]
- Wong, K.; Haque, M. Dynamic load modelling of a paper mill for small signal stability studies. IET Gener. Transm. Distrib. 2014, 8, 131–141. [Google Scholar] [CrossRef]
- Navarro, I. Dynamic Load Models for Power Systems-Estimation of Time-Varying Parameters during Normal Operation; Department of Industrial Electrical Engineering and Automation, Lund Institute of Technology: Lund, Sweden, 2002. [Google Scholar]
- Collin, A.; Acosta, J.; Hayes, B.; Djokic, S. Component-Based Aggregate Load Models for Combined Power Flow and Harmonic Analysis. In Proceedings of the 7th Mediterranean Conference and Exhibition on Power Generation, Transmission, Distribution and Energy Conversion (MedPower 2010), Agia Napa, Cyprus, 7–10 November 2010. [Google Scholar] [CrossRef]
- Chassin, F.; Mayhorn, E.; Elizondo, M.; Lu, S. Load Modeling and Calibration Techniques for Power System Studies. In Proceedings of the 2011 North American Power Symposium, Boston, MA, USA, 4–6 August 2011. [Google Scholar] [CrossRef]
- Morison, K.; Hamadani, H.; Wang, L. Load Modeling for Voltage Stability Studies. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006. [Google Scholar] [CrossRef]
- Hajagos, L.; Danai, B. Laboratory measurements and models of modern loads and their effect on voltage stability studies. IEEE Trans. Power Syst. 1998, 13, 584–592. [Google Scholar] [CrossRef]
- Price, W.W.; Taylor, C.W.; Rogers, G.J. Standard load models for power flow and dynamic performance simulation. IEEE Trans. Power Syst. 1995, 10, 1302–1313. [Google Scholar] [CrossRef]
- Ju, P.; Shi, K.; Tang, Y.; Shao, Z.; Chen, Q.; Yang, W. Comparisons between the Load Models with Considering Distribution Network Directly or Indirectly. In Proceedings of the 2008 Joint International Conference on Power System Technology and IEEE Power India Conference, New Delhi, India, 12–15 October 2008. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, A.; Chen, Z.; Gao, K. Dynamic synthesis load modeling approach based on load survey and load curves analysis. In Proceedings of the 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008. [Google Scholar] [CrossRef]
- Lin, C.J.; Chen, A.T.; Chiou, C.Y.; Huang, C.H.; Chiang, H.D.; Wang, J.C.; Fekih-Ahmed, L. Dynamic load models in power systems using the measurement approach. IEEE Trans. Power Syst. 1993, 8, 309–315. [Google Scholar] [CrossRef]
- Knyazkin, V.; Canizares, C.; Soder, L. On the parameter estimation and modeling of aggregate power system loads. IEEE Trans. Power Syst. 2004, 19, 1023–1031. [Google Scholar] [CrossRef]
- Price, W.W.; Wirgau, K.A.; Murdoch, A.; Mitsche, J.V.; Vaahedi, E.; El-Kady, M. Load modelling for power flow and transient stability computer studies. IEEE Trans. Power Syst. 1998, 3, 180–187. [Google Scholar] [CrossRef]
- Bostanci, M.; Koplowitz, J.; Taylor, C. Identification of power system load dynamics using artificial neural networks. IEEE Trans. Power Syst. 1997, 12, 1468–1473. [Google Scholar] [CrossRef]
- Billinton, R.; Kumar, S.; Chowdhury, N.; Chu, K.; Debnath, K.; Goel, L.; Khan, E.; Kos, P.; Nourbakhsh, G.; Oteng-Adjei, J. A reliability test system for educational purposes-basic data. IEEE Power Eng. Rev. 1989, 9, 67–68. [Google Scholar] [CrossRef]
- Allan, R.N.; Billinton, R.; Sjarief, I.; Goel, L.; So, K.S. Reliability test system for education purposes—Basic distribution system data and results. IEEE Trans. Power Syst. 1991, 6, 813–820. [Google Scholar] [CrossRef]

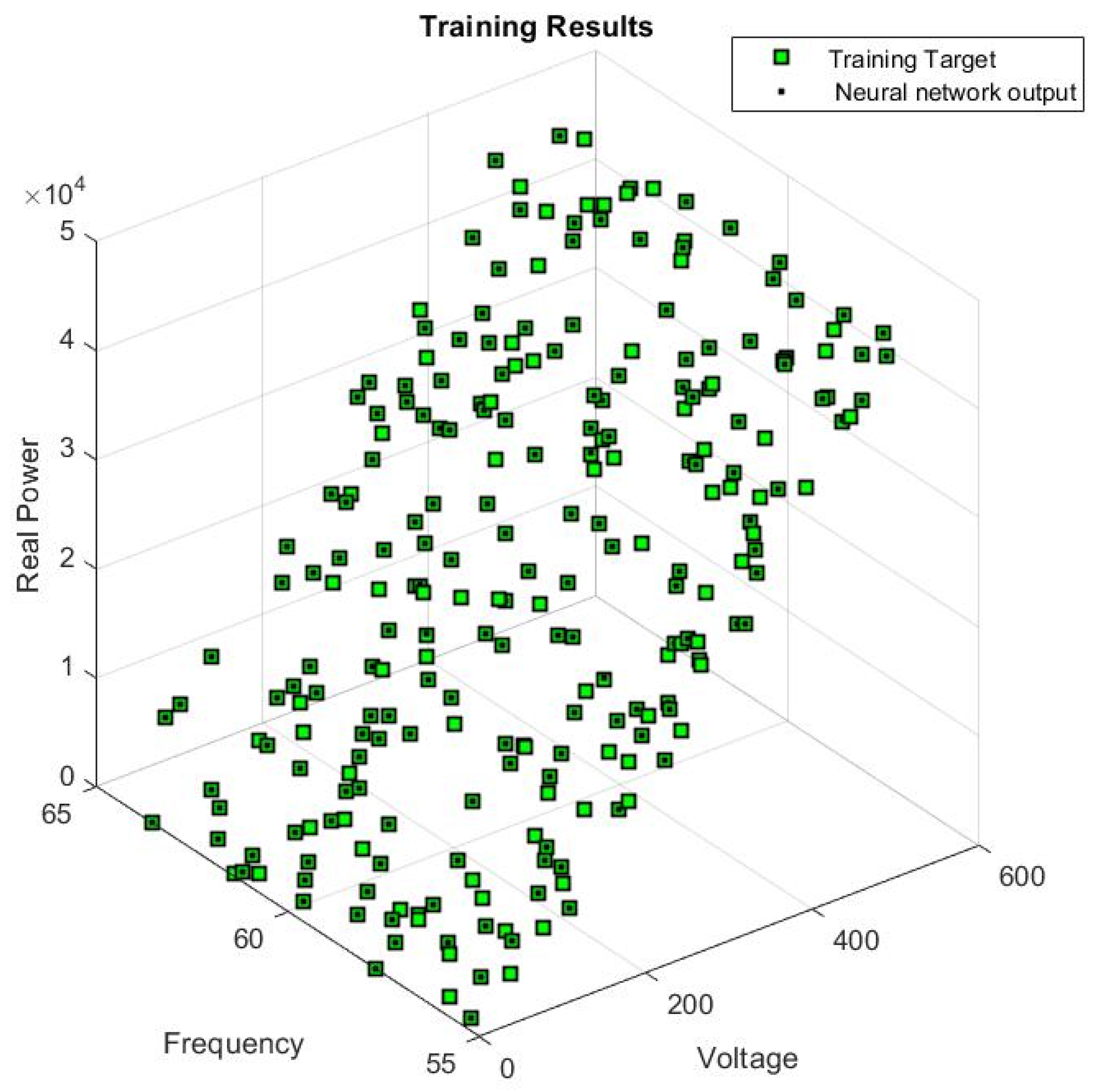
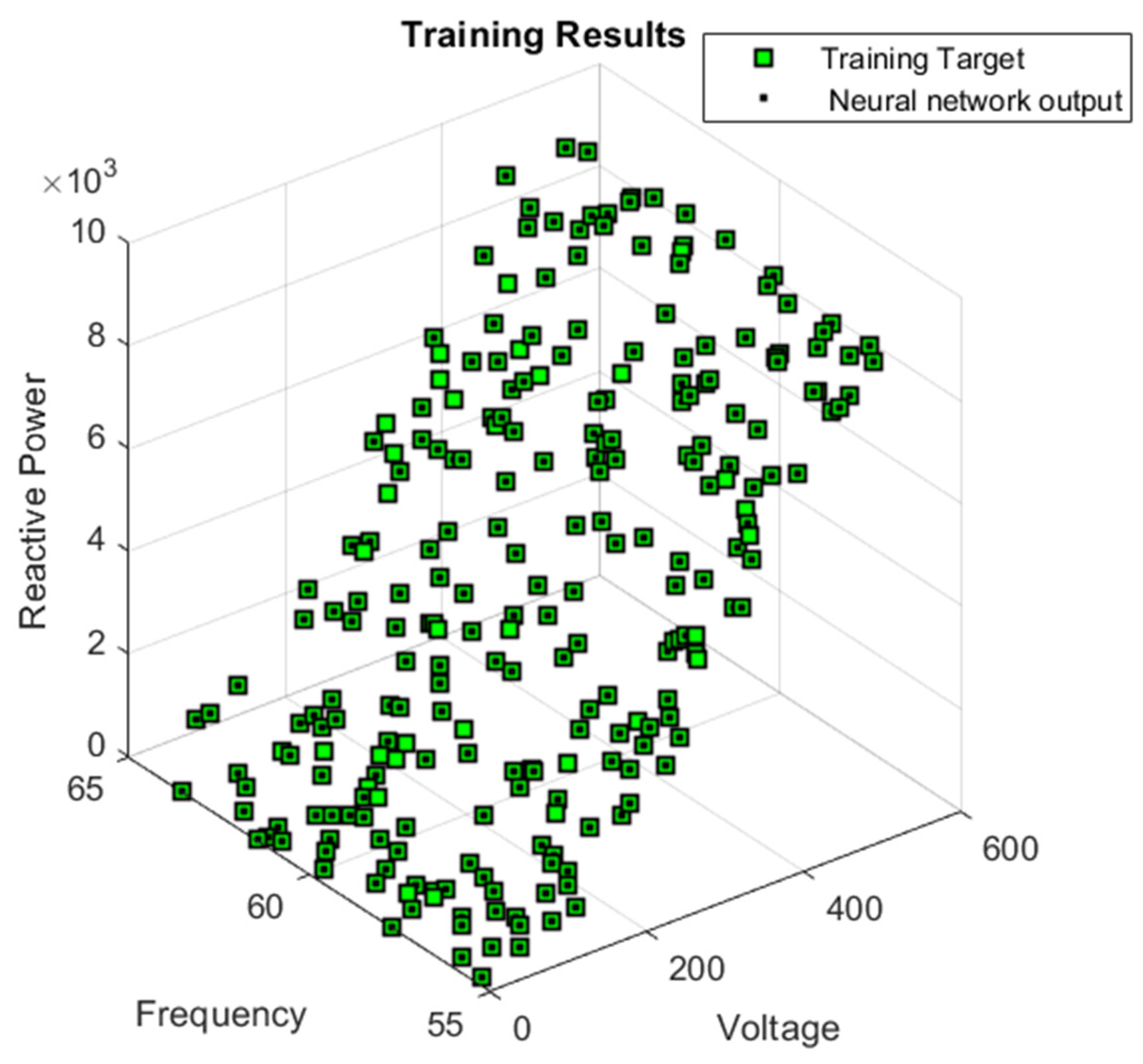
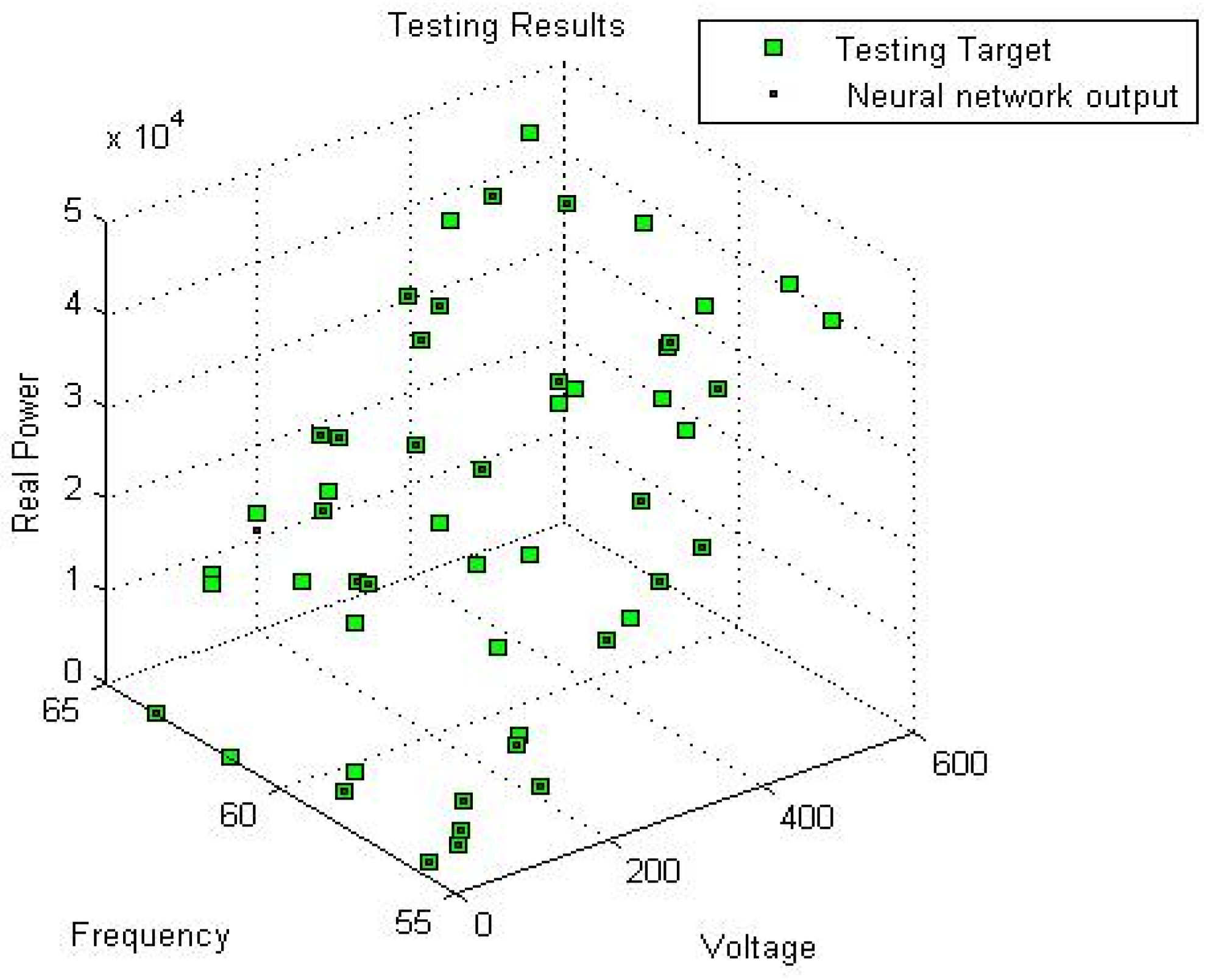
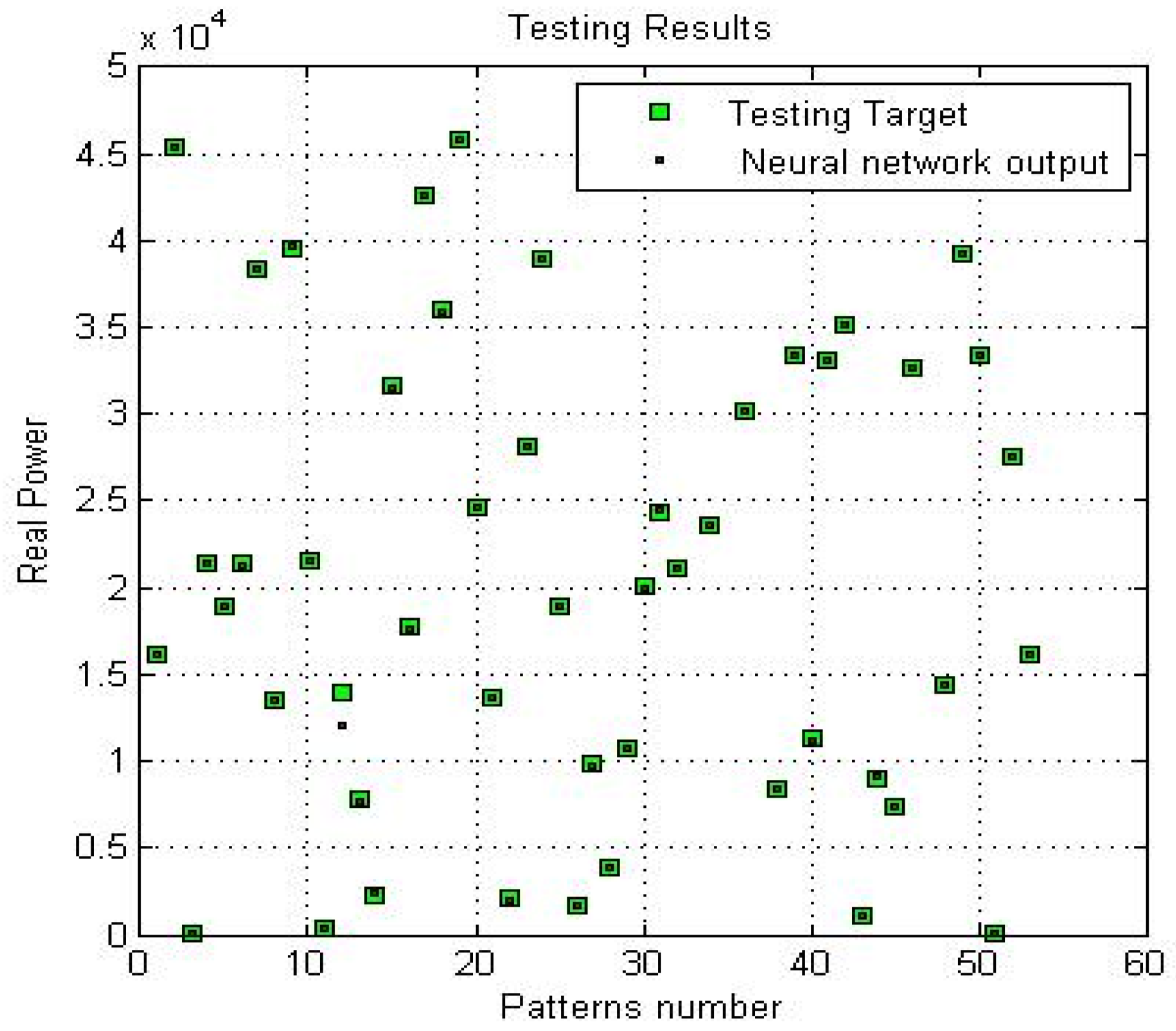
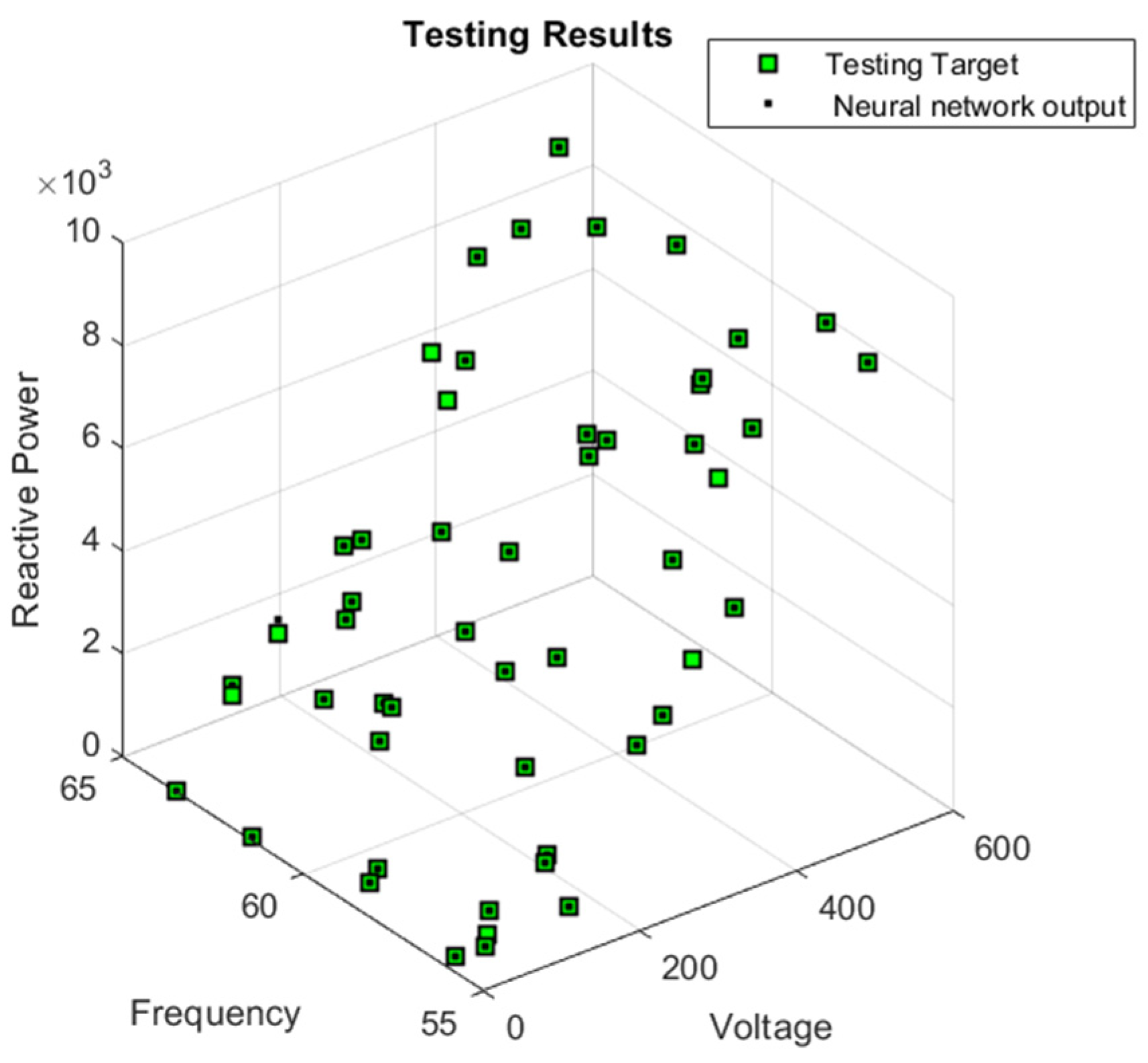
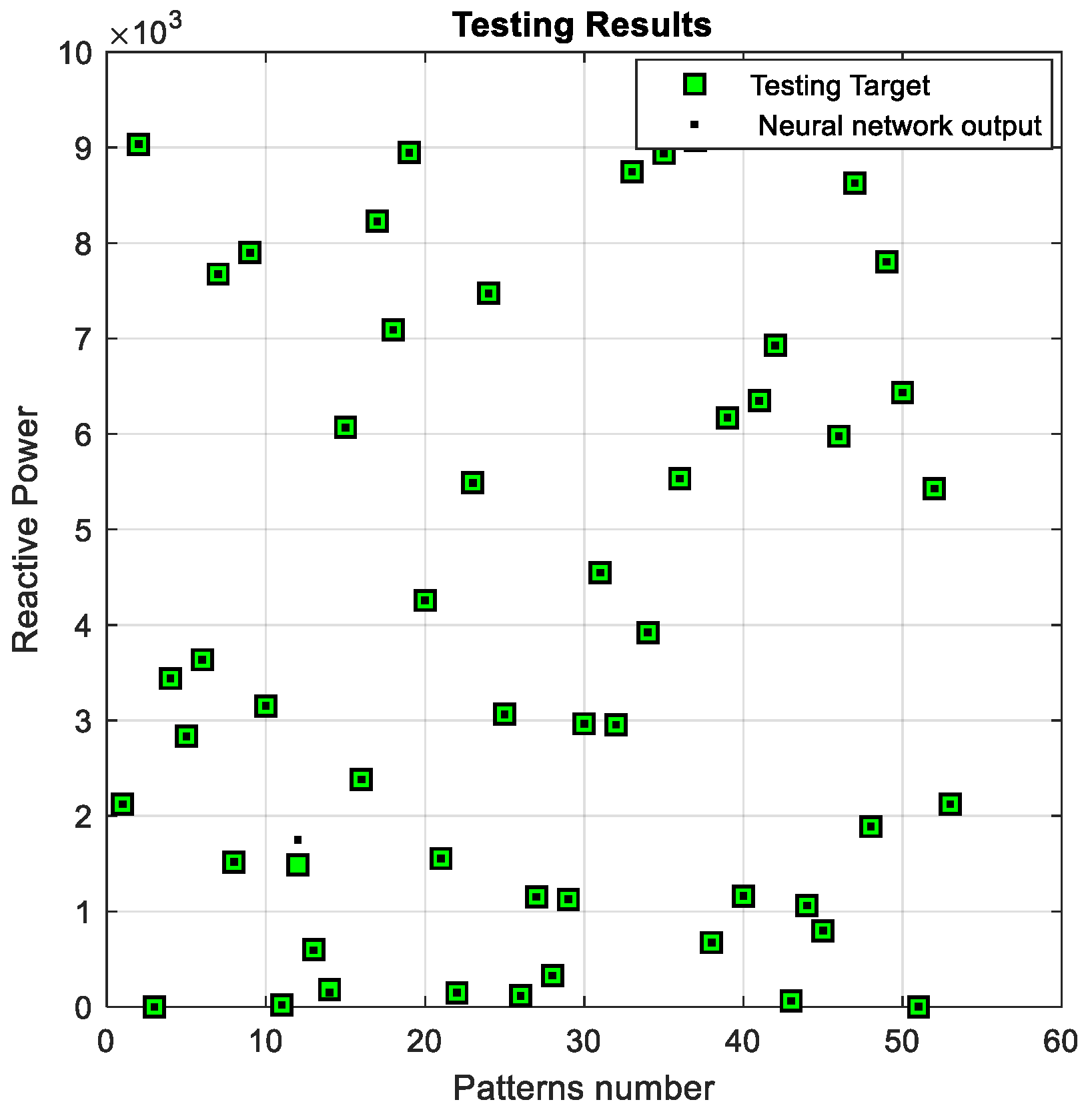
| # | Voltage (V) | Frequency (HZ) | Active Power | Reactive Power |
|---|---|---|---|---|
| 1 | 339.9 | 55.92 | 18,038.40 | 3259.17 |
| 2 | 311.9 | 57.37 | 17,798.47 | 3217.36 |
| 3 | 529.0 | 57.43 | 19,573.18 | 2951.85 |
| 4 | 410.3 | 56.04 | 18,573.67 | 3228.48 |
| 5 | 364.3 | 63.58 | 18,218.23 | 3259.64 |
| 6 | 287.8 | 61.98 | 17,414.89 | 3043.77 |
| 7 | 142.9 | 62.33 | 9424.49 | 899.88 |
| Component | Number |
|---|---|
| Buses | 60 |
| Cables | 60 |
| Transformers | 24 |
| Source | 1 |
| Loads | 22 |
| Operating Voltage (kV) | Feeder Type | Max Length (km) | Cross-Sectional Area (mm2) | R (Ω) | X (Ω) |
|---|---|---|---|---|---|
| 11 | XPLE | 15 | 150 | 265 | 133.2 |
| 0.4 | XPLE | 0.3 | 95 | 410 | 142.8 |
| Operating Voltage(V) | Type | Rating (MVA) | R% | X% |
|---|---|---|---|---|
| 33/11 | Liquid-Filled | 7 | 0.575 | 6.976 |
| 11/0.4 | Liquid-Filled | 0.5 | 1.001 | 5.103 |
| 11/0.4 | Liquid-Filled | 0.6 | 1.408 | 5.575 |
| 11/0.4 | Liquid-Filled | 1.1 | 0.802 | 5.694 |
| Component | Voltage (kV) | Failure Rate (Failures/Year) | Mean Repair Time (h) |
|---|---|---|---|
| Buses | 0.4 | 0.001 | 2 |
| 11 | |||
| 33 | |||
| Cables | 11 | 0.02 | 25 |
| Transformers | 11/0.4 | 0.015 | 200 |
| 33/11 | 0.0041 | 378 | |
| Circuit breakers | 11 | 0.003 | 50 |
| 0.4 | |||
| 33 | 0.0036 | 62.4 |
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |
|---|---|---|---|---|
| SAIFI | 2.1444 | 2.1463 | 2.1574 | 2.1648 |
| SAIDI | 43.2316 | 43.4029 | 44.4309 | 45.1162 |
| CAIDI | 20.160 | 20.222 | 20.594 | 20.840 |
| ASAI | 0.9951 | 0.9950 | 0.9949 | 0.9948 |
| EENS | 447.304 | 451.215 | 821.736 | 1030.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maraaba, L.; Almuhaini, M.; Habli, M.; Khalid, M. Neural Networks Based Dynamic Load Modeling for Power System Reliability Assessment. Sustainability 2023, 15, 5403. https://doi.org/10.3390/su15065403
Maraaba L, Almuhaini M, Habli M, Khalid M. Neural Networks Based Dynamic Load Modeling for Power System Reliability Assessment. Sustainability. 2023; 15(6):5403. https://doi.org/10.3390/su15065403
Chicago/Turabian StyleMaraaba, Luqman, Mohammad Almuhaini, Malek Habli, and Muhammad Khalid. 2023. "Neural Networks Based Dynamic Load Modeling for Power System Reliability Assessment" Sustainability 15, no. 6: 5403. https://doi.org/10.3390/su15065403
APA StyleMaraaba, L., Almuhaini, M., Habli, M., & Khalid, M. (2023). Neural Networks Based Dynamic Load Modeling for Power System Reliability Assessment. Sustainability, 15(6), 5403. https://doi.org/10.3390/su15065403








