From Individual Motivation to Geospatial Epidemiology: A Novel Approach Using Fuzzy Cognitive Maps and Agent-Based Modeling for Large-Scale Disease Spread
Abstract
1. Introduction
2. Background Theory
2.1. FCM
- is the value of concept at time ,
- is the value of concept at time t,
- is the weight value from concept to concept ,
- f is the activation function.
2.2. ABM
2.3. SEIR Model
- is the effective infection rate,
- is the disease-induced death rate,
- is the developing rate of exposed humans becoming infectious,
- is the rate of recovered humans,
- is the rate recovered humans enter ‘S’.
3. Methodology
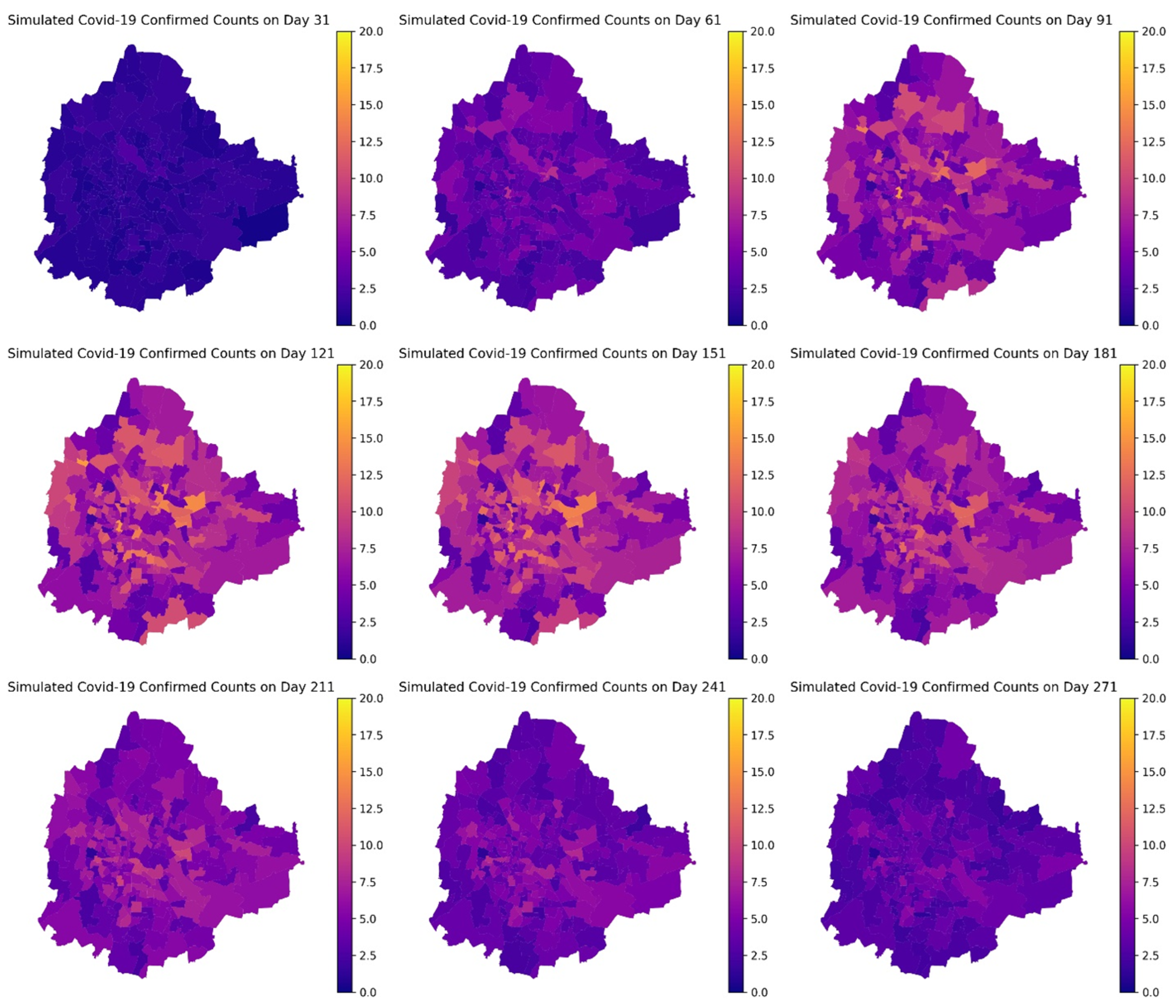
3.1. Study Area
3.2. Datasets
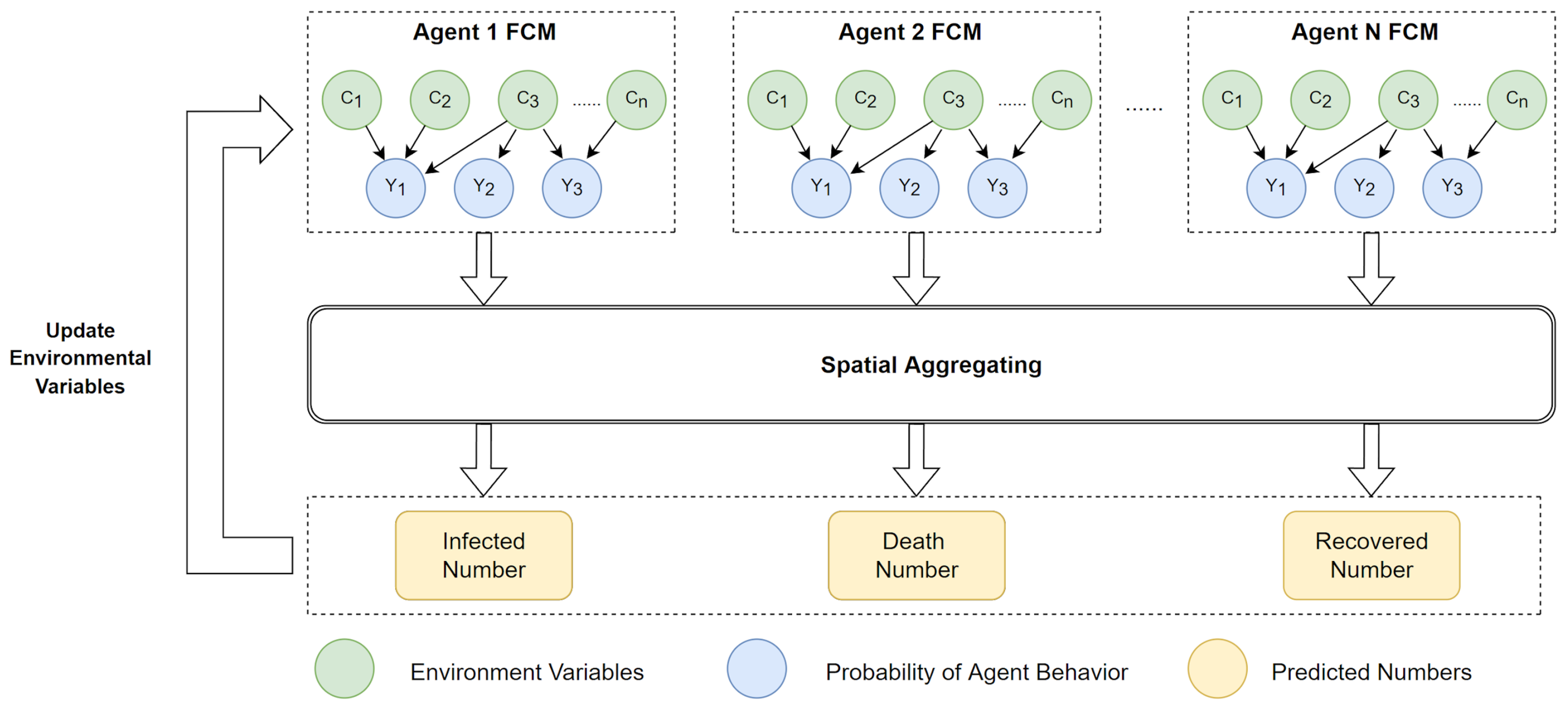
3.3. FCM Model Design
- Inputs (e.g., cognition of the epidemiological situation).
- Internal status (e.g., emotions).
- Outputs, which need to be estimated for observation from outside.
3.4. ABM and SEIR Model Design
| Algorithm 1 FCM–ABM Simulating SEIR Pseudo-Code |
|
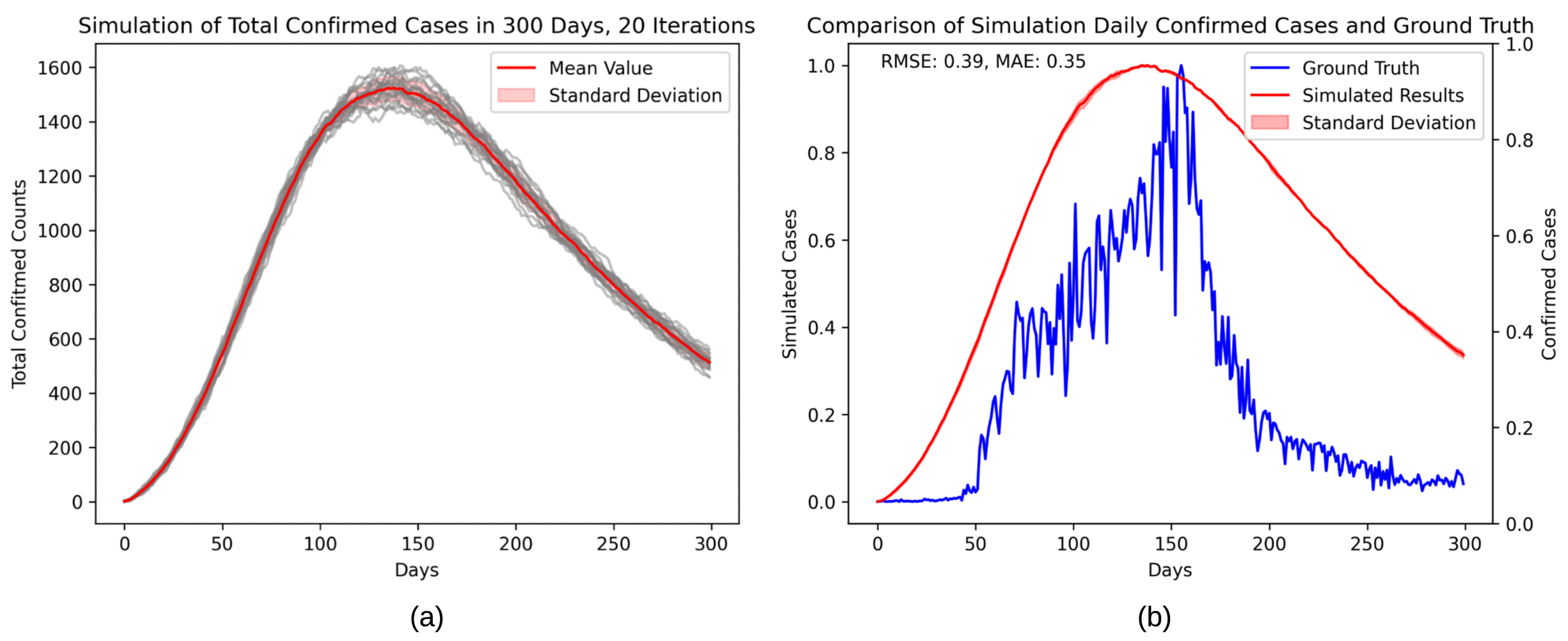
4. Results
5. Discussion
5.1. Future Work
5.2. Broader Impact
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FCM | Fuzzy Cognitive Map |
| ABM | Agent-Based Modeling |
| SEIR | “Susceptible—Exposed—Infectious—Removed” Model |
| NPI | Non-Pharmaceutical Interventions |
| NHL | Non-Linear Hebbian Learning |
| DOC | Desired Output Concept |
References
- WHO COVID-19 Cases|WHO COVID-19 Dashboard. 2023. Available online: https://data.who.int/dashboards/covid19/cases (accessed on 12 March 2022).
- Picoli, S.; Teixeira, J.; Ribeiro, H.; Malacarne, L.; Paupitz, R.; Mendes, R. Spreading patterns of the influenza A (H1N1) pandemic. PLoS ONE 2011, 6, e17823. [Google Scholar] [CrossRef] [PubMed]
- Hunt, A. Exponential growth in Ebola outbreak since May 14, 2014. Complexity 2014, 20, 8–11. [Google Scholar] [CrossRef]
- Maier, B.; Brockmann, D. Effective containment explains subexponential growth in recent confirmed COVID-19 cases in China. Science 2020, 368, 742–746. [Google Scholar] [CrossRef] [PubMed]
- Kermack, W.; McKendrick, A. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Van Den Driessche, P.; Watmough, J. A simple SIS epidemic model with a backward bifurcation. J. Math. Biol. 2000, 40, 525–540. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Paré, P.; Du, E.; Sun, Z. A Networked SIS Disease Dynamics Model with a Waterborne Pathogen. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019. [Google Scholar] [CrossRef]
- Osman, M.; Adu, I.; Chen, Y. A simple SEIR mathematical model of malaria transmission. Asian Res. J. Math. 2017, 7, 1–22. [Google Scholar] [CrossRef]
- Almeida, R. Analysis of a fractional SEIR model with treatment. Appl. Math. Lett. 2018, 84, 56–62. [Google Scholar] [CrossRef]
- Bjørnstad, O.; Shea, K.; Krzywinski, M.; Altman, N. The SEIRS model for infectious disease dynamics. Nat. Methods 2020, 17, 557–558. [Google Scholar] [CrossRef]
- de Lima, L.M.M.; de Sá, L.R.; dos Santos Macambira, A.F.U.; de Almeida Nogueir, J.; de Toledo Vianna, R.P.; de Moraes, R.M. A new combination rule for Spatial Decision Support Systems for epidemiology. Int. J. Health Geogr. 2019, 18, 24. [Google Scholar] [CrossRef]
- Kosko, B. Fuzzy cognitive maps. Int. J. Man-Mach. Stud. 1986, 24, 65–75. [Google Scholar] [CrossRef]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M.; Schlickeiser, R. Analytical solution of the SIR-model for the temporal evolution of epidemics. Part A: Time-independent reproduction factor. J. Phys. Math. Theor. 2020, 53, 505601. [Google Scholar] [CrossRef]
- Davis, C.; Giabbanelli, P.; Jetter, A. The Intersection of Agent Based Models and Fuzzy Cognitive Maps: A Review of an Emerging Hybrid Modeling Practice. In Proceedings of the 2019 Winter Simulation Conference (WSC), National Harbor, MD, USA, 8–11 December 2019. [Google Scholar] [CrossRef]
- Chen, T.; Rui, J.; Wang, Q.; Zhao, Z.; Cui, J.; Yin, L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 2020, 9, 18–25. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.; Lau, E.; Wong, J.; et al. Early transmission dynamics in Wuhan, China, of novel Coronavirus–Infected pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Lyu, F.; Kang, J.; Wang, S.; Han, S.; Li, Z.; Wang, S. Multi-scale CyberGIS analytics for detecting spatiotemporal patterns of COVID-19. Hum. Dyn. Smart Cities 2021, 217–232. [Google Scholar] [CrossRef] [PubMed]
- Perez, L.; Dragićević, S. An agent-based approach for modeling dynamics of contagious disease spread. Int. J. Health Geogr. 2009, 8, 50. [Google Scholar] [CrossRef] [PubMed]
- Bian, L. A conceptual framework for an individual-based spatially explicit epidemiological model. Environ. Plan. Plan. Des. 2004, 31, 381–395. [Google Scholar] [CrossRef]
- Giabbanelli, P.; Fattoruso, M.; Norman, M. CoFluences: Simulating the spread of social influences via a hybrid Agent-Based/Fuzzy cognitive maps architecture. In Proceedings of the 2019 ACM SIGSIM Conference on Principles of Advanced Discrete Simulation, Chicago, IL, USA, 3–5 June 2019. [Google Scholar] [CrossRef]
- Dickerson, J.; Kosko, B. Virtual worlds as fuzzy cognitive maps. Presence Teleoperators Virtual Environ. 1994, 3, 173–189. [Google Scholar] [CrossRef]
- Xirogiannis, G.; Stefanou, J.; Glykas, M. A fuzzy cognitive map approach to support urban design. Expert Syst. Appl. 2004, 26, 257–268. [Google Scholar] [CrossRef]
- Mei, S.; Zhu, Y.; Qiu, X.; Zhou, X.; Zu, Z.; Boukhanovsky, A.; Sloot, P. Individual Decision Making Can Drive Epidemics: A Fuzzy Cognitive Map Study. IEEE Trans. Fuzzy Syst. 2014, 22, 264–273. [Google Scholar] [CrossRef]
- Gilbert, G.; Troitzsch, K. Simulation for the Social Scientist. 1999. Available online: http://www.pensamientocomplejo.com.ar/docs/files/Gilbert%20and%20Troitzsch%20-%20Simulation%20for%20the%20social%20scientist.pdf (accessed on 10 May 2023).
- Macal, C.; North, M. Tutorial on agent-based modelling and simulation. J. Simul. 2010, 4, 151–162. [Google Scholar] [CrossRef]
- He, S.; Peng, Y.; Sun, K. SEIR modeling of the COVID-19 and its dynamics. Nonlinear Dyn. 2020, 101, 1667–1680. [Google Scholar] [CrossRef] [PubMed]
- Weiss, H. The SIR model and the foundations of public health. Mater. Mat. 2013, 2013, 1–17. [Google Scholar]
- Covid19india GitHub—Covid19india/Data. 2023. Available online: https://github.com/covid19india/data/ (accessed on 10 May 2023).
- Tamrakar, V.; Srivastava, A.; Saikia, N.; Parmar, M.; Shukla, S.; Shabnam, S.; Boro, B.; Saha, A.; Debbarma, B. District level correlates of COVID-19 pandemic in India during March-October 2020. PLoS ONE 2021, 16, e0257533. [Google Scholar] [CrossRef] [PubMed]
- Alam, S.; Schlecht, E.; Reichenbach, M. Impacts of COVID-19 on Small-Scale Dairy Enterprises in an Indian Megacity—Insights from Greater Bengaluru. Sustainability 2022, 14, 2057. [Google Scholar] [CrossRef]
- Bauza, V.; Sclar, G.; Bisoyi, A.; Owens, A.; Ghugey, A.; Clasen, T. Experience of the COVID-19 pandemic in rural Odisha, India: Knowledge, preventative actions, and impacts on daily life. Int. J. Environ. Res. Public Health 2021, 18, 2863. [Google Scholar] [CrossRef] [PubMed]
- OpenCity. BBMP Ward Information. OpenCity. 2020. Available online: https://data.opencity.in/dataset/bbmp-ward-information (accessed on 10 December 2023).
- Papageorgiou, E.; Groumpos, P. A new hybrid method using evolutionary algorithms to train Fuzzy Cognitive Maps. Appl. Soft Comput. 2005, 5, 409–431. [Google Scholar] [CrossRef]
- Nuzzo, J.; Meyer, D.; Snyder, M.; Ravi, S.; Lapascu, A.; Souleles, J.; Andrada, C.; Bishai, D. What makes health systems resilient against infectious disease outbreaks and natural hazards? Results from a scoping review. BMC Public Health 2019, 19, 1310. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Rahman, M.; Khanam, R. The impact of the government response on pandemic control in the long run—A dynamic empirical analysis based on COVID-19. PLoS ONE 2022, 17, e0267232. [Google Scholar] [CrossRef]
- Khan, M.; Nazli, A.; Al-Furas, H.; Asad, M.; Ajmal, I.; Khan, D.; Shah, J.; Farooq, M.; Jiang, W. An overview of viral mutagenesis and the impact on pathogenesis of SARS-CoV-2 variants. Front. Immunol. 2022, 13, 1034444. [Google Scholar] [CrossRef]
- Saeed, H.; Eslami, A.; Nassif, N.; Simpson, A.; Lal, S. Anxiety linked to COVID-19: A systematic review comparing anxiety rates in different populations. Int. J. Environ. Res. Public Health 2022, 19, 2189. [Google Scholar] [CrossRef] [PubMed]
- Czepiel, D.; McCormack, C.; Da Silva, A.; Seblova, D.; Moro, M.; Restrepo-Henao, A.; Martínez, A.; Afolabi, O.; Alnasser, L.; Alvarado, R.; et al. Inequality on the frontline: A multi-country study on gender differences in mental health among healthcare workers during the COVID-19 pandemic. Glob. Ment. Health 2024, 11, e34. [Google Scholar] [CrossRef] [PubMed]
- Times, N. Covid in the U.S.: Latest Maps, Case and Death Counts. 2023. Available online: https://www.nytimes.com/interactive/2021/us/covid-cases.html (accessed on 12 May 2024).
- CSSEGISandData GitHub—CSSEGISandData/COVID-19: Novel Coronavirus (COVID-19) Cases, Provided by JHU CSSE. 2023. Available online: https://github.com/CSSEGISandData/COVID-19 (accessed on 12 May 2024).
- University of Illinois at Urbana-Champaign WhereCOVID-19 by CyberGIS Center for Advanced Digital and Spatial Studies. 2020. Available online: https://wherecovid19.cigi.illinois.edu/ (accessed on 12 May 2024).
- Abbasi, K. COVID-19: Fail to prepare, prepare to fail. J. R. Soc. Med. 2020, 113, 131. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Zhang, H. The uniform l1 long-time behavior of time discretization for time-fractional partial differential equations with nonsmooth data. Appl. Math. Lett. 2022, 124, 107644. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H.; Zhang, Q.; Yuan, G.; Sheng, Z. The finite volume scheme preserving maximum principle for two-dimensional time-fractional Fokker–Planck equations on distorted meshes. Appl. Math. Lett. 2019, 97, 99–106. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H.; Zhang, Q.; Yuan, G. Simple positivity-preserving nonlinear finite volume scheme for subdiffusion equations on general non-conforming distorted meshes. Nonlinear Dyn. 2022, 108, 3859–3886. [Google Scholar] [CrossRef]
- Roosa, K.; Lee, Y.; Luo, R.; Kirpich, A.; Rothenberg, R.; Hyman, J.; Yan, P.; Chowell, G. Real-time forecasts of the COVID-19 epidemic in China from February 5th to February 24th, 2020. Infect. Dis. Model. 2020, 5, 256–263. [Google Scholar] [CrossRef] [PubMed]
- Desjardins, M.R.; Hohl, A.; Delmelle, E.M. Rapid surveillance of COVID-19 in the United States using a prospective space-time scan statistic: Detecting and evaluating emerging clusters. Appl. Geogr. 2020, 118, 102202. [Google Scholar] [CrossRef] [PubMed]
- Grasselli, G.; Pesenti, A.; Cecconi, M. Critical care utilization for the COVID-19 outbreak in Lombardy, Italy. JAMA 2020, 323, 1545. [Google Scholar] [CrossRef]
- Anderson, R.; Heesterbeek, H.; Klinkenberg, D.; Hollingsworth, T. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet 2020, 395, 931–934. [Google Scholar] [CrossRef]
- Wilder-Smith, A.; Freedman, D. Isolation, quarantine, social distancing and community containment: Pivotal role for old-style public health measures in the novel coronavirus (2019-nCoV) outbreak. J. Travel Med. 2020, 27, taaa020. [Google Scholar] [CrossRef] [PubMed]


| Description | Category | Initial Value | |
|---|---|---|---|
| Number of infected individuals | Input | 0.0 | |
| Number of recovered individuals | Input | 0.0 | |
| Health state of individual | Internal | 0.0 | |
| Knowledge of local epidemic situation | Internal | 0.0 | |
| Knowledge of global epidemic situation | Input | 0.5 | |
| Epidemiological situation | Internal | 0.0 | |
| Optimism level | Internal | 0.0 | |
| Memory of situations | Internal | 0.0 | |
| Instant reactions | Internal | 0.0 | |
| 1 | Rate of getting influenced by the pandemic | Output | 0.1 |
| Category | Name | Description | Value |
|---|---|---|---|
| System Parameters | ‘population’ | Total population simulated | 10,000 |
| ‘days’ | # of days in simulation | 300 | |
| ‘iterations’ | # of simulation iterations | 20 | |
| Model Parameters | ‘infect_rate’ | Infectious Rate 1 | 0.2 |
| ‘death_rate’ | Disease Death Rate 2 | 0.0193 | |
| ‘recovery_days’ | Average # of days to recover | 7 | |
| ‘recovery_sd’ | Standard deviation of ‘recovery_days’ | 3 | |
| ‘neighborhood_contact’ | # of people met per person under local spread | 40 | |
| ‘hotspot_contact’ | # of people met per person under no intervention | 120 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Z.; Zhang, Z.; Lyu, F.; Bishop, M.; Liu, J.; Chi, Z. From Individual Motivation to Geospatial Epidemiology: A Novel Approach Using Fuzzy Cognitive Maps and Agent-Based Modeling for Large-Scale Disease Spread. Sustainability 2024, 16, 5036. https://doi.org/10.3390/su16125036
Song Z, Zhang Z, Lyu F, Bishop M, Liu J, Chi Z. From Individual Motivation to Geospatial Epidemiology: A Novel Approach Using Fuzzy Cognitive Maps and Agent-Based Modeling for Large-Scale Disease Spread. Sustainability. 2024; 16(12):5036. https://doi.org/10.3390/su16125036
Chicago/Turabian StyleSong, Zhenlei, Zhe Zhang, Fangzheng Lyu, Michael Bishop, Jikun Liu, and Zhaohui Chi. 2024. "From Individual Motivation to Geospatial Epidemiology: A Novel Approach Using Fuzzy Cognitive Maps and Agent-Based Modeling for Large-Scale Disease Spread" Sustainability 16, no. 12: 5036. https://doi.org/10.3390/su16125036
APA StyleSong, Z., Zhang, Z., Lyu, F., Bishop, M., Liu, J., & Chi, Z. (2024). From Individual Motivation to Geospatial Epidemiology: A Novel Approach Using Fuzzy Cognitive Maps and Agent-Based Modeling for Large-Scale Disease Spread. Sustainability, 16(12), 5036. https://doi.org/10.3390/su16125036







