Response of Sustainable Solar Photovoltaic Power Output to Summer Heatwave Events in Northern China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites and Data
2.2. Methods
2.2.1. Selection Criteria for Heatwave and Background Days
2.2.2. Machine Learning Algorithms
2.2.3. Metrics for Evaluating Model Performance
2.2.4. Pearson Correlation Coefficient Analysis
3. Results and Discussion
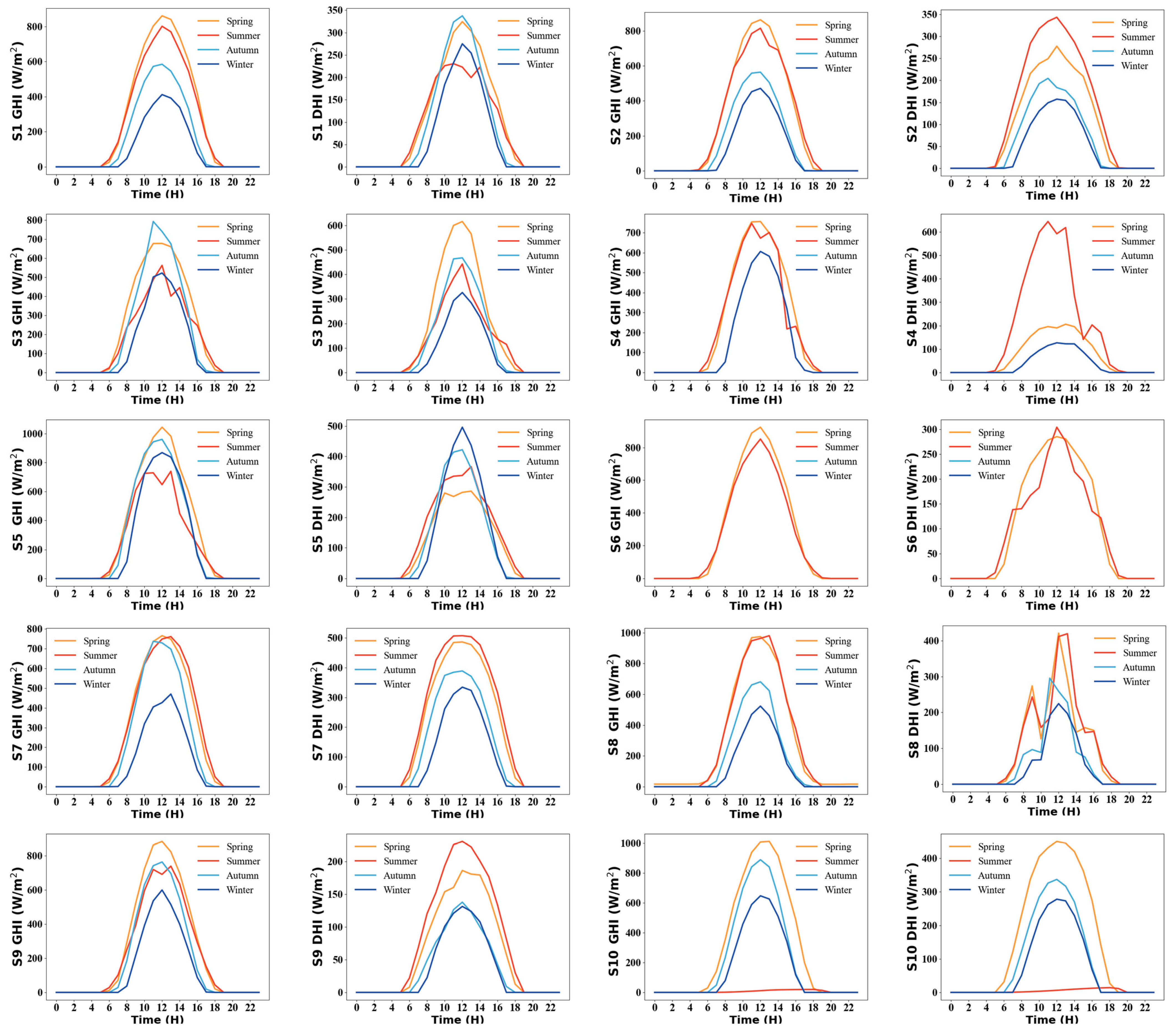
3.1. Spatio-Temporal Patterns of Solar PV Energies
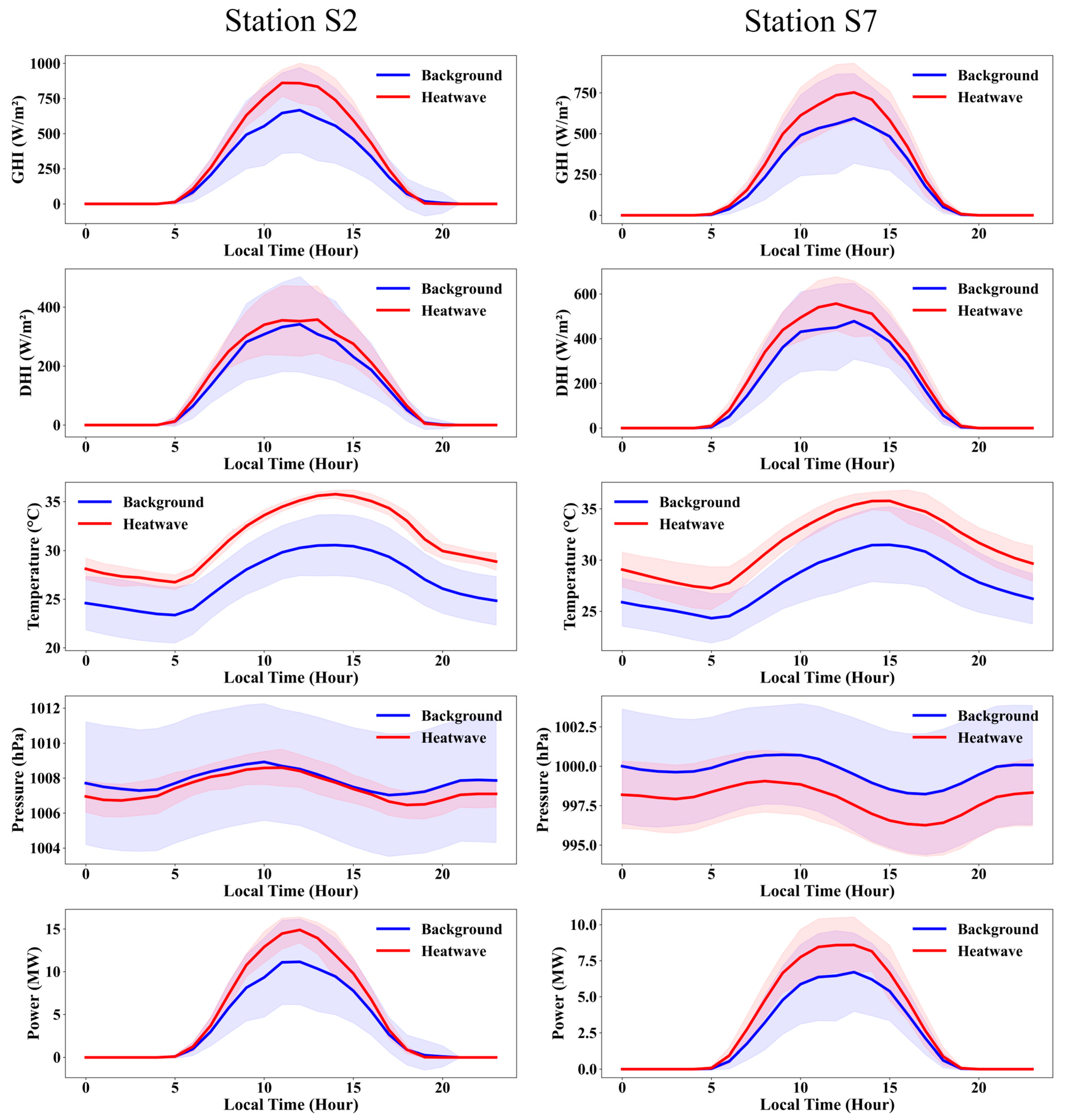
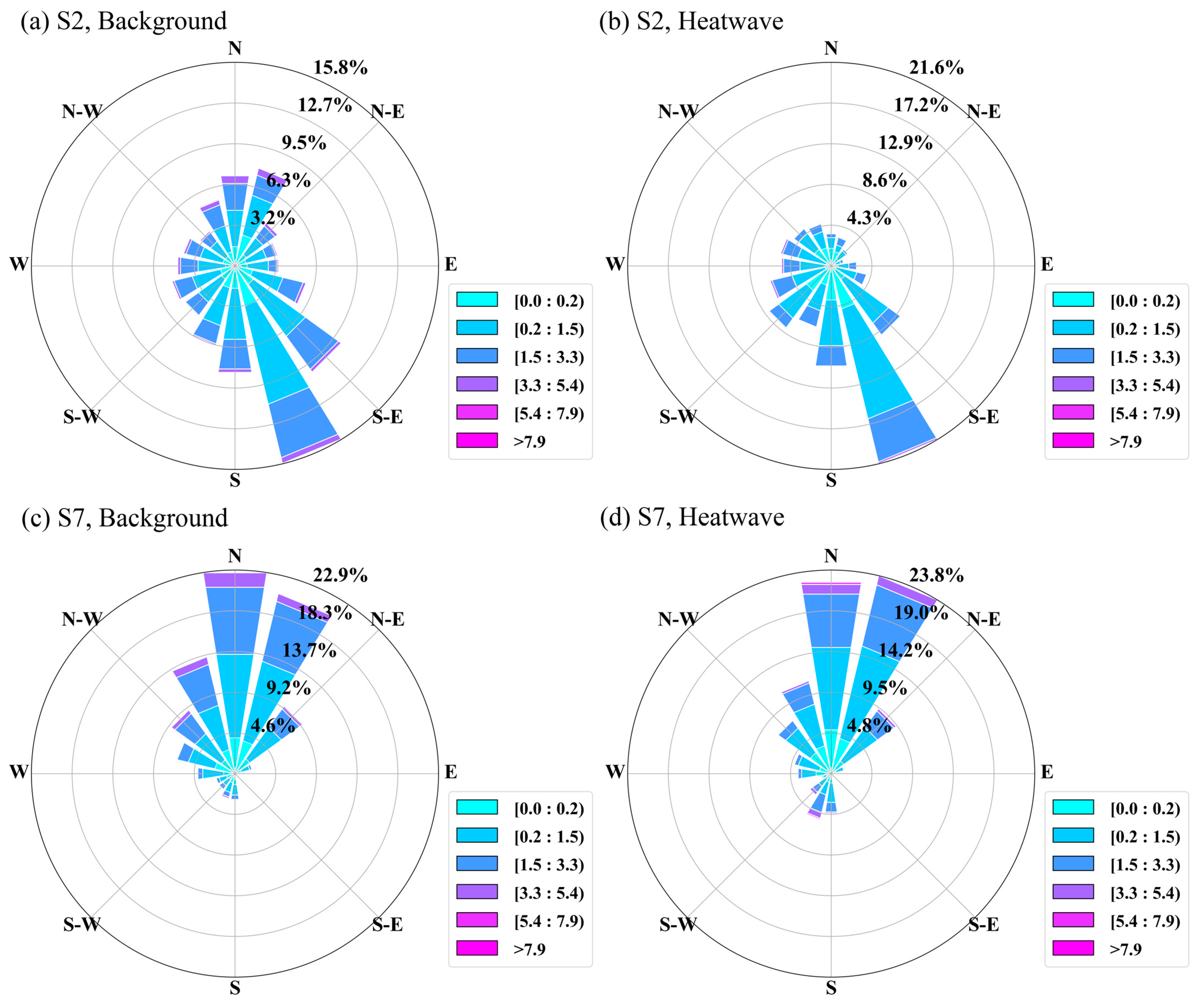
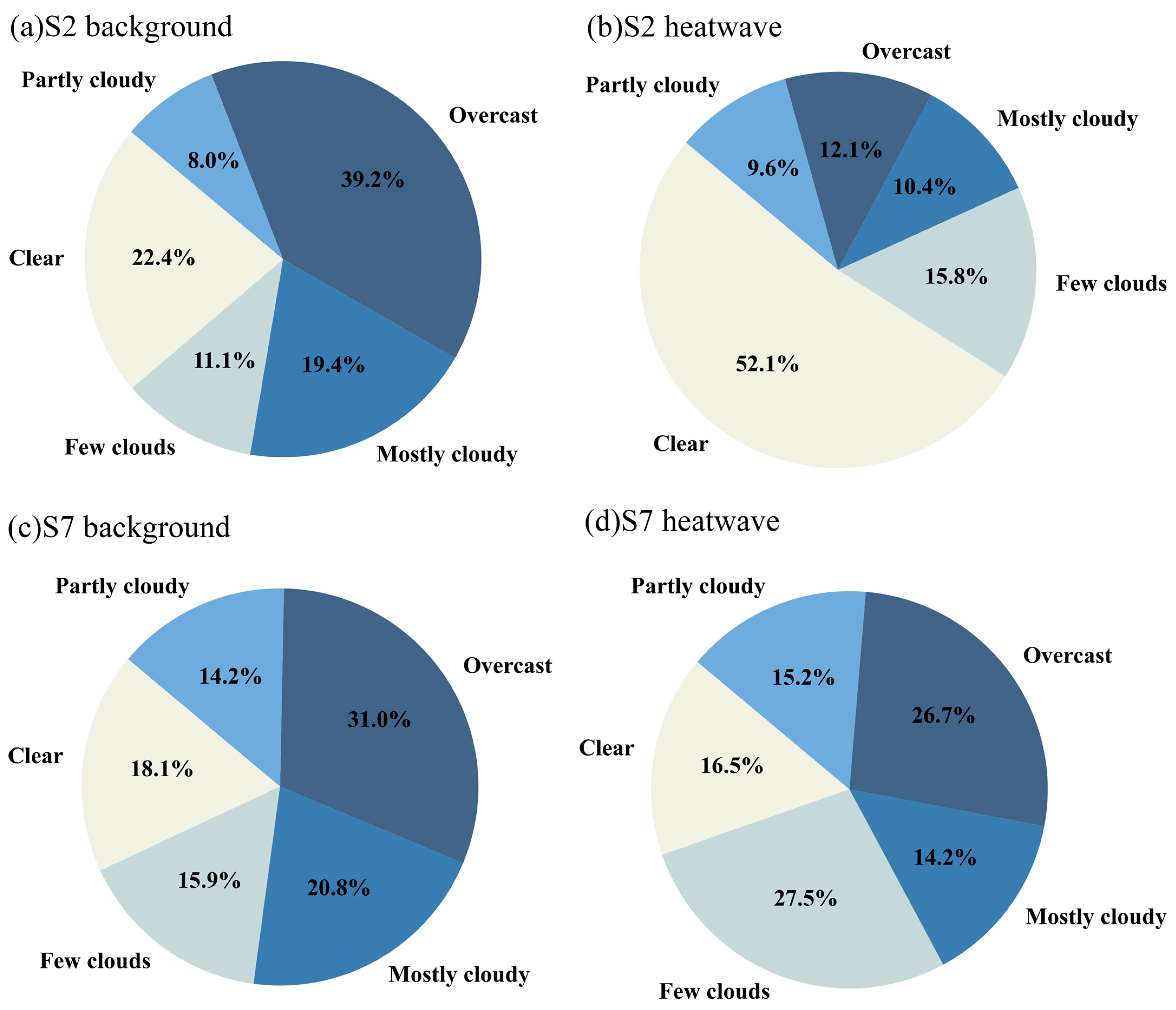
3.2. Meteorological Conditions under Heatwave and Background Days
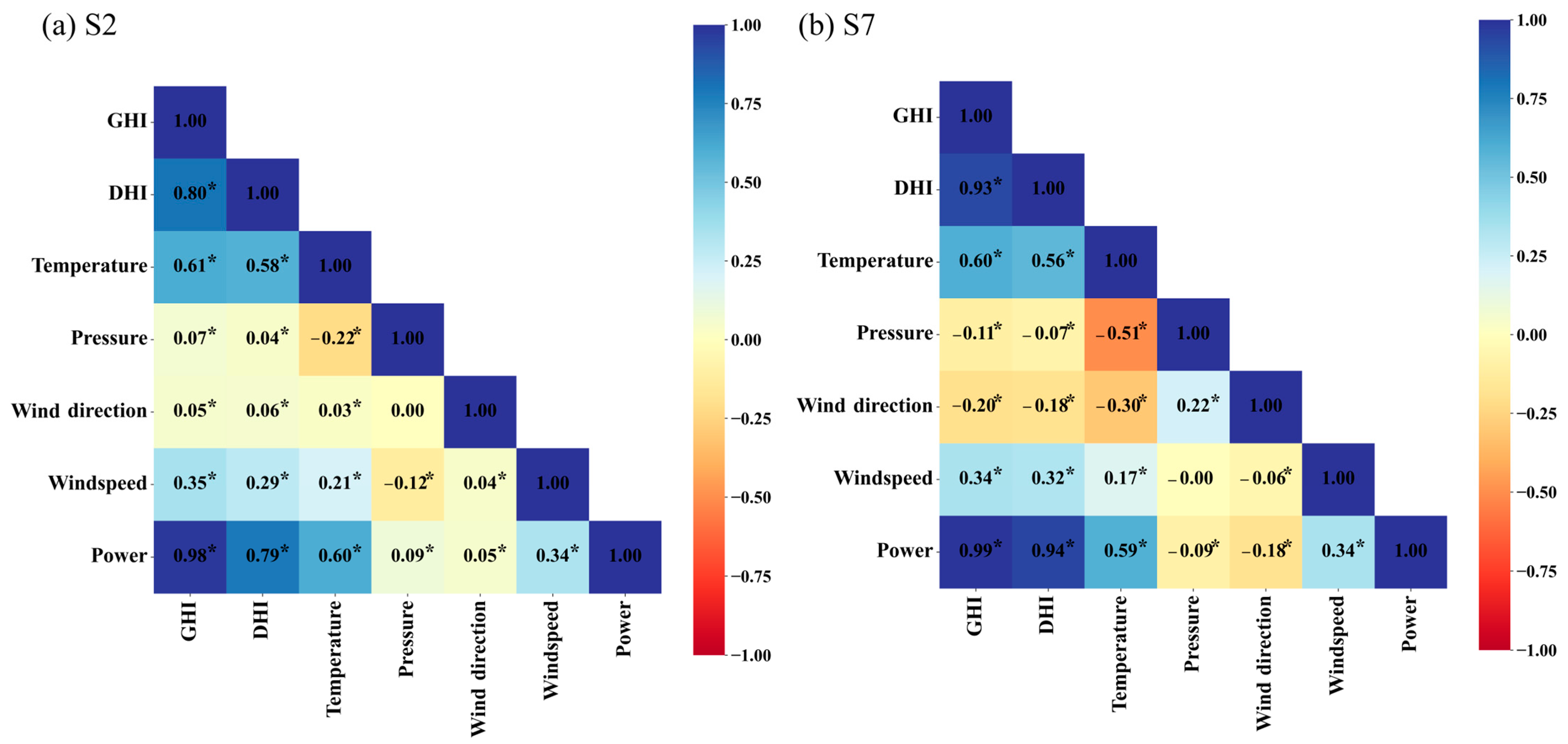
3.3. Driving Factors of PV on a Seasonal Scale
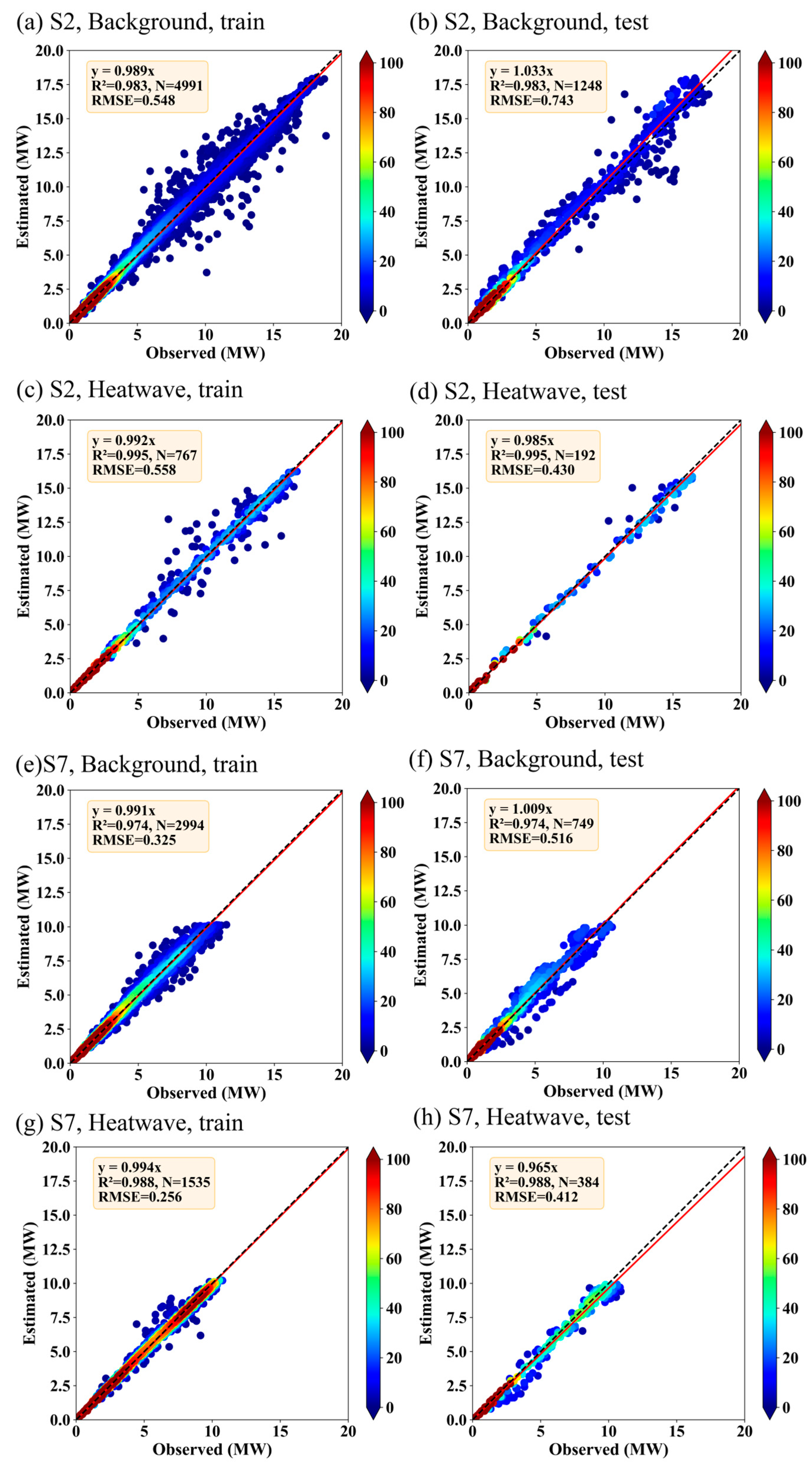
3.4. Random Forest Model Evaluation
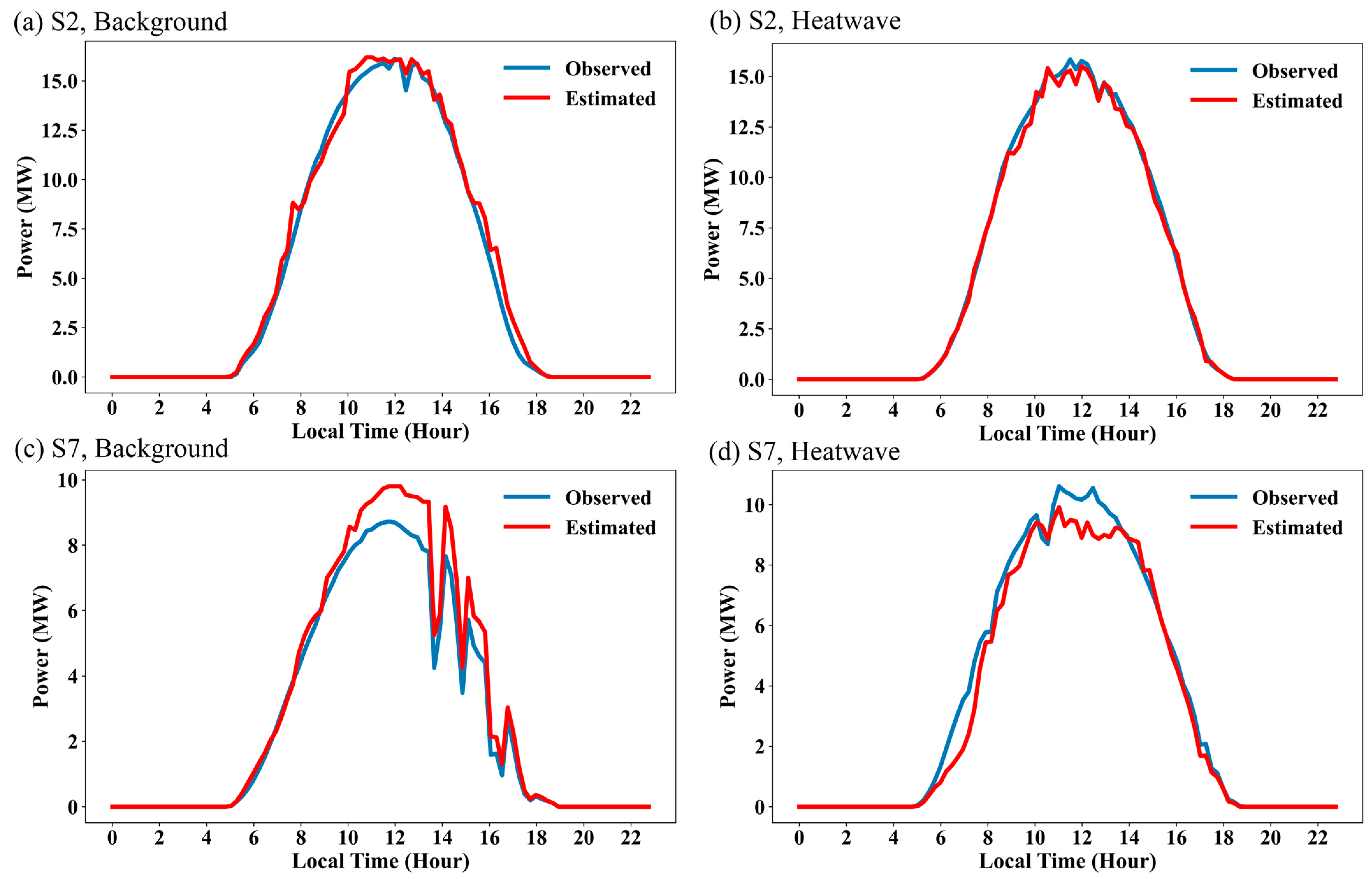
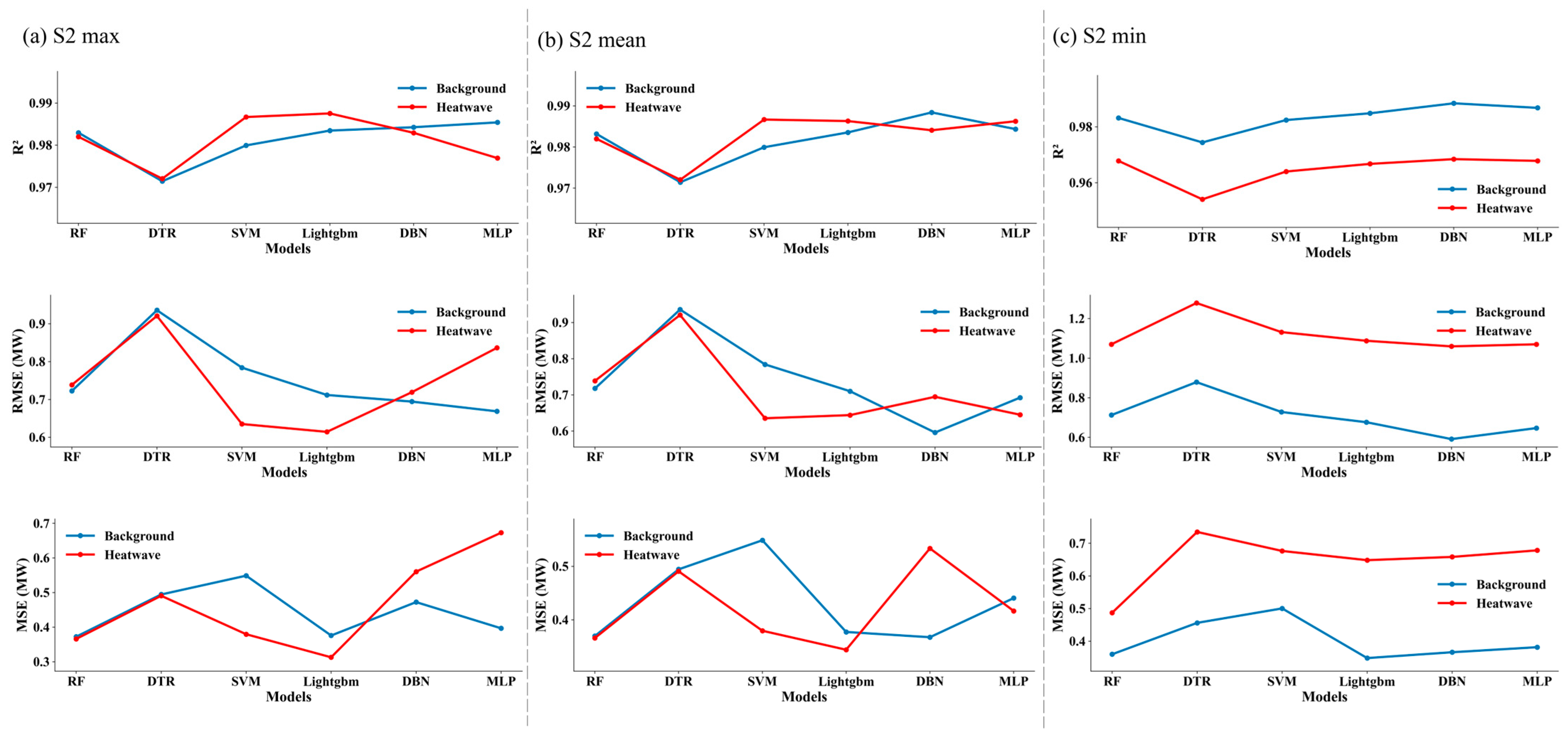
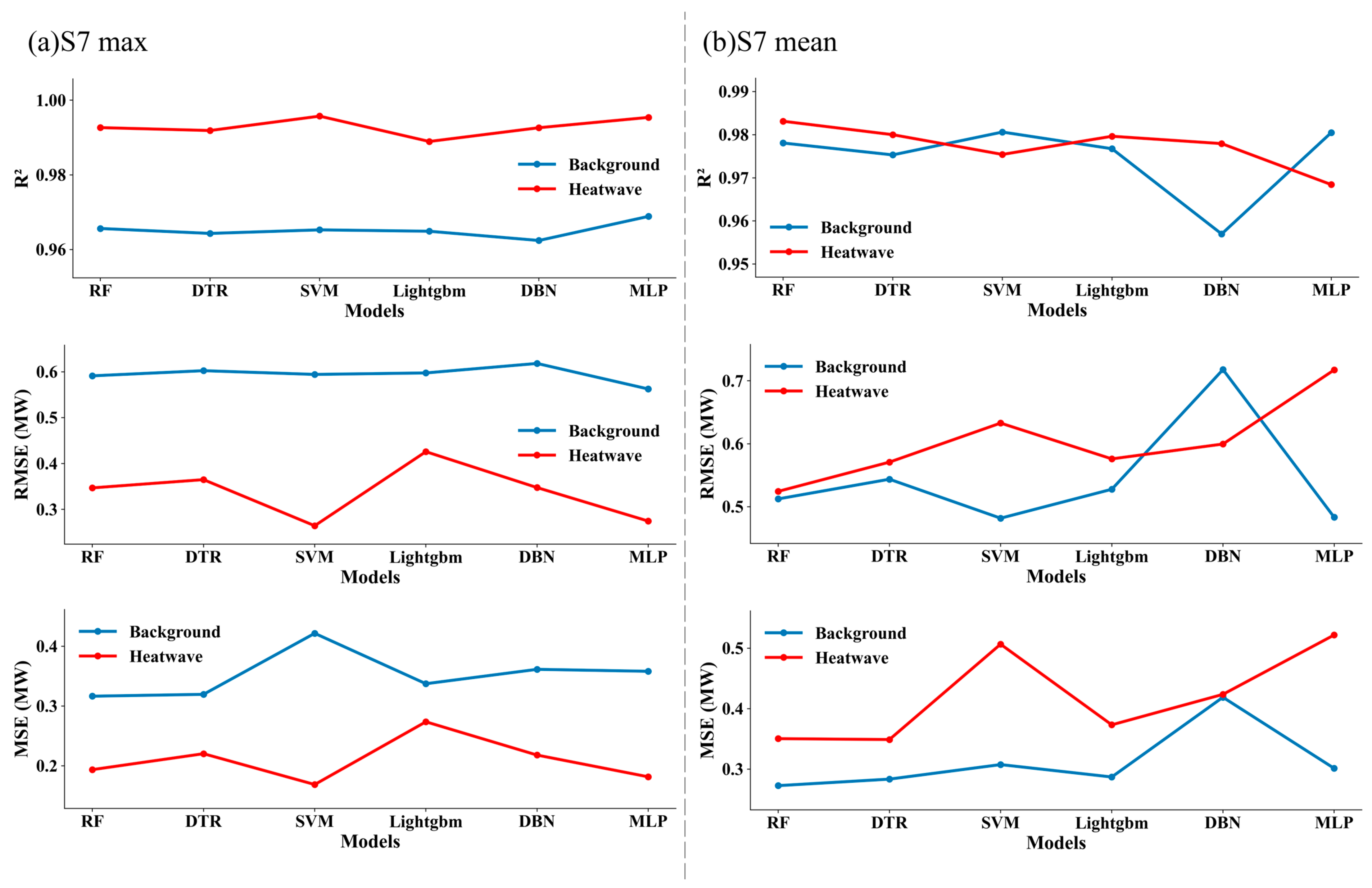
3.5. Performance of Diverse Models under Heatwave and Non-Heatwave Conditions
3.6. The Impact of Cloud Cover on the Prediction of Photovoltaic Power Generation
3.7. The Impact of Different Definitions on PV Power Forecasting
3.8. Complexity of the Drivers of Spatio-Temporal Variation in PV
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- You, V.; Kakinaka, M. Modern and traditional renewable energy sources and CO2 emissions in emerging countries. Environ. Sci. Pollut. Res. Int. 2022, 29, 17695–17708. [Google Scholar] [CrossRef] [PubMed]
- Fang, W.; Huang, Q.; Huang, S.; Yang, J.; Meng, E.; Li, Y. Optimal sizing of utility-scale photovoltaic power generation complementarily operating with hydropower: A case study of the world’s largest hydro-photovoltaic plant. Energy Convers. Manag. 2017, 136, 161–172. [Google Scholar] [CrossRef]
- Jackson, N.D.; Gunda, T. Evaluation of extreme weather impacts on utility-scale photovoltaic plant performance in the United States. Appl. Energy 2021, 302, 117508. [Google Scholar] [CrossRef]
- Brás, T.A.; Simoes, S.G.; Amorim, F.; Fortes, P. How much extreme weather events have affected European power generation in the past three decades? Renew. Sustain. Energy Rev. 2023, 183, 113494. [Google Scholar] [CrossRef]
- Gopi, A.; Sudhakar, K.; Ngui, W.; Kirpichnikova, I.; Cuce, E. Energy analysis of utility-scale PV plant in the rain-dominated tropical monsoon climates. Case Stud. Therm. Eng. 2021, 26, 101123. [Google Scholar] [CrossRef]
- Tobin, I.; Greuell, W.; Jerez, S.; Ludwig, F.; Vautard, R.; van Vliet, M.T.H.; Bréon, F.-M. Vulnerabilities and resilience of European power generation to 1.5 °C, 2 °C and 3 °C warming. Environ. Res. Lett. 2018, 13, 044024. [Google Scholar] [CrossRef]
- Li, P.; Gao, X.; Li, Z.; Zhou, X. Effect of the temperature difference between land and lake on photovoltaic power generation. Renew. Energy 2022, 185, 86–95. [Google Scholar] [CrossRef]
- Bošnjaković, M.; Stojkov, M.; Katinić, M.; Lacković, I. Effects of Extreme Weather Conditions on PV Systems. Sustainability 2023, 15, 16044. [Google Scholar] [CrossRef]
- Feron, S.; Cordero, R.R.; Damiani, A.; Jackson, R.B. Climate change extremes and photovoltaic power output. Nat. Sustain. 2021, 4, 270–276. [Google Scholar] [CrossRef]
- do Nascimento, L.R.; de Souza Viana, T.; Campos, R.A.; Rüther, R. Extreme solar overirradiance events: Occurrence and impacts on utility-scale photovoltaic power plants in Brazil. Sol. Energy 2019, 186, 370–381. [Google Scholar] [CrossRef]
- Berardi, U.; Graham, J. Investigation of the impacts of microclimate on PV energy efficiency and outdoor thermal comfort. Sustain. Cities Soc. 2020, 62, 102402. [Google Scholar] [CrossRef]
- Patel, A.; Swathika, O.V.G.; Subramaniam, U.; Babu, T.S.; Tripathi, A.; Nag, S.; Karthick, A.; Muhibbullah, M. A Practical Approach for Predicting Power in a Small-Scale Off-Grid Photovoltaic System using Machine Learning Algorithms. Int. J. Photoenergy 2022, 2022, 1–21. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, T. Stacking Model for Photovoltaic-Power-Generation Prediction. Sustainability 2022, 14, 5669. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, B. Short-Term Prediction Method of Solar Photovoltaic Power Generation Based on Machine Learning in Smart Grid. Math. Probl. Eng. 2022, 2022, 1–10. [Google Scholar]
- Wang, Y.; Liao, W.; Chang, Y. Gated Recurrent Unit Network-Based Short-Term Photovoltaic Forecasting. Energies 2018, 11, 2163. [Google Scholar] [CrossRef]
- Zhou, N.R.; Zhou, Y.; Gong, L.H.; Jiang, M.L. Accurate prediction of photovoltaic power output based on long short-term memory network. IET Optoelectron. 2020, 14, 399–405. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, F.; Li, D.; He, H.; Zhang, T.; Yang, S. Prediction of Photovoltaic Power by the Informer Model Based on Convolutional Neural Network. Sustainability 2022, 14, 13022. [Google Scholar] [CrossRef]
- Cañadillas-Ramallo, D.; Moutaoikil, A.; Shephard, L.E.; Guerrero-Lemus, R. The influence of extreme dust events in the current and future 100% renewable power scenarios in Tenerife. Renew. Energy 2022, 184, 948–959. [Google Scholar] [CrossRef]
- Gómez-Amo, J.L.; Freile-Aranda, M.D.; Camarasa, J.; Estellés, V.; Utrillas, M.P.; Martínez-Lozano, J.A. Empirical estimates of the radiative impact of an unusually extreme dust and wildfire episode on the performance of a photovoltaic plant in Western Mediterranean. Appl. Energy 2019, 235, 1226–1234. [Google Scholar] [CrossRef]
- Guo, J.; Li, R.; Cai, P.; Xiao, Z.; Fu, H.; Guo, T.; Wang, T.; Zhang, X.; Wang, J.; Song, X. Risk in solar energy: Spatio-temporal instability and extreme low-light events in China. Appl. Energy 2024, 359, 122749. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, Y.; Chandio, A.A.; Sargani, G.R.; Ankrah Twumasi, M. Measuring the Effects of Climate Change on Wheat Production: Evidence from Northern China. Int. J. Environ. Res. Public Health 2022, 19, 12341. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Li, Y.; Hao, F.; Ajaz, T. Role of green energy technology on ecological footprint in China: Evidence from Beijing-Tianjin-Hebei region. Front. Environ. Sci. 2022, 10, 965679. [Google Scholar] [CrossRef]
- Gao, M.; Wang, F.; Ding, Y.; Wu, Z.; Xu, Y.; Lu, X.; Wang, Z.; Carmichael, G.R.; McElroy, M.B. Large-scale climate patterns offer preseasonal hints on the co-occurrence of heat wave and O3 pollution in China. Proc. Natl. Acad. Sci. USA 2023, 120, e2218274120. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Zhang, B.; Huang, H.; Zeng, J.; Wang, X.; Jiao, W. Spatiotemporal Characteristics of Drought in the North China Plain over the Past 58 Years. Atmosphere 2021, 12, 844. [Google Scholar] [CrossRef]
- Du, J.; Wang, K.; Wang, J.; Ma, Q. Contributions of surface solar radiation and precipitation to the spatiotemporal patterns of surface and air warming in China from 1960 to 2003. Atmos. Chem. Phys. 2017, 17, 4931–4944. [Google Scholar] [CrossRef]
- Yao, T.; Wang, J.; Wu, H.; Zhang, P.; Li, S.; Wang, Y.; Chi, X.; Shi, M. A photovoltaic power output dataset: Multi-source photovoltaic power output dataset with Python toolkit. Sol. Energy 2021, 230, 122–130. [Google Scholar] [CrossRef]
- Abrams, M.; Crippen, R.; Fujisada, H. ASTER Global Digital Elevation Model (GDEM) and ASTER Global Water Body Dataset (ASTWBD). Remote. Sens. 2020, 12, 1156. [Google Scholar] [CrossRef]
- Yu, S.; Han, R.; Zhang, J. Reassessment of the potential for centralized and distributed photovoltaic power generation in China: On a prefecture-level city scale. Energy 2023, 262, 125436. [Google Scholar] [CrossRef]
- Wang, P.; Tang, J.; Sun, X.; Wang, S.; Wu, J.; Dong, X.; Fang, J. Heat Waves in China: Definitions, Leading Patterns, and Connections to Large-Scale Atmospheric Circulation and SSTs. J. Geophys. Res. Atmos. 2017, 122, 10,679–10,699. [Google Scholar] [CrossRef]
- Zhang, J.; You, Q.; Ullah, S. Changes in photovoltaic potential over China in a warmer future. Environ. Res. Lett. 2022, 17, 114032. [Google Scholar] [CrossRef]
- Raj, V.; Dotse, S.-Q.; Sathyajith, M.; Petra, M.I.; Yassin, H. Ensemble Machine Learning for Predicting the Power Output from Different Solar Photovoltaic Systems. Energies 2023, 16, 671. [Google Scholar] [CrossRef]
- Pan, M.; Li, C.; Gao, R.; Huang, Y.; You, H.; Gu, T.; Qin, F. Photovoltaic power forecasting based on a support vector machine with improved ant colony optimization. J. Clean. Prod. 2020, 277, 123948. [Google Scholar] [CrossRef]
- Wang, J.; Li, P.; Ran, R.; Che, Y.; Zhou, Y. A Short-Term Photovoltaic Power Prediction Model Based on the Gradient Boost Decision Tree. Appl. Sci. 2018, 8, 689. [Google Scholar] [CrossRef]
- Liu, L.; Liu, F.; Zheng, Y. A Novel Ultra-Short-Term PV Power Forecasting Method Based on DBN-Based Takagi-Sugeno Fuzzy Model. Energies 2021, 14, 6447. [Google Scholar] [CrossRef]
- Huang, C.; Cao, L.; Peng, N.; Li, S.; Zhang, J.; Wang, L.; Luo, X.; Wang, J.-H. Day-Ahead Forecasting of Hourly Photovoltaic Power Based on Robust Multilayer Perception. Sustainability 2018, 10, 4863. [Google Scholar] [CrossRef]
- Ding, W.; Liu, S. Impact assessment of air pollutants and greenhouse gases on urban heat wave events in the Beijing-Tianjin-Hebei region. Environ. Geochem. Health 2023, 45, 7693–7709. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zuo, Y.; Wang, N.; Yuan, F.; Zhu, X.; Zhang, L.; Zhang, J.; Sun, Y.; Guo, Z.; Guo, Y.; et al. Comparative Analysis of Two Machine Learning Algorithms in Predicting Site-Level Net Ecosystem Exchange in Major Biomes. Remote. Sens. 2021, 13, 2242. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Chen, Q. Study on the impacts of meteorological factors on distributed photovoltaic accommodation considering dynamic line parameters. Appl. Energy 2020, 259, 114133. [Google Scholar] [CrossRef]
- Son, N.; Jung, M. Analysis of Meteorological Factor Multivariate Models for Medium- and Long-Term Photovoltaic Solar Power Forecasting Using Long Short-Term Memory. Appl. Sci. 2020, 11, 316. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, H.; Zheng, J.; Dai, Y.; Huang, L.; Shang, W.; Liang, Y. A point prediction method based automatic machine learning for day-ahead power output of multi-region photovoltaic plants. Energy 2021, 223, 120026. [Google Scholar] [CrossRef]
- Li, G.; Wei, X.; Yang, H. Decomposition integration and error correction method for photovoltaic power forecasting. Measurement 2023, 208, 112462. [Google Scholar] [CrossRef]
- Cai, J.; Xu, K.; Zhu, Y.; Hu, F.; Li, L. Prediction and analysis of net ecosystem carbon exchange based on gradient boosting regression and random forest. Appl. Energy 2020, 262, 114566. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Z.; Yin, W.; Zhao, C.; Wang, F.; Li, Y. A study on depth classification of defects by machine learning based on hyper-parameter search. Measurement 2022, 189, 110660. [Google Scholar] [CrossRef]
- Rimal, Y.; Sharma, N.; Alsadoon, A. The accuracy of machine learning models relies on hyperparameter tuning: Student result classification using random forest, randomized search, grid search, bayesian, genetic, and optuna algorithms. Multimedia Tools Appl. 2024. [Google Scholar] [CrossRef]
- Zhang, X.; Song, Y.; Nam, W.H.; Huang, T.; Gu, X.; Zeng, J.; Huang, S.; Chen, N.; Yan, Z.; Niyogi, D. Data fusion of satellite imagery and downscaling for generating highly fine-scale precipitation. J. Hydrol. 2024, 631, 130665. [Google Scholar] [CrossRef]
- Xu, H.; Deng, Y. Dependent Evidence Combination Based on Shearman Coefficient and Pearson Coefficient. IEEE Access 2018, 6, 11634–11640. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; She, J.; Peng, X. Assimilating remote sensing data into GIS-based all sky solar radiation modeling for mountain terrain. Remote Sens. Environ. 2019, 231, 111239. [Google Scholar] [CrossRef]
- Alfaro-Contreras, R.; Zhang, J.; Campbell, J.R.; Holz, R.E.; Reid, J.S. Evaluating the impact of aerosol particles above cloud on cloud optical depth retrievals from MODIS. J. Geophys. Res. Atmos. 2014, 119, 5410–5423. [Google Scholar] [CrossRef]
- Russak, V. Changes in solar radiation and their influence on temperature trend in Estonia (1955–2007). J. Geophys. Res. Atmos. 2009, 114, D00D01. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Z. Rapid rises in the magnitude and risk of extreme regional heat wave events in China. Weather Clim. Extremes 2021, 34, 100379. [Google Scholar] [CrossRef]
- Yoon, D.; Cha, D.H.; Lee, G.; Park, C.; Lee, M.I.; Min, K.H. Impacts of Synoptic and Local Factors on Heat Wave Events Over Southeastern Region of Korea in 2015. J. Geophys. Res. Atmos. 2018, 123, 12081–12096. [Google Scholar] [CrossRef]
- Seo, J.M.; Ganbat, G.; Han, J.-Y.; Baik, J.-J. Theoretical calculations of interactions between urban breezes and mountain slope winds in the presence of basic-state wind. Theor. Appl. Climatol. 2015, 127, 865–874. [Google Scholar] [CrossRef]
- Kong, J.; Zhao, Y.; Strebel, D.; Gao, K.; Carmeliet, J.; Lei, C. Understanding the impact of heatwave on urban heat in greater Sydney: Temporal surface energy budget change with land types. Sci. Total Environ. 2023, 903, 166374. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Yu, C.; Deng, X.; He, D.; Zhao, Z.; Mo, H.; Mo, J.; Wu, Y. Mechanism for synoptic and intra-seasonal oscillation of visibility in Beijing-Tianjin-Hebei region. Theor. Appl. Climatol. 2020, 143, 1005–1015. [Google Scholar] [CrossRef]
- Danso, D.K.; Anquetin, S.; Diedhiou, A.; Lavaysse, C.; Hingray, B.; Raynaud, D.; Kobea, A.T. A CMIP6 assessment of the potential climate change impacts on solar photovoltaic energy and its atmospheric drivers in West Africa. Environ. Res. Lett. 2022, 17, 044016. [Google Scholar] [CrossRef]
- Hasan, K.; Yousuf, S.B.; Tushar, M.S.H.K.; Das, B.K.; Das, P.; Islam, M.S. Effects of different environmental and operational factors on the PV performance: A comprehensive review. Energy Sci. Eng. 2021, 10, 656–675. [Google Scholar] [CrossRef]
- Tiba, C.; Beltrão, R.E.d.A. Siting PV plant focusing on the effect of local climate variables on electric energy production—Case study for Araripina and Recife. Renew. Energy 2012, 48, 309–317. [Google Scholar] [CrossRef]
- Tian, Y.; Ghausi, S.A.; Zhang, Y.; Zhang, M.; Xie, D.; Cao, Y.; Mei, Y.; Wang, G.; Zhong, D.; Kleidon, A. Radiation as the dominant cause of high-temperature extremes on the eastern Tibetan Plateau. Environ. Res. Lett. 2023, 18, 074007. [Google Scholar] [CrossRef]
- Skoplaki, E.; Palyvos, J.A. On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Sol. Energy 2009, 83, 614–624. [Google Scholar] [CrossRef]
- Sengupta, S. Atmospheric Thermal Emission Effect on Chandrasekhar’s Finite Atmosphere Problem. Astrophys. J. 2022, 936, 139. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Huang, H. Stratospheric Water Vapor Feedback Disclosed by a Locking Experiment. Geophys. Res. Lett. 2020, 47, e2020GL087987. [Google Scholar] [CrossRef]
- Si, Z.; Yang, M.; Yu, Y.; Ding, T. Photovoltaic power forecast based on satellite images considering effects of solar position. Appl. Energy 2021, 302, 117514. [Google Scholar] [CrossRef]
- Park, S.; Kim, Y.; Ferrier, N.J.; Collis, S.M.; Sankaran, R.; Beckman, P.H. Prediction of Solar Irradiance and Photovoltaic Solar Energy Product Based on Cloud Coverage Estimation Using Machine Learning Methods. Atmosphere 2021, 12, 395. [Google Scholar] [CrossRef]
- Jiang, Y.; Yi, B. An Assessment of the Influences of Clouds on the Solar Photovoltaic Potential over China. Remote Sensing 2023, 15, 258. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, Y.; Chen, F.; Shang, E.; Yao, W.; Liu, J.; Long, A. Estimation of Photovoltaic Energy in China Based on Global Land High-Resolution Cloud Climatology. Remote. Sens. 2022, 14, 2084. [Google Scholar] [CrossRef]
- Stull, R.B. Meteorology for Scientists and Engineers. Cengage Learn. Emea 2000. [Google Scholar]
- Ding, S.; Chen, A. Comprehensive assessment of daytime, nighttime and compound heatwave risk in East China. Nat. Hazards 2024, 120, 7245–7263. [Google Scholar] [CrossRef]
- Russo, S.; Sillmann, J.; Sterl, A. Humid heat waves at different warming levels. Sci. Rep. 2017, 7, 7477. [Google Scholar] [CrossRef]
- Shi, Z.; Xu, X.; Jia, G. Urbanization Magnified Nighttime Heat Waves in China. Geophys. Res. Lett. 2021, 48, e2021GL093603. [Google Scholar] [CrossRef]
- Fenner, D.; Holtmann, A.; Krug, A.; Scherer, D. Heat waves in Berlin and Potsdam, Germany—Long-term trends and comparison of heat wave definitions from 1893 to 2017. Int. J. Climatol. 2018, 39, 2422–2437. [Google Scholar] [CrossRef]
- Donat, M.G.; Alexander, L.V.; Yang, H.; Durre, I.; Vose, R.; Dunn, R.J.; Willett, K.M.; Aguilar, E.; Brunet, M.; Caesar, J.; et al. Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The HadEX2 dataset. J. Geophys. Res. Atmos. 2013, 118, 2098–2118. [Google Scholar] [CrossRef]
- Alexander, L.V.; Perkins, S.E. On the Measurement of Heat Waves. J. Clim. 2013, 26, 4500–4517. [Google Scholar]
- Russo, S.; Dosio, A.; Graversen, R.G.; Sillmann, J.; Carrao, H.; Dunbar, M.B.; Singleton, A.; Montagna, P.; Barbola, P.; Vogt, J.V. Magnitude of extreme heat waves in present climate and their projection in a warming world. J. Geophys. Res. Atmos. 2014, 119, 12,500–12,512. [Google Scholar] [CrossRef]
- Xu, Z.; FitzGerald, G.; Guo, Y.; Jalaludin, B.; Tong, S. Impact of heatwave on mortality under different heatwave definitions: A systematic review and meta-analysis. Environ. Int. 2016, 89–90, 193–203. [Google Scholar] [CrossRef]
- Russo, S.; Sillmann, J.; Fischer, E.M. Top ten European heatwaves since 1950 and their occurrence in the coming decades. Environ. Res. Lett. 2015, 10, 124003. [Google Scholar] [CrossRef]
- Na, Y.; Lu, R.; Lu, B.; Chen, M.; Miao, S. Impact of the Horizontal Heat Flux in the Mixed Layer on an Extreme Heat Event in North China: A Case Study. Adv. Atmos. Sci. 2018, 36, 133–142. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, X.; Li, J.; Zhang, R.; Kang, Y.; Huang, W.; Xia, Y.; Liu, D.; Sun, X. The Large-Scale Circulation Patterns Responsible for Extreme Precipitation Over the North China Plain in Midsummer. J. Geophys. Res. Atmos. 2019, 124, 12794–12809. [Google Scholar] [CrossRef]
- Lin, Z. Impacts of two types of northward jumps of the East Asian upper-tropospheric jet stream in midsummer on rainfall in eastern China. Adv. Atmos. Sci. 2013, 30, 1224–1234. [Google Scholar] [CrossRef]
- Giovannini, L.; Ferrero, E.; Karl, T.; Rotach, M.W.; Staquet, C.; Castelli, S.T.; Zardi, D. Atmospheric Pollutant Dispersion over Complex Terrain: Challenges and Needs for Improving Air Quality Measurements and Modeling. Atmosphere 2020, 11, 646. [Google Scholar] [CrossRef]
- Jin, X.; Cai, X.; Huang, Q.; Wang, X.; Song, Y.; Zhu, T. Atmospheric Boundary Layer—Free Troposphere Air Exchange in the North China Plain and its Impact on PM2.5 Pollution. J. Geophys. Res. Atmos. 2021, 126, e2021JD034641. [Google Scholar] [CrossRef]
- Kang, S.; Eltahir, E.A.B. North China Plain threatened by deadly heatwaves due to climate change and irrigation. Nat. Commun. 2018, 9, 2894. [Google Scholar] [CrossRef] [PubMed]




| Station | Period | n_Estimators | Max_Depth | Min_Samples_Split | Min_Samples_Leaf |
|---|---|---|---|---|---|
| S2 | background | 130 | 10 | 6 | 5 |
| heatwave | 100 | 10 | 8 | 5 | |
| S7 | background | 190 | 16 | 6 | 3 |
| heatwave | 190 | 18 | 2 | 14 |
| Name | Clear | Few Clouds | Partly Cloudy | Mostly Cloudy | Overcast |
|---|---|---|---|---|---|
| Sky Cover | 0–0.1 | 0.1–0.3 | 0.3–0.5 | 0.5–0.9 | 0.9–1 |
| Station | Period | RF | DTR | SVM | LightGBM | DBN | MLP |
|---|---|---|---|---|---|---|---|
| S2 | clear | 0.986 | 0.972 | 0.982 | 0.987 | 0.995 | 0.975 |
| cloud | 0.988 | 0.986 | 0.950 | 0.979 | 0.985 | 0.977 | |
| S7 | clear | 0.982 | 0.983 | 0.985 | 0.982 | 0.956 | 0.964 |
| cloud | 0.975 | 0.974 | 0.967 | 0.968 | 0.965 | 0.962 |
| Definition | Variable | Minimum Duration (Day) | Type and Value of Threshold (at Potsdam) | S2 Background | S2 Heatwave | S7 Background | S7 Heatwave |
|---|---|---|---|---|---|---|---|
| HW01 [73] | Tmax | 3 | Dynamic; 90th perc. | 6720 | 480 | 5376 | 288 |
| HW02 [74] | Tmean | 3 | Dynamic; 90th perc. | 6720 | 480 | 5376 | 288 |
| HW03 [75] | Tmin | 3 | Dynamic; 90th perc. | 6912 | 288 | / | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Duan, Z.; Zhang, Y.; Ji, T. Response of Sustainable Solar Photovoltaic Power Output to Summer Heatwave Events in Northern China. Sustainability 2024, 16, 5254. https://doi.org/10.3390/su16125254
Huang Z, Duan Z, Zhang Y, Ji T. Response of Sustainable Solar Photovoltaic Power Output to Summer Heatwave Events in Northern China. Sustainability. 2024; 16(12):5254. https://doi.org/10.3390/su16125254
Chicago/Turabian StyleHuang, Zifan, Zexia Duan, Yichi Zhang, and Tianbo Ji. 2024. "Response of Sustainable Solar Photovoltaic Power Output to Summer Heatwave Events in Northern China" Sustainability 16, no. 12: 5254. https://doi.org/10.3390/su16125254
APA StyleHuang, Z., Duan, Z., Zhang, Y., & Ji, T. (2024). Response of Sustainable Solar Photovoltaic Power Output to Summer Heatwave Events in Northern China. Sustainability, 16(12), 5254. https://doi.org/10.3390/su16125254






