Generalized-Norm-Based Robustness Evaluation Model of Bus Network under Snowy Weather
Abstract
:1. Introduction
- (1)
- Considering the vehicle speed reduction and the space congestion within buses under snow conditions, the weighted adjacency matrix is constructed, and a robustness evaluation model of the bus transit network system based on the generalized norm is proposed. When there are enough data, the proposed evaluation model can analyze the network robustness under any vehicle speed and congestion;
- (2)
- The proposed robustness evaluation model is applied to the bus network under the two classic network topology types of chessboard and ring radiation. The results show that the robustness of the chessboard and ring-radiation bus networks is reduced by 38% and 39%, respectively;
- (3)
- The unit with the highest importance for the system robustness in the checkerboard network is C910, and the central area unit is always more important than the peripheral units. However, in the ring-radial network, the units that are more important for system robustness are on the ring line, such as C916. In addition, the failure of Ring Line 5 has a great impact on both the checkerboard and ring-radial networks, causing the system robustness to decrease by 43% and 50%, respectively.
2. Effects of Snowy Conditions on the Operations of Bus Network
2.1. Snow Intensity and Road Condition
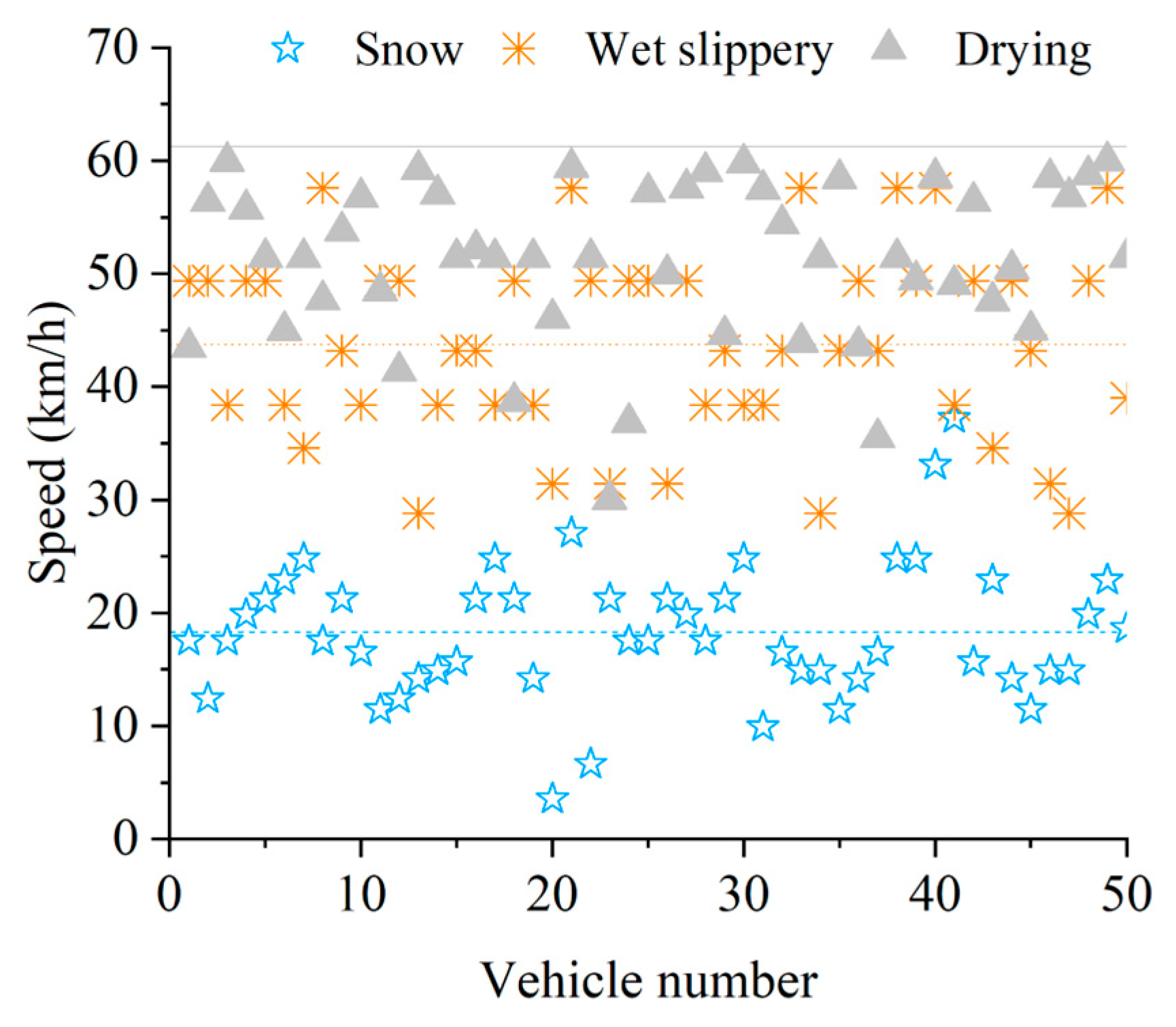
2.2. Bus Speed
- (1)
- In the free flow state, under the same road conditions, the average speed of vehicles at night is lower than that in the day. For example, on the water road, the average speeds of Changchun Road during the day and night are reduced by 16% and 19%, respectively, and the average speeds of Cuizhu Street during the day and night are reduced by 15% and 23%, respectively;
- (2)
- Comparing speeds of different road conditions during the day, the speeds of snowy roads are lower than that of water roads. Compared with the speeds of dry roads during the day, the average speeds of Changchun Road and Cuizhu Street are reduced by 60% and 64%, respectively, under snowy conditions. Under water road conditions, the average speeds of Changchun Road and Cuizhu Street are reduced by 16% and 15%, respectively. This is because drivers are unable to fully determine the snow thickness of the road, and the snowy conditions will affect drivers’ perception and psychology. Additionally, water roads have a higher friction coefficient than snowy roads, so, in order to ensure their safety, drivers will take lower speed;
- (3)
- Changchun Road and Cuizhu Street are both main roads, but the average speed of Changchun Road is higher than that of Cuizhu Street under the same road conditions, mainly because the cross-sectional structure and the surrounding environment of the two roads are different. Changchun Road is a two-way six-lane road, while Cuizhu Street is a two-way four-lane road, and there are residential areas and primary schools on Cuizhu Street. There are more pedestrians and non-motor vehicles on Cuizhu Street, and its speed will be affected.
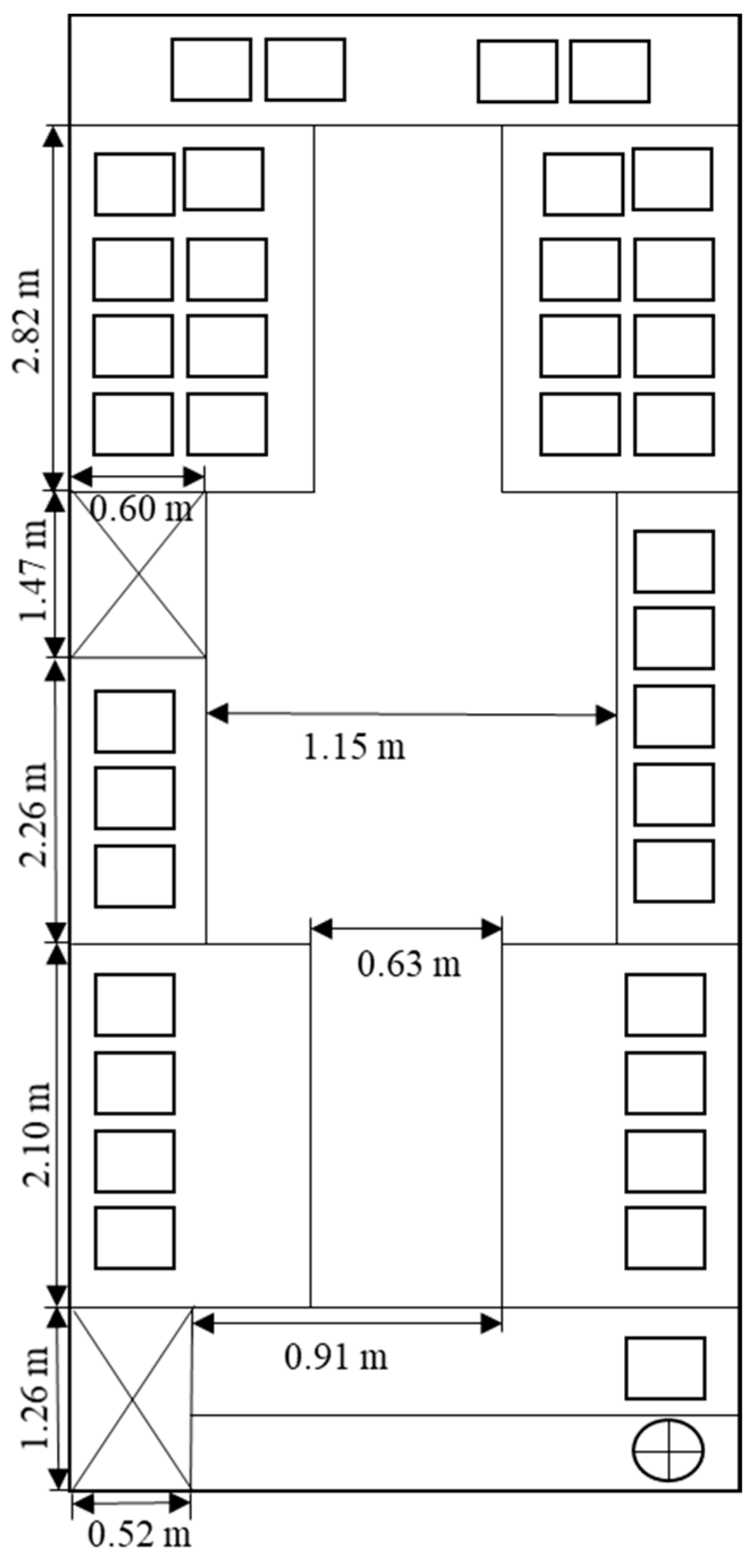
2.3. Congestion Degree within Bus
3. Methodology
3.1. Spectral-Radius-Based Robustness Evaluation Model
3.2. Robustness Evaluation Model under Snowy Conditions
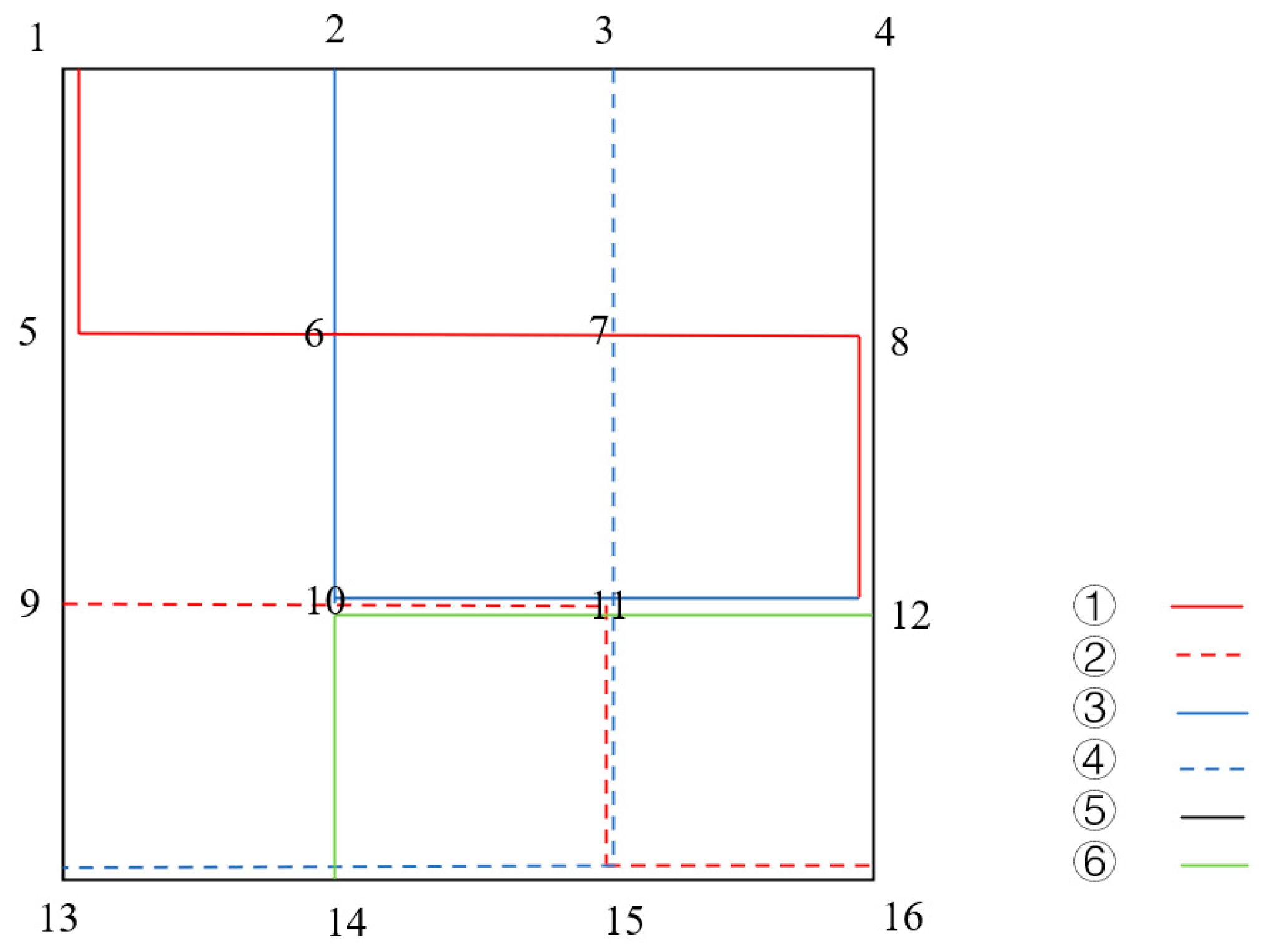
4. Case Study
4.1. Parameter Setting
- (1)
- Network parameters
- (2)
- Speed
- (3)
- Congestion degree thresholds
4.2. Network Robustness
4.3. Importance Ranking of Units in Network
- (1)
- On the whole, the most peripheral units in the network have little effect on the network robustness, whether it is a checkerboard or a ring-radiating network topology, that is, the importance of the unit is low. This is because, in the network design, the road grade of the most peripheral unit is higher, and the standard speed is larger under snowy conditions. Although the passenger flows on the ring line are large, only one unit is deleted at a time, and there are many lines connected to the ring line. When the unit fails, there are other alternative paths, and the failure of a unit in the internal structure of the network may cause the two stations to detour far away to complete the trip;
- (2)
- In the ranking of the unit importance of the chessboard network, the importance of the unit at the center of the inner ring is relatively high. For example, the reduction values of the robustness of C610, C1011, and C710 are all higher than 0.6, and the unit C910 has the highest importance in the network. The main reason is that the importance of the unit is not only related to the location of the unit in the network, but also related to the passenger flows allocated on the unit, that is, the congestion degree within the bus on the unit. Under the snowstorm scenario, the bus line on the C910 unit still runs, and the congestion degree within the bus on the unit is large. If the C910 unit is deleted, the passenger flows on the unit need to be redistributed to other units in the network, which has a greater impact on the operation of other units, that is, the importance of the unit C910 is higher;
- (3)
- In the unit importance ranking of the ring-radial network, the importance of the unit at the center of the inner ring is also relatively high. Different from the unit importance ranking in the checkerboard network, the unit with the highest importance, C916, is located on the inner ring, followed by C1516. The direct reason is that the passenger flows from node 9 to node 16 and node 9 to node 15 in the network are large, and the shortest paths of the two pairs of OD pairs pass through unit C916.
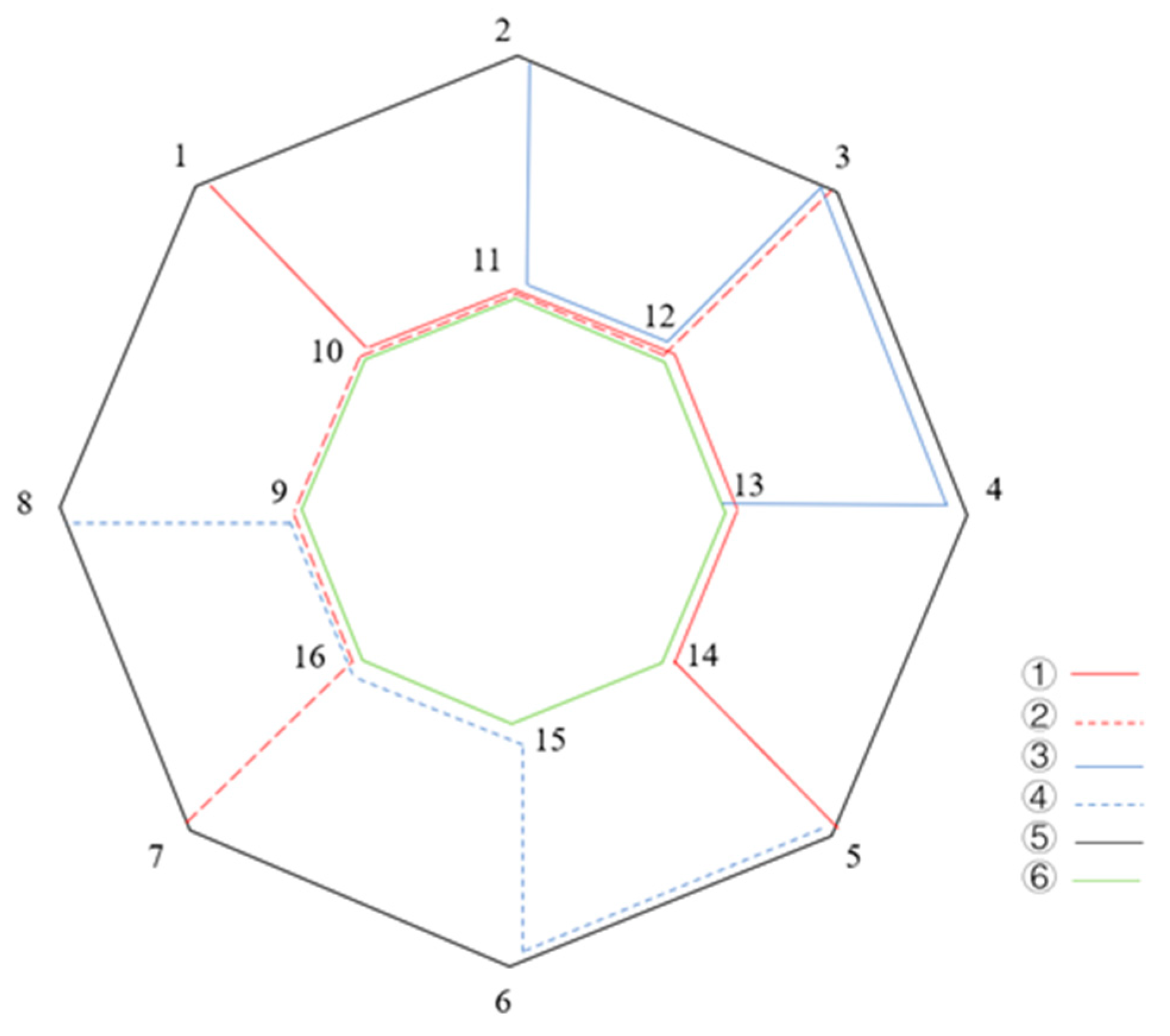
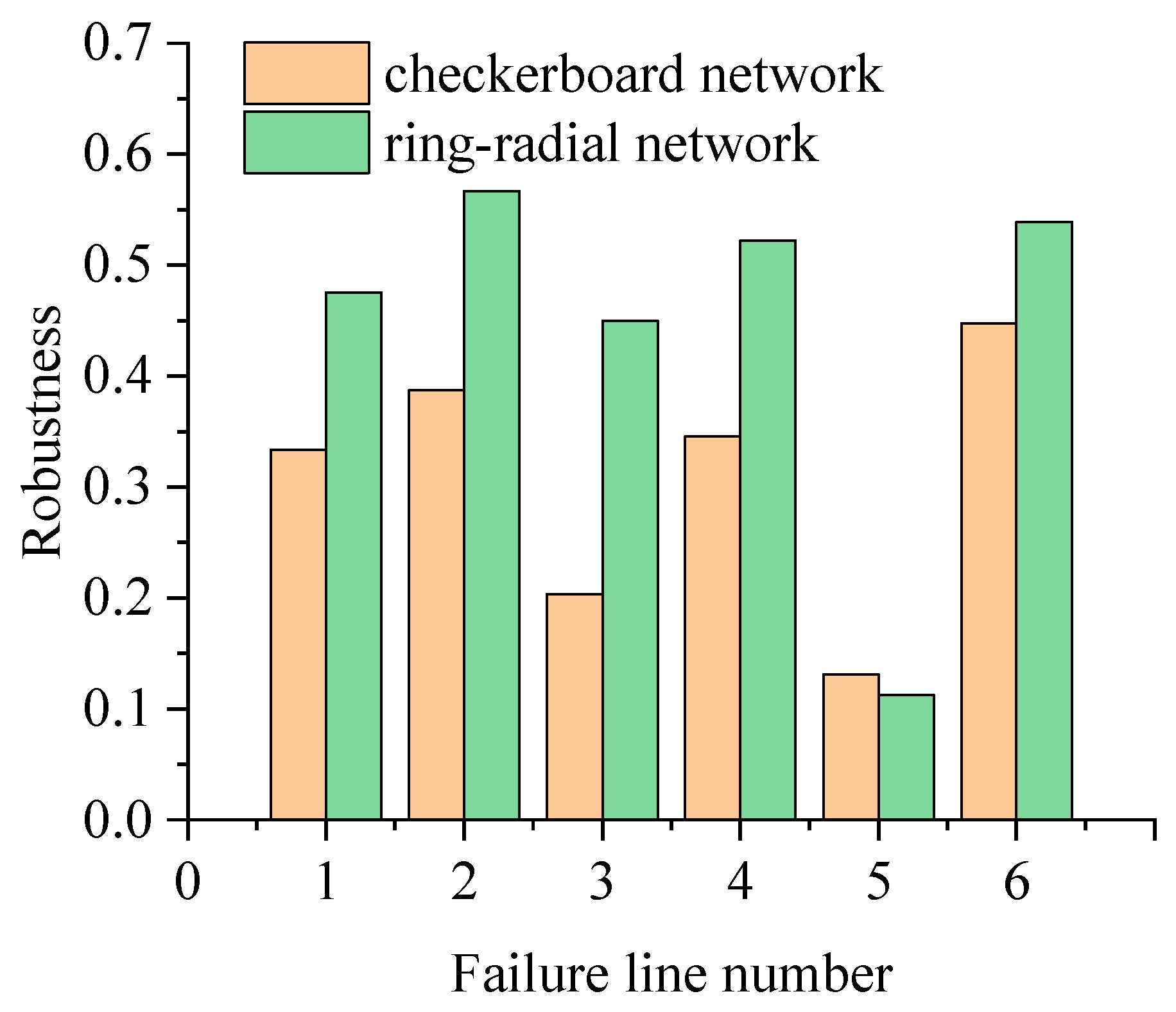
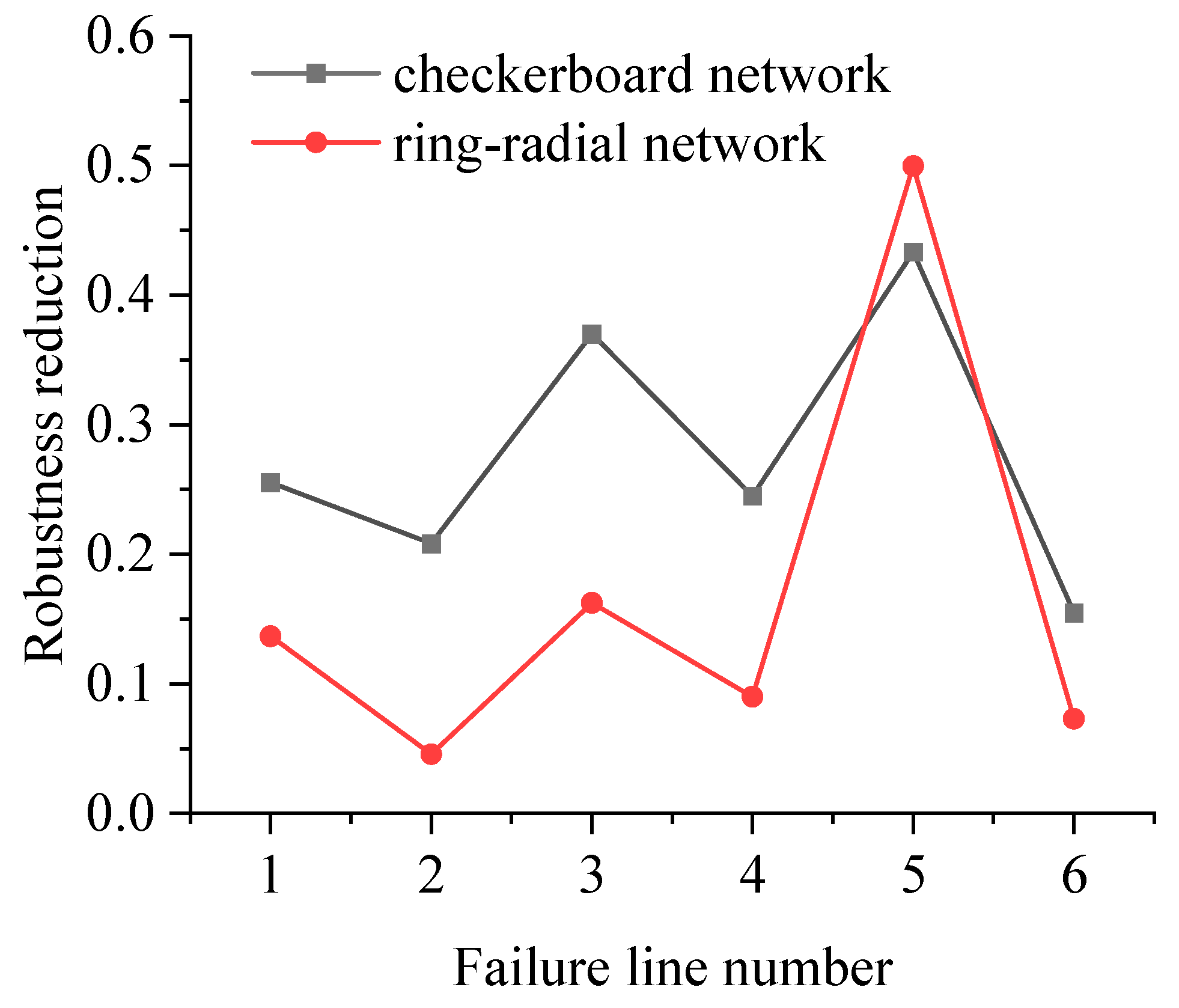
4.4. Importance Ranking of Lines
- (1)
- The robustness of the two network types with the same number of bus lines is different. The robustness of the ring-radial network is about 1.14 times that of the checkerboard network;
- (2)
- When different lines in the network fail, Ring Line 5 of both the checkerboard and the ring-radial network structure types has the highest importance, and the failure of the line will have the greatest impact on the network. If the ring line fails, the passenger flows on the line will be redistributed to other lines in the network, which will lead to a significant increase in passenger flows on other lines. Therefore, compared with other lines in the network, the ring line is more important. For both checkerboard and ring-radiation networks, the failure of Ring Line 5 significantly impacts the network, reducing system resilience by 43% and 50%, respectively;
- (3)
- When Line 1, 2, 3, 4, or 6 fails, the robustness reduction of the ring-radial network is smaller than that of the checkerboard network because there are more overlaps between the lines in the ring-radial network. When one of the lines fails, the passenger flows can be redistributed to other lines. When a line in the checkerboard network fails, passengers may need to bypass the path for a long time. Therefore, the failure of a single line will have a greater impact on the robustness of the checkerboard network;
- (4)
- Based on the robustness of the network, the results are shown in Figure 14, and the importance ranking of the lines in the checkerboard network is Line 5, 3, 1, 4, 2, and 6, and the importance ranking of the lines in the ring-radial network is Line 5, 3, 1, 4, 6, and 2.
5. Conclusions
- (1)
- Under different snowfall intensities, urban road surface conditions and residents’ travel choice behaviors are different, which leads to different changes in bus speed and in-vehicle congestion, and the corresponding weighted adjacency matrix pages of the network change accordingly. Therefore, future research can further analyze the selection of model parameter thresholds and the application of the model under different snowfall intensities;
- (2)
- There are differences in the initial robustness of different cities. For example, cities with perennial snow cover have higher robustness to deal with snowfall, and their speed reduction coefficients and congestion change coefficients are different. In the follow-up study, the network structure of specific cities can be used to analyze the robustness of different structural networks;
- (3)
- When calculating the robustness of the network in this paper, only the ground bus network is considered, but the actual urban bus network also has rail transit, taxi, and other modes, and other public transport will be considered in the future;
- (4)
- The model in this paper only evaluates the robust performance of the network, but the future research will consider the robust performance of the bus system, operating costs, passenger satisfaction, and other factors [42,43], and an optimization model will be established to find an urban bus optimization scheme for snowy conditions and provide the basis for the operation of the urban bus system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Horner, M.W. Sustainable Transportation: Problems and Solutions. Ann. Assoc. Am. Geogr. 2011, 101, 454–456. [Google Scholar] [CrossRef]
- Miller, P.; de Barros, A.G.; Kattan, L.; Wirasinghe, S.C. Public transportation and sustainability: A review. Ksce J. Civ. Eng. 2016, 20, 1076–1083. [Google Scholar] [CrossRef]
- Climate Change Center of China Meteorological Administration. China Climate Change Blue Book(2023); Science Press: Beijing, China, 2023. [Google Scholar]
- Hao, Z.C.; Singh, V.P. Compound Events under Global Warming: A Dependence Perspective. J. Hydrol. Eng. 2020, 25, 03120001. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, Z.H. Measuring the performance of airport resilience to severe weather events. Transp. Res. Part D Transp. Environ. 2020, 83, 102362. [Google Scholar] [CrossRef]
- AR6 Synthesis Eport: Climate Change 2023. Available online: https://www.ipcc.ch/ar6-syr/ (accessed on 9 May 2024).
- Tianjin Public Transportation Group (Holdings) Co., Ltd. Tianjin Bus. Urban Public Transp. 2024, 307, 45. [Google Scholar]
- Chester, M.V.; Allenby, B. Toward adaptive infrastructure: Flexibility and agility in a non-stationarity age. Sustain. Resilient Infrastruct. 2019, 4, 173–191. [Google Scholar] [CrossRef]
- Markolf, S.A.; Hoehne, C.; Fraser, A.; Chester, M.V.; Underwood, B.S. Transportation resilience to climate change and extreme weather events—Beyond risk and robustness. Transp. Policy 2019, 74, 174–186. [Google Scholar] [CrossRef]
- Bruneau, M.; Reinhorn, A. Exploring the concept of seismic resilience for acute care facilities. Earthq. Spectra 2007, 23, 41–62. [Google Scholar] [CrossRef]
- Cats, O. The robustness value of public transport development plans. J. Transp. Geogr. 2016, 51, 236–246. [Google Scholar] [CrossRef]
- Kim, H.; Kim, C.; Chun, Y. Network Reliability and Resilience of Rapid Transit Systems. Prof. Geogr. 2016, 68, 53–65. [Google Scholar] [CrossRef]
- Xing, Y.; Lu, J.; Chen, S.; Dissanayake, S. Vulnerability analysis of urban rail transit based on complex network theory: A case study of Shanghai Metro. Public Transp. 2017, 9, 501–525. [Google Scholar] [CrossRef]
- Yang, Y.H.; Liu, Y.X.; Zhou, M.X.; Li, F.X.; Sun, C. Robustness assessment of urban rail transit based on complex network theory: A case study of the Beijing Subway. Saf. Sci. 2015, 79, 149–162. [Google Scholar] [CrossRef]
- Derrible, S.; Kennedy, C. The complexity and robustness of metro networks. Phys. A Stat. Mech. Appl. 2010, 389, 3678–3691. [Google Scholar] [CrossRef]
- Wang, X.; Koc, Y.; Derrible, S.; Ahmad, S.N.; Pino, W.J.A.; Kooij, R.E. Multi-criteria robustness analysis of metro networks. Phys. A Stat. Mech. Appl. 2017, 474, 19–31. [Google Scholar] [CrossRef]
- Tang, J.J.; Li, Z.T.; Gao, F.; Zong, F. Identifying critical metro stations in multiplex network based on D-S evidence theory. Phys. A Stat. Mech. Appl. 2021, 574, 126018. [Google Scholar] [CrossRef]
- Qi, Q.J.; Meng, Y.Y.; Zhao, X.F.; Liu, J.Z. Resilience Assessment of an Urban Metro Complex Network: A Case Study of the Zhengzhou Metro. Sustainability 2022, 14, 11555. [Google Scholar] [CrossRef]
- Ding, R.; Fu, J.; Du, Y.M.; Du, L.Y.; Zhou, T.; Zhang, Y.L.; Shen, S.W.; Zhu, Y.Q.; Chen, S.H. Structural Evolution and Community Detection of China Rail Transit Route Network. Sustainability 2022, 14, 12342. [Google Scholar] [CrossRef]
- Yu, W.; Chen, J.; Yan, X.C. Space-Time Evolution Analysis of the Nanjing Metro Network Based on a Complex Network. Sustainability 2019, 11, 523. [Google Scholar] [CrossRef]
- Li, J.Y.; Teng, J.; Wang, H. Measuring robustness in uncertain topologies: A study of on-demand bus networks. Transp. A Transp. Sci. 2024, 1–27. [Google Scholar] [CrossRef]
- Liao, J.; Guo, C.; Xu, Y.; Zhang, J.; Yang, K. Quantitative analysis and calculation of traffic social cost during the construction of open-cut subway station. IOP Conf. Ser. Mater. Sci. Eng. 2020, 741, 012032. [Google Scholar] [CrossRef]
- Bajaj, G.; Singh, P. Understanding Preferences of Delhi Metro Users Using Choice-Based Conjoint Analysis. IEEE Trans. Intell. Transp. Syst. 2021, 22, 384–393. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, P.Y.; Yang, S.F.; Zheng, F.; Yu, H.; Tang, J.; Lu, Y.; Chen, G.M.; Lu, X.Q.; Zhang, X.P.; et al. The impact of Typhoon Lekima (2019) on East China: A postevent survey in Wenzhou City and Taizhou City. Front. Earth Sci. 2022, 16, 109–120. [Google Scholar] [CrossRef]
- Zhang, L.J.; Li, L.S. People-oriented emergency response mechanism-An example of the emergency work when typhoon Meranti stroked Xiamen. Int. J. Disaster Risk Reduct. 2019, 38, 101185. [Google Scholar] [CrossRef]
- Jain, D.; Singh, S. Adaptation of trips by metro rail users at two stations in extreme weather conditions: Delhi. Urban Clim. 2021, 36, 100766. [Google Scholar] [CrossRef]
- Novales, M.; Orro, A.; Pérez-López, J.B.; Feal, J.; Bugarín, M.R. Increasing Boarding Lost Time at Regular Bus Stops during Rainy Conditions: A Case Study. J. Public Transp. 2021, 23, 63–80. [Google Scholar] [CrossRef]
- Abdelaty, H.; Foda, A.; Mohamed, M. The Robustness of Battery Electric Bus Transit Networks under Charging Infrastructure Disruptions. Sustainability 2023, 15, 3642. [Google Scholar] [CrossRef]
- Li, Z.C.; Huang, J.L. How to Mitigate Traffic Congestion Based on Improved Ant Colony Algorithm: A Case Study of a Congested Old Area of a Metropolis. Sustainability 2019, 11, 1140. [Google Scholar] [CrossRef]
- Cao, N.; Cao, H.Q. Exploring the robustness of urban bus network: A case from Southern China. Chin. J. Phys. 2020, 65, 389–397. [Google Scholar] [CrossRef]
- Abdelaty, H.; Mohamed, M.; Ezzeldin, M.; El-Dakhakhni, W. Quantifying and classifying the robustness of bus transit networks. Transp. A Transp. Sci. 2020, 16, 1176–1216. [Google Scholar] [CrossRef]
- Pan, H.Y.; Zhang, W.H.; Hu, B.Y.; Liu, Z.Y.; Wang, Y.G.; Zhang, X. Construction and robustness analysis of urban weighted subway-bus composite network. J. Jilin Univ. (Eng. Technol. Ed.) 2022, 52, 2582–2591. [Google Scholar]
- GB/T 28592-2012; Grade Division of Precipitation. Standards Press of China: Beijing, China, 2012.
- Cheng, G.Z.; Mo, X.Y.; Mao, C.Y. Urban Road Traffic Safety Evaluation Method under the Condition of lce and Snow Pavement. J. Transp. Syst. Eng. Inf. Technol. 2011, 11, 130–134. [Google Scholar]
- Sun, H.Y.; Yang, J.S.; Li, L.B.; Wu, B. Research Review of the lmpacts of Adverse Weather Events on RoadTransport System. J. Transp. Inf. Saf. 2012, 30, 26–32. [Google Scholar]
- CJJ/T 119-2008; Terminology Standard for Urban Public Transport Engineering. China Building Industry Press: Beijing, China, 2008.
- GB7258-2017; Safety Technical Conditions for Motor Vehicle Operation. Standards Press of China: Beijing, China, 2017.
- Reggiani, A.; Nijkamp, P.; Lanzi, D. Transport resilience and vulnerability: The role of connectivity. Transp. Res. Part A-Policy Pract. 2015, 81, 4–15. [Google Scholar] [CrossRef]
- Lyu, S.Y. Redundancy Analysis and Optimization Design of Urban Road Network under the Influence of Rainfall. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2022. [Google Scholar]
- Hong, J.; Tamakloe, R.; Lee, S.; Park, D. Exploring the Topological Characteristics of Complex Public Transportation Networks: Focus on Variations in Both Single and Integrated Systems in the Seoul Metropolitan Area. Sustainability 2019, 11, 5404. [Google Scholar] [CrossRef]
- American Transportation Research Council. Transit Capacity and Quality of Service Manual, 3rd ed.; The National Academies Press: Washington, DC, USA, 2019. [Google Scholar]
- Ji, J.; Bie, Y.; Shi, H.; Wang, L. Energy-saving speed profile planning for a connected and automated electric bus considering motor characteristic. J. Clean. Prod. 2024, 448, 141721. [Google Scholar] [CrossRef]
- Ji, J.; Bie, Y.; Wang, L. Optimal electric bus fleet scheduling for a route with charging facility sharing. Transp. Res. Part C Emerg. Technol. 2023, 147, 104010. [Google Scholar] [CrossRef]







| Snow Intensity Grade | 12 h of Snowfall (mm) | 24 h of Snowfall (mm) |
|---|---|---|
| sporadic snow | <0.1 | <0.1 |
| light snow | 0.1–0.9 | 0.1–2.4 |
| medium snow | 1.0–2.9 | 2.5–4.9 |
| heavy snow | 3.0–5.9 | 5.0–9.9 |
| snowstorm | 6.0–9.9 | 10.0–19.9 |
| heavy snowstorm | 10.0–14.9 | 20.0–29.9 |
| severe snowstorm | ≥15.0 | ≥30.0 |
| Road | Cross-Sectional Type | Day | Night | ||
|---|---|---|---|---|---|
| Dry | Water | Dry | Snowy | ||
| Changchun Road | Four | 52.63 | 44.37 | 50.44 | 20.46 |
| Cuizhu Street | Three | 51.27 | 43.71 | 46.02 | 16.57 |
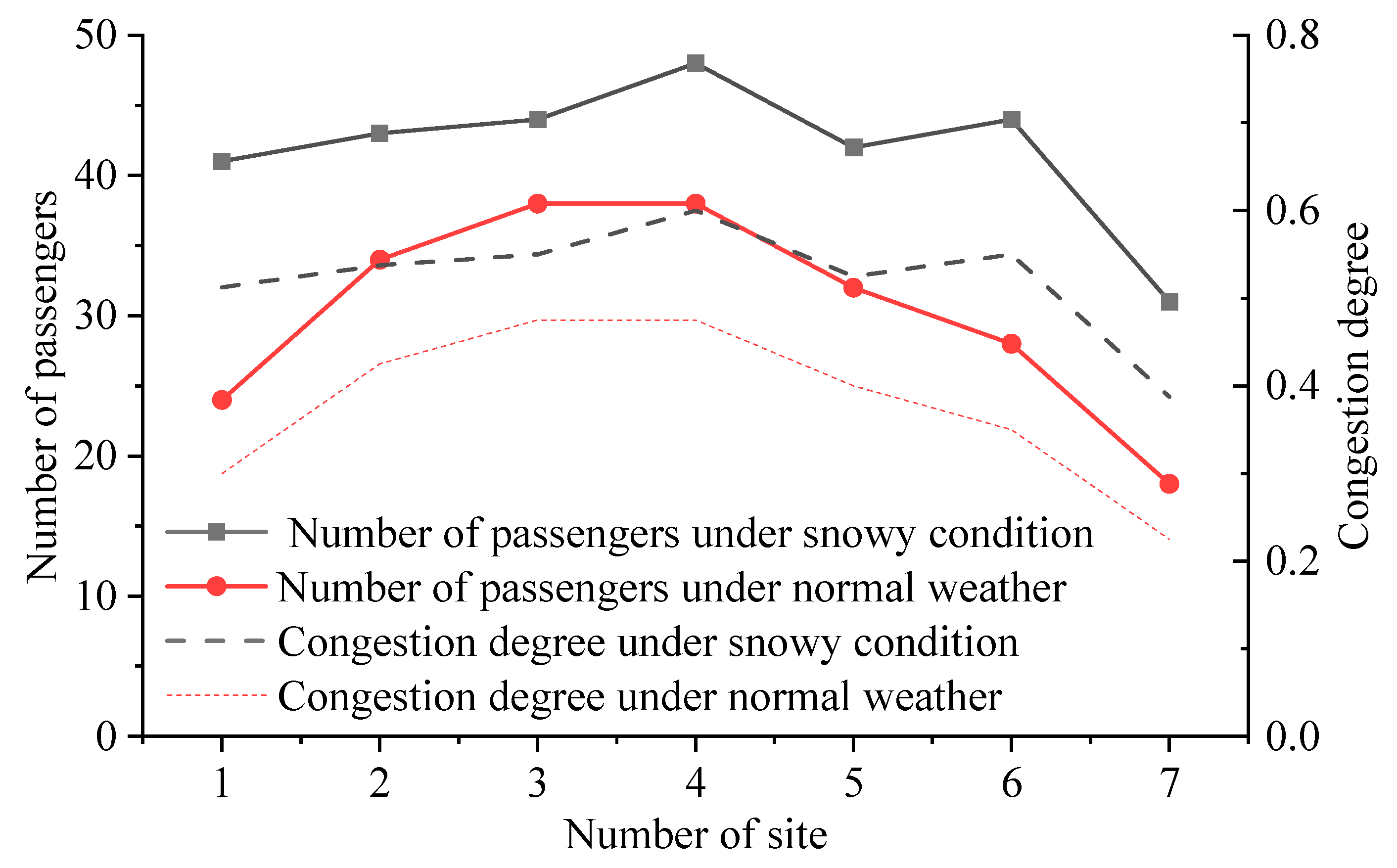
| Weather Conditions | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Mean Value |
|---|---|---|---|---|---|---|---|---|
| Normal weather | 0.3000 | 0.4250 | 0.4750 | 0.4750 | 0.4000 | 0.3500 | 0.2250 | 0.3786 |
| Snowy conditions | 0.5125 | 0.5375 | 0.5500 | 0.6000 | 0.5250 | 0.5500 | 0.3875 | 0.5232 |
| O | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | |||||||||||||||||
| 1 | 0 | 42 | 30 | 46 | 41 | 22 | 39 | 33 | 50 | 26 | 22 | 15 | 8 | 14 | 10 | 6 | |
| 2 | 42 | 0 | 14 | 25 | 24 | 14 | 26 | 23 | 48 | 34 | 37 | 32 | 23 | 46 | 42 | 30 | |
| 3 | 30 | 14 | 0 | 1 | 2 | 1 | 4 | 4 | 12 | 10 | 14 | 15 | 13 | 31 | 34 | 27 | |
| 4 | 46 | 25 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 4 | 5 | 5 | 13 | 16 | 14 | |
| 5 | 41 | 24 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 3 | 5 | 7 | 8 | 23 | 30 | 29 | |
| 6 | 22 | 14 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 4 | 6 | 7 | |
| 7 | 39 | 26 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 13 | 22 | 25 | |
| 8 | 33 | 23 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 4 | 7 | 30 | 56 | 74 | |
| 9 | 50 | 48 | 12 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 4 | 20 | 45 | 67 | |
| 10 | 26 | 34 | 10 | 2 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 3 | 6 | |
| 11 | 22 | 37 | 14 | 4 | 5 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 4 | 8 | |
| 12 | 15 | 32 | 15 | 5 | 7 | 1 | 2 | 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 13 | 8 | 23 | 13 | 5 | 8 | 1 | 3 | 7 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 14 | 14 | 46 | 31 | 13 | 23 | 4 | 13 | 30 | 20 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 15 | 10 | 42 | 34 | 16 | 30 | 6 | 22 | 56 | 45 | 3 | 4 | 0 | 0 | 0 | 0 | 0 | |
| 16 | 6 | 30 | 27 | 14 | 29 | 7 | 25 | 74 | 67 | 6 | 8 | 1 | 1 | 0 | 0 | 0 | |
| Road | Cross-Sectional Type | Day | Night | ||||
|---|---|---|---|---|---|---|---|
| Dry | Water | Snowy | Dry | Water | Snowy | ||
| Changchun Road | Four | 0.8772 | 0.7395 | 0.3570 | 0.8407 | 0.7087 | 0.3410 |
| Cuizhu Street | Three | 0.8545 | 0.7285 | 0.3050 | 0.7670 | 0.6885 | 0.2762 |
| Network Structure | Standard Speed | Speed Reduction Coefficient | Congestion Degree | Robustness | ||
|---|---|---|---|---|---|---|
| Inside Units | Outside Units | Inside Units | Outside Units | |||
| Chessboard | 0.3050 | 0.3570 | 0.6430 | 0.5930 | 0.4343 | 0.6238 |
| Ring-radial | 0.3050 | 0.3570 | 0.6430 | 0.5930 | 0.3755 | 0.6132 |
| Failure Line Number | Chessboard Network | Ring-Radial Network |
|---|---|---|
| 1 | 0.2554 | 0.1367 |
| 2 | 0.2082 | 0.0457 |
| 3 | 0.3699 | 0.1625 |
| 4 | 0.2449 | 0.0902 |
| 5 | 0.4332 | 0.4996 |
| 6 | 0.1550 | 0.0731 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Su, B.; Chen, Z. Generalized-Norm-Based Robustness Evaluation Model of Bus Network under Snowy Weather. Sustainability 2024, 16, 5260. https://doi.org/10.3390/su16125260
Yan Y, Su B, Chen Z. Generalized-Norm-Based Robustness Evaluation Model of Bus Network under Snowy Weather. Sustainability. 2024; 16(12):5260. https://doi.org/10.3390/su16125260
Chicago/Turabian StyleYan, Yadan, Bohui Su, and Zhiju Chen. 2024. "Generalized-Norm-Based Robustness Evaluation Model of Bus Network under Snowy Weather" Sustainability 16, no. 12: 5260. https://doi.org/10.3390/su16125260
APA StyleYan, Y., Su, B., & Chen, Z. (2024). Generalized-Norm-Based Robustness Evaluation Model of Bus Network under Snowy Weather. Sustainability, 16(12), 5260. https://doi.org/10.3390/su16125260






