A Performance and Data-Driven Method for Optimization of Traditional Courtyards
Abstract
:1. Introduction
1.1. Previous Studies on Energy Consumption and Comfort in Traditional Villages of Cold Regions
1.2. Introduction to Performance and Data-Driven Design
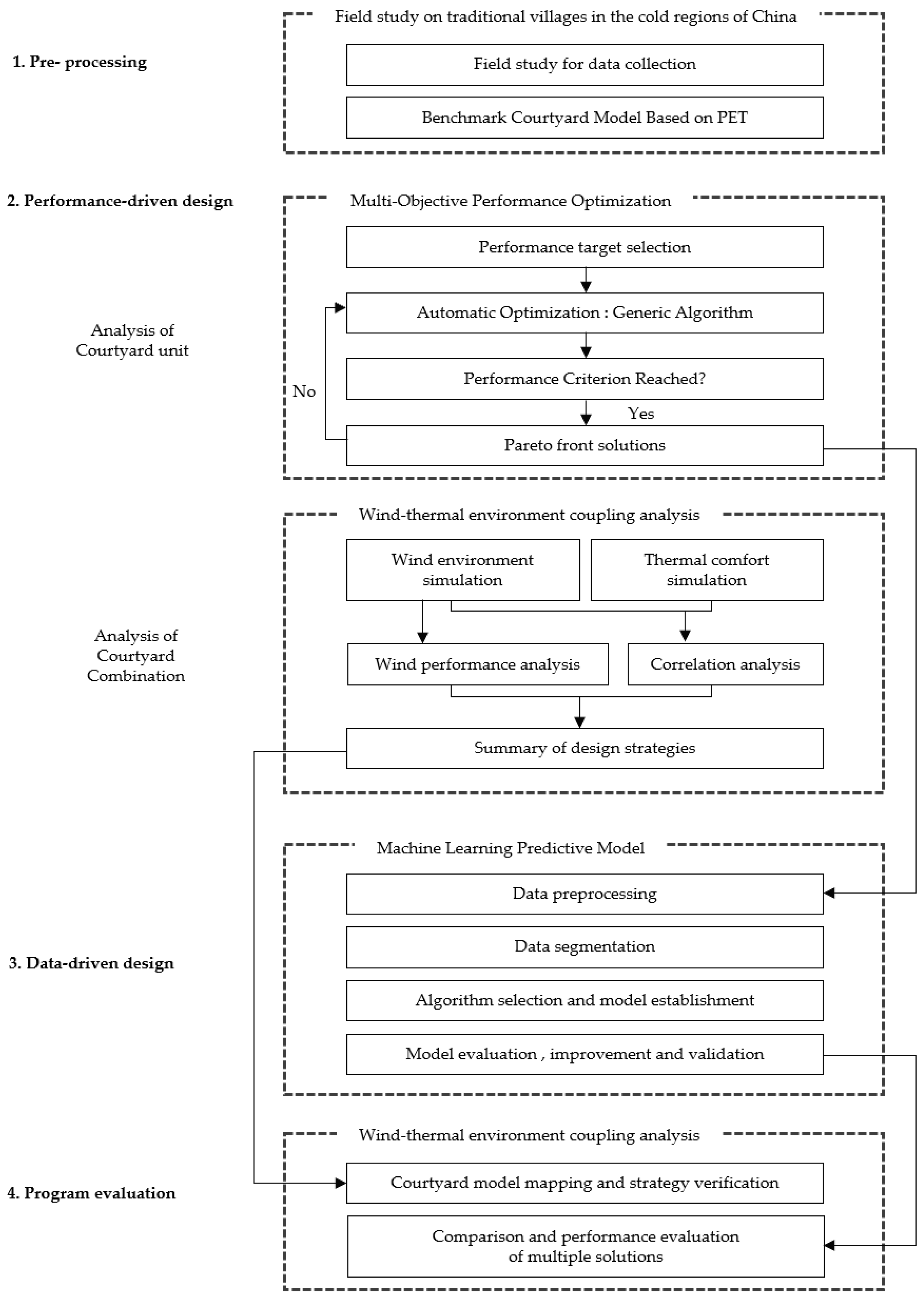
1.3. Overview Workflow
- (1)
- Pre-processing: A baseline courtyard model is selected based on the simulation and ranking of PET values for various courtyard types.
- (2)
- Performance-driven design: This stage consists of two parts: analysis of courtyard units and courtyard combinations. The former involves detailed adjustments to the baseline courtyard model through performance-based multi-objective optimization, generating a dataset for the next stage’s machine learning. The latter extracts design strategies for courtyard combinations from the perspective of wind efficiency based on a correlation analysis of wind and thermal environments. Together, these form the courtyard design strategies.
- (3)
- Data-driven design: The dataset from the courtyard unit analysis is input into the Sci-kit learn 1.3 software and trained using the XGBoost algorithm to develop a predictive model for courtyard performance.
- (4)
- Program evaluation: The baseline model and design strategies from the previous steps are applied to the project design, generating multiple plans based on design requirements. The parameter information of each scheme is then input into the algorithm model obtained in the third step for performance evaluation, allowing the selection of the optimal scheme in terms of performance.
2. Pre-Processing: Study Areas and Data Sources
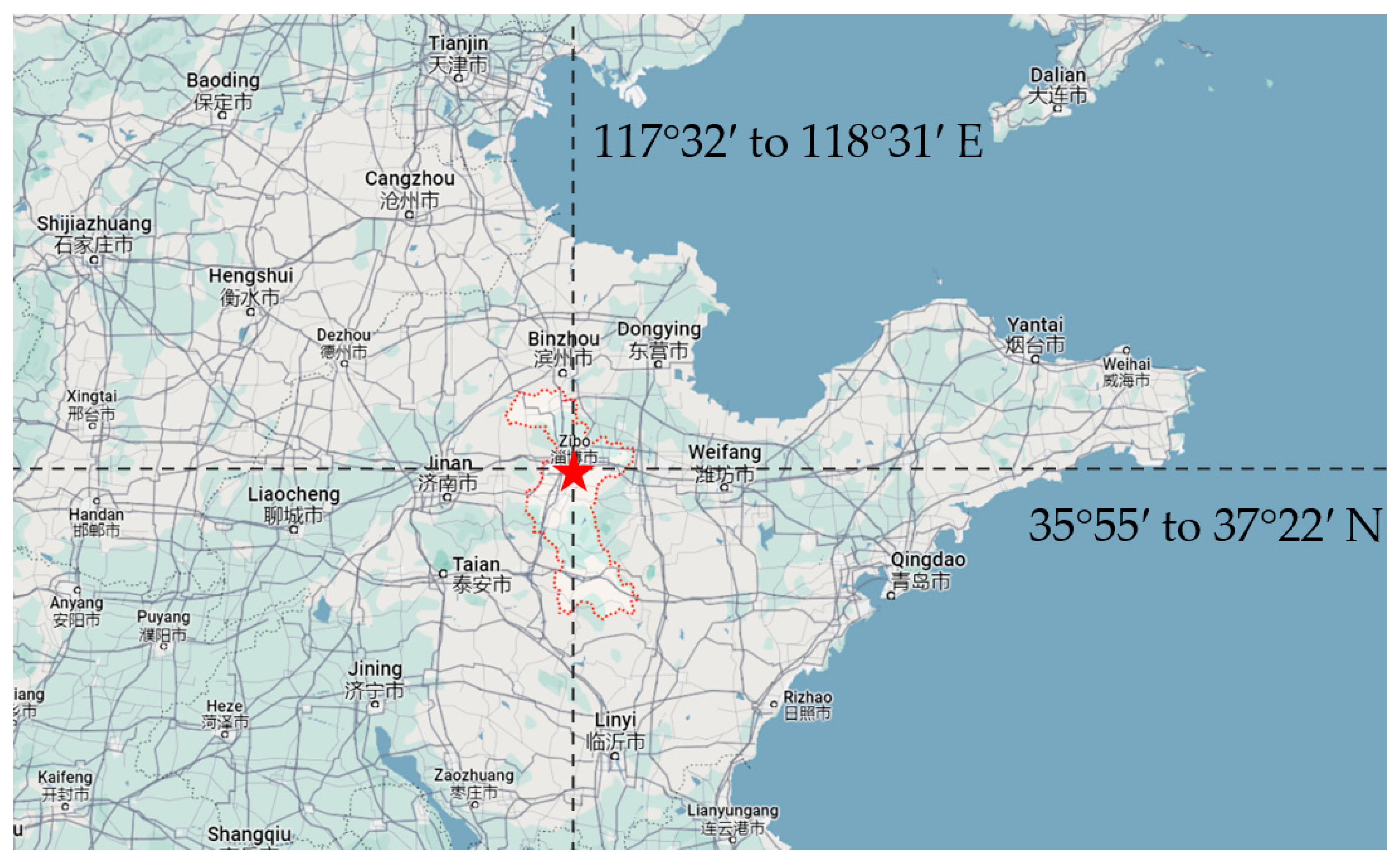
2.1. Field Study of Traditional Villages in Cold Regions of China
2.1.1. Study Areas
2.1.2. Microclimate Measurement and Validation
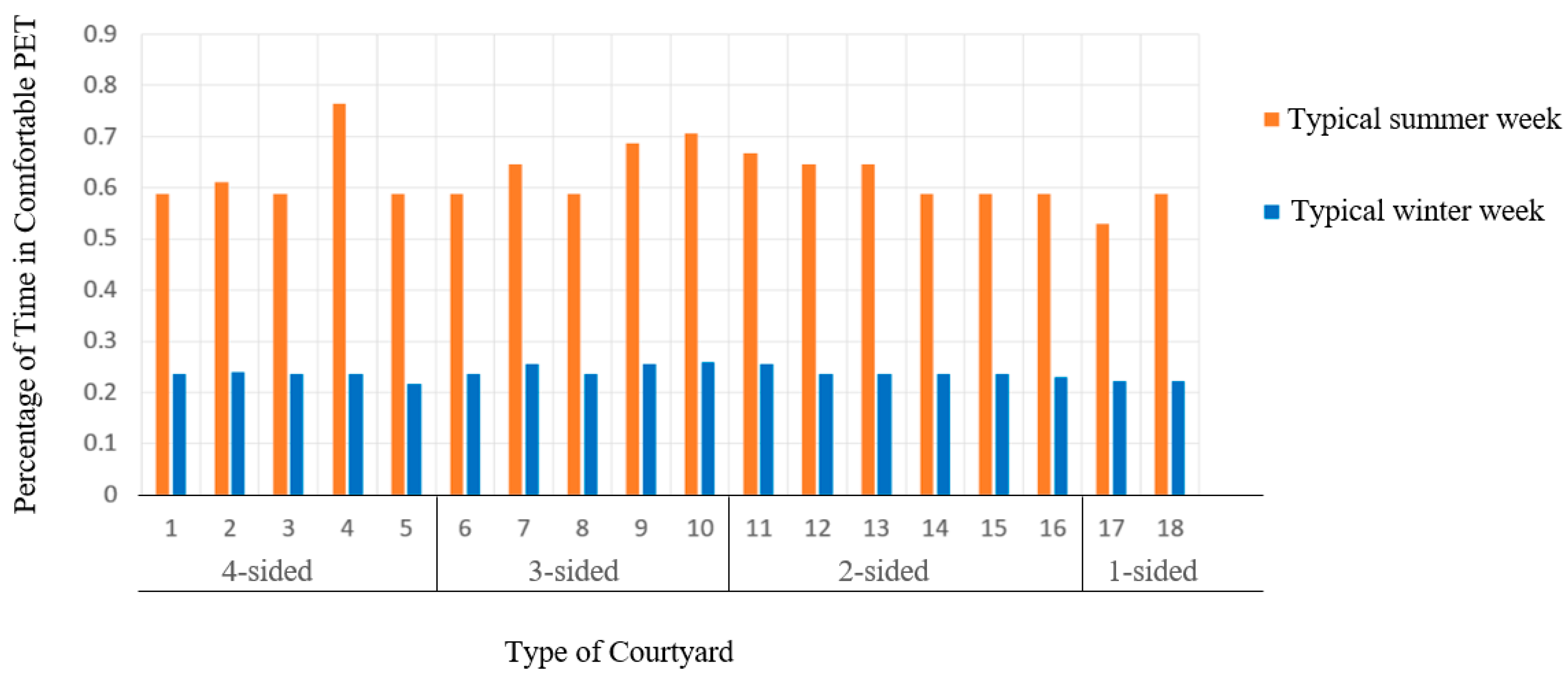
2.2. Baseline Courtyard Model Based on PET
3. Research Process
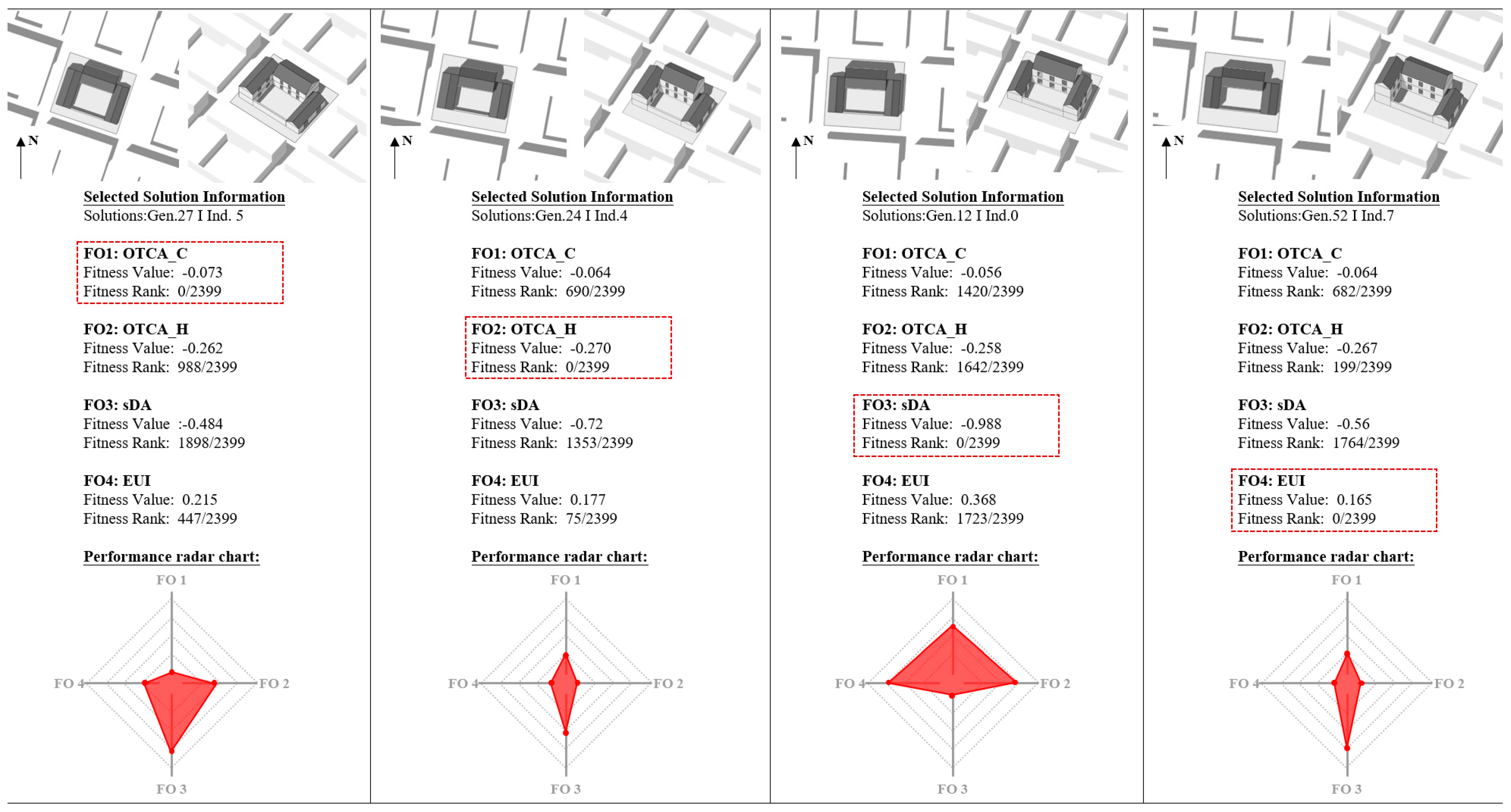
3.1. Multi-Objective Performance Optimization
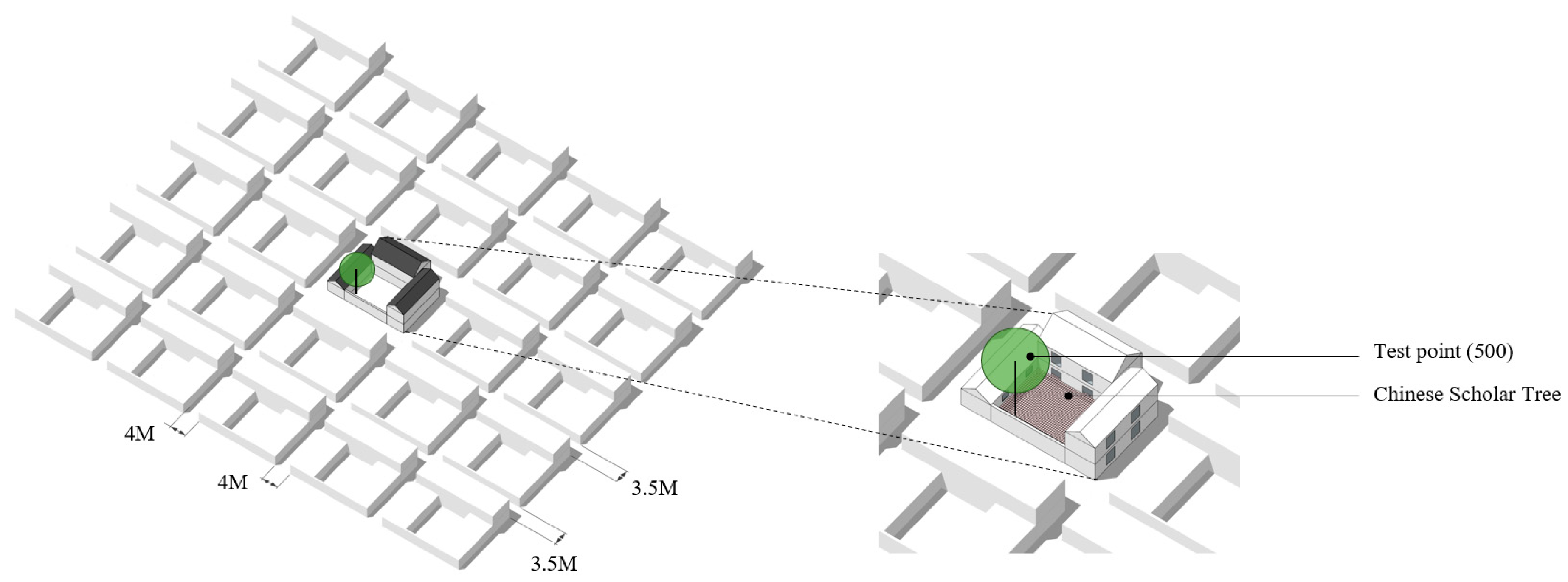
3.1.1. Baseline Model and Site Environment Settings
3.1.2. Performance Objective Selection
- (1)
- Courtyard width refers to the length of the courtyard in the east-west direction. Based on the surveyed courtyard areas in the village, the courtyard area is set at 120 m2, with the base area of each of the three buildings within the courtyard set at 60 m2. This way, once the courtyard width is determined, all the planar parameters of the courtyard are set.
- (2)
- Standard floor height refers to the floor height of each building within the courtyard, with a range of [2.7, 4.0] m. To simplify calculations, Height_N, Height_E, and Height_W represent the heights of the main building to the north, the secondary building to the east, and the secondary building to the west, respectively. This metric is related to secondary-house floor control.
- (3)
- Orientation refers to the courtyard’s angle based on the orientation of the main building to the north. From preliminary research and experience, aside from significant deviations due to terrain, the courtyard angle in cold regions typically does not exceed ±45°.
- (4)
- Secondary-house floor control refers to the number of floors of the secondary buildings within the courtyard. An input value of “−1” indicates both secondary houses have one floor; “0” indicates the left secondary house has one floor and the right one has two floors; “1” indicates the left secondary house has two floors and the right one has one floor. In cold regions, the main building to the north generally has the highest number of floors to shield against winter winds. Given the small space needs of a courtyard typically housing 3 to 5 people, usually only one secondary house has two floors, so the secondary-house floor control only considers these three scenarios.
- (5)
- Window-to-wall ratio (WWR) refers to the ratio of window area to wall area. To simplify calculations and improve efficiency, the same WWR is set for the upper and lower sides of a building. Additionally, since the indoor energy consumption simulation is conducted under steady-state air conditioning conditions, door openings are not considered. The WWR settings for the three buildings in the courtyard are as follows: W_N and W_S refer to the WWR for the north and south sides of the main building; W_W1 and W_E1 refer to the WWR for the west and east sides of the left secondary house; and W_W2 and W_E2 refer to the right secondary house. Considering the characteristics of local traditional dwellings, courtyard buildings typically have fewer windows on the sides, so no side windows are included in this study.
3.1.3. Generate Design Parameter Settings and Simulation
3.2. Wind-Thermal Environment Coupling Analysis
3.2.1. Parametric Settings
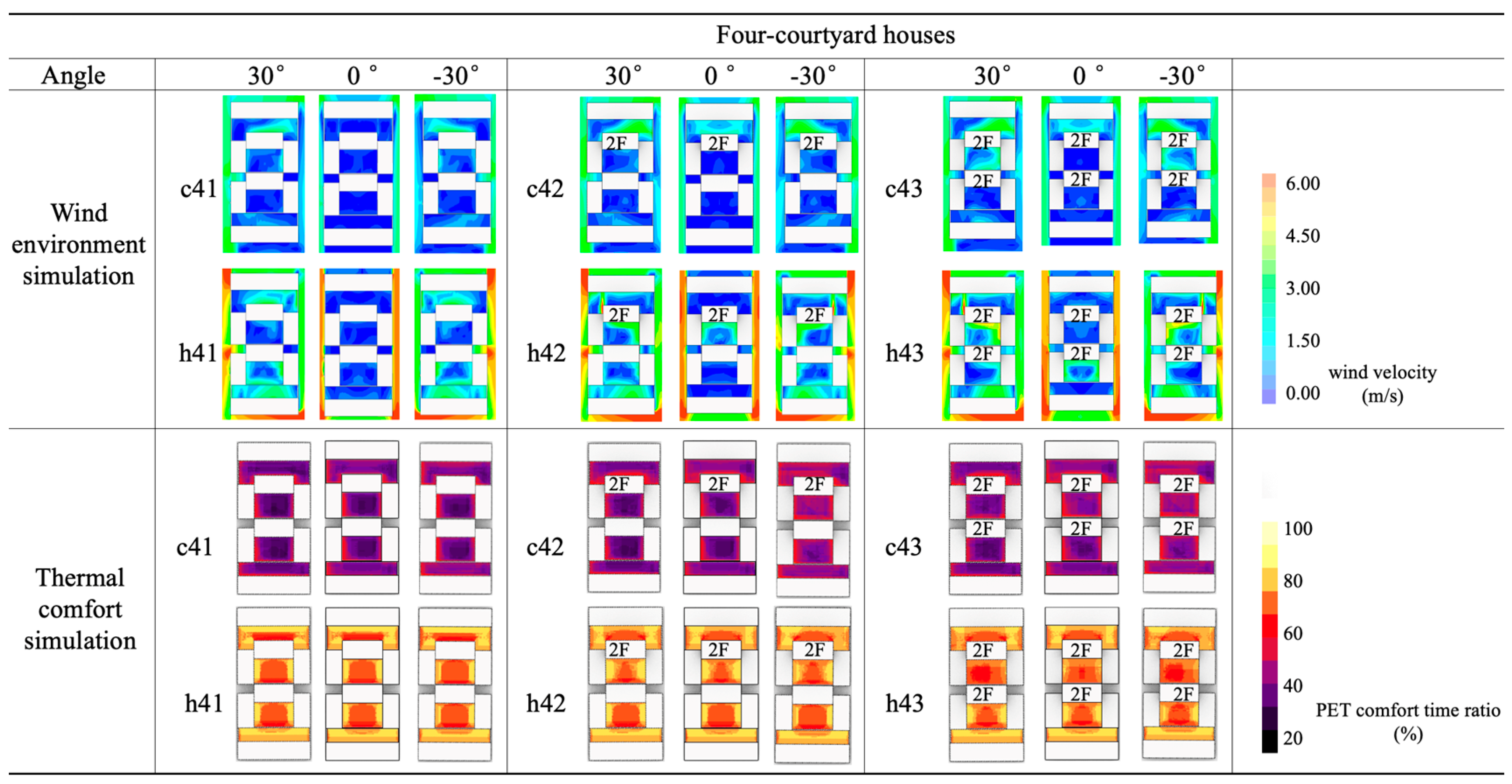
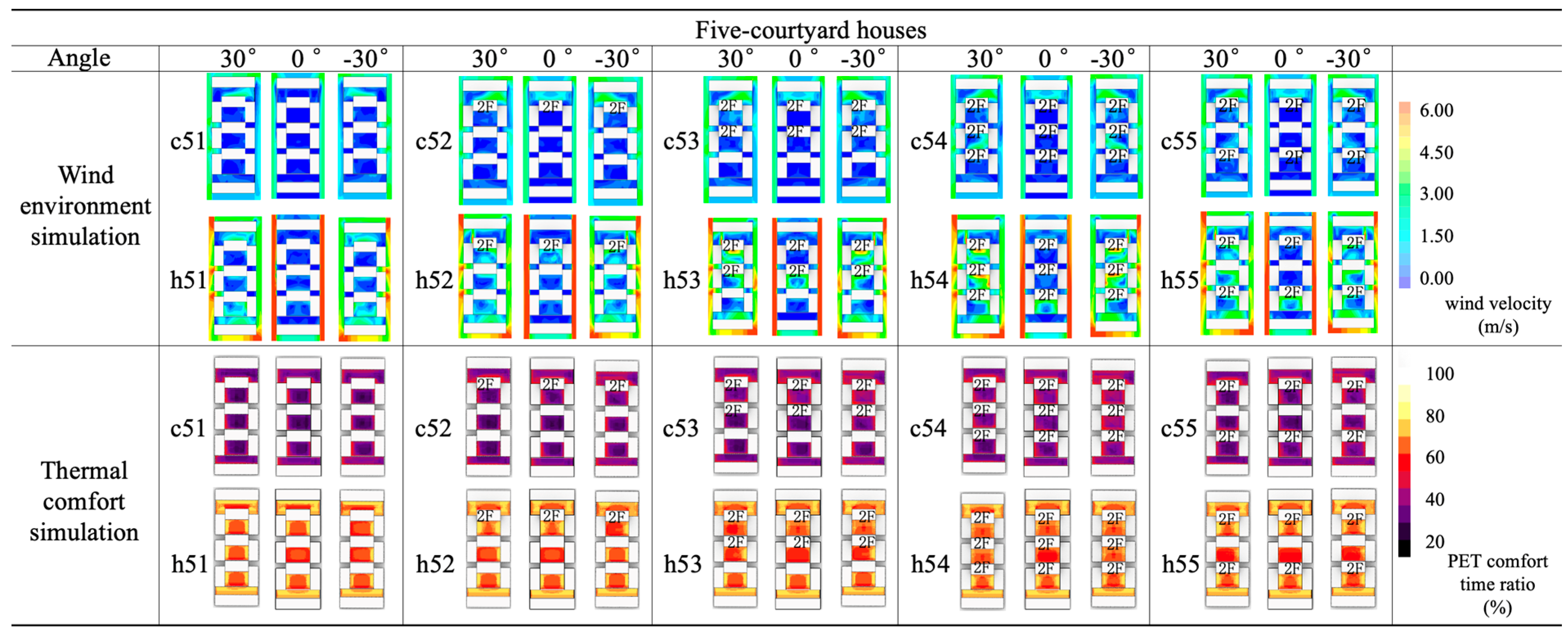
3.2.2. Wind-Thermal Environment Simulation
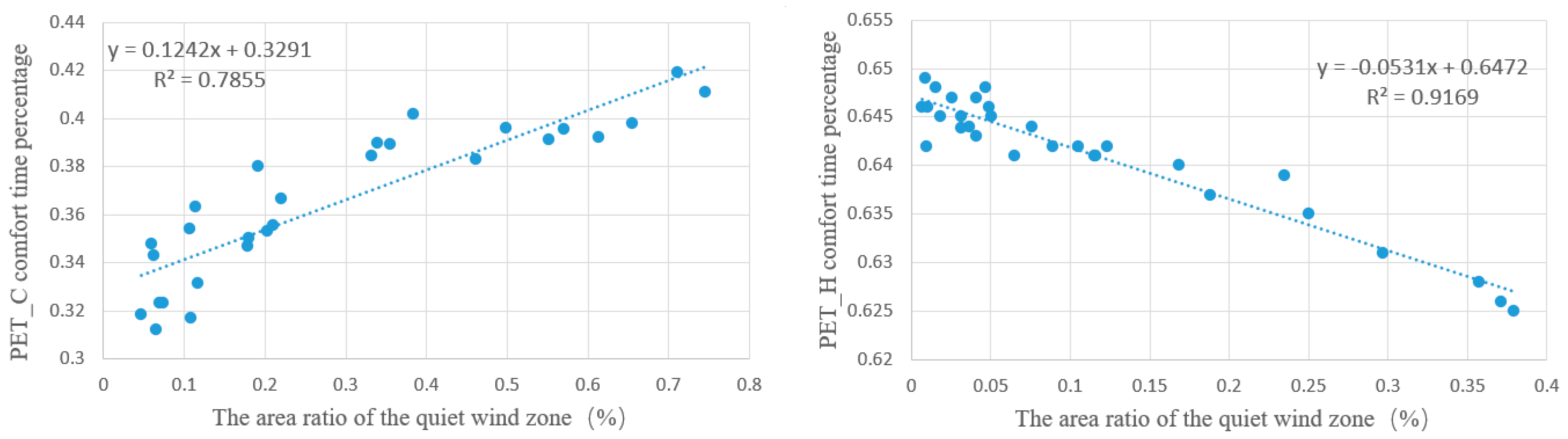
3.2.3. Correlation Analysis
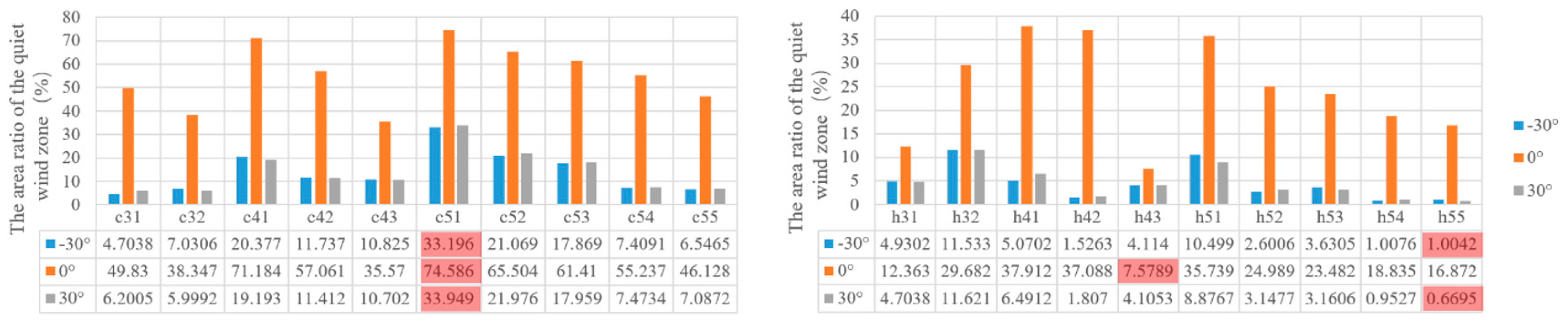
3.2.4. Wind Performance Analysis
- (1)
- Vertical Layout: In winter, local building heightening has a limited impact on improving the regional climate. However, a staggered arrangement of taller buildings from south to north (h55) in summer enhances overall climate conditions and promotes air circulation.
- (2)
- Horizontal Layout: Increasing spatial depth weakens the correlation with overall microclimate conditions. Stacking the same courtyard type generally reduces wind speed, but increasing building height vertically can offset this effect.
- (3)
- Courtyard Combination: From the perspective of overall wind environment comfort, the three-courtyard house is optimal for summer heat insulation and winter wind protection. This aligns with previous research indicating that traditional villages predominantly feature single-courtyard houses with few multi-courtyard layouts, especially in mountainous areas.
3.3. Machine Learning Predictive Model
3.3.1. Data Preprocessing
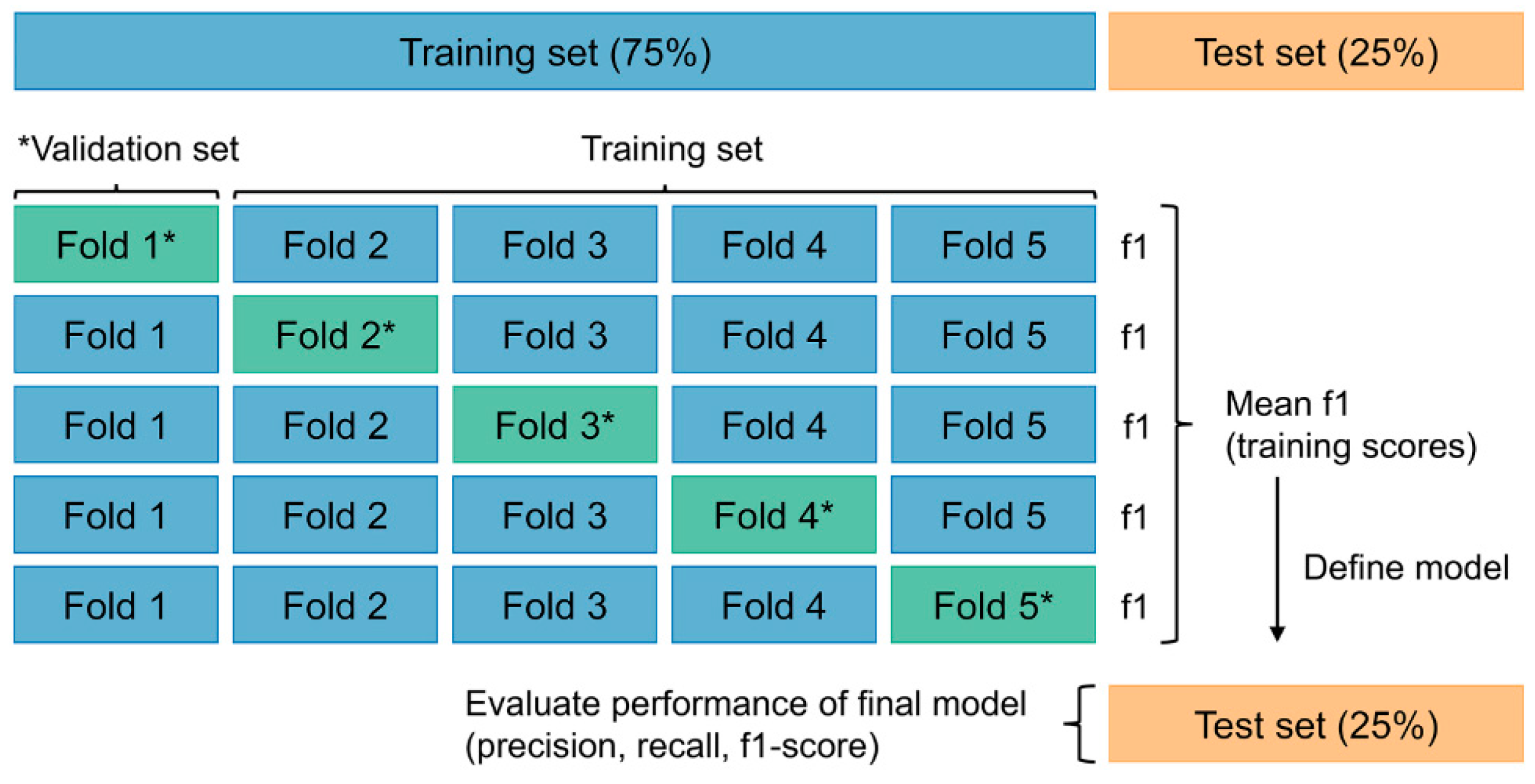
3.3.2. Data Segmentation
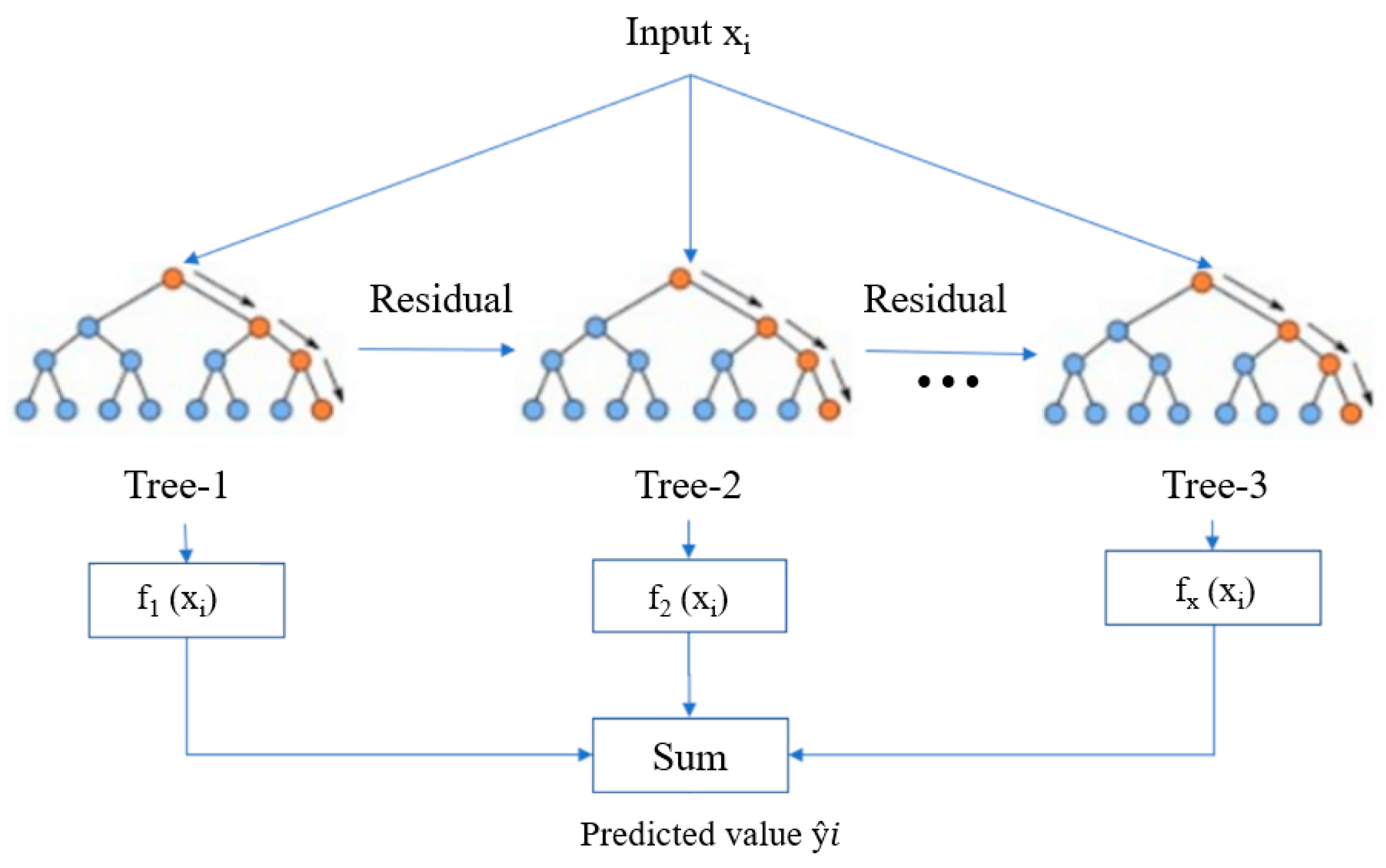
3.3.3. Algorithm Selection and Model Establishment
3.3.4. Model Evaluation, Improvement, and Validation
4. Results: Program Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pata, U.K. Linking renewable energy, globalization, agriculture, CO2 emissions and ecological footprint in BRIC countries: A sustainability perspective. Renew. Energy 2021, 173, 197–208. [Google Scholar] [CrossRef]
- Cao, X.; Dai, X.; Liu, J. Building energy-consumption status worldwide and the state-of-the-art technologies for zero-energy buildings during the past decade. Energy Build. 2016, 128, 198–213. [Google Scholar] [CrossRef]
- Chen, M.; Liu, W.; Tao, X. Evolution and assessment on China’s urbanization 1960–2010: Under-urbanization or over-urbanization? Habitat. Int. 2013, 38, 25–33. [Google Scholar] [CrossRef]
- Long, H.; Zou, J.; Pykett, J.; Li, Y. Analysis of rural transformation development in China since the turn of the new millennium. Appl. Geogr. 2011, 31, 1094–1105. [Google Scholar] [CrossRef]
- Wang, X.R.; Hui, E.C.M.; Choguill, C.; Jia, S.H. The new urbanization policy in China: Which way forward? Habitat. Int. 2015, 47, 279–284. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhang, J.; Yan, Y.; Sun, S.; Xu, X.; Higueras, E. Effect of the spatial form of Jiangnan traditional villages on microclimate and human comfort. Sustain. Cities Soc. 2022, 87, 104136. [Google Scholar] [CrossRef]
- Lyu, Y.; Zhang, L.; Liu, X.; Ma, X. Microclimate-Adaptive Morphological Parametric Design of Streets and Alleys in Traditional Villages. Buildings 2024, 14, 152. [Google Scholar] [CrossRef]
- Zang, H.Y.; Hsieh, C.M.; Cang, Y.; Gu, M. Microclimate adaptability analysis of waterfront traditional villages: A case study of Mingyuewan Village in Suzhou. J. Water Clim. Chang. 2023, 14, 3329–3344. [Google Scholar] [CrossRef]
- Sun, M.; Xue, Y.; Wang, L. Research on Optimized Design of Rural Housing in Cold Regions Based on Parametrization and Machine Learning. Sustainability 2024, 16, 667. [Google Scholar] [CrossRef]
- Zhu, L.; Liao, H.; Hou, B.; Cheng, L.; Li, H. The status of household heating in northern China: A field survey in towns and villages. Environ. Sci. Pollut. Res. 2020, 27, 16145–16158. [Google Scholar] [CrossRef]
- Jin, H.; Ling, W. External wall structure of green rural houses in Daqing, China, based on life cycle and ecological footprint theories. Front. Arch. Res. 2015, 4, 212–219. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, B.; Sun, Y. Multi-objective optimization for energy consumption, daylighting and thermal comfort performance of rural tourism buildings in north China. Build. Environ. 2020, 176, 106841. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, D.; He, B.J.; Wang, Q.; Yu, H.; Ma, W.; Jin, G. Evaluating potentials of passive solar heating renovation for the energy poverty alleviation of plateau areas in developing countries: A case study in rural Qinghai-Tibet Plateau, China. Sol. Energy 2019, 187, 95–107. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, M.; Li, Y.Z.; Li, C. Numerical investigation on the impact of an on-top sunspace passive heating approach for typical rural buildings in northern China. Sol. Energy 2019, 186, 300–310. [Google Scholar] [CrossRef]
- Li, D.; Zhang, C.; Li, Q.; Liu, C.; Arıcı, M.; Wu, Y. Thermal performance evaluation of glass window combining silica aerogels and phase change materials for cold climate of China. Appl. Therm. Eng. 2020, 165, 114547. [Google Scholar] [CrossRef]
- Martinelli, L.; Matzarakis, A. Influence of height/width proportions on the thermal comfort of courtyard typology for Italian climate zones. Sustain. Cities Soc. 2017, 29, 97–106. [Google Scholar] [CrossRef]
- Andreou, E. The effect of urban layout, street geometry and orientation on shading conditions in urban canyons in the Mediterranean. Renew. Energy 2014, 63, 587–596. [Google Scholar] [CrossRef]
- Taleghani, M.; Tenpierik, M.; van den Dobbelsteen, A. Indoor thermal comfort in urban courtyard block dwellings in the Netherlands. Build. Environ. 2014, 82, 566–579. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, G.; Wang, Y.; Zhou, H.; Ma, L. A quantitative analysis of the impact of residential cluster layout on building heating energy consumption in cold IIB regions of China. Energy Build. 2021, 253, 111515. [Google Scholar] [CrossRef]
- Chatzipoulka, C.; Compagnon, R.; Kaempf, J.; Nikolopoulou, M. Sky view factor as predictor of solar availability on building façades. Sol. Energy 2018, 170, 1026–1038. [Google Scholar] [CrossRef]
- Röck, M.; Hollberg, A.; Habert, G.; Passer, A. LCA and BIM: Visualization of environmental potentials in building construction at early design stages. Build. Environ. 2018, 140, 153–161. [Google Scholar] [CrossRef]
- Leatherbarrow, D. Architecture Oriented Otherwise, 1st ed.; Princeton Architectural Press: New York, NY, USA, 2009. [Google Scholar]
- Negroponte, N. The architecture machine. Comput. Aided Des. 1975, 7, 190–195. [Google Scholar] [CrossRef]
- Xiao, T.; Sheng, L.; Zhang, S.; Zheng, L.; Shui, T. Thermal Comfort Improvement Strategies for Outdoor Spaces in Traditional Villages Based on ENVI-Met: Shimengao Village in Chizhou City. Sustainability 2023, 15, 11785. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, L.; Pang, Y. Analysis on climate adaptability of traditional villages in Lingnan, China–World Cultural Heritage Site of Majianglong Villages as example. Procedia Eng. 2017, 205, 2011–2018. [Google Scholar] [CrossRef]
- Yao, X.; Han, S.; Dewancker, B. Wind environment simulation accuracy in traditional villages with complex layouts based on CFD. Int. J. Environ. Res. Public Health 2021, 18, 8644. [Google Scholar] [CrossRef]
- Molake, A.; Zhang, R.; Zhou, Y. Multi-Objective Optimization of Daylight Performance and Thermal Comfort of Enclosed-Courtyard Rural Residence in a Cold Climate Zone, China. Sustainability 2023, 15, 7953. [Google Scholar] [CrossRef]
- Xi, H.; Gao, H.; Hou, W.; Yin, B.; Zuo, J.; Zhao, H. Multi-Objective Optimization for Winter Heating Retrofit in Rural Houses of Cold Regions: A Case Study in the Wusu Area. Appl. Sci. 2024, 14, 3760. [Google Scholar] [CrossRef]
- Reynolds, P.; Pavic, A.; Ibrahim, Z. A remote monitoring system for stadia dynamics. Proc. Inst. Civ. Eng.-Struct. Build. 2004, 157, 385–393. [Google Scholar] [CrossRef]
- Bouyer, J.; Vinet, J.; Delpech, P.; Carré, S. Thermal comfort assessment in semi-outdoor environments: Application to comfort study in stadia. J. Wind Eng. Ind. Aerod. 2007, 95, 963–976. [Google Scholar] [CrossRef]
- Haghighat, E.; Juanes, R. SciANN: A Keras/TensorFlow wrapper for scientific computations and physics-informed deep learning using artificial neural networks. Comput. Methods Appl. Mech. Eng. 2021, 373, 113552. [Google Scholar] [CrossRef]
- Li, Q.; Yang, Y.; Guo, Y.; Li, W.; Liu, Y.; Liu, H.; Kang, Y. Performance evaluation of deep learning classification network for image features. IEEE Access 2021, 9, 9318–9333. [Google Scholar] [CrossRef]
- Satrio, P.; Mahlia, T.M.I.; Giannetti, N.; Saito, K. Optimization of HVAC system energy consumption in a building using artificial neural network and multi-objective genetic algorithm. Sustain. Energy Technol. Assess. 2019, 35, 48–57. [Google Scholar]
- Cannistraro, G.; Cannistraro, M.; Restivo, R. The local media radiant temperature for the calculation of comfort in areas characterized by radiant surfaces. Int. J. Heat Technol. 2015, 33, 115–122. [Google Scholar] [CrossRef]
- Cannistraro, M.; Trancossi, M. Enhancement of indoor comfort in the presence of large glazed radiant surfaces by a local heat pump system based on Peltier cells. Therm. Sci. Eng. Prog. 2019, 14, 100388. [Google Scholar] [CrossRef]
- Jović, S.; Arsić, N.; Vilimonović, J.; Petković, D. Thermal sensation prediction by soft computing methodology. J. Therm. Biol. 2016, 62, 106–108. [Google Scholar] [CrossRef]
- Yan, H.; Yan, K.; Ji, G. Optimization and prediction in the early design stage of office buildings using genetic and XGBoost algorithms. Build. Environ. 2022, 218, 109081. [Google Scholar] [CrossRef]
- Mi, J.; Hong, B.; Zhang, T.; Huang, B.; Niu, J. Outdoor thermal benchmarks and their application to climate–responsive designs of residential open spaces in a cold region of China. Build. Environ. 2020, 169, 106592. [Google Scholar] [CrossRef]
- Yuan, T.; Hong, B.; Qu, H.; Liu, A.; Zheng, Y. Outdoor thermal comfort in urban and rural open spaces: A comparative study in China’s cold region. Urban Clim. 2023, 49, 101501. [Google Scholar] [CrossRef]
- GB/T50034-2024; Standard for Lighting Design of Buildings. China Architecture & Building Press: Beijing, China, 2024.
- Albadr, M.A.; Tiun, S.; Ayob, M.; Al-Dhief, F. Genetic algorithm based on natural selection theory for optimization problems. Symmetry 2020, 12, 1758. [Google Scholar] [CrossRef]
- Hashempour, N.; Taherkhani, R.; Mahdikhani, M. Energy performance optimization of existing buildings: A literature review. Sustain. Cities Soc. 2020, 54, 101967. [Google Scholar] [CrossRef]
- Kiss, B.; Szalay, Z. Modular approach to multi-objective environmental optimization of buildings. Automat. Constr. 2020, 111, 103044. [Google Scholar] [CrossRef]
- Sijgers, L.; Sorensen, T.; Soulby, A.; Boyle, P.; Dalbert, A.; Röösli, C.; Jablonski, G.E.; Hamacher, V.; Greisiger, R.; Jiang, D.; et al. Classification of Acoustic Hearing Preservation After Cochlear Implantation Using Electrocochleography. Trends Hear. 2023, 27, 23312165231220997. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Mo, H.; Sun, H.; Liu, J.; Wei, S. Developing window behavior models for residential buildings using XGBoost algorithm. Energy Build. 2019, 205, 109564. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Wu, L.; Zhou, H.; Zhang, F.; Yu, X.; Lu, X.; Xiang, Y. Comparison of Support Vector Machine and Extreme Gradient Boosting for predicting daily global solar radiation using temperature and precipitation in humid subtropical climates: A case study in China. Energy Convers. Manag. 2018, 164, 102–111. [Google Scholar] [CrossRef]
- Wang, W.; Chakraborty, G.; Chakraborty, B. Predicting the risk of chronic kidney disease (ckd) using machine learning algorithm. Appl. Sci. 2020, 11, 202. [Google Scholar] [CrossRef]
- Pan, S.; Zheng, Z.; Guo, Z.; Luo, H. An optimized XGBoost method for predicting reservoir porosity using petrophysical logs. J. Pet. Sci. Eng. 2022, 208, 109520. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef]
- Teshnehdel, S.; Mirnezami, S.; Saber, A.; Pourzangbar, A.; Olabi, A.G. Data-driven and numerical approaches to predict thermal comfort in traditional courtyards. Sustain. Energy Technol. Assess. 2020, 37, 100569. [Google Scholar] [CrossRef]
- Wang, W.; Liu, K.; Zhang, M.; Shen, Y.; Jing, R.; Xu, X. From simulation to data-driven approach: A framework of integrating urban morphology to low-energy urban design. Renew. Energy 2021, 179, 2016–2035. [Google Scholar] [CrossRef]
- Cheng, F.; Cui, C.; Cai, W.; Zhang, X.; Ge, Y.; Li, B. A novel data-driven air balancing method with energy-saving constraint strategy to minimize the energy consumption of ventilation system. Energy 2022, 239, 122146. [Google Scholar] [CrossRef]
- Yang, S.; Yu, J.; Gao, Z.; Zhao, A. Energy-saving optimization of air-conditioning water system based on data-driven and improved parallel artificial immune system algorithm. Energy Convers. Manag. 2023, 283, 116902. [Google Scholar] [CrossRef]
- Tahmasebi, F.; Mahdavi, A. An inquiry into the reliability of window operation models in building performance simulation. Build. Environ. 2016, 105, 343–357. [Google Scholar] [CrossRef]
- Jannat, N.; Hussien, A.; Abdullah, B.; Cotgrave, A. A comparative simulation study of the thermal performances of the building envelope wall materials in the tropics. Sustainability 2022, 12, 4892. [Google Scholar] [CrossRef]


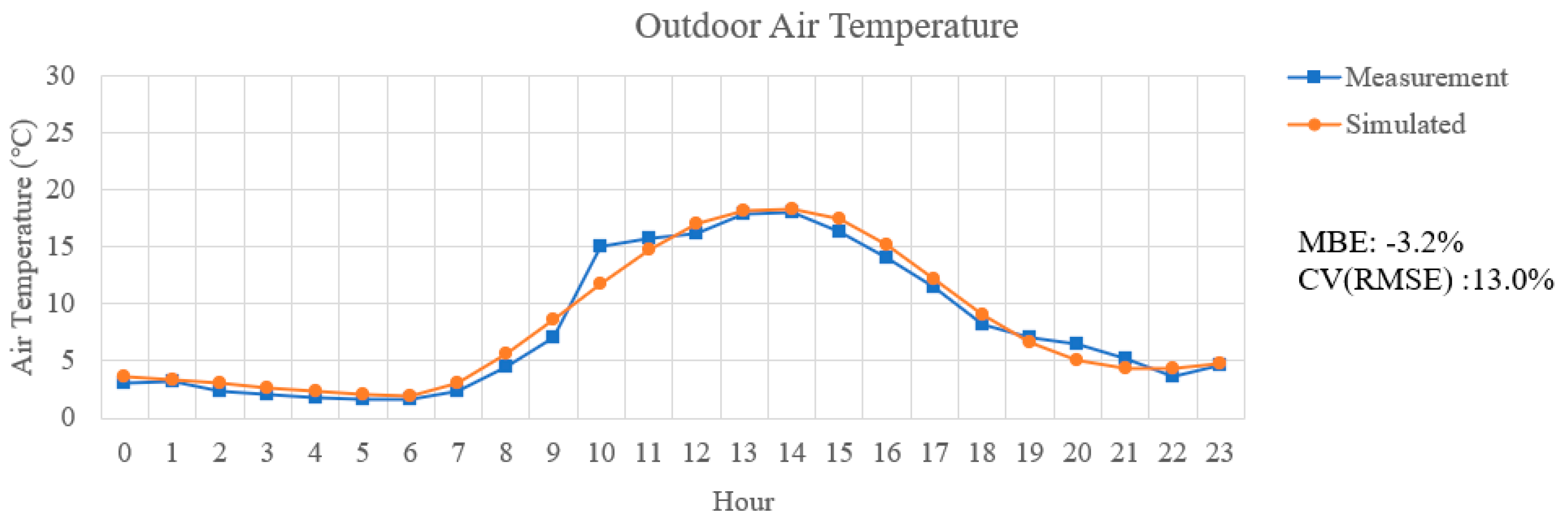
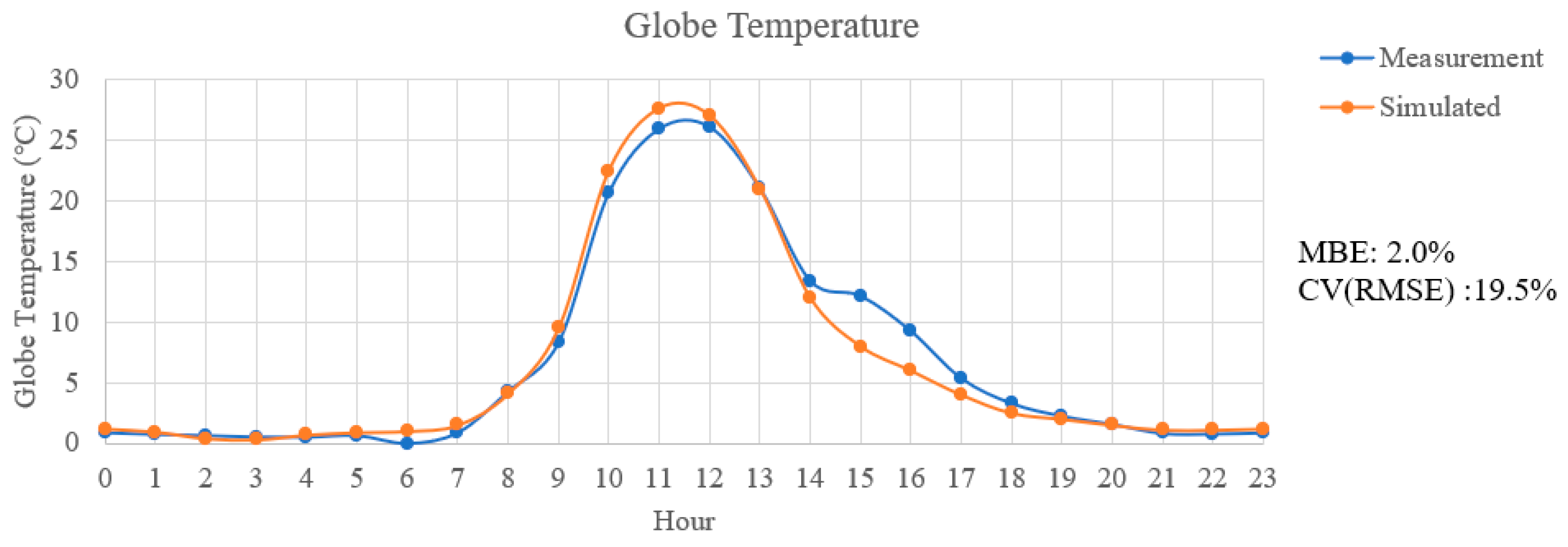

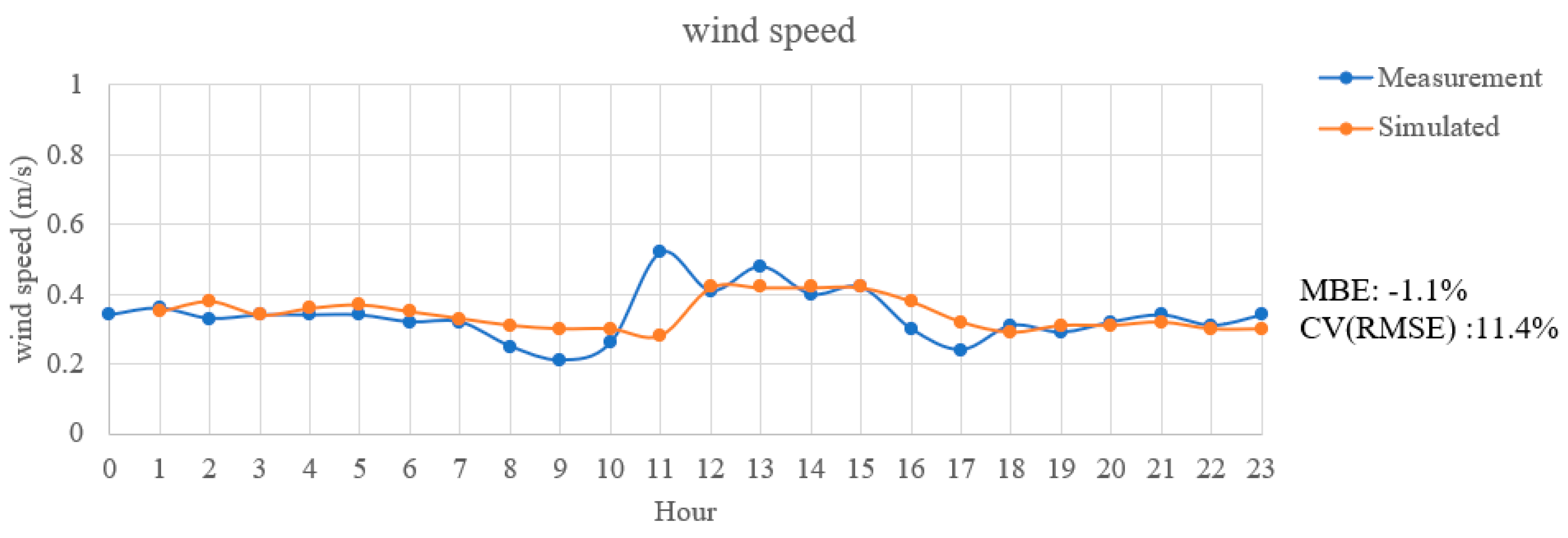






| Standard/Guideline | Hourly Criteria | |
|---|---|---|
| MBE (%) | CV(RMSE) (%) | |
| ASHARE Guideline 14 | 10 | 30 |
| IPMVP | 5 | 20 |
| FEMP | 10 | 30 |
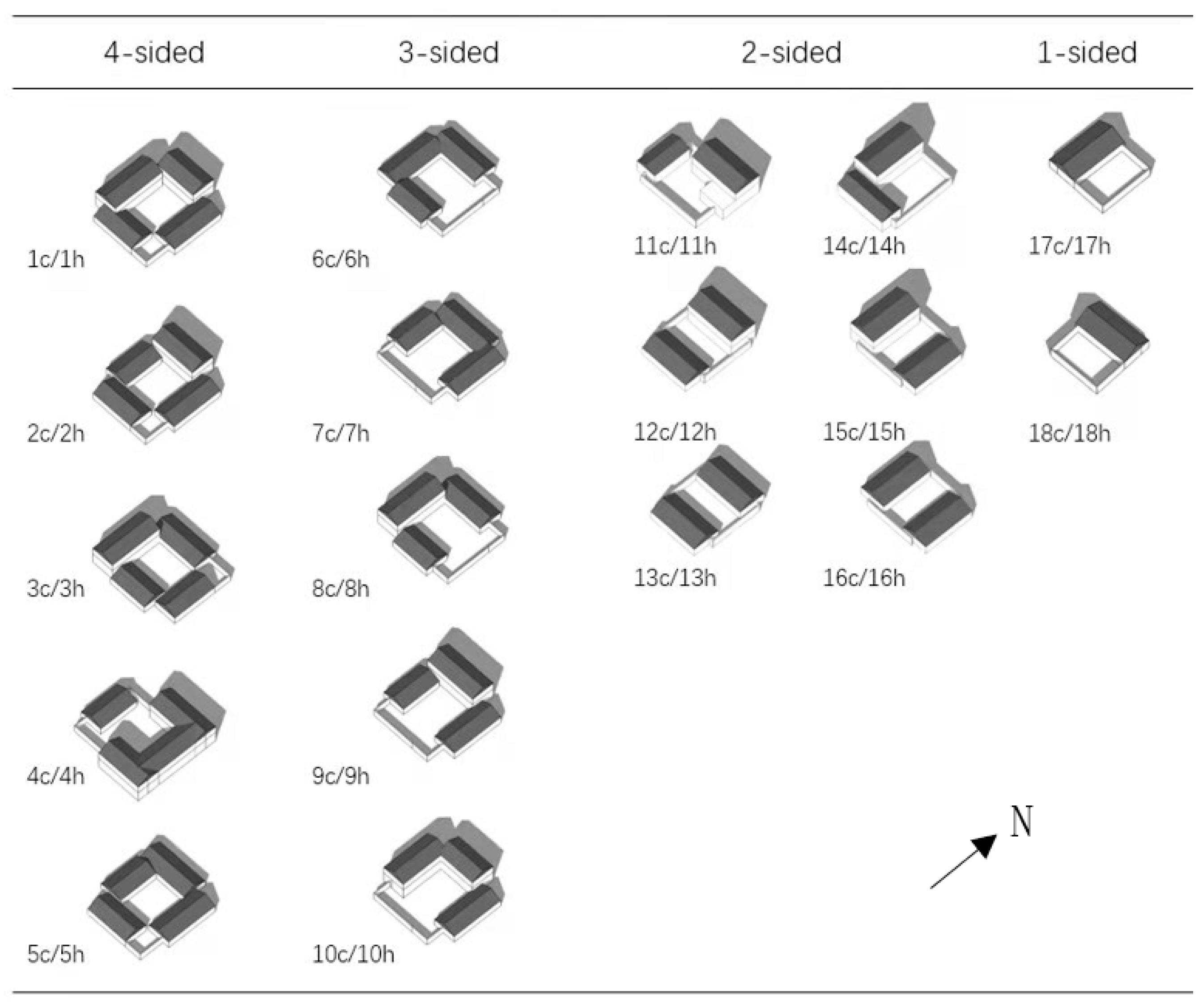
| Classification | No. | Orientation | Courtyard Location | No. Floors of the Main House | Category Code ** | Total Categories | |
|---|---|---|---|---|---|---|---|
| Traditional Courtyards (34) | 4-sided | 3 | North-south | Central | 2 * | 1c/1h | 18 |
| 2 | 2c/2h | ||||||
| 1 | 5c/5h | ||||||
| East-west | Central | 2 * | 4c/4h | ||||
| 2 | 3c/3h | ||||||
| 3-sided | 7 | North-south | South | 2 * | 10c/10h | ||
| 2 | 9c/9h | ||||||
| 1 | 7c/7h | ||||||
| East-west | East | 2 | 8c/8h | ||||
| 1 | 6c/6h | ||||||
| 2-sided | 11 | North-south | Central | 2 | 12c/12h | ||
| 1 | 13c/13h | ||||||
| Southeast | 2 | 11c/11h | |||||
| East-west | Central | 2 | 15c/15h | ||||
| 1 | 16c/16h | ||||||
| Northeast | 2 | 14c/14h | |||||
| 1-sided | 13 | North-south | South | 1 | 18c/18h | ||
| East-west | East | 1 | 17c/17h | ||||
| Index | Energy Model Parameters |
|---|---|
| Wall | 5 mm Cement mortar + 370 mm Fired claybrick U-value = 1.72 W·m−2·K−1 |
| Floor | 10 mm Ceramic tile + 100 mm Concrete + 1500 mm Plain soil compaction U-value = 0.47 W·m−2·K−1 |
| Roof | Color steel plate + 10 mm Asphalt felt + 10 mm Grass clay + 200 mm Cement mortar U-value = 1.94 W·m−2·K−1 |
| Glazing | Wooden Glass U-value = 5.03 W·m−2·K−1 SHGC = 0.6 |
| Shading | Not applied |
| Equipment loads per area | 3.8 W·m−2 |
| Infiltration rate per area | 0.4 cfm/sf facade @ 75 Pa |
| Lighting density per area | 11.8 W·m−2 |
| Num. of people per area | 0.03 people·m−2 |
| Schedules | Default Honeybee residential schedules |
| HVAC | Ideal mechanical system |
| Heating setpoint | 16 °C |
| Cooling setpoint | 26 °C |
| Design Variables | Unit | Scope | Distribution Type |
|---|---|---|---|
| Courtyard width | m | [9, 12] | Continuous |
| Standard floor height | m | [2.7, 4.0] | Continuous |
| Orientation | ° | [−45, 45] | Continuous |
| Secondary-house Floor Control | - | [−1, 1] | Discrete |
| WWR | - | [0, 0.35] | Continuous |
| Design Variables | ||||||
|---|---|---|---|---|---|---|
| Courtyard width | Height_N | Height_E | Height_W | Orientation | Secondary-house Floor Control | W_N/W_S/W_W1/W_E1/W_W2/W_E2 |
| 10.8 m | 6.3 m | 2.9 m | 6 m | −19° | 0 | 0.1/0.3/0.1/0.3/0.4/0.1 |
| Performance Objectives | |||
|---|---|---|---|
| FO1: OTCA_C | FO2: OTCA_H | FO3: sDA | FO4: EUI |
| −0.06 | −0.26 | −0.79 | 0.31 |
| No. of Courtyards | Index | Average No. of Floors | Height Distribution | Vc (m/s) | Vh (m/s) |
|---|---|---|---|---|---|
| 3 | c31/h31 | 1 | - | 0.1 | 2.5 |
| c32/h32 | 1.3 | - | 0.3 | 1.9 | |
| 4 | c41/h41 | 1 | - | 0.1 | 2.3 |
| c42/h42 | 1.25 | - | 0.3 | 2.1 | |
| c43/h43 | 1.5 | - | 0.4 | 2.2 | |
| 5 | c51/h51 | 1 | - | 0.1 | 1.9 |
| c52/h52 | 1.2 | - | 0.1 | 1.8 | |
| c53/h53 | 1.4 | Centralized | 0.2 | 1.7 | |
| c55/h55 | 1.4 | Dispersed | 0.3 | 2.0 | |
| c54/h54 | 1.6 | - | 0.3 | 1.9 |
| Index | W | H_N | H_W | H_E | D | W_N/W_S/W_W1/W_E1/W_W2/W_E2 | True Label | Predicted Label |
|---|---|---|---|---|---|---|---|---|
| 1 | 11 | 7.4 | 7.1 | 3.9 | 3 | 0.1/0.2/0.1/0.1/0.1/0.1 | A | A |
| 2 | 11.1 | 6.4 | 5.9 | 3.1 | −21 | 0.1/0.2/0.1/0.3/0.3/0.1 | B | B |
| 3 | 10.5 | 6.1 | 2.9 | 6 | −19 | 0.1/0.2/0.1/0.3/0.4/0.1 | C | C |
| 4 | 11.3 | 5.8 | 5.6 | 3.9 | −21 | 0.2/0.2/0.1/0.2/0.1/0.3 | D | C |
| 5 | 11.8 | 7.3 | 6.8 | 3.1 | 9 | 0.2/0.3/0.1/0.1/0.2/0.3 | E | E |
| 6 | 9.7 | 5.8 | 3.4 | 7.4 | 11 | 0.3/0.3/0.1/0.3/0.1/0.1 | F | F |
| Index | Functional Division | Total Floor Area (m2) | Performance Rating | Overall Performance Score |
| Status of the Base | Master workshop | 720 | D4 | 59.12 |
| Business community | 1840 | E5 | ||
| Guesthouse | 1620 | E5 | ||
| Cultural exhibitions | 1510 | D4 | ||
| Plan 1 | Master workshop | 550 | C3 | 61.75 |
| Business community | 1770 | B2 | ||
| Guesthouse | 1460 | A1 | ||
| Cultural exhibitions | 1410 | C3 | ||
| Plan 2 | Master workshop | 720 | B2 | 71.12 |
| Business community | 1840 | B2 | ||
| Guesthouse | 1620 | B2 | ||
| Cultural exhibitions | 1510 | B2 | ||
| Plan 3 | Master workshop | 720 | A1 | 85.62 |
| Business community | 1790 | B2 | ||
| Guesthouse | 1620 | A1 | ||
| Cultural exhibitions | 1550 | B2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Huang, X.; Zheng, X.; Deng, J.-Y.; Sun, B. A Performance and Data-Driven Method for Optimization of Traditional Courtyards. Sustainability 2024, 16, 5779. https://doi.org/10.3390/su16135779
Xu Z, Huang X, Zheng X, Deng J-Y, Sun B. A Performance and Data-Driven Method for Optimization of Traditional Courtyards. Sustainability. 2024; 16(13):5779. https://doi.org/10.3390/su16135779
Chicago/Turabian StyleXu, Zhixin, Xia Huang, Xin Zheng, Ji-Yu Deng, and Bo Sun. 2024. "A Performance and Data-Driven Method for Optimization of Traditional Courtyards" Sustainability 16, no. 13: 5779. https://doi.org/10.3390/su16135779
APA StyleXu, Z., Huang, X., Zheng, X., Deng, J.-Y., & Sun, B. (2024). A Performance and Data-Driven Method for Optimization of Traditional Courtyards. Sustainability, 16(13), 5779. https://doi.org/10.3390/su16135779







