Integrated Absorption–Adsorption Process for Waste-Free Decontamination of Gases from Sulfur Dioxide, Part 2: CFD Modeling and Experimental Investigation of a Bubble-Cap Tray
Abstract
:1. Introduction
State-of-the-Art FGD Using Ion-Exchange Resins
2. Investigation Methods and Experimental Set-Up
- Determination of the flow conditions, in accordance with the experience and the data in the literature on bubble-cap trays, as well as the scale of the laboratory model;
- Dimensioning of the model, according to the liquid level, the column diameter, and the gas velocity;
- Testing different configurations of the bubble-cap tray by CFD simulation of the fluid flow. Analysis of the results leads to the proper configuration of the bubble-cap tray.
2.1. CFD Model Details
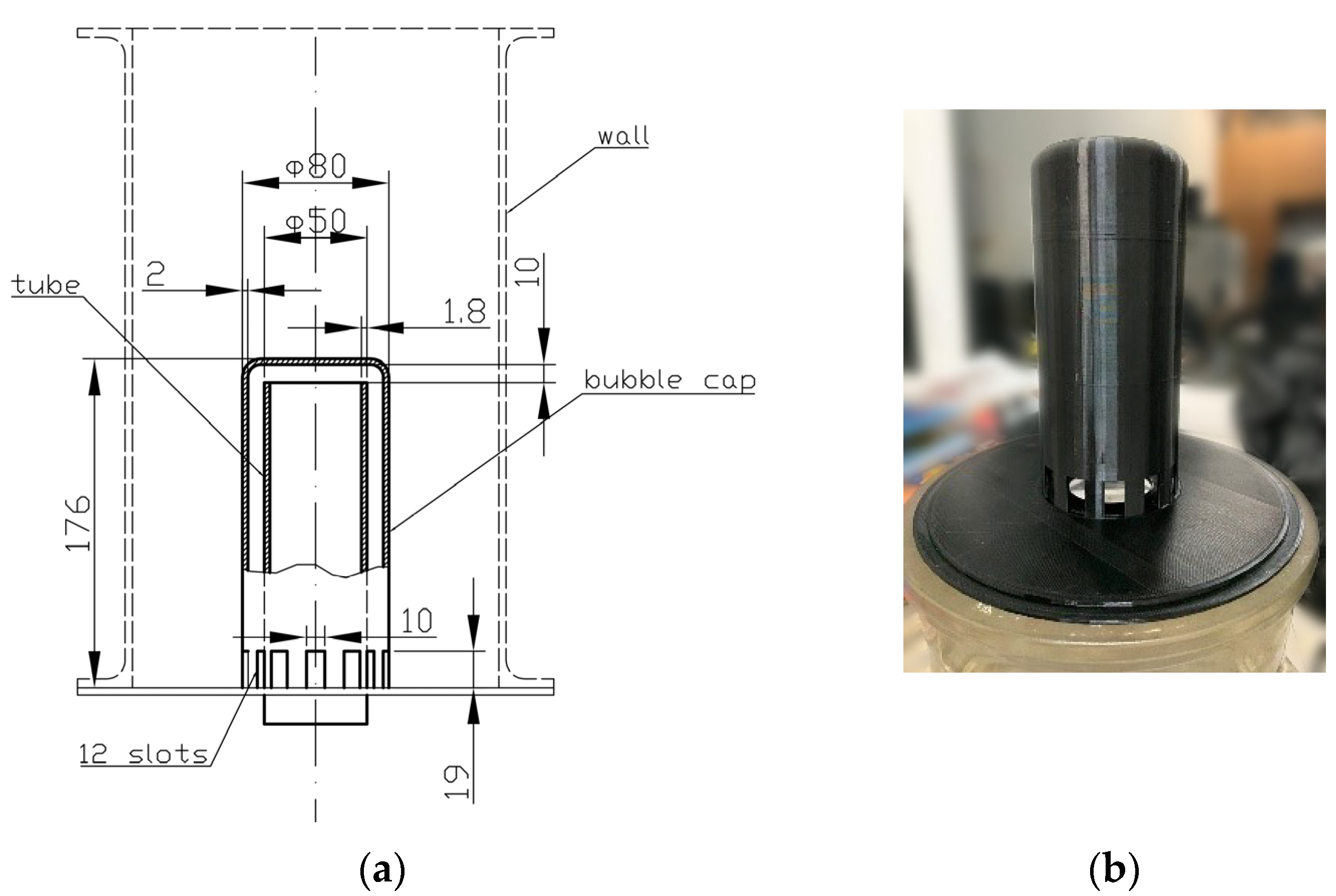
2.2. Additive Technology
Manufacturing of the Bubble-Cap Tray
- Adapting the 3D CAD model of the bubble-cap tray in accordance with the 3D printer’s working volume and the properties of the material used;
- 2.
- Reprocessing (slicing) of the 3D CAD model by specialized software and setting of the printing machine;
- 3.
- Drying of the polymer before printing to ensure the necessary quality of the part;
- 4.
- Test printing of a test object before printing the main part;
- 5.
- Printing of the physical model (for the bubble cap it took about 12 h; for the tray—about 8).
2.3. Choice of Anion-Exchange Resin
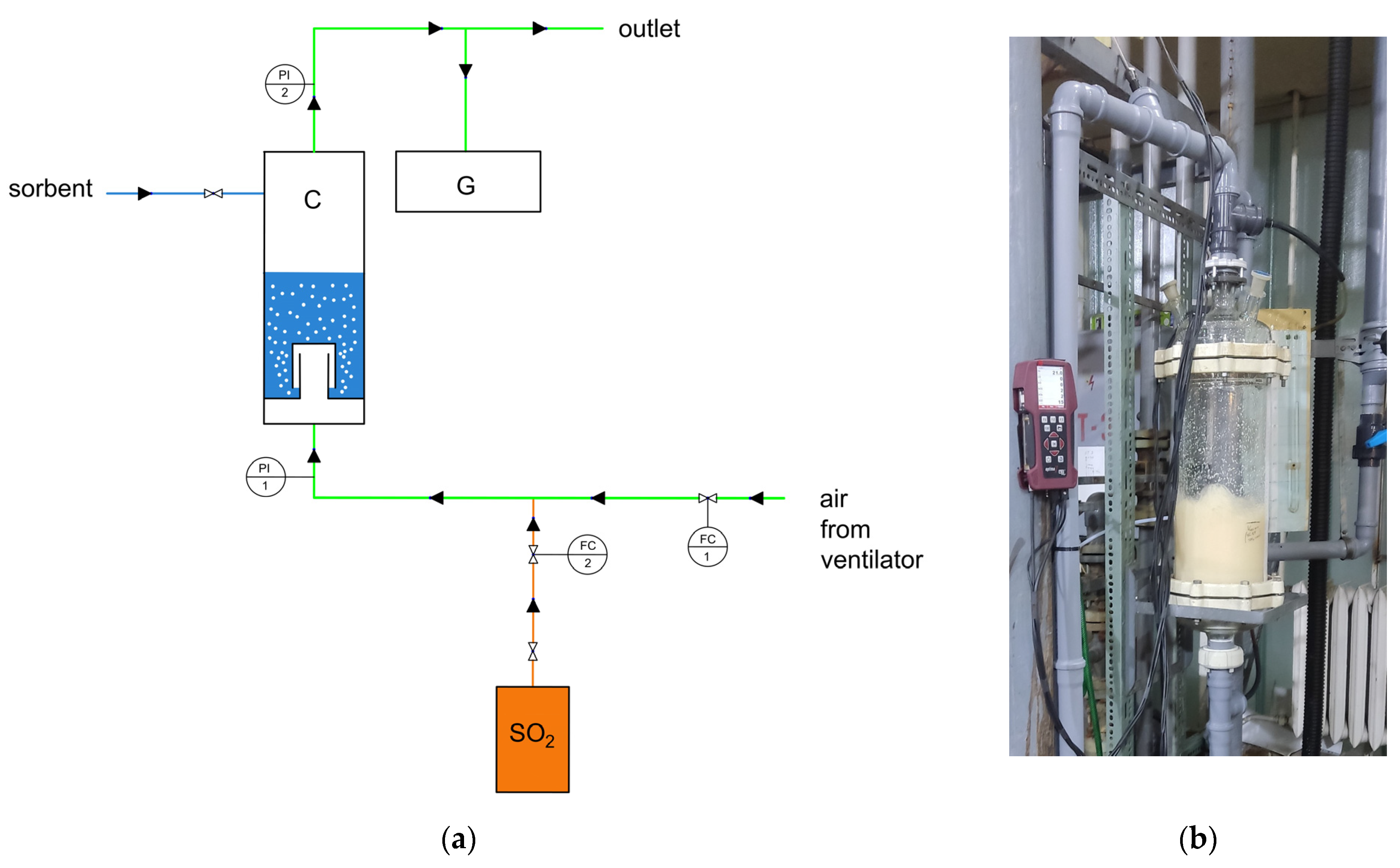
2.4. Experimental Set-Up
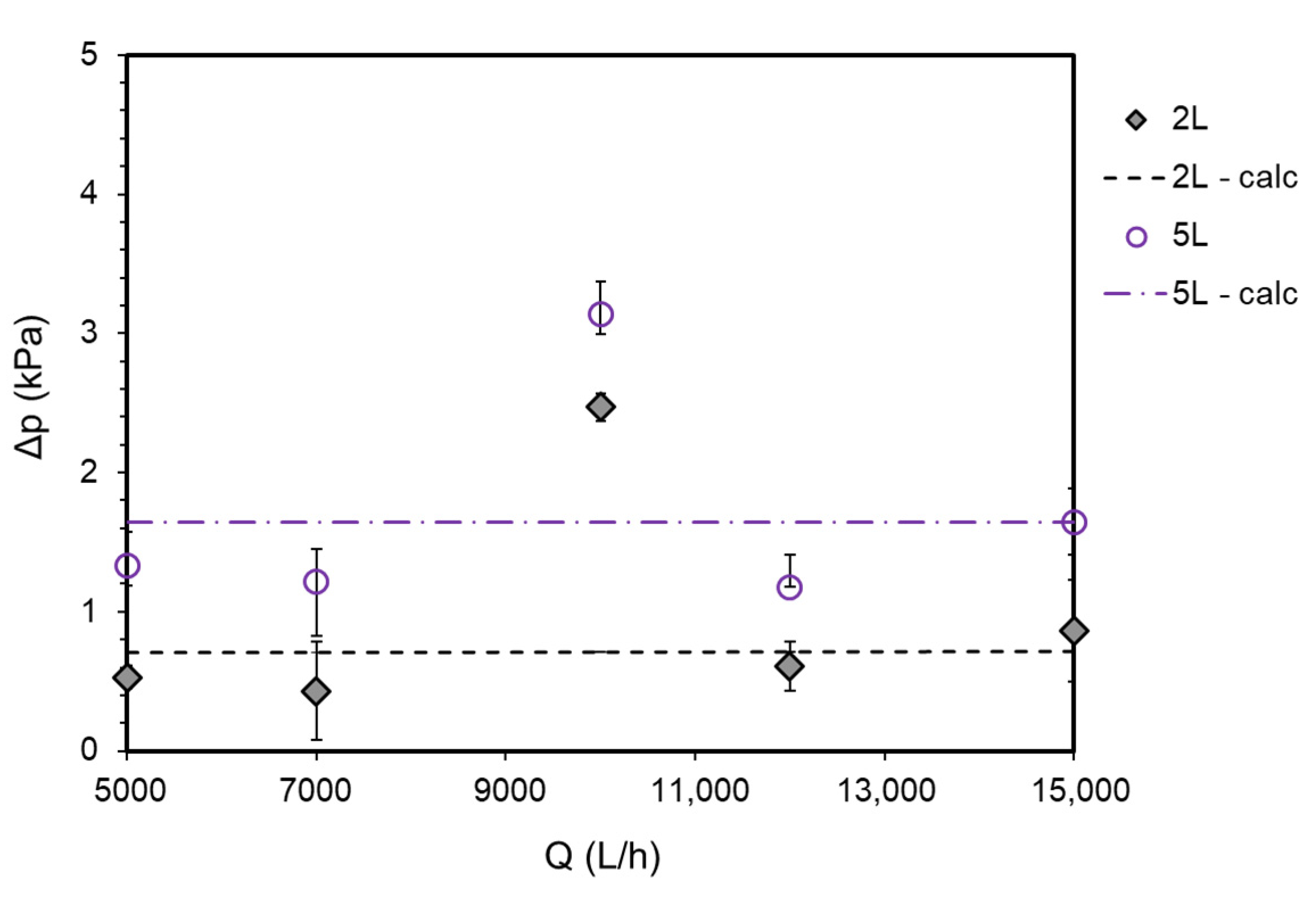
2.5. Pressure Drop Measurements
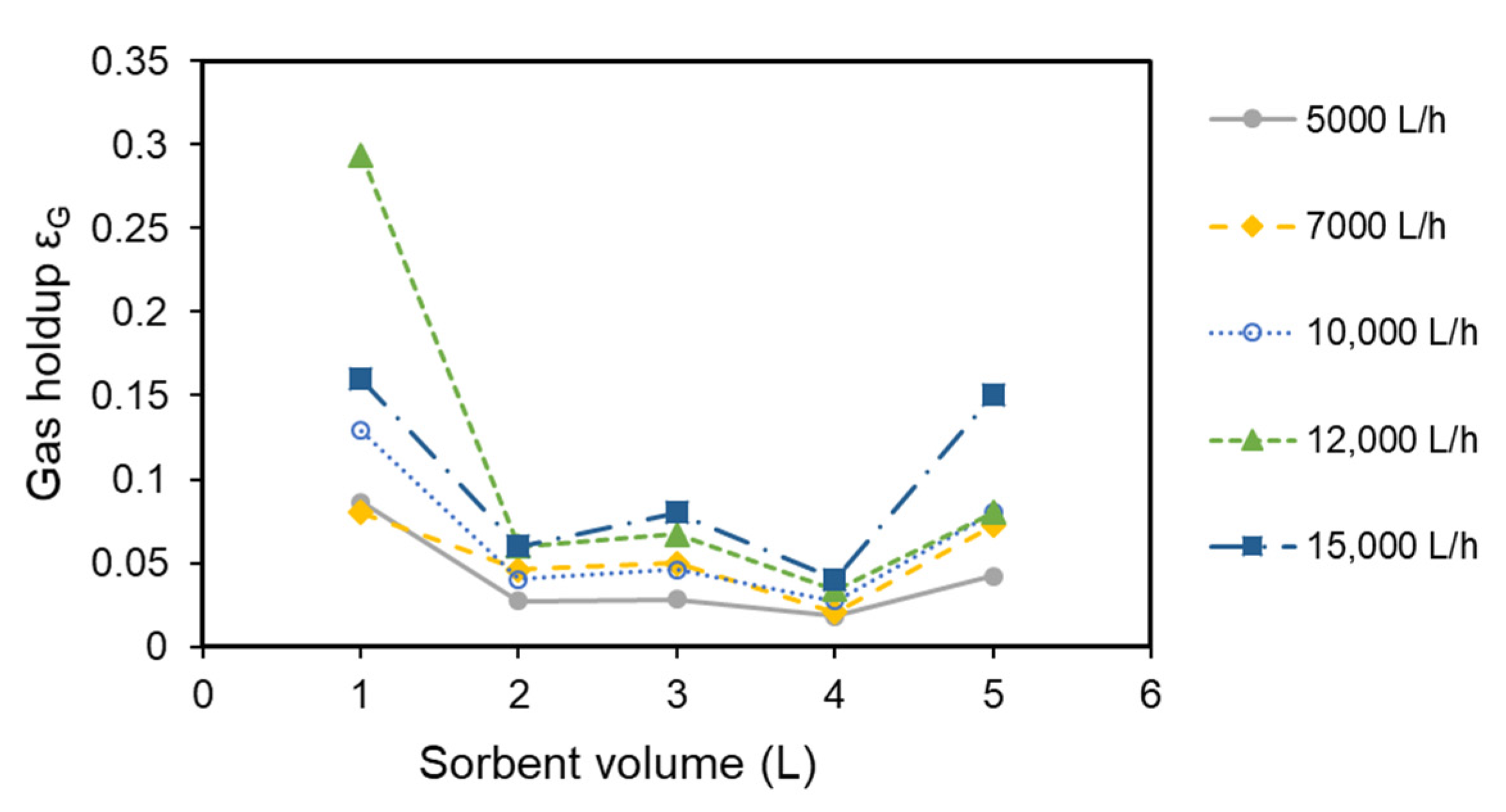
2.6. Gas Holdup Measurements
2.7. Kinetics of the Gas Absorption–Adsorption Process
3. Results and Discussion
3.1. CFD Simulations
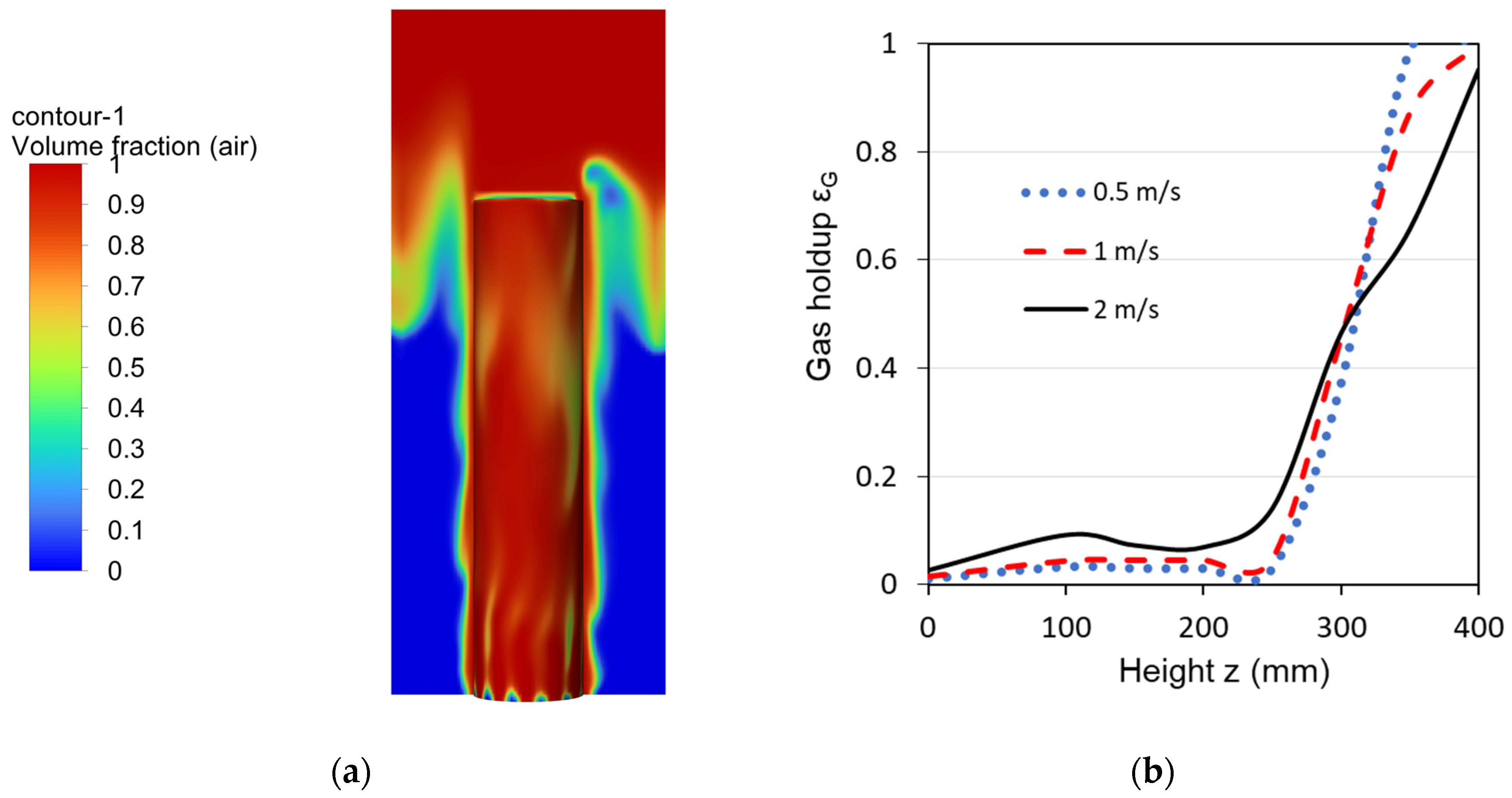
3.1.1. Reference Bubble-Cap Design
3.1.2. Enhancement of Mixing by Lowering the Liquid Level
3.1.3. Enhancement of Mixing by Increasing the Number of Bubble Caps
3.2. Experimental Results for Pressure Drop and Gas Holdup
3.3. Kinetics of the Gas Absorption–Adsorption Process
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| b | slot width (m); |
| C0 | inlet SO2 concentration in the gas before treatment (ppm v/v); |
| Ce | outlet SO2 concentration in the gas after treatment (ppm v/v); |
| d | outside diameter of the bubble cap (mm); |
| D | inside diameter of the model section (mm); |
| G | gas treated per volume of dry resin (m3/m3); |
| h | height of the bubble cap (mm); |
| hp | distance from the upper edge of the slots to the liquid level of the tray (m); |
| H | height of the liquid level at a given gas flow rate (mm); |
| H0 | height of the liquid level in the absence of gas flow (mm); |
| Hs | height of the model section for the CFD simulation (mm); |
| l | slot height (m); |
| inter–momentum exchange term between the two phases p and q, which accounts for inter–phase coupling forces (N); | |
| Mr | mass of dry resin in the sorbent mixture (kg); |
| P | pressure (Pa); |
| Q | gas flow rate (L/h); |
| t | time of operation (s); |
| average velocity of phase q (m/s); | |
| wG | average gas velocity at the surface area of the slots (m/s); |
| z | vertical coordinate (height) (mm); |
| Greek symbols: | |
| αg | gas volume fraction (-); |
| αl | liquid volume fraction (-); |
| αq | volume fraction of phase q (-); |
| γG | specific weight of air (γG = 11.81 N/m3 at 20 °C) (N/m3); |
| γw | specific weight of water (γw = 9807 N/m3 at 20 °C) (N/m3); |
| Δp | gas pressure drop caused by the bubble-cap tray (Pa); |
| Δp1 | pressure drop of the dry tray with fully open slots (Pa); |
| Δp2 | pressure drop due to surface tension forces (Pa); |
| Δp3 | hydrostatic pressure of the liquid column at the open slots (Pa); |
| Δp4 | static pressure of the liquid column above the upper edge of the slots (Pa); |
| εG | gas holdup (gas volume fraction) (-); |
| ξ | coefficient of slot resistance (ξ = 2) (-); |
| η | removal efficiency (%); |
| ρq | density of phase q (kg/m3); |
| ρr | dry resin density (kg/m3); |
| σ | surface tension at a water–air interface (σ = 0.0728 N/m at 20 °C) (N/m); |
| τq- | stress-strain tensor of phase q (Pa); |
| Abbreviations: | |
| BC | boundary conditions; |
| CAD | computer aided design; |
| CFD | computational fluid dynamics; |
| FC | flow control; |
| FGD | flue gas desulfurization; |
| OD | outside diameter; |
| MR | macroreticular; |
| PETG | polyethylene terephthalate glycol; |
| PP | polypropylene; |
| PI | pressure indicator. |
References
- The World Bank Annual Report 1998 (English); World Bank Group: Washington, DC, USA, 1988; Available online: http://documents.worldbank.org/curated/en/390771468320070967/The-World-Bank-annual-report-1998 (accessed on 28 November 2023).
- EPA Agency, USA. Available online: https://www.epa.gov/acidrain/acid-rain-program (accessed on 28 November 2023).
- 2022 Report on the State of the Ecology and Environment in China, Ministry of Ecology and Environment, PR China. Available online: https://english.mee.gov.cn/Resources/Reports/soe/SOEE2019/202312/P020231206607194894058.pdf (accessed on 11 January 2024).
- Wang, L.; Liu, C.; Meng, X.; Niu, Y.; Lin, Z.; Liu, Y.; Liu, J.; Qi, J.; You, J.; Tse, L.A.; et al. Associations between short-term exposure to ambient sulfur dioxide and increased cause-specific mortality in 272 Chinese cities. Environ. Int. 2018, 117, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, R.K. Controlling SO2 Emissions: A Review of Technologies; Nova Science: Washington, DC, USA, 2003. [Google Scholar]
- Kohl, A.L.; Nielsen, R.B. Chapter 7—Sulfur Dioxide Removal. In Gas Purification, 5th ed.; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Atanes, E.; Nieto-Márquez, A.; Cambra, A.; Ruiz-Pérez, M.C.; Fernández-Martínez, F. Adsorption of SO2 onto waste cork powder-derived activated carbons. Chem. Eng. J. 2012, 211–212, 60–67. [Google Scholar] [CrossRef]
- Namba, H.; Tokunaga, O.; Hashimoto, S.; Tanaka, T.; Ogura, Y.; Doi, Y.; Aoki, S.; Izutsu, M. Pilot-scale test for electron beam purification of flue gas from coal-combustion boiler. Radiat. Phys. Chem. 1995, 46, 1103–1106. [Google Scholar] [CrossRef]
- Yan, W.; Ninghui, W.; Yimin, Z.; Yanbin, Z. SO2 removal from industrial flue gases using pulsed corona discharge. J. Electrostat. 1998, 44, 11–16. [Google Scholar] [CrossRef]
- Poullikkas, A. Review of Design, Operating, and Financial Considerations in Flue Gas Desulfurization Systems. Int. J. Energy Technol. Policy 2015, 2, 92–103. [Google Scholar] [CrossRef]
- Alexandratos, S.D. Ion-Exchange Resins: A Retrospective from Industrial and Engineering Chemistry Research. Ind. Eng. Chem. Res. 2009, 48, 388–398. [Google Scholar] [CrossRef]
- Cole, R.; Shulman, H.L. Adsorbing Sulfur Dioxide on Dry Ion Exchange Resins. Ind. Eng. Chem. 1960, 52, 859–860. [Google Scholar] [CrossRef]
- Vaidyanathan, A.S.; Youngquist, G.R. Sorption of Sulfur Dioxide, Hydrogen Sulfide, and Nitrogen Dioxide by Ion-Exchange Resins. Ind. Eng. Chem. Prod. Res. Develop. 1973, 12, 288–293. [Google Scholar] [CrossRef]
- Quinn, R. Ion Exchange Resins as Reversible Acid Gas Absorbents. Sep. Sci. Technol. 2003, 38, 3385–3407. [Google Scholar] [CrossRef]
- Chen, T.-W.; Pinto, N.G. Fixed-bed adsorption of acid gases on a macroreticular ion-exchange resin. React. Polym. 1991, 14, 151–168. [Google Scholar] [CrossRef]
- Boyadzhiev, K.; Pantofchieva, L.; Khristov, I. Sulfur dioxide adsorption in a fixed bed of a synthetic anionite. Theor. Found. Chem. Eng. 2000, 34, 141–144. [Google Scholar] [CrossRef]
- Chen, T.-W.; Pinto, N.G. Stability and equilibrium properties of macroreticular resins for flue gas desulfurization. Ind. Eng. Chem. Res. 1990, 29, 440–447. [Google Scholar] [CrossRef]
- Al-Asheh, S.; Aidan, A. A Comprehensive Method of Ion Exchange Resins Regeneration and Its Optimization for Water Treatment. In Promising Techniques for Wastewater Treatment and Water Quality Assessment; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Holub, M.; Pavlikova, P.; Balintova, M.; Smolakova, M. Application of ion-exchange resins for removing sulphate ions from acidic solutions. Chem. Technol. 2017, 68, 18–22. [Google Scholar] [CrossRef]
- Geraud, D. Ion Exchange Experiments—Water Softening and Deionization, 2016, 345, Honors Research Projects. Available online: http://ideaexchange.uakron.edu/honors_research_projects/345/ (accessed on 28 November 2023).
- Kratochvil, D.; Bratty, M. Selective Sulphate Removal by Exclusive Anion Exchange from Hard Water Waste Streams. United States of America Patent US8551340B2, 23 September 2014. [Google Scholar]
- Sheth, A.C.; Butler, W.A. Desulfurization Process. U.S. Patent 4917874, 17 April 1990. [Google Scholar]
- Gao, J.; Wang, S.; Wang, J.; Cao, L.; Tang, S.; Xia, Y. Effect of SO2 on the amine-based CO2 capture solvent and improvement using ion exchange resins. Int. J. Greenh. Gas Control 2015, 37, 38–45. [Google Scholar] [CrossRef]
- Ghorbani, A.; Bayati, B.; Poerio, T.; Argurio, P.; Kikhavani, T.; Namdari, M.; Ferreira, L.M. Application of NF Polymeric Membranes for Removal of Multicomponent Heat-Stable Salts (HSS) Ions from Methyl Diethanolamine (MDEA) Solutions. Molecules 2020, 25, 4911. [Google Scholar] [CrossRef] [PubMed]
- Matsuura, H.; Sun, Z.; Yanase, M.; Ihara, T.; Kida, K.; Jyo, A. Separation of Sulfuric Acid and Monosaccharides with a Strong-Base Anion Exchange Resin Containing Polystyrenesulfonate as Polymeric Counter Ion to Reduce Tailing of Sulfuric Acid. J. Ion Exch. 2014, 25, 81–87. [Google Scholar] [CrossRef]
- Stefanov, S.; Razkazova-Velkova, E. Integrated absorption-adsorption process for waste-free decontamination of gases from sulfur dioxide. Part 1. Choice of ion-exchange resin and adsorption and desorption parameters. Bulg. Chem. Commun. 2020, 52, 57–63. [Google Scholar]
- Boyadjiev, C.B.; Boyadjiev, B.C. Absorption-Adsorption Apparatus for Purification of Gases from Sulfur Dioxide. Bulgarian Patent 2196, 31 March 2016. (In Bulgarian). [Google Scholar]
- Boyadjiev, C.B.; Boyadjiev, B.C.; Doychinova, M.D.; Popova-Krumova, P. Method and Apparatus for Purification of Gases from Sulfur Dioxide. Bulgarian Patent 66757, 11 October 2018. (In Bulgarian). [Google Scholar]
- ANSYS Fluent Theory Guide; Release 2023 R1; ANSYS, Inc.: Canonsburg, PA, USA, 2023.
- Dimitrov, D.; Schreve, K.; de Beer, N. Advances in three dimensional printing—State of the art and future perspectives. Rapid Prototyp. J. 2006, 12, 136–147. [Google Scholar] [CrossRef]
- Sans, V.; Dragone, V.; Cronin, L. Applications of 3D Printing in Synthetic Process and Analytical Chemistry. In Handbook of Green Chemistry; Wiley Online Books: Hoboken, NJ, USA, 2019; pp. 215–256. [Google Scholar] [CrossRef]
- Kolev, N. Chapter 2—Investigation of the main performance characteristics of packed bed columns. In Packed Bed Columns, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Kasatkin, A.G. Basic Processes and Equipment of Chemical Technology; Izdat. Coskhimizdat: Moscow, Russia, 1955. (In Russian) [Google Scholar]
- Optima MRU—Emission Monitoring Systems. Available online: https://www.mru.eu/en/products/detail/optima7/ (accessed on 30 November 2023).
- Ferguson, J.B. The Iodometric Determination of Sulfur Dioxide and the Sulfites. J. Am. Chem. Soc. 1917, 39, 364–373. [Google Scholar] [CrossRef]
- Stupin, W.J.; Kister, H.Z. System Limit: The Ultimate Capacity of Fractionators. Chem. Eng. Res. Des. 2003, 81, 136–146. [Google Scholar] [CrossRef]
- Totev, T.; Boycheva, S.; Ignatov, B.; Angelov, B.; Todorov, K. SO3 emission control for Thermal Power Plants burning lignite coals. In Proceedings of the 15 Scientific Conference—Faculty of Power Engineering and Power Machines (PEPM), Sozopol, Bulgaria, 16–19 September 2010; Technical University Sofia: Sofia, Bulgaria; Volume I, pp. 135–141. (In Bulgarian). [Google Scholar]




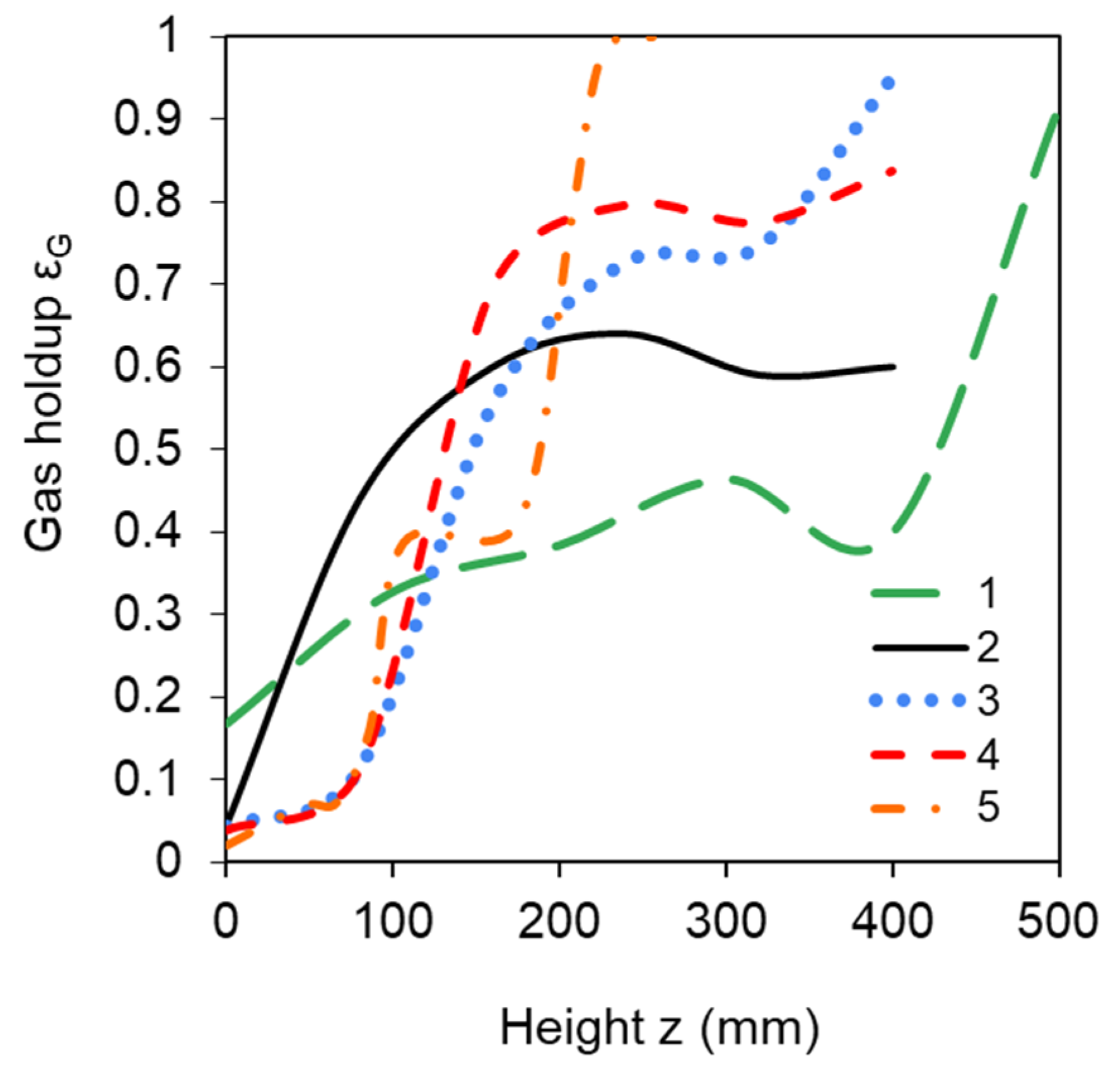
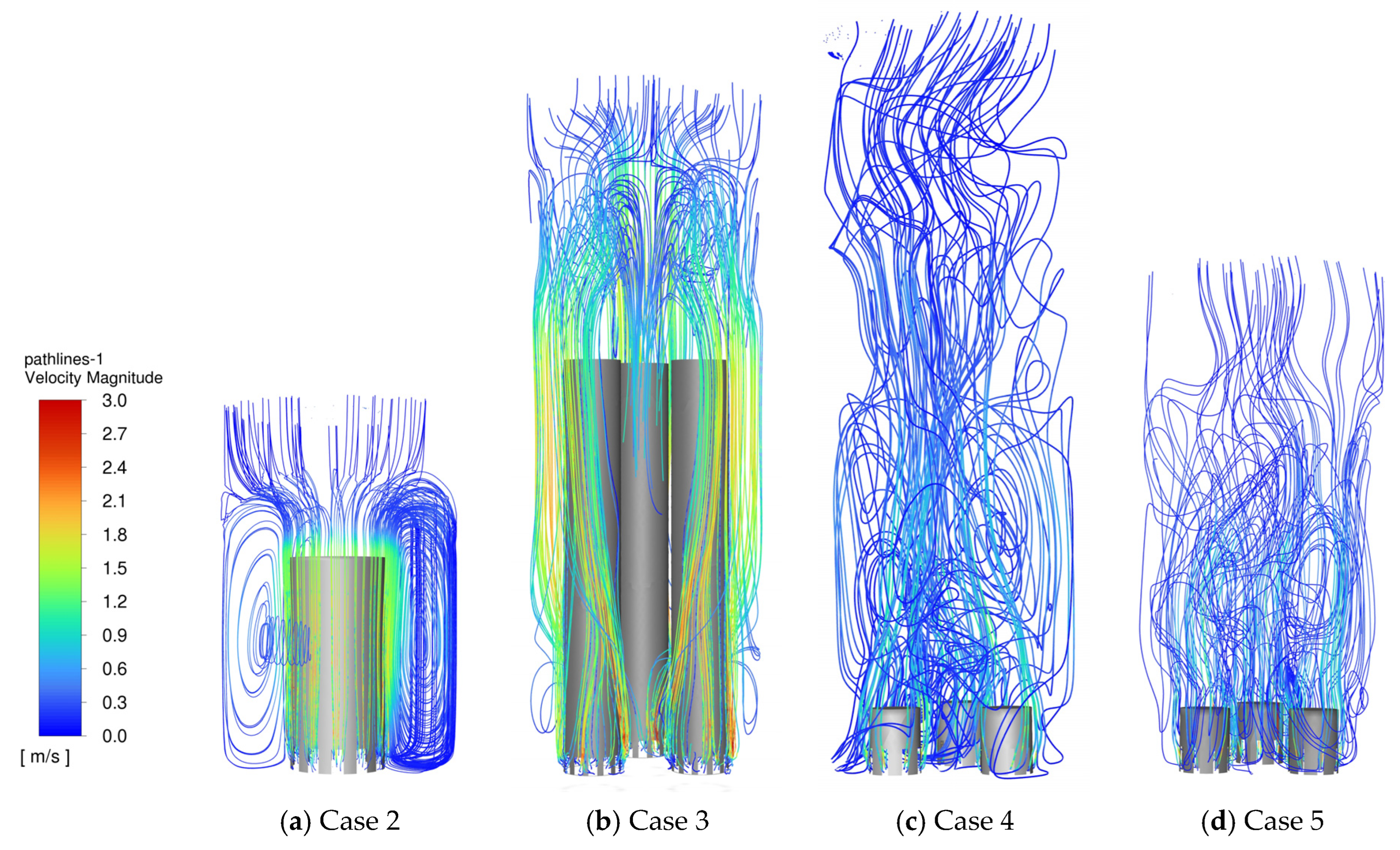

| Case No | Number of Bubble Caps | Bubble-Cap Diameter d (mm) | Bubble-Cap Height h (mm) | Liquid Level H0 (mm) |
|---|---|---|---|---|
| Case 1 | 1 | 80 | 360 | 300 |
| Case 2 | 1 | 80 | 180 | 150 |
| Case 3 | 3 | 40 | 360 | 300 |
| Case 4 | 3 | 40 | 50 | 300 |
| Case 5 | 3 | 40 | 50 | 150 |
| Plot No | C0 (ppm) | Q (L/h) | Mr (g) |
|---|---|---|---|
| 1 | 1500 | 5000 | 250 |
| 2 | 1500 | 5000 | 500 |
| 3 | 3500 | 5000 | 500 |
| 4 | 1500 | 15,000 | 500 |
| 5 | 1500 | 5000 | 0 (water only) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apostolov, A.; Panyovska, S.; Stefanov, S.; Dzhonova-Atanasova, D.; Razkazova-Velkova, E.; Michev, S. Integrated Absorption–Adsorption Process for Waste-Free Decontamination of Gases from Sulfur Dioxide, Part 2: CFD Modeling and Experimental Investigation of a Bubble-Cap Tray. Sustainability 2024, 16, 2472. https://doi.org/10.3390/su16062472
Apostolov A, Panyovska S, Stefanov S, Dzhonova-Atanasova D, Razkazova-Velkova E, Michev S. Integrated Absorption–Adsorption Process for Waste-Free Decontamination of Gases from Sulfur Dioxide, Part 2: CFD Modeling and Experimental Investigation of a Bubble-Cap Tray. Sustainability. 2024; 16(6):2472. https://doi.org/10.3390/su16062472
Chicago/Turabian StyleApostolov, Apostol, Stela Panyovska, Stefan Stefanov, Daniela Dzhonova-Atanasova, Elena Razkazova-Velkova, and Stefan Michev. 2024. "Integrated Absorption–Adsorption Process for Waste-Free Decontamination of Gases from Sulfur Dioxide, Part 2: CFD Modeling and Experimental Investigation of a Bubble-Cap Tray" Sustainability 16, no. 6: 2472. https://doi.org/10.3390/su16062472





