Abstract
This paper investigates a competitive market consisting of two new energy vehicle (NEV) firms with a technology gap and consumers with green preferences. By employing a Hotelling model, we obtain the equilibrium outcomes of two competing firms without and with segmented consumer subsidy (SCS) following Nash game theory. We further explore the incentive effect, effective scope of SCS policy and the impacts of subsidy threshold and technology improvement on it, which fills the gap in the literature and provides managerial insights. We find that SCS can only play a role when the threshold is intermediate, and the government can expand the effective scope of subsidies by cultivating consumers’ green preferences and strengthening the intensity of subsidies. Moreover, the government can change the competitiveness and green level gap of two firms through the threshold. When threshold is small (large), increasing it can narrow (expand) the green level gap between two firms but widen (narrow) the market gap. We also find that implementing an SCS policy has a positive impact on environmental benefits and technological improvement is more likely to cause environmental damage. However, the government can effectively decrease the degree and probability of damage by raising the subsidy threshold and reducing the subsidy amount.
1. Introduction
Reducing greenhouse gas emissions and addressing climate change have become crucial aspects of global sustainable development [1]. As of September 2023, more than 150 countries have made carbon neutral commitments, covering more than 80% of the global carbon dioxide emissions, GDP and population. However, with the rapid development of society and the improvement in people’s living standards, the public’s demand for cars continues to grow, and the increasing energy consumption and carbon dioxide emissions pose serious threats to the environment [2]. According to global carbon emission industry structure data, highway transportation accounts for 11.9% of total carbon emissions [3]. Because, compared with conventional fuel vehicles, new energy vehicles (NEVs) use green clean energy and can reduce carbon emissions by 30–50% [4], developing NEVs to reduce the transportation industry’s carbon emissions is becoming a significant way to achieve carbon neutrality [3,5,6]. However, there are many obstacles hindering the development of NEVs, such as imperfect key technologies and high vehicle purchase costs [7,8,9]. Government subsidies have become an important means of stimulating consumer demand for NEVs and promoting the innovation vitality of NEV firms. Among these subsidies, consumer subsidies are one of the most common and effective policies [10].
Many studies have shown that high upfront purchase costs are the biggest barrier to NEV adoption [7,11], with the average price of an electric vehicle estimated to be about USD 2800 higher than an average gasoline vehicle [12]. In the initial stage of NEV development, many governments provide cash subsidies, tax incentives and other purchase incentives for consumers to buy NEVs, so as to encourage consumers to buy NEVs [10]. With the support of these policies, sales of NEVs have increased annually. From 2014 to 2023, the delivery of electric vehicles rose from 3.2 million to over 14 million, resulting in a market share increase from 0.4% to 15.8% [13]. However, excessive subsidies have caused some firms to rely on subsidies and even to engage in improper acts to defraud subsidies, thus hindering their efficiency and the technological innovation of NEVs [14]. To address these issues, the government has recently begun to take technical criteria such as greenness as a measure of whether to subsidize and formulated a consumer subsidy policy with greenness or other criteria as the subsidy threshold. For example, the United States can provide NEV purchase incentives ranging from USD 2500 to 7500 depending on different battery capacities [10]. Such subsidies are mainly segmented consumer subsidies (SCSs) based on standards such as the green level of NEVs, and consumers can only obtain subsidies when the green level of an NEV purchased reaches the subsidy threshold. SCS not only improves consumers’ willingness to buy NEVs, but also stimulates firms to produce products with higher green levels. This study aims to contribute to the literature by examining the role of SCS in improving NEV green levels and its mechanism of action.
This paper examines the following interesting questions: Firstly, it is curious whether introducing a subsidy threshold to SCS can effectively play the role of subsidy compared with no subsidy; how should the subsidy threshold be set? Secondly, in recent years, the NEV industry has seen the emergence of numerous firms with varying technical levels. Unfortunately, low-tech firms have not only captured a significant portion of the market share of high-tech NEVs, but they have also had a detrimental impact on environmental benefits. Therefore, considering the varying technical levels of NEV firms, how will the impact of SCS on these firms be different? To promote the development of high-tech NEV firms, how should the government adjust the subsidy threshold and intensity in the SCS? Finally, due to both market demand and subsidy policies, the technical level of NEV firms is expected to continue improving, which we refer to as a technological improvement phenomenon. This will result in a gradual narrowing of the technological gap between firms, leading to changes in the market structure and increased competition, which has to prompt us to think about how the technological improvements will affect the environmental benefits. Furthermore, we seek to know how the government can modify the SCS to facilitate the growth of the NEV industry in response to the effects of technological advancements.
To answer the questions above, we analyze a competitive market consisting of two NEV firms with different technical capabilities and consumers with green preferences. We construct a competitive game model with and without SCS policy and analyze the equilibrium green input and price decisions of the firms. The analysis of relevant parameters provides valuable insights for policymakers in the NEV market on how to design appropriate SCS. These parameters include the impact of the SCS policy, subsidy threshold, subsidy intensity, and technical capability on the equilibrium decision and environmental benefits.
Our main contribution can be divided into two aspects: On the one hand, most of the literature focuses on the traditional subsidy policy, where the government subsidizes all consumers regardless of the technical level of the product, ignoring the impact of the subsidy threshold in the consumer subsidy on the subsidy’s effect. We introduce the concept of subsidy threshold into the consumer subsidy, construct the segmented consumer subsidy (SCS), and reveal the influence of relevant parameters on the equilibrium decision. On the other hand, existing research rarely considers the reality of unbalanced technological development and technological improvement in the NEV market, which is inconsistent with the reality. We examine the impact of SCS policy on NEV firms and environmental benefits, taking into account technological gaps and improvements. These findings offer policy design recommendations for governments.
The rest of this paper is organized as follows: Section 2 summarizes the relevant literature. Section 3 describes research problem and presents the model in detail. Section 4 analyzes and compares the equilibrium results with and without SCS policies. Section 5 examines the impact of technological improvement on environmental benefits. Section 6 presents managerial insights and implications, theoretical implications, limitations and future research directions.
2. Literature Review
2.1. Environmental Benefits of NEVs
Road infrastructure, economic growth and industrialization have created a complex transport infrastructure but at the same time increased the energy consumption and pollutant emissions of road transport [15]. Due to the use of clean energy, NEVs are widely regarded as an effective means of reducing carbon emissions and achieving carbon neutrality [3]. Li et al. [16] argued that the development of NEVs has shown promising potential in addressing the issues of energy shortage and air pollution when compared to traditional petroleum-fueled vehicles. According to an IPCC report, Tang et al. [17] claimed that electric vehicles offer the environmental benefit of reducing CO2 emissions. This could lead to significant market penetration in the future [18]. Okada et al. [19] thought that the use of electric vehicles can help against global warming by reducing CO2 emissions. Spangher et al. [20] confirmed the positive impact of electric vehicles on carbon reduction by quantifying the effect of electric vehicle sales on CO2 emissions. In addition, Ahmed et al. [21] suggested that environmental protection policies should focus on supporting green energy projects, such as NEVs, which can positively impact the environment in many ways. In recent years, governments have increasingly supported the development of NEVs. This includes consumer subsidies for car purchases and tax breaks, as well as other policy measures aimed at reducing carbon emissions and reversing the effects of climate and environmental degradation [22].
2.2. Consumer Subsidies
Looking back at the relevant research on consumer subsidy policy, we found that the existing research mainly focuses on the subsidy effect and subsidy selection. Huijts et al. [23] and Jabeen et al. [24] showed that consumers’ acceptance of NEVs is related to perceived costs, risks and benefits. Consumer subsidies can lower the cost and risk of purchasing a car, which can increase consumer acceptance of NEVs and promote the development of the NEV industry. Luo et al. [25] suggested that the government can implement effective price discount programs, such as discount rates and subsidy caps, to stimulate sales of electric vehicles. They found that both measures may be more effective under different circumstances of manufacturers’ product costs. HAO et al. [26] analyzed the policy changes regarding subsidies for NEVs in China. They concluded that consumer subsidies could effectively reduce the ownership cost of NEVs in the short term. Huang et al. [27] investigated the supply chain of electric and fuel vehicles under a government subsidy incentive program. Their research indicated that incentive programs are more effective in boosting electric vehicle sales when consumers have greater bargaining power. Shao et al. [28] analyzed the automobile market under the government’s fixed subsidy and price discount incentive schemes. They found that the government is more willing to implement the subsidy incentive program because of the low expenditure. Fu et al. [29] examined two types of subsidies, fixed subsidies and discounted subsidies, that are considered applicable to different participants, such as BSs, EVMs or consumers. In addition, they found that in the fixed subsidy scheme (discounted subsidy scheme), it is optimal to provide the subsidy to consumers (suppliers).
Among these policies, the consumer subsidy policy is considered effective and necessary, particularly in the initial stage of the development of the NEV market. However, some scholars argued that excessive subsidies make NEVs too reliant on them, which can negatively impact the R&D and innovation of firms and reduce the efficiency of subsidies [14]. Based on a dynamic mathematical model and a numerical analysis of industrial organization, Jeanjean [30] found that the government’s subsidy policy has a more significant effect on the “demand side” than other measures. However, when subsidies are removed, consumers are less willing to buy. Therefore, the impact of subsidy policies on consumers is limited and not sustainable. Hirte and Tscharaktschiew [31] investigated whether the government should provide subsidies for NEVs and the optimal level of subsidies. The results showed that the emphasis that consumers place on factors such as the utility value, the cost of purchase and the risk of driving will change with subsidies. Continued large consumption subsidies will increase the financial burden of the government, and guiding the attraction of non-subsidy factors will become the future development direction.
2.3. Segmented Subsidies Considering the Subsidy Threshold
NEV market subsidy policy now prioritizes greenness, with a segmented approach to stimulate consumer demand for and the green innovation of NEV firms. Under this policy, subsidies are only granted to firms and consumers when an NEV’s green degree is not lower than the subsidy threshold. This incentivizes firms to improve the greenness of their products by reducing car prices or firm costs. However, there is currently limited research on green segmented subsidies. Liu et al. [32] analyzed the impact of subsidy thresholds and consumer environmental preferences on product R&D, profits and the environment in two symmetrical NEV firms. The study found that the product R&D strategy is determined by the level of subsidy threshold. Chen and Fan [33] analyzed a two-stage supply chain comprising a battery supplier (BS) and an electric vehicle manufacturer (EVM) to investigate the effect of increased subsidy thresholds on BS driving range investment decisions. Their findings indicated that a low (high) subsidy threshold leads to BS increasing the driving range to above (below) the subsidy threshold. When the subsidy threshold is moderately increased, the decision-making is influenced by the degree of subsidy threshold increase and the technical ceiling. Liu et al. [34] developed a Cournot game model to investigate the investment decisions of two electric vehicle manufacturers regarding carbon emission reduction technologies under the subsidy threshold. The study found that the manufacturers make the same investment decisions when the subsidy threshold is low or high, but opposite investment decisions when it is in the middle. However, all of the above studies focus on automobile firms as the recipients of the subsidies and do not take into account the subsidy threshold for consumer subsidies.
Based on the above research, this study considers the realistic background of the unbalanced development of NEV technology and technology improvement. It builds a competitive market composed of two NEV firms with a gap in technology level and consumers with green preferences. Taking consumers as subsidy objects, this paper analyzes the design of segmented subsidy policy based on product green level as a subsidy threshold and its impact on the environment and the production decisions of automobile firms.
3. The Base Model
We consider two new energy vehicle (NEV) firms, labelled by firm 1 and 2, competing in the same market by offering NEVs. We denote the NEV offered by firm i as NEV i (i ∈ {1,2}). The green level for NEV is denoted by , which is the level of technology or performance of a NEV developed by NEV firm [14]. For instance, firms can enhance the green level (such as increasing carbon reduction of 100 km) of NEVs by optimizing the motor design and control system, which can improve motor efficiency, reduce power consumption per 100 km, and ultimately increase the NEV’s carbon reduction per 100 km [32]. Firm invests R&D costs in improving the green level of its NEVs. Following Zhang et al. [35] and Hafezalkotob [36], we use the following function form to capture the unit R&D cost of NEV :
where is the coefficient reflecting the effect of an increase in the green level of the NEV on the unit R&D cost. A higher implies that it is costlier for firm to increase the green level of the NEV and if firm has a higher level of green technology capacity associated with increasing green level, the cost factor is lower and so is the total R&D cost. Without loss of generality, we assume that , implying that firm 1 possesses a higher green technology capacity than firm 2 [35].
In the NEV market, governments frequently provide various subsidy policies to promote the sale of NEVs, of which consumer subsidy policies are the most widely used. Taking the NEV market in China as an example, in the consumer subsidy policy implemented by the national government in 2021, the consumer purchasing pure EVs with a range of 300–400 km (including 300 km) receives a subsidy of CNY 13,000 (USD 1821), and a range of over 400 km (including 400 km) receives a subsidy of CNY 18,000 (USD 2511). Similarly, the latest consumer subsidy policy for NEVs implemented by the government in South Korea in 2023 proposes that if consumers purchase a NEV adopting “V2L” technology, they will receive a subsidy of 150,000 Korean won (USD 115). In these consumer subsidy cases, we find that the amount of the consumer subsidy is a segmented subsidy depending on the green level of the NEV. We call such a consumer subsidy policy the segmented consumer subsidy (SCS) policy. For the sake of simplicity, we assume a two-segment consumer subsidy policy, denoted by , where is specified as the threshold of subsidy (a green level value) and is the amount of the subsidy. In such an SCS policy, a consumer purchasing an NEV with a green level will receive a subsidy , which is given by
We utilize the Hotelling model to illustrate the consumer’s heterogeneous preference towards two firms [37]. The consumers are uniformly distributed on a [0, 1] line, with the two firms located at either end. Denote as the distance from a customer’s location to firm 1, and thus is the distance between the customer and firm 2. If the firm decides to produce the NEV, it will charge the price . Then, for the consumers purchasing NEV under the SCS policy, their utility, denoted by , is specified as follows:
where is a basic valuation parameter, and reflects consumers’ preferences to the green levels of the NEVs due to social responsibility or energy cost saving during use of NEVs. A higher value of implies that consumers pay more attention to the environmental attributes of NEVs. is specified as the strength of consumer’s brand preference, and a higher value of means that consumers are more loyal to the brand [38].
We assume the basic valuation parameter is sufficiently large so that the market is fully covered. This assumption is standard in Hoteling models (e.g., Shaffer and Zhang [39]; Jain [40]), and it enables both firms to compete for limited market demand. We further assume that the total market demand is, without loss of generality, normalized to 1. We can easily derive the total demand for NEV under the SCS policy, denoted by :
Therefore, firm ’s profit function can be given as follows:
To analyze the effects of the segmented consumer subsidy (SCS) policy on the environment, we define a metric for measuring the total environment benefits of the production of NEVs. Specifically, we use a general function to characterize the environmental benefits of a NEV with green level [10,41]. Following Cohen et al. [38], we assume that indicates that a higher green level of the NEV corresponds to a greater environmental benefit (i.e., less negative environmental impact). Then, we define the total environmental benefits, denoted by , by factoring in the demand for each NEV, i.e.,
The timing of events is as follows: Firstly, given the government, both firms simultaneously decide the green levels for NEVs, and . Then, both firms simultaneously determine prices for NEVs, and . It is worth noting that there is no information asymmetry between firms and consumers; thus, all consumers can observe green levels of both NEVs. Finally, given the green levels and prices of both NEVs, consumers make purchasing decisions by comparing their utilities and given in (3) and (4), respectively.
4. Analysis of Equilibrium Results
We analyze the two firms’ equilibrium outcomes without and with SCS in Section 4.1 and Section 4.2, respectively, and then compare them to find out the effect of SCS on the NEV firms and the environment.
4.1. The Case without SCS
In this section, we consider that the government provides no SCS for consumers (i.e., , ). We develop a Nash perfect equilibrium in the following proposition. We use superscript “” to denote the equilibrium outcomes.
Proposition 1.
When the government does not provide any consumer subsidy for consumers, for and , we have , , , and .
By the sensitivity analysis on Proposition 1, we can obtain Corollary 1.
Corollary 1.
(i) ; , ; (ii) , .
Corollary 1 indicates an intuitive result, that is, firms are more likely to produce higher green levels for NEVs if they have higher green technology capabilities or if consumers are more environmentally conscious. However, improving firms’ green technology capabilities, which reduces the cost of producing NEVs with the same green level, leads to an increase in the price of NEVs. In recent years, the cost of batteries for electric vehicles has been declining, which is equivalent to a reduction of in the model. However, the costs of EVs have not decreased. This is because firms do not pass on the cost savings to consumers. Instead, they choose to increase the green levels of NEVs, which ultimately increases the prices of NEVs.
4.2. The Case with SCS
This subsection discusses the government’s SCS under which the consumer can receive the subsidy only if the green level of the NEV purchased exceeds a threshold. Therefore, subsidies obtained by consumers, denoted as , are related to the green level of NEVs (see Equation (2)). There are four possible SCS situations: (1) the green level of either NEV does not exceed the subsidy threshold (i.e., ), and consumers cannot receive subsidies for purchasing any NEV, denoted as Case ; (2) only the green level of NEV 1 exceeds the subsidy threshold (i.e., ), and consumers who purchase it are eligible for subsidies, denoted as Case ; (3) only the green level of NEV 2 exceeds the subsidy threshold (i.e., ), and subsidies are only available to consumers who purchase NEV 2, denoted as Case ; (4) the green levels of both NEVs exceed the subsidy threshold and consumers who purchase either NEV can receive the subsidies, denoted as Case .
Given the government’s SCS policy, utilizing Kuhn–Tucker conditions, the local optimal profits of both firms under Cases , , and , denoted as , are written in Table 1; details can be found in Appendix A.

Table 1.
The profits of the two firms in Cases NN, EN, NE and EE.
The Nash perfect equilibrium under SCS policy based on Table 1 is developed and shown in Table 2. We use superscript “” to denote the equilibrium outcomes under SCS policy.

Table 2.
Nash perfect equilibrium outcomes under SCS policy.
Proposition 2.
Under the SCS policy, both firms’ equilibrium decisions of productions are as follows: (i) when the threshold level for the subsidy is low, such as , both firms produce NEVs with high green levels for subsidies; (ii) when the threshold level for the subsidy is moderate, such as , only the firm 1 produces NEVs with high green levels for subsidies; (iii) when the threshold level for the subsidy is sufficiently large, such as , both firms produce NEVs with low green levels and no subsidies.
According to Proposition 2, Figure 1 displays the Nash equilibrium production decisions of both firms where the parameters are set. As the threshold level for the subsidy increases, both firms’ equilibrium product strategies show a changing trend of . It is worth noting that Case does not belong to the equilibriums. This is because that it is evident that if firm 2, with lower green technology capability, adopts a technology-leading strategy, it will suffer from cost disadvantages and profit loss. Moreover, a sufficiently high threshold level for the subsidy (i.e., ) will lead to Case in which the SCS policy loses its incentive effect on firms’ R&D and there will be no difference between Case and the non-SCS case. Therefore, we define an efficient SCS policy satisfying where ).
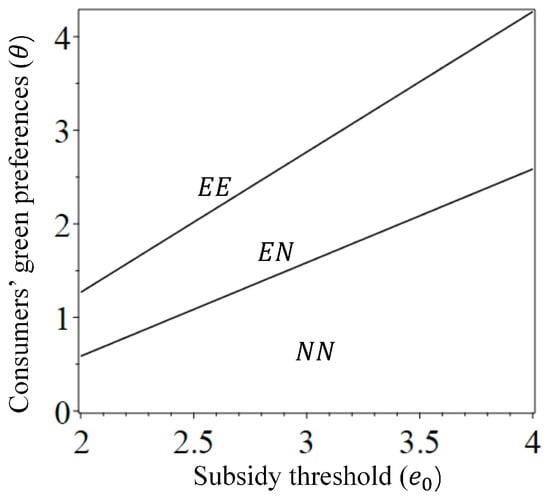
Figure 1.
Equilibrium production decisions of firms under SCS policy.
Further analysis of the impact of , and on shows that higher technology capabilities of firms, higher government consumer subsidies and stronger environmental awareness of consumers can increase the effective range of SCS policy. This is because the higher the technology capability of the firm, the higher the consumer’s environmental awareness, and the higher the subsidy amount, the more incentive firms have to produce higher green level NEVs. In practice, in order to improve the effective range of its SCS policy, the Chinese government has set up special projects since 2001 for cultivating specialists and invested a large amount of money to support the R&D of green technologies in order to reduce the R&D costs of NEVs. Moreover, in terms of improving the environmental awareness of consumers, the government has actively promoted concepts of the energy saving and emission reduction of NEVs to consumers since 2009.
In order to further analyze the impact of the SCS policy on the two competing firms, Proposition 3 analyzes the impact of the SCS policy on the green levels and prices of NEVs under the cases where the SCS policy is effective (i.e., Cases and ), and Proposition 4 summarizes the impact of the SCS policy on the sales volume and profits of both firms.
Proposition 3.
(i) ; , ; (ii) if , otherwise ; if , otherwise .
Proposition 3 demonstrates how firms’ technology capabilities affect the green level and price of NEVs under the SCS policy. The effects of firms’ technology capabilities and consumers’ environmental awareness on the green level of NEVs under the SCS policy are consistent with the no-subsidy policy. Corollary 1 indicates that as firms become more technologically advanced, the green level of NEVs is improved, resulting in higher product prices. However, Proposition 3(ii) demonstrates that increased technology capability of firms does not always raise the price of NEVs. For firm 1 with higher technology capabilities, when is small, the NEV green level is mainly affected by the technology capabilities of the firm, and the higher the technology capabilities of the firm (the smaller the ), the higher the NEV green level, which contributes to higher product prices. When the subsidy threshold is high, the firm will have to increase the NEV green level to the subsidy threshold to obtain the government subsidy, which deviates from the firm’s optimal decisions on green levels of NEVs. With the advancement of technology, the firm will not continue to increase the green level of its NEVs, and the reduced technology cost will be reflected in the price. For firm 2 with lower technology capability, when the subsidy threshold is very low, higher technology capability will result in higher product prices, but as the subsidy threshold increases, firm 2 will have to raise the NEV green level to the subsidy threshold, at which higher technology capability helps to reduce the cost on firm 2, which in turn reduces the NEV price. It is important to note that when the subsidy threshold is high, firm 2 will give up access to the subsidy before firm 1. This will cause the price of NEV 2 to rise as firm 2’s technology capability increases.
Proposition 4.
(i) , , , if , otherwise , , , ; (ii) .
Setting parameters , Figure 2 demonstrates the differentiated impacts of the subsidy threshold on NEV sales and profits of competing firms. Proposition 4(i) reveals that neither firm can always benefit from an increase in subsidy threshold in a competitive environment (see Figure 2). When the subsidy threshold is small, both firms’ NEVs receive subsidies. As increases, firm 2 will have to invest in more than its optimal R&D efforts to continue receiving subsidies. This leads to a significant increase in R&D costs, resulting in higher product prices, lower sales and lower profits. Accordingly, increasing the subsidy threshold reduces the green level difference between the two firms but strengthens the competitive advantage of firm 1. Therefore, firm 1 will benefit from the subsidy threshold increase. When the subsidy threshold is higher, firm 2 gives up the NEV subsidy, while firm 1 exerts R&D efforts beyond its optimal level to obtain the subsidy. This increase in the R&D costs of firm 1 leads to higher NEV prices, lower sales and lower profits. As a result, the increase in the subsidy threshold widens the green level gap between the two firms but reduces the competitive advantage of firm 1, ultimately benefiting firm 2. Unlike the subsidy threshold, Proposition 4(ii) shows that firm 1 always benefits from higher subsidies while firm 2 benefits from lower subsidies. This means that an increase in subsidy will always increase firm 1’s competitive advantage.
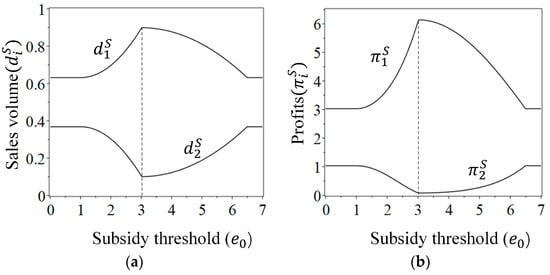
Figure 2.
(a) The impact of the subsidy threshold on the firms’ sales volume; (b) the impact of the subsidy threshold on the firms’ profits.
In summary, changing the subsidy threshold in a competitive environment has inconsistent impacts on firms 1 and 2. To promote the development of technologically advantageous firms in the market and accelerate industrial upgrading, the government should fully consider the green level of NEVs in the market when offering SCSs. For instance, if the government offers a moderate subsidy threshold, firms with high technological capacity are more likely to receive subsidy, while those with low technological capacity may struggle to obtain it. Therefore, increasing the subsidy threshold or amount may not only benefit environmentally friendly firms but also have a negative impact on those with low environmental benefits. This can help eliminate backward firms in the process of NEV industry upgrading. The conclusion confirms the validity of the NEV subsidy threshold in China. In 2022, most NEVs have a range of 100–600 km, while Tesla’s mainstream NEVs have a stable range of over 400 km. According to SCS policy in 2022, consumers who buy NEVs with a range of 300–400 km and those with a range of over 400 km are eligible for subsidies of CNY 9100/12,600, respectively. Therefore, consumers of most mainstream models with high range can be subsidized. The SCS has promoted the technological development of Tesla and other mainstream brand automobile firms. This policy has also eliminated a number of small- and micro-vehicle firms with backward technology and helped to realize industrial upgrading.
4.3. Comparative Analysis
This subsection compares and analyzes the equilibrium outcomes for firms in and scenarios and explores the impact of SCS policy on environmental benefits.
Proposition 5.
Comparing green levels of NEVs, prices, and profits under and scenarios yields: (i) , ; (ii) ; if , and otherwise; (iii) , .
Proposition 5(i) demonstrates the positive impact of SCS policy on the green level of NEVs. However, Proposition 5(ii) shows that under the SCS policy, firm 1 will increase the product price, while firm 2 may set a lower price due to the high subsidy threshold. In addition, it is worth noting that if the subsidy threshold is too low () or too high (), there is no difference between the case and the case decision. When the subsidy threshold is not high (), firm 2 designs a higher green level for the product, resulting in increased costs and prices and firm 1 may also take advantage of this opportunity to increase prices Because its consumer can obtain a subsidy and higher green level (when ). As the subsidy threshold increases , consumers of firm 2—with its lower technological capability—cannot obtain subsidies. Meanwhile, firm 1’s consumers can obtain subsidies due to its higher green levels. Therefore, firm 1 will raise the price of NEV 1 to earn more marginal profit. However, firm 2 does not allow for its consumers to obtain subsidies under competitive situations, so it has to lower its prices to improve its competitiveness.
The findings of Proposition 5(iii) indicate that while the SCS policy offers economic support to both firms, it does not always enhance the economic benefits of both firms in a competitive market. Specifically, firm 2, with weaker technological capability, does not benefit from the SCS policy, while firm 1, with stronger technological capability, does benefit from it. The SCS policy favors firms with stronger technological capabilities. This means that the stronger the technical capabilities of a firm, the higher the green level of its products and the easier it is for its consumers to obtain subsidies. In other words, the SCS policy exacerbates the impact of a technological gap between NEVs, which in turn magnifies the competitive disadvantage of firm 2.
Proposition 6 further demonstrates the impact of the SCS policy on the environmental benefit.
Proposition 6.
Comparing the total environmental benefits with and without the SCS policy yields .
Proposition 6 demonstrates that SCS policy has a positive impact on overall environmental benefits. This is because SCS policy encourages all firms to produce greener NEVs and incentivize consumers to purchase NEVs with higher levels of greenness. Corollary 2 further explores the effect of specific subsidy parameters on overall environmental benefits.
Corollary 2.
(i) ; (ii) if equilibrium occurs and holds, and otherwise, where .
Corollary 2(i) shows that an increase in the subsidy results in a corresponding increase in overall environmental benefits. This is because the SCS policy subsidizes NEVs with higher levels of greenness, which not only improves the overall greenness of NEVs, but also promotes consumers to buy NEVs with higher levels of greenness. Both of these factors contribute to the improvement of environmental benefits. Corollary 2(i) suggests that reduced subsidies have a negative effect on environmental benefits during the subsidy disappearance stage. However, Corollary 2(ii) indicates a possible positive impact of increasing subsidy thresholds on environmental benefits. Specifically, when is at a lower level (i.e., the equilibrium case), the subsidy threshold mainly constrains NEV 2. A higher subsidy threshold could incentivize firm 2 to increase the green level of NEV 2, enabling its consumers to qualify for the subsidy. This could lead to firm 2’s decisions that deviate from its optimal decisions, potentially strengthening the competitive advantage of NEV 1 and improving environmental benefits. In the equilibrium case, where is at a higher level, the subsidy threshold constrains NEV 1, weakening its competitive advantage. In this situation, consumers are more likely to be attracted to the lower-priced NEV 2 when their loyalty to the firm is low (). This ultimately makes the higher green level of NEV 1 less appealing to consumers, reduces the sales volume of NEV 1, and results in the loss of environmental benefits. During the stage of subsidy disappearance in the NEV market, these results partially alleviate public concerns about the potential damage to environmental benefits.
5. Analysis of Technology Improvement
The development of NEV technology will lead to a reduction in and in the model, resulting in an inevitable change in the sales structure. This change will have an impact on environmental benefits. To analyze the impact of technological improvements on environmental benefits, we assume that the cost coefficients of firm 1 and 2 drop from and to and , respectively, with the improvement in technological capability of NEVs, and . In Proposition 7, we analyze the impact of technological improvement on environmental benefit without SCS, and represents the overall environmental benefit after technological improvement.
Proposition 7.
With the improvement of NEV technology, if the following conditions can be satisfied: (i) , ; (ii) , , we can achieve , where can be found in the Appendix A.
Technological improvements have increased the green level of NEVs to some extent (). However, it is surprising that Proposition 7 suggests that such improvements may result in poorer overall environmental benefits. The following reasoning explains this result: Firstly, the technical levels of the two firms do not show significant improvement. Specifically, one manifestation of this is seen in , indicating that the technological advancement of firm 2 has not yet reached the level of firm 1’s previous technological advancement. However, following the technological improvement, firm 2 has increased its market share, i.e., (simplify to ). The second aspect concerns the performance in , indicating that the technological improvement of firm 1 is not significant, resulting in a decrease in its market share. In other words, there is a difference in the degree of technological improvement between firms 1 and 2, leading to firm 2 occupying the market share of firm 1. Secondly, there is a significant gap between the two firms prior to technological improvements (). As a result, firm 2 has more potential for technical improvement and is more likely to benefit from technological improvement. Finally, consumer brand loyalty is not high (). This means that when the green level of product 2 is improved, consumers are more willing to buy. In summary, although the technological improvement in NEVs has increased the green level of products, the uneven development of technology may prompt consumers to buy more low-green products, resulting in damage to environmental benefits.
The technology gap among NEV firms is narrowing due to the rapid development of automobile technology. For example, Xpeng Motor has significantly improved its technical level in a short period of time by adopting a strategy of constantly learning from Tesla’s electronic and electrical architecture. In 2020 and 2021, Xpeng’s delivery volume increased by approximately 112% and 263%, respectively. During this period, the government implemented several subsidy policies to encourage the growth of high-tech car firms and increase sales of high-tech products. These policies were implemented in response to the market situation, with the aim of reducing the negative impact on the environment.
In Proposition 8, we analyze the impact of technological improvement on environmental benefit with SCS, and represents the overall environmental benefit after technological improvement.
Proposition 8.
Proposition 8 demonstrates that even with the implementation of SCS policy, the technological imbalance of firms may continue to harm the overall environmental benefits, as is also seen in Proposition 7 without SCS policy. To further analyze the impact of SCS policy, we set parameters . Figure 3 shows the range of environmental benefit loss / caused by technological improvement when the government does not have an SCS policy/has an SCS policy. If , we can have ; if , we can achieve . Figure 3 shows that is a subset of , indicating that the range of environmental damage caused by technological improvement under SCS policy will not be eliminated, but may be further expanded compared to the situation without SCS. The reason is that when the technological improvement appears, SCS policy stimulates the sales of low-green-level products more than high-green-level products, resulting in a large increase in market share of low-green-level products and a decline in environmental benefits.
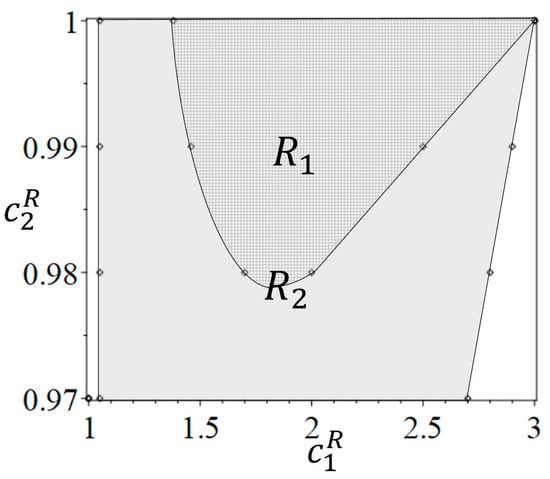
Figure 3.
The impact of technological improvement on the damaged range of environmental benefits.
The analysis of Corollary 2 suggests that, unlike Proposition 1, adjusting the subsidy threshold and amount under SCS policy can affect the environmental benefits. This provides valuable reference for the government when making policies. Giving the parameters values such as , we can depict the effect of changes in SCS policy on the interval of environmental benefit loss in Figure 4. It is evident that reducing lessens the damage range of environmental benefits, as the negative impact of technological improvement on environmental benefits weakens when the subsidy amount is reduced. However, it is important to note that in the situation, raising the subsidy threshold can improve environmental benefits only when consumers have a strong brand preference. In addition, if the situation is , when most firms have a mature technology level and can easily obtain subsidies, regulating the subsidy threshold and amount cannot reduce losses. This suggests that government policies cannot remain unchanged with technological improvement, and it is necessary to regulate the subsidy threshold and subsidy amount to reduce the loss of environmental benefits to a certain extent.
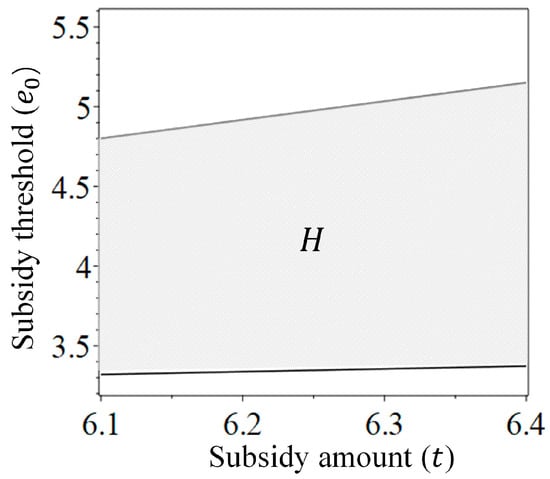
Figure 4.
Influence of subsidy amount on the range of environmental benefit loss.
6. Conclusions and Future Research
To promote the development of the NEV industry, governments of some countries or cities provide subsidies to consumers who buy NEVs. This study considers a competitive market under the segmented consumer subsidy (SCS) policy. We construct a competitive market composed of a high-tech NEV firm, a low-tech NEV firm and consumers with green preferences, and determine the optimal decision (green level, price) under the SCS policy. In addition, the effects of SCS policy, subsidy threshold, subsidy amount, technical capability and other relevant parameters are analyzed with respect to equilibrium decisions and environmental benefits. Our paper provides valuable insights for policymakers in the NEV market on how to design appropriate SCS.
6.1. Managerial Insights and Implications
In this section, we show our main findings and provide managerial insights by answering our research questions mentioned in the introduction.
(1) Can SCS effectively play the role of subsidy compared with no subsidy, and how should the subsidy threshold be set?
We found that the SCS policy has a positive effect on the green level and environmental benefits of products. However, only when the subsidy threshold is relatively moderate can SCS effectively play the role of subsidy incentive. In addition, improving technical capability, subsidy intensity and consumer green awareness can expand the effective scope of SCS policy. Therefore, to ensure that NEV firms are able to innovate technologically, the government needs to set a moderate subsidy threshold to avoid wasting money on ineffective subsidies. To expand the effective scope of SCS subsidies, the government should conduct in-depth environmental awareness education for consumers and provide high-level subsidies for key innovative technologies. This will enable consumers to form stricter requirements for green products, fully mobilize the vitality of high-tech innovation of firms, and promote the healthy development of the NEV market.
(2) How does the SCS affect firms with different technical levels? To promote the development of high-tech NEV firms, how should the government set the subsidy threshold and subsidy intensity?
Our results revealed that the SCS policy has an inconsistent impact on firms with superior or inferior technical capabilities in a competitive environment. Specifically, the SCS policy benefits technologically superior firms while harming disadvantaged ones. This is because the SCS policy is essentially more supportive of firms with stronger technical capabilities, and the stronger the technical capabilities, the greener the product, the easier it is for consumers to obtain subsidies. In addition, the subsidy threshold can adjust the green level difference and the competitive pattern of the two competing firms. If the subsidy threshold is low, an increase in the subsidy threshold may reduce the green level difference between the two firms, but it may increase the market gap. This is because currently, the firm with low technical capacity invests more in R&D to reach the subsidy threshold, resulting in higher prices and lower product competitiveness. When the subsidy threshold is high, the technologically inferior firm gives up the subsidy, while the advantaged firm invests more in R&D to reach the subsidy threshold, leading to a significant increase in costs and prices. At this time, the increase in the subsidy threshold has widened the gap in green level between the two firms but has weakened the competitiveness of the advantaged firm. Therefore, adjusting the subsidy threshold in a competitive environment can affect the competitive situation of firms and promote the reasonable and healthy development of the NEV industry.
The government can draw some inspiration from these results. For example, the government can use the SCS policy to eliminate tail firms and help upgrade the NEV industry. Specifically, the subsidy threshold can regulate the market competition pattern, so the government can design the subsidy threshold and subsidy amount according to market demand, such as in the northern region; meet a certain technical standard of battery charging speed that can be subsidized to consumers; and control the technical standard in a certain range to enhance the competitive advantage of high-tech firms, so as to promote the healthy development of the NEV industry.
(3) In a market with unbalanced technological development, how does technological improvement affect environmental benefits, and how should the government use SCS policy to regulate the impact of technological improvement?
This paper found that whether or not the SCS policy is implemented, technological improvement can lead to damage to environmental benefits. In particular, environmental benefits are more likely to be damaged under SCS policy, but raising the subsidy threshold and reducing the subsidy amount under certain conditions can effectively reduce the degree and probability of environmental benefits being damaged. This is because when consumers have a high brand preference, raising the subsidy threshold is more conducive to the development of technologically advantageous firms, and lowering the subsidy amount mitigates the negative impact of technological improvement on environmental benefits. This conclusion to some extent indicates the trend of the future change in SCS policy and reveals that the government should pay attention to the damage to environmental benefits caused by technological improvement under the SCS. In order to reduce the probability and degree of damage, the government should adjust the subsidy parameters in a timely manner according to the market development cycle, such as regular consumer loyalty and subsidy surveys, so as to punctually raise the subsidy threshold and reduce subsidy intensity.
6.2. Theoretical Implications
This paper extends the literature on government subsidy policies and new energy vehicles. Firstly, the existing literature on subsidy thresholds fails to consider the influencing factors of consumer subsidy and the technology gap [32,33,34]. This paper further reveals the impact of SCS (subsidy threshold and subsidy intensity) on the two competing firms with technology gap. The results show that the SCS has different impact trends on the profits of the two firms within different subsidy thresholds, which provides suggestions for the rational design of policies to promote the healthy development of the NEV industry. Secondly, previous studies have examined the impact of subsidy thresholds [33,34] and consumers’ environmental preferences [32] on environmental benefits. However, they have not yet considered the impact of technological improvement. We examined the potential impact of technological improvement on environmental benefits and policy design, concluding that technological improvement may have negative effects on the environment, but the degree of damage can be reduced by adjusting the subsidy threshold and subsidy intensity.
6.3. Future Research
We propose several directions for future research. Firstly, we considered the independent R&D of NEV firms without considering the superior suppliers. In the future, we can consider the upstream and downstream cooperation of the supply chain and the cooperative R&D of firms. Secondly, we have only considered fixed subsidies for the green level. In the future, we can consider more types of subsidies, such as price subsidies and R&D subsidies, and explore the optimal subsidy decision, which may be more valuable. Finally, we considered two NEV firms with different technological capabilities, but ignored the possibility of technology spillovers affecting the decision-making between the two NEV firms. In future research, it may be interesting to consider the impact of technology spillovers on firms’ decision making.
Author Contributions
Conceptualization, J.Z. and Y.C.; methodology, J.Z.; validation, J.Z. and Y.C.; writing—original draft preparation, J.Z. and Y.C.; writing—review and editing, J.Z.; visualization, J.Z. and Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Fundamental Research Funds for the Central Universities (No. B210202156).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The financial support mentioned in the Funding part is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Proofs
Proof of Proposition 1.
When the government does not provide SCS, we have ,. Substituting into Equations (5) and (6), we can obtain the firms’ profits:
We have and . In consequence, the optimal prices can be acquired through solving the first-order conditions , simultaneously leading to the optimal prices:
Substituting (A2) into (A1) leads to the following profits:
We can obtain the equilibrium green level by calculating . Thus, we have the following:
Substituting into and , we obtain the equilibrium prices and profits. As a result, we can obtain the equilibrium demands. Finally, let us check the constraints. Note . □
Proof of Corollary 1.
Recall Proposition 1, we obtain , ; , . □
Proof of Proposition 2.
□
Similar to the proof of Proposition 1, we can obtain the equilibrium result of the four cases , , , and in Section 4.2. We use superscript “” to denote the corresponding equilibrium outcomes.
- (a)
- ()
① When , ; ② when , ; ③ when , .
- (b)
- ()
① When , ; ② when , ; ③ when , .
- (c)
- ()
① When , ; ② when , ; ③ when , .
- (d)
- ()
① When , ; ② when , ; ③ when , .
According to the results of (a), (b), (c) and (d), we can obtain the demand and profit of the corresponding situation. Note . Firstly, the optimal strategy choice of firm 2 is derived on the premise of the given strategy choice of firm 1, and then the optimal strategy choice of firm 1 is derived on the basis of given strategy choice of firm 2. Finally, according to the optimal strategy selection of firm 1 and firm 2, the global Nash game equilibrium strategy of firm 1 and firm 2 is obtained. Table 1 is constructed. Below, we use as an example for Nash equilibrium analysis.
In the interval , we can easily obtain
With the assumption and , we can easily prove , , , . Solving , we can obtain condition or and , otherwise . To conclude the discussions above, for the assumed conditions that or and , the firms only consider the case. Similarly, if and , the firms only consider the case. Similar to , we can obtain the equilibrium solutions of the firms under and . The summary analysis results are in Table 2. Substituting the results of Table 2 into the profit and sales formula, we obtain Table A1 and Table A2.



Table A1.
Equilibrium green level, price, sales volume and profit of the two firms.
Table A1.
Equilibrium green level, price, sales volume and profit of the two firms.

Table A2.
Equilibrium green level, price, sales volume and profit of the two firms.
Table A2.
Equilibrium green level, price, sales volume and profit of the two firms.
Note , we can get that :
Proof of Proposition 3.
Recall Table 2: we have or , or ; we can also easily prove that if , otherwise ; similarly, we have if , otherwise . □
Proof of Proposition 4.
From (A10), we can easily prove that and if , otherwise and . From (A11), ① we can easily show that ; ② when , we can obtain . Denote in and in . We can easily know that and , and have the same sign. With the assumptions , we can easily prove that and . Thus, we can obtain and . The analysis for the remaining cases is similar. Thus, we ignore it here.
(2) From Table A1 and Table A2, it is easy to obtain . ① In the and cases, we can easily obtain . ② In case, we can easily obtain . We can also have that and when . Denote in and in . We can easily know that and , and have the same sign. With the assumptions , we can easily prove that and . Thus, we can obtain and . The analysis for the remaining cases is similar. Thus, we ignore it here. □
Proof of Proposition 5.
(1) Recall the Proposition 1 and Table 1; we can easily prove that .
(2) Let , it is easy to obtain the following:
① When ,, we can know that . ② When , we can easily obtain . Solving , we can obtain . Thus, we can obtain ; ③ when , we can easily obtain . Solving , we can obtain . Thus, we can obtain ; the rest of the proof process is similar to the above proof process. Therefore, we ignore it here. □
Proof of Proposition 6.
Substituting , , and into Equation (7), we can obtain and .
From (A13) and (A14): ① When or , we can easily obtain , . ② When , we can easily obtain . Denote , and we can easily know that and have the same sign. With the assumptions , we can easily prove that . Thus, we can obtain and . ③ When , we can easily obtain . Thus, with the assumptions , we can easily prove that . ④ When , we can easily obtain and . ⑤ When , we can easily obtain . Solving , we can obtain . With this condition, it can be concluded that . Otherwise, we can have that . □
Proof of Corollary 2.
From (A14), we can easily obtain ① when , ; ② when , ; ③ when or or , . Recall Proof of Proposition 6; we can prove (ii) of Corollary 2. □
Proof of Proposition 7.
From (A13), we can obtain = . Thus, it is easy to obtain . Solving , we can obtain conditions and , otherwise . If , we can have . In summary, if we want , the , should be hold.
With the assumption and , we can easily see that decreases and then increases with and when . Thus, if , there must exist and . In summary, if , , and , we can prove that . □
Proof of Proposition 8.
From (A14), we can see that when . Thus, it is easy to obtain . Solving , we can obtain condition , otherwise . If , we can have for any . Thus, the condition should be hold if we want . With the assumption , we can easily see that increases with . Thus, we can see . If , there must exist and . In summary, if , and if , we can prove that . □
References
- Zheng, Y.; Li, Z.; Chai, J. Progress and prospects of international carbon peaking and carbon neutral research–based on bibliometric analysis (1991–2022). Front. Energy Res. 2023, 11, 1121639. [Google Scholar] [CrossRef]
- Degirmenci, K.; Breitner, M.H. Consumer purchase intentions for electric vehicles: Is green more important than price and range? Transp. Res. Part D Transp. Environ. 2017, 51, 250–260. [Google Scholar] [CrossRef]
- Shi, Z.; Cheng, J. How do government subsidies and consumers’ low-carbon preference promote new energy vehicle diffusion? A tripartite evolutionary game based on energy vehicle manufacturers, the government and consumers. Heliyon 2023, 9, e14327. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Li, J.; Zhao, D. The impact of policy measures on consumer intention to adopt electric vehicles: Evidence from China. Transp. Res. Part A Policy Pract. 2017, 105, 14–26. [Google Scholar] [CrossRef]
- Li, J.; Ku, Y.; Yu, Y.; Liu, C.; Zhou, Y. Optimizing production of new energy vehicles with across-chain cooperation under China’s dual credit policy. Energy 2020, 194, 116832. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Q.; Liu, B.; McLellan, B.; Gao, Y.; Tang, Y. Substitution effect of new-energy vehicle credit program and corporate average fuel consumption regulation for green-car subsidy. Energy 2018, 152, 223–236. [Google Scholar] [CrossRef]
- Avci, B.; Girotra, K.; Netessine, S. Electric vehicles with a battery switching station: Adoption and environmental impact. Manag. Sci. 2015, 61, 772–794. [Google Scholar] [CrossRef]
- Peng, J.; Lin, Z. Eco-Innovation in New Energy Vehicle Supply Chains under Government Subsidies. Sustainability 2022, 14, 15216. [Google Scholar] [CrossRef]
- Zhang, H.; Cai, G. Subsidy strategy on new-energy vehicle based on incomplete information: A Case in China. Phys. A Stat. Mech. Its Appl. 2020, 541, 123370. [Google Scholar] [CrossRef]
- Li, K.; Wang, L. Optimal electric vehicle subsidy and pricing decisions with consideration of EV anxiety and EV preference in green and non-green consumers. Transp. Res. Part E Logist. Transp. Rev. 2023, 170, 103010. [Google Scholar] [CrossRef]
- Halvorson, B. Cost Remains the Biggest Barrier against EV Adoption, Study Finds. Available online: https://www.greencarreports.com/news/1126706_cost-remains-the-biggestbarrier-against-ev-adoption-study-finds (accessed on 2 February 2024).
- Lindwall, C. Electric vs. Gas: Is It Cheaper to Drive an EV. Available online: https://www.nrdc.org/stories/electric-vs-gas-cars-it-cheaper-drive-ev (accessed on 2 February 2024).
- Irle, R. Global EV Sales for 2023. Available online: https://www.ev-volumes.com/ (accessed on 14 March 2024).
- Wang, Y.; Meng, W.; Huang, B.; Li, Y. Study of the retreating product subsidy policy based on technology thresholds of new energy vehicle consumers. Front. Energy Res. 2022, 10, 959864. [Google Scholar] [CrossRef]
- Wang, Z.; Ahmed, Z.; Zhang, B.; Wang, B. The nexus between urbanization, road infrastructure, and transport energy demand: Empirical evidence from Pakistan. Environ. Sci. Pollut. Res. 2019, 26, 34884–34895. [Google Scholar] [CrossRef]
- Li, F.; Ou, R.; Xiao, X.; Zhou, K.; Xie, W.; Ma, D.; Liu, K.; Song, Z. Regional comparison of electric vehicle adoption and emission reduction effects in China. Resour. Conserv. Recycl. 2019, 149, 714–726. [Google Scholar] [CrossRef]
- Tang, B.-J.; Wu, X.-F.; Zhang, X. Modeling the CO2 emissions and energy saved from new energy vehicles based on the logistic-curve. Energy Policy 2013, 57, 30–35. [Google Scholar] [CrossRef]
- Wu, X.; Freese, D.; Cabrera, A.; Kitch, W.A. Electric vehicles’ energy consumption measurement and estimation. Transp. Res. Part D Transp. Environ. 2015, 34, 52–67. [Google Scholar] [CrossRef]
- Okada, T.; Tamaki, T.; Managi, S. Effect of environmental awareness on purchase intention and satisfaction pertaining to electric vehicles in Japan. Transp. Res. Part D Transp. Environ. 2019, 67, 503–513. [Google Scholar] [CrossRef]
- Spangher, L.; Gorman, W.; Bauer, G.; Xu, Y.; Atkinson, C. Quantifying the impact of US electric vehicle sales on light-duty vehicle fleet CO2 emissions using a novel agent-based simulation. Transp. Res. Part D Transp. Environ. 2019, 72, 358–377. [Google Scholar] [CrossRef]
- Ahmed, Z.; Cary, M.; Le, H.P. Accounting asymmetries in the long-run nexus between globalization and environmental sustainability in the United States: An aggregated and disaggregated investigation. Environ. Impact Assess. Rev. 2021, 86, 106511. [Google Scholar] [CrossRef]
- Su, C.-W.; Yuan, X.; Tao, R.; Umar, M. Can new energy vehicles help to achieve carbon neutrality targets? J. Environ. Manag. 2021, 297, 113348. [Google Scholar] [CrossRef]
- Huijts, N.M.A.; Molin, E.J.E.; Steg, L. Psychological factors influencing sustainable energy technology acceptance: A review-based comprehensive framework. Renew. Sustain. Energy Rev. 2012, 16, 525–531. [Google Scholar] [CrossRef]
- Jabeen, F.; Olaru, D.; Smith, B.; Braunl, T.; Speidel, S. Acceptability of Electric Vehicles: Findings from a driver survey. 2014. Available online: https://www.researchgate.net/publication/265883429_Acceptability_of_Electric_Vehicles_Findings_from_a_driver_survey (accessed on 2 February 2024).
- Luo, C.; Leng, M.; Huang, J.; Liang, L. Supply chain analysis under a price-discount incentive scheme for electric vehicles. Eur. J. Oper. Res. 2014, 235, 329–333. [Google Scholar] [CrossRef]
- Hao, H.; Ou, X.; Du, J.; Wang, H.; Ouyang, M. China’s electric vehicle subsidy scheme: Rationale and impacts. Energy Policy 2014, 73, 722–732. [Google Scholar] [CrossRef]
- Huang, J.; Leng, M.; Liang, L.; Liu, J. Promoting electric automobiles: Supply chain analysis under a government’s subsidy incentive scheme. IIE Trans. 2013, 45, 826–844. [Google Scholar] [CrossRef]
- Shao, L.; Yang, J.; Zhang, M. Subsidy scheme or price discount scheme? Mass adoption of electric vehicles under different market structures. Eur. J. Oper. Res. 2017, 262, 1181–1195. [Google Scholar] [CrossRef]
- Fu, J.; Chen, X.; Hu, Q. Subsidizing strategies in a sustainable supply chain. J. Oper. Res. Soc. 2018, 69, 283–295. [Google Scholar] [CrossRef]
- Jeanjean, F. Subsidising the next generation infrastructures. Consumer-side or supply-side? Info 2010, 12, 95–120. [Google Scholar] [CrossRef]
- Hirte, G.; Tscharaktschiew, S. The optimal subsidy on electric vehicles in German metropolitan areas: A spatial general equilibrium analysis. Energy Econ. 2013, 40, 515–528. [Google Scholar] [CrossRef]
- Liu, J.; Nie, J.; Zhang, W.; Li, L.; Yuan, H. Product development strategies of electric vehicle manufacturers: Considering government subsidy and consumers’ environmental preferences. Technol. Forecast. Soc. Chang. 2024, 201, 123222. [Google Scholar] [CrossRef]
- Chen, Z.; Fan, Z.-P. Improvement strategies of battery driving range in an electric vehicle supply chain considering subsidy threshold and cost misreporting. Ann. Oper. Res. 2023, 326, 89–113. [Google Scholar] [CrossRef]
- Liu, J.; Nie, J.; Yuan, H. Electric vehicle manufacturers’ decisions on investing in carbon-reduction technology under government subsidy: A Cournot game model. IMA J. Manag. Math. 2023, 34, 71–100. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Zhao, H. The impact of consumer subsidy on green technology innovations for vehicles and environmental impact. Int. J. Environ. Res. Public Health 2020, 17, 7518. [Google Scholar] [CrossRef] [PubMed]
- Hafezalkotob, A. Competition, cooperation, and coopetition of green supply chains under regulations on energy saving levels. Transp. Res. Part E Logist. Transp. Rev. 2017, 97, 228–250. [Google Scholar] [CrossRef]
- Zhang, T.; Huo, Y.; Zhang, X.; Shuai, J. Endogenous third-degree price discrimination in Hotelling model with elastic demand. J. Econ. 2019, 127, 125–145. [Google Scholar] [CrossRef]
- Cohen, M.A.; Cui, S.; Gao, F. The Effect of Government Support on Green Product Design and Environmental Impact. 2019. Available online: https://www.researchgate.net/publication/329600621_The_Effect_of_Government_Support_on_Green_Product_Design_and_Environmental_Impact (accessed on 2 February 2024).
- Shaffer, G.; Zhang, Z.J. Competitive coupon targeting. Mark. Sci. 1995, 14, 395–416. [Google Scholar] [CrossRef]
- Jain, S. Digital piracy: A competitive analysis. Mark. Sci. 2008, 27, 610–626. [Google Scholar] [CrossRef]
- Chen, C. Design for the environment: A quality-based model for green product development. Manag. Sci. 2001, 47, 250–263. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).